实验二 伯努利实验报告
流体力学伯努利方程实验报告

流体力学伯努利方程实验报告一、实验目的1、深入理解流体力学中伯努利方程的基本原理和物理意义。
2、通过实验测量,验证伯努利方程在不同流体流动情况下的正确性。
3、掌握测量流体流速、压力等参数的实验方法和仪器使用。
4、培养观察、分析和解决问题的能力,提高实验操作技能。
二、实验原理伯努利方程是描述理想流体在稳定流动时,流速、压力和高度之间关系的方程,表达式为:\p +\frac{1}{2}\rho v^2 +\rho gh = C\其中,\(p\)为流体的压强,\(\rho\)为流体的密度,\(v\)为流体的流速,\(g\)为重力加速度,\(h\)为流体所处的高度,\(C\)为常数。
在水平管道中,\(h\)不变,伯努利方程可简化为:\p +\frac{1}{2}\rho v^2 = C\这表明在同一流线上,流速大的地方压强小,流速小的地方压强大。
三、实验设备1、伯努利实验仪:包括水箱、管道、测压管、调节阀等。
2、流量计:用于测量流体的流量。
3、秒表:用于记录时间。
四、实验步骤1、熟悉实验设备,了解各部分的功能和作用。
2、检查实验设备是否完好,水箱中加满水,确保管道无漏水现象。
3、调节调节阀,改变流体的流速,观察测压管中液面的高度变化。
4、用流量计测量不同流速下的流量,并记录相应的时间。
5、记录不同位置测压管的液面高度,以及对应的流速和流量。
五、实验数据记录与处理|流速(m/s)|流量(m³/h)|测压管高度(cm)|||||| 10 | 15 | 150 || 15 | 225 | 120 || 20 | 30 | 90 || 25 | 375 | 60 |根据实验数据,计算出不同流速下的动压、静压和总压。
动压:\(\frac{1}{2}\rho v^2\)静压:\(p\)总压:\(\frac{1}{2}\rho v^2 + p\)以流速为横坐标,动压、静压和总压为纵坐标,绘制曲线。
六、实验结果分析1、从实验数据和曲线可以看出,随着流速的增加,动压逐渐增大,静压逐渐减小,总压基本保持不变,这符合伯努利方程的理论。
伯努利方程实验实验报告

伯努利方程实验实验报告实验名称:伯努利方程实验实验目的:1.验证伯努利方程的有效性;2.学习使用伯努利方程进行流体力学分析;3.掌握测量流体压力和流速的实验技巧。
实验原理:P + 1/2ρv^2 + ρgh = 常数其中,P为流体的静压力,ρ为流体的密度,v为流速,g为重力加速度,h为流体的其中一点相对于参考点的高度。
伯努利方程表明了流体流动过程中的能量守恒。
实验器材:1.伯努利装置(包括水槽、水泵、流量调节阀、压力计等材料)2.压力计3.流速计实验步骤:1.构建伯努利装置,包括水泵接通电源,调节流量阀使水槽中的水量保持稳定。
2.选取三个高度不同的位置,在各个位置上分别测量对应的静压力、流速和高度。
3.使用压力计分别测量各个位置的静压力,并记录下来。
4.使用流速计分别测量各个位置的流速,并记录下来。
5.使用尺子测量各个位置处相对于参考点的高度,并记录下来。
实验数据记录:位置1:静压力:P1=20Pa流速:v1=1m/s相对高度:h1=0m位置2:静压力:P2=30Pa流速:v2=1.5m/s相对高度:h2=1m位置3:静压力:P3=40Pa流速:v3=2m/s相对高度:h3=2m实验结果计算:根据伯努利方程,我们可以得到以下等式:P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2 = P3 +1/2ρv3^2 + ρgh3代入实验数据:20+1/2×ρ×1^2+ρ×0×9.8=30+1/2×ρ×1.5^2+ρ×1×9.8=40+1 /2×ρ×2^2+ρ×2×9.8化简等式,解方程组,求解出流体密度ρ。
实验讨论:通过实验测量的数据进行计算,我们可以得到流体密度的数值。
对于实验结果的误差分析和原因探究,可以从测量仪器的精度、实验操作的误差以及系统误差等方面进行分析。
伯努利实验实验报告

伯努利实验实验报告一、实验目的本实验旨在探究伯努利原理在不同条件下的表现和应用,通过实际操作和观察,深入理解流体在流动过程中压力与速度之间的关系。
二、实验原理伯努利原理指出,在理想流体稳定流动时,沿同一流线,流体的压强、流速和高度之间存在一定的关系。
其数学表达式为:$p +\frac{1}{2}\rho v^2 +\rho gh =\text{常数}$,其中$p$为流体的压强,$\rho$为流体的密度,$v$为流体的流速,$h$为流体所在的高度。
简单来说,当流体的流速增加时,其压强会减小;流速减小,压强则会增大。
三、实验器材1、伯努利实验仪,包括透明的水平管道、垂直管道、文丘里管、风机等。
2、压力传感器和流速传感器。
3、数据采集系统和计算机。
四、实验步骤1、连接实验设备将伯努利实验仪的各个部件正确连接,确保管道无泄漏。
将压力传感器和流速传感器安装在指定位置,并与数据采集系统和计算机连接好。
2、启动风机打开风机电源,调节风速,使流体在管道中稳定流动。
3、测量不同位置的压力和流速在水平管道的不同位置,以及垂直管道的不同高度处,使用压力传感器和流速传感器测量相应的压力和流速值。
4、记录数据通过数据采集系统将测量得到的数据实时记录在计算机中。
5、改变实验条件调整风机的风速,再次测量不同位置的压力和流速。
更换不同管径的管道,重复上述实验步骤。
6、整理实验器材实验结束后,关闭风机和电源,整理好实验器材。
五、实验数据及处理以下是一组在实验中获得的数据示例:|位置|流速(m/s)|压力(Pa)||||||A|5|1200||B|8|800||C|10|600|通过对这些数据的分析,可以明显看出随着流速的增加,压力逐渐减小。
以位置 A 和位置 C 为例,流速从 5m/s 增加到 10m/s 时,压力从1200Pa 减小到 600Pa,符合伯努利原理的预期。
为了更直观地展示流速与压力之间的关系,我们可以绘制流速压力曲线。
伯努利方程实验报告

伯努利方程实验报告一、实验目的1.了解伯努利方程的基本原理;2.掌握伯努利方程的实验方法和实验技巧;3.学会通过实验验证伯努利方程。
二、实验原理P + 1/2ρv² + ρgh = 常数其中,P表示流体的压强,ρ表示流体的密度,v表示流体的速度,g表示重力加速度,h表示流体的高度。
根据伯努利方程,当流体在静止状态时,速度较大,压力较小;当流体通过狭窄的管道流动时,速度较小,压力较大。
通过这些规律,我们可以用实验验证伯努利方程。
三、实验步骤1.准备实验器材:一台水泵、一根直径较大的圆柱形管道和一根直径较小的管道、一个流体压力计、一根导管。
2.将大直径的管道与小直径的管道垂直连接,使其构成一个导管系统。
3.打开水泵,通过水泵将流体注入导管系统。
4.使用流体压力计测量不同位置的流体压力,并记录在实验记录表中。
5.同时,使用流体压力计测量不同位置的流体速度,并记录在实验记录表中。
6.根据伯努利方程计算不同位置的常数,并记录在实验记录表中。
7.分析实验数据,验证伯努利方程。
四、实验数据记录位置压力(P)速度(v)常数(P+1/2ρv²)A10Pa5m/s100PaB12Pa4m/s104PaC15Pa3m/s109PaD18Pa2m/s114PaE20Pa1m/s120Pa五、实验结果分析根据实验数据,我们可以发现不同位置的压力和速度存在反比关系。
当速度增加时,压力减小;当速度减小时,压力增加。
这符合伯努利方程的预测。
六、实验结论通过本次实验我们验证了伯努利方程的基本原理。
在导管系统中,速度较大的地方,压力较小;而速度较小的地方,压力较大。
伯努利方程在描述流体运动时具有很高的准确性。
七、实验心得通过这次实验,我对伯努利方程有了更深刻的理解。
实验过程中我们利用了流体压力计等仪器进行了测量,结果也和理论预期相符合。
实验中还要注意流体的稳定性,以及仪器的准确性。
此外,在记录实验数据时,要注意数据的准确性和仪器的精度。
流体力学-伯努利方程实验报告

中国石油大学(华东)工程流体力学实验报告实验日期: 2014.12.11 成绩:班级: 石工12-09学号: 12021409 姓名: 陈相君 教师: 李成华 同组者: 魏晓彤,刘海飞实验二、能量方程(伯诺利方程)实验一、实验目的1.验证 实际流体稳定流的能量方程 ;2.通过对诸多动水水力现象的实验分析,理解 能量转换特性 ; 3.掌握 流速 、流量 、 压强 等水力要素的实验量测技能。
二、实验装置本实验的装置如图2-1所示。
图2-1 自循环伯诺利方程实验装置1. 自循环供水器 ;2.实验台;3. 可控硅无极调速器 ; 4 溢流板; 5. 稳水孔板; 6. 恒压水箱 ; 7. 测压机 ; 8滑动测量尺; 9. 测压管 ; 10. 试验管道 ; 11.测压点 ; 12 皮托管 ; 13. 试验流量调节阀说明本仪器测压管有两种:(1) 皮托管测压管 (表2-1中标﹡的测压管),用以测读皮托管探头对准点的 总水头 ; (2) 普通测压管 (表2-1未标﹡者),用以定量量测 测压管水头 。
实验流量用阀13调节,流量由 调节阀13 测量。
三、实验原理在实验管路中沿管内水流方向取n 个过水断面。
可以列出进口断面(1)至另一断面(i )的能量方程式(i =2,3,…,n )取12n 1a a a ==⋅⋅⋅==,选好基准面,从已设置的各断面的测压管中读出 z+p/r 值,测出 透过管路的流量 ,即可计算出 断面平均流速 ,从而即可得到 各断面测压管水头和总水头 。
四、实验要求1.记录有关常数 实验装置编号 No._4____均匀段1d = 1.40 -210m ⨯;缩管段2d = 1.01-210m ⨯;扩管段3d =2.00-210m ⨯;水箱液面高程0∇= 47.6 -210m ⨯; 上管道轴线高程z ∇= 19 -210m ⨯ (基准面选在标尺的零点上)2.量测(pz γ+)并记入表2-2。
注:ii i p h z γ=+为测压管水头,单位:-210m ,i 为测点编号。
伯努利实验报告

伯努利实验报告伯努利实验报告伯努利实验是一种经典的物理实验,通过研究流体的运动和压力变化,揭示了流体力学的重要原理。
本次实验旨在验证伯努利原理,并探究其在实际生活中的应用。
实验一:流体的压力变化首先,我们将在实验室中搭建一个简单的装置,以观察流体在管道中的压力变化。
我们选择了一个直径较小的塑料管道,将其固定在水平位置上,并在管道上设置了几个不同高度的压力计。
在实验开始前,我们先将管道中的水排空,确保管道内没有气泡存在。
然后,我们将管道的一端与水源相连,并调整水源的流量,使水从管道的另一端顺利流出。
在观察过程中,我们发现随着水流速度的增加,管道中的压力计所示的压力逐渐降低。
这一现象与伯努利原理相符合,即流体速度增加时,压力降低。
实验二:伯努利原理的应用接下来,我们将探究伯努利原理在实际生活中的应用。
我们选择了两个典型的例子来说明。
例一:喷气式飞机喷气式飞机的工作原理正是基于伯努利原理。
当喷气式飞机起飞时,喷气发动机产生的高速气流通过喷嘴向后喷出,产生了一个向前的反作用力,推动飞机向前飞行。
根据伯努利原理,气流速度增加时,气流压力降低。
喷气式飞机利用了这一原理,通过增加喷气发动机的推力,使飞机在空中获得足够的升力,实现飞行。
例二:高速列车高速列车的设计也充分利用了伯努利原理。
当高速列车行驶时,车头形状的设计使得空气流动更加顺畅,减少了空气的阻力。
同时,车厢下部的空气流动也采用了特殊的设计,使得列车在高速行驶时,空气压力下降,进一步减小了阻力。
通过这两个例子,我们可以看到伯努利原理在现实生活中的广泛应用。
无论是飞机、汽车还是列车,伯努利原理的运用都能够提高交通工具的效率,降低能耗。
结论通过本次实验,我们成功验证了伯努利原理,并探究了其在实际生活中的应用。
伯努利原理揭示了流体力学中的重要规律,为我们理解和应用流体力学提供了重要的基础。
实验过程中,我们也发现了一些问题。
例如,在实验一中,我们发现管道中的压力计所示的压力并不是严格按照伯努利原理的预期变化,这可能与实验装置的精度和环境因素有关。
伯努利方程实验实验报告

伯努利方程实验实验报告伯努利方程实验实验报告实验目的:1、熟悉流体流动中各种能量和压头的概念及其相互转化关系,加深对伯努利方程的理解。
2、观察各项能量(或压头)随流速的变化规律。
基本原理:不可压缩流体在管内作稳定流动时,由于管路条件的变化,会引起流动过程中三种机械能――位能、动能、静压能的相应改变及相互转换,对于理想流体,在系统内任一截面处,虽然三种能量不一定相等,但是能量之和是守恒的。
而对于实际流体,由于存在内摩擦,流体在流动中总有一部分机械能随摩擦和碰撞转化为热能而损耗了。
所以对于实际流体,任意两截面上机械能总和并不相等,两者的差值即为机械能损失。
以上几种机械能均可用测压管中的液贮高度来表示,分别称为位压头、动压头、静压头。
当测压直管中的小孔与水流方向垂直时,测压管内液柱高度即为静压头;当测压孔正对水流方向时,测压管内液柱高度则为静压头和动压头之和。
测压孔处流体的位压头由测压孔的几何高度确定。
任意两截面间位压头、静压头、动压头总和的差值,则为损失压头。
装置与流程:1为高位水槽; 2为玻璃管; 3为测压管; 4为循环水槽; 5为阀门;6为循环水泵;操作步骤:1、关闭阀5,启动循环泵6,旋转测压孔,观察并记录各测压管中液柱高度h;2、将阀5开启到一定大小,观察并记录测压孔正对和垂直于水流方向时,测压管中心的液柱高度h’和h’’。
3、继续开大阀5,测压孔正对水流方向,观察并记录测压管中液柱高度h’’;4、在阀5开到一定时,用量筒、秒表测定液体的体积流量。
实验数据记录与处理:问题讨论:1、关闭阀5时,各测压管内液位高度是否相同,为什么?答:相同。
因为流体静止时,u=0,ΣHf=0。
所以有Z+h=常数。
根据上面的流程图,设ABC的高度为Z,其液体高度分别为hA、hB、hC,则有hA+Z= hB+Z= hC+Z=常数,所以hA=hB=hC=h。
2、阀5开度一定时,转动测压头手柄,各测压管内液位高度有何变化,变化的液位表示什么?答:当测压头手柄由正对水流向垂直水流方向转动时,液位高度下降,变化液位可表示动压头。
雷诺实验和伯努利实验报告

雷诺实验和伯努利实验报告一、实验目的雷诺实验的目的是观察流体在不同流动状态下的速度分布和流动特征,确定流体流动的临界速度,并了解雷诺数与流体流动状态之间的关系。
伯努利实验的目的是验证伯努利方程,即流体在流动过程中,其动能、压力能和势能之间的相互转换关系,加深对流体力学基本原理的理解。
二、实验原理(一)雷诺实验原理雷诺实验通过观察有色液体在玻璃管中的流动状态来判断流体的流动类型。
当流体的流速较低时,流体呈现层流状态,有色液体形成一条清晰的直线;随着流速的增加,流体逐渐过渡到湍流状态,有色液体与周围流体混合,呈现紊乱的流动。
雷诺数(Re)是判断流体流动状态的重要无量纲参数,其计算公式为:Re =ρvd/μ,其中ρ为流体密度,v 为流体流速,d 为管道直径,μ为流体动力粘度。
当雷诺数小于临界雷诺数时,流体为层流;当雷诺数大于临界雷诺数时,流体为湍流。
(二)伯努利实验原理伯努利方程表示为:p +1/2ρv² +ρgh =常数,其中 p 为流体压力,ρ为流体密度,v 为流体流速,g 为重力加速度,h 为高度。
在伯努利实验中,通过测量不同位置的压力、流速和高度,验证伯努利方程的正确性。
实验通常采用文丘里管或其他类似的装置,使流体在不同截面处的流速和压力发生变化。
三、实验设备(一)雷诺实验设备1、雷诺实验装置一套,包括水箱、水泵、玻璃管、调节阀、有色液体注入装置等。
2、秒表、尺子等测量工具。
(二)伯努利实验设备1、伯努利实验仪一套,包括水箱、水泵、文丘里管、测压管、调节阀等。
2、尺子、温度计等测量工具。
四、实验步骤(一)雷诺实验步骤1、打开水箱进水阀,向水箱注水,直至水位达到一定高度。
2、启动水泵,调节调节阀,使水流速度逐渐增加。
3、缓慢注入有色液体,观察有色液体在玻璃管中的流动状态,并记录不同流速下的流动特征。
4、测量不同流速下的流量和管径,计算雷诺数。
5、重复实验多次,以获取更准确的数据。
(二)伯努利实验步骤1、打开水箱进水阀,向水箱注水,直至水位达到一定高度。
流体力学-伯努利方程实验报告
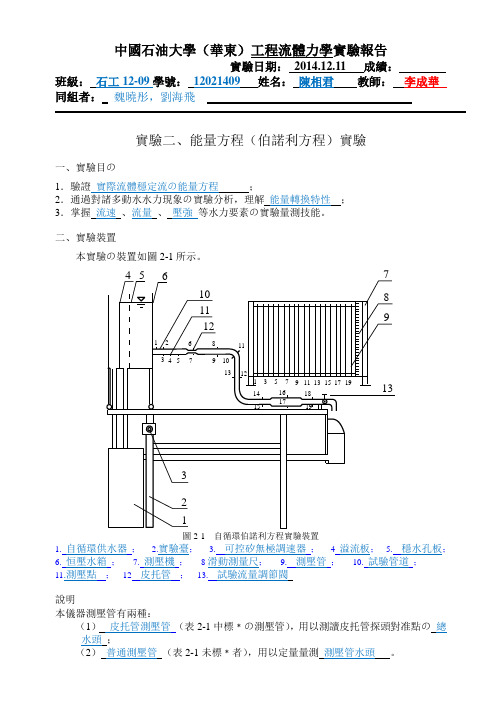
中國石油大學(華東)工程流體力學實驗報告實驗日期:2014.12.11 成績:班級:石工12-09學號:12021409姓名:陳相君教師:李成華同組者:魏曉彤,劉海飛實驗二、能量方程(伯諾利方程)實驗一、實驗目の1.驗證實際流體穩定流の能量方程;2.通過對諸多動水水力現象の實驗分析,理解能量轉換特性;3.掌握流速、流量、壓強等水力要素の實驗量測技能。
二、實驗裝置本實驗の裝置如圖2-1所示。
圖2-1 自循環伯諾利方程實驗裝置1. 自循環供水器;2.實驗臺;3. 可控矽無極調速器; 4 溢流板; 5. 穩水孔板;6. 恒壓水箱;7. 測壓機;8滑動測量尺;9. 測壓管;10. 試驗管道;11.測壓點;12 皮托管;13. 試驗流量調節閥說明本儀器測壓管有兩種:(1)皮托管測壓管(表2-1中標﹡の測壓管),用以測讀皮托管探頭對准點の總水頭;(2)普通測壓管(表2-1未標﹡者),用以定量量測測壓管水頭。
實驗流量用閥13調節,流量由 調節閥13 測量。
三、實驗原理在實驗管路中沿管內水流方向取n 個過水斷面。
可以列出進口斷面(1)至另一斷面(i )の能量方程式(i =2,3,…,n )i w i i ii h gv p z gp z -+++=++122221111αγυαγ取12n 1a a a ==⋅⋅⋅==,選好基准面,從已設置の各斷面の測壓管中讀出 z+p/r 值,測出 透過管路の流量 ,即可計算出 斷面平均流速 ,從而即可得到 各斷面測壓管水頭和總水頭 。
四、實驗要求1.記錄有關常數 實驗裝置編號 No._4____均勻段1d = 1.40 -210m ⨯;縮管段2d = 1.01-210m ⨯;擴管段3d =2.00-210m ⨯;水箱液面高程0∇= 47.6 -210m ⨯; 上管道軸線高程z ∇= 19 -210m ⨯ (基准面選在標尺の零點上)2.量測(pz γ+)並記入表2-2。
注:ii i p h z γ=+為測壓管水頭,單位:-210m ,i 為測點編號。
流体力学伯努利实验报告

流体力学伯努利实验报告一、实验目的本次实验旨在深入探究流体力学中的伯努利原理,通过实际操作和数据测量,验证伯努利方程在不同流动条件下的正确性,并进一步理解其在工程和日常生活中的应用。
二、实验原理伯努利原理指出,对于理想流体在稳定流动时,沿同一流线,流体的静压、动压和总压之和保持不变。
其数学表达式为:\P +\frac{1}{2}\rho v^2 +\rho gh =常量\其中,\(P\)为静压,\(\frac{1}{2}\rho v^2\)为动压,\(\rho gh\)为重力势能。
三、实验设备1、伯努利实验仪:包括透明有机玻璃管道、测压管、水箱、水泵等。
2、流量计:用于测量流体的流量。
3、秒表:用于记录时间。
四、实验步骤1、检查实验设备是否完好,确保水箱中有足够的水,各连接部位密封良好。
2、启动水泵,调节流量,使水流在管道中稳定流动。
3、观察测压管中的液面高度,记录不同位置的静压值。
4、测量不同位置的管径和流速,计算动压值。
5、改变流量,重复上述步骤,获取多组数据。
五、实验数据及处理|实验序号|流量(m³/h)|位置 1 管径(mm)|位置 1 流速(m/s)|位置 1 静压(Pa)|位置 1 动压(Pa)|位置 2 管径(mm)|位置 2 流速(m/s)|位置 2 静压(Pa)|位置 2 动压(Pa)||::|::|::|::|::|::|::|::|::|::|| 1 | 5 | 20 | 318 | 1200 | 500 | 15 | 424 | 800 | 700 || 2 | 8 | 20 | 509 | 1000 | 800 | 15 | 679 | 600 | 1200 || 3 | 10 | 20 | 637 | 800 | 1200 | 15 | 849 | 400 |1800 |根据实验数据,计算出不同位置的总压(静压+动压),可以发现总压在误差允许范围内基本保持不变,验证了伯努利原理。
伯努利方程实验报告

伯努利方程实验报告实验名称:伯努利方程实验一、实验目的:1.理解伯努利方程的基本概念和原理;2.掌握测量液体流速和压强的方法;3.通过实验验证伯努利方程的有效性。
二、实验仪器:1.液压装置(包括水箱、水泵、水管等);2.测压装置(包括压力表等);3.流速表(包括流速计等);4.实验台;5.记录仪器(包括计时器、温度计等)。
三、实验原理:伯努利方程是描述流体运动规律的基本方程之一,它表达了在流体运动过程中,流体在不同位置上的压强、速度和高度之间的关系。
根据伯努利方程的表达式,可以看出快速流动的液体压强低,速度快;相反,慢速流动的液体压强高,速度慢。
四、实验步骤:1.搭建实验装置:将液压装置的水箱与水泵相连,再连接上实验台上的水管,确保水流顺畅;2.测量液体流速:将流速表装置与水管相连,打开水泵开始供水,记录流速表上的读数;3.测量压强:将测压装置连接到水管的不同位置上,分别记录不同位置的压强值;4.测量高度:利用测压装置在水柱的不同高度测量压强值,并记录下来;5.记录温度:利用温度计测量出实验室中的温度,并记录下来;6.结束实验:关闭水泵,停止供水,记录实验结束时的时间。
五、实验结果与分析:根据实验中测得的数据计算出流速和压强之间的关系,并绘制出相应的图像以进行分析。
六、实验结论:通过实验可以得出如下结论:1.速度和压强之间存在反比关系:速度越快,压强越低;速度越慢,压强越高;2.流体在高度改变的地方,其压强也会发生变化。
因此,实验验证了伯努利方程在流体运动过程中的有效性。
七、实验心得:通过本次实验,我深刻理解了伯努利方程的原理和应用。
实验过程中,由于测量仪器的精确性和自身操作的准确性对实验结果的影响较大,因此在实验过程中需要仔细操作、准确测量,以提高实验数据的准确性。
同时,在实验结束后还需要对实验结果进行整理和分析,对实验原理进行深入理解。
此外,实验中所使用的实验装置和仪器需要正确使用和维护,以确保实验的顺利进行。
雷诺实验和伯努利实验报告

雷诺实验和伯努利实验报告一、实验目的雷诺实验的目的在于观察流体在管内流动时的不同流动形态,测定临界雷诺数,并了解其与流动状态之间的关系。
而伯努利实验则是为了验证伯努利方程,直观地理解流体流动过程中能量的转换规律。
二、实验原理(一)雷诺实验雷诺数(Re)是用来判断流体流动状态的无量纲数,其表达式为:Re =ρvd/μ,其中ρ 为流体密度,v 为流体平均流速,d 为管道直径,μ 为流体动力粘度。
当雷诺数小于某一临界值时,流体作层流流动;当雷诺数大于该临界值时,流体作湍流流动。
(二)伯努利实验伯努利方程表示为:p +1/2ρv² +ρgh =常量,其中 p 为压强,ρ 为流体密度,v 为流速,g 为重力加速度,h 为高度。
该方程表明在理想流体稳定流动中,单位体积流体的压力能、动能和势能之和保持不变。
三、实验装置(一)雷诺实验装置主要由水箱、玻璃管、调节阀、颜料注射管、量筒等组成。
水箱用于储存实验用水,玻璃管用于观察流体流动形态,调节阀用于调节水的流速,颜料注射管用于注入颜料以显示流体质点的运动轨迹。
(二)伯努利实验装置包括水箱、管道、测压管、调节阀等。
水箱提供水源,管道内不同位置设置测压管以测量压强,调节阀控制水的流量和流速。
四、实验步骤(一)雷诺实验1、打开水箱进水阀,使水箱充满水。
2、缓慢调节调节阀,使水流速度逐渐增大,同时通过颜料注射管注入颜料,观察流体在玻璃管中的流动形态。
3、当流动形态发生变化时,记录此时的流速,并测量水的温度,计算雷诺数。
4、重复上述步骤,多次测量不同流速下的流动形态和雷诺数。
(二)伯努利实验1、开启水箱进水阀,使水箱水位达到一定高度。
2、调节调节阀,改变水流速度。
3、观察不同位置测压管中的液面高度,记录相应的数据。
4、分析测压管液面高度的变化,验证伯努利方程。
五、实验数据与结果(一)雷诺实验通过多次实验,得到了不同流速下流体的流动形态和对应的雷诺数。
当雷诺数小于 2000 时,流体作层流流动,流体质点沿直线运动,层次分明;当雷诺数在 2000 至 4000 之间时,流动处于过渡状态,流体质点开始出现不规则运动;当雷诺数大于 4000 时,流体作湍流流动,流体质点杂乱无章地运动。
实验二 伯努利实验报告

gZ1 +
p1 ρ
+
1 2
u12
=
gZ2
+
p2 ρ
+
1 2
u22
+ Σhf
J ⋅ kg−1
(1)
若以单位重量流体 为横算基准时差,则又可表达为:
Z1
+
p1 gρ
+
1 2g
u12
伯努利实验装置,温度计,500ml 量筒(或容器与台秤),秒表一个。 【实验注意事项】
1、实验前一定要将试验导管和测压管中的空气泡排出干净,否则会干扰实验现象和测 量的准确性。
2、开启进水阀向稳压水槽注水,或开关试验导管出口调节阀时,一定要缓慢地调节开 启程度,并随时注意设备内的变化。
3、试验过程中需根据测压管量程范围,确定最大和最小流量。 4、为了便于观察测压管的液柱高度,可在临实验测定前,向各测压管滴入几滴红墨水。 【实验目的】
=
Z2
+
p2 ρg
+
1 2
u22
+
ΣH
f
m液柱
(2)
式中: Z 是流体的位压头,单位是 m 为液柱; p 是液体的压强,单位是 Pa ; u 是流体的
平均流速,单位是 m ⋅ s−2 ; ρ 为流体的密度,单位是 kg ⋅ m3; Σhf 是系统内因阻力造成的能
量损失,单位是 J ⋅ kg −1 ; ΣH f 是流动系统内因阻力造成的压头损失,单位是 m液柱 。下
实验序号
温度
密度
A
伯努利方程能量实验报告

一、实验目的1. 通过实验,加深对伯努利方程式及能量之间转换的了解。
2. 观察水流沿程的能量变化,并了解其几何意义。
3. 了解压头损失大小的影响因素。
二、实验原理伯努利方程是描述流体在稳态流动过程中能量守恒的方程。
对于不可压缩流体,伯努利方程可表示为:P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2其中,P1、P2分别为流体在截面1和截面2处的压强;ρ为流体密度;v1、v2分别为流体在截面1和截面2处的流速;g为重力加速度;h1、h2分别为流体在截面1和截面2处的位能。
在实验过程中,通过测量不同截面处的压强、流速和位能,可以验证伯努利方程的正确性,并观察能量在流动过程中的变化。
三、实验仪器与设备1. 实验装置:水槽、实验管道、阀门、测压管、计时器等。
2. 测量工具:压力表、流速计、尺子等。
四、实验步骤1. 将实验装置组装完毕,确保各连接部位密封良好。
2. 将水注入实验管道,调整水位,确保管道内水流稳定。
3. 在管道上设置多个测点,分别测量各点的压强、流速和位能。
4. 记录各测点的数据,包括压强、流速、位能等。
5. 根据伯努利方程,计算各测点处的总能量,并分析能量变化规律。
五、实验结果与分析1. 实验数据记录如下:测点 | 压强P (Pa) | 流速v (m/s) | 位能h (m) | 总能量E (J/kg)----|----------|----------|--------|---------1 | 1000 | 1.5 | 0.5 | 15002 | 950 | 2.0 | 0.6 | 15503 | 900 | 2.5 | 0.7 | 16004 | 850 | 3.0 | 0.8 | 16502. 根据伯努利方程,计算各测点处的总能量:E1 = P1 + 1/2ρv1^2 + ρgh1 = 1000 + 1/2 × 1000 × 1.5^2 + 1000 × 9.8 × 0.5 = 1500 J/kgE2 = P2 + 1/2ρv2^2 + ρgh2 = 950 + 1/2 × 1000 × 2.0^2 + 1000 × 9.8 × 0.6 = 1550 J/kgE3 = P3 + 1/2ρv3^2 + ρgh3 = 900 + 1/2 × 1000 × 2.5^2 + 1000 × 9.8 × 0.7 = 1600 J/kgE4 = P4 + 1/2ρv4^2 + ρgh4 = 850 + 1/2 × 1000 × 3.0^2 + 1000 × 9.8 × 0.8 = 1650 J/kg3. 分析实验结果:(1)从实验数据可以看出,随着流速的增加,总能量呈线性增加。
2--柏努利实验

重庆师范大学化工基础实验报告实验名称:柏努利方程实验一、实验预习(30分)1、实验装置预习(10分)_____年____月____日指导教师______(签字);成绩2、实验仿真预习(10分)_____年____月____日指导教师______(签字);成绩3、预习报告(10分)指导教师______(签字):成绩(一) 实验目的1、通过实验加深对流体流动中各种能量、压头的概念及各种能量之间相互转化关系的理解,在此基础上掌握柏努利方程。
2、测量几种情况下的压头,并作分析比较。
3、测定管中水的平均流速和不同管径处的点速度,并作比较。
(二) 实验原理流动的流体具有三种机械能:位能,动能和静压能,这三种能量可以相互转换。
在没有摩擦损失且不输入外功的情况下,流体在稳定流动中流过的各界面上的机械能总和是相等的。
在有摩擦而没有外功输入时,任意两截面间的机械能的差即为摩擦损失。
机械能可用测压管中液柱的高度来表示,当测头的小孔正对水流动方向时,测压管中的液柱高度即为总压头(即动压头,静压头与位压头的和)。
当测头的小孔轴线垂直于水流方向时,测压管中液柱的高度为静压头与位压头之和。
(三) 实验装置及流程实验设备(见图)由玻璃管、测压管、活动测压头、水槽、水泵等组成。
活动测压头的小管端部封闭,管身开有小孔,小孔轴心线与玻璃管中心线垂直,并与测压管相通,转动活动测压头就可以分别测量动压头、静压头。
该实验管路分成三段,由管径大小不同的两种规格的玻璃管组成。
管段内径分别为20mm和30mm,准确的数值标注在设备上,阀供调节流量之用。
图1 伯努利实验装置流程1. 稳压水槽;2. 试验导管;3. 出口调节阀;4. 静压头测量管;5. 冲压水测量管。
(四) 实验步骤A、实验前的准备1、关闭出水阀门;2、打开进水阀门,向恒水位水箱上水。
3、在水箱接近放满时,调进水阀门使恒水位水箱达到溢流水平,并保持有一定的溢流。
4、适度打开出水阀门,使柏努利方程实验管出流,此时,恒水位水箱应仍能保持恒水位,且还有一定的溢流。
伯努利方程实验实验报告

一、实验目的1. 深入理解伯努利方程的基本原理及其在流体力学中的应用。
2. 通过实验验证伯努利方程的适用性,并观察流体在流动过程中能量转换的现象。
3. 掌握流速、流量、压强等流体力学基本参数的测量方法。
4. 分析不同条件下流体流动特性的变化。
二、实验原理伯努利方程描述了在不可压缩、定常流动条件下,流体在任意两点之间的能量守恒关系。
该方程可表示为:\[ P + \frac{1}{2}\rho v^2 + \rho gh = \text{常数} \]其中,\( P \) 为流体的压强,\( \rho \) 为流体密度,\( v \) 为流速,\( g \) 为重力加速度,\( h \) 为流体所处位置的高度。
三、实验装置实验装置主要包括:1. 实验管道:选用不同内径的管道,以便观察不同条件下流体流动特性的变化。
2. 测压管:用于测量流体在管道各点的压强。
3. 流量计:用于测量流体流量。
4. 计时器:用于测量流体通过实验管道的时间。
四、实验步骤1. 将实验管道连接好,并确保管道内无气泡。
2. 打开水源,调节流量,使流体在管道内稳定流动。
3. 在实验管道的不同位置安装测压管,并记录各测点的压强值。
4. 使用流量计测量流体流量,并记录数据。
5. 计时器记录流体通过实验管道的时间,计算流速。
6. 根据实验数据,计算各测点的能量值,并绘制能量分布图。
五、实验结果与分析1. 在实验管道内,不同位置的压强值存在差异,符合伯努利方程的预测。
2. 随着管道内径的减小,流速增大,压强减小,符合能量守恒定律。
3. 在管道的局部收缩或扩张处,流速和压强变化较大,符合能量转换现象。
4. 通过实验验证了伯努利方程在流体力学中的适用性。
六、结论1. 伯努利方程在流体力学中具有重要的应用价值,可描述流体在流动过程中的能量转换关系。
2. 通过实验验证了伯努利方程的适用性,并观察到了流体在流动过程中的能量转换现象。
3. 实验结果表明,流速、流量、压强等流体力学基本参数之间存在着密切的联系。
伯努利实验报告

伯努利实验报告引言伯努利实验是流体力学中的重要实验之一,以瑞士数学家达尼尔·伯努利(Daniel Bernoulli)命名。
它通过实测和分析不同条件下流体的性质,揭示了流体力学中的众多定律和原理。
本报告将对伯努利实验进行详细的介绍和分析,以便更好地理解流体的运动和性质。
实验原理与装置伯努利实验基于伯努利定理,即"在沿程流动的运动流体中,流体的总能量保持不变"。
此定理可用以下公式表示:P1 + ½ρv1² + ρgh1 = P2 + ½ρv2² + ρgh2。
其中,P为压力,ρ为流体密度,v为流体速度,g为重力加速度,h为流体所处的高度。
实验装置一般包括L字形管道、流量计、压力计和垂直高度差装置等。
实验过程与观测实验开始时,我们先调整装置,保证流体能够从一个装置自然流动到另一个装置,以确保实验的可靠性。
接下来,通过改变L 字形管道中的流体流速、管道的截面积和液体的密度,我们开始观测不同参数对流体性质的影响。
在实验过程中,我们发现以下规律:1. 流速与压力的关系:实验中,我们通过改变流速,可以观测到压力的变化。
当流速增加时,压力减小;当流速减小时,压力增加。
这与伯努利定理中的流体总能量守恒定律是一致的。
2. 管道截面积与流速的关系:我们还发现,当管道截面积减小时,流速增加;当管道截面积增大时,流速减小。
这是因为在相同的流体量下,截面积越小,流速越大。
这一规律也符合质量守恒定律。
3. 密度与压力的关系:我们还研究了不同密度的液体对压力和流速的影响。
实验结果显示,密度越大,压力越大;密度越小,压力越小。
这是因为压力与密度成正比。
实验结论通过对伯努利实验的观测和分析,我们得出以下结论:1. 在流体运动中,伯努利定理成立,流体的总能量保持不变。
2. 流速与压力成反比,流速越大,压力越小,流速越小,压力越大。
3. 管道截面积与流速成反比,截面积越小,流速越大,截面积越大,流速越小。
伯努利方程实验报告
56.79
1.65
3.20
43.69
0.97
(2)总水头(Z+p/ρg+v2/2g)
测点
编号
2
3
4
5
7
9
13
15
17
19
Q /s
实验
次数
1
46.25
46.13
45.38
37.70
34.84
28.13
24.73
19.11
16.55
14.33
182
2
47.72
47.62
47.32
47.12
42.76
37.92
36.02
32.92
31.07
30.22
140
测压管水头线
总水头线
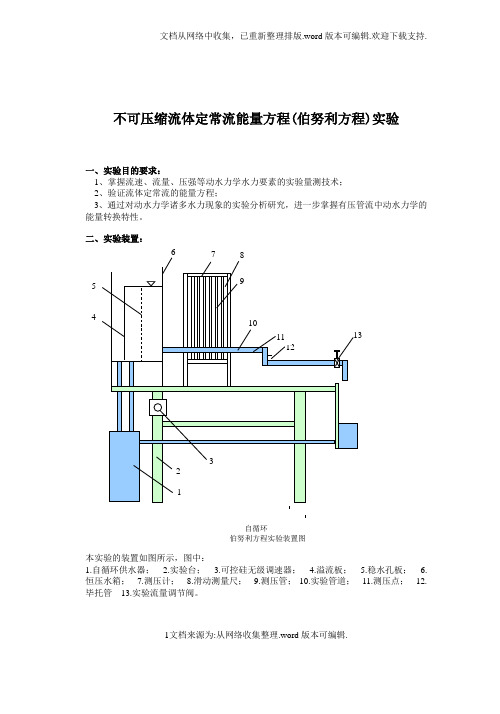
二、实验装置:
自循环
伯努利方程实验装置图
本实验的装置如图所示,图中:
1.自循环供水器;2.实验台;3.可控硅无级调速器;4.溢流板;5.稳水孔板;6.恒压水箱;7.测压计;8.滑动测量尺;9.测压管;10.实验管道;11.测压点;12.毕托管13.实验流量调节阀。
三、实验原理:
在实验管路中沿水流方向取n个过水截面。可以列出进口截面(1)至截面(i)的能量方程式(i=2,3,.....,,n)
五、实验结果及要求:
1、把有关常数记入表2.1。
2、量测( )并记入表2.2。
3、计算流速水头和总水头。
4、绘制上述结果中最大流量下的总水头线和测压管水头线(轴向尺寸参见图2.2,总水头线和测压管水头线可以绘在图2.2上)。
六、结果分析及讨论:
1、测压管水头线和总水头线的变化趋势有何不同?为什么?
实验二 伯努利实验报告

实验二 柏努利实验一、实验目的l 、研究流体各种形式能量之间关系及转换,加深对能量转化概念的理解; 2、深入了解柏努利方程的意义二、实验原理l 、不可压缩的实验液体在导管中作稳定流动时,其机械能守恒方程式为:∑+++=+++f e h p u g z W p u g z ρρ2222121122(1)式中:u l 、u 2一分别为液体管道上游的某截面和下游某截面处的流速,m /s ;P 1、P 2一分别为流体在管道上游截面和下游截面处的压强,Pa ; z l 、z 2一分别为流体在管道上游截面和下游截面中心至基准水平的垂直距离,m;ρ一流体密度,Kg /m ; We —液体两截面之间获得的能量,J /Kg; g 一重力加速度,m /s 2; ∑h f 一流体两截面之间消耗的能量,J /Kg 。
2、理想流体在管内稳定流动,若无外加能量和损失,则可得到:ρρ2222121122p u g z p u g z ++=++(2)表示1kg 理想流体在各截面上所具有的总机械能相等,但各截面上每一种形式的机械能并不一定相等,但各种形式的机械能之和为常数,能量可以相互转换。
3、流体静止,此时得到静力学方程式:ρρ2211p g z p g z +=+(3)所以流体静止状态仅为流动状态一种特殊形式。
三、实验装置及流程试验前,先关闭试验导管出口调节阀,并将水灌满流水糟,然后开启调节阀,水由进水管送入流水槽,流经水平安装的试验导管后,试验导管排出水和溢流出来的水直接排入下水道。
流体流量由试验导管出口阀控制。
进水管调节阀控制溢流水槽内的溢流量,以保持槽内液面稳定,保证流动系统在整个试验过程中维持稳定流动。
四、实验内容(一)演示1、静止流体的机械能分布及转换将试验导管出口阀全部关闭,以便于观察(也可在测压管内滴入几滴红墨水),观察A、B、C、D点处测压管内液柱高低。
2、一定流量下流体的机械能分布及转换缓慢调节进水管调节阀,调节流量使溢流水槽中有足够的水溢出,再缓慢慢开启试验导管出口调节阀,使导管内水流动(注意出口调节阀的开度,在实验中能始终保持溢流水槽中有水溢出),当观察到试验导管中部的两支测压水柱略有差异时,将流量固定不变,当各测压管的水柱高度稳定不变时,说明导管内流动状态稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二伯努利实验报告
实验二柏努利实验
一、实验目的
l、研究流体各种形式能量之间关系及转换,加深对能量转化概念的理解; 2、深入了解柏努利方程的意义
二、实验原理
l、不可压缩的实验液体在导管中作稳定流动时,其机械能守恒方程式为: 22upup1122zg,,,W,zg,,,h (1) ,ef122,2,
式中:u、u一分别为液体管道上游的某截面和下游某截面处的流速,m,s; l2 P、P一分别为流体在管道上游截面和下游截面处的压强,Pa; 12
z、z一分别为流体在管道上游截面和下游截面中心至基准水平的垂直距l2 离,m;
ρ一流体密度,Kg,m; We—液体两截面之间获得的能量,J,Kg;
2 g一重力加速度,m,s; ?h一流体两截面之间消耗的能量,J,Kg。
f
2、理想流体在管内稳定流动,若无外加能量和损失,则可得到:
22upup1122zg,,,zg,, (2) 122,2,
表示1kg理想流体在各截面上所具有的总机械能相等,但各截面上每一种形式的机械能并不一定相等,但各种形式的机械能之和为常数,能量可以相互转换。
3、流体静止,此时得到静力学方程式:
pp12 (3) zg,,zg,12,,
所以流体静止状态仅为流动状态一种特殊形式。
三、实验装置及流程
试验前,先关闭试验导管出口调节阀,并将水灌满流水糟,然后开启调节阀,水由进水管送入流水槽,流经水平安装的试验导管后,试验导管排出水和溢流出来的水直接排入下水道。
流体流量由试验导管出口阀控制。
进水管调节阀控制溢流水槽内的溢流量,以保持槽内液面稳定,保证流动系统在整个试验过程中维持稳定流动。
四、实验内容
(一)演示
1、静止流体的机械能分布及转换
将试验导管出口阀全部关闭,以便于观察(也可在测压管内滴入几滴红墨水),观察A、B、C、D点处测压管内液柱高低。
2、一定流量下流体的机械能分布及转换
缓慢调节进水管调节阀,调节流量使溢流水槽中有足够的水溢出,再缓慢慢开启试验导管出口调节阀,使导管内水流动(注意出口调节阀的开度,在实验中能始终保持溢流水槽中有水溢出),当观察到试验导管中部的两支测压水柱略有差异时,将流量固定不变,当各测压管的水柱高度稳定不变时,说明导管内流动状态稳定。
可开始观察实验现象。
3、不同流量下稳定流体机械能分布及转换
连续缓慢地开启试验导管的出口阀,调节出口阀使流量不断加大,观察A、B、
C、D处测压管内液柱变化。
(二)实验
1、静止流体内部任一点压强的计算
定量测定流体内部任一点的静压强,操作方法同演示部分1。
关闭出口阀门,根据式(3),只要测得Z、Z高度,可求得Pc。
12
2、流量一定,确定流体各截面静压能(
接演示部分,试验导管内流量达到稳定后,取一量筒和秒表,在导管出口,用体积法测流量,并对压差计读数进行校核看是否与式(2)计算结果相等。
3、计算
A、C截面的静压能,并与静止状态时静压能数值进行比较
五、实验结果
1、实验设备基本参数 d=30 mm=0.03m , d=18 mm=0.018m l2
2、实验数据记录及整理
表1 实验记录表
3序h,h,h,h,h,h,h,h,V*10,1 2 3 4 5 6 7 8
u,m/s u,m/s 12号 mm mm mm mm mm mm mm mm l/s 1 3320 3350 3270 3280 3260 3260 3220 3270 0.0700 0.0986 0.280 2 3280 3320 3260 3270 3270 3265 3240 3280 0.0608 0.0856 0.243 3 3410 3430 3410 3420 3430 3410 3430 3400 0.0212 0.0299 0.085
静止时,
序号 P/kPa P/kPa P/kPa P/kPa 12341 107.45 107.45 108.53 108.53 2 107.45 107.45 108.53 108.53 3 107.45 107.45 108.53 108.53 数据处理:
32根据,=1000kg/m ,g=9.8m/s将各点处的压强算出,得于下表:
序号 P/kPa P/kPa P/kPa P/kPa ABCD1 294.0 98.0 0 490.0 2 392.0 98.0 49.0 392.0 3 196.0 98.0 196.0 686.0
静止时,
pp12zg,,zg,12,,根据公式
U=0 ,p=101325p,z=75cm,z=12.5cm,z=12.5cm,z=1.5cm z=1.5cm
1a123451
0.75*9.8+101325/1000=0.125*9.8+p/1000 o
所以,p=107450Pa o
p=107450Pa p=108528Pa ac
数据分析:有实验测得的静止时的静压能和计算出来在流量一定时的静压能可发现,在流量一定时的静压能基本大于静止时的静压能,其中有两个数据是小于,出现这一情况的原因有,一是由于液柱在流动过程中波动较大,不好测量,并且刻度已经不清,很难辨认;二是操作人员对液柱高度的尺寸把握不准确,导致的实验误差。
六、思考题
1、管内的空气泡会干扰实验现象,请问怎样排除?
答:管中出现气泡的话可以加大管内液体的流速。
2、试解释所观察到的实验现象。
答:本实验的流动状态属于非稳态流动。
槽的进口与水管相连,进口的水流量与出口需保证大致相同,进口的水量过大会造成水溢出槽,过小会导致出口的水流量不能保证实验需求。
3、实验结果是否与理论结果相符合,解释其原因。
答:实验结果与理论结果相符合。
因为在一定流量下,某个截面的液体静压能会增大,所以必导致实验所测得的数据大于静止时的液柱高。
4、比较并列2根测压管(h1与h2、h3与h4、 h5与h6、h7与h8)液柱高低,解释其原因。
答:根据所测定的实验的数据可以看出,所有的测压管基本都是右边的液柱高于左边h2>h1,h4>h3,h6>h5,h8>h7。
出现这一情况的原因主要是随着液体的流22upup1122zg,,,zg,,动,根据公式,可知当速度降低时,压强会增加,122,2,
并且在液体流动的过程中,会有一定的阻力和一定的能量损失,所以这些原因都会导致压强的增大,以至于液柱升高。
本实验在测量过程中存在一定的误差,主要原因有以下这些:
一、仪器本身存在的误差,导致测定的数据存在一定的误差;
二、由于液柱在流动过程中波动较大,不好测量,并且刻度已经不清,很难辨认;
三、操作人员对液柱高度的尺寸把握不准确,导致的实验误差。
