伯努利方程实验

合集下载

不可压缩流体恒定流能量方程(伯努利)实验

不可压缩流体恒定流能量方程(伯努利)实验
伯努利方程是描述不可压缩流体恒定流动过程中能量守恒的方程。

伯努利方程的数学表达式为：
P + 1/2ρv^2 + ρgh = constant
其中，P为流体的静压力，ρ为流体的密度，v为流体的流速，g为重力加速度，h为流体的高度。

这个方程说明了，如果不
可压缩流体在一段管道中沿一定方向流动，其沿途的总能量相同，即静压力、动压力和位能之和不变。

为了验证伯努利方程的可靠性，可以进行以下实验：
实验材料：
- 一条直径较小的降压管
- 一个水箱
- 测压计
- 尺子
- 水
实验步骤：
1. 将降压管的一个端口插入水箱底部，另外一个端口向上，调整好降压管的位置使其与水箱水平。

2. 在降压管的高度处放置测压计，测量降压管水柱的压力。

3. 打开水箱的水龙头，让水自由流入降压管。

观察水流的流速和降压管压力的变化。

4. 重复实验3，但这次在降压管进口处用尺子测量水的流速。

并且将降压管移至不同高度，重复实验3。

实验结果：
实验结果应该证实伯努利方程的成立性，即随着流速增加，静压力降低。

除非有能量损失，沿途的总能量相同。

通过实验结果可以验证伯努利方程。

流体力学实验-伯努利方程

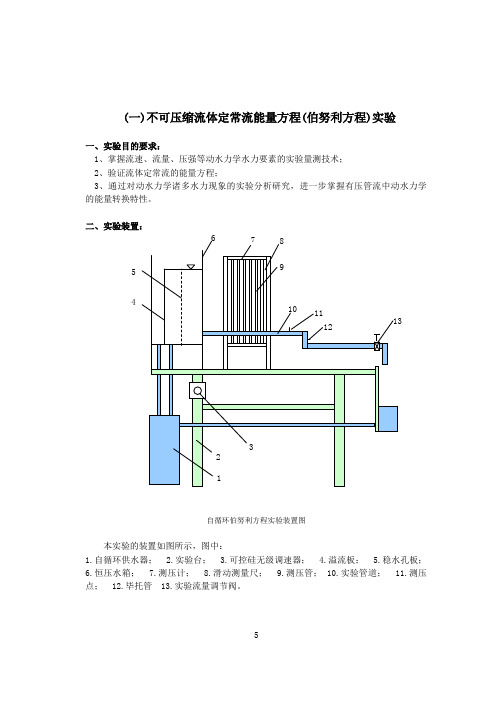
(一)不可压缩流体定常流能量方程(伯努利方程)实验一、实验目的要求：1、掌握流速、流量、压强等动水力学水力要素的实验量测技术；2、验证流体定常流的能量方程；3、通过对动水力学诸多水力现象的实验分析研究，进一步掌握有压管流中动水力学的能量转换特性。

自循环伯努利方程实验装置图本实验的装置如图所示，图中：1.自循环供水器；2.实验台；3.可控硅无级调速器；4.溢流板；5.稳水孔板；6.恒压水箱；7.测压计；8.滑动测量尺；9.测压管； 10.实验管道； 11.测压点； 12.毕托管 13.实验流量调节阀。

56三、实验原理：在实验管路中沿水流方向取n 个过水截面。

可以列出进口截面(1)至截面(i)的能量方程式（i=2,3,.....,，n)W i hg g p Z g g p Z i i i -+++=++12222111νρνρ选好基准面，从已设置的各截面的测压管中读出g p Z ρ+值,测出通过管路的流量,即可计算出截面平均流速ν及动压g 22ν，从而可得到各截面测管水头和总水头。

四、实验方法与步骤：1、熟悉实验设备，分清各测压管与各测压点，毕托管测点的对应关系。

2、打开开关供水，使水箱充水，待水箱溢流后，检查泄水阀关闭时所有测压管水面是否齐平，若不平则进行排气调平(开关几次）。

3、打开阀13，观察测压管水头线和总水头线的变化趋势及位置水头、压强水头之间的相互关系，观察当流量增加或减少时测压管水头的变化情况。

4、调节阀13开度，待流量稳定后，测记各测压管液面读数，同时测记实验流量(与毕托管相连通的是演示用，不必测记读数)。

5、再调节阀13开度1～2次，其中一次阀门开度大到使液面降到标尺最低点为限，按第4步重复测量。

五、实验结果及要求：1、把有关常数记入表2.1。

2、量测(g pZ ρ+)并记入表2.2。

3、计算流速水头和总水头。

4、绘制上述结果中最大流量下的总水头线和测压管水头线(轴向尺寸参见图2.2，总水头线和测压管水头线可以绘在图2.2上)。

能量方程(伯努利方程)实验

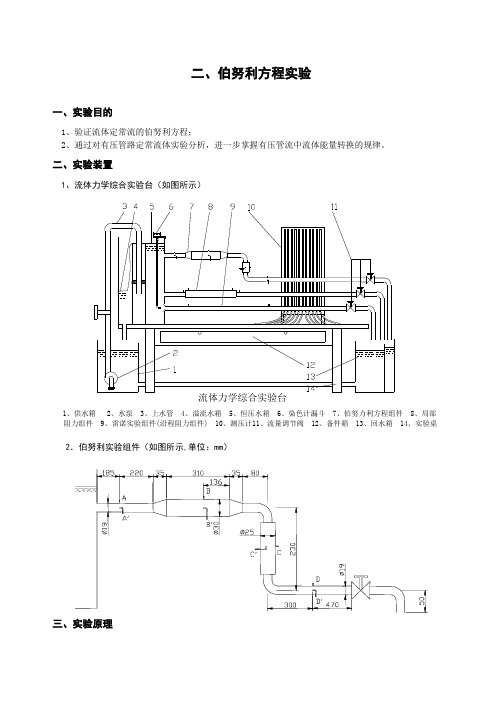
能量方程(伯努利方程)实验能量方程（伯努利方程）实验姓名：史亮班级：9131011403学号：913101140327处的7根皮托管测压管测量总水头或12根普通测压管测量测压管水头，其中测点1、6、8、12、14、16和18均为皮托管测压管（示意图见图3.2），用于测量皮托管探头对准点的总水头H ’（=2gu2++r p Z ），其余为普通测压管（示意图见图3.3），用于测量测压管水头。

图3.2 安装在管道中的皮托管测压管示意图图3.3安装在管道中的普通测压管示意图3.3 实验原理当流量调节阀旋到一定位置后，实验管道内的水流以恒定流速流动，在实验管道中沿管内水流方向取n 个过水断面，从进口断面（1）至另一个断面（i ）的能量方程式为：2g v2111++r p Z =fiih r p Z +++2gv 2i=常数（3.1）式中：i=2，3，······ ，n ；Z ──位置水头；rp──压强水头； 2gv 2──速度水头；fh ──进口断面（1）至另一个断面（i ）的损失水头。

从测压计中读出各断面的测压管水头（r pZ +），通过体积时间法或重量时间法测出管道流量，计算不v2，从同管道内径时过水断面平均速度v及速度水头2g而得到各断面的测压管水头和总水头。

3.4 实验方法与步骤1)观察实验管道上分布的19根测压管，哪些是普通测压管，哪些是皮托管测压管。

观察管道内径的大小，并记录各测点管径至表3.1。

2)打开供水水箱开关，当实验管道充满水时反复开或关流量调节阀，排除管内气体或测压管内的气泡，并观察流量调节阀全部关闭时所有测压管水面是否平齐（水箱溢流时）。

如不平，则用吸气球将测压管中气泡排出或检查连通管内是否有异物堵塞。

确保所有测压管水面平齐后才能进行实验，否则实验数据不准确。

3)打开流量调节阀并观察测压管液面变化，当最后一根测压管液面下降幅度超过50%时停止调节阀门。

伯努利方程实验

伯努利方程实验我们知道，物理学是研究自然界物质的基本运动规律的。

为了突出主要矛盾，人们往往设定一些理想物理模型，如质点，刚体，理想气体等等。

在这里涉及的理想物理模型是理想流体。

理想流体的主要特征指的是不可压缩和没有粘滞性，所谓不可压缩指的是流体中任意一定体积的流体团无论其压强、位置、形状如何变化总是保持体积不变；所谓没有粘滞性指的是流体中一部分流体相对于相邻流体流动时它们之间没有相互作用力(或：固体球或棒在理想流体中运动时不受阻力)。

在设定流体为理想流体，且在作定常流动时，即流体中任一点的流速不随时间变化时，按照欧拉法，可用速度场表示流体，其中的场线就是流线，流线上任一点的切线就表示该点的流速。

由流线围成的闭合细管称为流管。

由于设定流体为理想流体，没有粘滞性，流动过程中没有能量损耗，机械能守恒。

再由质点系的功能原理，把流管中的一段流体体元作为质点系，当它在流管中运动时，外力功等于体元的机械能的变化。

由此得到伯努利方程其中，ρ为流体的密度；v为流体元的速度；g为重力加速度；h为流体元的高度；p为流体在流体元处的压强；C为常量，它表示流体元中单位体积的机械能。

实验表明，几乎一切流体都具有黏滞性。

在物理学史上，先辈们对流体物理图像的理解曾经经历过曲折的过程。

在20世纪之前，人们研究流体力学的兴趣和精力都集中在无黏滞假设下一个又一个优美的数学解上。

冯·诺埃曼(John von Neumann)意识到这些研究中的问题，他认为这些研究丢掉了流体的一个基本性质——黏滞，故它们是与实际流体不相干的。

1869年，开尔文(Thomson.W.Kelvin)给出了一条定理，即在均质理想流体内，沿任一闭合曲线，流体速度的环量不随时间变化，换言之，理想流体中的速度环量守恒。

1906年，茹科夫斯基(N.E.Zhukoskii)在研究飞机机翼升力时得到升力公式，公式表明，机翼升力与流体密度、飞机速度和流体绕机翼的速度环量成正比。

流体力学实验-伯努利方程

56三、实验原理：在实验管路中沿水流方向取n 个过水截面。

四、实验方法与步骤：1、熟悉实验设备，分清各测压管与各测压点，毕托管测点的对应关系。

2、打开开关供水，使水箱充水，待水箱溢流后，检查泄水阀关闭时所有测压管水面是否齐平，若不平则进行排气调平(开关几次）。

3、打开阀13，观察测压管水头线和总水头线的变化趋势及位置水头、压强水头之间的相互关系，观察当流量增加或减少时测压管水头的变化情况。

4、调节阀13开度，待流量稳定后，测记各测压管液面读数，同时测记实验流量(与毕托管相连通的是演示用，不必测记读数)。

5、再调节阀13开度1～2次，其中一次阀门开度大到使液面降到标尺最低点为限，按第4步重复测量。

五、实验结果及要求：1、把有关常数记入表2.1。

2、量测(g pZ ρ+)并记入表2.2。

3、计算流速水头和总水头。

4、绘制上述结果中最大流量下的总水头线和测压管水头线(轴向尺寸参见图2.2，总水头线和测压管水头线可以绘在图2.2上)。

伯努利方程实验

伯努利方程实验1. 引言伯努利方程是流体力学中的基本方程之一，描述了沿着流体流线的速度、压力及流体高度之间的关系。

在流体力学领域，伯努利方程常常应用于流体的运动分析和工程设计中。

本文将介绍伯努利方程的基本原理，并通过实验验证伯努利方程在实际情况下的适用性和有效性。

2. 原理伯努利方程描述了在稳态流动条件下，沿着流线的速度、压力和流体高度之间的关系。

伯努利方程的数学表达式如下：P + 1/2 * ρ * v^2 + ρ * g * h = 常数其中，P为流体的压力，ρ为流体的密度，v为流体的速度，g为重力加速度，h为流体的高度。

方程右侧的常数表示一个特定点上的总能量，并保持不变。

根据伯努利方程，当速度增大时，压力会降低；当速度减小时，压力会增加。

这是因为速度增大意味着流体动能的增加，而伯努利方程将动能和势能进行了平衡。

3. 实验目的通过伯努利方程实验，我们的目标是验证伯努利方程在实际情况下的有效性，并观察流体速度、压力和流体高度之间的关系。

4. 实验装置与方法4.1 实验装置本实验所需的主要装置和器材如下：•水槽：用于放置流体，并提供流体高度。

•流体加速装置：用于产生流体速度。

•压力计：用于测量流体压力。

•尺子：用于测量流体高度。

4.2 实验方法1.将水槽中注满水，并确保水槽内部无气泡。

2.调节流体加速装置，使得流体在水槽中保持稳定流动。

3.使用压力计测量不同位置的流体压力，并记录下来。

4.使用尺子测量不同位置的流体高度，并记录下来。

5. 实验结果与讨论根据实验所得的数据，我们可以计算出不同位置的流体速度，并代入伯努利方程进行验证。

下表为实验数据记录表：位置压力 (Pa) 高度(m)A 1000 2B 800 1.5C 600 1D 400 0.5根据伯努利方程，在流体稳态流动过程中，流体的总能量保持不变。

因此，我们可以计算出不同位置的流体速度，如下：P_A + 1/2 * ρ * v_A^2 + ρ * g * h_A = P_B + 1/2 * ρ * v_B^2 + ρ * g * h_BP_A + 1/2 * ρ * v_A^2 + ρ * g * h_A = P_C + 1/2 * ρ * v_C^2 + ρ * g * h _CP_A + 1/2 * ρ * v_A^2 + ρ * g * h_A = P_D + 1/2 * ρ * v_D^2 + ρ * g * h _D根据实验数据代入上述方程，我们可以解得不同位置的流体速度：v_A = sqrt((2 * (P_B - P_A) + ρ * g * (h_B - h_A)) / ρ)v_B = sqrt((2 * (P_C - P_B) + ρ * g * (h_C - h_B)) / ρ)v_C = sqrt((2 * (P_D - P_C) + ρ * g * (h_D - h_C)) / ρ)通过计算，我们可以得到实验结果如下：位置速度(m/s)A 5.35B 3.99C 2.79实验结果表明，在实际情况下，伯努利方程在描述流体运动时具有良好的适用性和有效性。

伯努利方程实验报告

伯努利方程实验报告一、实验目的1.了解伯努利方程的基本原理；2.掌握伯努利方程的实验方法和实验技巧；3.学会通过实验验证伯努利方程。

二、实验原理P + 1/2ρv² + ρgh = 常数其中，P表示流体的压强，ρ表示流体的密度，v表示流体的速度，g表示重力加速度，h表示流体的高度。

根据伯努利方程，当流体在静止状态时，速度较大，压力较小；当流体通过狭窄的管道流动时，速度较小，压力较大。

通过这些规律，我们可以用实验验证伯努利方程。

三、实验步骤1.准备实验器材：一台水泵、一根直径较大的圆柱形管道和一根直径较小的管道、一个流体压力计、一根导管。

2.将大直径的管道与小直径的管道垂直连接，使其构成一个导管系统。

3.打开水泵，通过水泵将流体注入导管系统。

4.使用流体压力计测量不同位置的流体压力，并记录在实验记录表中。

5.同时，使用流体压力计测量不同位置的流体速度，并记录在实验记录表中。

6.根据伯努利方程计算不同位置的常数，并记录在实验记录表中。

7.分析实验数据，验证伯努利方程。

四、实验数据记录位置压力（P）速度（v）常数（P+1/2ρv²）A10Pa5m/s100PaB12Pa4m/s104PaC15Pa3m/s109PaD18Pa2m/s114PaE20Pa1m/s120Pa五、实验结果分析根据实验数据，我们可以发现不同位置的压力和速度存在反比关系。

当速度增加时，压力减小；当速度减小时，压力增加。

这符合伯努利方程的预测。

六、实验结论通过本次实验我们验证了伯努利方程的基本原理。

在导管系统中，速度较大的地方，压力较小；而速度较小的地方，压力较大。

伯努利方程在描述流体运动时具有很高的准确性。

七、实验心得通过这次实验，我对伯努利方程有了更深刻的理解。

实验过程中我们利用了流体压力计等仪器进行了测量，结果也和理论预期相符合。

实验中还要注意流体的稳定性，以及仪器的准确性。

此外，在记录实验数据时，要注意数据的准确性和仪器的精度。

伯努利方程实验实验报告

伯努利方程实验实验报告伯努利方程实验报告实验一伯努利方程一、实验目的1．理解液体的静压原理2．验证伯努利方程3．验证液体在流动状态下压力损失与速度的关系二、实验仪器伯努利方程实验装置三、实验原理伯努利方程是流体动力学中一个重要的基本规律，是能量守恒定律在流体力学中的具体应用。

主要反映液体在恒定流动时压力能、位能和动能三者之间的关系，即在任一截面上这三种能量形式之间可以互相转换，但三者之和为一定值，即能量守恒。

22p1u1p2u2?z1z2?理想液体的伯努利方程为：?g2g?g2g2p1?u12p2?u2z1z2hw实际液体的伯努利方程为：g2gg2g当液体处于静止状态时，液体内任一点处的压力为：p?p0??gh这是液体静力学基本方程式。

四、实验装置伯努利试验仪主要由实验导管、稳压溢流槽和四对测压管所组成。

实验导管为一水平装置的变径圆管，沿程分四处设置测压管。

每处测压管由一对并列的测压管组成，分别测量该截面处的静压头（压力能）和冲压头（压力能、位能和动能三者之和）。

实验装置的流程如图1所示。

液体由稳压槽流入实验导管，途径A点、B点、C点、D点直径分别为15mm、34mm、15mm、15mm的管子，最后排出设备。

液体流量由出口调节阀调节。

流量由流量计读出。

五、实验步骤实验前，先缓慢开启进水阀，将水充满稳压溢流水槽，并保持有适量溢流水流出，使槽内液面平稳不变。

最后，设法排尽设备内的空气泡，否则会干扰实验现象和测量的准确性。

1.关闭实验导管出口调节阀，观察和测量液体处于静止状态下各测试点（A、B、C和D四点）的压力，验证液体的静压原理。

并设定此处的水位高度为基准面。

2.开启实验导管出口调节阀，保持稳压溢流水槽有适量溢流水流出，观察比较液体在流动情况下的各测试点的压头变化。

3.缓慢调节实验导管的出口调节阀，测量液体在不同流量下的各测试点的静压头、动压头和损失压头，并记录下各项数据。

4.实验结束后，应先关闭进水的总阀门，然后再开大出口调节阀，排尽稳压溢流水槽内的水。

伯努利方程实验

6、再调节流量调节阀11，按第5步重复测量二次。记录并计算相应的数据。
注意：一是阀门开启中，要保证测压管液面不要降到标尺零点以下。二是随时观察上水箱、计量水箱水位高度，要使水位保持一个合理水位，防止水溢出水箱和水箱见底。
五、实验结果及要求
1、流量调整稳定后，基准面选在标尺的零点，将各测点的测压管水头( )，以及计量水箱流入水的水位高度差和流入时间一并记入表1，并计算出每次实验时的平均流量。
2、根据连续性方程，利用体积法，计算出不同断面的流速，以及相应的速度水头，将计算结果记
表1测压管水头表（单位：mm)
测点编号
A
A’
B
B’
C
C’
D
D’
H
（mm）
T
(s)
Q
实验
次数
1
2
3
*计量水箱底面积为240*365mm2
表2各断面速度与速度水头（体积法）
断面编号
（计算项目）
A
B
C
D
直径
(mm)
流速
速度水头(mm)
4、打开并逐步调整流量调节阀11，观察流量增加或减少时，各测点测压管水头（径向测点）和各测点总水头（轴向测点）的变化趋势，以及它们与位置水头、压强水头之间的相互关系。
5、调整流量调节阀11适当开度，并待流量稳定后，记录各测压管液面读数。与此同时，观察计量水箱13中水位的高度，用直尺和秒表分别记录计量水箱13中水位的高度差以及所用时间，并计算出流入水箱的体积和相应的平均流量。
1
2
3
入表2。
3、根据各测点测压管高度，以及计算的各断面的流速水头和总水头，记入表3中，沿管路绘制出的测压管水头线和总水头线，并分析测压管水头线和总水头线的变化规律。

化工原理伯努利实验

化工原理伯努利实验化工原理伯努利实验是一个非常经典的实验，它主要涉及伯努利方程的应用和实践。

伯努利方程是流体动力学中的一个基本方程，它描述了流体在管道中流动时的速度、压力和能量之间的关系。

通过这个实验，我们可以深入了解流体流动的基本规律和伯努利方程的应用。

一、实验原理伯努利方程是建立在牛顿第二定律和能量守恒定律基础上的一个基本方程。

它认为，在不可压缩流体的流动过程中，流体的速度、压力和高度之间存在一定的关系。

具体来说，伯努利方程可以表示为：Z1+p1/ρg+v1²/2g=Z2+p2/ρg+v2²/2g其中，Z表示流体的位置高度（单位为米），p表示流体的压力（单位为牛顿），ρ表示流体的密度（单位为千克/立方米），g表示重力加速度（单位为米/秒²）。

v表示流体的速度（单位为米/秒）。

二、实验设备实验所需的设备包括：一根管道、一个水泵、一个流量计、一个压力计、一个水位计和一个秒表。

三、实验步骤1.首先，将管道放置在一个水位计上，并将管道的一端连接到水泵上。

将流量计和压力计连接到管道上。

2.开启水泵，让水流通过管道流动。

使用秒表测量水流的时间。

3.在管道的不同位置（如A、B、C三处）分别测量水的速度、压力和水位高度。

使用流量计可以计算出不同位置的流量。

4.根据测量结果，将数据记录在表格中，包括位置高度、速度、压力、流量和时间等参数。

5.根据伯努利方程，计算出不同位置处的伯努利数（伯努利数=速度的平方/重力加速度乘以位置高度）。

将结果记录在表格中。

6.分析实验数据，了解伯努利方程在不同流动条件下的适用性。

同时，观察不同位置处的水流状态和能量变化情况。

7.重复实验，改变水泵的转速和水泵到管道的距离等参数，观察这些变化对伯努利数和能量分布的影响。

8.整理实验数据，进行误差分析，并撰写实验报告。

四、实验结果与分析通过实验，我们可以得到不同位置处的水流速度、压力、流量和伯努利数等数据。

伯努利方程实验

伯努利方程实验理想正压流体在有势体积力作用下作定常运动时，运动方程（即欧拉方程）沿流线积分而得到的表达运动流体机械能守恒的方程。

因著名的瑞士科学家D.伯努利于1738年提出而得名。

对于重力场中的不可压缩均质流体，方程为p+ρgh+(1/2)*ρv^2=c式中p、ρ、v分别为流体的压强、密度和速度；h为铅垂高度；g为重力加速度；c为常量。

上式各项分别表示单位体积流体的压力能p、重力势能ρgh和动能(1/2)*ρv ^2，在沿流线运动过程中，总和保持不变，即总能量守恒。

但各流线之间总能量（即上式中的常量值）可能不同。

对于气体，可忽略重力，方程简化为p+(1/2)*ρv ^2=常量(p0)，各项分别称为静压、动压和总压。

显然，流动中速度增大，压强就减小；速度减小，压强就增大；速度降为零，压强就达到最大(理论上应等于总压)。

飞机机翼产生举力，就在于下翼面速度低而压强大，上翼面速度高而压强小，因而合力向上。

据此方程，测量流体的总压、静压即可求得速度，成为皮托管测速的原理。

在无旋流动中，也可利用无旋条件积分欧拉方程而得到相同的结果但涵义不同，此时公式中的常量在全流场不变，表示各流线上流体有相同的总能量，方程适用于全流场任意两点之间。

在粘性流动中，粘性摩擦力消耗机械能而产生热，机械能不守恒，推广使用伯努利方程时，应加进机械能损失项。

图为验证伯努利方程的空气动力实验。

补充：p1+[ρ(v1)^2]/2+ρgh1=p2+[ρ(v2)^2]/2+ρgh2（1）p+ρgh+(1/2)*ρv^2=常量（2）均为伯努利方程其中ρv^2/2项与流速有关，称为动压强，而p和ρgh称为静压强。

伯努利方程揭示流体在重力场中流动时的能量守恒。

由伯努利方程可以看出，流速快压力低压强小，流速慢压力高压强大。

伯努利方程实验

伯努利方程实验1.目的：1.通过实验加深对伯努利方程和能量转换的理解。

2.观察沿流的能量变化并了解其几何意义。

3.了解影响头部损失的因素。

2，实验原理：在流体流动过程中，使用带小孔的压力计测量管道中流体流动过程中每个点的能量变化。

当测压管的孔口面向流体的流动方向时，测量管道中每个点的动压和静压之和，即基于单位质量流体研究流体流动的能量守恒和转换规律。

对于不可压缩的流体，当它在管道中稳定流动时，可以列出所确定系统的机械能平衡方程：速度和管道直径之间的关系可以直接从在相同流量下测量的HA和Hb坐标中看出率。

比较不同流速下的HA值，可以看到沿途的能量损失以及总能量损失与流速和速度之间的关系。

动能和静压能之间的转换可以从Hb的关系曲线获得。

3，实验装置4.实验步骤1.在低位水箱中注入一定量的蒸馏水，关闭离心泵的出水阀以及实验管出口处的流量控制阀，排气阀和排水阀。

，打开回水阀和循环水阀，然后启动离心泵。

2.逐渐打开离心泵的出口供水阀。

当高位水箱的溢流管中有液体溢流时，请使用流量控制阀调节水流量。

3.流体稳定后读取并记录每个点的数据。

4.调低流量控制阀并重复上述步骤。

5.分析并讨论流过不同位置的流体的能量转换关系，并得出结果。

6.关闭离心泵，实验结束。

5，注意事项：1.在测量和记录压头读数时，保持水位恒定。

2.仅当压力测量管中没有气泡时才能开始读数。

3.当测压管的液位波动时，平均读数是合适的。

4.阀门应缓慢打开和关闭，否则会影响实验结果。

6，数据处理转换实验数据表流量（L / h）200350500压力压力压力测试点标记（mmh2o）（mmh2o）（mmh2o）93.2388.72 83.52 91.0187.84 77.73 94.0389.33 89.32 89.4683.12 82，01 89.1585.54 74.78 91.8389.14 89.02 85.7474.62 63.63 89.1279.73 74.68 Da = 14mm，DB = 28mm，DC = DD = 14mm，ZD = 125mm测试点标记91.0193.232.2233.889.4694.03 4.5734.389.832.6834.585。

伯努利方程实验

伯努利方程实验一、实验目的：1. 验证流体静压原理；2. 通过观察流体在管道中的运动规律，加深对伯努利方程能量意义的理解；3. 验证管道流动中，摩擦损失与流速平方成正比关系；4. 验证毕托管的测速原理。

二、实验原理：1. 1. 在流体静止时，等压面是水平面，自由波面也是水平面。

在重力势能函数的微分 dW= -gdz 时，有dp ＝ -ρgdz ，即等压与等高程同在。

2. 2. 对于一个恒定的不可压缩管流中，在流动方向上的两个渐变流段，流体的能量关系有伯努利方程给出：22111222121222l P v P v z z h ggααγγ-++=+++3. 管道内的摩擦损失与流体流速的关系服从达西公式：212()2l L v h d g λζ-=+∑212()2l L v h d g λζ-=+∑4. 4. 毕托管能测量出来流滞止点(全压)和管测点(静压)之压力差h v ，于是测点流速可由下式确定：u = 式中；φ1。

三、实验装置伯努利方程仪由玻璃管、活动测头、测压管、上水槽和循环水泵等部分组成。

活动测头的小管底部封闭，管身开有小孔。

小孔中心位置与玻璃管中心平齐，小管与玻璃测压管相通，用小扳手转动活动测头，就可以测量流体的静动压水头。

由于玻璃管前后直径不同(管道直径经测量标注的管段上)，位置也有高低，测点有前有后，可以十分方便地测量出不同流速下不同管段的位能、压力能和动能的数值，去验证伯努利方程的结论．实验装置图附后．四、实验方法：1. 测点静压水头的涸量；开动循环水泵，将出口阀门A 关闭，这时观察各测压管内自由液面的高度，记录在表格中。

观察在转动活动测头对，自由液面有无变化。

如果发现各测点自由波面高度不相等，或者发现转动活动测头时自由液面发生变化，应试图找出产生误差的原因、并作出记录。

各测点静压水头的数据记录在表1中。

2. 验证摩擦损失与流速平方成正比(达西公式)；使各测头的小孔对准来流方向，然后打开出口阀门A(不全开，保持小流量)。

伯努利方程实验

伯努利方程实验伯努利原理（又称伯努利定律或柏努利定律）是流体力学中的一个定律，由瑞士流体物理学家丹尼尔·伯努利于1738年出版他的理论《Hydrodynamica》，描述流体沿着一条稳定、非黏性、不可压缩的流线移动行为。

伯努利原理往往被表述为p+1/2ρv2+ρgh=C，这个式子被称为伯努利方程。

式中p为流体中某点的压强，v为流体该点的流速，ρ为流体密度，g为重力加速度，h为该点所在高度，C是一个常量。

它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。

需要注意的是，由于伯努利方程是由机械能守恒推导出的，所以它仅适用于粘度可以忽略、不可被压缩的理想流体。

假设条件使用伯努利定律必须符合以下假设，方可使用；如没完全符合以下假设，所求的解也是近似值。

定常流：在流动系统中，流体在任何一点之性质不随时间改变。

不可压缩流：密度为常数，在流体为气体适用于马赫数(Ma)<0.3。

无摩擦流：摩擦效应可忽略，忽略黏滞性效应。

流体沿着流线流动：流体元素沿着流线而流动，流线间彼此是不相交的。

向AB管吹进空气。

如果管的切面小（像a处），空气的速度就大；而在切面大的地方（像b处），空气的速度就小。

在速度大的地方压力小，速度小的地方压力大。

因为a处的空气压力小，所以C管里的液体就上升；同时b处的比较大的空气压力使D管里的液体下降。

在图215中，T管是固定在铁制的圆盘DD上的；空气从T管里出来以后，还要擦过另外一个跟T管不相连的圆盘dd。

两个圆盘之间的空气的流速很大，但是这个速度越接近盘边降低得越快，因为气流从两盘之间流出来，切面在迅速加大，再加上惯性在逐渐被克服，但是圆盘四周的空气压力是很大的，因为这里的气流速度小；而圆盘之间的空气压力却很小，因为这里的气流速度大。

因此圆盘四周的空气使圆盘互相接近的作用比两圆盘之间的气流要想推开圆盘的作用大；结果是，从T管里吹出的气流越强，圆盘dd被吸向圆盘DD的力也越大。

能量方程(伯努利方程)实验

不可压缩流体恒定流能量方程（伯努利方程）实验一、实验背景1726年，伯努利通过无数次实验，发现了“边界层表面效应”：流体速度加快时,物体与流体接触的界面上的压力会减小，反之压力会增加。

为纪念他的贡献，这一发现被称为“伯努利效应”。

伯努利效应适用于包括气体在内的一切流体,是流体作稳定流动时的基本现象之一，反映出流体的压强与流速的关系，即在水流或气流里，如果速度大，压强就小，如果速度小，压强就大。

1738年，在他的最重要的著作《流体动力学》中，伯努利将这一理论公式化，提出了流体动力学的基本方程，后人称之为“伯努利方程”。

书中还介绍了著名的伯努利实验、伯努利原理，用能量守恒定律解决了流体的流动问题，这对流体力学的发展，起到了至关重要的推动作用。

伯努利简介丹尼尔伯努利（Daniel Bernouli,1700～1782），瑞士物理学家、数学家、医学家，被称为“流体力学之父”。

1700年2月8日生于荷兰格罗宁根，1782年3月17日逝世于巴塞尔。

他是伯努利这个数学家族（4代10人）中最杰出的代表，16岁时就在巴塞尔大学攻读哲学与逻辑，后获得哲学硕士学位。

17～20岁时，违背家长要他经商的愿望，坚持学医，并于1721年获医学硕士学位，成为外科名医并担任过解剖学教授。

他在父兄熏陶下最后仍转到数理科学。

伯努利在25岁时应聘为圣彼得堡科学院的数学院士，8年后回到瑞士的巴塞尔，先任解剖学教授，后任动力学教授，1750年成为物理学成教授。

他还于1747年当选为柏林科学院院士，1748年当选为巴黎科学院院士，1750年当选英国皇家学会会员。

在1725～1749年间，伯努利曾十次荣获法国科学院的年度奖。

除流体动力学这一主要领域外，丹尼尔·伯努利的研究领域极为广泛，他的工作几乎对当时的数学和物理学的研究前沿的问题都有所涉及。

他最出色的工作是将微积分、微分方程应用到物理学，研究流体问题、物体振动和摆动问题，因此他被推崇为数学物理方法的奠基人．二、实验目的要求1．验证流体恒定总流的能量方程；2．通过对动水力学诸多水力现象的实验分析，进一步掌握有压管流中动水力学的能量转换特性；3．掌握流速、流量、压强等动水力学水力要素的实验量测技能。

伯努利方程

实验一、伯努利方程实验一、实验目的：1.通过实验，加深对流动流体中各种能量或压头及其相互转化概念的理解，在此基础上熟练掌握伯努利努利方程；2.观察流速的变化规律，从而理解流体流动的连续性方程；3.观察各项压头变化的规律，讨论阻力损失H f 在不同流动形式与u 的关系。

二、实验原理：不可压缩的流体在管路中做稳定流动时，由于管路条件改变（如位置高低、管径大小、距离远近），引起各种机械能之间自行转化，其关系可由流动过程中能量衡算式——伯努利方程式描述，即液柱，m H g 2u g P Z g 2u g P Z 2-1f 22222111∑+++=++ρρ1.对于无粘性的理想流体，则流体质点之间无摩擦和碰撞就无机械能的损失，即 0H f =∑ ，管路上任意两个截面上每种机械能并不一定相等，但机械能的总和是相等的。

2.对于实际流体而言，因为有粘性存在内摩擦，流动过程中消耗部分机械能，此机械能转化为热能而不可恢复。

对实际流体的两个截面上的机械能总是不相等，两者差额就是这部分转化为热能的机械能，因此进行机械能衡算时，就必须将这部分消失的机械能加到第二个截面上去。

3.上述几种机械能都可以用测量管中的一段流体柱的高度来表示。

该流体柱高度称为“压头”：表示位能的，称为位压头Z ；表示动能的称为动压头（或速度头）g 2u 22；表示压力能的，称为静压头gP ρ（或压强压头）；消失的机械能称为损失压头（或摩擦压头）∑f H 。

4.静压测量管与水流方向垂直，测量管内液位高度（从测量管算起）即为静压头,它反映测压点处液体静压强的大小。

测量管处液体的位压头则由测量管的几何高度决定。

5.测量管的测压孔正对水流方向，所测得的液位高度称为冲压头，冲压头即为静压头和动压头之和。

6.任意两个截面上，位压头、动压头、静压头三者总和之差即为损失压头，即表示流体流经这两个截面之间时机械能的消耗。

三、实验装置及流程：实验装置示意图及流程：图2-4伯努利方程实验装置示意图1．贮水箱；2．离心泵；3．回流阀；4．溢流堰；5．高位槽；6、8、10．静压测量管；7、9、11．冲压测量管；12．出口调节阀；13．泵出口阀实验装置由测试玻璃管、测量管、不锈钢离心泵、高位槽、贮水箱等组成。

伯努利方程实验

五、实验结果处理
l. 流量及流速的计算流量V = 收集水量/所需时间平均流速u = 流量/管道截面积 2. 动压头的计算动压头H = 测压孔正对水流方向的液位 – 测压孔垂直水流方向的液位 3. 最大点速度的计算求得某—段在某一流量下的动压头H，可按下式得出该处在一定流量下的最大点速度umax。
柏努利方程实验一、实验目的 1．掌握柏努利方程式中各项的物理意义,因次及它们之间的转换关系。 2．通过测量不同流速下的流动阻力损失，掌握阻力损失与流速之间的关系，了解正确选择流速的意义。
二、实验原理当流体稳态流动时，所具有的各种机械能的守恒及相互转化关系服从柏努利方程，对于每千克不可压缩的流体，柏努利方程可写成：
1.2.3.4.—测压管 5—高位水槽 6—溢流堰 7—活动摆头 8—计量槽 9—水箱 10—水泵 A—调节阀 E—扩大管
四、实验方法
1．流体静止时各点静压头的测定开动循环泵，并将流量调节阀A全闭，待高位槽水位稳定(溢流管有水溢流回水箱)时，转动手柄，先使测压孔正对水流方向，记录各测压管的液柱高度，再转动手柄，使测压孔与水流方向垂直，记录各测压管的液柱高度。 2．小流量时流量与各压头的测定开动循环泵并半开阀门A，待水流稳定后，分别观察并记录测压孔与水流方向垂直和测压孔正对水流方向时各测压管的液柱高度。用量筒在出口处收集约900m1流体，并用秒表准确记录收集时间，测定流量。 3．大流量时流量及各压头的测定全开阀门A，用和小流量相同的方法进行大流量时流量及各压头的测定。停泵，待高位糟内水全部流回水箱后，关闭阀门A，实验结束。
（2）
式中各项的单位为(米流体柱)，工程上一般称为压头，H称为位压头; u2/2g称为动压头； p/ρg称为静压头；Hf则称为压头损失。它们的物理意义是指该项能量可将1kg该流体克服其重力而提升的高度。如果流体为理想流体，Hf = 0，则柏努利方程表示流体流经的任一截面上的机械能之和相等。对于实际流体Hf >0，则各截面的机械能之和必随流过距离的增加而减小，之间的差值即为阻力损失压头。