自动控制常见MATLAB函数的应用
MATLAB在《自动控制原理》课程教学中的应用
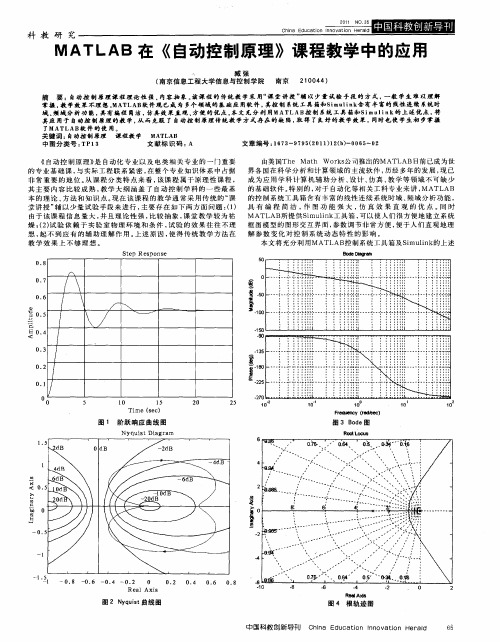
【】俞 倩 兰 . 用 MA A 辅 助 Ⅸ 5 利 TL B 自动控 制原 理 》 学 [ . 教 J 常熟 理 工 】 学院 学 报 , 0 8 20.
4 5 6 7 8 9 1
6 6
中 国科教创 新导刊 C i d c t n I o a in H r l hn E u a i n v t e ad a o n o
参 考 文 献
[】刘永 强 , 1 董翠 敏 . 谈Ⅸ自动 控 制原 理 》 程 教 学改 革 【】 湖南 农 浅 课 J. 机 , 0 8 1 20 ,. []胡 寿 松 . 2 自动 控 制 原 理 ( 5 ) . 学 出 版 社 , 0 7 6 第 版 【 科 M】 20 , . 【]张志 涌 . 3 精通 MA L B . 版 [ . T A 6 5 M】北京 航 空航 天 出版 社 , 0 3 20 . [1朱 成 志 . 4 MATLAB在 自动 控 制 原理 理 论 教 学 中的 应 用【】 铜陵 J. 职 业 技 术 学 院 学报 , 0 . 2 08
)
=
[() ef+
r +
]
Ke +ie) Kdt P)K[ +ae) ( t (
() 然 以 传递 函数 为 G s i 2仍 ()
的线 性 系统 为例 , 用 利 以 开环 传递 函数 为 G() 2 0 s =— +1— 0的单 位 反 馈 系 统 为 例 s s+2
利用 S mu i k i l 提供 的P D 块 , 建 系 统框 图如 图5 n I模 搭 N示 。 双 击 P D控制 模 块 , 得 到 函数 参 数 模 块 , 而 可 直 接 对P D调 I 可 进 I 节 器 的 三 个 参 数 , , 进 行 调 节 , 到 系 统 不 同 的 阶跃 响应 曲 得 线 。 如 当取 K =1 , i 0 , a 0时 , 得 到 如 下 曲线 ( 图6 。 例 0 K =1 0K =1 可 如 ) 通 过 不 断 调 整三 个 参 数 , 应 地 可 得 到 不 同 的 阶 跃 响 应 函数 , 相 进 而 研 究 参 数 变 化 对 系 统输 出 的 影 响 , 这里 不 再 一 一 罗列 。 当然 , MAT AB 件 的功 能 不局 限于 上 述 两 个方 面 。 于更 深 L 软 至 层次 的应 用 , 要 结 合 具 体 课 程 内 容 和 教 学 目标 要 求 加 以 进 一 步 需 的分析 , 这里 不 再 一 一 赘 述 。
matlab中pid控制器的应用实例

matlab中pid控制器的应用实例Matlab中PID控制器的应用实例引言PID控制器是一种常用的控制器,可以广泛应用于自动控制系统中。
其中,P代表比例,I代表积分,D代表微分。
PID控制器通过对误差、误差的积分和误差的微分进行加权求和,以便更好地控制系统的输出。
在本文中,我们将使用Matlab来演示PID控制器的应用实例。
我们将从控制物理实验中的水位控制系统开始,然后详细介绍PID控制器的原理和参数调整,最后使用Matlab进行仿真实验和结果分析。
一、实验背景我们考虑一个简单的水位控制系统。
系统由一个水箱和一个控制阀组成。
当水箱的水位低于设定水位时,控制阀将打开,往水箱中注水,当水位达到设定水位时,控制阀将关闭。
我们的目标是设计一个PID控制器,以便精确控制水箱中的水位。
二、PID控制器介绍在介绍PID控制器之前,我们需要了解一些基本的概念。
1. 比例控制(P)比例控制是根据误差的大小来调整控制量的大小。
比例增益参数Kp用于调整误差和控制量之间的比例关系。
控制量可通过以下公式计算:Control = Kp * Error其中,Error是设定值与测量值之间的差异。
2. 积分控制(I)积分控制用于减小系统的稳态误差。
积分增益参数Ki用于计算控制量的积分部分。
控制量可通过以下公式计算:Control = Kp * Error + Ki * \int Error dt其中,\int Error dt表示误差的积分。
3. 微分控制(D)微分控制用于减小系统的瞬态误差。
微分增益参数Kd用于计算控制量的微分部分。
控制量可通过以下公式计算:Control = Kp * Error + Ki * \int Error dt + Kd * \frac{{dError}}{{dt}}其中,\frac{{dError}}{{dt}}表示误差的微分。
三、PID控制器参数调整PID控制器中的三个参数(Kp,Ki,Kd)对控制器的性能有着重要的影响。
matlab在自动控制中的应用

matlab在自动控制中的应用
Matlab在自动控制中有广泛的应用。
以下是几个常见的应用
领域:
1. 系统建模和仿真:Matlab可以用于系统建模和仿真,可以
根据实际物理系统的特性来建立数学模型,并通过仿真来验证系统的性能。
2. 控制系统设计:Matlab提供了丰富的控制系统设计工具箱,可以用于设计各种类型的控制器,如比例-积分-微分(PID)
控制器、线性二次调节器(LQR)等。
3. 系统分析和优化:Matlab可以用于分析控制系统的性能,
如稳定性、鲁棒性和灵敏度等。
还可以用于系统参数优化,通过调整控制器的参数来达到期望的控制效果。
4. 多变量控制系统:Matlab可以处理多变量控制系统,可以
对多输入多输出(MIMO)系统进行建模、仿真和控制设计。
5. 自适应控制:Matlab提供了自适应控制工具箱,可以用于
设计具有自适应性能的控制器,可以根据系统动态特性自动调整控制参数。
6. 状态估计和观测器设计:Matlab可以用于设计状态估计器
和观测器,用于估计系统的状态变量,从而实现对系统的观测和控制。
7. 非线性控制系统:Matlab可以处理非线性控制系统,可以
用于建立非线性控制系统的数学模型,并进行仿真和控制设计。
总的来说,Matlab在自动控制中提供了丰富的工具和功能,
可以帮助工程师和研究人员进行控制系统的分析、建模、仿真和控制设计等工作。
MATLAB在“自动控制原理”课程中的应用研究

HEBEINONGJI摘要:“自动控制原理”是电气与自动化专业重要的专业基础课,内容抽象、复杂,学生理解困难。
近年来,随着MATLAB引入自动控制原理教学实践中,利用其强大的数值计算及绘图功能,对教学形式和内容进行了有力改革,从而有效地提高了课堂教学效率及教学效果。
关键词:自动控制原理;MATLAB;教学改革MATLAB在“自动控制原理力课程中的应用研究河北农业大学李珊珊孔德刚弋景刚袁永伟刘江涛引言自动控制原理是电气与自动化专业一门重要的专业技术基础课,该课程在内容体系中起着承上启下的作用。
主要介绍讨论了单输入一单输出定常系统的控制问题,讲授经典控制理论的三大分析方法一时域分析法、根轨迹分析法和频域分析法,自动控制系统综合与校正的一般方法和非线性系统等内容,课程具有一定的抽象性,包含大量的数学内容和复杂计算。
通过学习,要求学生系统掌握自动控制的基本原理和基本方法,并能对控制系统进行定性分析、定量计算和综合设计。
学生普遍反映难以理解,内容枯燥。
基于此,需要对教学内容及教学方法进行更新,在教学中引入了MATLAB编程语言。
1现代教育理念1.1以学生为中心美国人本主义心理学家卡尔•罗杰斯于1952年提出“以学生为本”的教育理念,主张促进学生个性发展、人格完善和潜能发挥,使他们能够愉快地、创造性地学习和工作。
目前,这种教育理念仍然作为一种基本的现代教育理念。
1.2创新发展的理念党的十八届五中全会提出“创新、协调、绿色、开放、共享”五大发展理念,其中创新被置于首位。
随着互联网技术的迅速发展,知识更新换代速度加快,对复合创新型人才的需求愈发强烈,人才培养要摒弃传统的知识灌溉模式,应将教学重点转移到重视研究方法学习、培养创新精神上。
1.3OBE教育理念OBE为"Outcomes-based Education"的缩写,OBE教育理念即基于成果导向的教育理念。
美国的Spady在《基于产出的教育模式:争议与答案》一书中把OBE定义为“关注和组织教育体系,以确保学生在未来的生活中获得实质性的成功经验”。
自动控制原理MATLAB仿真实验(于海春)

自动控制原理MATLAB仿真实验(于海春)实验一典型环节的MATLAB仿真一、实验目的1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK 的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB软件,在命令窗口栏“>>”提示符下键入imulink命令,按Enter键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK仿真环境下。
2.选择File菜单下New下的Model命令,新建一个imulink仿真环境常规模板。
图1-1SIMULINK仿真界面图1-2系统方框图3.在imulink仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击imulink下的“Continuou”,再将右边窗口中“TranferFen”的图标用左键拖至新建的“untitled”窗口。
2)改变模块参数。
在imulink仿真环境“untitled”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的imulink的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math”右边窗口“Gain”的图标。
4)选取阶跃信号输入函数。
用鼠标点击imulink下的“Source”,将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口,形成一个阶跃函数输入模块。
5)选择输出方式。
控制系统matlab常用函数的使用

4.residue多项式模型转化为部分分式展开式模型,或反过来,根据输入参数不同而异5.zp2tf6.tf2zp7.series串联连接8.parallel并联连接10.linmod将结构图模型(Simulink结构图)转化成状态空间模型先建立simulink结构图,保存在当前目录下,文件名取为“sysmodel.mdl”如图0所示。
编写程序,便可得到图0对应模型的解析表达。
图1图2可见当w一定时,系统随着阻尼比ζ的增大,闭环极点的实部在s左半平面的位置更加远n离原点。
图3可见,当ζ一定时,随着w增大,系统响应加速,振荡频率增大,系统调整时间缩短,但n是超调量没变化。
19.spline插值函数,用于由若干实验点估算实验点之外的函数值,下面的程序由插值函数“rltool ”命令,然后回车即可。
24. rlocfind 对给定根计算对应的增益与极点25. nichols 绘制尼科尔斯图,尼科尔斯图的作用同伯德图,不过纵坐标表示的是|G(jw)|,而横坐标则为∠G(jw)。
26. dcgain 求连续系统的稳态增益。
27. residue 部分分式展开。
28. linspace 构造线性分布的向量。
29. roots 求多项式根。
30. limit 求极限,可用于求解系统的稳态位置、速度与加速度误差系数。
例:已知某稳定单位负反馈系统的闭环传递函数为25()556s s s Φ=++。
试求系统的稳定位置、速度与加速度误差系数Kp 、Kv 和Ka 。
32.pade用于近似求取纯延迟时间函数33.tf2ss传递函数到状态空间转换34.subs变量替换参考文献[1]熊晓君.自动控制原理实验教程(硬件模拟与MATLAB仿真)[M].北京:机械工业出版社, 2009.[2]黄忠霖. 自动控制原理的MATLAB实现[M]. 北京:国防工业出版社,2007.谭彩铭2012-3-27南京理工大学基础实验楼。
智能控制及MATLAB实现—水箱液位模糊控制仿真设计

智能控制及MATLAB实现—水箱液位模糊控制仿真设计智能控制是一种利用先进的智能技术和算法来实现自动控制的方法。
在智能控制中,模糊控制是一种常见且有效的方法之一、模糊控制通过将模糊逻辑应用于控制系统中的输入和输出,根据模糊规则来进行决策和控制。
水箱液位控制是一个典型的控制问题,常常用于工业和民用领域中的自动化系统。
在许多控制应用中,水箱液位的控制是一个关键的问题,因为它需要根据系统的液位情况来实现稳定的控制。
在模糊控制中,首先需要建立一套模糊规则系统,该系统包括模糊化、模糊推理和解模糊化这三个步骤。
模糊化是将实际输入转换为模糊集合的过程。
在水箱液位控制中,可以将液位分为低、中和高三个模糊集合。
通过将实际液位值映射到这些模糊集合中的一个,来表示液位状态。
模糊推理是根据一组模糊规则,将模糊输入转换为模糊输出的过程。
通过将输入和规则进行匹配,确定输出的模糊集合。
在水箱液位控制中,可以使用如下规则:如果液位低且液位变化小,则控制信号为增大水流量;如果液位高且液位变化大,则控制信号为减小水流量;如果液位中等且液位变化适中,则控制信号为不变。
解模糊化是将模糊输出转换为实际的控制信号的过程。
在水箱液位控制中,可以使用模糊加权平均值的方法来进行解模糊化。
通过将模糊集合和其对应的权重进行加权平均计算,得到最终的控制信号。
在MATLAB中,可以使用Fuzzy Logic Toolbox来实现水箱液位模糊控制仿真设计。
首先需要建立输入和输出的模糊化和解模糊化函数,然后根据实际的模糊规则,构建模糊系统。
最后通过设定输入的模糊值,使用模糊系统进行推理和解模糊,得到最终的控制信号。
总结起来,智能控制及MATLAB实现水箱液位模糊控制仿真设计包括建立模糊规则系统,进行模糊化、模糊推理和解模糊化三个步骤,通过Fuzzy Logic Toolbox来实现模糊控制系统的构建和仿真。
通过利用模糊控制的方法,可以实现水箱液位的自动稳定控制,并提高了控制系统的鲁棒性和适应性。
第八章 matlab在自动控制原理中的应用

>> get(s1) num: {[0 0 3 4 5]} den: {[1 3 5 0 9]} Variable: 's' Ts: 0 ioDelay: 0 InputDelay: 0 OutputDelay: 0 InputName: {''} OutputName: {''} InputGroup: [1x1 struct] OutputGroup: [1x1 struct] Notes: {} UserData: []
>> s3=ss(s1) a= x1 x2 x3 x4 x1 -3 -1.25 0 -1.125 x2 4 0 0 0 x3 0 2 0 0 x4 0 0 1 0 b= u1 x1 1 x2 0 x3 0 x4 0 c= x1 x2 x3 x4 y1 0 0.75 0.5 0.625 d= u1 y1 0 Continuous-time model.
>> s4=ss(s2) a= x1 x2 x3 x4 x1 -1.891 1.737 -0.745 0 x2 -1.737 -1.891 -0.05194 0 x3 0 0 0.3913 2.201 x4 0 0 -0.5503 0.3913 b= u1 x1 0 x2 0 x3 0 x4 1.651 c= x1 x2 x3 x4 y1 2.714 0 0.8255 0 d= u1 y1 0 Continuous-time model.
使用时,只要输入环节的名称,不必输入其参 数矩阵。
控制系统工具箱LTI对象运算优先等级为 “状态空间>零极增益>传递函数”
实现的算法:以并联为例 算法:
f ( s) f A ( s) g B ( s) f B ( s) g A ( s) W ( s) g ( s) g A ( s) g B ( s)
自动控制原理Matlab仿真应用

控制系统的MATLAB 仿真1 MATLAB 简介MATLAB 是Mathworks 公司开发的一种集数值计算、符号计算和图形可视化三大基本功能于一体的功能强大、操作简单的优秀工程计算应用软件。
MATLAB 不仅可以处理代数问题和数值分析问题,而且还具有强大的图形处理及仿真模拟等功能。
从而能够很好的帮助工程师及科学家解决实际的技术问题。
MATLAB 的含义是矩阵实验室(Matrix Laboratory ),最初主要用于方便矩阵的存取,其基本元素是无需定义维数的矩阵。
经过十几年的扩充和完善,现已发展成为包含大量实用工具箱(Toolbox )的综合应用软件,不仅成为线性代数课程的标准工具,而且适合具有不同专业研究方向及工程应用需求的用户使用。
MATLAB 最重要的特点是易于扩展。
它允许用户自行建立完成指定功能的扩展MATLAB 函数(称为M 文件),从而构成适合于其它领域的工具箱,大大扩展了MATLAB 的应用范围。
目前,MATLAB 已成为国际控制界最流行的软件,控制界很多学者将自己擅长的CAD 方法用MATLAB 加以实现,出现了大量的MATLAB 配套工具箱,如控制系统工具箱(control systems toolbox ),系统识别工具箱(system identification toolbox ),鲁棒控制工具箱(robust control toolbox ),信号处理工具箱(signal processing toolbox )以及仿真环境SIMULINK 等。
(1) MATLAB 的安装本节将讨论操作系统为Microsoft Windows 环境下安装MATLAB6的过程。
将MATLAB6的安装盘放入光驱,系统将自动运行auto-run.bat 文件,进行安装;也可以执行安装盘内的setup.exe 文件启动MATLAB 的安装程序。
启动安装程序后,屏幕将显示安装MATLAB 的初始界面,根据Windows 安装程序的常识,不断单击[Next],输入正确的安装信息,具体操作过程如下:输入正确的用户注册信息码;选择接收软件公司的协议;输入用户名和公司名;选择MATLAB 组件(Toolbox );选择软件安装路径和目录;单击[Next]按钮进入正式的安装界面。
MATLAB在《自动控制原理》教学中的应用

{
l
鬻
j一
。
图 1 单 位 负 反 馈 控 制 系统 特 性 曲线
1 教 学 现 状 及 改进 方 法 的 图解 方法 , 绘 制根 轨 迹 步 骤 较 多 , 但 需要 求 出 系 统 的零 、 点 和 分 极 《 自动控制原理》 课程 内容理论性强、 公式应用灵活、 前后联 系紧 离 点 。 系统 传 递 函数 的分 子 或 分 母 为 高 次 方程 时 , 用代 数法 求得 当 使 密 , 要应 用 大 量 的 物 理及 高等 数 学 相 关 知 识 。 与成 人 教 育 中 学 员 且 这 系统 的零 、 点和 分离 点 比较 困难 。 系 统 零 、 点 和 分 离 点 若 不 能确 极 极 学 习基 础 参 差 不 齐形 成 鲜 明 的矛 盾 。 仅通 过~ 张 黑 板 一 支 粉 笔 , 部 按 定 , 轨 迹 也 就 无 法 绘 制 。 MA L B 工具 可 以 很 方 便 绘 制 控 制 系 统 根 TA 就 班 传 统 教 学 方式 , 绝 大 多数 学 员 感 到 课 程 内容 抽 象 , 以理 解 。 使 难 的根 轨 迹 , 数 命 令 r c sg。 同 时 , 过 gi 选 项 可 得 到 等 函 l u () o 通 r d的 随着 计 算 机 多媒 体 技 术 在 教 学 中 的 应 用 ,教 学 软 件 在 一 定 程 度 上 丰 线族和等 c ^ 族 的根 轨迹 。 ) 线 富了教学手段 , 由于 自动控制原理 实例的复杂性 , 但 现有 的《 自动控 制原理》 计算机多媒体软件 , 并不能从根 本上解决本课程 的理论教学 与 工 程 实践 脱 节 的 问题 。 制 闭环 系统 的根 轨迹 。 MA L 丁 AB是 由 Mah ok tW rs公 司开 发 并 推 出 的 程 序 计 算 语 言 , 在 MA L B 中编 程 序 为 TA 它不仅集数值分析 、 阵运算 、 号处理和 图形显示于一体 , 矩 信 并且一 n m=[ 1 : u 1, 】 直 面 向控 制 理 论 和 控 制 工 程 为其 核 心应 用 领 域 。 目前 MA L 的应 T AB d =c n ( 4, 0】【 3) en o v【 1, 8, ,1, 】; 用 已从 经典 控 制 理 论 的应 用 发展 到 最 优 控 制 、 系统 辨 识 、 型 预 测 控 模 g= f u , e ) t( m d n ; n 制 、 棒 控 制 、 经 网 络控 制 、 鲁 神 模糊 控 制 等领 域 ” 】 。 r c sg l u () o 2M T A A L B在《 自动控制原理》 教学 中的应用 MA L B包含 了进行控 制系统 分析 与设计所 必须 的工具 箱函 TA 数 , 以分 析 连 续 系统 , 可 以 分析 离 散 系 统 , 可 以进 行 极 点 配 置 可 也 并 控 制器 设 计 和最 优 控 制 系统 设 计 等 多 项 操作 。现 以连 续 系统 中 的 时 域 分析 法 、 域 分 析 法 及 根 轨 迹 分析 法 为例 介 绍 。 频 21 时 域 分析 应 用 [ . 3 1时域 分 析 法 是 根 据 自动 控 制 系统 微 分 方 程 求解 系统 动 态 响应 的过 程 曲线 以及 响 应指 标 , 运用 解 析 法进 行 分 析 时 , 数 学 推 导 过 程 比较 复 杂 , 其 需要 进 行 大 量 的人 工 计 算 , 为课 作 堂 教 学 , 在 计 算 和 推 导 过程 中花 费过 多的 时 间 , 师 的教 学 容 易显 若 教 得 主 次 不 清 , 生 往 往 把 注 意 力集 中在 数 学 推 导 过 程 上 , 对 真 正 需 学 而 要 理 解 和 掌 握 的概 念 规 律 , 却被 忽 略 了。 图 2 某 单 位 负 反 馈 系 统 根 轨迹 图 如 : 单 位 负 反 馈 控 制 系统 该 系统 的 闭环 传 递 函 数 为 某 3 MA L B在 自动 控 制 原 理 中的 合 理 应 用 TA
matlab_自动控制传递函数计算幅值对应频率的方法

matlab 自动控制传递函数计算幅值对应频率的方法1. 引言1.1 概述本篇文章旨在介绍在自动控制系统中计算幅值对应频率的方法,并重点关注利用Matlab进行计算的技巧和步骤。
自动控制传递函数是控制系统设计和分析中常用的数学模型,对于了解系统稳定性、频率响应以及滤波器设计等方面起着至关重要的作用。
1.2 文章结构本文分为五个主要部分,首先在引言部分简要概述了文章内容和结构。
接下来,在第二部分将详细介绍什么是自动控制传递函数以及其在控制系统中的重要性。
第三部分将讨论幅值与频率之间的关系以及幅值对应频率在控制系统中的作用,并通过实际案例进行深入分析。
第四部分将重点介绍Matlab中计算幅值对应频率的方法,包括频域分析工具的介绍、使用Matlab进行计算的步骤以及示例演示与讨论。
最后,第五部分总结本文的结论并展望未来研究方向和工作。
1.3 目的本篇文章旨在帮助读者了解自动控制传递函数的定义和意义,并特别关注幅值对应频率的重要性。
通过介绍Matlab中计算幅值对应频率的方法,读者可以更加方便地进行相关计算和分析。
文章还将通过实际案例和示例演示,帮助读者深入理解幅值对应频率在控制系统中的作用,并为读者提供未来研究方向和工作的展望。
2. 自动控制传递函数:2.1 什么是自动控制传递函数:自动控制传递函数是描述线性时不变系统在频域中输入与输出之间关系的数学模型。
它是一种对系统进行建模和分析的标准工具。
通过使用自动控制传递函数,我们可以获得系统的稳定性、响应速度以及频率响应等关键信息,从而更好地设计和优化控制系统。
2.2 控制系统的模型表示:控制系统通常由多个组件组成,包括传感器、执行器和控制器等。
为了方便分析和设计,可以将整个控制系统抽象为一个输入输出之间的数学模型。
这个模型通常可以表示为一个或多个差分方程或微分方程,并用传递函数进行描述。
2.3 传递函数的定义与意义:传递函数是描述线性时不变系统频率响应特性的重要工具。
matlab在自动控制原理中的应用毕业论文

建筑与技术学院MATLAB在自动控制原理中的应用毕业设计(论文)原件及使用授权说明原始语句我保证我提交的毕业设计(论文)是我在导师指导下所做的研究工作和成果。
据我所知,除文中特别标注和注明的地方外,不包含其他人或组织已发表的研究成果,也不包含我曾用来与其他教育机构取得学位或学历的材料。
对本研究有所帮助和贡献的个人或集体,都做出了明确的解释,并表达了对本文的兴趣。
作者签名:日期:讲师签名:日期:授权说明本人完全理解学校关于毕业设计(论文)收集、保存和使用的规定,即按照学校的要求提交毕业设计(论文)的印刷版和电子版;学校有权保留毕业设计(论文)的印刷版和电子版,并提供目录检索和阅读服务;学校可以采用影印、减印、数字化或其他复制手段保存论文;在不盈利的前提下,学校可以发表论文的部分或全部内容。
签名:日期:目录摘要3第1章绪论41.1研究目的41.2相关研究现状41.3研究方法41.4本次设计的主要容以与目前学术届近一步研究的趋势61. 4. 1本次设计的主要容61. 4. 2目前学术界近一步研究的趋势6第2章开发工具82.1 MATLAB编程语言发展历程与特点82.2 MATLAB系统构成92.3 MATLAB的GUI设计102.4本章小结11第3章控制系统性能指标与校正装置分类123.1控制系统的性能指标123. 2控制系统校正的分类143.3本章小结16第4章基于频率法的控制系统的校正设计174.1基于频率法的串联超前校正174.1.1 串联超前校正网络设计的算法步骤174.1.2超前校正装置的评价184.2基于频率法的串联滞后校正184.2.1串联滞后校正网络设计的算法步骤194. 2. 2滞后校正装置的评价194.3基于频率法的串联超前滞后校正194.3.1串联超前滞后校正网络设计的算法步骤204.3.2滞后超前校正装置的评价204. 4三种校正方法的效果对比214.5本章小结21第5章控制系统的仿真与校正对比分析225.1程序方式225. 1. 1控制系统校正前的性能指标225. 1. 2校正装置的设计过程与其性能指标的仿真285. 1. 3控制系统校正后的性能指标305.2Multisim电路设计仿真方式38第6章设计总结416. 1总结416. 2心得41附英文文献:43摘要本文将讨论如何根据用户对自动控制系统的要求来设计串级补偿器,这具有非常重要的现实意义。
matlab ode45函数用法

MATLAB ODE45函数用法在MATLAB中,ODE45函数是用于求解常微分方程(ODE)的一种常用工具。
它采用龙格-库塔法(Runge-Kutta)来数值求解微分方程,通常适用于非刚性的微分方程问题。
在本文中,我们将深入探讨ODE45函数的用法,并通过具体例子来演示它的实际应用。
1. ODE45函数概述ODE45函数的基本语法如下:```matlab[t, y] = ode45(@odefun, tspan, y0)```其中,@odefun是一个用户自定义的函数,用于定义微分方程的形式;tspan是时间范围;y0是初始条件。
这个函数返回两个参数:t是时间向量,y是对应时间点的解向量。
2. ODE45函数的详细用法2.1. 自定义微分方程函数在使用ODE45函数之前,我们需要先定义微分方程的形式。
通常,我们将微分方程表示为一个函数的形式,例如:```matlabfunction dydt = odefun(t, y)dydt = % 根据微分方程的具体形式对dydt进行计算end```在这个函数中,dydt表示微分方程的导数,t表示时间,y表示状态变量。
我们需要根据具体的微分方程形式来计算dydt的值。
2.2. 设定时间范围和初始条件在使用ODE45函数时,我们需要设定时间范围和初始条件。
时间范围可以用一个包含起始时间和结束时间的向量来表示,例如tspan = [0, 10];初始条件则是微分方程在起始时间点的状态变量值,例如y0 = 1。
2.3. 求解微分方程并获取结果一旦定义了ODE45函数的参数,我们就可以用它来求解微分方程了。
调用ODE45函数后,它将返回时间向量t和对应时间点的解向量y,我们可以利用这些结果来进行进一步的分析和应用。
3. ODE45函数的实际案例为了更好地理解ODE45函数的用法,让我们通过一个具体的案例来演示。
假设我们有一个简单的一阶微分方程:```matlabfunction dydt = odefun(t, y)dydt = -2*t*y;end```我们希望求解该微分方程在时间范围tspan = [0, 5],初始条件y0 = 1的情况下的解。
自控实验-自动控制系统的MATLAB仿真分析

实验名称:自动控制系统的MATLAB仿真分析一、实验目的1.熟悉MATLAB在自动控制系统仿真中的应用;2.对自动控制系统进行仿真研究;3.掌握用MATLAB绘制自动控制系统根轨迹及对数频率特性的方法,掌握根据系统根轨迹及对数频率特性分析自动控制系统性能的方法。
二、实验设备1.计算机2.MATLAB软件三、实验内容1.用MATLAB提供的Simulink仿真软件工具对实验一中的各个典型环节及二阶系统进行阶跃响应仿真研究,将仿真获得的阶跃响应结果与模拟电路获得的阶跃响应结果进行比较。
(1)比例环节传递函数为200 ()51 G s=建立仿真模型,得到的输出结果如图所示:(2)积分环节传递函数为9.8 ()G ss=建立仿真模型,得到的输出结果如图所示:(3)一阶惯性环节传递函数为3.9 ()0.21G ss=+建立仿真模型,得到的输出结果如图所示:(4)比例积分环节传递函数为0.39781 ()0.102sG ss+=建立仿真模型,得到的输出结果如图所示:(5)比例微分环节传递函数为10 ()220s G ss=++建立仿真模型,得到的输出结果如图所示:(6)比例微分积分环节传递函数为51050 ()220sG ss s+=+++建立仿真模型,得到的输出结果如图所示:(7) 二阶系统的阶跃响应 ①0.325K ξ==传递函数为2()250()10250C s R s s s =++ 建立的仿真模型与阶跃响应仿真波形如下图所示:②0.510K ξ==传递函数为2()100()10100C s R s s s =++ 建立的仿真模型与阶跃响应仿真波形如下图所示:③0.75K ξ==传递函数为2()50()1050C s R s s s =++ 建立的仿真模型与阶跃响应仿真波形如下图所示:2. 单位负反馈系统的开环传递函数为:(1)()()(21)k s G s H s s s +=+仿真绘制K 从0~∞变化时的根轨迹,分析系统的稳定性。
Matlab基础与应用

rand(3,3)= 0.2311 0.8913 0.0185
0.6068 0.7621 0.8214
382/859 1627/1765 583/1437
Format rat rand(3,3) = 989/1607 313/424 2131/2278
609/769 355/2014 2571/2804
例:求下列极限。 Problem 1:
syms a m x; f=(x*(exp(sin(x))+1)-2*(exp(tan(x))-1))/(x+a); limit(f,x,a) ans = (1/2*a*exp(sin(a))+1/2*a-exp(tan(a))+1)/a Problem 2: syms x t; limit((1+2*t/x)^(3*x),x,inf) ans = exp(6*t)
级数求和
4. 级数(级数求和) 级数求和运算是数学中常见的一种运算。例 如: f(x)=a0+a1x+a2x2+a3x3+…+anxn 函数symsum可以用于此类对符号函数f的求和 运算。该函数的引用时,应确定级数的通项 式S,变量的变化范围a和b。该函数的引用格 式为:
symsum(s, a, b)
Plot绘图
例一:画出衰减震荡曲线
y
t
e3
sin
3t
及其包
络线
y0
t
e3
t的取值范围是
[0,4 ]
程序如下:
t=0:pi/50:4*pi; y0=exp(-t/3); y=exp(-t/3).*sin(3*t); plot(t,y,'-r',t,y0,':b',t,-y0,':b')
matlab的功能及应用

matlab的功能及应用Matlab是一种功能强大且广泛应用的数学软件,它具有众多功能和应用,可以满足科学计算、数据分析、图像处理、机器学习等领域的需求。
本文将介绍Matlab的一些主要功能及其应用。
一、数学计算功能Matlab具有强大的数学计算能力,可以进行各种数值计算、符号计算和矩阵运算。
例如,可以使用Matlab进行线性方程组的求解、数值积分、微分方程的数值解法等。
这些功能在科学研究、工程计算等领域应用广泛。
二、数据分析功能Matlab提供了丰富的数据分析工具,可以对各种数据进行统计分析、数据可视化和建模预测。
例如,可以使用Matlab进行数据的描述统计分析、假设检验、方差分析等。
此外,Matlab还支持数据可视化,可以绘制各种统计图表,如柱状图、折线图、散点图等,直观展示数据的分布和趋势。
这些功能在市场调研、金融分析、医学统计等领域有广泛应用。
三、图像处理功能Matlab拥有强大的图像处理功能,可以对图像进行各种操作和处理,如图像的读取、显示、滤波、增强、分割等。
例如,可以使用Matlab对医学图像进行肿瘤检测、对遥感图像进行地物提取、对数字图像进行特征提取等。
此外,Matlab还支持图像的压缩和编码,可以对图像进行压缩存储和传输。
这些功能在计算机视觉、图像识别、图像检索等领域有广泛应用。
四、机器学习功能Matlab提供了丰富的机器学习工具箱,可以进行各种机器学习算法的实现和应用。
例如,可以使用Matlab进行数据预处理、特征选择、模型训练和模型评估等。
Matlab支持各种常见的机器学习算法,如线性回归、逻辑回归、支持向量机、决策树、随机森林等。
这些功能在数据挖掘、模式识别、智能推荐等领域有广泛应用。
五、信号处理功能Matlab具有丰富的信号处理工具箱,可以进行各种信号的分析和处理。
例如,可以使用Matlab进行信号的滤波、频谱分析、时频分析、谱估计等。
这些功能在通信系统、音频处理、雷达信号处理等领域有广泛应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制常见MATLAB 函数的应用
1、在matlab 中采用roots 函数求解多项式的根,采用conv 函数实
现多项式的积,相互连接的模块的模型求解也相当简单(1)、串联连接命令G=G1*G2(2)、并联连接命令G=G 1±G2(3)、反馈连接命令G=feedback (G1,G2,Sign )(sign 用来表示系统是正反馈或负反馈,sign=-1为负反馈)
例如:①
程序如下:
>>p=[1304];
>>roots(p)
ans =
-3.3553
0.1777+1.0773i
0.1777-1.0773i
②、用matlab 实现:
程序如下:
>>p=[321];q=[14];
>>n=conv(p,q)
n =
31494③、一个传递函数模型,可以由下面的命令输入:32()34p s s s =++2
()(321)(4)n s s s s =+++325()345
s G s
s s s +=+++
>>num=[15];den=[1345];
>>G=tf(num,den)
Transfer function:
s +5
---------------------
s^3+3s^2+4s +5
④、如下图所示,前向传递函数为G (S )
,反馈回路传递函数为H(S),利用feedback 计算系统的闭环传递函数
程序如下:
>>numg=[1];deng=[50000];
>>numh=[11];denh=[12];
>>[num,den]=feedback(numg,deng,numb,denh,-1);
>>[num,den]=feedback(numg,deng,numh,denh,-1);
>>G=tf(num,den)
()
R S −−−→
Transfer function:
s +2
--------------------------
500s^3+1000s^2+s +1
2、在matlab 中,可以轻松的求解系统的所有极点,从而判断其稳定性
例子:系统的传递函数为:用matlab 判断其稳定性,程序如下:
>>num=[1,7,24,24];
>>den=[1:9];
>>roots(den)
ans =
-1.2888+0.4477i
-1.2888-0.4477i
-0.7244+1.1370i
-0.7244-1.1370i
0.1364+1.3050i
0.1364-1.3050i
0.8767+0.8814i
0.8767-0.8814i
可见4个极点带有正实部,所以系统不稳定
3287653272424()2346789
S S S G S S S S S S S S +++=+++++++
3、MATLAB 中给出了一个函数step ()直接求取线性系统的阶跃
响应,该函数的调用方式如下:y=step (G,t )(G 为系统的传递函数,t 为要计算的点到所在时刻的值组成的时间向量,t 一般可以由t=0:dt :t_end 等步长地产生,t-end 为终值时间,而dt 为步长;y 为系统的输出量)
例子:系统的传递函数为:线性系统的稳态值可以通过dcgain ()来求得,impulse ()函数可以求出系统的脉冲响应
程序如下:>>num=[1,7,24,24];den=[1,10,35,50,24];
>>G=tf(num,den);
>>t=0:0.1:10;
>>y=step(G,t);
>>plot(t,y)
>>Y=dcgain(G)
Y =
1
>>hold on
>>y1=impulse(G,t);
>>plot(t,y1)
3272424()S S S G S +++=++++
例子:控制精度变化时,系统的闭环传递函数为:
应用如下MATLAB 语言,可得到=10、=40、=80时的系统响应。
可见,当
时,系统响应速度明显加快,但出现振荡
程序如下:
>>ka=80;
>>nf=[5000];df=[11000];
>>ng=[1];dg=[1200];>>[num,den]=series(ka*nf,df,ng,dg);
>>[n,d]=cloop(num,den);
>>t=[0:0.01:2];
>>y=step(n,d,t);
>>plot(t,y,'black'),grid
on
a k 123212()()5000()1()()1020200005000a a a a
k G S G S K s k G S G S s s s k φ==++++a k a k a k 80
a k =
4、用matlab绘制根轨迹
MTLAB中提供了rlocus()函数,用来绘制给定的根轨迹,该函数
的调用方式为:R=rlocus(G,K)
(G为系统的模型,
输入变量k为用户自己选择的增益,返回的变量R为根轨迹各点构成的复数矩阵)如果k值不给定,则该函数自动选择k,在这种情况下,调用格式为[,]()
R K r l o c u s G
这样产生的k值可以用来确定闭环系统稳定的增益范围
如果在函数调用中不返回任何参数,则将在图形窗口中自动绘制系统
根轨迹曲线Rlocus(G)
Rlocufind ()函数允许用户求取根轨迹上指定点处的开环增益,并将该增益下的所有的闭环极点显示出来:
[K P]=rlocufind(G)
例子:闭环系统的闭环传递函数为:特征方程可以写为:在解题前,必须将特征方程写成下面形式:K 为所关心的参数,变化范围从0到
,绘制的根轨迹如下:程序如下:
>>num=[11];
>>den=[1560];
>>G=tf(num,den);
>>hold on;rlocus(G);
>>[K,P]=rlocfind(G)
Select a point in the graphics window
selected_point =
-2.4621+0.0248i
K =
0.4196
P =
-2.4655+0.0246i
-2.4655-0.0246i (1)(2)()(2)(3)(1)K s s s s s s K s φ++=++++110(2)(3)s K
s s s ++=++()10()
P s K Q s +=+∞
-0.0690
例子:研究系统根轨迹曲线和阶跃响应曲线之间的关心,考虑系统输
出:输入为单位阶跃信号时:程序如下:>>t=0:0.2:15;
>>K=16.2859;
>>num=K*[143];
>>den=[156+K K];
>>G=tf(num,den);
>>y=step(G,t);
>>plot(t,y)
>>grid
on
(1)(2)()()()()K s s C s s R s R s φ++==
++++
5、在MATLAB中,使用较多的频域稳定性函数有bode函数、
nyquist函数、nichols函数、margin函数,pade函数,ngrid函数等。
MATLAB的控制系统工具箱中提供了bode()函数来求取、绘制给给定线性系统的伯德图,函数调用方式如下:
[mag,pha]=bode(G.,w)
其中G为系统的对象模型,变量w为用户制定频率点构成的向量,该函数在这些频率点上对系统进行频率分析。
mag、pha对应系统的幅值和相位向量,相位的单位为角度。
同时经常要将幅值向量转换成分贝形式,MATLAB命令为:
该函数的另一种调用格式为:[mag ,pha ,w]=bode (G.)
这时w 可以自动生成,如果在调用bode 函数时不返回变量,则MATLAB 自动生成系统的伯德图。
一般和计算增益裕度和相角裕度的函数margin 结合使用
例子:考虑系统传递函数:则可以用下面的命令绘出系统的伯德图,计算出增益裕度和相角裕度,程序如下:
>>w=logspace(-1,1,200);
>>num=[13];
>>den=[conv([11],[12]),0];
>>G=tf(num,den);
>>[x y w]=bode(G,w);
>>margin(x,y,w)magdB=20*log10(mag )
3()(1)(2)
s G s s s s +=++
例子:考虑系统传递函数则可用下面命令绘出系统的奈氏图>>num=[0.5];
>>den=[1210.5];
>>[re,im]=nyquist(num,den);>>plot(re,im),grid on 3
20.5()20.5G s s s s =+++。
