理论力学例题
理论力学典型例题答案及解析(适用于邓国红版)

联立求解上式,并注意到
JC
1 ml2 12
可得
3g cos j
2l
w
3g l
(sin
j0
sin
j
)
以C点为基点,则A点的加速度为 注: 亦可由加速度合成法求出
aAaCaA tCaA nC
在运动开始时, 到y 轴上,得
w=0,
故
aAnC=0
, 将上式投影
0aCy aA tCsinq
aC yaA tCsinq2 lsinq (4)
知识点:动能定理的运用
分析:对m1与m2进行整体分 析,分别写出初末状态下的动 能,运用动能定理进行求解
解:
系统的初动能T1 0,当转过j角度时有
T2
1 2
Jw2
1 2
m2v2
W12 Mj m2grj sinq fm2grj cosq
由T2 T1 W12求出w,然后对w求导得到
11.15
大小
√
√
?
?
求出滑枕B的加速度
7.15 轮只滚不滑,I点为瞬心
求B点与C点的速度
vA
vB
vC
分析可知:AB杆为瞬时平动,则有
wB
vBvAwO A 2m/s I
wBvB/B I4rad/s
vCwBC I2.8m 3 /s
取A点为基点,对B点作加速度分析 y
an BatBaAan B AatBAaA
vr vo v e
L z2
Jw
M z (mv e mv r )
Jw
m • OM
2 w mv 0 • MA
其中 MA = l cos j r
OM 2 (l r cos j ) 2 (r sin j ) 2
理论力学考试题及答案详解

理论力学考试题及答案详解一、选择题(每题2分,共10分)1. 牛顿第一定律又称为惯性定律,它指出:A. 物体在受力时,会改变运动状态B. 物体在不受力时,会保持静止或匀速直线运动C. 物体在受力时,会做圆周运动D. 物体在受力时,会保持原运动状态答案:B2. 根据胡克定律,弹簧的弹力与弹簧的形变量成正比,比例系数称为:A. 弹性系数B. 刚度系数C. 硬度系数D. 柔度系数答案:A3. 在理论力学中,一个系统动量守恒的条件是:A. 系统外力为零B. 系统外力和内力都为零C. 系统外力和内力之和为零D. 系统外力和内力之差为零答案:C4. 一个物体做自由落体运动,其加速度为:A. 0B. g(重力加速度)C. -gD. 取决于物体的质量答案:B5. 刚体的转动惯量与以下哪个因素无关?A. 质量B. 质量分布C. 旋转轴的位置D. 物体的形状答案:A二、填空题(每空2分,共10分)6. 一个物体受到三个共点力平衡,如果撤去其中两个力,而保持第三个力不变,物体的加速度将________。
答案:等于撤去的两个力的合力除以物体质量7. 根据动能定理,一个物体的动能等于工作力与物体位移的________。
答案:标量乘积8. 在光滑水平面上,两个冰球相互碰撞后,它们的总动能将________。
答案:守恒9. 一个物体在水平面上做匀速圆周运动,其向心力的方向始终________。
答案:指向圆心10. 刚体的角速度与角动量的关系是________。
答案:成正比三、简答题(共20分)11. 什么是达朗贝尔原理?请简述其在解决动力学问题中的应用。
答案:达朗贝尔原理是分析动力学问题的一种方法,它基于牛顿第二定律,用于处理作用在静止或匀速直线运动的物体上的力系。
在应用达朗贝尔原理时,可以将物体视为受力平衡的状态,即使物体实际上是在加速运动。
通过引入惯性力的概念,可以将动力学问题转化为静力学问题来求解。
12. 描述一下什么是科里奥利力,并解释它在地球上的表现。
理论力学

1、运动分析。----说明机构中主要构件的运动形式。 2、作速度分析,需要画出相关速度,求一点速度或图形角
速度。(若要分析加速度,一般需要求图形的角速度)
画速度 (1)沿点的运动轨迹切线,与相关的角速度方向协调。
(2)要符合速度投影定理。
3、作加速度分析,需要画出相关加速度,求一点加速度 或图形角加速度。 画加速度
例8-10
如图所示,在椭圆规的机构中,曲柄OD以匀角速度ω绕O 轴转动。
OD=AD=BD=l。求:当 60 时,尺AB的角加速度和点A的加速度。
B ABC AB D
O O
O
A A
vD
O
aA
n a BA
a A B
aD
v A
aD
n a AD y’ a AD
n a AD l 2
n x’ a A cos aD cos 2 a AD
y’ n a A 0 aD sin aAD cos a AD sin
x’
若OD变速转动,有什么变化?
a A l
2
a 0 AD AD
a AD 0 AD
解:
(1)动点:OA上的A点
动系:摇杆O1B
(2)运动分析: 绝对运动: 圆周运动。 相对运动: 直线运动。 牵连运动: 摇杆转动。
(3)速度分析与计算
v a r
ve
O ω
va
B vr
A ω1
vr va cos
ve va sin
r 2 O1 1 2 2 O1 A l r ve
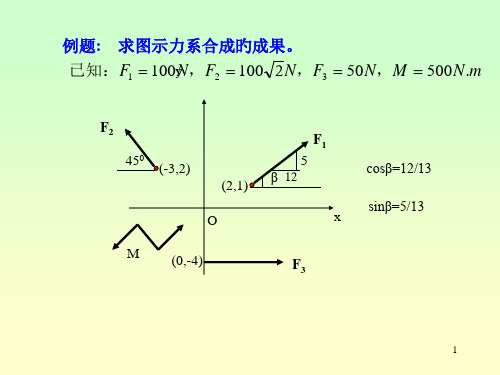
理论力学5平面任意力系
P
1m
q
C
2m
A
2m
B
43
P
1m
q
C
XA
2m
A
YA
2m
XB
B
YB
解: ( 1 ) 取整体为研究对象,画受力图.
44
P
1m
q
C
XA
2m
A
2m
XB
B
YA
MA( F ) = 0
YB
- 4 × 3 × 1.5 - 20 × 3 + 4 YB = 0
YB = 19.5 kN
45
P
1m
q
C
XA
2m
2m
A
FR 0, M O (F ) 0
(一)基本平衡方程
Fx = 0 Fy = 0 Mo ( F ) = 0
(一力矩式)
能解 3 个未知量
16
(二)平面任意力系平衡方程旳其他形式
(1) 二力矩式
MA ( Fi ) = 0 MB ( Fi ) = 0 Fx = 0
投影轴 x 不能与矩心 A 和 B 旳连线垂直.
a
G3 A
C
e G1 L G2
B
NA
b
NB
1、满载时,当重物距离右轨最远时,易右翻。 当起重机平衡 m B( F ) = 0 - G1 ·e - G2 ·L - NA ·b+ G3 ·(a+ b) = 0
NA = [ - G1 ·e - G2 ·L + G3 ·( a+ b)] / b
33
a
G3 A
XA = 14.14 kN
Fy = 0
YA
理论力学试题及答案

理论力学试题及答案一、选择题(每题2分,共20分)1. 牛顿第一定律描述的是:A. 物体在受力时的运动状态B. 物体在不受力时的运动状态C. 物体在受力时的加速度D. 物体在受力时的位移答案:B2. 根据牛顿第二定律,物体的加速度与作用力和物体质量的关系是:A. 加速度与作用力成正比,与质量成反比B. 加速度与作用力成反比,与质量成正比C. 加速度与作用力成正比,与质量成正比D. 加速度与作用力成反比,与质量成反比答案:A3. 以下哪个不是刚体的运动特性?A. 刚体的质心保持静止或匀速直线运动B. 刚体的各部分相对位置不变C. 刚体的各部分速度相同D. 刚体的各部分加速度相同答案:C4. 角动量守恒定律适用于:A. 只有重力作用的系统B. 只有内力作用的系统C. 外力矩为零的系统D. 外力为零的系统答案:C5. 以下哪个是能量守恒定律的表述?A. 一个封闭系统的总动能是恒定的B. 一个封闭系统的总势能是恒定的C. 一个封闭系统的总能量是恒定的D. 一个封闭系统的总动量是恒定的答案:C二、简答题(每题10分,共20分)6. 简述牛顿第三定律的内容及其在实际中的应用。
答案:牛顿第三定律,又称作用与反作用定律,表述为:对于两个相互作用的物体,它们之间的作用力和反作用力总是大小相等、方向相反。
在实际应用中,例如在推门时,门对人的作用力和人对门的作用力大小相等,方向相反。
7. 描述什么是简谐振动,并给出一个生活中的例子。
答案:简谐振动是一种周期性振动,其回复力与位移成正比,且总是指向平衡位置。
生活中的例子包括弹簧振子,当弹簧被拉伸或压缩后释放,它会在原始平衡位置附近做周期性的往复运动。
三、计算题(每题15分,共30分)8. 一个质量为m的物体,从静止开始,沿着一个斜面下滑,斜面的倾角为θ。
如果斜面的摩擦系数为μ,求物体下滑的加速度。
答案:首先,物体受到重力mg的作用,分解为沿斜面方向的分力mg sinθ和垂直斜面方向的分力mg cosθ。
理论力学试题及答案

理论力学试题及答案一、选择题(每题2分,共10分)1. 一个物体在水平面上以速度v匀速直线运动,其动摩擦因数为μ,若物体所受的摩擦力为F,则F等于:A. μvB. μmgC. μND. μ(v^2)答案:B2. 根据牛顿第二定律,物体的加速度与作用在物体上的合外力成正比,与物体的质量成反比。
这一定律的数学表达式为:A. F = maB. F = m/aC. a = F/mD. a = mF答案:A3. 一个物体从静止开始自由下落,其下落的高度h与时间t的关系为:A. h = gt^2B. h = 1/2gt^2C. h = 2gtD. h = gt答案:B4. 两个物体A和B用轻杆连接,A的质量为mA,B的质量为mB,系统在水平面上以共同速度v向右做匀速直线运动。
若杆的力为F,则F的方向是:A. 向左B. 向右C. 不确定D. 无法判断答案:B5. 一个物体在竖直平面内做圆周运动,当物体通过最高点时,其向心力的来源是:A. 重力B. 杆的支持力C. 绳子的张力D. 重力和杆的支持力的合力答案:D二、填空题(每空2分,共10分)1. 一个物体的质量为2kg,受到的合外力为10N,根据牛顿第二定律,其加速度为______ m/s²。
答案:52. 一个物体做匀加速直线运动,初速度为3m/s,加速度为2m/s²,经过4秒后的速度为______ m/s。
答案:153. 在光滑水平面上,一个物体受到一个大小为5N,方向向右的恒定力作用,物体的质量为1kg,其加速度为______ m/s²。
答案:54. 一个物体在竖直上抛运动中,当其上升的最大高度为20m时,其初速度为______ m/s。
答案:205. 根据动能定理,物体的动能变化等于合外力做的功,若一个物体的动能增加了30J,合外力做的功为______ J。
答案:30三、简答题(共20分)1. 解释什么是科里奥利力,并给出其表达式。
理论力学精选80题

图示机构由四根杆组成,已知:各杆重均为P,长均为L,弹簧原长为L。,弹性系数为K,B端在光滑水平面上。没弹簧受压时不会失隐,试用虚位移原理求系统的平衡位置θ。
计算题
图示结构由AC、CE、ED三个刚杆组成,已知:P=3KN,M=1KN·m,L=1m,用虚位面刚架中,自重不计,已知:q1=10KN,m,q2=20KN/m,P=16KN。试求:支座A、B、E的反力。
计算题:
计算题
构架由AC、CD、DB三根杆用铰链C和D连接,其他支承和载荷如图所示。在杆DB的中点E作用集中力F=8kN,均布载荷集度q=4kN/m,力偶矩M=10kN•m,尺寸a=1m。如果不计杆件重,求固定端A的约束力。
理论力学精选80题
北京科技大学理论力学课程组编
计算题
平面结构如图,A、B为固定铰支座,已知:а=1m,α=30o,在铰链D处作用一铅直载荷Q=1KN,在AC杆的中点作用一水平载荷P=0.4KN,各构件自重不计,试求支座A、B的反力及杆CB,杆CD的内力。
计算题
构架如图,在水平杆AD的中点E和D点,各铰接一直杆EG及DG,此二杆在G点与GH杆铰接,GH杆为铅直方向,其在H点又与水平直杆BH及直角弯杆CH铰接,在D、G铰上各装一个定滑轮Ⅰ及Ⅱ,半径相同,一无重绳跨过此二滑轮,其一端固于BH杆的K点,另一端挂一重为P的重物,细绳LK与BH垂直,已知:P=100N,q=200N/m,R=0.4m,a=1m,b=0.6m,滑轮及各杆重不计,求固定铰支座A、B、C的反力。
计算题
在平面机构中,已知:AB=CD=EH=r,AC=BD= r, K、E分别是AC、BD的中点,图示瞬时,D点正好在KH的连线上,且DH= r,不计自重及摩擦。已知 ,用虚位移原理求平衡时力偶M的大小。
理论力学练习题

理论力学练习题一、选择题1. 质点系的动量守恒定律适用于以下哪种情况?A. 质点系内部作用力远大于外力B. 质点系内部作用力远小于外力C. 质点系内部作用力与外力相等D. 质点系内部作用力与外力都为零2. 以下哪项不是牛顿运动定律的内容?A. 物体的加速度与作用力成正比B. 物体的加速度与物体质量成反比C. 物体的加速度方向与作用力方向相反D. 物体的加速度方向与作用力方向相同3. 根据角动量守恒定律,以下说法正确的是:A. 角动量守恒定律只适用于刚体B. 角动量守恒定律只适用于质点C. 角动量守恒定律适用于所有物体D. 角动量守恒定律不适用于任何物体二、计算题1. 一个质量为m的物体在水平面上以速度v做匀速直线运动,求其动量大小。
2. 一个质量为m的物体在竖直方向上受到大小为F的力作用,物体的加速度为a。
如果物体从静止开始运动,求物体在t秒后的速度。
3. 一个质量为m的物体在光滑水平面上以角速度ω绕一个固定点做匀速圆周运动,求其向心力大小。
三、简答题1. 描述牛顿第三定律的内容,并举例说明。
2. 简述动量守恒定律的条件和应用。
3. 说明角动量守恒定律在天体物理中的应用。
四、分析题1. 一个质量为m的物体从高度h处自由落体,忽略空气阻力。
请分析其在落地时的动能,并与从同一高度以初速度v0水平抛出时的动能进行比较。
2. 一个质量为m的物体在光滑水平面上,受到一个恒定的力F作用,力的方向与水平面成θ角。
请分析物体的运动状态,并求出其加速度大小。
3. 考虑一个质量为m的物体在光滑水平面上,受到一个大小为F,方向始终与速度方向垂直的力作用。
请分析物体的运动状态,并求出其速度随时间的变化关系。
五、应用题1. 一个质量为2kg的物体在水平面上以5m/s的速度做匀速直线运动,若突然施加一个大小为10N的力,方向与运动方向相反,求物体在2秒后的速度。
2. 一个质量为3kg的物体从静止开始,受到一个大小为20N的恒定力作用,求物体在5秒后的速度和位移。
(完整版)理论力学计算题及答案

1. 图示圆盘受一平面力系作用,已知圆盘半径R =0.1m ,F 1=100N ,F 2=200N ,M 0=400Nm 。
求该平面任意力系的合力及其作用线与AC 或其延长线的交点位置。
平面任意力系简化191.42,54.82,199.12391.347.16R xyF N F N F NM NmOE m==-==-=∑∑∑2. 求图示桁架中各杆的内力。
桁架内力计算,截面法与节点法:13F F =3. 已知图示结构中2m a =,在外力5kN F =和力偶矩=10kN m M ⋅作用下,求A 、B 和D处的约束反力。
力系的平衡条件的应用,隔离体与整体分析:()()()1010D Ax Ay Bx By A F F F F F kN M kNm↑=→=↓====4. 已知图示结构中1m =60,a οθ=,在外力10kN F =和力偶矩0=20kN m M ⋅作用下,求A 、C 处的约束反力。
同上()20,0,20,17.32Ax Ay A c F kN F M kNm F kN =→===5. 图示构件截面均一,图中小方形边长为b ,圆形半径均为R ,若右图中大方形和半圆形材料密度分别为12,ρρ,试计算确定两种情况下平面图形的质心位置。
以圆心为原点:()()3222c b x =-R b π→-左以方形下缘中点为原点:()()()12212123238c 2x =ρπρρρπρ++↑+右6. 斜坡上放置一矩形匀质物体,质量m=10kg ,其角点A 上作用一水平力F ,已知斜坡角度θ=30°,物体的宽高比b/h=0.3,物体与斜坡间的静摩擦系数s f =0.4。
试确定不致破坏平衡时F 的取值范围。
计算滑动和翻倒两种情况得到(1)滑动平衡范围14.12124.54N F N -≤≤,(2)翻倒平衡范围:8.6962.27N F N ≤≤7. 如图机构,折杆OBC 绕着O 轴作顺时针的匀速定轴转动,角速度为ω,试求此时扣环M 的速度和加速度。
理论力学练习册及答案同济

理论力学练习册及答案同济一、静力学基础1. 题目:一个均匀的木杆,长度为2m,重量为50kg,一端固定在墙上,另一端自由。
求木杆的重心位置。
答案:木杆的重心位于其几何中心,即木杆的中点。
由于木杆均匀,其重心距离固定端1m。
2. 题目:一个质量为10kg的物体,受到三个力的作用:F1=20N向右,F2=30N向上,F3=15N向左。
求物体的合力大小和方向。
答案:合力F = F1 + F2 + F3 = (20N, 0) + (0, 30N) + (-15N, 0) = (5N, 30N)。
合力大小F = √(5² + 30²) = √(25 + 900) = √925 ≈30.41N。
合力方向与水平线的夹角θ满足tanθ = 30N / 5N = 6,所以θ ≈ 80.53°。
二、动力学基础1. 题目:一个质量为2kg的物体,从静止开始沿直线运动,加速度为5m/s²。
求物体在第3秒末的速度和位移。
答案:速度v = at = 5m/s² × 3s = 15m/s。
位移s = 0.5at² = 0.5 × 5m/s² × (3s)² = 22.5m。
2. 题目:一个质量为5kg的物体,以20m/s的初速度沿直线运动,受到一个恒定的阻力,大小为10N。
求物体在第5秒末的速度。
答案:加速度a = F/m = -10N / 5kg = -2m/s²。
速度v = v0 + at = 20m/s - 2m/s² × 5s = 0m/s。
三、转动动力学1. 题目:一个半径为0.5m的均匀圆盘,质量为10kg,绕通过其中心的轴旋转。
若圆盘的角加速度为10rad/s²,求圆盘的转动惯量。
答案:转动惯量I = mr² = 10kg × (0.5m)² = 2.5kg·m²。
理论力学题库及答案详解

理论力学题库及答案详解一、选择题1. 在经典力学中,牛顿第一定律描述的是:A. 物体在没有外力作用下,将保持静止或匀速直线运动状态B. 物体在受到外力作用时,其加速度与所受合力成正比,与物体质量成反比C. 物体的动量守恒D. 物体的角动量守恒答案:A2. 以下哪一项不是牛顿运动定律的内容?A. 惯性定律B. 力的作用与反作用定律C. 动量守恒定律D. 力的独立作用定律答案:C二、填空题1. 根据牛顿第二定律,物体的加速度 \( a \) 与作用力 \( F \) 和物体质量 \( m \) 的关系是 \( a = \frac{F}{m} \)。
2. 一个物体在水平面上以初速度 \( v_0 \) 滑行,摩擦力 \( f \) 与其质量 \( m \) 和加速度 \( a \) 的关系是 \( f = m \cdot a \)。
三、简答题1. 简述牛顿第三定律的内容及其在实际问题中的应用。
答案:牛顿第三定律,也称为作用与反作用定律,指出作用力和反作用力总是成对出现,大小相等、方向相反,作用在两个不同的物体上。
在实际问题中,如火箭发射时,火箭向下喷射气体产生向上的推力,这是作用力;而气体向下的反作用力则推动火箭向上运动。
2. 解释什么是刚体的转动惯量,并给出计算公式。
答案:刚体的转动惯量是描述刚体绕某一轴旋转时惯性大小的物理量,其计算公式为 \( I = \sum m_i r_i^2 \),其中 \( m_i \) 是刚体各质点的质量,\( r_i \) 是各质点到旋转轴的垂直距离。
四、计算题1. 一个质量为 \( m \) 的物体在水平面上以初速度 \( v_0 \) 滑行,受到一个大小为 \( \mu mg \) 的摩擦力作用,求物体滑行的距离\( s \)。
答案:首先应用牛顿第二定律 \( F = ma \),得到 \( \mu mg = ma \)。
解得加速度 \( a = \mu g \)。
【精】理论力学经典例题

m2vB
(m1
vr 2ve 20 cm/s
vr C
O
M
w
ve va A
B
小环M的加速度分析如图所示 :
aa ae ar aC
O
aC 2wvr 2 0.5 20 w
B
20 cm/s2
aen M ar C
ac
a aA
y
aen w 2 OM
a 向y方向投影,有: a
0.52
cos
20
aen
5 cm/s2
2w
4ew
3
1
8ew 2
3
B h
aC aa
art
A
aen q
arn
C
O
w
aa cosq aen cosq arn aC
aa
2 (2ew2
3
3 16ew2 8ew2 ) 2 ew2
2 33
3
9
例13 图示曲杆OBC绕O轴转动,使套在其上的小环M沿固定直 杆OA滑动。已知OB=10 cm,OB与BC垂直,曲杆的角速度为 0.5rad/s,求当φ=60°时小环M的速度和加速度。
va ve vr
va
vr
A
ve
ve w OA
q
va ve tanq w OA
32 3
3ew
3
C O w
vr
ve
cosq
2ew
3
4
3ew
3
2
加速度分析如图
aa ae ar aC
aen OA w 2 2ew 2
arn
vr 2 R
16ew 2
33
aC
2wvr
《理论力学》章节典型例题(含详解)—精品文档
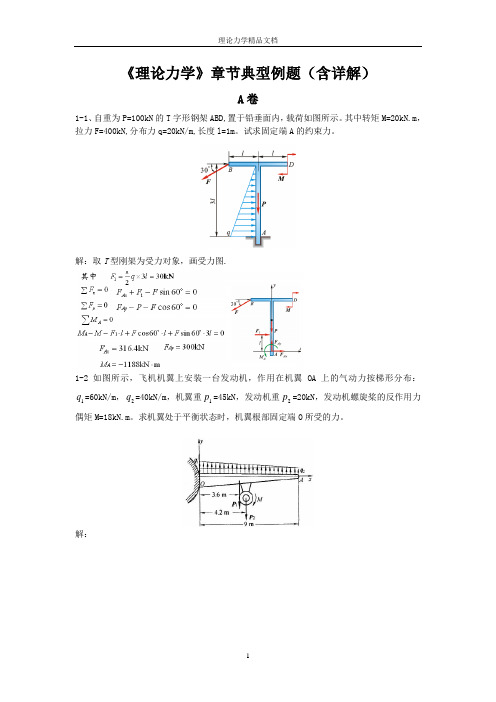
《理论力学》章节典型例题(含详解)A 卷1-1、自重为P=100kN 的T 字形钢架ABD,置于铅垂面内,载荷如图所示。
其中转矩M=20kN.m ,拉力F=400kN,分布力q=20kN/m,长度l=1m 。
试求固定端A 的约束力。
解:取T 型刚架为受力对象,画受力图.1-2 如图所示,飞机机翼上安装一台发动机,作用在机翼OA 上的气动力按梯形分布:1q =60kN/m ,2q =40kN/m ,机翼重1p =45kN ,发动机重2p =20kN ,发动机螺旋桨的反作用力偶矩M=18kN.m 。
求机翼处于平衡状态时,机翼根部固定端O 所受的力。
解:1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸如图。
求固定端A处及支座C的约束力。
1-4 已知:如图所示结构,a, M=Fa, 12F F F ==, 求:A ,D 处约束力.解:1-5、平面桁架受力如图所示。
ABC 为等边三角形,且AD=DB 。
求杆CD 的内力。
1-6、如图所示的平面桁架,A 端采用铰链约束,B 端采用滚动支座约束,各杆件长度为1m 。
在节点E 和G 上分别作用载荷E F =10kN ,G F =7 kN 。
试计算杆1、2和3的内力。
解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面内,且与铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆的内力。
2-2 杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向F。
在节点C沿CH边铅直向下作用力F。
如铰链B,L和H是固定的,杆重不计,作用力D求各杆的内力。
2-3 重为1P =980 N ,半径为r =100mm 的滚子A 与重为2P =490 N 的板B 由通过定滑轮C 的柔绳相连。
《理论力学》考试试题解答解析

z
C
E
D
F
O
30°
By
A
x
2012~2013 学年第一学期《理论力学》考试试题及解答
2、圆盘以匀角速度ω 绕定轴 O 转动,如图所示,盘上动点 M 在半 径为 R 的圆槽内以速度 v 相对圆盘作等速圆周运动,以圆盘为动系, 求点 M 的科氏加速度。
M v
ω R
O
2012~2013 学年第一学期《理论力学》考试试题及解答
l2 R2
R l2 R2
轮
aB R
r 2
l2 R2
2011~2012 学年第二学期《理论力学》考试试题及解答
五、如图所示两均质圆轮质量均为 m ,半径为 R ,A 轮绕固定轴 O
转动,B 轮在倾角为θ 的斜面上作纯滚动,B 轮中心的绳绕到 A 轮
上。若 A 轮上作用一力偶矩为 M 的力偶,忽略绳子的质量和轴承
《理论力学》考试试题 及解答
2012~2013 学年第一学期《理论力学》考试试题及解答
一、简单计算题(每题5分,共15分) 1、正三棱柱的底面为等腰三角形,OA=OB=a,在平面ABED内
有一沿对角线AE作用的力F,F与AB边的夹角θ=30º,大小为F。 求该力在x、y、z 轴上的投影及对y、z 轴的矩。
五、图示纯滚动的均质圆轮与物块 A 的质量均为 m ,圆轮半径为 r , 斜面倾角为θ,物块 A 与斜面间的摩擦系数为 f 。 杆 OA 与斜面平 行,不计杆的质量。试求:⑴ 物块 A 的加速度;⑵ 圆轮所受的摩 擦力;⑶ 杆 OA 所受的力。(20分)
A
O
θ
2012~2013 学年第一学期《理论力学》考试试题及解答
A
D
u O
理论力学精选80题

木支架结构的尺寸如图所示,各杆在A、D、E、F处均以螺栓连接,C、D处用铰链与地面连接,在水平杆AB的B端挂一重物,其重W= 5kN。若不计各杆的重,试求C、G、A、E各点的约束力。
计算题
图示结构各杆自重不计,DE杆靠在AC杆的C端,接触面光滑,已知:P,M=Pa,q=P/a,试求固定端A及铰支座E的约束反力。
计算题
如图所示滑块连杆铰结系统中,滑块A、B重量均为100N,摩擦因数f=0.5,试求平衡时作用在铰C的铅垂向下力F的大小。
计算题
在图示刚架,已知:P=10kN,M=56kN·m,θ=60°,L=2m,B、C处为铰接,各构件的自重不计。试求:(1)固定端支座A的反力;(2)铰链C的约束力。
计算题
构架由直角杆AC、CD和直杆DB用铰链C和D连接,其他支承和载荷如图所示。销钉穿过AC和CD两杆,在销钉C上作用铅垂力F=4kN,三角形分布载荷集度q=2kN/m,力偶矩M=6kN•m,图中长度单位为m。如果不计杆件重量,求固定端A的约束力以及销钉C对杆AC和杆CD的作用力。
计算题
如右下图所示平面结构。杆AC与杆DF 互相平行,A、B、C、D、E处均为光滑铰链。已知: 力 的大小,其方向与AC垂直; F处作用一矩为 的力偶。各杆自重不计。试求:
(1)铰A处的反力;
(2)杆BD和杆CE的内力。
计算题
计算题
计算题:
图示构架受载荷MP q作用。已指:长度a,略去各杆重及各处摩擦。试求固定支座A和活动铰支座B的反力。(力的单位为KN,长度单位为 m。)
计算题
在平面刚架中,自重不计,已知:q1=10KN,m,q2=20KN/m,P=16KN。试求:支座A、B、E的反力。
计算题:
计算题
理论力学超典型例题

第2页/共21页
例题
最后得杆 AB 的角加速度
3g sin
(c)
4l
利用关系 d d d 把上式化成积分 dt d d
d 3g
sin d
0
4l 0
求得杆 AB的角速度
3g 2l
(cos 0
cos
)
(d )
第3页/共21页
例题
杆开始脱离墙壁时它与墙壁所成的角度 1:
MxC N A
第8页/共21页
例题
杆的惯性力合成为一个作用在质心
的力 RQ 和一个力偶,两者都在运动平面 内, RQ 的两个分量大小分别是
RxQ = maCx , RyQ = maCy
aAt y
T aC
ε
y
C aCx
x
G
力偶矩 MCQ 的大小是
MCQ = JCz´ε
旋向与ε相反( 如图b)
第9页/共21页
例题
第14页/共21页
例题6-7
根据虚位移原理的平衡方程,有
δW F δ xC mg δ yD mg δ yE
F 2l(cos1 δ1 cos2 δ2 ) mgl sin 1 δ1 mgl(2sin 1 δ1 sin 2 δ2 )
0
即
mg
F mg
(2F cos1 3mg sin 1)l δ1 (2F cos2 mg sin 2 )l δ2 0
aA = aAn + aA = aCx + aCy + aAC + aACn
第10页/共21页
例题
aA = aAn + aA = aCx + aCy + aAC + aACn
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-1画出下列各图中物体A ,ABC 或构件AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
(b)(b1)2N 3N(c) (c1)B(e)(e1)Bq(f) (f1)(j) (j1)BF (k) (k1)1-2画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所有接触处均为光滑接触。
22N(a) (a1)2AxFAx(a2) (a3)3N(b) (b1)N3F ′ (b2) (b3)(h) (h1)2-3F F AxC(i) (i1) (i2)F (i3)(i4)如图2-5a 所示,刚架的点B 作用1水平力F ,刚架重量不计。
求支座A ,D 的约束力。
(a)(b)图2-5解 研究对象:刚架。
由三力平衡汇交定理,支座A 的约束力F A 必通过点C ,方向如图2-5b 所示。
取坐标系Cxy ,由平衡理论得052,0=×−=∑A x F F F(1)051,0=×−=∑A D y F F F(2)式(1)、(2)联立,解得F F F A 12.125==,FF D 5.0=2-6 在图示结构中,各构件的自重略去不计,在构件BC 上作用一力偶矩为M 的力偶,各尺寸如图。
求支座A 的约束力。
解一、研究对象:BC ,受力如图(b)二、列平衡方程,求F B 、F C为构成约束力偶,有解2-8已知梁AB 上作用1力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图2-12a ,2-12b ,2-12c 三种情况下支座A 和B 的约束力。
BAF(a)BF(b)B(c)(c1)图2-12解(a )梁AB ,受力如图2-12a1所示。
B A F F ,组成力偶,故 BA F F =0=∑A M ,0=−M l F B , l M F B =,l M F A = (b )梁AB ,受力如图2-12b1所示。
0=∑A M , 0=−M l F B , l M F F A B ==(c )梁AB ,受力如图2-12c1所示。
0=∑A M ,0cos=−M l F B θ,θcos l MF F A B ==解)三、研究对象:ADC ,受力如图(c )四、列平衡方程,求F A(方向如图)2-13如图3-5a 所示,飞机机翼上安装1台发动机,作用在机翼OA 上的气动力按梯形分布:kN/m 40,kN/m 6021==q q ,机翼重为kN 451=P ,发动机重为kN 202=P ,发动机螺旋桨的作用力偶矩m kN 18⋅=M 。
求机翼处于平衡状态时,机翼根部固定端O 的受力。
M (a)(b)图3-5解 研究对象:机翼(含螺旋桨),受力如图3-5b 所示。
梯形分布载荷看作三角形分布载荷(21q q −)和均布载荷2q 两部分合成。
三角形分布载荷21q q −的合力N 00009m 9)(21211=×−=q q F 均布载荷q 2的合力000360m 922=×=q F N2F 位于离O m .54处。
,02121=−−++=∑P P F F F F O y 2121F F P P F O −++=N 000385−=kN385−=0=∑O M ,0m 2.4m 6.3m 54m 32121=−×−×−⋅×+×+M P P F F M O=O M m kN 6621⋅ (逆)2-203-12a 在图,图3-12b 各连续梁中,已知q ,M ,a 及θ,不计梁的自重,求各连续梁在A ,B ,C 三处的约束力。
B′F(a)(a2)AxFC(b)(b1)(b2)图3-12解(a )(1)梁BC ,受力如图3-12a2所示。
该力系为一力偶系,则:CB F F =0=∑M ,M a F C =θcos ,=C F θcos a MF B =(2)梁AB ,受力如图3-12a1所示 0=∑x F ,θθtan sin 'a MF F B Ax == 0=∑y F ,aM F F B Ay −=−=θcos '0=∑B M ,0=−a F M Ay A ,)(顺M M A −=解(b )(1)梁BC ,受力如图3-12b2所示0=∑B M ,0cos 2/2=⋅+−a F qa C θ,θcos 2qaF C =2-210=∑x F , θθtan 2sin qaF F C Bx ==0=∑y F , 2/qa F By =(2)梁AB ,受力如图3-12b1所示0=∑x F ,θtan 2'qaF F Bx Ax ==0=∑y F ,2/'qa F F ByAy ==0=∑A M ,2/2qa M A = 由AC 和CD 构成的组合梁通过铰链C 连接。
它的支承和受力如图3-13a 所示。
已知kN/m 10=q ,m kN 40⋅=M ,不计梁的自重。
求支座A ,B ,D 的约束力和铰链C受力。
F C ′DF q(a)(b)(c)图3-13解(1) 梁CD ,受力如图3-13c 所示 0=∑C M ,0m 4m)2(212=×+−×−D F M qkN154/)2(=+=q M F D0=∑y F ,0m 2=×−+q F F D C ,kN 5=C F (2)梁AC ,受力如图3-13b 所示0=∑A M ,0m 3m 2m 4m 2'=×⋅−×−×q F F C B kN402/)64('=+=q F F C B0=∑y F ,0m 2'=×−−+q F F F C B A ,kN15−=A4-21杆系由球铰连接,位于正方体的边和对角线上,如图4-21a 所示。
在节点D 沿对角线LD 方向作用力F D 。
在节点C 沿CH 边铅直向下作用F 。
如球铰B ,L 和H 是固定的,杆重不计,求各杆的内力。
(a)(b)图4-21解 (1) 节点D 为研究对象,受力如图4-21b 所示 0=∑y F ,021211=×−×F F D ,D F F =1(拉)0=∑z F ,021216=×−×F F D ,D F F =6(拉)2-30构架由杆AB,AC和DF铰接而成,如图3-19a所示,在杆DEF上作用1力偶矩为M的力偶。
各杆重力不计,求杆AB上铰链A,D和B受力。
FDx′(a)图3-19解(1)整体,受力如图3-19b所示,0==∑BxxFFaMFMByC2,0==∑(↓)(2) 杆DE,受力如图3-19c所示aMFMDyE==∑,0(↓)(3)杆ADB,受力如图3-19d所示,0==∑DxAFM,0==∑AxxFF=∑yF,aMFAy2−=(↓)=∑xF,()02/1)(613=×++FFF,DFF23−=(压)(2) 节点C为研究对象,受力如图4-21b所示=∑xF,()03/143=×−−FF,DFF64−=(拉)=∑yF,()03/142=×−−FF,DFF22−=(压)=∑zF,03/145=×−−−FFF,DFFF25−−=(压)3-12=∑z F,015sin30sin45sin30sin45sin=−°−°°−°°−PFFFCBA(3)P=10 kN解得kN4.26−==BAFF(压)kN5.33=CF(拉)空间构架由3根无重直杆组成,在D端用球铰链连接,如图4-7a所示。
A,B和C端则用球铰链固定在水平地板上。
如果挂在D端的物重P=10kN,求铰链A,B和C的约束力。
解取节点D为研究对象,设各杆受拉,受力如图4-7b所示。
平衡:=∑x F,045cos45cos=°−°ABFF(1)0=∑y F,015cos30cos45sin30cos45sin=°−°°−°°−CBAFFF(2)3-263-25(a)(b)图4-7工字钢截面尺寸如图4-23a 所示,求此截面的几何中心。
20(a) 图4-23解把图形的对称轴作轴x ,如图4-23b 所示,图形的形心C 在对称轴x 上,即=C y mm 902015020200202002102015010020200)10(20200=×+×+×××+××+−××=Δ∑⋅Δ∑=i i i C A x A x 均质块尺寸如图4-24所示,求其重心的位置。
解)604080304020104040()206040801030402060104040(××+××+×××××+×××+×××=∑∑=g g P x P x ii i C ρρmm72.21=)604080304020104040()406040806030402020104040(××+××+×××××+×××+×××=∑∑=g g P y P y ii i C ρρmm69.40=)604080304020104040())30(60408015304020)5(104040(××+××+××−×××+×××+−×××=∑∑=g g P z P z i i i C ρρ mm62.23−=图4-24 图4-255-37-75-1 图6-1所示为曲线规尺的各杆,长为mm 200==AB OA ,mm 50====AE AC DE CD 。
如杆OA 以等角速度rad/s 5π=ω绕O 轴转动,并且当运动开始时,杆OA 水平向右,求尺上点D 的运动方程和轨迹。
解 如图所示t AOB ω=∠,则点D 坐标为 t OA x D ωcos =,t AC t OA y D ωωsin 2sin −=代入数据,得到点D 的运动方程为:mm 5πcos200t x =,mm 5πsin 100t y =把以上两式消去t 得点D 轨迹方程:1100004000022=+y x (坐标单位:mm )因此,D 点轨迹为中心在(0,0),长半轴为0.2 m ,短半轴为0.1 m的椭圆。
