近5年高考数学全国卷2、3试卷分析
全国Ⅱ卷理科数学2013-2018年高考分析

全国Ⅱ卷理科数学2013-2018年高考分析2019年高考,除北京、天津、上海、江苏、浙江等5省市自主命题外,其他26个省市区全部使用全国卷。
研究发现,全国卷的试卷结构和题型具有一定的稳定性和连续性,每个题型考查的知识点、考查方法、考查角度、思维方法等相对固定。
掌握了全国卷的各种题型,就把握住了全国卷的灵魂,基于此,笔者潜心研究近6年全国高考理科数学Ⅱ卷和高考数学考试说明,精心分类汇总了全国卷近6年所有题型。
为了便于读者使用,所有题目分类(共21类)列于表格之中,按年份排序,高考题的小题(选择和填空)的答案都列在表格的第三列,便于同学们及时解答对照答案,所有解笞题的答案直接列在题目之后,方便查看。
1、集合与常用逻辑用语小题(1)集合小题:6年6考,每年1题,都是交并补子运算为主,多与不等式交汇,新定义运算也有较小的可能,但是难度较低;基本上是每年的送分题,相信命题小组对集合题进行大幅变动的决心不大。
(2)常用逻辑用语小题:6年0考,这个考点一般与其他知识交汇出题,单独出题的可3、平面向量小题6年6考,每年1题,向量题考的比较基本,突出向量的几何运算或代数运算,不4、线性规划小题:6年5考,2016年没考,线性规划题考的比较基本,一般不与其他知识结合难度不大。
5、三角函数小题:题目难度较小,主要考公式熟练运用,平移,由图像性质、化简求值角形等问题(含应用题),基本属于“送分题”。
三角不考大题时,考3个小题,三角数性质,三角恒等变换,解三角形各1个,三角考大题时,只考1个小题6、立体几何小题6年12考,每年2题,一般考三视图和球,主要计算表面积和体积,2018年7、推理与证明小题6年2考,也不是常规的数学考法,倒是很像一道公务员考试的逻辑推理题,但这是个信号。
8、概率小题6年4考,难度较小,一般考查古典概型和几何概型,2014年考了条件概率。
9、统计小题6年2考,统计一般在大题考,这个考点内容实在太多:抽样方法、频率分布表方图、茎叶图,众数,平均数、中位数、方差、标准差、散点图、回归分析、独立10、数列小题:6年6考,全国2理数的数列解答题和三角函数解答题每年只考一个,考解答题考小题,不考解答题时,就考两个小题,一般等差数列和等比数列各考一个,交错奇数年或偶数年12、圆锥曲线小题6年12考,每年2题!太稳定了!太重要了!!全国卷注重考查基础知识和基本概念,综合一点的小题側重考查直线与圆锥曲线位置关系,多数题目比较单一,一般一个容易的,一个较难的13、函数小题6年14考,可见其重要性!主要考查基本初等函数图象和性质,包括:定义域、最值、单调性性、周期性、对称性、平移、导数、切线、定积分、零点等,分段函数是重要载体!函数已是值得学生“恐惧”的了吧?14、排列组合二项式定理:6年5考二项式定理出现较多,这一点很合理,因为排列组合可以在概率统计中考察排列组合考题的难度不大,无需投入过多时间,而且排列组合难题无数处理好分配问题及掌握好分类讨论思想即可,二项式定理通项问题出现较多。
高考全国Ⅱ卷数学试题综合解析

高考全国Ⅱ卷数学试题综合解析_年高考数学试题设计围绕高中数学的核心内容,重点知识重点考查,通性通法着力考查;围绕学生的学习和生活实际,考查数学知识的综合与应用,体现数学的文化及教育价值.下面是小编为大家带来的_高考全国Ⅱ卷数学试题综合解析,希望你喜欢._年高考数学科目考试结束后,省教育考试院邀请西安电子科技大学数学与统计学院部分教授和部分中学特.高级数学教师对我省数学科目试题进行了简要分析.本年度陕西省高考数学试题依然采用全国Ⅱ卷,从大多数考生的答题情况分析得1_分容易,_0分以上难,特别是阅读量的增加,解答题顺序的调整,不难感受到学科素养下命题的导向新变化.试题特点一:试题相对稳定,顺序有所调整_年试题仍然延续了全国高考数学新课标卷稳中求变的风格,主干知识保持不变.试题注重对基础知识与基本技能的考查,贴近教学实际,〝三角函数〞〝立体几何〞〝概率统计〞〝解析几何〞〝函数与导数〞等六大板块依旧是考查重点,体现了高考对主干知识的重视程度,如理科试题中,概率统计_分.立体几何_分.解析几何_分.纯粹三角_分,参数方程与极坐标_分.绝对值不等式_分.函数与导数37分,导数与三角结合与往年不同,但一.二问难度不大,较往年分值增加,尽管放_题的位置,但难度稳定.变化较大的还是解答题顺序上有调整,_题由立体几何换成解析几何,与往年相比运算量减小,_题由常规的解析几何变更为立体几何题,但难度不大,问题的设置常规,证明线线平行.面面垂直及线面夹角的正弦值,只要考生有较好的运算能力和问题分析能力就能解决.压轴_题的导数问题在预料之中,相比_年难度略有提高,但第一.第二问容易入手,难度适中,所以可以看到试题在整体平稳的基础上,试题顺序进行动态调整,排列顺序上依然是由易到难,循序渐进.试题特点二:创设生活情境落实科学育人全国Ⅱ卷发挥学科特色,以中国抗击新冠肺炎疫情中的真实素材设计数学试题的问题情境.理科第3题(文科第4题)以志愿者参加某超市的配货工作为背景设计,疫情防控期间大规模的网购.配货,是考生身边的真实情境,试题考查的知识和方法很基本,考生只要读懂了试题内容,运用概率的基本知识便可求得问题的答案,对考生提高获得感及稳定考试心态都有良好的作用.试题考查考生分析问题和解决问题的基本能力,体现了对核心素养与关键能力的考查;同时,试题的情境具有时代性,对考生具有积极的教育意义.这些材料试题考查学生的阅读理解能力与运用数学模型解决实际问题的能力,同时也较好地考查学生的知识迁移水平和应用能力,对推理步骤的严谨性,答题过程的条理性,解题过程的探索性都有较高的要求,具有浓厚的时代气息,体现了数学与社会的密切联系.试题特点三:聚焦数学思想突出核心素养试题整体运算量不大,注重了数学思维的考查,侧重对逻辑推理.分析和解决问题能力的考查,如理科第 4.5.7.8.9._._._题等;注重通性通法和对数学思想的考查,淡化了特殊方法.技巧解题,如理科第1.2. 6._._._._(1)题等.蕴含数形结合思想的试题有:理科第 5.9._题,文科第8._._题;蕴含转化与化归思想的试题有:理科第_._._题,文科第_._题;考查直观想象素养的试题有:理科第7._._._题,文科第_._._题;考查数学运算素养的试题有:理科第5.6.8._._._._._._题,文科第 5.6.8.9._._._._._题;考查逻辑推理素养的试题有:文科第_._题,理科第_题的二三问.总之命题从知识立意到能力立意,再到学科素养立意,都是以数学知识为载体,培养学生的理性思维和数学品质,考查学生理性思维的广度和深度,体现了数学思想.通性通法的重要性.高中历史重要知识点高中的历史的学习重点是掌握课本知识,所以我们在学习必修一的历史课本时,就要理解好_全国1卷高考语文作文范文精选5篇关注语文教学发展,解决语文学习困惑.从_年的高考语文作文可以看出,我们的作文_全国1卷语文作文范文精选 _年备受关注的高考语文作文试题已经出炉,_全国1卷语文作文是〝对齐桓公.中国面孔高考满分作文范文5篇每一个口罩下都是一张美丽的面孔,_年让我们致敬奋斗战役一线的工作者吧,下面就是。
近年高考数学试题分析

近年高考数学试题分析
本文旨在分析过去几年高考数学试题的趋势和难点,提供有用
的备考参考。
考试趋势
近年来,高考数学试题主要体现以下趋势:
1. 呈现出多元化、综合性的特点,注重考查数学知识的应用能力;
2. 出现更多的跨学科、跨领域的知识点和题型,如统计、概率、二次函数等等;
3. 注重团队协作与实际应用,考查学生的综合素质。
难点分析
一般来说,近年来高考数学试题的难点主要集中在以下几个方面:
1. 组合数学和概率论;
2. 解析几何;
3. 向量;
4. 常微分方程。
需要指出的是,高考数学试题的难点不断变化,备考的关键仍在于不断跟进,掌握解题的基本方法和技巧。
题型解析
根据过去几年的趋势,高考数学试题的题型主要分为选择题和解答题两种。
选择题难度较低,但需要学生对各种知识点掌握得较为熟练;解答题难度较高,需要学生在解题方法上有较强的拓展性和应用能力。
总结
以上是本文对近年来高考数学试题的分析和总结。
备考过程中,学生需要注重掌握各种数学知识点的应用能力,把握数学试题的出
题规律和趋势,合理调配备考时间,保持研究的热情和动力。
祝愿各位考生在高考数学试题中取得优异的成绩!。
全国二卷文科数学2015-2019年五年高考考试试题分析(共23张PPT)

二是随机事件的基本研究过程:随机事件一事件概率→基本概型。
随机事件
事件概率
基本概型
两种常见事件:随机事件,基本事件 三种常见求法 :用频率估计概率 两种概率模型古典概型 ,几
,利用基本概型
何概型
3、教学策略(包括教学内容处理、教学方法和考题导向等)
重点突出——立足数学核心
本模块考点多,但也并非杂乱无章,大题多以交汇性的形式考查,交汇点主要有两种:一是两图(频
文科数学五年高考试题分析
综述
总体来说近几年全国II卷文科数学试题进一步以“立德树人、服务选才、引导教学”作 为高考的核心功能,加强“必备知识、关键能力、学科素养、核心价值”四个层次的考 查,体现“基础性、综合性、应用性、创新性”四个方面的要求。试卷以知识为载体, 以思维为核心,考查学生的数学核心素养,充分体现了数学学科特点。试题坚持新题不 难、难题不怪的命题方向,并注重知识的生成,遵循考纲又体现新课改精神,考查基础 又适当增加创新、灵活成分,强调重点、兼顾全面,体现出侧重能力的考查。
1中 18
古典概型,题不好理解(保费 表,)
2 中 古典概型,题不好理解
17
3 中 加权平均值
1易
通过频率分布直方图求相应组的 概率
19 2 中
独立性检验(新旧网箱水产养殖 问题)
17
3中
作频率分布直方图,并求加权平 均值,判断两组数据的优劣
1 易 利用已知回归方程求预测值
18 2易
判定回归模型的可靠性(环境基 础设施投资图)
求前n项和公式,并用二次函 数求最值
由基本公式建立简单的方程组 求a1,和q再求通项(等比,)
对数运算,再等差求和
总分 年限
10
高考数学全国卷试题评析

高考数学全国卷试题评析
题目评析主要从以下几个方面进行分析:
1. 题目类型:高考数学试卷中通常包含选择题、填空题、解答题和证明题等不同类型的题目。
评析时可以分别对每种类型的题目进行讨论,分析其难度、命题角度和解题思路等。
2. 题目分值:高考数学试卷中每道题目都有相应的分值,根据分值的大小可以评估题目的重要性。
通常来说,分值较高的题目要求考生熟练掌握相关知识和解题技巧,并能灵活运用。
3. 命题思路:高考数学试题的命题思路一般包括应用、推理、证明等不同的思维方法。
评析时可以分析每道题目所涉及的命题思路,评估其对考生思维能力和应用能力的要求。
4. 题目难度:对于每道题目,可以从难易程度的角度进行评析。
难度较低的题目通常是基础知识和基本解题方法的应用,而难度较高的题目则需要考生较为深入地理解和运用相关知识。
5. 解题思路:对于每道题目,可以分析其可以采用的不同解题思路和方法。
评析时可以指出不同解法的优缺点,并提供相应的解题思路和指导,帮助考生更好地解答题目。
6. 错解分析:对于一些常见的错误解题思路或常见错误答案,可以进行分析和讨论,帮助考生避免类似的错误。
综上所述,高考数学全国卷试题评析主要从题目类型、分值、
命题思路、难度、解题思路和错解分析等方面进行,旨在帮助考生更好地理解和应用相关知识,并提高解题能力。
2023年全国卷新高考II卷数学真题解析

新高考二卷参考答案1.(2023·新高考Ⅱ卷·1·★)在复平面内,(13i)(3i)+−对应的点位于( ) (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限 答案:A解析:2(13i)(3i)3i 9i 3i 68i +−=−+−=+,所以该复数对应的点为(6,8),位于第一象限.2.(2023·新高考Ⅱ卷·2·★)设集合{0,}A a =−,{1,2,22}B a a =−−,若A B ⊆,则a =( ) (A )2 (B )1 (C )23(D )1− 答案:B解析:观察发现集合A 中有元素0,故只需考虑B 中的哪个元素是0, 因为0A ∈,A B ⊆,所以0B ∈,故20a −=或220a −=,解得:2a =或1, 注意0B ∈不能保证A B ⊆,故还需代回集合检验,若2a =,则{0,2}A =−,{1,0,2}B =,不满足A B ⊆,不合题意; 若1a =,则{0,1}A =−,{1,1,0}B =−,满足A B ⊆. 故选B.3.(2023·新高考Ⅱ卷·3·★)某学校为了解学生参加体育运动的情况,用比例分配的分层随机抽样作抽样调查,拟从初中部和高中部两层共抽取60名学生,已知该校初中部和高中部分别有400名和200名学生,则不同的抽样结果共有( )(A )4515400200C C ⋅种 (B )2040400200C C ⋅种 (C )3030400200C C ⋅种 (D )4020400200C C ⋅种答案:D解析:应先找到两层中各抽多少人,因为是比例分配的分层抽取,故各层的抽取率都等于总体的抽取率, 设初中部抽取x 人,则60400400200x =+,解得:40x =,所以初中部抽40人,高中部抽20人, 故不同的抽样结果共有4020400200C C ⋅种.4.(2023·新高考Ⅱ卷·4·★★)若21()()ln 21x f x x a x −=++为偶函数,则a =( ) (A )1− (B )0 (C )12(D )1 答案:B解法1:偶函数可抓住定义()()f x f x −=来建立方程求参, 因为()f x 为偶函数,所以()()f x f x −=,即2121()ln ()ln 2121x x x a x a x x −−−−+=+−++ ①,而121212121lnln ln()ln 21212121x x x x x x x x −−−+−−===−−+−++,代入①得:2121()(ln )()ln 2121x x x a x a x x −−−+−=+++,化简得:x a x a −=+,所以0a =.解法2:也可在定义域内取个特值快速求出答案, 210(21)(21)021x x x x −>⇔+−>+,所以12x <−或12x >,因为()f x 为偶函数,所以(1)(1)f f −=,故1(1)ln 3(1)ln 3a a −+=+ ①,而11ln ln 3ln 33−==−,代入①得:(1)ln3(1)ln3a a −+=−+,解得:0a =.5.(2023·新高考Ⅱ卷·5·★★★)已知椭圆22:13x C y +=的左、右焦点分别为1F ,2F ,直线y x m =+与C 交于A ,B 两点,若1F AB ∆的面积是2F AB ∆面积的2倍,则m =( ) (A )23 (B(C) (D )23−答案:C解析:如图,观察发现两个三角形有公共的底边AB ,故只需分析高的关系,作1F G AB ⊥于点G ,2F I AB ⊥于点I ,设AB 与x 轴交于点K ,由题意,121212212F AB F ABAB F G S S AB F I ∆∆⋅==⋅, 所以122F G F I=,由图可知12F KG F KI ∆∆∽,所以11222F K FG F KF I==,故122F K F K =,又椭圆的半焦距c =,所以122F F c ==21213F K F F ==,故11OK OF F K =−=,所以K ,代入y x m =+可得0m =,解得:m =6.(2023·新高考Ⅱ卷·6·★★★)已知函数()e ln x f x a x =−在区间(1,2)单调递增,则a 的最小值为( ) (A )2e (B )e (C )1e − (D )2e − 答案:C解析:()f x 的解析式较复杂,不易直接分析单调性,故求导, 由题意,1()e x f x a x'=−,因为()f x 在(1,2)上,所以()0f x '≥在(1,2)上恒成立,即1e 0x a x−≥ ①, 观察发现参数a 容易全分离,故将其分离出来再看,不等式①等价于1ex a x ≥,令()e (12)x g x x x =<<, 则()(1)e 0x g x x '=+>,所以()g x 在(1,2)上,又(1)e g =,2(2)2e g =,所以2()(e,2e )g x ∈,故21111(,)()e 2e ex g x x =∈,因为1e x a x ≥在(1,2)上恒成立,所以11e e a −≥=,故a 的最小值为1e −.7.(2023·新高考Ⅱ卷·7·★★)已知α为锐角,1cos 4α=sin 2α=( )(A(B(C(D答案:D解析:22cos12sin sin22ααα=−=⇒=,此式要开根号,不妨上下同乘以2,将分母化为24,所以2sin2α==,故sin2α=,又α为锐角,所以(0,)24απ∈,故sin2α=8.(2023·新高考Ⅱ卷·8·★★★)记nS为等比数列{}na的前n项和,若45S=−,6221S S=,则8S=()(A)120 (B)85 (C)85−(D)120−答案:C解法1:观察发现2S,4S,6S,8S的下标都是2的整数倍,故可考虑片段和性质,先考虑q是否为1−,若{}na的公比1q=−,则414[1(1)]1(1)aS−−==−−,与题意不符,所以1q≠−,故2S,42S S−,64S S−,86S S−成等比数列①,条件中有6221S S=,不妨由此设个未知数,设2S m=,则621S m=,所以425S S m−=−−,64215S S m−=+,由①可得242262()()S S S S S−=−,所以2(5)(215)m m m−−=+,解得:1m=−或54,若1m=−,则21S=−,424S S−=−,6416S S−=−,所以8664S S−=−,故8664216485S S m=−=−=−;到此结合选项已可确定选C,另一种情况我也算一下,若54m=,则254S=>,而2222412341212122()(1)(1)S a a a a a a a q a q a a q S q=+++=+++=++=+,所以4S与2S同号,故4S>,与题意不符;综上所述,m只能取1−,此时885S=−.解法2:已知和要求的都只涉及前n项和,故也可直接代公式翻译,先看公比是否为1,若{}na的公比1q=,则612162142S a S a=≠=,不合题意,所以1q≠,故414(1)51a qSq−==−−①,又6221S S=,所以6211(1)(1)2111a q a qq q−−=⋅−−,化简得:62121(1)q q−=−②,又62322411()(1)(1)q q q q q−=−=−++,代入②可得:2242(1)(1)21(1)q q q q−++=−③,两端有公因式可约,但需分析21q−是否可能为0,已经有1q≠了,只需再看q是否可能等于1−,若1q=−,则414[1(1)]1(1)aS−−==−−,与题意不符,所以1q≠−,故式③可化为24121q q++=,整理得:42200q q+−=,所以24q=或5−(舍去),故要求的8241118(1)[1()]255111a q a q aSq q q−−===−⋅−−−④,只差11a q−了,该结构式①中也有,可由24q =整体计算它, 将24q =代入①可得21(14)51a q−=−−,所以1113a q =−,代入④得81255853S =−⨯=−. 9.(2023·新高考Ⅱ卷·9·★★★)(多选)已知圆锥的顶点为P ,底面圆心为O ,AB 为底面直径,o 120APB ∠=,2PA =,点C 在底面圆周上,且二面角P AC O −−为o 45,则( )(A )该圆锥的体积为π(B )该圆锥的侧面积为(C )AC =(D )PAC ∆答案:AC解析:A 项,因为2PA =,o 120APB ∠=,所以o 60APO ∠=,cos 1OP AP APO =⋅∠=,sin OA AP APO =⋅∠=,从而圆锥的体积211133V Sh ππ==⨯⨯⨯=,故A 项正确;B 项,圆锥的侧面积2S rl ππ===,故B 项错误;C 项,要求AC 的长,条件中的二面角P AC O −−还没用,观察发现PAC ∆和OAC ∆都是等腰三角形,故取底边中点即可构造棱的垂线,作出二面角的平面角,取AC 中点Q ,连接PQ ,OQ ,因为OA OC =,PA PC =,所以AC OQ ⊥,AC PQ ⊥, 故PQO ∠即为二面角P AC O −−的平面角,由题意,o 45PQO ∠=,所以1OQ OP ==,故AQ =,所以2AC AQ ==,故C 项正确;D 项,PQ =11222PAC S AC PQ ∆=⋅=⨯=,故D 项错误. POCABQ10.(2023·新高考Ⅱ卷·10·★★★)(多选)设O 为坐标原点,直线1)y x =−过抛物线2:2(0)C y px p =>的焦点,且与C 交于M ,N 两点,l 为C 的准线,则( )(A )2p = (B )83MN = (C )以MN 为直径的圆与l 相切 (D )OMN ∆为等腰三角形答案:AC解析:A 项,在1)y x =−中令0y =可得1x =,由题意,抛物线的焦点为(1,0)F ,所以12p=, 从而2p =,故A 项正确;B 项,此处可以由直线MN 的斜率求得MFO ∠,再代角版焦点弦公式22sin pMN α=求MN ,但观察发现后续选项可能需要用M ,N 的坐标,所以直接联立直线与抛物线,用坐标版焦点弦公式来算,设11(,)M x y ,22(,)N x y,将1)y x =−代入24y x =消去y 整理得:231030x x −+=,解得:13x =或3, 对应的y−(3,M −,1(3N ,从而121163233MN x x p =++=++=,故B 项错误;C 项,判断直线与圆的位置关系,只需将圆心到直线的距离d 和半径比较, 12523x x MN +=⇒的中点Q 到准线:1l x =−的距离8132d MN ==, 从而以MN 为直径的圆与准线l 相切,故C 项正确; D 项,M ,N 的坐标都有了,算出OM ,ON 即可判断,OMON ==, 所以OM ,ON ,MN 均不相等,故D 项错误.11.(2023·新高考Ⅱ卷·11·★★★)(多选)若函数2()ln (0)b cf x a x a x x =++≠既有极大值也有极小值,则( ) (A )0bc > (B ) 0ab > (C )280b ac +> (D )0ac < 答案:BCD解析:由题意,223322()(0)a b c ax bx cf x x x x x x −−'=−−=>,函数()f x 既有极大值,又有极小值,所以()f x '在(0,)+∞上有2个变号零点, 故方程220ax bx c −−=在(0,)+∞上有两个不相等实根,所以212120()(()4(2)020)()b a c c x x a b x x a ⎧⎪∆=−−−>⎪⎪=−>⎨⎪⎪+=>⎪⎩保证有两根保证两根同号保证两根只能同③正①②,由①可得280b ac +>,故C 项正确;由②可得0ca<,所以a ,c 异号,从而0ac <,故D 项正确; 由③可得a ,b 同号,所以0ab >,故B 项正确;因为a ,c 异号,a ,b 同号,所以b ,c 异号,从而0bc <,故A 项错误.12.(2023·新高考Ⅱ卷·12·★★★★)(多选)在信道内传输0,1信号,信号的传输相互独立. 发送0时,收到1的概率为(01)αα<<,收到0的概率为1α−;发送1时,收到0的概率为(01)ββ<<,收到1的概率为1β−. 考虑两种传输方案:单次传输和三次传输. 单次传输是指每个信号只发送1次,三次传输是指每个信号重复发送3次. 收到的信号需要译码,译码规则如下:单次传输时,收到的信号即为译码;三次传输时,收到的信号中出现次数多的即为译码(例如,若依次收到1,0,1,则译码为1).( )(A )采用单次传输方案,若依次发送1,0,1,则依次收到1,0,1的概率为2(1)(1)αβ−− (B )采用三次传输方案,若发送1,则依次收到1,0,1的概率为2(1)ββ− (C )采用三次传输方案,若发送1,则译码为1的概率为23(1)(1)βββ−+−(D )当00.5α<<时,若发送0,则采用三次传输方案译码为0的概率大于采用单次传输方案译码为0的概率 答案:ABD解析:A 项,由题意,若采用单次传输方案,则发送1收到1的概率为1β−,发送0收到0的概率为1α−, 所以依次发送1,0,1,则依次收到1,0,1的概率为2(1)(1)(1)(1)(1)βαβαβ−−−=−−,故A 项正确; B 项,采用三次传输方案,若发送1,则需独立重复发送3次1,依次收到1,0,1的概率为2(1)(1)(1)βββββ−−=−,故B 项正确;C 项,采用三次传输方案,由B 项的分析过程可知若发送1,则收到1的个数~(3,1)X B β−, 而译码为1需收2个1,或3个1,所以译码为1的概率为22332333(2)(3)C (1)C (1)3(1)(1)P X P X ββββββ=+==−+−=−+−,故C 项错误;D 项,若采用单次传输方案,则发送0译码为0的概率为1α−;若采用三次传输方案,则发送0等同于发3个0,收到0的个数~(3,1)Y B α−,且译码为0的概率为22332333(2)(3)C (1)C (1)3(1)(1)P Y P Y αααααα=+==−+−=−+−,要比较上述两个概率的大小,可作差来看,2323(1)(1)(1)(1)[3(1)(1)1](1)(12)ααααααααααα−+−−−=−−+−−=−−,因为00.5α<<,所以233(1)(1)(1)(1)(12)0ααααααα−+−−−=−−>, 从而233(1)(1)1αααα−+−>−,故D 项正确.13.(2023·新高考Ⅱ卷·13·★★)已知向量a ,b满足−a b 2+=−a b a b ,则=b _____.解析:条件涉及两个模的等式,想到把它们平方来看, 由题意,22223−=+−⋅=a b a b a b ①,又2+=−a b a b ,所以222+=−a b a b ,故2222244++⋅=+−⋅a b a b a b a b ,整理得:220−⋅=a a b , 代入①可得23=b ,即23=b,所以=b .14.(2023·新高考Ⅱ卷·14·★★)底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为2,高为3的正四棱锥,所得棱台的体积为_____. 答案:28解析:如图,四棱锥1111P A B C D −与P ABCD −相似,它们的体积之比等于边长之比的立方,故只需求四棱锥1111P A B C D −的体积,11113112111()4228P A B C D P ABCD V A B AB V −−==⇒==,所以11118P ABCD P A B C D V V −−=,故所求四棱台的体积11117P A B C D V V −=,由题意,1111212343P A B C D V −=⨯⨯=,所以7428V =⨯=.P 1D 1A 1B 1CD ABCO423【反思】相似图形的面积之比等于边长之比的平方,体积之比等于边长之比的立方.15.(2023·新高考Ⅱ卷·15·★★★)已知直线10x my −+=与⊙22:(1)4C x y −+=交于A ,B 两点,写出满足“ABC ∆的面积为85”的m 的一个值_____.答案:2(答案不唯一,也可填2−或12或12−) 解析:如图,设圆心(1,0)C 到直线AB 的距离为(0)d d >,则12ABC S AB d ∆=⋅, 注意到AB 也可用d 表示,故先由85ABC S ∆=求d ,再将d 用m 表示,建立关于m 的方程,又AB ==12ABC S d ∆=⨯=由题意,85ABC S ∆=85,结合0d >解得:d =,又d ====,解得:2m =±或12±.16.(2023·新高考Ⅱ卷·16·★★★★)已知函数()sin()f x x ωϕ=+,如图,A ,B 是直线12y =与曲线()y f x =的两个交点,若6AB π=,则()f π=_____.答案:2−解法1:6AB π=这个条件怎么翻译?可用12y =求A ,B 横坐标的通解,得到AB ,从而建立方程求ω, 不妨设0ω>,令1sin()2x ωϕ+=可得26x k πωϕπ+=+或526k ππ+,其中k ∈Z ,由图知26A x k πωϕπ+=+,526B x k πωϕπ+=+,两式作差得:2()3B A x x πω−=,故23B A x x πω−=, 又6B A AB x x π=−=,所以336ππω=,解得:4ω=,则()sin(4)f x x ϕ=+, 再求ϕ,由图知23π是零点,可代入解析式,注意,23π是增区间上的零点,且sin y x =的增区间上的零点是2n π,故应按它来求ϕ的通解, 所以82()3n n πϕπ+=∈Z ,从而823n πϕπ=−,故82()sin(42)sin(4)33f x x n x πππ=+−=−,所以222()sin(4)sin()sin 333f πππππ=−=−=−=. 解法2:若注意横向伸缩虽会改变图象在水平方向上的线段长度,但不改变长度比例,则可先分析sin y x =与12y =交点的情况,再按比例对应到本题的图中来, 如图1,直线12y =与函数sin y x =在y 轴右侧的三个I ,J ,K 的横坐标分别为6π,56π,136π, 所以52663IJ πππ=−=,1354663JK πππ=−=,:1:2IJ JK =,故在图2中:1:2AB BC =, 因为6AB π=,所以3BC π=,故2AC AB BC π=+=,又由图2可知AC T =,所以2T π=,故24Tπω==,接下来同解法1.2图【反思】①对于函数sin()(0)yx ωϕω=+>,若只能用零点来求解析式,则需尽量确定零点是在增区间还是减区间. “上升零点”用2x n ωϕπ+=来求,“下降零点”用2x n ωϕππ+=+来求;②对图象进行横向伸缩时,水平方向的线段长度比例关系不变,当涉及水平线与图象交点的距离时,我们常抓住这一特征来求周期.17.(2023·新高考Ⅱ卷·17·★★★)记ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知ABC ∆D 为BC 的中点,且1AD =. (1)若3ADC π∠=,求tan B ;(2)若228b c +=,求b ,c . 解:(1)如图,因为3ADC π∠=,所以23ADB π∠=,(要求tan B ,可到ABD ∆中来分析,所给面积怎么用?可以用它求出ABD S ∆,从而得到BD ) 因为D 是BC 中点,所以2ABC ABD S S ∆∆=,又ABC S ∆=ABD S ∆=,由图可知112sin 1sin 223ABD S AD BD ADB BD π∆=⋅⋅∠=⨯⨯⨯==2BD =,(此时ABD ∆已知两边及夹角,可先用余弦定理求第三边AB ,再用正弦定理求角B )在ABD ∆中,由余弦定理,2222212cos 12212()72AB AD BD AD BD ADB =+−⋅⋅∠=+−⨯⨯⨯−=,所以AB由正弦定理,sin sin AB ADADB B =∠,所以1sin sin AD ADB B AB⋅∠==由23ADB π∠=可知B为锐角,从而cos B ==,故sin tan cos B B B ==. (2)(已有关于bc 的一个方程,若再建立一个方程,就能求b 和c ,故把面积和中线都用b ,c 表示)由题意,1sin 2ABC S bc A ∆==sin bc A =①,(中线AD 怎样用b ,c 表示?可用向量处理) 因为D 为BC 中点,所以1()2AD AB AC =+,从而2AD AB AC =+,故22242AD AB AC AB AC =++⋅, 所以222cos 4c b cb A ++=,将228b c +=代入上式化简得cos 2bc A =− ②,(我们希望找的是b ,c 的方程,故由①②消去A ,平方相加即可) 由①②得222222sin cos 16b c A b c A +=,所以4bc = ③, 由228b c +=可得2()28b c bc +−=,所以4b c +==,结合式③可得2b c ==.ADBC118.(2023·新高考Ⅱ卷·18·★★★★)已知{}n a 为等差数列,6,2,n n n a n b a n −⎧⎪=⎨⎪⎩为奇数为偶数,记n S ,n T 分别为{}n a ,{}n b 的前n 项和,432S =,316T =. (1)求{}n a 的通项公式; (2)证明:当5n >时,n n T S >.解:(1)(给出了两个条件,把它们用1a 和d 翻译出来,即可建立方程组求解1a 和d ) 由题意,414632S a d =+= ①,31231231111(6)2(6)62()26441216T b b b a a a a a d a d a d =++=−++−=−++++−=+−= ②,由①②解得:15a =,2d =,所以1(1)23n a a n d n =+−=+.(2)由(1)可得21()(523)422n n n a a n n S n n +++===+, (要证结论,还需求n T ,由于n b 按奇偶分段,故求n T 也应分奇偶讨论,先考虑n 为偶数的情形) 当(5)n n >为偶数时,12n n T b b b =++⋅⋅⋅+ 12341(6)2(6)2(6)2n n a a a a a a −=−++−++⋅⋅⋅+−+ 13124()62()2n n na a a a a a −=++⋅⋅⋅+−⨯+++⋅⋅⋅+ ③, 因为131,,,n a a a −⋅⋅⋅和24,,,n a a a ⋅⋅⋅分别也构成等差数列,所以211131()(521)32242n n na a n n n n a a a −−++++++⋅⋅⋅+===,2224()(723)52242n n na a n n n n a a a ++++++⋅⋅⋅+===,代入③化简得:222353732222n n n n n n nT n +++=−+⨯=, (要由此证n n T S >,可作差比较)所以2237(4)022n n n n n n T S n n 2+−−=−+=>,故n n T S >;(对于n 为奇数的情形,可以重复上述计算过程,但更简单的做法是补1项凑成偶数项,再减掉补的那项)当(5)n n >为奇数时,2113(1)7(1)2n n n n n T T b +++++=−=−2213(1)7(1)351022(25)22n n n n n a n +++++−=−+=, 所以223510(4)2n n n n T S n n +−−=−+ 2310(2)(5)022n n n n −−+−==>,故n n T S >;综上所述,当5n >时,总有n n T S >.19.(2023·新高考Ⅱ卷·19·★★★)某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该项指标的频率分布直方图:患病者未患病者利用该指标制定一个检测标准,需要确定临界值c ,将该指标大于c 的人判定为阳性,小于或等于c 的人判定为阴性. 此检测标准的漏诊率是将患病者判定为阴性的概率,记为()p c ;误诊率是将未患病者判定为阳性的概率,记为()q c . 假设数据在组内均匀分布. 以事件发生的频率作为相应事件发生的概率. (1)当漏诊率()0.5%p c =时,求临界值c 和误诊率()q c ;(2)设函数()()()f c p c q c =+. 当[95,105]c ∈时,求()f c 的解析式,并求()f c 在区间[95,105]的最小值.解:(1)(给的是漏诊率,故先看患病者的图,漏诊率为0.5%即小于或等于c 的频率为0.5%,可由此求c )由患病者的图可知,[95,100)这组的频率为50.0020.010.005⨯=>,所以c 在[95,100)内, 且(95)0.0020.005c −⨯=,解得:97.5c =;(要求()q c ,再来看未患病者的图,()q c 是误诊率,也即未患病者判定为阳性(指标大于c )的概率) 由未患病者的图可知指标大于97.5的概率为(10097.5)0.0150.0020.035−⨯+⨯=,所以() 3.5%q c =. (2)([95,105]包含两个分组,故应分类讨论)当95100c ≤<时,()(95)0.002p c c =−⨯,()(100)0.0150.002q c c =−⨯+⨯,所以()()()0.0080.82f c p c q c c =+=−+, 故()0.0081000.820.02f c >−⨯+= ①;当100105c ≤≤时,()50.002(100)0.012p c c =⨯+−⨯,()(105)0.002q c c =−⨯, 所以()()()0.010.98f c p c q c c =+=−,故()(100)0.011000.980.02f c f ≥=⨯−= ②; 所以0.0080.82,95100()0.010.98,100105c c f c c c −+≤<⎧=⎨−≤≤⎩,且由①②可得min ()0.02f c =.20.(2023·新高考Ⅱ卷·20·★★★)如图,三棱锥A BCD −中,DA DB DC ==,BD CD ⊥,o 60ADB ADC ∠=∠=,E 为BC 的中点. (1)证明:BC DA ⊥;(2)点F 满足EF DA =,求二面角D AB F −−的正弦值.CDABEF解:(1)(BC 和DA 是异面直线,要证垂直,需找线面垂直,可用逆推法,假设BC DA ⊥,注意到条件中还有DB DC =,所以BC DE ⊥,二者结合可得到BC ⊥面ADE ,故可通过证此线面垂直来证BC DA ⊥)因为DA DB DC ==,o 60ADB ADC ∠=∠=,所以ADB ∆和ADC ∆是全等的正三角形,故AB AC =, 又E 为BC 中点,所以BC AE ⊥,BC DE ⊥,因为AE ,DE ⊂平面ADE ,AE DE E =,所以BC ⊥平面ADE ,又DA ⊂平面ADE ,所以BC DA ⊥.(2)(由图可猜想AE ⊥面BCD ,若能证出这一结果,就能建系处理,故先尝试证明) 不妨设2DA DB DC ===,则2AB AC ==, 因为BDCD ⊥,所以BC =故12DE CE BE BC ====AE 所以2224AE DE AD +==,故AE DE ⊥,所以EA ,EB ,ED 两两垂直,以E为原点建立如图所示的空间直角坐标系,则A,D,B ,所以(DA =−,(0,AB =,由EF DA =可知四边形ADEF 是平行四边形,所以(2,0,0)FA ED ==, 设平面DAB 和平面ABF 的法向量分别为111(,,)x y z =m ,222(,,)x y z =n ,则11112020DA AB y ⎧⋅=−+=⎪⎨⋅==⎪⎩m m ,令11x =,则1111y z =⎧⎨=⎩,所以(1,1,1)=m 是平面DAB 的一个法向量,2222020AB y FA x ⎧⋅==⎪⎨⋅==⎪⎩n n ,令21y =,则2201xz =⎧⎨=⎩,所以(0,1,1)=n 是平面ABF 的一个法向量, 从而cos ,⋅<>===⋅m n m n m n D AB F −−.21.(2023·新高考Ⅱ卷·21·★★★★)已知双曲线C 的中心为坐标原点,左焦点为(−. (1)求C 的方程;(2)记C 的左、右顶点分别为1A ,2A ,过点(4,0)−的直线与C 的左支交于M ,N 两点,M 在第二象限,直线1MA 与2NA 交于点P ,证明:点P 在定直线上.解:(1)设双曲线方程为()222210,0x y a b a b−=>>,由焦点坐标可知c =则由ce a==2a =,4b ==,双曲线方程为221416x y −=.(2)由(1)可得()()122,0,2,0A A −,设()()1122,,,M x y N x y , 显然直线的斜率不为0,所以设直线MN 的方程为4x my =−,且1122m −<<, 与221416x y −=联立可得()224132480m y my −−+=,且264(43)0m ∆=+>,则1212223248,4141m y y y y m m +==−−,直线1MA 的方程为()1122y y x x =++,直线2NA 的方程为()2222y y x x =−−,联立直线1MA 与直线2NA 的方程可得:()()()()()2121121211212121222222266y x y my my y y y y x x y x y my my y y +−−+++==−−=−− 112221122483216222141414148483664141m mm y y m m m m m y y m m −⋅−⋅++−−−===−⨯−−−−,由2123x x +=−−可得=1x −,即1P x =−, 据此可得点P 在定直线=1x −上运动.【点睛】关键点点睛:求双曲线方程的定直线问题,意在考查学生的计算能力,转化能力和综合应用能力,其中根据设而不求的思想,利用韦达定理得到根与系数的关系可以简化运算,是解题的关键.22.(2023·新高考Ⅱ卷·22·★★★★)(1)证明:当01x <<时,2sin x x x x −<<; (2)已知函数2()cos ln(1)f x ax x =−−,若0x =是()f x 的极大值点,求a 的取值范围. 解:(1)构建()()sin ,0,1F x x x x =−∈,则()1cos 0F x x '=−>对()0,1x ∀∈恒成立, 则()F x 在()0,1上单调递增,可得()()00F x F >=,所以()sin ,0,1x x x >∈; 构建()()()22sin sin ,0,1G x x x xxx x x =−−=−+∈,则()()21cos ,0,1G x x x x '=−+∈,构建()()(),0,1g x G x x '=∈,则()2sin 0g x x '=−>对()0,1x ∀∈恒成立,则()g x 在()0,1上单调递增,可得()()00g x g >=,即()0G x '>对()0,1x ∀∈恒成立,则()G x 在()0,1上单调递增,可得()()00G x G >=,所以()2sin ,0,1x x x x >−∈;综上所述:sin x x x x 2−<<.(2)令210x −>,解得11x −<<,即函数()f x 的定义域为()1,1−,若0a =,则()()()2ln 1,1,1f x x x =−−∈−,因为ln y u =−在定义域内单调递减,21y x =−在()1,0−上单调递增,在()0,1上单调递减,则()()2ln 1f x x =−−在()1,0−上单调递减,在()0,1上单调递增,故0x =是()f x 的极小值点,不合题意,所以0a ≠. 当0a ≠时,令0b a =>因为()()()()()222cos ln 1cos ln 1cos ln 1f x ax x a x x bx x =−−=−−=−−,且()()()()()22cos ln 1cos ln 1f x bx x bx x f x ⎡⎤−=−−−−=−−=⎣⎦, 所以函数()f x 在定义域内为偶函数,由题意可得:()()22sin ,1,11xf x b bx x x =−−∈'−−, (i )当202b <≤时,取1min ,1m b ⎧⎫=⎨⎬⎩⎭,()0,x m ∈,则()0,1bx ∈,由(1)可得()()()2222222222sin 111x b x b x xf x b bx b x x x x +−'=−−>−−=−−−, 且22220,20,10b x b x >−≥−>,所以()()2222201x b x b f x x+−'>>−,即当()()0,0,1x m ∈⊆时,()0f x ¢>,则()f x 在()0,m 上单调递增, 结合偶函数的对称性可知:()f x 在(),0m −上单调递减, 所以0x =是()f x 的极小值点,不合题意;(ⅱ)当22b >时,取()10,0,1x b ⎛⎫∈⊆ ⎪⎝⎭,则()0,1bx ∈,由(1)可得()()()2233223222222sin 2111x x xf x b bx b bx b x b x b x b x b x x x'=−−<−−−=−+++−−−−, 构建()33223212,0,h x b x b x b x b x b ⎛⎫=−+++−∈ ⎪⎝⎭,则()3223132,0,h x b x b x b x b ⎛⎫'=−++∈ ⎪⎝⎭,且()33100,0h b h b b b ⎛⎫''=>=−> ⎪⎝⎭,则()0h x '>对10,x b ⎛⎫∀∈ ⎪⎝⎭恒成立,可知()h x 在10,b ⎛⎫ ⎪⎝⎭上单调递增,且()21020,20h b h b ⎛⎫=−<=> ⎪⎝⎭,所以()h x 在10,b ⎛⎫⎪⎝⎭内存在唯一的零点10,n b ⎛⎫∈ ⎪⎝⎭,当()0,x n ∈时,则()0h x <,且20,10x x >−>, 则()()3322322201xf x b x b x b x b x'<−+++−<−, 即当()()0,0,1x n ∈⊆时,()0f x '<,则()f x 在()0,n 上单调递减, 结合偶函数的对称性可知:()f x 在(),0n −上单调递增, 所以0x =是()f x 的极大值点,符合题意;综上所述:22b >,即22a >,解得a >a <故a 的取值范围为((),2,−∞+∞.。
近五年的高考试题分析
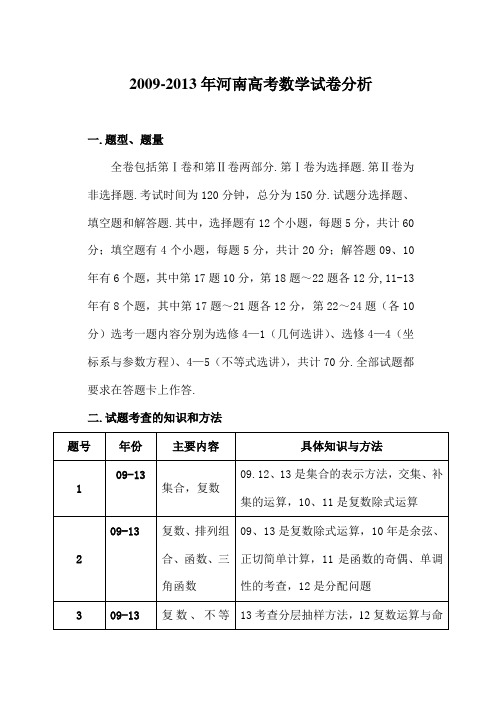
2009-2013年河南高考数学试卷分析
一.题型、题量
全卷包括第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题.第Ⅱ卷为非选择题.考试时间为120分钟,总分为150分.试题分选择题、填空题和解答题.其中,选择题有12个小题,每题5分,共计60分;填空题有4个小题,每题5分,共计20分;解答题09、10年有6个题,其中第17题10分,第18题~22题各12分,11-13年有8个题,其中第17题~21题各12分,第22~24题(各10分)选考一题内容分别为选修4—1(几何选讲)、选修4—4(坐标系与参数方程)、4—5(不等式选讲),共计70分.全部试题都要求在答题卡上作答.
二.试题考查的知识和方法。
近三年高考数学试卷分析

近三年高考数学试卷分析近三年高考数学试卷分析近三年高考数学试卷(文科)分析高3年级数学组一、2021年高考数学试卷分析(一)试卷总体评价2021年高考数学新课标全国卷是以《课程标准》、《考试大纲》为依据, 试卷的结构保持了新课程高考数学试卷的一贯风格, 试题设计体现了“大稳定、小创新”的稳健、成熟设计理念. 今年试卷贴近中学教学实际, 在坚持对五个能力、两个意识考查的同时, 注重对数学思想与方法的考查, 体现了数学的基础性、应用性和工具性的学科特色. 以支撑学科知识体系的重点内容为考点来挑选合理背景, 善于应用知识之间的内在联系进行融合构建试卷的主体结构, 在新课程新增内容和传统内容的结合处寻找创新点, 考查更加科学. 试卷从多视角、多维度、多层次地考查数学思维品质, 考查考生对数学本质的理解, 考查考生的数学素养和学习潜能. 从考试性质上审视这份试卷, 它有利于中学数学教学和课程改革, 有利于高校选拔有学习潜能的新生, 是具有较高的信度、效度, 必要的区分度和适当的灵活度的可圈可点的试卷.(二)试卷考点内容及所占分值试卷考点内容统计及所占分值(三)试卷特点评析1. 注重基础考查试题区分度明显纵观全卷, 选择题简洁平稳, 填空题难度适中, 解答题层次分明. 选择、填空题考查知识点单一, 注重了对基础知识、基本方法、基本技能及高中数学主干知识的考查, 有利于稳定考生情绪, 也有助于考生发挥出自己理想的水平. 而在解答题中, 每道题均以多问形式出现, 其中第一问相对容易, 大多数考生能顺利完成; 而第二问难度逐渐加大, 灵活性渐强, 对知识的迁移和应用知识解决问题的能力要求较高, 给个性品质优秀、数学成绩良好的考生留有较大的展示空间.2. 淡化技巧重视通法能力立意强化思维试题淡化特殊技巧, 注重通性通法和对数学思想方法的考查. 如第(5)、(11)、(16)题考查了数形结合思想; 第(8)、(12)、(21)题涉及函数与方程思想及分类讨论思想等.试卷突出对五个能力和两个意识的考查. 如第 (6)、(16)、(21)题重点考查数学思维能力; 第 (9)、(15)、(18)题考查空间想象能力; 第(4)、(10)、(12)、(20)题综合考查思维能力、运算能力、实践能力、创新意识和应用意识等.3. 诠释考试说明内涵运算能力决定成败试题以高中内容为主, 但高层次包括低层次的内容, 例如在立体几何中考查平面几何的性质和数值的运算, 在解三角形和解析几何中包含着方程思想, 试题表述比较常规, 运算能力与运算手段决定了考试的成败.二、2021年高考数学试卷分析2021年高考数学新课标试题从试卷的形式和结构上看与往年的课标卷一样, 基本遵循“稳中有变、立足基础、突出能力、锐意求新”的命题指导思想,全卷设计基本合理、梯度基本适中,覆盖面广。
近5年高考数学试卷分析
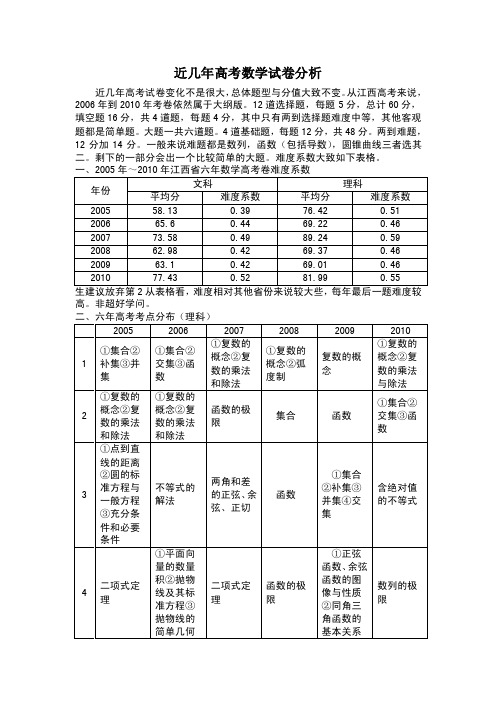
近几年高考数学试卷分析近几年高考试卷变化不是很大,总体题型与分值大致不变。
从江西高考来说,2006年到2010年考卷依然属于大纲版。
12道选择题,每题5分,总计60分,填空题16分,共4道题,每题4分,其中只有两到选择题难度中等,其他客观题都是简单题。
大题一共六道题。
4道基础题,每题12分,共48分。
两到难题,12分加14分。
一般来说难题都是数列,函数(包括导数),圆锥曲线三者选其二。
剩下的一部分会出一个比较简单的大题。
难度系数大致如下表格。
一、2005年~2010年江西省六年数学高考卷难度系数年份文科理科平均分难度系数平均分难度系数2005 58.13 0.39 76.42 0.51 2006 65.6 0.44 69.22 0.46 2007 73.58 0.49 89.24 0.59 2008 62.98 0.42 69.37 0.46 2009 63.1 0.42 69.01 0.46 2010 77.43 0.52 81.99 0.55生建议放弃第2从表格看,难度相对其他省份来说较大些,每年最后一题难度较高。
非超好学问。
二、六年高考考点分布(理科)2005 2006 2007 2008 2009 20101 ①集合②补集③并集①集合②交集③函数①复数的概念②复数的乘法和除法①复数的概念②弧度制复数的概念①复数的概念②复数的乘法与除法2 ①复数的概念②复数的乘法和除法①复数的概念②复数的乘法和除法函数的极限集合函数①集合②交集③函数3 ①点到直线的距离②圆的标准方程与一般方程③充分条件和必要条件不等式的解法两角和差的正弦、余弦、正切函数①集合②补集③并集④交集含绝对值的不等式4 二项式定理①平面向量的数量积②抛物线及其标准方程③抛物线的简单几何二项式定理函数的极限①正弦函数、余弦函数的图像与性质②同角三角函数的基本关系数列的极限性质5 周期函数①不等式的解法②导数的概念③利用导数研究函数的单调性和极值正弦函数、余弦函数的图像与性质数列导数的几何意义基本导数公式6 ①向量②向量的加法与减法③平面向量的数量积函数①集合②简单的线性规划①正弦函数、余弦函数的图像与性质②正切函数的图像和性质①椭圆及其标准方程②椭圆的简单几何性质二项式定理7 ①函数的单调性、奇偶性②导数的概念③导数的几何意义①向量②等差数列的前n项和公式①三垂线定理及其逆定理②直线和平面垂直的判定与性质③直线和平面所成的角①平面向量的数量积②椭圆的简单几何性质二项式定理余弦定理8 函数的极限二项式定理①球②棱锥二项式定理数列①点到直线的距离②不等式的解法9 ①球②两平面垂直的判定与性质①双曲线及其标准方程②圆的标准方程和一般方程①椭圆及其标准方程②椭圆的简单几何性质③圆的标准方程和一般方程不等式的性质①正多面体②棱锥③直线和平面平行的判定和性质④异面直线所成的角⑤二面角及其平面角①函数②互为反函数的函数图像间的关系③周期函数10 指数函数①排列、组合②等可能事件的概率①等可能事件的概率②分类计数原理与分步计数原理③等差数列及其通项(新概念问题)等可能事件的概率异面直线所成的角11 ①平面向量的数量积②二倍角的正弦余弦、正切③正弦函数余弦函数的图像与性质棱锥①函数的单调性、奇偶性②周期函数③导数的几何意义等可能事件的概率(新概念问题)等可能事件的概率①利用导数研究函数的单调性和极值②基本导数公式③充分条件和必要条件12 ①等差数列及其通项公式②组合③随机事件的概率函数的运用函数函数导数的几何意义13 ①函数的单调性、奇偶性②对数③对数的运算性质数列的极限①函数②反函数①平面向量的数量积②线段的定比分点平面向量的坐标表示平面向量的数量积14 简单的线性规划问题①对数函数②反函数数列不等式的性质①棱锥②球①排列②排列数公式③组合④组合数公式15 (立体图形的展开)棱柱①向量②向量的加法与减法①抛物线及其标准方程②抛物线的简单几何性质不等式的解法(无理不等式)双曲线及其标准方程16 ①双曲线及其标准方程②椭圆及其标准方程③椭圆的简单几何性质④双曲线的简单几何性质①圆的标准方程和一般方程②点到直线的距离③直线方程的点斜式和两点式①圆的标准方程与一般方程②点到直线的距离①棱柱②棱锥①圆的标准方程与一般方程②点到直线的距离①棱锥②点到平面的距离17 不等式的解法①几种常见函数的导数②两个函数的和、差、积、商的导数③利用导数研究函数的单调性和极值④函数的最大值和最小值①函数的连续性②不等式③不等式的解法①正弦、余弦的诱导公式②①两个函数的和、差、积、商的导数②利用导数研究函数的单调性和极值③不等式的解法①同角三角函数间的基本关系②二倍角的正弦、余弦、正切③正弦函数、余弦函数的图像和性质18 ①平面向量的数量积②几种常见函数的导数③两个函数的和、差、积、商的导数①等可能事件的概率②离散型随机变量的分布列③离散型随机变量的期望值和方差①几种常见函数的导数②正弦函数、余弦函数的图像与性质①等可能事件的概率②离散型随机变量的分布列③离散型随机变量的期望值和方差①等可能事件的概率②离散型随机变量的分布列③离散型随机变量的期望值和方差①等可能事件的概率②离散型随机变量的分布列③离散型随机变量的期望值和方差19 ①相互独立事件同时发生的概率②离散型随机变量的期望值和方差①正弦定理②两角和与差的正弦、余弦、正切③正切函数的图像和性质①相互独立事件同时发生的概率②离散型随机变量的期望值和方差①等差数列及其通项公式②等比数列及其通项公式③不等式的证明①正弦定理②两角和与差的正弦、余弦、正切③同角三角函数的基本关系①基本导数公式②利用导数研究函数的单调性和极值③函数的最大值和最小值20 ①三垂线定理及其逆定理②线面垂直的性质③点到平面的距离④二面角及其平面角①直线和平面垂直的判定与性质②三垂线定理及其逆定理③二面角及其平面角④余弦定理⑤直线和平面所成的角①直线和平面平行的判定与性质②直线和平面垂直的判定与性质③三垂线定理及其逆定理④二面角及其平面角⑤棱锥⑥棱柱①直线和平面平行的判定与性质②直线和平面垂直的判定与性质③直线和平面所成的角④点到平面的距离①两个平面垂直的判定与性质②直线和平面垂直的判定与性质③三垂线定理及其逆定理④二面角及其平面角⑤棱锥⑥棱柱①直线和平面垂直的判定与性质②两个平面垂直的判定与性质③点到平面的距离④二面角及其平面角21 ①数学归纳法②数学归纳法的运用③数列①椭圆及其标准方程②曲线与方程的概念③椭圆的简单几何性质④正弦、余弦函数的图像和性质①双曲线及其标准方程②曲线与方程的概念③由已知条件列出曲线方程④平面向量的数量积①双曲线及其标准方程②线段的定比分点③由已知条件列出曲线方程④直线的点斜式和两点式①双曲线及其标准方程②双曲线的简单几何性质③由已知条件列出曲线方程④圆的标准方程和一般方程①椭圆及其标准方程②椭圆的简单几何性质③由已知条件列出曲线方程22 ①导数的几何意义②几种常见函数的导数③点到直线的距离(向量的数量积)①等比数列及其通项②数学归纳法③数学归纳法的运用④不等式的证明①数列②数学归纳法③数学归纳法的运用④不等式的证明①利用导数研究函数的单调性和极值②两个函数的和、差、积、商的导数③不等式的证明①数列②等比数列及其通项公式①数列②等差数列及其通项③数论从2011年开始到2013年,江西高考开始改为新课标版。
2023年全国高考数学卷三试卷分析

2023年全国高考数学卷三试卷分析
本文旨在对2023年全国高考数学卷三试卷进行分析,以下是
对试卷不同部分的评述:
一、选择题部分
选择题部分共有X道题目,涵盖了高中数学各个知识点。
试卷整体难度适中,题目设置合理。
其中,有部分题目考察了思维灵活
性和数学推理能力,对学生的综合能力有一定要求。
二、计算题部分
计算题部分共有X道题目,包括了代数、几何等不同题型。
题目难度分布均匀,既考察了学生的计算能力,也考察了对数学知识
的理解和运用能力。
部分题目设置了较大的难度,对学生的思考能
力和解题技巧提出了一定的挑战。
三、证明题部分
证明题部分共有X道题目,涉及了几何证明和代数证明。
题目难度适中,要求学生能够熟练运用所学的数学理论进行推导和证明。
同时,也考察了学生的逻辑思维和论证能力。
综上所述,2023年全国高考数学卷三试卷内容全面,难度适中,能够全面考察学生在各个数学知识点上的掌握程度和综合应用能力。
希望考生能够认真复习相关知识,合理备考,取得好成绩。
2019届高考数学全国卷近五年试题评析及命题趋势分析预测

2013
[命题分析] 1.高考对导数的几何意义的考查,多在选择、填空题中出现, 难度较小. 2.高考重点考查导数的应用,即利用导数研究函数的单调性、 极值、最值问题,多在选择、填空的后几题中出现,难度中等.有时 也会作为压轴题出现,属于综合性问题,难度中等偏上. 3.近几年全国课标卷对定积分及其应用的考查极少,题目一般比 较简单,但也不能忽略.
(三)平面向量
年份 2018 卷别 具体考查内容及命题位置
Ⅰ卷 ห้องสมุดไป่ตู้面向量的线性运算·T6
Ⅱ卷 平面向量数量积的运算·T4 Ⅲ卷 平面向量的坐标运算及共线问题·T13
2017
2016
Ⅰ卷 向量模的运算·T13
甲卷 向量垂直的应用·T3 乙卷 向量模的运算·T13
丙卷 向量的夹角问题·T3
2015 2014 Ⅰ卷 平面向量的线性运算·T7 Ⅱ卷 平面向量共线定理的应用·T13
(七)统计与统计案例
年份 2018 2017 卷别 Ⅰ卷 Ⅱ卷 Ⅲ卷 Ⅲ卷 统计图表·T3 回归分析及应用·T18 茎叶图及独立性检验·T18 折线图·T3 统计图表的应用·T4 折线图、相关性检验、线性回归方程及其应用·T18 散点图、求回归方程、回归分析·T19 条形图、两变量间的相关性·T3 频率分布直方图、用样本的数字特征估计总体的数 字特征、正态分布、数学期望·T18 线性回归方程及其应用、最小二乘法·T19 具体考查内容及命题位置
(二)函数的图象与性质
年份 2018 卷别 Ⅰ卷 Ⅱ卷 具体考查内容及命题位置 函数图象的判断·T3 函数的奇偶性、对称性、周期性·T11
高中数学试卷分析与反思_高中数学试卷分析

【 - 高中作文】**年普通高考山东数学卷,继承了以往山东试卷的特点。
试题在具有了连续性和稳定性的基础上,更具有了山东特色,适合山东中学教学实际,对山东省平稳推进素质教育起到很好的导向作用。
不仅如此,试卷还体现新课程改革中对情感、态度、价值观和探究能力考查的理念,丰富了数学试卷的内涵品质,在有利于高校选拔人才的同时,具备了一定的评价功能,同时还有利于课程改革的纵深推进。
试卷形式保持稳定,主要体现在大纲理念、试卷结构、题目数量以及题型等方面与20**年基本相同,保证了试题年度间的连续稳定。
另外在全国20**年全面推进新课程标准的大背景下,作为首批进入课程改革的实验省,20**年的试卷在保持“稳定”的基调下,进一步加深对课程改革的渗透,既体现了知识运用的灵活性和创造性,又兼顾了试题的连续和谐与稳定发展。
一、遵循考试说明,注重基础试卷紧扣我省的考试说明,体现了新课程理念,贴近教学实际,从考生熟悉的基础知识入手,无论是必修内容,还是选修内容,许多试题都属于常规题。
部分题目“源于教材,高于教材”,做足教材文章。
如文、理科的选择、填空以及解答题的入手题(17)和(18)题,均侧重于中学数学学科的基础知识和基本技能的考查,这对正确地引导中学数学教学都起到良好的促进作用。
二、考查全面,注重知识交汇点但是,在本套试卷中还有我们经常关注的知识本次没有涉及,是否会说明一些问题,三视图在经历了新课标必考的阶段之后,今年没有涉及,另外抽样方法、频率分布直方图、二项式定理我们复习时认为重要的点也没有涉及,特别是二项式定理已经连续两年没有涉及,这也值得我们注意。
三、注重能力立意,体现文理差异四、重视创新意识,凸显新课程理念总之,20**年山东省高考数学文、理两份试卷,均具有较高的信度、效度和有效的区分度,达到了“考基础、考能力、考素质、考潜能”的考试目标。
(二)如果想考进大学,数学高考成绩应该在120以上,特别是想考重点大学数学成绩应该在130以上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013----2017年高考全国卷2、3试卷分析从2012年云南进入新课标高考至今,已有六年时间,数学因为容易拉分,加上难度变幻不定,可以说是我省考生最为害怕的一个学科,第一天下午开考的数学考得如何直接决定着考生第二天的考试情绪。
近5年全国卷数学试题从试卷的结构和试卷的难度上逐渐趋于平稳,稳中有新,难度都属于较为稳定的状态。
选择、填空题会以基础题呈现,属于中等难度。
选择题在前六题的位置,填空题在前二题的位置;解答题属于中等难度,且基本定位在前三题和最后一题的位置。
一、近五年高考数学考点分布统计表:从近五年数学试题知识点分布及分值分布统计表不难看出,试题坚持对基础知识、数学思想方法进行考查,重点考查了高中数学的主体内容,兼顾考查新课标的新增内容,在此基础上,突出了对考生数学思维能力和数学应用意识的考查,体现了新课程改革的理念。
具体来说几个方面:1.整体稳定,覆盖面广高考数学全国卷2、3全面考查了新课标考试说明中各部分的内容,可以说教材中各章的内容都有所涉及,如复数、旋转体、简易逻辑、概率等教学课时较少的内容,在试卷中也都有所考查。
有些内容这几年轮换考查,如统计图、线性回归、直线与圆、线性规划,理科的计数原理、二项式定理、正态分布、条件概率等。
2.重视基础,难度适中试题以考查高中基础知识为主线,在基础中考查能力。
理科前8道选择题都是考查基本概念和公式的题型,相当于课本习题的变式题型。
填空题前三题的难度相对较低,均属常规题型。
解答题的前三道题分别考查解三角形,分布列、数学期望,空间线面位置关系等基础知识,利用空间直角坐标系求二面角,属中低档难度题。
4.全面考查新增内容,体现新课改理念如定积分、函数的零点、三视图、算法框图、直方图与茎叶图、条件概率、几何概型、全称命题与特称命题等。
5.突出通性通法、理性思维和思想方法的考查数学思想方法是对数学知识的最高层次的概括与提炼,是适用于中学数学全部内容的通法,是高考考查的核心。
数形结合的思想、方程的思想、分类讨论的思想等在高考中每年都会考查。
尤其数形结合,每年还专门有一道“新函数”的大致图象问题6.注重数学的应用和创新近三年的试题加强了应用问题的考查,涉及线性规划、统计图表、线性回归等,文理科每年都有解答题考查概率统计,2009(理科)和2011年都在21题位置上设置了函数与导数的应用题。
7.注重能力考查,有效区分不同思维层次的学生鼓励考生宽口径、多角度的思考和解决问题,不拘泥于某一成法,不局限考生的思想,设置的题目尽可能让考生可以从不同角度入手,均能得出结果。
二、2017高考题师生感觉初做2017年高考试题,第一感觉是,今年的高考试题难于2016年高考数学试题。
而且,从知识点的布点来看,今年的高考题更加合理,具有较强的综合考察学生掌握知识程度的作用。
2017年高考试题保持了数学一贯的严密体系,还是把对数学基本概念的理解和把握摆在首要考察的地位,侧重于考察学生的基本知识和基本技能,达到了“考基础、考能力、考素质、考潜能”的考试目标。
今年高考题,选择题注重双基的考察,当然其中也有数学思想方法的考察,比如第11题的等价转化与化归及数形结合思想,第12题的坐标化运用等,16题,需要学生有很强的空间想象能力,而解答题特别突出计算能力,思维能力,虽然说题目不偏不怪,包括20,21都还是算常规,有一定灵活,比如选做题中,22题的参数方程求轨迹方程的问题,可以说我们平时的复习备考基本都到不了这样的高度,这也为我们以后的备考提出新的思考。
从而导致多数学生叫苦叫难的,此次数学试题稳中有变,总体较2016年有较好的区分度,试卷关注社会热点、贴近实际,充分利用数学学科特点,突出创新。
其中,立体几何题题干不常规,解析几何考查抛物线和圆,第一问就提高难度。
函数与导数大题第二问给出关于正整数命题,其实我们还真不能说不常规,我们不妨冷静的分析一下前5年我们云南省的高考题,18题,前五年就出现过两次这种概率加分段函数讨论的问题,19题,常规的锥体,没有动点,没有参数,20题,前五年就很注重抛物线与圆相结合考察的问题,对于21题就更不用说了,围绕y=lnx和y=x-1的基本模型展开,第二问需要用第一问结论巧妙赋值即可。
但是高考,不但考知识,还考心态,谁的心态好,谁时间分配合理,就能考高分。
今年的高考仍然有特别强的延续性,常规重点仍然是反复出现,专家家从命题到应试,各个方面都非常具体到位,小题练基本功,练竞争意识。
所以平时我们非常有必要给学生总结一些常用的结论,做到省时,高效,提高竞争力。
诸如中点弦,分点弦,以及常见的切线等结论。
大题中重通法,强规范。
要说专家压中了多少题,这个还真不好判断,四、高考复习备考策略分析1.注重基础,全面复习我们的高考无论如何变化,对基础知识和基本技能的考核,永远是不会变的,注重回归课本、扎实基础,努力提高学生的能力,既要引导学生掌握好新教材中的新内容,又要引导学生掌握好旧的内容,在教学中要体现过程教学,精选习题,有效训练。
高考试题总是以重点基础知识为主线组织全卷的内容的,从今年乃至近几年甚至自高考以来, 不重视“双基”的考生,不可能取得取得高分。
每年试题的框架主体都是考查数学的基础知识,基本技能和通性通法, 如函数的单调性、奇偶性、零点、图像性质及变换;三角函数及其图像的基本性质;向量的基本运算;圆锥曲线的基本概念、性质及应用;数列的基本性质及应用;空间图形的识别及线面的位置关系(包括面积、体积和理科的夹角和距离);古典概型的方法;统计的基本方法(包括散点图、茎叶图、直方图、回归直线方程、方差、标准差)等。
2.注重思想方法,思维灵活如数形结合思想,新课程加强了和“图”有关的内容.如:三视图、统计图、程序框图、函数的图像性质及变换、空间线面位置关系、平面直线与圆锥曲线的位置关系等;函数与方程的思想方法,如函数的性质及围绕研究函数性质的相关知识和方法(导数、数列、解析几何等)、、特殊与一般的思想方法、变换的思想方法;还有数据的收集、整理、分析和应用,如统计与概率、线性规划等相关的应用问题,体现或然和必然的数学思想。
在复习过程中要熟悉知识的来龙去脉,“知其然,更要知其所以然”,克服急功近利的思想。
如对“不等式放缩法”,有一些常见的放缩技巧,但更要明白为什么要放缩,然后才是放缩技巧的问题,放缩的本质我感觉是目标逼近,根据你的需要,逐步向目标逼近。
对知识的掌握要做到策略化。
3.通法为主,变法为辅重视中学数学的通性通法,倡导举一反三、一题多解和多题一解,努力培养学生“六种能力、二个意识”.数学能力包括运算求解能力、数据处理能力、空间想象能力、抽象概括能力、推理论证能力、实践能力和创新意识.能力的分类和要求与以前有不同,必然要反映在命题中.特别应注意新增加的“数据处理能力”和“实践能力和创新意识”.前者与统计有关,后者与应用问题有关.另外,“推理论证能力”有别于先前四大能力之一的“逻辑思维能力”,逻辑思维能力注重是演绎推理,“合情推理”也应引起我们的重视,它可以有效地培养学生的创新意识,这正是我们国家现在大力提倡的.我们鼓励考生思维活跃, 提倡考生发散思维, 就应该给与特殊方法,特殊技能一定的地位, 针对具体问题, 采用具体的方法,这是很重要的处理问题的方法.我们强调通性通法的重要,并不意味着完全否定其他的特殊方法, 其他的方法也是处理问题的一个重要方面,在整个数学科的发展过程中, 也很重要的, 也应该有所体现.4.重视数学语言,提高素养.数学素养的高低在某种意义上来说就是其数学语言掌握和运用的程度的差异.因此,数学学习的过程可以理解为就是数学语言的学习过程.无论学生将来从事何种工作,经过高中(包括基础教育)阶段的数学学习,具备初步的数学语言理解、转化和表达能力是非常重要的,是一个人具备一定的数学素养的基本标志.尤其是当前高考考试形式主要考查的是书面表达能力.试卷能否得分,不唯你会做,重要的是你要准确的表达出来,卷面上的文字表述务必正确、简洁;文字书写力求工整.因此,在日常教学中要重视对学生口头和书面表述(包括作图)能力的培养,以求达到数学语言运用的准确性、逻辑性、完整性和流畅性.5.重视创新能力和应用意识的培养创新能力的培养是新课改的一个重要理念,我们的教学对象,不应该仅仅是接受知识的口袋,而更应该是创造知识的机器,我们的教学对象,是蓄势待发的火箭,他们将来应该能够独立地翱翔于知识的太空,应该能够独立的探索未知的世界,而我们,作为教师,应该像点火者一样,激发学生的能动性,赋予他们能够创新的基本知识,激活他们的创新意识,让学生能够在已有的知识基础上,探索未知的知识领域.只有这样,我们和我们的教学对象才能真正体会“生知也有涯,而知也无涯”的境界,只有这样,我们的知识水平才能不断的增加,我们的认知能力才能不断地提高,教师永远要记住:培养学生的创新能力和探索能力,永远是重要的.培养数学的应用意识也是非常重要的,数学对我们大多数人而言,应该是一个工具,是处理其它实际问题的工具,如何将已有的数学知识应用到我们面临的实际问题中,如何利用我们已掌握的数学知识,处理我们面对的实际问题,这都是很重要的,我们教育的目的,是使我们的学生将来走向生活,走向社会,并且能够适应社会,这就要求他们必须将现在的“所学”和将来的“所遇”有一个好的衔接,这样的能力不是自然产生的,需要一个培养的过程,要有意识的培养学生的数学应用意识,高考命题中很好的体现了这一点,我们的高考题中有相当数量的题目是数学的应用题,需要考生面对实际问题,将他们转化为数学问题,然后运用所学的知识,解决这个数学问题,最后再将所得到的数学结果,还原到实际背景中,并合理的解释实际的问题,这就是数学的应用过程,这就是数学的建模过程,这也是我们的教学对象,将来走向社会后,需要面对和解决问题的主要过程,培养学生适应这个解决问题的方法和过程是非常重要的.。
