考研数一真题试卷2012

合集下载

考研(数学一)历年真题试卷汇编1(题后含答案及解析)

考研（数学一）历年真题试卷汇编1(题后含答案及解析)题型有：1. 选择题 2. 填空题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．(2011)已知当x→0时，函数f(x)=3sin．x=sin 3x与cxk是等价无穷小，则( )A．k=1，c=4．B．k=1，c=4．C．k=3，c=4．D．k=3，c=-4．正确答案：C解析：因为当x→0时，函数f(x)=3sin x=sin 3x与cxk是等价无穷小，所以从而k-1=2，即k=3，于是故应选C．2．(2012)设函数f(x)=(ex-1)(e2x-2).….(enx-n)，其中n为正整数，则f’(0)=( ) A．(-1)n-1(n-1)!．B．(-1)n(n-1)!．C．(-1)n-1n!．D．(-1)nn!．正确答案：A解析：利用导数的定义求f’(0)．故应选A．3．(2012)曲线的渐近线的条数为( )A．0．B．1．C．2．D．3．正确答案：C解析：应同时考虑水平渐近线、铅直渐近线与斜渐近线．因为所以y=1是曲线的水平渐近线，同时说明曲线无斜渐近线．又因为所以x=1是曲线的铅直渐近线，x=-1不是曲线的铅直渐近线．综上所述，应选C．4．(2009)设A，B均为2阶矩阵，A*，B*分别为A，B的伴随矩阵．若｜A｜=2，｜B｜=3，则分块矩阵的伴随矩阵为( )A．B．C．D．正确答案：B解析：本题主要考查分块矩阵的行列式、伴随矩阵的相关公式以及分块矩阵的逆矩阵．由=(-1)2×2｜A｜｜B｜=6知，矩阵可逆，从而故应选B．5．(2006)设A、B为两个随机事件，且P(B)＞0，P(A｜B)=1，则必有( ) A．P(A∪B)＞P(A)．B．P(A∪B)＞P(B)．C．P(A∪B)=P(A)．D．P(A∪B)=-P(B)．正确答案：C解析：本题主要考查乘法公式与加法公式．由已知条件与乘法公式有P(AB)=P(B)P(A｜B)=P(B)，再由加法公式有P(A∪B)=P(A)+P(B)-P(AB)=P(A)．故应选C．6．(2003)设函数f(x)在(-∞，+∞)内连续，其导函数的图形如图1所示，则f(x)有( )A．一个极小值点和两个极大值点．B．两个极小值点和一个极大值点．C．两个极小值点和两个极大值点．D．三个极小值点和一个极大值点．正确答案：C解析：本题主要考查导函数y=f’(x)与函数y=f(x)的图形的关系与一元函数的极值(点)．由于已知函数是抽象函数，无法用推理法及反例排除法解决．考虑用y=f’(x)与y=f(x)的图形之间的关系画出y=f(x)的图形，利用定性分析的方法解决该问题．根据y=f’(x)的图形画出y=f(x)的图形，如图2所示，根据y=f(x)的图形知，f(x)有两个极小值点和两个极大值点．故应选C．7．(2011)函数f(x)=ln｜(x-1)(x-2)(x-3)｜的驻点个数为( )A．0．B．1．C．2．D．3．正确答案：C解析：因为，所以x=1，x=2，x=3是曲线y=f(x)的铅直渐近线．又，由此可画出f(x)=ln｜(x-1)(x-2)(x-3)｜的草图，如图3所示，由图形可知，存在两点x1，x2，使得f’(x1)=f’(x2)=0，即f(x)有两个驻点．故应选C．8．(2006)设函数y=f(x)具有二阶导数，且f’(x)＞0，f’’(x)＞0，△x为自变量x在点x0处的增量，△y与dy分别为f(x)在点x0处对应的增量与微分，若△x＞0，则( )A．0＜dy＜△y．B．0＜△y＜dy．C．△y＜dy＜0．D．dy＜△y＜0．正确答案：A解析：△y=f(x0+△x)-(x0)=f’(ξ)△x (x0＜ξ＜x0+△x)．因为f’’(x)＞0，所以f’(x)单调增加，从而f’(ξ)＞f’(x0)，于是△y=f’(ξ)△x＞f’(x0)△x=dy．又因为f’(x)＞0，所以0＜dy＜△y．故应选A．9．(1999)设两个相互独立的随机变量X和Y分别服从正态分布N(0，1)和N(1，1)，则( )A．P{X+Y≤0}=B．P{X+Y≤1}=C．P{X-Y≤0}=D．P{X-Y≤1}=正确答案：B解析：由于均服从正态分布且相互独立的随机变量的线性组合仍然服从正态分布，所以由正态分布的几何意义知，正态分布的密度函数关于均值左右对称，于是其小于均值的概率为，从而P{X+Y≤1}=故应选B．10．(2002)设函数y=f(x)在(0，+∞)内有界且可导，则( )A．B．C．D．正确答案：B解析：取，因为排除A、C、D．故应选B．11．(2005)以下四个命题中，正确的是( )A．若f’(x)在(0，1)内连续，则f(x)在(0，1)内有界．B．若f(x)在(0，1)内连续，则f(x)在(0，1)内有界．C．若f’(x)在(0，1)内有界，则f(x)在(0，1)内有界．D．若f(x)在(0，1)内有界，则f’(x)在(0，1)内有界．正确答案：C解析：取f’(x)=，在(0，1)内连续，但f(x)=lnx在(0，1)内无界，排除A．取f(x)=，在(0，1)内连续，但f(x)在(0，1)内无界，排除B．取f(x)=，在(0，1)内有界，但f’(x)=在(0，1)内无界，排除D．故应选C．12．(2004)设f’(x)在[a，b]上连续，且f’(a)＞0，f’(b)＜0，则下列结论中错误的是( )A．至少存在一点x0∈(a，b)，使f(x0)＞f(a)．B．至少存在一点x0∈(a，b)，使f(x0)＞f(b)．C．至少存在一点x0∈(a，b)，使f’(x0)=0．D．至少存在一点x0∈(a，b)，使f(x0)=0．正确答案：D解析：取f(x)=2-x2，x∈[-1，1]，则f’(x)=-2x在[a，b]=[-1，1]上连续，且f’(a)=f’(-1)=2＞0，f’(b)=f’(1)=-2＜0，满足已知条件．由f(x)=2-x2的图形可知，在(-1，1)内，f(x)＞1，即对任意x0∈(-1，1)，都有f(x0)≠0，这表明D选项是错误的．故应选D．13．(2001)设f(x)的导数在x=a处连续，又，则( )A．x=a是f(x)的极小值点．B．x=a是f(x)的极大值点．C．(a，f(a))是曲线y=f(x)的拐点．D．x=a不是f(x)的极值点，(a，f(a))也不是曲线y=f(x)的拐点．正确答案：B解析：由f(x)的导数在x=a处连续及=f’(a)=0，即x=a是f(x)的驻点．从而所以x=a是f(x)的极大值点．故应选B．14．(2003)设f(x)为不恒等于零的奇函数，且f’(0)存在，则函数g(x)=( ) A．在x=0处左极限不存在．B．有跳跃间断点x=0．C．在x=0处右极限不存在．D．有可去间断点x=0．正确答案：D解析：因为f(x)为不恒等于零的奇函数，所以f(0)=0，又f’(0)存在．所以故x=0是g(x)的可去间断点．应选D．15．(2005)设函数u(x，y)=φ(x+y)+φ(x+y)+其中函数φ具有二阶导数，ψ具有一阶导数，则必有( )A．B．C．D．正确答案：B解析：取φ(x)=x2，ψ(x)=0，则u(x，y)=(x+y)2+(x-y)2=2x2+2y2．于是由此可知，选项A、C、D都不正确．故应选B．16．(2005)设an＞0，n=1，2，…，若收敛，则下列结论正确的是( ) A．B．C．D．正确答案：D解析：取收敛，但发散，排除A；发散，排除B；发散，排除C．故应选D．17．(2002)设A是m×n矩阵，B是n×m矩阵，则线性方程组(AB)X=0( ) A．当n＞m时仅有零解．B．当n＞m时必有非零解．C．当m＞n时仅有零解．D．当m＞n时必有非零解．正确答案：D解析：(推理法)因为当n＜m时，齐次线性方程组BX=0有非零解，从而线性方程组(AB)X=0有非零解，故应选D．18．(2002)设向量组α1，α2，α3线性无关，向量β1可由α1，α2，α3线性表示，而向量β2不能由α1，α2，α3线性表示，则对任意常数k，必有( )A．α1，α2，α3，kβ1+β2线性无关．B．α1，α2，α3，kβ1+β2线性相关．C．α1，α2，α3，β1+kβ2线性无关．D．α1，α2，α3，β1+kβ2线性相关．正确答案：A解析：因为β2不能由α1，α2，α3线性表示，则α1，α2，α3，β2线性无关．取k=0，由B知，α1，α2，α3，β2线性相关，与α1，α2，α3，β2线性无关矛盾，排除B．取k=0，由C知，α1，α2，α3，β1线性无关，则β1不能由α1，α2，α3线性表示，与已知条件矛盾，排除C．取k=1，由D知，α1，α2，α3．β1+β2线性相关，因为α1，α2，α3线性无关，所以β1+β2可由α1，α2，α3线性表示，而β1可由α1，α2，α3线性表示，于是β2可由α1，α2，α3线性表示，与已知条件矛盾，排除D．故应选A．填空题19．(2000)=_____，正确答案：解析：由定积分的几何意义，表示由直线x=0，x=1，y=0与曲线y=所围成的图形的面积，如图5所示，所以(其中S为单位圆(x-1)2+y2≤1的面积)．20．(2001)(x3+sin2x)cos2xdx=_______．正确答案：解析：21．(2012)设区域D是由曲线y=sinx，x=，y=1围成，则(x5y-1)dxdy=_______.正确答案：-π解析：22．(2008)设D={(x，y)｜x2+y2≤1}，则(x2-y)dxdy=______．正确答案：解析：因为积分区域D关于x轴对称，函数y关于y是奇函数，所以．由轮换对称性以及极坐标下二重积分的计算方法，有23．(2009)设Ω={(x，y，z)｜x2+y2+z2≤1}，则z2dxdydz=_______.正确答案：解析：利用轮换对称性，有再利用球坐标下三重积分的计算有24．(2007)设曲面∑：｜x｜+｜y｜+｜z｜=1，则=_______.正确答案：解析：因为∑关于yOz平面对称，x关于x为奇函数，所以．由轮换对称性，其中S是∑的表面积，记∑在第一卦限部分的面积为S1．如图8所示，则。

2012年考研数学一真题及答案详解

（7）设随机变量 x 与 y 相互独立，且分别服从参数为 1 与参数为 4 的指数分布，则 px y （）
( A) 1 5 ( B) 1 3 (C ) 2 5 ( D) 4 5
（ 8 ）将长度为 1m 的木棒随机地截成两段，则两段长度的相关系数为（） 1 1 ( A) 1 ( B) (C ) ( D) 1 2 2 二、填空题：914 小题，每小题 4 分，共 24 分，请将答案写在答题纸指定位置．．．上. （9）若函数 f ( x) 满足方程 f '' ( x) f ' ( x) 2 f ( x) 0 及 f ' ( x) f ( x) 2e x ，则 f ( x) =________。（10） x 2 x x 2 dx ________。
x2 x y 2 x 1 渐近线的条数为（）（1）曲线
（A）0 （B）1 （C）2 （D）3 【答案】：C
x2 x lim 2 x 1 x 1 【解析】：，所以 x 1 为垂直的 lim x2 x 1 x x 2 1 ，所以 y 1 为水平的，没有斜渐近线故两条选 C
2012 年全国硕士研究生入学统一考试数学(一)试卷
一、选择题：1～8 小题，每小题 4 分，共 32 分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸指定位置上. （1）曲线 y （A）0 （D）3
x2 x 渐近线的条数为（） x2 1
（B）1
（C）2
列向量组线性相关的是（（A） 1 , 2 , 3
）（C） 1 , 3 , 4 （D）
（B） 1 , 2 ,4
第 1 页共 17 页

考研数学一二维随机变量及其分布历年真题试卷汇编2_真题(含答案与解析)-交互

考研数学一（二维随机变量及其分布）历年真题试卷汇编2(总分150, 做题时间180分钟)选择题1.[2009年] 设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y(z)为随机变量Z=XY的分布函数，则函的概率分布P(Y=0)=P(Y=1)=1／2．记FZ数F(z)的间断点的个数为( )．ZSSS_SINGLE_SELAB1C2D3分值: 7.5答案:BF(z)=P(Z≤z)=P(XY≤z)=P(XY≤z｜Y=0)P(Y=0)+P(XY≤z｜Y=1)P(Y=1)Z=[P(XY≤z｜Y=0)+P(XY≤z｜Y=1)]／5．又X，Y相互独立，故 F(z)=[P(X·0≤z)+P(X≤z)]／2．Z(z)=[+ф(z)]／2=ф(z)／2．当z＜0时， FZ(z)=[P(Ω)+P(X≤z)]／2=[1+ф(z)]／2．当z≥0时， FZ综上所述，得到因(z)只有一个间断点z=0．仅B入选．所以FZ2.[2012年] 设随机变量X与Y相互独立，且分别服从参数为1和参数为4的指数分布，则P(X＜Y)=( )．SSS_SINGLE_SELA1／5B1／3C2／5D4／5分值: 7.5答案:A由题设有而X与Y相互独立，故f(x，y)=fX (x)fY(y)=则P(X＜Y)= f(x，y)dxdy=∫0+∞∫x+∞4e-(x+4y)dxdy=一∫+∞e-x dx∫x+∞e-4y d(一4y)=∫0+∞e-x·e-4x dx=∫+∞e-5x dx=仅A入选．3.[2005年] 设二维随机变量(X，Y)的概率分布为若随机事件{X=0}与{X+Y=1}相互独立，则( )．SSS_SINGLE_SELAa=0．2，b=0．3Ba=0．4，b=0．1Ca=0．3，b=0．2Da=0．1，b=0．4分值: 7.5答案:B由=(a+0．4)+(b+0．1)=a+b+0．5=1(归一性)知，a+b=0．5．又由事件{X=0}与{X+Y=1}相互独立，有P(X=0，X+Y=1)=P(X=0)P(X+Y=1)，而P(X=0，X+Y=1)=P(X=0，Y=1)=a，P(X=0)=a+0．4，P(X+Y=1)=P(X=0，Y=1)+P(X=1，Y=0)=a+b，故 a=(a+0．4)(a+b)=(a+0．4)×0．5．①所以a=0．4．从而b=0．5一a=0．1．填空题4.[2003年] 设二维随机变量(X，Y)的概率密度为则P(X+Y≤1)=______．SSS_FILL分值: 7.5答案:首先求出积分区域D ∩ G．D ∩ G实质上是G={(x，y)｜0≤x≤y≤1}与D={(x，y)｜x+y≤1}交集．可知，0≤x≤y≤1是在y=x上方的区域，而x+y≤1是直线x+y=1下方的区域．两者之交即为D ∩ G(见图)，故5.[2015年] 设二维随机变量(X，Y)服从正态分布N(1，0；1，1；0)，则P{XY—Y＜0}=_______．SSS_FILL分值: 7.5答案:因(X，Y)～N(1，1；0，1；0)，ρ=0，故X，Y相互独立，则P{XY—y＜0}=P{(X一1)Y＜0}=P{X一1＜0，Y＞0}+P{X一1＞0，Y＜0}=P{X＜1}P{Y＞0}+P{X＞1}P{Y＜0}．因X～N(1，1)，故P{X＜1}=P{X＞1}=．因Y～N(0，1)，故P{Y＞0}=P{Y＜0}=．所以6.[2006年] 设随机变量X与Y相互独立，且均服从区间[0，3]上的均匀分布，则P(max{X，Y}≤1)=______．SSS_FILL分值: 7.5答案:1/9P(max(X，Y)≤1)=P({X≤1}{Y≤1})=P(X≤1，Y≤1)=P(X≤1)P(Y≤1)=[(1一0)／(3—0)][(1一0)／(3一0)]=(1／3)×(1／3)=1／9．解答题[2008年] 设随机变量X与Y相互独立，X的概率分布为P(X=i)=1／3(i=一1，0，1)，Y的概率密度为记Z=X+Y．SSS_TEXT_QUSTI7.求P(Z≤1／2｜X=0)；分值: 7.5答案:由于X，Y相互独立，有P(Z≤1／2 ｜X=0)=P(X+Y≤1／2｜X=0)=P(y≤1／2｜X=0)SSS_TEXT_QUSTI8.求Z的概率密度fZ(z)．分值: 7.5答案:因X的可能取值为一1，0，1，而fY(y)取非零值的自变量的变化范围为0≤y≤1，一1≤z=x+y≤2．(1)当z≥2时，X，Y的所有取值均满足上式，故F(z)=P(Z≤z)=P(X+Y≤z)=1．(2)当z=x+y＜一1时，X，Y的取值为空值，则P(X+Y≤z)==0．(3)当一1≤z＜2时，下面用全概率公式求出FZ(z)的表示式：FZ(z)=P(Z≤z)=P(X+Y≤z)=P(X+Y≤z｜X=一1)P(X=一1)+P(X+Y≤z｜X=0)P(X=0)+P(X+Y≤z｜X=1)P(X=1)(Fy(z)为y的分布函数)，则fZ (z)=F'Z(z)=[FY(z+1)+fY(z)+fY(z—1)]．当0＜z+1＜1或0＜z＜1或0＜z—1＜1，即一1＜z＜2时，FZ(z)=；其他情况下，fZ(z)=0．[2017年] 设随机变量X，Y相互独立，，Y的概率密度为fY(y)=SSS_TEXT_QUSTI9.求P{Y≤E(Y)}；分值: 7.5答案:因E(Y)=∫-∞+∞yfY(y)dy=∫1y·2ydy=，故SSS_TEXT_QUSTI10.求Z=X+Y的概率密度．分值: 7.5答案:Z的分布函数FZ(Z)=P{X+Y≤z，X=0}+P{X+Y≤z，X=2} =P{X=0，Y≤z}+P{X=2，Y+2≤z}=，故Z的概率密度函数为[2014年] 设随机变量X的概率分布为P(X=1)=P(X=2)=，在给定X=i的条件下，随机变量y服从均匀分布U(0，i)(i=1，2)．SSS_TEXT_QUSTI11.求Y的分布函数F(y)；Y分值: 7.5答案:记U(0，i)的分布函数为F(x)(i=1，2)，则i(y)=p(Y≤Y)=P(x=1)P(Y≤y｜X=1)+P(X=2)P(Y≤y｜X=2)于是FY因在X=i的条件下，Y服从均匀分布U(0，i)(i=1，2)，故当y≤0时，(y)=0．Fi当0＜y≤1时，当1＜y＜2时，当y≥2时，所以SSS_TEXT_QUSTI12.求期望E(Y)．分值: 7.5答案:(y)可得概率密度函数为由Y的分布函数FY+∞yfy(y)dy=故E(Y)=∫-∞[2013年] 设随机变量X的概率密度为令随机变量，SSS_TEXT_QUSTI13.求y的分布函数；分值: 7.5答案:+∞f(x)dx=，得到a=9．此时，X的利用概率密度函数的归一性，由1=∫-∞概率密度为(y)．由题设知，Y的取值范围为1≤Y≤2，故设Y的分布函数为FY(y)=P{Y≤y}=0；P(1≤Y≤2)=1．因而当y＜1时，FY当1≤Y＜2时，F(y)=P{Y≤y}=P{Y＜1}+P{Y=1}+P{1＜Y≤y}Y=0+P{X≥2}+P{1＜X≤Y}=(y)=P{Y≤y}=P{Y≤2}=1．当Y≥2时，FY综上得到y的分布函数为SSS_TEXT_QUSTI14.求概率P{X≤Y}．分值: 7.5答案:由随机变量y的分段表示式易看出，满足x≤y的x的取值范围为x＜2．因而所求概率为P{X≤Y}=P{X＜2}=[2016年]设二维随机变量(X，Y)在区域D=((x，y)｜0＜x＜1，x2＜y＜)上服从均匀分布．令SSS_TEXT_QUSTI15.写出(X，Y)的概率密度；分值: 7.5答案:易求得区域D的面积，故(X，Y)的概率密度SSS_TEXT_QUSTI16.问U与X是否相互独立?并说明理由；分值: 7.5答案:考查事件{U=0}与乘积的概率是否与事件{U=0}的概率的乘积相等．事实上，它们不相等．易求得显然，故U与X不独立．SSS_TEXT_QUSTI17.求Z=U+X的分布函数FZ(z)．分值: 7.5答案:下面用全集分解法求f(u，v)的分布函数FZ(z)=P(Z≤z)=P(U+X≤z)．FZ(z)=P(U+X≤z)=P(U=0，U+X≤z)+P(U=1，U+X≤z)=P(U=0，X≤z)+P(U=1，U≤z—1)=P(X＞y，X≤z)+P(X≤Y，X≤z一1)注意到x取值的边界点为0，1，而U取值边界点也为0，1，因而z的取值的分段点为0，1，2．于是应分下述四种情况分别求出FZ(z)的表示式．①z＜0时，则P(X≤z)==0，P(X≤z—1)==0，故FZ(z)=0．②0≤z＜1时，③1≤z＜2时，④z≥2时，FZ(z)=P(X＞Y)+P(X≤y)=P(U=0)+P(U=1)=1．综上所述，Z的分布函数为[2009年] 袋中有一个红球、两个黑球、三个白球．现在有放回地从袋中取两次，每次取一个，以X，Y，Z分别表示两次取球所取得的红球、黑球与白球个数．SSS_TEXT_QUSTI18.求P(X=1｜Z=0)；分值: 7.5答案:(I)用缩减样本空间的方法求之．求时应注意两次取球取到的是不同类的球，要讲次序．因而两次都没取到白球(Z=0)的条件下，只能取红、黑两种球，且每次都要取到一个红球，其可能性为C11×C21+C21×C11=4，总的可能性为C 31×C31=3×3=9，故SSS_TEXT_QUSTI19.求二维随机变量(X，Y)的概率分布．分值: 7.5答案:由题设知X与Y的所有可能取值均为0，1，2，而取值的概率可由古典概率的计算公式得到．计算时要注意两次取球取到的是不同类的球要讲次序，取到的是同类的球不讲次序．故(X，Y)的概率分布为20.设随机变量X的概率密度为f(x)=e-｜x｜／2，一∞＜x＜+∞，问随机变量X 与｜X｜是否相互独立?为什么?SSS_TEXT_QUSTI分值: 7.5答案:因X和｜X｜为两个随机变量，下面证明对于给定的a(0＜a＜+∞)，式P(X＜x，Y＜y)=P(X＜x)P(Y＜y)不成立，从而X与｜X｜不相互独立．事实上，因事件{｜X｜＜a}包含在事件{X＜a}之中，即{X＜a} {｜X｜＜a}，故P(X＜a，｜X｜＜a)=P({X＜a}∩{｜X｜＜a})=P(｜X｜＜a)．又P(X＜a)＜1，P(｜X｜＜a)＞0，因而P(X＜a)P(｜X｜＜a)＜P(｜X｜＜a)．于是P(X＜a，｜X｜＜a)=P(｜X｜＜a)＞P(X＞a)P(｜X｜＜a)，故P(X＞a，｜X｜＜a)≠P(X＜a)P(｜X｜＜a) (0＜a＜+∞)．可知，X与｜X｜不相互独立．1。

2012考研数学一真题及解析

2012考研数学一真题及解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸指定位置上.（1）【答案】：C【解析】：221lim1x x xx →+=∞-，所以1x =为垂直的 22lim 11x x xx →∞+=-，所以1y =为水平的，没有斜渐近线故两条选C（2）【答案】：C 【解析】：'222()(2)()(1)(22)()(1)(2)()x x nx x x nx x x nx f x e e e n e e e n e e ne n =--+---+---所以'(0)f =1(1)!n n -- （3）【答案】：【解析】：由于(,)f x y 在()0,0处连续，可知如果22(,)limx y f x y x y →→+存在，则必有0(0,0)lim (,)0x y f f x y →→== 这样，220(,)limx y f x y x y →→+就可以写成2200(,)(0,0)lim x y f x y f x y ∆→∆→∆∆-∆+∆，也即极限220(,)(0,0)limx y f x y f x y ∆→∆→∆∆-∆+∆存在，可知lim 0x y ∆→∆→=，也即(,)(0,0)00f x y f x y o∆∆-=∆+∆+。

由可微的定义可知(,)f x y 在(0,0)处可微。

（4）【答案】：(D) 【解析】：2sin kx k eI e xdx =⎰看为以k 为自变量的函数，则可知()2'sin 0,0,k k I e k k π=≥∈，即可知2sin kx k eI e xdx =⎰关于k 在()0,π上为单调增函数，又由于()1,2,30,π∈，则123I I I <<，故选D（5）【答案】：（C ）【解析】：由于()13411341111,,011011c c c c ααα--=-==-，可知134,,ααα线性相关。

中国科学院大学2012年《概率论与数理统计》考研专业课真题试卷

服从 [0, ] 上的均匀分布.
（a）试求针与线相交的概率；（b）设计一个投针实验用以估计圆周率 .
3 （共 15 分）有一个实验需要三个步骤才能完成，第一个步骤能按时完成的概率为 0.7，已知第一个步骤完成的条件下，第二个步骤能按时完成的概率为 0.8，科目名称：概率论与数理统计第1页共3页
cov( X , Y ).
5. （共 20 分）设 X 和 Y 是两个相互独立的服从同一指数分布（参数为）的随机变量，现记：
Z
min( X , Y ) . max( X , Y )
任意给定 c (0, 1), 试求概率 P( Z c).
6．（每小题 15 分，共 30 分）植物学家通常假定野外每单位面积的区域上有某种植物的个数服从泊松分布，现在考察 n 个互不叠交的面积分别为
科目名称：概率论与数理统计
第2页
共3页
问：（a）检验统计量是什么？为什么 n 充分大时它近似服从正态分布，请给出你所知道的理由；（b）根据调查数据，我们是否能拒绝 H 0 ? （提示： z 0.01 2.33, 即 1 (2.33) 0.01, ( x ) 是标准正态分布函数）；（c）如果实际比例是 0.4，请问犯第二类错误的概率是多少？（提示：可将 102 近似算作 10， 6 近似算作 2.45， (0.34) 0.6631 ）.
前两个步骤能按时完成的条件下，第三个步骤能按时完成的概率为 0.9，问前二个步骤能按时完成，但第三个步骤却失败的概率是多少？
4
(共 15 分) 一个盒子中有 5 个红球和 8 个蓝球，从中无放回地抽 3 个球，设X
是 3 次中得到红球的次数， Y 是 3 次中得到蓝球的次数，试求 X 与 Y 的协方差

[考研类试卷]考研数学一(常微分方程)历年真题试卷汇编1.doc

[考研类试卷]考研数学一（常微分方程）历年真题试卷汇编1一、选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1 (1998年)已知函数y=y(x)在任意点x处的增量且当△x→0时，α是△x的高阶无穷小，y(0)=π，则y(1)等于( )（A）2π（B）π（C）（D）2 (2016年)若是微分方程y′+p(x)y=q(x)的两个解，则q(x)=( )（A）3x(1+x2)（B）一3x(1+x2)（C）（D）3 (2008年)在下列微分方程中，以y=C1e x+C2cos2x+C3sin2x(C1，C2，C3为任意常数)为通解的是( )（A）y"′+y"一4y′一4y=0（B）y"′+y"+4y′+4y=0（C）y"′一y"一4y′+4y=0（D）y"′一y"+4y′一4y=04 (2015年)设是二阶常系数非齐次线性微分方程y"+ay′+by=ce x的一个特解，则( )（A）a=一3，b=2，c=一1（B）a=3，b=2，c=一1（C）a=一3，b=2，c=1（D）a=3，b=2，c=1二、填空题5 (2006年)微分方程的通解是__________。

6 (2008年)微分方程xy′+y=0满足条件y(1)=1的解是y=___________。

7 (2014年)微分方程xy′+y(lnx—lny)=0满足y(1)=e3的解为y=____________。

8 (2005年)微分方程xy′+2y=zlnx满足的解为___________。

9 (2011年)微分方程y′+y=e-x cosx满足条件y(0)=0的解为y=__________。

10 (2000年)微分方程xy"+3y′=0的通解为_____________。

11 (2002年)微分方程xy"+y′2=0满足初始条件的特解是____________。

考研数学一(多元函数微分学)历年真题试卷汇编4(题后含答案及解析)

考研数学一（多元函数微分学）历年真题试卷汇编4(题后含答案及解析)题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．(2006年)若f(x，y)与φ(x，y)均为可微函数，且φ’y(x，y)≠0．已知(x0，y0)是f(x，y)在约束条件φ(x，y)=0下的一个极值点，下列选项正确的是A．若f’x(x0，y0)=0，则f’y(x0，y0)=0．B．若f’0(x0，y0)=0．则f’(x0，y0)≠0．C．若f’x(x0，y0)≠0，则f’y(x0，y0、)=0．D．若f’x(x0，y01)≠0，则f’y(x0，y0)≠0．正确答案：D解析：由拉格朗日乘数法知，若(x0，y0)是f(x．y)在约束条件φ(x，y)=0下的极值点。

则必有若f’x(x0，y0)≠0，由①式知，λ≠0，加之原题设φ’y(x，y)≠0，由②式知，λφ’(x0，y0)≠0，从而必有f’y(x0，y0)≠0，故应选(D)．知识模块：多元函数微分学2．(2008年)函数在点(0，1)处的梯度等于A．iB．一iC．jD．一j正确答案：A解析：解1 由知则f’x(0，1)=1，f’(0，1)=0，所以gradf(0，1)=i 解2 由知则gradf(0．1)=i 知识模块：多元函数微分学3．(2010年)设函数z=z(x，y)由方程确定，其中F为可微函数，且F’2≠0，则A．x．B．z．C．一x．D．一z．正确答案：B解析：由隐函数求导公式得则解 2 等式分别对x，y求偏导得(1)式乘x2加(2)式乘xy得(一z)F’2+F’2(xzx+yzy)=0则xzx+yzy=z (F’2≠0) 知识模块：多元函数微分学4．(2011年)设函数f(x)具有二阶连续导数，且f(x)＞0，f’(0)=0，则函数z=f(x)lnf(y)在点(0，0)处取得极小值的一个充分条件是A．f(0)＞1，f”(0)＞0．B．f(0)＞1，f”(0)＜0．C．f(0)＜1，f”(0)＞0．D．f(0)＜1，f”(0)＜0．正确答案：A解析：则AC—B2＞0故应选(A)．知识模块：多元函数微分学5．(2012年)如果f(x，y)在(0，0)处连续，那么下列命题正确的是A．若极限存在，则f(x，y)在(0，0)处可微．B．若极限存在，则f(x，y)在(0，0：)处可微．C．若f(x，y)在(0，0)处可微，则极限存在．D．若f(x，y)在(0，0)处可微，则极限存在．正确答案：B解析：解l 由f(x，y)在(0，0)处连续可知，如果存在，则必有又极限则由存在知即由微分的定义知f(x，y)在(0，0)处可微．解2 排除法：取f(x，y)=|x|+|y|，显然，存在，但f(x，y)=|x|+|y|在(0，0)处不可微，这是由于f(x，0)=|x|，而|x|在x=0处不可导，则fx(0，0)不存在．则排除(A)；若取f(x，y)=x，显然，f(x，y)在(0，0)处可微，但不存在，则不存在，排除(C)．又则不存在，排除(D)．故应选(B)．知识模块：多元函数微分学6．(2013年)曲面x2+cos(xy)+yz+x=0在点(0，1，一1)处的切平面方程为A．x—y+z=一2．B．x+y+z=0．C．x一2y+z=一3．D．x—y一z=0．正确答案：A解析：令F(x，y，z)=x2+cos(xy)一yz+x，则则所求切平面方程为x一(y 一1)+(z+1)=0即x—y+z=一2 知识模块：多元函数微分学7．(2017年)函数f(x，y，z)=x2y+z2在点(1，2，0)处沿向量n=(1，2，2)的方向导数为A．12．B．6．C．4．D．2．正确答案：D解析：fx(1，2，0)=2xy|(1，2，0)=4 fy(1，2，0)=x2|(1，2，0)=1 fz(1，2，0)=3z2|(1，2，0)=0 向量n={1，2，2}的方向余弦为则知识模块：多元函数微分学填空题8．(2003年)曲面z=x2+y2与平面2x+4y一z—0平行的切平面方程是_____________．正确答案：2x+4y—z=5解析：曲面z=x2+y2在点(x0，y0，z0)处切平面的法向量为n1={2x0，2y0，一1)而平面2x+4y一z=0的法向量为n2={2，4，一1}．由题设知n1／／n2，则从而有x0=1，y0=2，代入z=x2+y2 得z0=5，n1={2，4，一1}则所求切平面方程为2(x一1)+4(y一2)一(z一5)=0即2x+4y—z=5 知识模块：多元函数微分学9．(2005年)设函数单位向量则正确答案：解析：ux(1，2，3)=uy(1，2，3)=uz(1，2，3)=则知识模块：多元函数微分学10．(2007年)设f(u，v)为二元可微函数，z=f(xy，yx)，则正确答案：yxy-1f’1+y2lnyf’2．解析：由复合函数求导法知知识模块：多元函数微分学11．(2009年)设函数f(u，v)具有二阶连续偏导数，z=f(x，xy)，则正确答案：f’2+xf”12+xyf”22解析：知识模块：多元函数微分学12．(2011年)设函数则正确答案：4解析：解1 △解2 由偏导数定义知知识模块：多元函数微分学13．(2012年)正确答案：(1，1，1)解析：知识模块：多元函数微分学14．(2014年)曲面z=z2(1一siny)+y2(1一sinx)在点(1，0，1)处的切平面方程为_____________．正确答案：2x—y一z=1．解析：由z=x2(1一siny)+y2(1一sinx)得z’x=2x(1一siny)一y2cosx，z’x(1，0)=2 z’y=一x2cosy+2y(1一sinx)，z’ y(1，0)=一1所以，曲面z=x2(1一siny)+y2(1一sinx)在点(1．0．1)处的法向量为[*]=(2．一1，一1)，该点处切平面方程为2(x-1)一y一(z一1)=0即2x—y一z=1．知识模块：多元函数微分学15．(2015年)若函数z=z(x，y)由方程ez+xyz+x+cosx=2确定，则dz|(0，1)=_____________．正确答案：一dx解析：将x=0，y=1代入ez+xyz+x+cosx=2 中得ez+1=2，则z=0．方程ez+xyz+x+cosx=2两端微分得ezdz+yzdx+xzdy+xydz+dx—sinxdx=0 将x=0，y=1．z=0代入上式得dx+dz=0则dz|(0,1)=一dx 知识模块：多元函数微分学16．(2016年)设函数f(u，v)可微，z=z(x，y)由方程(x+1)z—y2=x2f(x一z，y)确定，则dz|(0，1)=___________.正确答案：一dz+2dy．解析：解1 由原方程知，当x=0，y=1时，z=1．方程(x+1)z一y2=xf(x —z，y)两边求全微分zdx+(x+1)dz一2ydy=2xf(x一z，y)dx+x2[f’1·(dx一dz)+f’2dy] 将x=0，y=1，z=1代入上式得dz|(0，1)=-dx+2dy 解2 由原方程知，当x=0，y=1时，z=1．方程两边分别对x、y求偏导数，有把x=0，y=1，z=1代入上式得所以dz|(0，1)=-dx+2dy 知识模块：多元函数微分学解答题解答应写出文字说明、证明过程或演算步骤。

2012考研数一真题解析

【答案】 3 12
【考点】曲面积分的计算【难易度】★★★★ 【详解】本题涉及到的主要知识点：
8 第 8 页，共 21 页
梦想不会辜负每一个努力的人
曲面积分公式：
x 1
的间断点只有
x
1 .
由于 lim y ，故 x 1是垂直渐近线. x1
（而 lim y lim x(x 1) 1 ，故 x 1不是渐近线）. x1 x1 (x 1)(x 1) 2
1 1
又 lim y lim x 1，故 y 1是水平渐近线.（无斜渐近线）
x
x 1
1 x2
综上可知，渐近线的条数是 2.故选 C.
lim
x0
f (x, y) x2 y2
lim x0
f
(x, y) f (0, 0) x2 y2
A
y0
y0
由极限与无穷小的关系
f (x, y) f (0, 0) x2 y2
A
o(1)
x y
0 0
，
其中 o(1) 为无穷小. f (x, y) f (0, 0) A(x2 y2) (x2 y2)o(1)
【答案】D 【考点】定积分的基本性质【难易度】★★★ 【详解】本题涉及到的主要知识点：
b
c
b
设 a c b ，则 f (x)dx f (x)dx f (x)dx .
a
a
c
在本题中，
I1
0
ex2
sin
xdx
，
I2
2 0
ex2
sin
xdx ，
I3
3 ex2 sin xdx
0
I2 I1
y0
可微，但 lim x0

考研数学一(一元函数微分学)历年真题试卷汇编3(题后含答案及解析)

考研数学一（一元函数微分学）历年真题试卷汇编3(题后含答案及解析)题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．(2004年)设函数f(x)连续，且f’(0)＞0，则存在δ＞0。

使得A．f(x)在(0，δ)内单调增加B．f(x)在(一δ，0)内单凋减少C．对任意的x∈(0，δ)有f(x)＞f(0)D．对任意的x∈(一δ，0)有f(x)＞f(0)正确答案：C解析：由于由极限的保号性知，存在δ＞0，当x∈(一δ，0)或x∈(0，δ)时，而当∈(0，δ)时x＞0，则此时f(x)一f(0)＞0，即f(x)＞f(0)，故应选(C)．知识模块：一元函数微分学2．(2005年)设函数则f(x)在(一∞，+∞)内A．处处可导B．恰有一个不可导点C．恰有两个不可导点D．至少有三个不可导点正确答案：C解析：当|x|≤1时，当|x|＞1时，则而f’+(一1)≠f’-(一1)，则f(x)在x=一1不可导．同理则f(x)在x=1处不可导，故应选(C)．知识模块：一元函数微分学3．(2006年)设函数y=f(x)具有二阶导数，且f’(x)＞0．f”(x)＞0，△x为自变量x在x11处的增量，△y与dy分别为f(x)在点x0处对应的增量与微分，若△x＞0，则A．0＜dy＜△yB．0＜△y＜dyC．△y＜dy＜0D．dy＜△y＜0正确答案：A解析：解1 直接法：dy=f’(x0)△x，△y=f(x0+△x)一f(x0)=f’(ξ)△x，x0＜ξ＜x0+△x由于f”(x)＞0，则f’(x)单调增，从而有f(x0)＜f’(ξ)，故dy＜△y 由于f’(x)＞0，△x＞0，则0＜dy＜△y，故应选(A)．解2 排除法：取f(x)=x2，在(0，+∞)上，f’(x)=2x＞0，f”(x)一2＞0，取x0=1，则dy=f’(x0)△x=2△x △y=f(1+△x)一f(1)=(1+△x)2一1=2△x+(△x)2由于△x＞0，显然有0＜dy＜△y，由此可知，选项(B)，(C)，(D)均不正确，故应选(A)。

2012年考研数学真题及参考答案(数学一)

=
⎧ ⎨
y,
⎩
x
−
z y2
,
1⎫
y
⎬ ⎭
( 2,1,1)
= {1,1,1}
（12）设 ∑ = {(x, y, z) x + y + z = 1, x ≥ 0, y ≥ 0, z ≥ 0}, 则 ∫∫ y2ds = ________。 ∑
【答案】： 3 12
∫∫ ∫∫ ∫∫ 【解析】：由曲面积分的计算公式可知 y2ds = y2 1+ (−1)2 + (−1)2 dxdy = 3 y2dxdy ，其中
所以 f ' (0) = (−1)n−1n!
（3）如果 f (x, y) 在 (0, 0) 处连续，那么下列命题正确的是（）
（A）若极限 lim f (x, y) 存在，则 f (x, y) 在 (0, 0) 处可微
x→0 y→0
x+ y
（B）若极限 lim x→0 y→0
f (x, y) x2 + y2
2
4
三、解答题：15—23 小题，共 94 分.请将解答写在答．题．纸．指定位置上.解答应写出文字说明、证明过程或
演算步骤.
（15）（本题满分 10 分）
证明： x ln 1+ x + cos x ≥ 1+ x2 , −1 < x < 1
1− x
2
【解析】：令 f ( x) = x ln 1+ x + cos x −1− x2 ，可得
( ) 化的，故它的秩等于它非零特征值的个数，也即 r E − xxT = 2 。
（14）设
A,

考研数学历年真题(1987-2012)年数学一_可直接打印(纯试题)

1987年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上) (1)当x =_____________时,函数2xy x =⋅取得极小值.(2)由曲线ln y x =与两直线e 1y x =+-及0y =所围成的平面图形的面积是_____________.1x =(3)与两直线 1y t =-+及121111x y z +++==都平行且过原点的平面方程为_____________.2z t =+(4)设L 为取正向的圆周229,x y +=则曲线积分2(22)(4)Lxy y dx x x dy -+-⎰Ñ= _____________. (5)已知三维向量空间的基底为123(1,1,0),(1,0,1),(0,1,1),===ααα则向量(2,0,0)=β在此基底下的坐标是_____________.二、(本题满分8分)求正的常数a 与,b 使等式201lim 1sin x x bx x →=-⎰成立.三、(本题满分7分)(1)设f 、g 为连续可微函数,(,),(),u f x xy v g x xy ==+求,.u v x x ∂∂∂∂(2)设矩阵A 和B 满足关系式2,+AB =A B 其中301110,014⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A 求矩阵.B四、(本题满分8分)求微分方程26(9)1y y a y ''''''+++=的通解,其中常数0.a >五、选择题(本题共4小题,每小题3分,满分12分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内) (1)设2()()lim1,()x af x f a x a →-=--则在x a =处 (A)()f x 的导数存在,且()0f a '≠ (B)()f x 取得极大值(2)设()f x 为已知连续函数0,(),s t I t f tx dx =⎰其中0,0,t s >>则I 的值(A)依赖于s 和t (B)依赖于s 、t 和x (C)依赖于t 、x ,不依赖于s(D)依赖于s ,不依赖于t(3)设常数0,k >则级数21(1)nn k nn ∞=+-∑ (A)发散 (B)绝对收敛(C)条件收敛(D)散敛性与k 的取值有关(4)设A 为n 阶方阵，且A 的行列式||0,a =≠A 而*A 是A 的伴随矩阵，则*||A 等于 (A)a(B)1a(C)1n a -(D)n a六、（本题满分10分）求幂级数1112n nn x n ∞-=∑g 的收敛域，并求其和函数.七、（本题满分10分）求曲面积分2(81)2(1)4,I x y dydz y dzdx yzdxdy ∑=++--⎰⎰其中∑是由曲线13()0z y f x x ⎧=≤≤⎪=⎨=⎪⎩绕y 轴旋转一周而成的曲面,其法向量与y 轴正向的夹角恒大于.2π八、（本题满分10分）设函数()f x 在闭区间[0,1]上可微,对于[0,1]上的每一个,x 函数()f x 的值都在开区间(0,1)内,且()f x '≠1,证明在(0,1)内有且仅有一个,x 使得().f x x =九、（本题满分8分）问,a b 为何值时,现线性方程组123423423412340221(3)2321x x x x x x x x a x x b x x x ax +++=++=-+--=+++=-有唯一解,无解,有无穷多解?并求出有无穷多解时的通解.十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)设在一次实验中,事件A 发生的概率为,p 现进行n 次独立试验,则A 至少发生一次的概率为____________;而事件A 至多发生一次的概率为____________.(2)有两个箱子,第1个箱子有3个白球,2个红球, 第2个箱子有4个白球,4个红球.现从第1个箱子中随机地取1个球放到第2个箱子里,再从第2个箱子中取出1个球,此球是白球的概率为____________.已知上述从第2个箱子中取出的球是白球,则从第一个箱子中取出的球是白球的概率为____________.(3)已知连续随机变量X的概率密度函数为221(),xx f x -+-=则X 的数学期望为____________,X 的方差为____________.十一、（本题满分6分）设随机变量,X Y 相互独立,其概率密度函数分别为()X f x = 1001x ≤≤其它,()Y f y = e 0y - 00y y >≤,求2Z X Y =+的概率密度函数.1988年全国硕士研究生入学统一考试数学(一)试卷一、(本题共3小题,每小题5分,满分15分)(1)求幂级数1(3)3nnn x n ∞=-∑的收敛域. (2)设2()e ,[()]1x f x f x x ϕ==-且()0x ϕ≥,求()x ϕ及其定义域. (3)设∑为曲面2221x y z ++=的外侧,计算曲面积分333.I x dydz y dzdx z dxdy ∑=++⎰⎰Ò二、填空题(本题共4小题,每小题3分,满分12分.把答案填在题中横线上) (1)若21()lim (1),tx x f t t x→∞=+则()f t '= _____________.(2)设()f x 连续且31(),x f t dt x -=⎰则(7)f =_____________.(3)设周期为2的周期函数,它在区间(1,1]-上定义为()f x =22x1001x x -<≤<≤,则的傅里叶()Fourier 级数在1x =处收敛于_____________.(4)设4阶矩阵234234[,,,],[,,,],==A αγγγB βγγγ其中234,,,,αβγγγ均为4维列向量,且已知行列式4,1,==A B 则行列式+A B = _____________.三、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设()f x 可导且01(),2f x '=则0x ∆→时,()f x 在0x 处的微分dy 是 (A)与x ∆等价的无穷小 (B)与x ∆同阶的无穷小 (C)比x ∆低阶的无穷小(D)比x ∆高阶的无穷小(2)设()y f x =是方程240y y y '''-+=的一个解且00()0,()0,f x f x '>=则函数()f x 在点0x 处 (A)取得极大值(B)取得极小值 (C)某邻域内单调增加(D)某邻域内单调减少(3)设空间区域2222222212:,0,:,0,0,0,x y z R z x y z R x y z Ω++≤≥Ω++≤≥≥≥则 (A)124xdv dv ΩΩ=⎰⎰⎰⎰⎰⎰(B)124ydv ydv ΩΩ=⎰⎰⎰⎰⎰⎰(C)124zdv zdv ΩΩ=⎰⎰⎰⎰⎰⎰(D)124xyzdv xyzdv ΩΩ=⎰⎰⎰⎰⎰⎰(4)设幂级数1(1)nn n a x ∞=-∑在1x =-处收敛,则此级数在2x =处 (A)条件收敛(B)绝对收敛(C)发散(D)收敛性不能确定(5)n 维向量组12,,,(3)s s n ≤≤αααL 线性无关的充要条件是 (A)存在一组不全为零的数12,,,,s k k k L 使11220s s k k k +++≠αααL (B)12,,,s αααL 中任意两个向量均线性无关(C)12,,,s αααL 中存在一个向量不能用其余向量线性表示 (D)12,,,s αααL 中存在一个向量都不能用其余向量线性表示四、(本题满分6分)设()(),x yu yf xg y x=+其中函数f 、g 具有二阶连续导数,求222.u u x yx x y ∂∂+∂∂∂五、(本题满分8分)设函数()y y x =满足微分方程322e ,xy y y '''-+=其图形在点(0,1)处的切线与曲线21y x x =--在该点处的切线重合,求函数().y y x = 六、（本题满分9分）设位于点(0,1)的质点A 对质点M 的引力大小为2(0kk r>为常数,r 为A 质点与M 之间的距离),质点M沿直线y =自(2,0)B 运动到(0,0),O 求在此运动过程中质点A 对质点M 的引力所作的功.七、（本题满分6分）已知,=AP BP 其中100100000,210,001211⎡⎤⎡⎤⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦B P 求5,.A A八、（本题满分8分）已知矩阵20000101x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A 与20000001y ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦B 相似. (1)求x 与.y(2)求一个满足1-=P AP B 的可逆阵.P九、（本题满分9分）设函数()f x 在区间[,]a b 上连续,且在(,)a b 内有()0,f x '>证明:在(,)a b 内存在唯一的,ξ使曲线()y f x =与两直线(),y f x a ξ==所围平面图形面积1S 是曲线()y f x =与两直线(),y f x b ξ==所围平面图形面积2S 的3倍.十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)设在三次独立试验中,事件A 出现的概率相等,若已知A 至少出现一次的概率等于19,27则事件A 在一次试验中出现的概率是____________. (2)若在区间(0,1)内任取两个数,则事件”两数之和小于65”的概率为____________. (3)设随机变量X 服从均值为10,均方差为0.02的正态分布,已知22(),(2.5)0.9938,u xx du φφ-==⎰则X 落在区间(9.95,10.05)内的概率为____________.十一、（本题满分6分）设随机变量X 的概率密度函数为21(),(1)X f x x π=-求随机变量1Y =-的概率密度函数().Y f y1989年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上) (1)已知(3)2,f '=则0(3)(3)lim2h f h f h→--= _____________.(2)设()f x 是连续函数,且1()2(),f x x f t dt =+⎰则()f x =_____________.(3)设平面曲线L为下半圆周y =则曲线积分22()Lx y ds +⎰=_____________.(4)向量场div u 在点(1,1,0)P 处的散度div u =_____________.(5)设矩阵300100140,010,003001⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A I 则矩阵1(2)--A I =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内) (1)当0x >时,曲线1siny x x= (A)有且仅有水平渐近线 (B)有且仅有铅直渐近线(C)既有水平渐近线,又有铅直渐近线(D)既无水平渐近线,又无铅直渐近线(2)已知曲面224z x y =--上点P 处的切平面平行于平面2210,x y z ++-=则点的坐标是 (A)(1,1,2)- (B)(1,1,2)- (C)(1,1,2)(D)(1,1,2)--(3)设线性无关的函数都是二阶非齐次线性方程的解是任意常数,则该非齐次方程的通解是 (A)11223c y c y y ++(B)1122123()c y c y c c y +-+(C)1122123(1)c y c y c c y +---(D)1122123(1)c y c y c c y ++--(4)设函数2(),01,f x x x =≤<而1()sin ,,nn S x bn x x π∞==-∞<<+∞∑其中102()sin ,1,2,3,,n b f x n xdx n π==⎰L 则1()2S -等于(A)12- (B)14-(C)14 (D)12(5)设A 是n 阶矩阵,且A 的行列式0,=A 则A 中 (A)必有一列元素全为0 (B)必有两列元素对应成比例 (C)必有一列向量是其余列向量的线性组合(D)任一列向量是其余列向量的线性组合三、(本题共3小题,每小题5分,满分15分)(1)设(2)(,),z f x y g x xy =-+其中函数()f t 二阶可导,(,)g u v 具有连续二阶偏导数,求2.zx y ∂∂∂(2)设曲线积分2()cxy dx y x dy ϕ+⎰与路径无关,其中()x ϕ具有连续的导数,且(0)0,ϕ=计算(1,1)2(0,0)()xy dx y x dy ϕ+⎰的值.(3)计算三重积分(),x z dv Ω+⎰⎰⎰其中Ω是由曲面z =与z =所围成的区域.四、(本题满分6分) 将函数1()arctan 1xf x x+=-展为x 的幂级数.五、(本题满分7分) 设0()sin ()(),xf x x x t f t dt =--⎰其中f 为连续函数,求().f x六、（本题满分7分）证明方程0ln e x x π=-⎰在区间(0,)+∞内有且仅有两个不同实根. 七、（本题满分6分）问λ为何值时,线性方程组13x x λ+=123422x x x λ++=+ 1236423x x x λ++=+有解,并求出解的一般形式.八、（本题满分8分）假设λ为n 阶可逆矩阵A 的一个特征值,证明 (1)1λ为1-A 的特征值. (2)λA为A 的伴随矩阵*A 的特征值.九、（本题满分9分）设半径为R 的球面∑的球心在定球面2222(0)x y z a a ++=>上,问当R 为何值时,球面∑在定球面内部的那部分的面积最大?十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)已知随机事件A 的概率()0.5,P A =随机事件B 的概率()0.6P B =及条件概率(|)0.8,P B A =则和事件A B U 的概率()P A B U =____________.(2)甲、乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率为____________. (3)若随机变量ξ在(1,6)上服从均匀分布,则方程210x x ξ++=有实根的概率是____________.十一、（本题满分6分）设随机变量X 与Y 独立,且X 服从均值为1、标准差(均方差)的正态分布,而Y 服从标准正态分布.试求随机变量23Z X Y =-+的概率密度函数.1990年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)2x t=-+(1)过点(1,21)M-且与直线34y t=-垂直的平面方程是_____________.1z t=-(2)设a为非零常数,则lim()xxx ax a→∞+-=_____________.(3)设函数()f x=111xx≤>,则[()]f f x=_____________.(4)积分222e yxdx dy-⎰⎰的值等于_____________.(5)已知向量组1234(1,2,3,4),(2,3,4,5),(3,4,5,6),(4,5,6,7),====αααα则该向量组的秩是_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设()f x是连续函数,且e()(),xxF x f t dt-=⎰则()F x'等于(A)e(e)()x xf f x----(B)e(e)()x xf f x---+(C)e(e)()x xf f x---(D)e(e)()x xf f x--+(2)已知函数()f x具有任意阶导数,且2()[()],f x f x'=则当n为大于2的正整数时,()f x的n阶导数()()nf x是(A)1![()]nn f x+(B)1[()]nn f x+(C)2[()]nf x(D)2![()]nn f x(3)设a为常数,则级数21sin()[nnan∞=∑(A)绝对收敛(B)条件收敛(C)发散(D)收敛性与a的取值有关(4)已知()f x在0x=的某个邻域内连续,且()(0)0,lim2,1cosxf xfx→==-则在点0x=处()f x(A)不可导(B)可导,且(0)0f'≠(C)取得极大值(D)取得极小值(5)已知1β、2β是非齐次线性方程组=AX b的两个不同的解1,α、2α是对应其次线性方程组=AX0的基础解析1,k、2k为任意常数,则方程组=AX b的通解(一般解)必是(A)1211212()2k k-+++ββααα(B)1211212()2k k++-+ββααα(C)1211212()2k k-+++ββαββ(D)1211212()2k k++-+ββαββ三、(本题共3小题,每小题5分,满分15分)(1)求12ln(1).(2)xdxx+-⎰(2)设(2,sin),z f x y y x=-其中(,)f u v具有连续的二阶偏导数,求2.zx y∂∂∂(3)求微分方程244e xy y y -'''++=的通解(一般解).四、(本题满分6分) 求幂级数(21)nn n x∞=+∑的收敛域,并求其和函数.五、(本题满分8分) 求曲面积分2SI yzdzdx dxdy =+⎰⎰其中S 是球面2224x y z ++=外侧在0z ≥的部分.六、（本题满分7分）设不恒为常数的函数()f x 在闭区间[,]a b 上连续,在开区间(,)a b 内可导,且()().f a f b =证明在(,)a b 内至少存在一点,ξ使得()0.f ξ'> 七、（本题满分6分）设四阶矩阵1100213401100213,0011002100010002-⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥==⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦B C 且矩阵A 满足关系式1()-''-=A E C B C E其中E 为四阶单位矩阵1,-C 表示C 的逆矩阵,'C 表示C 的转置矩阵.将上述关系式化简并求矩阵.A八、（本题满分8分）求一个正交变换化二次型22212312132344448f x x x x x x x x x =++-+-成标准型.九、（本题满分8分）质点P 沿着以AB 为直径的半圆周,从点(1,2)A 运动到点(3,4)B 的过程中受变力F r 作用(见图).F r的大小等于点P 与原点O 之间的距离,其方向垂直于线段OP 且与y 轴正向的夹角小于.2π求变力F r 对质点P 所作的功.十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上) (1)已知随机变量X 的概率密度函数1()e ,2xf x x -=-∞<<+∞则X 的概率分布函数()F x =____________.(2)设随机事件A 、B 及其和事件的概率分别是0.4、0.3和0.6,若B 表示B 的对立事件,那么积事件AB 的概率()P AB =____________.(3)已知离散型随机变量X 服从参数为2的泊松()Poisson 分布,即22e {},0,1,2,,!k P X k k k -===L 则随机变量32Z X =-的数学期望()E Z =____________.十一、（本题满分6分）设二维随机变量(,)X Y 在区域:01,D x y x <<<内服从均匀分布,求关于X 的边缘概率密度函数及随机变量21Z X =+的方差().D Z1991年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)设21cos x t y t=+=,则22d ydx =_____________.(2)由方程xyz =(,)z z x y =在点(1,0,1)-处的全微分dz =_____________.(3)已知两条直线的方程是1212321:;:.101211x y z x y zl l ---+-====-则过1l 且平行于2l 的平面方程是_____________. (4)已知当0x →时123,(1)1ax +-与cos 1x -是等价无穷小,则常数a =_____________.(5)设4阶方阵52002100,00120011⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦A 则A 的逆阵1-A =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内) (1)曲线221e 1ex x y --+=- (A)没有渐近线 (B)仅有水平渐近线(C)仅有铅直渐近线(D)既有水平渐近线又有铅直渐近线(2)若连续函数()f x 满足关系式20()()ln 2,2tf x f dt π=+⎰则()f x 等于 (A)e ln 2x (B)2e ln 2x (C)e ln 2x +(D)2e ln 2x +(3)已知级数12111(1)2,5,n n n n n a a ∞∞--==-==∑∑则级数1n n a ∞=∑等于(A)3 (B)7(C)8(D)9(4)设D 是平面xoy 上以(1,1)、(1,1)-和(1,1)--为顶点的三角形区域1,D 是D 在第一象限的部分,则(cos sin )Dxy x y dxdy +⎰⎰等于(A)12cos sin D x ydxdy ⎰⎰(B)12D xydxdy ⎰⎰(C)14(cos sin )D xy x y dxdy +⎰⎰(D)0(5)设n 阶方阵A 、B 、C 满足关系式,=ABC E 其中E 是n 阶单位阵,则必有 (A)=ACB E (B)=CBA E (C)=BAC E (D)=BCA E三、(本题共3小题,每小题5分,满分15分)(1)求20).x π+→(2)设n r 是曲面222236x y z ++=在点(1,1,1)P 处的指向外侧的法向量,求函数u =P 处沿方向n r 的方向导数.(3)22(),x y z dv Ω++⎰⎰⎰其中Ω是由曲线 220y zx ==绕z 轴旋转一周而成的曲面与平面4z =所围城的立体.四、(本题满分6分)过点(0,0)O 和(,0)A π的曲线族sin (0)y a x a =>中,求一条曲线,L 使沿该曲线O 从到A 的积分3(1)(2)Ly dx x y dy +++⎰的值最小.五、(本题满分8分)将函数()2(11)f x x x =+-≤≤展开成以2为周期的傅里叶级数,并由此求级数211n n∞=∑的和. 六、（本题满分7分）设函数()f x 在[0,1]上连续,(0,1)内可导,且1233()(0),f x dx f =⎰证明在(0,1)内存在一点,c 使()0.f c '=七、（本题满分8分）已知1234(1,0,2,3),(1,1,3,5),(1,1,2,1),(1,2,4,8)a a ===-+=+αααα及(1,1,3,5).b =+β (1)a 、b 为何值时,β不能表示成1234,,,αααα的线性组合?(2)a 、b 为何值时,β有1234,,,αααα的唯一的线性表示式?写出该表示式.八、（本题满分6分）设A 是n 阶正定阵,E 是n 阶单位阵,证明+A E 的行列式大于1.九、（本题满分8分）在上半平面求一条向上凹的曲线,其上任一点(,)P x y 处的曲率等于此曲线在该点的法线段PQ 长度的倒数(Q 是法线与x 轴的交点),且曲线在点(1,1)处的切线与x 轴平行.十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)若随机变量X 服从均值为2、方差为2σ的正态分布,且{24}0.3,P X <<=则{0}P X <=____________.(2)随机地向半圆0y a <<为正常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,则原点和该点的连线与x 轴的夹角小于4π的概率为____________.十一、（本题满分6分）设二维随机变量(,)X Y 的密度函数为(,)f x y =(2)2e 0,00 x y x y -+>>其它求随机变量2Z X Y =+的分布函数.1992年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上) (1)设函数()y y x =由方程ecos()0x yxy ++=确定,则dydx=_____________.(2)函数222ln()u x y z =++在点(1,2,2)M -处的梯度grad Mu =_____________.(3)设()f x =211x -+0x x ππ-<≤<≤,则其以2π为周期的傅里叶级数在点x π=处收敛于_____________.(4)微分方程tan cos y y x x '+=的通解为y =_____________.(5)设111212121212,n n n n n n a b a b a b a b a b a b a b a b a b ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A L L L L L L L其中0,0,(1,2,,).i i a b i n ≠≠=L 则矩阵A 的秩()r A =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)当1x →时,函数1211e 1x x x ---的极限 (A)等于2 (B)等于0(C)为∞(D)不存在但不为∞(2)级数1(1)(1cos )(nn an∞=--∑常数0)a >(A)发散 (B)条件收敛(C)绝对收敛(D)收敛性与a 有关(3)在曲线23,,x t y t z t ==-=的所有切线中,与平面24x y z ++=平行的切线 (A)只有1条 (B)只有2条 (C)至少有3条(D)不存在(4)设32()3,f x x x x =+则使()(0)n f存在的最高阶数n 为(A)0 (B)1 (C)2(D)3(5)要使12100,121⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ξξ都是线性方程组=AX 0的解,只要系数矩阵A 为(A)[]212-(B)201011-⎡⎤⎢⎥⎣⎦(C)102011-⎡⎤⎢⎥-⎣⎦(D)011422011-⎡⎤⎢⎥--⎢⎥⎢⎥⎣⎦三、(本题共3小题,每小题5分,满分15分)(1)求x x →(2)设22(e sin ,),xz f y x y =+其中f 具有二阶连续偏导数,求2.zx y ∂∂∂(3)设()f x = 21e xx -+ 00x x ≤>,求31(2).f x dx -⎰四、(本题满分6分) 求微分方程323e xy y y -'''+-=的通解.五、(本题满分8分)计算曲面积分323232()()(),x az dydz y ax dzdx z ay dxdy ∑+++++⎰⎰其中∑为上半球面z =.六、（本题满分7分）设()0,(0)0,f x f ''<=证明对任何120,0,x x >>有1212()()().f x x f x f x +<+七、（本题满分8分）在变力F yzi zxj xyk =++r r r r 的作用下,质点由原点沿直线运动到椭球面2222221x y z a b c++=上第一卦限的点(,,),M ξηζ问当ξ、η、ζ取何值时,力F r所做的功W 最大?并求出W 的最大值.八、（本题满分7分）设向量组123,,ααα线性相关,向量组234,,ααα线性无关,问: (1)1α能否由23,αα线性表出?证明你的结论. (2)4α能否由123,,ααα线性表出?证明你的结论. 九、（本题满分7分）设3阶矩阵A 的特征值为1231,2,3,λλλ===对应的特征向量依次为1231111,2,3,149⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ξξξ又向量12.3⎛⎫⎪= ⎪ ⎪⎝⎭β(1)将β用123,,ξξξ线性表出. (2)求(nn A β为自然数).十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上) (1)已知11()()(),()0,()(),46P A P B P C P AB P AC P BC ======则事件A 、B 、C 全不发生的概率为____________. (2)设随机变量X 服从参数为1的指数分布,则数学期望2{e }XE X -+=____________.十一、（本题满分6分）设随机变量X 与Y 独立,X 服从正态分布2(,),N Y μσ服从[,]ππ-上的均匀分布,试求Z X Y =+的概率分布密度(计算结果用标准正态分布函数Φ表示,其中22()e)t xx dt --∞Φ=⎰.1993年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上) (1)函数1()(2(0)xF x dt x =->⎰的单调减少区间为_____________.(2)由曲线223212x y z +==绕y 轴旋转一周得到的旋转面在点处的指向外侧的单位法向量为_____________.(3)设函数2()()f x x x x πππ=+-<<的傅里叶级数展开式为01(cos sin ),2n n n a a nx b nx ∞=++∑则其中系数3b 的值为_____________. (4)设数量场u =则div(grad )u =_____________.(5)设n 阶矩阵A 的各行元素之和均为零,且A 的秩为1,n -则线性方程组=AX 0的通解为_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内) (1)设sin 2340()sin(),(),xf x t dtg x x x ==+⎰则当0x →时,()f x 是()g x 的(A)等价无穷小 (B)同价但非等价的无穷小 (C)高阶无穷小(D)低价无穷小(2)双纽线22222()x y x y +=-所围成的区域面积可用定积分表示为(A)402cos 2d πθθ⎰(B)404cos 2d πθθ⎰(C)2θ(D)2401(cos 2)2d πθθ⎰(3)设有直线1158:121x y z l --+==-与2:l 623x y y z -=+=则1l 与2l 的夹角为 (A)6π(B)4π (C)3π(D)2π(4)设曲线积分[()e ]sin ()cos x Lf t ydx f x ydy --⎰与路径无关,其中()f x 具有一阶连续导数,且(0)0,f =则()f x 等于(A)e e 2x x --(B)e e 2x x --(C)e e 12x x-+-(D)e e 12x x-+-(5)已知12324,369t ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦Q P 为三阶非零矩阵,且满足0,=PQ 则 (A)6t =时P 的秩必为1(B)6t =时P 的秩必为2 (C)6t ≠时P 的秩必为1(D)6t ≠时P 的秩必为2三、(本题共3小题,每小题5分,满分15分) (1)求21lim(sincos ).x x x x →∞+(2)求.x(3)求微分方程22,x y xy y '+=满足初始条件11x y ==的特解.四、(本题满分6分) 计算22,xzdydz yzdzdx z dxdy ∑+-⎰⎰Ò其中∑是由曲面z =与z =.五、(本题满分7分)求级数20(1)(1)2n nn n n ∞=--+∑的和.六、(本题共2小题,每小题5分,满分10分) (1)设在[0,)+∞上函数()f x 有连续导数,且()0,(0)0,f x k f '≥><证明()f x 在(0,)+∞内有且仅有一个零点. (2)设,b a e >>证明.b a a b >七、（本题满分8分）已知二次型22212312323(,,)2332(0)f x x x x x x ax x a =+++>通过正交变换化成标准形22212325,f y y y =++求参数a 及所用的正交变换矩阵.八、（本题满分6分）设A 是n m ⨯矩阵,B 是m n ⨯矩阵,其中,n m <I 是n 阶单位矩阵,若,=AB I 证明B 的列向量组线性无关.九、（本题满分6分）设物体A 从点(0,1)出发,以速度大小为常数v 沿y 轴正向运动.物体B 从点(1,0)-与A 同时出发,其速度大小为2,v 方向始终指向,A 试建立物体B 的运动轨迹所满足的微分方程,并写出初始条件.十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)一批产品共有10个正品和2个次品,任意抽取两次,每次抽一个,抽出后不再放回,则第二次抽出的是次品的概率为____________.(2)设随机变量X 服从(0,2)上的均匀分布,则随机变量2Y X =在(0,4)内的概率分布密度()Y f y =____________.十一、（本题满分6分）设随机变量X 的概率分布密度为1()e ,.2xf x x -=-∞<<+∞ (1)求X 的数学期望EX 和方差.DX(2)求X 与X 的协方差,并问X 与X 是否不相关? (3)问X 与X 是否相互独立?为什么?1994年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)011limcot ()sin x x xπ→-= _____________.(2)曲面e 23xz xy -+=在点(1,2,0)处的切平面方程为_____________.(3)设e sin ,xx u y -=则2u x y ∂∂∂在点1(2,)π处的值为_____________.(4)设区域D 为222,x y R +≤则2222()Dx y dxdy a b +⎰⎰=_____________.(5)已知11[1,2,3],[1,,],23==αβ设,'=A αβ其中'α是α的转置,则n A =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设4342342222222sin cos ,(sin cos ),(sin cos ),1x M xdx N x x dx P x x x dx x ππππππ---==+=-+⎰⎰⎰则有 (A)N P M << (B)M P N << (C)N M P <<(D)P M N <<(2)二元函数(,)f x y 在点00(,)x y 处两个偏导数00(,)x f x y '、00(,)y f x y '存在是(,)f x y 在该点连续的 (A)充分条件而非必要条件 (B)必要条件而非充分条件(C)充分必要条件(D)既非充分条件又非必要条件(3)设常数0,λ>且级数21nn a ∞=∑收敛,则级数1(1)nn ∞=-∑(A)发散(B)条件收敛 (C)绝对收敛(D)收敛性与λ有关(4)2tan (1cos )lim2,ln(12)(1)x x a x b x c x d e -→+-=-+-其中220,a c +≠则必有(A)4b d = (B)4b d =- (C)4a c =(D)4a c =-(5)已知向量组1234,,,αααα线性无关,则向量组 (A)12233441,,,++++αααααααα线性无关 (B)12233441,,,----αααααααα线性无关 (C)12233441,,,+++-αααααααα线性无关 (D)12233441,,,++--αααααααα线性无关三、(本题共3小题,每小题5分,满分15分)(1)设2221cos()cos()t x t y t t udu==-⎰,求dydx 、22d y dx 在t =. (2)将函数111()ln arctan 412x f x x x x +=+--展开成x 的幂级数.(3)求.sin(2)2sin dxx x +⎰四、(本题满分6分)计算曲面积分2222,Sxdydz z dxdy x y z +++⎰⎰其中S 是由曲面222x y R +=及,(0)z R z R R ==->两平面所围成立体表面的外侧.五、(本题满分9分)设()f x 具有二阶连续函数,(0)0,(0)1,f f '==且2[()()][()]0xy x y f x y dx f x x y dy '+-++=为一全微分方程,求()f x 及此全微分方程的通解.六、(本题满分8分)设()f x 在点0x =的某一邻域内具有二阶连续导数,且0()lim 0,x f x x →=证明级数11()n f n ∞=∑绝对收敛.七、（本题满分6分）已知点A 与B 的直角坐标分别为(1,0,0)与(0,1,1).线段AB 绕x 轴旋转一周所成的旋转曲面为.S 求由S 及两平面0,1z z ==所围成的立体体积.八、（本题满分8分）设四元线性齐次方程组(Ⅰ)为122400x x x x +=-=,又已知某线性齐次方程组(Ⅱ)的通解为12(0,1,1,0)(1,2,2,1).k k +- (1)求线性方程组(Ⅰ)的基础解析.(2)问线性方程组(Ⅰ)和(Ⅱ)是否有非零公共解?若有,则求出所有的非零公共解.若没有,则说明理由. 九、（本题满分6分）设A 为n 阶非零方阵*,A 是A 的伴随矩阵,'A 是A 的转置矩阵,当*'=A A 时,证明0.≠A十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)已知A 、B 两个事件满足条件()(),P AB P AB =且(),P A p =则()P B =____________. (2)设相互独立的两个随机变量,X Y 具有同一分布率,且X 的分布率为则随机变量max{,}Z X Y =的分布率为____________.十一、（本题满分6分）设随机变量X 和Y 分别服从正态分布2(1,3)N 和2(0,4),N 且X 与Y 的相关系数1,2xy ρ=-设,32X Y Z =+ (1)求Z 的数学期望EZ 和DZ 方差.(2)求X 与Z 的相关系数.xz ρ (3)问X 与Y 是否相互独立?为什么?1995年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)2sin 0lim(13)xx x →+=_____________.(2)202cos x d x t dt dx⎰= _____________.(3)设()2,⨯=a b c g 则[()()]()+⨯++a b b c c a g =_____________.(4)幂级数2112(3)n n nn nx ∞-=+-∑的收敛半径R =_____________. (5)设三阶方阵,A B 满足关系式16,-=+A BA A BA 且100310,41007⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A 则B =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)(1)设有直线:L 321021030x y z x y z +++=--+=,及平面:4220,x y z π-+-=则直线L(A)平行于π (B)在π上 (C)垂直于π(D)与π斜交(2)设在[0,1]上()0,f x ''>则(0),(1),(1)(0)f f f f ''-或(0)(1)f f -的大小顺序是 (A)(1)(0)(1)(0)f f f f ''>>- (B)(1)(1)(0)(0)f f f f ''>-> (C)(1)(0)(1)(0)f f f f ''->>(D)(1)(0)(1)(0)f f f f ''>->(3)设()f x 可导,()()(1sin ),F x f x x =+则(0)0f =是()F x 在0x =处可导的 (A)充分必要条件 (B)充分条件但非必要条件(C)必要条件但非充分条件 (D)既非充分条件又非必要条件(4)设(1)ln(1nn u =-则级数 (A)1nn u∞=∑与21nn u∞=∑都收敛(B)1nn u∞=∑与21nn u∞=∑都发散(C)1nn u∞=∑收敛,而21nn u∞=∑发散 (D)1nn u∞=∑收敛,而21nn u∞=∑发散(5)设11121311121321222321222312313233313233010100,,100,010,001101a a a a a a a a a a a a a a a a a a ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦A B P P 则必有(A)12AP P =B (B)21AP P =B (C)12P P A =B(D)21P P A =B三、(本题共2小题,每小题5分,满分10分) (1)设2(,,),(,e ,)0,sin ,yu f x y z x z y x ϕ===其中,f ϕ都具有一阶连续偏导数,且0.z ϕ∂≠∂求.du dx(2)设函数()f x 在区间[0,1]上连续,并设1(),f x dx A =⎰求11()().xdx f x f y dy ⎰⎰四、(本题共2小题,每小题6分,满分12分)(1)计算曲面积分,zdS ∑⎰⎰其中∑为锥面z =在柱体222x y x +≤内的部分.(2)将函数()1(02)f x x x =-≤≤展开成周期为4的余弦函数.五、(本题满分7分)设曲线L 位于平面xOy 的第一象限内,L 上任一点M 处的切线与y 轴总相交,交点记为.A 已知,MA OA =且L 过点33(,),22求L 的方程.六、(本题满分8分)设函数(,)Q x y 在平面xOy 上具有一阶连续偏导数,曲线积分2(,)Lxydx Q x y dy +⎰与路径无关,并且对任意t恒有(,1)(1,)(0,0)(0,0)2(,)2(,),t t xydx Q x y dy xydx Q x y dy +=+⎰⎰求(,).Q x y七、（本题满分8分）假设函数()f x 和()g x 在[,]a b 上存在二阶导数,并且()0,()()()()0,g x f a f b g a g b ''≠====试证:(1)在开区间(,)a b 内()0.g x ≠(2)在开区间(,)a b 内至少存在一点,ξ使()().()()f f g g ξξξξ''=''八、（本题满分7分）设三阶实对称矩阵A 的特征值为1231,1,λλλ=-==对应于1λ的特征向量为101,1⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ξ求.A九、（本题满分6分）设A 为n 阶矩阵,满足('=AA I I 是n 阶单位矩阵,'A 是A 的转置矩阵),0,<A 求.+A I十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上) (1)设X 表示10次独立重复射击命中目标的次数,每次射中目标的概率为0.4,则2X 的数学期望2()E X =____________.(2)设X 和Y 为两个随机变量,且34{0,0},{0}{0},77P X Y P X P Y ≥≥=≥=≥=则{max(,)0}P X Y ≥=____________.十一、（本题满分6分）设随机变量X 的概率密度为()X f x = e 0x - 0x x ≥<,求随机变量e X Y =的概率密度().Y f y1996年全国硕士研究生入学统一考试数学(一)试卷一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)(1)设2lim()8,xx x a x a→∞+=-则a =_____________.(2)设一平面经过原点及点(6,3,2),-且与平面428x y z -+=垂直,则此平面方程为_____________. (3)微分方程22e xy y y '''-+=的通解为_____________. (4)函数ln(u x =+在点(1,0,1)A 处沿点A 指向点(3,2,2)B -方向的方向导数为_____________.(5)设A 是43⨯矩阵,且A 的秩()2,r =A 而102020,103⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦B 则()r AB =_____________.二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内) (1)已知2()()x ay dx ydyx y +++为某函数的全微分,a 则等于 (A)-1 (B)0 (C)1(D)2(2)设()f x 具有二阶连续导数,且0()(0)0,lim1,x f x f x→'''==则 (A)(0)f 是()f x 的极大值 (B)(0)f 是()f x 的极小值(C)(0,(0))f 是曲线()y f x =的拐点(D)(0)f 不是()f x 的极值,(0,(0))f 也不是曲线()y f x =的拐点 (3)设0(1,2,),n a n >=L 且1n n a ∞=∑收敛,常数(0,),2πλ∈则级数21(1)(tan )n n n n a n λ∞=-∑ (A)绝对收敛(B)条件收敛(C)发散(D)散敛性与λ有关(4)设有()f x 连续的导数22,(0)0,(0)0,()()(),x f f F x x t f t dt '=≠=-⎰且当0x →时,()F x '与k x 是同阶无穷小,则k 等于(A)1 (B)2 (C)3 (D)4(5)四阶行列式112233440000000a b a b a b b a 的值等于(A)12341234a a a a b b b b -(B)12341234a a a a b b b b + (C)12123434()()a a b b a a b b --(D)23231414()()a a b b a a b b --三、(本题共2小题,每小题5分,满分10分) (1)求心形线(1cos )r a θ=+的全长,其中0a >是常数.四、(本题共2小题,每小题6分,满分12分)(1)计算曲面积分(2),Sx z dydz zdxdy ++⎰⎰其中S 为有向曲面22(01),z x y x =+≤≤其法向量与z 轴正向的夹角为锐角.(2)设变换 2u x y v x ay =-=+可把方程2222260z z z x x y y ∂∂∂+-=∂∂∂∂简化为20,zu v∂=∂∂求常数.a五、(本题满分7分) 求级数211(1)2nn n ∞=-∑的和.六、(本题满分7分)设对任意0,x >曲线()y f x =上点(,())x f x 处的切线在y 轴上的截距等于01(),xf t dt x ⎰求()f x 的一般表达式.七、（本题满分8分）设()f x 在[0,1]上具有二阶导数,且满足条件(),(),f x a f x b ''≤≤其中,a b 都是非负常数,c 是(0,1)内任意一点.证明()2.2b f c a '≤+设,T A =-I ξξ其中I 是n 阶单位矩阵,ξ是n 维非零列向量,Tξ是ξ的转置.证明 (1)2=A A 的充分条件是 1.T=ξξ (2)当1T=ξξ时,A 是不可逆矩阵. 九、（本题满分8分）已知二次型222123123121323(,,)55266f x x x x x cx x x x x x x =++-+-的秩为2, (1)求参数c 及此二次型对应矩阵的特征值. (2)指出方程123(,,)1f x x x =表示何种二次曲面.十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)设工厂A 和工厂B 的产品的次品率分别为1%和2%,现从由A 和B 的产品分别占60%和40%的一批产品中随机抽取一件,发现是次品,则该次品属A 生产的概率是____________.(2)设,ξη是两个相互独立且均服从正态分布2)N 的随机变量,则随机变量ξη-的数学期望()E ξη-=____________.十一、（本题满分6分）设,ξη是两个相互独立且服从同一分布的两个随机变量,已知ξ的分布率为1(),1,2,3.3P i i ξ=== 又设max(,),min(,).X Y ξηξη==(1)写出二维随机变量的分布率:(2)求随机变量X 的数学期望().E X。

(2013考研必备)考研数学一历年真题(1987-2012年)-文字版无水印免积分

2012年全国硕士研究生入学统一考试数学一试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸．．．指定位置上. （1）曲线221x x y x +=-渐近线的条数为（）（A ）0 （B ）1 （C ）2 （D ）3 【答案】：C【解析】：221lim 1x x x x ®+=¥-，所以1x =为垂直的22lim 11x x xx ®¥+=-，所以1y =为水平的，没有斜渐近线故两条选C（2）设函数2()(1)(2)()x x nx f x e e e n =---L ，其中n 为正整数，则'(0)f = （A ）1(1)(1)!n n ---（B ）(1)(1)!nn --（C ）1(1)!n n -- （D ）(1)!nn - 【答案】：C 【解析】：'222()(2)()(1)(22)()(1)(2)()x x nx x x nx x x nx f x e e e n e e e n e e ne n =--+---+---L L L L 所以'(0)f =1(1)!n n --（3）如果(,)f x y 在()0,0处连续，那么下列命题正确的是（）（A ）若极限00(,)lim x y f x y x y ®®+存在，则(,)f x y 在(0,0)处可微（B ）若极限2200(,)limx y f x y x y ®®+存在，则(,)f x y 在(0,0)处可微（C ）若(,)f x y 在(0,0)处可微，则极限0(,)limx y f x y x y ®®+存在（D ）若(,)f x y 在(0,0)处可微，则极限2200(,)limx y f x y x y®®+存在【答案】：【解析】：由于(,)f x y 在()0,0处连续，可知如果22(,)limx y f x y x y®®+存在，则必有00(0,0)lim (,)0x y f f x y ®®==这样，2200(,)limx y f x y x y ®®+就可以写成2200(,)(0,0)lim x y f x y f x y D ®D ®D D -D +D ，也即极限220(,)(0,0)limx y f x y f x y D ®D ®D D -D +D 存在，可知lim 0x y D ®D ®=，也即(,)(0,0)00f x y f x y oD D -=D +D +。

考研数学一选择题专项强化真题试卷12(题后含答案及解析)

考研数学一选择题专项强化真题试卷12(题后含答案及解析)题型有：1.1．(2013年)设L1：x2+y2=1，L2：x2+y2=2，L3：x2+2y2=2．L4：2x2+y2=2为四条逆时针方向的平面曲线．记则max{I1，I2，I3，I4}=A．I1．B．I2．C．I3．D．I4．正确答案：D解析：由格林公式得其中Di为Li围成的平面域(i=1，2，3，4) 显然，在D1和D4上则0＜I1＜I4又I2＜I4，I3＜I4，则max{I1，I2，I3，I4)=I4 知识模块：多元函数积分学2．(2017年)函数f(x，y，z)=x2y+z2在点(1，2，0)处沿向量n=(1，2，2)的方向导数为A．12．B．6．C．4．D．2．正确答案：D解析：fx(1，2，0)=2xy|(1，2，0)=4 fy(1，2，0)=x2|(1，2，0)=1 fz(1，2，0)=3z2|(1，2，0)=0 向量n={1，2，2}的方向余弦为则知识模块：多元函数微分学3．设X1，X2，…，Xn(n≥2)为来自总体N(0．1)的简单随机样本，X为样本均值，S2为样本方差，则A．n～N(0，1)B．nS2～χ2(n)C．～t(n－1)D．～F(1，n－1)正确答案：D 涉及知识点：概率论与数理统计4．(2012年)设函数_f(x)=(ex一1)(e2x一2)…(enx一n)，其中n为正整数，则f’(0)=A．(一1)n-1一(n一1)!B．(一1)n(n一1)!C．(一1)n-1n!D．(一1)nn!正确答案：A解析：解1 记g(x)=(e2x一2)(e3x一3)…(enx一n)，则f(x)=(ex一1)g(x) f’(x)=exg(x)+(ex一1)g’(x)则f’(0)=g(0)=(一1)(一2)…(一(n一1))=(一1)n-1(n一1)! 故应选(A)．△解2 由导数定义得△解3 排除法：当n=2时，f(x)=(ex一1)(e2x一2) f’(x)=ex(e2x一2)+2e2x(ex一1)，f’(0)=一1 显然，(B)(C)(D)都不正确，故应选(A)．知识模块：一元函数微分学5．设α是n维单位列向量，E为n阶单位矩阵，则( )A．E－ααT不可逆B．E+ααT不可逆C．E+2ααT不可逆D．E－2ααT不可逆正确答案：A解析：由α是n维单位列向量可知(ααT)α=α(αTα)=α，且1≤r(ααT)≤r(α)=1，即1是矩阵ααT的特征值，且r(ααT)=1，所以ααT的特征值为0(n－1重)和1。

2012.10考研管理类联考初数真题(有答案)

2012年10月真题一、问题求解：第1~15小题，每小题3分，共45分。

下列每题给出的A 、B 、C 、D 、E 五个选项中，只有一项是符合试题要求的。

请在答题卡．．．上将所选项的字母涂黑。

1.将3700元奖金按112::235的比例分给甲、乙、丙三人，则乙应得奖金（） .1000.1050.1200.1500.1700A B C D E 2.设实数,x y 满足23x y +=，则222x y y ++的最小值为（）.4.5.6.51.51A B C D E -+3.若菱形两条对角线的长分别为6和8，则这个菱形的周长和面积分别为（）.14;24.14;48.20;12.20;24.20;48A B C D E4.第一季度甲公司的产值比乙公司的产值低20%，第二季度甲公司的产值比第一季度增长了20%，乙公司的产值比第一季度增长了10%，第二季度甲、乙两公司的产值之比是（）11:10.25:24.55:48.115:92.115:96.E D C B A5.在等差数列{}n a 中，244,8a a ==。

若111521n k k k a a =+=∑，则n =（） .16.17.19.20.21A B C D E6.如图是一个简单的电路图123,,S S S 表示开关，随时闭合123,,S S S 中的两个，灯泡发光的概率是（）31.41.61.C B A 32.21.E D7.设{}n a 是非负等比数列，若)(1,41,18153===∑=n na a a 。

32255.16255.8255.4255.255.E D C B A8.某次乒乓球单打比赛，先将8名选手等分为2组进行小组单循环赛，若一位选手只打1场比赛后因故退赛，则小组赛的实际比赛场数是( )。

10.11.12.19.24.E D C B A9.甲、乙、丙三人同时在起点出发进行1000米自行车比赛（假若他们各自保持速度不变），甲到终点时，乙距终点还有10米，丙距终点还有64米，那么乙到达终点时，丙距终点（）米。

2012数学一考研真题答案解析

2012年全国硕士研究生考试数学一试题答案解析一、选择题1. 解析：C由lim 1,1x y y →∞==得为水平渐近线由1lim 1x y x →=∞=得为垂直渐近线12.)3.4. 解析： D22222111sin |sin |.xxI I e xdx I ex dx I ππππ=+=-<⎰⎰2223312|sin |sin .xxI I ex dx e xdx ππππ=-+⎰⎰而2232()2sin sin xt e xdx x t etdt ππππππ+=+-⎰⎰2222()|sin ||sin |.x xex dx ex dx πππππ+=>⎰⎰31312..I I I I I ∴>∴>>5. 解析：C343400c c αα⎛⎫ ⎪+= ⎪ ⎪+⎝⎭,34αα+ 与1α成比例.6.110111010012012 ⎪ ⎪ ⎪ ⎪=-= ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭7. 解析：A~(1)X E ，,0~(4)()0,x x e x Y E f x x -⎧>⇒=⎨≤⎩.4,40()0,0y Y e y f y y -⎧>=⎨≤⎩.,X Y ∴独立.44,0,0(,)0,x y e e x y f x y --⎧>>∴=⎨⎩其他8.cov(,)(1)(1)X Y EX X EX E x =---2()[1]E X X EX EX =--- 22()EX EX EX EX =-+ 22()EXEX DX =-+=-1ρ∴=，选项D二、填空题1. 解析：212202,1λλλλ+-=⇒=-=212()()2()0(),xxf x f x f x f x C e C e -"+'-=⇒=+代入12()()20, 1.xf x f x e C C '+===得2.3.4.121,:1(0,0)z x y D x y x y =--+≤≥≥112222x Dy ds y dx y dy δ-=⋅=⎰⎰⎰⎰⎰1134(1)(1)31212x dx x =-=--=⎰5. 解析：2.设2,TA E XX A A =-=()() 3.r A r E A ⇒+-=()()()1Tr E A r XX r X -=== () 2.r A ∴=6.11xx --2211lnsin 11x x x x xx++=+--- 01x <<时. 1ln01x x+>-,2211x x x x+≥-，又sin x x ≤.()0x ϕ∴>’；10x -<<时，1ln01x x+<-，2211x x x x+≤-,又sin x x ≥.()0x ϕ∴<’.0x ⇒=为()x ϕ在（-1，1）内最小点，而ϕ（0）=0 ∴当-1<x<1时. ϕ()0x ≥，即21x x+20A C B -> 且0A >，0y ∴⎨=⎩为极小点.极小值为12(1,0).f e--=-当1x y =⎧⎨=⎩时，11222,0,,A e B C e --=-==-2100,0x AC B A y =⎧-><∴⎨=⎩ 且为极大点极大值为12(1,0)f e -=3. 解：由1lim1n x na a +→∞=得R =1.当∴令n ==n ∞=⎛= ⎝⎛= ⎝当当x ≠0时，xS 1(x )=021n n =+∑[]2121()1nn xS x xx∞===-∑’111111()ln,()ln.2121x x xS x S x xxx++=∴=--223,0()111ln ,110(1)1x S x x xx x x x x =⎧⎪∴=++⎨+-<<≠⎪--⎩且4. 解析： ①/sin ./()dy dy dt t k dxdx dtf t -==='x ⇒ (f ②=⎰5. 解析：012:0(2,0)L L L L x y y I +====-⎰⎰22(313)x x d =+-σ=⎰2d dx σ=-而20⎰∴∴∴（（当1a =时，A =11 0 0 1⎛⎫ ⎪0 1 1 0 -1⎪ ⎪0 0 1 1 0 ⎪1 0 0 1 0⎝⎭→100120101100110000⎛⎫⎪-- ⎪ ⎪⎪⎝⎭通解为12111010x k -⎛⎫⎛⎫ ⎪ ⎪-⎪ ⎪=+ ⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭ 当1a =-时.A 11001100100110101011001100011011000--⎛⎫⎛⎫⎪ ⎪---- ⎪⎪=→ ⎪ ⎪-- ⎪ ⎪-⎝⎭⎝⎭通解为10111010x k ⎛⎫⎛⎫ ⎪ ⎪- ⎪⎪=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭7. 解析：A T A=1010010111a a -⎛⎫ ⎪ ⎪ ⎪-⎝⎭1010111001a a⎛⎫ ⎪ ⎪ ⎪- ⎪-⎝⎭22201011113a aa a aa -⎛⎫⎪=+-⎪ ⎪--+⎝⎭TT(A A )x x 秩为2. ∴TT(A A )2((A A )(A )2)r r r ===也可以利用 ⇒TA A 01a =⇒=- ( T22A A (3)(1)a a =++)(II)令T202A A =B =022224⎛⎫ ⎪ ⎪ ⎪⎝⎭ 由E λ-20-2λ-B =0λ-2-2-2-2λ-4=λ(λ-2)(λ-6)=0解λ当λ当λ当λ取r 令2223111.12026Q f x x x Q y y y T=-⎝=B = +8. 解析：(1)(2)=X ∴D 2222cov(,)13333X Y Y -=-⨯-=-.9. 解析：22~(,),~(,2)X N Y N μσμσ，,X Y 独立，0σ>，未知Z X Y =-. 解：（1）Z 的密度2(,)f z σ22~(,),~(,2),,X N Y N X Yμσμσ独立.2~(0,3)Z X Y Nσ=-22222236(,)z zf zσσσ--⋅∴==（2）设1nZ Z…样本.2n2~(0,3)iZ Nσ，~(0,1)ZN-∴，iZ是简单随机样本.221~(),niZnχ=⎛⎫⎝∑223iZE nσ∑∴=，223iE Z nσ∑=.。

考研数学一(向量代数和空间解析几何、多元函数微分学)历年真题

考研数学一（向量代数和空间解析几何、多元函数微分学）历年真题试卷汇编1(题后含答案及解析)题型有：1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中，只有一个选项符合题目要求。

1．[2018年] 过点(1，0，0)与(0，1，0)，且与曲面z=x2+y2相切的平面方程为( )．A．z=0与x+y-z=1B．z=0与2x+2y一z=2C．y=x与x+y一z=1D．y=x与2x+2y一z=2正确答案：B解析：设切点的坐标为(x0，y0，x02+y02)，由题意可知切平面的法向量为n=(2x0，2y0，一1)，则切平面的方程为2x0(x—x0)+2y0(y—y0)一[z一(x02+y02)]=0 ，即2x0x+2y0y-z一(x02+y02)=0．(*)将点(1，0，0)与(0，1，0)代入上式得解得x0=y0=0或x0=y0=1．将x0，y0的值代入(*)式，可得z=0或2x+2y-z=2．仅B入选．知识模块：向量代数和空间解析几何2．设直线L：及平面π：4x-2y+z一2=0，则直线L( )．A．平行于πB．在π上C．垂直于πD．与π斜交正确答案：C解析：易求得直线L的方向向量为而平面π的法向量为，n=(4，一2，1)，故s与n共线，即l的方向向量s与平面π的法向量n平行．因而直线L和平面π垂直．仅C入选．知识模块：向量代数和空间解析几何3．[2002年] 设有三个不同平面的方程ai1x+ai2y+ai3z=bi，i=1，2，3，它们所组成的线性方程组的系数矩阵与增广矩阵的秩为2，则这三个平面可能的位置关系为( )．A．B．C．D．正确答案：B解析：由题设，建立线性方程组系数矩阵和增广矩阵的秩相等且为2，小于未知数个数3．由线性方程组解的理论知，此方程组有无穷多组解，即三个平面有无穷多个交点．对照四个选项，A只有一个交点，C、D无交点，只有B符合要求．仅B入选．知识模块：向量代数和空间解析几何4．设矩阵是满秩的，则直线( )．A．相交于一点B．重合C．平行但不重合D．异面正确答案：A解析：因秩，又经初等行变换得到而经初等行变换，矩阵的秩不变，故两行向量(a1一a2，b1一b2，c1一c2)，(a2一a3，b2一b3，c2一c3)线性无关，所以它们不共线．因而两直线的方向向量不平行，也不重合．B、C不能入选．又因两直线分别过点M3(a3，b3，c3)，M1(a1，b1，c1)．而三向量=(a3-a1，b3-b1，c3-c1)，s1=(a1一a2，b1—b2，c1一c2)，s2=(a2一a3，b2—b3，c2一c3)共面．这是因为故此两直线不是异面直线，而是共面直线．又因它们不平行，所以必相交．仅A入选．知识模块：向量代数和空间解析几何5．[2008年] 设A为三阶实对称矩阵，如果二次曲面方程[x，y，z]A[x，y，z]T=1在正交变换下的标准方程的图形如图所示，则A的正特征值的个数为( )．A．0B．1C．2D．3正确答案：B解析：由图可知二次曲面为旋转双叶双曲面，其标准方程应为从而方程左端对应二次型的正惯性指数为1，即正特征值的个数为1．仅B入选．知识模块：向量代数和空间解析几何6．[2016年] 设二次型f(x1，x2，x3)=x12+x22+x32+4x1x2+4x1x3+4x2x3，则f(x1，x2，x3)=2在空间直角坐标下表示的二次曲面为( )．A．单叶双曲面B．双叶双曲面C．椭球面D．柱面正确答案：B解析：由f(x1，x2，x3)=x12+x22+x32+4x1x2+4x1x3+4x2x3易求得其矩阵为易知A的特征值为λ1=a+(n一1)b=1+(3—1)×2=5，λ2=λ3=a—b=1—2=一1.或直接计算由｜λE—A｜==(λ一5)(λ+1)2=0得到λ1=5，λ2=λ3=一1．故此二次型在正交变换X=QY下的标准形为f(y1，y2，y3)=5y12一y22一y32，因而f(y1，y2，y3) 5y12一y22一y32=2，表示双叶双曲面．仅B入选．知识模块：向量代数和空间解析几何7．二元函数在点(0，0)处( )．A．连续，偏导数存在B．连续，偏导数不存在C．不连续，偏导数存在D．不连续，偏导数不存在正确答案：C解析：仅C入选．二元函数f(x，y)在点(0，0)处不连续．这是因为当y=kx 时，有k取不同值时，也不同，故不存在，因而在点(0，0)处f(x，y)不连续．或由点(x，y)沿直线y=x趋于点(0，0)时极限存在但不等于f(0，0)=0证之．事实上，有由偏导数的定义知，fx’(0，0)=，再由对称性有fy’(0，0)=0，故f(x，y)在点(0，0)处的两个偏导数都存在．知识模块：多元函数微分学8．[2012年] 如果函数f(x，y)在点(0，0)处连续，则下列命题正确的是( )．A．若极限存在，则f(x，y)在点(0，0)处可微B．若极限存在，则f(x，y)在点(0，0)处可微C．若f(x，y)在点(0，0)处可微，则极限存在D．若f(x，y)在点(0，0)处可微，则极限存在正确答案：B解析：设(k为常数)，则，因而f(x，y)～k(x2+y2)(x→0，y→0)．因f(x，y)在点(0，0)处连续，故又则故f(x，y)在点(0，0)处可微．仅B入选．知识模块：多元函数微分学9．[2002年] 考虑二元函数f(x，y)在点(x0，y0)处下面4条性质：(1)f(x，y)在点(x0，y0)处连续；(2)f(x，y)在点(x0，y0)处的两个偏导数连续；(3)f(x，y)在点(x0，y0)处可微；(4)f(x，y)在点(x0，y0)处的两个偏导数存在．若用“P=＞Q”表示可由性质P推出性质Q，则有( )．A．(2)=＞(3)=＞(1)B．(3)=＞(2)=＞(1)C．(3)=＞(4)=＞(1)D．(3)=＞(1)=＞(4)正确答案：A解析：若f(x，y)在点(x0，y0)处的两个偏导数连续，则f(x，y)在点(x0，y0)处可微，而f(x，y)在(x0，y0)处可微时，又必有f(x，y)在(x0，y0)处连续．因而有(2)=＞(3)=＞(1)．仅A入选．知识模块：多元函数微分学10．[2005年] 设有三元方程xy—zlny+exz=1，根据隐函数存在定理，存在点(0，1，1)的一个邻域，在此邻域内该方程( )．A．只能确定一个具有连续偏导数的隐函数z=z(x，y)B．可确定两个具有连续偏导数的隐函数y=y(x，z)和z=z(x，y)C．可确定两个具有连续偏导数的隐函数x=x(y，z)和z=z(x，y)D．可确定两个具有连续偏导数的隐函数x=x(y，z)和y=y(x，z)正确答案：D解析：仅D入选．F(x，y，z)=0，其中F(x，y，z)=xy—zlny+exy一1．显然，F在点(0，1，1)附近对x，y，z均有连续偏导数，且F(0，1，1)=0．相应的三个偏导数为F’z｜(0，1，1)=(lny+xexz)｜(0，1，1)=0，F’y｜(0，1，1)==一1≠0，F’x｜(0，1，1)=(y+zexz)｜(0，1，1)=2≠0．由隐函数存在定理知，在点(0，1，1)的一个邻域内，由方程F(x，y，z)=xy—zlny+exz一1=0可以确定两个具有连续偏导数的隐函数y=y(x，z)，x=x(y，z)．知识模块：多元函数微分学11．[2010] 设函数z=z(x，y)由方程确定，其中F为可微函数，且F’z≠0，则= ( )．A．xB．zC．一xD．一z正确答案：B解析：用直接法求之．设，在方程两边对x求偏导．由于x是x，y的函数，求关于x的偏导数时必须也要对z求偏导，得到易解得再在方程两边对y求偏导，同样必须对z也要对y求偏导，得到解得则仅B入选．知识模块：多元函数微分学12．[2005年] 设函数u(x，y)=φ(x+y)+φ(x—y)+∫x-yx+yψ(t)dt，其中φ具有二阶导数，ψ具有一阶导数，则必有( )．A．B．C．D．正确答案：B解析：知识模块：多元函数微分学填空题13．设(a×n)·c=2，则[(a+b)×(b+c)]·(c+a)=______．正确答案：4解析：由叉积对加法的分配律得[(a+b)×(b+c)]·(c+a)=[(a×b)+(a×c)+(b×b)+(b×c)]·(c+a)，其中b×b=0．再由点积对加法的分配律得原式=(a×b)·c+(a ×b)·a+(a×c)·c+(a×c)·a+(b×c)·c+(b×c)·a．由混合积的性质知，若a，b，c中有两个相同，则(a×b)·c=0，且(a×b)·c中相邻两向量互换，混合积变号，从而原式=2(a×b)·c=4．知识模块：向量代数和空间解析几何14．设一平面过原点及点A(6，一3，2)，且与平面4x—y+2z=8垂直，则此平面方程为______．正确答案：2x+2y-3z=0解析：已知平面的法向量n1=(4，一1，2)，又，由可取所求平面的法向量为n=(2，2，一3)．由点法式得所求平面方程为2(x一6)+2(y+3)一3(z一2)=2x+2y 一3z=0．知识模块：向量代数和空间解析几何15．[2006年] 点(2，1，0)到平面3x+4y一5z=0的距离d=______．正确答案：解析：由点到平面的距离公式得到知识模块：向量代数和空间解析几何16．[2007年] 设f(u，v)为二元可微函数，z=f(xy，yx)，则=______.正确答案：f’1·yxy-1+f’2·yxlny解析：设u=xy，v=yx，得到=f’1`yxy-1+f’2·yxlny．知识模块：多元函数微分学17．[2009年] 设函数f(u，v)具有二阶连续偏导数，z=f(x，xy)，则=______.正确答案：xf’’22+f’2+xyf’’22解析：=f’1(x，xy)+yf’2，则=xf’12+f’2(x，xy)+yxf’’22(x，xy)=xf’’22+f’2+xyf’’22．知识模块：多元函数微分学18．[2011年]设函数F(x，y)=则=______.正确答案：4解析：故知识模块：多元函数微分学19．[2015年] 若函数z=z(x，y)由方程ez+xyz+x+cosx=2确定，则dz｜(0，1)=______．正确答案：-dx解析：在所给方程两边求全微分，得到d(ez+xyz+z+cosx)=dez+d(xyz)+dx+dcosx=d(2)=0，ezdz+xydz+xzdy+yzdx+dx—sinx dx=0，整理得(ez+xy)dz=(sinx—yz-1)dx-xzdy，将x=0，y=1代入所给方程得到ez+1=2，得到z=0．将x=0，y=1，z=0代入式①，得到知识模块：多元函数微分学解答题解答应写出文字说明、证明过程或演算步骤。

2012年考研数学一试题分值特点及分布

线性代数
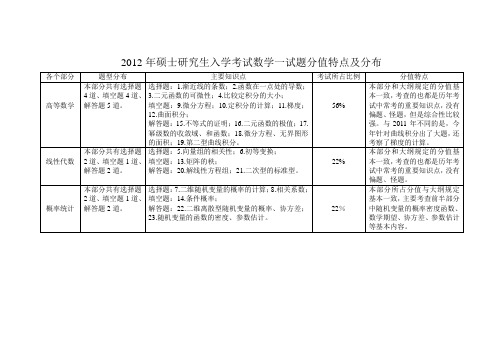
本部分共有选择题2道、填空题1道、解答题2道。
选择题：5.向量组的相关性；6.初等变换；
填空题：13.矩阵的秩；
解答题：20.解线性方程组；21.二次型的标准型。
22%
本部分和大纲规定的分值基本一致，考查的也都是历年考试中常考的重要知识点，没有偏题、怪题。
概率统计
本部分共有选择题2道、填空题1道、解答题2道。
解答题：15.不等式的证明；16.二元函数的极值；17.幂级数的收敛域、和函数；18.微分方程、无界图形的面积；19.第二型曲线积分。
56%
本部分和大纲规定的分值基本一致，考查的也都是历年考试中常考的重要知识点，没有偏题、怪题，但是综合性比较强。与2011年不同的是，今年针对曲线积分出了大题，还考察了梯度的计算。
2012年硕士研究生入学考试数学一试题分值特点及分布
各个部分
题型分布
主要知识点
考试所占比例
分值特点
高数学
本部分共有选择题4道、填空题4道、解答题5道。
选择题：1.渐近线的条数；2.函数在一点处的导数；3.二元函数的可微性；4.比较定积分的大小；
填空题：9.微分方程；10.定积分的计算；11.梯度；12.曲面积分；
选择题：7.二维随机变量的概率的计算；8.相关系数；
填空题：14.条件概率；
解答题：22.二维离散型随机变量的概率、协方差；23.随机变量的函数的密度、参数估计。
22％
本部分所占分值与大纲规定基本一致，主要考查前半部分中随机变量的概率密度函数、数学期望、协方差、参数估计等基本内容。

2012考研数一真题答案及详细解析

2012年（数一）真题答案解析一、选择题Cl) C解函数y=X +x x z —l 的间断点为x =土l 由lim y =lim x 2 +x 工]X 丑Cx +l)(x�, ==, 故X =l 是垂直渐近线．又lim y =lim X (x+ l ) 1 ＝—,故X =-l 不是渐近线．工-I 工-1(x + 1) (x -1) 2 考察x -=时函数的极限1 —+1X 由lim y = lim = 1 , 故y =l 是水平渐近线．x-=工-= 1 1-—X 2 y 2因为lim —=limx +x =O, 故无斜渐近线．工-00X x -00 X (x 2 -1) 故应选C,有2条渐近线．(2)A解J '(x)=矿(e 红-2)(e 3x —3)…(e"x -n ) + (e x -1) (2 e 2x ) (e 3x -3)…(e 杠-n )+……+ce—l)(e 2x -2)(e 3x -3)···(ne 杠）当X =O 时e 工—1=0故J '(0) = 1• (1—2) (1 -3)…0-n )=(—l)n -1 (n —1) ! 故应选A .(3)Bf (x,y) 解A项用枚举法：设f (x,y )=l x l +I Y I 则lim x -。

l x l +I Y I 存在，y 一o 但儿(0,0),儿(0,0)都不存在即f (x,y )在(0,0)处不可微.A错误B项．由lim f (x,y) 工-o x z + y z =AC存在），则lim f (x,y ) =0, x 一o y-0 y 一0又f (x ,y )在点(0,0)处连续，故f (O,O )=0; X -0 且时f(x,y )是x 2+ y z 的高阶无穷小y-o:. lim f (x,y )—f (O,O ) f (x ,y) =lim =O.B 正确芦心2+ y 2�=g 心：2 + y 2 C、D项用枚举法.f (x,y )=x 满足条件，但lim f (x ,y) f (x ,y) 与lim 2 芦gl x l +I Y I�二g X + y 2 错误．故应选B.(4)D均不存在故C、D 解I 2 =『：六矿sin x d x =『矿sin x d x +厂矿sinxdx=!1 +厂矿sinxd x O 兀又兀<x<加时e x 2sin x < 0故厂心血d x < o 故l2< l1Ia =厂矿sinx dx =厂矿sinxdx +厂矿sinx dx = 12 +厂产sinx dx 0 02又纭<x<玩时e "'2sinx > 0 故厂矿si nx dx > 0 故12< Ia, Ia =厂尸sinx dx = I: 矿sinx dx +厂矿sinx dx = 11 +厂产sinx dx 厂e x 2si n x d x =『六e 工2sinx d x + f "矿sinx dx =『lt穴矿sin .x d x +『穴"e"五）'sin (t +:)d(t +亢）＝厂矿sinx dx --J : e <工妇）2 si n xdx = J: [e 工2_ e (x 五）2 ]sin x d x > 0:. 13 > I 1 综上I a>I 1 > 12. 故应选D .(5)C解0 1 -1 l a 1,a3,a4I = O -1 1 =C11 C1 c3 c4 1 -1 =O-1 1 故U1,U3,U4线性相关．故应选C.(6)B 1 O O 1 O 0 解Q =(a,+a,,a,心）=(a,,a,,a,+ I o ]=+ I o ] 0 0 1 0 0 1 Q 一'A Q = [i � �r P -'A P[三三子］＝［—又��][1 I J [上三�]=[I I J 故应选B.(7)A e -x,X>0,解八(x)= { o,X¾O , 由X,Y相互独立，故fy (y )=t e 五，y>O ,o , y�o. f (x ,y ) =八(x )•八(y )= {4e 玉如，x>O ,y>O , 0 ' 其他P{X<Y}= JI f (x ,y )d xd y= II 4e 玉+4y )dx d y (8)D <y 1 5．故应选A.解设两段木棒的长度为x,y 则X +y =1⇒ y =-x + 1由定理：若y =a x +b 则I P x Y I = 1,若心a <O则p xy = -1,®a >O 则p xy = 1.故px y =—1. 故应选D.1 2 ．． l +x(l —X)2 s m x -x l —xl+x ＋ 2x =l n-s m x -x l —X Cl+工:)(1—x) l+x =l n +x 1—x 1 +x 1 1 =l n1 十—sm x —x -x l —x I+x XE (O,l) /} 1 } } f (x) = + + + -cosx —1l+x 1—.r (1—x)2 O +x )2 x E (0,1)1 广(x)=—+ 12 2 —+O+x)2 Cl-x)2 (1—x)3 Cl+x)3 + s inx x E (0 , 1)因为O< 1 1 1 X <}时，>o, 1 (l-x)2-(l+x )2 (1-x)3-(l+x )3 > O,sinx > 0,故J"(x)> 0.又因为J'(x)在[O'1)是连续的，故J'(x)在[0,1)上是单调增加的，f I (X ) > f I (0) = 2 > 0 同理，f(x )在[O,1)上也是单调增加的，f(x )>f(O)=O,故F(x)在[O,1)上是单调增加的，F(x)> F (O) =O; 又因为F(x )是偶函数，则F(x)> O ,x E (—1,1) ,x #-0. 又因为F(O)=O, 故F(x )�o,即原不等式成立，证毕．(16)解先求出驻点叮＾迁王丑+Y 2,-2+_v 2 —=e 一一+x e ——亡• (—x)=Cl -x 2)e-—广0.2 、丿。

考研数学一常微分方程历年真题试卷汇编4_真题-无答案

考研数学一（常微分方程）历年真题试卷汇编4(总分150,考试时间180分钟)选择题1. 1.[2004年] 微分方程y''+y=x2+1+sinx的特解形式可设为( )．A. y*=ax2+bx+c+x(Asinx+Bcosx)B. y*=x(ax2+bx+c+Asinx+Bcosx)C. y*=ax2+bx+c+AsinxD. y*=ax2+bx+c+Acosx2. 2.[2008年] 在下列微分方程中以y=C1ex+C2cos2x+C3sin2x (C1，C2，C3为任意常数)为通解的是( )．A. y'''+y''一4y'一4y=0B. y'''+y''+4y'+4y=0C. y'''一y''一4y'+4y=0D. y'''-y''+4y'-4y=03. 3.[2015年] 设是二阶常系数非齐次线性微分方程y''+ay'+by=cex的一个特解，则( )．A. a=一3，b=2，c=一1B. a=3，b=2，c=一1C. a=一3，b=2，c=1D. a=3，b=2，c=14. 4.[2016年] 若y=(1+x2)2一，y=(1+x2)2+再是微分方程y'+p(x)y=q(x)的两个解，则q(x)=( )．A. 3x(1+x2)B. 一3x(1+x2)C.D.填空题5. 5.[2006年] 微分方程y'=y(1一x)／x的通解是______．6. 6.[2008年] 微分方程xy'+y=0满足条件y(1)=1的解为______．7. 7.[2014年] 微分方程xy'+y(lnx—lny)=0满足条件y(1)=e3的解为y=______.8. 8.[2011年] 微分方程y'+y=e-xcosx满足条件y(0)=0的解为y=______．9. 9.[2005年] 微分方程xy'+2y=xlnx满足y(1)=一1／9的特解为______．10. 10.[2013年] 已知y1=e3x—xe2x，y2=ex一xe2x，y3=一xe2x是某二阶常系数非齐次线性微分方程的3个解，则该方程的通解为y=______．11. 11.[2002年] 微分方程yy''+y'2=0满足初始条件y｜x=0=1，y'｜x=0=1／2的特解是______．12. 12.[2007年] 二阶常系数非齐次线性微分方程y''-4y'+3y=2e2x的通解为______．13. 13.[2012年] 若函数f(x)满足方程f''(x)+f'(x)-2f(x)=0及f''(x)+f(x)=2ex，则f(x)=______．14. 14.[2017年] 微分方程y''+2y'+3y=0的通解为y=______．15. 15.微分方程xy''+3y'=0的通解为______．16. 16.[2004年] 欧拉方程(x＞0)的通解是______．17. 17.[2009年] 若二阶常系数线性齐次微分方程y''+ay'+by=0的通解为y=(C1+C2x)ex，则非齐次方程y'+ay'+by=x满足条件y(0)=2，y'(0)=0的解为______．解答题[2018年] 已知微分方程y'+y=f(x)，其中f(x)是R上的连续函数．18. 18.若f(x)=x，求方程的通解．19. 19.若f(x)为周期函数，试证微分方程有解与其对应，且该解也为周期函数．20. 20.求微分方程x2y'+xy=y2满足初始条件y｜x=1=1的特解．21. 21.设f(x)具有二阶连续导数，f(0)=0，f'(0)=1，且[xy(x+y)-f(x)y]dx+[f'(x)+x2y]dy=0为一全微分方程，求f(x)及此全微分方程的通解．22. 22.[2010年]求微分方程y''一3y'+2y=2xex的通解．[2003年] 设函数y=y(x)在(一∞，+∞)内具有二阶导数，且y'≠0，x=x(y)是y=y(x)的反函数．23. 23.试将x=x(y)所满足的微分方程变换为y=y(x)满足的微分方程；24. 24.求变换后的微分方程满足初始条件y(0)=0，y'(0)=3／2的解．25. 25.[2005年] 用变量代换x=cost(0＜t＜π)化简微分方程(1一x2)y''-xy'+y=0，并求其满足y｜x=0=1，y'｜x=0=2的特解．26. 26.[2015年] 设函数f(x)在定义域I上的导数大于零，若对任意x0∈I，曲线y=f(x)在点(x0，f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4，且f(0)=2，求f(x)的表达式．27. 27.从船上向海中沉放某种探测仪器，按探测要求，需确定仪器的下沉深度y(从海平面算起)与下沉速度v之间的函数关系．设仪器在重力作用下，从海平面由静止开始铅直下沉，在下沉过程中还受到阻力和浮力的作用．设仪器的质量为m，体积为B，海水密度为ρ，仪器所受的阻力与下沉速度成正比，比例系数为k(k＞0)．试建立y与v所满足的微分方程，并求出函数关系式y=y(v)．28. 28.[2004年] 某种飞机在机场降落时，为了减少滑行距离，在触地瞬间，飞机尾部张开降落伞以增大阻力使飞机迅速减速并停下．现有一质量为9000 kg的飞机，着陆时的水平速度为700 km／h．经测试，减速伞打开后飞机所受的阻力与飞机的速度成正比(比例系数k=6．0×106)．问从着陆点算起，飞机滑行的最大距离是多少(注：kg表示千克，km／h表示千米／小时)．。