《三角形复习课》精品PPT课件
合集下载
全等三角形复习课通用课件

详细描述
根据ASA全等定理,如果两个三角形 的两角和它们之间的夹边分别相等, 则这两个三角形全等。
适用情况
适用于已知三角形两角和夹边相等的 情况。
证明方法
通过比较两个三角形的两组对应角和 夹边是否相等来证明两个三角形是否 全等。
角角边(AAS)
总结词
详细描述
当两个三角形的两角和其中一个角的对边 分别相等时,这两个三角形全等。
详细描述
根据SAS全等定理,如果两个 三角形的两边和它们之间的夹 角分别相等,则这两个三角形 全等。
适用情况
适用于已知三角形一边和邻接 角相等的情况。
证明方法
通过比较两个三角形的两组对 应边和夹角是否相等来证明两
个三角形是否全等。
角边角(ASA)
总结词
当两个三角形的两角和它们之间的夹 边分别相等时,这两个三角形全等。
解决实际问题
总结词
全等三角形在实际问题中有着广泛的应用,可以帮助解决各种与几何相关的问题。
详细描述
全等三角形在实际问题中有着广泛的应用,例如在建筑设计、机械制造、测量等领域中都可以利用全等三角形的 性质来解决各种问题。通过全等三角形的性质,可以方便地解决与几何相关的问题,提高解决问题的效率和质量 。
综合练习题
总结词
培养学生综合运用全等三角形与其他数学知识的能力
详细描述
设计一些涉及多个知识点和解题技巧的题目,要求学 生能够灵活运用全等三角形的知识与其他数学知识( 如平行线、角平分线等)来解决实际问题。
感谢您的观看
THANKS
帮助学生掌握全等三角形的基本性质和判定 方法
详细描述
设计一系列基础题目,包括选择题、填空题 和简答题,旨在帮助学生回顾全等三角形的 定义、性质和判定定理,如SSS、SAS、 ASA、AAS等。
三角形全等判定复习ppt课件
N 明方法与前题基本相同,只
须证明⊿ABN≌⊿BCM
A
C
B
变式4:如图,⊿ABD,⊿ACE都是正三角形, 求证CD=BE
D
A
E
B
C
分析:此题实质上是把题目中的条件B,A,C三点改为 不共线,证明方法与前题基本相同.
变式6:如图,分别以⊿ABC的边AB,AC为一边 画正方形AEDB和正方形ACFG,连结CE,BG.
求证BG=CE
E
分析:此题是把两个三
角形改成两个正方形而
D
A
G 以,证法类同
FBBiblioteka C小结:1.证明两个三角形全等,要结合题目的条件 和结论,选择恰当的判定方法
2.全等三角形,是证明两条线段或两个角相 等的重要方法之一,证明时
①要观察待证的线段或角,在哪两个可能全等的三 角形中。
②分析要证两个三角形全等,已有什么条件,还缺 什么条件。
AB=CB
A
AD=CD
BD=BD
_
=
P
∴ △ABD≌△CBD(SSS)
B
D
∴∠ABD=∠CBD
_
=
在△ABP和△CBP中
C
AB=BC
∠ABP=∠CBP
BP=BP
∴ △ABP ≌ △CBP(SAS)
∴PA=PC
例4。已知:如图AB=AE,∠B=∠E,BC=ED AF⊥CD 求证:点F是CD的中点
分析:要证CF=DF可以考虑CF 、 DF所在的两个三角形全等,为此可 添加辅助线构建三角形全等 ,如何 添加辅助线呢?
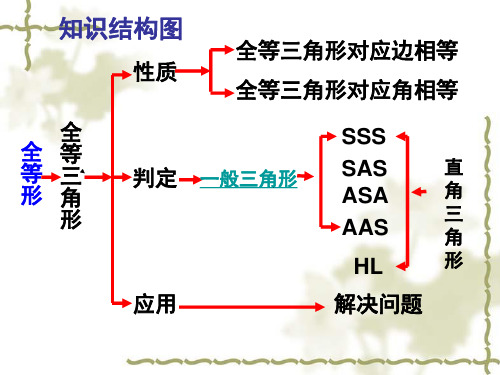
知识结构图
性质
全等三角形对应边相等 全等三角形对应角相等
全 全等 等三 形角
形
完整版-全等三角形总复习PPT教学课件

AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
2024/3/9
29
6. 如图A、B、C在一直线上,△ABD,△BCE都是等边 三角形,AE交BD于F,DC交BE于G,求证:BF=BG。
AB
=
DB
∠ABE = ∠ DBC
BE=BC ∴△ABE≌△DBC(SAS)
D
C
2
1
A
B
思路3: 已知一边一角(边与角相邻):
找夹这个角的另一边
AD=CB (SAS)
找夹这条边的另一角
∠ACD=∠CAB(ASA)
找边的对角
∠D=∠(B AAS)
15
如图,已知∠B= ∠E,要识别△ABC≌ △AED,需 要添加的一个条件是--------------
A
D
C
E
思路4:
找夹边
AB=AE (ASA)
∴ △ADC ≌ △EDB
D
C
∴ AC = EB
在△ABE中,AE < AB+BE=AB+AC
E
即 2AD < AB+AC
∴ AD 1 (AB AC) 2
2024/3/9
35
12.如图,已知AC∥BD,EA、EB分别平分∠CAB和∠DBA, CD过点E,则AB与AC+BD相等吗?请说明理由。
C A
∵ QD⊥OA,QE⊥OB,QD=QE(已知). ∴点Q在∠AOB的平分线上.(到角的两边的距
离相等的点在角的平分线上)
2024/3/9
10
2.如图, △ABC的角平分线BM,CN相交于点P, 求证:点P到三边AB、BC、CA的距离相等
三角形中考复习PPT课件

2.按角分
直角三角形
三角形斜三角形② ①
锐角 钝角
三角形 三角形
第23页/共100页
返回目录 23
第四单元 三角形
考点2 三角形的基本性质
1.三角形的三边关系 如图①,我们知道“连接两点的所有连线中,线段 最短”,因此有:AC+CB>AB,BA+AC>BC, AB+BC>AC.由此可见,三角形三边之间有如下 关系: 三角形任意两边之和③ 大于 第三边.
例1.已知:如图5,AB∥CD,
A
1
E2
BF
求证:∠B+∠D=∠BED.
C
D
证明:过点E作EF∥AB,
(图5)
∴∠B=∠1(两直线平行,内错角相等).
∵AB∥CD(已知),
又∵EF∥AB(已作),
∴EF∥CD(平行于同一直线的两条直线互相平行).
∴∠D=∠2(两直线平行,内错角相等).
又∵∠BED=∠1+∠2,
线段,任选其中的三条线段组成一个三角形,则最多
能组成三角形的个数为(C )
A.1
B.2
C.3 D.4
【解析】①3、6、8,3+6>8,能构成;②3、6、9,
3+6=9,不能构成;③3、8、9,3+8>9,能构成;④
6、8、9,6+8>9,能构成.故最多能组成三个三角
形.
第30页/共100页
返回目录 30
第四单元 三角形
【点评与拓展】(1)三边关系定理:①三角形两边之和
大于第三边;②三角形的两边之差小于第三边;实际
操作时,只要验证:两条较短的线段长度之和大于第
三条线段的长度即可.(2)三角形的三边关系一般和不
第十一章 三角形 复习课件

6、同上题图,若
A
△ACD的面积为
630cm2,则△ABC 的面积为1_62_00_cc_mm_2。2 B D C
填一填Байду номын сангаас
7、如图,在△ABC中,CE,
BF是两条高,若∠A= 56705°,
∠ 是B24C50E°=,3205°,则∠EBF的A 度数
∠FBC的度
E
F
数是__24_0_°_。
B
C
看你会不会
第十一章 三角形 复习课件
你学会了哪些?
三角形的边
与三角形有关
高
三
的线段
中线
角
角平分线
形
三角形的内角和 多边形的内角和
三角形的外角
多边形的外角和
如图,在△ABC中,AD是BC边上的中线,△ADC的周
例1 长比△ABD的周长多3cm, AB与AC的和为13cm,求AC的
长。
解:∵AD是BC边上的中线, ∴D为BC的中点, ∴CD=BD。 ∵C△ADC-C△ABD=3, ∴AC-AB=3, 又∵AB+AC=13, ∴AC=8cm,即AC的长度是8cm。
8、如图, AD、AF分别是△ABC 的高和角平线,C 76,B 36 则 DAF =______度。
填一填
9、若三角形三个内角的度数
之比为12∶23∶346 ,则这三个内角 的度数分别是_143_8_00_0、、__5_64_00_0、、__1_890_0_80_0。
10、在△ABC中,根据下列条 件,求∠C的度数。 ③①②∠∠ABB=A⊥4=03B08C,0,∠∠A∶AB=∠3753C0 =,3∶4
∠∠CC== 68590500
填一填
八年级数学全等三角形复习课件(高效)-PPT

就知道∠ABC=∠ADC。请用所学的知识给予
说明。
18
5.如图(4)AE=CF,∠AFD=∠CEB,DF=BE, △AFD与△ CEB全等吗?为什么?
A 解:∵AE=CF(已知)
∴AE-FE=CF-EF(等量减等量,差相等)
即AF=CE
F
在△AFD和△CEB中,
AF=CE(已证)
∠AFD=∠CEB(已知)
17
三、熟练转化“间接条件”
判全等
A
D
5如图,AE=CF,∠AFD=∠CEB,DF=BE, △AFD与△ CEB全等吗?为什么?
6.如图(5)∠CAE=∠BAD,∠B=∠D,
AC=AE,△ABC与△ADE全等吗?
E
FE
B
C
B
D
为什么?
C
A
7.“三月三,放风筝”如图(6)是小东同学自己
做的风筝,他根据AB=AD,BC=DC,不用度量,
B
DF=BE(已知)
∴△AFD≌△CEB (SAS)
D E
C
19
6.如图(5)∠CAE=∠BAD,∠B=∠D, AC=AE,△ABC与△ADE全等吗?为什么?
B
解:∵ ∠CAE=∠BAD(已知)
E
D
∴ ∠CAE+∠BAE=∠BAD+∠BAE
C
A
(等量减等量,差相等) 即∠BAC=∠DAE
在△ABC和△ADE中, ∠B=∠D(已知)
角”与
“对角”的不同含义;
(2):表示两个三角形全等时,表示对应顶点的 字母要写在对应的位置上;
(3):要记住“有三个角对应相等”或“有两边及 其中一边的对角对应相等”的两个三角形不一定全等;
《三角形复习课》PPT教学课件

11. 三角形外角和定理 三角形的外角和等于3600
7
12. 三角形的外角与内角的关系 三角形的一个外角等于与它不相邻的
两个内角的和。 三角形的一个外角大于与它不相邻的
任何一个内角。
8
13、n边形的内角和等于(n-2)·180 多边形的外角和都等于360°.
我们通过把多边形划分为若干个三
角形,用三角形内角和去求多边形内角
20
例3、如图所示,∠B=45°, ∠A=30°,∠C=25°, 求∠ADC的度数
A
D
B
C
21
析:利用转化思想,把四边形转化成 几个三角形,再利用三角形内角和定 理来解答。
A
A
D
D
B
C
B
A
C
D
22
例4、如图所示:
求∠A+∠B+∠C+∠D+ ∠E+∠F+∠G的度数
C
F
G
D
B
A
分析
E
C
:
B
F
G
D
A
B
DC
27
2、有一六边形,截去一三角形,内角和会发生 怎样变化?请画图说明。
内角和减少180O 内角和不变 内角和增加180O
28
29
16
3.如图,已知:AD是△ABC 的中线,△ABC的面积为 60cm2 ,求
△ABD的面积
A
解:作AE BC,垂足为E, AD是 ABC的中线,
BD CD,
B
DE
C
又 S ABC 60cm2
S
ABD
1 BD AE, 2
S
ADC
1 CD AE, 2
7
12. 三角形的外角与内角的关系 三角形的一个外角等于与它不相邻的
两个内角的和。 三角形的一个外角大于与它不相邻的
任何一个内角。
8
13、n边形的内角和等于(n-2)·180 多边形的外角和都等于360°.
我们通过把多边形划分为若干个三
角形,用三角形内角和去求多边形内角
20
例3、如图所示,∠B=45°, ∠A=30°,∠C=25°, 求∠ADC的度数
A
D
B
C
21
析:利用转化思想,把四边形转化成 几个三角形,再利用三角形内角和定 理来解答。
A
A
D
D
B
C
B
A
C
D
22
例4、如图所示:
求∠A+∠B+∠C+∠D+ ∠E+∠F+∠G的度数
C
F
G
D
B
A
分析
E
C
:
B
F
G
D
A
B
DC
27
2、有一六边形,截去一三角形,内角和会发生 怎样变化?请画图说明。
内角和减少180O 内角和不变 内角和增加180O
28
29
16
3.如图,已知:AD是△ABC 的中线,△ABC的面积为 60cm2 ,求
△ABD的面积
A
解:作AE BC,垂足为E, AD是 ABC的中线,
BD CD,
B
DE
C
又 S ABC 60cm2
S
ABD
1 BD AE, 2
S
ADC
1 CD AE, 2
人教版 八年级上册 《三角形》 复习课件(共34张PPT)

B A
小莉的设计方案:先在池塘旁取一个能
直接到达A和B处的点C,连结AC并延长至
D点,使AC=DC,连结BC并延长至E点,
使BC=EC,连结CD,用米尺测出DE的长,
这个长度就等于A,B两点的距离。请你说
明理由。
解: AC=DC
∠ACB=∠DCE
A
B
BC=EC
C
△ACB≌△DCE(SAS)
E
D
AB=DE
: ①两边和一角对应相等;②两角和一边对应
相等; ③两个直角三角形中斜边和一条直角边
对应相等;④三个角对应相等;其中能判定这两
个三角形全等的条件是( )
A、①和②
B、 ①和④
C、②和③
D、③和④
1、如图AB=CD,AC=BD,则 △ABC≌△DCB吗?说明理由。
解:△ABC≌△DCB
A 在△ABC与△DCB中
如图,已知AB=AC,AD=AE。 A 求证:∠B=∠C
证明:在△ABD和△ACE中 E
AB=AC(已知)
A=A(公共角)
B A
AD=AE(已知)
∴△ABD≌△ACE(SAS) D
∴∠B=∠C(全等三角形
D C
A
E
对应角相等)
B
C
如图,∠B=∠E,AB=EF,BD=EC,那 么△ABC与 △FED全等吗?为什么?
2
。
(3,3,1;2,2,3)
1、如图,求△ABC各内角的度数。 A
解:3x + 2x + x = 180
35xx
6x=180
X=30
23xx
B
xx C
∴三角形各内角的度数分别为:30°,60°,90°
小莉的设计方案:先在池塘旁取一个能
直接到达A和B处的点C,连结AC并延长至
D点,使AC=DC,连结BC并延长至E点,
使BC=EC,连结CD,用米尺测出DE的长,
这个长度就等于A,B两点的距离。请你说
明理由。
解: AC=DC
∠ACB=∠DCE
A
B
BC=EC
C
△ACB≌△DCE(SAS)
E
D
AB=DE
: ①两边和一角对应相等;②两角和一边对应
相等; ③两个直角三角形中斜边和一条直角边
对应相等;④三个角对应相等;其中能判定这两
个三角形全等的条件是( )
A、①和②
B、 ①和④
C、②和③
D、③和④
1、如图AB=CD,AC=BD,则 △ABC≌△DCB吗?说明理由。
解:△ABC≌△DCB
A 在△ABC与△DCB中
如图,已知AB=AC,AD=AE。 A 求证:∠B=∠C
证明:在△ABD和△ACE中 E
AB=AC(已知)
A=A(公共角)
B A
AD=AE(已知)
∴△ABD≌△ACE(SAS) D
∴∠B=∠C(全等三角形
D C
A
E
对应角相等)
B
C
如图,∠B=∠E,AB=EF,BD=EC,那 么△ABC与 △FED全等吗?为什么?
2
。
(3,3,1;2,2,3)
1、如图,求△ABC各内角的度数。 A
解:3x + 2x + x = 180
35xx
6x=180
X=30
23xx
B
xx C
∴三角形各内角的度数分别为:30°,60°,90°
第四章《 三角形 》复习总结 ppt课件

本章总结提升
[点析]本题以构成三角形三边关系为载体,主要考查了整式 计算与三角形的有关边知识的理解与运用,在探究等腰三角形的 形状时要注意分类讨论,构建方程分析与解决实际问题.
本章总结提升
► 类型二 等腰三角形
例3 一个三角形的两条边相等,周长为18 cm,三角形一边 长为4 cm,求其他两边长.
本章总结提升
例10 如图4-T-8,AB=AE,∠B=∠E,BC=ED,F是CD的
中点,则AF⊥CD吗?试说明理由.
图4-T-8
本章总结提升
解:连接AC,AD,由AB=AE,∠B=∠E,BC=DE,根据 “SAS”可知△ABC≌△AED,
根据全等三角形的对应边相等可知AC=AD. 由AC=AD,CF=DF,AF=AF(公共边), 根据“SSS”可知△ACF≌△ADF. 根据全等三角形的对应角相等可知∠AFC=∠AFD. 又由于F在直线CD上,可得∠AFC=90°, 即AF⊥CD.
[解析] 本题分两种情况:①腰长为4 cm,②底边长为4 cm. 解答时要注意求出的边长要符合“三角形两边之和大于第三边” .
本章总结提升
解:①当腰长为 4 cm 时,则底边长为 18-4×2=10(cm),此 时,三角形三边长为 4 cm,4 cm,10 cm,因为 4+4<10,不符合 三角形三边关系,所以当三角形的腰长为 4 cm 时不合题意,舍去; ②当底边长为 4 cm 时,则腰长为182-4=7(cm),此时三角形的三 边长为 4 cm,7 cm,7 cm,4+7>7,符合三角形三边关系,所以, 该三角形其他两边长为 7 cm,7 cm.
图4-T-4
本章总结提升
解:如图4-T-5所示.①先画射线BC;
图4-T-5
人教版11章《三角形》全章复习(共25张PPT)

例5 如图,在锐角△ABC中,CD、BE 分别是AB、AC边上的高,且CD、BE 交于一点P,若∠A=50°,则∠BPC的 度数是(B)
A.150° B.130° C.120° D.100°
例6 如图所示,BE与CD相交于点A,CF为∠BCD 的平分线,EF为∠BED的平分线。 (1)试探求∠F与∠B、∠D间有何等量关系。
(2)根据你的猜想,当n=4时说明∠BO3C的 度数成立.
解:当n=4时,代入所猜想的公式得 ∠BO3C=(1/4)×180°+(3/4)×∠A。
另外,在△BO3C中由三角形内角和定理 得:
∠BO[3]C=180°-(∠O3BC+∠O3CB) =180°-(3/4)(∠ABC+∠ACB) =180°-(3/4)(180°-∠A) =(1/4)×180°+(3/4)∠A
解:(1)∠D+∠B=2∠F ∵EF平分∠BED,CF平分∠BCD ∴∠DEF=(1/2)DEB,∠FCD=(1/2)∠BCD 而∠EMC=∠D+(1/2)∠BED,
∠EMC=∠F+(1/2)∠BCD ∴∠D+(1/2)∠BED=∠F+(1/2)∠BCD ① 同理可得: ∠B+(1/2)∠BCD=∠F+(1/2)∠BED ②
11章《三角形》 章末复习
R·八年级上册
知识框架
回顾思考
1.本章的主要内容是: 三角形的概念, 三角形的三边关系定理, 三角形的三条重要线段(高、中线和角平分线), 三角形内角和定理。
三角形的外角,多边形的内、外角和定理,简单 的平面镶嵌。
三角形的稳定性和四边形的不稳定性。
2.经历三角形内角和等于180°的验证与证明过 程,初步体验对一个规律的发展到发现确认艰 辛历程。体会证明的重要性,初步接触辅助线 在几何研究中不 可或缺的作用。
三角形复习课ppt课件

2、三角形的三边长分别不3㎝,8㎝,x㎝,且x为整
数,那么x应满足的不等式是_5_㎝__<___x_<__1_1_㎝___,可能 取的值共有____5____个。
3+8>x 11 >x x<11
8-3<x 5<x x>5
∴ 5㎝<x<11㎝
知 识 要 点
B
1
四、三角形的角的性质
★1.三角形三个内角的和等于180°
可求∠BAC
例3 如图,已知∠B=28°,∠C=56°,AD 是高线, AE是∠BAC的平分线求∠DAAE的度数.
解 ∵ ∠BAC+∠B+∠C=180°
(三角形的内角和等于360) ∴ ∠BAC=180°- ∠B-∠C =180°-28°-56°=96°. B 28°
56° C
∵AE是∠BAC的平分线 (已知)
★2.三角形的一个外角等于 和它不相邻的两个内角 的和
★3.三角形的一个外角大于 任何一个和它不相邻的内角
A
∵∠1是△ABC的一个外角
∴(1)∠ 1= ∠B+ ∠C
(三角形的一个外角等于
和它不相邻的两个内角
C
的和 )
(2)∠1>∠B,∠1>∠C.
(三角形的一个外角大于 任何一个和它不相邻的内角)
四、三角形的角的性质
知识系统
概念与分类
三
画法
角
角
形
性质
边
有关线段
一、三角形及有关概念
不在同一条直线上的三条线段首尾顺次连 结组成的图形叫做三角形。
A 顶点
角
边
边
记作△ABC
角
角 外角
B
边
C
D
A
斜边
数,那么x应满足的不等式是_5_㎝__<___x_<__1_1_㎝___,可能 取的值共有____5____个。
3+8>x 11 >x x<11
8-3<x 5<x x>5
∴ 5㎝<x<11㎝
知 识 要 点
B
1
四、三角形的角的性质
★1.三角形三个内角的和等于180°
可求∠BAC
例3 如图,已知∠B=28°,∠C=56°,AD 是高线, AE是∠BAC的平分线求∠DAAE的度数.
解 ∵ ∠BAC+∠B+∠C=180°
(三角形的内角和等于360) ∴ ∠BAC=180°- ∠B-∠C =180°-28°-56°=96°. B 28°
56° C
∵AE是∠BAC的平分线 (已知)
★2.三角形的一个外角等于 和它不相邻的两个内角 的和
★3.三角形的一个外角大于 任何一个和它不相邻的内角
A
∵∠1是△ABC的一个外角
∴(1)∠ 1= ∠B+ ∠C
(三角形的一个外角等于
和它不相邻的两个内角
C
的和 )
(2)∠1>∠B,∠1>∠C.
(三角形的一个外角大于 任何一个和它不相邻的内角)
四、三角形的角的性质
知识系统
概念与分类
三
画法
角
角
形
性质
边
有关线段
一、三角形及有关概念
不在同一条直线上的三条线段首尾顺次连 结组成的图形叫做三角形。
A 顶点
角
边
边
记作△ABC
角
角 外角
B
边
C
D
A
斜边
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
BD
C
练一练
3、下列条件中能组成三角形的是( C )
A、 5cm, 13cm, 7cm B、 3cm, 5cm, 9cm C、 14cm, 9cm, 6cm D、 5cm, 6cm, 11cm
4、三角形的两边为7cm和5cm,则第三边x的 范围是_2_c_m__右图,AD是BC边上的高,BE 是 △ ABD的角平分线,∠1=40°, ∠2=30°,则∠C=6_0_°__∠BED=65°。
2 X X 2 X 1800
5X 1800
11. 三角形外角和定理 三角形的外角和等于3600
12. 三角形的外角与内角的关系
三角形的一个外角等于与它不相邻的 两个内角的和。
三角形的一个外角大于与它不相邻的 任何一个内角。
13、n边形的内角和等于(n-2)·180 多边形的外角和都等于360°.
我们通过把多边形划分为若干个三 角形,用三角形内角和去求多边形内角 和,从而得到多边形的内角和公式为 (n-2)× 180°。这种化未知为已 知的转化方法,必须在学习中逐渐掌握。 由于多边形外角和为360°,与边数无 关,所以常把多边形内角和的问题转化 为外角和来处理。
6. 三角形的三条角平分线交于三角形 内部一点。
7. 三角形的分类
(1) 按角分
斜三角形
三角形
锐角三角形 钝角三角形
直角三角形
(2) 按边分
三角形
不等边三角形
腰和底不等的等腰三角形
等腰三角形 等边三角形
8. 三角形的主要线段 三角形的高线定义:
从三角形的一个顶点向它的对边所在直线作垂线, __ 顶点__和__垂__足__之__间__的线段叫做三角形的高线.
BD CD,
B
DE
C
又 S ABC 60cm2
S
ABD
1 BD AE, 2
S
ADC
1 CD AE, 2
S
ADC
S
ABD
1S 2
ABC 1 60 2
30(cm2 )
5.已知B 420, A 100 1, ACD 640,说明AB // CD。
D
C
1
A
解: A B 1 1800 (三角形内角和等于1800 ) 又 B 420, 1 A 100 B A 420 A 100 1800 (等量代换) 2A=1280,A 640 又 ACD 640 A ACD AB // CD(内错角相等,两直线平行)
7.如图, △ABC中, ∠A= ∠ABD, ∠C= ∠BDC= ∠ABC,求∠DBC的度数
A
解:设A X 0
A ABD,ABD X 0
BDC A ABD 2 X 0
D
又 C ABC BDC
C ABC 2 X 0
DBC ABC ABD
B
C 2X 0 X 0 X 0
又 C DBC BDC 1800
解:当腰长为5cm时,它的周长为: 5+5+8=18(cm) 当腰长为8cm时,它的周长为: 8+8+5=21(cm)
∴这个三角形的周长为18cm或21cm
3.如图,已知:AD是△ABC 的中线,△ABC的面积为 60cm2 ,求
△ABD的面积
A
解:作AE BC,垂足为E, AD是 ABC的中线,
6.已知.1 2, 3 4, A 1000,求X的值。
B 1 2 A X
34
C
解 :
A 1 2 3 4 1800
又 A 1000, 1 2, 3 4
1000 22 24 1800
2(2 4) 800
2 4 400
又 2 4 X 1800
X 1800 400 1400
14、镶嵌
1、拼接在同一个点的各个角 的和等于360度
2、任意三角形一定可以镶嵌. 3、任意四边形一定可以镶嵌 4、正六边形可以镶嵌.
注意:只用正五边形、正八边 形一种图形不能镶嵌.
练一练
1.在△ABC中, (1)∠B=100°,∠A=∠C,则∠C= 40°; (2)2∠A=∠B+∠C,则∠A= 60°。 2.如图,_∠_A__D_B_是△ACD的外角, ∠ADB= 115°,∠CAD= 80°则∠C =__3_5°.
A BDC
知识应用
1、已知两条线段的长分别是3cm、8cm , 要想拼成一个三角形,且第三条线段a的 长为奇数,问第三条线段应取多少长?
解: 由三角形两边之和大于第三边,
两边之差小于第三边得:
8-3<a<8+3,
∴ 5 <a<11
又∵第三边长为奇数,
∴ 第三条边长为 7cm、9cm。
2、有两边相等的三角形一边的长是5 cm, 另一边的长是8cm,求它的周长
三角形知识结构图
三角形的边
与三角形有 关的线段
三
角
形
与三角形有
关的角
三角形的分类
中线 角平分线 三角形内角和 三角形外角和 内角与外角关系
定义
多
边 形
多边形的内外角和
镶嵌
1. 三角形的三边关系:
(1) 三角形两边的和大于第三边 (2) 三角形两边的差小于第三边
2. 判断三条已知线段a、b、c能否 组成三角形.
B
A
12 E
D
C
6.直角三角形的两个锐角相等,则每一个锐角等于 __4_5__度。
7、在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大 30°,则∠C的外角为_____7度5°,这个三角形是____ 三钝角形
8、如图,已知:AD是△ABC 的中线,△ABC的面积为50cm2 ,则△ABD的面积是___2_5_c_m_2.
当a最长,且有b+c>a时,就可构成三角形.
3. 确定三角形第三边的取值范围:
两边之差<第三边<两边之和.
4. 三角形的三条高线(或高线所在直线) 交于一点
锐角三角形三条高线交于三角形内部一点, 直角三角形三条高线交于直角顶点, 钝角三角形三条高线所在直线交于三角形 外部一点。
5.三角形的三条中线交于三角形内部一点。
三角形角平分线的定义:
三个角角形的一顶个点角与的交平点分之线间与的它线的段对叫边做相三交角,形这的 角平分线。
三角形的中线定义
连结三角形一个 顶点与它对边中点 的线段 叫做三角形的中线。
9. 三角形木架的形状不会改变,而四边形木 架的形状会改变.这就是说,三角形具有稳定 性,而四边形没有稳定性。
10. 三角形内角和定理 三角形的内角和等于1800 直角三角形的两个锐角互余。
BD
C
练一练
3、下列条件中能组成三角形的是( C )
A、 5cm, 13cm, 7cm B、 3cm, 5cm, 9cm C、 14cm, 9cm, 6cm D、 5cm, 6cm, 11cm
4、三角形的两边为7cm和5cm,则第三边x的 范围是_2_c_m__右图,AD是BC边上的高,BE 是 △ ABD的角平分线,∠1=40°, ∠2=30°,则∠C=6_0_°__∠BED=65°。
2 X X 2 X 1800
5X 1800
11. 三角形外角和定理 三角形的外角和等于3600
12. 三角形的外角与内角的关系
三角形的一个外角等于与它不相邻的 两个内角的和。
三角形的一个外角大于与它不相邻的 任何一个内角。
13、n边形的内角和等于(n-2)·180 多边形的外角和都等于360°.
我们通过把多边形划分为若干个三 角形,用三角形内角和去求多边形内角 和,从而得到多边形的内角和公式为 (n-2)× 180°。这种化未知为已 知的转化方法,必须在学习中逐渐掌握。 由于多边形外角和为360°,与边数无 关,所以常把多边形内角和的问题转化 为外角和来处理。
6. 三角形的三条角平分线交于三角形 内部一点。
7. 三角形的分类
(1) 按角分
斜三角形
三角形
锐角三角形 钝角三角形
直角三角形
(2) 按边分
三角形
不等边三角形
腰和底不等的等腰三角形
等腰三角形 等边三角形
8. 三角形的主要线段 三角形的高线定义:
从三角形的一个顶点向它的对边所在直线作垂线, __ 顶点__和__垂__足__之__间__的线段叫做三角形的高线.
BD CD,
B
DE
C
又 S ABC 60cm2
S
ABD
1 BD AE, 2
S
ADC
1 CD AE, 2
S
ADC
S
ABD
1S 2
ABC 1 60 2
30(cm2 )
5.已知B 420, A 100 1, ACD 640,说明AB // CD。
D
C
1
A
解: A B 1 1800 (三角形内角和等于1800 ) 又 B 420, 1 A 100 B A 420 A 100 1800 (等量代换) 2A=1280,A 640 又 ACD 640 A ACD AB // CD(内错角相等,两直线平行)
7.如图, △ABC中, ∠A= ∠ABD, ∠C= ∠BDC= ∠ABC,求∠DBC的度数
A
解:设A X 0
A ABD,ABD X 0
BDC A ABD 2 X 0
D
又 C ABC BDC
C ABC 2 X 0
DBC ABC ABD
B
C 2X 0 X 0 X 0
又 C DBC BDC 1800
解:当腰长为5cm时,它的周长为: 5+5+8=18(cm) 当腰长为8cm时,它的周长为: 8+8+5=21(cm)
∴这个三角形的周长为18cm或21cm
3.如图,已知:AD是△ABC 的中线,△ABC的面积为 60cm2 ,求
△ABD的面积
A
解:作AE BC,垂足为E, AD是 ABC的中线,
6.已知.1 2, 3 4, A 1000,求X的值。
B 1 2 A X
34
C
解 :
A 1 2 3 4 1800
又 A 1000, 1 2, 3 4
1000 22 24 1800
2(2 4) 800
2 4 400
又 2 4 X 1800
X 1800 400 1400
14、镶嵌
1、拼接在同一个点的各个角 的和等于360度
2、任意三角形一定可以镶嵌. 3、任意四边形一定可以镶嵌 4、正六边形可以镶嵌.
注意:只用正五边形、正八边 形一种图形不能镶嵌.
练一练
1.在△ABC中, (1)∠B=100°,∠A=∠C,则∠C= 40°; (2)2∠A=∠B+∠C,则∠A= 60°。 2.如图,_∠_A__D_B_是△ACD的外角, ∠ADB= 115°,∠CAD= 80°则∠C =__3_5°.
A BDC
知识应用
1、已知两条线段的长分别是3cm、8cm , 要想拼成一个三角形,且第三条线段a的 长为奇数,问第三条线段应取多少长?
解: 由三角形两边之和大于第三边,
两边之差小于第三边得:
8-3<a<8+3,
∴ 5 <a<11
又∵第三边长为奇数,
∴ 第三条边长为 7cm、9cm。
2、有两边相等的三角形一边的长是5 cm, 另一边的长是8cm,求它的周长
三角形知识结构图
三角形的边
与三角形有 关的线段
三
角
形
与三角形有
关的角
三角形的分类
中线 角平分线 三角形内角和 三角形外角和 内角与外角关系
定义
多
边 形
多边形的内外角和
镶嵌
1. 三角形的三边关系:
(1) 三角形两边的和大于第三边 (2) 三角形两边的差小于第三边
2. 判断三条已知线段a、b、c能否 组成三角形.
B
A
12 E
D
C
6.直角三角形的两个锐角相等,则每一个锐角等于 __4_5__度。
7、在△ABC中,∠A是∠B的2倍,∠C比∠A+∠B还大 30°,则∠C的外角为_____7度5°,这个三角形是____ 三钝角形
8、如图,已知:AD是△ABC 的中线,△ABC的面积为50cm2 ,则△ABD的面积是___2_5_c_m_2.
当a最长,且有b+c>a时,就可构成三角形.
3. 确定三角形第三边的取值范围:
两边之差<第三边<两边之和.
4. 三角形的三条高线(或高线所在直线) 交于一点
锐角三角形三条高线交于三角形内部一点, 直角三角形三条高线交于直角顶点, 钝角三角形三条高线所在直线交于三角形 外部一点。
5.三角形的三条中线交于三角形内部一点。
三角形角平分线的定义:
三个角角形的一顶个点角与的交平点分之线间与的它线的段对叫边做相三交角,形这的 角平分线。
三角形的中线定义
连结三角形一个 顶点与它对边中点 的线段 叫做三角形的中线。
9. 三角形木架的形状不会改变,而四边形木 架的形状会改变.这就是说,三角形具有稳定 性,而四边形没有稳定性。
10. 三角形内角和定理 三角形的内角和等于1800 直角三角形的两个锐角互余。
