中考培优中考综合题面积平分问题
初中数学培优专题学习专题25 图形面积的计算
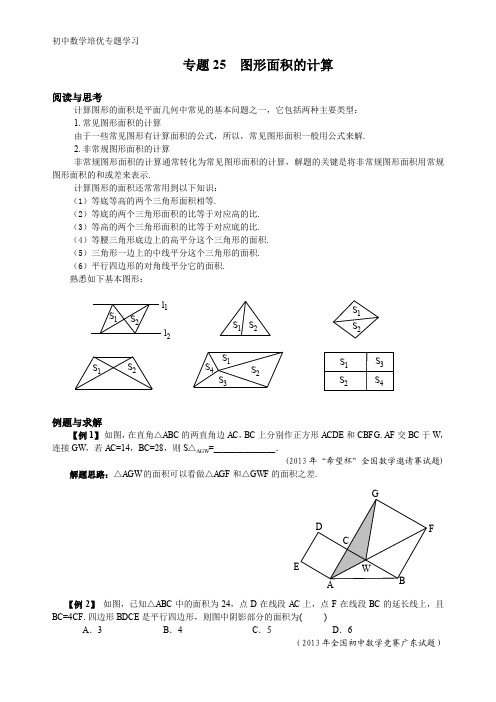
专题25 图形面积的计算阅读与思考计算图形的面积是平面几何中常见的基本问题之一,它包括两种主要类型: 1.常见图形面积的计算由于一些常见图形有计算面积的公式,所以,常见图形面积一般用公式来解. 2.非常规图形面积的计算非常规图形面积的计算通常转化为常见图形面积的计算,解题的关键是将非常规图形面积用常规图形面积的和或差来表示.计算图形的面积还常常用到以下知识:(1)等底等高的两个三角形面积相等.(2)等底的两个三角形面积的比等于对应高的比. (3)等高的两个三角形面积的比等于对应底的比. (4)等腰三角形底边上的高平分这个三角形的面积. (5)三角形一边上的中线平分这个三角形的面积. (6)平行四边形的对角线平分它的面积. 熟悉如下基本图形:S 3S 4S 3S 4S 1S 2S 1S 2S 1S 2S 1S 2S 1S 2S 2S 1l 2l 1例题与求解【例1】 如图,在直角△ABC 的两直角边AC ,BC 上分别作正方形ACDE 和CBFG .AF 交BC 于W ,连接GW ,若AC =14,BC =28,则S △AGW =______________.(2013年“希望杯”全国数学邀请赛试题)解题思路:△AGW 的面积可以看做△AGF 和△GWF 的面积之差.WFGEDCBA【例2】 如图,已知△ABC 中的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且BC =4CF .四边形BDCE 是平行四边形,则图中阴影部分的面积为( )A .3B .4C .5D .6(2013年全国初中数学竞赛广东试题)解题思路:设△ABC 底边BC 上的高为h .本例关键是通过适当变形找出h 和DE 之间的关系.FC BDEA【例3】 如图,平行四边形ABCD 的面积为30cm 2,E 为AD 边延长线上的一点,EB 与DC 交于F 点,已知三角形FBC 的面积比三角形DEF 的面积大9cm 2,AD =5cm ,求DE 长.(北京市“迎春杯”竞赛试题)解题思路:由面积求相关线段,是一个逆向思维的过程,解题的关键是把条件中图形面积用DE 及其它线段表示.BACFDE【例4】 如图,四边形ABCD 被AC 与DB 分成甲、乙、丙、丁4个三角形,已知BE =80 cm ,CE =60 cm ,DE =40 cm ,AE =30 cm ,问:丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?(“华罗庚杯”竞赛决赛试题)解题思路:甲、乙、丙、丁四个三角形面积可通过线段的比而建立联系,找出这种联系是解本例的突破口.丁乙丙甲E BCDA【例5】 如图,△ABC 的面积为1,D ,E 为BC 的三等分点,F ,G 为CA 的三等分点,求四边形PECF 的面积.解题思路:连CP ,设S △PFC =x ,S △PEC =y ,建立x ,y 的二元一次方程组.QP F GEDCBA【例6】如图,E ,F 分别是四边形ABCD 的边AB ,BC 的中点, DE 与AF 交于点P ,点Q 在线段DE 上,且AQ ∥PC .求梯形APCQ 的面积与平行四边形ABCD 的面积的比值.(2013年”希望杯“数学邀请赛试题)解题思路:连接EF ,DF ,AC ,PB ,设S □ABCD =a ,求得△APQ 和△CPQ 的面积.FEPQDCBA能力训练A 级1.如图,边长为1的正方形ABCD 的对角线相交于点O .过点O 的直线分别交AD ,BC 于E ,F ,则阴影部分面积是______.FOEDCB A(海南省竞赛试题)2.如图,在长方形ABCD 中,E 是AD 的中点,F 是CE 的中点,若△BDF 的面积为6平方厘米,则长方形ABCD 的面积是_____________平方厘米.EFDCBA(“希望杯”邀请赛试题)3.如图,ABCD 是边长为a 的正方形,以AB ,BC ,CD ,DA 分别为直径画半圆,则这四个半圆弧所围成的阴影部分的面积是____________.DCBA(安徽省中考试题)4.如图,已知AB ,CD 分别为梯形ABCD 的上底、下底,阴影部分总面积为5平方厘米,△AOB 的面积是0.625平方厘米,则梯形ABCD 的面积是_________平方厘米.DOCBA(“祖冲之杯”邀请赛试题)5.如图,长方形ABCD 中,E 是AB 的中点,F 是BC 上的一点,且CF =BC 31,则长方形ABCD的面积是阴影部分面积的( )倍.A .2B . 3C . 4D .5DF CBEA6.如图,是一个长为a ,宽为b 的长方形,两个阴影图形都是一对长为c 的底边在长方形对边上的平行四边形,则长方形中未涂阴影部分的面积为( ).A .c b a ab )(+-B . c b a ab )(--C .))((c b c a --D .))((c b c a +-cccc7.如图,线段AB =CD =10cm ,BC 和DA 是弧长与半径都相等的圆弧,曲边三角形BCD 的面积是以D 为圆心、DC 为半径的圆面积的41,则阴影部分的面积是( ). A .25π B . 100 C .50π D .200CBD A(“五羊杯”竞赛试题)8.如图,一个大长方形被两条线段AB 、CD 中分成四个小长方形,如果其中图形Ⅰ,Ⅱ,Ⅲ的面积分别为8,6,5,那么阴影部分的面积为( ). A .29 B .27 C .310 D .815 ⅢⅡⅠCBDA9.如图,长方形ABCD 中,E ,F 分别为AD ,BC 边上的任一点,△ABG ,△DCH 的面积分别为15和20,求阴影部分的面积.HGEDCF B A(五城市联赛试题)10.如图,正方形ABCD ,正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,已知正方形BEFG 的边长为4,求△DEK 的面积.RKP GF EC B AD(广西壮族自治区省南宁市中考试题)B 级1.如果图中4个圆的半径都为a ,那么阴影部分的面积为_____________.(江苏省竞赛试题)2.如图,在长方形ABCD 中,E 是BC 上的一点,F 是CD 上的一点,若三角形ABE 的面积是长方形ABCD 面积的31,三角形ADF 的面积是长方形ABCD 面积的52,三角形CEF 的面积为4cm 2,那么长方形ABCD 的面积是_________cm 2.DCFE BA(北京市“迎春杯”邀请赛试题)3.如图,边长为3厘米与5厘米的两个正方形并排放在一起,在大正方形中画一段以它的一个顶点为圆心,边长为半径的圆弧,则阴影部分的面积为___________________.(“希望杯”邀请赛试题)4.如图,若正方形APHM ,BNHP ,CQHN 的面积分别为7,4,6,则阴影部分的面积是_____.CMNDQPB A(“五羊杯”竞赛试题)5.如图,把等边三角形每边三等分,使其向外长出一个边长为原来的31的小等边三角形,称为一次“生长”,在得到的多边上类似“生长”,一共“生长”三次后,得到的多边形的边数=________,面积是原三角形面积的______倍.第2次生长第1次生长原图(“五羊杯”竞赛试题)6.如图,在长方形ABCD 中,AE =BG =BF =21AD =31AB =2,E ,H ,G 在同一条直线上,则阴影部分的面积等于( ).A .8B .12C .16D .20F BGCHDE A7.如图,边长分别为8cm 和6cm 的两个正方形,ABCD 与BEFG 并排放在一起,连接EG 并延长交AC 于K ,则△AKE 的面积是( ).A .48cm 2B .49cm 2C .50cm 2D .51cm 2KGFEC B A D(2013年“希望杯”邀请赛试题)8.在一个由8×8个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆经过的所有小方格的圆内部分的面积之和记为S 1,把圆周经过的所有小方格的圆外部分的面积之和记为S 2,则21S S 的整数部分是( ).A .0B .1C .2D .3(全国初中数学联赛试题)9.如图,△ABC 中,点D ,E ,F 分别在三边上,E 是AC 的中点,AD ,BE ,CF 交于一点G ,BD =2DC ,S △GEC =3,S △GDC =4,则△ABC 的面积是( ).A .25B .30C .35D .40GFE CBDA10.已知O (0,0),A (2,2),B (1,a ),求a 为何值时,S △ABO =5?11.如图,已知正方形ABCD 的面积为1,M 为AB 的中点,求图中阴影部分的面积.GCBMAD(湖北省武汉市竞赛试题)12.如图,△ABC 中,21===FA FB EC EA DB DC .求的面积△的面积△ABC GHI 的值. G IHEDCBFA(“华罗庚金杯”邀请赛试题)。
中考25题常考类型------面积均分问题

中考 25 题常考类型 ------ 面积均分问题本节课讲了两种类型,第一种三角形和不规则四边形面积均分问题;第二种特殊的四边形面积均分问题。
在讲三角形面积均分时学生很容易就理解三角形的中线就能均分三角形面积。
但是在具体的题中要求过三角形一边的某一个定点均分三角形面积。
这道题学生觉得有难度,需要老师架一个梯度,帮助学生突破这种过定点等分的情形,其中需要用到蝴蝶模型,所以在讲过定点面积等分问题前给学生铺垫了蝴蝶模型。
即就是平行线剪的三角形面积相等,借助同底等高,不仅可以面积相等,还可以根据平行线做的位置不同转变三角形的位置。
引入:等腰三角形面积等分---一般三角形面积等分得到结论:三角形的中线能够等分三角形的面积。
师:在没有任何条件限制下,等分三角形面积我们知道找三角形中线即可。
那么要是有条件限制呢?比如过三角形ABC一边BC上的一定点P的直线如何等分三角形面积?先抛出问题,引发学生独立思考,再进行小组合作。
师:在解决这个问题前我们先来看一个模型---蝴蝶模型。
引入蝴蝶模型。
小结:我们发现蝴蝶模型存在等积转化的方法,即可以构造平行线,转化面积。
师:我们思考这个问题,已经会用中线等分面积了,那如何使得过定点的直线等分三角形面积?生:(思考中)生:(小组合作中)生:我考虑借助蝴蝶模型进行等积转化。
师:很好,给其他同学也提供了思路,可以朝这个方向思考。
再思考蝴蝶模型在什么线中产生的?生:平行线中产生,所以要构造平行线。
师:很棒,那么我们是等积转化,如何转化?在什么情况下可以转化成等分面积的情形呢?生:在已知中线可以等分面积的基础上,考虑结合中点构造平行线和蝴蝶模型。
生:我连接AP,取BC边上的中点M,连接AM,过M作MD平行于AP交AB于点D,连接DP,构造平行线,得到等积模型,从而得到三角形APM和三角形ADP面积相等,将这两个三角形面积进行转化,得到四边形DPCA的面积等于三角形AMC的面积,即就是四边形DPCA的面积等于三角形ABC的一半,即直线DP即为所求的直线。
中考压轴题全解——解答题之面积问题

中考压轴题全解——解答题之面积问题
中考压轴题全解——解答题之面积问题
一、面积最大值
当一个三角形(或其他多边形)的形状或大小发生变化时,会产生面积变化。
利用已知条件求出变化过程中该三角形的面积。
主要有以下几种方法:
•1.直接法求三角形面积
•2.补全法求三角形面积
•3.分制法求三角形面积
•4,平移法求三角形面积
二、面积最小值
面积最小问题是指一个图形在变化过程中,面积存在一个最小值。
通常情况下,三角形有一条边不变,只要使得这条边上的高的值最小即可。
三、图形面积比值
四、重叠部分面积
当对一个图形进行平移、旋转或轴对称变换时,与另外一个图形产生的重叠部分面积会发生变化。
求两个图形重叠部分面积时,通常要找出临界位置,画出图形,再分别求出相应的面积即可。
五、面积大加、减、乘、除
666。
2023年中考数学专题复习:二次函数综合题(面积问题)
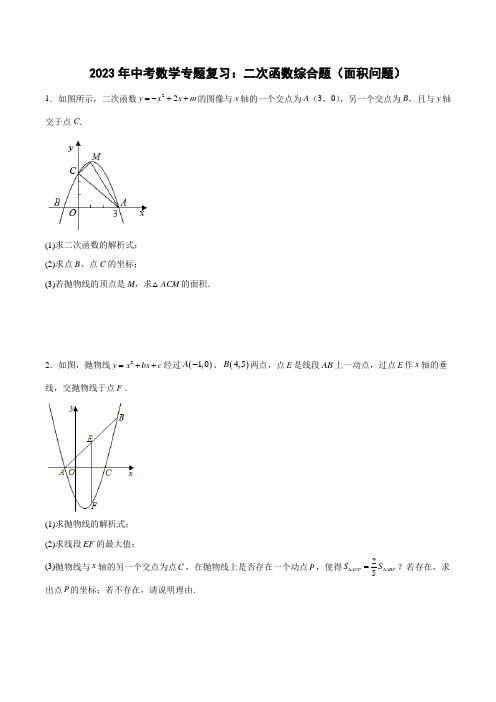
2023年中考数学专题复习:二次函数综合题(面积问题)1.如图所示,二次函数22y x x m =-++的图像与x 轴的一个交点为A (3,0),另一个交点为B ,且与y 轴交于点C .(1)求二次函数的解析式;(2)求点B 、点C 的坐标;(3)若抛物线的顶点是M ,求△ACM 的面积.2.如图,抛物线2y x bx c =++经过()1,0A -、()4,5B 两点,点E 是线段AB 上一动点,过点E 作x 轴的垂线,交抛物线于点F .(1)求抛物线的解析式;(2)求线段EF 的最大值;(3)抛物线与x 轴的另一个交点为点C ,在抛物线上是否存在一个动点P ,使得25ACP ABC S S ∆∆=?若存在,求出点P 的坐标;若不存在,请说明理由.3.如图,二次函数23y ax bx=++的图像与x正半轴相交于点B,负半轴相交于点A,其中A点坐标是(-1,0),B点坐标是(3,0).(1)求此二次函数的解析式;(2)如图1,点P在第一象限的抛物线上运动,过点P作PD x⊥轴于点D,交线段BC于点E,线段BC把△CPD 分割成两个三角形的面积比为1∶2,求P点坐标;(3)如图2,若点H在抛物线上,点F在x轴上,当以B、C、H、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.4.如图,已知直线y=43x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.(1)求抛物线的表达式;(2)D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;(3)若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.5.如图,已知在平面直角坐标系xOy中,抛物线y=-12x2+bx+c经过点A(-2,0).与点C(0,4).与x轴的正半轴交于点B.(1)求抛物线的表达式;(2)如果D是抛物线上一点,AD与线段BC相交于点E,且AD将四边形ABDC分成面积相等的两部分,求DE AE的值;(3)如果P是x轴上一点,∠PCB=∠ACO,求∠PCO的正切值.6.如图,抛物线23y ax bx =+-交x 轴于()30A -,,()10B ,两点,与y 轴交于点.C 连接AC ,BC .(1)求抛物线的解析式;(2)如图1,点P 为抛物线在第三象限的一个动点,PM x ⊥轴于点M ,交AC 于点G ,PE AC ⊥于点E ,当PGE 的面积为1时,求点P 的坐标;(3)如图2,若Q 为抛物线上一点,直线OQ 与线段AC 交于点N ,是否存在这样的点Q ,使得以A ,O ,N 为顶点的三角形与ABC 相似.若存在,请求出此时点Q 的坐标;若不存在,请说明理由.7.在平面直角坐标系中,已知抛物线经过A (-4,0),B (0,-4),C (2,0)三点.(1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.(3)若点P 是抛物线上的动点,点Q 是直线y =-x 上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.8.如图,二次函数23y ax bx =++的图象经过点A (-1,0),B (3,0),与y 轴交于点C .(1)求二次函数的解析式;(2)第一象限内的二次函数23y ax bx =++图象上有一动点P ,x 轴正半轴上有一点D ,且OD =2,当S △PCD =3时,求出点P 的坐标;(3)若点M 在第一象限内二次函数图象上,是否存在以CD 为直角边的Rt MCD ,若存在,求出点M 的坐标,若不存在,请说明理由.9.如图,在平面直角坐标系中,已知抛物线y =ax 2+4x +c 与直线AB 相交于点A (0,1)和点B (3,4).(1)求该抛物线的解析式;(2)设C 为直线AB 上方的抛物线上一点,连接AC ,BC ,以AC ,BC 为邻边作平行四边形ACBP ,求四边形ACBP 面积的最大值;(3)将该抛物线向左平移2个单位长度得到抛物线y =a 1x 2+b 1x +c 1(a 1≠0),平移后的抛物线与原抛物线相交于点D ,是否存在点E 使得△ADE 是以AD 为腰的等腰直角三角形?若存在,直接写出....点E 的坐标;若不存在,请说明理由.10.如图,在平面直角坐标系中,抛物线2(0)y ax bx c a =++≠与x 轴交于A ,B 两点(A 在B 的左侧),与y 轴的交点为C ()0,3-,顶点为()1,4D -.(1)求抛物线的表达式;(2)若平行于x轴的直线与抛物线交于M,N两点,与抛物线的对称轴交于点H,若点H到x轴的距离是线,求线段MN的长;段MN长的12(3)若经过C,D两点的直线与x轴相交于点E,F是y轴上一点,且AF∥CD,在抛物线上是否存在点P,使直线PB恰好将四边形AECF的周长和面积同时平分?如果存在, 求出点P的坐标;如果不存在,请说明理.11.如图,已知抛物线y=ax2+4x+c经过A(2,0)、B(0,﹣6)两点,其对称轴与x轴交于点C.(1)求该抛物线和直线BC的解析式;(2)设抛物线与直线BC相交于点D,求△ABD的面积;(3)在该抛物线的对称轴上是否存在点Q,使得△QAB的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.12.如图,抛物线y =ax 2+bx +c 与x 轴交于A (﹣2,0)、B (6,0)两点,与y 轴交于点 C .直线l 与抛物线交于A 、D 两点,与y 轴交于点E ,点D 的坐标为(4,3).(1)求抛物线的解析式与直线l 的解析式;(2)若点P 是抛物线上的点且在直线l 上方,连接P A 、PD ,求△P AD 面积最大值;(3)由(2)并求出点 P 的坐标.13.已知抛物线2y ax c =+过点()2,0A -和()1,3D -两点,交x 轴于另一点B .(1)求抛物线解析式;(2)如图1,点P 是BD 上方抛物线上一点,连接AD ,BD ,PD ,当BD 平分ADP 时,求P 点坐标;(3)将抛物线图象绕原点O 顺时针旋转90°形成如图2的“心形”图案,其中点M ,N 分别是旋转前后抛物线的顶点,点E 、F 是旋转前后抛物线的交点.①直线EF 的解析式是______;②点G 、H 是“心形”图案上两点且关于EF 对称,则线段GH 的最大值是______.14.如图,抛物线2142y x x =-++与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C .(1)求A ,B ,C 三点的坐标,并直接写出直线AC 的函数表达式;(2)若D 是第一象限内抛物线上一动点,且△BCD 的面积等于△AOC 的面积,求点D 的坐标;(3)在(2)的条件下,连接AD ,试判断在抛物线上是否存在点M ,使∠MDA =∠ACO ?若存在,请直接写出点M 的坐标;若不存在,请说明理由.15.综合与探究如图,在平面直角坐标系中,直线y x b =+与x 轴交于点()4,0A ,与y 轴交于点B ,过A ,B 两点的抛物线交x 轴于另一点C ,且2OA OC =,点F 是直线AB 下方抛物线上的动点,连接F A ,FB .(1)求抛物线解析式;(2)当点F 与抛物线的顶点重合时,ABF 的面积为______;.(3)求四边形F AOB 面积的最大值及此时点F 的坐标.(4)在(3)的条件下,点Q 为平面内y 轴右侧的一点,是否存在点Q 及平面内另一点M ,使得以A ,F ,Q ,M 为顶点的四边形是正方形?若存在,直接写出点Q 的坐标;若不存在,说明理由.16.抛物线224y ax ax =--交x 轴于(2,0)A -、B 两点,交y 轴于C ;直线AD 交抛物线于第一象限内点D ,且D 的横坐标为5,(1)求抛物线解析式;(2)点E 为直线AD 下方抛物线上一动点,且21ADE S =,求点E 的坐标;(3)抛物线上是否存在点P ,使PCO DAO CBO ∠+∠=∠,若存在,请求出此时点P 的坐标;若不存在,请说明理由.17.如图,在平面直角坐标系中,矩形OABC 的两边OA ,OC 分别在x 轴和y 轴上,3OA =,4OC =,抛物线24y ax bx =++经过点B ,且与x 轴交于点()1,0D -和点E .(1)求抛物线的表达式:(2)若P 是第一象限抛物线上的一个动点,连接CP ,PE ,当四边形OCPE 的面积最大时,求点P 的坐标,此时四边形OCPE 的最大面积是多少;(3)若N 是抛物线对称轴上一点,在平面内是否存在一点M ,使以点C ,D ,M ,N 为顶点的四边形是矩形?若存在,请直接写出点M 的坐标;若不存在,说明理由.18.如图,抛物线与x 轴交于点()2,0B -、()4,0C 两点,与y 轴交于点()0,2A ;(1)求出此抛物线的解析式;(2)如图1,在直线AC 上方的抛物线上有一点M ,求AMC S △的最大值;(3)如图2,将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90°得到线段O A '',若线段O A ''与抛物线只有一个公共点,请结合函数图象,求m 的取值范围;19.如图,已知抛物线2y x bx c =++与x 轴交于点A ,B (点A 在点B 的左侧),与y 轴交于点C ,OA =OC =3.(1)求抛物线的函数表达式;(2)若点P 为直线AC 下方抛物线上一点,连接BP 并交AC 于点Q ,若AC 分ABP △的面积为1:2两部分,请求出点P 的坐标;(3)在y 轴上是否存在一点N ,使得45BCO BNO ∠+∠=︒,若存在,请求出点N 的坐标;若不存在,请说明理由.20.已知二次函数2(0)y x bx c a =++≠的图像与x 轴的交于A 、(1,0)B 两点,与y 轴交于点(0,3)C -.(1)求二次函数的表达式及A 点坐标;(2)D 是二次函数图像上位于第三象限内的点,求点D 到直线AC 的距离取得最大值时点D 的坐标;(3)M 是二次函数图像对称轴上的点,在二次函数图像上是否存在点N .使以M 、N 、B 、O 为顶点的四边形是平行四边形?若有,请写出点N 的坐标(不写求解过程).答案1.(1)2y x 2x 3=-++(2)()0,3C 、()1,0B -(3)32.(1)223y x x =-- (2)254(3)存在,点P 的坐标为(12)或(12)+或()12-或(12)-3.(1)2y x 2x 3=-++(2)P 点坐标115(,)24或(2,3)(3)F 点坐标为:(1,0)、(5,0)、)2,0、()2-4.(1)y =﹣43x 2﹣83x +4 (2)S 最大=252,D (﹣32,5) (3)存在,Q (﹣2,198)5.(1)抛物线解析式为y =-12x 2+x +4; (2)14DE AE =; (3)∠PCO 的正切值13或3.6.(1)223y x x =+-(2)()14P --,或()23--,(3)存在,坐标为⎝⎭或⎝⎭或或(-7.(1)2142y x x =+- (2)24=--S m m ,4(3)()4,4Q -或(2-+-或(2--+或()4,4-8.(1)2+23y x x =-+(2)P 1(32,154),P 2(2,3)(3)存在点M 其坐标为1M 43539(,)或2M9.(1)241y x x =-++ (2)274(3)存在,E (4,3)或(-2,5)或(-3,2)或(3,0).10.(1)223y x x =--(2)1或1-(3)在抛物线上存在点3(4P -,15)16-,使直线PB 恰好将四边形AECF 的周长和面积同时平分11.(1)y =﹣12x 2+4x ﹣6,y =32x ﹣6 (2)152(3)存在,点Q 的坐标为(4,﹣2)12.(1)(1)y =-14x 2+x +3,y =12x +1 (2)274(3)(1,154)(2)232,39P ⎛⎫ ⎪⎝⎭(3)①y x =; 14.(1)A (-2,0),B (4,0),C (0,4),24y x =+(2)(2,4)(3)存在,(-23,289)或(-6,-20)15.(1)2142y x x =-- (2)3(3)FAOB S 四边形有最大值12,此时点F 的坐标为()2,4-(4)存在,点Q 的坐标()18,2Q -,()26,6Q -,()35,3Q -,()41,1Q -16.(1)2142y x x =-- (2)191,2E ⎛⎫- ⎪⎝⎭;E 2(2,-4) (3)存在,(8,20)17.(1)y =-x 2+3x +4(2)P (2,6);四边形OCPE 的面积最大为16(3)存在; M 113,28⎛⎫- ⎪⎝⎭或M 252728,⎛⎫ ⎪⎝⎭或M 355,22⎛⎫- ⎪⎝⎭或M 453,22⎛⎫- ⎪⎝⎭18.(1)211242y x x =-++ (2)2(3)34m -≤-或32m -≤(2)(-2,-3)或(-1,-4)(3)(0,2)或(0,-2)20.(1)223y x x =+-,(3,0)A - (2)315,24D ⎛⎫-- ⎪⎝⎭(3)存在,(2,3)--或(0,3)-或(2,5)。
2020年中考复习讲义 用面积解决几何问题大全

用面积解决几何问题许多数学问题,表面上看来似与面积无关,但灵活运用面积法,往往能使问题顺利获解。
面积法的常用解题思路:1.分解法:通常把一个复杂的图形,分解成几个三角形。
2.作平行线法找出同高(或等高)的三角形。
3. 利用有关性质法:比如利用中点、中位线等性质。
4.还可以利用面积解决其它问题。
一、用面积法证线段不等1. 如图,在△ABC 中,已知AB>AC ,∠A 的平分线交BC 于D. 求证:BD>CD证明:过点D 作DE ⊥AB, DF ⊥AC, 垂足分别为E 、F 。
∵AD 平分∠BAC ,∴DE=DF.∵S △ADB =21AB ·DE, S △ADC =21AC ·DF,又 AB>AC,∴S △ADB >S △ADC .即21BD ·h>21DC ·h∴BD>DC. 二、用面积法证比例式或等积式2. 如图,AD 是△ABC 的角平分线。
求证:DCBD =AC AB 证明 :过D 作DE ⊥AB,DF ⊥AC, AH ⊥BC,垂足分别为E 、F 、H.∵AD 是△ABC 的角平分线,∴DE=DF.∵S △ABD =21AB ·DE, S △ACD =21AC ·DF. ∴AC AB =S S ADC ΔABD Δ. 又∵S △ABD =21BD ·AH, S △ACD =21DC ·AH,∴DC BD =S S ADC ΔABD Δ. ∴ACAB =DC BD . 三、用面积比求线段的比3.如图,在△ABC 中,已知BC 、AC 边上的中线AD 、BF 交于M 。
求证:MD=21AM 。
证明:作BG ⊥AD 垂足为G ,连接CM 。
∵AF 是△ABC 的中线,∴S △ABF =S △BCF ,S △MAF =S △MCF ,∴S △ABM =S △BCM .∵DB=DC,∴S △DBM = 21 S △BCM =21 S △BAM .∵S △BAM =21AM ·BG,S △BDM =21DM ·BG,∴21×21AM ·BG=21DM ·BG, ∴DM=21AM. 4.已知菱形的边长为a 同两条对角线长为m ,n 且a 2=mn 。
初中平分面积周长问题

ECD图1ABCD图21.如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.如,平行四边形的一条对线所在的直线就是平行四边形的一条面积等分线.(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有________;(2)如图1,梯形ABCD 中,AB ∥DC ,如果延长DC 到E ,使CE =AB ,连接AE ,那么有S梯形ABCD=S △ABE .请你给出这个结论成立的理由,并过点A 作出梯形ABCD的面积等分线(不写作法,保留作图痕迹);(3)如图,四边形ABCD 中,AB 与CD 不平行,S △ADC >S △ABC ,过点A 能否作出四边形ABCD 的面积等分线?若能,请画出面积等分线,并给出证明;若不能,说明理由.2如图1,在△ABC 中,AB =BC ,且BC ≠AC ,在△ABC 上画一条直线,若这条直线..既平分△ABC 的面积,又平分△ABC 的周长,我们称这条线为△ABC 的“等分积周线”. (1)请你在图1中用尺规作图作出一条△ABC 的“等分积周线”;(2)在图1中过点C 能否画出一条“等分积周线”?若能,说出确定的方法;若不能,请说明理由;(3)如图2,若AB =BC =5cm ,AC =6cm ,请你找出△ABC 的所有“等分积周线”,并简要说明确定的方法.3在△ABC 中,∠C =90°,AC =3,BC =4,CD 是斜边AB 上的高,点E 在斜边AB 上,过点E 作直线与△ABC 的直角边相交于点F ,设AE =x ,△AEF 的面积为y . (1)求线段AD 的长;A B C 图2A B C 图1(2)若EF⊥AB,当点E在线段AB上移动时,①求y与x的函数关系式(写出自变量x的取值范围)②当x取何值时,y有最大值?并求其最大值;(3)若F在直角边AC上(点F与A、C两点均不重合),点E在斜边AB上移动,试问:是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.4问题探究(1)请你在图①中作一条..直线,使它将矩形ABCD分成面积相等的两部分;(2)如图②,点M是矩形ABCD内一定点,请你在图②中过点M作一条直线,使它将矩形ABCD分成面积相等的两部分;问题解决(3)如图③,在平面直角坐标系中,直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图,其中DC∥OB,OB=6,BC=4,CD=4.开发区综合服务管理委员会(其占地面积不计)设在点P(4,2)处.为了方便驻区单位,准备过点P修一条笔直的道路(路的宽度不计),并且使这条路所在的直线l将直角梯形OBCD分成面积相等的两部分.你认为直线l是否存在?若存在,求出直线lDBC①②③ABC图1P 1 P 2R 2R 15.如图,直角梯形ABCD 中,AD ∥BC ,∠ABC=90°,已知AD=AB=3,BC=4,动点P 从B 点出发,沿线段BC 向点C 作匀速运动;动点Q 从点D 出发,沿线段DA 向点A 作匀速运动.过Q 点垂直于AD 的射线交AC 于点M ,交BC 于点N .P 、Q 两点同时出发,速度都为每秒1个单位长度.当Q 点运动到A 点,P 、Q 两点同时停止运动.设点Q 运动的时间为t 秒.(1)求NC ,MC 的长(用t 的代数式表示);(2)当t 为何值时,四边形PCDQ 构成平行四边形;(3)是否存在某一时刻,使射线QN 恰好将△ABC 的面积和周长同时平分?若存在,求出此时t 的值;若不存在,请说明理由;(4)探究:t 为何值时,△PMC 为等腰三角形.6(江苏省苏州市)如图,在△ABC 中,∠C =90°,AC =8,BC =6.P 是AB 边上的一个动点(异于A 、B 两点),过点P 分别作AC 、BC 边的垂线,垂足为M 、N .设AP =x . (1)在△ABC 中,AB =_________;(2)当x =_________时,矩形PMCN 的周长是14; (3)是否存在x 的值,使得△PAM 的面积、△PBN 的面积与矩形PMCN 的面积同时相等?请说出你的判断,并加以说明.7某课题研究小组就图形面积问题进行专题研究,他们发现如下结论: (1)有一条边对应相等的两个三角形面积之比等于这条边上的对应高之比; (2)有一个角对应相等的两个三角形面积之比等于夹这个角的两边乘积之比;…现请你继续对下面问题进行探究,探究过程可直接应用上述结论.(S 表示面积) 问题1:如图1,现有一块三角形纸板ABC ,P 1,P 2三等分边AB ,R 1,R 2三等分边AC .经探究知2121R R P P S 四边形=13 S △ADE ,请证明.N A CP M BAB图2P 1P 2R 2R 1DQ 1Q 2问题2:若有另一块三角形纸板,可将其与问题1中的拼合成四边形ABCD ,如图2,Q 1,Q 2三等分边DC .请探究2211P Q Q P S 四边形与S 四边形ABCD 之间的数量关系.问题3:如图3,P 1,P 2,P 3,P 4五等分边AB ,Q 1,Q 2,Q 3,Q 4五等分边DC .若S 四边形ABCD=1,求3322P Q Q P S 四边形.问题4:如图4,P 1,P 2,P 3四等分边AB ,Q 1,Q 2,Q 3四等分边DC ,P 1Q 1,P 2Q 2,P 3Q 3将四边形ABCD 分成四个部分,面积分别为S 1,S 2,S 3,S 4.请直接写出含有S 1,S 2,S 3,S 4的一个等式.1.如图,一次函数7-x y +=与正比例函数x \y 34=的图象交于点A ,且与x 轴交于点B 。
中考培优-中考综合题-------面积平分问题
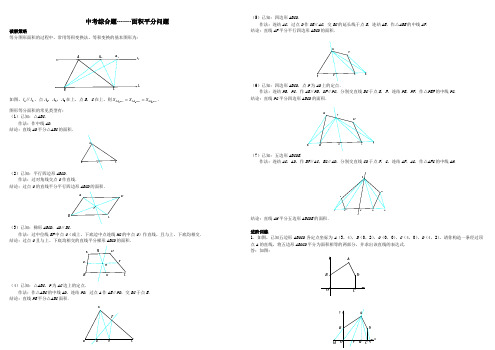
中考综合题-------面积平分问题破解策略等分图形面积的过程中,常用等积变换法,等积变换的基本图形为:如图,12l l ∥,点123A A A ,,在上,点B ,C 在上,则123A BC A BC A BC S S S ∆∆∆==. 图形等分面积的常见类型有: (1)已知:△ABC .作法:作中线AD .结论:直线AD 平分△ABC 的面积.(2)已知:平行四边形ABCD .作法:过对角线交点O 作直线.结论:过点O 的直线平分平行四边形ABCD 的面积.(3)已知:梯形ABCD ,AD ∥BC .作法:过中位线EF 中点O (或上、下底边中点连线HG 的中点O )作直线,且与上、下底均相交. 结论:过点O 且与上、下底均相交的直线平分梯形ABCD 的面积.(4)已知:△ABC ,P 为AC 边上的定点.作法:作△ABC 的中线AD ,连结PD ,过点A 作AE ∥PD ,交BC 于点E . 结论:直线PE 平分△ABC 面积.(5)已知:四边形ABCD .作法:连结AC ,过点D 作DE ∥AC ,交BC 的延长线于点E ,连结AE ,作△ABE 的中线AF . 结论:直线AF 平分平行四边形ABCD 的面积.(6)已知:四边形ABCD ,点P 为AD 上的定点.作法:连结PB ,PC .作AE ∥PB ,DF ∥PC ,分别交直线BC 于点E ,F ,连结PE ,PF ,作△PEF 的中线PG . 结论:直线PG 平分四边形ABCD 的面积.(7)已知:五边形ABCDE .作法:连结AC ,AD ,作BF ∥AC ,EG ∥AD ,分别交直线CD 于点F ,G ,连结AF ,AG ,作△AFG 的中线AH .结论:直线AH 平分五边形ABCDE 的面积.进阶训练1.如图,已知五边形ABOCD 各定点坐标为A (3,4),B (0,2),O (0,0),C (4,0),D (4,2),请你构造一条经过顶点A 的直线,将五边形ABOCD 平分为面积相等的两部分,并求出该直线的表达式. 答:如图:AD21直线的表达式为843y x =-. 【提示】 连结AO ,作BM ∥AO 交x 轴于点M ,连结AC ,作DN ∥AC 交x 轴于点N ,取MN 中点F ,则直线AF 将五边形ABOCD 分为面积相等的两部分.作AH ⊥x 轴于点H ,则△BMO ∽△AOH ,可得点M 的坐标.同理可得点N 的坐标.从而求得点F 的坐标.确定直线AF 的表达式.2.过四边形ABCD 的一个顶点画一条直线,把四边形ABCD 的面积分成1:2的两部分.答:如图:【提示】 连结AC ,过点D 作DE ∥AC 交BC 的延长线于点E ,取BE 的一个三等分点F 或G ,则直线AF 或AG 即为所求. 3.设w 是一个平面图形,如果用直尺和圆规经过有限步作图(简称尺规作图),画出一个正方形与w 的面积相等(简称等积),那么这样的等积转化称为w 的“化方”. (1)阅读填空 如图1,已知矩形ABCD ,延长AD 到点E ,使DE =DC ,以AE 为直径作半圆,延长CD 交半圆于点H ,以DH 为边作正方形DFGH ,则正方形DFGH 与矩形ABCD 等积.理由:连结AH ,EH .因为AE 为直径,所以∠AHE =90°, 所以∠HAE +∠HEA =90°.因为DH ⊥AE ,所以∠ADH =∠EDH =90°. 所以∠AHD =∠HED ,所以△ADH ∽. 所以AD DH DH DE=,即2=DH AD DE ⋅ 因为DE =DC ,所以2DH =,即正方形DFGH 与矩形ABCD 等积(2)操作实践平行四边形的“化方”思路是:先把平行四边形转化为等积的矩形,再把矩形转化为等积的正方形.如图2,请作出与平行四边形ABCD 等积的正方形(不要求写出具体作法,保留作图痕迹). (3)解决问题三角形的“化方”思路是:先把三角形转化为等积的(填写图形名称),再转化为等积的正方形.如图3,△ABC 的顶点再正方形网格的格点上,请作出与△ABC 等积的正方形(不要求写具体作法,保留作图痕迹,不通过计算△ABC 面积作图). 3.(1)△HDE ;AD ·DC ; (2)作图如下:(3)矩形;作图如下:(4)作图如下:【提示】(2)作法:①分别过点A ,D 作直线BC 的垂线,垂足分别为11B C ,; ②延长AD 至点E ,使得1DE DC =; ③以AE 为直径作半圆;图2DCBA图1HGFED C B A11AD EFGHEGFABCDDCBA④延长1C D交半圆于点H;⑤以DH为边向右作正方形DFGH.则正方形DFGH与平行四边形ABCD等积.(3)作法:①作△ABC的中位线MN;②分别过点B,C作MN的垂线,垂足分别为E,D;③延长BC至点F,使得CF=CD;④以BF为直径作半圆;⑤延长DC交半圆于点G;⑥以CG为边向右作正方形CGHI.则正方形CGHI与△ABC等积.(4)作法:①连结BD,过点A作AE∥BD交CD的延长线于点E;②作△EBC的中位线MN;③分别过点B,C作MN的垂线,垂足分别为F,G;④延长BC至点H使得CH=CG;⑤以BH为直径作半圆;⑥延长GC交半圆于点I;⑦以CI为边向右作正方形CIJK.则正方形CIJK 与四边形ABCD等积.n边形(n>3)的“化方”思路之一是:把村边形转化,为等积的”1边形.…一直至转化为等积的三角形,从而实现化方.如图4,四边形ABCD的顶点在正方形网格的格点上,请作出与四边形ABCD等积的正方形(不要求写具体作法,保留作图痕迹,不通过计算四边形ABCD面积作圈)练习题1.问题探究:(1)请在图①中作出两条直线,使它们将圆面四等分;(2)如图②,M是正方形ABCD内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M)使它们将正方形ABCD的面积四等分,并说明理由.问题解决:(3)如图③,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点,如果AB=a,CD=b,且b >a,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?如若存在,求出BQ的长;若不存在,说明理由.AB CAB CD2.探索发现:(1)如图1,在△ABC中,AD是BC边上的中线,若△ABC的面积为S,则△ACD 的面积为.联系拓展:(2)在图2中,E、F分别是▱ABCD的边AB、BC的中点,若▱ABCD的面积为S,求四边形BEDF的面积?并说明理由.(3)在图3中,E、F分别是▱ABCD 的边AB、BC上的点,且AE=AB,BF=BC,若▱ABCD的面积为S,则四边形BEDF的面积为.解决问题:(4)如图4中,矩形ABCD中,AB=nBC(n为常数,且n>0).E是AB边上的一个动点,F是BC边上的一个动点.若在两点运动的过程中,四边形BEDF的面积始终等于矩形面积的,请探究线段AE、BF 应满足怎样的数量关系,并说明理由.3.如果图1,已知直线m∥n,A、B为直线n上两定点,C、D为直线m上两动点,容易证明:△ABC的面积=△ABD的面积;问题探究(1)在图2中画出与四边形ABCD面积相等且以AB为一条边的三角形.(2)在图3中,已知正方形ABCD的边长为4,G是边CD上一点,以CD为边作正方形GCEF,当CG=a 时,求△BDF的面积.问题解决(3)李大爷家有一块正方形的果园如图4所示,由于修建道路,图中三角形BCE区域将被占用,现决定在DE右侧补给一块土地,补偿后,果园将调整为四边形ABMD,要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BE上.请你在图4中通过画图来确定M点的位置,并简要叙述画法和理由;若AB=4,CE=a,求出上图中tan∠MDC的值.4.问题提出(1)如图①,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为;问题探究(2)如图②,在矩形ABCD中,AB=12,AD=18,如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.问题解决(3)某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌.)同时,再合理设计好喷灌龙头喷水的射程就可以了.如图③,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB交于点E,又测得DE=8m.请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)5.提出问题:爸爸出差回家带了一个分布均匀的等腰三角形蛋糕礼物给儿子(如图1,AB=BC,且BC≠AC),在蛋糕的边缘均匀分布着巧克力,双胞胎儿子大毛和小毛决定只切一刀将这块蛋糕平分吃(要求分得的蛋糕和巧克力质量都一样).背景介绍:这条分割直线即平分了三角形的面积,又平分了三角形的周长,我们称这条线为三角形的“等分积周线”.尝试解决:(1)大毛很快就想到了一条分割直线,而且用尺规作图作出.请你帮大毛在图1中作出这条“等分积周线”,从而平分蛋糕.(2)小毛觉得大毛的方法很好,所以自己模仿着在蛋糕上过点C画了一条直线CD交AB于点D.你觉得小毛会成功吗?如能成功,说出确定的方法;如不能成功,请说明理由.(用图2说明)(3)若AB=BC=5cm,AC=6cm,如图3,你能找出几条△ABC的“等分积周线”,请分别画出,并简要说明确定的方法.6.(1)请在图①中画出与△ABC面积相等的三个三角形:△ABC1、△ABC2、△ABC3,其中点C1、C2、C3为△ABC所在平面上异于点C的三个不同点;(2)请在图②中射线BC上通过画图确定一点E,使得S△ABE =S四边形ABCD,并简要叙述画法和理由;问题解决(4)李大爷家有一块果园如图③中的四边形ABCD,由于修路,图中三角形CEF区域将被占用,现决定在DF的右侧补给他一块土地,要求补偿前后的总面积不变,已知∠A=135°,∠B=60°,∠D=105°,AB=350m,BE=(100+50)m,CF=300m,DF=100m,若所补区域为三角形DFG,且点G在射线EF上,请求出符合条年的FG的长度.7.问题探究(1)如图1,点E为矩形ABCD内一点,请过点E作一条直线,将矩形ABCD的面积分为相等的两部分;(2)如图2,在矩形ABCD中,AB=8,BC=6,P为对角线AC上一点,且AC=3AP,请问在边CD上是否存在一点E,使得直线PE将矩形ABCD的面积分为2:3两部分,如果存在求出DE的长;如果不存在,请说明理由;解决问题(3)如图3,现有一块矩形空地ABCD,AB=80米,BC=60米,P为对角线AC上一点,且PC=3AP,计划在这块空地上修建一个四边形花园AECF,使得E、F分别在线段AD、AB上,且EF经过点P,若每平方米的造价为100元,请求出修建该花园所需费用的范围(其他费用不计).8.平面上有三点M、A、B,若MA=MB,则称点A、B为点M的等距点.问题探究:(1)如图①,在△ABC中,AB=AC,点P为AB上一点,试在AC上确定一点Q,使点P、Q 为点A的等距点;(2)如图②,平行四边形ABCD的对角线AC、BD交于点O,点P是AD边上一定点,试在BC边上找点Q,使点P、Q为点O的等距点,并说明理由.问题解决:(3)如图③,在正方形ABCD中,AB=1,点P是对角线AC上一动点,在边CD上是否存在点Q,使点B、Q为点P的等距点,同时使四边形BCQP的面积为正方形ABCD面积的一半?若存在这样的点Q,求出CQ 的长;若不存在,说明理由.9.提出问题在一个图形上画一条直线,若这条直线既平分该图形的面积,又平分该图形的周长,我们称这条直线为这个图形的“等分积周线”.探究问题(1)如图①,在Rt△ABC中,∠ACB=90°,∠ABC=45°,AB=4,请你过点C画出△ABC的一条“等分积周线”,与AB交于点D,并求出CD的长;(2)如图②,在△ABC中,AB=BC,且BC≠AC,过点C画一条直线CE,其中点E为AB上一点,你觉得CE可能是△ABC的“等分积周线”吗?请说明理由;解决问题(3)西安市区的环境越来越美,随处可见的街心花园成为人们休闲的好去处.在某地的街心花园中有一块如图③所示的空地ABCD,其中∠A=∠B=90°,AB=4,BC=6,CD=5,现要在这块空地上修建一条笔直的水渠(渠宽不计),使这条水渠所在的直线既平分四边形ABCD的周长,又平分四边形ABCD的面积,且要求这条水渠必须经过BC边.请你画出所有满足条件的水渠,说明理由,并求出该水渠与BC边的交点到点B的距离.10.我们定义:在一个图形上画一条直线,若这条直线既平分该图形的面积,又平分该图形的周长,我们称这条直线为这个图形的“等分积周线”.(1)如图1,在△ABC中,AB=BC,且BC≠AC,请你在图1中用尺规作图作出△ABC的一条“等分积周线”;(2)在图1中,过点C能否画出一条“等分积周线”?若能,说出确定的方法‘若不能,请说明理由.(3)如图2,四边形ABCD中,∠B=∠C=90°,EF垂直平分AD,垂足为F,交BC于点E,已知AB=3,BC=8,CD=5.求证:直线EF为四边形ABCD的“等分积周线”;(4)如图3,在△ABC中,AB=BC=6cm,AC=8cm,请你不过△ABC的顶点,画出△ABC的一条“等分积周线”,并说明理由.。
中考几何平分面积问题方法总结

中考几何平分面积问题方法总结1、三角形的面积平分①三角形的中线将三角形面积平分②构造以下模型,通过等面积转换,作出面积平分线如图,在梯形ABCD中,易证△OAB和△OCD面积相等,我们不妨称之为“蝴蝶模型”。
构造蝴蝶模型的关键点:平行线构造蝴蝶模型的目的:等面积转换例1、如图,过△ABC的底边BC上一定点P,求作一直线l,使其平分△ABC的面积.简答:取BC中点M,连接AM,则△ABM和△ACM的面积相等,连接AP,过M作AP的平行线MN,构造“蝴蝶模型”如图,∵△OAN和△OPM面积相等,∴△BNP和四边形ACPN面积相等。
2、平行四边形的面积平分结论1:过平行四边形中心的任意一条直线,平分该平行四边形的面积。
结论2:任何图形,只要能找到它的中心,那么过中心的直线平分这个图形的面积。
例2、如图平行四边形ABCD中,点P是AB边上一点,过点P求作一条直线,使其平分平行四边形ABCD的面积。
简答:连接BD、AC交于O点,则直线PO即为所求作的直线。
可用全等证明,过程略。
例3、现有如图的铁片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,工人师傅想用一条直线将其分割成面积相等的两部分,请你帮师傅设计三种不同的分割方案.简答:如图所示,三种方法都是取大小两个平行四边形的中心,连接即可。
3、梯形的面积平分结论1:梯形上下底中点的连线平分该梯形的面积。
结论2:过梯形上下底中点的连线的中点,且与上下底有交点的直线,平分该梯形的面积。
例4、如图:五边形ABCDE可以看成是由一个直角梯形和一个矩形构成.⑴ 请你作一条直线,使直线平分五边形ABCDE的面积;⑵ 这样的直线有多少条?请你用语言描述出这样的直线.简答:(1)取梯形上下两底中点连线的中点O,取矩形的中心P,则直线OP即为所求作直线l;(2)这样的直线有无数条,设直线l与AE交于M,与BC交于N,取MN中点G,则过G点且与线段AE、BC均有交点的直线平分五边形ABCDE的面积。
中考复习微专题----利用对称平分图形面积

A ������������DM来自������������
O
B
C
(三)作一条直线平分组合图形面积
【基本方法】若一个不规则图形可以分为两个规则图形,可找到它们的对称中心,那么 连接两个规则图形对称中心的直线即可将这个不规则图形分成面积相等的两部分。
【问题解决】:如图,在平行四边形一个角上剪 去一个平行四边形,得到一个六边形ABCDEF,请
(4)对于任何中心对称图形,只要能找到它的对称中心点O,那么过点 O和已知点M的直线即可将这个图形分成面积相等的两部分。
本节课你的收获是什么?
A
B M
A y
E
B
O
(图1)
DC
N
b
(图2)
Ba
C
P (图3) AF x
【知识归纳】:本专题主要探究了: (1)等腰或等边三角形为轴对称图形,作其底边上的高即可平分其面积; (2)平行四边形、矩形、菱形、正方形均为中心对称图形,过它们的对称 中心(对角线交点)的任意一条直线均可将它们的面积分成相等的两部分; (3)圆、正多边形均为轴对称对称图形,对称轴所在的直线均可将它们的 面积分成相等的两部分;
l
【基本模型】(3)圆、正多边形均为轴对
称对称图形,对称轴所在的直线均可将它们
的面积分成相等的两部分。
O
(二)过一点M作直线等分图形面积
【基本方法】不论已知点M在所给图形内部或者边上,借助图形的对称中心解决问题: 对于任何中心对称图形,只要能找到它的对称中心点O,那么过点O和已知点M的直线 即可将这个图形分成面积相等的两部分。
B
DC
(一)任作一条直线等分图形面积
【基本模型】(2)平行四边形、矩形、菱形、正方形均为中心对称图形,过它 们的对称中心(对角线交点)的任意一条直线均可将它们的面积分成相等的两 部分;两条对角线能四等分它们的面积。
陕西省中考数学试题研究类型面积平分问题练习

类型1 面积平分问题1. 问题探究(1)定义:两组邻边对应相等的四边形为筝形.写出一个你所学过的是筝形的特殊四边形:______;如图①,已知筝形ABCD ,连接AC ,试证明直线AC 平分该筝形ABCD 的面积; (2)如图②,已知四边形ABCD ,AB =AD ,BC =DC .在四边形ABCD 中找一点P ,连接PB 、PD ,使折线B —P —D 平分筝形ABCD 的面积,并说明理由; 问题解决(3)现有一块如图③所示的菜田ABCD ,且D 处有一水井,现要过水井D 修一条灌溉水渠,该水渠近似为一条直线,且水渠两边菜田的面积相等,已知AB =AD =20 m ,BC =DC =20 5 m ,∠BAD =90°,则是否能修出这样的水渠?若能,求出该水渠的长度;若不能,请说明理由.第1题图解:(1)菱形(或正方形); 证明:如解图①,第1题解图①在△ABC 和△ADC 中,⎩⎪⎨⎪⎧AB =AD BC =DC AC =AC, ∴△ABC ≌△ADC (SSS). ∴直线AC 平分筝形ABCD 的面积;(2)如解图②,连接AC ,取AC 的中点P ,连接BP 、DP ,则折线B —P —D 平分筝形ABCD 的面积.第1题解图②理由如下:∵S △ABP =S △BPC ,(三角形等底同高面积相等) ∴S △ABP =12S △ABC ,同理,S △ADP =12S △ADC ,∴S △ABP +S △ADP =12S △ABC +12S △ADC .∴S 四边形ABPD =12S 四边形ABCD .即S 四边形ABPD =S 四边形BCDP .∴折线B —P —D 平分筝形ABCD 的面积; (3)能.如解图③,设直线DG 平分筝形ABCD 的面积,连接AC 、BD 交于点O ,第1题解图③∵OC >OA ,则S △ABD <S △CBD , ∴点G 在BC 边上.过点D 作线段DG 交BC 于点G ,设BG =x ,△DBG 的边BG 上的高为h , ∵AB =AD =20,∠BAD =90°, ∴BD =20 2.又∵△CBD 是等腰三角形,则有CO =DC 2-DO 2=2000-200=302, ∴12BC ·h =12BD ·CO =12×205h =12×202×30 2 =600,∴h =12 5.若△DGC 的面积等于四边形ABGD 的面积,即S △DCG =S △ABD +S △BDG ,则有12(205-x )h =12×20×20+12xh ,即105h -12xh =200+12xh ,∴x =2035,即BG =13BC .过点G 作GH ⊥BD 于点H ,∵AC ⊥BD ,GH ⊥BD ,∴GH ∥AC ,△BGH ∽△BCO , 则BH =13BO ,GH =13CO ,∴BH =16BD ,DH =BD -BH =56BD =5032,GH =13CO =102,∴GD =DH 2+GH 2=2500×29+200=20317. ∴能修出这样的水渠,该水渠的长度为20317 m.2. 问题提出(1)如图①,已知△ABC ,过点A 作线段AD 交BC 边于点D ,使得AD 平分△ABC 的面积; 问题探究(2)如图②,在平行四边形ABCD 中,AB =6,BC =8,∠B =60°,AM =2,在BC 边上确定一点Q ,使得线段MQ 平分平行四边形ABCD 的面积,并求出MQ 的长; 问题解决(3)如图③,在平面直角坐标系中有四边形ABCD ,A (0,2)、B (2,0)、C (4,0)、D (6,4),过点A 作线段AE 交DC 于点E ,使得AE 平分四边形ABCD 的面积,并求点E 的坐标.第2题图解:(1)如解图①,取BC 边上的中点D ,连接AD ,线段AD 即为所求;第2题解图① 第2题解图②(2)如解图②,连接AC 、BD 交于点O ,连接MO 并延长,交BC 于点Q , 则MQ 即可平分平行四边形ABCD 的面积,且AM =CQ , 过点A 作AE ⊥BC 于点E ,过点M 作MF ⊥BC 于点F , ∵在▱ABCD 中,AD ∥BC ,∴四边形AEFM 是矩形,AE =MF ,AM =EF =2. 在Rt △ABE 中,∠B =60°,AB =6, ∴BE =3,AE =33,∴FQ =BC -BE -EF -QC =8-3-2-2=1,在Rt △MFQ 中,∠MFQ =90°,FQ =1,MF =AE =33, ∴MQ =FQ 2+MF 2=12+(33)2=27;(3)如解图③,连接BD ,取BD 的中点P ,连接AP 、PC ,则BP =PD , ∴S △ABP =S △ADP ,S △BCP =S △CDP ,∵S 四边形ABCP =S △ABP +S △BCP ,S 四边形ADCP =S △ADP +S △DCP , ∴S 四边形ABCP=S 四边形ADCP ,第2题解图③连接AC ,过点P 作PE ∥AC 交CD 于点E ,连接AE 交PC 于点F ,则S △APE =S △CPE , ∴S △APF =S △CEF , ∴S △ADE =S 四边形ABCE ,∴线段AE 平分四边形ABCD 的面积.设直线AC 的解析式为y AC =kx +b (k ≠0),将点A (0,2),C (4,0)代入, 可求得直线AC 的解析式为y AC =-12x +2,∵B (2,0),D (6,4),∴线段BD 的中点P 的坐标为(4,2), ∵AC ∥PE,∴设直线PE 的解析式为y PE =-12x +m ,将点P (4,2)代入,可求得直线PE 的解析式为y PE =-12x +4.设直线CD 的解析式为y CD =ax +n , 将点C (4,0),D (6,4)代入,可求得直线CD 的解析式为y CD =2x -8, ∵直线y CD =2x -8与y PE =-12x +4交点为E ,∴⎩⎪⎨⎪⎧y =2x -8y =-12x +4,解得⎩⎪⎨⎪⎧x =245y =85, ∴点E 的坐标为(245,85).3. 问题提出(1)如图①,已知直线a ∥b ,点A 、B 分别是直线a 上不同的两点,分别过点A 、B 作AC ⊥b ,BD ⊥b ,垂足记为点C 、D ,则线段AC 和线段BD 的数量关系为AC ________BD ;(填“>”,“<”或“=”) 问题探究(2)如图②,在△ABC 中,点M 、N 分别是AB 、AC 的中点,过点A 作直线a ∥BC ,点P 是直线a 上的任意一点,连接PM 、PN 、MN ,若四边形BCNM 的面积为3,则△PMN 的面积为________; 问题解决(3)如图③,有一块四边形空地ABCD, AD ∥BC ,∠B =60°,AB =10米,AD =30米,BC =8米,点E 是BC 上一点,且BE =2米.市政为了美化城市,计划将这块空地改造成一片牡丹园,为了方便行人行走,计划在牡丹园中间过点E 修一条笔直的小路(路的宽度不计),使得小路的另一出口在AD 上的点F 处,且EF 恰好将四边形ABCD 的面积平分.请你帮助市政设计出小路EF 的位置(在图中画出EF ),并求EF 的长(结果保留根号).第3题图解:(1)=;【解法提示】两平行线间的距离处处相等. (2)1;【解法提示】在△ABC 中,M 、N 分别是AB 、AC 的中点, ∴MN ∥BC ,MN =12BC ,∴S △AMN =14S △ABC ,∴S 四边形MNCB =3S △AMN , ∴S △AMN =1.又∵直线a ∥BC ,MN ∥BC ,∴直线a ∥MN , ∴S △PMN =S △AMN =1.(3)如解图,在CD 上取点G ,使得CG =DG ,过点G 作HK ∥AB ,分别交AD 于点H ,交BC 的延长线于点K ,连接BH 、AK ,相交于点O ,连接EO 并延长交AD 于点F ,此时EF 即为所求.第3题解图过点A 作AQ ⊥BC 于点Q ,在Rt △ABQ 中,AB =10米,∠ABQ =60°, ∴BQ =5米,AQ =53米. ∵BE =2米,∴EQ =3米.过点E 作EP ⊥DA 交DA 的延长线于点P ,则四边形EQAP 是矩形, ∴PE =AQ =53米,AP =EQ =3米. ∵G 是CD 的中点,CK ∥HD ,∴∠KCG =∠HDG ,∠CKG =∠DHG ,CG =DG , ∴△CKG ≌△DHG (AAS),∴CK =DH ,又由作图及题知HK ∥AB ,AD ∥BC , ∴四边形ABKH 是平行四边形, ∴AH =BK ,∴AH =BC +CK =BC +HD =AD -HD , ∴HD =12(AD -BC )=12×(30-8)=11米,∴AH =AD -HD =30-11=19米, ∵FH =BE =2米,∴AF =AH -FH =17米,∴PF =PA +AF =3+17=20米,在Rt △EPF 中,由勾股定理得EF =PE 2+PF 2=(53)2+202=519米.。
中考面积平分问题
思考:对于不规则图形如何做面积平分线?
作业:如图,四边形ABCD是某商业用地示意图,现准备过点A修一 条笔直的道路(宽度不计),使其平分四边形ABCD的面积.请你在 图中作出这条路所在的直线,写出作法,并说明理由.
A
D
B
C
如图,在同学们放学路上,有一块矩形的 草坪,很多同学为了少走一些路,就从草 坪上面踩过,学校既为了方便学生行走又 为了保护小草,于是决定,从草坪中铺一 条小路(宽度不计),小路可以怎么样 来铺?
为了铺好路之后草坪看起来更加 美观,要求小路两边的草坪面积 要相等,应该怎么样来铺小路?
面积平分问题
简单的面积平分问题
—三角形面积平分问题
A
证明:过点A作直线AE⊥BC于点E.
∵AD是中线 ∴BD=CD
B D E C
思考:对于任意三角形是否有三角形中线平分三角形面积?
探索:
三角形中,高相同,底相等,则面积相等 三角形任意边的中线都将这个三角形分为 等底同高的两个面积相等的三角形
结论:三角形的中线平分三角形的面积
四边形的面积平分问题
例:如图,在平行四边形中ABCD中,
对角线AC、BD相交于点O,点M是四边形内一定点 请你做出一条直线,过点M且平分平行四边形 ABCD的面积.
分析:AC将平行四边形分为两个等底等高的两个三角形,所以 AC平分四边形ABCD的面积,同理得:BD也平分四边形ABCD的 面积. AC、BD都过点O,O又是平行四边形ABCD的中心. 猜想:过点M、O的直线平分平行四边形ABCD. 验证:连接MO并延长交AB于点E,CD于点F . A D
F
C
.M
O
E
B
∴EF平分平行四边形ABCD,EF所在的直线即为所求.
中考数学专题探究-----面积问题(含详细解答)

中考数学专题探究-----面积问题面积问题在中考中占有很重要的地位,一般情况下,计算一些基本图形的面积,可以直接运用图形的面积公式,对于一些不规则的图形面积的计算,可以对图形进行转化,这类问题虽然解题方法比较灵活多样,但难度一般不太大。
但是,在中考压轴题中,有关面积的问题常常以动态的方式出现,经常与函数知识联系起来,有时还需要分类讨论。
因此,对考生要求较高,在解题时,要注意分清其中的变量和不变量,并把运动的过程转化成静止的状态,做到动静结合,以静求动。
考点一:面积的函数关系式问题典型例题:1、(2009年湖南衡阳)如图12,直线4+-=x y 与两坐标轴分别相交于A 、B 点,点M 是线段AB 上任意一点(A 、B 两点除外),过M 分别作MC ⊥OA 于点C ,MD ⊥OB 于D . (1)当点M 在AB 上运动时,你认为四边形OCMD 的周长是否发生变化?并说明理由;(2)当点M 运动到什么位置时,四边形OCMD 的面积有最大值?最大值是多少?(3)当四边形OCMD 为正方形时,将四边形OCMD 沿着x 轴的正方向移动,设平移的距离为)40<<a a (,正方形OCMD 与△AOB 重叠部分的面积为S .试求S 与a 的函数关系式并画出该函数的图象.解:(1)设点M 的横坐标为x ,则点M 的纵坐标为-x+4(0<x<4,x>0,-x+4>0); 则:MC =∣-x+4∣=-x+4,MD =∣x ∣=x ;∴C 四边形OCMD =2(MC+MD )=2(-x+4+x )=8∴当点M 在AB 上运动时,四边形OCMD 的周长不发生变化,总是等于8; (2)根据题意得:S 四边形OCMD =MC ·MD =(-x+4)· x =-x 2+4x =-(x-2)2+4∴四边形OCMD 的面积是关于点M 的横坐标x (0<x<4)的二次函数,并且当x =2,即当点M 运动到线段AB 的中点时,四边形OCMD 的面积最大且最大面积为4; (3)如图10(2),当20≤<a 时,42121422+-=-=a aS ; 如图10(3),当42<≤a 时,22)4(21)4(21-=-=a a S ;∴S 与a 的函数的图象如下图所示:图12(1)图12(2)图12(3)2、(2009宁夏)已知:等边三角形ABC 的边长为4厘米,长为1厘米的线段MN 在ABC △的边A B 上沿A B 方向以1厘米/秒的速度向B 点运动(运动开始时,点M 与点A 重合,点N 到达点B 时运动终止),过点M N 、分别作A B 边的垂线,与ABC △的其它边交于P Q 、两点,线段MN 运动的时间为t 秒.(1)线段MN 在运动的过程中,t 为何值时,四边形M N Q P 恰为矩形?并求出该矩形的面积; (2)线段MN 在运动的过程中,四边形M N Q P 的面积为S ,运动的时间为t .求四边形M N Q P的面积S 随运动时间t 变化的函数关系式,并写出自变量t 的取值范围. 解:(1)过点C 作CD AB ⊥,垂足为D . 则2A D =,当MN 运动到被CD 垂直平分时,四边形M N Q P 是矩形, 即32A M =时,四边形M N Q P 是矩形,32t ∴=秒时,四边形M N Q P 是矩形.tan 60PM AM = °=,M N Q P S ∴=四边形(2)1°当01t <<时,1()2M N Q P S P M Q N M N =+四边形·11)2t ⎤=++⎦2=+))4<≤aC PQBA M NC PQBA MN2°当12t ≤≤时1()2M N Q P S P M Q N M N =+四边形·1)12t ⎤=+-⎦·= 3°当23t <<时,1()2M N Q P S P M Q N M N =+四边形·1))2t t ⎤=-+-⎦=+3、(2010年辽宁丹东)如图,平面直角坐标系中有一直角梯形OMNH ,点H 的坐标为(-8,0),点N 的坐标为(-6,-4).(1)画出直角梯形OMNH 绕点O 旋转180°的图形OABC ,并写出顶点A ,B ,C 的坐标(点M 的对应点为A , 点N 的对应点为B , 点H 的对应点为C ); (2)求出过A ,B ,C 三点的抛物线的表达式;(3)截取CE =OF =AG =m ,且E ,F ,G 分别在线段CO ,OA ,AB 上,求四边形...BEFG 的面积S 与m 之间的函数关系式,并写出自变量m 的取值范围;面积S 是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由;(4)在(3)的情况下,四边形BEFG 是否存在邻边相等的情况,若存在,请直接..写出此时m 的值,并指出相等的邻边;若不存在,说明理由.解:(1) 利用中心对称性质,画出梯形OABC . ∵A ,B ,C 三点与M ,N ,H 分别关于点O 中心对称, ∴A (0,4),B (6,4),C (8,0)CPQA M N CPQA MN(2)设过A ,B ,C 三点的抛物线关系式为2y ax bx c =++, ∵抛物线过点A (0,4),∴4c =.则抛物线关系式为24y ax bx =++. 将B (6,4), C (8,0)两点坐标代入关系式,得3664464840a b a b ++=⎧⎨++=⎩,. 解得1432a b ⎧=-⎪⎪⎨⎪=⎪⎩,.所求抛物线关系式为:213442y x x =-++.(3)∵OA =4,OC =8,∴AF =4-m ,OE =8-m .∴AG F EO F BEC EFG B ABC O S S S S S =---△△△四边形梯形 21=OA (AB +OC )12-AF ·AG 12-OE ·OF 12-CE ·OAm m m m m 421)8(21)4(2186421⨯-----+⨯⨯=)(2882+-=m m ( 0<m <4)∵2(4)12S m =-+. ∴当4m =时,S 的取最小值. 又∵0<m <4,∴不存在m 值,使S 的取得最小值. (4)当2m =-+GB =GF ,当2m =时,BE =BG .4、如图所示,菱形ABCD 的边长为6厘米,60B ∠=°.从初始时刻开始,点P 、Q 同时从A 点出发,点P 以1厘米/秒的速度沿A C B →→的方向运动,点Q 以2厘米/秒的速度沿A B C D →→→的方向运动,当点Q 运动到D 点时,P 、Q 两点同时停止运动,设P 、QO MN HA CE FDB↑→ -8(-6,-4)x y运动的时间为x 秒时,APQ △与ABC △重叠部分....的面积为y 平方厘米(这里规定:点和线段是面积为O 的三角形),解答下列问题:(1)点P 、Q 从出发到相遇所用时间是 秒;(2)点P 、Q 从开始运动到停止的过程中,当APQ △是等边三角形时x 的值是 秒; (3)求y 与x 之间的函数关系式. 解:(1)6. (2)8.(3)①当03x <≤时,2111sin 6022222AP Q y S AP AQ x x x ==︒==13△1·····. ②当3x <≤6时,1222222121sin 6021(12-2)22A P Q y S A P P Q A P C Q x x ==︒=△= ····=2.2x -+③当69x ≤≤时,设33P Q 与AC 交于点O . (解法一)过3Q 作3,Q E CB ∥则3CQ E △为等边三角形.33333212..Q E C E C Q x Q E C B C O P EO Q ∴===-∴ ∥△∽△(第28题)Q 1B C D Q 2 P 3 Q 3 EP 2 P 1 O3361,212211(212),33C P O C x O EEQ x O C C E x -∴===-∴==-3333311sin 60sin 6022AQ P AC P C O P y S S C P AC O C C P ===-△△△-S ··°··°111(6)(212)(6)22232x x x =-⨯-⨯--⨯·6.262x x =-+-.(解法二)如右图,过点O 作3OF CP ⊥于点F ,3O G C Q ⊥,于点,G 过点3P 作3P H DC ⊥交DC 延长线于点H .,.A CB ACD O F O G ∠=∠∴=又33,6,2122(6),C P x C Q x x =-=-=-3312C Q P C O Q S S ∴=△△3333321,3113211(212)(6)322(6).6C O P C P Q S S C Q P H x x x ∴==⨯=⨯--=-△△···又331sin 602AC P S C P AC =△··°1(6)6226).2x x =-⨯⨯=-P 3OABC DQ 3G H F3A O P y S ∴=△3326)6)26AC P O C P S S x x =-=---△△262x x =-+-考点2、面积最值问题典型例题:1、(2008年广东广州)如图11,在梯形ABCD 中,AD ∥BC ,AB=AD=DC=2cm ,BC=4cm ,在等腰△PQR 中,∠QPR=120°,底边QR=6cm ,点B 、C 、Q 、R 在同一直线l 上,且C 、Q 两点重合,如果等腰△PQR 以1cm/秒的速度沿直线l 箭头所示方向匀速运动,t 秒时梯形ABCD 与等腰△PQR 重合部分的面积记为S 平方厘米 (1)当t=4时,求S 的值(2)当4t ≤≤10,求S 与t 的函数关系式,并求出S 的最大值解.(1)t =4时,Q 与B 重合,P 与D 重合, 重合部分是BDC ∆=3232221=⋅⋅(2)当时,如图104≤≤tQB=DP=t-4,CR=6-t,AP=6-t 由PQR ∆∽BQM ∆∽CRN ∆图11得2)324(-=∆∆t S S PQRBQM2)326(t S S PQRCRN -=∆∆22)4(43)324(-=-=∆∆t S t S PQR BQM ,22)6(43)326(t S t S PQR CRN -=-=∆∆S =3255)-(t 23t)-(6434t 4333222+-=---)(当t 取5时,最大值为325当t 取6时,有最大值32 综上所述,最大值为325二、名题精练:1、(2009湖南永州)如图,在平面直角坐标系中,点A C 、的坐标分别为(10)(0--,、,,点B在x 轴上.已知某二次函数的图象经过A 、B 、C 三点,且它的对称轴为直线1x =,点P 为直线BC 下方的二次函数图象上的一个动点(点P 与B 、C 不重合),过点P 作y 轴的平行线交BC 于点F .(1)求该二次函数的解析式;(2)若设点P 的横坐标为m ,用含m 的代数式表示线段P F(3)求PBC △面积的最大值,并求此时点P 的坐标. 解:(1)设二次函数的解析式为2(0)y ax bx c a a b c =++≠,、、为常数,由抛物线的对称性知B 点坐标为(30),,依题意得:093a b c a b c c ⎧-+=⎪++=⎨⎪=⎩(第25题)解得:33a b c ⎧=⎪⎪⎪⎪=-⎨⎪⎪⎪=⎪⎩∴所求二次函数的解析式为233y x x =--(2)P 点的横坐标为m ,P ∴点的纵坐标为233m m --设直线BC 的解析式为(0)y kx b k k b =+≠,、是常数,依题意,得30k b b +=⎧⎪⎨=⎪⎩3k b ⎧=⎪∴⎨⎪=⎩ 故直线BC的解析式为3y x =-∴点F的坐标为3m ⎛-⎝⎭2(03)3PF m ∴=-+<<(3)PBC △的面积12C P F B P F S S S P F B O =+=△△·=2213323228m ⎛⎫⎫⨯-+⨯=--+ ⎪⎪ ⎪⎝⎭⎝⎭∴当32m =时,PBC △的最大面积为8把32m =代入233y m m =--4y =-∴点P的坐标为324⎛⎫-⎪ ⎪⎝⎭,(第25题)2、(2007年淮安)在平面直角坐标系中,放置一个如图所示的直角三角形纸片AOB ,已知OA=2 ∠AOB=30°,D 、E 两点同时从原点O 出发,D 点以每秒3个单位长度的速度沿x 轴的正方向运动,E 点以每秒1个单位长度的速度沿y 轴的正方向运动,设D 、E 两点运动的时间为t 秒。
中考平分面积问题的探究(齐福德)
平分面积问题的探究近年来,中考中常遇到用一条直线平分一个平面图形面积的作图题,如何迅速解决这类问题呢,首先要掌握好以下一些常用的基本规律。
一.中心对称图形的面积平分在初中数学阶段,我们经常遇到的中心对称图形有圆和平行四边形等。
1. 圆我们知道,圆的对称中心就它的圆心,只要经过圆的圆心作一条直线,便可以将这个圆的面积平分。
2. 平行四边形我们知道,平行四边形的对称中心是两条对角线的交点,只要经过对角线的交点作一条直线,便可以将这个平行四边形的面积平分。
矩形、菱形、正方形都是特殊的平行四边形,同样也可以用这种方式将面积平分。
一般地,对于中心对称图形,我们经过它的对称中心作一条直线便可以将它的面积平分。
二、组合图形的面积平分掌握了中心对称图形的面积平分规律,我们再来解决组合图形的面积平分就不是什么难事了,一般只要通过适当的方法将图形分解成两个中心对称图形的组合,问题便解决了。
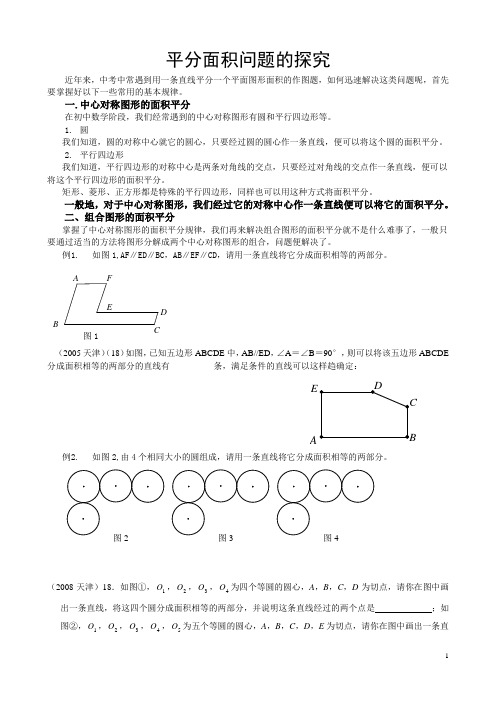
例1. 如图1,AF ∥ED ∥BC ,AB ∥EF ∥CD ,请用一条直线将它分成面积相等的两部分。
(2005天津)(18)如图,已知五边形ABCDE 中,AB//ED ,∠A =∠B =90°,则可以将该五边形ABCDE 分成面积相等的两部分的直线有__________条,满足条件的直线可以这样趋确定: ____________________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________例2. 如图2,由4个相同大小的圆组成,请用一条直线将它分成面积相等的两部分。
备战2020中考数学一轮专项训练:面积平分问题(含解析)

备战2020中考数学一轮专项训练:面积平分问题前言:“一学就会,一考就废?”,正是因为考试后缺少了这个环节从小学到初中,学生们经历了无数次考试。
通过考试可以检测同学们对知识的理解、掌握情况,提高应试能力。
但对待考试,部分同学只关注自己的分数,而对试卷的分析和总结缺乏重视。
结果常常出现一些题在考试中屡次出现,但却一错再错的情况。
这样,学生们无法从考试中获益,考试也就失去了它的重要意义。
做好试卷分析和总结是十分有必要的。
那么,怎样做好试卷分析呢?我认为,应从下面两点做起:一.失分的原因主要有如下四方面:(1)考试心理:心理紧张,马虎大意;(2)知识结构:知识面窄,基础不扎实;(3)自身能力:审题不清,读不懂题意;(4)解题基本功:答题规范性差。
只有查出、找准原因,才能对症下药,从弱项方面加强训练,以提高成绩。
二.“扭转乾坤”的方法做题的过程中对每一道题要试图问如下几个问题?(1)怎样做出来的?——想解题方法;(2)为什么这样做?——思考解题原理;(3)怎样想到这种方法?——想解题的基本思路;(4)题目体现什么样的思想?——揭示本质,挖掘规律;(5)是否可将题目变化?——一题多变,拓宽思路;(6)题目是否有创新解法?——创新、求异思维。
转变,让我们从一轮复习开始。
按照上面两点认真完成后面练习题。
希望每一位同学经过一轮复习后,能够扭转“一考就废”的局面,最后决胜中考。
1. 问题探究在矩形ABCD 中,AD =a ,AB =b (b >a ),P 为AB 边上一点,且PB =m (m <a ),在CD 边上有两点M 、N .(1)如图①,求证:△MPB 的面积与△NPB 的面积相等;(2)如图②,延长AB 到点S ,使BS =PB ,以BS 为边在直线AB 上方作正方形BSRQ ,连接AR 、AQ 、AC 、CR ,若△ACR 的面积等于矩形ABCD 面积的14,试确定a 、b 、m 的关系;第1题图问题解决(3)如图③,有一片矩形绿地ABCD ,现要修建一条高速公路,该公路要占用绿地△ABE ,按照施工要求,高速公路的边缘AE 不能超过BC 的中点,为补偿占用的绿地,试在AE 的延长线上找出一点F ,使四边形ADCF 的面积与原矩形ABCD 的面积相等,试在图③中画出图形并说明理由. (1)证明:如解图①,∵△MPB 与△NPB 同底等高, ∴S △MPB =S △NPB ;第1题解图①(2)解: S △ACR =S △ACQ +S △AQR +S △CQR =12b (a -m )+12m 2+12m (a -m )=12(ab +am -bm ),∵S △ACR =14S 矩形ABCD ,∴12(ab +am -bm )=14ab ,∴ab +2am -2bm =0;(3)解:如解图②,连接AC ,过点B 作BF ∥AC 交AE 的延长线于点F ,连接CF .第1题解图②设AC 到BF 的距离为h ,则S △ABC =12AC ·h ,S △ACF =12AC ·h , ∴S △ABC =S △ACF , ∴S △ABE =S △CEF , ∴S 矩形ABCD =S 四边形ADCF .2. 问题探究(1)如图①,在△ABC 中,AD 是BC 边上的中线,若△ABC 的面积为S ,则△ACD 的面积为________;(2)在图②中,当点E 、F 分别是平行四边形ABCD 的边AB 、BC 的中点时,记四边形BEDF 的面积为S 1;当点E 、F 分别在平行四边形ABCD 的边AB 、BC 上时,且满足AE =13AB ,BF =13BC ,记此时的四边形BEDF 的面积为S 2.证明:S 1=S 2; (3)如图③,在矩形ABCD 中,AB =nBC (n 为常数,且n >0),点E 是AB 边上任意一点,点F 是BC 边上任意一点,若四边形BEDF 的面积始终等于矩形面积的12,请探究线段AE 、BF应满足怎样的数量关系,并说明理由.第2题图(1)解:12S ;【解法提示】∵ AD 为△ABC 中BC 边的中线, ∴DC 为BC 的一半,由图可知△ABC 与△ADC 同高,又知△ABC 的面积为S ,∴S △ACD =12S ; (2)证明:如解图①,连接BD, 当点E 、F 分别为AB 、BC 上的中点,第2题解图①由(1)可知S △BED =12S △ABD , S △BDF =12S △BCD ,又∵根据平行四边形的性质可知S △ABD =S △BCD =12S ▱ABCD , ∴S 1=S △BED +S △BDF =12S ▱ABCD ,当点E 、F 分别在平行四边形ABCD 的边AB 、BC 上时,且满足AE =13AB ,BF =13BC ,∴BE =23AB ,则S △BDE =23S △ABD ,S △BFD =13S △BCD , 又∵S △ABD =S △BCD =12S ▱ABCD , ∴S 2=S △BDE +S △BFD =12S ▱ABCD . 综上所述,可证:S 1=S 2;(3)解:如解图②,连接BD ,第2题解图②由题意可知四边形BEDF 的面积始终等于矩形面积的12,即根据等面积可知:AB ·BC =2(12BE ·AD +12BF ·AB ), ∵AB =nBC ,∴AB ·BC =2(12BE ·1n AB +12BF ·AB )=BE ·1n AB +BF ·AB ,∴BC =1n BE +BF , ∴1n AB =1n BE +BF , ∴AE =nBF .。
2024中考数学总复习冲刺专题:利用平行线解决函数中的面积问题 通用版

《用平行线解函数中的三角形面积问题》一、考点梳理:函数与三角形面积相结合的综合题常常出现在中考的压轴题中,是中考压轴题的难点之一。
主要考查学生的综合分析问题能力,考察学生数形结合思想,分类讨论思想、转化思想等。
热点考题是:面积比问题,面积定值问题、面积最值问题,面积之间的和、差、比值等问题。
常见的解题方法有多种,例如:1、利用铅垂高、水平宽解决问题;2、利用割补法解决问题;3、利用面积比等于相似比的平方解决问题;4、利用平行线转移面积解决问题等。
在二次函数与一次函数相结合的题目中求面积或者与面积相关的问题时,我们通常过三角形的某个已知顶点作对边的平行线,利用平滑定理来求解,问题就会变得简单许多,近年来,多地的中考试题中也出现了这样的题目,值得我们重视。
二、本节课学习目标:1.利用平行线转移三角形面积,并解决问题;2.利用平行线把面积比转化为线段比;3.通过直线与曲线相切求面积的最值;三、新课学习:知识铺垫:知识铺垫:任何两条夹在平行线间的垂线段长度相等;(1)如图1,若直线a∥b,则有MN=PQ=S△BCD(2)如图2,直线a∥b,则S△ABC我们先来了解什么是平滑定理:两个三角形共用同一底,且顶点都在与底平行的同一条直线上,那么由三角形的面积公式可知,这两个三角形的面积必然相等。
所以平滑定理需要两个条件:(1)共底或者底在同一直线上但相等;(2)三角形的顶点都在与底平行的同一条直线上知识铺垫2:一次函数y=k1x+b1图像与一次函数y=k2x+b2图像平行则可以推出k1=k2反之若k1=k2则可推出一次函数y=k1x+b1图像与一次函数y=k2x+b2图像平行,其中b1≠b2.模块一(利用平行转换面积)典例精讲:如图,已知二次函数y =﹣x 2+x +4的图象与y 轴交于点A (0,4).与x 轴交于点B ,C ,点C 坐标为(8,0),连接AB 、AC .若点N 在线段BC 上运动(不与点B ,C 重合),过点N 作NM ∥AC ,交AB 于点M ,当△AMN 面积等于5时,求此时点N 的坐标;解法1:A (0,4),B (-2,0),C (8,0)b 1b2y=kx+b 1y=kx y=kx+b 2设NC=m ,连接MC ,MH BC⊥作∵MNB ACB∆∆∽∴MH BN AO BC =∴10m 410MH -=∴2(10m)5MH -=∵NM ∥AC∴S △AMN =S △CMN=12NC MH ⨯=12(10m)25m -⨯(10m)5m -=∴当△AMN 面积是5时,m =5,此时N 点坐标为(3,0)学生练习:已知:如图,抛物线y =x 2+4x +3交x 轴于E 、F 两点,交y 轴于A 点,若Q 为抛物线上一点,连接QE ,QA ,设点Q 的横坐标为t (t <﹣3),△QAE 的面积为S ,求S 与t 函数关系式;【解答】解:易得A (0,3),E (-3,0),AE:y =x+3.作QH//AE ,交y 轴于点H ,设Q (t ,t 2+4t +3),设HQ :y =x+b把Q 点坐标代入y =x+b可得HQ:2y=33x t t +++∴H (0,233t t ++),AH=23t t +,2212139(3)3222AEQ AEP S S AH OE t t t t ∆∆==⨯⨯=⨯+⨯=+模块二(同底三角形面积比问题)典例精讲:1、如图,在平面直角坐标系中,抛物线y =-x 2+2x+3与交x 轴于点A ,与y 轴交于点C .点M 的坐标为(4,-5),在抛物线上是否存在点P (不与点A 重合),使△PMC 的面积与△AMC 的面积相等?若存在,直接写出点P 的坐标;若不存在,请说明理由.【解答】解:当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则A(3,0),当x=0时,y=﹣x2+2x+3=3,则C(0,3)设直线CM的解析式为y=mx+n,把C(0,3),M(4,﹣5)代入得m=﹣2,n=3,∴直线MC的解析式为y=﹣2x+3,∵△PMC的面积与△AMC的面积相等,∴AP∥MC,设AP的解析式为y=﹣2x+p,把A(3,0)代入得p=6,∴AP的解析式为y=﹣2x+6,解方程组得或,此时P点坐标为(1,4);直线AP的解析式为y=﹣2x+6与y轴的交点坐标为(0,6),∵6﹣3=3,把直线CM向下平移3个单位得到y=﹣2x,解方程得或,此时P点坐标为(2+,﹣4﹣2),(2﹣,﹣4+2),综上所述,P点坐标为(1,4)或(2+,﹣4﹣2)或(2﹣,﹣4+2),典例精讲:2.如图,抛物线y=﹣x2+3x+8与x轴交于点A、B点,与y轴交于点C点,P是抛物线上第一象限上的动点,连接PB,PC,当35PBCABCSS∆∆=时,求点P的坐标.P解:易得A (-2,0),B (8,0),C (0,8)作AD//BC ,交y 轴于D ,易求BC :y =﹣x +8AD :y =﹣x -2,∴CD=10,在C 点上方截取CE=6,过E 作EP//BC,交抛物线于点P ,则P 为所求的点PQ :y =﹣x +14,联立方程组,2141382y x y x x =-+⎧⎪⎨=-++⎪⎩可得点P 的坐标为(2,12)或P (6,8)例题精讲:如图,在平面直角坐标系内抛物线21y=42x x --与x 轴交于点A ,点B ,与y 轴交于点C .过点A 的直线y =x +2与抛物线交于点E .点P 为第四象限内抛物线上的一个动点.在点P 的运动过程中,是否存在点P 使得△AEP 的面积最大,若存在,请求出点P的坐标.解:存在点P 使得△AEP 的面积最大,理由如下:在直线AE 的下方作MN//AE ,当MN 与抛物线有唯一交点P 时,此时△AEP 的面积最大,P 为所求的点设MN :y=x b+联立方程组2142y x b y x x =+⎧⎪⎨=--⎪⎩可得212402x x b ---=144(4)02b ∆=-⨯--=解得6b =-联立方程组261382y x y x x =-⎧⎪⎨=-++⎪⎩可得P (2,﹣4).此时S △APE =32,学生练习:如图,一次函数y =﹣x +4的图象与反比例函数y =(k 为常数,且k ≠0)的图象交于A 、B 两点.点P 在反比例函数第三象限的图象上,使得△PAB 的面积最小,求满足条件的P 点坐标及△PAB 面积的最小值.【解答】解:联立方程组可得:,∴点B(3,1);如图,将直线AB平移,当与双曲线第三象限的图象只有一个交点P时,此时△PAB的面积有最小值,设平移的直线解析式为y=﹣x由题意可得:﹣x+b=,∴x2﹣bx+3=0,∵两图象只有一个交点,∴Δ=b2﹣4×3=0,∴b=±2,∵直线y=﹣x+b与y轴交在负半轴,∴b=﹣2,∴平移后的解析式为y=﹣x﹣2,∴﹣x﹣2=,∴x=﹣,∴y=﹣,∴点P(﹣,﹣),过点P作PH⊥AB于H,设直线y=﹣x+4与x轴交于点D,与y轴交于点C,设直线y=﹣x﹣2与x轴交于点E,与y轴交于点F,∴点C(0,4),点D(4,0),点E(﹣2,0),点F(0,﹣2),∴CO=DO=4,EO=FO=2,∴CD=4,EF=2,△COD和△EOF是等腰直角三角形,∴点O到EF的距离为,点O到CD的距离为2,∴PH=+2,∵点A坐标为(1,3),点B(3,1),∴AB==2,∴△PAB面积的最小值=×2×(+2)=2+4.三、课后作业1、如图,抛物线y=﹣x2+2x+3经过A(﹣1,0)、B(3,0)、C(0,3)三点,对称轴与抛物线相交于点P、与BC E,连接PB.抛物线上是否存在一点Q,使△QPB 与△EPB的面积相等,若存在,请求出点Q的坐标;若不存在,说明理由.由y=﹣x2+2x+3=﹣(x﹣1)2+4,则顶点P(1,4),对称轴为直线x=1,∴H(1,0),∴PH=4,BH=2,∵B(3,0),C(0,3),∴直线BC解析式为y=﹣x+3,∴点E(1,2),如图,过点E作EQ∥BC,交抛物线于Q,此时△QPB与△PEB的面积相等,由点P、B的坐标得,直线PB的表达式为:y=﹣2(x﹣3),则直线QE的表达式为:y=﹣2(x﹣1)+2②,联立①②并整理得:x2﹣4x+1=0,解得:x=2,则点Q的坐标为(2﹣,2)或(2+,﹣2);对于直线QE,设QE交x轴于点R,令y=﹣2(x﹣1)+2=0,解得:x=2,即点R(2,0则BR=3﹣2=1,取点R′使BR=BR′,过点R′作PB的平行线l,如上图,则点R′(4,0),则直线l的表达式为:y=﹣2(x﹣4),联立y=﹣x2+2x+3和y=﹣2(x﹣4)得:x2﹣4x+5=0,则Δ=16﹣20<0,无解,故在点B的右侧不存在点Q,综上,点Q的坐标为(2﹣,2)或(2+,﹣2)2.已知二次函数与x 轴交于A 、B 两点,A 在B 点的左边,与y 轴交于C 点,点P 在第一象限的抛物线上,且在对称轴右边.S △P AC =4,求P 点坐标.如图:解当y =0时,=0,解得x 1=1,x 2=3,即A (1,0),B (3,0).当x =0时,y =2,即C (0,2)过点P 作PE ∥AC ,则S △P AC =S △EAC =4设点E 为(a ,0)得421a 214OC AE 21=⨯-=⨯)(,即解得a=5,所以E (5,0)设直线y ac =kx+b ,分别代入A (1,0)、C (0,2)得b 2bk 0=+=解得k=-2,b=2.所以y ac =-2x+2因为PE ∥AC ,所以可设y pe =-2x+b 代入E (5,0)得0=-2x5+b ,解得b=10所以y pe =-2x+10,联立方程组得y=-2x+10解得:x 1=4x 2=-3y 1=2y 2=16答:P 点坐标是(4,2).3.如图,抛物线223y x x =-++的顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B (0,3).抛物线上第一象限内是否存在一动点P ,使S △PAB =98S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由。
中考数学考点 方法突破精讲练—利用对称平分图形面积

如解图④,先将六边形ABCDEF分割成两个规则的图形:矩形AGEF和矩
形GBCD,然后分别连接两个矩形的对角线,找出两个矩形的对称中心M 和N,连接MN,则直线MN将六边形ABCDEF分成面积相等的两部分(解法 不唯一).
利用对称平分图形面积
方法突破精讲练
2.对于过一点M 作直线平分图形面积的问题,需掌握:不论点在所给图
形内部或者边上,借助图形的中心点解决问题:
①对于任何图形,只要能找到它的中心点O,那么过点O、M的直线将这个
图形分成面积相等的两部分;
②对于正n(n≥3)边形,若点O为它的中心点,若直线OM与另一条过O点的
部分;在图②中作出两条直线,使它们将☉O的面积四等分;在图③中作
一条直线,使它平分以BC为底的等腰三角形ABC的面积;在图④中作两
条直线,使它们将正方形ABCD的面积四等分.
第1题图
利用对称平分图形面积
方法突破精讲练
解:如解图①,连接BD,则BD所在直线将▱ABCD的面积平分(解法不唯一); 如解图②,在圆中作两条互相垂直的直径,则这两条直径所在直线可将☉O 的面积四等分;
直线l能四等分它的周长,则直线OM与l四等分所给正n边形的面积;
③对于菱形和圆,方法②同样适用.
3.若一个不规则图形可以分为两个规则图形,则连接两个规则图形中心
的直线平分这个不规则图形的面积.
利用对称平分图形面积
方法突破精讲练
针对训练
1. 请你在图①中作一条直线,使它将平行四边形ABCD分成面积相等的两
图①
图②
图③ 第2题解图
图④
利用对称平分图形面积
方法突破精讲练
如解图②,连接Aቤተ መጻሕፍቲ ባይዱ、BD,交于点P,则点P为矩形ABCD的对称中心,作 直线MP,则直线MP平分矩形ABCD的面积;
2025年九年级数学中考专题复习--探索平分图形面积的直线+课件+

(三)平分梯形的面积
. .
•• .(1)两底中点所在直线 (2)变形为等积的平行四边形
(3)变形为等积的三角形
注意:所作直 线必须与梯形 两底都相交
二、平分组合图形的面积
问题情境一 做一条直线同时平分四边形ABCD和四边形EFGH
连接AC和BD交于M, A 连接EG和FH交于N,作 直线MN,沿MN修水渠 可把土地平分.
部分
A
B
P
E
C
F
D
解题策略: 任意四知识点
• (1)平分三角形面积:找中线.
• (2)平分平行四边形面积:找过中心的直线.
• (3)平分梯形面积:找两底中点所在直线;
•
变形成等积三角形;
•
变形成等积平行四边形.
• (4)平分一般四边形面积:变形为等积的三 角形.
方法三(补法): 如图,补成一个大长方形.
分别作两条对角线的交点,过 两交点作直线即平分面积.
反思:探究到此结束吗?平分面积的直线还有吗?
如图,在五边形ABCD E中,AB∥ED,∠A =∠B=90°, 则可以将五边形ABCD
E分成面积相等的直线有 几条?
方法一:上下分成梯形和矩形.
E
D
C
作梯形中位线和两底中点所
B 思考:问题就这样轻易解决吗? 你发现水渠的位置有什么特点?
D
M
H
G
N
C
EF
问题情境二 请你在图中画一条直线把它分成面积相等的两
部分.
方法一(割法):
如图,分割成上下两个长 方形.
分别作两条对角线的交点,过 两交点作直线即平分面积.
方法二(割法):
如图,分割成左右两个长 方形.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年4月35日中考综合题-------面积平分问题
1.问题探究:
(1)请在图①中作出两条直线,使它们将圆面四等分;
(2)如图②,M是正方形ABCD内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M)使它们将正方形ABCD的面积四等分,并说明理由.
问题解决:
(3)如图③,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点,如果AB=a,CD=b,且b >a,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?如若存在,求出BQ的长;若不存在,说明理由.
2.探索发现:
(1)如图1,在△ABC中,AD是BC边上的中线,若△ABC的面积为S,则△ACD的面积为.联系拓展:
(2)在图2中,E、F分别是▱ABCD的边AB、BC的中点,若▱ABCD的面积为S,求四边形BEDF的面积?并说明理由.
(3)在图3中,E、F分别是▱ABCD的边AB、BC上的点,且AE=AB,BF=BC,若▱ABCD的面积为S,则四边形BEDF的面积为.
解决问题:
(4)如图4中,矩形ABCD中,AB=nBC(n为常数,且n>0).E是AB边上的一个动点,F是BC边上的一个动点.若在两点运动的过程中,四边形BEDF的面积始终等于矩形面积的,请探究线段AE、BF应满足怎样的数量关系,并说明理由.
3.如果图1,已知直线m∥n,A、B为直线n上两定点,C、D为直线m上两动点,容易证明:△ABC 的面积=△ABD的面积;
问题探究
(1)在图2中画出与四边形ABCD面积相等且以AB为一条边的三角形.
(2)在图3中,已知正方形ABCD的边长为4,G是边CD上一点,以CD为边作正方形GCEF,当CG=a 时,求△BDF的面积.
问题解决
(3)李大爷家有一块正方形的果园如图4所示,由于修建道路,图中三角形BCE区域将被占用,现决定在DE右侧补给一块土地,补偿后,果园将调整为四边形ABMD,要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BE上.请你在图4中通过画图来确定M点的位置,并简要叙述画法和理由;若AB=4,CE=a,求出上图中tan∠MDC的值.
4.问题提出
(1)如图①,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为;
问题探究
(2)如图②,在矩形ABCD中,AB=12,AD=18,如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.
问题解决
(3)某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌.)同时,再合理设计好喷灌龙头喷水的射程就可以了.
如图③,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB交于点E,又测得DE=8m.
请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)
5.提出问题:爸爸出差回家带了一个分布均匀的等腰三角形蛋糕礼物给儿子(如图1,AB=BC,且BC≠AC),在蛋糕的边缘均匀分布着巧克力,双胞胎儿子大毛和小毛决定只切一刀将这块蛋糕平分吃(要求分得的蛋糕和巧克力质量都一样).
背景介绍:这条分割直线即平分了三角形的面积,又平分了三角形的周长,我们称这条线为三角形的“等分积周线”.
尝试解决:
(1)大毛很快就想到了一条分割直线,而且用尺规作图作出.请你帮大毛在图1中作出这条“等分积周线”,从而平分蛋糕.
(2)小毛觉得大毛的方法很好,所以自己模仿着在蛋糕上过点C画了一条直线CD交AB于点D.你觉得小毛会成功吗?如能成功,说出确定的方法;如不能成功,请说明理由.(用图2说明)
(3)若AB=BC=5cm,AC=6cm,如图3,你能找出几条△ABC的“等分积周线”,请分别画出,并简要说明确定的方法.
6.(1)请在图①中画出与△ABC面积相等的三个三角形:△ABC1、△ABC2、△ABC3,其中点C1、C2、C3为△ABC所在平面上异于点C的三个不同点;
(2)请在图②中射线BC上通过画图确定一点E,使得S
△ABE =S
四边形ABCD
,并简要叙述画法和理由;
问题解决
(4)李大爷家有一块果园如图③中的四边形ABCD,由于修路,图中三角形CEF区域将被占用,现决定在DF的右侧补给他一块土地,要求补偿前后的总面积不变,已知∠A=135°,∠B=60°,∠D=105°,AB=350m,BE=(100+50)m,CF=300m,DF=100m,若所补区域为三角形DFG,且点G在射线EF 上,请求出符合条年的FG的长度.
7.问题探究
(1)如图1,点E为矩形ABCD内一点,请过点E作一条直线,将矩形ABCD的面积分为相等的两部分;
(2)如图2,在矩形ABCD中,AB=8,BC=6,P为对角线AC上一点,且AC=3AP,请问在边CD上是
否存在一点E,使得直线PE将矩形ABCD的面积分为2:3两部分,如果存在求出DE的长;如果不存在,请说明理由;
解决问题
(3)如图3,现有一块矩形空地ABCD,AB=80米,BC=60米,P为对角线AC上一点,且PC=3AP,计划在这块空地上修建一个四边形花园AECF,使得E、F分别在线段AD、AB上,且EF经过点P,若每平方米的造价为100元,请求出修建该花园所需费用的范围(其他费用不计).
8.平面上有三点M、A、B,若MA=MB,则称点A、B为点M的等距点.
问题探究:(1)如图①,在△ABC中,AB=AC,点P为AB上一点,试在AC上确定一点Q,使点P、Q为点A的等距点;
(2)如图②,平行四边形ABCD的对角线AC、BD交于点O,点P是AD边上一定点,试在BC边上找点Q,使点P、Q为点O的等距点,并说明理由.
问题解决:
(3)如图③,在正方形ABCD中,AB=1,点P是对角线AC上一动点,在边CD上是否存在点Q,使点B、Q为点P的等距点,同时使四边形BCQP的面积为正方形ABCD面积的一半?若存在这样的点Q,求出CQ的长;若不存在,说明理由.
9.提出问题
在一个图形上画一条直线,若这条直线既平分该图形的面积,又平分该图形的周长,我们称这条直线
为这个图形的“等分积周线”.
探究问题
(1)如图①,在Rt△ABC中,∠ACB=90°,∠ABC=45°,AB=4,请你过点C画出△ABC的一条“等分积周线”,与AB交于点D,并求出CD的长;
(2)如图②,在△ABC中,AB=BC,且BC≠AC,过点C画一条直线CE,其中点E为AB上一点,你觉得CE可能是△ABC的“等分积周线”吗?请说明理由;
解决问题
(3)西安市区的环境越来越美,随处可见的街心花园成为人们休闲的好去处.在某地的街心花园中有一块如图③所示的空地ABCD,其中∠A=∠B=90°,AB=4,BC=6,CD=5,现要在这块空地上修建一条笔直的水渠(渠宽不计),使这条水渠所在的直线既平分四边形ABCD的周长,又平分四边形ABCD 的面积,且要求这条水渠必须经过BC边.请你画出所有满足条件的水渠,说明理由,并求出该水渠与BC边的交点到点B的距离.。
