斯坦福密码课程05.2-integrity-macs-based-on-PRFs

合集下载

网络安全05高级加密标准

1997年4月15日，NIST发起征集高级加密标准的活动，活动目的是确定一个非保密的、可以公开技术细节的、全球免费使用的分
组密码算法，作为新的数据加密标准。
1997年9月12日，美国联邦登记处公布了正式征集AES候选算法的通告。作为进入AES候选过程的一个条件，开发者承诺放弃被选中算法的知识产权。
processes data as block of 4 columns of 4 bytes operates on entire data block in every round
designed to be:
resistant against known attacks speed and code compactness on many CPUs design simplicity
有限域GF（28）上的一个固定可逆方阵A乘
乘法是GF(28)定义中定义的，素多项式为：
m(x) =x8+x4+x3+x+1
29
精选ppt
30
精选ppt
§5.2.3 列混淆（Mix Column）变换
例子
31
精选ppt
§5.2.4 轮密钥加（Add Round Key）变换
一个简单地按位异或的操作
c7 , c6 , c0 , =（01100011）2
26
精选ppt
§5.2.2 行移位(shift Row)变换
正向和逆向变换
27
精选ppt
§5.2.2 行移位(shift Row)变换
例子
28
精选ppt
§5.2.3 列混淆变换（Mix Column）
正向和逆向变换
代替操作，将状态的列看作有限域GF（28）上的4维向量并被

斯坦福2017机器学习人工智能教程课程讲义 bolcskei-stats385-slides

Task: Separate two categories of data through a linear classiﬁer
Φ(f ) =
f 1
1
: w, f > 0 : w, f < 0
not possible!
: w, Φ(f ) > 0 : w, Φ(f ) < 0
possible with w =
Why non-linear feature extractors?
Task: Separate two categories of data through a linear classiﬁer
1
: w, f > 0 : w, f < 0 not possible!
Why non-linear feature extractors?
ImageNet
ImageNet
ski rock
plant coﬀee
ImageNet
ski rock
plant coﬀee
CNNs win the ImageNet 2015 challenge [He et al., 2015 ]
Describing the content of an image
Translation invariance
Handwritten digits from the MNIST database [LeCun & Cortes, 1998 ] Feature vector should be invariant to spatial location ⇒ translation invariance
1 −1
Why non-linear feature extractors?

密码编码学与网络安全(第五版)答案

Chapter 1: Introduction (5)Chapter 2: Classical Encryption Techniques (7)Chapter 3: Block Ciphers and the Date Encryption Standard (13)Chapter 4: Finite Fields (21)Chapter 5: Advanced Encryption Standard (28)Chapter 6: More on Symmetric Ciphers (33)Chapter 7: Confidentiality Using Symmetric Encryption (38)Chapter 8: Introduction to Number Theory (42)Chapter 9: Public-Key Cryptography and RSA (46)Chapter 10: Key Management; Other Public-Key Cryptosystems (55)Chapter 11: Message Authentication and Hash Functions (59)Chapter 12: Hash and MAC Algorithms (62)Chapter 13: Digital Signatures and Authentication Protocols (66)Chapter 14: Authentication Applications (71)Chapter 15: Electronic Mail Security (73)Chapter 16: IP Security (76)Chapter 17: Web Security (80)Chapter 18: Intruders (83)Chapter 19: Malicious Software (87)Chapter 20: Firewalls (89)A NSWERS TO Q UESTIONS1.1The OSI Security Architecture is a framework that provides a systematic way of definingthe requirements for security and characterizing the approaches to satisfying thoserequirements. The document defines security attacks, mechanisms, and services, and the relationships among these categories.1.2 Passive attacks have to do with eavesdropping on, or monitoring, transmissions.Electronic mail, file transfers, and client/server exchanges are examples oftransmissions that can be monitored. Active attacks include the modification of transmitted data and attempts to gain unauthorized access to computer systems.1.3 Passive attacks: release of message contents and traffic analysis. Active attacks:masquerade, replay, modification of messages, and denial of service.1.4 Authentication: The assurance that the communicating entity is the one that it claims to be.Access control: The prevention of unauthorized use of a resource (i.e., this service controls who can have access to a resource, under what conditions access can occur, and what those accessing the resource are allowed to do).Data confidentiality: The protection of data from unauthorized disclosure.Data integrity: The assurance that data received are exactly as sent by an authorized entity(i.e., contain no modification, insertion, deletion, or replay).Nonrepudiation: Provides protection against denial by one of the entities involved in a communication of having participated in all or part of the communication.Availability service: The property of a system or a system resource being accessible and usable upon demand by an authorized system entity, according to performancespecifications for the system (i.e., a system is available if it provides services according to the system design whenever users request them).1.5 See Table 1.3.C HAPTER 2C LASSICAL E NCRYPTION T ECHNIQUESR2.1 Plaintext, encryption algorithm, secret key, ciphertext, decryption algorithm.2.2 Permutation and substitution.2.3 One key for symmetric ciphers, two keys for asymmetric ciphers.2.4 A stream cipher is one that encrypts a digital data stream one bit or one byte at atime. A block cipher is one in which a block of plaintext is treated as a whole and used to produce a ciphertext block of equal length.2.5 Cryptanalysis and brute force.2.6 Ciphertext only. One possible attack under these circumstances is the brute-forceapproach of trying all possible keys. If the key space is very large, this becomesimpractical. Thus, the opponent must rely on an analysis of the ciphertext itself, generally applying various statistical tests to it. Known plaintext. The analyst may be able to capture one or more plaintext messages as well as their encryptions.With this knowledge, the analyst may be able to deduce the key on the basis of the way in which the known plaintext is transformed. Chosen plaintext. If the analyst is able to choose the messages to encrypt, the analyst may deliberately pickpatterns that can be expected to reveal the structure of the key.2.7 An encryption scheme is unconditionally secure if the ciphertext generated by thescheme does not contain enough information to determine uniquely thecorresponding plaintext, no matter how much ciphertext is available. Anencryption scheme is said to be computationally secure if: (1) the cost of breaking the cipher exceeds the value of the encrypted information, and (2) the timerequired to break the cipher exceeds the useful lifetime of the information.2.8 The Caesar cipher involves replacing each letter of the alphabet with the letterstanding k places further down the alphabet, for k in the range 1 through 25.2.9 A monoalphabetic substitution cipher maps a plaintext alphabet to a ciphertextalphabet, so that each letter of the plaintext alphabet maps to a single unique letter of the ciphertext alphabet.2.10 The Playfair algorithm is based on the use of a 5 5 matrix of letters constructedusing a keyword. Plaintext is encrypted two letters at a time using this matrix.2.11 A polyalphabetic substitution cipher uses a separate monoalphabetic substitutioncipher for each successive letter of plaintext, depending on a key.2.12 1. There is the practical problem of making large quantities of random keys. Anyheavily used system might require millions of random characters on a regularbasis. Supplying truly random characters in this volume is a significant task.2. Even more daunting is the problem of key distribution and protection. For everymessage to be sent, a key of equal length is needed by both sender and receiver.Thus, a mammoth key distribution problem exists.2.13 A transposition cipher involves a permutation of the plaintext letters.2.14 Steganography involves concealing the existence of a message.2.1 a. No. A change in the value of b shifts the relationship between plaintext lettersand ciphertext letters to the left or right uniformly, so that if the mapping isone-to-one it remains one-to-one.b. 2, 4, 6, 8, 10, 12, 13, 14, 16, 18, 20, 22, 24. Any value of a larger than 25 isequivalent to a mod 26.c. The values of a and 26 must have no common positive integer factor other than1. This is equivalent to saying that a and 26 are relatively prime, or that thegreatest common divisor of a and 26 is 1. To see this, first note that E(a, p) = E(a,q) (0 ≤ p≤ q < 26) if and only if a(p–q) is divisible by 26. 1. Suppose that a and26 are relatively prime. Then, a(p–q) is not divisible by 26, because there is noway to reduce the fraction a/26 and (p–q) is less than 26. 2. Suppose that a and26 have a common factor k > 1. Then E(a, p) = E(a, q), if q = p + m/k≠ p.2.2 There are 12 allowable values of a (1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25). There are 26allowable values of b, from 0 through 25). Thus the total number of distinct affine Caesar ciphers is 12 26 = 312.2.3 Assume that the most frequent plaintext letter is e and the second most frequentletter is t. Note that the numerical values are e = 4; B = 1; t = 19; U = 20. Then we have the following equations:1 = (4a + b) mod 2620 = (19a + b) mod 26Thus, 19 = 15a mod 26. By trial and error, we solve: a = 3.Then 1 = (12 + b) mod 26. By observation, b = 15.2.4 A good glass in the Bishop's hostel in the Devil's seat—twenty-one degrees andthirteen minutes—northeast and by north—main branch seventh limb east side—shoot from the left eye of the death's head— a bee line from the tree through the shot fifty feet out. (from The Gold Bug, by Edgar Allan Poe)2.5 a.The first letter t corresponds to A, the second letter h corresponds to B, e is C, sis D, and so on. Second and subsequent occurrences of a letter in the keysentence are ignored. The resultciphertext: SIDKHKDM AF HCRKIABIE SHIMC KD LFEAILAplaintext: basilisk to leviathan blake is contactb.It is a monalphabetic cipher and so easily breakable.c.The last sentence may not contain all the letters of the alphabet. If the firstsentence is used, the second and subsequent sentences may also be used untilall 26 letters are encountered.2.6The cipher refers to the words in the page of a book. The first entry, 534, refers topage 534. The second entry, C2, refers to column two. The remaining numbers are words in that column. The names DOUGLAS and BIRLSTONE are simply words that do not appear on that page. Elementary! (from The Valley of Fear, by Sir Arthur Conan Doyle)2.7 a.2 8 10 7 9 63 14 54 2 8 1056 37 1 9ISRNG BUTLF RRAFR LIDLP FTIYO NVSEE TBEHI HTETAEYHAT TUCME HRGTA IOENT TUSRU IEADR FOETO LHMETNTEDS IFWRO HUTEL EITDSb.The two matrices are used in reverse order. First, the ciphertext is laid out incolumns in the second matrix, taking into account the order dictated by thesecond memory word. Then, the contents of the second matrix are read left toright, top to bottom and laid out in columns in the first matrix, taking intoaccount the order dictated by the first memory word. The plaintext is then read left to right, top to bottom.c.Although this is a weak method, it may have use with time-sensitiveinformation and an adversary without immediate access to good cryptanalysis(e.g., tactical use). Plus it doesn't require anything more than paper and pencil,and can be easily remembered.2.8 SPUTNIK2.9 PT BOAT ONE OWE NINE LOST IN ACTION IN BLACKETT STRAIT TWOMILES SW MERESU COVE X CREW OF TWELVE X REQUEST ANYINFORMATION2.10 a.b.2.11 a. UZTBDLGZPNNWLGTGTUEROVLDBDUHFPERHWQSRZb.UZTBDLGZPNNWLGTGTUEROVLDBDUHFPERHWQSRZc. A cyclic rotation of rows and/or columns leads to equivalent substitutions. Inthis case, the matrix for part a of this problem is obtained from the matrix ofProblem 2.10a, by rotating the columns by one step and the rows by three steps.2.12 a. 25! ≈ 284b. Given any 5x5 configuration, any of the four row rotations is equivalent, for atotal of five equivalent configurations. For each of these five configurations,any of the four column rotations is equivalent. So each configuration in factrepresents 25 equivalent configurations. Thus, the total number of unique keysis 25!/25 = 24!2.13 A mixed Caesar cipher. The amount of shift is determined by the keyword, whichdetermines the placement of letters in the matrix.2.14 a. Difficulties are things that show what men are.b. Irrationally held truths may be more harmful than reasoned errors.2.15 a. We need an even number of letters, so append a "q" to the end of the message.Then convert the letters into the corresponding alphabetic positions:The calculations proceed two letters at a time. The first pair:The first two ciphertext characters are alphabetic positions 7 and 22, whichcorrespond to GV. The complete ciphertext:GVUIGVKODZYPUHEKJHUZWFZFWSJSDZMUDZMYCJQMFWWUQRKRb. We first perform a matrix inversion. Note that the determinate of theencryption matrix is (9 ⨯ 7) – (4 ⨯ 5) = 43. Using the matrix inversion formulafrom the book:Here we used the fact that (43)–1 = 23 in Z26. Once the inverse matrix has beendetermined, decryption can proceed. Source: [LEWA00].2.16 Consider the matrix K with elements k ij to consist of the set of column vectors K j,where:andThe ciphertext of the following chosen plaintext n-grams reveals the columns of K:(B, A, A, …, A, A) ↔ K1(A, B, A, …, A, A) ↔ K2:(A, A, A, …, A, B) ↔ K n2.17 a.7 ⨯ 134b.7 ⨯ 134c.134d.10 ⨯ 134e.24⨯ 132f.24⨯(132– 1) ⨯ 13g. 37648h.23530i.1572482.18 key: legleglegleplaintext: explanationciphertext: PBVWETLXOZR2.19 a.b.2.20your package ready Friday 21st room three Please destroy this immediately.2.21 y the message out in a matrix 8 letters across. Each integer in the key tellsyou which letter to choose in the corresponding row. Result:He sitteth between the cherubims. The isles may be gladthereof. As the rivers in the south.b.Quite secure. In each row there is one of eight possibilities. So if the ciphertextis 8n letters in length, then the number of possible plaintexts is 8n.c. Not very secure. Lord Peter figured it out. (from The Nine Tailors)3.1 Most symmetric block encryption algorithms in current use are based on the Feistelblock cipher structure. Therefore, a study of the Feistel structure reveals theprinciples behind these more recent ciphers.3.2 A stream cipher is one that encrypts a digital data stream one bit or one byte at atime. A block cipher is one in which a block of plaintext is treated as a whole and used to produce a ciphertext block of equal length.3.3 If a small block size, such as n = 4, is used, then the system is equivalent to aclassical substitution cipher. For small n, such systems are vulnerable to a statistical analysis of the plaintext. For a large block size, the size of the key, which is on the order of n 2n, makes the system impractical.3.4 In a product cipher, two or more basic ciphers are performed in sequence in such away that the final result or product is cryptographically stronger than any of the component ciphers.3.5 In diffusion, the statistical structure of the plaintext is dissipated into long-rangestatistics of the ciphertext. This is achieved by having each plaintext digit affect thevalue of many ciphertext digits, which is equivalent to saying that each ciphertext digit is affected by many plaintext digits. Confusion seeks to make the relationship between the statistics of the ciphertext and the value of the encryption key ascomplex as possible, again to thwart attempts to discover the key. Thus, even if the attacker can get some handle on the statistics of the ciphertext, the way in which the key was used to produce that ciphertext is so complex as to make it difficult todeduce the key. This is achieved by the use of a complex substitution algorithm. 3.6 Block size: Larger block sizes mean greater security (all other things being equal)but reduced encryption/decryption speed. Key size: Larger key size means greater security but may decrease encryption/decryption speed. Number of rounds: The essence of the Feistel cipher is that a single round offers inadequate security but that multiple rounds offer increasing security. Subkey generation algorithm:Greater complexity in this algorithm should lead to greater difficulty ofcryptanalysis. Round function: Again, greater complexity generally means greater resistance to cryptanalysis. Fast software encryption/decryption: In many cases, encryption is embedded in applications or utility functions in such a way as topreclude a hardware implementation. Accordingly, the speed of execution of the algorithm becomes a concern. Ease of analysis: Although we would like to make our algorithm as difficult as possible to cryptanalyze, there is great benefit inmaking the algorithm easy to analyze. That is, if the algorithm can be concisely and clearly explained, it is easier to analyze that algorithm for cryptanalyticvulnerabilities and therefore develop a higher level of assurance as to its strength.3.7 The S-box is a substitution function that introduces nonlinearity and adds to thecomplexity of the transformation.3.8 The avalanche effect is a property of any encryption algorithm such that a smallchange in either the plaintext or the key produces a significant change in theciphertext.3.9 Differential cryptanalysis is a technique in which chosen plaintexts with particularXOR difference patterns are encrypted. The difference patterns of the resultingciphertext provide information that can be used to determine the encryption key.Linear cryptanalysis is based on finding linear approximations to describe thetransformations performed in a block cipher.3.1 a. For an n-bit block size are 2n possible different plaintext blocks and 2n possibledifferent ciphertext blocks. For both the plaintext and ciphertext, if we treat theblock as an unsigned integer, the values are in the range 0 through 2n– 1. For amapping to be reversible, each plaintext block must map into a uniqueciphertext block. Thus, to enumerate all possible reversible mappings, the blockwith value 0 can map into anyone of 2n possible ciphertext blocks. For anygiven mapping of the block with value 0, the block with value 1 can map intoany one of 2n– 1 possible ciphertext blocks, and so on. Thus, the total numberof reversible mappings is (2n)!.b. In theory, the key length could be log2(2n)! bits. For example, assign eachmapping a number, from 1 through (2n)! and maintain a table that shows themapping for each such number. Then, the key would only require log2(2n)! bits, but we would also require this huge table. A more straightforward way todefine the key is to have the key consist of the ciphertext value for eachplaintext block, listed in sequence for plaintext blocks 0 through 2n– 1. This iswhat is suggested by Table 3.1. In this case the key size is n⨯ 2n and the hugetable is not required.3.2 Because of the key schedule, the round functions used in rounds 9 through 16 aremirror images of the round functions used in rounds 1 through 8. From this fact we see that encryption and decryption are identical. We are given a ciphertext c.Let m' = c. Ask the encryption oracle to encrypt m'. The ciphertext returned by the oracle will be the decryption of c.3.3 a.We need only determine the probability that for the remaining N – t plaintextsP i, we have E[K, P i] ≠ E[K', P i]. But E[K, P i] = E[K', P i] for all the remaining P iwith probability 1 – 1/(N–t)!.b.Without loss of generality we may assume the E[K, P i] = P i since E K(•) is takenover all permutations. It then follows that we seek the probability that apermutation on N–t objects has exactly t' fixed points, which would be theadditional t' points of agreement between E(K, •) and E(K', •). But apermutation on N–t objects with t' fixed points is equal to the number of wayst' out of N–t objects can be fixed, while the remaining N–t–t' are not fixed.Then using Problem 3.4 we have thatPr(t' additional fixed points) = ⨯Pr(no fixed points in N – t – t' objects)=We see that this reduces to the solution to part (a) when t' = N–t.3.4Let be the set of permutations on [0, 1, . . ., 2n– 1], which is referredto as the symmetric group on 2n objects, and let N = 2n. For 0 ≤ i≤ N, let A i be all mappings for which π(i) = i. It follows that |A i| = (N– 1)! and= (N–k)!. The inclusion-exclusion principle states thatPr(no fixed points in π)=== 1 – 1 + 1/2! – 1/3! + . . . + (–1)N⨯ 1/N!= e–1 +Then since e–1≈ 0.368, we find that for even small values of N, approximately37% of permutations contain no fixed points.3.53.6 Main key K = 111…111 (56 bits)Round keys K1 = K2=…= K16 = 1111..111 (48 bits)Ciphertext C = 1111…111 (64 bits)Input to the first round of decryption =LD0RD0 = RE16LE16 = IP(C) = 1111...111 (64 bits)LD0 = RD0 = 1111...111 (32 bits)Output of the first round of decryption = LD1RD1LD1 = RD0= 1111…111 (32 bits)Thus, the bits no. 1 and 16 of the output are equal to ‘1’.RD1 = LD0 F(RD0, K16)We are looking for bits no. 1 and 16 of RD1 (33 and 48 of the entire output).Based on the analysis of the permutation P, bit 1 of F(RD0, K16) comes from thefourth output of the S-box S4, and bit 16 of F(RD0, K16) comes from the second output of the S-box S3. These bits are XOR-ed with 1’s from the correspondingpositions of LD0.Inside of the function F,E(RD0) ≈ K16= 0000…000 (48 bits),and thus inputs to all eight S-boxes are equal to “000000”.Output from the S-box S4 = “0111”, and thus the fourth output is equal to ‘1’,Output from the S-box S3 = “1010”, and thus the second output is equal to ‘0’.From here, after the XOR, the bit no. 33 of the first round output is equal to ‘0’, and the bit no. 48 is equal to ‘1’.3.7 In the solution given below the following general properties of the XOR functionare used:A ⊕ 1 = A'(A ⊕ B)' = A' ⊕ B = A ⊕ B'A' ⊕ B' = A ⊕ BWhere A' = the bitwise complement of A.a. F (R n, K n+1) = 1We haveL n+1 = R n; R n+1 = L n⊕ F (R n, K n+1) = L n⊕ 1 = L n'ThusL n+2 = R n+1 = L n' ; R n+2 = L n+1 = R n'i.e., after each two rounds we obtain the bit complement of the original input,and every four rounds we obtain back the original input:L n+4 = L n+2' = L n ; R n+2 = R n+2' = R nTherefore,L16 = L0; R16 = R0An input to the inverse initial permutation is R16 L16.Therefore, the transformation computed by the modified DES can berepresented as follows:C = IP–1(SWAP(IP(M))), where SWAP is a permutation exchanging the positionof two halves of the input: SWAP(A, B) = (B, A).This function is linear (and thus also affine). Actually, this is a permutation, the product of three permutations IP, SWAP, and IP–1. This permutation ishowever different from the identity permutation.b. F (R n, K n+1) = R n'We haveL n+1 = R n; R n+1 = L n⊕ F(R n, K n+1) = L n⊕ R n'L n+2 = R n+1 = L n⊕ R n'R n+2 = L n+1⊕ F(R n+1, K n+2) = R n≈ (L n⊕ R n')' = R n⊕ L n⊕ R n'' = L nL n+3 = R n+2 = L nR n+3 = L n+2⊕ F (R n+2, K n+3) = (L n≈ R n') ⊕ L n' = R n' ⊕1 = R ni.e., after each three rounds we come back to the original input.L15 = L0; R15 = R0andL16 = R0(1)R16 = L0⊕ R0' (2)An input to the inverse initial permutation is R16 L16.A function described by (1) and (2) is affine, as bitwise complement is affine,and the other transformations are linear.The transformation computed by the modified DES can be represented asfollows:C = IP–1(FUN2(IP(M))), where FUN2(A, B) = (A ⊕ B', B).This function is affine as a product of three affine functions.In all cases decryption looks exactly the same as encryption.3.8 a. First, pass the 64-bit input through PC-1 (Table 3.4a) to produce a 56-bit result.Then perform a left circular shift separately on the two 28-bit halves. Finally,pass the 56-bit result through PC-2 (Table 3.4b) to produce the 48-bit K1.:in binary notation: 0000 1011 0000 0010 0110 01111001 1011 0100 1001 1010 0101in hexadecimal notation: 0 B 0 2 6 7 9 B 4 9 A 5b. L0, R0 are derived by passing the 64-plaintext through IP (Table 3.2a):L0 = 1100 1100 0000 0000 1100 1100 1111 1111R0 = 1111 0000 1010 1010 1111 0000 1010 1010c. The E table (Table 3.2c) expands R0 to 48 bits:E(R0) = 01110 100001 010101 010101 011110 100001 010101 010101d. A = 011100 010001 011100 110010 111000 010101 110011 110000e. (1110) = (14) = 0 (base 10) = 0000 (base 2)(1000) = (8) = 12 (base 10) = 1100 (base 2)(1110) = (14) = 2 (base 10) = 0010 (base 2)(1001) = (9) = 1 (base 10) = 0001 (base 2)(1100) = (12) = 6 (base 10) = 0110 (base 2)(1010) = (10) = 13 (base 10) = 1101 (base 2)(1001) = (9) = 5 (base 10) = 0101 (base 2)(1000) = (8) = 0 (base 10) = 0000 (base 2)f. B = 0000 1100 0010 0001 0110 1101 0101 0000g. Using Table 3.2d, P(B) = 1001 0010 0001 1100 0010 0000 1001 1100h. R1 = 0101 1110 0001 1100 1110 1100 0110 0011i. L1 = R0. The ciphertext is the concatenation of L1 and R1. Source: [MEYE82]3.9The reasoning for the Feistel cipher, as shown in Figure 3.6 applies in the case ofDES. We only have to show the effect of the IP and IP–1 functions. For encryption, the input to the final IP–1 is RE16|| LE16. The output of that stage is the ciphertext.On decryption, the first step is to take the ciphertext and pass it through IP. Because IP is the inverse of IP–1, the result of this operation is just RE16|| LE16, which isequivalent to LD0|| RD0. Then, we follow the same reasoning as with the Feistel cipher to reach a point where LE0 = RD16 and RE0 = LD16. Decryption is completed by passing LD0|| RD0 through IP–1. Again, because IP is the inverse of IP–1, passing the plaintext through IP as the first step of encryption yields LD0|| RD0, thusshowing that decryption is the inverse of encryption.3.10a.Let us work this from the inside out.T16(L15|| R15) = L16|| R16T17(L16|| R16) = R16|| L16IP [IP–1 (R16|| L16)] = R16|| L16TD1(R16|| L16) = R15|| L15b.T16(L15|| R15) = L16|| R16IP [IP–1 (L16|| R16)] = L16|| R16TD1(R16 || L16) = R16|| L16 f(R16, K16)≠ L15|| R153.11PC-1 is essentially the same as IP with every eighth bit eliminated. This wouldenable a similar type of implementation. Beyond that, there does not appear to be any particular cryptographic significance.3.13a.The equality in the hint can be shown by listing all 1-bit possibilities:We also need the equality A ⊕ B = A' ⊕ B', which is easily seen to be true. Now, consider the two XOR operations in Figure 3.8. If the plaintext and key for anencryption are complemented, then the inputs to the first XOR are alsocomplemented. The output, then, is the same as for the uncomplementedinputs. Further down, we see that only one of the two inputs to the secondXOR is complemented, therefore, the output is the complement of the outputthat would be generated by uncomplemented inputs.b.In a chosen plaintext attack, if for chosen plaintext X, the analyst can obtain Y1= E[K, X] and Y2 = E[K, X'], then an exhaustive key search requires only 255rather than 256 encryptions. To see this, note that (Y2)' = E[K', X]. Now, pick atest value of the key T and perform E[T, X]. If the result is Y1, then we knowthat T is the correct key. If the result is (Y2)', then we know that T' is the correctkey. If neither result appears, then we have eliminated two possible keys withone encryption.3.14 The result can be demonstrated by tracing through the way in which the bits areused. An easy, but not necessary, way to see this is to number the 64 bits of the key as follows (read each vertical column of 2 digits as a number):2113355-1025554-0214434-1123334-0012343-2021453-0202435-0110454- 1031975-1176107-2423401-7632789-7452553-0858846-6836043-9495226-The first bit of the key is identified as 21, the second as 10, the third as 13, and so on.The eight bits that are not used in the calculation are unnumbered. The numbers 01 through 28 and 30 through 57 are used. The reason for this assignment is to clarify the way in which the subkeys are chosen. With this assignment, the subkey for the first iteration contains 48 bits, 01 through 24 and 30 through 53, in their naturalnumerical order. It is easy at this point to see that the first 24 bits of each subkey will always be from the bits designated 01 through 28, and the second 24 bits of each subkey will always be from the bits designated 30 through 57.3.15 For 1 ≤ i ≤ 128, take c i∈ {0, 1}128 to be the string containing a 1 in position i andthen zeros elsewhere. Obtain the decryption of these 128 ciphertexts. Let m1,m2, . . . , m128 be the corresponding plaintexts. Now, given any ciphertext c which does not consist of all zeros, there is a unique nonempty subset of the c i’s which we can XOR together to obtain c. Let I(c) ⊆ {1, 2, . . . , 128} denote this subset.ObserveThus, we obtain the plaintext of c by computing . Let 0 be the all-zerostring. Note that 0 = 0⊕0. From this we obtain E(0) = E(0⊕0) = E(0) ⊕ E(0) = 0.Thus, the plaintext of c = 0 is m = 0. Hence we can decrypt every c ∈ {0, 1}128.3.16a. This adds nothing to the security of the algorithm. There is a one-to-onereversible relationship between the 10-bit key and the output of the P10function. If we consider the output of the P10 function as a new key, then thereare still 210 different unique keys.b. By the same reasoning as (a), this adds nothing to the security of the algorithm.3.17s = wxyz + wxy + wyz + wy + wz + yz + w + x + zt = wxz + wyz + wz + xz + yz + w + y3.18OK4.1 A group is a set of elements that is closed under a binary operation and that isassociative and that includes an identity element and an inverse element.4.2 A ring is a set of elements that is closed under two binary operations, addition andsubtraction, with the following: the addition operation is a group that iscommutative; the multiplication operation is associative and is distributive over the addition operation.C HAPTER 4F INITE F IELDS。

密码算法国际标准

密码算法国际标准
以下是一些常见的密码算法国际标准：
1. 对称密码算法：
* 数据加密标准（DES）：ISO/IEC 18033-3标准，ITU-T X.1035标准。

* 高级数据加密标准（AES）：ISO/IEC 18033-3和ISO/IEC 19772标准，ITU-T X.1035和ITU-T X.1036标准。

* 国际数据加密算法（IDEA）：ISO/IEC 18033-3和ISO/IEC 9797-1标准。

2. 非对称密码算法：
* RSA密码算法：RSA密码算法是美国麻省理工学院的Rivest、Shamir和Adleman这3位学者于1978年提出的。

RSA密码算法方案是唯一被广泛接受并实现的通用公开密码算法，它能够抵抗目前为止已知的绝大多数密码攻击，已经成为公钥密码的国际标准。

它是第一个既能用于数据加密，又能通用数字签名的公开密钥密码算法。

在Internet中，电子邮件收、发的加密和数字签名软件PGP就采用了RSA密码算法。

人工智能国外经典课程

人工智能国外经典课程人工智能是当今科技领域的热门话题，国外有许多经典课程涵盖了人工智能的各个领域和技术。

下面我将列举一些国外经典的人工智能课程，这些课程涵盖了人工智能的基础理论、算法和应用等方面。

1. Stanford University - CS229: Machine Learning这门课程由斯坦福大学的吴恩达教授主讲，是机器学习领域的经典之作。

课程内容包括监督学习、无监督学习、强化学习等各种机器学习算法和方法。

2. Massachusetts Institute of Technology - 6.034: Artificial Intelligence这门课程由麻省理工学院的Patrick Henry Winston教授主讲，涵盖了人工智能的基础知识、推理和规划、感知和学习等方面。

课程通过讲解经典的人工智能方法和案例，帮助学生理解人工智能的核心概念和技术。

3. University of California, Berkeley - CS188: Introduction to Artificial Intelligence这门课程是加州大学伯克利分校的经典人工智能课程，内容包括搜索、规划、机器学习、自然语言处理等方面。

课程通过理论讲解和实践项目，培养学生的人工智能编程能力和解决实际问题的能力。

4. Carnegie Mellon University - 10-701: Introduction to这门课程由卡内基梅隆大学的Tom Mitchell教授主讲，介绍了机器学习的基本理论和算法。

课程内容包括统计学习理论、监督学习和无监督学习方法等，旨在帮助学生理解机器学习的原理和应用。

5. University of Washington - CSE 446: Machine Learning这门课程由华盛顿大学的Pedro Domingos教授主讲，涵盖了机器学习的基本概念、算法和应用。

stanford nlp 用法-概述说明以及解释

stanford nlp 用法-概述说明以及解释1.引言1.1 概述概述部分旨在介绍本文的主题——Stanford NLP，并提供一些背景信息。

Stanford NLP是由斯坦福大学自然语言处理（Natural Language Processing，简称NLP）小组开发的一套自然语言处理工具包。

它提供了丰富的功能和算法，能够帮助研究人员和开发者进行文本分析、语言理解和信息提取等任务。

自然语言处理是人工智能领域的一个重要分支，涉及了对人类语言的理解和生成。

随着互联网和数字化时代的到来，海量的文本数据成为了研究和应用的宝贵资源。

然而，人类语言的复杂性和多样性给文本处理带来了挑战。

Stanford NLP应运而生，旨在利用先进的技术和算法帮助研究人员和开发者解决这些挑战。

在本文中，我们将探讨Stanford NLP的主要功能和用途。

首先，我们将介绍Stanford NLP的简介，包括其目标和诞生背景。

然后，我们将详细讨论Stanford NLP在各个领域的应用，包括文本分类、命名实体识别、情感分析等。

最后，我们将总结Stanford NLP的应用优势，并展望其未来的发展潜力。

在阅读本文之前，读者需要对自然语言处理的基本概念有一定的了解，同时，具备一定的编程和机器学习知识也将有助于更好地理解本文。

本文将从大的框架上介绍Stanford NLP的用法，并提供一些具体的实例和应用场景，以帮助读者更好地理解和使用Stanford NLP。

接下来，让我们深入探索Stanford NLP的世界，了解它的用途和优势，并展望它在自然语言处理领域的未来发展。

文章结构部分的内容可以如下所示：1.2 文章结构本文主要分为引言、正文和结论三个部分。

引言部分（Section 1）首先概述了本文的主题和目的，然后简要介绍了Stanford NLP的概念及其在自然语言处理领域的重要性。

接下来，给出了本文的整体结构安排。

正文部分（Section 2）详细介绍了Stanford NLP的应用。

斯坦福大学公开课：机器学习课程note1翻译分析解析

CS229 Lecture notesAndrew Ng监督式学习让我们开始先讨论几个关于监督式学习的问题。

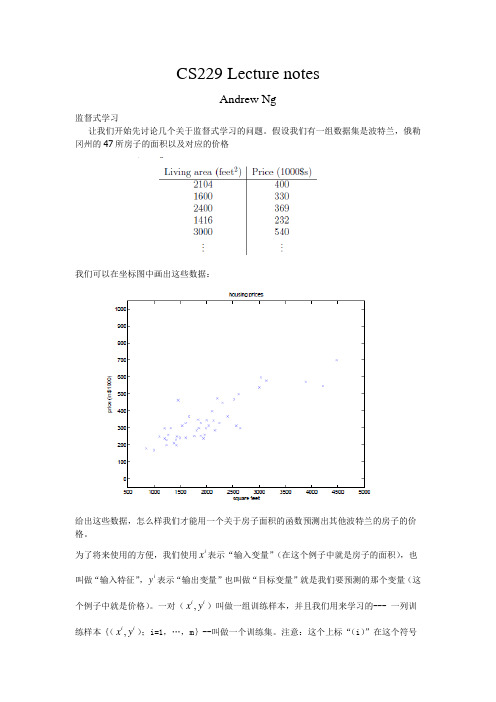
假设我们有一组数据集是波特兰，俄勒冈州的47所房子的面积以及对应的价格我们可以在坐标图中画出这些数据：给出这些数据，怎么样我们才能用一个关于房子面积的函数预测出其他波特兰的房子的价格。

为了将来使用的方便，我们使用i x表示“输入变量”（在这个例子中就是房子的面积），也叫做“输入特征”，i y表示“输出变量”也叫做“目标变量”就是我们要预测的那个变量（这x y）叫做一组训练样本，并且我们用来学习的--- 一列训个例子中就是价格）。

一对（,i ix y）；i=1，…，m｝--叫做一个训练集。

注意：这个上标“（i）”在这个符号练样本｛（,i i表示法中就是训练集中的索引项，并不是表示次幂的概念。

我们会使用χ表示输入变量的定义域，使用表示输出变量的值域。

在这个例子中χ=Y=R为了更正式的描述我们这个预测问题，我们的目标是给出一个训练集，去学习产生一个函数h ：X → Y 因此h(x)是一个好的预测对于近似的y 。

由于历史性的原因，这个函数h 被叫做“假设”。

预测过程的顺序图示如下：当我们预测的目标变量是连续的，就像在我们例子中的房子的价格，我们叫这一类的学习问题为“回归问题”，当我们预测的目标变量仅仅只能取到一部分的离散的值（就像如果给出一个居住面积，让你去预测这个是房子还是公寓，等等），我们叫这一类的问题是“分类问题”PART ILinear Reression为了使我们的房子问题更加有趣，我们假设我们知道每个房子中有几间卧室：在这里，x 是一个二维的向量属于2R 。

例如，1i x 就是训练集中第i 个房子的居住面积， 2i x 是训练集中第i 个房子的卧室数量。

（通常情况下，当设计一个学习问题的时候，这些输入变量是由你决定去选择哪些，因此如果你是在Portland 收集房子的数据，你可能会决定包含其他的特征，比如房子是否带有壁炉，这个洗澡间的数量等等。

斯坦福密码课程05.3-integrity-cbc-mac-and-nmac

there exists an eff. adversary B s.t.:
AdvPRF[A, FECBC] AdvPRP[B, F] + 2 q2 / |X|
AdvPRF[A, FNMAC] q⋅L⋅AdvPRF[B, F] + q2 / 2|K|
CBC-MAC is secure as long as q << |X|1/2 NMAC is secure as long as q << |K|1/2
cascade
m[0] m[1] m[3]
(nested MAC)
m[4]
k
>
F
>
F
>
F
>
F
t
t ll fpad
Let F: K × X ⟶ K be a PRF
k1
>
tag
F
Define new PRF FNMAC : K2 × X≤L ⟶ K
Dan Boneh
Why the last encryption step in ECBC-MAC and NMAC?
obtain ( mi, ti ) for i = 1 ,…, |Y|1/2
step 2: find a collision tu = tv for u≠v (one exists w.h.p by b-day paradox) step 3: choose some w and query for t := FBIG(k, mullw) step 4: output forgery (mvllw, t). Indeed t := FBIG(k, mvllw)
• Then both PRFs (ECBC and NMAC) have the following extension property: ∀x,y,w: FBIG(k, x) = FBIG(k, y) ⇒ FBIG(k, xllw) = FBIG(k, yllw)

密码学参考书

密码学参考书
以下是密码学相关的参考书：
1.《Real-World Cryptography》：这本书从名字可以大概了解其主要内容，是一本注重应用的书，理论方面也有一定的深度，并且非常全面。

2.《A Graduate Course in Applied Cryptography》：这本书是Coursera 上非常火的斯坦福密码学课程的主讲老师写的，目前还在更新，可以直接在 A Graduate Course in Applied Cryptography下载。

3.《Introduction To Modern Cryptography (Jonathan Katz, Yehuda Lindell)》：2012年刚出了第三版，有时间可以看一下。

4.《古今密码学趣谈》：这本书介绍了密码学的历史和基础知识，适合初学者入门。

5.《密码学原理与实践》：这本书涵盖了对称、公钥两个领域的内容，对密码学有较全面的介绍。

6.《密码编码学与网络安全》：这本书介绍了密码编码学和网络安全的基本原理和技术，包括加密算法、数字签名、身份认证等。

7.《椭圆曲线密码学导论》：这本书介绍了椭圆曲线密码学的基本原理和应用，是密码学领域的经典著作之一。

8.《密码学家的工具箱》：这本书涵盖了密码学中常用的工具和技术，包括对称密码与公钥密码、单项散列函数、消息认证码和伪随机数生成器等。

以上书籍可以作为学习密码学的参考书，选择适合自己的书籍深入学习，掌握密码学的原理和应用。

1。

网络安全密码技术全文-移动互联网-

空间复杂性和时间复杂性往往是可以相互转换的。比如，可以预算某些明文和密文对，分析时只需使用查询即可，这样计算的时间就转换成了存储空间。
假如T(n)=O(nc)（c>0），那么称该算法运算的时间是多项式阶的，假如T(n)=O(ap(n))（a>0），则称该算法运算的时间是指数阶的。其中P(n)是n的一个多项式。对于指数阶的运算时间算法，适当增大n，计算将变成不可能。因此，一般认为，如果破译一个密码体制所需的时间是指数阶的，则它在计算上是安全的，因而实际上也是安全的。
2．1．2 密码技术基础
1．基本概念
密码技术（或密码学）是研究通信安全保密的一门学科，它包含两个相对独立的分支：密码编码学和密码分析学。
密码编码学是研究把信息（明文）变换成没有密钥就不能解读或很难解读的密文的方法，从事此行的称为密码编码者。
密码分析学是研究分析破译密码的方法，从事此行的称为密码分析者。
合，即：K×M→C，（m，k） Ek(m)；
5
解密算法D，由加密密钥控制的加密变换的集
合，即：K×C→M，（c，k） Dk(c)。对m∈M，k∈K，有Dk(Ek(m))=m。以上描述的五元
组（M，C，K，E，D）就称为一个密码体制。
•一个完整的保密通信系统是由一个密码体制、一个信源、一个信宿、一个攻击者或密码分析者构成。
可证明安全性和计算安全性统称为实际安全性。
什么是计算复杂性理论？
计算复杂性理论是密码安全性理论的基础，它为分析不同密码技术和算法的“复杂性”提供了一种方法，它对不同的密码算法和技术进行比较，从而给出问题求解困难性的数量指标，并确定它们的安全性。
（1）密码分析所需的计算量则是密码体制安全性的生命指标。如果用n 表示问题的大小（或输入的长度），则计算复杂性可以用两个参数来表示：运算所需的时间T和存储空间S。它们都是n的函数，表示为： T(n)和S(n)，也分别称为空间复杂性和时间复杂性。

Experimental quantum cryptography

1 2
2
approach to implement quantum key distribution 19] (making use of EPR and Bell's theorem), but a simpli ed | and no less secure | version of his scheme is shown in 10] to be equivalent to the idealized quantum key distribution protocol originally put forward by Bennett and Brassard in 1984 3]. Let us also mention that Bennett, Brassard, and Crepeau have developed practical quantum protocols to achieve oblivious transfer, bit commitment and coin-tossing 8]. See also 14]. The principle of quantum cryptography has been described in major popular magazines such as Scienti c American 25], The Economist 20], New Scientist 18] and Science News 23]. In New Scientist , Deutsch wrote that \Alan Turing's theoretical
Francois Bessette z
Gilles Brassard {
September 1991

密码培训教程

对称密码
1. 对称密码：加密密钥与解密密钥相同。 2. 优点是：
• 安全性高 • 加解密速度快 3. 缺点是： • 随着网络规模的扩大，密钥管理成为一
个难点；
• 无法解决消息确认问题；（不过可以采用一些业务方法弥补，如：商户号终端号等方式但对内部人员无效）
• 缺乏自动检测密钥泄露的能力。举例：21.80.66.254 /usr/btssrc/twb/encrypt
非对称密码
1. 非对称密码：加密密钥与解密密钥不同，而且解密密钥不能根据加密密钥计算出来。
2. 优点是：不需要安全信道来传送密钥。
3. 缺点是：算法复杂，加解密速度慢，一般比单钥密码慢1000倍。
攻击分类
被动攻击
主动攻击
窃听获取消息内容流量分析
中断
修改
伪造
破坏可用性破坏完整性破坏真实性
• 传统密码学的缺陷： 1、受限制，只能在一个组织内使用。大家必须知道相应的加解密算法。 2、对人要求过高，一旦一个用户离开组织就会使保密荡然无存。（这就是为什么风语者中：为什么要保护密码员，为什么当密码员被抓的时候，宁可杀死他也不能落到敌人手里的原因。） 3、受限制的密码算法不可能进行质量控制或者标准化。
2. 保证交易信息在传输、交换过程中的完整性。 3. 安全的密钥管理。这是保证上述两点的必要
条件。
银行网络解决之道
• 建立基于硬件加密设备的安全体系，是解决银行卡网络系统安全的有效办法。
• 现在的银行卡网络安全系统采用的是基于DES/3DES算法的对称密码体制。
DES算法
• DES算法来自IBM。
加密方式:软件加密
• 缺点Байду номын сангаас安全性差、速度慢、造价高。

斯坦福密码课程sit08.4-odds-and-ends

is negligible.
Dan Boneh
Example 1: the trivial construction
Let (E,D) be a secure PRP, E: K × X ⟶ X .
• The trivial tweakable construction:
(suppose K = X)
Dan Boneh
sector 1 PRP(k, ⋅) sector 1
sector 2 PRP(k, ⋅) sector 2
sector 3 PRP(k, ⋅) sector 3
Problem: sector 1 and sector 3 may have same content • Leaks same information as ECB mode Can we do better?
Dan Boneh
End of Segment
Dan Boneh
Disk encryption using XTS
sector # t:
block 1 block 2 block n
tweak: (t,1)
tweak: (t,2)
tweak: (t,n)
• note: block-level PRP, not sector-level PRP. • Popular in disk encryption products: Mac OS X-Lion, TrueCrypt, BestCrypt, …
x Yes, it is secure
c
No: E(k, (t,1), P(t,2)) ⨁ E(k, (t,2), P(t,1)) = P(t,1) ⨁ P(t,2) No: E(k, (t,1), P(t,1)) ⨁ E(k, (t,2), P(t,2)) = P(t,1) ⨁ P(t,2) No: E(k, (t,1), P(t,1)) ⨁ E(k, (t,2), P(t,2)) = 0

密码算法与应用基础

11
Playfair cipher
5×5变换矩阵: I与J视为同一字符
CRYPT
OGAHB
D E F I K (cryptography)
LMNQS
UVWXZ
加密规则:按成对字母加密成对反复字母加分隔符(如x)
balloon ba lx lo on 同行取右边: rt YC 同列取下边:fw NY 其他取交叉:ly NC, GK BE
19
Transposition
换位密码把明文按列写入,按行读出密钥包括3方面信息: 行宽,列高,读出顺序
key:
4312567
plaintext: a t t a c k p
ostpone
duntilt
woamxyz
ciphertext:TTNAAPTMTSUOAODWCOIXPETZ
完全保存字符旳统计信息使用多轮加密可提升安全性
9
பைடு நூலகம்onoalphabetic cipher
Caesar cipher E(p) = (p+3) mod 26 abcdefghijklmnopqrstuvwxyz
DEFGHIJKLMNOPQRSTUVWXYZABC 例子: crypt => FUBSW 任意旳单表替代密码 abcdefghijklmnopqrstuvwxyz
22
Feistel 构造图
Institute of Computer Science & Technology, Peking University
23
Feistel构造定义
加密: Li = Ri-1; Ri = Li-1F(Ri-1,Ki) 解密: Ri-1 = Li

无需记忆的密码系统问世让黑客束手无策

无需记忆的密码系统问世让黑客束手无策
无需记忆的密码系统问世让黑客束手无策
问题是即使是世界上最安全的密码你也不得不记住它，而且如果你能记住它，那就意味着一名电脑黑客或者是一名法官就能说服你把它交出来。

但是来自斯坦福大学、西北大学和斯坦福国际研究所的研究人员们在Hristo Bojinov的带领下已经研制出一种程序可以让你在甚至不了解密码的情况下进行输入。

科学家设计的游戏能让你无意之中记住密码序列
它利用的事实上就是你在无意中所记忆的一些事情，即使输入密码靠的也是它。

它或许会耗费你一段时间来重新创建准确的键盘布局，但是你能快速输入并且毫不迟疑。

同样的，研究人员认为通过一个名为“隐性学习”的过程，你应该能够“了解”一个你无法写出或者背诵的密码。

为了演示这一过程，他们开发了一种游戏，使用者必须连续的敲击键盘并且精确定时，它并不像“劲爆热舞”和“吉他英雄”这样的普通节奏游戏。

在研究人员的游戏当中，使用者会获得半随机的序列，其中之一在这个训练项目或者游戏当中多次重复出现，这就是他们的“密码”。

两个周以后，当使用者再次玩这个游戏的时候，相比随机的序列他们会更好的准确记录他们的密码序列。

改善的并不多只有10%-15%，但是足够使它稳定并且可察觉。

然而使用者甚至没有注意到他们正在输入一个密码，而且或许甚至并未
它对于每日密码使用或许并不实用，但是它仍然是有趣的研究，它表明我们的密码或许不一定是一组简单的字母数字序列或者生物识别。

Bojinov的发现将会在下个月的高级计算机系统学会安全讨论会上展示，但是你可以从他的网站阅读到这篇论文。

你可以在这里玩一下游戏，但是你不会像研究的参与者一样获得报酬。