2.3 重要：MATLAB常微分方程(组)的数值解法

合集下载

重要：MATLAB常微分方程(组)数值解法

Matlab常微分方程求解问题分类
边值问题：
初值问题：
• 定解附加条件在自变量的一端
• 一般形式为： y' f (x, y)
y(a)
y0
• 初值问题的数值解法一般采用步进法，如 Runge-Kutta法
➢ 在自变量两端均给定附加条件
y' f (x, y)
➢ 一般形式：y(a)y1, y(b)y2
1.根据常微分方程要求的求解精度与速度要求
求解初值问题：
y
'
y
2x y
y ( 0 ) 1
(0x1)
比较ode45和ode23的求解精度和速度
ode45和ode23的比较-1
function xODE clear all clc
format long
y0 = 1; [x1,y1] = ode45(@f,[0,1],y0); [x2,y2] = ode23(@f,[0,1],y0); plot(x1,y1,'k-',x2,y2,'b--') xlabel('x') ylabel('y')
rD = k(3)*C(2)-k(5)*C(4);
rE = k(4)*C(3)+k(5)*C(4);
% Mass balances dCdt = [rA; rB; rC; rD; rE];
三个串联的CSTR等温反应器（例4-3）
function IsothermCSTRs clear all clc CA0 = 1.8; % kmol/m^3 CA10 = 0.4; % kmol/m^3 CA20 = 0.2; % kmol/m^3 CA30 = 0.1; % kmol/m^3 k = 0.5; % 1/min tau = 2; stoptime = 2.9; % min [t,y] = ode45(@Equations,[0 stoptime],[CA10 CA20 CA30],[],k,CA0,tau); disp(' Results:') disp(' t CA1 CA2 CA3') disp([t,y]) plot(t,y(:,1),'k--',t,y(:,2),'b:',t,y(:,3),'r-') legend('CA_1','CA_2','CA_3') xlabel('Time (min)') ylabel('Concentration') % -----------------------------------------------------------------function dydt = Equations(t,y,k,CA0,tau) CA1 = y(1); CA2 = y(2); CA3 = y(3); dCA1dt = (CA0-CA1)/tau - k*CA1; dCA2dt = (CA1-CA2)/tau - k*CA2; dCA3dt = (CA2-CA3)/tau - k*CA3; dydt = [dCA1dt; dCA2dt; dCA3dt];

MATLAB求解常微分方程数值解

MATLAB求解常微分方程数值解利用MATLAB求解常微分方程数值解1.内容简介把《高等工程数学》看了一遍，增加对数学内容的了解，对其中数值解法比较感兴趣，这大概是因为在其它各方面的学习和研究中经常会遇到数值解法的问题。

理解模型然后列出微分方程，却对着方程无从下手，无法得出精确结果实在是让人难受的一件事情。

实际问题中更多遇到的是利用数值法求解偏微分方程问题，但考虑到先从常微分方程下手更为简单有效率，所以本文只研究常微分方程的数值解法。

把一个工程实际问题弄出精确结果远比弄清楚各种细枝末节更有意思，因此文章中不追求非常严格地证明，而是偏向如何利用工具实际求解出常微分方程的数值解，力求将课程上所学的知识真正地运用到实际方程的求解中去，在以后遇到微分方程的时候能够熟练运用MATLAB得到能够在工程上运用的结果。

文中求解过程中用到MATLAB进行数值求解，主要目的是弄清楚各个函数本质上是如何对常1微分方程进行求解的，对各种方法进行MATLAB 编程求解，并将求得的数值解与精确解对比，其中源程序在附录中。

最后考察MATLAB中各个函数的适用范围，当遇到实际工程问题时能够正确地得到问题的数值解。

2.Euler Method(欧拉法)求解Euler法求解常微分方程主要包括3种形式，即显式Euler法、隐式Euler法、梯形公式法，本节内容分别介绍这3种方法的具体内容，并在最后对3种方法精度进行对比，讨论Euler法的实用性。

本节考虑实际初值问题使用解析法，对方程两边同乘以得到下式两边同时求积分并采用分部积分得到解析2解：本节后面将对此方程进行求解，并与精确解进行对比，分析Euler的可行性。

2.1.显式Euler法和隐式Euler法显式和隐式Euler法都属于一阶方法，显式Euler法的迭代公式简单，如下所示：对过上述公式对式进行迭代，其中步长3图2.1 显式Euler法精确解和数值解图像从图2.1中可以看出，显式Euler法在斜率很大的时候存在非常大的误差。

MATLAB常微分方程的数值解法

MATLAB常微分⽅程的数值解法MATLAB常微分⽅程的数值解法⼀、实验⽬的科学技术中常常要求解常微分⽅程的定解问题，所谓数值解法就是求未知函数在⼀系列离散点处的近似值。

⼆、实验原理三、实验程序1. 尤拉公式程序四、实验内容选⼀可求解的常微分⽅程的定解问题，分别⽤以上1, 4两种⽅法求出未知函数在节点处的近似值，并对所求结果与分析解的（数值或图形）结果进⾏⽐较。

五、解答1. 程序求解初值问题取n=10源程序：euler23.m:function [A1,A2,B1,B2,C1,C2]=euler23(a,b,n,y0)%欧拉法解⼀阶常微分⽅程%初始条件y0h = (b-a)/n; %步长h%区域的左边界a%区域的右边界bx = a:h:b;m=length(x);%前向欧拉法y = y0;for i=2:my(i)=y(i-1)+h*oula(x(i-1),y(i-1));A1(i)=x(i);A2(i)=y(i);endplot(x,y,'r-');hold on;%改进欧拉法y = y0;for i=2:my(i)=y(i-1)+h/2*( oula(x(i-1),y(i-1))+oula(x(i),y(i-1))+h*(oula(x(i-1),x(i-1))));B1(i)=x(i);B2(i)=y(i);endplot(x,y,'m-');hold on;%欧拉两步公式y=y0;y(2)=y(1)+h*oula(x(1),y(1));for i=2:m-1y(i+1)=y(i-1)+2*h*oula(x(i),y(i));C1(i)=x(i);C2(i)=y(i);endplot(x,y,'b-');hold on;%精确解⽤作图xx = x;f = dsolve('Dy=-3*y+8*x-7','y(0)=1','x');%求出解析解y = subs(f,xx); %将xx代⼊解析解，得到解析解对应的数值plot(xx,y,'k--');legend('前向欧拉法','改进欧拉法','欧拉两步法','解析解');oula.m:function f=oula(x,y)f=-3*y+8*x-7;2. 运算结果A1,A2为前向欧拉法在节点处的近似值，B1,B2为改进的欧拉法在节点处的近似值，C1,C2为欧拉公式法在节点处的近似值。

MATLAB应用第8章常微分方程的数值求解

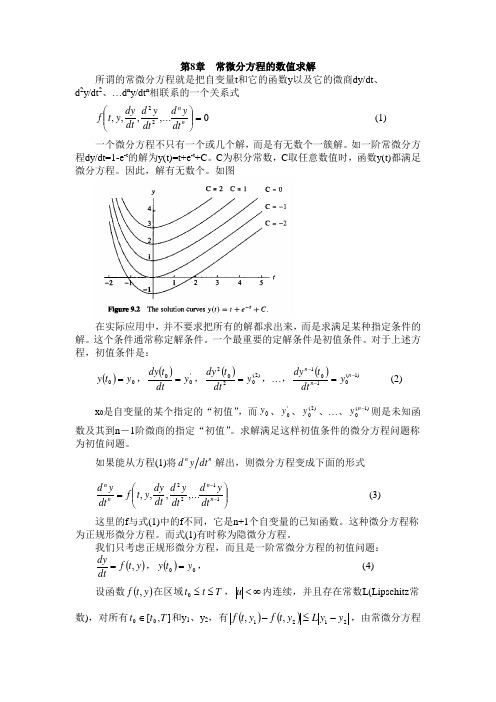
第8章常微分方程的数值求解所谓的常微分方程就是把自变量t 和它的函数y 以及它的微商dy/dt 、d 2y/dt 2、…d n y/dt n 相联系的一个关系式0,...,,,22=⎪⎪⎭⎫ ⎝⎛n n dt y d dt y d dt dy y t f (1) 一个微分方程不只有一个或几个解，而是有无数个一簇解。

如一阶常微分方程dy/dt=1-e -t 的解为y(t)=t+e -t +C 。

C 为积分常数，C 取任意数值时，函数y(t)都满足微分方程。

因此，解有无数个。

如图在实际应用中，并不要求把所有的解都求出来，而是求满足某种指定条件的解。

这个条件通常称定解条件。

一个最重要的定解条件是初值条件。

对于上述方程，初值条件是：()00y t y =，()'00y dt t dy =，())2(0202y dt t dy =，…，())1(0101---=n n n y dt t dy (2) x 0是自变量的某个指定的“初值”，而0y 、'0y 、)2(0y 、…、)1(0-n y 则是未知函数及其到n －1阶微商的指定“初值”。

求解满足这样初值条件的微分方程问题称为初值问题。

如果能从方程(1)将n n dt y d 解出，则微分方程变成下面的形式⎪⎪⎭⎫ ⎝⎛=--1122,...,,,n n n n dt y d dt y d dt dy y t f dt y d (3) 这里的f 与式(1)中的f 不同，它是n+1个自变量的已知函数。

这种微分方程称为正规形微分方程。

而式(1)有时称为隐微分方程。

我们只考虑正规形微分方程，而且是一阶常微分方程的初值问题： ()y t f dtdy,=，()00y t y =， (4) 设函数()y t f ,在区域T t t ≤≤0，∞<u 内连续，并且存在常数L(Lipschitz 常数)，对所有],[00T t t ∈和y 1、y 2，有()()2121,,y y L y t f y t f -≤-，由常微分方程理论得知，初值问题(4)在区间[t 0, T]有唯一解，且连续可微。

matlab_常微分方程数值解法

d2x 2x2 0
dt 2
简朴问题可以求得解析解，多数实际问题靠数值求解。
第4页
一阶常微分方程(ODE )初值问题： ODE ：Ordinary Differential Equation
dy
f
(x,
y)
dx
x0 x xn
y(x0 ) y0
数值解法就是求y(x)在某些分立旳节点 xn 上旳近似值 yn，用以近似y(xn)
x0
y0
x1 f y(x), x dx
x0
x2 f y(x), x dx
x1
y(x1) f y(x1), x1 h
第17页
同样，在[x0,xn+1] ，积分采用矩形近似，得：
y(xn1) y0
f xn1
x0
y(x), x dx
y(xn ) f y(xn ), xn h
yn y(xn )
第5页
2、欧拉近似办法
2.1 简朴欧拉(L.Euler, 1707-1783)办法。
dy
dx
f
(y, x)
y(x0 ) y0
欧拉数值算法就是由初值通过递推求解，递推求解
就是从初值开始，后一种函数值由前一种函数值得到。核心是构造递推公式。
y0 y1 y2 yn
第6页
i 1,2,...
第36页
没有一种算法可以有效地解决所有旳 ODE 问题，因此 MATLAB 提供了多种ODE函数。
函数 ODE类
特点
阐明
型
ode45
非刚性单步法；4，5 阶 R-K 措施；合计大部分场合旳首选措施
截断误差为 (△x)3
ode23
非刚性单步法；2，3 阶 R-K 措施；合计使用于精度较低旳情形

matlab数值求解常微分方程快速方法

MATLAB是一种用于科学计算和工程应用的高级编程语言和交互式环境。

它在数学建模、模拟和分析等方面有着广泛的应用。

在MATLAB 中，常微分方程的数值求解是一个常见的应用场景。

在实际工程问题中，通常需要对常微分方程进行数值求解来模拟系统的动态行为。

本文将介绍MATLAB中对常微分方程进行数值求解的快速方法。

1. 基本概念在MATLAB中，可以使用ode45函数来对常微分方程进行数值求解。

ode45是一种常用的Runge-Kutta法，它可以自适应地选取步长，并且具有较高的数值精度。

使用ode45函数可以方便地对各种类型的常微分方程进行求解，包括一阶、高阶、常系数和变系数的微分方程。

2. 函数调用要使用ode45函数进行常微分方程的数值求解，需要按照以下格式进行函数调用：[t, y] = ode45(odefun, tspan, y0)其中，odefun表示用于描述微分方程的函数，tspan表示求解的时间跨度，y0表示初值条件，t和y分别表示求解得到的时间序列和对应的解向量。

3. 示例演示为了更好地理解如何使用ode45函数进行常微分方程的数值求解，下面我们以一个具体的例子来进行演示。

考虑如下的一阶常微分方程：dy/dt = -2*y其中，y(0) = 1。

我们可以编写一个描述微分方程的函数odefun：function dydt = odefun(t, y)dydt = -2*y;按照上述的函数调用格式，使用ode45函数进行求解：tspan = [0 10];y0 = 1;[t, y] = ode45(odefun, tspan, y0);绘制出解曲线：plot(t, y);4. 高级用法除了基本的函数调用方式外，MATLAB中还提供了更多高级的方法来对常微分方程进行数值求解。

可以通过设定选项参数来控制数值求解的精度和稳定性，并且还可以对刚性微分方程进行求解。

5. 性能优化在实际工程应用中，常常需要对大规模的常微分方程进行数值求解。

matlab微分方程常用数值解法

一、概述Matlab作为一种常用的科学计算软件，在微分方程的数值解法领域具有广泛的应用。

微分方程是描述自然现象中变化规律的数学工具，而数值解法则是指使用计算机进行近似求解微分方程的方法。

在Matlab 中，有多种常用的数值解法可以用来求解微分方程，例如欧拉法、改进的欧拉法、四阶龙格-库塔法等。

本文将对这些数值解法进行介绍和比较，以帮助读者更好地理解和应用微分方程求解数值方法。

二、欧拉法欧拉法是微分方程的最简单的数值解法之一，它通过离散化微分方程进行近似求解。

具体而言，对于一阶常微分方程dy/dx=f(x,y)，可以利用欧拉法进行数值解。

欧拉法的基本思想是将自变量x的增量Δx分成n个小区间，然后根据微分方程的数值近似公式y(x+Δx)=y(x)+f(x,y)Δx对每个小区间进行迭代计算。

欧拉法的优点是简单易实现，但由于它是一阶的数值方法，因此对于某些微分方程求解效果可能不够准确。

三、改进的欧拉法改进的欧拉法是对欧拉法的一种改进，它通过在每个小区间内使用平均斜率来提高求解的精度。

具体而言，对于微分方程dy/dx=f(x,y)，改进的欧拉法可以通过以下迭代公式进行数值求解：y(x+Δx)=y(x)+Δx/2[f(x,y)+f(x+Δx,y+Δx*f(x,y))]改进的欧拉法相比于欧拉法具有更高的数值精度，但计算量也相对增加。

四、四阶龙格-库塔法四阶龙格-库塔法是一种常用的数值微分方程求解方法，它通过四次迭代计算来获得微分方程的数值解。

具体而言，对于微分方程dy/dx=f(x,y)，四阶龙格-库塔法可以用以下公式进行数值求解：k1=f(x,y)k2=f(x+Δx/2,y+Δx/2*k1)k3=f(x+Δx/2,y+Δx/2*k2)k4=f(x+Δx,y+Δx*k3)y(x+Δx)=y(x)+Δx/6*(k1+2*k2+2*k3+k4)四阶龙格-库塔法相比于欧拉法和改进的欧拉法具有更高的数值精度和稳定性，但计算量也相对较大。

matlab常微分方程和常微分方程组求解方法

并做出解函数的曲线图。 6．完成实验报告。
为：
[X,Y]=dsolve('Dx+2*x-Dy=10*cos(t),Dx+Dy+2*y=4*exp(-2*t)','x(0)=2','y(0)=0' ) 以上这些都是常微分方程的精确解法，也称为常微分方程的符号解。但是，我们知道，有大量的常微分方程虽然从理论上讲，其解是存在的，但我们却无法求出其解析解，此时，我们需要寻求方程的数值解，在求常微分方程数值解方面， MATLAB 具有丰富的函数，我们将其统称为 solver，其一般格式为： [T,Y]=solver(odefun,tspan,y0) 该函数表示在区间 tspan=[t0,tf]上，用初始条件 y0 求解显式常微分方程
[X,Y]=dsolve('Dx+5*x+y=exp(t),Dy- x-3*y=exp(2*t)','t')
dy dx 2x 10 cos t , x t 0 2 dt dt dx dy 2 y 4e2t , y 0 t 0 dt dt 例 4：求常微分方程组通解的 MATLAB 程序
常微分方程和常微分方程组的求解
一、实验目的：熟悉 Matlab 软件中关于求解常微分方程和常微分方程组的各种命令，掌握利用 Matlab 软件进行常微分方程和常微分方程组的求解。二、相关知识在 MATLAB 中，由函数 dsolve()解决常微分方程（组）的求解问题，其具体格式如下： X=dsolve(‘eqn1’,’eqn2’,…) 函数 dsolve 用来解符号常微分方程、方程组，如果没有初始条件，则求出通解，如果有初始条件，则求出特解。

常微分方程数值解及其MATLAB实现

常微分方程数值解及其MATLAB实现常微分方程是数学中的一个重要分支，研究的是含有导数或微分的方程。

由于常微分方程往往难以求得精确解，因此数值解方法成为研究常微分方程的重要手段之一、本文将介绍常微分方程的数值解方法，并给出MATLAB实现。

首先介绍欧拉法，该方法是最简单的一种数值解法。

对于形如y'=f(x,y)的一阶常微分方程，将自变量x的范围分割为若干小区间，设步长为h。

在每个区间内，通过近似斜率来估计下一个点的函数值。

具体的递推关系式为：y_{n+1}=y_n+h*f(x_n,y_n)其中，y_n表示第n个解，x_n表示第n个点，f(x,y)表示一阶常微分方程右侧的函数。

下面给出欧拉法的MATLAB实现代码：function y = euler_method(f, x_range, y0, h)x = x_range(1):h:x_range(2);y = zeros(size(x));y(1)=y0;for i = 1:length(x)-1y(i+1)=y(i)+h*f(x(i),y(i));endend使用该函数只需提供函数句柄f，自变量范围x_range，初始条件y0和步长h即可。

函数返回数值解y。

改进欧拉法是对欧拉法的一种改进，通过使用函数连续两个点的斜率来估计下一个点的函数值。

具体的递推关系式为：y_{n+1}=y_n+h/2*[f(x_n,y_n)+f(x_{n+1},y_n+h*f(x_n,y_n))]下面给出改进欧拉法的MATLAB实现代码：function y = improved_euler_method(f, x_range, y0, h)x = x_range(1):h:x_range(2);y = zeros(size(x));y(1)=y0;for i = 1:length(x)-1k1=f(x(i),y(i));k2=f(x(i+1),y(i)+h*k1);y(i+1)=y(i)+h/2*(k1+k2);endend四阶龙格-库塔法是一种更精确的数值解法，通过使用函数四个点的斜率来估计下一个点的函数值。

实验七用matlab求解常微分方程(最新整理)

实验七用matlab 求解常微分方程一、实验目的：1、熟悉常微分方程的求解方法，了解状态方程的概念；2、能熟练使用dsolve 函数求常微分方程（组）的解析解；3、能熟练应用ode45\ode15s 函数分别求常微分方程的非刚性、刚性的数值解；4、掌握绘制相图的方法二、预备知识：1．微分方程的概念未知的函数以及它的某些阶的导数连同自变量都由一已知方程联系在一起的方程称为微分方程。

如果未知函数是一元函数，称为常微分方程。

常微分方程的一般形式为),,",',,()(=n y y y y t F 如果未知函数是多元函数，成为偏微分方程。

联系一些未知函数的一组微分方程组称为微分方程组。

微分方程中出现的未知函数的导数的最高阶解数称为微分方程的阶。

若方程中未知函数及其各阶导数都是一次的，称为线性常微分方程，一般表示为)()(')()(1)1(1)(t b y t a y t a y t a y n n n n =++++-- 若上式中的系数ni t a i ,,2,1),( =均与t 无关，称之为常系数。

2．常微分方程的解析解有些微分方程可直接通过积分求解.例如,一解常系数常微分方程1+=y dt dy可化为dt y dy=+1,两边积分可得通解为1-=tce y .其中c 为任意常数.有些常微分方程可用一些技巧,如分离变量法,积分因子法,常数变异法,降阶法等可化为可积分的方程而求得解析解.线性常微分方程的解满足叠加原理,从而他们的求解可归结为求一个特解和相应齐次微分方程的通解.一阶变系数线性微分方程总可用这一思路求得显式解。

高阶线性常系数微分方程可用特征根法求得相应齐次微分方程的基本解，再用常数变异法求特解。

一阶常微分方程与高阶微分方程可以互化，已给一个n 阶方程),,",',()1()(-=n n y y y t f y 设)1(21,,',-===n n y y y y y y ，可将上式化为一阶方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧====-),,,,(''''2113221n n nn y y y t f y yy y y y y反过来，在许多情况下，一阶微分方程组也可化为高阶方程。

matlab 求微分方程组数值解

matlab 求微分方程组数值解使用Matlab求解微分方程组是一种常见的数值方法。

微分方程组是描述自然界中许多现象的数学模型，它们可以用一组关于未知函数及其导数的方程来表示。

通过求解微分方程组，我们可以得到未知函数在给定条件下的数值解。

在Matlab中，求解微分方程组可以使用ode45函数。

该函数是一个常用的求解常微分方程初值问题的函数，它使用四阶龙格-库塔法（RK4）进行数值求解。

使用ode45函数求解微分方程组的步骤如下：定义微分方程组。

在Matlab中，可以使用匿名函数或函数句柄的方式定义微分方程组。

例如，对于一个二阶微分方程组：dy1/dt = f1(t, y1, y2)dy2/dt = f2(t, y1, y2)可以定义一个匿名函数：f = @(t, y) [f1(t, y(1), y(2)); f2(t, y(1), y(2))]其中，t是自变量，y是未知函数的向量。

接下来，指定求解的时间区间和初值条件。

时间区间可以通过指定起始时间和结束时间来确定。

初值条件是指在起始时间处未知函数的值。

初值条件可以通过一个向量来表示。

例如，对于一个二阶微分方程组，初值条件可以表示为一个长度为2的向量。

然后，调用ode45函数进行求解。

ode45函数的输入参数包括定义的微分方程组、时间区间和初值条件。

该函数会返回数值解和对应的时间点。

可以通过绘制图形或打印数值解来展示结果。

Matlab提供了丰富的绘图函数，可以方便地将数值解可视化。

需要注意的是，求解微分方程组时，应选择合适的数值方法和步长，以保证数值解的精度和稳定性。

对于复杂的微分方程组，可能需要进行参数调整和迭代求解，以得到满意的结果。

使用Matlab求解微分方程组是一种便捷而有效的数值方法。

通过定义微分方程组、指定时间区间和初值条件，调用ode45函数进行求解，可以得到微分方程组的数值解。

这种方法在科学研究和工程实践中具有广泛的应用，可以帮助我们更好地理解和分析自然界中的现象。

matlab 求解常微分方程组

一、概述随着科技的发展，数学在各个领域中都扮演着非常重要的角色。

微分方程作为数学中的一个重要分支，在物理、工程、生物等领域都有着广泛的应用。

而 MATLAB 作为一个强大的数学软件工具，可以帮助我们快速高效地求解各种类型的微分方程组，从而为各领域的研究和应用提供有力的支持。

本文将详细介绍如何使用 MATLAB 求解常微分方程组的方法及步骤。

二、常微分方程组的定义常微分方程组是指这样一类微分方程组：一个或多个未知函数及其导数的方程组。

一般形式为：dx1/dt=f1(t,x1,x2,...,xn),dx2/dt=f2(t,x1,x2,...,xn),..., dxn/dt=fn(t,x1,x2,...,xn)。

其中x1,x2,...,xn 是未知函数，t是自变量，f1,f2,...,fn 是关于 t 和x1,x2,...,xn 的已知函数。

三、求解常微分方程组的方法MATLAB 提供了多种方法来求解常微分方程组，常用的方法有：欧拉法、四阶龙格库塔法、常微分方程组函数 ode45、ode23、ode113 等。

下面将分别介绍各种方法的具体步骤。

四、使用欧拉法求解常微分方程组欧拉法是一种简单粗糙的数值解法，通过分割等间距的步长满足微分方程初值问题。

其具体步骤如下：1. 定义微分方程组的初始条件和步长：x0=[x1(0),x2(0),...,xn(0)],h=步长。

2. 使用欧拉法逐步逼近微分方程组的解：for i=1:Nt(i)=t(i-1)+h;x(:,i+1)=x(:,i)+h*f(t(i),x(:,i));end其中 x(:,i)=[x1(i),x2(i),...,xn(i)] 为微分方程组在第 i 个时间节点的解。

五、使用四阶龙格库塔法求解常微分方程组四阶龙格库塔法是一种常用的数值解法，通过多次近似来计算微分方程组的数值解。

其具体步骤如下：1. 定义微分方程组的初始条件和步长：x0=[x1(0),x2(0),...,xn(0)],h=步长。

第12章 MATLAB常微分方程(组)数值求解方程与方程组的数值解

基于修正的二阶Rosenbrock公式。由于是单步解算器，当精度要求不高时，它效率可能会高于ode15s。它可以解决一些
ode15s求解起来效率不太高的刚性问题。
ode23t可以用来求解微分代数方程。
ode23tb 刚性
低
当方程是刚性的，并且求解要求精度不高
时可以使用。
2020/6/19
© 吴鹏, MATLAB从零到进阶.
常微分方程数值解
【例12.4-1】的结果图：
方法 1计算结果图 1
方法 2计算结果图 1
方法 3计算结果图 1
0.8
0.8
0.8
0.6
0.6
0.6
0.4
0.4
0.4
0.2
0.2
0.2
0
0
0
-0.2
-0.4 0
2020/6/19
y1(t)
-0.2
y2(t)
y3(t)
-0.4
在某段时间区间内的变化来看。非刚性问题变化相对缓慢，而刚性问题在某段时间内会发生剧烈变化，即很短的时间内，解的变化巨大。对于刚性问题不适合用 ode45来求解，如果硬要用ode45来求解的话，达到指定精度所耗费的时间往往会非常长。
2020/6/19
© 吴鹏, MATLAB从零到进阶.
二、非刚性问题举例
这些函数可以求解非刚性问题，刚性问题，隐式
微分方程，微分代数方程等初值问题，也可以求解延迟微分方程，以及边值问题等。
2020/6/19
© 吴鹏, MATLAB从零到进阶.
二、初值问题求解函数
常微分方程数值解
1. 提供的函数
ode23, ode45, ode113, ode15s, ode23s, ode23t, ode23tb，这些函数统一的调用格式如下：

常微分方程的数值解的matlab命令实现方法

常微分方程的数值解的matlab命令实现方法常微分方程的数值解在 MATLAB 中可以通过 ode 函数或 dsolve 函数进行求解。

其中，ode 函数可以求解一阶常微分方程，而 dsolve 函数可以求解二阶及以上的常微分方程。

下面是具体的实现方法:1. 一阶常微分方程的求解对于一阶常微分方程，可以使用 ode 函数求解。

假设我们要求解的常微分方程为:dx/dt = f(x, t)可以使用以下命令进行求解:y0 = [a, 0]; % 初值条件tspan = [0, 20]; % 时间区间[t, y] = ode45(@(t, y) odefun(t, y, a), tspan, y0); % 求解其中，odefun 函数用于定义常微分方程的解，它是一个自定义函数，其形式可以为:dy/dt = f(t, y)其中，dy 是 y 的求导，f(t, y) 是常微分方程的系数矩阵。

在 MATLAB 中，可以使用 dy[] 函数来计算 y 的求导，例如:dy = dy[](t, y);最后，使用 ode45 函数求解常微分方程的解，其中 tspan 是时间区间，y0 是初值条件。

2. 二阶常微分方程的求解对于二阶常微分方程，可以使用 dsolve 函数求解。

假设我们要求解的二阶常微分方程为:d2y/dt2 + p(t)dyy/dt + q(t)dy/dt + r(t)y = 0可以使用以下命令进行求解:syms t pqr;y0 = [a1, a2, a3]; % 初值条件[t, y] = dsolve(@(t, y) dy0(t, y), t, y0); % 求解其中，dy0 函数用于定义二阶常微分方程的解，其形式可以为:d2y/dt2 + p(t)dyy/dt + q(t)dy/dt + r(t)y = 0其中，d2y/dt2 是 y 的二阶求导，其它项是 y 的求导。

在 MATLAB 中，可以使用 dy0[] 函数来计算 y 的二阶求导。

matlab算法-求解微分方程数值解和解析解

MATLAB是一种用于数学计算、工程和科学应用程序开发的高级技术计算语言和交互式环境。

它被广泛应用于各种领域，尤其在工程和科学领域中被用于解决复杂的数学问题。

微分方程是许多工程和科学问题的基本数学描述，求解微分方程的数值解和解析解是MATLAB算法的一个重要应用。

1. 求解微分方程数值解在MATLAB中，可以使用各种数值方法来求解微分方程的数值解。

其中，常见的方法包括欧拉法、改进的欧拉法、四阶龙格-库塔法等。

这些数值方法可以通过编写MATLAB脚本来实现，从而得到微分方程的近似数值解。

以常微分方程为例，可以使用ode45函数来求解微分方程的数值解。

该函数是MATLAB中用于求解常微分方程初值问题的快速、鲁棒的数值方法，可以有效地得到微分方程的数值解。

2. 求解微分方程解析解除了求解微分方程的数值解外，MATLAB还可以用于求解微分方程的解析解。

对于一些特定类型的微分方程，可以使用符号计算工具箱中的函数来求解微分方程的解析解。

通过符号计算工具箱，可以对微分方程进行符号化处理，从而得到微分方程的解析解。

这对于研究微分方程的性质和特点非常有帮助，也有助于理论分析和验证数值解的准确性。

3. MATLAB算法应用举例在实际工程和科学应用中，MATLAB算法求解微分方程问题非常常见。

在控制系统设计中，经常需要对系统的动态特性进行分析和设计，这通常涉及到微分方程的建模和求解。

通过MATLAB算法，可以对系统的微分方程进行数值求解，从而得到系统的响应曲线和动态特性。

另外，在物理学、生物学、经济学等领域的建模和仿真中，也经常需要用到MATLAB算法来求解微分方程问题。

4. MATLAB算法优势相比于其他数学软件和编程语言，MATLAB在求解微分方程问题上具有明显的优势。

MATLAB提供了丰富的数值方法和工具，能够方便地对各种微分方程进行数值求解。

MATLAB具有直观的交互式界面和强大的绘图功能，能够直观地展示微分方程的数值解和解析解，有利于分析和理解问题。

matlab解常微分方程的特别方法

求解具体ODE的基本过程：
（2）运用数学中的变量替换：
yn=y(n-1),yn-1=y(n-2),…,y2=y‘,y1=y，把高阶（大于2阶）的方程（组）写成一阶
微分方程组：
y
y1 y2
yn
f1 ( t , f2 (t,
fn (t,
y)
y
)
y
)
y1 (0 ) y 0
有效值： on、off 缺省值： off
为‘on’时，控制解向量范数的相对误差，使每步计算中，满足： norm(e)<=max(RelTol* norm(y),AbsTol)
Events
有效值：为‘on’时，返回相应的 on、off 事件记录
参数设置
属性名
OutputFcn
取值
含义
若无输出参量，则
-x(2)+0.02*x(1)*x(2)+0.04*t];
运行命令文件
[t,x]=ode45('function3',[0,20],[30 ;20]);
plot(t,x); xlabel('time t0=0,tt=20'); ylabel('x values
x1(0)=30,x2(0)=20');
求解器 Solver
ode23s
ode23tb
OD
E类
特点
型
刚性
一步法；2阶 Rosebrock算法；低精度
刚梯形算法；低精性度
说明
当精度较低时，计算时间比 ode15s短当精度较低时，计算时间比 ode15s短
参数设置
属性名 AbsTol
RelTol