材料力学惯性矩ppt
惯性矩

1、静矩(求形心)⎰=AZ ydA S⎰=Ay zdA SSz 、Sy 分别定义为图形对z 轴和y 轴的静矩,也称为图形对z 轴和y 轴的一次矩。
平面图形的静矩是对某一坐标而言的,同一图形对不同的坐标轴,其静矩也就不同。
静矩的数值可能为正值,可能为负值,也可能为零。
静矩的量纲是长度的三次方。
静矩用来求平面图形的形心坐标:A zdAz A ydAy AA⎰⎰==对于规则的形状,可以将其划分为若干个规则的简单图形,通过组合求的形心。
212211212211A A z A z A z A A y A y A y ++=++=注:A 为简单图形的面积(空心面积可以为负值),y 、z 为简单图形的形心坐标值2、惯性矩⎰⎰==Ay AZ dAz I dAy I 22Iz 、Iy 分别定义为图形对z 轴和y 轴的惯性矩,也称为图形对z 轴和y 轴的二次轴矩。
惯性矩始终为正值,惯性矩的量纲是长度的四次方。
计算步骤123222332202202bh bx dx x b x bdx dA z I h h Ay =⨯=⨯=⨯⨯==⎰⎰⎰左图三角形面积对z轴的惯性矩1243)()(44322hyhydyyyhydyyhI hhz=-=-=⨯-=⎰⎰右图关于z轴的惯性矩为左图的四倍34hIz=惯性距的平行移轴定理:有了它规则形状的物体就不用通过积分来求惯性矩了,省时省力(但精准度差了一些)截面图形对某轴的惯性矩,等于它对该轴平行的形心轴的惯性矩,加上两轴间距离的平方乘以截面面积。
A a I I xc x 2+=Ix ——截面图形对目标轴的惯性矩(目标轴:组合图形的形心轴) Ixc ——截面图形对形心轴的惯性矩(注意理解:此处的形心轴是指划分的规则截面的形心轴)a ——两轴之间的距离 A ——截面图形的面积3、极惯性矩图形对于任意一对互相垂直的轴的惯性矩之和,等于它对该两轴交点的极惯性矩。
I p=I z+I y4、惯性积在平面图形的坐标(x ,y )处,取微面积dA ,遍及整个图形面积的积分⎰=AyzyzdA I ,定义为图形对y ,z 轴的惯性积。
《材料力学惯性矩》课件

PART 04
惯性矩的应用
REPORTING
弯曲应力计算
总结词
在计算梁的弯曲应力时,惯性矩是一 个重要的参数。
详细描述
通过利用惯性矩的计算公式,可以确 定梁在承受垂直或水平力时的弯曲应 力分布。惯性矩的大小决定了弯曲变 形的程度,进而影响应力分布。
剪切应力计算
总结词
在分析剪切应力时,惯性矩起到关键作用。
建筑结构中的惯性矩问题
高层建筑在风力和地震作用下,需要具备足 够的惯性矩来抵抗侧向和扭转力。建筑设计 时需充分考虑不同方向的惯性矩,以确保结
构安全。
利用惯性矩优化结构设计
优化截面尺寸
根据工程需求,调整结构件的截面尺寸,以改变其惯性矩,从而提高结构的承载能力和 稳定性。
减重与加强
在满足强度要求的前提下,通过优化结构设计,减小不必要的材料使用,降低结构重量 。同时,对关键部位进行加强,提高其惯性矩,确保结构安全。
应力分析是研究物体在受力后内部应力的分布和大小
的过程。
方法
02 通过理论分析、实验测试和数值模拟等方法进行应力
分析。
重要性
03
确保结构在各种工况下的安全性和可靠性,防止因应
力集中、疲劳或过载等原因导致的断裂或失效。
应变分析
定义
应变分析是研究物体在外力作用下产生的变形和位移的过程。
方法
通过测量物体的尺寸变化、观察表面变形和利用有限元等方法进 行应变分析。
在稳定性分析中,惯性矩是评估结构稳定性 的重要参数。
详细描述
结构的稳定性与惯性矩的大小密切相关。通 过分析不同受力情况下惯性矩的变化,可以 预测结构的失稳趋势,并采取相应的措施提 高结构的稳定性。
PART 05
材料力学截面法PPT

概述: 讨论的问题:介绍与截面形状和尺寸有关的几何量
(静矩、惯性矩、惯性积)的定义及计算方法;平行移轴 公式,转轴公式等。
在实际工程中发现,同样的材料,同截面积,由于 横截面的形状不同,构件的强度、刚度有明显不同,如 一张纸(或作业本),两端放在铅笔上,明显弯曲,更 不能承载东西了.但把同一张纸折成波浪状(象石棉瓦 状) ,这时纸的两端再搁在铅笔上,不仅不弯曲,再放 上一支铅笔,也不弯曲.可见,材料截面的几何形状对强度、 刚度是有一定影响的,研究截面几何性质的目的就是解
y
ry
A
rz2 A I z
rz
Iz A
o
rz z
ry2 A I y
例4—3中的矩形截面:
ry
Iy A
rz
Iz A
bh3 12 h
h 0.289h
bh
12 2 3
h
y
oz b
• 补充例子:试计算圆弧右上方阴影部分面积的惯性积 I zy.
解:因为惯性矩与惯性积等于各微
y C
B
r
元面积的惯性矩或惯性积之和,
i
sz yci Ai y1 A1 y2 A2
i
15 300 30 270 30 270 50 23.625 105 (mm)2 ,
2
• 4-2 惯性矩和惯性积
一、惯性矩的定义
------面积对坐标轴的二次矩.
y
y
dA
o
z
z
设一平面图形,取一元面积 dA,坐 标为(z,y),距原点的距离为 ,方位
服务特 权
共享文档下载特权
VIP用户有效期内可使用共享文档下载特权下载任意下载券标价的文档(不含付费文档和VIP专享文档),每下载一篇共享文
惯性矩 静距

静矩,惯性矩,极惯性矩等问题静矩(截面一次矩):微元面积(把微元面积视为垂直于图形的力)对坐标轴的矩的积分,即微元面积与微元到坐标轴距离的乘积的积分。
应用:1形心:图形几何形状的中心。
若将微元面积视为垂直于图形平面的力,则形心即为合力的作用点。
利用平衡力系求得。
下式中Yc和Zc就是图形的形心坐标静矩与坐标轴有关,同一平面内对不同坐标轴有不同的静矩,可以为正,也可以为负。
它的量纲是长度的三次方。
对于通过形心的坐标轴,图形静矩等于零。
静矩和形心相互关联,知道其中一个就可求出另一个。
静矩的力学意义是:如果截面上作用有均匀分布载荷,其值以单位面积上的量表示,则载荷对于某个轴的合力矩就等于分布载荷乘以截面对该轴的静矩。
静矩是求截面形心和计算截面内各点剪应力的必要数据。
2:静矩在材料力学中主要应用于弯曲剪应力的计算,考虑剪应力平行于剪力,并且剪应力在截面宽度方向上均匀分布,此时,矩形截面,工字梁,圆截面的剪应力的表达式为:τ=QS/Ib,这里Q为剪力,S为距离中性面y以外面积对中性轴的静矩,b为截面的宽度,I为截面对中性轴的惯性矩。
3:求解静定结构的位移的单位载荷法,当研究对象为线弹性体的时候,即为莫尔定理,或者莫尔积分。
在求解莫尔积分的时候,被积函数中有一个函数为线性函数的时候,便可以采用莫尔积分图乘法。
原理是当被积函数一个为线性函数的时候,该函数可以表示为x*tan(θ),而tan(θ)对于莫尔积分来讲是常数,可以提到积分号以外,因此,原来的积分便可以表示为x与另一个函数相乘的积分,而其物理意义即为该函数曲线围成的曲面面积到y轴的静矩,所以该积分的解可以由该曲面的面积乘以形心的x坐标。
因此对于原始积分来讲需要乘以tan(θ),所以莫尔积分的图乘法的结果是曲线面积乘以形心的纵坐标。
惯性矩(截面二次矩):微元面积(把微元面积视为垂直于图形的力)对到坐标轴距离的平方的积分。
极惯性矩(截面二次极矩):对某点的极惯性矩为该微元面积对到该点距离的平方的积分。
截面惯性矩(材料力学)

B 解:1、计算各杆件的轴力。 (设斜杆为1杆,水平杆为2杆)
F 用截面法取节点B为研究对象
Fx 0 x Fy 0
FN1 cos 45 FN 2 0 FN1 sin 45 F 0
FN1 28.3kN
FN 2 20kN
截面上的应力
A 1
45°
C
2
FN1
y
FN 2 45° B
F
FN1 28.3kN FN 2 20kN
20 100 50=32 104mm3
§I-2 惯性矩、惯性积、极惯性矩
1、惯性矩:(惯性矩是一个物理量,通常被用作描述一个物 体抵抗扭动,扭转的能力 )
它是图形面积与它对轴的距离的平方之积表达式为
Ix y2dA
A
I y x2dA
A
注意:
1)同一截面对不同的轴惯性 矩不同;
2)惯性矩永远为正值;
m
合。所以称为轴力。
F FN
FN
3、轴力正负号:拉为正、
F 压为负
Fx 0 FN F 0
FN F
4、轴力图:轴力沿杆件轴 线的变化
轴力和轴力图
例题3-1
A
F1 F1 F1
FN kN
1 B 2 C 3D
已知F1=10kN;F2=20kN; F3=35kN;F4=25kN;试画
1 F2
2
F3
2
2
I Z1
Iy
IZ 2
Iy
IZ 2
cos 2a
I yz sin 2a
2.三个公式:设新坐标系由原坐标系逆转α角而得,且有
I y1
Iy
IZ 2
Iy
IZ 2
c os 2a
截面惯性矩(材料力学)

A 1
45°
C
2
FN1
y
FN 2 45° B
F
图示结构,试求杆件AB、CB的
应力。已知 F=20kN;斜杆AB为直
径20mm的圆截面杆,水平杆CB为 15×15的方截面杆。
B 解:1、计算各杆件的轴力。 (设斜杆为1杆,水平杆为2杆)
F 用截面法取节点B为研究对象
Fx 0 x Fy 0
b2h23 12
20Байду номын сангаас
20
100
3
12
16.67 105
3)求对整个截面形心ZC轴的惯性矩 IzC (Iz1 a12 A1) (Iz2 a22 A2 ) 66.67103 302 200016.67105 302 2000 53.34105 mm4
F
F 作用线也与杆件的轴线重
m
合。所以称为轴力。
F FN
FN
3、轴力正负号:拉为正、
F 压为负
Fx 0 FN F 0
FN F
4、轴力图:轴力沿杆件轴 线的变化
轴力和轴力图
例题3-1
A
F1 F1 F1
FN kN
1 B 2 C 3D
已知F1=10kN;F2=20kN; F3=35kN;F4=25kN;试画
杆件的基本变形: 拉(压)、剪切、扭转、弯曲
拉压变形
剪切变形
扭转变形
弯曲变形
二、杆件的轴向拉压变形分析
一、轴向拉伸和压缩的概念
特点:
作用在杆件上的外力合力的作用线与 杆件轴线重合,杆件变形是沿轴线方向的伸 长或缩短。
杆的受力简图为
拉伸
材料力学惯性矩

材料力学惯性矩材料力学是研究物质内部力的作用和变形规律的一门学科,而惯性矩则是材料力学中非常重要的一个概念。
在工程实践中,我们经常需要计算和应用惯性矩来分析和设计结构。
因此,对于材料力学惯性矩的理解和掌握是非常必要的。
首先,我们来了解一下惯性矩的概念。
惯性矩是描述物体抵抗转动的能力的物理量,它与物体的质量和形状密切相关。
惯性矩的大小取决于物体的质量分布和旋转轴的位置。
在工程中,我们通常需要计算关于惯性矩的一些参数,比如转动惯量、极转动半径等,以便进行结构设计和分析。
其次,惯性矩的计算方法有很多种,根据不同的情况可以采用不同的计算公式。
比如对于一般的平面图形,我们可以利用基本的几何学知识来计算其惯性矩;对于复杂的三维结构,我们则需要运用积分或者数值计算的方法来求解。
在实际工程中,我们经常会遇到各种各样的结构和形状,因此掌握多种计算方法是非常重要的。
另外,惯性矩的计算还需要考虑材料的弹性模量和截面的形状。
对于不同的材料和截面形状,其惯性矩的计算方法也会有所不同。
比如对于矩形截面和圆形截面,它们的惯性矩计算公式就是不同的。
因此,在实际工程中,我们需要根据具体情况选择合适的计算方法,并结合材料的力学性能参数来进行计算。
最后,惯性矩的应用非常广泛,不仅可以用于结构设计和分析,还可以用于动力学和振动学的研究。
比如在机械设计中,我们需要计算零件的惯性矩来确定其转动惯量,从而分析其转动特性;在航天航空领域,惯性矩也是非常重要的参数,它关系到飞行器的稳定性和控制性能。
总之,材料力学惯性矩是工程领域中非常重要的概念,它涉及到结构设计、力学分析、动力学和振动学等多个领域。
掌握惯性矩的计算方法和应用技巧,对于工程师来说是非常必要的。
希望本文的介绍能够帮助大家更好地理解和应用惯性矩的知识。
4-截面惯性矩(材料力学)

FN3 F4 25kN
x
2、绘制轴力图。
三、应力概念、拉(压)杆横截面上的应力
杆件的强度不仅与轴力有关,还与横截面面 积有关。必须用应力来比较和判断杆件的强度。
——横截面上的应力
——横截面上的应力
FN
A
——横截面上的应力
该式为横截面上的正应力σ计 算公式。正应力σ和轴力FN同号。 即拉应力为正,压应力为负。
D4
32
o
z
IP Iy0 Iz0
I y0
Iz0
IP 2
D4
64
§ I-3 惯性积
1.定义:图形对两个坐标轴的两个坐标之积的积分。
§ I-3 惯性积
2.表达式:
y
I yz yzdA
A
3.说明: h
1)同一图形对不同轴的惯性积不同; A1 A2
z
2)惯性积可正,可负,可为零。
x
IP 2dA
A
2 x2 y2 IP (x2 y2 )dA I y I x
A
IP Ix I y 图形对正交坐标轴的惯性矩之和等于它 对此二轴交点的极惯性矩
例求圆形截面对形心轴的惯性矩。 y
解: D
IP
A
2dA
2 0
2 2d
I x
y 2dA
A
xC
A ( yC b)2 dA
A ( yC2 2byC b2 )dA
x
I xC 2bSxC b2 A
SxC AyC 0 I x I xC b2 A 返
§Ⅰ- 4平行移轴公式 y
材料力学复习 PPT课件
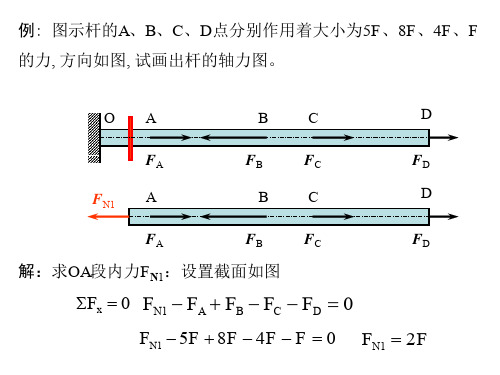
M c y1 Iz
[sc ]
y1 y2
[st ] [s c ]
20 y
20
F
q=F/b
A
CB
D
b
b
b
Fb/2
C截面的强度条件由最大的拉应
力控制。
Fb/4
s t max
MC y1 Iz
( F 2) 0.134 4 5493108
30 106
F 24.6 kN
B截面
s t max
T 0.2d 3
T
1930
d 3 0.2tmax 3 0.2 66.7 106 0.053 m 5.3 cm
A空 8.5 0.303 A实 28.2
可见, 采用钢管时, 其重量只有实心圆 轴的30%, 耗费的材料要少得多。
例: 作内力图。已知F1=F2=2 kN, Me=10 kN·m, q=1 kN/m。
s t max
My1 Iz
s cmax
My2 Iz
60 280
sc max
Oz
st max
s t max y1 [s t ] 1 s c max y2 [s c ] 3
y1 1 y2 3
d
60 280
y
y2
y1 y2 280 mm
由上两式确定出
Oz
y1
y
y y2 210 mm
80
120 20
y1
B截面
st
M B y1 Iz
4000 0.052 763108
27.2106 Pa 27.2 MPa [s t]
材料力学第五章
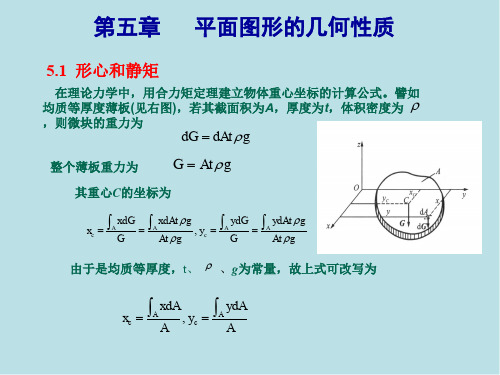
xC
Sy A
n
x C
Ai
i 1
n
Ai
i 1
n
yC
Sx A
i 1 n
y C
Ai
Ai
i 1
第五章 平面图形的几何性质
270
30
y [例1] 已知:图形尺寸如图
Ⅱ
所示。
求:图形的形心。
50
C2
Ⅰ
C C1
yc
z
解:1、将图形分解为 简单图形的组合
第五章 平面图形的几何性质
静矩与形心坐标之间的关系
S y
zdA
A
S z
ydA
A
Sy AzC
Sz AyC
yC
Sz A
ydA
A
A
zC
Sy A
zdA
A
A
已知静矩可以确定图形的形心坐标 已知图形的形心坐标可以确定静矩
第五章 平面图形的几何性质
构件截面的图形往往是由矩形、圆形等简单图形 组成,称为组合图形。
xc
A
G
A At g
, yc
A
G
A At g
由于是均质等厚度,t、 、g为常量,故上式可改写为
xdA
ydA
xc
A
A
, yc
A
A
第五章 平面图形的几何性质
1. 静矩的定义
对 z 轴静矩 对 y 轴静矩
Sz
ydA
A
Sy
材料力学惯性矩ppt课件

取微面积dA=dzdy,则:I zy 0;
例5-3 圆形截面对其形心轴的惯性矩。 解:取yoz坐标系。取微面积dA=2zdy,则:
2 R 2 2 2
I z y dA 2 y R y dy ; A R 4 64 D 4 由对称性:I y I z ; 由几何关系: 2=y 2 z 2 , 64
返回 下一张 上一张 小结
3
第二节 惯性矩和惯性积
一、极惯性矩: 定义:平面图形中任一微面积dA与它到坐 标原点O的距离ρ平方的乘积ρ2dA,称为该面积 dA对于坐标原点o的极惯性矩。
截面对坐标原点o的极惯性矩为:
I P 2 dA;
A
简单图形的极惯性矩可由定义式积分计算。
实心圆截面: I P 2dA 32 ; D 4 d 空心圆截面: I P (1 4 ); ( )
5
例5-2 求矩形截面对其对称轴的惯性矩和惯性积。 解:取yoz坐标系。取微面积dA=bdy,则:
bh3 I z y dA y bdy ; A h / 2 12
2 h/2 2
取微面积dA=hdz,则:
2 b/2 2
hb3 I y z dA z hdz ; A b / 2 12
2 I z1 z a 2 A; y1 y b A;
I z1 y1 I zy abA ;
注意:y、z轴必须是形心轴。 二、转轴公式:
2
I z1 y1 dA ( y cos z sin ) 2 dA;
I z1
I y1
Iz Iy
R 4
D 4
I P 2 dA ( y 2 z 2 )dA I Z I y .
转动惯量-惯性矩

d d ,切应力为 G dx dx
进一步推导可得
d T (7) dx GI p
此处 I p 即为极惯性矩(参见式 1) (2)弯曲问题——惯性矩 由材料力学相关推导可得,对于一根对称等截面 梁以中性层曲率表达的弯曲变形公式为:
1
M EI z
(8)
横截面上 y 处的弯曲正应力为
(2)
空心圆截面极惯性矩为 I p
D4 d 4
32
(3)
1.2 截Байду номын сангаас的惯性矩(对坐标轴)
任意截面 A 对坐标轴的惯性矩为:
I z y 2 dA A 2 I y z dA A
(4)
I z 、 I y 分别称为截面对 z 轴和 y 轴的惯性矩。
实心圆截面直径惯性矩 I d
惯性矩与转动惯量
1 惯性矩(Products of Inertia) 1.1 截面的极惯性矩(对坐标原点)
任意截面 A 对坐标原点 O 的极惯性矩为:
I p 2 dA
A
(1)
由以上定义公式可见,截面极惯性矩恒为正,量 纲为长度的四次方,即 L4 实心圆截面极惯性矩为 I p
d4
32
i 1
J z MRz2 ,M 为刚体总质量, Rz 为刚体等效为一质点 M 时,对 z 轴的回转半径。
由上可知转动惯量的量纲为 ML2 , 国际单位制下为 kg m2
2.2 常用转动惯量表
Note:薄盘转动惯量近似满足 I d
1 Ip 2
3 常用软件中相关问题说明
UG 中“Moments of Inertia (WCS)”下求得 I x , I y , I z 即为依照上式(9)所得, Radii of Gyration (WCS)为对应于各坐标轴的回转半径; ANSYS 中“Operate-Calc Geom Items-Of Volumes”项下”MOMENTS OF INERTIA” 求得 I xx , I yy 及 I zz 同样依照上式(9)所得。 ANSYS 的 mass21 中加的 Rotary Inertia 为转动惯量, 可用实体模型求得或者用 2.2 节中的公式求得。注意:mass21 中的转动惯量值是相对于 element coordinate 求得的! 默认为,坐标原点为 mass21 单元的中心,坐标方向与总体坐标系相同。
惯性矩

截面惯性矩编辑同义词截面矩一般指截面惯性矩计算公式编辑常见截面的惯性矩公式矩形b*h^3/12 其中:b—宽;h—高三角形b*h^3/36 其中:b—底长;h—高圆形π*d^4/64 其中:d—直径圆环形π*D^4*(1-α^4)/64; α=d/D 其中:d—内环直径;D—外环直径惯性矩编辑惯性矩I=质量X垂直轴二次)the moment of inertiacharacterize an object's angular acceleration due to torque.静矩静矩(面积X面内轴一次)把微元面积与各微元至截面上指定轴线距离乘积的积分称为截面的对指定轴的静矩Sx= ydF。
截面惯性矩截面惯性矩(I=面积X面内轴二次)截面惯性矩:the area moment of inertiacharacterized an object's ability to resist bending and is required to calculate displacement.截面各微元面积与各微元至截面某一指定轴线距离二次方乘积的积分Ix= y↑2dF。
截面极惯性矩截面极惯性矩(Ip=面积X垂直轴二次)。
扭转惯性矩Ip: the torsional moment of inertia极惯性矩the polar moment of inertia截面各微元面积与各微元至垂直于截面的某一指定轴线二次方乘积的积分Ip= P↑2dF。
a quantity to predict an object's ability to resist torsion, to calculate the angular displacement of an object subjected to a torque.相互关系截面惯性矩和极惯性矩的关系截面对任意一对互相垂直轴的惯性矩之和,等于截面对该二轴交点的极惯性矩Ip=Iy+Iz。
材料力学附录I 平面图形的几何性质2形心主轴和形心主惯性矩

10 150yC x1
x
由于对称知: xC=0
材料力学 附录I 平面图形的几何性质
§I-2 惯性矩和惯性半径
一、惯性矩
Iz
y 2 d A,
A
Iy
z2dA
A
工程中常把惯性矩表示为平面图 形的面积与某一长度平方的乘积, 即
Iy A iy2
或
iy
Iy A
Iz A iz2
或
iz
Iz A
4
③ 建立形心坐标系;求:IyC , IxC , I xCy
材料力学 附录I 平面图形的几何性质
I xC I矩xC I圆xC I矩x A矩 y 2[I圆x1A圆 (0.5dy)2 ]
1.5d
(2d )3
3d 2 (0.177 d )2
d 4
[
d 2
(0.5d
0.177 d )2 ]
0.685 d 4
A
dA
zdy
h1
y2 b2
dy
dz
z
yC C y
O b
A
y
dA
A
b 0
h1
y2 b2
dy
2bh 3
材料力学 附录I 平面图形的几何性质
z
h yC C z O y dy
b
Sz
y
ydA
A
b 0
yh1
y2 b2
dy
b2h 4
yC
Sz A
3b 8
z
dz
z
yC C y
y
O b
Sy
4bh2 15
材料力学 附录I 平面图形的几何性质
§I-1 静矩和形心 §I-2 惯性矩和惯性半径 §I-3 惯性积 §I-4 平行移轴公式 §I-5 转轴公式 主惯性轴
《材料力学 第2版》_顾晓勤第05章第2节 截面的惯性矩、惯性积和惯性半径

2 2 2 22
64
第 2 节 截面的惯性矩、惯性积和惯性半径 第五章 截面的几何性质
例 5-4 如图所示,计算圆形截面对于 x 轴和 y轴
的惯性矩、惯性半径,以及极惯性矩、第一象限部
分对 x、y轴的惯性积。
解 取平行于 x 轴的狭
长条作为微面积 dA,则
dA b(y)dy 2 d 22 y2dy
dy
dA bdy
y
矩形截面对于 x 轴的惯性矩为
H
Ix A y2dA 2h2 y2bdy 2 2b [( H )3 ( h )3 ] 32 2 b (H 3 h3) 12
第 2 节 截面的惯性矩、惯性积和惯性半径 第五章 截面的几何性质
矩形截面对于 x 轴的惯性半径为
ix
Ix A
b 12
圆形截面对于 x 轴的惯性矩为
Ix A y2dA
d2
d 2
y2
2
d 2 2 y2 dy
πd 4 64
第 2 节 截面的惯性矩、惯性积和惯性半径 第五章 截面的几何性质
圆形截面对于 x 轴的惯性半径为
ix
Ix A
πd 4 πd 2
64 4
d 4
x 轴和 y 轴都与圆的直径重合,由
于对称的原因,有
第 2 节 截面的惯性矩、惯性积和惯性半径 第五章 截面的几何性质
设任意平面图形其面积
为A。x 轴和 y 轴为图形所在 平面内的坐标轴。在 ( x ,y )
处取微面积 dA,则定义图形
对于x 轴和 y轴 y2dA I y A x2dA
注意
由于 x2 和 y 2总是正的,所以 I x 和 I y 也恒
是正值。
惯性矩的量纲为长度的四次方。
材料力学第四章 平面图形的几何性质

§4.1 静矩和形心
一、静矩,即面积对轴的矩:(与力矩类似)
z
是面积与它到轴的距离之积。
图形对y轴和z轴的静矩为
dA
Sz
ydA
A
z
Sy
zdA
A
特点:
y▲静矩的量纲为长度的三次方;
第四章 平面图形的几何性质
§4.1 静矩和形心 §4.2 惯性矩和惯性半径 §4.3 惯性积 §4.4 平行移轴公式 §4.5 转轴公式 主惯性轴
第四章 平面图形的几何性质
【基本内容】
一、静矩、形心 二、惯性矩、惯性积、惯性半径 三、主轴、主惯性矩、形心主惯性平面的概念 四、平行移轴公式、转轴公式
跟踪训练
1.图示矩形截面的I.Ⅱ两部分对z轴的静矩的关 系是( )
例 1 求下列各图的图形形心位置。
za
y1
1 2
a,
y2
3 2
a
z1
a,
z2
1 2
a
2a o
A1
y
n
Ai yi
i 1
n
Ai
2a2
1a 2 2a2
a2 a2
3 2
a
5 6
a
i 1
A2
a
yz
n
Ai zi
i 1
n
Ai
2a2 a a2 1 a 2
I z1
Iy
2
Iz
Iy
Iz 2
cos2
I yz sin 2
I y1z1
Iy
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节 • 静矩和形心 第二•节 惯性矩和惯性积
第三• 节 •
惯性矩和惯性积的 平行移轴和转轴公式
第• 四节 主惯性轴和主惯性矩
• 第五节 组合截面惯性矩的计算
•
小结
-
返回
第六章 截面的几何性质
• 第一节 静矩和形心
一、静矩(面积矩)定义: 微面积dA对 z轴和y轴的静矩分别为 ydA 和 zdA
当Sz=0或Sy=0时,必有yc=0或zc=0,可知截面对某轴的
静矩为零时,该轴必通过截面形心;反之,若某轴通过形心,
则截面对该轴的静矩为零。 -
返回 下一张 上一张 小结
二、形心公式:
yc
Sz ; A
zc
Sy . A
三、组合截面的静矩:n个简单图形组成的截面,其静矩为:
n
Sz Ai yci; i1
返回 下一张 上一张 小结
第三节 惯性矩和惯性积的平行移轴和转轴公式
一、平行移轴公式:
z1 y1dA (ya)2dA A
y2dA2a ydAa2 dA
Iz1za2A; y1 y b2A;
Iz1y1 Izyab;A
注意:y、z轴必须是形心轴。
二、转轴公式:
Iz 1A y 1 2 d A A (y co z s si)2 n d;A
空心圆截面: IP3D42(14)(;D d) 二、惯性矩:
定义:平面图形中任一微面积dA对z轴、y轴的惯性矩分别为: y2dA和Z2dA;则整个图形(面积为A)对z轴、y轴的惯性矩分别为:
Iz
y2dA;
A
Iy
z2dA;
A-
返回 下一张 上一张 小结
惯性矩是对某轴而言的,同一截面对不同轴的惯性矩值不同。 惯性矩单位:m4或mm4; 惯性矩恒为正值。 简单图形对轴的惯性矩由定义式积分计算。
第五节 组合截面惯性矩的计算 工程中常遇到组合截面。计算其形心主惯性矩时,应先确定形 心位置、形心主轴,再求形心主惯性矩。
-
返回 下一张 上一张 小结
例Байду номын сангаас–4:试计算图示T形截面的形心主惯性矩。 解:(1)确定形心坐标yc.
yc
1y1 1
2y2 2
50055001025 20cm;
500500
(2)计算形心主惯性矩:
截面(面积A)对z轴和y轴的静矩分
别为:
Sz
ydA;
A
Sy
zdA;
A
静矩为代数值。静矩单位:m3;mm3; 不同截面对同一坐标轴的静矩不同;同
一截面对不同坐标轴的静矩也不同。
若截面形心坐标为zc、yc,将面积视为平行力(即看作等 厚、均质薄板的重力),由合力矩定理可得:
SzAydA Ayc; SyA zdA Azc;
例5-3 圆形截面对其形心轴的惯性矩。
解:取yoz坐标系。取微面积dA=2zdy,则:
由 Iz 对 A y 2 称 dIy A 性 R IR z2 y : 2 6D 44R ;2 由 y 几 2 d 何 y 关 R 4 4 系 2= : 6 D y24 ;4 z2,
IP A2 d A A (y 2 z 2 ) d A I Z Iy . -
返回 下一张 上一张 小结
第二节 惯性矩和惯性积
一、极惯性矩:
定义:平面图形中任一微面积dA与它到坐 标原点O的距离ρ平方的乘积ρ2dA,称为该面积 dA对于坐标原点o的极惯性矩。
截面对坐标原点o的极惯性矩为:
IP
2dA;
A
简单图形的极惯性矩可由定义式积分计算。
实心圆截面: IP0D 222dA 3D42;
主惯性矩(主惯矩)—截面对主惯性轴的惯性矩;
形心主惯性轴(形心主轴)—通过形心的主惯性轴;
形心主惯性矩(形心主惯矩)—截面对形心主轴的惯性矩。
特点:①两个形心主惯性矩是截面对过形心所有各轴的惯性矩 中的极大值和极小值;
②有一根对称轴的截面,形心主轴是对称轴和与之垂直 的形心轴;
③有两根对称轴的截面,形心主轴是两根对称轴; ④无对称轴的截面,由转轴公式求对形心的惯性积为零 的 o 角,即 形心主惯性轴。
y 若c 分A 解1 A y 1 为1 1A A 2 2 、y 2 2 、0 .0 3三0 7 .0 2 个.4 矩2 7 形0 6 0 .4 .,4 2 则 8 1 8 .2 1 .3m ;6
y'c0 0 ..6 6 2 2 ..5 5 2 2 2 (1 .2 0 .2 6 1 2 .2 .4 )0 .1m 6 ;-
单位: m4,mm4;
-
返回 下一张 上一张 小结
例5-2 求矩形截面对其对称轴的惯性矩和惯性积。 解:取yoz坐标系。取微面积dA=bdy,则:
IzAy2dA hh//22y2bdyb 13 h2;
取微面积dA=hdz,则:
IyAz2dA bb//22z2hdzh 13b 2;
取微面积dA=dzdy,则:Izy 0;
Iz1Iz 2IyIz 2Iyco 2 sIzy si2n ;
Iy 1Iz 2IyIz 2Iyco 2 sIzy si2n ;
Iz1y1Iz 2Iysi2nIzyco2- s;
返回 下一张 上一张 小结
第四节 主惯性轴和主惯性矩:
主惯性轴(主轴)—使截面对zo、yo轴的惯性积 Izoyo 0 的这对 正交坐标轴;
(z、y轴即形心主轴)
z1z1a12151 012302 052501 0.1 7150cm 4;
z2z2a22211 052303 52025002.1 7150cm 4;
n
Sy Ai zci; i1
n
四、组合截面形心公式:
A i y ci
yc
i1 n
;
Ai
i1
例5-1 求图示T形截面形心位置。
n
A i z ci
zc
i1 n
;
Ai
i1
解:取参考坐标轴y、z,由对称图形,zc=0。 分解图形为1、2两个矩形,则
A 1 0 . 0 m 2 , 7 y 1 2 . 4 2 m ; A 2 6 0 . 4 m 2 ,y 8 2 1 . 2 m ;
三、惯性积:
定义:平面图形内,微面积dA与其两个 坐标z、y的乘积zydA在整个图形内的积分称 为该图形对z、y轴的惯性积。
Iz
y
z
A
ydA;
特点:①惯性积是截面对某两个正交
坐标轴而言。不同截面对同一对轴或同一截面对不同轴的惯性积
均不同。惯性积是代数值。
②若截面有一根为对称轴,则该截面对包括此对称轴在 内的一对正交坐标轴的惯性积必为零。
