内部排序算法的实现与比较

合集下载

数据结构-内排序

Shell排序的性能分析
Shell排序的时间复杂度在O(nlog2n)和O(n2)间， Knuth的统计结论是，平均比较次数和记录平均移动次数在n1.25与 1.6n1.25之间
Shell排序是一种不稳定的排序方法
最后谈一下delta的取法。 Shell最初的方案是delta=n/2， delta=delta/2，直到delta=1。Knuth的方案是delta=delta/3 +1。其它方案有：都取奇数为好；或delta互质为好等等。而使用象1, 2, 4, 8, …或1, 3, 6, 9, …这样的增量序列就不太合适，因为这样会使几个元素多次被分到一组中，从而造成重复排序，产生大量无用的比较操作
另外，在无序子表中向前移动的过程中，如果没有交换元素，则说明无序子表已有序，无须再做排序
24
冒泡排序算法实现
1 void bubble_sort(RecType R[ ], int n) { 2 //待排序元素用一个数组R表示，数组有n个记录
3 int i, j; 4 bool swap=TRUE; //判断无序子表是否已有序的变量
内排序和外排序按照排序过程中使用内、外存的不同将排序方法分为内排序和外排序。若待排序记录全部在内存中，称为内排序；若待排序记录的数量很大，以致内存一次不能容纳全部记录，在排序过程中需要进行内、外存交换，称为外排序。本章仅讨论内排序
内排序可分为五大类：插入排序、交换排序、选择排序、归并排序和基数排序
直接插入排序(straight insert sort) 折半插入排序(binary insert sort) Shell排序(Shell sort)
10
10.2.1 直接插入排序举例

数据结构-第十章-内部排序

0
1
2
3
4
5
6
7
8
i=5
MAXINT 49 2 3
MAXINT 49 6 3 MAXINT 49 6 3 MAXINT 49 6 8
38 1
38 1 38 1 38 1
65 97 5 0
65 5 65 5 65 5 97 0 97 0 97 0
76 4
76 4 76 4 76 4
13
27
49
i=6

最坏情况下,待排记录按关键字非递增有序排列（逆序）时，第 i 趟时第 i＋1 个对象必须与前面 i 个对象都做排序码比较, 并且每做1次比较就要做1次数据移动。总比较次数为 (n+2)(n-1)/2 次，总移动次数为 (n+4)(n-1)/2。在平均情况下的排序码比较次数和对象移动次数约为 n2/4。因此，直接插入排序的时间复杂度为 O(n2)。直接插入排序是一种稳定的排序方法。
折半插入排序 (Binary Insertsort)
基本思想既然每个要插入记录之前的纪录已经按关键字有序排列，在查找插入位臵时就没有必要逐个关键字比较，可以使用折半查找来实现。由此进行的插入排序称之为折半插入排序。
折半插入排序的算法
void BInsertSort (SqList &L){ for (i=2;i<=L.length;++i){ L.r[0]=L.r[i]; low=1;high=i-1; //查找范围由1到i-1 while(low<=high){ m=(low+high)/2; if LT(L.r[0].key,L.r[m].key) high=m-1; else low=m+1; }//while 折半查找 for (j=i-1;j>=high+1;--j) L.r[j+1]=L.r[j]; //折半查找结束后high+1位臵即为插入位臵 L.r[high+1]=L.r[0]; }//for }//BInsertSort

河北工业大学-数据结构实验报告-内部排序算法效率比较平台的设计与实现

实验五内部排序算法效率比较平台的设计与实现1.试验内容1、问题描述各种内部排序算法的时间复杂度分析结果只给出了算法执行时间的阶，或大概执行时间。

设计和实现内部排序算法效率比较平台，通过随机的数据比较各算法的关键字比较次数和关键字移动次数，以取得直观的感受。

2、基本要求（1）对以下6种常用的内部排序算法进行比较：起泡排序、直接插入排序、简单选择排序、快速排序、希尔排序、堆排序。

（2）待排序的表长不小于100；其中的数据要用伪随机数产生程序产生；至少要用5组不同的输入数据作比较；比较的指标为有关键字参加的比较次数和关键字的移动次数（关键字交换计为3次移动）。

（3）最后要对结果作出简单分析，包括对各组数据得出结果波动大小的解释。

3、测试数据由随机数产生器生成。

4、实现提示主要工作是设法在已知算法中的适当位置插入对关键字的比较次数和移动次数的计数操作。

程序还可以考虑几组数据的典型性，如，正序、逆序和不同程度的乱序。

注意采用分块调试的方法。

2.试验目的掌握多种排序方法的基本思想，如直接插入、冒泡、简单选择、快速、堆、希尔排序等排序方法，并能够用高级语言实现。

3.流程图4.源程序代码#include<iostream.h>#include<string.h>#include<stdlib.h>#define le 100struct point{char key[11];};//冒泡法void maopao(point c[]){point a,b[le];int i,j,jh=0,bj=0,q;for(i=0;i<le;i++){b[i]=c[i];};for(i=0;i<le;i++){for(j=le-1;j>i;j--){bj=bj+1;q=strcmp(b[i].key,b[j].key);if(q==1){a=b[i];b[i]=b[j];b[j]=a;jh=jh+3;};};};cout<<"冒泡法:"<<endl<<"完成的序列如下:"<<endl;for(i=0;i<le;i++){cout<<b[i].key<<" ";};cout<<endl<<"共进行比较"<<bj<<"次,进行交换"<<jh<<"次"<<endl<<"***************************"<<endl;};//直接插入排序void zhijiecharu(point c[]){point b[le+1];int i,j,jh=0,bj=0,q;for(i=0;i<le;i++){b[i+1]=c[i];};for(i=2;i<=le+1;i++){q=strcmp(b[i].key,b[i-1].key);bj=bj+1;if(q==-1){b[0]=b[i];b[i]=b[i-1];jh=jh+2;q=strcmp(b[0].key,b[i-2].key);bj=bj+1;for(j=i-2;q==-1;j--){b[j+1]=b[j];jh=jh+1;q=strcmp(b[0].key,b[j-1].key);bj=bj+1;};b[j+1]=b[0];jh=jh+1;};};cout<<"直接插入排序:"<<endl<<"完成的序列如下:"<<endl;for(i=1;i<le+1;i++){cout<<b[i].key<<" ";};cout<<endl<<"共进行比较"<<bj<<"次,进行交换"<<jh<<"次"<<endl<<"***************************"<<endl;};//void shellinsert(point c[],int dk,int d[]){int j,i,q;point a;for(i=dk+1;i<le+1;i++){q=strcmp(c[i].key,c[i-dk].key);d[0]=d[0]+1;if(q==-1){a=c[i];q=strcmp(a.key,c[i-dk].key);d[0]=d[0]+1;d[1]=d[1]+1;for(j=i-dk;j>0&&q==-1;j=j-dk){c[j+dk]=c[j];d[1]=d[1]+1;q=strcmp(a.key,c[j-dk].key);};c[j+dk]=a;d[1]=d[1]+1;};};};void shellsort(point c[],int dlta[],int t){int k,d[2],i;d[0]=0;d[1]=0;point b[le+1];for(k=0;k<le;k++){b[k+1]=c[k];};for(k=0;k<t;k++)shellinsert(b,dlta[k],d);cout<<"希尔排序:"<<endl<<"完成的序列如下:"<<endl;for(i=1;i<le+1;i++){cout<<b[i].key<<" ";};cout<<endl<<"共进行比较"<<d[0]<<"次,进行交换"<<d[1]<<"次"<<endl<<"***************************"<<endl;};//希尔排序void xier(point c[]){int dlta[20],t,i;t=le/2;for(i=0;i<20;i++){dlta[i]=t+1;if(t==0)break;t=t/2;};t=i+1;shellsort(c,dlta,t);};//简单选择排序void jiandanxuanze(point c[]){point a,b[le];int i,j,jh=0,bj=0,q,w;for(i=0;i<le;i++){b[i]=c[i];};for(i=0;i<le-1;i++){q=i;for(j=i+1;j<le;j++){bj=bj+1;w=strcmp(b[q].key,b[j].key);if(w==1)q=j;};if(q==i)continue;else {a=b[i];b[i]=b[q];b[q]=a;jh=jh+3;};};cout<<"简单选择排序排序:"<<endl<<"完成的序列如下:"<<endl;for(i=0;i<le;i++){cout<<b[i].key<<" ";};cout<<endl<<"共进行比较"<<bj<<"次,进行交换"<<jh<<"次"<<endl<<"***************************"<<endl;};int partition(point c[],int low,int high,int d[]){point a,b;int jh=0,bj=0,q;a=c[low];while(low<high){q=strcmp(c[high].key,a.key);d[0]=d[0]+1;while(low<high&&q!=-1){high--;q=strcmp(c[high].key,a.key);d[0]=d[0]+1;};b=c[low];c[low]=c[high];c[high]=b;d[1]=d[1]+3;q=strcmp(c[low].key,a.key);d[0]=d[0]+1;while(low<high&&q!=1){low++;q=strcmp(c[low].key,a.key);d[0]=d[0]+1;};b=c[low];c[low]=c[high];c[high]=b;d[1]=d[1]+3;};return(low);};void qsort(point c[],int low,int high,int d[]){int pivotloc;if(low<high){pivotloc=partition(c,low,high,d);qsort(c,low,pivotloc-1,d);qsort(c,pivotloc+1,high,d);};};//快速排序void kuaisu(point c[]){point b[le];int i,d[2];d[0]=0;d[1]=0;for(i=0;i<le;i++){b[i]=c[i];};qsort(b,0,le-1,d);cout<<"快速排序:"<<endl<<"完成的序列如下:"<<endl;for(i=0;i<le;i++){cout<<b[i].key<<" ";};cout<<endl<<"共进行比较"<<d[1]<<"次,进行交换"<<d[0]<<"次"<<endl<<"***************************"<<endl;};void diu(point b[],int we,int *jh,int *bj){point a;int i,q;for(i=we/2-1;i>=0;i--){q=strcmp(b[i].key,b[2*i].key);*bj=*bj+1;if(q==-1){a=b[i];b[i]=b[2*i];b[2*i]=a;*jh=*jh+3;};if(2*i+1<we){q=strcmp(b[i].key,b[2*i+1].key);*bj=*bj+1;if(q==-1){a=b[i];b[i]=b[2*i+1];b[2*i+1]=a;*jh=*jh+3;};};};a=b[we-1];b[we-1]=b[0];b[0]=a;*jh=*jh+3;};//堆排序void diup(point c[]){point b[le];int i,jh=0,bj=0,*j,*bl;j=&jh;bl=&bj;for(i=0;i<le;i++){b[i]=c[i];};for(i=le;i>1;i--){diu(b,i,j,bl);};cout<<"堆排序:"<<endl<<"完成的序列如下:"<<endl;for(i=0;i<le;i++){cout<<b[i].key<<" ";};cout<<endl<<"共进行比较"<<bj<<"次,进行交换"<<jh<<"次"<<endl<<"***************************"<<endl;};void main(){int i,j,n=10,ans,an;char b[]="abcdefghijklmnopqrstuvwxyz";point a[le];for(i=0;i<le;i++){n=10;an=rand()*(n-1)/RAND_MAX+1;n=26;for(j=0;j<an;j++){ans=rand()*(n-0)/RAND_MAX+0;a[i].key[j]=b[ans];};a[i].key[j]='\0';};for(i=0;i<le;i++){cout<<a[i].key<<endl;};zhijiecharu(a);maopao(a);xier(a);jiandanxuanze(a);kuaisu(a);diup(a);}参考自百度文库5.实验结果运行结果如下：直接插入排序:完成的序列如下:***************************冒泡法:完成的序列如下:***************************希尔排序:完成的序列如下:*************************** 简单选择排序排序:完成的序列如下:*************************** 快速排序:完成的序列如下:*************************** 堆排序:完成的序列如下:。

第三章内部排序算法比较

第三章内部排序算法比较3.1. 问题描述3.1.1 题目内容设计程序实现六种方法的内部排序：起泡排序、直接插入排序、简单选择排序、快速排序、希尔排序、堆排序。

并对各个内部排序算法进行实测比较。

3.1.2 基本要求程序分别对六种常用的内部排序算法进行实测比较：起泡排序、直接插入排序、简单选择排序、快速排序、希尔排序、堆排序。

待排序表的表长不小于100，其中数据要用随机数产生程序产生，要求用多组不同的输入数据进行比较，比较的指标为：有关键字参加的比较次数和关键字的移动次数（关键字交换计为3次的移动）。

3.1.3 待测试数据因为所产生的数据是随机数，所以只需要用户输入要产生的随机数的个数。

所以可根据需要设置以下一组数：5，10，50，300，1000，7000，20000，50000。

3.2. 需求分析3.2.1 程序的基本功能首先用户输入要测试的随机数的个数，然后可以进行各个选项对数据进行不同的测试，程序能分别输出用起泡排序、直接插入排序、简单选择排序、快速排序、希尔排序、堆排序所用的移动关键字的步数，以便比较各个排序算法的效率。

3.2.2 输入值的形式和范围程序设定输入的整型数据在100000之内。

3.2.3 输出形式程序将产生的随机数以数组的形式储存，并在屏幕上依次输出，排序后得到的有序数组也同样依次输出，同时输出跟踪的来的总移动步数。

3.2.4 测试数据要求在调试时，为了能方便判断得出的结果是否正确可使用数量小的随机数，如3、4、5。

在调试确定算法能得出正确结果后测试数据要求每组随机数的个数应大于100，最好更长，这样才能更加容易得出各个排序算法在时间上的不同。

3.3. 概要设计3.3.1 主程序流程及模块调用关系（1）主程序流程图：一. 产生随机数。

二. 各个排序算法图 3-1 程序流程图（2）模块调用关系图见下页：图 3-23.3.2 核心的粗线条伪码算法设置一个类class Algorithm{……..将各个排序算法的函数作为类中的构造函数……..}A;Algorithm Sorting( )1. 输入随机数的个数N；2. 调用随机数产生函数产生个N随机数并储存到Array[1]~~Array[N]中.3. 输入选择功能4．switch(c){case '1':调用起泡法对所产生的随机数进行排序;case '2':调用直接插入法对所产生的随机数进行排序;case '3':调用简单选择法对所产生的随机数进行排序;case '4':调用快速排序法对所产生的随机数进行排序;case '5':调用Shell排序对所产生的随机数进行排序;case '6':调用堆排序对所产生的随机数进行排序;case '7':产生下一组随机数据case '8':结束并退出程序3.4. 详细设计3.4.1 实现概要设计的数据类型.定义一个类，将每个算法都现在该类中：Class Algorithm{Public:Bubblesort(){……….}StraightInsertsort(){……….}Selectsort(){……….}Quiksort(){……….}Shellsort(){……….}Heapesort(){……….}}A;3.4.2 每个操作的伪码算法.（1）.起泡法排序伪码算法：Algorithm BubbleSort( ){while(k>1){//i>1表明上一趟曾进行过记录交换设定一个记录最后一次交换位置的整型int lastExchangeIndex=1;for(int j=1;j<k;j++){作循环当后一个元素小于前一个时L.elem[j+1].key<L.elem[j].key{相互交换元素的值.记录交换的元素的位置}将一趟排序中无序序列中最后一个记录的位置传递给k,做下一次循环（2）.直接插入排序的伪算法：Algorithm InsertSort()for(int i=2;i<=L.length;++i)判断如果第i个元素的值小于第i-1元素的值时{ 需将第i个元素插入有序子表将i元素复制为哨兵for(int j=i-1;L.elem[0].key<L.elem[j].key;--j)将元素记录后移然后将哨兵插入到正确位置}（3）.Shell排序伪算法Algorithm ShellSort(){设置一个整型变量福初始值为5（dlta=5; ）{ 做运算dlta = dlta/3+1;调用ShellInsert函数}当设置的整型变量大于1;ShellInsert( ) //ShellInsert函数{for(int i=dk+1;i<=L.length;++i)if(L.elem[i].key<L.elem[i-dk].key){ //需将L.elem.[i]插入有序增量子表L.elem[0]=L.elem[i];//暂存在L.elem.[0]int j=i-dk;do{ L.elem[j+dk] = L.elem[j];j = j - dk;}while(j > 0&&L.elem[0].key < L.elem[j].key); //记录后移，查找插入位置插入操作L.elem[j+dk]=L.elem[0];}（4）. 快速排序伪算法：Algorithm QuikSort(){判断需要排序的数组长度，如果大于1{调用Partition函数，将Low 到Hight一分为二分别调用QSort函数，分别对高低子表进行递归排序} }Partition(sqlist &R,int low,int high) //划分函数{//对记录子序列R[low....high]进行一趟快速排序，并返回枢轴记录所在位置，//使得在它之前的记录的关键字均不大于它的关键字，在它之后的记录的关键//字均不小于它的关键字将枢轴记录移至数组的闲置地方；枢轴记录关键字；从表的两端交替地向中间扫描；将比枢轴记录小的记录移到底端将比枢轴记录大的记录移到高端枢轴记录移到正确位置（R.elem[low] = R.elem[0]）返回枢轴的位置return low}void QSort(sqlist &R,int low,int high) 函数对记录序列R[s....t]进行快速排序{ 如果子表长度大于1{ 调用Partition对R[s...t]进行一次划分，并返回枢轴位置对底端子序列递归排序(QSort(R,low,pivotloc-1) ).对高断子序列递归排序(QSort(R,pivotloc+1,high) ).}3.4.3 主程序和其它模块的伪码算法.Algorithm main( )1. 函数运行，并先后调用菜单函数和随机数产生函数2. 进入while循环，再次调用菜单函数3．进入如下一个Switch语句，对各个功能进行调用switch(c){ case '1':调用起泡法对所产生的随机数进行排序;case '2':调用直接插入法对所产生的随机数进行排序;……….case '6':调用堆排序对所产生的随机数进行排序;case '7':产生下一组随机数据case '8':结束并退出程序3.5. 调试分析3.5.1 设计与调试过程中遇到的问题及分析、体会在程序的最初调试中因为没有把握好各个函数之间的调用关系，因而出现了许多错误，比如得不到排序结果等，然后将所有排序的函数都写在了一个类中，这样，只要声明一次，以后就可以非常方便，准确的调用各个函数了。

所有排序的原理

所有排序的原理排序是将一组数据按照某种特定顺序进行排列的过程。

在计算机科学中，排序是一种基本的算法问题，涉及到许多常见的排序算法。

排序算法根据其基本原理和实现方式的不同，可以分为多种类型，如比较排序、非比较排序、稳定排序和非稳定排序等。

下面将详细介绍排序的原理和各种排序算法。

一、比较排序的原理比较排序是指通过比较数据之间的大小关系来确定数据的相对顺序。

所有常见的比较排序算法都基于这种原理，包括冒泡排序、插入排序、选择排序、归并排序、快速排序、堆排序等。

比较排序算法的时间复杂度一般为O(n^2)或O(nlogn)，其中n是待排序元素的数量。

1. 冒泡排序原理冒泡排序是一种简单的比较排序算法，其基本思想是从待排序的元素中两两比较相邻元素的大小，并依次将较大的元素往后移，最终将最大的元素冒泡到序列的尾部。

重复这个过程，直到所有元素都有序。

2. 插入排序原理插入排序是一种简单直观的比较排序算法，其基本思想是将待排序序列分成已排序和未排序两部分，初始状态下已排序部分只包含第一个元素。

然后，依次将未排序部分的元素插入到已排序部分的正确位置，直到所有元素都有序。

3. 选择排序原理选择排序是一种简单直观的比较排序算法，其基本思想是每次从待排序的元素中选择最小（或最大）的元素，将其放到已排序部分的末尾。

重复这个过程，直到所有元素都有序。

4. 归并排序原理归并排序是一种典型的分治策略下的比较排序算法，其基本思想是将待排序的元素不断地二分，直到每个子序列只包含一个元素，然后将相邻的子序列两两归并，直到所有元素都有序。

5. 快速排序原理快速排序是一种常用的比较排序算法，其基本思想是通过一趟排序将待排序的元素分割成两部分，其中一部分的元素均比另一部分的元素小。

然后，对这两部分元素分别进行快速排序，最终将整个序列排序完成。

6. 堆排序原理堆排序是一种常用的比较排序算法，其基本思想是利用堆这种数据结构对待排序的元素进行排序。

内部排序算法的性能分析与探讨

表，采用不同的测试组数，测试了６种常用的内部排序算法的关键字比较次数和移动次数，从时
间复杂度方面给出了６种排序算法的优劣．关键词：算法评价；随机乱序；内排序；比较次数；移动次数中图分类号：Ｔ３１２Ｐ１．１５文献标识码：Ａ文章编号：１７ — ５０（０１５００ — ７６２０２２１）０ — ０３２
收稿日期：２１— ６８０１０ —１
作者简介：申雪琴（９３）１７一，女，甘肃张掖人，河西学院信息技术与传媒学院讲师，研究方向：计算机软
件与理论．
・
５・Ｏ
申雪琴：内部排序算法的性能分析与探讨
动次数的记数操作．
２１可排序表的抽象数据类型的定义．
Ｏ引言
排序是数据处理中经常使用的一种运算．排序的方法很多，应用也很广泛．排序过程中，文在
件放在内存的称为 “ 内排序” ；排序过程中，不仅需要内存，还需要外存的称为 “ 排序 ”．外按所
用策略的不同，排序方法又可以分为五种：插入排序、选择排序、交换排序、分配排序和并归排
Ｌｓｍｔ（／ｉＥｐ）／ｔｙ若可排序表为空表，则返回Ｔｕ，否则返回Ｆｌｒｅａｅｓ
● ● ● ● ● ●
】ＤｒｅａｌｉＡＴＯｄｒｂｅｓｌｔ
上述定义中，括号里面都各包含２参数Ｃ，还应包括返回上述６个和Ｓ种排序算法的关键字比较次数和移动次数的函数．别为：Ｂｂｌｏ）ｎｅｔｒ）ｅｃｏ）ｕｋｏ）ｈｌ分ｕｂｅｒ、Ｉｓｒｏｔ（、Ｓｌｔｒ、ＱｉＳｒ、Ｓｅ — Ｓｔ（ＳｅＳｔ（ｃｔ（ｌＳｒ）ｅｐｏｔ（其功能依次是冒泡排序、插入排序、选择排序、快速排序、希尔排序、堆ｏｔ（、ＨａＳｒ）．排序，返回关键字比较次数Ｃ和移动次数Ｓ．２．随机乱序算法的实现２

数据结构之各种排序的实现与效率分析

各种排序的实现与效率分析一、排序原理（1）直接插入排序基本原理：这是最简单的一种排序方法，它的基本操作是将一个记录插入到已排好的有序表中，从而得到一个新的、记录增1的有序表。

效率分析：该排序算法简洁，易于实现。

从空间来看，他只需要一个记录的辅助空间，即空间复杂度为O（1）.从时间来看，排序的基本操作为：比较两个关键字的大小和移动记录。

当待排序列中记录按关键字非递减有序排列（即正序）时，所需进行关键字间的比较次数达最小值n-1，记录不需移动；反之，当待排序列中记录按关键字非递增有序排列（即逆序）时，总的比较次数达最大值（n+2）(n-1)/2，记录移动也达到最大值（n+4）(n-2)/2.由于待排记录是随机的，可取最大值与最小值的平均值，约为n²/4.则直接插入排序的时间复杂度为O（n²）.由此可知，直接插入排序的元素个数n越小越好，源序列排序度越高越好（正序时时间复杂度可提高至O（n））。

插入排序算法对于大数组，这种算法非常慢。

但是对于小数组，它比其他算法快。

其他算法因为待的数组元素很少，反而使得效率降低。

插入排序还有一个优点就是排序稳定。

（2）折半插入排序基本原理：折半插入是在直接插入排序的基础上实现的，不同的是折半插入排序在将数据插入一个有序表时，采用效率更高的“折半查找”来确定插入位置。

效率分析：由上可知该排序所需存储空间和直接插入排序相同。

从时间上比较，折半插入排序仅减少了关键字间的比较次数，为O(nlogn)。

而记录的移动次数不变。

因此，折半查找排序的时间复杂度为O(nlogn)+O（n²）= O（n²）。

排序稳定。

（3）希尔排序基本原理：希尔排序也一种插入排序类的方法，由于直接插入排序序列越短越好，源序列的排序度越好效率越高。

Shell 根据这两点分析结果进行了改进，将待排记录序列以一定的增量间隔dk 分割成多个子序列，对每个子序列分别进行一趟直接插入排序, 然后逐步减小分组的步长dk，对于每一个步长dk 下的各个子序列进行同样方法的排序,直到步长为1 时再进行一次整体排序。

用Java实现常见的8种内部排序算法

⽤Java实现常见的8种内部排序算法⼀、插⼊类排序插⼊类排序就是在⼀个有序的序列中，插⼊⼀个新的关键字。

从⽽达到新的有序序列。

插⼊排序⼀般有直接插⼊排序、折半插⼊排序和希尔排序。

1. 插⼊排序1.1 直接插⼊排序/*** 直接⽐较，将⼤元素向后移来移动数组*/public static void InsertSort(int[] A) {for(int i = 1; i < A.length; i++) {int temp = A[i]; //temp ⽤于存储元素，防⽌后⾯移动数组被前⼀个元素覆盖int j;for(j = i; j > 0 && temp < A[j-1]; j--) { //如果 temp ⽐前⼀个元素⼩，则移动数组A[j] = A[j-1];}A[j] = temp; //如果 temp ⽐前⼀个元素⼤，遍历下⼀个元素}}/*** 这⾥是通过类似于冒泡交换的⽅式来找到插⼊元素的最佳位置。

⽽传统的是直接⽐较，移动数组元素并最后找到合适的位置*/public static void InsertSort2(int[] A) { //A[] 是给定的待排数组for(int i = 0; i < A.length - 1; i++) { //遍历数组for(int j = i + 1; j > 0; j--) { //在有序的序列中插⼊新的关键字if(A[j] < A[j-1]) { //这⾥直接使⽤交换来移动元素int temp = A[j];A[j] = A[j-1];A[j-1] = temp;}}}}/*** 时间复杂度：两个 for 循环 O(n^2)* 空间复杂度：占⽤⼀个数组⼤⼩，属于常量，所以是 O(1)*/1.2 折半插⼊排序/** 从直接插⼊排序的主要流程是：1.遍历数组确定新关键字 2.在有序序列中寻找插⼊关键字的位置* 考虑到数组线性表的特性，采⽤⼆分法可以快速寻找到插⼊关键字的位置，提⾼整体排序时间*/public static void BInsertSort(int[] A) {for(int i = 1; i < A.length; i++) {int temp = A[i];//⼆分法查找int low = 0;int high = i - 1;int mid;while(low <= high) {mid = (high + low)/2;if (A[mid] > temp) {high = mid - 1;} else {low = mid + 1;}}//向后移动插⼊关键字位置后的元素for(int j = i - 1; j >= high + 1; j--) {A[j + 1] = A[j];}//将元素插⼊到寻找到的位置A[high + 1] = temp;}}2. 希尔排序希尔排序⼜称缩⼩增量排序，其本质还是插⼊排序，只不过是将待排序列按某种规则分成⼏个⼦序列，然后如同前⾯的插⼊排序⼀般对这些⼦序列进⾏排序。

算法21--内部排序--归并排序

2019/10/20
实现这种递归调用的关键是为过程建立递归调用工作栈。通常，在一个过程中调用另一过程时，系统需在运行被调用过程之前先完成3件事:
（1）将所有实参指针，返回地址等信息传递给被调用过程；（2）为被调用过程的局部变量分配存储区；（3）将控制转移到被调用过程的入口。在从被调用过程返回调用过程时，系统也相应地要完成3件事：（1）保存被调用过程的计算结果；（2）释放分配给被调用过程的数据区；（3）依照被凋用过程保存的返回地址将控制转移到调用过程.
实际的意义：可以把一个长度为n 的无序序列看成是 n 个长度为 1 的有序子序列，首先做两两归并，得到 n/2 个长度为 2 的子序列；再做两两归并，…，如此重复，直到最后得到一个长度为 n
的有序序列。
归并排序
初始序列
[49] [38] [65] [97 [76] [13] [27]
第一步第二步
T(1)=1 T(n)=kT(n/m)+f(n)
2019/10/20
归并排序时间复杂性分析
• 合并趟数： log2n • 每趟进行比较的代价 n • 总的代价为 T(n) = O ( nlog2n ) • 在一般情况下：
c
n=1
T(n) =
T( n/2 ) + T( n/2 ) + cn n>1
优缺点：Ω的这个定义的优点是与O的定义对称，缺点是当 f(N) 对自然数的不同无穷子集有不同的表达式，且有不同的阶时，未能很好地刻画出 f(N)的下界。
2019/10/20
f(n) cg(n)
n0
n
2019/10/20
代入法解递归方程
方法的关键步骤在于预先对解答作出推测，然后用数学归纳法证明推测的正确性。

数据结构(C语言版)实验报告 (内部排序算法比较)

《数据结构与算法》实验报告一、需求分析问题描述：在教科书中，各种内部排序算法的时间复杂度分析结果只给出了算法执行时间的阶，或大概执行时间。

试通过随机数据比较各算法的关键字比较次数和关键字移动次数，以取得直观感受。

基本要求：（l）对以下6种常用的内部排序算法进行比较：起泡排序、直接插入排序、简单选择排序、快速排序、希尔排序、堆排序。

（2）待排序表的表长不小于100000；其中的数据要用伪随机数程序产生；至少要用5组不同的输入数据作比较；比较的指标为有关键字参加的比较次数和关键字的移动次数（关键字交换计为3次移动）。

（3）最后要对结果作简单分析，包括对各组数据得出结果波动大小的解释。

数据测试：二．概要设计1.程序所需的抽象数据类型的定义：typedef int BOOL; //说明BOOL是int的别名typedef struct StudentData { int num; //存放关键字}Data; typedef struct LinkList { int Length; //数组长度Data Record[MAXSIZE]; //用数组存放所有的随机数} LinkList int RandArray[MAXSIZE]; //定义长度为MAXSIZE的随机数组void RandomNum() //随机生成函数void InitLinkList(LinkList* L) //初始化链表BOOL LT(int i, int j,int* CmpNum) //比较i和j 的大小void Display(LinkList* L) //显示输出函数void ShellSort(LinkList* L, int dlta[], int t,int* CmpNum, int* ChgNum) //希尔排序void QuickSort (LinkList* L, int* CmpNum, int* ChgNum) //快速排序void HeapSort (LinkList* L, int* CmpNum, int* ChgNum) //堆排序void BubbleSort(LinkList* L, int* CmpNum, int* ChgNum) //冒泡排序void SelSort(LinkList* L, int* CmpNum, int* ChgNum) //选择排序void Compare(LinkList* L,int* CmpNum, int* ChgNum) //比较所有排序2 .各程序模块之间的层次（调用）关系：二、详细设计typedef int BOOL; //定义标识符关键字BOOL别名为int typedef struct StudentData //记录数据类型{int num; //定义关键字类型}Data; //排序的记录数据类型定义typedef struct LinkList //记录线性表{int Length; //定义表长Data Record[MAXSIZE]; //表长记录最大值}LinkList; //排序的记录线性表类型定义int RandArray[MAXSIZE]; //定义随机数组类型及最大值/******************随机生成函数********************/void RandomNum(){int i; srand((int)time(NULL)); //用伪随机数程序产生伪随机数for(i=0; i小于MAXSIZE; i++) RandArray[i]<=(int)rand(); 返回;}/*****************初始化链表**********************/void InitLinkList(LinkList* L) //初始化链表{int i;memset(L,0,sizeof(LinkList));RandomNum();for(i=0; i小于<MAXSIZE; i++)L->Record[i].num<=RandArray[i]; L->Length<=i;}BOOL LT(int i, int j,int* CmpNum){(*CmpNum)++; 若i<j) 则返回TRUE; 否则返回FALSE;}void Display(LinkList* L){FILE* f; //定义一个文件指针f int i;若打开文件的指令不为空则//通过文件指针f打开文件为条件判断{ //是否应该打开文件输出“can't open file”;exit(0); }for (i=0; i小于L->Length; i++)fprintf(f,"%d\n",L->Record[i].num);通过文件指针f关闭文件;三、调试分析1.调试过程中遇到的问题及经验体会:在本次程序的编写和调试过程中，我曾多次修改代码，并根据调试显示的界面一次次调整代码。

三种常用内部排序算法探讨

３简单选择排序
３１基本思想．在待排序的一组数据元素中．出最小的一个数据元素与第一个选位置的数据元素交换：然后在剩下的数据元素当中再找最小的与第二个位置的数据元素交换．如此循环到只剩下最后一个数据元素为止。３排序过程．２关键字：３１８７４１第一趟（将最小值１出与第一个数８选交换位置）：
０引言
排序是程序设计中非常重要的内容．每一种语言都涉及到排序，它的功能是将一组无序的数据变成有序．结果有两种：升序或者降序。排序依据所涉及的存储器不同．分为两大类：分别是内部排序和外部排序本文主要介绍内部排序．指待排序列完全存放在内存中所进行的排序过程．适合不太大的元素序列常用的内部排序方法有：冒泡法排序、简单选择排序、直接插入排序，每一种排序方法的基本思想、排序过程各不相同．现将该三种排序方法进行分析．主要从排序的思想、排序的过程以及算法的稳定性三个方面进行探讨
２１年０１
第２期９
ＳＩＮＥＥＨ０ＯＹＩＦＲＡＩＮＣＥＣ＆ＴＣＮＬＧＯＭＴＯＮ
ＯＩ论坛。Ｔ
科技信息
三种常用内部排序算法探讨
袁利芬郑道都（商丘职业技术学院软件学院河南商丘４６０）７００
【要】摘排序是计算机程序设计中一项经常而又重要的操作，研究排序算法具有重要的理论意义和广泛的应用价值。本文论述了常用的三种内部排序算法，并比较了它们的异同，最后得出一定指导意义的结论。【关键词】排序算法；冒泡排序；简单选择排序；直１４７】第二次【１４７】结果【】４１７

排序算法比较系统实验报告

排序算法比较系统一．项目计划书1.项目的选题意义随着计算机科学技术的快速发展，排序成为了计算机程序设计中的一种重要操作。

它在计算机图形、计算机辅助设计、机器人、模式识别及统计学等领域具有广泛应用。

在实际应用当中比如数据统计等方面都会用到。

而且对一组数据进行排序也方便了后面对数据查找的操作。

要知道在一个有序数组中查找和在一个随机无序数组中的查找的时间复杂度和系统消耗是有天壤之别的。

它的的功能是将一个数据元素（或记录）的任意序列，重新排列成一个关键字有序的序列。

由于排序法很多，但就其全面性能而言，很难提出一种被认为是最好的方法，每一种方法都有各自的优缺点，适合在不同的的环境下使用。

一般情况下，采用不同的排序算法效率会不一样。

因此，在不同的环境下选择相对效率最高的排序算法，能够有效加快工程实施的进度。

为了方便大家了解不同排序算法的时间效率，特建立一种排序算法比较系统，实现比较不同排序算法效率的目的。

2.项目的主要内容和目标排序算法比较系统主要实现的下列十种功能:一．简单选择排序；二．折半插入排序；三．直接插入排序；四．冒泡排序；五．希尔排序；六．快速排序；七．归并排序；八．堆排序；九．清屏；十．退出系统；3．项目的技术基础、特点及实施的条件该项目可用C语言实现，适于在单机环境下运行。

小组成员均已学习过C语言程序设计、数据结构、算法等课程，具有一定的开发能力。

4.项目人员分工所有人都参与了项目的选题、设计、实现及测试工作，项目负责人归纳整理小组成员讨论成果，并确定最终方案。

在实践阶段，按照功能模块具体分工如下：项目组负责人：李齐，构建模型、设计算法、设计界面、实现功能二、四、五、六、七、十项目组成员：刘运皇，初始化数据、实现功能一、三、八、九二．设计方案1.算法思想的选择与设计此项目来源于实际问题。

通常，在排序的过程中需进行下列两种基本操作：（1）比较两个关键字的大小；（2）将记录从一个位置移动至另一个位置。

常用排序算法的分析与比较

在数组序列ａｎ中，第１数与第２个数到第ｎ【１将个
２排序算法的分类
依据待排序的问题大小（记录数量ｎ的不同。）排序
过程中需要的存储器空间也不同．由此将排序算法分为两大类：排序、排序。内排序指待排序数据记录内外存放于计算机随机存储器ＲＭ中所进行的排序过程．Ａ
收稿日期：０２５２２１￣０ — ５修稿日期：０２０ —２２１—６５
个数依次比较．找出最小值，记下其位置Ｐ。比较完一轮后，存放了１ｎ个数中最小值所在的位置。交换ａ１Ｐ－［Ｏ与ａ】［的值。这时ａ】ｐ［为原ａ０到ａ — 】ｎ个数据记０［】［ｌｎ的
关键词：排序算法；时间复杂度；空间复杂度；定性；＋代码稳ｃ＋源
１排序的概念
随着计算机的发展与应用领域的越来越广．基于
内排序又分为：比较交换排序、择排序、泡排序、选冒插
录中的最小次比较，找出第２数到第ｎ数中的最小值．个个记
作者简介：德超（９４，，庆人，教授，士，究方向为计算机应用、法设计与分析王１６－）男重副博研算
则使序列（）关键字序列（）增（序）递减１按２递升或

排序算法实验报告

数据结构实验报告八种排序算法实验报告一、实验内容编写关于八种排序算法的C语言程序，要求包含直接插入排序、希尔排序、简单项选择择排序、堆排序、冒泡排序、快速排序、归并排序和基数排序。

二、实验步骤各种内部排序算法的比较：1.八种排序算法的复杂度分析〔时间与空间〕。

2.八种排序算法的C语言编程实现。

3.八种排序算法的比较，包括比较次数、移动次数。

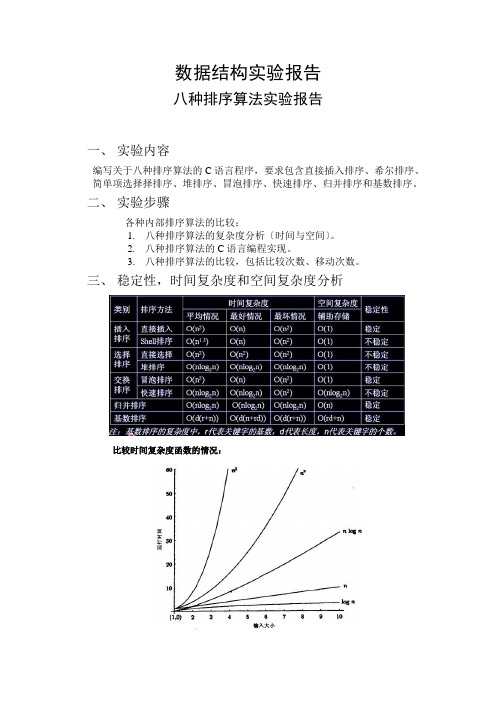
三、稳定性，时间复杂度和空间复杂度分析比较时间复杂度函数的情况：时间复杂度函数O(n)的增长情况所以对n较大的排序记录。

一般的选择都是时间复杂度为O(nlog2n)的排序方法。

时间复杂度来说：(1)平方阶(O(n2))排序各类简单排序:直接插入、直接选择和冒泡排序；(2)线性对数阶(O(nlog2n))排序快速排序、堆排序和归并排序；(3)O(n1+§))排序,§是介于0和1之间的常数。

希尔排序(4)线性阶(O(n))排序基数排序，此外还有桶、箱排序。

说明：当原表有序或基本有序时，直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数，时间复杂度可降至O〔n〕；而快速排序则相反，当原表基本有序时，将蜕化为冒泡排序，时间复杂度提高为O〔n2〕；原表是否有序，对简单项选择择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。

稳定性：排序算法的稳定性:假设待排序的序列中，存在多个具有相同关键字的记录，经过排序，这些记录的相对次序保持不变，则称该算法是稳定的；假设经排序后，记录的相对次序发生了改变，则称该算法是不稳定的。

稳定性的好处：排序算法如果是稳定的，那么从一个键上排序，然后再从另一个键上排序，第一个键排序的结果可以为第二个键排序所用。

基数排序就是这样，先按低位排序，逐次按高位排序，低位相同的元素其顺序再高位也相同时是不会改变的。

另外，如果排序算法稳定，可以防止多余的比较；稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序四、设计细节排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

数据结构内部排序算法比较

内部排序算法比较第一章问题描述排序是数据结构中重要的一个部分，也是在实际开发中易遇到的问题，所以研究各种排算法的时间消耗对于在实际应用当中很有必要通过分析实际结合算法的特性进行选择和使用哪种算法可以使实际问题得到更好更充分的解决！该系统通过对各种内部排序算法如直接插入排序，冒泡排序，简单选择排序，快速排序，希尔排序，堆排序、二路归并排序等，以关键码的比较次数和移动次数分析其特点，并进行比较，估算每种算法的时间消耗，从而比较各种算法的优劣和使用情况！排序表的数据是多种不同的情况，如随机产生数据、极端的数据如已是正序或逆序数据。

比较的结果用一个直方图表示。

第二章系统分析界面的设计如图所示：|******************************||-------欢迎使用---------||-----（1）随机取数-------||-----（2）自行输入-------||-----（0）退出使用-------||******************************|请选择操作方式：如上图所示该系统的功能有：（1）：选择 1 时系统由客户输入要进行测试的元素个数由电脑随机选取数字进行各种排序结果得到准确的比较和移动次数并打印出结果。

（2）选择 2 时系统由客户自己输入要进行测试的元素进行各种排序结果得到准确的比较和移动次数并打印出结果。

（3）选择0 打印“谢谢使用！！”退出系统的使用！！第三章系统设计（I）友好的人机界面设计：（如图3.1所示）|******************************||-------欢迎使用---------||-----（1）随机取数-------||-----（2）自行输入-------||-----（0）退出使用-------||******************************|（3.1）（II）方便快捷的操作：用户只需要根据不同的需要在界面上输入系统提醒的操作形式直接进行相应的操作方式即可！如图（3.2所示）|******************************||-------欢迎使用---------||-----（1）随机取数-------||-----（2）自行输入-------||-----（0）退出使用-------||******************************|请选择操作方式：（用户在此输入操作方式）（3.2）（III）系统采用定义结构体数组来存储数据。

算法22-- 内部排序--基数排序

yes a<c<b
a<c no
c<a<b
c<b<a
• 注意：树高代表比较的代价。因此只要知道了树高和结点数 n 的关系，就可以求出用比较法进行排序时的时间代价。另外，n 个结点的分类序列，其叶子结点共有 n! 片。
17
9.7 内部排序方法的比较
比较次数排序方法最好最差最好最差移动次数
269
184 278 f[7] 083 f[8] f[9]
930
f[3] f[4] f[5]
063 f[6]
r[0]→ 505
008
109
930
063
269
278
083
184
589
2018/10/16
第二趟收集的结果：
r[0]0
063
269
278
083
184
589
第三趟分配（按最高位 i = 1 ） e[0] 083 063 008 f[0] 第三趟收集 184 109 f[1] 278 269 f[2] f[3] f[4] 589 505 f[5] f[6] f[7] f[8] 930 f[9] e[1] e[2] e[3] e[4] e[5] e[6] e[7] e[8] e[9]
2018/10/16

j = 0; // 开始从0号队列（总共radix个队）开始收集 while ( f [j] == 0 ) j++; // 若是空队列则跳过 r[0].next=p = f [j]; //建立本趟收集链表的头指针 int last = e[j]; //建立本趟收集链表的尾指针 for ( k = j+1; k < radix; k++) // 逐个队列链接（收集） if ( f [k] ) { //若队列非空 r[last].next=f [k]; last = e[k]; //队尾指针链接 } r[last].next=0; //本趟收集链表之尾部应为0 } } // RadixSort

常见内部排序算法综述

【关键词】内部排序
基本思想比较
性能的排序方法应综合考虑下列因素
表１
１排序的相关概念．排序是计算机程序设计中的一种重要操作，它的功能是将一个数据元素的任意序列，重新排列成一个按关键字有序的序列。在程序设计中，排序是数据运算中的一种重要操作。根据排序过程中涉及的存储器不同，可以将排序方法分为两大类：一类是内部排序，指的是待排序地记录存放在计算机随机存储器中进行的排序过程。另一类是外部排序，指的是排需要对外存储器进行访问的排序过程。本课题主要研究内部排序，根据排序思想的不同，通常会将内部排序分为插入排序、选择排序、交换排序、归并排序和分配排序等五类。常见的有冒泡排序、快速排序、简单选择排序、堆排序、直接插入排序、归并排序。
．
排序方法最坏情况最好情况平均时间辅助存储稳定性
冒泡排序
快速排序
Ｏｎ（）
０（ｎ）
Ｏｎ（）
Ｏｎ）（
Ｏ１（）
稳定
０（ｌｎ０ｎｏｎ０１）不稳定ｎｏ）（ｌ）（唧ｇｇＯ（ｎ）Ｏｎ）（０（）不稳定１
Ｏｎｇ）Ｏｎｇ）Ｏｎｇ）Ｏｎ（ｌｎｏ（ｌ￣ｏ（ｌｎｏ（）
有序性非常敏感的排序算法。
（肤速排序。它是冒泡排序的改进算法，２基于分治策略。基本思想是，通过一趟排序将待排记录分割成独立的两部分，中一部分记录的其关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，已达到整个序列有序。若初始记录序列按关键字有序或基本有序时，快速排序将蜕化为冒泡排序，这是最坏的情况。当每次都能将序列恰好分成两个相等序列时，出现了快速排序的最佳情况，时ｎ个此关键需要做ｌ２趟排序，每一趟中所有划分关键字的和是ｎｏｎｇ在。（）３简单选择排序。基本思想是在待排序的一组数据元素中，出最选小的一个数据元素与第一个位置的数据元素交换；然后在剩下的数据元素当中再找最小的与第二个位置的数据元素交换，循环到只剩下最后一个数据元素为止。它的比较次数是一定的：（１２ｎ一）。因此无论何种序ｎ／列，正序和反序数据耗时相差不多，差的只是数据移动时间，相对数据的有序性不敏感。它虽然比较次数多，但它的数据交换量却很少。一般情况下还是快于冒泡排序。（）４堆排序。用大根堆排序的基本思想（当然也可以采用小根堆排序）先将初始文件建成一个大根堆，：此堆为初始的无序区；再选得一个关键字为最大的记录并与序列中最后一个记录交换，然后对序列中前ｎ１一个记录进行筛选，重新将它调整为一个“ 大顶堆 ” 如此反复直至排，序结束。由于它在直接选择排序的基础上利用了比较结果形成，效率提高很大。它完成排序的总比较次数为Ｏｎｏ２）它也是对数据的有序性（ｌｇｎ。不敏感的一种算法。但堆排序将需要做两个步骤：一是建堆，排序二是（调整堆）所以一般在小规模的序列中不合适，。但对于较大的序列，将表现出优越的性能。（埴接插人排序。直接插入排序是一种简单的排序方法，的基本５它排序思想是依次将待排序的记录逐一地按其关键字值的大小插入到一个已排好序的有序序列中，得到一个新的有序序列，直到所有的记录插完为止，而实现排序！从直接插入法也是一种对数据的有序性非常敏感的算法。在有序情况下只需要经过ｔ次比较，ｌ一１在最坏情况下，需要将ｎ玎１，比较。（一）２次（）６二路归并排序。基本思想是排序开始时将待排序列看成ｎ个已排好序的子序列，每一个子序列中只含有一个记录。将两个相邻的子序按算法ｍｅｇ逐一两两合并，ｒｅ得到ｎ２个有序子序列，对子序列进行／再上述过程。如此类推，直到最后归并得到一个有序序列为止。归并排序是一种非就地排序，需要与待排序序列一样多的辅助空间。在使用归并排序对两个已有序的序列归并时，将有很大的优势。对数据的有序性不敏感，但可改造成索引操作，效果将非常出色。３排序方法的性能比较及选择．（）１性能总结我们可以通过一些基本的性能标准对各个排序方法进行总结对比，表１见：（）响排序效果的因素２影因为不同的排序方法适应不同的应用环境和要求，以选择合适所

数据结构中内部排序算法的分析

・
３・８
ＣｏｕｅａＮｏ６２０１ｍｐｔｒＥｒ．０
数据结构中内部排序算法的分析
吴红芝，郭麦成，吴浩（长江大学计算机科学学院研究生院，湖北荆州４４２）３０３
摘要：排序是计算机程序设计中经常遇到的一个重要内容，它的功能是将一个数据集合，关键字重新排列成一个有按
序的序列。然而，由于排序算法程序须考虑设计路线、时间复杂度及稳定性等因素，学者在理解上存在较大的困难，初文
章针对这些具体问题，提供一些行之有效的解决方法。
关键词：排序；算法；稳定性；时间复杂度
ＡｎａｙｓｓｆＩｔｒｌＳｏｔｎｇＡｌｏｒｔｌｉｏｎｅｎａｒｉｇｉｈｍｉＤａａｔｕｃｕｒｎｔＳｒｔｅ
从排序的稳定性来看，稳定的排序有：直接插入排序、折半
与其他算法相比，序也是数据结构中的一种算法，排只不插入排序、冒泡排序和归并排序，稳定的排序有：尔排序、不希快速排序、简单选择排序和堆排序；从排序算法的时间复杂度它也涉及到一种算法的设计思想、参数的引用及时间复杂度等来看，直接插入排序、半插入排序、折冒泡排序、简单选择排序
ｄｔｉｍｓｎｏｎｒｅｅｓｑｅｃｂｋｙｒ．Ｈｏｖｒｂｃｕｓｏｈｆｃｏｓｗｈｉｈａａｔｅｉｔａｏｄｒｄｅｕｎｅｙｅｗｏｄｗｅｅ，ｅａｅｆｔｅａｔｒｃｍｕｔｅｏｓｄｒｄｎｏｔｎｐｏｒｍ，ｓｂｃｎｉｅｅｉｓｒｉｇｒｇａ

内部排序实验报告总结

内部排序实验报告总结引言内部排序是指对内存中的数据进行排序的过程。

在计算机科学中，排序是一项基础且重要的任务。

通过对大量数据进行排序，可以提高数据的查找和处理效率。

本次实验旨在比较和分析不同的内部排序算法的性能和效果。

实验目的•熟悉常见的内部排序算法•掌握内部排序算法的实现方法•比较和分析不同内部排序算法的性能和效果实验过程数据准备首先，我们需要准备一组待排序的数据。

在本次实验中，我们选择了随机生成的10000个整数作为待排序的数据。

冒泡排序冒泡排序是一种简单但效率较低的排序算法。

它的基本思想是通过不断交换相邻的元素，将最大的元素逐渐“冒泡”到数组的末尾。

冒泡排序的实现代码如下：def bubble_sort(arr):n = len(arr)for i in range(n):for j in range(0, n-i-1):if arr[j] > arr[j+1]:arr[j], arr[j+1] = arr[j+1], arr[j]插入排序插入排序是一种简单且高效的排序算法。

它的基本思想是将待排序的元素逐个插入到已排序的部分中，直到所有元素都插入完毕。

插入排序的实现代码如下：def insertion_sort(arr):n = len(arr)for i in range(1, n):key = arr[i]j = i - 1while j >= 0 and arr[j] > key:arr[j+1] = arr[j]j -= 1arr[j+1] = key快速排序快速排序是一种高效的排序算法。

它的基本思想是通过选择一个基准元素，将数组分割成两个子数组，其中一个子数组的所有元素都小于基准元素，另一个子数组的所有元素都大于基准元素。

然后对这两个子数组分别进行快速排序。

快速排序的实现代码如下：def quick_sort(arr, low, high):if low < high:pi = partition(arr, low, high)quick_sort(arr, low, pi-1)quick_sort(arr, pi+1, high)def partition(arr, low, high):i = low - 1pivot = arr[high]for j in range(low, high):if arr[j] < pivot:i += 1arr[i], arr[j] = arr[j], arr[i]arr[i+1], arr[high] = arr[high], arr[i+1]return i+1归并排序归并排序是一种稳定的排序算法。