几个幂函数图像
幂函数与函数图像_课件

► 探究点2 幂函数的图象与性质
例 2 已知幂函数 f ( x)m22m3 (m∈N*)的图象关
于 y 轴 对 称 , 且 在 (0 , + ∞) 上 是 减 函 数 , 求 满 足
m
m
(a 1) 3 (3 2a) 3 的 a 的取值范围.
[思路] 利用幂函数的奇偶性和单调性确定m的值, 再由幂函数的单调性确定a的值.
y=f(x)―y―×a→y=af(x);
Ⅱ、函数 y=f(ax)(a>0)的图象可以将函数 y=f(x) 的图象中的每一点纵坐标不变横坐标伸长(a>1)或压缩
(0<a<1)为原来的1a倍得到.
y=f(x)―x―×a→y=f(ax).
(3)识图:图象的分布范围、变化趋势、对 称性、周期性等等.
3.函数图象的应用 (1)利用函数图象,研究函数的几何性质,如单调性、 周期性、奇偶性、最值、零点、值域及定义域、对称性 等; (2)利用函数图象、数形结合的思想方法解题,将代 数问题转化为平面解析几何问题处理.
[点评] (1)利用描点法作函数图象的步骤是:列表、 描点、连线,若对函数图象的形状比较熟悉,可不必列 表,直接描点、连线;(2)利用图象变换作函数图象, 关键是找出基本初等函数,将函数的解析式分解为只有 单个变换的函数链,然后依次进行单一变换,最终得到 所要的函数图象.
已知图象变换:①关于 y 轴对称;②关于 x 轴
方法三:函数 y=ex 的图象向左平移 1 个单位得 y= ex+1 的图象,然后横坐标缩短为原来的一半,纵坐标不变 得函数 y=e1+2x 的图象,最后关于 y 轴对称得函数 y= e1+2(-x)=e1-2x 的图象;
方法四:函数 y=ex 的图象向左平移 1 个单位得 y =ex+1 的图象,然后关于 y 轴对称得函数 y=e-x+1 的图 象,最后横坐标缩短为原来的一半,纵坐标不变得函数 y=e-2x+1.
经典数学函数图像大全
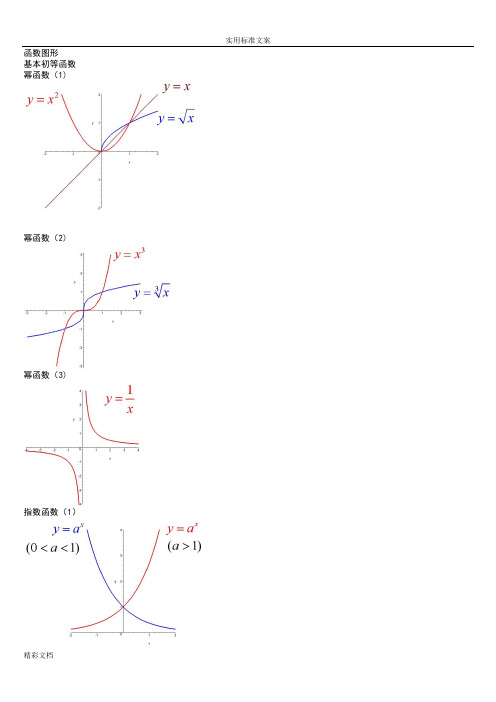
函数图形 基本初等函数 幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质) 极限的性质 (4) (局部有界性) 极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x 的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e 的值(1)e 的值(2)等价无穷小(x->0)sinx 等价于xarcsinx等价于xtanx等价于xarctanx 等价于x 1-cosx 等价于x^2/2sinx 等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线实用标准文案精彩文档y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1) 夹逼定理(2) 数列的夹逼性 (1) 数列的夹逼性 (2)。
2.3 幂函数图像与性质

(指数函数)
y x1
(幂函数)
y 3x
(指数函数)
1
y x2
(幂函数)
y 5x
(指数函数)
y5 x
(幂函数)
幂函数的图象及性质
对于幂函数,我们只讨论 =1,2,3,1 , 2
-1时的情形。
五个常用幂函数的图像和性质
(1) y x (2) y x2 (3) y x3
2
(4,2)
1
(-1,1)
(1,1)
y=x-1
2、在第一象限内, k >0,在
4
6 k <0,在(0,+∞)上为减函数.
-1
(-1,-1)
-2
3、k为奇数时,幂函数为奇函数,
k为偶数时,幂函数为偶函数.
-3
-4
4、幂函数图像不过第四象限。
例3
若m
4
1 2
23 4
3 4… 27 64 …
3 2…
1
y=x 2
x
函数 y x3 的图像
定义域: R 值 域: R
奇偶性:在R上是奇函数 单调性:在R上是增函数
1
函数 y x 2 的图像
定义域:[0,)
值 域:[0,)
奇偶性:非奇非偶函数
单调性:在[0,)上是增函数
4
3
2
1
(1,1)
-6
意
2、定义域与k的值有关系.
例1、下列函数中,哪几个函
数是幂函数? 答案:(1)(4)
(1)y = 1
x2
(3)y=2x
(2)y=2x2
(4)y=
1 x
(5) y=x2 +2
幂函数的图像及性质

函数,∴由 (a ?1)3 ? (3? 2a)3 ,得a-1<3+2a 即a>-4 .
∴所求a的取值范围是 (-4,+∞).
幂函数的图像及性质
【变形训练】
1、已知幂函数 y ? (mm2 ? ? 1)xm2?2m?3 ,当x∈
(0,+ ∞)时为减函数,则该幂函数的解析式是什么 ?奇偶性如何?单调性如何?
(2)由(1)知,f(x)的单调减区间为 (0,+∞), ∴函数 f(x) 在[1,+ ∞)上是减函数, ∴函数f(x)在[1,+∞)上的最大值为 f(1)=2.
幂函数的图像及性质
【典型例题】
2、已知幂函数 y=xp-3 (p∈N*)的图象关于 y轴
对称,且在 (0,+∞)上是减函数,求满足
p
p
(a ? 1) 3 ? (3 ? 2a ) 3 的a的取值范围 .
解:函数 f(x)在(0,+∞)上是减函数. 证明如
下:
任f(x取1)-x1、f(xx22)∈=(0x,212 +? x∞222),? 且2(xxx21122<?xx2x22,12)
?
2(x1
? x2)(x2 x12 x22
?
x1)
幂函数的图像及性质
【典型例题】
∵0<x 1<x2,∴ x1+x2>0,x2-x1>0, x12x22>0. ∴f(x1)-f(x2)>0,即f(x1)>f(x2). ∴函数f(x)在(0,+∞)上是减函数 .
解:∵函数 y=xp-3在(0,+∞)上是减函数,
∴p -3<0,即 p<3 ,
又∵ p ∈N*,∴ p =1,或 p =2.
∵函数y=xp-3的图象关于 y轴对称,∴ p-3是偶数,
常用函数图像
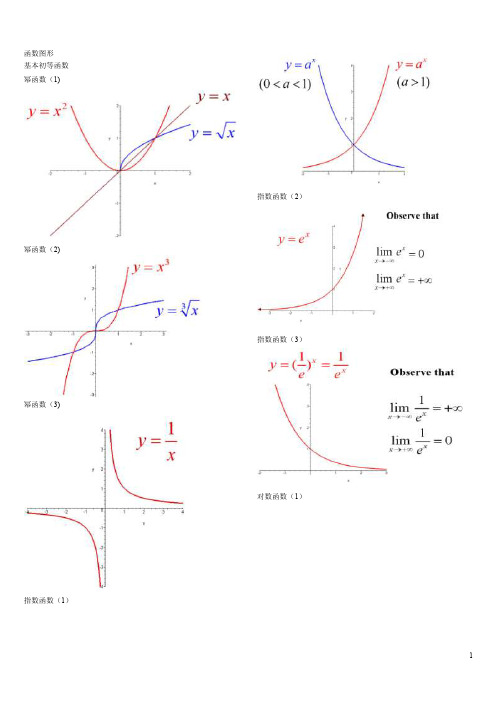
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1) 极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性) 极限的性质(3) (不等式性质) 极限的性质(4) (局部有界性) 极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)等价无穷小(x->0)sinx等价于xarcsinx等价于x tanx等价于x arctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2)数列的夹逼性(1) 数列的夹逼性(2) pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了文案编辑词条B 添加义项?文案,原指放书的桌子,后来指在桌子上写字的人。
经典数学函数图像大全-数学函数图像-函数图像全
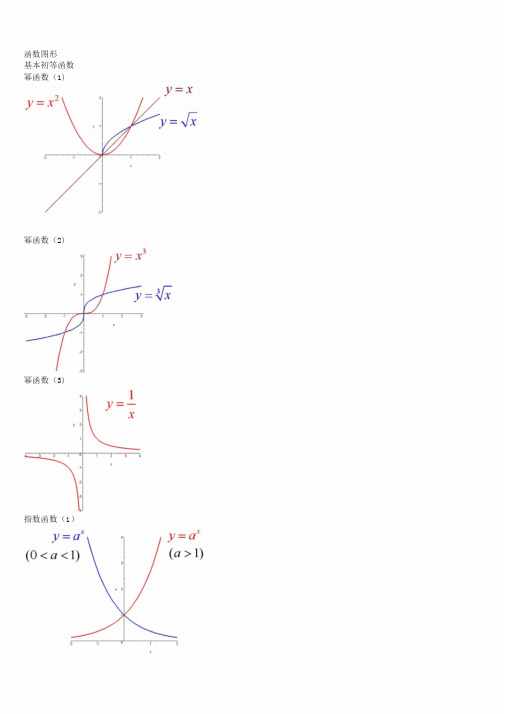
函数图形基本初等函数幂函数(1)幂函数(2) 幂函数(3) 指数函数(1)指数函数(3)对数函数(1)对数函数(2)三角函数(2)三角函数(3)三角函数(4)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(5)反三角函数(6)反三角函数(7)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(6)y=sin(1/x)(1) y=sin(1/x)(2)WOIRD格式y=[1/x](2 )y=sin(1/x)(3)y=sin(1/x)(4)y=[1/x](1)y=21/xy=21/x(2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx(x->∞)绝对值函数y=|x| 符号函数y=sgnx 取整函数y=[x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1)(局部保号性) 极限的性质(2)(局部保号性)极限的性质(3)(不等式性质) 极限的性质(4)(局部有界性) 极限的性质(5)(局部有界性)两个重要极限y=sinx/x(1)y=sinx/x(2)limsinx/x的一般形式y=(1+1/x)^x(1)y=(1+1/x)^x(2)lim(1+1/x)^x的一般形式(1) lim(1+1/x)^x的一般形式(2) lim(1+1/x)^x的一般形式(3) e的值(1)e的值(2)等价无穷小(x->0)sinx等价于x arcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线WOIRD格式y=(x+1)/(x-1)数列的夹逼性(1) y=sinx/x(x->∞)数列的夹逼性(2) 夹逼定理(1)夹逼定理(2)。
幂函数的图像与性质

x 1, x 1, 解析: x 1 ,有 解得 x<1, e 2 x 1 1n2,
x 1 x 1, 或 1 有 解得 1≤x≤8, x8 3 x 2
综上所述, {x|x≤8}.
这节课你有什么收获?
总结 (1)幂函数的定义; (2) 幂函数的图像与性质;
(慢增) (快增)
提高训练
练习 如图所示,曲线是幂函数 y = xa 在第一象限内
的图象,已知 a分别取
1 四个值,则相 1,1, , 2 2
C4 C2 C3 C1 应图象依次为:________
1
范例讲解 考点三:幂函数的单调性 例1. 利用单调性判断下列各值的大小。 (1)5.20.8 与 5.30.8 (2)0.20.3 与 0.30.3
y=x0
6
-1
-2
-3
-4
幂函数在第一象限的图像
幂函数图象在第一象限的分布情况:
1
1
=1
0 1
0
1
在直线x=1的右侧,从下往上, 幂指数增大
0< <1
图 像 特 点
第一象限
>1
y y
<0
y
1 o 1 x
1 o
1
1
x
o
1
x
性 质
都经过定点(1,1) 在[0,+∞)为 在[0,+∞)为 在(0,+∞)为 单调增函数. 单调增函数. 单调减函数.
3
2
1
(-1,1)
-6 -4 -2
(1,1)
2 4 6
-1
(-1,-1)
经典数学函数图像大全-数学函数图像-函数图像 全
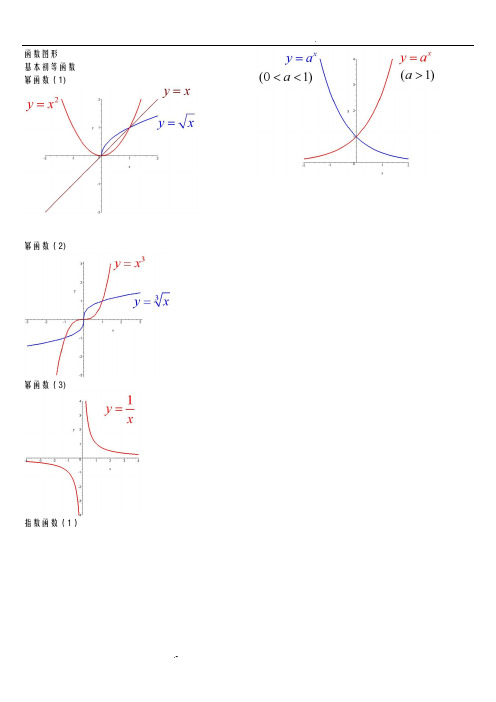
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2) y=xsin(1/x) y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1) 极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性) 极限的性质(2) (局部保号性)极限的性质(3) (不等式性质) 极限的性质(4) (局部有界性) 极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3) e的值(1)e的值(2)等价无穷小(x->0)sinx等价于x arcsinx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。
幂函数图像与性质

… … …
-2 -8 /
-1 -1 /
y 8
0 0 0
1 1 1
2 8
2
3 27
4 … 64 …
3
2 …
y=x3
6
4 2
y=x
1 2 3 4 x
1 2
-3
-2
-1
0 -2 -4 -6 -8
yx
(-2,4)
2
4
yx
3
3
(2,4)
y=x
2
yx
(1,1)
2 4 6
1 2
(-1,1)
1
yx
-4
1
三都民族中学高一数学备课组
2015年、10月、19日
问题引入
我们先看几个具体问题:
(1) 如果张红购买了每千克1元的蔬菜w千克,那么她需
要支付p= w 元 (2) 如果正方形的边长为a,那么正方形的面积
S
yx
2
a
2
yx
y x
1 2
(3) 如果立方体的边长为a,那么立方体的体积
V
a
3
3
(4)如果一个正方形场地的面积为S,那么这个正方形的 边长 a 度
x2 0,
所以f ( x1 ) f ( x2 ) 即幂函数f ( x ) x在[0,)上的增函数 .
例3 若 m 4
1 2
3 2m ,
1 2
1 2
则求m的取值范围.
解: 幂函数f ( x) x 的定义域是(0, ) 且在定义域上是减函数, 0 3 2m m 4 1 3 m ,即为m的取值范围. 3 2
2
α 为偶数时,幂函数为偶函数.
幂函数图像及性质

幂函数图像及性质一、什么是幂函数在数学中,幂函数是一种形式为 f(x) = x^a 的函数,其中 a 是实数。
当 a = 1 时,幂函数就是我们熟悉的一次函数,而当a > 1 时,幂函数的图像呈现出特定的形状。
二、幂函数的图像特点1. 当 a > 1 时•当 a > 1 时,幂函数的图像呈现出向上凹曲的形状。
•随着 x 的增大,函数值快速增加,增长迅猛。
•函数图像在第一象限,并在原点围绕原点对称。
2. 当 a = 1 时•当 a = 1 时,幂函数就是一次函数,函数图像为一条过原点的直线。
3. 当 0 < a < 1 时•当 0 < a < 1 时,函数的增长趋于缓慢,图像在第一象限被压缩,所占的范围变小。
三、幂函数的性质1. 定义域和值域•对于幂函数 f(x) = x^a,当 a 为奇数时,定义域为实数集,值域也为实数集;当 a 为偶数时,定义域为非负实数集,值域也为非负实数集。
2. 奇偶性•当 a 为奇数时,幂函数是奇函数,关于原点对称;•当 a 为偶数时,幂函数是偶函数,关于 y 轴对称。
3. 单调性•当 a > 1 时,幂函数是增函数;•当 0 < a < 1 时,幂函数是减函数。
4. 特殊情况•当 a < 0 时,幂函数的图像为反比例函数的图像。
四、实例分析示例 1考虑函数 f(x) = x^2,这是一个以原点为中心向上开口的抛物线图像。
随着 x 的增大,函数值快速增加,形成一个向上凸起的形状。
示例 2当考虑函数 f(x) = x^0.5 时,函数的图像呈现出一个缓慢上升的曲线,范围也变小了,整体呈现出一种被压缩的状态。
五、总结幂函数是数学中非常重要的一类函数,通过本文的讨论,我们了解了幂函数的图像特点和性质。
无论是在理论研究还是实际应用中,对于幂函数的理解都具有重要的意义。
希望本文内容能够帮助读者更深入地理解幂函数及其性质。
经典数学函数图像大全-数学函数图像
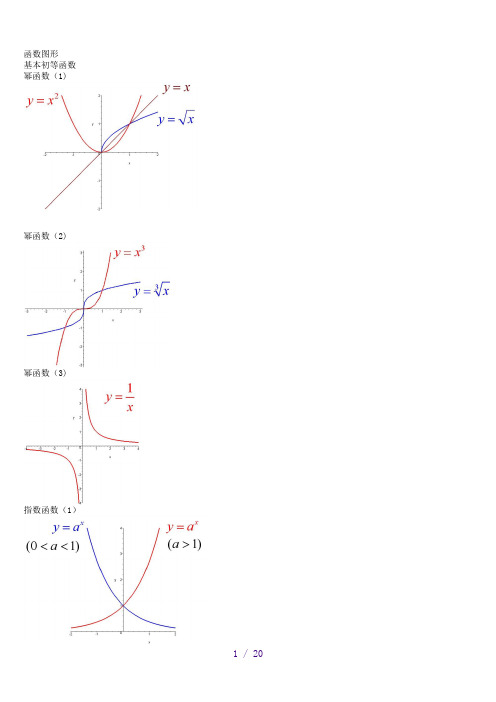
基本初等函数
幂函数(1)
幂函数(2)
幂函数(3)
指数函数(1)
指数函数(2)
指数函数(3)
对数函数(1)
对数函数(2)
三角函数(1)
三角函数(2)
三角函数(3)
三角函数(4)
三角函数(5)
反三角函数(1)
反三角函数(2)
反三角函数(3)
反三角函数(4)
反三角函数(5)
反三角函数(6)
反三角函数(7)
y = [1/x](1)
y = [1/x](2)
y=21/x
y=21/x (2)
y=xsin(1/x)
y=arctan(1/x)
y=e1/x
y=sinx (x->∞)
绝对值函数 y = |x|
符号函数 y = sgnx
取整函数 y= [x]
极限的几何解释 (1)
极限的几何解释 (2)
极限的几何解释 (3)
海涅定理
渐近线
水平渐近线
铅直渐近线
y=(x+1)/(x-1)
y=sinx/x (x->∞)
夹逼定理(1)
夹逼定理(2)
数列的夹逼性 (1)
数列的夹逼性 (2)
(注:文档可能无法思考全面,请浏览后下载,供参考。可复制、编制,期待你的好评与关注)
极限的性质 (1) (局部保号性)
极限的性质 (2) (局部保号性)
极限的性质 (3) (不等式性质)
极限的性质 (4) (局部有界性)
极限的性质 (5) (局部有界性)
两个重要极限
y=sinx/x (1)
y=sinx/x (2)
limsinx/x的一般形式
5、幂函数图像与性质

函数 y x 的图像
2
定义域:
R
值 域:[0,) 奇偶性: 在R上是偶函数 单调性: 在[0,)上是增函数
在(,0]上是减函数
函数 y x
1
的图像
定义域:{x x 0} 值 域:{ y
y 0}
奇偶性:在{x x 0}上是奇函数
单调性: 在(0,)上是减函数
问题引入
我们先看几个具体问题:
(1) 如果张红购买了每千克1元的蔬菜w千克,那么她需
要支付p= w 元 (2) 如果正方形的边长为a,那么正方形的面积
S
yx
2
a
2
yx
y x
1 2
(3) 如果立方体的边长为a,那么立方体的体积
V
a
3
3
(4)如果一个正方形场地的面积为S,那么这个正方形的 边长 a 度
幂函数的图象及性质
1 -1, 2 , 时的情形。
对于幂函数,我们只讨论 =1,2,3,
五个常用幂函数的图像和性质
3 2 y x y x (1) (2) y x (3)
(4) y x
1 2
(5) y x
1
函数 y x 的图像
定义域: 值 域:
R R
奇偶性:在R上是奇函数
单调性:在R上是增函数
函数 y x 的图像
1 2性:在[0,)上是增函数
幂函数的定义域、值域、奇偶性和单调性,随常 数α取值的不同而不同.
y=x
定义域 值域 R R
y = x2
R [0,+∞) 偶函数
y=
x3
y x
[0,+∞) [0,+∞) 非奇非偶 函数
幂函数9种图像总结

幂函数9种图像总结
幂函数的图像总结有9种:
1、当b>1时,y=x^b的图像是从原点开始向右上方延伸的曲线;
2、当0<b<1时,y=x^b的图像是从原点开始向右下方延伸的曲线;
3、当b=-1时,y=x^b的图像是一条水平线;
4、当b<-1时,y=x^b的图像是一条折线,从原点开始先向右上方,再向右下方延伸;
5、当b=0时,y=x^b的图像是一条垂直线;
6、当b>0且b不是整数时,y=x^b的图像是一条弯曲的折线,从原点开始向右上方延伸;
7、当b<0且b不是整数时,y=x^b的图像是一条弯曲的折线,从原点开始向右下方延伸;
8、当b是正整数时,y=x^b的图像是一条折线,从原点开始向右上方延伸;
9、当b是负整数时,y=x^b的图像是一条折线,从原点开始向右下方延伸。
幂函数的图像

幂函数的认识
对于课本上的幂函数,相信大家都可以熟练地画出它们的图像,并且能说出它们的性质。
但是对于其它的幂函数,你们也能画出它们的图像,并且能说出它们的性质吗?比如y=x -2,y=x 2/3,y=x -2/3,等等。
下面听听我的看法吧!
如果您仔细研究了幂函数的图像及性质,就会发现,其实课本上介绍的不仅仅是五个幂函数,而是所有的幂函数。
为什么这样说呢?画函数的图像,无非就是根据其定义域、值域、单调性、奇偶性等等来解决。
课本上介绍的五个幂函数,实际上是四类幂函数,即0<a<1、a=1、a>1、a<0 四种情形。
比如y=x -2这个函数,我们知道,-2是小于0的,所以她的定义域是())(+∞⋃∞-,00,,我们可以先画出它在第一象限的图像,它的图像与y=x -1的图像是相似的,所以先画出第一象限的图像,再看它的奇偶性,因为(-x)-2=x-2,所以它是偶函数。
而偶函数的图像是关于y 轴对称的,所以可以根据对称性画出剩余部分的图像。
如果x 不能小于0,那么只要画出第一象限的图像就可以了。
所以说,幂函数的图像只要按照下面四步做就可以了:第一步,根据a 的取值画出第一象限的图像;第二步,研究其定义域,如果x 不能小于0,那么所画的第一象限的图像即为该函数的图像,否则,进行下一步;第三步,研究其奇偶性,如果它是奇函数,则根据图像关于原点对称,可以画出其余的图像;如果它是偶函数,则根据图像关于y 轴对称,可以画出其余的图像。
幂函数并不神秘,试试吧!。
