勾股定理与面积计算
勾股定理解析三角形面积和边长之间的关系
勾股定理解析三角形面积和边长之间的关系勾股定理是初中数学中最基础的知识点之一，它指出：在一个直角三角形中，直角边的长度的平方等于另外两条边的长度平方之和。
用数学符号来表示就是：a² + b² = c²，其中c为斜边的长度，a、b为直角边的长度。
该定理的证明方法有很多种，其中最著名的莫过于毕达哥拉斯的证明。
面积和长度的关系三角形是初中数学中的另一个基础知识点，它有许多性质和公式，例如，三角形的面积可以用底边和高来表示，即面积等于底边长度乘以高的长度再除以2，公式可以表示为：S = 1/2 * a * h。
而在勾股定理中，三角形的斜边可以用另外两条直角边的长度表示，此时三角形的面积可以表示为：S = 1/2 * a * b。
三角形的面积公式中的“底边”和“高”都是用长度表示的，而勾股定理中的“直角边”和“斜边”也是用长度表示的。
这就说明，三角形的面积和边长之间存在着某种关系。
为了探究这种关系，我们可以结合勾股定理和三角形的面积公式来进行推导。
在勾股定理中，有c² = a² + b²，两边同时乘以2再除以c²，可以得到：2S/c² = 2ab/c²这里，S表示三角形的面积，c为斜边的长度，a、b为直角边的长度。
式子左边表示三角形的面积与斜边的平方之间的比值，式子右边表示直角边之积与斜边的平方之间的比值。
进一步移项得到：S = ab/c这就是三角形面积和边长之间的关系式。
结论：在任意一个三角形中，其面积等于底边长度和高的乘积再除以2，也等于任意两边长度之积再除以第三边的长度。
这两个公式是等价的。
结语通过对勾股定理和三角形面积公式的推导过程，我们可以发现它们之间存在着紧密的关系。
这不仅可以加深我们对数学知识的理解，还有助于我们更加灵活地运用它们，更好地解决实际问题。
勾股定理面积问题
1 S1 S2
2 S2
若变为作其它任意正 多边形，情形会怎样？ S3
B
C
S2
a c
B
b
A
S3 A S2
S1
C
S1
四变： 如图，分别以直角△ABC三边 为直径向外作三个半圆，其面积分别用S1、 S2、S3表示，则S1、S2、S3有什么关系？ 不难证明S3=S1+S2 .
C S1 a B
S2
b c
A
S3
观察下列图形，正方形1的边长为7，则 正方形2、3、4、5的面积之和为多少？ 规律：
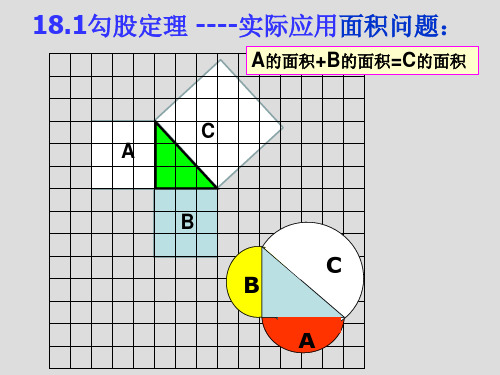
18.1勾股定理 ----实际应用面积问题：
A的面积+B的面积=C的面积
C
A
B
B A
C
D
二变：如图，分别以Rt △ABC三边为 斜边向外作三个等腰直角三角形，其面 积分别用S1、S2、S3表示，则S1、S2、S3 之间的关系是 S1 S2 S3，请说理。
C
S3
A
b
a c
S2
B
S1
三变：如图，分别以Rt △ABC三边为 边向外作三个正三角形，其面积分别用 S1、S2、S3表示，则S1、S2、S3之间的关 系是 S1 S2 S3 ，请说理。
2 3 4 5
S2+S3+S4+S5= S1
1
二.y=0 复习面积法证明勾股定理
已知S1=1,S2=3,S3=2,S4=4,求 S5、S6、S7的值
S3
S4
S2
结论:
S1+S2+S3+S4 =S5+S6 =S7
S1
S5
S6
勾股定理常用个公式
勾股定理常用个公式勾股定理是数学中一个非常重要的定理，它是平面几何中的基础定理，常用来求解直角三角形的边长和角度。
根据勾股定理，我们可以推导出多个相关的公式来解决各种问题。
在本篇文章中，我将介绍11个常用的勾股定理公式，每个公式都会附带一个解析和一个示例。
1.三角形斜边的长度(已知两边长度)：c=√(a²+b²)，其中a和b分别是直角三角形的两条直角边的长度，c是斜边的长度。
示例：已知一个直角三角形的两条直角边的长度分别为3和4，求斜边的长度。
解析：根据公式，c=√(3²+4²)=√(9+16)=√25=5、因此，斜边的长度为52.直角三角形的直角边长度(已知斜边长度和另一直角边长度)：a=√(c²-b²)，其中b是已知直角边的长度，c是斜边的长度。
示例：已知一个直角三角形的斜边长度为5，另一直角边的长度为4，求第二个直角边的长度。
解析：根据公式，a=√(5²-4²)=√(25-16)=√9=3、因此，第二个直角边的长度为33.直角三角形的直角边长度(已知斜边长度和另一直角边长度)：b=√(c²-a²)，其中a是已知直角边的长度，c是斜边的长度。
示例：已知一个直角三角形的斜边长度为5，另一直角边的长度为3，求第二个直角边的长度。
解析：根据公式，b=√(5²-3²)=√(25-9)=√16=4、因此，第二个直角边的长度为44.直角三角形的面积(已知两个直角边的长度)：A=1/2*a*b，其中a和b为直角三角形的两个直角边的长度。
示例：已知一个直角三角形的两个直角边的长度分别为3和4，求其面积。
解析：根据公式，A=1/2*3*4=6、因此，直角三角形的面积为65.直角三角形的周长(已知两个直角边的长度)：P=a+b+c，其中a和b分别为直角三角形的两个直角边的长度，c为斜边的长度。
利用勾股定理求面积
S2
π 8
a2,S3
π 8
b 2 ,S1
π 8
c2
S2 S3 S1
总结：与直角三角形三边相连的正方 形、等腰直角三角形、等边三角形以 及半圆甚至正多边形都有相同的结论： 即两直角边上图形面积的和等于斜边 上的图形的面积。
பைடு நூலகம்
1、如图，所有的四边形都是正方形，所有的三 角形都是直角三角形，其中最大的正方形的边 和长为7cm,则正方形A，B，C，D的面积之和为
a2 b2 c2
3 2
c2
S2
S3
S1
探究二：向外拓展半圆
1、如图，已知在△ABC中，∠ACB=90°，
AC=b,BC=a,AB=c，分别以Rt △ABC三边为 边向外作三个半圆，其面积分别用S1，S2， S3表示，求证：S1 S2 S3
ACB 90
a2 b2 c2
由以上探究知：SDCA SCBF SABE
即：S1 S4 S3 S5 S2 S4 S5 S6
S1
S3
S2
S6
68 2
24
勾股定理在求图形面积中的应用
如图，已知在△ABC中，∠ACB=90°，
AC=b,BC=a,AB=c，分别以Rt △ABC三边为边向 外作三个正方形，其面积分别用S1，S2，S3表 示，容易得出S1，S2，S3之间的关系
为 S1 S2 S3 ．
探究一：向外拓展三角形
1、如图，已知在△ABC中，∠ACB=90°，
AC=b,BC=a,AB=c，分别以Rt △ABC三边为
边向外作三个等腰直角三角形，其面积分
教材回归(二)勾股定理与图形面积课件
勾股定理在矩形中主要应用于计算矩形的对角线长度，以及 与矩形相关的直角三角形的斜边长度。
详细描述
在矩形中，勾股定理的应用通常涉及已知矩形的两条边长， 然后利用勾股定理计算出矩形的对角线长度。这个对角线长 度也可以用于计算与矩形相关的直角三角形的斜边长度。
勾股定理在三角形中的应用
总结词
勾股定理在三角形中主要用于确定三角形是否为直角三角形，以及计算直角三角形的斜 边长度。
详细描述
三角形面积的计算公式是底乘以高再 除以2，即A=1/2bh，其中A表示面 积，b表示底，h表示高。
圆形面积的计算
总结词
圆形面积可以通过半径的平方乘以π来计算。
详细描述
圆形面积的计算公式是π乘以半径的平方，即A=πr²，其中A表示面积，r表示半径。
03
勾股定理与图形面积的关 联
勾股定理在矩形中的应用
在车辆设计中，勾股定理可用于确定 车辆的尺寸和性能参数，如确定车辆 的长度、宽度和高度，以确保车辆的 安全性和稳定性。
在航空中，勾股定理可用于确定飞机 的航向、飞行高度和飞行距离，以确 保飞机的安全和准确飞行。
05
练习与思考
勾股定理的练习题
总结词
掌握勾股定理的应用
总结词
理解勾股定理的证明方法
总结词
等结构的尺寸和位置。
施工测量
在建筑施工过程中，勾股定理可用 于确定建筑物的角度、长度和高度 ，以确保施工的准确性和安全性。
桥梁工程
在桥梁设计中，勾股定理可用于确 定桥梁的斜率、长度和高度，以确 保桥梁的稳定性和安全性。
勾股定理在物理学中Байду номын сангаас应用
01
02
03
机械运动
勾股定理 定义
勾股定理定义
勾股定理是一种数学定理，通常用来计算三角形的边、角和面积等问题。
它的定义如下：
在一个直角三角形中，直角对边所对的角度为90度，另外两条边分别
为a和b，则有a²+b²=c²（c为斜边）。
这个定理是由公元前6世纪中国数学家毕达哥拉斯所发现的。
勾股定理的应用非常广泛，我们可以用它来解决各种问题。
下面我们
来一步步了解勾股定理的应用。
第一步，首先我们要确定一个三角形是否为直角三角形，这个很简单，只需要看这个三角形的两个边是否垂直即可。
第二步，我们要分别测量三角形的三个边的长度，这个也比较容易，
使用尺子或者测量仪器即可。
第三步，我们要根据勾股定理的公式进行计算：a²+b²=c²。
将值代入
即可得出斜边的长度。
除了计算斜边长度之外，我们还可以利用勾股定理计算角度。
如何计
算呢？我们可以使用反正切函数，即tan-1（b/a）来计算相应的角度。
此外，勾股定理还有一个重要的应用，就是解决三角形的面积问题。
如何计算三角形的面积呢？我们可以利用斜边长、底边长来计算。
设
三角形的底边为a，斜边为c，高为h，则三角形面积为S=1/2ah，而h 则为：h=c*sinB，其中B为底边a和斜边c所夹的角度。
以上就是勾股定理的一些应用方法。
这个定理虽然简单，但却非常实用，可以帮助我们解决很多实际问题。
我们要好好学习和应用这个定理，让它发挥更大的作用。
正方形面积法证明勾股定理
正方形面积法证明勾股定理正方形面积法证明勾股定理引言：勾股定理是数学中著名的定理之一，它是指在直角三角形中，斜边的平方等于直角两边的平方和。
这个定理被广泛地应用于各个领域，如物理、工程等。
本文将通过正方形面积法来证明勾股定理。
一、正方形面积法的原理二、证明勾股定理1. 画出直角三角形ABC2. 构造正方形ABDE和ACFG3. 求解正方形ABDE和ACFG的面积4. 推导出勾股定理三、结论一、正方形面积法的原理正方形面积法是指在一个平面直角坐标系中，通过构造两个相同的正方形来证明一个几何问题。
这种方法可以利用平面几何中图形的对称性和相似性来得到结论。
二、证明勾股定理1. 画出直角三角形ABC首先，在平面直角坐标系中画出一个直角三角形ABC。
假设AB为斜边，AC为邻边，BC为对边。
2. 构造正方形ABDE和ACFG其次，在BC上构造正方形ABDE，使D点在BC的延长线上。
在AC 上构造正方形ACFG，使F点在AC的延长线上。
3. 求解正方形ABDE和ACFG的面积由于正方形ABDE和ACFG是相同的，所以它们的面积也相等。
因此，我们只需要求出其中一个正方形的面积即可。
设AB=c, AC=b, BC=a，则BD=a-c，CF=a-b。
根据勾股定理可知：BD²+AD²=AB²CF²+AF²=AC²将BD和CF带入上式得：(a-c)²+AD²=c²(a-b)²+AF²=b²化简得：a²-2ac+c²+AD²=c²a²-2ab+b²+AF²=b²移项得：AD²=2ac-a^2AF^2=2ab-b^24. 推导出勾股定理因为ABDE和ACFG都是正方形，所以它们的面积分别为：S1 = AD×AD = (2ac-a^2)/4S2 = AF×AF = (2ab-b^2)/4同时，由于直角三角形ABC中斜边AB与直角边AC垂直，所以S1+S2=S(ABC)，即：(2ac-a^2)/4 + (2ab-b^2)/4 = ab/2移项得：a^2+b^2=c^2这就是勾股定理。
半圆的面积关系勾股定理
半圆的面积关系勾股定理
半圆的面积与勾股定理之间存在着一定的关系。
首先，让我们来看一下半圆的面积计算公式。
假设半圆的半径为r，则半圆的面积S可以通过以下公式计算，S = (1/2)πr^2，其中π是圆周率，约为3.14159。
这是基本的半圆面积的计算方法。
现在让我们来谈谈勾股定理。
勾股定理是指直角三角形中，直角边的平方等于另外两条边的平方和。
具体而言，如果一个直角三角形的两条直角边长分别为a和b，斜边长为c，那么勾股定理可以表示为，a^2 + b^2 = c^2。
将这两个概念结合起来，我们可以得出一个有趣的结论。
考虑一个半径为r的半圆，我们可以将其看作一个直角三角形的斜边，而半圆的直径就是这个直角三角形的斜边。
根据勾股定理，直角三角形的两条直角边的平方和等于斜边的平方，即(r/2)^2 + r^2 = c^2，化简得到，r^2/4 + r^2 = c^2，进一步化简得到，5r^2/4 = c^2。
因此，半圆的直径的平方等于5/4倍半圆的面积。
综上所述，半圆的面积与勾股定理之间的关系可以通过半圆的直径和半圆的面积之间的关系来体现。
这种关系为我们提供了一种
有趣的方式来理解几何形状之间的数学关系，并展示了数学在不同领域之间的重要应用。
希望这个回答能够帮助你更好地理解半圆的面积和勾股定理之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
图14.1.3G F E D
C B A 勾股定理与面积计算
1.（1）如图①，S 1、S 2和S 3分别是以直角三角形的两直
角边和斜边长为直径的半圆的面积，你能找出S 1、S 2和S 3之间的关
系吗请说明
理由
（2）如图②，如果直角三角形的两直角边分别为6cm ，8cm ，你能根据（1）的结论求出阴影部分的面积吗你能得出什么结论吗
2.如图（2）Rt ⊿ABC 中，∠ACB=900，AC=6，BC=8，S 1、S 2和S 3分
别是以直角三角形的两直角边和斜边长为边长的等边三角形。
你能找出S 1、S 2和S 3之间的关系吗请说明理由
3. 如图（3）Rt ⊿ABC 中，∠ACB=900，AB=3，S 1、S 2和S 3分别是以直角三角形的三边为斜边
的等腰直角三角形，则图中阴影部分的面积为 。
4. 如图（4） 以Rt ⊿ABC 的三边为边长向形外画正方形，以AB 为边的正方形的 面积为100cm 2，则这三个正方形的面积共为 cm 2。
（2）
（3） (41
242334图14.1.4
B 8题图
5、如图，所有的四边形都是正方形，所有的三角形都是直角三角形，
其中最大的正方形E的面积为81cm2，则正方形A、B、C、D的面积之和为。
6、如图14.1.4，是一个“羊头型”的图案，其作法是：从正方形1开始以它的一边为斜边向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形2，依次类推。
若正方形1的面积为64cm2，则正形7的边长为。
7.如图所示的弦图中，大正方形的面积为13，小正方形的面积为1，直角三角形的短直角边为a，较长直角边为b，求（a+b）= 。
8. 有一块土地的形状如图，∠B=∠D=90°，AB=20m，BC=15m，CD=7m，请计算这块土地面积。