【奥赛】小学数学竞赛：任意四边形、梯形与相似模型(三).教师版解题技巧 培优 易错 难

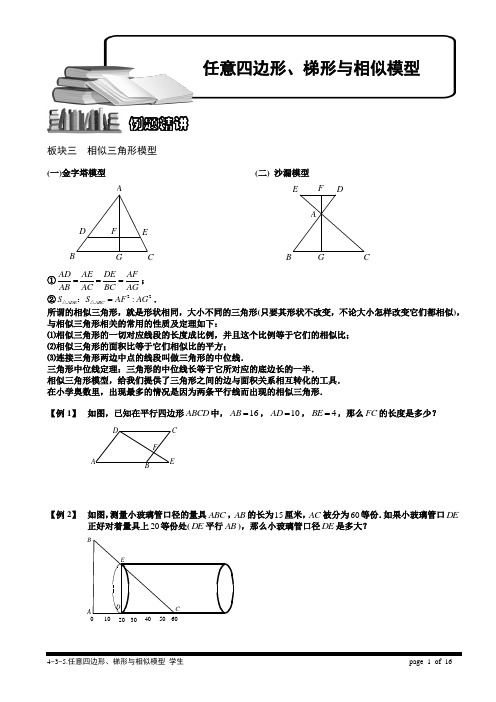
板块三 相似三角形模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===； ②22:ADE ABC S S AF AG =△△：．所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方；⑶连接三角形两边中点的线段叫做三角形的中位线．三角形中位线定理：三角形的中位线长等于它所对应的底边长的一半．相似三角形模型，给我们提供了三角形之间的边与面积关系相互转化的工具． 在小学奥数里，出现最多的情况是因为两条平行线而出现的相似三角形．【例 1】 如图，已知在平行四边形ABCD 中，16AB =，10AD =，4BE =，那么FC 的长度是多少？FE DCBA【考点】相似三角形模型 【难度】2星 【题型】解答 【解析】 图中有一个沙漏，也有金字塔，但我们用沙漏就能解决问题，因为AB 平行于CD ，所以::4:161:4BF FC BE CD ===，所以410814FC =⨯=+．【答案】8【例 2】 如图，测量小玻璃管口径的量具ABC ，AB 的长为15厘米，AC 被分为60等份．如果小玻璃管口DE正好对着量具上20等份处(DE 平行AB )，那么小玻璃管口径DE 是多大？例题精讲任意四边形、梯形与相似模型605040302010EA D C B【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 有一个金字塔模型，所以::DE AB DC AC =，:1540:60DE =，所以10DE =厘米． 【答案】10【例 3】 如图，DE 平行BC ，若:2:3AD DB =，那么:ADE ECB S S =△△________．A ED CB【考点】相似三角形模型 【难度】2星 【题型】填空 【解析】 根据金字塔模型:::2:(23)2:5AD AB AE AC DE BC ===+=，22:2:54:25ADE ABC S S ==△△， 设4ADE S =△份，则25ABC S =△份，255315BEC S =÷⨯=△份，所以:4:15ADE ECB S S =△△． 【答案】4:15【例 4】 如图， ABC △中，DE ，FG ，BC 互相平行，AD DF FB ==，则::ADE DEGF FGCB S S S =△四边形四边形 ．EGF A D CB【考点】相似三角形模型 【难度】3星 【题型】填空 【解析】 设1ADE S =△份，根据面积比等于相似比的平方，所以22::1:4ADE AFG S S AD AF ==△△，22::1:9ADE ABC S S AD AB ==△△，因此4AFG S =△份，9ABC S =△份，进而有3DEGF S =四边形份，5FGCB S =四边形份，所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形【答案】1:3:5【巩固】如图，DE 平行BC ，且2AD =，5AB =，4AE =，求AC 的长．A ED CB【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 由金字塔模型得:::2:5AD AB AE AC DE BC ===，所以42510AC =÷⨯= 【答案】10【巩固】如图， ABC △中，DE ，FG ，MN ，PQ ，BC 互相平行，AD DF FM MP PB ====，则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 ．Q E GNMF PA D CB【考点】相似三角形模型 【难度】3星 【题型】填空 【解析】 设1ADE S =△份，22::1:4ADE AFG S S AD AF ==△△，因此4AFG S =△份，进而有3DEGF S =四边形份，同理有5FGNM S =四边形份，7MNQP S =四边形份，9PQCB S =四边形份．所以有::::1:3:5:7:9ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形【总结】继续拓展，我们得到一个规律：平行线等分线段后，所分出来的图形的面积成等差数列． 【答案】1:3:5:7:9【例 5】 已知ABC △中，DE 平行BC ，若:2:3AD DB =，且DBCE S 梯形比ADE S △大28.5cm ，求ABC S △．A ED CB【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 根据金字塔模型::2:(23)2:5AD AB DE BC ==+=，22:2:54:25ADE ABC S S ==△△，设4ADE S =△份，则25ABC S =△份，25421DBCE S =-=梯形份，DBCE S 梯形比ADE S △大17份，恰好是28.5cm ，所以212.5cm ABC S =△【答案】12.5【例 6】 如图：MN 平行BC ， :4:9MPN BCP S S =△△，4cm AM =，求BM 的长度NMPA C B【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 在沙漏模型中，因为:4:9MPN BCP S S =△△，所以:2:3MN BC =，在金字塔模型中有：::2:3AM AB MN BC ==，因为4cm AM =，4236AB =÷⨯=cm ，所以642cm BM =-=【答案】2【巩固】如图，已知DE 平行BC ，:3:2BO EO =，那么:AD AB =________．OED C BA【考点】相似三角形模型【难度】3星【题型】填空【解析】由沙漏模型得::3:2BO EO BC DE==，再由金字塔模型得::2:3AD AB DE BC==．【答案】2:3【例 7】如图，ABC∆中，1 4AE AB=，1 4AD AC=，ED与BC平行，EOD∆的面积是1平方厘米．那么AED∆的面积是平方厘米．AB CDEO【考点】相似三角形模型【难度】3星【题型】填空【解析】因为14AE AB=，14AD AC=，ED与BC平行，根据相似模型可知:1:4ED BC=，:1:4EO OC=，44COD EODS S∆∆==平方厘米，则415CDES∆=+=平方厘米，又因为::1:3AED CDES S AD DC∆∆==，所以15533AEDS∆=⨯=(平方厘米)．【答案】53【例 8】如下图，正方形ABCD边长为l0厘米，BO长8厘米。

AE=____厘米。

EOD CBA【考点】相似三角形模型【难度】3星【题型】填空【关键词】走美杯，5年级，决赛，第4题，10分【解析】△AOB与△EDA相似，对应边成比例。

AB：BO=AE：AD，AE=AB×AD÷BO=10×10÷8=12.5(厘米)。

【答案】12.5【例 9】如图，已知正方形ABCD的边长是12厘米，E是CD边上的中点，连接对角线AC，交BE于点O，则三角形AOB的面积是（）平方厘米。

A、24B、36C、48D、60【考点】相似三角形模型【难度】3星【题型】选择【关键词】华杯赛，五年级，初赛【解析】C【答案】C【例 10】 在图中的正方形中，A ，B ，C 分别是所在边的中点，CDO V 的面积是ABO V 面积的几倍？ABCDO E FABCD O【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 连接BC ，易知OA ∥EF ，根据相似三角形性质，可知::OB OD AE AD =，且::1:2OA BE DA DE ==，所以CDO V 的面积等于CBO V 的面积；由1124OA BE AC ==可得3CO OA =，所以3CDO CBO ABO S S S ==V V V ，即CDO V 的面积是ABO V 面积的3倍．【答案】3【例 11】 图30-10是一个正方形，其中所标数值的单位是厘米．问：阴影部分的面积是多少平方厘米?【考点】相似三角形模型 【难度】4星 【题型】解答 【解析】 如下图所示，为了方便所叙，将某些点标上字母，并连接BG ．A设△AEG 的面积为x ，显然△EBG 、△BFG 、△FCG 的面积均为x ，则△ABF 的面积为3x ，120101002ABF S ∆=⨯⨯=即1003x =，那么正方形内空白部分的面积为40043x =.所以原题中阴影部分面积为400800202033⨯-= (平方厘米)． 【答案】8003【例 12】 如图，线段AB 与BC 垂直，已知4AD EC ==，6BD BE ==，那么图中阴影部分面积是多少？A BDA BDA BD【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 解法一：这个图是个对称图形，且各边长度已经给出，不妨连接这个图形的对称轴看看．作辅助线BO ，则图形关于BO 对称，有ADO CEO S S =V V ，DBO EBO S S =V V ，且:4:62:3ADO DBO S S ==V V ． 设ADO V 的面积为2份，则DBO V 的面积为3份，直角三角形ABE 的面积为8份．因为610230ABE S =⨯÷=V ，而阴影部分的面积为4份，所以阴影部分的面积为308415÷⨯=．解法二：连接DE 、AC ．由于4AD EC ==，6BD BE ==，所以DE ∥AC ，根据相似三角形性质，可知::6:103:5DE AC BD BA ===，根据梯形蝴蝶定理，()()22:::3:35:35:59:15:15:25DOE DOA COE COA S S S S =⨯⨯=V V V V ，所以()():1515:915152515:32ADEC S S =++++=阴影梯形，即1532ADECS S=阴影梯形； 又11101066=3222ADEC S =⨯⨯-⨯⨯梯形，所以151532ADEC S S ==阴影梯形．【答案】15【例 13】 如图，四边形ABCD 和EFGH 都是平行四边形，四边形ABCD 的面积是16，:3:1BG GC =，则四边形EFGH 的面积=________．G ECBA【考点】相似三角形模型 【难度】3星 【题型】填空 【关键词】华杯赛，精英邀请赛 【解析】 因为FGHE 为平行四边形，所以//EC AG ，所以AGCE 为平行四边形．:3:1BG GC =，那么:1:4GC BC =，所以1116444AGCE ABCD S S =⨯=⨯=Y Y ．又AE GC =，所以::1:3AE BG GC BG ==，根据沙漏模型，::3:1FG AF BG AE ==，所以334344FGHE AGCE S S ==⨯=Y Y ．【答案】3【例 14】 已知三角形ABC 的面积为a ，:2:1AF FC =，E 是BD 的中点，且EF ∥BC ，交CD 于G ，求阴影部分的面积．【考点】相似三角形模型 【难度】4星 【题型】解答 【解析】 已知:2:1AF FC =，且EF ∥BC ，利用相似三角形性质可知::2:3EF BC AF AC ==，所以23EF BC =，且:4:9AEF ABC S S =V V ． 又因为E 是BD 的中点，所以EG 是三角形DBC 的中位线，那么12EG BC =，12::3:423EG EF ==，所以:1:4GF EF =，可得:1:8CFG AFE S S =V V ，所以:1:18CFG ABCS S =V V ，那么18CFG aS =V ．【答案】18a【例 15】 已知正方形ABCD ，过C 的直线分别交AB 、AD 的延长线于点E 、F ，且10cm AE =，15cmAF =，求正方形ABCD 的边长．FAEDCB【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 方法一：本题有两个金字塔模型，根据这两个模型有::BC AF CE EF =，::DC AE CF EF =，设正方形的边长为cm x ，所以有1BC DC CE CF AF AE EF EF +=+=，即11510x x+=，解得6x =，所以正方形的边长为6cm ．方法二：或根据一个金字塔列方程即151015x x-=，解得6x =【答案】6【例 16】 如图，三角形ABC 是一块锐角三角形余料，边120BC =毫米，高80AD =毫米，要把它加工成正方形零件，使正方形的一边在BC 上，其余两个顶点分别在AB 、AC 上，这个正方形零件的边长是多少？HGNPAD CB【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 观察图中有金字塔模型5个，用与已知边有关系的两个金字塔模型，所以有PN AP BC AB =，PH BPAD AB=，设正方形的边长为x 毫米，PN PH BC AD +=1AP BP AB AB +=，即112080x x+=，解得48x =，即正方形的边长为48毫米．【答案】48【巩固】如图，在ABC △中，有长方形DEFG ，G 、F 在BC 上，D 、E 分别在AB 、AC 上，AH 是ABC △边BC 的高，交DE 于M ，:1:2DG DE =，12BC =厘米，8AH =厘米，求长方形的长和宽．E H GMFAD CB【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 观察图中有金字塔模型5个，用与已知边有关系的两个金字塔模型，所以DE AD BC AB =，DG BDAH AB=，所以有1DE DG AD BD BC AH AB AB +=+=，设DG x =，则2DE x =，所以有21128x x +=，解得247x =，4827x =，因此长方形的长和宽分别是487厘米，247厘米．【答案】长487，宽247【例 17】 图中ABCD 是边长为12cm 的正方形，从G 到正方形顶点C 、D 连成一个三角形，已知这个三角形在AB 上截得的EF 长度为4cm ，那么三角形GDC 的面积是多少？ ABCD E FGNMABCDE FG【考点】相似三角形模型 【难度】4星 【题型】解答 【解析】 根据题中条件，可以直接判断出EF 与DC 平行，从而三角形GEF 与三角形GDC 相似，这样，就可以采用相似三角形性质来解决问题． 做GM 垂直DC 于M ，交AB 于N ．因为EF ∥DC ，所以三角形GEF 与三角形GDC 相似，且相似比为:4:121:3EF DC ==， 所以:1:3GN GM =，又因为12MN GM GN =-=，所以()18GM cm =，所以三角形GDC 的面积为()2112181082cm ⨯⨯=．【答案】108【例 18】 如图，将一个边长为2的正方形两边长分别延长1和3，割出图中的阴影部分，求阴影部分的面积是多少？E【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 根据相似三角形的对应边成比例有：31223NF =++；12312EM =++， 则59NF =，53EM =，19512225330S ⎛⎫⎛⎫=⨯-⨯-= ⎪ ⎪⎝⎭⎝⎭阴【答案】130【例 19】 图中的大小正方形的边长均为整数(厘米)，它们的面积之和等于52平方厘米，则阴影部分的面积是 ．H【考点】相似三角形模型 【难度】3星 【题型】填空 【关键词】101中学 【解析】 设大、小正方形的边长分别为m 厘米、n 厘米(m n >)，则2252m n +=，所以8m <．若5m ≤，则222525052m n +<⨯=<，不合题意，所以m 只能为6或7．检验可知只有6m =、4n =满足题意，所以大、小正方形的边长分别为6厘米和4厘米．根据相似三角形性质，::6:43:2BG GF AB FE ===，而6BG GF +=，得 3.6BG =(厘米)，所以阴影部分的面积为：16 3.610.82⨯⨯=(平方厘米)． 【答案】10.8【例 20】 如图，O 是矩形一条对角线的中点，图中已经标出两个三角形的面积为3和4，那么阴影部分的一块直角三角形的面积是多少？DBDB【考点】相似三角形模型 【难度】4星 【题型】解答【解析】 连接OB ,面积为4的三角形占了矩形面积的14，所以431OEB S =-=△,所以:1:3OE EA =,所以:5:8CE CA =,由三角形相似可得阴影部分面积为25258()88⨯=．【答案】258【例 21】 已知长方形ABCD 的面积为70厘米，E 是AD 的中点，F 、G 是BC 边上的三等分点，求阴影EHO △的面积是多少厘米？DCBAABC D【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 因为E 是AD 的中点，F 、G 是BC 边上的三等分点，由此可以说明如果把长方形的长分成6份的话，那么3ED AD ==份、2BF FG GC ===份，大家能在图形中找到沙漏EOD △和BOG △：有34ED BG ∶=∶，所以34OD BO =∶∶，相当于把BD 分成(34+)7份，同理也可以在图中在次找到沙漏：EHD △和BHF △也是沙漏，32ED BF =∶∶，由此可以推出：32HD BH =∶∶, 相当于把BD 分成(32+)5份，那么我们就可以把BD 分成35份(5和7的最小公倍数)其中OD 占15份，BH 占14份，HO 占6份，连接EB 则可知BED △的面积为357042÷=，在BD 为底的三角形中HO 占6份，则面积为：3563235⨯=(平方厘米).【答案】3【例 22】 ABCD 是平行四边形，面积为72平方厘米，E 、F 分别为AB 、BC 的中点，则图中阴影部分的面积为 平方厘米．BB【考点】相似三角形模型 【难度】4星 【题型】填空 【解析】 方法一：注意引导学生利用三角形的中位线定理以及平行线的相关性质．设G 、H 分别为AD 、DC 的中点，连接GH 、EF 、BD ．可得1=4AED ABCD S S V 平行四边形，对角线BD 被EF 、AC 、GH 平均分成四段，又OM ∥EF ，所以23::2:344DO ED BD BD ==，()()::32:31:3OE ED ED OD ED =-=-=，所以 11117263434AEO ABCD S S =⨯=⨯⨯=V 平行四边形(平方厘米)，212ADO AEO S S =⨯=V V (平方厘米)．同理可得6CFM S =V 平方厘米，12CDM S =V 平方厘米．所以 366624ABC AEO CFM S S S --=--=V V V (平方厘米)， 于是，阴影部分的面积为24121248++=(平方厘米)．方法二：寻找图中的沙漏，::1:2AE CD AO OC ==，::1:2FC AD CM AM ==，因此,O M 为AC 的三等分点，11721266ODM ABCD S S ==⨯=△平行四边形(平方厘米)，11122644AEO OCD S S ==⨯⨯=△△(平方厘米)，同理6FMC S =△(平方厘米)，所以72126648S =---=阴影(平方厘米)．【答案】48【例 23】 如图，三角形PDM 的面积是8平方厘米，长方形ABCD 的长是6厘米，宽是4厘米，M 是BC 的中点，则三角形APD 的面积是 平方厘米．ABCDP MKN ABCDP M【考点】相似三角形模型 【难度】4星 【题型】填空 【解析】 本题在矩形内连接三点构成一个三角形，而且其中一点是矩形某一条边的中点，一般需要通过这一点做垂线．取AD 的中点N ，连接MN ，设MN 交PD 于K ．则三角形PDM 被分成两个三角形，而且这两个三角形有公共的底边MK ，可知三角形PDM 的面积等于182MK BC ⨯⨯=(平方厘米)，所以8MK=3(厘米)，那么84433NK =-=(厘米)．因为NK 是三角形APD 的中位线，所以823AP NK =⨯=(厘米)，所以三角形APD 的面积为186823⨯⨯=(平方厘米)． 【答案】8【例 24】 如图，长方形ABCD 中，E 为AD 的中点，AF 与BE 、BD 分别交于G 、H ，OE 垂直AD 于E ，交AF 于O ，已知5cm AH =，3cm HF =，求AG ．ABCDEF GHO【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 由于AB ∥DF ，利用相似三角形性质可以得到::5:3AB DF AH HF ==，又因为E 为AD 中点，那么有:1:2OE FD =，所以3:5:10:32AB OE ==，利用相似三角形性质可以得到::10:3AG GO AB OE ==，而()()11534cm 22AO AF ==⨯+=，所以()10404cm 1313AG =⨯=．【答案】4013【例 25】 右图中正方形的面积为1， E 、F 分别为AB 、BD 的中点，13GC FC =．求阴影部分的面积．AB EABE【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 题中条件给出的都是比例关系，由此可以初步推断阴影部分的面积要通过比例求解，而图中出现最多的就是三角形，那么首先想到的就是利用相似三角形的性质．阴影部分为三角形，已知底边为正方形边长的一半，只要求出高，便可求出面积． 可以作FH 垂直BC 于H ，GI 垂直BC 于I ．根据相似三角形性质，::1:3CI CH CG CF ==，又因为CH HB =，所以:1:6CI CB =，即():61:65:6BI BC =-=，所以115522624BGE S =⨯⨯=V ．【答案】524【例 26】 梯形ABCD 的面积为12，2AB CD =，E 为AC 的中点，BE 的延长线与AD 交于F ，四边形CDFE的面积是 ．ABC D EFGABCD EF【考点】相似三角形模型 【难度】4星 【题型】填空 【解析】 延长BF 、CD 相交于G ．由于E 为AC 的中点，根据相似三角形性质，2CG AB CD ==，1122GD GC AB ==，再根据相似三角形性质，::2:1AF FD AB DG ==，:1:3GF GB =，而::2:1ABD BCD S S AB CD ∆∆==，所以1112433BCD ABCD S S ∆==⨯=，28GBC BCD S S ∆∆==．又111236GDF GBC S S ∆∆=⨯=，12EBC GBC S S ∆∆=，所以111812633CDFE GBC GBC S S S ∆∆⎛⎫=--== ⎪⎝⎭．【答案】83【例 27】 如图，三角形ABC 的面积为60平方厘米，D 、E 、F 分别为各边的中点，那么阴影部分的面积是 平方厘米．BCBCB【考点】相似三角形模型 【难度】4星 【题型】填空 【解析】 阴影部分是一个不规则的四边形，不方便直接求面积，可以将其转化为两个三角形的面积之差．而从图中来看，既可以转化为BEF ∆与EMN ∆的面积之差，又可以转化为BCM ∆与CFN ∆的面积之差． (法1)如图，连接DE ．由于D 、E 、F 分别为各边的中点，那么BDEF 为平行四边形，且面积为三角形ABC 面积的一半，即30平方厘米；那么BEF ∆的面积为平行四边形BDEF 面积的一半，为15平方厘米．根据几何五大模型中的相似模型，由于DE 为三角形ABC 的中位线，长度为BC 的一半，则::1:2EM BM DE BC ==，所以13EM EB =；::1:1EN FN DE FC ==，所以12EN EF =．那么EMN ∆的面积占BEF ∆面积的111236⨯=，所以阴影部分面积为115112.56⎛⎫⨯-= ⎪⎝⎭(平方厘米)．(法2)如图，连接AM ．根据燕尾定理，::1:1ABM BCM S S AE EC ∆∆==，::1:1ACM BCM S S AD DB ∆∆==，所以11602033BCO ABC S S ∆∆==⨯=平方厘米，而11603022BDC ABC S S ∆∆==⨯=平方厘米，所以17.54FCN BDC S S ∆∆==平方厘米，那么阴影部分面积为207.512.5-=(平方厘米)．【总结】求三角形的面积，一般有三种方法：⑴利用面积公式：底⨯高2÷； ⑵利用整体减去部分；⑶利用比例和模型．【答案】12.5【例 28】 如图,ABCD 是直角梯形，4,5,3AB AD DE ===，那么梯形ABCD 的面积是多少?OEDCBAOED AFCB【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 延长EO 交AB 于F 点，分别计算,,,AOD AOB DOC BOC △△△△的面积，再求和． 31DE BF DO OB ==∶∶∶ ∴31AOD AOB S S =△△∶∶；31DOC BOC S S ==△△∶ AOD BOC S S =△△又∵145102ABD S =⨯⨯=△∴37.54AOD ABD S S ==△△, 2.5,7.5,337.522.5AOB BOC DOC BOC S S S S ====⨯=△△△△∴7.5 2.57.522.540ABCD S =+++=梯形【答案】40【例 29】 边长为8厘米和12厘米的两个正方形并放在一起，那么图中阴影三角形的面积是多少平方厘米？CB【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 给图形标注字母，按顺时针方向标注，大正方形为ABCD ，小正方形为MNDE ，EB 分别交,AC AD于,O H 两点， 122035AO OC AB EC ===∶∶∶∶，35AH BC AO OC ==∶∶∶ ∴38AO AC =∶∶，35AH AD =∶∶，940AHO ADC S S =△△∶∶ ∵2112722ADC S =⨯=△∴997216.24040AHO ADC S S ==⨯=△△【答案】16.2【例 30】 如右图，长方形ABCD 中，16EF =，9FG =，求AG 的长．DABC EFG【考点】相似三角形模型 【难度】3星 【题型】解答【解析】 因为DA ∥BE ，根据相似三角形性质知DG AGGB GE=， 又因为DF ∥AB ，DG FGGB GA=， 所以AG FGGE GA=，即2225922515AG GE FG =⋅=⨯==，所以15AG =． 【答案】15【例 31】 如图，已知正方形ABCD 的边长为4，F 是BC 边的中点，E 是DC 边上的点，且:1:3DE EC =，AF 与BE 相交于点G ，求ABG S △GFAEDC BM GFAEDCBGFAEDCB【考点】相似三角形模型 【难度】4星 【题型】解答 【关键词】迎春杯 【解析】 方法一：连接AE ，延长AF ，DC 两条线交于点M ，构造出两个沙漏，所以有::1:1AB CM BF FC ==，因此4CM =，根据题意有3CE =，再根据另一个沙漏有::4:7GB GE AB EM ==，所以4432(442)471111ABG ABE S S ==⨯⨯÷=+△△． 方法二：连接,AE EF ，分别求4224ABF S =⨯÷=△，4441232247AEF S =⨯-⨯÷-⨯÷-=△，根据蝴蝶定理::4:7ABF AEF S S BG GE ==△△，所以4432(442)471111ABG ABE S S ==⨯⨯÷=+△△． 【答案】3211【例 32】 如图所示，已知平行四边形ABCD 的面积是1，E 、F 是AB 、AD 的中点， BF 交EC 于M ，求BMG ∆的面积．MHGF E D CBAA【考点】相似三角形模型 【难度】4星 【题型】解答【解析】 解法一：由题意可得，E 、F 是AB 、AD 的中点，得//EF BD ，而::1:2FD BC FH HC ==，::1:2EB CD BG GD ==所以::2:3CH CF GH EF ==， 并得G 、H 是BD 的三等分点，所以BG GH =，所以 ::2:3BG EF BM MF ==，所以25BM BF =，11112224BFD ABD ABCD S S S ∆∆==⨯=Y ；又因为13BG BD =，所以1212113535430BMG BFD S S ∆∆=⨯⨯=⨯⨯=．解法二：延长CE 交DA 于I ，如右图， 可得，::1:1AI BC AE EB ==， 从而可以确定M 的点的位置， ::2:3BM MF BC IF ==，25BM BF =，13BG BD =(鸟头定理)，可得2121115353430BMG BDF ABCD S S S ∆∆=⨯=⨯⨯=Y【答案】130【例 33】 正方形ABCD 的面积是120平方厘米，E 是AB 的中点，F 是BC 的中点，四边形BGHF 的面积是平方厘米．H GFEDC BAMH GFEDCBA【考点】相似三角形模型 【难度】4星 【题型】填空 【关键词】清华附中，入学测试 【解析】 欲求四边形BGHF 的面积须求出EBG ∆和CHF ∆的面积．由题意可得到：::1:2EG GC EB CD ==，所以可得：13EBG BCE S S ∆∆=将AB 、DF 延长交于M 点，可得： :::1:1BM DC MF FD BF FC ===，而1::():3:22EH HC EM CD AB AB CD ==+=，得25CH CE =，而12CF BC =，所以121255CHF BCE BCE S S S ∆∆∆=⨯=11112030224BCE S AB BC ∆=⨯⨯=⨯=1177301451515EBC EBC EBC EBC BGHF S S S S S ∆∆∆∆=--==⨯=四边形．EF ，确定H 的位置(也就是:FH HD )，同样也能解出． 【答案】14【例 34】 如图，已知14ABC S =△,点,,D E F 分别在,,AB BC CA 上，且2,5,AD BD AF FC ===，ABE DBEF S S =△四边形则ABE S △是多少？FEDCBAFEDCBA【考点】相似三角形模型 【难度】4星 【题型】解答 【解析】 ABC △的面积已知，若知道ABE △的面积占ABC △的几分之几就可以计算出ABE △的面积．连接CD ．∵ABE DBEF S S =△四边形∴DEF ADE S S =△△ ∴AC 与DE 平行，∴ADE CDE S S =△△∴ABE CDB S S =△△ ∵2AD =，5BD = ∴:2:5ACD CDB S S =V V∴55141077ABC ABB CDB S S S ===⨯=△△△【答案】10【例 35】 如图，长方形ABCD 中，E 、F 分别为CD 、AB 边上的点，DE EC =，2FB AF =，求::PM MN NQ ．PMNQ FEDCBA GPMNQ FEDCBA【考点】相似三角形模型 【难度】4星 【题型】解答 【解析】 如图，过E 作AD 的平行线交PQ 于G ．由于E 是DC 的中点，所以G 是PQ 的中点．由于DE EC =，2FB AF =，所以:2:3AF DE =，:4:3BF CE =．根据相似性，:::2:3PM MG AM ME AF DE ===，:::3:4GN NQ EN NB EC BF ===，于是25PM PG =，33365735MN PG GQ PG =+=，4477NQ GQ PG ==，所以2364::::7:18:105357PM MN NQ ==．【答案】7:18:10【例 36】 如下图，D 、E 、F 、G 均为各边的三等分点，线段EG 和DF 把三角形ABC 分成四部分，如果四边形FOGC 的面积是24平方厘米，求三角形ABC 的面积．EDOGC F B AED OGCFBA【考点】相似三角形模型 【难度】3星 【题型】解答 【解析】 设三角形以AB 为底的高为h ，由于:2:3FG AB =，所以:1:2ED FG =；所以三角形OGF 以GF 为底的高是122339h h ⨯=；又因为三角形CFG 以FG 为底的高是23h ，所以三角形OGF 的面积与三角形CGF 的面积之比22:1:393h h ==，所以三角形CFG 的面积为3241831⨯=+(平方厘米)，而三角形CFG 的面积占三角形ABC 的224339⨯=，所以三角形ABC的面积是41840.59÷=(平方厘米)．【答案】40.5【例 37】如图，ABCD为正方形，1cmAM NB DE FC====且2cmMN=，请问四边形PQRS的面积为多少？CACA【考点】相似三角形模型【难度】4星【题型】解答【关键词】香港保良局小学数学世界邀请赛【解析】(法1)由//AB CD，有MP PCMN DC=，所以2PC PM=，又MQ MBQC EC=，所以12MQ QC MC==，所以111236PQ MC MC MC=-=，所以SPQRS占AMCFS的16，所以121(112)63SPQRS=⨯⨯++=2(cm)．(法2)如图，连结AE，则14482ABES∆=⨯⨯=(2cm)，而RB ERAB EF=，所以2RB ABEF EF==，22168333ABR ABES S∆∆==⨯=(2cm)．而1134322MBQ ANSS S∆∆==⨯⨯⨯=(2cm)，因为MN MPDC PC=，所以13MP MC=，则11424233MNPS∆=⨯⨯⨯=(2cm)，阴影部分面积等于164233333ABR ANS MBQ MNPS S S S∆∆∆∆--+=--+=(2cm)．【答案】23【例 38】如图12-6所示，在三角形ABC中，DC=3BD，DE=EA．若三角形ABC的面积是1．则阴影部分的面积是多少?【考点】相似三角形模型【难度】4星【题型】解答【关键词】奥林匹克，5题【解析】△ABC、△ADC同高，所以底的比等于面积比，那么有33.44ADC ABC ABCDCS S SBC∆∆∆=⨯=⨯=而E为AD中点，所以13.28DEC ADCS S∆∆==连接FD，△DFE、△FAE面积相等，设,FEAS x∆=则．FDES∆的面积也为x，11.44ABD ABCS S∆∆==12,4BDF ABD FEA FDE S S S S x ∆∆∆∆=--=-而3.8FDC FDE DEC S S S x ∆∆∆=+=+ 13:(2);()1:348BDF FDC S S x x ∆∆=-+=，解得356x =.所以，阴影部分面积为333.8567DEC FEA S S ∆∆+=+=【答案】37【例 39】 一个等腰直角三角形和一个正方形如图摆放，①、②、③这三块的面积比依次为1:4:41．那么，④、⑤这两块的面积比是______．⑤④③②①HKJG IF DCEB A ⑤④③②①【考点】相似三角形模型 【难度】3星 【题型】填空 【关键词】迎春杯，六年级，初赛 【解析】 如图∵()()12:1:4S S =，∴:1:2AB BC =，∴:1:5ABE BCHE S S ∆=，()():415:156:1EHIF AEHC S S =-+=，:6:1EF AE =，又∵:1:2AE CD =，∴:7:2AF CD =，∴::7:3AF AC AF DH ==，∴()()()451:66:7379:142S S ⎛⎫=⨯⨯-⨯=⎡⎤ ⎪⎣⎦⎝⎭． 【答案】9:14【例 40】 下图中，四边形ABCD 都是边长为1的正方形，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的重点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn，那么，m ＋n 的值等于__________。