七年级数学下册第二单元测试题和答案
七年级数学下册第二章单元测试题及答案

校铭数学内部资料第二章相交线与平行线单元测试卷(一)班级姓名学号得分评卷人得分一、单选题(注释)1、如图,直线 a、b、c、d,已知 c⊥a,c⊥b,直线 b、c、d 交于一点,若∠1=500,则∠2 等于【】A.600B.50C.40D.300 002、如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么,∠ABE 与∠DCF 的位置与大小关系是( )A.是同位角且相等B.不是同位角但相等;C.是同位角但不等D.不是同位角也不等3、如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能()A.相等B.互补C.相等或互补D.相等且互补4、下列说法中,为平行线特征的是()①两条直线平行,同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行;④垂直于同一条直线的两条直线平行。
A.①B.②③C.④D.②和④5、如图,AB∥CD∥EF,若∠ABC=50°,∠CEF=150°,则∠BCE=()A.60°B.50°C.30°D.20°6、如图,如果 AB∥CD,则角α、β、γ之间的关系为( )A.α+β+γ=360°B.α-β+γ=180°C.α+β—γ=180°D.α+β+γ=180°7、如图,由 A 到 B 的方向是( )D.北偏西 60°A.南偏东 30°B.南偏东 60° C.北偏西 30° 8、如图,由 AC∥ED,可知相等的角有()A.6 对B.5 对C.4 对D.3 对9、如图,直线 AB、CD 交于 O,EO⊥AB 于 O,∠1 与∠2 的关系是()A.互余B。
对顶角 C.互补D。
相等10、若∠1 和∠2 互余,∠1 与∠3 互补,∠3=120°,则∠1 与∠2 的度数分别为() A.50°、40°B.60°、30°C.50°、130°D.60°、120°11、下列语句正确的是()A.一个角小于它的补角B.相等的角是对顶角C.同位角互补,两直线平行D.同旁内角互补,两直线平行12、图中与∠1 是内错角的角的个数是()A.2 个B.3 个C.4 个D.5 个13、如图,直线AB 和 CD 相交于点 O,∠AOD 和∠BOC 的和为 202°,那么∠AOC 的度数为()A.89°B.101°C.79°D.110°14、如图,∠1 和∠2 是对顶角的图形的个数有()A.1 个B.2 个C.3 个D.0 个15、如图,直线 a、b 被直线 c 所截,现给出下列四个条件:①∠1=∠5,②∠1=∠7,③∠2+∠3=180°,④∠4=∠7,其中能判定 a∥b 的条件的序号是()A.①②B.①③C.①④D.③④评卷人得分二、填空题(注释)16、如图,∠ACD=∠BCD,DE∥BC 交 AC 于 E,若∠ACB=60°,∠B=74°,则∠EDC=___°,∠CDB=____°。
北师大版七年级下册数学第二章相交线与平行线测试题(附答案)

北师大版七年级下册数学第二章相交线与平行线测试题(附答案)北师大版七年级下册数学第二章相交线与平行线测试题(附答案)一、单选题1.如图,已知直线l1∥l2,将一块直角三角板ABC按如图所示方式放置,若∠1=39°,则∠2等于()A。
39° B。
45° C。
50° D。
51°2.如图.直线a∥b,直线L与a、b分别交于点A,B,过点A作AC⊥b于点C.若∠1=50°,则∠2的度数为()A。
130° B。
50° C。
40° D。
25°3.如图,三点共线A、B、C,D、E、F三点共线,且AD∥CF,BE∥CD,下列结论错误的是()A。
∠ABE=∠XXX∠ABE=∠CDEC。
∠ABE=∠XXX∠ABE=∠BDF4.如图,平行线AB∥CD,EF⊥CD,垂足为G,图中∠AGE=()A。
90° B。
45° C。
30° D。
60°5.如图,互余的角有()A。
1个 B。
2个 C。
3个 D。
4个6.如图,AB∥CD,EF∥GH,则下列等式正确的是()A。
∠AEF=∠GHF B。
∠AEF=∠HGFC。
∠XXX∠GHF D。
∠XXX∠HGF7.已知同一平面内的三条直线AB,CD,EF,AB∥CD,CD∥EF,则下列结论错误的是()A。
AB∥EF B。
AB∥CD C。
EF∥CD D。
AB∥EF8.如果a<b,且a+b=5c,如果c<a,b<c,比a与b 的和的3倍少2,那么a与b的位置关系是()A。
a<b B。
a>b C。
a=b D.无法确定9.如图,已知AB∥CD,AE=2cm,EC=3cm,则图中互相平行的线段是()A。
AB//CD B。
AE//DC C。
BE//CD D。
AB//EC10.如图,AB∥CD,点E在直线AD上,且∠AEC=34°,则∠BED的大小为()A。
七年级数学下册《第二单元》单元检测卷及答案(沪科版)

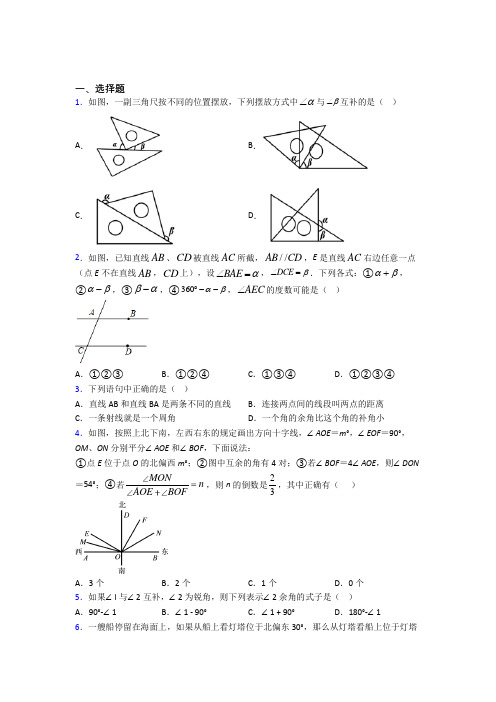
七年级数学下册《第二单元》单元检测卷及答案(沪科版)一、选择题(共40分)1. 如果m >n 那么下列结论错误的是( ) A. m +2>n +2 B. m −2>n −2 C. 2m >2nD. −2m >−2n2. 实数a b c 在数轴上对应的点的位置如图所示 则下列式子中正确的是( )A. a −c >b −cB. a +c <b +cC. ac >bcD. a b <cb 3. 不等式9−2x >x +1的正整数解的个数是( ) A. 1B. 2C. 3D. 无数个4. 不等式3x −2>x +2的解集在数轴上表示正确的是( ) A.B.C.D.5. 若不等式(a −1)x >a −1的解集是x <1 则a 的取值范围是( ) A. a >1B. a <1C. a ≥1D. a ≤16. 把不等式组{3x >x −61−2x 3≤x−42中每个不等式的解集在同一条数轴上表示出来 正确的是( )A.B.C.D.7. 不等式组{x−12≤1x −2<4(x +1)的正整数解有( )A. 1个B. 2个C. 3个D. 4个8. 已知a >b >0 则下列不等式组中无解的是( ) A. {x <a,x >−bB. {x >−a,x <−bC. {x >−a,x <bD. {x >a,x <−b9. 文德中学初二年级为了奖励在英语演讲比赛中胜出的学生 年级购买了若干本课外读物准备送给他们.如果每人送4本 则还余9本;如果每人送5本 则最后一人能得到课外读物但不足2本.设初二年级有x 名学生获奖.则下列不等式组表示正确的是( )A. {4x +9−5(x −1)>04x +9−5(x −1)<2 B. {4x −9−5(x −1)>04x −9−5(x −1)<2 C. {4x +9−5(x −1)>04x +9−5(x −1)≤2D. {4x −9−5(x −1)>04x −9−5(x −1)≤210. 疫情的发生 各地积极响应政府“管住门 看住人”的要求 温华物业管理有限公司 对管辖的各小区实行门绳拦截管理 对符合3天出门一次采购生活用品的人员才能签证放行 为此 他们要把长19米的绳子剪成2米或1米的绳子 分发给各小区 请帮助公司设计有裁剪方案.( )A. 10B. 9C. 8D. 7二、填空题(共20分)11. 若a <b <0 则−4a ______ −4b(用< >连接). 12. 不等式3−2x >7的解集为______.13. 某种出租车的收费标准是起步价8元(即距离不超过3km 都付8元车费) 超过3km 以后 每增加1km 加收1.2元(不足1km 按1km 计).若某人乘这种出租车从甲地到乙地经过的路程是xkm 共付车费14元 那么x 的最大值是____________.14. 关于x 的不等式组{x−12−x+23≤1x −a >2只有3个整数解 求a 的取值范围 .三、计算题15. (8分) 解不等式3(x +2)≥4(x −1)+7 并把它的解集在数轴上表示出来.16. (8分) 解不等式组{5x −3≤2x +9,①3x >x+102,②并写出它的所有整数解. 四 解答题.17. (8分)规定:{x}表示不小于x 的最小整数 如{4}=4 {−2.6}=−2 {−5}=−5 在此规定下任意数x 都能写出如下形式:x ={x}−b 其中0⩽b <1. (1)直接写出{x} x x +1的大小关系:___________; (2)根据(1)中的关系式解决下列问题: ①满足{x +7}=4的x 的取值范围是______; ②求适合{3.5x −2}=2x +14的x 的值.18. (8分) 友谊商店A 型号笔记本电脑的售价是a 元/台.最近 该商店对A 型号笔记本电脑举行促销活动 有两种优惠方案.方案一:每台按售价的九折销售;方案二:若购买不超过5台 每台按售价销售;若超过5台 超过的部分每台按售价的八折销售.某公司一次性从友谊商店购买A 型号笔记本电脑x 台.(1)当x =8时 应选择哪种方案 该公司购买费用最少?最少费用是多少元? (2)若该公司采用方案二购买更合算 求x 的取值范围.19. (8分)为应对新冠肺炎疫情 某服装厂决定转型生产口罩 根据现有厂房大小决定购买10条口罩生产线 现有甲 乙两种型号的口罩生产线可供选择.经调查:购买3条甲型口罩生产线比购买2条乙型口罩生产线多花14万元 购买4条甲型口罩生产线与购买5条乙型口罩生产线所需款数相同. (1)求甲 乙两种型号口罩生产线的单价;(2)已知甲型口罩生产线每天可生产口罩9万只 乙型口罩生产线每天可生产口罩7万只 若每天要求产量不低于75万只 预算购买口罩生产线的资金不超过90万元 该厂有哪几种购买方案?哪种方案最省钱?最少费用是多少?20. (8分)某中学为了加强学生体育锻炼 准备购进一批篮球和足球.据调查 某体育器材专卖店销售40个足球和60个篮球一共9200元;销售100个足球和30个篮球一共11000元. (1)求足球和篮球的单价;(2)该校计划使用10420元资金用于购买足球和篮球120个 且篮球数量不少于足球数量的2倍.购买时恰逢该专卖店在做优惠活动 信息如下表:球类 购买数量低于50个购买数量不低于50个足球 原价销售 八折销售 篮球原价销售九折销售21. (12分)(1)观察发现:材料:解方程组{x +y =4 ①3(x +y)+y =14 ②将①整体代入② 得3×4+y =14 解得y =2把y =2代入① 得x =2 所以{x =2y =2这种解法称为“整体代入法” 你若留心观察 有很多方程组可采用此方法解答 请直接写出方程组{x −y −1=0, ①4(x −y)−y =5, ②的解为____(2)实践运用:请用“整体代入法”解方程组{2x −3y −2=0, ①2x −3y +57+2y =9, ②(3)拓展运用:若关于x y 的二元一次方程组{2x +y =−3m +2x +2y =4的解满足x +y <−23请求出m 的最小整数值.参考答案1.【答案】D2.【答案】B3.【答案】B4.【答案】A5.【答案】B7.【答案】C8.【答案】D 9.【答案】A10.【答案】A11.【答案】>12.【答案】x<−213.【答案】814.【答案】8≤a<9【解析】解:{x−12−x+23≤1①x−a>2②解①得解②得∴不等式组的解集为:2+a<x≤13∵不等式组只有3个整数解∴10≤2+a<11解得故答案为8≤a<9.15.【答案】解:不等式的解集为x≤3.16.【答案】解:2<x≤4.不等式组的所有整数解为34.17.【答案】解:(1)由题意可得x≤{x}<x+1(2)①∵x≤{x}<x+1∴{x+7≤44<x+7+1解得−4<x≤−3②∵{3.5x−2}=2x+1 4∴由(1)得:3.5x−2≤{3.5x−2}<(3.5x−2)+1且2x+14为整数∴3.5x−2≤2x+14<(3.5x−2)+1解得:56<x≤32∴11112<2x+14≤314∴整数2x+14是2或3当2x +14=2时 得x =78当2x +14=3时 得x =118∴适合{3.5x −2}=2x +14的x 的值是x =78或x =118. 18.【答案】(1)解:设购买A 型号笔记本电脑x 台时的费用为w 元当x =8时方案一:w =90%a ×8=7.2a方案二:w =5a +(8−5)a ×80%=7.4a a 为正数 所以7.2a <7.4a∴当x =8时 应选择方案一 该公司购买费用最少 最少费用是7.2a 元;(2)若x ⩽5 方案一每台按售价九折销售 方案二每台按售价销售 所以采用方案一购买合算; 若x >5方案一:w =90%ax =0.9ax 方案二:当x >5时 则0.9ax >a +0.8axx >10∴x 的取值范围是x >10且x 为正整数.19.【答案】解:(1)设甲型号口罩生产线的单价为x 万元 乙型号口罩生产线的单价为y 万元由题意得: {3x −2y =144x =5y解得:{x =10y =8答:甲型号口罩生产线的单价为10万元 乙型号口罩生产线的单价为8万元. (2)设购买甲型号口罩生产线m 条 则购买乙型号口罩生产线(10−m)条 由题意得:{10m +8(10−m)≤909m +7(10−m)≥75解得:2.5≤m ≤5 又∵m 为整数∴m =3 或m =4 或m =5 因此有三种购买方案: ①购买甲型3条 乙型7条; ②购买甲型4条 乙型6条; ③购买甲型5条 乙型5条.当m =3时 购买资金为:10×3+8×7=86(万元) 当m =4时 购买资金为:10×4+8×6=88(万元)当m =5时 购买资金为:10×5+8×5=90(万元)∵86<88<90∴最省钱的购买方案为:选购甲型3条 乙型7条 最少费用为86万元.20.【答案】解:(1)设足球的单价为x 元 篮球的单价为y 元依题意得 {40x +60y =9200100x +30y =11000 解得{x =80y =100答:足球的单价为80元 篮球的单价为100元; (2)设购买a 个足球 则购买篮球数为(120−a)个 依题意得 120−a ≥2a∴a ≤40 ∴120−a ≥80∴购买足球按原价 购买篮球按九折计算∴80a +90(120−a)≤10420∴a ≥38∴38≤a ≤40∵a 为整数 ∴a =38 39∴可有以下三种购买方案: 方案1:购买38个足球 82个篮球 共10420元; 方案2:购买39个足球 81个篮球 共10410元; 方案3:购买40个足球 80个篮球 共10400元. ∴购买40个足球 80个篮球共10400元 费用最少.21.【答案】解:(1)由①得:x −y =1③将③代入②得:4−y =5 即y =−1 将y =−1代入③得:x =0 则方程组的解为{x =0 y =−1.故答案为{x =0 y =−1.(2)由①得:2x −3y =2③将③代入②得:1+2y =9 即y =4 将y =4代入③得:2x −12=2 解得x =7则方程组的解为{x =7y =4(3){2x+y=−3m+2 ①x+2y=4 ②①+②得:3(x+y)=−3m+6即x+y=−m+2代入不等式得:−m+2<−23解得:m>83则满足条件m的最小整数值是3.。
北师大版七年级下册数学第二单元测试卷及答案

北师大版七年级下册数学第二单元测试卷及答案单元测试(二)——相交线与平行线(B卷)一、选择题(每小题3分,共30分)1.与30度的角互为余角的角的度数是()A.30B.60C.70D.902.如图,若∠AOC增大50°,则∠BOD()A.减少50B.不变C.增大50D.增大1303.如图,直线AB与直线CD相交于点O,点E是∠AOD内一点,已知OE⊥AB,∠COE=135°,则∠BOD的度数是()A.35°B.45°C.50°D.55°4.如图,下列条件中能判定AE//CD的是()A.∠A=∠CB.∠A+∠ABC=180°C.∠C=∠XXXD.∠A=∠XXX5.如图,有三条公路,其中AC与AB垂直,XXX和XXX分别沿AC,BC同时出发骑车到C城。
若他们同时到达,则下列判断中正确的是()A.XXX骑车的速度快B.XXX骑车的速度快C.两人一样快D.因为不知道公路的长度,所以无法判断他们速度的快慢6.如图,已知a//b,直角三角板的直角顶点在直线b上。
若∠1=60°,则下列结论错误的是()A.∠5=40°B.∠2=60°C.∠3=60°D.∠4=120°7.如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点。
若∠1=50°,则∠2=()A.60°B.50°C.40°D.30°8.如图,XXX,∠ABC=46°,∠CEF=154°,则∠XXX等于()A.23°B.16°C.20°D.26°9.将一条两边平行的纸带按如图所示方式折叠,若∠1=52°,则∠2等于()A.52°B.58°C.64°D.60°10.如图,直线MN分别与直线AB,CD相交于点E,F,∠XXX与∠CFE互补,∠BEF的平分线与∠DFE的平分线交于点P,与直线CD交于点G,GH//PF交MN于点H,则下列说法中错误的是()A.XXXB.∠XXX∠XXXXXXD.∠XXX∠EGD二、填空题(每小题4分,共20分)11.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是__直角__角。
(常考题)人教版初中数学七年级数学下册第二单元《实数》检测卷(包含答案解析)

一、选择题1.如图,数轴上O 、A 、B 、C 四点,若数轴上有一点M ,点M 所表示的数为m ,且5m m c -=-,则关于M 点的位置,下列叙述正确的是( )A .在A 点左侧B .在线段AC 上 C .在线段OC 上D .在线段OB 上 2.若15的整数部分为a ,小数部分为b ,则a-b 的值为()A .615-B .156-C .815-D .158- 3.在实数3-,-3.14,0,π,364中,无理数有( )A .1个B .2个C .3个D .4个 4.已知122=,224=,328=,4216=,5232=,……,根据这一规律,20192的个位数字是( )A .2B .4C .8D .6 5.下列说法中,正确的是 ( ) A .64的平方根是8B .16的平方根是4和-4C .()23-没有平方根D .4的平方根是2和-26.如图,在数轴上表示1,3的对应点分别为A B 、,点B 关于点A 的对称点为C ,则点C 表示的数为( )A .31-B .13-C .23-D .32- 7.已知n 是正整数,并且n -1<326+<n ,则n 的值为( )A .7B .8C .9D .108.下列各式中,正确的是( ) A .16=±4 B .±16=4 C .3273-=-D .2(4)4-=- 9.数轴上表示下列各数的点,能落在A ,B 两个点之间的是( )A .3B 7C 11D 1310.下列命题中真命题的个数( )①无理数包括正无理数、零和负无理数;②经过直线外一点有且只有一条直线与已知直线平行;③和为180°的两个角互为邻补角;④49的算术平方根是7;⑤有理数和数轴上的点一一对应;⑥垂直于同一条直线的两条直线互相平行.A.4 B.3 C.2 D.1-的整数部分11.已知无理数m的小数部分与5的小数部分相同,它的整数部分与5π相同,则m为()π-A.5B.10C.51-D.512.若将2-,7,11分别表示在数轴上,其中能被如图所示的墨迹覆盖的数是()A.2-B.7C.11D.无法确定二、填空题13.教材中的探究:如图,把两个边长为1的小正方形沿对角线剪开,用所得到的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法(数轴的单位长度为1).(1)阅读理解:图1中大正方形的边长为________,图2中点A表示的数为________;(2)迁移应用:请你参照上面的方法,把5个小正方形按图3位置摆放,并将其进行裁剪,拼成一个大正方形.①请在图3中画出裁剪线,并在图3中画出所拼得的大正方形的示意图.-+的点,并比较它②利用①中的成果,在图4的数轴上分别标出表示数-0.5以及35们的大小.14.对于结论:当a+b=0时,a3+b3=0也成立.若将a看成a3的立方根,b看成是b3的立方根,由此得出这样的结论:“如果两数的立方根互为相反数,那么这两数也互为相反数”.(1)试举一个例子来判断上述结论的猜测是否成立?(2)若332x -与35x +的值互为相反数,求12x -的值. 15.求下列各式中x 的值(1)()328x -=(2)21(3)753x -= 16.把下列各数填入相应的集合里:﹣3,|﹣5|,+(13-),﹣3.14,0,﹣1.2121121112…,﹣(﹣2.5),34,﹣|45-|,3π 正数集合:{_____________…};整数集合:{_____________…};负分数集合:{_____________…};无理数集合:{_____________…}.17.计算:38642-+--.18.计算:31891224-++-+.19.比较大小:3- _______-2.(填“>”“=”或“<”)20.8的相反数是_____;16的平方根为_____;()34-的立方根是_____.三、解答题21.求下列各式中的x 的值(1)21(1)82x +=;(2)3(21)270x -+=22.计算(1)22234x +=;(2)38130125x +=(3)21|12|(2)16-----;(4)(x +2)2=25.23.如图,数轴上点A ,B ,C 所对应的实数分别为a ,b ,c ,试化简()323|-|b a c a b -++.24.观察下列各式:322111124==⨯⨯,33221129234+==⨯⨯,33322112336344++==⨯⨯,33332211234100454+++==⨯⨯;…回答下面的问题:(1)猜想:33333123(1)n n ++++-+=_________;(直接写出你的结果)(2)根据(1)中的结论,直接写出13+23+33+......+93+103的值是_________; (3)计算:213+223+233+......+293+303的值.25.(1)计算:|3|-.(2)求下列各式中x 的值:③22536x =;④3(1)64x --=.26.求满足下列条件的x 的值:(1)3(3)27x +=-;(2)2(1)218x -+=.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据A 、C 、O 、B 四点在数轴上的位置以及绝对值的定义即可得出答案.【详解】∵|m-5|表示点M 与5表示的点B 之间的距离,|m−c|表示点M 与数c 表示的点C 之间的距离,|m-5|=|m−c|,∴MB =MC .∴点M 在线段OB 上.故选:D .【点睛】本题考查的是实数与数轴,熟知实数与数轴上各点是一一对应的关系是解答此题的关键. 2.A解析:A【分析】先根据无理数的估算求出a 、b 的值,由此即可得.【详解】91516<<,<<34<<,3,3a b ∴==,)336a b ∴-=-=, 故选:A .【点睛】 本题考查了无理数的估算,熟练掌握估算方法是解题关键.3.B解析:B【分析】根据无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数,进行判断即可.【详解】=4,所给数据中无理数有:π,共2个.故选:B .【点睛】本题考查了无理数的知识,解答本题的关键是掌握无理数的三种形式.4.C解析:C【分析】通过观察122=,224=,328=,4216=,,5232=…知,他们的个位数是4个数一循环,2,4,8,6,…因为2019÷4=504…3,所以20192的个位数字与32的个位数字相同是8.【详解】解:仔细观察122=,224=,328=,4216=,,5232=…;可以发现他们的个位数是4个数一循环,2,4,8,6,…∵2019÷4=504…3,∴20192的个位数字与32的个位数字相同是8.故答案是:8.【点睛】本题考查了尾数特征,解题的关键是根据已知条件,找出规律:2的乘方的个位数是每4个数一循环,2,4,8,6,….5.D解析:D【分析】根据平方根的定义与性质,结合各选项进行判断即可.【详解】A、64的平方根是±8,故本选项错误;=,4的平方根是±2,故本选项错误;B4-=,9的平方根是±3,故本选项错误;C、()239D、4的平方根是±2,故本选项正确.故选:D.【点睛】本题考查了平方根的知识,如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.注意,一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.6.C解析:C【分析】首先根据表示1A、点B可以求出线段AB的长度,然后根据点B 和点C关于点A对称,求出AC的长度,最后可以计算出点C的坐标.【详解】解:∵表示1A、点B,∴AB−1,∵点B关于点A的对称点为点C,∴CA=AB,∴点C的坐标为:1−1)=故选:C.【点睛】本题考查的知识点为实数与数轴,解决本题的关键是求数轴上两点间的距离就让右边的数减去左边的数.知道两点间的距离,求较小的数,就用较大的数减去两点间的距离.7.C解析:C【分析】根据实数的大小关系比较,得到5<6,从而得到n的值.【详解】解:∵<5<6,∴8<<9,∴n=9.故选:C.【点睛】8.C解析:C【分析】根据算术平方根与平方根、立方根的定义逐项判断即可得.【详解】A4=,此项错误;B、4=±,此项错误;C3=-,此项正确;D4==,此项错误;故选:C.【点睛】本题考查了算术平方根与平方根、立方根,熟记各定义是解题关键.9.B解析:B【分析】首先确定A,B对应的数,再分别估算四个选项的数值进行判断即可.【详解】解:由数轴得,A点对应的数是1,B点对应的数是3,A.-2<<-1,不符合题意;B.2<3,符合题意;C、34,不符合题意;D. 34,不符合题意;故选:B【点睛】本题主要考查了对无理数的估算.10.D解析:D【分析】根据无理数、平行公理、邻补角、算术平方根、实数与数轴、平行线的判定逐个判断即可得.【详解】①无理数包括正无理数和负无理数,此命题是假命题;②经过直线外一点有且只有一条直线与已知直线平行,此命题是真命题;③和为180︒的两个角不一定互为邻补角,此命题是假命题;=,此命题是假命题;7⑤实数和数轴上的点一一对应,此命题是假命题;⑥在同一平面内,垂直于同一条直线的两条直线互相平行,此命题是假命题; 综上,真命题的个数是1个,故选:D .【点睛】本题考查了无理数、平行公理、邻补角、实数与数轴等知识点,熟练掌握各定义与公理是解题关键.11.C解析:C【分析】m 的整数部分与小数部分,进而可得答案.【详解】解:因为23, 3.14π≈,2,5π-的整数部分为1,所以无理数m 的整数部分是12,所以121m =+=.故选:C .【点睛】m 的整数部分与小数部分是解题的关键.12.B解析:B【分析】首先利用估算的方法分别得到间),从而可判断出被覆盖的数.【详解】 ∵221,23<<,34<<而墨迹覆盖的范围是1-3∴故选B.【点睛】本题考查了实数与数轴的对应关系,以及估算无理数大小的能力.二、填空题13.(1);(2)①见解析;②见解析【分析】(1)设正方形边长为a 根据正方形面积公式结合平方根的运算求出a 值则知结果;(2)①根据面积相等利用割补法裁剪后拼得如图所示的正方形;②由题(1)的原理得出大正解析:(1)2,2-;(2)①见解析;②见解析, 350.5-+<-【分析】(1)设正方形边长为a ,根据正方形面积公式,结合平方根的运算求出a 值,则知结果; (2) ① 根据面积相等,利用割补法裁剪后拼得如图所示的正方形;②由题(1)的原理得出大正方形的边长为5,然后在数轴上以-3为圆心,以大正方形的边长为半径画弧交数轴的右方与一点M ,再把N 点表示出来,即可比较它们的大小.【详解】解:设正方形边长为a ,∵a 2=2,∴a=2±,故答案为:2,2-;(2)解:①裁剪后拼得的大正方形如图所示:②设拼成的大正方形的边长为b ,∴b 2=5,∴b=±5,在数轴上以-3为圆心,以大正方形的边长为半径画弧交数轴的右方与一点M ,则M 表示的数为-3+5,看图可知,表示-0.5的N 点在M 点的右方,∴比较大小:350.5-+<-.【点睛】本题主要考查平方根与算术平方根的应用及实数的大小比较,熟练掌握平方根与算术平方根的意义及实数的大小比较是解题的关键.14.(1)见解析;(2)【分析】(1)这个结论很简单可选择则2与﹣2互为相反数进行说明(2)利用(1)的结论列出方程(3﹣2x )+(x+5)=0从而解出x 的值代入可得出答案【详解】解:(1)答案不唯一如解析:(1)见解析;(2)123x =-【分析】(10=,则2与﹣2互为相反数进行说明.(2)利用(1)的结论,列出方程(3﹣2x )+(x +5)=0,从而解出x 的值,代入可得出答案.【详解】解:(10=,则2与﹣2互为相反数;(2)由已知,得(3﹣2x )+(x +5)=0,解得x =8,∴1=1=1﹣4=﹣3.【点睛】本题考查立方根的知识,难度一般,注意一个数的立方根有一个,它和这个数正负一致,本题的结论同学们可以记住,以后可直接运用.15.(1);(2)或【分析】(1)利用立方根的定义得到然后解一次方程即可;(2)先变形为然后利用平方根的定义得到的值【详解】(1)∵∴∴;(2)整理得:∴或∴或【点睛】本题考查了解一元一次方程平方根和立 解析:(1)4x =;(2)18x =或12x =-.【分析】(1)利用立方根的定义得到22x -=,然后解一次方程即可;(2)先变形为()23225x -=,然后利用平方根的定义得到x 的值.【详解】(1)∵()328x -=,∴22x -=,∴4x =;(2)21(3)753x -=,整理得:()23225x -=,∴315x -=或315x -=-,∴18x =或12x =-.【点睛】本题考查了解一元一次方程,平方根和立方根,熟练掌握各自的定义是解本题的关键. 16.|﹣5|﹣(﹣25)3π﹣3|﹣5|0+()﹣314﹣||﹣12121121112…3π【分析】先根据绝对值的定义及化简符号的法则去掉绝对值的符号及多重符号再根据正数整数负分数无理数的定义求解即可【解析:|﹣5|,﹣(﹣2.5),34,3π ﹣3,|﹣5|,0 +(13-),﹣3.14,﹣|45-| ﹣1.2121121112 (3)【分析】先根据绝对值的定义及化简符号的法则去掉绝对值的符号及多重符号,再根据正数、整数、负分数、无理数的定义求解即可.【详解】解:|﹣5|=5,+(13-)13=-,﹣(﹣2.5)=2.5,﹣|45-|45=-, 17.4【分析】原式利用平方根立方根定义及绝对值化简计算即可得到结果【详解】解:原式【点睛】本题考查了实数的运算熟练掌握平方根立方根定义是解本题的关键解析:4【分析】原式利用平方根、立方根定义及绝对值化简计算即可得到结果.【详解】解:原式282=-+-4=【点睛】本题考查了实数的运算,熟练掌握平方根、立方根定义是解本题的关键.18.【分析】先根据开方的意义绝对值的意义进行化简最后计算即可求解【详解】解:原式【点睛】本题考查了实数的混合运算理解开方的意义能正确去绝对值是解题关键解析:1【分析】先根据开方的意义,绝对值的意义进行化简,最后计算即可求解.【详解】解:原式123122=-+++⨯1=+ 【点睛】本题考查了实数的混合运算,理解开方的意义,能正确去绝对值是解题关键. 19.>【分析】两个负数比较绝对值大的反而小由此得到答案【详解】∵∴故答案为:>【点睛】此题考查实数的大小比较:负实数都比0小正实数都比0大两个负实数比较大小绝对值大的反而小解析:>【分析】两个负数比较绝对值大的反而小,由此得到答案.【详解】 ∵2<,∴2>-,故答案为:>.【点睛】此题考查实数的大小比较:负实数都比0小,正实数都比0大,两个负实数比较大小,绝对值大的反而小.20.【分析】分别根据算术平方根相反数平方根和立方根的概念直接计算即可求解【详解】解:=所以的相反数是;16的平方根为;的立方根是故答案为:;±4;-4【点睛】本题考查了算术平方根平方根和立方根的概念进行解析:- 4± 4-【分析】分别根据算术平方根、相反数、平方根和立方根的概念直接计算即可求解.【详解】-;16的平方根为4±;()34-的立方根是4-.故答案为:—±4;-4【点睛】本题考查了算术平方根、平方根和立方根的概念进行求解即可.注意一个正数有两个平方根,它们互为相反数,正的平方根即为它的算术平方根.立方根的性质:一个正数的立方根是正数,一个负数的立方根是负数,0的立方根是0. 三、解答题21.(1)3x =或5x =-;(2)1x =-.【分析】(1)适当变形后,利用平方根的定义即可解方程;(2)适当变形后,利用立方根的定义即可解方程.【详解】解:(1)21(1)82x += 两边乘以2得,2(1)16x +=,开平方得,14x +=±,即14x +=或14x +=-,∴3x =或5x =-;(2)3(21)270x -+=移项得,3(21)27x -=-,开立方得,213x -=-,解得,1x =-.【点睛】本题考查的是利用平方根,立方根的含义解方程,掌握平方根与立方根的定义和等式的性质是解题的关键.22.(1)12x x ==-2)x=35;(3)12;(4)123,7x x ==-. 【分析】 (1)方程整理后,利用平方根定义开方即可求出解;(2)先求出x 3的值,再根据立方根的定义解答;(3)直接利用绝对值的性质、平方根定义和负指数幂的性质分别化简得出答案; (4)依据平方根的定义求解即可.【详解】(1)22234x +=,2x²=32,x²=18,,∴12x x ==-(2)38130125x +=, 327125x =-, x=35;(3)2|12|(2)--- =1-1144-=311442-= (4)(x +2)2=25,(x+2)=±5,x+2=5,x+2=-5,∴123,7x x ==-.【点睛】本题考查了利用平方根和立方根解方程,绝对值的性质和负指数幂的性质,掌握有关性质是解题的关键.23.2a-c【分析】根据数轴得到a<b<0<c ,由此得到a-c<0,a+b<0,依此化简各式,再合并同类项即可.【详解】由数轴得a<b<0<c ,∴a-c<0,a+b<0,∴|-|a c=-b-(c-a )+(a+b)=-b-c+a+a+b=2a-c.【点睛】此题考查数轴上的点表示数,利用数轴比较数的大小,绝对值的性质,立方根的化简,整式的加减法计算法则,解题的关键是依据数轴确定各式子的符号由此化简各式. 24.(1)221(1)4n n ⨯⨯+;(2)3025;(3)172125【分析】(1)根据题中所给各式可直接进行分析求解;(2)由(1)可直接代入求值即可;(3)根据(1)可直接进行求解.【详解】解:(1)根据题意可得出:33333123(1)n n ++++-+=221(1)4n n ⨯⨯+; (2)将n =10代入221(1)4n n ⨯⨯+, 原式221×1010130254=⨯+=(); (3)原式=22221130(301)20(201)44⨯⨯+-⨯⨯+=172125.【点睛】本题主要考查实数的运算,熟练掌握实数的运算是解题的关键.25.(1)①13;②9-2)③65x =±;④5x =. 【分析】①先计算根式,再加减计算.②先计算根式和绝对值,再加减计算.(2)③两边除以25,再开算术平方根.④先除以-1,再开立方根.【详解】(1)-+1322=-+13=|3|-1153=-+-9=-(2)③22536x =23625x =65x =± ④3(1)64x --=3(641)x -=-14x -=-5x =【点睛】本题考查根式的化简求值,关键在于化简. 26.(1)6x =-;(2)3x =-或5【分析】(1)根据立方根,即可解答; (2)根据平方根,即可解答.【详解】解:(1)3(3)27x +=-33x +=-6x =-;(2)2(1)218x -+=2(1)16x -=14x -=±∴3x =-或5.【点睛】本题考查了平方根、立方根,解决本题的关键是熟记平方根、立方根的定义.。
(完整版)北师大版七年级下学期数学第二单元测试题及答案
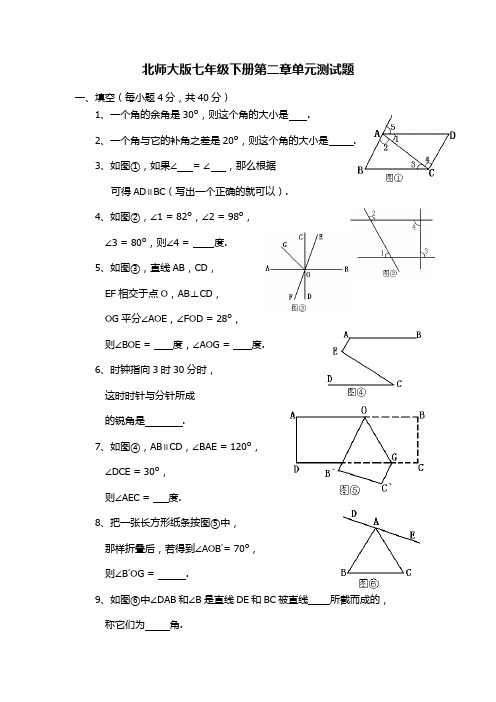
北师大版七年级下册第二章单元测试题一、填空(每小题4分,共40分)1、一个角的余角是30º,则这个角的大小是 .2、一个角与它的补角之差是20º,则这个角的大小是 .3、如图①,如果∠ = ∠ ,那么根据可得AD ∥BC (写出一个正确的就可以).4、如图②,∠1 = 82º,∠2 = 98º,∠3 = 80º,则∠4 = 度.5、如图③,直线AB ,CD ,EF 相交于点O ,AB ⊥CD ,OG 平分∠AOE ,∠FOD = 28º,则∠BOE = 度,∠AOG = 度.6、时钟指向3时30分时,这时时针与分针所成的锐角是 .7、如图④,AB ∥CD ,∠BAE = 120º,∠DCE = 30º,则∠AEC = 度.8、把一张长方形纸条按图⑤中,那样折叠后,若得到∠AOB ′= 70º,则∠B ′OG = .9、如图⑥中∠DAB 和∠B 是直线DE 和BC 被直线 所截而成的,称它们为 角.10、如图⑦,正方形ABCD 边长为8,M 在DC 上,且DM = 2,N 是AC上一动点,则DN + MN 的最小值为 .二、选择题(每小题3分,共18分)11、下列正确说法的个数是( )①同位角相等 ②对顶角相等③等角的补角相等 ④两直线平行,同旁内角相等A . 1, B. 2, C. 3, D. 412、如图⑧,在△ABC 中,AB = AC ,∠A = 36º,BD平分∠ABC ,DE ∥BC ,那么在图中与△ABC 相似的三角形的个数是( )A. 0,B. 1,C. 2,D. 313、下列图中∠1和∠2是同位角的是( )A. ⑴、⑵、⑶,B. ⑵、⑶、⑷,C. ⑶、⑷、⑸,D.⑴、⑵、⑸14、下列说法正确的是( )A.两点之间,直线最短;B.过一点有一条直线平行于已知直线;C.和已知直线垂直的直线有且只有一条;D.在平面内过一点有且只有一条直线垂直于已知直线.15、一束光线垂直照射在水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为()A. 45º,B. 60º,C. 75º,D. 80º16、如图⑨,DH ∥EG ∥EF ,且DC ∥EF ,那么图中和∠1相等的角的个数是( )A. 2,B. 4,C. 5,D. 6三、解答题:17、按要求作图(不写作法,但要保留作图痕迹)(3分)已知点P 、Q 分别在∠AOB 的边OA ,OB 上(如图 ).)①作直线PQ ,②过点P 作OB 的垂线,③过点Q 作OA 的平行线.18、已知线段AB,延长AB到C,使BC∶AB=1∶3,D为AC中点,若DC = 2cm,求AB的长. (7分)分)19、如图,,已知AB∥CD,∠1 = ∠2.求证.:∠E=∠F (620、如图所示,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个判断:⑴ AD = CB⑵ AE = FC⑶∠B = ∠D⑷ AD∥BC请用其中三个作为已知条件,余下一个作为结论,编一道数学问题,并写出解答过程. (8分)21、如图,ABCD是一块釉面砖,居室装修时需要一块梯形APCD的釉面砖,且使∠APC=120º.请在长方形AB边上找一点P,使∠APC=120º.然后把多余部分割下来,试着叙述怎样选取P点及其选取P点的理由.(8分)22、如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E =分)140º,求∠BFD的度数. (10第二单元答案一、填空题:1.60°;2.100°;3.∠5= ∠B,同位角相等,两直线平行;4.80°;5.62°,59°;6.75°;7.90°;8.55°;9.AB,内错;10.10.二、选择题:11.B; 12.C; 13.D; 14.D; 15.A; 16.C.三、解答题:17. 略;18. AB=3cm;19.略;20. 比如:已知:⑴⑵⑷.求证:⑶;求证过程略;21. 以C为顶点,CD为一边,在∠DCB内画∠DCP=60°,交AB于P,则P点为所选取的点.证明略;22.∠BFD=70°;。
七年级数学下册第二章《整式加减》综合测试卷-人教版(含答案)

七年级数学下册第二章《整式加减》综合测试卷-人教版(含答案)( 时间:90分钟 总分:100分)一、选择题:(本大题共12小题,每小题2分,共计24分)1.下列说法中,正确的是( )A. 单项式b 的次数是0B. 是一次单项式C. 24x 3是7次单项式D. -5是单项式2.对于单项式-的系数和次数分别是( )A. -2,2B. -2,3C. -,2D. -,33.下列单项式中,书写规范的是( )A. 1aB. x ·2C. 0.5xD. 1mn4.若21213n x y --是7次单项式,则n =( ) A. 1 B. 2 C. 3 D. 45.下列说法正确的是( )A. -x +3x 三次二项式B. x -1二次二项式C. x 2-2x +34是二次三项式D. -5x 5+2x 4y 2-1是八次三项式6.一个n 次多项式(n 为正整数),它的每一项的次数是( )A. 都等于nB. 都小于nC. 都不小于nD. 都不大于n7.设M ,N 都是关于x 的五次多项式,则M +N 是( )A.十次多项式B.五次多项式C.次数不大于5的多项式D.次数不大于5的整式8.-3x 4与3y 是同类项,则mn 的值为( )A. 6B. 8C. 2D. 19.化简:ab-(2ab-3ab2)结果是()A.3a2b+3abB.-3ab2-abC.3ab2-abD.-3ab2+3ab10.若x 是两位数,y是一位数,如果把y 置于x左边所得的三位数是()A.100y+xB. 100y+10xC.10y+xD. yx11.减去2-3x等于6x2-3x-8的代数式是()A.6x2-6x-10B.6x2-10C.6x2-6D.6x2-6x-612.若a2b+4=0,则代数式3a2b-(a2b-3a2b)的值为()A. 20B. -20C. 4D. -4二、填空题:(本大题共8小题,每小题2分,共16分)13.用式子表示“数a的3倍与3的差的一半”是.14.把多项式6+2x4-3x2+7x3按各项的次数从高到低重新排列为.15.某项工程。
2024年人教版七年级下册数学第二单元课后练习题(含答案和概念)

2024年人教版七年级下册数学第二单元课后练习题(含答案和概念)试题部分一、选择题:1. 在下列各数中,3的相反数是()A. 3B. 3C. 0D. (3)2. 下列各数中,最小的数是()A. |3|B. 3C. |3|D. 33. 下列各数中,有理数是()A. √1B. √3C. √3D. √34. 如果|a|=5,那么a的值可能是()A. 5B. 5C. 3D. 35. 有理数的乘法中,下列说法错误的是()A. 两个负数相乘得正数B. 两个正数相乘得正数C. 两个负数相乘得负数D. 一个正数和一个负数相乘得负数6. 在数轴上,点A表示的数是2,那么点A关于原点对称的点是()A. 2B. 2C. 0D. 17. 下列各式中,正确的是()A. (2)³ = 6B. (2)² = 4C. (2)³ = 8D. (2)² = 48. 如果a、b互为相反数,那么a+b的值是()A. aB. bC. 0D. 无法确定9. 下列各式中,等式成立的是()A. |3| = 3B. |3| = 3C. |3| = 3D. |3| = 310. 下列各数中,无理数是()A. 2πB. √9C. 1.5D. 0.333…二、判断题:1. 两个负数相加,和一定是负数。
()2. 两个正数相乘,积一定是正数。
()3. 0的相反数是0。
()4. 任何数的平方都是正数。
()5. 互为相反数的两个数的和为0。
()6. 有理数和无理数统称为实数。
()7. 负数的绝对值是它本身。
()8. 两个负数相乘,积一定是正数。
()9. 数轴上的点到原点的距离叫做这个点的绝对值。
()10. 互为倒数的两个数,它们的乘积为1。
()三、计算题:1. 计算:3 + 72. 计算:5 (2)3. 计算:4 × 64. 计算:8 ÷ (2)5. 计算:|5|6. 计算:|7|7. 计算:(3/4) × (16)8. 计算:9 ÷ (1/3)9. 计算:(2/5) ÷ (10)10. 计算:|5 + 3 × 2|11. 计算:4²12. 计算:(3)³13. 计算:√(49)14. 计算:√(64)15. 计算:|3 5| + 216. 计算:(4 7) × (3)17. 计算:(6) ÷ (3) + 218. 计算:(8 ÷ 2)² 519. 计算:3 × (2)²20. 计算:(5 3) × (2 + 4)四、应用题:1. 小华的零花钱比小丽多5元,小丽的零花钱是20元,那么小华有多少零花钱?2. 一个数加上3后等于8,求这个数。
浙教版七年级数学下册第2章测试题及答案

浙教版七年级数学下册第2章测试题及答案2.1 二元一次方程一.选择题(共5小题)1.在下列方程中:(1)3x+=8;(2)+2y=4;(3)3x+=1;(4)x2=5y+1;(5)y=x;(6)2(x﹣y)﹣3(x+)=x+y是二元一次方程的有()A.2个B.3个C.4个D.5个2.若x|k|+ky=2+y是关于x、y的二元一次方程,则k的值为()A.1 B.﹣1 C.1或﹣1 D.03.若(m﹣2018)x|m|﹣2017+(n+4)y|n|﹣3=2018是关于x,y的二元一次方程,则()A.m=±2018,n=±4 B.m=﹣2018,n=±4C.m=±2018,n=﹣4 D.m=﹣2018,n=44.下列方程中,二元一次方程的个数有()①x2+y2=3;②3x+=4;③2x+3y=0;④+=7A.1 B.2 C.3 D.45.在下列方程中:(1)3x+=8;(2)+2y=4;(3)3x﹣3(y+x)=1;(4)x2=5y+1;(5)y=x是二元一次方程的有()A.2个B.3个C.4个D.5个二.填空题(共5小题)6.关于x,y的方程x2m﹣n﹣2+4y m+1=6是二元一次方程,则m+n=.7.已知(m﹣2)x|m﹣1|+y=0是关于x,y的二元一次方程,则m=.8.已知方程x2m﹣n﹣2+4y m+n+1=6是关于x,y的二元一次方程,则m=,n=.9.在方程①2x+3y=4,②+2y=3,③xy+2=0,④x2+3y=0,⑤4y﹣3=2﹣y中,是二元一次方程的是.(填序号)10.已知3x n﹣2﹣y2m+1=0是关于x,y的二元一次方程,则m=,n=.三.解答题(共8小题)11.方程2x m+1+3y2n=5是二元一次方程,求m,n.12.已知关于x,y的方程(m2﹣4)x2+(m+2)x+(m+1)y=m+5.(1)当m为何值时,它是一元一次方程?(2)当m为何值时.它是二元一次方程?13.已知方程(m﹣2)x|m|﹣1+(n+3)=6是关于x,y的二元一次方程.(1)求m,n的值;(2)求x=时,y的值.14.已知关于x的方程(2a﹣6)x|b|﹣1+(b+2)=0是二元一次方程,求a、b的值.15.已知和是二元一次方程mx﹣3ny=5的两个解.(1)求m、n的值;(2)若x<﹣2,求y的取值范围.参考答案一.1.B 2.B 3.D 4.B 5.B二.6.﹣3 7.0 8.1、﹣1 9.①10.0, 3三.11.解:根据二元一次方程的定义,m+1=1,2n=1,解得m=0,n=.12.解:(1)依题意,得m2﹣4=0且m+2=0,或m2﹣4=0且m+1=0,解得m=﹣2.即当m=﹣2时,它是一元一次方程.(2)依题意,得m2﹣4=0且m+2≠0、m+1≠0,解得m=2.即当m=2时,它是二元一次方程.13.解:(1)因为,已知方程(m﹣2)x|m|﹣1+(n+3)=6是关于x,y的二元一次方程,所以,解这个不等式组,得m=﹣2,n=3即m=﹣2,n=3(2)因为,当m=﹣2,n=3时,二元一次方程可化为:﹣4x+6y=6所以,当x=时,有﹣4×+6y=6y=即求x=时,y的值为14.解:∵(2a﹣6)x|b|﹣1+(b+2)=0是二元一次方程,∴,且2a﹣6≠0,b+2≠0,解得a=﹣3,b=2.15.解:(1)把和代入方程得:,①×2+②,得15n=15,解得n=1,把n=1代入①,得m=2,(2)当时,原方程变为:2x﹣3y=5,解得x=,∵x<﹣2,∴<﹣2,解得y<﹣3.故y的取值范围是y<﹣3.2.2 二元一次方程组一.选择题(共5小题)1.在方程组,,,,中,是二元一次方程组的有()A.2个B.3个C.4个D.5个2.下列不是二元一次方程组的是()A.B.C.D.3.若解得x、y的值互为相反数,则k的值为()A.4 B.﹣2 C.2 D.﹣44.如果方程组的解同时满足3x+y=﹣2,则k的值是()A.﹣4 B.﹣3 C.﹣2 D.﹣15.方程组的解为,则被遮盖的两个数分别为()A.2,1 B.2,3 C.5,1 D.2,4二.填空题(共5小题)6.已知x,y满足方程组,则无论k取何值,x,y恒有关系式是.7.若方程组的解为,则方程组的解是.8.已知关于x,y的方程组.给出下列结论:②当k=时,x,y的值互为相反数;③若方程组的解也是方程x+y=4﹣k的解,则k=1;④若2x•8y=2z,则z=1.其中正确的是.9.方程组的解满足方程x+y+a=0,那么a的值是.10.已知是方程组的解,则代数式a+b的值为.三.解答题(共5小题)11.已知方程组,甲正确地解得,而乙粗心地把C看错了,得,试求出a,b,c 的值.12.已知关于x,y的方程组,给出下列结论:①当t=﹣1时,方程组的解也是方程x+2y=2的解;②当x=y时,t=﹣;③不论t取什么实数,x+2y的值始终不变;④若z=﹣xy,则z的最小值为﹣1.请判断以上结论是否正确,并说明理由.13.已知关于x、y的方程组.(1)若x、y是互为相反数,求a的值;(2)若x﹣y=2,求方程组的解和a的值.14.在解关于x,y的方程组时,老师告诉同学们正确的解是,粗心的小勇由于看错了系数c,因而得到的解为,试求abc的值.15.已知关于x,y的方程组(1)请直接写出方程x+2y﹣6=0的所有正整数解;(2)若方程组的解满足x+y=0,求m的值;(3)无论实数m取何值,方程x﹣2y+mx+5=0总有一个固定的解,请直接写出这个解?(4)若方程组的解中x恰为整数,m也为整数,求m的值.参考答案一.1.A 2.A 3.D 4.B 5.C二.6.x+y=1 7.8.①②④9.1 10.0三.11.解:根据题意,得,解得,把代入方程5x﹣cy=1,得到:10﹣3c=1,解得c=3.故a=3,b=﹣1 c=3.12.解:①把t=﹣1代入方程组得,解得,把代入x+2y=2得:左边=﹣6+2=﹣4≠右边,不符合题意;②由y=x,得到,解得t=﹣,符合题意;③,①+②得2y=2t+16,即y=t+8,①﹣②得2x=﹣4﹣4t,即x=﹣2t﹣2,x+2y=﹣2t﹣2+2t+16=14,符合题意;④z=﹣(t+8)(﹣2t﹣2)=(t+8)(t+1)=t2+9t+8=(t+)2+≥,不符合题意.13.解:(1)由题意,得x+y=0,方程组两方程相加,得3(x+y)=3a﹣3,即x+y=a﹣1,可得a﹣1=0,解得a=1;(2)方程组两方程相减,得x﹣y=﹣a﹣5,代入x﹣y=2得﹣a﹣5=2,解得a=﹣7,方程组为,①×2﹣②,得3y=15,解得y=5,把y=5代入②,得x=﹣8,则方程组的解为.14.解:把和代入ax+by=2中,得,解得,把代入cx﹣7y=8中,得c=﹣2,则abc=﹣40.15.解:(1)方程x+2y﹣6=0,2x+y=6,解得x=6﹣2y,当y=1时,x=4;当y=2时,x=2,方程x+2y﹣6=0的所有正整数解为,;(2)由题意得,解得,把代入x﹣2y+mx+5=0,解得m=﹣;(3)x﹣2y+mx+5=0,(1+m)x﹣2y=﹣5,∴当x=0时,y=2.5,即固定的解为,(4),①+②得2x﹣6+mx+5=0,(2+m)x=1,x=,∵x恰为整数,m也为整数,∴2+m是1的约数,2+m=1或﹣1,m=﹣1或﹣3.2.3 解二元一次方程组一.选择题(共9小题)1.已知方程组的解满足x﹣y=m﹣1,则m的值为()A.﹣1 B.﹣2 C.1 D.22.如果|x﹣2y+1|+|x+y﹣5|=0,那么xy=()A.2 B.3 C.5 D.63.若x,y满足方程组,则x﹣y的值等于()A.﹣1 B.1 C.2 D.34.已知关于x,y的方程组,甲看错a得到的解为,乙看错了b得到的解为,他们分别把a、b错看成的值为()A.a=5,b=﹣1 B.a=5,b=C.a=﹣l,b=D.a=﹣1,b=﹣15.若关于x、y的二元一次方程组的解满足x+y=9,则k的值是(()A.1 B.2 C.3 D.46.若方程组的解x和y相等,则a的值为()A.1 B.2 C.3 D.47.若5x2a+b y2与﹣4x3y3a﹣b是同类项,则a﹣b的值是()A.0 B.1 C.2 D.38.已知方程组的解满足x﹣y=m﹣1,则m的值为()A.﹣1 B.﹣2 C.1 D.29.如果(x+y﹣5)2与|3x﹣2y+10|互为相反数,则x,y的值为()A.x=3,y=2 B.x=2,y=3 C.x=0,y=5 D.x=5,y=0二.填空题(共3小题)10.若实数x,y满足,则代数式2x+3y﹣2的值为.11.已知方程组与有相同的解,则m=,n=.12.如果方程组与方程组的解相同,则m=,n=.三.解答题(共13小题)13.已知方程组和有相同的解,求a2﹣2ab+b2的值.14.解下列方程组:(1)(2)15.解下列方程组:(1)用代入法解方程组:(2)用加减法解方程组:16.下列解方程组:(1)(2)17.解下列方程组:(1)(2)参考答案一.1.D 2.D 3.A 4.A 5.B 6.C 7.A 8.A 9.C 二.10.4 11.,12 12.3,2三.13.解:解方程组得,把代入第二个方程组得,解得,则a2﹣2ab+b2=22﹣2×2×1+12=1.14.解:(1),①×2+②,得到5x=20,∴x=4,把x=4代入①得到y=﹣1,∴.(2),①﹣②×2得到19y=﹣38,y=﹣2,把y=﹣2代入②得到:x=3,∴15.解:(1)由①得y=2x﹣5 ③,把③代入②,得3x+4(2x﹣5)=2,解得x=2,把x=2代入③,得y=2×2﹣5=﹣1,∴方程组的解为.(2)把①×3得9x+12y=48 ③,把②×2得10x﹣12y=66 ④,③+④得19x=114解得x=6,把x=6代入①得18+4y=16,解得y=﹣,∴方程组的解为.16.解:(1),①×3﹣②×2,得11x=22,解得x=2,将x=2代入①,得10﹣2y=4,解得y=3,所以方程组的解为;(2),②代入①,得4x﹣3(7﹣5x)=17,解得x=2,将x=2代入②,得y=﹣3,所以方程组的解为.17.解:(1),①×4+②,得11x=22,解得x=2,将x=2代入①,得4﹣y=5,解得y=﹣1,所以方程组的解为;(2),①﹣②,得2y=﹣8,解得y=﹣4,将y=﹣4代入②,得x﹣4=2,解得x=12,所以方程组的解为.2.4 二元一次方程组的应用一.选择题(共5小题)1.我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为()A.B.C.D.2.我国古代数学著作《九章算术》卷七有下列问题:“今有共买物,人出八,盈三:人出七,不足四,问人数、物价几何?”意思是:现在有几个人共同出钱去买件物品,如果每人出8钱,则剩余3钱:如果每人出7钱,则差4钱.问有多少人,物品的价格是多少?设有x人,物品的价格为y元,可列方程(组)为()A.B.C.D.=3.甲、乙两人骑自行车比赛,若甲先骑30分钟,则乙出发后50分钟可追上甲,设甲、乙每小时分别骑x 千米、y千米,则可列方程()A.30x=50y B.C.(30+50)x=50y D.4.如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是()(第4题图)A.0.6x+0.4y+100=500 B.0.6x+0.4y﹣100=500C.0.4x+0.6y+100=500 D.0.4x+0.6y﹣100=5005.某市举办花展,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为()(第5题图)A.8 B.13 C.16 D.20二.填空题(共4小题)6.以绳测井,若将绳三折测之,绳多五尺;若将绳四折测之,绳多一尺,绳长,井深各几何若设绳长x 尺,井深y尺,则可列方程组为.7.算筹是中国古代用来记数、列式和进行各种数与式演算的一种工具.在算筹计数法中,以“立”,“卧”两种排列方式来表示单位数目,表示多位数时,个位用立式,十位用卧式,百位用立式,千位用卧式,以此类推.《九章算术》的“方程”一章中介绍了一种用“算筹图”解决一次方程组的方法.如图1,从左向右的符号中,前两个符号分别代表未知数x,y的系数.因此,根据此图可以列出方程:x+10y=26.请你根据图2列出方程组.(第7题图)8.老王家去年收入x元,支出y元,而今年收入比去年多15%,支出比去年少10%,结果今年结余30000元,根据题意可列出的方程为.9.盒子里有若干个大小相同的白球和红球,从中任意摸出一个球,摸到红球得2分,摸到白球得3分.某人摸到x个红球,y个白球,共得12分.列出关于x、y的二元一次方程:.三.解答题(共2小题)10.下列各个图是由若干个花盆组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数是s.(第10题图)按此规律推断,以s、n为未知数的二元一次方程是.11.某工厂用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图2所示的竖式与横式两种无盖的长方体纸盒.设加工竖式纸盒x个,横式纸盒y个.(第11题图)(1)根据题意,完成以下表格:(2)工人李娟从仓库领来了长方形纸板2012张,正方形纸板1003张,请你帮她计划竖式纸盒、横式纸盒各加工多少个,恰好将领来的纸板全部用完;(3)李娟有一张领取材料的清单,上面写着:长方形纸板a张(碰巧a处的数字看不清了,她只记得不超过142张),正方形纸板90张.并且领来的材料恰好全部用于加工上述两种纸盒,试求出她加工这两种盒子各多少个?参考答案与试题解析一.1.C 2.A 3.D 4.A 5.C二.6.7.8.(1+15%)x﹣(1﹣10%)y=300009.2x+3y=12三.10.解:由图可知:第一图:有花盆3个,每条边有花盆2个,那么s=3×2﹣3;第二图:有花盆6个,每条边有花盆3个,那么s=3×3﹣3;第二图:有花盆9个,每条边有花盆4个,那么s=3×4﹣3;…由此可知以s,n为未知数的二元一次方程为s=3n﹣3.11.解:(1)完成表格如下所示:(2)由题意,得,解得,答:竖式纸盒加工203个,横式纸盒加工400个.(3)由题意,得,解得y=72﹣a,x=90﹣2y,∵a≤142,∴y≥43.6.∵x>0,∴90﹣2y>0,∴y<45,∴43.6≤y<45.∵y为正整数,∴y=44,x=2.答:他做竖式纸盒2个,横式纸盒44个.2.5 三元一次方程组及其解法(选学)一.选择题(共5小题)1.解下面的方程组时,要使解法较为简便,应()A.先消去x B.先消去y C.先消去z D.先消去常数2.三元一次方程组,消去未知数z后,得到的二元一次方程组是()A.B.C.D.3.下列四组数值中,()是方程组的解.A.B.C.D.4.甲、乙、丙三种商品,若购买甲3件、乙2件、丙1件,共需130元钱,购甲1件、乙2件、丙3件共需210元钱,那么购甲、乙、丙三种商品各一件共需()A.105元B.95元C.85 元D.88元5.如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是()(第5题图)A.2 B.7 C.8 D.15二.填空题(共2小题)6.方程组的解是.7.已知:,则x+y+z=.三.解答题(共4小题)8.解三元一次方程组:.9.解方程组:.10.甲地到乙地全程是142千米,一段上坡、一段平路、一段下坡,如果保持上坡每小时行驶28千米,平路每小时行驶30千米,下坡每小时行驶35千米,从甲地行驶到乙地需4小时30分钟,从乙地行驶到甲地需4小时42分钟,问:从甲地到乙地时,上坡、平路、下坡的路程各是多少?11.吃仙果的趣味问题:三种仙果红紫白,八戒共吃十一对;白果占紫三分一,紫果正是红二倍;三种仙果各多少?看谁算得快又对.(1)小明分析:如果设红果x个,紫果y个,则白果有(22﹣x﹣y)个,根据题意,可列二元一次方程组为;(2)小敏分析,如果设红果x个,紫果y个,白果z个,根据题意,可列三元一次方程组为;(3)请你先填出上述小题中相应的方程组,然后选一种分析思路求解本题.参考答案一.1.C 2.A 3.B 4.C 5.C二.6.7.6三.8.解:①+②,得2y=﹣5﹣1,解得y=﹣3.②+③,得2x=﹣1+15,解得x=7,把x=7,y=﹣3代入①,得﹣3+z﹣7=﹣5,解得z=5,方程组的解为.9.解:①+②,得4x+3z=18④,①+③,得2x﹣2z=2⑤⑤×2﹣④,得﹣7z=﹣14,解得z=2,把z=2代入①,得x=3,把x=3,z=2代入①,得y=1,则方程组的解为.10.解:设从甲地到乙地时,上坡、平路、下坡的路程各是x、y、z千米,4小时30分钟=4.5小时,4小时42分钟=4.7小时,根据已知可得,解得.答:从甲地到乙地时,上坡、平路、下坡的路程各是42、30和70千米.11.解:(1)设红果x个,紫果y个,则白果(22﹣x﹣y)个.根据题意,得,(2)设红果x个,紫果y个,白果z个.依题意得.(3)二元一次方程组:设红果x个,紫果y个,则白果(22﹣x﹣y)个.根据题意,得,解得.则红果6个,紫果12个,白果4个;三元一次方程组:设红果x个,紫果y个,白果z个.依题意,得.解得.则红果6个,紫果12个,白果4个.。
七年级下册数学第二单元测试卷

七年级数学下册第二章单元测试题一、 选择题每题3分,共30分1.以下说法错误..的是 A .两直线平行,内错角相等 B .两直线平行,同旁内角相等 C .同位角相等,两直线平行D .对顶角相等2.如果一个角的补角是120°,那么这个角的余角的度数是 °°° °3.如图1,所示是一条街道的路线图AB 2∠AB CE //////AB EF DC EG BD 1∠a b ,c a b∥160∠=°2∠=° 17.如图11:如果∠1=∠3,可以推出一组平行线为 ;10 图1118.如图11,AB ∥ED,则∠A +∠C +∠D = 三、 解答题第19题每空2分,共18分,第20题8分,第21,22题每题10分,共46分19.1如图,已知∠A =∠F,∠C =∠D,根据图形填空,并在括号内注明理由; 解: ∠A =∠FAC ∥________内错角相等,两直线平行∠1 =∠D_________________________________∠1 =∠D ∠C =∠D∠1=___________等量代换BD ∥______________________________________________________ 2已知:如图,AB ∥CD,∠A = ∠D,试说明 AC ∥DE 成立的理由; 下面是某同学进行的推理,请你将他的推理过程补充完整;6分 解:∵ AB ∥ CD 已知∴ ∠A = ∠ 两直线平行,内错角相等 又∵ ∠A = ∠D∴ ∠ = ∠ 等量代换∴ AC ∥ DE20、 如图,EF ∥AD,∠1 =∠2,∠BAC = 70°;将求∠AGD 的过程填写完整;A B CEA BC D O 12B C E ADA图9A BC E DO BA12图7ca bA B CDEAACADAEABAFA1BAD解:∵EF∥AD,∴∠2 = ;又∵∠1 = ∠2,∴∠1 = ∠3;∴ AB∥ ;∴∠BAC + = 180°;又∵∠BAC = 70°,∴∠AGD = ;21、如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,你能算出∠BAD、∠EAC、∠C的度数吗22、如图,已知AB证:AC。
新人教版七年下册数学第二单元(实数)测试卷及答案

2022——2023学年度第二学期七年级数学测试卷第六章 实数学校:___________姓名:___________班级:___________考号:___________一、单选题(每题3分,共30分)1.下列各数中,是无理数的是( )A .74-B .0C .πD .0.122.数轴上表示实数a 的点的位置如图所示,化简|1|a -的结果为( )A .1a -B .1a -C .1a +D .1a --3n 和1n +之间,则n 的值是( )A .4B .3C .2D .1 4.在实数2π-,0,1-中,最小的是( ) A.2π- B .0 C D .1- 5.在实数1-17,3.14中,属于无理数的是( ) A .1- B C .17 D .3.146.下列各数中是无理数的是( )1.34,12π,0.020020002...,6.57896. A .2个 B .3个 C .4个 D .5个 7.估算7 )A .3和4之间B .4和5之间C .5和6之间D .6和7之间8.已知3既是5a +的平方根,也是721a b -+的立方根,则关于x 的方程()2290a xb --=的解是( ).A .12x =B .72x =C .43x =或83D .12x =或729.下列各数:π2,00.2,227,0.303003(相邻两个3之间依次多一个0),1 )10.下列说法中:①不是正数的数一定是负数;①227不仅是无理数,而且是分数;①多项式223x xy ++是二次三项式;①单项式22xyz π-的系数和次数分别是2π-和4.其中错误的说法的个数为( )A .1个B .2个C .3个D .4个二、判断题(每题2分,共10分)11.判断对错:(正确的画“√”,错误的画“×”)(1)任何数都有算术平方根 ( )(2)一个数的算术平方根一定是正数 ( )(3)所有无限小数都是无理数; ( )(4)所有无理数都是无限小数; ( )(5)不是有限小数的不是有理数. ( )三、填空题(每空4分,共52分)12.写出一个比0小的整数__________.13.若()229x +=,则x =_______.143π-=_____.15.若01x <<1x 、2x 的大小关系是________.16.16的平方根是________________.17()220y -=,则xy 的值为______.18.计算:|2022|-=________,2023(1)-=________=________.29.已知实数a 、b 满足()2350a b +++=,则a b +的立方根是_______.20.已知57≤, 46≤ _____.21.一个两位数m 的十位上的数字是a ,个位上的数字是b ,我们把十位上的数字a 与个位上的数字b 的和叫做这个两位数m 的“衍生数”,记作()f m ,即()f m a b =+.如()52527f =+=.现有2个两位数x 和y ,且满足100x y +=,则()()f x f y +=______.四、解答题(6个小题共58分)22.计算:(16分)(1). 321|(|)-+- (2). 23()(15273)-++-⨯(3). (4). ()()232--23. 已知一个正数a 的平方根分别是25a -和21a +,另一个实数b 的立方根是2,c(8分) 求:(1)a ,b ,c 的值(2)求224a b c +-的平方根.24.我们用[]a 表示不大于a 的最大整数,[]a a -的值称为数a 的相对小数部分.如[]2.132=,2.13的相对小数部分为[]2.13 2.130.13-=. (12分)(1)= ,= . 3.2-的相对小数部分= .(2)m ,求)m 的值.(3)设2x ,y 为有理数.若()x x y +的值为有理数,求()x x y +的值.25.对于任意一个四位正整数m ,若m 的各位数字都不为0,且千位数字与百位数字不相等,十位数字与个位数字不相等,那么称这个数为“不同数”.将一个“不同数”m 的任意一个数位上的数字去掉后得到四个新三位数,把这四个新三位数的和与3的商记为F(m ).例 如,“不同数”1234m =,去掉其中任意一位数后得到的四个新三位数分别为:234、134、124、123,这四个三位数之和为234134124123615+++=,6153205÷=,所以()1234205F =. (10分)(1)计算()1245F 和()2134F ;(2)若“不同数”340010n x y =++(13x ≤≤,18y ≤≤,x 、y 都是正整数),()n F 的百位数字与个位数字不相同且()n F 能被6整除,求n 的值.26.一个三位自然数的各位数字均不为0,它的十位与个位数字之和等于百位的两倍.那么这样的数叫“好数”,对于一个好数m ,将其十位与个位对调得到一个数m ',记()111m m F m '+=. 例如:324x =,因为24632+==⨯,所以x 是“好数”,()3243426111F x +== 212y =,因为12322+=≠⨯,所以y 不是“好数” (12分)(1)判断435m =和523n =是不是“好数”,如果是“好数”,求出()F m 或()F n ;(2)若一个好数“t ”的百位数字是a ,十位数字是b ,个位数字是c ,14a ≤≤,18b ≤≤且()1T F t t =++能被7整除,求出所有t 的值.参考答案:1.C【分析】根据无理数的定义:无限不循环小数,进行判断即可.【详解】解:A 、74-是有理数,不符合题意; B 、0是有理数,不符合题意;C 、π是无理数,符合题意;D 、0.12是有理数,不符合题意;故选C .【点睛】本题考查无理数,熟练掌握无理数的定义,是解题的关键.2.B【分析】根据绝对值化简的方法,即可化简求值.【详解】①从数轴上观察出a<0①10a -<①()|1|11a a a -=--=-故选:B【点睛】本题考查绝对值的化简,解题的关键是掌握绝对值化简的方法.3.C【分析】根据459得到23<<,即可得到答案. 【详解】解:①459,①23<,①2n =,故选:C .【点睛】此题考查了无理数的估算,正确掌握无理数的估算方法是解题的关键.4.A【分析】根据实数的大小比较法则即可得到答案.【详解】解:102π-<-<< ∴最小的数是2π-, 故选A .【点睛】本题考查了实数的大小比较,解题关键是熟练掌握实数的大小比较法则:负数都小于0;负数都小于正数;两个负数,其绝对值大的反而小.5.B【分析】根据无理数的定义判断即可.1-是整数,17,3.14是分数,都属于有理数, 故选B .【点睛】本题考查了无理数,能熟记无理数的定义是解此题的关键,注意:无理数是指无限不循环小数.6.B【分析】根据无理数就是无限不循环小数,逐项判断即可.【详解】无理数有12π,0.020020002…,共3个 故选:B【点睛】本题主要考查无理数的定义,包括:①开方开不尽的根式,①含π的,①一些有规律的数;明确无理数指的是无限不循环小数是解题的关键.7.A【分析】估算34<,进而即可求解.【详解】解:①91316<<①34<,①43-<- ①374<,故选:A .【点睛】本题考查了无理数的估算,正确的估算出34<是解题的关键.8.D【分析】根据平方根和立方根的概念可得59a +=,72127a b -+=,求解可得4a =,1b =,然后带入原方程,利用平方根解方程即可.【详解】解:根据题意,3既是5a +的平方根,也是721a b -+的立方根,可得2539a +==,3721327a b -+==,解得4a =,1b =,则关于x 的方程()2290a x b --=即为()22904x --=, ①29(2)4x -=, ①322x -=±, 解得 12x =或72x =. 故选:D .【点睛】本题主要考查了平方根和立方根的知识,熟练掌握相关概念是解题关键.9.B【分析】根据无理数的定义求解即可.【详解】π2是无理数,03=是有理数,0.2是有理数,227是有理数,0.303003(相邻两个3之间依次多一个0)是无理数,1故无理数的个数有3个,故选:B .【点睛】此题主要考查了无理数的定义:无限不循环的小数为无理数,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.303003(相邻两个3之间依次多一个0),等有这样规律的数.10.C【分析】分别根据有理数的分类,无理数的定义,多项式的定义,单项式的定义逐一判断即可.【详解】解:①不是正数的数一定是负数或0,故①不正确; ①227不仅是有理数,而且是分数,故①不正确; ①多项式223x xy ++是三次三项式,故①不正确;①单项式22xyz π-的系数和次数分别是2π-和4,故①正确, 错误的说法个数是3个,故选:C .【点睛】本题考查了多项式,单项式,无理数,正数和负数,熟练掌握这些数学概念是解题的关键.11. × × × √ ×【分析】根据算术平方根的定义分析即可.【详解】解:(1)①负数没有算术平方根,①任何数都有算术平方根 (× );(2) ①0的算术平方根是0,①一个数的算术平方根一定是正数(×);解:(3)无限小数包括无限循环小数和无限不循环小数,无限循环小数是有理数, ∴(3)错误;(4)无限不循环小数是无理数,∴(4)正确;(5)有理数包括整数、分数、有限小数和无限循环小数,∴(5)错误;故答案为:①×①×①×①√5×.【点睛】题目主要考查有理数和无理数的常见类别,理解有理数和无理数的分类是解题关键. 12.1-##2-【分析】判断无理数的取值范围,直接求解即可.【详解】因为2232-<<-,所以32-<<-,则比0小的整数有1-或2-.故答案为:填1-或2-均可.【点睛】此题考查无理数的估算,解题关键是直接算出取值范围.13.1或5-##5-或1【分析】利用平方根定义开方即可求解.【详解】解:方程()229x +=,开方得:23x +=±,解得:1x =或5x =-.故答案为:1或5-.【点睛】本题考查了平方根的定义,熟练掌握平方根的定义是解答本题的关键. 14.π【分析】直接利用立方根的性质以及绝对值的性质和算术平方根的性质分别化简,然后计算得出答案.|3|π-363π=-++-π=.故答案为:π.【点睛】本题主要考查了立方根的性质以及绝对值的性质和算术平方根的性质,正确化简各数是解题关键.15.21x x> 【分析】由实数的比较大小的法则进行比较,即可得到答案.【详解】解:由01x <<,得x >,11x>,21x ,故答案为:21x x >. 【点睛】本题考查了实数的比较大小,解题的关键是熟练掌握实数比较大小的法则. 16. 4± 2【分析】根据平方根和算术平方根的定义即可得到结论.【详解】解:因为4±的平方是16,所以16的平方根是4±,4=,且2的平方是4,2.故答案为:4±;2.【点睛】本题考查了平方根和算术平方根的定义,熟记定义是解题的关键.17.4-【分析】根据非负数的性质分别求出x y ,,代入计算即可. 【详解】解:()220x y y ++-=, 020x y y ∴+=-=,,解得:22x y =-=,,224xy ∴=-⨯=-,故答案为:4-,【点睛】本题考查的是非负数的性质和代数式求值,掌握算术平方根的非负性、偶次方的非负性是解题的关键.18. 2022 1- 4【分析】根据负数的绝对值为正数,有理数的乘方运算,求一个数的算术平方根计算即可.【详解】解:|2022|2022-=,2023(1)1-=-,4,故答案为:①2022;①1-;①4.【点睛】题目主要考查绝对值的化简,有理数的乘方运算,求一个数的算术平方根,熟练掌握运算法则是解题关键.19.2-【分析】先根据非负数的性质求出a 、b 的值,进而求出a b +的值,再根据立方根的定义进行求解即可.【详解】解:①()2350a b +++=,()25030a b ++≥≥,, ①()23500a b ++==,,①3050a b +=+=,,①35a b =-=-,,①()358a b +=-+-=-,①a b +的立方根是2-,故答案为:2-.【点睛】本题主要考查了求一个数的立方根,非负数的性质,正确根据非负数的性质求出a 、b 的值,进而求出a b +的值是解题的关键.20.6,7,8,9【详解】解:①57≤,46≤,①2549a ≤≤,1636b ≤≤,①4185a b ≤+≤,6,7,8,9.故答案为:6,7,8,9.【点睛】本题考查了估算无理数的大小,解决本题的关键是掌握估算的方法.21.19或10【分析】x 和y 的取值分两种情况分别分析即可得解.【详解】解:设两位数x 的十位数字为c ,个位数字为d ,两位数y 的十位数字为p ,个位数字为q ,根据题意100x y +=,则x 和y 的取值有两种情况,①x y ≠时,此时9c p +=,10d q +=,()()19f x f y c d p q +=+++=∴,②50x y ==时,此时5c p ==,0d q ==,()()10f x f y c d p q +=+++=∴,故答案为:19或10.【点睛】此题考查了用字母表示数的新定义,理解题意并进行分类讨论是解题关键. 22.(1)2- (2)51 (3)154(4)40-【分析】(1)根据绝对值,有理数的乘方运算,求一个数的立方根,进行计算即可求解.(2)根据有理数的混合运算进行计算即可求解.(3)先计算算术平方根,然后计算加减即可;(4)先计算立方根和算术平方根以及平方,然后计算加减,【详解】(1)解:原式213=-- 2=-;(2)解:原式25271=+-521=-51=.(3)554=-+ 154=;(4()()232--6304=---40=-.【点睛】此题考查了立方根和算术平方根的运算,平方的运算,解题的关键是熟练掌握以上运算法则.23.(1)1a =,8b =,3c =(2)5±【分析】(1)由平方根的性质知25a -和21a +互为相反数,可列式,解之可求得a 的值;根据立方根定义可得b 的值;根据34<<可得c 的值;(2)分别将a ,b ,c 的值代入224a b c +-中,即可求得它的值及平方根.【详解】(1)解:①一个正数的平方根分别是25a -和21a +,另一个实数b 的立方根是2, 25210a a ∴-++=,8b =,解得:1a =则a 的值是1,b 的值是8;91516<<,34∴<,3,3c ∴=,综上所述,1a =,8b =,3c =;(2)解:1a =,8b =,3c =,224a b c ∴+-2329=+-25= 25的平方根5±,224a b c ∴+-的平方根5±.【点睛】本题主要考查了立方根、平方根及无理数的估算,解题的关键是熟练掌握平方根和立方根的定义.24.(1)22,0.8(2)1(3)2-【分析】(1)根据题目给的定义进行计算即可;(2)根据题目给的定义求出m 值,再代入式子求解即可;(3)根据题目给的定义求出x ,再根据y 和()x x y +都是有理数进行求解即可.【详解】(1)23<,①2=的相对小数部分2=,3.2-的相对小数部分为()3.2 3.2 3.20]48[.---=---=,故答案为:22,0.8;(2)由题意得:2=,2m =,①))221m ==;(3)由题意得: ()22213x ⎡==-=⎣ ()()33y x x y +=,若使y 和()x x y +都为有理数,则33x y y +==-此时()(33792x x y +=-=-=-.【点睛】本题考查了无理数的估算,新定义问题,无理数有理化等知识点,能够根据题目给的定义进行推理是解题的关键.25.(1)213,265(2)n 的值为3426,3435【分析】(1)根据新定义计算,即可分别求得.(2)首先可求得()4607F n x y =++,再根据()F n 能被6整除,可得x y +能被6整除,且13x ≤≤,18y ≤≤,x ,y 都是正整数,x y ≠,可得029x y ≤-++≤且x y ≠,分类讨论,即可求得.【详解】(1)()()12451241251452453213F =+++÷=,()()21342132142341343265F =+++÷=;(2)“不同数”340010n x y =++,去掉千位:40010x y ++,去掉百位:30010x y ++,去掉十位:340y +,去掉个位:340x +()()400103001034034034607F n x y x y y x x y =+++++++++÷=++,()F n 能被6整除, ①460+727766x y x y x +-++=++ x y ∴+能被6整除,且13x ≤≤,18y ≤≤,x ,y 都是正整数,x y ≠,①029x y ≤-++≤且x y ≠,①20x y -++=或26x y -++=①当20x y -++=时,1x y ==,不合题意;①当26x y -++=时,8x y +=,当x =1,y =7时,()474F n =,不合题意;当x =2,y =6时,()480F n =,n =3426;当x =3,y =5时,)486Fn =(,n =3435; 综上所述,n 的值为3426,3435.【点睛】本题考查了新定义下的运算,理解新定义,采用分类讨论的思想是解决此类题的关键.26.(1)435m =是“好数”,523n =不是“好数”, ()8F m =(2)315或453【分析】(1)先根据“好数”的定义可以得到435m =是“好数”,523n =不是“好数”,再根据()F m 的定义求出()F m 的值即可;(2)先根据题意得到2b c a +=,10010t a b c =++,10010t a c b '=++,进而求出()2F t a =,再根据已知条件式得到10491a b ++能被7整除,据此求解即可.【详解】(1)解:①3542+=⨯,①435m =是“好数”,①453m '=,①()4354538111F m +==; (2)解:①一个好数“t ”的百位数字是a ,十位数字是b ,个位数字是c ,①2b c a +=,10010t a b c =++,10010t a c b '=++,①()10010100102001111200222111111111a b c a c b a b c a a F t a ++++++++====, ①()1T F t t =++能被7整除,①210010*********a a b c a a b a b ++++=+++-+能被7整除,①10491a b ++能被7整除,当1a =时,7b =,此时5c =-,不符合题意;当2a =时,4b =,此时0c ,不符合题意;当3a =时,1b =,此时5c =,符合题意;当4a =时,5b =,此时3c =,符合题意;综上所述,符合题意的t 的值为315或453.【点睛】本题主要考查了新定义的实数运算,正确理解题意是解题的关键.。
七年级数学下册《第二章 二元一次方程组》单元测试卷及答案(浙教版)

七年级数学下册《第二章 二元一次方程组》单元测试卷及答案(浙教版)一、选择题1.下列选项中,是二元一次方程的是( )A .a+3=5.B .x+y2=1.C .m+n=3.D .xy=6.2.已知关于x 、y 的方程组05mx y x ny +=⎧⎨+=⎩,解是13x y =-⎧⎨=-⎩,则2m+n 的值为( )A .-8B .-6C .-4D .03.若方程组34221x y x y -=⎧⎨=-⎩用代入法消去x ,所得关于y 的一元一次方程为( )A .32142y y ---=B .()31242y y --=C .()32142y y --=D .3242y y --=4.如图,宽为40cm 的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为( )A .256cm 2B .320cm 2C .360cm 2D .400cm 25.已知12x y =⎧⎨=⎩是方程5ax by +=的解,则代数式246a b +-的值为( )A .4B .2C .1D .56.方程组23x y x y +=⎧⎨+=⎩的解为2x y =⎧⎨=⎩,则被遮盖的两个数分别为( )A .2,1B .2,3C .5,1D .2,47.已知关于x 、y 的方程组343x y ax y a+=-⎧⎨-=-⎩的解互为相反数,则a 的值是( )A .4B .0C .1-D .18.已知关于x ,y 的方程组{4x +3y =1(k −1)x +3ky =3的解中x 与y 互为相反数,则k 的值为( )A .2B .0C .2-D .4-9.方程组233730x y x z x y z +=⎧⎪-=⎨⎪-+=⎩的解为( )A .211x y z =⎧⎪=⎨⎪=-⎩B .211x y z =⎧⎪=-⎨⎪=⎩C .211x y z =⎧⎪=-⎨⎪=-⎩D .211x y z =⎧⎪=⎨⎪=⎩10.我国古代数学名著《九章算术》中记载:“今有甲、乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十,问甲、乙持钱各几何?”题目大意是:今有甲、乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其23的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?若设甲持钱为x ,乙持钱为y ,则下列方程组中正确的是( )A .{12x +y =50y +23x =50 B .{x +12y =50y +x =50C .{x +12y =5023y +x =50D .15022503x y y x ⎧+=⎪⎪⎨⎪+=⎪⎩二、填空题11.若{x =1y =-2是关于x 和y 的二元一次方程ax+y=1的解,则a 的值等于 .12.若二元一次方程32kx y -=的一组解是12x y =⎧⎨=-⎩,则k 的值为 .13.在方程b y ax =-中,当2x =-时3y =,当1x =时,0y =,那么2a b += .14.如图,在长为20m ,宽为16m 的长方形空地上,沿平行于各边分割出三个形状、大小一样的小长方形花圃,则其中一个小长方形花圃的长为 m.三、解答题15.已知关于 ,x y 的方程组 2143x y m x y m -=+⎧⎨+=+⎩的解也是二元一次方程 237x y -= 的一个解,求m 的值.16.解关于x ,y 的方程组932ax by x cy +=⎧⎨-=-⎩时,甲正确的解出24x y =⎧⎨=⎩,乙因为把c 抄错了,误解为41x y =⎧⎨=-⎩,求a 、b ,c 的值. 17.已知关于x 、y 的二元一次方程组231mx ny mx ny +=⎧⎨-=⎩的解为11x y =⎧⎨=-⎩,求2m n -的值.18.有一个三位数,个位数字是百位数字的3倍,十位数字比百位数字大5,若将此数的个位数与百位数互相对调,所得新数比原数的2倍多35,求原数.19.用铁皮材料做罐头盒,每张铁皮可制盒身30个,或制盒底50个,一个盒身与两个盒底配成一套.现有33张铁皮材料,分别用多少张制盒身、盒底,才能保证既恰好用完铁皮材料,又使盒身和盒底正好配套?四、综合题20.薇菜蕨类植物中紫萁科紫萁类植物是中国目前出口创汇的重要蔬菜之一,具有杀菌消炎,抗病毒,防止脑神经老化等多重功效,珍宝岛地区在扶贫攻坚战中为了推动农民创收,特别研发出保鲜包装和干制两种新产品再将两种产品包装成A ,B 两种型号的礼盒,每个A 型礼盒含2斤干薇菜和2袋鲜薇菜,每个B 型礼盒含4斤干薇菜和2袋鲜薇菜.现有1000斤干薇菜和400袋鲜薇菜需要包装销售(包装费用暂时忽略不计)两种礼盒的成本和售价如下表所示(单位:元)A 型礼盒B 型礼盒 成本 340 410 售价400500根据以上信息,解答下列问题(1)将上述干薇菜和鲜薇菜全部包装成A 型和B 型礼盒,求包装成的两种礼盒的数量各是多少?(2)若将上述干薇菜和鲜薇菜包装成280个礼盒后全部销售,包装后剩余的干薇菜和鲜薇菜不计入成本和利润,那么怎样包装可获得最大利润?最大利润是多少?(3)在(2)的条件下,将包装后剩余的干薇菜和鲜薇菜以成本价在当地销售,销售所得用来购买薇菜根苗在养植基地进行无土栽培,若每株薇菜根苗价格为15元,那么可以购买多少株?21.已知关于x ,y 的二元一次方程组53212x y m x y m +=-⎧⎨-=-+⎩,,的解满足3x y +=.(1)求m 的值; (2)求原方程组的解.22.水是生命之源,“节约用水,人人有责”.为了加强公民的节水意识,合理利用水资源,我市居民生活用水按阶梯式水价计费,下表是该市居民“一户一表”生活用水及阶梯计费价格表的部分信息(注:水费按月份结算,3m 表示立方米)每户每月用水量3(m ) 自来水销售价格(元3/m )污水处理价格(元3/m ) 不超出36m 部分a1.10 超出36m 不超出310m 的部分 b 1.10 超出310m 的部分7.001.10(注:①每户产生的污水量等于该户自来水用水量;②水费=自来水费用+污水处理费用). 已知2023年三月份,小红家用水38m ,交水费32.8元,小智家用水310m ,交水费44元. (1)请你根据以上信息,求表中a ,b 的值:(2)由于七月份正值夏天,小红家预计用水315m ,求小红家七月份预计应缴水费多少元? (3)若小智家四、五月份共用水320m ,其中四月份的用水量低于五月份的用水量,共缴水费89元,则小智家四、五月份的用水量各是多少?答案解析部分1.【答案】C【解析】【解答】解: A :a+3=5,只含有一个未知数,不是二元一次方程,不符合题意;B :x+y 2=1,含有未知数的最高次数是2次,不是二元一次方程,不符合题意;C :m+n=3,是二元一次方程,符合题意;D :xy=6,含未知数的项的次数是2次,不是二元一次方程,不符合题意; 故答案为:C.【分析】根据二元一次方程的定义对每个选项一一判断即可。
七年级数学下第二章相交线与平行线单元达标检测试卷含答案

第二章相交线与平行线达标检测卷一、选择题(每题3分,共30分)1.在同一平面内两条直线的位置关系可能是()A.相交或垂直B.垂直或平行C.平行或相交D.平行或相交或垂直2.a,b,c是同一平面内任意三条直线,交点可能有()A.1个或2个或3个B.0个或1个或2个或3个C.1个或2个D.都不对3.如图,是同位角关系的是()A.∠3和∠4B.∠1和∠4C.∠2和∠4D.不存在4.下列语句叙述正确的有()①如果两个角有公共顶点且没有公共边,那么这两个角是对顶角;②如果两个角相等,那么这两个角是对顶角;③连接两点的线段长度叫做两点间的距离;④直线外一点到这条直线的垂线段叫做这点到直线的距离.A.0个B.1个C.2个D.3个5.下列说法正确的是()A.两点之间的距离是两点间的线段B.同一平面内,过一点有且只有一条直线与已知直线平行C.与同一条直线垂直的两条直线也垂直D.同一平面内,过一点有且只有一条直线与已知直线垂直6.∠1和∠2是直线AB和CD被直线EF所截得到的同位角,那么∠1和∠2的大小关系是()A.∠1=∠2B.∠1>∠2C.∠1<∠2D.无法确定7.如图,有三条公路,其中AC与AB垂直,小明和小亮分别从A,B两点沿AC,BC同时出发骑车到C城,若他们同时到达,则下列判断中正确的是()A.小亮骑车的速度快B.小明骑车的速度快C.两人骑车的速度一样快D.因为不知道公路的长度,所以无法判断他们骑车速度的快慢8.下列说法中,正确的是()A.过点P不能画线段AB的垂线B.P是直线AB外一点,Q是直线AB上一点,连接PQ,使PQ⊥ABC.在同一平面内,过一点有且只有一条直线垂直于已知直线D.过一点有且只有一条直线平行于已知直线9.如图,如果AB ∥CD ,则∠α,∠β,∠γ之间的关系是()A. ∠α+∠β+∠γ=180°B. ∠α-∠β+∠γ=180°C.∠α+∠β-∠γ=180°D.∠α+∠β+∠γ=270°10.如图,已知A1B∥A n C,则∠A1+∠A2+…+∠A n=()A.180°nB.(n+1)180°C.(n-1)180°D.(n-2)180°二、填空题(每题3分,共24分)11.尺规作图是指用____________画图.12. 如图,直线a,b相交,∠1=60°,则∠2=__________,∠3=__________,∠4=__________.13.如图,直线AB与CD的位置关系是_________,记作_________于点_________,此时∠AOD=_________=_________=_________=90°.14.如图,AB∥CD,EF分别交AB,CD于G,H两点,若∠1=50°,则∠EGB=_________.15.如图,请写出能判断CE∥AB的一个条件,这个条件是:_________或_________或_________.16.如图,已知AB∥CD,CE,AE分别平分∠ACD,∠CAB,则∠1+∠2=_________.17.同一平面内的三条直线a,b,c,若a⊥b,b⊥c,则a__________c.若a∥b,b∥c,则a_________c.若a∥b,b⊥c,则a_________c.18.如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地间同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西.三、解答题(19~21题每题8分,25题12分,其余每题10分,共66分)19.如图,点P是∠ABC内一点.(1)画图:①过点P画BC的垂线,垂足为D;②过点P画BC的平行线交AB 于点E,过点P画AB的平行线交BC于点F.(2)∠EPF等于∠B吗?为什么?(3)请你用直尺和圆规作图,作一个角,使它等于2∠ABC.(要求用尺规作图,不必写作法,但要保留作图痕迹)20.如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:解:因为AD∥BC(已知),所以∠1=∠3(___________).因为∠1=∠2(已知),所以∠2=∠3.所以BE∥___________ (___________).所以∠3+∠4=180°(___________).21.如图,已知∠1=∠2,AC平分∠DAB,你能判定哪两条直线平行?说明理由.22.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.(1)试说明:CF∥AB;(2)求∠DFC的度数.23.如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH,求∠KOH的度数.24.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.试说明:AD∥BC.25.如图,已知AB∥CD,分别探讨下面的四个图形中∠APC与∠PAB,∠PCD的关系,请你从所得关系中任意选取一个加以说明.参考答案一、1.【答案】C2.【答案】B解:三条直线两两平行,没有交点;三条直线交于一点,有一个交点;两条直线平行与第三条直线相交,有两个交点;三条直线两两相交,不交于同一点,有三个交点,故选B.本题考查了相交线,分类讨论是解题关键,注意不要漏掉任何一种情况.3.【答案】B解:同位角的特征:在截线同旁,在两条被截直线同一方向上.4.【答案】B5.【答案】D6.【答案】D解:因为不知道直线AB和CD是否平行,平行时同位角相等,不平行时同位角不相等,所以无法确定同位角的大小关系,故选D.7.【答案】A8.【答案】C解:过一点画线段的垂线,即过一点画线段所在直线的垂线,故A错误;P是直线AB外一点,Q是直线AB上一点,如果P点不在过Q点且与AB垂直的直线上,或Q点不在过P点且与AB垂直的直线上,连接PQ,不可能有PQ⊥AB,故B错误;过一点画直线的平行线,这点不能在直线上,否则是同一条直线,故D错误;故C正确.9.【答案】C解:如图,过点E向右作EF∥CD,则∠FED=∠γ;由AB∥CD,可知EF∥AB,所以∠α+∠AEF=180°,即∠AEF=180°-∠α.不难看出∠β=∠FED+∠AEF,由此得到∠β=∠γ+∠AEF=∠γ+180°-∠α,即∠α+∠β-∠γ=180°,故选C.10.【答案】C解:如图,过点A2向右作A2D∥A1B,过点A3向右作A3E∥A1B,……因为A1B∥A n C,所以A3E∥A2D∥…∥A1B∥A n C,所以∠A1+∠A1A2D=180°,∠DA2A3+∠A2A3E=180°,…,所以∠A1+∠A1A2A3+…+∠A n-1A n C=(n-1)180°.二、11.【答案】圆规和没有刻度的直尺12. 【答案】120°;60°;120°13.【答案】垂直;AB⊥CD; O;∠BOD; ∠BOC;∠AOC14.【答案】50°解:因为AB∥CD,所以∠1=∠AGF.因为∠AGF与∠EGB是对顶角,所以∠EGB=∠AGF.故∠EGB=50°.15.【答案】∠DCE=∠A;∠ECB=∠B;∠A+∠ACE=180°16.【答案】90°解:因为AB∥CD,所以∠BAC+∠ACD=180°.因为CE,AE分别平分∠ACD,∠CAB,所以∠1+∠2=90°.17.【答案】∥;∥;⊥18.【答案】48°三、19.解:(1)如图,①直线PD即为所求;②直线PE,PF即为所求.(2)∠EPF=∠B.理由:因为PE∥BC(已知),所以∠AEP=∠B(两直线平行,同位角相等).又因为PF∥AB(已知),所以∠EPF=∠AEP(两直线平行,内错角相等),所以∠EPF=∠B(等量代换).(3)作∠MGH=∠ABC,以GH为一边在外侧再作∠HGN=∠ABC,即∠MGN=2∠ABC.20.解:因为AD∥BC(已知),所以∠1=∠3(两直线平行,内错角相等).因为∠1=∠2(已知),所以∠2=∠3.所以BE∥DF(同位角相等,两直线平行).所以∠3+∠4=180°(两直线平行,同旁内角互补).21.解:DC∥AB,理由如下:因为AC平分∠DAB,所以∠1=∠3.又因为∠1=∠2,所以∠2=∠3.所以DC∥AB(内错角相等,两直线平行).22.解:(1)因为CF平分∠DCE,所以∠1=∠2=∠DCE.因为∠DCE=90°,所以∠1=45°.因为∠3=45°,所以∠1=∠3.所以CF∥AB(内错角相等,两直线平行).(2)因为∠D=30°,∠1=45°,所以∠DFC=180°-30°-45°=105°.23.解:因为∠1+∠2=180°,所以AB∥CD.所以∠3=∠GOD.因为∠3=100°,所以∠GOD=100°.所以∠DOH=180°-∠GOD=180°-100°=80°.因为OK平分∠DOH,所以∠KOH=∠DOH=×80°=40°.24.解:因为AE平分∠BAD,所以∠1=∠2.因为AB∥CD,∠CFE=∠E,所以∠1=∠CFE=∠E.所以∠2=∠E.所以AD∥BC.25.解:题图①:∠APC+∠PAB+∠PCD=360°.理由:过点P向右作PE∥AB,如图①,因为AB∥CD,所以AB∥PE∥CD.所以∠A+∠1=180°,∠2+∠C=180°.所以∠A+∠1+∠2+∠C=360°.所以∠APC+∠PAB+∠PCD=360°.题图②:∠APC=∠PAB+∠PCD.理由:过点P向左作PE∥AB, 如图②,因为AB∥CD,所以AB∥PE∥CD.所以∠1=∠A,∠2=∠C.所以∠APC=∠1+∠2=∠PAB+∠PCD.题图③:∠APC=∠PAB-∠PCD.理由: 延长BA交PC于E, 如图③, 因为AB∥CD,所以∠1=∠C.因为∠PAB=180°-∠PAE=∠1+∠P,所以∠PAB=∠APC+∠PCD.所以∠APC=∠PAB-∠PCD.题图④:∠APC=∠PCD-∠PAB.理由:设AB与PC交于点Q,如图④,因为AB∥CD,所以∠1=∠C.因为∠1=180°-∠PQA=∠A+∠P, 所以∠P=∠1-∠A.所以∠APC=∠PCD-∠PAB.。
七年级数学下册第二单元测试题和答案

七年级数学下册各单元测试题第二章《相交线与平行线》测试卷一、选择题(每小题3分,共30分)1、如图所示,∠1和∠2是对顶角的是()A12B12C 112D2如图AB ∥CD 可以得到()A 、∠1=∠2B 、∠2=∠3C 、∠1=∠4D 、∠3=∠4AD2c1121234b B34365(第2题)C(第三题)78a(第4题)3、直线AB 、CD 、EF 相交于O ,则∠1+∠2+∠3=()A 、90°B 、120°C 、180°D 、140°4、如图所示,直线a 、b 被直线c 所截,现给出下列四种条件:①∠2=∠6②∠2=∠8③∠1+∠4=180°④∠3=∠8,其中能判断是a ∥b 的条件的序号是()A 、①②B 、①③C 、①④D 、③④5、某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是()A 、第一次左拐30°,第二次右拐30°B 、第一次右拐50°,第二次左拐130°DCC 、第一次右拐50°,第二次右拐130°D 、第一次向左拐50°,第二次向左拐130°6、下列哪个图形是由左图平移得到的()A(第7题)BA BCD2、7、如图,在一个有4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD 面积的比是()A 、3:4B 、5:8C 、9:16D 、1:28、下列现象属于平移的是()①打气筒活塞的轮复运动,②电梯的上下运动,③钟摆的摆动,④转动的门,⑤汽车在一条笔直的马路上行走A 、③B 、②③C 、①②④D 、①②⑤9、下列说法正确的是()A 、有且只有一条直线与已知直线平行B 、垂直于同一条直线的两条直线互相垂直C 、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
D 、在平面内过一点有且只有一条直线与已知直线垂直。
(必考题)初中数学七年级数学下册第二单元《相交线与平行线》测试(有答案解析)(1)
一、选择题1.如图,一副三角尺按不同的位置摆放,下列摆放方式中α∠与β∠互补的是( ) A . B . C . D .2.如图,已知直线AB 、CD 被直线AC 所截,//AB CD ,E 是直线AC 右边任意一点(点E 不在直线AB ,CD 上),设BAE α∠=,DCE β∠=.下列各式:①αβ+,②αβ-,③βα-,④360αβ︒--,AEC ∠的度数可能是( )A .①②③B .①②④C .①③④D .①②③④ 3.下列语句中正确的是( )A .直线AB 和直线BA 是两条不同的直线B .连接两点间的线段叫两点的距离C .一条射线就是一个周角D .一个角的余角比这个角的补角小 4.如图,按照上北下南,左西右东的规定画出方向十字线,∠AOE =m °,∠EOF =90°,OM 、ON 分别平分∠AOE 和∠BOF ,下面说法:①点E 位于点O 的北偏西m °;②图中互余的角有4对;③若∠BOF =4∠AOE ,则∠DON =54°;④若MON n AOE BOF ,则n 的倒数是23,其中正确有( )A .3个B .2个C .1个D .0个 5.如果∠l 与∠2互补,∠2为锐角,则下列表示∠2余角的式子是( ) A .90°-∠1 B .∠1 - 90° C .∠1 + 90° D .180°-∠1 6.一艘船停留在海面上,如果从船上看灯塔位于北偏东30°,那么从灯塔看船上位于灯塔的( )A .北偏东30°B .北偏东60°C .南偏西30°D .南偏西60° 7.如图,//AB CD ,120BAE ∠=︒,40DCE ∠=︒,则AEC ∠=( )A .70︒B .80︒C .90︒D .100︒8.如图,∠BCD =70°,AB ∥DE ,则∠α与∠β满足( )A .∠α+∠β=110°B .∠α+∠β=70°C .∠β﹣∠α=70°D .∠α+∠β=90° 9.将一直角三角板与等宽的纸条如图放置,顶点C 在纸条边FG 上,且DE//FG ,当132∠=︒时,∠2的度数是( )A .48°B .32°C .58°D .64°10.在同一平面内,a 、b 、c 是直线,下列说法正确的是( )A .若a ∥b ,b ∥c 则 a ∥cB .若a ⊥b ,b ⊥c ,则a ⊥cC .若a ∥b ,b ⊥c ,则a ∥cD .若a ∥b ,b ∥c ,则a ⊥c11.如图,直线AB ,CD 相交于点O ,EO ⊥AB ,若∠AOC =24°,则∠DOE 的度数是( )A .24°B .54°C .66°D .76°12.下面四个图形中∠1与∠2为互为对顶角的说法正确的是( )A .都互为对顶角B .图1、图2、图3中的∠1、∠2互为对顶角C .都不互为对顶角D .只有图3中的∠1、∠2互为对顶角二、填空题13.如果一个角的补角是120°,那么这个角的余角的度数是________.14.如图,点A 在直线m 上,点B 在直线l 上,点A 到直线l 的距离为a ,点B 到直线m 的距离为b ,线段AB 的长度为c ,通过测量等方法可以判断在a ,b ,c 三个数据中,最大的是_____________.15.如图,直线AB ,CD 相交于点O ,OE ⊥AB ,O 为垂足,∠EOD=26°,则∠AOC=____,∠COB=___.16.如图,直线AB 、CD 相交于点O ,OM AB ⊥于点O ,若42MOD ∠=,则COB ∠=__________度.17.如图,172∠=︒,262∠=︒,362∠=︒,则4∠的度数为__________.18.在直线AB 上任取一点O ,过点O 作射线OC 、OD ,使∠COD =90°,当∠AOC =50°时,∠BOD 的度数是____________.19.如图,已知AB//CD ,120AFC ∠=︒,13EAF EAB ∠=∠,13ECF ECD ∠=∠,则AEC ∠=____度.20.将如图1的长方形ABCD 纸片()//AD BC 沿EF 折叠得到图2,折叠后DE 与BF 相交于点P .如果70,EPF ∠=︒则PEF ∠的度数为____.三、解答题21.小明同学在完成七年级上册数学的学习后,遇到了一些问题,请你帮他解决一下.(1)如图1,已知//AB CD ,则∠AEC=∠BAE +∠DCE 成立吗?请说明理由;(2)如图2,已知//AB CD ,BE 平分∠ABC ,DE 平分∠ADC .BE 、DE 所在直线交于点E ,若∠FAD=60°,∠ABC=40°,求∠BED 的度数;(3)将图2中的点B 移到点A 的右侧,得到图3,其他条件不变,若∠FAD=α°,∠ABC=β°,请你求出∠BED 的度数(用含α,β的式子表示).22.如图,直线AB 与CD 相交于点O ,OF ,OD 分别是AOE ∠,∠BOE 的平分线. (1)写出DOE ∠的补角;(2)若64BOE ∠=︒,求AOD ∠和BOF ∠的度数;(3)射线OD 与OF 之间的夹角DOF ∠等于多少度?请说明理由.23.如图,已知PE 平分,BEF PF ∠平分,135,255DFE ∠∠=︒∠=︒.(1)试说明://AB CD ;(2)求AEP CFP EPF ∠+∠+∠的度数.24.如图,直线AB 与CD 相交于点O ,90AOF ∠=︒,90COE ∠=︒,60DOF ∠=︒,OH 平分∠BOE .求:(1)∠BOE 的度数;(2)AOH ∠的度数.25.如图,直线AB ,CD 相交于点O ,OE 平分∠BOC ,FO ⊥CD 于点O ,若∠BOD ∶∠EOB=2∶3,求∠AOF 的度数.26.如图,∠AGF=∠ABC,∠1+∠2=180°,(1)求证;BF∥DE(2)如果DE垂直于AC,∠2=150°,求∠AFG的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据同角的余角相等,等角的补角相等和邻补角的定义对各小题分析判断即可得解.【详解】解:A、图中∠α+∠β=180°﹣90°=90°,∠α与∠β互余,故本选项不符合题意;B、图中∠α=∠β,不一定互余,故本选项错误;C、图中∠α+∠β=180°﹣45°+180°﹣45°=270°,不是互余关系,故本选项错误;D、图中∠α+∠β=180°,互为补角,故本选项正确.故选:D.【点睛】本题考查了余角和补角,是基础题,熟记概念与性质是解题的关键.2.A解析:A【分析】根据点E有3种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.【详解】解:(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,∵∠AOC=∠BAE1+∠AE1C,∴∠AE1C=β-α.(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,∴∠AE2C=α+β.(3)当点E在CD的下方时,同理可得,∠AEC=α-β.综上所述,∠AEC的度数可能为β-α,α+β,α-β.即①α+β,②α-β,③β-α,都成立.故选A.【点睛】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同位角相等;两直线平行,内错角相等.3.D解析:D【分析】根据射线、直线的定义,余角与补角,周角的定义,以及线段的性质即可求解.【详解】A、直线AB和直线BA是一条直线,原来的说法是错误的,不符合题意;B、连接两点间的线段的长度叫两点的距离,原来的说法是错误的,不符合题意;C、周角的特点是两条边重合成射线.但不能说成周角是一条射线,原来的说法是错误的,不符合题意;D 、一个角的余角比这个角的补角小是正确的,符合题意;故选:D .【点睛】本题考查了射线、直线的定义,余角与补角,周角的定义,以及线段的性质,是基础题,熟记相关概念与性质是解题的关键.4.B解析:B【分析】根据方位角的定义,以及角平分线的定义,分别求出所需角的度数,然后分别进行判断,即可得到答案.【详解】解:∵∠AOE =m °,∴∠EOD=90°-m°,∴点E 位于点O 的北偏西90°-m °;故①错误;∵∠EOF =90°,∴∠EOD+∠DOF =90°,∠AOE+∠BOF=90°,∵∠AOD =∠BOD=90°,∴∠AOE+∠EOD=90°,∠DOF+∠FOB=90°,∠AOM+∠MOD=90°,∠BON+∠DON=90°,∵OM 、ON 分别平分∠AOE 和∠BOF ,∴∠AOM=∠EOM ,∠BON=∠FON ,∴∠EOM+∠MOD=90°,∠FON+∠DON=90°,∴图中互余的角共有8对,故②错误;∵∠BOF =4∠AOE ,∠AOE+∠BOF=90°,∴∠BOF=72°,∴∠BON=36°,∴∠DON=90°-36°=54°;故③正确;∵∠AOE+∠BOF=90°,∴∠MOE+∠NOF=11()904522AOE BOF , ∴9045135MON , ∴1353902MON n AOE BOF , ∴n 的倒数是23,故④正确; ∴正确的选项有③④,共2个;故选:B .【点睛】本题考查了角平分线的定义,余角的定义,方位角的表示,以及角度的和差关系,解题的关键是熟练掌握题意,正确找出图中角的关系进行判断.5.B解析:B【分析】首先根据补角的定义可得∠2=180°-∠1,再根据余角定义可得∠2余角的式子是90°-∠2,再进行等量代换即可.【详解】解:∵∠1与∠2互补,∴∠1+∠2=180°,∴∠2=180°-∠1,∴∠2余角的式子是,90°-∠2=90°-(180°-∠1)=∠1-90°,故选:B.【点睛】本题主要考查了补角和余角,关键是掌握余角和补角的定义.6.C解析:C【分析】根据方向角的表示方法,可得答案.【详解】解:设此船位于海面上的C处,灯塔位于D处,射线CA、DB的方向分别为正北方向与正南方向,如图所示.∵从船上看灯塔位于北偏东30°,∴∠ACD=30°.又∵AC∥BD,∴∠CDB=∠ACD=30°.即从灯塔看船位于灯塔的南偏西30°.故选:C.【点睛】本题考查了方向角,理解题意画出图形是解题的关键.7.D解析:D【分析】过点E 作//EF AB ,先根据平行线的判定可得//EF CD ,再根据平行线的性质分别可得AEF ∠和CEF ∠的度数,然后根据角的和差即可得.【详解】如图,过点E 作//EF AB ,120BAE ∠=︒,18060AEF BAE ∴∠=︒-∠=︒,又//AB CD ,//EF CD ∴,40DCE CEF ∴=∠=∠︒,6040100AEC AEF CEF ∴∠=∠+∠=︒+︒=︒,故选:D .【点睛】本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解题关键. 8.B解析:B【分析】过点C 作CF ∥AB ,根据平行线的性质得到∠BCF =∠α,∠DCF =∠β,由此即可解答.【详解】如图,过点C 作CF ∥AB ,∵AB ∥DE ,∴AB ∥CF ∥DE ,∴∠BCF =∠α,∠DCF =∠β,∵∠BCD =70°,∴∠BCD =∠BCF +∠DCF =∠α+∠β=70°,∴∠α+∠β=70°.故选B .【点睛】本题考查了平行线的性质,正确作出辅助线,熟练掌握平行线的性质进行推理证明是解决9.C解析:C【分析】先根据平行线的性质,求得∠3的度数,再根据平角的定义,求得∠2的度数.【详解】解:如图,∵DE∥FG,∠1=32°,∴∠3=32°,∴∠2=180°-90°-32°=58°.故选:C.【点睛】本题主要考查的是平行线的性质,解决问题的关键是掌握:两直线平行,同位角相等.10.A解析:A【分析】根据线段垂直平分线上的定义,平行公理以及平行线的性质对各选项分析判断后利用排除法求解.【详解】解:A.在同一平面内,若a∥b,b∥c,则a∥c正确,故本选项正确;B.在同一平面内,若a⊥b,b⊥c,则a∥c,故本选项错误;C.在同一平面内,若a∥b,b⊥c,则a⊥c,故本选项错误;D.在同一平面内,若a∥b,b∥c,则a∥c,故本选项错误.故选:A.11.C解析:C【分析】根据对顶角相等求∠BOD,由垂直的性质求∠BOE,根据∠DOE=∠BOE−∠BOD求解.【详解】∵直线AB,CD相交于点O,∠AOC=24°,∴∠BOD=∠AOC=24°,∵EO⊥AB,∴∠BOE=90°,∴∠DOE=∠BOE−∠BOD=90°−24°=66°.【点睛】本题考查了对顶角,垂直的定义.解题的关键是采用形数结合的方法得到∠DOE=∠BOE−∠BOD.12.D解析:D【分析】根据对顶角的定义来判断,两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做对顶角.【详解】解:根据对顶角的定义可知:C中∠1、∠2属于对顶角,故选:D.【点睛】本题考查对顶角的定义,是需要熟记的内容.二、填空题13.30°【分析】根据余角和补角的定义即可解答【详解】解:∵一个角的补角是120°∴这个角为:180°−120°=60°∴这个角的余角为:90°−60°=30°故答案为:30°【点睛】本题考查了余角和补解析:30°【分析】根据余角和补角的定义,即可解答.【详解】解:∵一个角的补角是120°,∴这个角为:180°−120°=60°,∴这个角的余角为:90°−60°=30°,故答案为:30°.【点睛】本题考查了余角和补角的定义,解决本题的关键是熟记余角和补角的定义.14.【分析】过点A作AD垂直于垂足为D过点B作BH垂直于垂足为H连接AB根据点到直线垂线段最短可知AB>ADAB>BH可得最大【详解】过点A作AD垂直于垂足为D过点B作BH垂直于垂足为H连接AB由题意得解析:c【分析】过点A作AD垂直于l垂足为D,过点B作BH垂直于m垂足为H,连接AB,根据点到直线垂线段最短,可知AB>AD,AB>BH,可得c最大.【详解】过点A作AD垂直于l垂足为D,过点B作BH垂直于m垂足为H,连接AB,由题意得:AD=a, BH=b,AB=c;根据点到直线垂线段最短,可知AB>AD,AB>BH∴c>a,c>b;∴c最大故答案:c【点睛】本题主要考查了垂线段最短的性质,熟记性质是解题的关键.15.64°116°【分析】根据垂线的定义进行作答【详解】由OE⊥AB得到∠AOE=90°所以∠AOC=180°-∠EOD-∠AOE=64°;因为∠BOD=64°∠COB=180°-∠BOD=116°【点解析:64° 116°.【分析】根据垂线的定义进行作答.【详解】由OE⊥AB,得到∠AOE=90°,所以∠AOC=180°-∠EOD-∠AOE=64°;因为∠BOD=64°,∠COB=180°-∠BOD= 116°.【点睛】本题考查了垂线的定义,熟练掌握垂线的定义是本题解题关键.16.132【分析】先根据垂直定义得到∠AOM=90°求出∠AOD的度数然后根据对顶角的性质求解即可【详解】∵∴∠AOM=90°∵∴∠AOD=90+42=132°∴∠AOD=132°故答案为:132【点睛解析:132【分析】先根据垂直定义得到∠AOM=90°,求出∠AOD的度数,然后根据对顶角的性质求解即可.【详解】,∵OM AB∴∠AOM=90°,∵42MOD ∠=,∴∠AOD=90+42=132°,∴COB ∠=∠AOD=132°.故答案为:132.【点睛】本题考查了垂直的定义,对顶角的性质,熟练掌握对顶角相等是解答本题的关键. 17.108【分析】先根据题意得出a ∥b 再由平行线的性质即可得出结论【详解】解:如图∵∴∠2=∠3∴a ∥b ∵∠1=72°∴∠5=180°-72°=108°∴∠4=∠5=108°故答案为:108【点睛】本题解析:108【分析】先根据题意得出a ∥b ,再由平行线的性质即可得出结论.【详解】解:如图,∵262∠=︒,362∠=︒,∴∠2=∠3,∴a ∥b .∵∠1=72°,∴∠5=180°-72°=108°,∴∠4=∠5=108°.故答案为:108.【点睛】本题考查的是平行线的判定与性质,先根据题意得出直线a ∥b 是解答此题的关键. 18.40°或140°【分析】先根据题意可得OC 分在AB 同侧和异侧两种情況讨论并画出图然后根据OC ⊥OD 与∠AOC =50°计算∠BOD 的度数【详解】解:当OCOD 在直线AB 同侧时如图∵∠COD =90°∠A解析:40°或140°【分析】先根据题意可得OC 分在AB 同侧和异侧两种情況讨论,并画出图,然后根据OC ⊥OD 与∠AOC =50°,计算∠BOD 的度数.【详解】解:当OC 、OD 在直线AB 同侧时,如图∵∠COD=90°,∠AOC=50°∴∠BOD=180°-∠COD-∠AOC=180°-90°-50°=40°当OC、OD在直线AB异侧时,如图∵∠COD=90°,∠AOC=50°∴∠BOD=180-∠AOD=180°-(∠DOC-∠AOC)=180°-(90°-50°)=140°.故答案为:40°或140°【点睛】解答此类问题时,要注意对不同的情况进行讨论,避免出现漏解.19.90【详解】解:如图过点E作EH∥AB过点F作FG∥AB∵AB∥CD∴AB∥FG∥CDAB∥EH∥CD∴又∵∴∴∴即:∴故答案为:90【点睛】本题考查了平行线的性质平行公理作辅助线构造内错角是解题的解析:90【详解】解:如图,过点E作EH∥AB,过点F作FG∥AB,∵AB∥CD,∴AB∥FG∥CD,AB∥EH∥CD,∴AFG FAB,GFC FCD,AFG FAB,GFC FCD,又∵13EAF EAB∠=∠,13ECF ECD∠=∠,∴3EAB EAF,3ECD ECF,∴4FAB EAF,4ECD ECF,∴44120AFC AFG GFC FAB ECD EAF ECF,即:30EAF ECF,∴33390AEC EAB ECD EAF ECF EAF ECF.故答案为:90.【点睛】本题考查了平行线的性质,平行公理,作辅助线构造内错角是解题的关键.20.55°【分析】根据翻折可知对应角都相等另外两直线平行同旁内角互补利用这两条性质即可解答【详解】解:∵AE∥BF∴∠AEP=∠FPE=70°又∵折叠后DE 与BF相交于点P设∠PEF=x即∠AEP+2∠解析:55°【分析】根据翻折可知对应角都相等.另外两直线平行,同旁内角互补.利用这两条性质即可解答.【详解】解:∵AE∥BF,∴∠AEP=∠FPE=70°.又∵折叠后DE与BF相交于点P,设∠PEF=x,即∠AEP+2∠PEF=180°,即70°+2x=180°,x=55°.即∠PEF=55°,故答案为:55°.【点睛】解答此题的关键是要明白图形翻折变换后与原图形全等,对应的角和边均相等.三、解答题21.(1)成立,理由见解析;(2)50︒;(3)1118022βα-+.【分析】(1)根据平行线的性质即可得到结论;(2)先过点E作EH∥AB,根据平行线的性质和角平分线的定义,即可得到结论;(3)过E作EG∥AB,根据平行线的性质和角平分线的定义,即可得到结论.【详解】解:(1)如图1中,作EF//AB,则有EF//CD,∴∠1=∠BAE ,∠2=∠DCE ,∴∠AEC=∠1+∠2=∠BAE+∠DCE .(2)如图2,过点E 作EH ∥AB ,∵AB//CD ,∠FAD=60°,∴∠FAD=∠ADC=60°,∵DE 平分∠ADC ,∠ADC=60°,∴∠EDC=12∠ADC=30°, ∵BE 平分∠ABC ,∠ABC=40°, ∴∠ABE=12∠ABC=20°, 由(1)的结论,得203050BED ABE EDC ∠=∠+∠=︒+=︒︒. (3)如图3,过点E 作//EG AB .∵BE 平分ABC ∠,DE 平分ADC ∠, ABC β∠=︒,FAD ADC α∠=∠=︒ ∴1122ABE ABC β∠=∠=︒,1122CDE ADC α∠=∠=︒ ∵//AB CD ,////AB CD EG ∴11801802BEG ABE β∠=-∠=-,12CDE DEG α∠=∠=1118022BED BEG DEG βα∠=∠+∠=-+ 【点睛】本题主要考查了平移的性质,平行线的性质以及角平分线的定义的运用,解决问题的关键是正确的作出辅助线.22.(1)∠COE,∠AOD,∠BOC;(2)∠AOD=148°,∠BOF=122°;(3)90°,见解析【分析】(1)根据互补的定义结合角平分线的定义确定∠DOE的补角;(2)先根据角平分线的定义得出∠BOD的度数,再由邻补角定义可得∠AOD=180°-∠BOD;先根据邻补角定义可得∠AOE=180°-∠BOE,再由角平分线的定义得出∠AOF的度数,从而求解;(3)运用平角的定义和角平分线的定义,证明∠DOF是90°,得直线OD、OF的位置关系.【详解】解:(1)由直线AB与CD相交于点O∴∠DOE+∠COE=180°;∠BOD+∠AOD=180°又∵OD平分 BOE∴∠DOE=∠BOD∴∠DOE+∠AOD=180°又∵∠AOD=∠BOC∴∠DOE+∠BOC=180°∴∠DOE的补角为∠COE,∠AOD,∠BOC;(2)因为OD是∠BOE的平分线,∠BOD=12∠BOE=32°,所以∠AOD=180°-∠BOD=148°,因为∠AOE=180°-∠BOE=116°,OF是∠AOE的平分线,所以∠AOF=12∠AOE=58°,所以∠BOF=180°-∠AOF=122°即∠AOD=148°,∠BOF=122°;(3)因为OF,OD分别是∠AOE,∠BOE的平分线,所以∠DOF=∠DOE+∠EOF=12∠BOE+12∠EOA=12(∠BOE+∠EOA)=12×180°=90°.【点睛】本题考查了角平分线、补角、垂线的定义以及角的计算,属于基础题型,比较简单.23.(1)见解析;(2)360°【分析】(1)由PE 与PF 分别为角平分线,得到两对角相等,根据∠1与∠2的度数求出∠BEF 与∠EFD 的度数之和为180°,利用同旁内角互补两直线平行即可得证;(2)过点P 作//PG AB ,得//PG CD ,再根据平行线的性质可得结论.【详解】解:(1)证明:∵PE 平分∠BEF ,PF 平分∠DFE ,∠1=35°,∠2=55°,∴∠1=∠BEP=12∠BEF ,∠2=∠PFD=12∠EFD , ∴∠BEF=70°,∠EFD=110°,即∠BEF+∠EFD=180°,∴AB ∥CD ;(2)过点P 作//PG AB// ,AB CD//,PG CD ∴180,AEP GPE ∴∠+∠=︒180,CFP GPF ∴∠+∠=︒360AEP CFP EPF ∴∠+∠+∠=︒【点睛】此题考查了平行线的性质性质和判定,熟练掌握平行线的判定方法是解本题的关键. 24.(1)60︒;(2)150︒.【分析】(1)根据∠FOB=90︒及∠DOF=60︒,可求出∠DOB ,根据∠BOE=∠DOE-∠DOB ,可求出∠BOE ;(2)根据OH 平分∠BOE 及∠BOE=60︒,可知∠BOH=∠EOH ,则∠AOH=180︒-∠BOH .【详解】解:(1)∵∠AOF=90︒,∠COE=90︒,∴∠DOE=90︒,∠FOB=90︒,∵∠DOF=60︒,∴∠DOB=∠FOB-∠FOD=906030︒-︒=︒,∴∠BOE=∠DOE-∠DOB=903060︒-︒=︒;(2)∵OH 平分∠BOE ,∠BOE=60︒,∴∠BOH=∠EOH=30︒,∴∠AOH=180********BOH ︒-∠=︒-︒=︒.【点睛】本题考查余角、补角及角平分线,找到互为余角和补角的角是解题的关键.25.45︒.【分析】设2BOD x ∠=,从而可得3EOB x ∠=,先根据角平分线的定义3EOC EOB x ∠=∠=,再根据平角的定义可得求出x 的值,然后根据垂直的定义可得90DOF ∠=︒,最后根据平角的定义即可得.【详解】设2BOD x ∠=,则3EOB x ∠=,∵OE 平分BOC ∠,∴3EOC EOB x ∠=∠=,180BOD EOB EOC ∠+∠+∠=︒,233180x x x ∴++=︒,解得22.5x =︒,45BOD ∴∠=︒,FO CD ⊥,90DOF ∴∠=︒,又180BOD DOF AOF ∠+∠+∠=︒,4590180AOF ∴︒+︒+∠=︒,解得45AOF ∠=︒.【点睛】本题考查了角平分线的定义、平角的定义、垂直的定义等知识点,熟练掌握并理解各定义是解题关键.26.(1)证明见解析;(2)∠AFG=60°.【分析】(1)根据平行线的判定定理,由∠AGF =∠ABC ,可判断GF ∥BC ,由平行线的性质可得∠1=∠3,由∠1+∠2=180°得出∠3+∠2=180°,即可判断出BF ∥DE ;(2)由BF ∥DE ,BF ⊥AC 得到DE ⊥AC ,由∠2=150°得出∠1=30°,从而得出结论.【详解】(1)BF ∥DE ,理由如下:∵∠AGF =∠ABC ,∴GF ∥BC ,∴∠1=∠3,∵∠1+∠2=180°,∴∠3+∠2=180°,∴BF ∥DE ;(2)∵BF ∥DE ,BF ⊥AC ,∴DE ⊥AC ,∵∠1+∠2=180°,∠2=150°,∴∠1=30°,∴∠AFG =90°﹣30°=60°.【点睛】本题考查了平行线的判定与性质.解题的关键是熟练掌握平行线的判定与性质.。
(必考题)初中数学七年级数学下册第二单元《相交线与平行线》检测卷(包含答案解析)

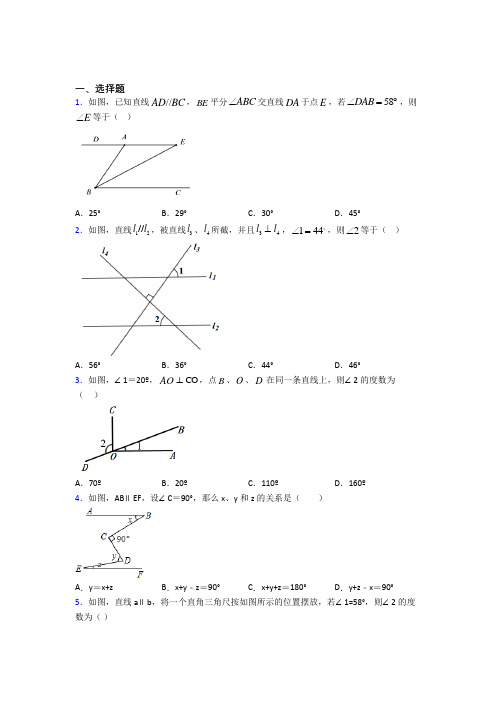
一、选择题1.下列说法不正确...的是( ) A .对顶角相等B .两点确定一条直线C .一个角的补角一定大于这个角D .垂线段最短 2.已知一个角是这个角的余角的13,则这个角的度数是( ). A .45︒ B .60︒ C .67.5︒ D .22.5︒ 3.下列说法正确的是( )A .锐角的补角一定是钝角B .一个角的补角一定大于这个角C .锐角和钝角一定互补D .两个锐角一定互为余角4.一个角的余角是它的补角的25,这个角是( ) A .30B .60︒C .120︒D .150︒ 5.如果∠l 与∠2互补,∠2为锐角,则下列表示∠2余角的式子是( ) A .90°-∠1B .∠1 - 90°C .∠1 + 90°D .180°-∠1 6.已知A ∠与B 互补,B 与C ∠互余,若120A ∠=︒,则C ∠的度数是( )A .70︒B .60︒C .30D .20︒ 7.一个角的余角是它的补角的25,则这个角等于 ( ) A .60°B .45°C .30°D .75° 8.用一副三角板不能画出的角是( ).A .75°B .105°C .110°D .135° 9.我们利用尺规作图可以作一个角()''A O B ∠等于已知角()AOB ∠,如下所示:(1)作射线OA ;(2)以O 为圆心,任意长为半径作弧,交OA 于C ,交OB 于D ;(3)以O '为圆心,OC 为半径作弧,交OA '于'C ;(4)以C '为圆心,OC 为半径作弧,交前面的弧于D ;(5)连接'O D '作射线,O B ''则A O B '''∠就是所求作的角.以上作法中,错误的一步是( )A .()2B .()3C .()4D .()510.已知点P 为直线m 外一点,点A ,B ,C 为直线m 上三点,PA =4 cm ,PB =5 cm ,PC =2 cm ,则点P 到直线m 的距离为( )A .4 cmB .5 cmC .小于2 cmD .不大于2 cm 11.如图,计划把河水引到水池A 中,可以先引AB CD ⊥,垂足为B ,然后沿AB 开渠,则能使所开的渠最短,这样设计的依据是( )A .垂线段最短B .两点之间,线段最短C .两点确定一条直线D .以上说法都不对12.下列图形中,1∠与2∠是对顶角的是( )A .B .C .D .二、填空题13.一个角的补角比它的余角的3倍少20︒,这个角的度数是_______度.14.已知n (3n ≥,且n 为整数)条直线中只有两条直线平行,且任何三条直线都不交于..........同一个点.....如图,当3n =时,共有2个交点;当4n =时,共有5个交点;当5n =时,共有9个交点;…依此规律,当图中有n 条直线时,共有交点________个.15.已知70AOB ∠=︒,COB ∠与AOB ∠互余,则AOC ∠的度数为______.16.如图,将矩形ABCD 沿对角线BD 折叠,点C 落在点E 处,BE 交AD 于点F ,已知∠BDC=62°,则∠DFE 的度数为_______.17.如图,一环湖公路的AB 段为东西方向,经过四次拐弯后,又变成了东西方向的FE 段,则B C D E ∠+∠+∠+∠的度数是______.18.将一副直角三角板如图放置,点E 在AC 边上,且ED//BC ,∠C=30°,∠F=∠DEF=45°,则∠AEF=_____度.19.如图,//AB CD ,点E 在CB 的延长线上,若60ABE ∠=︒,则ECD ∠的度数为__________.20.如图,直线a ∥b ,点A ,B 位于直线a 上,点C ,D 位于直线b 上,且AB :CD =1:2,如果△ABC 的面积为10,那么△BCD 的面积为_____.三、解答题21.如图,AD BE ⊥,BC BE ⊥,A C ∠=∠,点C ,D ,E 在同一条直线上.(1)请说明AB 与CD 平行.(2)若3ABC E ∠=∠,求E ∠的度数.22.如图,在三角形ABC 中,D 、E 、G 分别是AC 、AB 、BC 上的点,CF 是ACB ∠的平分线,已知3ACB ∠=∠,45180︒∠+∠=.(1)图中1∠与3∠是一对______,2∠与5∠是一对______,3∠与4∠是一对______.(填“同位角”或“内错角”或“同旁内角”)(2)判断CF 与DE 是什么位置关系?并说明理由.(3)若CF AB ⊥,垂足为F ,56︒∠=A ,则ACB ∠的度数为______,ADE ∠的度数为______.23.如图,将长方形纸片的一角折叠,使顶点A 落在A '处,EF 为折痕,点F 在线段AD 上,且点F 不与点D 重合,点E 在线段AB 上,此时∠AFE 和∠AEF 互为余角,若EA '恰好平分∠FEB ,回答下列问题.(1)求∠AEF 的度数;(2)∠A FD '= 度.24.在一张地图上有、、A B C 三地,但地图被墨迹污染,C 地具体位置看不清楚,但知道C 地在A 地的北偏东30°方向,在B 地南偏东45°方向.(1)根据以上条件,在地图上画出C 地的位置;(2)直接写出ACB ∠的度数.25.如图,O 是直线AB 上的一点,90BOD COE ∠=∠=︒.(1)图中与1∠互余的角有______;(2)写出图中相等的角______;(直角除外)(3)3∠的补角是______.26.补全解答过程:如图,EF∥AD,∠1=∠2,若∠BAC=70°,求∠AGD.解:∵EF∥AD,(已知)∴∠2=,(两直线平行,同位角相等).又∵∠1=∠2,(已知)∴∠1=∠3,(等量代换)∴AB∥,()∴∠AGD+∠BAC=180°.()∵∠BAC=70°,(已知)∴∠AGD=.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据对顶角的性质,直线的性质,补角的定义,垂线段的性质依次判断即可得到答案.【详解】解:A、对顶角相等,故该项不符合题意;B、两点确定一条直线,故该项不符合题意;C、一个角的补角一定不大于这个角,故该项符合题意;D、垂线段最短,故该项不符合题意;故选:C.【点睛】此题考查对顶角的性质,直线的性质,补角的定义,垂线段的性质,正确理解各性质及定义是解题的关键.2.D解析:D【分析】设这个角的度数为x ,则它的余角为90°-x ,再根据题意列出方程,求出x 的值即可;【详解】解:设这个角的度数为x ,则它的余角为90°-x , 依题意得:()1903x x =︒- , 解得:x=22.5,故选:D .【点睛】 本题考查的是余角的定义,能根据题意列出关于x 的方程是解题的关键.3.A解析:A【分析】根据余角和补角的概念判断.【详解】解:A 、锐角的补角一定是钝角,本选项说法正确;B 、一个角的补角一定大于这个角,本选项说法错误,例如:120°的补角是60°,而60°<120°;C 、锐角和钝角一定互补,本选项说法错误,例如20°+120°=140°,20°与120°不互补;D 、两个锐角一定互为余角,本选项说法错误,30°与30°不是互为余角;故选:A .【点睛】此题考查余角和补角的概念,熟记概念是解题的关键.4.A解析:A【分析】设这个角的度数是x°,根据题意得出方程2901805x x -=-(),求出方程的解即可.【详解】 解:设这个角的度数是x°,则2901805x x -=-(),解得:x=30,即这个角的度数是30°,故选A .【点睛】本题考查了余角和补角,注意:∠A 的余角是90°-∠A ,∠A 的补角是180°-∠A . 5.B解析:B【分析】首先根据补角的定义可得∠2=180°-∠1,再根据余角定义可得∠2余角的式子是90°-∠2,再进行等量代换即可.【详解】解:∵∠1与∠2互补,∴∠1+∠2=180°,∴∠2=180°-∠1,∴∠2余角的式子是,90°-∠2=90°-(180°-∠1)=∠1-90°,故选:B .【点睛】本题主要考查了补角和余角,关键是掌握余角和补角的定义.6.C解析:C【分析】先根据互补角的定义可得60B ∠=︒,再根据互余角的定义即可得.【详解】 A ∠与B 互补,且120A ∠=︒,18060B A ∴∠=︒-∠=︒,又B ∠与C ∠互余,9030C B ∴∠=︒-∠=︒,故选:C .【点睛】本题考查了互补角、互余角,熟练掌握互补角与互余角的定义是解题关键.7.C解析:C【分析】设这个角的度数是x°,根据余角是这个角的补角的25,即可列出方程,求得x 的值. 【详解】解:设这个角的度数是x°,根据题意得:90-x=25(180-x ), 解得:x=30,所以,这个角等于30°故选:C .【点睛】本题考查了余角和补角的定义,正确列出方程,解方程是关键.8.C解析:C【分析】105°=60°+45°,105°角可以用一幅三角板中的60°角和45°角画;75°=45°+30°,75°角可以用一幅三角板中的45°角和30°角画;135°=90°+45°,135°角可以用一幅三角板中的直角和90°角或45°角画;110°角用一副三角板不能画出.【详解】解:105°角可以用一幅三角板中的60°角和45°角画;75°角可以用一幅三角板中的45°角和30°角画;110°角用一副三角板不能画出;135°角可以用一幅三角板中的直角和90°角或45°角画。
北师大版七年级数学下册第二章《相交线与平行线》单元测试卷附答案

第二章《相交线与平行线》单元测试卷(新题型卷共23小题,满分120分,考试用时90分钟)一、选择题(本大题共10小题,每小题3分,共30分)1.已知∠A=25°,则∠A的补角等于()A.65°B.75°C.155°D.165°2.如图,直线a与直线c相交于点O,则∠1的度数是()A.60°B.50°C.40°D.30°第2题图第3题图第4题图3.如图,∠1=15°,AO⊥CO,直线BD经过点O,则∠2的度数为()A.75°B.105°C.100°D.165°4.如图,直线c与直线a,b都相交.若a∥b,∠1=55°,则∠2=()A.60°B.55°C.50°D.45°5.如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2=()A.55°B.65°C.75°D.85°第5题图第6题图第7题图第8题图6.如图,下列说法中正确的是()A.若∠2=∠4,则AB∥CDB.若∠BAD +∠ADC=180°,则AB∥CDC.若∠1=∠3,则AD∥BCD.若∠BAD +∠ABC=180°,则AB∥CD7.(传统文化)一条古称在称物时的状态如图所示,已知∠1=80°,则∠2=()A.20°B.80°C.100°D.120°8.如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2=()A.90°B.65°C.60°D.50°9.如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4等于()。
(必考题)初中数学七年级数学下册第二单元《相交线与平行线》测试题(有答案解析)(3)
一、选择题1.如图,已知直线//AD BC ,BE 平分ABC ∠交直线DA 于点E ,若58DAB ∠=︒,则E ∠等于( )A .25°B .29°C .30°D .45°2.如图,直线12l l //,被直线3l 、4l 所截,并且34l l ⊥,144∠=,则2∠等于( )A .56°B .36°C .44°D .46° 3.如图,∠1=20º,AO ⊥CO ,点B 、O 、D 在同一条直线上,则∠2的度数为( )A .70ºB .20ºC .110ºD .160º4.如图,AB ∥EF ,设∠C =90°,那么x 、y 和z 的关系是( )A .y =x+zB .x+y ﹣z =90°C .x+y+z =180°D .y+z ﹣x =90° 5.如图,直线a ∥b ,将一个直角三角尺按如图所示的位置摆放,若∠1=58°,则∠2的度数为( )A .30°B .32°C .42°D .58°6.如图,AB ∥CD , ∠BED=110°,BF 平分∠ABE,DF 平分∠CDE,则∠BFD= ( )A .110°B .115°C .125°D .130°7.如图,∠BCD =70°,AB ∥DE ,则∠α与∠β满足( )A .∠α+∠β=110°B .∠α+∠β=70°C .∠β﹣∠α=70°D .∠α+∠β=90° 8.如图,直线a b ∥,三角板的直角顶点放在直线b 上,两直角边与直线a 相交,如果160∠=︒,那么2∠等于( )A .30B .︒40C .50︒D .60︒9.如图,直线a ,b 被直线c 所截,//a b ,若140∠=︒,则( )A .250∠=︒B .350∠=︒C .4160∠=︒D .540∠=︒ 10.如图,已知∠1=∠2,∠3=30°,则∠B 的度数是( )A .20B .30C .40D .6011.如图,平面内直线////a b c ,点,,A B C 分别在直线,,a b c 上,BD 平分ABC ∠,并且满足a β∠>∠,则,,a βγ∠∠∠关系正确的是( )A . 2a βγ∠=∠+∠B .22a βγ∠=∠-∠C .a βγ∠=∠+∠D . 2a βγ∠=∠-∠12.如图,直线a b 、被直线c 所截,若//a b ,则下列不正确的是( )A .12∠=∠B .24∠∠=C .14∠=∠D .15∠=∠二、填空题13.一个角的补角比它的余角的3倍少20︒,这个角的度数是_______度.14.已知70AOB ∠=︒,COB ∠与AOB ∠互余,则AOC ∠的度数为______. 15.小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板ABC ,并将边AC 延长至点P ,第二步将另一块三角板CDE 的直角顶点与三角板ABC 的直角顶点C 重合,摆放成如图所示,延长DC 至点F ,PCD ∠与ACF ∠就是一组对顶角,若30ACF ∠=,则PCD ∠=__________,若重叠所成的(090)BCE n n ∠=<<,则PCF ∠的度数__________.16.如图是“步步高”超市里购物车的侧面示意图,扶手AB 与车底CD 平行,1100∠=︒,24829'∠=︒,则3∠的度数是________.17.已知直线//a b ,将一个含有45度角的直角三角板(90︒∠=C )按如图位置摆放,若160∠=︒,则2∠的度数是_____________.18.如图,一环湖公路的AB 段为东西方向,经过四次拐弯后,又变成了东西方向的FE 段,则B C D E ∠+∠+∠+∠的度数是______.19.将一副三角板(30A ∠=︒)按如图所示方式摆放,使得AB EF ,则1∠等于______度.20.如图,点O 为线段AB 上一点,若点,D E 不在线段AB 上,,40OD OE AOD ⊥∠=︒,则∠BOE 度数为____________________.三、解答题21.如图,180,AEM CDN EC ︒∠+∠=平分AEF ∠.若62EFC ︒∠=,求C ∠的度数.根据提示将解题过程补充完整.解:180CDM CDN ︒∠+∠=(平角的意义),180AEM CDN ︒∠+∠=(已知), AEM CDM ∴∠=∠//AB CD ∴(___________________)AEF ∴∠+(________)180︒=(两直线平行,同旁内角互补)62EFC ︒∠=,118AEF ︒∴∠= EC 平分AEF ∠,59AEC ︒∴∠=(_________)//AB CD ,59C AEC ︒∴∠=∠=(___________________)22.如图,直角三角板ABC 的直角顶点C 在直线DE 上,CF 平分.BCD ∠()1如图①,若30BCE ∠=,求ACF ∠的度数;()2将图①中的三角板ABC 绕顶点C 转动到图②的位置,若140BCE ∠=,试求出,ACF ACE ∠∠的度数.23.在如图所示的方格中,每个小正方形的边长为1,点A B C D 、、、在方格纸中小正方形的顶点上.(1)画线段AB ;(2)画图并说理:①画出点C 到线段AB 的最短线路CE ,理由是 ;②画出一点P ,使AP DP CP EP +++最短,理由是 .24.直线AB 、CD 相交于点O ,OE 平分AOD ∠,90FOC ,50BOF ∠=︒,求AOC ∠与AOE ∠的度数.25.如图,已知∠1=∠2,∠A =29°,求∠C 的度数.26.如图,点P 是AOB ∠内部一点,//PM OA 交OB 于点C .请你画出射线PN ,并且PN //OB ,PN 或PN 的反向延长线交OA 于点D .(1)补全图形;(2)判断AOB ∠与MPN ∠的数量关系,并证明.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】根据平行线的性质可知∠ABC=58°,再根据角平分线的性质可求∠EBC=29°,再利用平行线的性质可求∠E .【详解】解:∵//AD BC ,∴58ABC DAB ∠=∠=︒,∵BE 平分ABC ∠, ∴1292EBC ABC ∠=∠=︒, ∵//AD BC ,∴29E EBC ∠=∠=︒,故选B .【点睛】本题考查了平行线的性质和角平分线的性质,灵活运用这两个性质是解题关键. 2.D解析:D【分析】依据l 1∥l 2,即可得到∠1=∠3=44°,再根据l 3⊥l 4,可得∠2=90°-44°=46°.【详解】解:如图,∵l1∥l2,∴∠1=∠3=44°,又∵l3⊥l4,∴∠2=90°-44°=46°,故选:D.【点睛】本题主要考查了平行线的性质,解题时注意:两直线平行,同位角相等.3.C解析:C【分析】由AO⊥CO和∠1=20º求得∠BOC=70º,再由邻补角的定义求得∠2的度数.【详解】∵AO⊥CO和∠1=20º,∴∠BOC=90 º-20 º=70º,又∵∠2+∠BOC=180 º(邻补角互补),∴∠2=110º.故选:C.【点睛】考查了邻补角和垂直的定义,解题关键是利用角的度数之间的和差的关系求未知的角的度数.4.B解析:B【分析】过C作CM∥AB,延长CD交EF于N,根据三角形外角性质求出∠CNE=y﹣z,根据平行线性质得出∠1=x,∠2=∠CNE,代入求出即可.【详解】解:过C作CM∥AB,延长CD交EF于N,则∠CDE=∠E+∠CNE,即∠CNE=y﹣z∵CM∥AB,AB∥EF,∴CM∥AB∥EF,∴∠ABC=x=∠1,∠2=∠CNE,∵∠BCD=90°,∴∠1+∠2=90°,∴x+y﹣z=90°.故选:B.【点睛】本题考查了平行线的性质和三角形外角性质的应用,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.5.B解析:B【解析】试题分析:如图,过点A作AB∥b,∴∠3=∠1=58°,∵∠3+∠4=90°,∴∠4=90°﹣∠3=32°,∵a∥b,AB∥B,∴AB∥b,∴∠2=∠4=32°,故选B.考点:平行线的性质.6.C解析:C【分析】先过点E作EM∥AB,过点F作FN∥AB,由AB∥CD,即可得EM∥AB∥CD∥FN,然后根据两直线平行,同旁内角互补,由∠BED=110°,即可求得∠ABE+∠CDE=250°,又由BF平分∠ABE,DF平分∠CDE,根据角平分线的性质,即可求得∠ABF+∠CDF的度数,又由两直线平行,内错角相等,即可求得∠BFD的度数.【详解】解:如图,过点E作EM∥AB,过点F作FN∥AB,∵AB∥CD,∴EM∥AB∥CD∥FN,∴∠ABE+∠BEM=180°,∠CDE+∠DEM=180°,∴∠ABE+∠BED+∠CDE=360°,∵∠BED=110°,∴∠ABE+∠CDE=250°∵BF平分∠ABE,DF平分∠CDE,∴∠ABF=12∠ABE,∠CDF=12∠CDE,∴∠ABF+∠CDF=12(∠ABE+∠CDE)=125°,∵∠DFN=∠CDF,∠BFN=∠ABF,∴∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=125°.故选:C.【点睛】此题考查了平行线的性质与角平分线的定义,解题的关键是注意数形结合思想的应用,注意辅助线的作法.7.B解析:B【分析】过点C作CF∥AB,根据平行线的性质得到∠BCF=∠α,∠DCF=∠β,由此即可解答.【详解】如图,过点C作CF∥AB,∵AB∥DE,∴AB∥CF∥DE,∴∠BCF=∠α,∠DCF=∠β,∵∠BCD=70°,∴∠BCD =∠BCF+∠DCF=∠α+∠β=70°,∴∠α+∠β=70°.故选B.【点睛】本题考查了平行线的性质,正确作出辅助线,熟练掌握平行线的性质进行推理证明是解决本题的关键.8.A解析:A【分析】先由直线a∥b,根据平行线的性质,得出∠3=∠1=60°,再由已知直角三角板得∠4=90°,然后由∠2+∠3+∠4=180°求出∠2.【详解】已知直线a∥b,∴∠3=∠1=60°(两直线平行,同位角相等),∠4=90°(已知),∠2+∠3+∠4=180°(已知直线),∴∠2=180°-60°-90°=30°.故选:A.【点睛】此题考查平行线性质的应用,解题关键是由平行线性质:两直线平行,同位角相等,求出∠3.9.D解析:D【分析】根据平行线的性质、对顶角相等、邻补角的定义解答即可.【详解】∵a∥b,∴∠2=∠1=40°,∵∠3与∠1是对顶角,∠5与∠2是对顶角,∴∠3=∠5=40°,∵∠4+∠1=180°,∴∠4=180°-∠1=140°,故选:D.【点睛】此题考查相交线与平行线,掌握平行线的性质、对顶角相等、邻补角的定义是解题的关键. 10.B解析:B【分析】根据内错角相等,两直线平行,得AB∥CE,再根据性质得∠B=∠3.【详解】因为∠1=∠2,所以AB∥CE所以∠B=∠3=30故选B【点睛】熟练运用平行线的判定和性质.11.A解析:A【分析】由平行线的性质可得∠ABC=a β∠+∠,然后根据1=2ABC βγ∠+∠∠求解即可. 【详解】解:∵////a b c ,∴∠ABE=∠α,∠CBE=∠β,∴∠ABC=a β∠+∠,∵BD 平分ABC ∠,∴∠CBD 1=2ABC ∠, ∴()1=2βγαβ∠+∠∠+∠, ∴2a βγ∠=∠+∠.故选A .【点睛】本题考查了角平分线的定义,以及平行线的性质,熟练掌握平行线的性质是解答本题的关键.平行线的性质:①两直线平行同位角相等,②两直线平行内错角相等,③两直线平行同旁内角互补.12.D解析:D【分析】根据平行线的性质得出∠2=∠4,∠1=∠4,根据对顶角相等和邻补角互补得出∠1=∠2,∠1+∠5=180°,即可得出选项.【详解】解:∵a ∥b ,∴∠2=∠4,∠1=∠4,∵∠4+∠5=180°,∴∠1+∠5=180°,∵∠1=∠2(对顶角相等),所以选项A 、B 、C 答案正确,只有选项D 答案错误;故选:D .【点睛】本题考查了平行线的性质,对顶角相等,邻补角互补等知识点,能灵活运用知识点进行推理是解此题的关键.二、填空题13.35【分析】设这个角为x 度根据一个角的补角比它的余角的3倍少20°构建方程即可解决问题【详解】解:设这个角为x 度则180°-x=3(90°-x )-20°解得:x=35°答:这个角的度数是35°故答案解析:35【分析】设这个角为x 度.根据一个角的补角比它的余角的3倍少20°,构建方程即可解决问题.【详解】解:设这个角为x 度.则180°-x=3(90°-x )-20°,解得:x=35°.答:这个角的度数是35°.故答案为:35.【点睛】本题考查余角、补角的定义,一元一次方程等知识,解题的关键是学会用方程分思想思考问题,属于中考常考题型.14.90°或50°【分析】根据互余的特点分射线OC 在内部和外部进行求解即可;【详解】∵与互余∴当OC 在内部时;当OC 在外部时;故答案是90°或50°【点睛】本题主要考查了角的计算准确计算是解题的关键解析:90°或50°【分析】根据互余的特点,分射线OC 在AOB ∠内部和外部进行求解即可;【详解】∵70AOB ∠=︒,COB ∠与AOB ∠互余,∴20COB ∠=︒,当OC 在AOB ∠内部时,702050AOC ∠=︒-︒=︒;当OC 在AOB ∠外部时,702090AOC ∠=︒+︒=︒;故答案是90°或50°.【点睛】本题主要考查了角的计算,准确计算是解题的关键.15.30°180°-n°【分析】(1)根据对顶角相等可得答案;(2)根据角的和差可得答案【详解】解:(1)若∠ACF=30°则∠PCD=30°理由是对顶角相等(2)由角的和差得∠ACD+∠BCE=∠AC解析:30° 180°-n°【分析】(1)根据对顶角相等,可得答案;(2)根据角的和差,可得答案.【详解】解:(1)若∠ACF=30°,则∠PCD=30°,理由是对顶角相等.(2)由角的和差,得∠ACD+∠BCE=∠ACB+∠BCD+∠BCE=∠ACB+∠DCE=180°, ∴∠ACD=180°-∠BCE=180°-n°.故答案为:30°,180°-n°.【点睛】本题考查了对顶角的性质、角的和差,由图形得到各角之间的数量关系是解答本题的关键.16.【分析】根据两直线平行内错角相等可得∠1=∠2+∠3据此可求【详解】解:∵AB ∥CD ∴∠1=∠2+∠3∴∠3=∠1-∠2=-=故答案是:【点睛】此题主要考查了平行线的性质关键是正确理解题意掌握两直线解析:5131︒.【分析】根据两直线平行内错角相等可得∠1=∠2+∠3,据此可求.【详解】解:∵AB ∥CD ,∴∠1=∠2+∠3∴∠3=∠1-∠2=100︒-4829︒'=5131︒,故答案是:5131︒.【点睛】此题主要考查了平行线的性质,关键是正确理解题意,掌握两直线平行内错角相等. 17.75°【分析】先根据对顶角的性质求得∠4=60°然后由三角形外角的性质得∠5=105°然后根据补角的定义求得∠3最后运用平行线的性质解答即可【详解】解:如图所示∵∠4=∠1=60°∠B=45°∴∠5解析:75°【分析】先根据对顶角的性质求得∠4=60°,然后由三角形外角的性质得∠5=105°,然后根据补角的定义求得∠3,最后运用平行线的性质解答即可.【详解】解:如图所示.∵∠4=∠1=60°,∠B=45°∴∠5=∠4+∠B=60°+45°=105°,∵∠5+∠3=180°∴∠3=180°-∠5=75°∵直线a//b.∴∠2=∠3=75°.故答案为:75°.【点睛】本题考查了等腰直角三角形的性质、平行线的性质、三角形外角的性质等知识:根据三角形外角的性质以及邻补角互补求得∠3的度数是解答本题的关键.18.540°【分析】分别过点CD作AB的平行线CGDH进而利用同旁内角互补可得∠B+∠BCD+∠CDE+∠E的大小【详解】解:如图根据题意可知:AB∥EF 分别过点CD作AB的平行线CGDH所以AB∥CG解析:540°【分析】分别过点C,D作AB的平行线CG,DH,进而利用同旁内角互补可得∠B+∠BCD+∠CDE +∠E的大小.【详解】解:如图,根据题意可知:AB∥EF,分别过点C,D作AB的平行线CG,DH,所以AB∥CG∥DH∥EF,则∠B+∠BCG=180°,∠GCD+∠HDC=180°,∠HDE+∠DEF=180°,∴∠B+∠BCG+∠GCD+∠HDC+∠HDE+∠DEF=180°×3=540°,∴∠B+∠BCD+∠CDE+∠E=540°.故答案为:540°.【点睛】考查了平行线的性质,解题的关键是作辅助线,利用平行线的性质计算角的大小. 19.105°【分析】依据AB ∥EF 即可得∠BDE=∠E=45°再根据∠A=30°可得∠B=60°利用三角形外角性质即可得到∠1=∠BDE+∠B=105°【详解】∵AB ∥EF ∴∠BDE=∠E=45°又∵∠解析:105°【分析】依据AB ∥EF ,即可得∠BDE=∠E=45°,再根据∠A=30°,可得∠B=60°,利用三角形外角性质,即可得到∠1=∠BDE+∠B=105°.【详解】∵AB ∥EF ,∴∠BDE=∠E=45°,又∵∠A=30°,∴∠B=60°,∴∠1=∠BDE+∠B=45°+60°=105°,【点睛】本题考查平行线的性质和三角形外角的性质,解题的关键是掌握平行线的性质和三角形外角的性质.20.或【分析】可分两种情况当位于线段同侧时或异侧时根据垂线的定义结合平角的定义可计算求解【详解】解:当位于线段同侧时如图1;当位于线段两侧时如图2故答案为:或【点睛】本题主要考查垂线的定义理解好题意分类 解析:50或130【分析】可分两种情况当OD ,OE 位于线段AB 同侧时或异侧时,根据垂线的定义,结合平角的定义可计算求解.【详解】解:当OD ,OE 位于线段AB 同侧时,如图1,OD OE ⊥,90DOE ∴∠=︒,180AOD DOE BOE ∠+∠+∠=︒,40AOD ∠=︒,180904050BOE ∴∠=︒-︒-︒=︒;当OD ,OE 位于线段AB 两侧时,如图2,OD OE ⊥,90DOE ∴∠=︒,40AOD ∠=︒,904050AOE ∴∠=︒-︒=︒,180AOE BOE ∠+∠=︒,18050130BOE ∴∠=︒-︒=︒.故答案为:50︒或130︒.【点睛】本题主要考查垂线的定义,理解好题意,分类讨论,灵活运用垂线的定义计算角的度数是解题的关键.三、解答题21.见解析【分析】根据同角的补角相等可得出∠AEM=∠CDM ,利用“同位角相等,两直线平行”可得出AB ∥CD ,由“两直线平行,同旁内角互补”及∠EFC=62°可求出∠AEF=118°,结合角平分线的定义可求出∠AEC 的度数,再利用“两直线平行,内错角相等”即可求出∠C 的度数.【详解】解:∵∠CDM+∠CDN=180°(平角的意义),∠AEM+∠CDN=180°(已知),∴∠AEM=∠CDM ,∴AB ∥CD ,(同位角相等,两直线平行)∴∠AEF+∠EFC=180°,(两直线平行,同旁内角互补)∵∠EFC=62°,∴∠AEF=118°,∵EC 平分∠AEF ,∴∠AEC=59°,(角平分线的定义)∵AB ∥CD ,∴∠C=∠AEC=59°.(两直线平行,内错角相等).【点睛】本题考查了平行线的判定与性质以及角平分线,牢记各平行线的判定与性质定理是解题的关键.22.(1)15ACF ∠=︒;(2)70ACF ∠=,130ACE ∠=.【分析】(1)、结合平角的定义和角平分线的定义解答;(2)、根据角平分线的定义、平角的定义以及角的和差关系解答即可.【详解】解:()1如题图①,因为90,30ACB BCE ∠=︒∠=︒,所以180903060,180ACD BCD ∠=︒-︒-︒=︒∠=︒30150-︒=︒又因为CF 平分,BCD ∠ 所以1752DCF BCF BCD ∠=∠=∠=︒, 所以756015ACF DCF ACD ∠=∠-∠=︒-=︒;()2如题图②,因为140BCE ∠=︒,所以40BCD ∠=因为CF 平分,BCD ∠所以20BCF FCD ∠=∠=︒,所以9070ACF BCF ∠=︒-∠=,9050ACD BCD ∠=︒-∠=,所以180130ACE ACD ∠=︒-∠=.【点睛】考查了角的计算和角平分线的定义,主要考查学生的计算能力,求解过程类似. 23.(1)图见解析;(2)图见解析,点到直线的距离垂线段最短;(3)图见解析,两点之间线段最短.【分析】(1)根据题意画图即可;(2)①借助网格作CE ⊥AB ,根据点到直线距离垂线段最短可得符合条件的E 点; ②连接AD 和CE 交于P 点,根据两点之间线段最短可得AP DP CP EP AD CE +++=+.【详解】(1)连接AB 如下图所示;(2)①如图所示CE 为最短路径,理由是点到直线的距离垂线段最短,故答案为:点到直线的距离垂线段最短;②如图所示P 点为AP DP CP EP +++最短,理由是:两点之间线段最短,故答案为:两点之间线段最短.【点睛】本题考查两点之间的距离,垂线段最短和根据要求画线段.理解点到直线的距离垂线段最短和两点之间线段最短是解题关键.24.40AOC ∠=︒;70AOE ∠=︒【分析】先利用平角定义与90FOC求出90FOD ∠=︒,再利用互余关系求=40BOD ∠︒,利用对顶角性质求40AOC ∠=︒,利用邻补角定义,求出140AOD ∠=︒,利用角平分线定义便可求出AOE ∠.【详解】 解:90FOC ∠=︒,∴1801809090FOD FOC ∠=︒-∠=︒-︒=︒, ∵50BOF ∠=︒,90-50=40BOD FOD BOF ∴∠=∠-∠=︒︒︒,AOC ∠与BOD ∠是对顶角,40AOC BOD ∴∠=∠=︒;COD ∠是一个平角,∴∠AOC+∠AOD=180º,∵40AOC ∠=︒,140AOD ∴∠=︒, OE 平分AOD ∠,12AOE AOD ∴∠=∠, 70AOE ∴∠=︒.【点睛】本题考查的知识点是对顶角、邻补角、两角互余、角平分线的意义,解题关键是熟练利用角平分线定理.25.∠C的度数是151°.【分析】根据对顶角相等,等量代换得∠1=∠3,根据同位角相等判断两直线平行,再由两直线平行得同旁内角互补则可解答.【详解】解:如图,∵∠1=∠2又∵∠2=∠3∴∠1=∠3∴AB∥CD∴∠A+∠C=180°,又∵∠A=29°∴∠C=151°答:∠C的度数是151°.【点睛】本题考查了对顶角的性质、平行线的性质和判定,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系;平行线的性质是由平行关系来寻找角的数量关系.26.(1)见解析;(2)∠AOB与∠MPN相等或互补;证明见解析.【分析】(1)根据几何语言画出对应的几何图形;(2)如图1,根据平行线的性质得到∠AOB=∠PCB,∠MPN=∠PCB,则∠AOB=∠MPN;如图2,利用平行线的性质得到∠AOB=∠PCB,∠MPN+∠PCB=180°,从而得到∠AOB+∠MPN=180°.【详解】解:(1)(2)∠AOB与∠MPN相等或互补.证明:如图1,∵PM∥OA,∴∠AOB=∠PCB,∵PN∥OB,∴∠MPN=∠PCB,∴∠AOB=∠MPN;如图2,∵PM∥OA,∴∠AOB=∠PCB,∵PN∥OB,∴∠MPN+∠PCB=180°,∴∠AOB+∠MPN=180°.综上所述,∠AOB与∠MPN相等或互补.【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行线的性质.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
23
(第三题)
A
B C
D
1
234
(第2题)
1
23
45
67
8
(第4题)
a
b c
A
B
C
D (第7题)
七年级数学下册各单元测试题
第二章《相交线与平行线》测试卷
一、选择题(每小题3分,共 30 分) 1、如图所示,∠1和∠2是对顶角的是( )
A
B
C D
1
2
1
2
1
2
1
2
2、
如图AB ∥CD 可以得到( )
A 、∠1=∠2
B 、∠2=∠3
C 、∠1=∠4
D 、∠3=∠4
3、直线AB 、CD 、EF 相交于O ,则∠1+∠2+∠3=( ) A 、90° B 、120° C 、180° D 、140°
4、如图所示,直线a 、b 被直线c 所截,现给出下列四种条件: ①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断 是a ∥b 的条件的序号是( )
A 、①②
B 、①③
C 、①④
D 、③④
5、某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相 同,这两次拐弯的角度可能是( )
A 、第一次左拐30°,第二次右拐30°
B 、第一次右拐50°,第二次左拐130°
C 、第一次右拐50°,第二次右拐130°
D 、第一次向左拐50°,第二次向左拐130° 6、下列哪个图形是由左图平移得到的( )
B
D
A B C
D
E
(第10题)
(第14题)
A B
C
D E
F
G
H
第13题
7、如图,在一个有4×4个小正方形组成的正方形网格中,阴影 部分面积与正方形ABCD 面积的比是( ) A 、3:4 B 、5:8 C 、9:16 D 、1:2 8、下列现象属于平移的是( )
① 打气筒活塞的轮复运动,② 电梯的上下运动,③ 钟摆的摆动,④ 转动的门,⑤ 汽车在一条笔直的马路上行走
A 、③
B 、②③
C 、①②④
D 、①②⑤ 9、下列说法正确的是( ) A 、有且只有一条直线与已知直线平行 B 、垂直于同一条直线的两条直线互相垂直
C 、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离。
D 、在平面内过一点有且只有一条直线与已知直线垂直。
10、直线AB ∥CD ,∠B =23°,∠D =42°,则∠
E =( ) A 、23° B 、42° C 、65° D 、19°
二、填空题(本大题共6小题,每小题3分,共18分)
11、直线AB 、CD 相交于点O ,若∠AOC =100°,则∠AOD =___________。
12、若AB ∥CD ,AB ∥EF ,则CD ____EF ,其理由是___________________。
13、如图,在正方体中,与线段AB 平行的线段有______________________。
14、奥运会上,跳水运动员入水时,形成的水花是评委评分的一个标准,如图所示为一跳水运动员的入水前的路线示意图。
按这样的路线入水时,形成的水花很大,请你画图示意运动员如何入水才能减小水花? 15、把命题“等角的补角相等”写成“如果……那么……”的形式是:_________________________。
16、如果两条平行线被第三条直线所截,一对同旁内角的度数之比是2:7,那么这两个角分别是_______。
1
A B
O
F
D
E
C (第18题)
第17题
A B C
D
M
N
1
2
A B
D
G
E
H C
(第18题)
A
B C
三 、(每题5分,共15分)
17、如图所示,直线AB ∥CD ,∠1=75°,求∠2的度数。
18、如图,直线AB 、CD 相交于O ,OD 平分∠AOF ,OE ⊥CD 于点O ,∠1=50°,求∠COB 、∠BOF 的度数。
19、如图,在长方形ABCD 中,AB =10cm ,BC =6cm ,若此长方形以2cm/S 的速度沿着A →B 方向移动,则经过多长时间,平移后的长方形与原来长方形重叠部分的面积为24?
四、(每题6分,共18分) 20、△ABC 在网格中如图所示, 请根据下列提示作图
(1)向上平移2个单位长度。
(2)再向右移3个单位长度。
21、如图,选择适当的方向击打白球,可使白球反弹后将红球撞入袋中。
此时,∠1=∠2,∠3=∠4,如果红球与洞口的连线与台球桌面边缘的夹角∠5=30°,那么∠1等于多少度时,才能保证红球能直接入袋?
A
O
D
B E C
A B C
D
E
F
14
23第19题)
22、把一张长方形纸片ABCD 沿EF 折叠后ED 与BC 的交点为G ,D 、C 分别在M 、N 的位置上,若∠EFG =55°,求∠1和∠2的度数。
五、(第23题9分,第24题10分,共19分)
23、如图,E 点为DF 上的点,B 为AC 上的点,∠1=∠2,∠C =∠D ,那么DF ∥AC ,请完成它成立的理由
∵∠1=∠2,∠2=∠3 ,∠1=∠4( ) ∴∠3=∠4( ) ∴________∥_______ ( ) ∴∠C =∠ABD ( ) ∵∠C =∠D ( ) ∴∠D =∠ABD ( ) ∴DF ∥AC ( )
24、如图,DO 平分∠AOC ,OE 平分∠BOC ,若OA ⊥OB , (1)当∠BOC =30°,∠DOE =_______________ 当∠BOC =60°,∠DOE =_______________ (2)通过上面的计算,猜想∠DOE 的度数与∠AOB
B
A C
D E
F G M
N
1
2
第二章《相交线与平行线》测试卷答案
一、1、D ;2、C ;3、C ;4、A ;5、A ;6、C ;7、B ;8、D ;9、D ;10、C 二、11、80°; 12、11,平行于同一条直线的两条直线互相平行;13、EF 、HG 、DC ;14、过表示运动员的点作水面的垂线段;15、如果两个角相等,那么这两个角的补角也相等;16、40°,140°。
三、17、105°;18、∠COB =40°,∠BOF =100°;19、3秒 四、20、略;21、∠1=60°;22、∠1=70°,∠2=110° 五、23、略;24、(1)45°,45°,(2)∠DOE =
2
1
∠AOB。
