7.1.2《用坐标表示平移》同步练习题(2)及答案
七年数学同步练习:7.2.2 用坐标表示平移(含答案)

二、达标体验
1、将点(-2,5)向右平移3个单位长度,再向下平移7个单位长度得到点(1,-2).
分析:-2+3=1;5-7= -2.
2、在平面直角坐标系中,将点(-2,3)平移后得到点B(-2,-3),则点A向下平移了6个单位长度。
分析:-2-(-2)=0;-3-3=-6.
3、在平面直角坐标系中,已知线段AB的两个端点的坐标分别为A(-4,-1),B(0,1),将线段AB平移后得到线段CD,点A,B的对应点分别为点C,D.若点C的坐标为(-2,2),则点D的坐标为(2,4).
3、一般地,在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向___(或向___)平移____个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向___(或向___)平移___个单位长度。
二、达标体验
1、将点(-2,5)向右平移3个单位长度,再向已知点M(a,b),N(c,d),请写出线段MN的中点P的坐标。
四、中考链接
11、(大连)在平面直角坐标系中,将点(2,3)向上平移1个单位长度,所得到的点的坐标是( ).
A.(1,3) B.(2,2) C(2,4) D.(3,3)
12、(安顺)将点A(-2,-3)向右平移3个单位长度得到点B,则点B所在的象限是( )
(1)画出三角形ABC及三角形A1B1C1;
(2)写出三角形A1B1C1各顶点的坐标.
7.2.2 用坐标表示平移(2)
5 4 3 2 1
y
(x-5,y+3)
o -1 -2 -3
-4
1
2 3 (2,-2) P
4
5 (5,-2) x Q
R (3,-4)
尝试练习一、
课本P54的练习3(解答题)(平移n个单位长度后求新坐标) 课本P54的练习4、6(选择题)(平移n个单位长度后求新坐标)
3、如图,长方形ABCD四个顶点分别是A(-3,2),B(3,-2),C(3,-2),D(3,2).将长方形向左平移2个单位长度 各个顶点的坐标变为多少?将它向上平移3个单位 y A2 D2 5 长度呢?分别画出平移后的图形
• 6、线段CD是由线段AB平移得到的。
点A(–1,4)的对应点为C (4,7),则点B(–4,–1)的对 (1,2) 应点D的坐标为________。
12 7.已知A(1,4),B(-4,0),C(2,0).△ABC的面积是__
8.将△ABC向左平移三个单位后,点A、B、C的
坐标分别变为______,______,____. (-2,4) (-7,0) (-1,0)
y 4 3 D -4 -3 -2 -1 2 1 1 -1 -2 -3 -4 B 2 3 4 C x
O
A
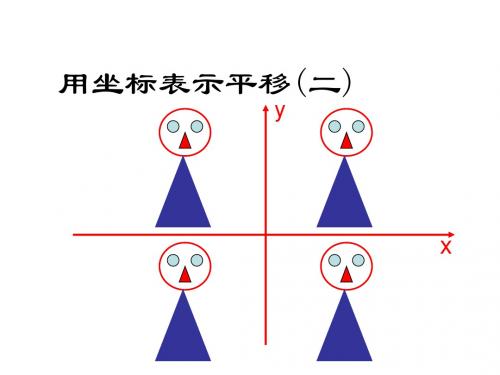
用坐标表示平移(二)
y
x
复习1:点的平移
(1)左右平移: 点(x,y) , 向右平移a个单位 (x+a,y)
点(x,y) , 向左平移a个单位 (x-a,y)
(2)上下平移:
点(x,y) , 向上平移b个单位 (x,y+b) 点(x,y) , 向下平移b个单位 (x,y-b)
点(x,y)
向右平移a个单位, , 向下平移b个单位
人教版数学七年级下册7.2.2《用坐标表示平移》同步练习 (含答案)

人教版数学七下7.2.2《用坐标表示平移》同步练习一、选择题1.将点A(2,1)向左平移2个单位长度得到点A′,则点A′的坐标是( )A.(2,3)B.(2,-1)C.(4,1)D.(0,1)2.在平面直角坐标系中,将点(2,3)向上平移1个单位,所得到的点坐标是( )A.(1,3)B.(2,2)C.(2,4)D.(3,3)3.如图,如果将三角形ABC向左平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为( )A.(5,1)B.(1,1)C.(7,1)D.(3,3)4.如图,将三角形PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )A.(-2,-4)B.(-2,4)C.(2,-3)D.(-1,-3)5.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )A.(2,5)B.(-8,5)C.(-8,-1)D.(2,-1)6.如果一个图案沿x轴负方向平移3个单位长度,那么这个图案上的点坐标变化为( )A.横坐标不变,纵坐标减少3个单位长度B.纵坐标不变,横坐标减少3个单位长度C.横纵坐标都没有变化D.横纵坐标都减少3个单位长度7.已知线段CD是由线段AB平移得到的,点A(-1,4)的对应点为点C(4,7),则点B(-4,-1)的对应点D的坐标为( )A.(1,2)B.(2,9)C.(5,3)D.(-9,-4)8.在如图所示的单位正方形网格中,三角形ABC经过平移后得到三角形A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,则P1点的坐标为( )A.(1.4,-1)B.(1.5,2)C.(-1.6,-1)D.(2.4,1)9.点G(-2,-2),将点G先向右平移6个单位长度,再向上平移5 个单位长度,得到G′,则G′的坐标为( )A.(6,5)B.(4,5)C.(6,3)D.(4,3)10.将点A(a,-3)先向右平移2个单位长度,再向上平移4个单位长度得到点B(4,b),则a和b的值分别为( )A.(1,4)B.(4,1)C.(2,1)D.(1,2)二、填空题11.在平面直角坐标系中,已知点O(0,0),A(1,3),将线段OA向右平移3个单位,得到线段O1A1,则点O1的坐标是,A1的坐标是 .12.将点A(-3,1)向右平移5个单位长度,再向上平移6个单位长度,可以得到对应点A′的坐标为 .13.在平面直角坐标系中,三角形ABC的三个顶点的横坐标保持不变,纵坐标都减去2个单位长度,则得到的新三角形与原三角形相比向平移了个单位长度.14.已知三角形ABC,若将三角形ABC平移后,得到三角形A′B′C′,且点A(1,0)的对应点A′的坐标是(-1,0),则三角形ABC是向平移个单位得到三角形A′B′C′.15.在平面直角坐标系中,已知线段AB的两个端点的坐标分别是A(4,-1)、B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2),则点B′的坐标为 .三、作图题16.如图所示,一小船,将其向左平移6个单位长度,再向下平移5个单位长度,试确定A,B,C,D,E,F,G平移后对应点的坐标并画出平移后的图形.17.如图,在边长均为1个单位的正方形网格图中,建立了直角坐标系xOy,按要求解答下列问题:(1)写出△ABC三个顶点的坐标;(2)画出△ABC向右平移6个单位后的图形△A1B1C1;(3)求△ABC的面积.四、解答题18.如图所示,三角形ABC三点坐标分别为A(-3,4),B(-4,1),C(-1,2).(1)说明三角形ABC平移到三角形A1B1C1的过程,并求出点A1,B1,C1的坐标;(2)由三角形ABC平移到三角形A2B2C2又是怎样平移的?并求出点A2,B2,C2的坐标.19.如图,三角形ABC是由三角形A1B1C1平移后得到的,三角形ABC中任意一点P(x,y)经平移后对应点为P1(x-3,y-5),求A1、B1、C1的坐标.。
人教版七年级数学下册:用坐标表示平移 课时作业(含答案)

人教版七年级下册数学同步课时作业第七章平面直角坐标系7.2坐标方法的简单应用7.2.2用坐标表示平移1. 在平面直角坐标系中,点A'(2,-2)可以由点A(-2,3)经过两次平移得到,则正确的是()A.先向左平移4个单位长度,再向上平移5个单位长度B.先向右平移4个单位长度,再向上平移5个单位长度C.先向左平移4个单位长度,再向下平移5个单位长度D.先向右平移4个单位长度,再向下平移5个单位长度2. 将点A(-2,-3)先向右平移3个单位长度,再向下平移2个单位长度得到点B,则点B所在象限是()A.第一象限B.第二象限C.第三象限D.第四象限3. 已知三角形ABC的三个顶点坐标分别是(-2,1),(2,3),(-3,-1),把三角形ABC移动到一个确定位置,则点A,B,C所对应的顶点坐标可能是()A.(0,3),(0,1),(-1,-1)B.(-3,2),(3,2),(-4,0)C.(1,-2),(3,2),(-1,-3)D.(-1,3),(3,5),(-2,1)4. 如图,在平面直角坐标系中,点A,B的坐标分别为A(0,6),B(-3,-3).将线段AB平移后,点A的对应点为A'(10,10),则点B的对应点B'的坐标为()A.(10,10)B.(-3,-3)C.(-3,3)D.(7,1)5. 在平面直角坐标系中,点P(1,2)平移后的坐标是P'(-3,3).若按照同样的规律平移其他点,则以下各点的平移变换中符合此种规律的是()A.(3,2)→(4,-2)B.(-1,0)→(-5,-4)C.(1.2,5)→(-3.2,6)D.(2.5,-13)→(-1.5,23)6. 如图,将线段AB平移到线段CD的位置,则a+b的值为()A.4B.3C.0D.-57. 如图是由边长为1的小正方形组成的网格图,点A,B,C都在格点上,若将线段AB沿BC方向平移,使点B与点C重合,则线段AB扫过的面积为()A.11B.10C.9D.88. 将画在透明胶片上的平行四边形ABCD放在如图所示的平面直角坐标系内,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A'(4,-2)处,则此平移是()A.先向右平移5个单位长度,再向下平移1个单位长度B.先向右平移5个单位长度,再向下平移3个单位长度C.先向右平移4个单位长度,再向下平移4个单位长度D.先向右平移4个单位长度,再向下平移3个单位长度9. 将点P(-3,y)向上平移3个单位长度,向左平移2个单位长度后得到点Q(x,-1),则xy的值为.10. A,B两点的坐标分别为(2,0),(0,2),若将线段AB平移至A1B1,点A1,B1的坐标分别为(1,a),(b,6),则b a =.11. 如图,将线段AB平移,使点B平移到点C,则平移后点A的坐标为.12. 如图,把“笑脸”放在平面直角坐标系中,已知左眼的坐标是(-2,3),嘴唇的坐标为(-1,1),则将此“笑脸”向右平移3个单位长度后,右眼的坐标是.13. 点A,B的坐标分别为(-7,0),(0,-6).若将线段AB平移到A1B1,点A1,B1的坐标分别为(-2,a),(b,5),则a+b的平方根是.14. 如图,在平面直角坐标系xOy中,将点A(2,4)向右平移4个单位长度,再向下平移2个单位长度得到点B.(1)标出点B的位置,并写出点B的坐标;(2)求出三角形OAB的面积.15. 已知三角形ABC与三角形A'B'C'在平面直角坐标系中的位置如图所示.(1)分别写出点B,B'的坐标:B,B';(2)若P(a,b)是三角形ABC内部一点,则平移后三角形A'B'C'内的对应点P'的坐标为;(3)求三角形ABC的面积.16. 如图,四边形ABCD的各顶点的坐标分别为A(-2,0),B(3,0),C(2,3),D(-1,2).(1)若各顶点的纵坐标不变,横坐标增加3,得到点A1,B1,C1,D1,写出点A1,B1,C1,D1的坐标;(2)若将(1)中点A1,B1,C1,D1依次连接起来,得到四边形A1B1C1D1,则四边形A1B1C1D1是由原四边形ABCD如何变化得到的?(3)若各顶点的横坐标不变,纵坐标增加3,得到的四边形A2B2C2D2是由原四边形ABCD如何变化得到的?参考答案1. D2. D3. D4. D5. D6. A7. B8. C9. 2010. 111. (-1,1)12. (3,3)13. ±4 14. 解:(1)图略;点B的坐标为(6,2).(2)S三角形OAB=6×4-12×4×2-12×4×2-12×6×2=10.15. 解:(1)(3,-4) (-2,0) (2)(a-5,b+4)(3)S三角形ABC=4×4-12×2×4-12×4×1-12×2×3=7.16. 解:(1)点A1(1,0),B1(6,0),C1(5,3),D1(2,2).(2)四边形A1B1C1D1是由原四边形ABCD向右平移3个单位长度得到的.(3)四边形A2B2C2D2是由原四边形ABCD向上平移3个单位长度得到的.。
人教版七年级数学下册7.2.2用坐标表示平移同步测试(含答案)

绝密★启用前用坐标表示平移班级:姓名:一、单项选择题1.已知点A( 5,﹣ 1),现将点 A 沿 x 轴正方向挪动 1 个单位长度后抵达点B,那么点 B 的坐标是()A.( 6,﹣ 1)B.( 5,0)C.(4,﹣ 1)D.(﹣ 5, 1)2.将点A 2, 1 向左平移 3 个单位长度,在向上平移4 个单位长度获得点B,则点B的坐标是()A.5,3B.5,5C.1, 5D.1,33.如图,已知点,的坐标分别为( 3,0 ),( 0,4),将线段平移到,若点的对应点的坐标为( 4,2 ),则的对应点的坐标为()A.( 1,6)B.( 2,5)C.( 6, 1)D.( 4, 6)4.将某图形的各极点的横坐标保持不变,纵坐标减去3,可将该图形()A.横向向右平移3个单位B.横向向左平移3个单位C.纵向向上平移3个单位D.纵向向下平移3个单位5.在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比()A.向右平移了 3 个单位B.向左平移了 3 个单位C.向上平移了 3 个单位D.向下平移了 3 个单位6.在内的随意一点经过平移后的对应点为,已知在经过此次平移后对应点的坐标为,则的值为()A.B.C.D.7.已知线段AB 在平面直角坐标系中,A, B 坐标分别为( m, n),( 2, 3),将线段AB 平移至A1B1, A1, B1坐标为( n-1,3-m ),( -1, -2),则 A 点的坐标是()A.( -5, 3)B.( -3, 5)C.( 3, -5)D.( 5, 3)8.如图,将点 A 先向右平移 3 个单位长度,在向下平移 5 个单位长度,获得A’;将点 B 先向下平移5 个单位长度,再向右平移 4 个单位长度,获得B’,则 A’与 B’相距()A. 4 个单位长度B. 5 个单位长度C.6 个单位长度D.7 个单位长度二、填空题9.在平面直角坐标系中,将点A(5,﹣8)向左平移获得点B( x+3,x﹣ 2),则点 B 的坐标为 _____.10.如图,将直角三角形ABC 沿 BC 方向平移必定距离获得三角形DEF ,若AB 8 , BE 3 ,DG 2 则图中暗影部分面积为_____.11.在平面直角坐标系中,将点Q 向下平移 4 个单位长度后获得点2, 6 ,则点 Q 的坐标是__________.12.如图,在△AOB 中, AO=AB,在直角坐标系中,点 A 的坐标是(2,2),点 O 的坐标是( 0,0),将△AOB 平移获得△ A′O′,B使′得点 A′在 y 轴上.点 O′、 B′在 x 轴上.则点 B'的坐标是 ______三、解答题13.如图,在平面直角坐标系中,△ ABC的三个极点的坐标分别为:A( -1, 2), B(-2, -1), C (2,0).( 1)作图:将△ ABC先向右平移4 个单位,再向上平移 3 个单位,则获得△ A1B1C1,作出△A1B1C1;(不要求写作法)(2)写出以下点的坐标: A1______ ;B1______; C1______.(3)求△ ABC 的面积 .一、单项选择题1.在平面直角坐标系中,将点A(﹣ 1,﹣ 2)向右平移 3 个单位长度获得点B,则点 B 对于 x 轴的对称点 B′的坐标为()A.(﹣ 3,﹣ 2)B.( 2, 2)C.(﹣ 2, 2)D.( 2,﹣ 2)2.在直角坐标系中 ,某三角形三个极点的横坐标不变,纵坐标都增添 2 个单位长度 ,则所得三角形与原三角形对比()A.形状不变 ,面积扩大 2 倍B.形状不变 ,地点向上平移 2 个单位长度C.形状不变 ,地点向右平移 2 个单位长度D.以上都不对3.将三角形 ABC的三个极点的纵坐标都加上3,横坐标不变,表示将该三角形()A.沿 x 轴的正方向平移了3个单位长度B.沿 x 轴的负方向平移了3个单位长度C.沿 y 轴的正方向平移了3个单位长度D.沿 y 轴的负方向平移了3个单位长度4.如图,已知一个直角三角板的直角极点与原点重合,另两个极点A, B 的坐标分别为(-1, 0),( 0, 3 ).现将该三角板向右平移使点 A 与点 O 重合,获得△ OCB’,则点 B 的对应点B’的坐标是()A.(1,0)B.(3, 3 )C.(1,3)D.(-1, 3 )5.如图,在 x 轴的正半轴和与x 轴平行的射线上各搁置一块平面镜,发光点(0,1)处沿如下图方向发射一束光,每当遇到镜面时会发生反射(反射时反射角等于入射角,认真看光芒与网格线和镜面的夹角),当光芒第20 次遇到镜面时的坐标为()A.( 60,0)B.( 58,0 )C.( 61,3)D.( 58,3)6.在平面直角坐标系中,线段CF是由线段AB 平移获得的;点A( -1,4)的对应点为C( 4, 1);则点 B( a, b)的对应点 F 的坐标为()A.( a+3, b+5)B.( a+5, b+3)C.( a-5,b+3)D.( a+5,b-3)7.将某图形的横坐标都减去2,纵坐标不变,则该图形()A.向右平移 2 个单位B.向左平移 2 个单位C.向上平移 2 个单位D.向下平移 2 个单位8.点 A(-3, -5)向右平移 2 个单位,再向下平移 3 个单位到点B,则点 B 的坐标为()A.(-5,-8)B. (-5,-2)C. (-1,-8)D. (-1,-2)二、填空题9.如图,△ ABC的极点都在网格点上,将△ ABC向右平移 3 个单位长度,再向上平移 2 个单位长度,则平移后获得的△ A′B′三C个′极点 A′、 B′、C′的坐标分别是 _____.10.如图,线段AB 经过平移获得线段A'B' ,此中点A,B的对应点分别为点A', B' ,这四个点都在格点上,若线段AB 上有一个点P a,b ,则点P在A'B'上的对应点P'的坐标为______.11.若将P 1,m向右平移 2 个单位长度后,再向上平移 1 个单位长度获得点Q n,3 ,则点 m,n的实质坐标是 ______ .12.线段 CD 是由线段 AB 平移获得的,此中点 A(﹣ 1,4)平移到点 C(﹣ 3, 2),点 B( 5,﹣ 8)平移到点 D,则 D 点的坐标是 ________.三、解答题13.如图,△ ABC在直角坐标系中,(1)请写出△ ABC各点的坐标 .(2)求出△ ABC的面积 .(3)若把△ ABC向上平移 2 个单位,再向右平移 2 个单位得△ A′B′,C在′图中画出△ ABC 变化地点。
人教版七年级下册7.2.2 用坐标表示平移(含答案).doc

7.2.2用坐标表示平移一、选择题1.在平面直角坐标系中,将点(1,1)向右平移2个单位后,得到的点的坐标是( )A.(3,1) B.(-1,1) C.(1,3) D.(1,-1)2.在平面直角坐标系中,将点P(-3,2)向下平移4个单位得到点P′,则点P′所在的象限为( ) A.第一象限B.第二象限C.第三象限D.第四象限3.在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( )A.(-1,1) B.(3,1) C.(4,-4) D.(4,0)4.如图,把三角形ABC先向右平移3个单位,再向上平移2个单位得到三角形DEF,则顶点C(0,-1)的对应点坐标为( )A.(0,0) B.(1,2) C.(1,3) D.(3,1)5.如图,点A(2,1),将线段OA先向上平移2个单位长度,再向左平移3个单位长度,得到线段O′A′,则点A的对应点A′的坐标是( )A.(-3,2) B.(0,4) C.(-1,3) D.(3,-1)6.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为( )A.(1,3) B.(5,1) C.(1,3)或(3,5) D.(1,3)或(5,1)7.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,3).现将该三角板向右平移使点A与点O重合,得到三角形OCB′,则点B的对应点B′的坐标是( )A.(1,0) B.(3,3) C.(1,3) D.(-1,3)二、填空题8.点N(-1,3)可以看作由点M(-1,-1)向平移个单位所得到的.9.已知点M(3a-9,1-a),将点M向左平移3个单位长度后落在y轴上,则a=. 10.如图,三角形OAB的顶点A,B的坐标分别为(3,5),(4,0),把三角形OAB沿x轴向右平移得到三角形CDE.如果CB=1,那么点D的坐标为.11.如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点A1(1,1);把点A1向上平移2个单位,再向左平移2个单位,得到点A2(-1,3);把点A2向下平移3个单位,再向左平移3个单位,得到点A3(-4,0);把点A3向下平移4个单位,再向右平移4个单位,得到点A4(0,-4)……按此做法进行下去,则点A10的坐标为.12.如图①是一个斜角坐标系,水平放置的轴称为横轴(记作a轴),斜向放置的轴称为斜轴(记作b轴).类似于直角坐标系,对于斜角坐标平面内的任意一点P,过点P分别作b轴、a轴的平行线交a轴、b轴于点M,N,若点M,N分别在a轴、b轴上所对应的实数为m与n,则称有序实数对(m,n)为点P的坐标.如图②,三角形ABC中,A(1,4),C(3,5),如果平移三角形ABC 得到三角形A′B′C′,使点A′与点C重合,在三角形ABC内部,有一任意点D(x,y),则平移后点D的对应点D′的坐标为________________.三、解答题13.如图,三角形ABC的顶点坐标分别为A(-2,3),B(-3,0),C(-1,-1).将三角形ABC 平移后得到三角形A′B′C′,且点A的对应点是A′(2,3),点B,C的对应点分别是B′,C′.(1)点A,A′之间的距离是;(2)请在图中画出三角形A′B′C′.14.如图,已知坐标平面内的三个点A(1,3),B(3,1),O(0,0).(1)平移三角形ABO至三角形A1B1O1,当点A1和点B重合时,求点O1的坐标;(2)平移三角形ABO至三角形A2B2O2,需要至少向下平移超过单位,并且至少向左平移超过个单位,才能使三角形A2B2O2位于第三象限.15.在平面直角坐标系中,三角形A′B′C′是由三角形ABC平移后得到的,已知三角形ABC内部的一点P(x0,y0)经平移后的对应点为P′(x0+5,y0-2).(1)三角形A′B′C′是由三角形ABC如何平移得到的?(2)若已知A(-1,2),B(-4,5),C(-3,0),请写出A′,B′,C′的坐标;(3)在(2)的条件下,求三角形A′B′C′的面积.16.如图,第一象限内有两点P(m-3,n),Q(m,n-2),将线段PQ平移,使点P,Q分别落在两条坐标轴上,求点P平移后的对应点的坐标.17.如图,在平面直角坐标系中,A(1,4),B(3,2),O为坐标原点,且OC∥AB,OC=AB.试用平移的知识求C点的坐标,并求四边形ABCO的面积.参考答案一、选择题1.在平面直角坐标系中,将点(1,1)向右平移2个单位后,得到的点的坐标是( A)A.(3,1) B.(-1,1) C.(1,3) D.(1,-1)2.在平面直角坐标系中,将点P(-3,2)向下平移4个单位得到点P′,则点P′所在的象限为( C) A.第一象限B.第二象限C.第三象限D.第四象限3.在平面直角坐标系中,将点A(1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B的坐标是( A)A.(-1,1) B.(3,1) C.(4,-4) D.(4,0)4.如图,把三角形ABC先向右平移3个单位,再向上平移2个单位得到三角形DEF,则顶点C(0,-1)的对应点坐标为( D)A.(0,0) B.(1,2) C.(1,3) D.(3,1)5.如图,点A(2,1),将线段OA先向上平移2个单位长度,再向左平移3个单位长度,得到线段O′A′,则点A的对应点A′的坐标是( C)A.(-3,2) B.(0,4) C.(-1,3) D.(3,-1)6.如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(0,1),将线段AB平移,使其一个端点到C(3,2),则平移后另一端点的坐标为( D)A.(1,3) B.(5,1) C.(1,3)或(3,5) D.(1,3)或(5,1)7.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0,3).现将该三角板向右平移使点A与点O重合,得到三角形OCB′,则点B的对应点B′的坐标是( C)A.(1,0) B.(3,3) C.(1,3) D.(-1,3)二、填空题8.点N(-1,3)可以看作由点M(-1,-1)向平移个单位所得到的.【答案】上 49.已知点M(3a-9,1-a),将点M向左平移3个单位长度后落在y轴上,则a=. 【答案】410.如图,三角形OAB的顶点A,B的坐标分别为(3,5),(4,0),把三角形OAB沿x轴向右平移得到三角形CDE.如果CB=1,那么点D的坐标为.【答案】(6,5)11.如图,在平面直角坐标系中,把一个点从原点开始向上平移1个单位,再向右平移1个单位,得到点A1(1,1);把点A1向上平移2个单位,再向左平移2个单位,得到点A2(-1,3);把点A2向下平移3个单位,再向左平移3个单位,得到点A3(-4,0);把点A3向下平移4个单位,再向右平移4个单位,得到点A4(0,-4)……按此做法进行下去,则点A10的坐标为.【答案】(-1,11)12.如图①是一个斜角坐标系,水平放置的轴称为横轴(记作a轴),斜向放置的轴称为斜轴(记作b轴).类似于直角坐标系,对于斜角坐标平面内的任意一点P,过点P分别作b轴、a轴的平行线交a轴、b轴于点M,N,若点M,N分别在a轴、b轴上所对应的实数为m与n,则称有序实数对(m,n)为点P的坐标.如图②,三角形ABC中,A(1,4),C(3,5),如果平移三角形ABC 得到三角形A′B′C′,使点A′与点C重合,在三角形ABC内部,有一任意点D(x,y),则平移后点D的对应点D′的坐标为________________.【答案】(x+2,y+1)三、解答题13.如图,三角形ABC的顶点坐标分别为A(-2,3),B(-3,0),C(-1,-1).将三角形ABC 平移后得到三角形A′B′C′,且点A的对应点是A′(2,3),点B,C的对应点分别是B′,C′.(1)点A,A′之间的距离是;(2)请在图中画出三角形A′B′C′.解:(1)4(2)如图所示,三角形A′B′C′即为所求.14.如图,已知坐标平面内的三个点A(1,3),B(3,1),O(0,0).(1)平移三角形ABO至三角形A1B1O1,当点A1和点B重合时,求点O1的坐标;(2)平移三角形ABO至三角形A2B2O2,需要至少向下平移超过单位,并且至少向左平移超过个单位,才能使三角形A2B2O2位于第三象限.解:(1)点O1的坐标为(2,-2).(2)3 315.在平面直角坐标系中,三角形A′B′C′是由三角形ABC平移后得到的,已知三角形ABC内部的一点P(x0,y0)经平移后的对应点为P′(x0+5,y0-2).(1)三角形A′B′C′是由三角形ABC如何平移得到的?(2)若已知A(-1,2),B(-4,5),C(-3,0),请写出A′,B′,C′的坐标;(3)在(2)的条件下,求三角形A′B′C′的面积.解:(1)三角形ABC先向右平移5个单位长度,再向下平移2个单位长度(或先向下平移2个单位长度,再向右平移5个单位长度)得到三角形A′B′C′.(2)A′(4,0),B′(1,3),C′(2,-2).(3)将三角形A ′B ′C ′补成如图所示的长方形,则S 三角形A ′B ′C ′=3×5-12×5×1-12×2×2-12×3×3=6.16.如图,第一象限内有两点P (m -3,n ),Q (m ,n -2),将线段PQ 平移,使点P ,Q 分别落在两条坐标轴上,求点P 平移后的对应点的坐标.解:设平移后点P ,Q 的对应点分别是P ′,Q ′.分两种情况:①P ′在y 轴上,Q ′在x 轴上,则P ′的横坐标为0,Q ′的纵坐标为0.∵0-(n -2)=-n +2,∴n -n +2=2.∴点P 平移后的对应点的坐标是(0,2).②P ′在x 轴上,Q ′在y 轴上,则P ′的纵坐标为0,Q ′的横坐标为0.∵0-m =-m ,∴m -3-m =-3.∴点P 平移后的对应点的坐标是(-3,0).综上可知,点P 平移后的对应点的坐标是(0,2)或(-3,0).17.如图,在平面直角坐标系中,A (1,4),B (3,2),O 为坐标原点,且OC ∥AB ,OC =AB .试用平移的知识求C 点的坐标,并求四边形ABCO 的面积.解:∵把A 点向左平移1个单位长度,再向下平移4个单位长度可得到原点O (0,0),又∵OC ∥AB ,OC =AB ,∴OC 可由AB 向左平移1个单位长度,再向下平移4个单位长度得到.∴点B (3,2)向左平移1个单位长度,再向下平移4个单位长度得到点C (2,-2).分别过A ,C 作x 轴的平行线,过B 作y 轴的平行线,交点为D ,E ,F ,G ,如图所示.S 四边形ABCO =S 长方形DEFG-S 三角形AOD -S 三角形COE -S 三角形BCF -S 三角形ABG =3×6-12×1×4-12×2×2-12×1×4-12×2×2=10.。
7.2.2用坐标表示平移(2)

第七章平面直角坐标系7.2.2 用坐标表示平移(2)一、新知探究坐标系下图形的平移:如图,三角形ABC三个顶点的坐标是A(4,3)、B(3,1)、C(1,2).(1)若将三角形ABC向左平移6个单位,写出A、B、C的对应点的坐标,并画出平移后的三角形。
(2)若将三角形ABC向下平移5个单位,写出A、B、C对应顶点的坐标,并画出平移后的三角形。
总结:一般地,在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向__ __(或向__ __)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数b,相应的新图形就是把原图形向__ __(或向_ ___)平移b个单位长度.简记:横坐标加a,向__ __平移a个单位长度;横坐标减a,向__ __平移a个单位长度;纵坐标加b,向__ __平移b个单位长度;纵坐标减b,向__ __平移b个单位长度.二、例题点拨例1:在直角三角形ABO中,∠OAB=90°,且点B的坐标为(4,2)。
(1)画出直角三角形ABO向下平移3个单位后的三角形A1B1O1;(2)写出A1,B1,O1的坐标;(3)求三角形A1B1O1的面积。
例2:如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点为P′(x0+5,y0﹣2).(1)已知A(﹣1,2),B(﹣4,5),C(﹣3,0),请写出A′、B′、C′的坐标;(2)试说明△A′B′C′是如何由△ABC平移得到的;(3)求出△A′B′C′的面积。
三、课堂练习1、如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(,)、B(,)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).(3)求△ABC的面积。
人教版七年级数学下册 7-2-2用坐标表示平移(同步练习)

第7章平面直角坐标系7.2坐标方法的简单应用-7.2.2用坐标表示平移班级:姓名:知识点1用坐标表示点的平移1.将点A(2,1)向左平移2个单位长度得到点A',则点A'的坐标是()A.(0,1)B.(2,-1)C.(4,1)D.(2,3)2.把点A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到B,点B的坐标是()A.(-5,3)B.(1,3)C.(1,-3)D.(-5,-1)3.点P(2,-3)先向左平移4个单位长度,再向上平移1个单位长度,得到点P'的坐标是.4.将点A(-3,-2)先沿y轴向上平移5个单位长度,再沿x轴向左平移4个单位长度得到点A',则点A'的坐标是.5.将点A(1,-3)向右平移2个单位长度,再向下平移2个单位长度后得到点B(a,b),则ab=.6.(1)如图,将点A向右平移几个单位长度可得到点B()A.3个单位长度B.4个单位长度C.5个单位长度D.6个单位长度(2)将点A向下平移5个单位长度后,将重合于图中的()A.点CB.点FC.点DD.点E(3)将点A先向右平移3个单位长度,再向下平移5个单位长度,得到A',将点B先向下平移5个单位长度,再向右平移3个单位长度,得到B',则A'与B'相距()A.4个单位长度B.5个单位长度C.6个单位长度D.7个单位长度(4)点G(-2,-2),将点G先向右平移6个单位长度,再向上平移5个单位长度,得到G',则G'的坐标为()A.(6,5)B.(4,5)C.(6,3)D.(4,3)7.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是()A.(2,5)B.(-8,5)C.(-8,-1)D.(2,-1)知识点2用坐标表示图形的平移8.将一个三角形的三个顶点的坐标分别向上平移1个单位长度,再向左平移4个单位长度所得点的坐标分别是(2,1),(-1,3),(4,-5),则平移前三个顶点的坐标分别是()A.(6,0),(3,2),(8,-6)B.(-1,-5),(2,-7),(3,-1)C.(1,5),(2,-7),(-3,1)D.(-1,5),(2,-7),(-3,1)9.如图,将三角形PQR向右平移2个单位长度,再向下平移3个单位长度,则点P平移后的坐标是()A.(-2,-4)B.(-2,4)C.(2,-3)D.(-1,-3)10.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2),(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是.11.如图,三角形OAB 的顶点B 的坐标为(4,0),把三角形OAB 沿x 轴向右平移得到三角形CDE.如果CB=1,那么OE 的长为.12.如图,A,B 的坐标分别为(1,0),(0,2),若将线段AB 平移至A 1B 1,A 1,B 1的坐标分别为(2,a),(b,3),则a+b=.13.如图,梯形A'B'C'D'可以由梯形ABCD 经过怎样的平移得到?对应点的坐标有什么变化?综合点学科内综合14.如图,点A,B 的坐标分别为(1,2),(4,0),将三角形AOB 沿x 轴向右平移,得到三角形CDE,已知DB=1,则点C 的坐标为.15.如图,三角形A'B'C'是由三角形ABC 平移后得到的,已知三角形ABC 中一点P(x 0,y 0)经平移后对应点为P'(x 0+5,y 0-2).(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A',B',C'的坐标;(2)试说明三角形A'B'C'是如何由三角形ABC平移得到的;(3)请直接写出三角形A'B'C'的面积为_____.拓展训练拓展点坐标中的规律探究16.如图,三角形DEF 是三角形ABC 经过某种变换后得到的图形,分别写出点A 与点D,点B 与点E,点C 与点F 的坐标,并观察它们的关系,如果三角形ABC 中任一点M 的坐标(x,y),那么它的对应点N的坐标是什么?第7章平面直角坐标系7.2坐标方法的简单应用-7.2.2用坐标表示平移答案与点拨1.A(点拨:点A'的横坐标为2-2=0,纵坐标为1,∴A'的坐标为(0,1).故选A.)2.B(点拨:∵A(-2,1)向上平移2个单位长度,再向右平移3个单位长度后得到B,∴1+2=3,-2+3=1;点B的坐标是(1,3).故选B.)3.(-2,-2)(点拨:点(2,-3)向左平移4个单位长度,横坐标为:2-4=-2,向上平移1个单位长度,纵坐标为:-3+1=-2,∴点P'(-2,-2).)4.(-7,3)(点拨:点A(-3,-2)先沿y轴向上平移5个单位长度,再沿x轴向左平移4个单位长度得到点A',∴A'的坐标是(-3-4,-2+5),即(-7,3).)5.-15(点拨:将点A向右平移2个单位长度,纵坐标不变,横坐标增加2,此时点的坐标为(3,-3),再向下平移2个单位长度,横坐标不变,纵坐标减2,此时的坐标为(3,-5),即点B坐标为(3,-5),∴a=3,b=-5,∴ab=3×(-5)=-15.)6.(1)B(2)D(3)A(点拨:先分别找到A',B'的位置,再观察它们之间的距离.)(4)D7.D(点拨:逆向思考,把点(-3,2)先向右平移5个单位长度,再向下平移3个单位长度可得到A点坐标.)8.A(点拨:将平移后各点横坐标加4,纵坐标减1,可得到平移前的点的坐标分别是:(2+4,1-1),(-1+4,3-1),(4+4,-5-1),即(6,0),(3,2),(8,-6).)9.A(点拨:由图形知点P的坐标为P(-4,-1),由平移规律得平移后P点的坐标是(-4+2,-1-3)即(-2,-4).故选A.)10.(5,4)(点拨:左眼坐标由(-4,2)到(3,4)是向右平移7个单位长度,又向上平移2个单位长度,右眼由(-2,2)作同样的平移得坐标为(5,4).)11.7(点拨:因为三角形OAB的顶点B的坐标为(4,0),所以OB=4,所以OC=OB-CB=4-1=3,因此平移的距离为3.因为把三角形OAB沿x轴向右平移得到三角形CDE,所以CE=OB=4,所以OE=OC+CE=3+4=7.)12.2(点拨:∵A,B的坐标分别为(1,0),(0,2),若将线段AB平移至A1B1,A1,B1的坐标分别为(2,a),(b,3),可知线段AB向右平移了1个单位长度,向上平移了1个单位长度,则a=0+1=1,b=0+1=1,则a+b=1+1=2.)13.可由ABCD向左平移7个单位长度,向上平移7个单位长度得到.各对应点的坐标横坐标减7,纵坐标加7.14.(4,2)(点拨:O与D是一对对应点,因此平移距离为OD=OB-DB=4-1=3,因此平行规律为向右平移3个单位长度,所以A(1,2)的对应点C的坐标为(4,2).)15.(1)A'(4,0),B'(1,3),C'(2,-2)(2)三角形ABC向右平移5个单位长度,再向下平移2个单位长度(或先下平移2个单位长度,再向右平移5个单位长度)即可得到三角形A'B'C'.(3)616.A(4,3),D(-4,-3),B(3,1),E(-3,-1),C(1,2),F(-1,-2);N(-x,-y)。
人教版七年级下第七章平面直角坐标系(用坐标表示平移)同步练习题含解析

人教版七年级下第七章平面直角坐标系(用坐标表示平移)同步练习题学校:___________姓名:___________班级:___________考号:___________一、填空题1.在平面直角坐标系内,把点A (5,-2)向右平移3个单位,再向下平移2个单位,得到的点B 的坐标为______.2.如图,在平面直角坐标系xOy 中,对正方形ABCD 及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一个实数t ,将得到的点先向右平移a 个单位,再向上平移b 个单位(a >0,b >0),得到正方形A B C D ''''及其内部的点,其中点A ,B 的对应点分别为A ',B '. ①a =__,b =__;①已知正方形ABCD 内部的一个点F 经过上述操作后得到的对应点F '与点F 重合,则点F 的坐标是 __.3.如图,平行四边形ABCD 的顶点A ,B ,C 的位置用数对分别表示为(4,6),(1,3),(5,3),则顶点D 的位置用数对表示为 ________.4.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC 的三个顶点均在格点(网格线的交点)上.以原点O 为位似中心,画出111A B C △,使它与△ABC 的相似比为2,且它与△ABC 在位似中心O 的两侧,并写出点B 的对应点1B 的坐标是______.二、单选题5.如图,平移①ABC 到①BDE 的位置,且点D 在边AB 的延长线上,连接EC ,CD ,若AB =BC ,那么在以下四个结论:①四边形ABEC 是平行四边形;①四边形BDEC 是菱形;①AC DC ⊥;①DC 平分①BDE ,正确的有( )A .1个B .2个C .3个D .4个6.将点P (﹣5,4)先向右平移4个单位长度,再向下平移2个单位长度后的坐标是( ) A .(﹣1,6)B .(﹣9,6)C .(﹣1,2)D .(﹣9,2)7.如图,将ABC 先向右平移3个单位,再绕原点O 旋转180︒,得到A B C ''',则点A 的对应点A '的坐标是( )A .(2,0)B .(2,3)--C .(1,3)--D .(3,1)--8.已知1y =4x y +的平方根为( )A B .C .2 D .±29.在平面直角坐标系中,将四边形格点的横坐标都减去2,纵坐标保持不变,所得图形与原图形相比( ) A .向右平移了2个单位 B .向左平移了2个单位 C .向上平移了2个单位D .向下平移了2个单位10.在平面直角坐标系中,将点A ()21,m 沿着y 轴的正方向向上平移()24+m 个单位后得到点B .有四个点E ()21,-m , F ()224,+m m , M ()21,3+m , N ()21,4m ,一定在线段AB 上的是( ) A .点EB .点FC .点MD .点N11.如图,在平面直角坐标系中,点M 到y 轴的距离为2,到x 轴的距离比到y 轴距离的2倍少1,则点M 的坐标为( )A .()3,2B .()3,2-C .()2,3-D .()2,3- 12.将点P (3,4)向下平移1个单位长度后,落在函数ky x=的图象上,则k 的值为( ) A .12k =B .10k =C .9k =D .8k13.A B C '''∆是由ABC ∆平移得到的,点()1,4A -的对应点为()1,7A ',点()1,1B 的对应点为()3,4B ',则点()4,1C --的对应点C '的坐标为( )A .()6,2-B .()6,4--C .()2,2-D .()2,4--三、解答题14.如图,能否通过平移、轴对称或旋转,由ABC 得到DEC ?15.阅读下列材料:问题:如图(1),已知正方形ABCD中,E、F分别是BC、CD边上的点,且①EAF=45°.解决下列问题:(1)图(1)中的线段BE、EF、FD之间的数量关系是______.(2)图(2),已知正方形ABCD的边长为8,E、F分别是BC、CD边上的点,且①EAF =45°,AG①EF于点G,求①EFC的周长.参考答案:1.(8,-4)【分析】直接利用平移中点的变化规律求解即可.【详解】解:原来点的横坐标是5,纵坐标是-2,向右平移3个单位,再向下平移2个单位得到新点的横坐标是5+3=8,纵坐标为-2-2=-4. 则点B 的坐标为(8,-4). 故答案为:(8,-4).【点睛】本题主要考查了坐标与图形变化-平移,平移中点的变化规律:左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加. 2.12##0.5 2 (1,4)【分析】首先根据点A 到A ',B 到B '的点的坐标可得方程组3102t a t b -+=-⎧⎨⨯+=⎩,3202t a t b +=⎧⎨⨯+=⎩,解可得t 、a 、b 的值,设F 点的坐标为(x ,y ),点F '点F 重合可列出方程组,再解可得F 点坐标.【详解】解:①由点A 到A ',可得方程组3102t a t b -+=-⎧⎨⨯+=⎩; 由B 到B ',可得方程组3202t a t b +=⎧⎨⨯+=⎩,解得12122t a b ⎧=⎪⎪⎪=⎨⎪=⎪⎪⎩,故答案为:12,2①设F 点的坐标为(x ,y ),点F '点F 重合得到方程组1122122x x y y ⎧+=⎪⎪⎨⎪+=⎪⎩,解得14x y =⎧⎨=⎩,即F (1,4).故答案为:(1,4).【点睛】此题主要考查了二元一次方程组的应用,关键是正确理解题意,根据点的坐标列出方程组. 3.(8,6)【分析】根据平行四边形的性质:对边平行且相等,得出点的平移方式,解答即可. 【详解】解:∵平行四边形ABCD 的顶点A ,B ,C 的位置用数对分别表示为(4,6),(1,3),(5,3),由A ,B 坐标可得B 向右平移3个单位,向上平移3个单位,可以得到点A ①点D 可由点C 向右平移3个单位,向上平移3个单位得到, ∵点C 坐标为(5,3) 则点D 坐标为(8,6); 故答案为:(8,6).【点睛】此题考查了坐标与图形,涉及了平行四边形的性质以及点的平移,掌握平行四边形的性质以及点的平移规律是解题的关键. 4.图见解析,点1B 的坐标是(-4,-2)【分析】直接利用位似图形的性质画出三角形顶点的对应点,再顺次连接即可画出图形,根据点1B 的位置写出坐标即可.【详解】解:如图所示:111A B C △就是所要求画的,点B 的对应点1B 的坐标是(-4,-2), 故答案为:(-4,-2).【点睛】此题主要考查了位似变换,正确得出对应点位置是解题关键. 5.D【分析】利用平移的性质、平行四边形的判定、菱形的判定与性质逐项判断即可. 【详解】解:①平移①ABC 到①BDE 的位置,且点D 在边AB 的延长线上, ①AD CE AC BE ∥,∥, ①四边形ABEC 是平行四边形, 故①正确;①平移①ABC 到①BDE 的位置, ①AB =BD=CE ,BC =DE , ①AB =BC ,①AB =BD=CE =BC =DE , ①四边形BDEC 是菱形, 故①正确;①四边形BDEC 是菱形, ①BE CD ⊥, ①AC BE ,AC CD ∴⊥, 故①正确;①四边形BDEC 是菱形, ①DC 平分①BDE , 故①正确; ①正确的有4个. 故选D .【点睛】本题主要考查了平移的性质、平行四边形的判定、菱形的判定与性质. 6.C【分析】直接利用平移中点的变化规律求解即可.【详解】将点()54P ﹣,先向右平移4个单位长度,再向下平移2个单位长度后的坐标是()5442+﹣,﹣,即()12﹣,, 故选:C .【点睛】本题主要考查了坐标与图形的变化-平移,在平面直角坐标系中,图形的平移与图形上某点的平移相同,平移点的变化规律是:横坐标右移加、左移减;纵坐标上移加、下移减. 7.C【分析】先画出平移后的图形,再利用旋转的性质画出旋转后的图形即可求解. 【详解】解:先画出①ABC 平移后的①DEF ,再利用旋转得到①A 'B 'C ', 由图像可知A '(-1,-3), 故选:C .【点睛】本题考查了图形的平移和旋转,解题关键是掌握绕原点旋转的图形的坐标特点,即对应点的横纵坐标都互为相反数. 8.B【分析】根据二次根式有意义列不等式组410140x x -≥⎧⎨-≥⎩,求出14x =与1y =,再求代数式的值,然后求平方根即可.【详解】解:410140x x -≥⎧⎨-≥⎩,解得14x =, 当14x =时,1y =, ①144124x y +=⨯+=,①4x y +的平方根为: 故选B .【点睛】本题考查二次根式有意义的条件,代数式的值,平方根,掌握二次根式有意义条件,代数式的值,平方根是解题关键.9.B【分析】根据平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,可得答案.【详解】解:在平面直角坐标系中,将四边形格点的横坐标都减去2,纵坐标保持不变,所得图形与原图形相比向左平移了2个单位.故选:B.【点睛】此题主要考查了坐标与图形变化﹣平移,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.10.C【分析】根据平移的过程以及四个点的坐标进行分析比较即可判断.【详解】解:①将A(1,m2)沿着y的正方向向上平移m2+4个单位后得到B点,①B(1,2m2+4),①m2≥0,①2m2+4>0,①线段AB在第一象限,点B在点A上方,且与y轴平行,距离y轴1个单位,因为点E(1,-m2)在点A下方,当m=0时,E点可以跟A点重合,点E不一定在线段AB 上.点F(m2+4,m2)距离y轴(m2+4)个单位,不在线段AB上;点M(1,m2+3)在点A上方,且距离y轴1个单位,在线段AB上;点N(1,4m2)是将A沿着y的正方向向上平移3m2个单位后得到的,不一定在线段AB上,有可能在线段AB延长线上.所以一定在线段AB上的是M点.故选:C.【点睛】本题考查了坐标与图形的变化-平移,解决本题的关键是掌握平移的性质.11.D【分析】根据题意得出点M到x轴的距离为2×2-1=3,然后结合图象即可确定点的坐标.【详解】解:①点M到y轴的距离为2,到x轴的距离比到y轴距离的2倍少1,①点M到x轴的距离为2×2-1=3,①点M在第四象限,①M(2,-3),故选:D.【点睛】题目主要考查坐标系中点到坐标轴的距离,理解题意,结合函数图象求解是解题关键.12.C【分析】首先求出P点平移后得到的点的坐标为(3,3),再利用待定系数法把点代入反比例函数关系式,即可求得k的值.【详解】解:点P(3,4)向下平移1个单位长度后得到点(3,3),把(3,3)代入函数kyx中,得k=9,故选C.【点睛】此题主要考查了求反比例函数解析式,根据平移方式求点的坐标,正确求出P点平移后的点的坐标是解题的关键.13.C【分析】直接利用平移中点的变化规律求解即可.【详解】由点A(−1,4)的对应点为A′(1,7)知平移方式为向右平移2个单位、向上平移3个单位,①点C(−4,−1)的对应点C′的坐标为(−2,2),故选C.【点睛】此题考查坐标与图形变化-平移,解题关键在于得到平移的方式.14.左图中①ACB绕着点C顺时针旋转90°能得到①DCE.右图中①ACB绕着点C顺时针旋转90°,再沿着BC翻折,能得到①DCE.【分析】根据旋转以及轴对称的性质解答即可.【详解】解:左图中①ACB绕着点C顺时针旋转90°得到①DCE.右图中①ACB绕着点C顺时针旋转90°,再沿着BC翻折,得到①DCE.【点睛】本题考查了图形的旋转以及对称翻折,熟知旋转以及轴对称的性质是解题的关键.15.(1)EF=BE+DF(2)过程见解析【分析】对于(1),先将①DAF 绕点A 顺时针旋转90°,得到①BAH ,可得①ADF ①①ABH ,再根据全等三角形的性质得AF=AH ,①EAF=①EAH ,然后根据“SAS ”证明①F AE ①①HAE ,根据全等三角形的对应边相等得出答案;对于(2),先根据(1),得①F AE ①①HAE ,可得AG=AB=AD ,再根据“HL ”证明Rt ①AEG ①Rt ①ABE ,得EG=BE ,同理GF=DF ,可得答案.(1)EF=BE+DF .理由如下:如图,将①DAF 绕点A 顺时针旋转90°,得到①BAH ,①①ADF ①①ABH ,①①DAF=①BAH ,AF=AH ,①①EAF=①EAH=45°.①AE=AE ,①①F AE ①①HAE ,①EF=HE=BE+HB ,①EF=BE+DF ;(2)由(1),得①F AE ①①HAE ,AG ,AB 分别是①F AE 和①HAE 的高,①AG=AB=AD=8.在Rt ①AEG 和Rt ①ABE 中,AE AE AG AB =⎧⎨=⎩, ①Rt ①AEG ①Rt ①ABE (HL ),①EG=BE ,同理GF=DF ,①①EFG 的周长=EC+EF+FC=EC+EG+GF+FC=EC+BE+DF+FC=BC+CD=16.【点睛】这是一道关于正方形和旋转的综合题目,考查了旋转的性质,正方形的性质,全等三角形的判定和性质等.。
人教版七年级数学下册7.2.2 用坐标表示平移(同步练习含答案)

7.2.2 用坐标表示平移一、选择题1.将点P(3,-2)先向左平移4个单位长度,再向上平移3个单位长度后得到点Q,则点Q的坐标是( )A.(-1,1)B.(7,1)C.(-1,-5)D.(-1,-2)2.线段AB是由线段PQ平移得到的,点P(-1,3)的对应点为A(4,7),则点Q(-3,1)的对应点B 的坐标是( )A.(2,5)B.(-6,-1)C.(-8,-3)D.(-2,-2)3.如图,A,B的坐标分别为(1,0),(0,2),若将线段AB平移至A1B1,则a-b的值为( )A.1B.-1C.0D.24.将线段AB在坐标系中进行平移,已知A(-1,2),B(1,1),将线段AB平移后,其两个端点的坐标变为A'(-2,1),B'(0,0),则它平移的情况是( )A.向上平移了1个单位长度,向左平移了1个单位长度B.向下平移了1个单位长度,向左平移了1个单位长度C.向下平移了1个单位长度,向右平移了1个单位长度D.向上平移了1个单位长度,向右平移了1个单位长度5.如图,已知△ABC在平面直角坐标系中的位置如图所示,将△ABC先向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是( )A.(5,-2)B.(1,-2)C.(2,-1)D.(2,-2)6.如图,将“笑脸”图标向右平移4个单位,再向下平移2个单位,点P的对应点P'的坐标是( )A.(-1,6)B.(-9,6)C.(-1,2)D.(-9,2)7.将点P(m+2,2m+4)向右平移1个单位到P',且P'在y轴上,那么P'的坐标是( )A.(-2,0)B.(0,-2)C.(1,0)D.(0,1)二、填空题8.点M(4,3)向(填“上”“下”“左”或“右”)平移个单位后落在y轴上;向(填“上”“下”“左”或“右”)平移个单位后落在x轴上.9.(2016黑龙江哈尔滨双城期末)在同一坐标系中,图形a是由图形b向上平移3个单位长度得到的,如果图形a中点A的坐标为(4,-2),则图形b中与点A对应的点A'的坐标为.10.在平面直角坐标系中有一点A(-2,1),将点A先向右平移3个单位,再向下平移2个单位,则平移后点A的坐标为.11.若点A(a-1,a+2)在x轴上,将点A向上平移4个单位长度得点B,则点B的坐标是.12.如图,点A、B的坐标分别为(1,2)、(4,0),将△AOB沿x轴向右平移,得到△CDE,已知DB=1,则点C的坐标为.13.三角形ABC中任意一点P(x0,y0)经平移后的对应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1,若A(-2,3),则A1的坐标为.14.在如图所示的直角坐标系中,△AOB经过平移后得到△A1O1B1(两个三角形的顶点都在格点上),已知在AO上一点P,平移后得到A1O1上一点P1(-3.5,-2),则P点的坐标为.三、解答题15.在平面直角坐标系xOy中,点A的坐标为(0,4),线段MN的位置如图所示,其中点M的坐标为(-3,-1),点N的坐标为(3,-2).(1)将线段MN平移得到线段AB,其中点M的对应点为A,点N的对称点为B.①点M平移到点A的过程可以是:先向平移个单位长度,再向平移个单位长度;②点B的坐标为;(2)在(1)的条件下,若点C的坐标为(4,0),连接AC,BC,求△ABC的面积.16.如图,直角坐标系中,△ABC的顶点都在格点上,其中,点C的坐标为(1,2).(1)填空:点A的坐标是,点B的坐标是;(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C'.请作出△A'B'C',并写出△A'B'C'的三个顶点坐标;(3)求△ABC的面积.答案1. A2. A3. C4. B5. B6. C7. B8.左;4;下;39.(4,1)10.(1,-1)11.(-3,4)12.(4,2)13.(3,6)14.(0.5,1)15.(1)如图,①点M平移到点A的过程可以是:先向右平移3个单位长度,再向上平移5个单位长度.②点B的坐标为(6,3).故为:右;3;上;5;(6,3).(2)如图,S △ABC =6×4-12×4×4-12×2×3-12×6×1=10.16. (1)点A 的坐标是(2,-1),点B 的坐标是(4,3).(2)如图,△A'B'C'为所求作的图形,A'(0,0),B'(2,4),C'(-1,3).(3)△ABC 的面积=3×4-12×2×4-12×3×1-12×3×1=5.。
《用坐标表示平移》练习题(含答案)

《⽤坐标表⽰平移》练习题(含答案)7.2.2 ⽤坐标表⽰平移1.(2014·厦门)在平⾯直⾓坐标系中,已知点O(0,0),A(1,3),将线段OA向右平移3个单位,得到线段O1A1,则点O1的坐标是__________,A1的坐标是__________.2.将点A(-3,1)向右平移5个单位长度,再向上平移6个单位长度,可以得到对应点A′的坐标为__________.3.在平⾯直⾓坐标系中,△ABC的三个顶点的横坐标保持不变,纵坐标都减去2个单位长度,则得到的新三⾓形与原三⾓形相⽐向__________平移了__________个单位长度.4.已知△ABC,若将△ABC平移后得到△A′B′C′,且点A(1,0)的对应点A′的坐标是(-1,0),则△ABC是向__________平移__________个单位得到△A′B′C′.5.在平⾯直⾓坐标系中,已知线段AB的两个端点分别是A(4,-1)、B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2),则点B′的坐标为__________.6.(2014·呼和浩特)已知线段CD是由线段AB平移得到的,点A(-1,4)的对应点为点C(4,7),则点B(-4,-1)的对应点D的坐标为( )A.(1,2)B.(2,9)C.(5,3)D.(-9,-4)7.(2013·泰安改编)在如图所⽰的单位正⽅形⽹格中,△ABC经过平移后得到△A1B1C1,已知在AC上⼀点P(2.4,2)平移后的对应点为P1,则P1点的坐标为( )A.(1.4,-1)B.(1.5,2)C.(-1.6,-1)D.(2.4,1)8.如图所⽰,在△ABC中,任意⼀点M(x0,y0)经平移后对应点为M1(x0-3,y0-5),将△ABC作同样平移,得到△A1B1C1,求△A1B1C1的三个顶点的坐标.9.如图所⽰,三⾓形ABC三点坐标分别为A(-3,4),B(-4,1),C(-1,2).(1)说明三⾓形ABC 平移到三⾓形A 1B 1C 1的过程,并求出点A 1,B 1,C 1的坐标;(2)由三⾓形ABC 平移到三⾓形A 2B 2C 2⼜是怎样平移的?并求出点A 2,B 2,C 2的坐标.10.在坐标平⾯内描出点A(2,0),B(4,0),C(-1,0),D(-3,0).(1)分别求出线段AB 中点,线段AC 中点及线段CD 中点的坐标,则线段AB 中点的坐标与点A,B 的坐标之间有什么关系?对线段AC 中点和点A,C 及线段CD 中点和点C,D 成⽴吗?(2)已知点M(a,0),N(b,0),请写出线段MN 的中点P 的坐标.参考答案1.(3,0) (4,3)2.(2,7)3.下 24.左 25.(-5,4)6.A7.C8.由M(x 0,y 0)平移后变为M 1(x 0-3,y 0-5)得到A 1(0-3,5-5),B 1(-1-3,2-5),C 1(5-3,1-5),即A 1(-3,0),B 1(-4,-3),C 1(2,-4).9.(1)三⾓形ABC 向下平移7个单位得到三⾓形A 1B 1C 1.A 1(-3,-3),B 1(-4,-6),C 1(-1,-5).(2)三⾓形ABC 向右平移6个单位,再向下平移3个单位得三⾓形A 2B 2C 2.A 2(3,1),B 2(2,-2),C 2(5,-1).10.(1)线段AB 中点的坐标为(242+,0),即(3,0);对AC 中点和点A,C 及线段CD 中点和点C,D 都成⽴. (2)线段MN 的中点P 的坐标为(2a b +,0)。
人教版数学七年级下册:7.2.2 用坐标表示平移 同步练习(附答案)

7.2.2 用坐标表示平移1.在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是( ) A.(3,0) B.(1,2)C.(5,2) D.(3,4)2.将点A(-2,-3)向左平移3个单位长度得到点B,则点B的坐标是( )A.(1,-3) B.(-2,0)C.(-5,-3) D.(-2,-6)3.在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是.4.平面直角坐标系中,将三角形各点的纵坐标都减去-3,横坐标保持不变,所得图形与原图形相比( )A.向上平移了3个单位长度B.向下平移了3个单位长度C.向右平移了3个单位长度D.向左平移了3个单位长度5.如图,如果将三角形ABC向右平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为( )A.(5,1)B.(1,1)C.(7,1)D.(3,3)6.如图,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,点P的对应点P′的坐标是( )A.(-1,6)B.(-9,6)C.(-1,2)D.(-9,2)7.线段CD是由线段AB平移得到的,点A(-2,3)的对应点为C(3,-2),则点B(-1,-2)的对应点D的坐标为( )A.(4,-7) B.(-2,-7) C.(4,-2) D.(-7,4)8.如图所示:(1)请写出在直角坐标系中的房子的A,B,C,D,E,F,G的坐标;(2)小影想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图形,并写出平移后7个对应点的坐标.9.已知坐标平面内的点A(-2,5),若将平面直角坐标系先向右平移3个单位长度,再向上平移4个单位长度,则点A在平移后的坐标系中的坐标是.10.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是( )A.(2,5) B.(-8,5)C.(-8,-1) D.(2,-1)11.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为( )A.(a-2,b+3)B.(a-2,b-3)C.(a+2,b+3)D.(a+2,b-3)12.点P(m+2,2m+1)向右平移1个单位长度后,正好落在y轴上,则m=.13.如图所示,三角形ABC三点坐标分别为A(-3,4),B(-4,1),C(-1,2).(1)说明三角形ABC平移到三角形A1B1C1的过程,并求出点A1,B1,C1的坐标;(2)由三角形ABC平移到三角形A2B2C2又是怎样平移的?并求出点A2,B2,C2的坐标.14.如图,把三角形ABC向上平移3个单位长度,再向右平移2个单位长度,得到三角形A′B′C′.(1)在图中画出三角形A′B′C′;(2)写出点A′,B′的坐标;(3)求三角形A′B′C′的面积;(4)在y轴上是否存在一点P,使得三角形BCP与三角形ABC面积相等?若存在,请直接写出点P的坐标;若不存在,说明理由.15.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一实数a,将得到的点先向右平移m个单位长度,再向上平移n个单位长度(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为点A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.7.2.2 用坐标表示平移1.在平面直角坐标系中,将点P(3,2)向下平移2个单位长度得到的点的坐标是(A) A.(3,0) B.(1,2)C.(5,2) D.(3,4)2.将点A(-2,-3)向左平移3个单位长度得到点B,则点B的坐标是(C)A.(1,-3) B.(-2,0)C.(-5,-3) D.(-2,-6)3.在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是(1,1).4.平面直角坐标系中,将三角形各点的纵坐标都减去-3,横坐标保持不变,所得图形与原图形相比(A)A.向上平移了3个单位长度B.向下平移了3个单位长度C.向右平移了3个单位长度D.向左平移了3个单位长度5.如图,如果将三角形ABC向右平移2格得到三角形A′B′C′,则顶点A′的位置用数对表示为(A)A.(5,1) B.(1,1)C.(7,1) D.(3,3)6.如图,将“笑脸”图标向右平移4个单位长度,再向下平移2个单位长度,点P的对应点P′的坐标是(C)A.(-1,6) B.(-9,6) C.(-1,2)7.线段CD是由线段AB平移得到的,点A(-2,3)的对应点为C(3,-2),则点B(-1,-2)的对应点D的坐标为(A)A.(4,-7) B.(-2,-7) C.(4,-2) D.(-7,4)8.如图所示:(1)请写出在直角坐标系中的房子的A,B,C,D,E,F,G的坐标;(2)小影想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图形,并写出平移后7个对应点的坐标.解:(1)A(2,3),B(6,5),C(10,3),D(3,3),E(9,3),F(3,0),G(9,0).(2)图略.向下平移3个单位长度,即所有点的纵坐标减去3,所以平移后7个对应点的坐标依次为(2,0),(6,2),(10,0),(3,0),(9,0),(3,-3),(9,-3).9.已知坐标平面内的点A(-2,5),若将平面直角坐标系先向右平移3个单位长度,再向上平移4个单位长度,则点A在平移后的坐标系中的坐标是(-5,1).10.在平面直角坐标系中,将点A(x,y)向左平移5个单位长度,再向上平移3个单位长度后与点B(-3,2)重合,则点A的坐标是(D)A.(2,5) B.(-8,5)C.(-8,-1) D.(2,-1)11.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为(D)A.(a-2,b+3) B.(a-2,b-3) C.(a+2,b+3)D .(a +2,b -3)12.点P(m +2,2m +1)向右平移1个单位长度后,正好落在y 轴上,则m =-3. 13.如图所示,三角形ABC 三点坐标分别为A(-3,4),B(-4,1),C(-1,2).(1)说明三角形ABC 平移到三角形A 1B 1C 1的过程,并求出点A 1,B 1,C 1的坐标; (2)由三角形ABC 平移到三角形A 2B 2C 2又是怎样平移的?并求出点A 2,B 2,C 2的坐标. 解:(1)三角形ABC 向下平移7个单位长度得到三角形A 1B 1C 1. A 1(-3,-3),B 1(-4,-6),C 1(-1,-5).(2)三角形ABC 向右平移6个单位长度,再向下平移3个单位长度得到三角形A 2B 2C 2. A 2(3,1),B 2(2,-2),C 2(5,-1).14.如图,把三角形ABC 向上平移3个单位长度,再向右平移2个单位长度,得到三角形A ′B ′C ′.(1)在图中画出三角形A ′B ′C ′; (2)写出点A ′,B ′的坐标; (3)求三角形A ′B ′C ′的面积;(4)在y 轴上是否存在一点P ,使得三角形BCP 与三角形ABC 面积相等?若存在,请直接写出点P 的坐标;若不存在,说明理由.解:(1)如图所示.(2)A ′(0,4),B ′(-1,1). (3)S 三角形A ′B ′C ′=12×4×3=6.(4)存在.设三角形BCP 的边BC 上的高为h , ∵三角形ABC 的面积和三角形BCP 的面积相等, ∴12×4×h =6,解得h =3. ∵点P 在y 轴上,∴点P 的坐标是(0,1)或(0,-5).15.如图,在平面直角坐标系xOy 中,对正方形ABCD 及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一实数a ,将得到的点先向右平移m 个单位长度,再向上平移n 个单位长度(m>0,n>0),得到正方形A ′B ′C ′D ′及其内部的点,其中点A ,B 的对应点分别为点A ′,B ′.已知正方形ABCD 内部的一个点F 经过上述操作后得到的对应点F ′与点F 重合,求点F 的坐标.解:易知AB =6,A ′B ′=3, ∴a =12.由(-3)×12+m =-1,得m =12. 由0×12+n =2,得n =2.设F(x ,y),变换后F ′(ax +m ,ay +n). ∵F 与F ′重合, ∴ax +m =x ,ay +n =y. ∴12x +12=x ,12y +2=y. 解得x =1,y =4. ∴点F 的坐标为(1,4).。
人教版七年级下第七章平面直角坐标系(用坐标表示平移)同步练习题含答案和解析

人教版七年级下第七章平面直角坐标系(用坐标表示平移)同步练习题学校:___________姓名:___________班级:___________考号:___________一、填空题1.如图,在平面直角坐标系中,动点P 从原点O 出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点()11,1P --;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点2P ;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点3P ;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点4P ,…,按此作法进行下去,则点2021P 的坐标为___________.2.如图,四边形ABCD 为平行四边形,则点B 的坐标为________.3.在平面直角坐标系中,点A ,B 的坐标分别为(1,0),(0,2),若将线段AB 平移到A 1B 1,点A 1,B 1的坐标分别为(2,a ),(b ,3),则a 2-2b 的值为______.4.如图,在平面直角坐标系中,P 与x 轴相切于原点O ,平行于y 轴的直线交P 于M ,N 两点.若点M 的坐标是(2,1)-,则点N 的坐标是__.二、单选题5.如图,点I 为ABC 的内心,4AB =,3AC =,2BC =,将ACB ∠平移使其顶点与I 重合,则图中阴影部分的周长为( )A .4.5B .4C .3D .56.在平面直角坐标系中,把点()3,2P -P '的坐标为( )A .(3,2--B .(3,2-+C .(32)-D .(32)-+ 7.如图,点()2,1A ,将线段OA 先向上平移2个单位长度,再向左平移3个单位长度,得到线段''O A ,则点A 的对应点'A 的坐标是( )A .()3,2-B .()0,4C .()1,3-D .()3,1-8.当x =1,代数式2x +2x +1的值是( )A .-4B .2C .4D .09.在平面直角坐标系中,将四边形格点的横坐标都减去2,纵坐标保持不变,所得图形与原图形相比( )A .向右平移了2个单位B .向左平移了2个单位C .向上平移了2个单位D .向下平移了2个单位10.如图,在平面直角坐标系中,已知点()2,1M ,()1,1N -,平移线段MN ,使点M 落在点()1,2M '-处,则点N 对应的点N '的坐标为( )A .()2,0-B .()0,2-C .()1,1-D .()3,1-- 11.如图,方格纸上有M ,N 两点,若以N 为原点建立平面直角坐标系,则点M 的坐标为(3,4);若以M 点为原点建立平面直角坐标系,则点N 的坐标为( )A .(-3,-4)B .(4,0)C .(0,-2)D .(2,0)12.已知()2M m -,为反比例函数6y x=-的图象上的一点,若将这个反比例函数的图象向右平移4个单位,则点M 的对应点的坐标为( )A .()23-,B .()21--,C .()23,D .()27, 13.A B C '''∆是由ABC ∆平移得到的,点()1,4A -的对应点为()1,7A ',点()1,1B 的对应点为()3,4B ',则点()4,1C --的对应点C '的坐标为( ) A .()6,2- B .()6,4-- C .()2,2- D .()2,4--三、解答题14.图,△ABC 是边长为 2 的等边三角形,将△ABC 沿直线 BC 平移到△DCE 的位置,连接 BD ,(1)△ABC 平移的距离为 ;(2)求 BD 的长.15.如图,点E 是正方形ABCD 内的一点,连接AE 、BE 、CE ,将ABE △绕点B 顺时针旋转90︒到CBF 的位置,连接EF ,EF 的长为(1)求BF 的长;(2)若1,3AE EC ==,求AEB ∠的度数.参考答案:1.(1011,1011)--【分析】先根据点坐标的平移变换规律求出点2345,,,P P P P 的坐标,再归纳类推出一般规律即可得.【详解】解:由题意得:2(12,12)P -+-+,即2(1,1)P ,3(13,13)P --,即3(2,2)P --,4(24,24)P -+-+,即4(2,2)P ,5(25,25)P --,即5(3,3)P --,观察可知,点1P 的坐标为(1,1)--,其中1211=⨯-,点3P 的坐标为(2,2)--,其中3221=⨯-,点5P 的坐标为(3,3)--,其中5231=⨯-,归纳类推得:点21n P -的坐标为(,)n n --,其中n 为正整数,2021210111=⨯-,∴点2021P 的坐标为(1011,1011)--,故答案为:(1011,1011)--.【点睛】本题考查了点坐标的平移变换规律、点坐标的规律探索,正确归纳类推出一般规律是解题关键.2.()2,1--【分析】根据平行四边形的性质以及点的平移即可得出结论. 【详解】解:四边形ABCD 为平行四边形,∴DA CB ∥,即将D 点平移到A 的过程与将C 点平移到B 的过程保持一致,将D 点平移到A 的过程是::134x --=-(向左平移4各单位长度);:220y -=(上下无平移);∴将C 点平移到B 的过程按照上述一致过程进行得到()24,1B --,即()2,1B --, 故答案为:()2,1--.【点睛】本题考查平行四边形的性质及点的平移,掌握点的平移的代数表示是解决问题的关键.3.-1【分析】根据点A 和点B 的坐标以及对应点的坐标确定出平移的方法,从而求出a 、b 的值,再代入代数式进行计算即可.【详解】解:∵A (1,0),A 1(2,a ),B (0,2),B 1(b ,3),∵平移方法为向右平移1个单位,向上平移1个单位,∵a =0+1=1,b =0+1=1,∵a 2-2b =1²-2×1=-1;故答案为:-1.【点睛】本题考查了平面直角坐标系-点的平移,根据题意得出平移方式是解本题的关键. 4.(2,4)-【分析】首先过点P 作P A ∵MN 于点A ,由垂径定理即可求得AM =12MN ,易证得四边形ABOP 是矩形,即可得AB =OP ,P A =OB =2,设OP =a ,在Rt △P AM 中,由PM 2=AM 2+P A 2,可得方程a 2=(a ﹣1)2+4,继而可求得答案.【详解】解:如图,过点P 作PA MN ⊥于点A ,∵12AM MN =,在平面直角坐标系中,P 与x 轴相切于原点O ,平行于y 轴的直线交P 于M ,N 两点,设MN 交x 轴于点B ,∵90POB PAB ABO ∠=∠=∠=︒,∵四边形ABOP 是矩形,∵AB OP =,2PA OB ==,设OP a =,则PM OP a ==,∵点M 的坐标是(2,1)-,∵BM =1,∵1AM a =-,在Rt ΔPAM 中,222PM AM PA =+,即22(1)4a a =-+,解得: 2.5a =,∵ 1.5AM =,∵23MN AM ==,∵134BN BM MN =+=+=,∵点N 的坐标为:(2,4)-.故答案为:(2,4)-.【点睛】此题考查了垂径定理、点与坐标的关系以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.5.B【分析】连接AI 、BI ,因为三角形的内心是角平分线的交点,所以AI 是CAB ∠的平分线,由平行的性质和等角对等边可得:AD DI =,同理BE EI =,所以图中阴影部分的周长就是边AB 的长.【详解】解:连接AI 、BI ,点I 为ABC ∆的内心,AI ∴平分CAB ∠,CAI BAI ∴∠=∠,由平移得://AC DI ,CAI AID ∴∠=∠,BAI AID ∴∠=∠,AD DI ∴=,同理可得:BE EI =,DIE ∴∆的周长4DE DI EI DE AD BE AB =++=++==,即图中阴影部分的周长为4,故选:B .【点睛】本题考查了三角形内心的定义、平移的性质及角平分线的定义等知识,熟练掌握三角形的内心是角平分线的交点是关键.6.C【分析】根据点坐标的平移变换规律即可得.【详解】解:由点坐标的平移变换规律得:点P'的坐标为(32)P-,故选:C.【点睛】本题考查了点坐标的平移变换规律,熟练掌握点坐标的平移变换规律是解题关键.7.C【分析】根据点向上平移a个单位,点向左平移b个单位,坐标P(x,y)⇒P(x,y+a)⇒P(x+a,y+b),进行计算即可.【详解】解:∵点A坐标为(2,1),∵线段OA向上平移2个单位长度,再向左平移3个单位长度,点A的对应点A′的坐标为(2-3,1+2),即(-1,3),故选C.【点睛】此题主要考查了坐标与图形的变化--平移,关键是掌握横坐标,右移加,左移减;纵坐标,上移加,下移减.8.C【分析】直接把x=1代入计算即可.【详解】解:当x=1时,2x+2x+1=21+2×1+1=1+2+1=4.故选:C.【点睛】本题考查代数式求值,有理数的混合运算,掌握有理数的运算法则和运算顺序是解决本题的关键.9.B【分析】根据平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减,可得答案.【详解】解:在平面直角坐标系中,将四边形格点的横坐标都减去2,纵坐标保持不变,所得图形与原图形相比向左平移了2个单位.故选:B .【点睛】此题主要考查了坐标与图形变化﹣平移,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.10.A【分析】根据()2,1M 平移后得到()1,2M '-,确定其平移规律是向左平移3个单位,后向上平移1个单位,根据规律确定点N 的平移坐标即可.【详解】∵()2,1M 平移后得到()1,2M '-,∵其平移规律是向左平移3个单位,后向上平移1个单位,∵()1,1N -,∵平移后的坐标为(1-3,-1+1)即()2,0-,故选A .【点睛】本题考查了坐标系中点的坐标平移,准确确定平移方向和平移距离,并熟记左减右加,上加下减的计算法则是解题的关键.11.A【解析】略12.C【分析】将()2M m -,代入6y x=-,即可求得M 点坐标,再根据平移方式即得出答案. 【详解】将()2M m -,代入6y x =-,得:632m =-=-, 即()23M -,. 将这个反比例函数的图象向右平移4个单位,即图象上的点也向右平移4个单位,∵点M 的对应点的坐标为(-2+4,3),即(2,3).故选C .【点睛】本题考查反比例函数图象上点的坐标特征,反比例函数图象的平移.掌握反比例函数图象上的点的坐标满足其解析式是解题关键.13.C【分析】直接利用平移中点的变化规律求解即可.【详解】由点A(−1,4)的对应点为A′(1,7)知平移方式为向右平移2个单位、向上平移3个单位,∵点C(−4,−1)的对应点C′的坐标为(−2,2),故选C.【点睛】此题考查坐标与图形变化-平移,解题关键在于得到平移的方式.14.(1)2(2)BD 的长为【分析】(1)根据平移的性质,即可求出平移距离;(2)首先证得BDE 是以BE 为斜边的直角三角形,利用勾股定理即可进行求值. (1)解:由题意可知,ABC 平移的距离为:BC =2,故答案为:2;(2)∵=60BCA ECD ∠=∠︒,∵=60ACD ∠︒,∵=120BCD ∠︒,∵=BC DC ,∵=30CBD ∠︒,∵=60E ∠︒,∵=90BDE ∠︒,∵BDE 是以BE 为斜边的直角三角形,∵由勾股定理得:222BE BD DE =+,答案第7页,共7页即:BD∵BD的长为【点睛】本题主要考查了平移的性质,以及勾股定理的应用,证出对应的直角三角形是解题的关键.15.(1)BF =2(2)∵AEB =135°【分析】(1)由旋转的性质得到∵BEF 为等腰直角三角形,根据勾股定理即可求出BF 的长; (2)根据AE =1,可得1CF AE ==,根据勾股定理逆定理(22221CF EF +=+=9=32=CE 2得出90EFC ∠=︒,根据等腰直角三角形可求45EFB ∠=︒,再求135BFC EFB EFC ∠=∠+∠=︒,根据旋转性质,可得135AEB BFC ∠=∠=︒即可. (1)解:∵∵ABE 绕点B 顺时针旋转90°得到∵CBF ,∵BE =BF ,∵EBF =∵ABC =90°∵∵BEF 为等腰直角三角形,设 BE =BF =x ,则x 2+x 2=(2 ,解得: x =2;(2)解:∵∵ABE 绕点B 顺时针旋转90°得到∵CBF ,∵∵AEB = ∵BFC ,AE =CF =1,在∵CEF 中,EF,CF =1,EC =3,∵CF 2+EF 2=12+()2=9,CE 2=9,∵CF 2+EF 2=CE 2,∵∵CEF 为直角三角形,∵EFC =90°,∵∵BFC =∵BFE +∵CFE =135°,∵∵AEB =135°.【点睛】本题考查正方形的性质,旋转性质,等腰直角三角形判定与性质,勾股定理逆定理,掌握,三角形旋转性质,等腰直角三角形判定与性质,勾股定理逆定理是解题关键.。
7.2.2用坐标表示平移(2)

欢 迎 指 导
(一) 回顾反思: 1、本节课还有哪些不清楚的问题? 2、谈谈本节课你有哪些收获?
(D) ( 1,4) (3,1) (-2,-1)
y
A(-1,4)4
3
2
1 B(1,1)
-5 -4 -3 -2 -1 0 1 2 3 4 x
C(-4,-1)
-1 -2
-3
如图,将⊿ABC向上平移3个单位长度,则平移后三个
顶点A、B、C的坐标分别是( )
C
(A) ( -1,7) (4,1) (-4,2)
(B) ( 2,4) (1,4) (-4,2)
(C) ( -1,7) (1,4) (-4,2)
(D) ( -1,7) (4,y1) (2,-4)
A(-1,4)4
3
2
1 B(1,1)
-5 -4 -3 -2 -1 0 1 2 3 4 x
C(-4,-1)
-1 -2
-3
y
如图,将⊿ABC向右
A(-1,4)4
问题1:
将坐标为 A(0,0),B(5,4), C(3,0),D(5,1),E(5,-1),F(3, 0),G(4,-2),的点用线 段依次连结起来, 观察所得图形, 你看它像什么?
y
B
4
3
2
D
1A
C
-5 -4 -3 -2 -1 0 1 2 3F 4
x
-1
E
-2
G
-3
-4
问题2:
如果将这个图形中的点 A(0,0),B(5,4), C(3,0),D(5,1),E(5,-1),F(3,0),G(4,-2), 作如下变化:纵坐标不变,横坐标分别减去5, 再将所得各点用线段依次连结起来,所得图案 与原图案相比有什么变化?
7.1.2《用坐标表示平移》同步练习题(3)及答案

4
4
6.如答图:
点拨:首先确定出平面直角坐标系的原点,x
轴、y 轴的正方向.
7.解:(1)平移后的小船如答图所示.
(2)如答图,点 A′与点 A 关于直线 L 成轴对称,连接 A′B 交直线 L 于点 P, 则点 P 为所求.
数学世界 小华用一种伸缩性很小的细线按交通网的形状和各条道路的长短比例,•编织成一副真
何图形割补的方法,同学们想一想,这是为什么?
4.(3,-2);(-3,-2);x 对称点是(a,-b),关于 y 轴的对称点是(-a,b),关
于原点的对称点是(-a,-b).
5.(1)(16,3);(32,0)
点拨:A(1,3),A1(2,3),A2(4,3),A3(8,3),其纵坐标都为 3,
3.(创新题)在直角坐标系中,A(3,4),B(-1,-2),O 为原点,求三 角形 AOB的面积.
爸爸出差前,留给小华一道题:
下图是某地区的交通网,其中小圈代表城镇,小圈间的连线代表道路,连线旁的 a 表
示该段道路的千米数,请你选择一条,从 A 到 B 的最短线路.
1
小华绞尽脑汁,想了一天还是没有眉目.吃过晚饭,他信步走进小树林,东瞅瞅,•西 瞧瞧,一眼落到一张硕大的蜘蛛网上,这张蜘蛛网,多像那张交通图啊!,突然,一只小 虫撞到网上,小虫奋力挣扎,于是便不断地拉紧连到网中心的最短的那根丝,•蜘蛛沿着那 根丝,迅速出击,抓住了小虫,小华若有所悟,口里直嚷嚷:“有了!有了!”很快地解 出了这道题,你知道小华是用什么方法解决这道题的吗?
7.1.2《用坐标表示平移》同步练习题(3) 知识点: P(x ,y)向右平移 a 个单位,对应点 P’(x+a,y) P(x ,y)向左平移 a 个单位,对应点 P’(x-a,y) P(x ,y)向上平移 a 个单位,对应点 P’(x,y+a) P(x ,y)向下平移 a 个单位,对应点 P’(x,y-a) 同步练习:
人教版七年级数学下册《7.2.2用坐标表示平移》同步练习【含答案】

人教版七年级数学下册《7.2.2用坐标表示平移》同步练习【含答案】1. 点M (-2,5)向右平移3个单位长度,所得对应点的坐标为 ;点N (4,6)向上平移6个,所得对应点的坐标为 .2. 在平面直角坐标系内,如果把平行四边形ABCD 的四个顶点的横坐标都减去5,那么所得平行四边形就是把原平行四边形向 平移 个单位长度;如果把平行四边形ABCD 各顶点的纵坐标都加5,那么所得平行四边形就是把原平行四边形向平移 个单位长度.3. 点P (-2,-3)向左平移1个单位长度,再向上平移3个单位长度,则所得到的点的坐标为 .4. 已知△ABC ,A (-3,2),B (1,1),C (-1,-2),现将△ABC 平移,使点A 1到点(1,-2)的位置上,则点B 1、C 1的坐标分别为________,________.5. 将点A 先向右平移4个单位长度,再向上平移6个单位长度,得到点B ,若点B 的坐标为(-6,-8),则点A 的坐标为 .6. 长方形ABCD 四个顶点的坐标分别为A (-2,1),B (-2,-2),C (3,-2),D(3,1).将长方形沿x 轴正方向平移一个单位长度,再沿y 轴正方向平移一个单位长度,则平移后的四个顶点坐标为 .7. 如图,将点A (3,2)向左平移5个单位长度,得到点A 1,请在图上标出这个点,并写出它的坐标.将点A 向下平移4个单位长度,得到点A 2,也请在图中标出这个点,也写出它的坐标.你能判断直线AA 1与x 轴,AA 2与y 轴的位置关系吗?8. 如图,在平面直角坐标系中,已知 点P 和三角形ABC .作三角形PQR , 使三角形PQR 是由三角形ABC 平移 得到的,分别写出平移的过程和点 Q 、R 的坐标.(第 7 题) -4 -5 -3 -2 -1 1 2 2 3 3 1 4 -1 -2 -3x y O ·A B A C (第 8 题) -4 -5 -3 -2 -1 1 2 2 3 314 -1 -2-3xyO ·P用坐标表示平移(2)1. 已知点A (-4,2),B (1,2),则线段AB 的长度是 ( )A .3个单位长度B .4个单位长度C .5个单位长度D .6个单位长度2. 已知点A (-3,-5),B (-3,7),则线段AB 的长度是 ( )A .2个单位长度B .4个单位长度C .12个单位长度D .14个单位长度3. 已知坐标平面内三点D (5,4),E (2,4),F (4,2),那么△DEF 的面积为( )A .3平方单位B .5平方单位C .6平方单位D .7平方单位4.如图,三角形DEF 是三角形ABC 经过某种变换后得到的图形,观察图形分别写出点A 和点D ,点B 和点E ,点C 和点F 的坐标.并根据它们之间的内在联系,试猜想三角形中任意一点P (x ,y )的对应点Q 的坐标是什么?5. 在直角坐标系中,描出点A (1,1),B (-1,-1),C (2,0),并求出△ABC 的面积.6. 如图,四边形ABCD 的四个顶点的位置在平面直角坐标系内,求四边形ABCD 的面积.-2 1 -1 -3 -4 -5 -4 -5 -3 -2 -1 1 2 3 4 5 x y O D A C B (第6题) B A C E O x 1234567 -6-5-4-3-2-1 y 4 3 2 1 -1 -2 -3 -4 D F用坐标表示平移(1)1.(1,5);(4,12) 2.左,5;上,5 3.(-1,0) 4.B 1(5,-3),C 1(3,-6)5.(-10,-14) 6.(-1,2),(-1,-1),(4,-1),(4,2) 7.A 1(-2,2),A 2(3,-2);AA 1∥x 轴,AA 2∥y 轴 8.向上平移3个单位长度,再向右平移6个单位长度,Q (1,0),R (4,0)用坐标表示平移(2)1.C 2.C 3.A 4. A (0,4),D (0,-4),B (-2,0),E (2,0),C (4,-3),F (-4,3);由上述对应点坐标的特点,猜想三角形ABC 中任意一点P (x ,y )的对应点Q 的坐标是(-x ,-y ) 5.2平方单位 6.平方单位 392。
7.2.2 用坐标表示平移 同步练习(含答案)

7.2.2 用坐标表示平移班级:________ 姓名:________ 得分:________一、选择题(每题5分,共25分)1.在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是()A.(-2,6)B.(-2,0)C.(-5,3)D.(1,3)2.将某图形的横坐标都减去2,纵坐标不变,则该图形()A. 向右平移2个单位B. 向左平移2个单位C. 向上平移2个单位D. 向下平移2个单位3.线段CD是由线段AB平移得到的,点A(﹣1.5)的对应点为C(4,8),则点B(﹣4,﹣2)的对应点D的坐标为()A.(﹣9,﹣5)B.(﹣9,1)C.(1,﹣5)D.(1,1)4.已知三角形ABC平移后得到三角形A1B1C1,且A(-2,3),B(-4,-1),C1(m,n),C(m+5,n+3),则A1,B1两点的坐标为()A.(3,6),(1,2)B.(-7,0),(-9,-4)C.(1,8),(-1,4)D.(-7,-2),(0,-9)5.如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是()A.(4,0) B. (5,0) C.(0,5) D.(5,5)第5题图第8题图第10题图二、填空题(每题5分,共25分)6.将点P(-3,4)向下平移3个单位,向左平移2个单位后得到点Q,则点Q的坐标为。
7.三角形ABC的三个顶点A(1,2),B(-1,-2),C(-2,3),将其平移到点A′(-1,-2)处,使A与A′重合,则B、C两点的坐标分别为__________,__________.8.如图,已知A(0,1),B(2,0),把线段AB平移后得到线段CD,其中C(1,a),D(b,1)则a+b = ;9.在平面直角坐标系中,若点M(1,3)与点N(x,3)之间的距离是5,则x的值是.10.如图,在直角坐标系中,右边的蝴蝶是由左边的蝴蝶飞过去以后得到的,左图案中左右翅尖的坐标分别是(-4,2)、(-2,2),右图案中左翅尖的坐标是(3,4),则右图案中右翅尖的坐标是.三、解答题(共50分)11.(10分)如图,在平面网格中每个小正方形的边长为1. (1)线段CD是线段AB经过怎样的平移后得到的?(2)线段AC是线段BD经过怎样的平移后得到的?12.(10分)如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,请画出平移后的图形,并写出△A′B′C′各顶点的坐标.13.(10分)如图,四边形ABCD各个顶点的坐标分别为(-2,8),(-11,6),(-14,0),(0,0).(1)确定这个四边形的面积,你是怎么做的?(2)如果四边形ABCD各个顶点的纵坐标保持不变,横坐标增加2,所得的新四边形的面积是多少?14.(10分)如图,方格纸中每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC 的顶点在格点上.且A (1,﹣4),B (5,﹣4),C (4,﹣1) (1)画出△ABC ; (2)求出△ABC 的面积;(3)若把△ABC 向上平移2个单位长度,再向左平移 4个单位长度得到△A ′B ′C ′,在图中画出△A ′B ′C ′,并写 出B ′的坐标.15.(10分)ABC ∆与C B A '''∆在平面直角坐标系中的位置如图.⑴分别写出下列各点的坐标:A ' ; B ' ;C ' ; ⑵说明C B A '''∆由ABC ∆经过怎样的平移得到: .⑶若点P (a ,b )是ABC ∆内部一点,则平移后C B A '''∆内的对应点P '的坐标为 ; ⑷求ABC ∆的面积.参考答案【解析】先根据点A和对应点C的坐标得到平移的规律为向右平移5个单位,再向上平移3个单位,然后根据此规律把点B进行平移,再写出平移后的对应点D的坐标.解:由于点A(﹣1,5)的对应点为C(4,8),即点A向右平移5个单位,再向上平移3个单位得到点C,因此点B(﹣4,﹣2)向右平移5个单位,再向上平移3个单位得到点D的坐标为(1,1).故选:D.4.B【解析】平面直角坐标系中点的坐标的平移规律:横坐标左减右加,纵坐标上加下减.5.B【解析】跳蚤运动的速度是每秒运动一个单位长度,(0,0)→(0,1)→(1,1)→(1,0)用的秒数分别是1秒,2秒,3秒,到(2,0)用4秒,到(2,2)用6秒,到(0,2)用8秒,到(0,3)用9秒,到(3,3)用12秒,到(4,0)用16秒,依此类推,到(5,0)用35秒.故第35秒时跳蚤所在位置的坐标是(5,0).故选:B.6.(-5,1)【解析】根据题意,点Q的横坐标为:-3-2=-5;纵坐标为4-3=-1;∴点Q的坐标是(-5,1).故答案填:(-5,1).7.(-3,-6),(-4,-1)【解析】平面直角坐标系中点的坐标的平移规律:横坐标左减右加,纵坐标上加下减..8.5【解析】∵两点A(0,1),B(2,0),把线段AB平移后A点对应点是C(1,a),B点对应点是D(b,1),∴线段是向右平移1个单位,再向上平移了1个单位,∴a=1+1=2,b=2+1=3,∴a+b=2+3=5,9.-4或6【解析】点M、N的纵坐标相等,则直线MN在平行于x轴的直线上,根据两点间的距离,可列出等式|x﹣1|=5,从而解得x的值.10.(5,4)【解析】根据左翅尖的坐标的变化规律可得所求坐标.解:∵左图案中左翅尖的坐标是(-4,2),右图案中左翅尖的坐标是(3,4),∴变化规律为横坐标加7,纵坐标加2,∵左图案中右翅尖的坐标是(-2,2),∴右图案中右翅尖的坐标是(5,4),故答案为:(5,4).11. 答案见解析.【解析】(1)将线段AB向右平移3个小格(向下平移4 个小格),再向下平移4个小格(向右平移3个小格),得线段CD.(2)将线段BD向左平移3个小格(向下平移1个小格),再向下平移1个小格(向左平移3个小格),得到线段AC.12. 答案见解析.【解析】解:如图所示:由图可知,A′(4,0),B′(1,3),C′(2,﹣2).13. 答案见解析.【解析】(1)可将这个四边形切割成三个三角形和一个长方形,S=12×3×6+12×9×2+12×2×8+9×6=9+9+8+54=80.(2)横坐标增加2,纵坐标不变,则四边形向右平移2个单位长度,形状和大小都不变,其面积仍是80.14. 答案见解析.【解析】解:(1)如图所示(2)过C作CD⊥AB于D,则S△ABC=AB?CD=×4×3=6;(3)如图所示:B′(1,﹣2).。
人教版七年级数学下册第七章第二节用坐标表示平移复习试题(含答案) (88)

人教版七年级数学下册第七章第二节用坐标表示平移习题(含答案)如图,在直角坐标系中,,,.(1)求的面积;(2)若把向下平移2个单位,再向右平移5个单位得到,请画出并写出的坐标.【答案】(1)7.5;(2),详见解析【解析】【分析】(1)根据直角坐标系首先求出ΔABC的高和底,利用三角形面积公式即可解答;(2)首先画出平移图形,再写出坐标即可.【详解】解:(1)根据直角坐标系知AB=5,AB边上的高为3,∴的面积是:;(2)作图如图所示,∴点的坐标为:【点睛】本题主要考查直角坐标系中图形的平移,熟知点的坐标平移方法是解答的关键.72.已知:如图把向上平移3个单位长度,再向右平移2个单位长度,得到.(1)在图中画出;(2)写出点的坐标:的坐标为______,的坐标为_________;的坐标为________.(3)在轴上是否存在一点P,使得的面积相等?若存在,请求出点P的坐标;若不存在,说明理由.【答案】(1)见解析;(2)(0,4),(−1,1),(3,1);(3)P(0,1)或(0,−5),理由见解析【解析】【分析】(1)根据图形平移的性质画出△A′B′C′即可;(2)根据各点在坐标系中的位置写出各点坐标即可;(3)根据同底等高的三角形面积相等即可得出结论.【详解】(1)A,B,C向上平移3个单位长度,再向右平移2个单位长度得到,,,连接,,,即可得到(2)由图可知,A′(0,4),B′(−1,1),C′(3,1)故答案为:(0,4),(−1,1),(3,1)(3)设P(0,y)∵△BCP与△ABC同底等高∴|y+2|=3,即y+2=3或y+2=−3解得y1=1,y2=−5∴P(0,1)或(0,−5)故答案为:P(0,1)或(0,−5),理由见解析【点睛】本题考查了作平移图形,一般步骤为:确定平移的方向和平移的距离;确定图形的关键点,如三角形、四边形等图形所有的顶点,圆的圆心等;过这些关键点作与平移的方向平行的射线,在射线上截取与平移的距离相等的线段,得到关键点的对应点;通过关键点作出平移后的图形.73.如图,平面直角坐标系中,的顶点都在网格点上,其中点坐标为.(1)填空:点的坐标是__________,点的坐标是________;(2)将先向左平移3个单位长度,再向上平移1个单位长度,画出平移后的;(3)求的面积.【答案】(1),;(2)画图见解析;(3)【解析】【分析】(1)利用点的坐标的表示方法写出A点和B点坐标;(2)利用点的坐标平移规律写出点、、的坐标,然后描点得到;(3)用一个矩形的面积分别减去三个三角形的面积可得到△ABC的面积.【详解】解:(1);(2)如图所示:即为所求;(3).【点睛】此题考查坐标与图形变化——平移,解题关键在于掌握在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.74.如图,每个小正方形的边长为1,△ABC经过平移得到△A′B′C′.根据下列条件,利用网格点和直尺画图:(1)补全△ABC;(2)作出中线CD;(3)画出BC边上的高线AE;(4)△ABC的面积为.【答案】(1)如图所示;见解析;(2)如图所示;见解析;(3)如图所示;见解析;(4)8.【解析】【分析】(1)利用B′,B得到平移规则,找到点A、C,连接A、B、C即可即可补全图形;(2)借助网格,找到AB的中点D,连接CD即可;(3)借助网格,过点A,作AE⊥BC,交线段BC的延长线于点E.(4)利用三角形的面积公式,结合网格计算即可.【详解】(1)如图所示;利用B′,B得到平移规则为向左平移4个单位,向下平移2个单位,分别画出点A′、C′的对应点A、C,连接A、B、C即可;(2)如图所示;(3)如图所示;(4).【点睛】此题主要考查了平移变换及三角形的有关线段和面积公式,熟练运用平移的性质是解题的关键,属于中考常考题型.75.在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的变换得到的?(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请求出三角形DEF的面积S.【答案】(1)图中格点△A′B′C′是由格点△ABC向右平移7个单位长度得到的;(2)5【解析】【分析】(1)直接根据图形平移的性质得到△A′B′C′即可;(2)根据△DEF所在的格点位置写出其坐标,连接GF,再根据三角形的面积公式求解;【详解】解:(1)图中格点△A′B′C′是由格点△ABC向右平移7个单位长度得到的;(2)如果以直线a、b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),则格点△DEF各顶点的坐标分别为D(0,-2),E(-4,-4),F(3,-3),S△DEF=S△DGF+S△GEF=×5×1+×5×1=5.【点睛】本题考查的是作图-平移变换及三角形的面积,熟知图形平移的性质是解答此题的关键.76.将△ABC向右平移3个单位长度,再向上平移2个单位长度,(1)在图上画出对应的三角形A1B1C1;写出点A1的坐标.(2)已知点P是x轴上的动点,求PB的最小值.(3)求出△的面积.【答案】(1)见解析;(2)2;(3)7【解析】【分析】(1)先平移三角形的三个顶点,再画出三角形A1B1C1;(2)直线外一点与直线上各点连接的所有线段中,垂线段最短;(3)利用割补法计算三角形面积.【详解】解:(1)如图所示,三角形A1B1C1即为所求.点A1的坐标为:(2,1)(2)∵点P是x轴上的动点∴当BP⊥x轴时,PB的长度最短,此时PB=2.(3)将△补成矩形ADEF,则【点睛】本题考查了图形的平移、垂线段公理以及割补法,正确画出图形是解决问题的关键.77.如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为_____.【答案】(a﹣2,b+3)【解析】【分析】先利用点A它的对应点A′的坐标特征确定平移方式,然后再根据平移方式写出点P(a,b)平移后的对应点P′的坐标.【详解】解:∵点A(1,﹣1)先向左平移2个单位,再向上平移3和单位得到点A′(﹣1,2),∴线段AB先向左平移2个单位,再向上平移3和单位得到线段A′B′,∴点P(a,b)平移后的对应点P′的坐标为(a﹣2,b+3).故答案为(a﹣2,b+3).【点睛】本题主要考查了坐标与图形的变化--平移,弄清题意、明确平移方式并掌握横坐标、右移加、左移减,纵坐标、上移加、下移减的平移规律是解答本题的关键.78.如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(,)、B(,);(2)求△ABC的面积;(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,画出△A′B′C′,写出A′、B′、C′三个点坐标.【答案】(1)A(2,﹣1)、B(4,3);(2)5;(3)图详见解析,A′(0,0)、B′(2,4)、C′(﹣1,3).【解析】【分析】(1)根据直角坐标系的特点写出对应点的坐标;(2)用△ABC所在的矩形面积减去三个小三角形的面积即可求解;(3)分别将点A、B、C先向左平移2个单位长度,再向上平移1个单位长度,得到点A′、B′、C′,然后顺次连接并写出坐标.【详解】解:(1)A(2,﹣1),B(4,3);(2)S△ABC=3×4﹣×2×4﹣×1×3﹣×3×1=5,故△ABC的面积为5;(3)所作图形如图所示:A′(0,0)、B′(2,4)、C′(﹣1,3).【点睛】本题考查了根据平移变换作图,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.79.如图,△ABC在平面直角坐标系中.(1)写出△ABC各顶点的坐标.(2)把△ABC向上平移2个单位,再向右平移2个单位得△A'B'C',在图中画出△A'B'C',并写出A'、B'、C'的坐标.(3)求出.【答案】(1)A(-1,-1) B(4,2) C(1,3) ;(2) 详见解析,A'(1,1),B'(6,4),C'(3,5);(3)7【解析】【分析】(1)根据各点所在象限的符号和距坐标轴的距离可得各点的坐标;(2)根据平移的规律,把△ABC的各顶点向上平移2个单位,再向右平移2个单位,顺次连接各顶点即为△A′B′C′;直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标;(3)利用△ABC所在的长方形的面积减去四周三个小直角三角形的面积列式计算即可得解.【详解】解:(1)A(-1,-1);B(4,2);C(1,3);(2)如图,A'(1,1),B'(6,4),C'(3,5).(3)SΔABC=5×4−×5×3−×1×3−×2×4=20-7.5-1.5-4=20-13=7.【点睛】用到的知识点为:图形的平移要归结为图形顶点的平移;格点中的三角形的面积通常整理为长方形的面积与几个三角形的面积的差;求点的坐标应根据所在象限确定符号,根据距离原点的水平距离和竖直距离确定具体坐标或者直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标.80.如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为A(﹣2,4),B(﹣5,﹣1),C(0,1),把三角形ABC向右平移2个单位长度,再向下平移4个单位长度后得到三角形A'B'C'.(1)画出三角形ABC和平移后A′B′C′的图形;(2)写出三个顶点A',B',C'的坐标;(3)求三角形ABC的面积.【答案】(1)见解析;(2)(0,0),(﹣3,﹣5),(2,﹣3);(3)9.5【解析】【分析】(1)(2)利用点平移的坐标变换规律写出点A',B',C'的坐标,然后描点得到△ABC和△A′B′C′为所作;(3)用一个矩形的面积分别减去三个三角形的面积去计算三角形ABC的面积.【详解】解:(1)如图,△ABC和△A′B′C′为所作;(2)点A',B',C'的坐标分别为(0,0),(﹣3,﹣5),(2,﹣3);(3)三角形ABC的面积=5×5﹣×2×3﹣×5×3×5×2=9.5.【点睛】本题考查了平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.。
人教版七年级数学下册第七章第二节用坐标表示平移复习试题(含答案) (28)

人教版七年级数学下册第七章第二节用坐标表示平移习题(含答案)如图,已知A(0,1),B(2,0),把线段AB平移后得到线段CD,其中C (1,a),D(b,1)则a+b =_________.【答案】5【解析】试题分析:∵两点A(0,1),B(2,0),把线段AB平移后A点对应点是C(1,a),B点对应点是D(b,1),∵线段是向右平移1个单位,再向上平移了1个单位,∵a=1+1=2,b=2+1=3,∵a+b=2+3=5,考点: 坐标与图形变化-平移92.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从顶点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…按这样的运动规律,经过第2010次运动后,动点P的坐标是_____.【答案】(2010,0)【解析】解:根据动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),∴第4次运动到点(4,0),第5次接着运动到点(5,1),…,∴横坐标为运动次数,经过第2010次运动后,动点P的横坐标为2010,纵坐标为1,0,2,0,每4次一轮,∴经过第2010次运动后,动点P的纵坐标为:2010÷4=502余2,故纵坐标为四个数中第二个,即为0,∴经过第2010次运动后,动点P 的坐标是:(2010,0).故答案为:(2010,0).点睛:本题考查了点的坐标规律,培养学生观察和归纳能力,从所给的数据和图形中寻求规律进行解题是解答本题的关键.93.在平面直角坐标系中,将点A(﹣3,2)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是_____.【答案】(0,0)【解析】【分析】根据坐标的平移规律解答即可.【详解】将点A(-3,2)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是(-3+3,2-2),即(0,0),故答案为(0,0).【点睛】此题主要考查坐标与图形变化-平移.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.94.如图,在平面直角坐标系中,ABC ∆位于第一象限,点A 的坐标是(4,3),把ABC ∆向左平移6个单位长度,得到111A B C ∆,则点1B 的坐标是__________.【答案】(3,1)-【解析】【分析】要求出点B 1的坐标,就需要确定出点B 的坐标;由点A 的坐标,结合图形即可得到点B 的坐标;接下来由平移的特点,结合坐标系内图形的平移的性质即可确定出答案.【详解】∵点A 的坐标为(4,3),∴由图可知点B 的坐标为(3,1),∴点B 向左平移6个单位长度后,由坐标系内图形的平移的性质,可得点B 1的坐标为(3-6,1),即(-3,1).【点睛】本题考查坐标系内图形的平移,解题的关键是掌握坐标系内图形的平移的性质.95.已知平面直角坐标系中两点A (-2,3),B (-3,1),连接AB ,平移线段AB 得到线段A 1B 1,若点A 的对应点A 1的坐标为(3,4),则点B 1的坐标为 .【答案】(2,2)【解析】根据题意:A、B两点的坐标分别为A(-2,3),B(-3,1),若A1的坐标为(3,4),即线段AB向上平移1个单位,向右平移5个单位得到线段A1B1;B1点的规律同以上规律,则B1的坐标为(2,2)96.线段AB是由线段CD平移得到,点A(﹣2,1)的对应点为C(1,1),则点B(3,2)的对应点D的坐标是______.【答案】(6,2).【解析】试题分析:由点A(﹣2,1)的对应点为C(1,1),坐标的变化规律可知:各对应点之间的关系是横坐标加3,纵坐标加0,故点D的横坐标为3+3=6;纵坐标为2+0=2;即所求点D的坐标为(6,2).考点:坐标与图形变化-平移.97.如图,在平面直角坐标系中,点A1(1,2),A2(2,0),A3(3,-2),A4(4,0)……根据这个规律,探究可得点A2017的坐标是________.【答案】(2017,2)【解析】分析:由图形得出点的横坐标依次是0、1、2、3、4、…、n,纵坐标依次是0、2、0、-2、0、2、0、-2、…,四个一循环,继而求得答案.详解:观察图形可知,点的横坐标依次是0、1、2、3、4、…、n,纵坐标依次是0、2、0、−2、0、2、0、−2、…,四个一循环,2017÷4=504…1,故点A2017坐标是(2017,2).故答案为(2017,2).点睛:本题考查了规律型:点的坐标,学生的观察图形的能力和理解能力,解本题的关键是根据图形得出规律.98.在平面直角坐标系中,点A(a,-3)向左平移3个单位得点A’,若点A和A’关于y轴对称,则a=_______.【答案】32【解析】【分析】根据平移规律得到A’的坐标,再根据两点关于y轴对称,纵坐标相等,横坐标互为相反数建立方程求解.【详解】∵点A(a,-3)向左平移3个单位得点A’,∴点A’的坐标为(a-3,-3)又∵点A和A’关于y轴对称,∴a+a-3=0,解得a=32. 故答案为32. 【点睛】本题考查了点的平移和对称,熟记平移规律与对称的性质是解题的关键.99.点()3,2P -先向上平移3个单位,再向左平移2个单元,得到的点的坐标为________.【答案】(1,1)【解析】【分析】直接利用平移中点的变化规律求解即可.【详解】解:原来点的横坐标是3,纵坐标是-2,向上平移3个单位,再向左平移2个单位,得到的新点的横坐标3-2=1,纵坐标是-2+3=1,所以新点的坐标是(1,1).故答案为:(1,1).【点睛】本题考查图形的平移变换,关键是要懂得左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.100.将点()1,1-向下平移3个单位,再向左平移5个单位后,所得点的坐标为__________.【答案】()6,2--【解析】【分析】利用平移时点的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减求解即可.【详解】解:将点(1,1)-向下平移3个单位,再向左平移5个单位后,所得点的坐标为(15,13)--.---,即(6,2)故答案为:(6,2)--.【点睛】本题考查图形的平移变换,关键是要懂得左右移动改变点的横坐标,左减、右加;上下移动改变点的纵坐标,下减、上加.。
人教版七年级数学下册7.1.2用坐标表示平移练习题及答案(1).doc

7.1.2《用坐标表示平移》同步练习题(2)知识点:P(x ,y)向右平移a个单位,对应点P’(x+a,y)P(x ,y)向左平移a个单位,对应点P’(x-a,y)P(x ,y)向上平移a个单位,对应点P’(x,y+a)P(x ,y)向下平移a个单位,对应点P’(x,y-a)同步练习:1.将点(-3,1)向右平移4个单位长度,再向上平移2个单位长度,可以得到对应点_______.2.三角形ABC三个顶点的坐标分别是A(2,1),B(1,3),C(3,0),将三角形ABC•向左平移3个单位长度,再向下平移1个单位长度,则平移后三个顶点的坐标为()A.(5,0),(4,2),(6,-1) B.(-1,0),(-2,2),(0,-1)C.(-1,2),(-2,4),(0,1) D.(5,2),(4,4),(6,1)3.在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)•一个正数a,相应的新图形就是把原图形向________(或向_______)平移______个单位长度.4.如图,菱形ABCD,四个顶点分别是A(-2,1),B(1,-3),C(4,-1),D (1,1).将菱形沿x轴负方向平移3个单位长度,各个顶点的坐标变为多少?将它沿y轴正方向平移4个单位长度呢?分别画出平移后的图形.5.如图,梯形A′B′C′D′可以由梯形ABCD经过怎样的平移得到?•对应点的坐标有什么变化?7.1.2《用坐标表示平移》同步练习题(2)答案:1.(1,3)2.B 点拨:将A、B、C三点的横坐标都减去3,纵坐标都减去1得(-1,0),(-2,2),(0,-1),故选B.3.右;左;a4.解:将菱形沿x轴负方向平移3个单位长度,各个顶点的坐标变为(-5,-1),(-2,-3),(1,-1),(-2,1).将它沿y轴正方向平移4个单位长度,各个顶点的坐标变为(-2,3),(1,1),(4,3),(1,5).图略.5.解:梯形A′B′C′D′可以由梯形ABCD先向左平移7个单位,再向上平移7个单位得到.点A、B、C、D的横坐标都减去7,纵坐标都加7,可以得到点A′、B′、C′、D′的坐标.A(1,-6)→A′(-6,1),B(6,-6)→B′(-1,1),C(5,-2)→C′(-2,5),D(3,-2)•→D′(-4,5).【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7
知识点:
P(x ,y)向右平移a个单位,对应点P’(x+a,y)
P(x ,y)向左平移a个单位,对应点P’(x-a,y)
P(x ,y)向上平移a个单位,对应点P’(x,y+a)
P(x ,y)向下平移a个单位,对应点P’(x,y-a)
同步练习:
1.将点(-3,1)向右平移4个单位长度,再向上平移2个单位长度,能够得到对应点_______.
2.三角形ABC三个顶点的坐标分不是A(2,1),B(1,3),C(3,0),将三角形ABC•向左平移3个单位长度,再向下平移1个单位长度,则平移后三个顶点的坐标为()
A.(5,0),(4,2),(6,-1)B.(-1,0),(-2,2),(0,-1)
C.(-1,2),(-2,4),(0,1)D.(5,2),(4,4),(6,1)3.在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)•一个正数a,相应的新图形确实是把原图形向________(或向______ _)平移______个单位长度.
4.如图,菱形ABCD,四个顶点分不是A(-2,1),B(1,-3),C(4,-1),D(1,1).将菱形沿x轴负方向平移3个单位长度,各个顶点的坐标变为多少?将它沿y轴正方向平移4个单位长度呢?分不画出平移后的图形.
5.如图,梯形A′B′C′D′能够由梯形ABCD通过如何样的平移得到?•对应点的坐标有什么变化?
7.1.2《用坐标表示平移》同步练习题(2)答案:
1.(1,3)
2.B 点拨:将A、B、C三点的横坐标都减去3,纵坐标都减去1得(-1,0),(-2,2),(0,-1),故选B.
3.右;左;a
4.解:将菱形沿x轴负方向平移3个单位长度,各个顶点的坐标变为(-5,-1),(-2,-3),(1,-1),(-2,1).
将它沿y轴正方向平移4个单位长度,各个顶点的坐标变为
(-2,3),(1,1),(4,3),(1,5).图略.
5.解:梯形A′B′C′D′能够由梯形ABCD先向左平移7个单位,再向上平移7个单位得到.点A、B、C、D的横坐标都减去7,纵坐标都加7,能够得到点A′、B′、C′、D′的坐标.
A(1,-6)→A′(-6,1),B(6,-6)→B′(-1,1),C(5,-2)→C′(-2,5),D(3,-2)•→D′(-4,5).。
