高考数学复习-程序框图
高考数学复习__《算法与程序框图》

开始
max w1
i2
.
Y
i6
Y
wi max
max wi
i i 1
输出
max 的号码球
结束
N N
w1, w2 , w3 , w4 , w5 , w6
N
i 10
Y
i 10
Y
N
S=S+i i=i+1
S=S+1/i i=i+1
输出S 结束
输出S 结束
P14练习A
3: 开始
P14练习B
3:
开始
x 1
x 10
Y
x 2 .4
N
x3
Y
N
y x2
输出
y x2
输出
y
y
x x 1
结束
x x 0 .6
结束
P15习题1—1(A)
P15习题1—1(A)
3: 设两位小数为a.bc ,其 中 a, b, c 都为整数,且 0 b 9,0 c 9 .
开始 输入实数
4:
开始
x 3
x3
Y
N
x a.bc
N
y x 2 3x 1
输出
Y
c5
x a 0.1 b
输出
x a 0.1 b 1
自然语言、数学语言、形式语言、框图。
程序框图
用一些通用图形符号构成一张图来 表示算法,这种图称作程序框图 (简称框图).
四种图框类型 输入、输出框 处理框 判断框 起止框
算法的三种基本逻辑结构和框图表示
顺序结构 条件分支结构 循环结构
A B A
高考数学一轮总复习:算法与程序框图、基本算法语句

算法与程序框图、基本算法语句[基础梳理]1.算法算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.2.程序框图(1)程序框图的定义:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.通常,程序框图由程序框和流程线组成,一个或几个程序框的组合表示算法中的一个步骤;流程线带有方向箭头,按照算法进行的顺序将程序框连接起来.(2)程序框图中图形符号的意义3.三种基本逻辑结构及相应语句(1)顺序结构:要解决的问题不需要分类讨论.(2)条件结构:要解决的问题需要分类讨论.(3)循环结构:要解决的问题要进行许多重复的步骤,且这些步骤之间有相同的规律.2.循环结构的两个形式的区别(1)当型循环结构:先判断是否满足条件,若满足条件,则执行循环体.(2)直到型循环结构:先执行循环体,再判断是否满足条件,直到满足条件时结束循环.3.理解赋值语句要注意的三点(1)赋值语句中的“=”称为赋值号,与等号的意义不同.(2)赋值语句的左边只能是变量的名字,而不能是表达式.(3)对于同一个变量可以多次赋值,变量的值始终等于最近一次赋给它的值,先前的值将会被替换.[四基自测]1.某居民区的物业公司按月向居民收取卫生费,每月收费方法是:4人和4人以下的住户,每户收取6元;超过4人的住户,每超出1人加收1.1元,相应收费系统的程序框图如图所示,则①处应填()A.y=6+1.1x B.y=15+1.1xC.y=6+1.1(x-4) D.y=15+1.1(x-4)答案:C2.如图所示的程序框图的运行结果是()A.2 B.2.5C.3.5 D.4答案:B3.阅读下边的程序框图,运行相应的程序,则输出i的值为()A.2 B.3C.4 D.5答案:C4.(2017·高考全国卷Ⅱ)执行如图所示的程序框图,如果输入的a=-1,则输出的S=()A.2 B.3C.4 D.5答案:B高考总复习数学(文)第十章算法初步、统计、统计案例5.已知函数y=lg|x-3|,如图所示程序框图表示的是给定x值,求其相应函数值y的算法,请将该程序框图补充完整,其中①处应填________,②处应填________.答案:x<3?y=lg(x-3)考点一求运行后的输出结果◄考基础——练透角度1 输出计算结果[例1](1)(2016·高考全国卷Ⅲ)执行如图所示的程序框图,如果输入的a=4,b =6,那么输出的n=()A.3B.4C.5 D.6解析:运行程序框图,第1次循环,a=2,b=4,a=6,s=6,n=1;第2次循环,a=-2,b=6,a=4,s=10,n=2;第3次循环,a=2,b=4,a=6,s=16,n=3;第4次循环,a=-2,b=6,a=4,s=20,n=4,结束循环,故输出的n=4.答案:B(2)(2018·高考天津卷)阅读如图所示的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为()A.1 B.2 C.3 D.4解析:输入N的值为20,第一次执行条件语句,N=20,i=2,Ni=10是整数,∴T=0+1=1,i=3<5;第二次执行条件语句,N=20,i=3,Ni=203不是整数,∴i=4<5;第三次执行条件语句,N=20,i=4,Ni=5是整数,∴T=1+1=2,i=5,此时i≥5成立,∴输出T=2.故选B.角度2 输出运算关系[例2]某流程图如图所示,现输入如下四个函数,则可以输出的函数是()A.f(x)=x2B.f(x)=|x| xC.f(x)=e x-e-x e x+e-xD.f(x)=1+sin x+cos x 1+sin x-cos x解析:由框图可知输出函数为奇函数且存在零点,依次判断各选项,A为偶函数,B不存在零点,不符合,对于C,由于f(-x)=e-x-e xe-x+e x=-f(x),即函数为奇函数,且存在零点为x=0,对于D,由于其定义域不关于原点对称,故其为非奇非偶函数,故选C.答案:C求程序框图运行结果的思路(1)要明确程序框图中的顺序结构、条件结构和循环结构.(2)要识别运行程序框图,理解框图所解决的实际问题.(3)按照题目的要求完成解答并验证.1.(2019·河北石家庄模拟)当n=4时,执行如图所示的程序框图,则输出的S 值为()A.9 B.15C.31 D.63解析:由程序框图可知,n=4,k=1,S=1,满足条件k≤4;执行循环体,S=3,k=2,满足条件k≤4;执行循环体,S=7,k=3,满足条件k≤4;执行循环体,S=15,k=4,满足条件k≤4;执行循环体,S=31,k=5,不满足条件k≤4,退出循环,输出S的值为31.故选C.答案:C2.执行下面的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足()A .y =2xB .y =3xC .y =4xD .y =5x解析:运行程序,第1次循环得x =0,y =1,n =2,第2次循环得x =12,y =2,n =3,第3次循环得x =32,y =6,此时x 2+y 2≥36,输出x ,y ,满足C 选项. 答案:C考点二 求输入的值◄考能力——知法[例3] (1)(2017·高考全国卷Ⅲ)执行如图所示的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A .5B .4C .3D .2解析:S =0+100=100,M =-10,t =2,100>91;S =100-10=90,M =1,t =3,90<91,输出S,此时,t=3不满足t≤N,所以输入的正整数N的最小值为2,故选D.答案:D(2)《九章算术》是中国古代数学名著,体现了古代劳动人民的数学智慧,其中有一竹节容量问题,某老师根据这一问题的思想设计了如图所示的程序框图,若输出的m的值为35,则输入的a的值为()A.4 B.5C.7 D.11解析:起始阶段有m=2a-3,i=1,第一次循环,m=2(2a-3)-3=4a-9,i=2;第二次循环,m=2(4a-9)-3=8a-21,i=3;第三次循环,m=2(8a-21)-3=16a-45,i=4;接着计算m=2(16a-45)-3=32a-93,跳出循环,输出m=32a-93,令32a-93=35,得a=4.答案:A(2019·湖南郴州模拟)秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出s的值为484,则输入n的值可为()A .6B .5C .4D .3解析:模拟程序的运行,可得x =3,k =0,s =0,a =4,s =4,k =1,不满足条件k >n ;执行循环体,a =4,s =16,k =2,不满足条件k >n ;执行循环体,a =4,s =52,k =3,不满足条件k >n ;执行循环体,a =4,s =160,k =4,不满足条件k >n ;执行循环体,a =4,s =484,k =5,由题意,此时应该满足条件k >n ,退出循环,输出s 的值为484,可得5>n ≥4,所以输入n 的值可为4.故选C. 答案:C考点三 完善程序框图◄考基础——练透 [例4] (1)(2018·高考全国卷Ⅱ)为计算S =1-12+13-14+…+199-1100,设计了如图所示的程序框图,则在空白框中应填入( ) A .i =i +1 B .i =i +2 C .i =i +3 D .i =i +4解析:把各循环变量在各次循环中的值用表格表循环次数①②③…○50N0+110+11+130+11+13+15…0+11+13+15+…+199T0+120+12+140+12+14+16…0+12+14+16+…+1100S1-121-12+13-141-12+13-14+15-16…1-12+13-14+…+199-1100因为N=N+i,由上表知i是1→3→5,…,所以i=i+2.故选B.答案:B(2)(2017·高考全国卷Ⅰ)如图所示的程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在和两个空白框中,可以分别填入()A.A>1 000和n=n+1B.A>1 000和n=n+2C.A≤1 000和n=n+1D.A≤1 000和n=n+2解析:程序框图中A=3n-2n,故判断框中应填入A≤1 000,由于初始值n=0,要求满足A=3n-2n>1 000的最小偶数,故执行框中应填入n=n+2,选D.解决此类问题,其关键点1.分两种循环直到型循环是“先循环,后判断,条件满足时终止循环”;当型循环则是“先判断,后循环,条件满足时执行循环”.两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反.2.理清所用变量(1)计数变量:用来记录某个事件发生的次数,如i=i+1.(2)累加变量:用来计算数据之和,如S=S+i.(3)累乘变量:用来计算数据之积,如p=p×i.(2019·许昌调研)如图给出的是计算12+14+…+1100的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是()A.i>100,n=n+1B.i>100,n=n+2 C.i>50,n=n+2 D.i≤50,n=n+2解析:因为12,14,…,1100共50个数,所以算法框图应运行50次,所以变量i应满足i>50,因为是求偶数的和,所以执行框图n满足n=n+2.故选C.逻辑推理、直观想象——传统文化中的程序框图的应用[例1](1)(2015·高考全国卷Ⅱ)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=()A.0B.2C.4 D.14解析:开始:a=14,b=18.第一次循环:14≠18且14<18,b=18-14=4;第二次循环:14≠4且14>4,a=14-4=10;第三次循环:10≠4且10>4,a=10-4=6;第四次循环:6≠4且6>4,a=6-4=2;第五次循环:2≠4且2<4,b=4-2=2;第六次循环:a=b=2,退出循环,输出a=2,故选B.答案:B(2)(2016·高考全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=()A.7B.12C.17 D.34解析:由程序框图知,第一次循环:x=2,n=2,a=2,s=0×2+2=2,k=1;第二次循环:a=2,s=2×2+2=6,k=2;第三次循环:a=5,s=6×2+5=17,k=3.结束循环,输出s的值为17,故选C.答案:C[例2](1)(2019·湖北荆州七校2月联考)宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n=()A.2B.3C.4D.5解析:程序运行如下:n=1,a=5+52=152,b=4,a>b,继续循环;n=2,a=152+12×152=454,b=8,a>b,继续循环;n=3,a=454+12×454=1358,b=16,a>b,继续循环;n=4,a=1358+12×1358=40516,b=32,此时,a<b.输出n=4,故选C.答案:C(2)(2019·河南开封模拟)我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的语句是()A.i<7,s=s-1i,i=2iB.i≤7,s=s-1i,i=2iC.i<7,s=s2,i=i+1D.i≤7,s=s2,i=i+1解析:由题意可知第一天后剩下12,第二天后剩下122,……,由此得出第7天后剩下127,则①应为i≤7,②应为s=s2,③应为i=i+1,故选D.答案:D(3)秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,3,则输出v的值为()A.20B.61C.183D.548解析:初始值n,x的值分别为4,3,程序运行过程如下所示:v=1,i=3;v=1×3+3=6,i=2;v=6×3+2=20,i=1,v=20×3+1=61,i=0;v=61×3+0=183,i=-1;跳出循环,输出v的值为183,故选C.答案:C课时规范练A组基础对点练1.阅读如图所示的程序框图,运行相应的程序,则输出S的值为()A.2B.4C.6 D.8解析:第一次:S=8,n=2,第二次:S=2,n=3,第三次:S=4,n=4,满足n>3,输出S=4.答案:B2.阅读如图的程序框图,运行相应的程序,若输入N的值为19,则输出N的值为()A.0B.1C.2D.3解析:阅读程序框图可得,程序执行过程如下:首先初始化数值为N=19,第一次循环:N=N-1=18,不满足N≤3;第二次循环:N=N3=6,不满足N≤3;第三次循环:N=N3=2,满足N≤3;此时跳出循环体,输出N=2.答案:C3.执行如图所示的程序框图,则输出的λ是() A.-4B.-2C.0D.-2或0解析:依题意,若λa+b与b垂直,则有(λa+b)·b =4(λ+4)-2(-3λ-2)=0,解得λ=-2;若λa+b 与b平行,则有-2(λ+4)=4(-3λ-2),解得λ=0.结合题中的程序框图,输出的λ是-2.答案:B4.执行如图所示的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=()A.203 B.165C.72 D.158解析:第一次循环:M=32,a=2,b=32,n=2;第二次循环:M=83,a=32,b=83,n=3;第三次循环:M=158,a=83,b=158,n=4.则输出的M=158,选D.答案:D5.执行如图所示的程序框图,如果输入的x,t均为2,则输出的S=()A.4 B.5 C.6 D.7解析:k=1≤2,执行第一次循环,M=11×2=2,S=2+3=5,k=1+1=2;k=2≤2,执行第二次循环,M=22×2=2,S=2+5=7,k=2+1=3;k=3>2,终止循环,输出S=7.故选D.答案:D6.阅读如图所示的程序框图,运行相应程序,则输出的i的值为()A.3 B.4C.5 D.6解析:第一次执行,i=1,a=2;第二次执行,i=2,a=5;第三次执行,i =3,a=16;第四次执行,i=4,a=65,此时满足条件a>50,跳出循环,故选B.答案:B7.执行如图所示的程序框图,如果输入的x的值是407,y的值是259,那么输出的x的值是()A.2 849 B.37C.74 D.77解析:输入x的值是407,y的值是259,第一次循环后,S=148,x=259,y =148;第二次循环后,S=111,x=148,y=111;第三次循环后,S=37,x =111,y=37;第四次循环后,S=74,x=74,y=37;第五次循环后,S=37,x=37,y=37,结束循环,所以输出的x的值是37.故选B.答案:B8.(2019·临沂模拟)某程序框图如图所示,若判断框内是k≥n,且n∈N时,输出的S=57,则判断框内的n应为________.解析:由程序框图,可得:S =1,k =1;S =2×1+2=4,k =2;S =2×4+3=11,k =3;S =2×11+4=26,k =4;S =2×26+5=57,k =5.答案:5B 组 能力提升练9.执行如图所示的程序框图,如果输入的t ∈[-1,3],则输出的s 属于( )A .[-3,4]B .[-5,2]C .[-4,3]D .[-2,5]解析:作出分段函数s =⎩⎨⎧ 3t ,-1≤t <1,-t 2+4t ,1≤t ≤3的图象(图略),可知函数s 在[-1,2]上单调递增,在[2,3]上单调递减,∴t ∈[-1,3]时,s ∈[-3,4].答案:A10.(2019·郑州一中质检)执行如图所示的程序框图,若输出y=-3,则输入的θ=()A.π6B.-π6C.π3D.-π3解析:对于A,当θ=π6时,y=sin θ=sin π6=12,则输出y=12,不合题意;对于B,当θ=-π6时,y=sin θ=sin(-π6)=-12,则输出y=-12,不合题意;对于C,当θ=π3时,y=tan θ=tan π3=3,则输出y=3,不合题意;对于D,当θ=-π3时,y=tan θ=tan(-π3)=-3,则输出y=-3,符合题意.故选D.答案:D11.执行如图所示的程序框图(算法流程图),输出的n为________.解析:第一次执行循环体a=32,n=2;此时|a-1.414|=|1.5-1.414|=0.086>0.005;第二次执行循环体a=75,n=3;此时|a-1.414|=|1.4-1.414|=0.014>0.005;第三次执行循环体a =1712,n =4;此时|a -1.414|<0.005,此时不满足判断框内的条件,输出n =4.答案:412.阅读如图所示的程序框图,运行相应的程序,输出的 结果S =________.解析:由程序框图知,S 可看成一个数列{a n }的前2 018 项的和,其中a n =1n (n +1)(n ∈N *,n ≤2 018), ∴S =11×2+12×3+…+12 018×2 019=⎝ ⎛⎭⎪⎫1-12+ ⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫12 018-12 019=1-12 019=2 0182 019.答案:2 0182 019。
高考数学复习考点知识剖析解题方法与技巧专题讲解92---程序框图

)
A.3
B.4
C.5
D.6
思路:循环的流程如下:
① i = 1, a = 2
② i = 2, a = 5
③ i = 3, a = 16
④ i = 4, a = 65
循环终止,所以 i = 4 答案:B
第2题
例 3:某程序框图如图所示,若输出的 S = 57 ,则判断框内为(
)
A. k > 4?
B. k &g:执行下图所示的程序框图,若输入 x = 2 ,则输出 y 的值为
.
思路:通过框图的判断语句可知 y 关于 x 的函数为:
2x − 1, x < 0
y
=
x
2
+
1, 0
≤
x
<
1,所以当
x
=
2
时,
y
=
23
+
2
⋅
2
=
12
x3 + 2x, x ≥ 1
答案:12
例 2:阅读右边的程序框图,运行相应的程序,则输出 i 的值为(
)
A. 120
B. 720
C. 1440
D. 5040
思路:循环的流程如下: ① p=1 ② k = 2, p = 2 ③ k = 3, p = 6
④ k = 4, p = 24 ⑤ k = 5, p = 120 ⑥ k = 6, p = 720 答案:B 例 5:右图是一个算法的流程图,则输出 S 的值是______
④ S = 20,n = 8,T = 20
⑤ S = 25,n = 10,T = 30 从而 T > S ,结束循环
所以 T = 30
《高三数学程序框图》PPT课件

2、怎么用程序框图表示呢? 3、i有什么作用?Sum呢? 4、如何使程序结束? h
i=i+1
Sum=Sum + i
5
程序框图 如图
开始 i=1 sum=0
i≤100? 否
输出sum
结束
h
i=i+1 sum=sum+1 是
6
例2 用二分法求解方程 求关于x的方程x2-2=0的根,精确到0.005
算法描述
算法初步
§1.1.2 程序框图
h
1
知识回忆 1、程序框图的概念 2、程序框图的图示和意义 3、顺序结构和条件结构的特点
h
2
程序框图又称流程图,是一种用规定的图形,指向线及 文字说明来准确、直观地表示算法的图形。
程序框
名称
功能
终端框(起 表示一个算法的起始和结束 止框)
输入、输出 表示算法的输入和输出的信
框
息
处理框(执 赋值、计算 行框)
判断框
判断一个条件是否成立,用
“是”、“否”或“Y”、“N”
h 标明
3
例1 设计一算法,求和:1+2+3+…+100
算法1:
第一步:确定首数a,尾 数b,项数n;
第二步:利用公式“总和 =(首数+尾数)×项数/2” 求和;
第三步:输出求和结果。
开始 输入a,b,n Sum=(a+b)*n/2 输出Sum
i=i+1
Sum=Sum*i
否 i>=100?
是 输出Sum
h
结束
10
小结
1、循环结构的特点 重复同一个处理过程 2、循环结构的框图表示 当型和直到型 3、循环结构有注意的问题 避免死循环的出现,设置好进入(结束)循环 体的条件。
高三数学框图试题

高三数学框图试题1.执行如图所示的程序框图,则输出的结果是()A.14B.15C.16D.17【答案】C【解析】根据程序框图,从到得到,因此将输出. 故选C.【考点】程序框图.2.右图是计算某年级500名学生期末考试(满分为100分)及格率的程序框图,则图中空白框内应填入()A.B.C.D.【答案】D.【解析】通过程序的判断语句可知,表示的是及格的人数,表示的是不及格的人数,∴.【考点】程序框图.3.执行如图所示的程序框图,若输入n的值为4,则输出S的值为 ( )A.5B.6C.7D.8【答案】C【解析】第一次循环后:S=1,i=2第二次循环后:S=2,i=3第三次循环后:S=4,i=4第四次循环后:S=7,i=5,故输出74.定义某种运算,运算原理如右图所示,则式子的值为【答案】13【解析】由算法知:,而【考点】新定义5.阅读右面的程序框图,运行相应的程序,输出的结果为()A.B.C.D.【答案】C【解析】第一次循环,第二次循环,第三次循环,第四次循环,,因此当时,【考点】循环体流程图6.执行如图所示的程序框图,则输出的k值是.【答案】3.【解析】由程序框图知,输出.【考点】程序框图.7.执行如图所示的程序框图.若输出,则框图中①处可以填入()A.B.C.D.【答案】B【解析】依次循环的结果为:;;;.因为输出,所以可满足,故选.【考点】程序框图.8.执行右面的程序框图,如果输入的t∈[-1,3],则输出的s属于( )A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]【答案】A;【解析】若,则;若,;综上所述.【考点】本题考查算法框图,考查学生的逻辑推理能力.9.如图,运行该程序后输出的值为()A.66B.55C.11D.10【答案】A【解析】由程序框图可以看出,本框图的作用就是计算的值,所以输出的.【考点】程序框图及其应用.10.如果执行框图,输入,则输出的数等于()A.B.C.D.【答案】D【解析】第一次循环,;第二次循环,;第三次循环,;第四次循环,;第五次循环,;此时不满足条件,输出,选D.【考点】算法与框图.11.程序框图如图所示,其输出结果是,则判断框中所填的条件是()A.B.C.D.【答案】B【解析】由题意可知第一次运行后,第二次运行后,第三次运行后,第四次运行后,第五次运行后,此时停止运算,又判断框下方是“是”,故应填.故选B.【考点】算法流程图.12.执行如图所示程序框图.若输入,则输出的值是()A.B.C.D.【答案】C【解析】通过程序循环计算,知道得到的x大于23就结束,即.【考点】考查程序框图.13.执行如图所示的程序框图,输出的S值为()A.1B.C.D.【答案】C【解析】第一次执行循环:,;第二次执行循环:,,满足≥2,结束循环,输出.【考点】本小题考查了对算法程序框图的三种逻辑结构的理解,考查了数据处理能力和算法思想的应用.14.如图所示,程序据图(算法流程图)的输出结果为()A.B.C.D.【答案】C【解析】;;,输出所以答案选择C【考点】本题考查算法框图的识别,逻辑思维,属于中等难题.15.随机抽取某产品件,测得其长度分别为,如图所示的程序框图输出样本的平均值,则在处理框①中应填入的式子是(注:框图中的赋值符号“=”也可以写成“←”“:=”)A.B.C.D.【答案】D,i=2时,s=,i=3【解析】如图所示的程序框图输出样本的平均值,当i=1时,s=a1时,…,因此,处理框①应填入的式子是,故选D。
高中数学复习:算法与程序框图

一般格式 ③ INPUT “提示内容”;变量 ④ PRINT “提示内容”;表达式 ⑤ 变量=表达式
教材研读 栏目索引
功能 输入信息 输出常量、变量的值和系统信息 将表达式的值赋给变量
(2)条件语句的格式及框图 a.IF-THEN格式
b.IF-THEN-ELSE格式
教材研读 栏目索引
(3)循环语句的格式及框图 a.UNTIL语句
教材研读 栏目索引
5.如图所示的程序框图的运行结果为
.
答案 2.5
6.执行如图所示的程序框图,则输出的A=
教材析 i=0,A=2;
A=2+ 1= 5,i=1;
22
2 12
A=2+ = ,i=2;
55
5 29
A=2+12=12 ,i=3;
A=2+
12 29
=
70 29
考点突破 栏目索引
规律方法 顺序结构和条件结构的运算方法 (1)顺序结构是最简单的算法结构,语句与语句之间、框与框之间是按 从上到下的顺序进行的. (2)条件结构中条件的判断关键是明确条件结构的功能,然后根据 “是”的分支成立的条件进行判断.对于条件结构,无论判断框中的条 件是否成立,都只能执行两个分支中的一个,不能同时执行两个分支.
2.程序框图
(1)程序框图又称流程图,是一种用程序框、流程线及文字说明来表示 算法的图形. (2)基本的程序框有终端框(起止框),输入、输出框,处理框(执行框),判断框.
3.三种基本逻辑结构
名称 顺序结构
条件结构
循环结构
教材研读 栏目索引
内 顺序结构是由若干个按 算法的流程根据条件 在一些算法中,会出现从某处开始,按照一
教材研读 栏目索引
高考文科数学 程序框图-知识点考法及解题方法

程序框图(算法初步)知识点、考法及解题方法算法的概念:算法通常是指可以用计算机来解决的某一类问题的明确和有限的步骤,这些步骤必须是确定的和能执行的,并且能够在有限步之内完成。
程序框图概念:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形。
一个程序框图包括哪几部分?实现不同算法功能的相对应的程序框;带箭头的流程线;程序框内必要的说明文字。
程序框与流程线:说明文字(基本算法语句-5种语句):常用程序符号(A ) (B ) (C ) (D ) 【例1】判断下列说法是否正确①算法执行以后可以有不同的结果; ②解决一个问题可以有不同的算法;③解决同一个问题采用不同算法得到的结果不同; ④算法的每个执行步骤都必须在有限的时间内完成; ⑤算法的每个步骤之间可以调换顺序; ⑥可以写出一个算法输出所有质数; ⑦算法只能用自然语言描述。
例2、)A. 输出a=10B. 赋值a=10C. 判断a=10D. 输入a=1例3、条件语句的一般形式如右图所示,其中B 表示的是( )A .条件B .条件语句C .满足条件时执行的内容D .不满足条件时执行的内容例4、下列图形中,是条件语句的一般格式的是( )例5、下列语句中,哪一个是输入语句 ( )A .PRINTB .IFC .INPUTD .WHILE高考考点:程序框图 解题方法:模拟分析法一般要求写出程序的运行结果,求输入参数,填空补全程序框图,指明算法的功能 解题方法分析:1、输出结果:(1)较简单或循环次数较少时,进行模拟分析,就是分析题意,看有多少个量就按多少列来模拟电脑列表分析;(2)较复杂或循环次数较多时,按题意先写出解析式(如分段函数)或通项公式(多次循环),最后代入数值求得结果。
2、求输入参数:进行逆向模拟分析3、填空补全:(1)补判断语句:答案不唯一,进行模拟分析,注意循环几次就出来,注意临界值,决定要谁不要谁;(2)补执行语句:进行模拟分析,看目的,注意看是否需要计数量,需要哪些计算量,怎么计算。
高考数学复习《流程图》
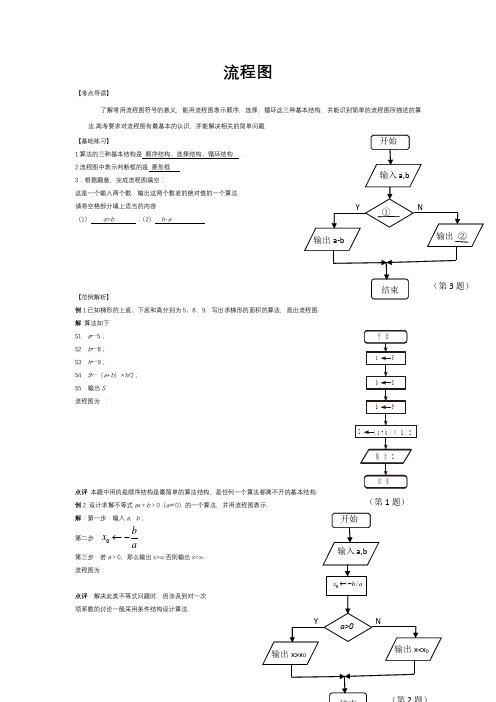
流程图【考点导读】了解常用流程图符号的意义,能用流程图表示顺序,选择,循环这三种基本结构,并能识别简单的流程图所描述的算法.高考要求对流程图有最基本的认识,并能解决相关的简单问题.【基础练习】1.算法的三种基本结构是顺序结构、选择结构、循环结构 .2.流程图中表示判断框的是菱形框 .3.根据题意,完成流程图填空:这是一个输入两个数,输出这两个数差的绝对值的一个算法.请将空格部分填上适当的内容(1)a>b;(2)b-a【范例解析】例1.已知梯形的上底、下底和高分别为5、8、9,写出求梯形的面积的算法,画出流程图.解算法如下S1 a←5;S2 b←8;S3 h←9;S4 S←(a+b)×h/2;S5 输出S.流程图为:点评本题中用的是顺序结构是最简单的算法结构,是任何一个算法都离不开的基本结构.例2 .设计求解不等式ax+b>0(a≠0)的一个算法,并用流程图表示.解:第一步输入a,b;第二步0bxa←-第三步若a>0,那么输出x>x0,否则输出x<x0流程图为:点评解决此类不等式问题时,因涉及到对一次项系数的讨论一般采用条件结构设计算法.(第1题)【反馈演练】1.如图表示的算法结构是 顺序 结构. 2.下面的程序执行后的结果是 4,1 .ba prb a b b a a b a ,int 31-←+←←← 解析:由题意得3,1==b a ,故执行到第三步时,把b a +的值给a ,这时4=a ,第四步,把b a -的值给b ,这时1=b .3 输入x 的值,通过函数y =⎪⎩⎪⎨⎧≥-<≤-<,10 113,101 12,1 x x x x x x 求出y 的值,现给出此算法流程图的一部分,请将空格部分填上适当的内容 ① x ② 1≤x <10 ③ 3x -114 如图所示,给出的是计算111124620++++L 的值的一个程序框图,其中判断框内应填入的条件是 i>20 .(第4题)(第3题)5. 给出以下一个算法的程序框图(如图所示).该程序框图的功能是求出a,b,c三数中的最小数 .6.根据下面的算法画出相应的流程图.算法:S1 T←0;S2 I←2;S3 T←T+I;S4 I←I+2;S5 如果I不大于200,转S3;S6 输出T .答案:解:这是计算2+4+6+…+200的一个算法.流程图如下:。
高三数学框图试题
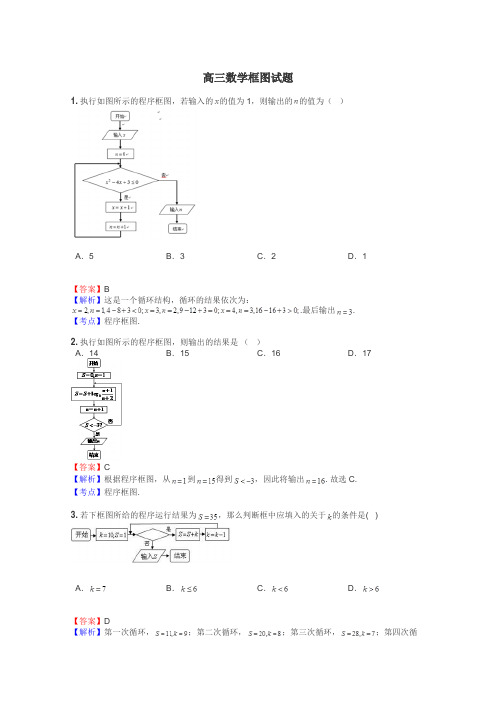
高三数学框图试题1.执行如图所示的程序框图,若输入的的值为1,则输出的的值为()A.5B.3C.2D.1【答案】B【解析】这是一个循环结构,循环的结果依次为:.最后输出.【考点】程序框图.2.执行如图所示的程序框图,则输出的结果是()A.14B.15C.16D.17【答案】C【解析】根据程序框图,从到得到,因此将输出. 故选C.【考点】程序框图.3.若下框图所给的程序运行结果为,那么判断框中应填入的关于的条件是( )A.B.C.D.【答案】D【解析】第一次循环,;第二次循环,;第三次循环,;第四次循环,,结束循环,输出,因此【考点】循环结构流程图4.阅读右图的程序框图,则输出S=( )A.14B.20C.30D.55【答案】C【解析】运行程序框图如下:故选C【考点】程序框图5.李强用流程图把早上上班前需要做的事情做了如下几种方案,则所用时间最少的方案是_______【答案】方案三【解析】方案一:所用时间为.方案二:所用时间为.方案三:所用时间为.所以所用时间最少的方案是方案三.【考点】流程图6.阅读右面的程序框图,运行相应的程序,输出的结果为()A.B.C.D.【答案】C【解析】第一次循环,第二次循环,第三次循环,第四次循环,,因此当时,【考点】循环体流程图7.某程序框图如图所示,现在输入下列四个函数,则可以输出函数是()A.B.C.D.【答案】B【解析】本题要从程序框图中发现函数的性质,第一个判断框说明是奇函数,第二个判断框说明方程有实解,即函数的图象与轴有交点,因此我们首先判断四个函数的奇偶性,可利用等式来判断,三个函数是奇函数,又,即或,从而,同样,因此两个函数图象与都无交点,只有中,,此函数图象与轴是相交的,因此选B.【考点】函数的奇偶性与函数的值域.8.下图是某算法的流程图,其输出值是 .【答案】.【解析】第一次循环,,不成立,执行第二次循环;,不成立,执行第三次循环;第三次循环,,不成立,执行第四次循环;第四次循环,,成立,跳出循环体,输出的值为.【考点】算法与程序框图9.阅读如图的程序框图,若输出的的值等于,那么在程序框图中判断框内应填写的条件是()A.?B.?C.?D.?【答案】A【解析】读懂框图可知求满足的值,易得所以.【考点】考查算法与框图.10.阅读程序框图(如图所示),若输入,,,则输出的数是.【答案】【解析】程序框图的功能是:输出中最大的数,∵,,,所以输出的数为.【考点】程序框图.11.某程序框图如图所示,该程序运行后输出的的值是()A.B.C.D.【答案】A【解析】第一步 ;第二步 ;第三步,第四步【考点】程序框图12.给出下面的程序框图,则输出的结果为_________.【答案】【解析】解:k=1,S=0+=,满足条件k≤5,执行循环,k=2,S=+,满足条件k≤5,执行循环,k=3,S=,满足条件k≤5,执行循环,k=4,S=,满足条件k≤5,执行循环,k=5,S=,满足条件k≤5,执行循环,k=6,S=,不满足条件k≤5,退出循环,输出S=故答案为:【考点】当型循环点评:本题主要考查了循环结构中的当型循环,以及程序框图,解题的关键是弄清循环次数,属于基础题13.如果右边程序框图的输出结果是10,那么在判断框中①表示的“条件”应该是()A.i≥3B.i≥4C.i≥5D.i≥6【答案】C【解析】第一执行,,第二执行,,第三次执行,,第四次执行,,因为输出结果为10,所以应填.选C.【考点】循环结构点评:本题考查循环结构,已知运算规则与最后运算结果,求运算次数的一个题,是算法中一种常见的题型.14.已知,由如右程序框图输出的为A.B.C.D. 0【答案】B【解析】因为,由程序框图,M<N,S=M=ln2,故选B。
高中数学程序框图专题

专题程序框图考点精要1.了解算法的含义,了解算法的思想;2.理解程序框图的三种基本逻辑结构:顺序结构、条件结构、循环结构;3.能熟练运用程序框图表示算法,由框图能指出其含义.热点分析重点侧重知识应用的考查,要求具备一定的逻辑推理能力,主要考查内容以程序框图为主.知识梳理1.算法的特征(1)确定性:算法的确定性是指一个算法中每一步操作都是明确的,不能模糊或有歧义,算法执行后一定产生明确的结果;(2)有穷性:算法的有穷性是指一个算法必须能够在有限个步骤之内把问题解决,不能无限的执行下去;(3)可行性:算法的可行性是指一个算法对于某一类问题的解决都必须是有效的,切实可行的,并且能够重复使用.2.程序框图(1)程序框图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;(2)构成程序框的图形符号及其作用程序框名称功能起止框表示一个算法的起始和结束,是任何算法程序框图不可缺少的.输入、输出框表示一个算法输入和输出的信息,可用在算法中任何需要输入、输出的位置.处理框赋值、计算.算法中处理数据需要的算式、公式等,它们分别写在不同的用以处理数据的处理框内.判断框判断某一条件是否成立,成立时在出口处标明“是”或“Y”;不成立时在出口处标明则标明“否”或“N”.流程线算法进行的前进方向以及先后顺序连结点连接另一页或另一部分的框图(3)程序框图的构成一个程序框图包括以下几部分:实现不同算法功能的相对应的程序框;带箭头的流程线;程序框内必要的说明文字.3.几种重要的结构(1)顺序结构顺序结构描述的是最自然的结构,它也是最基本的结构,其特点是:语句与语句之间,框与框之间是按从上到下的顺序进行,不能跳跃,不能回头,如右图表示的是顺序结构的示意图,它的功能是:A和B两个框是依次执行的,只有在执行完A框后,才能接着执行B框.(2)选择结构选择结构是依据指定条件选择不同的指令的控制结构.选择结构和实际问题中的分类处理与数学思想中的分类讨论思想是完全对应的.两种常见的选择结构如下左图和右图所示.左图的功能是先判断P是否成立,若成立,再执行A后脱离选择结构.右图的功能是根据给定的条件P是否成立而选择A框或B框,特别注意,无论条件P是否成立,只能执行A框或B框之一,不可能既执行A框又执行B 框,也不可能A框、B框都不执行,无论执行哪条路径,在执行完A框或B框之后,脱离本选择结构.(3)循环结构循环结构就是根据指定条件决定是否重复执行一条或多条指令的控制结构.它的特点是:从某处开始,按照一定的条件反复执行某一处理步骤,其中反复执行的处理步骤称为循环体.两种常见的循环结构如下左图和右图所示.左图的功能是先执行A框,然后判断给定的条件P是否成立,如果P条件不成立,再执行A,然后再对P条件作判断,如果P条件仍然不成立,又执行A,…,如此反复执行A,直到给定的P条件成立为止,此时不再执行A,脱离本循环结构(又称直到型循环).开始i=2, sum=0sum=sum+ii=i+2i ≥100? 否是输出sum结束右图的功能是先判断条件P 是否成立,若成立,则执行A 框,再判断条件P 是否成立,若成立,又执行A 框,…,直到不符合条件时终止循环(又称当型循环),执行本循环结构后的下一步程序.例题精讲例1.一个算法的程序框图如下图所示,若该程序输出的结果为56,则判断框中应填入的条件是A .4iB .5iC .5iD .6i例2.如下右图,给出的程序框图,那么输出的数是A .2450B .2550C .5050D .4900例3.如下左图所示的程序输出结果为sum=1320,则判断框中应填A .i ≥ 9B .i ≥ 10C .i ≤ 10D .i ≤ 9(例2题图)(例3题图)针对训练1.如下左图,阅读下列程序框图,该程序输出的结果是__________.2.如下中图,给出了一个程序框图,其作用是输入x 的值,输出相应的y 的值,若要使输入的x 的值与输出的y 的值相等,则这样的x 的值的集合为__________ 3.如下右图是一程序框图,则其输出结果为__________(1题图)(2题图)(3题图)4.按下列程序框图来计算:如果x=5, 应该运算__________次才停止.5.如下左边的程序框图输出结果S =__________否开始结束是x=3×x -2输入xx>200输出x1si12s si1i i 否输出s开始是是否开始i=0S =0S =S +2i 1 输出Si=i+2i ≥8(5题图)(6题图)6.如上右图给出的是计算111124620的值的一个框图,其中菱形判断框内应填入的条件是________7.程序框图(即算法流程图)如下左图所示,其输出结果是__________(7题图)(8题图)8.某算法的程序框如上右图所示,则输出量y 与输入量x 满足的关系式是__________9.随机抽取某产品n 件,测得其长度分别为12,,...,n a a a ,则下左图所示的程序框图输出的s=__________,s 表示的样本的数字特征是__________.(注:框图中的赋值符号“=”也可以写成“←”“:=”)10.执行下右边的程序框图,输出的T=__________.s输出否a=2a+1a=1结束100?a 开始输出a是T>S开始S =0, T=0, n=0是否(9题图)(10题图)11.阅读下左图的程序框图,若输入4m,6n ,则输出a _________.(11题图)(12题图)(13题图)12.某程序框图如上中图所示,该程序运行后输出的k 的值是A .4B .5C .6D .713.执行上图右边的程序框图,若0.8p ,则输出的n__________14.阅读如下左图的程序框图,则输出的S =A .26B .35C .40D .57开始1i n 整除a?是输入m n,结束a m i输出a i,1i i 否开始S 0 i 1开始10n S ,Sp ?是输入p结束输出n12nSS否1n n(14题图)(15题图)15.某地区为了解70~80岁老人的日平均睡眠时间(单位:h ),现随机地选择50位老人做调查,右表是50位老人日睡眠时间频率分布表。
高考数学专题—算法与程序框图
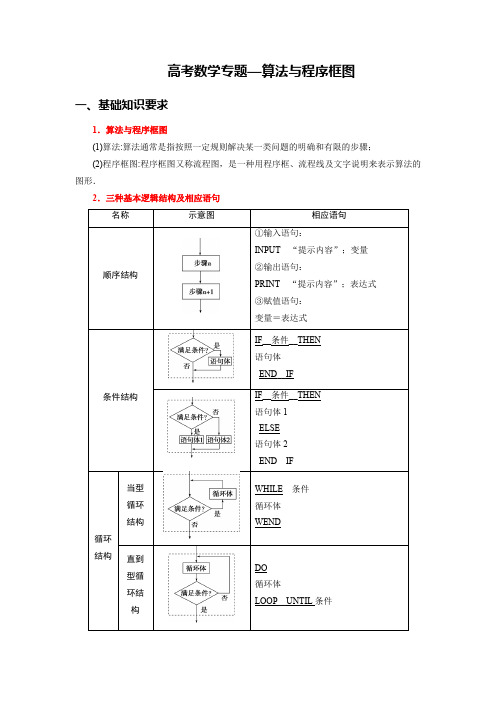
高考数学专题—算法与程序框图一、基础知识要求1.算法与程序框图(1)算法:算法通常是指按照一定规则解决某一类问题的明确和有限的步骤;(2)程序框图:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.2.三种基本逻辑结构及相应语句易错点:直到型循环是“先循环,后判断,条件满足时终止循环”;当型循环则是“先判断,后循环,条件满足时执行循环”;两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反.二、算法与程序框图常见题型:(共4种题型:由程序框图求输出结果、由输出结果判断输入量的值、辨析程序框图的算法功能、完善程序框图)1、由程序框图求输出结果:已知程序框图,求输出的结果,可按程序框图的流程依次执行,最后得出结果.例1、【2020年高考江苏】如图是一个算法流程图,若输出y 的值为2-,则输入x 的值是_____.【答案】3-【解析】由于20x >,所以12y x =+=-,解得3x =-. 故答案为:3-例2、【广西南宁市第三中学2020届高三适应性月考卷】运行如图所示的程序算法,则输出的结果为A .2B .12C .13D .132【答案】A【解析】当2a =时, 1k =;当132a =时,3k =; 当132132a ==时,5k =;…;当132a =时,99k =,当2a =时,101k =,跳出循环; 故选:A .例3、【河北省衡水中学2020届高三下学期第二次调研数学】执行如图所示的程序框图,输出的结果是A .5B .6C .7D .8【答案】B【解析】1i =,12n =, 第一次循环: 8n =,2i =, 第二次循环:31n =,3i =, 第三次循环:123n =,4i =, 第四次循环:119n =,5i =,第五次循环:475n =,6i =,停止循环, 输出6i =. 故选B .例4、【广东省深圳市2020届高三下学期第二次调研数学】执行如图的程序框图,如果输入的k =0.4,则输出的n =A .5B .4C .3D .2【答案】C【解析】模拟程序的运行,可得k =0.4,S =0,n =1, S 11133==⨯, 不满足条件S >0.4,执行循环体,n =2,S 11113352=+=⨯⨯(1111335-+-)25=,不满足条件S >0.4,执行循环体,n =3,S 11111335572=++=⨯⨯⨯(11111133557-+-+-)37=, 此时,满足条件S >0.4,退出循环,输出n 的值为3. 故选:C .例5、【甘肃省西北师大附中2020届高三5月模拟试卷】“辗转相除法”是欧几里得《原本》中记录的一个算法,是由欧几里得在公元前300年左右首先提出的,因而又叫欧几里得算法.如图所示是一个当型循环结构的“辗转相除法”程序框图.当输入2020m =,303n =时,则输出的m 是A .2B .6C .101D .202【答案】C【解析】输入2020m =,303n =,又1r =. ①10r =>,202r =,303m =,202n =; ②2020r =>,3032021101÷=,101r =,202m =,101n ;③1010r =>,0r =,101m =,0n =; ④0r =,则0r >否,输出101m =.故选:C.例6、【重庆市第一中学2019-2020学年高三下学期期中数学】冰雹猜想也称奇偶归一猜想:对给定的正整数进行一系列变换,则正整数会被螺旋式吸入黑洞(4,2,1),最终都会归入“4-2-1”的模式.该结论至今既没被证明,也没被证伪. 下边程序框图示意了冰雹猜想的变换规则,则输出的i=A.4B.5C.6D.7【答案】B【解析】由题意,第一次循环,12S Z∉,35116S=⨯+=,011i=+=,1S≠;第二次循环,12S Z∈,11682S=⨯=,112i=+=,1S≠;第三次循环,12S Z∈,1842S=⨯=,213i=+=,1S≠;第四次循环,12S Z∈,1422S=⨯=,314i=+=,1S≠;第五次循环,12S Z∈,1212S=⨯=,415i=+=,1S=;此时输出5i=.故选:B例7、【重庆市南开中学2019-2020学年高三下学期线上期中数学】若某程序框图如图所示,则输出的S 的值是A .31B .63C .127D .255【答案】C【解析】第一次运行,1i =,0S =,8i <成立,则2011S =⨯+=,112i =+=; 第二次运行,2i =,1S =,8i <成立,则2113S =⨯+=,213i =+=; 第三次运行,3i =,3S =,8i <成立,则2317S =⨯+=,314i =+=; 第四次运行,4i =,7=S ,8i <成立,则27115S =⨯+=,415i =+=; 第五次运行,5i =,15S =,8i <成立,则215131S =⨯+=,516i =+=; 第六次运行,6i =,31S =,8i <成立,则231163S =⨯+=,617i =+=; 第七次运行,7i =,63S =,8i <成立,则2631127S =⨯+=,718i =+=; 第八次运行,8i =,127S =,8i <不成立, 所以输出S 的值为127. 故选:C .2、由输出结果判断输入量的值例8、【2020·黑龙江哈尔滨六中期中】执行如图所示的程序框图,若输出的结果是1516,则输入的a 为( )A .3B .6C .5D .4【解析】 (1)第1次循环,n =1,S =12;第2次循环,n =2,S =12+122;第3次循环,n =3,S =12+122+123;第4次循环,n =4,S =12+122+123+124=1516.因为输出的结果为1516,所以判断框的条件为n <4,所以输入的a 为4.故选D.例9、我国古代数学著作《周髀算经》有如下问题:“今有器中米,不知其数.前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S =1.5(单位:升),则输入k 的值为( )A .4.5B .6C .7.5D .9【解析】选B.由程序框图知S =k -k 2-k 2×3-k 3×4=1.5,解得k =6,故选B.例10、执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A.5B.4C.3D.2【答案】D【解析】程序运行过程如下表所示:此时故选D. 例11、【2020届华大新高考联盟高三4月教学质量测评数学】执行如图所示的程序框图,设输出数据构成集合A ,从集合A 中任取一个元素m ,则事件“函数()2f x x mx =+在[)0,+∞上是增函数”的概率为A .14B .12C .34D .35【答案】C【解析】当20x y =-⇒=; 当2111x y =-+=-⇒=-; 当1100x y =-+=⇒=; 当0113x y =+=⇒=; 当1128x y =+=⇒=; 当213x =+=,退出循环. 所以{}0,1,3,8A =-,又函数()2f x x mx =+在[)0,+∞上是增函数,所以002mm -≤⇒≥. 函数()2f x x mx =+在[)0,+∞上是增函数的概率为34. 故选:C .3、辨析程序框图的算法功能:对于辨析程序框图功能问题,可将程序执行几次,即可根据结果作出判断.例12、执行右面的程序框图,如果输入的x=0,y=1,n=1,则输出x,y 的值满足 ( ) A.y=2x B.y=3x C.y=4x D.y=5x【答案】C【解析】由题图可知,x=0,y=1,n=1,执行如下循环: x=0,y=1,n=2;x=12,y=2,n=3;x=12+1=32,y=6,退出循环,输出x=32,y=6,验证可知,C 正确.例13、执行如图所示的程序框图,输出的结果为 ( )A.(-2,2)B.(-4,0)C.(-4,-4)D.(0,-8)【答案】B【解析】x=1,y=1,k=0,进入循环:s=1-1=0,t=1+1=2,x=0,y=2,k=0+1=1<3;s=0-2=-2,t=0+2=2,x=-2,y=2,k=1+1=2<3;s=-2-2=-4,t=-2+2=0,x=-4,y=0,k=2+1=3≥3,跳出循环,输出(x,y),即(-4,0).例14、执行下面的程序框图,如果输入的N=4,那么输出的S=( )A.1+12+13+14B.1+12+13×2+14×3×2C.1+12+13+14+15D.1+12+13×2+14×3×2+15×4×3×2 【答案】B【解析】由程序框图依次计算可得,输入N=4, T=1,S=1,k=2; T=12,S=1+12,k=3; T=13×2,S=1+12+13×2,k=4; T=14×3×2,S=1+12+13×2+14×3×2,k=5; 此时k 满足k>N,故输出S=1+1+1+1.例15、如果执行下边的程序框图,输入正整数N(N ≥2)和实数a 1,a 2,…,a N ,输出A,B,则( )A.A+B 为a 1,a 2,…,a N 的和B. A+B2为a 1,a 2,…,a N 的算术平均数C.A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数D.A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数 【答案】C【解析】随着k 的取值不同,x 可以取遍实数a 1,a 2,…,a N ,依次与A,B 比较,A 始终取较大的那个数,B 始终取较小的那个数,直到比较完为止,故最终输出的A,B 分别是这N 个数中的最大数与最小数.例16、【2020届清华大学中学生标准学术能力诊断性测试高三5月测试数学】下列程序框图的算法思想源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入16a =,10b =,则程序中需要做减法的次数为A .6B .5C .4D .3【答案】C【解析】由16a =,10b =,满足a b ,满足a b >,则16106a =-=;满足a b ,不满足a b >,则1064b =-=; 满足a b ,满足a b >,则642a =-=; 满足a b ,不满足a b >,则422b =-=; 不满足ab ,则输出2a =;则程序中需要做减法的次数为4, 故选:C .4、完善程序框图:完善程序框图问题,结合初始条件和输出结果,分析控制循环的变量应满足的条件或累加、累乘的变量的表达式.例17、【2020届河南省商丘周口市部分学校联考高三5月质量检测数学】宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:“松长六尺,竹长两尺,松日自半,竹日自倍,何日竹逾松长?”如图是解决此问题的一个程序框图,其中a 为松长、b 为竹长,则矩形框与菱形框处应依次填A .2a a a =+;a b <B .2aa a =+;a b < C .2a a a =+;a b ≥ D .2aa a =+;a b > 【答案】B【解析】松日自半,则表示松每日增加原来长度的一半,即矩形框应填2aa a =+;何日竹逾松长,则表示竹长超过松长,即松长小于竹长,即菱形框应填ab <. 故选:B例18、【2019·全国1·理T8文T9】下图是求12+12+12的程序框图,图中空白框中应填入( )A.A=12+A B.A=2+1A C.A=11+2AD.A=1+12A【答案】A【解析】执行第1次,A=12,k=1≤2,是,第一次应该计算A=12+12=12+A ,k=k+1=2;执行第2次,k=2≤2,是,第二次应该计算A=12+12+12=12+A,k=k+1=3;执行第3次,k=3≤2,否,输出,故循环体为A=12+A,故选A. 例19、【2018·全国2·理T7文T8】为计算S=1-12+13−14+…+199−1100,设计了右侧的程序框图,则在空白框中应填入( ) A.i=i+1 B.i=i+2 C.i=i+3 D.i=i+4【答案】B【解析】由于N=0,T=0,i=1,N=0+11=1,T=0+11+1=12,i=3,N=1+13,T=12+14,i=5…最后输出S=N-T=1-12+13−14+…+199−1100,一次处理1i 与1i+1两项,故i=i+2. 例20、下面程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在和两个空白框中,可以分别填入( ) A.A>1 000和n=n+1 B.A>1 000和n=n+2 C.A ≤1 000和n=n+1 D.A ≤1 000和n=n+2【答案】D【解析】因为要求A 大于1 000时输出,且程序框图中在“否”时输出,所以“”中不能填入A>1 000,排除A,B.又要求n 为偶数,且n 初始值为0,所以“”中n 依次加2可保证其为偶数,故选D.例21、执行下面的程序框图,当输入的x 的值为4时,输出的y 的值为2,则空白判断框中的条件可能为( ) A.x>3B.x>4C.x ≤4D.x ≤5【答案】B【解析】因为输入的x 的值为4,输出的y 的值为2,所以程序运行y=log 24=2. 故x=4不满足判断框中的条件,所以空白判断框中应填x>4.例22、【2020年高考浙江】设集合S ,T ,S ⊆N *,T ⊆N *,S ,T 中至少有2个元素,且S ,T 满足:①对于任意的x ,y ∈S ,若x ≠y ,则xy ∈T ;②对于任意的x ,y ∈T ,若x <y ,则y x∈S .下列命题正确的是A .若S 有4个元素,则S ∪T 有7个元素B .若S 有4个元素,则S ∪T 有6个元素C .若S 有3个元素,则S ∪T 有5个元素D .若S 有3个元素,则S ∪T 有4个元素 【答案】A【解析】首先利用排除法:若取{}1,2,4S =,则{}2,4,8T =,此时{}1,2,4,8ST =,包含4个元素,排除选项D ; 若取{}2,4,8S =,则{}8,16,32T =,此时{}2,4,8,16,32S T =,包含5个元素,排除选项C ;若取{}2,4,8,16S =,则{}8,16,32,64,128T =,此时{}2,4,8,16,32,64,128S T =,包含7个元素,排除选项B ;下面来说明选项A 的正确性:设集合{}1234,,,S p p p p =,且1234p p p p <<<,*1234,,,p p p p N ∈,则1224p p p p <,且1224,p p p p T ∈,则41p S p ∈, 同理42p S p ∈,43p S p ∈,32p S p ∈,31p S p ∈,21p S p ∈, 若11p =,则22p ≥,则332p p p <,故322p p p =即232p p =, 又444231p p p p p >>>,故442232p p p p p ==,所以342p p =, 故{}232221,,,S p p p =,此时522,p T p T ∈∈,故42p S ∈,矛盾,舍.若12p ≥,则32311p p p p p <<,故322111,p pp p p p ==即323121,p p p p ==, 又44441231p p p p p p p >>>>,故441331p p p p p ==,所以441p p =, 故{}2341111,,,S p p p p =,此时{}3456711111,,,,p p p p p T ⊆.若q T ∈, 则31q S p ∈,故131,1,2,3,4i q p i p ==,故31,1,2,3,4i q p i +==,即{}3456711111,,,,q p p p p p ∈,故{}3456711111,,,,p p p p p T =, 此时{}234456711111111,,,,,,,S T p p p p p p p p ⋃=即S T 中有7个元素.故A 正确.例23、【2020年高考全国II 卷理数】0-1周期序列在通信技术中有着重要应用.若序列12na a a 满足{0,1}(1,2,)i a i ∈=,且存在正整数m ,使得(1,2,)i m i a a i +==成立,则称其为0-1周期序列,并称满足(1,2,)i m i a a i +==的最小正整数m 为这个序列的周期.对于周期为m 的0-1序列12na a a ,11()(1,2,,1)m i i k i C k a a k m m +===-∑是描述其性质的重要指标,下列周期为5的0-1序列中,满足1()(1,2,3,4)5C k k ≤=的序列是A .11010B .11011C .10001D .11001【答案】C【解析】由i m i a a +=知,序列i a 的周期为m ,由已知,5m =,511(),1,2,3,45i i k i C k a a k +===∑对于选项A ,511223344556111111(1)()(10000)55555i i i C a a a a a a a a a a a a +===++++=++++=≤∑52132435465711112(2)()(01010)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满足; 对于选项B ,51122334455611113(1)()(10011)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满足; 对于选项D ,51122334455611112(1)()(10001)5555i i i C a a a a a a a a a a a a +===++++=++++=∑,不满足; 故选:C。
高考数学复习考点知识与题型专题讲解72 算法与程序框图

由题意,此时应该不满足条件,退出循环,输出 S 的值为 ; 故判断框中填写的内容可以是 n≤6. 故选:C.
D.n<9
【再练一题】 某程序框图如图所示,若输出的 S=26,则判断框内应填( )
7 / 32
A.k>3?
B.k>4?
C.k>5?
D.k>6?
【解答】解:程序在运行过程中,各变量的值变化如下表:
> ,是, = , = • = ( ) = ; k 0
k 1 S a1+S x0 a1+ a2+a3x0 x0 a1+a2x0+a3x02
> ,是, = , = • = . k 0
k 0 S a0+S x0 a0+a1x0+a2x02+a3x03
> ,否,输出 = . k 0
S a0+a1x0+a2x02+a3x03
高考数学复习考点知识与题型专题讲解
专题 72 算法与程序框图 考纲
1.了解算法的含义,了解算法的思想 2.理解程序框图的三种基本逻辑结构:顺序结构、条件结构、循环结构. 3.了解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.
基础知识融会贯通
1.算法与程序框图 (1)算法 ①算法通常是指按照一定规则解决某一类问题的明确和有限的步骤. ②应用:算法通常可以编成计算机程序,让计算机执行并解决问题. (2)程序框图 定义:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形. 2.三种基本逻辑结构
. 语句 b WHILE 条件 WHILE
循环体
WEND
重点难点突破
【题型一】算法的基本结构 【典型例题】
高考数学复习知识点归类与解题方法讲解8---程序框图

2 / 14
1.【广东省东莞市 2019 届高三第二学期高考冲刺试题(最后一卷)】执行如图的程序 框图,依次输入 x1 = 17,x2 = 19,x3 = 20,x4 = 21,x5 = 23,则输出的 S 值及其意 义分别是
A. S = 4 ,即 5 个数据的方差为 4 B. S = 4 ,即 5 个数据的标准差为 4 C. S = 20 ,即 5 个数据的方差为 20 D. S = 20 ,即 5 个数据的标准差为 20 【答案】A 【解析】根据程序框图,输出的 S 是 x1 = 17,x2 = 19,x3 = 20,x4 = 21,x5 = 23这 5
运算法是解决本题的关键. 4.【山东省临沂市、枣庄市 2019 届高三第二次模拟预测数学】执行如图所示的程序 框图,输出 n 的值为
A. 6 C. 8 【答案】C
B. 7 D. 9
【解析】由程序框图可知:
1
2
3
n
1 2 3 n
1
S = log2 2 + log2 3 + log2 4 + ⋅⋅⋅ + log2 n +1 = log2 2 ⋅ 3 ⋅ 4 ⋅⋅⋅ n +1 = log2 n +1 ,
A.14
高考数学复习:算法与程序框图、基本算法语句

A.6
B.7
C.8
D.12
【解析】选C.S=0,n=1,S>1 009? 否
2 020
S=0+(1 )1 ,n=1+1=2,S1>009 ? 否
3
2 020
S=0+(1 )1 (1,n)2=2+1=3,S>1 009? 否
33
2 020
由( 1 )1 ( 1 )2 ( 1 )3 ( 1 )m
A.1B.1C. 3D.1
4
2
4
3
【解析】选A.由题意,得2×[2×(2x+1)+1]+1≥55, 解得x≥6,所以输出的x不小于55的概率为 8-6=1 .
84
思想方法系列15——程序框图中的分类讨论思想 【思想诠释】每个数学结论都有其成立的条件,每一种 数学方法的使用也往往有其适用范围,在我们所遇到的 数学问题中,有些问题的结论不是唯一确定的,有些问 题的结论在解题中不能以统一的形式进行研究,还有些
由( 1 )1 ( 1 )2 ( 1 )3 ( 1 )m
33 3
3
1[1-( 1 )m ] 33
1 [1-( 1
)m ]>1
009 ,得
1-1
23
2 020
3
1 < 1 ,即3m>1 010,m≥7,”………………抓本质
3m 1 010
“由此可知S=0+ (1 )1 (1 )2 (1 )3 (1 )7,
第八章 算法、复数、推理与证明 第一节 算法与程序框图、
基本算法语句(全国卷5年11考)
【知识梳理】 1.算法 算法通常是指按照一定_规__则__解决某一类问题的 __明__确__和__有__限__的__步__骤__.这些步骤必须是_明__确__和_有__效__ 的,而且能够在有限步之内完成.
高三数学算法知识点总结之程序框图

高三数学算法知识点总结之程序框图1、程序框图基本概念:(一)程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。
一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。
(二)构成程序框的图形符号及其作用学习这部分知识的时候,要掌握各个图形的形状、作用及使用规则,画程序框图的规则如下:1、使用标准的图形符号。
2、框图一般按从上到下、从左到右的方向画。
3、除判断框外,大多数流程图符号只有一个进入点和一个退出点。
判断框具有超过一个退出点的唯一符号。
4、判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果。
5、在图形符号内描述的语言要非常简练清楚。
(三)、算法的三种基本逻辑结构:顺序结构、条件结构、循环结构。
1、顺序结构:顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,它是任何一个算法都离不开的一种基本算法结构。
顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤。
如在示意图中,A 框和B框是依次执行的,只有在执行完A框指定的操作后,才能接着执行B框所指定的操作。
2、条件结构:条件结构是指在算法中通过对条件的判断根据条件是否成立而选择不同流向的算法结构。
条件P是否成立而选择执行A框或B框。
无论P条件是否成立,只能执行A框或B框之一,不可能同时执行A框和B框,也不可能A框、B框都不执行。
一个判断结构可以有多个判断框。
3、循环结构:在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构,反复执行的处理步骤为循环体,显然,循环结构中一定包含条件结构。
循环结构又称重复结构,循环结构可细分为两类:(1)、一类是当型循环结构,如下左图所示,它的功能是当给定的条件P成立时,执行A框,A框执行完毕后,再判断条件P是否成立,如果仍然成立,再执行A框,如此反复执行A框,直到某一次条件P不成立为止,此时不再执行A框,离开循环结构。
高三数学程序框图

x1=x2? 否
输出两不等根x1,x2
原方程无实根
结束
例 5、 编写程序,输入 一元二次不等式 ax2+bx+c>0(a>0) 的系数,输出它
的结果.
开始 输入a,b,c
△=b24ac
p=-b/2a
q | | / 2a
否 △≥0? 是 x1=p+q,x2=p-q 是 x1=x2? 否 输出x>x1或x<x2 输出全体实数
x≠xx的全体实数
结束
开始
利用二分 法求 2 的 近似值.
f(x)=x2-2 x1=1 x2=2 m=(x1+x2)/2 f (m)=0 否 f(x1)f(m)>0 是 x1=m x2=m 是 x1=m x2=m 否
否
|x1-x2|<0.005 是 m=(x1+x2)/2
二分法解方程
输出所求的近似根m 结束
大话西游发布站 / 大话西游发布站 我顺着楼梯来到二楼,婴儿的啼哭声从卧室里传来。妻子敲开门,马天栓一见是肖燕,便赶紧把她往屋里让,“弟妹,你来得 正好,这小祖宗就要把人吵死了,你快去看看„„”说完,他如释重担地拉我去了客厅。 “六叔,”客厅的门半开着,念儿探进头跟我打着招呼,“我说六叔在我家,你还不信,怎么样?让我猜中了吧?”念儿嬉 笑着做了个鬼脸。 念儿和宝根背着书包走了进来。我起身要走,马天栓执意要我陪他喝酒谈心,我拗他不过,只好坐了下来。不一会儿,饭菜做 好了,我们两家人围坐在一起又吃起团圆大餐来。 “来,我们哥俩喝上两盅。”马天栓把酒杯倒满 “祝贺大哥喜得贵子。”我们哥俩碰起杯来。 “六弟,你什么都好,就是 这个老观念要改一改喽,现在的形势变了,男孩女孩都一样。依我看现在的社会,男孩却成了一种负担,又买楼又要车,你想 想看,这不是负担是什么?” “大哥,我们都是过来的人,话是这么说,但事却不能这么做„„有个儿子心里还是踏实„„” “你看,还是转不过弯来吧?别的不说,就说咱们村的张老汉,有七个姑娘,整天的不是这个姑娘来就是那个姑娘去,大包 小包的,你看把张老汉美得天天哼着小曲唱二黄„„”马天栓闷了口小酒,继续说:“远的不说就说你爹和你娘,八个儿子, 辛苦了一辈子,到头来,有哪一个在他们身边照顾他们的?” “天栓,你喝多了!”马大嫂急忙阻止他的话。马天栓摆了摆手,“我说的都是实情,六弟,你说我说的对不对?”我默然 了,无话以对。 “当然,我不是说我们做儿子的不孝敬父母,恰恰相反,我们这做儿子的被负担压地喘不过气来。” “天栓,别扯远了,你 忘了我们说好的,让六弟给孩子起个名字。”马大嫂打断了他的话。 “你不说我还真把这事给忘了,你就给我们的儿子起个名字吧。” “我可担当不起,现在的孩子可不像我们那个年代,起名 是有讲究的,你还是找个起名先生吧„„” “那些人我信不过,你的话我最爱听,你就随便来一个,叫啥都行。 “不是叫马奔驰吗?我听念儿妹妹说的„„”宝根插上 了话。 “不行不行„„”马天栓摇着手,“笨啊痴啊的,不吉利。” “骏马奔驰在辽阔的草原上„„你看大名叫马骏、小名叫苗苗 怎么样?„„” “好!这个名字我爱听!就叫马骏!就叫苗苗!”我的话还没说完,马天栓就拍案叫绝,把马骏的名字定了下来。 “来,感 谢六弟给我儿子起了个好名字,咱哥俩再干一杯!”我们俩又喝了起来。 肖艳和宝根回了家,临走时嘱咐我别忘了接小荷。马大嫂去了卧室,念儿也去做功课。我和马天栓喝了很多酒,谈到很晚很晚。 我忽然想起妻子嘱咐我的话,告辞了马天栓,踉踉跄跄地向学校走去„„ 来到街口的路灯下,我倚靠在电线杆旁。这是我最熟悉的地方,自从小荷上了高中,我便天天晚上到这儿接她,无论刮风下雨, 从来没有停歇过。 马天栓的话在我脑海中环绕„„ “一个姑娘,一等人;两个姑娘,上等人;三个姑娘,人上人„„你想过没有,如果大荷、 荷花和小荷都在你身边的话,那该有多好啊。” 想着想着,大荷、荷花和小荷背着书包,手拉手地向我走来„„
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
程序框图
A组
1.(2009年高考卷改编)阅读如图所示的程序框图,运行相应的程序,输出的结果是________.
解析:试将程序分步运行:
第一循环:S=
1
1-2
=-1,n=2;
第二循环:S=
1
1-(-1)
=
1
2
,n=3;
第三循环:S=
1
1-1
2
=2,n=4.答案:4
2.(2009年高考、卷改编)如果执行如图的程序框图,输入x=-2,h=0.5,那么输出的各个数的和等于________.
解析:由框图可知,当x=-2时,y=0;
当x=-1.5时,y=0;当x=-1时,y=0;
当x=-0.5时,y=0;当x=
时,y=0;
当x=0.5时,y=0.5;当x=1时,y=1;
当x=1.5时,y=1;当x=2时,y=1.
∴输出的各数之和为3.5. 答案:3.5
3.(2009年高考卷改编)执行下面的程序框图,输出的T=________.
第2题 第3题
解析:据框图依次为:
⎩⎨⎧ S =5,
n =2,
T =2,⎩⎨⎧ S =10,n =4,T =6,⎩⎨⎧ S =15,n =6,T =12,⎩⎨⎧ S =20,n =8,T =20,⎩⎨⎧ S =25,n =10,T =30,
故此时应输出T =30.答案:30
4.(2010年市高三调研)阅读下面的流程图,若输入a =6,b =1,则输出的结果是________.
解析:a =6,b =1,则x =5>2,再次进入循环得a =4,b =6,此时x =2,退出循环.故输出2.答案:2
5.(2010年、锡、常、镇四市高三调研)阅读如图所示的程序框图,若输入的n 是100,则输出的变量S 的值是多少?
第5题 第6题 解析:由循环结构可得S =100+99+…+3+2=5049.
故输出的变量S 的值为5049.答案:5049
6.(原创题)已知如图所示的程序框图(未完成),设当箭头a指向①时,输出的结果为S=m,当箭头a指向②时,输出的结果为S=n,求m+n的值.解:(1)当箭头a指向①时,输出S和i的结果如下:
S0+1 0+2 0+3 0+4 0+5
i 2 3 4 5 6
∴S=m=5.
(2)当箭头a指向②时,输出S和i的结果如下:
S0+1 0+1+2 0+1+2+3 0+1+2+3+4
i 2 3 4 5
S0+1+2+3+4+5
i 6
∴S=n=1+2+3+4+5=15,于是m+n=20.
B组
1.(2010年调研)如图是一算法的程序框图,若此程序运行结果为s=720,则在判断框中应填入的关于k的判断条件是__________.
解析:s=10×9×8,10≥8,9≥8,8≥8,判断条件为“是”时进入循环体,7≥8判断条件为“否”,跳出循环,输出s.答案:k≥8
(第1题)(第2题)(第3题)
2.若R=8,则下列流程图的运行结果为___4___.
3.给出一个如图所示的程序框图,若要使输入的x的值与输出的y的值相等,则x的可能值的个数为________.
解析:x≤2时,x2=x,∴x=0或x=1;2<x≤5时,2x-3=x,∴x=3;
x>5时,1
x
=x,∴x=-1或x=1(都舍去).所以共有3个可取值.答案:3
4.如图,该程序运行后输出的结果为________.
解析:A=1≤9,“是”,则S=0+1,A变为2;A=2≤9,“是”,则S =0+1+2,A变为3;…;A=9≤9,“是”,则S=0+1+…+9,A变为10;A=10≤9,“否”,则输出S=45.
答案:45
5.已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框①处应填____.
解析:a=1时进入循环,此时b=21=2;a=2时再进入循环,此时b=22=4;a=3时再进入循环,此时b=24=16,∴a=4时应跳出循环,∴循环满足的条件为a≤3,∴填3.
答案:3
(第4题)(第5题)(第6题)
6.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是________.
解析:A=1≤M,“是”,则S=2×1+1=3,A变为2;
A=2≤M,“是”,则S=2×3+1=7,A变为3;
A=3≤M,“是”,则S=2×7+1=15,A变为4;
A=4≤M,“是”,则S=2×15+1=31,A变为5;
A=5≤M,“是”,则S=2×31+1=63,A变为6;
A=6≤M,“否”,则跳出循环,故填5.
7.(2009年高考卷改编)某篮球队6名主力队员在最近三场比赛中投进的三分球
个数如下表所示: 队员i
1 2 3 4 5 6 三分球个数 a 1 a 2 a 3 a 4 a 5 a 6
则图中判断框应填______,输出的s =______.
(注:框图中的赋值符号“←”也可以写成“=”或“:=”)
(第7题) (第8题)
解析:由题意该程序框图实际上是求该6名队员在最近三场比赛中投进三分球总数,故判断框应填i ≤6或i <7,输出s 为a 1+a 2+a 3+a 4+a 5+a 6.
8.(2009年高考卷)某算法的程序框图如图所示,则输出量y 与输入量x 满足的
关系式是________.
解析:由程序框图的条件结构知:x >1时,y =x -2;x ≤1时,y =2x .
故y =⎩⎨⎧
2x (x ≤1),x -2 (x >1). 9.某流程如图所示,现输入如下四个函数 ①f (x )=x 2;②f (x )=1x ;③f (x )=ln x ;④f (x )=sin x .
则输入函数与输出函数为同一函数的是_____________.
解析:由程序框图易知只需函数为奇函数且存在零点时,输出与输入函数必是同一函数,分析上述四个函数,易知只有y =sin x 满足条件.答案:④
(第9题) (第10题)
10.如图所示的算法中,令a =tan θ,b =sin θ,c =cos θ,若在集合
⎩
⎨⎧⎭
⎬⎫θ⎪⎪⎪ -π4<θ<3π4,θ≠0,π4,π2中,给θ取一个值,输出的结果是sin θ,求θ值所在的围.
解:由框图知,要输出a 、b 、c 中最大的,当θ∈(
π2,34π)时,sin θ最大. ∴θ值所在的围为(π2,34π). 11.画出计算1+12+13+…+19+110
值的一个算法的流程图.
(第11题) (第12题)
12.到银行办理个人异地汇款(不超过100万元)时,银行要收取一定的手续费.汇
款额不超过100元,收取1元手续费;超过100元但不超过5000元,按汇款额的1%收取;超过5000元,一律收取50元手续费.设计算法求汇款额为x 元时,银行收取的手续费y 元,只画出流程图.
解:要计算手续费,首先要建立汇款数与手续费之间的函数关系式,依题意知y =⎩⎨⎧ 1 (0<x ≤100),
x ×0.01 (100<x ≤5000),
50 (5000<x ≤1000000).
流程图如上图所示.。
