第二章课后习题与答案要点
微观经济学原理课后习题及答案-第二章需求、供给和均衡价格

微观经济学原理课后习题及答案-第二章需求、供给和均衡价格第一部分教材配套习题本习题详解1. 下列各事件对x 商品的需求有何影响?(1) x 商品的生产厂商投入大量资金做广告宣传。
(2) 生产x 商品的工人的工资增加了。
(3) y 商品是x 商品的替代品,y 商品的价格下降了。
(4) 消费者的收入增加了。
解答:(1)x 商品的生产厂商投入大量资金做广告宣传,提高商品的知名度和消费者对商品的偏好,导致在每一价格下,消费者对商品需求量增加,使需求曲线向右移动。
(2) 生产x 商品的工人的工资增加了。
对x 商品的需求没有直接影响,需求曲线不变,但是工人的工资增加,增加了生产成本,使供给曲线向左上移动,需求不变供给减少,导致均衡价格上升,均衡数量减少。
(3) y商品是x 商品的替代品,y 商品的价格下降了,x 商品相对贵了,消费者用y 商品替代x 商品,导致在每一价格下,消费者对商品需求量减少,使需求曲线向左移动。
(4) 若消费者消费的是正常商品,消费者的收入增加了,在每一价格下,消费者对商品需求量增加,使需求曲线向右移动;若消费者消费的是劣商品(抵挡商品),导致在每一价格下,消费者对商品需求量减少,使需求曲线向左移动。
2. 下列各事件对棉花供给有何影响?(1) 气候恶劣导致棉花歉收。
(2) 种植棉花所需的化肥的价格上升。
(3) 政府对种植棉花的农户实施优惠政策。
(4) 棉花价格上升。
下列事件对棉花供给有何影响?(1)气候恶劣导致棉花歉收。
解答:( 1)棉花的供给曲线会左移。
因为恶劣气候导致的棉花歉收在棉花价格不变的情况下,会使棉花的供给数量减少,棉花的供给曲线会左移。
(2)棉花的供给曲线会左移。
因为化肥价格上升使得棉花的生产成本上升、利润下降,在任一价格水平下,农户都会缩小棉花种植面积,导致棉花供给数量下降, 棉花的供给曲线会左移。
(3)棉花的供给曲线会右移。
因为政府对种植棉花农户的优政策将激励农户的生产积极性,在任价格水平下,户都会大棉花种面积,导致棉花供给数量増加,棉花的供给曲线会右移。
2023版《概论》第二章 新民主主义革命理论--课后习题答案

第二章新民主主义革命理论1、什么是新民主主义革命的总路线?如何理解新民主主义革命的领导权问题?(1)1948年,毛泽东在《晋绥干部会议上的讲话》中完整地表述了新民主主义革命总路线的内容,即无产阶级领导的,人民大众的,反对帝国主义、封建主义和官僚资本主义的革命。
新民主主义的政治、经济、文化纲领是新民主主义革命总路线的展开和具体化,指明了新民主主义革命的发展方向。
中国革命必须走农村包围城市、武装夺取政权的革命道路。
新民主主义革命的总路线指明了革命的目的、对象、动力、领导力量以及革命的性质和前途。
具体内容如下:①新民主主义革命的目的新民主主义革命的目的是推翻买办的封建的生产关系以及腐朽的政治上层建筑,从根本上解放被束缚的生产力。
②新民主主义革命的对象近代中国社会的性质和主要矛盾,决定了中国革命的主要敌人就是帝国主义、封建主义和官僚资本主义。
帝国主义是中国革命的首要对象,是中国社会进步和发展的最大障碍,是近代中国贫困落后和一切灾难祸害的总根源。
封建地主阶级是帝国主义统治中国和封建军阀实行专制统治的社会基础,是中国经济现代化和政治民主化的主要障碍。
官僚资本主义是依靠帝国主义、勾结封建势力、利用国家政权力量而发展起来的买办的封建的国家垄断资本主义。
官僚资本主义对广大劳动人民的残酷剥削和对民族工商业的巧取豪夺,严重地束缚了中国社会生产力的发展,因此也是中国革命的对象。
③新民主主义革命的动力新民主主义革命的动力包括无产阶级、农民阶级、城市小资产阶级和民族资产阶级。
无产阶级是中国革命最基本的动力。
中国无产阶级是新的社会生产力的代表,是近代中国最进步的阶级,是中国革命的领导力量。
农民是中国革命的主力军,其中的贫农是无产阶级最可靠的同盟军,而中农是无产阶级可靠的同盟军。
城市小资产阶级是无产阶级的可靠同盟者。
民族资产阶级也是中国革命的动力之一。
④新民主主义革命的领导力量无产阶级的领导权是中国革命的中心问题,也是新民主主义革命理论的核心问题。
结构化学课后答案第2章习题原子的结构与性质

1. 简要说明原子轨道量子数及它们的取值范围?解:原子轨道有主量子数n ,角量子数l ,磁量子数m 与自旋量子数s ,对类氢原子(单电子原子)来说,原子轨道能级只与主量子数n 相关R n Z E n22-=。
对多电子原子,能级除了与n 相关,还要考虑电子间相互作用。
角量子数l 决定轨道角动量大小,磁量子数m 表示角动量在磁场方向(z 方向)分量的大小,自旋量子数s 则表示轨道自旋角动量大小。
n 取值为1、2、3……;l =0、1、2、……、n -1;m =0、±1、±2、……±l ;s 取值只有21±。
2. 在直角坐标系下,Li 2+ 的Schrödinger 方程为________________ 。
解:由于Li 2+属于单电子原子,在采取“B -O” 近似假定后,体系的动能只包括电子的动能,则体系的动能算符:2228ˆ∇-=mh T π;体系的势能算符:r e r Ze V 0202434ˆπεπε-=-= 故Li 2+ 的Schrödinger 方程为:ψψE r εe mh =⎥⎦⎤⎢⎣⎡π-∇π-20222438 式中:z y x ∂∂+∂∂+∂∂=∇2222222,r = ( x 2+ y 2+ z 2)1/23. 对氢原子,131321122101-++=ψψψψc c c ,其中 131211210,,-ψψψψ和都是归一化的。
那么波函数所描述状态的(1)能量平均值为多少?(2)角动量出现在 π22h 的概率是多少?,角动量 z 分量的平均值为多少?解: 由波函数131321122101-++=ψψψψc c c 得:n 1=2,l 1=1,m 1=0; n 2=2, l 2=1,m 2=1; n 3=3,l 3=1,m 3=-1;(1)由于131211210,,-ψψψψ和都是归一化的,且单电子原子)(6.1322eV nz E -=故(2) 由于 1)l(l M +=||, l 1=1,l 2=1,l 3=1,又131211210,,-ψψψψ和都是归一化的,故()eV c eV c c eV c eV c eV c E c E c E c E cE ii i 232221223222221323222121299.1346.13316.13216.13216.13-+-=⎪⎭⎫ ⎝⎛⨯-+⎪⎭⎫ ⎝⎛⨯-+⎪⎭⎫ ⎝⎛⨯-=++==∑2223232221212h h h M c M c M c M cM ii i ++==∑则角动量为π22h 出现的概率为:1232221=++c c c(3) 由于π2hm M Z ⨯=, m 1=0,m 2=1,m 3=-1; 又131211210,,-ψψψψ和都是归一化的, 故4. 已知类氢离子 He +的某一状态波函数为:()022-023021e 222241a r a r a ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛π (1)此状态的能量为多少?(2)此状态的角动量的平方值为多少? (3)此状态角动量在 z 方向的分量为多少? (4)此状态的 n , l , m 值分别为多少? (5)此状态角度分布的节面数为多少?解:由He +的波函数()002302/1222241a 2r 2-e a r a ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛π=ψ,可以得到:Z=2,则n =2, l =0, m =0 (1) He +为类氢离子,)(6.1322eV n z E -=,则eV eV eV n z E 6.13)(226.13)(6.132222-=⨯-=-=(2) 由l =0,21)l(l M+=2,得0)10(02=+=+=221)l(l M(3) 由|m |=0, m M Z =,得00=== m M Z(4) 此状态下n =2, l =0, m =0(5) 角度分布图中节面数= l ,又l =0 ,故此状态角度分布的节面数为0。
(完整版)机械振动课后习题和答案第二章习题和答案

2.1 弹簧下悬挂一物体,弹簧静伸长为δ。
设将物体向下拉,使弹簧有静伸长3δ,然后无初速度地释放,求此后的运动方程。
解:设物体质量为m ,弹簧刚度为k ,则:mg k δ=,即:n ω==取系统静平衡位置为原点0x =,系统运动方程为: δ⎧+=⎪=⎨⎪=⎩&&&00020mx kx x x (参考教材P14)解得:δω=()2cos n x t t2.2 弹簧不受力时长度为65cm ,下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放,试求物体的运动方程、振幅、周期及弹簧力的最大值。
解:由题可知:弹簧的静伸长0.850.650.2()m =-=V所以:7(/)n rad s ω=== 取系统的平衡位置为原点,得到:系统的运动微分方程为:20n x x ω+=&& 其中,初始条件:(0)0.2(0)0x x=-⎧⎨=⎩& (参考教材P14) 所以系统的响应为:()0.2cos ()n x t t m ω=- 弹簧力为:()()cos ()k n mg F kx t x t t N ω===-V因此:振幅为0.2m 、周期为2()7s π、弹簧力最大值为1N 。
2.3 重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置,另一重物2m 从高度为h 处自由落到1m 上而无弹跳,如图所示,求其后的运动。
解:取系统的上下运动x 为坐标,向上为正,静平衡位置为原点0x =,则当m 有x 位移时,系统有: 2121()2T E m m x =+& 212U kx =由()0T d E U +=可知:12()0m m x kx ++=&& 即:12/()n k m m ω=+系统的初始条件为:⎧=⎪⎨=-⎪+⎩&2020122m gx k m x gh m m (能量守恒得:221201()2m gh m m x =+&) 因此系统的响应为:01()cos sin n n x t A t A t ωω=+其中:ω⎧==⎪⎨==-⎪+⎩&200021122n m g A x k x m g ghk A k m m即:ωω=-2()(cos )n n m g x t t t k2.4 一质量为m 、转动惯量为I 的圆柱体作自由纯滚动,圆心受到一弹簧k 约束,如图所示,求系统的固有频率。
流体力学课后习题答案第二章

第二章 流体静力学2-1 密闭容器测压管液面高于容器内液面h=1.8m,液体密度为850kg/m3, 求液面压强。
解:08509.8 1.814994Pa p gh ρ==⨯⨯=2-2 密闭水箱,压力表测得压强为4900Pa,压力表中心比A 点高0.4米,A 点在液面下1.5m ,液面压强。
解:0()490010009.8(0.4 1.5) 49009800 1.15880PaM B A p p g h h ρ=+-=+⨯⨯-=-⨯=-2-3 水箱形状如图,底部有4个支座。
试求底面上的总压力和四个支座的支座反力,并讨论总压力和支座反力不相等的原因。
解:底面上总压力(内力,与容器内的反作用力平衡)()10009.81333352.8KN P ghA ρ==⨯⨯+⨯⨯=支座反力支座反力(合外力)3312()10009.8(31)274.4KN G g V V ρ=+=⨯⨯+=2-4盛满水的容器顶口装有活塞A ,直径d=0.4m ,容器底直径D=1.0m ,高h=1.8m 。
如活塞上加力为2520N(包括活塞自重)。
求容器底的压强和总压力。
解:压强2252010009.8 1.837.7kPa (0.4)/4G p gh A ρπ=+=+⨯⨯= 总压力 237.71/429.6KN P p A π=⋅=⨯⋅=2-5多管水银测压计用来测水箱中的表面压强。
图中高程单位为m ,试求水面的绝对压强。
解:对1-1等压面02(3.0 1.4)(2.5 1.4)p g p g ρρ+-=+-汞对3-3等压面 2(2.5 1.2)(2.3 1.2)a p g p g ρρ+-=+-汞将两式相加后整理0(2.3 1.2)(2.5 1.4)(2.5 1.2)(3.0 1.4)264.8kPap g g g g ρρρρ=-+-----=汞汞绝对压强 0.0264.8+98=362.8kPa abs a p p p =+=2-6水管A 、B 两点高差h 1=0.2m ,U 形管压差计中水银液面高差h 2=0.2m 。
计算机操作系统(第四版)课后习题答案第二章

第二章1.什么是前趋图?为什么要引入前趋图?答:前趋图(PrecedenceGraph)是一个有向无循环图,记为DAG(DirectedAcyclicGraph),用于描述进程之间执行的前后关系。
2.画出下面四条诧句的前趋图:S1=a:=x+y;S2=b:=z+1;S3=c:=a-b;S4=w:=c+1;答:其前趋图为:3.4.5.6.a.未建立任何进程的程序,都不能作为一个独立的单位来运行。
7.试说明PCB的作用?为什么说PCB是进程存在的唯一标志?a.PCB是进程实体的一部分,是操作系统中最重要的记录型数据结构。
PCB中记录了操作系统所需的用于描述进程情况及控制进程运行所需的全部信息。
因而它的作用是使一个在多道程序环境下不能独立运行的程序(含数据),成为一个能独立运行的基本单位,一个能和其它进程并发执行的进程。
b.在进程的整个生命周期中,系统总是通过其PCB对进程进行控制,系统是根据进程的PCB而不是任何别的什么而感知到该进程的存在的,所以说,PCB是进程存在的唯一标志。
11.试说明进程在三个基本状态之间转换的典型原因。
答:(1)就绪状态→执行状态:进程分配到CPU资源(2)执行状态→就绪状态:时间片用完(3)执行状态→阻塞状态:I/O请求(4)阻塞状态→就绪状态:I/O完成12.为什么要引入挂起状态?该状态有哪些性质?答:引入挂起状态处于五种不同的需要:终端用户需要,父进程需要,操作系统需要,对换需要和负荷调节需要。
处于挂起状态的进程不能接收处理机调度。
10.在3)。
17.在撤销一个进程时所要完成的主要工作是什么?答:(1)根据被终止进程标识符,从PCB集中检索出进程PCB,读出该进程状态。
(2)若被终止进程处于执行状态,立即终止该进程的执行,臵调度标志真,指示该进程被终止后重新调度。
(3)若该进程还有子进程,应将所有子孙进程终止,以防它们成为不可控进程。
(4)将被终止进程拥有的全部资源,归还给父进程,或归还给系统。
第二章课后习题答案

第二章习题(二)判断题1.用户构建单片机应用系统,只能使用芯片提供的信号引脚。
(T)2.程序计数器(PC)不能为用户使用,因此它没有地址。
(T)3.内部RAM的位寻址区,只能提供位寻址使用而不能供字节寻址使用。
(F)4.在程序执行过程中,由PC提供数据存储器的读/写地址。
(F)5.80C51共有21个专用寄存器,它们的位都是可用软件设置的,因此是可以进行位寻址的。
(T)(三)填空题1. MCS-51单片机引脚信号中,信号名称带上划线表示该信号低电平或下跳变有效。
2. MCS-51单片机内部RAM的寄存区共有32 个单元,分为4 组寄存器,每组8 个单元,以R7~R0 作为寄存器名称。
3. 单片机系统复位后,(PSW)=00H,因此内部RAM寄存区的当前寄存器是第0 组,8个寄存器的单元地址为00H ~07H 。
4.通过堆栈操作实现子程序调用,首先要把PC 的内容入栈,以进行断点保护。
调用返回时再进行出栈操作,把保护的断点送回PC 。
5. 为寻址程序状态字的F0位,可使用的地址和符号有D5H 、F0 、PSW.5和D5H.5 。
6. MCS-51单片机的时钟电路包括两部分内容,即芯片内的高增益反相放大器和芯片外跨接的晶体震荡器,微调电容。
7. 在MCS-51中,位处理器的数据位存储空间是由专用寄存器的可寻址位和内部RAM为寻址区的128 个位。
8. MCS-51的4个I/O口中,P0是真正的双向口,而其他口则为准双向口,这一区别在口线电路结构中表现在口的输出缓冲器的不同上。
(四)选择题1.单片机芯片内提供了一定数量的工作寄存器,这样做的好处不应包括(A)提高程序运行的可靠性(B)提高程序运行速度(C)为程序设计提供方便(D)减少程序长度2.内部RAM中的位寻址区定义的位是给(A)位操作准备的(B)移位操作准备的(C)控制转移操作准备的(D)以上都对3.对程序计数器PC的操作(A)是自动进行的(B)是通过传送进行的(C)是通过加“1”指令进行的(D)是通过减“1”指令进行的4.以下运算中对溢于言表标志位OV没有影响或不受OV影响的运算是(A)逻辑运算(B)符号数加减法运算(C)乘法运算(D)除法运算5.单片机程序存储器的寻址范围是由程序计数器PC的位数决定的,MCS-51的PC为16位,因此其寻址范围是(A)4KB (B)64KB (C)8KB (D)128KB6.在算术运算中,与辅助进位位AC有关的是(A)二进制数(B)八进制数(C)十进制数(D)十六进制数7.以下有关PC和DPTR的结论中错误的是(A)DPTR是可以访问的而PC是不能访问的(B)它们都是16位的寄存器(C)它们都具有加“1”的功能(D)DPTR可以分为2个8位的寄存器使用,但PC不能8.PC的值是(A)当前指令前一条指令的地址(B)当前正在执行指令的地址(C)下一条指令的地址(D)控制器中指令寄存器的地址9.假定设置堆栈指针SP的值为37H,在进行子程序调用时把断点地址进栈保护后,SP的值为(A)36H (B)37H (C)38H (D)39H10. 80C51中,可使用的堆栈最大深度为(A)80个单元(B)32个单元(C)128个单元(D)8个单元11. 位处理器是单片机面向控制应用的重要体现,下列中不属于位处理器资源的是(A)位累加器CY (B)通用寄存器的可寻址位(C)专用寄存器的可寻址位(D)位操作指令集12. 在MCS-51单片机的运算电路中,不能为ALU提供数据的是(A)累加器A (B)暂存器(C)寄存器B (D)状态寄存器PSW13. 在MCS-51中(A)具有独立的专用的地址线(B)在P0口和P1口的口线作地址线(C)在P0口和P2口的口线作地址线(D)在P1口和P2口的口线作地址线。
仪器分析课后习题答案第二章

(2)分离极性物质,选用极性固定液,这时试样中各组分主要按极性顺序分离,极 性小的先流出色谱柱,极性大的后流出色谱柱。
(3)分离非极性和极性混合物时,一般选用极性固定液,这时非极性组分先出峰, 极性组分(或易被极化的组分)后出峰。
桥路工作电流、热导池体温度、载气性质和流速、热敏元件阻值及 热导池死体积等均对检测器灵敏度有影响。
15.试述氢焰电离检测器的工作原理。如何考虑其操作条件?
解:对于氢焰检测器离子化的作用机理,至今还不十分清楚。目前认 为火焰中的电离不是热电离而是化学电离,即有机物在火焰中发生自 由基反应而被电离。化学电离产生的正离子( CHO+、H3O+)和电子(e)在 外加150~300v直流电场作用下向两极移动而产生微电流。经放大后, 记录下色谱峰。 氢火焰电离检测器对大多数的有机化合物有很高的灵 敏度,故对痕量有机物的分析很适宜。但对在氢火焰中不电离的元机 化合物例如CO、CO2、SO2、N2、NH3等则不能检测。
(4)对于能形成氢键的试样、如醉、酚、胺和水等的分离。一般选择极性的或是氢 键型的固定液,这时试样中各组分按与固定液分子间形成氢键的能力大小先后流出, 不易形成氢键的先流出,最易形成氢键的最后流出。
(5)对于复杂的难分离的物质可以用两种或两种以上的混合固定液。
以上讨论的仅是对固定液的大致的选择原则,应用时有一定的局限性。事实上在 色谱柱中的作用是较复杂的,因此固定液酌选择应主要靠实践。
担体的表面积越大,固定液的含量可以越高.
12. 试比较红色担体与白色担体的性能,何谓硅烷化担体?它有何优点? 答:
(见P27)
机械制造技术第二章课后答案

第二章加工设备自动化(课后习题)2-1.实现加工设备自动化的意义是什么? (P30)答:加工设备生产率得到有效提高的主要途径之一是采取措施缩短其辅助时 间,加工设备工作过程自动化可以缩短辅助时间,改善公认的劳动条件和减轻工 人的劳动强度。
加工设备自动化是零件整个机械加工工艺过程自动化的基本问题 之一,是机械制造厂实现零件加工自动化的基础。
2-2.为什么说单台加工设备的自动化是实现零件自动化加工的基础? (P30) 答:单台加工设备的自动化能较好地满足零件加工过程中某个或几个工序的加 工半自动化和自动化的需要,为多机床管理创造了条件,是建立自动化生产线和 过渡到全盘自动化的必要前提,是机械制造业更进一步向前发展的基础。
2-3.加工设备自动化包含的主要内容与实现的途径有哪些? (P30)答:加工设备自动化主要是指实现了机床加工循环自动化和实现了辅助工作自 动化的加工设备。
其主要内容如下:匚自动装卸工件实现加工设备自动化的途径主要有以下几种:(1) 对半自动加工设备通过配置自动上下料装置以实现加工设备的完全自动化;(2) 对通用加工设备运用电气控制技、数控技术等进行自动化改造;(3) 根据家公家的特点和工艺要求设计制造专用的自动化加工设备,如组合机床等;(4) 采用数控加工设备,包括数控机床、加工中心等。
2-4.试分析一下生产率与加工设备自动化的关系? (P32)答:生产率Q=K/(1+K*tf ),式中K ——理想的工艺生产率,K=1/tq ,tq —— 切削时间,tf ——空程辅助时间。
可知:tq 和tf 对机床生产的影响是相互制约 相互促进的。
当生产工艺发展到一定水平,即工艺生产率K 提高到一定程度时, 必须提高机床自动化程度,进一步减少空程辅助时间,促使生产率不断提高。
另 一方面,在相对落后的工艺基础上实现机床自动化,生产率的提高是有限的,为 了取得良好的效果,应当在先进的工艺基础上实现机床自动化。
概率论与数理统计第二章课后习题及参考答案.

概率论与数理统计第二章课后习题及参考答案1.离散型随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=≤=.4,1,42,7.0,21,2.0,1,0)()(x x x x x X P x F 求X 的分布律.解:)0()()(000--==x F x F x X P ,∴2.002.0)01()1()1(=-=----=-=F F X P ,5.02.07.0)02()2()2(=-=--==F F X P ,3.07.01)04()4()4(=-=--==F F X P ,∴X 的分布律为2.设k a k X P 32()(==, ,2,1=k ,问a 取何值时才能成为随机变量X 的分布律.解:由规范性,a a a n n k k 2321]32(1[32lim)32(11=--=⋅=+∞→∞+=∑,∴21=a ,此时,k k X P 32(21)(⋅==, ,2,1=k .3.设离散型随机变量X 的分布律为求:(1)X 的分布函数;(2)21(>X P ;(3))31(≤≤-X P .解:(1)1-<x 时,0)()(=≤=x X P x F ,11<≤-x 时,2.0)1()()(=-==≤=X P x X P x F ,21<≤x 时,7.0)1()1()()(==+-==≤=X P X P x X P x F ,2≥x 时,1)2()1()1()()(==+=+-==≤=X P X P X P x X P x F ,∴X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=.2,1,21,7.0,11,2.0,1,0)(x x x x x F .(2)方法1:8.0)2()1()21(==+==>X P X P X P .方法2:8.02.01)21(121(1)21(=-=-=≤-=>F X P X P .(3)方法1:1)2()1()1()31(==+=+-==≤≤-X P X P X P X P .方法2:101)01()3()31(=-=---=≤≤-F F X P .4.一制药厂分别独立地组织两组技术人员试制不同类型的新药.若每组成功的概率都是0.4,而当第一组成功时,每年的销售额可达40000元;当第二组成功时,每年的销售额可达60000元,若失败则分文全无.以X 记这两种新药的年销售额,求X 的分布律.解:设=i A {第i 组取得成功},2,1=i ,由题可知,1A ,2A 相互独立,且4.0)()(21==A P A P .两组技术人员试制不同类型的新药,共有四种可能的情况:21A A ,21A A ,21A A ,21A A ,相对应的X 的值为100000、40000、60000、0,则16.0)()()()100000(2121====A P A P A A P X P ,24.0)()()()40000(2121====A P A P A A P X P ,24.0)()()()60000(2121====A P A P A A P X P ,36.0)()()()0(2121====A P A P A A P X P ,∴X 的分布律为5.对某目标进行独立射击,每次射中的概率为p ,直到射中为止,求:(1)射击次数X 的分布律;(2)脱靶次数Y 的分布律.解:(1)由题设,X 所有可能的取值为1,2,…,k ,…,设=k A {射击时在第k 次命中目标},则k k A A A A k X 121}{-== ,于是1)1()(--==k p p k X P ,所以X 的分布律为1)1()(--==k p p k X P , ,2,1=k .(2)Y 的所有可能取值为0,1,2,…,k ,…,于是Y 的分布律为1)1()(--==k p p k Y P , ,2,1,0=k .6.抛掷一枚不均匀的硬币,正面出现的概率为p ,10<<p ,以X 表示直至两个面都出现时的试验次数,求X 的分布律.解:X 所有可能的取值为2,3,…,设=A {k 次试验中出现1-k 次正面,1次反面},=B {k 次试验中出现1-k 次反面,1次正面},由题知,B A k X ==}{,=AB ∅,则)1()(1p p A P k -=-,p p B P k 1)1()(--=,p p p p B P A P B A P k X P k k 11)1()1()()()()(---+-=+=== ,于是,X 的分布律为p p p p k X P k k 11)1()1()(---+-==, ,3,2=k .7.随机变量X 服从泊松分布,且)2()1(===X P X P ,求)4(=X P 及)1(>X P .X 100000060000400000P0.160.240.240.36解: )2()1(===X P X P ,∴2e e2λλλλ--=,∴2=λ或0=λ(舍去),∴224e 32e !42)4(--===X P .)1()0(1)1(1)1(=-=-=≤-=>X P X P X P X P 222e 31e 2e 1----=--=.8.设随机变量X 的分布函数为⎩⎨⎧<≥+-=-.0,0,0,e )1(1)(x x x x F x 求:(1)X 的概率密度;(2))2(≤X P .解:(1)⎩⎨⎧<≥='=-.0,0,0,e )()(x x x x F x f x ;(2)2e 31)2()2(--==≤F X P .9.设随机变量X 的概率密度为xx Ax f e e )(+=-,求:(1)常数A ;(2))3ln 210(<<X P ;(3)分布函数)(x F .解:(1)⎰⎰+∞∞--+∞∞-+==xAx x f xx d e e d )(1A A x A x x x 2|e arctan d e 21e 2π==+=∞+∞-∞+∞-⎰,∴π2=A .(2)61|e arctan 2d e e 12)3ln 210(3ln 2103ln 210==+=<<⎰-x xx x X P ππ.(3)x xx x xx t t f x F e arctan 2d e e 12d )()(ππ=+==⎰⎰∞--∞-.10.设连续型随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧>≤<-+-≤=.a x a x a a x B A a x x F ,1,,arctan ,,0)(其中0>a ,试求:(1)常数A ,B ;(2)概率密度)(x f .解:(1) 2arcsin (lim )0()(0)(π⋅-=+=+-=-=+-→B A a x B A a F a F a x ,1)(lim )0()(2==+==⋅++→x F a F a F B A a x π,∴21=A ,π1=B .(2)⎪⎩⎪⎨⎧≥<-='=.a x a x x a x F x f ,0,,1)()(22π.11.设随机变量X 的概率密度曲线如图所示,其中0>a .(1)写出密度函数的表达式,求出h ;(2)求分布函数)(x F ;(3)求)2(a X aP ≤<.解:(1)由题设知⎪⎩⎪⎨⎧≤≤-=其他.,0,0,)(a x x ah h x f 2d )(d )(10ahx x a h h x x f a=-==⎰⎰+∞∞-,∴ah 2=,从而⎪⎩⎪⎨⎧≤≤-=其他.,0,0,22)(2a x x a a x f .y hO a x(2)0<x 时,0d 0d )()(===⎰⎰∞-∞-xxt t t f x F ,a x <≤0时,220202d )22(d 0d )()(a x a x t t a a t t t f x F xx-=-+==⎰⎰⎰∞-∞-,a x ≥时,1)(=x F ,∴X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤-<=.a x a x axa x x x F ,1,0,2,0,0)(22.(3)41411(1)2()()2(=--=-=≤<a F a F a X a P .12.设随机变量X 在]6,2[上服从均匀分布,现对X 进行三次独立观察,试求至少有两次观测值大于3的概率.解:由题意知⎪⎩⎪⎨⎧≤≤=其他.,0,62,41)(x x f ,记3}{>=X A ,则43d 41)3()(63==>=⎰x X P A P ,设Y 为对X 进行三次独立观测事件}3{>X 出现的次数,则Y ~43,3(B ,所求概率为)3()2()2(=+==≥Y P Y P Y P )(()(333223A P C A P A P C +=3227)43(41)43(333223=+⋅=C C .13.设随机变量X 的概率密度为⎩⎨⎧<<=其他.,0,10,3)(2x x x f 以Y 表示对X 的三次独立重复观察中事件}21{≤X 出现的次数,求:(1)}21{≤X 至少出现一次的概率;(2)}21{≤X 恰好出现两次的概率.解:由题意知Y ~),3(p B ,其中81d 321(2102==≤=⎰x x X P p ,(1)}21{≤X 至少出现一次的概率为512169)811(1)1(1)0(1)1(33=--=--==-=≥p Y P Y P .(2)}21{≤X 恰好出现两次的概率为51221811(81()1()2(223223=-=-==C p p C Y P .14.在区间],0[a 上任意投掷一个质点,以X 表示这个质点的坐标.设这个质点落在],0[a 中任意小区间内的概率与这个小区间的长度成正比例.试求X 的分布函数.解:0<x 时,事件}{x X ≤表示X 落在区间],0[a 之外,是不可能事件,此时0)()(=≤=x X P x F ;a x ≤≤0时,事件}{x X ≤发生的概率等于X 落在区间],0[x 内的概率,它与],0[x 的长度x 成正比,即x k x X P x F =≤=)()(,a x =时,1)(=≤x X P ,所以a k 1=,则此时axx F =)(;a x ≥时,事件}{x X ≤是必然事件,有1)(=x F ,综上,⎪⎪⎩⎪⎪⎨⎧≥<≤<=,a x a x a x x x F ,1,0,,0,0)(.15.设X ~),2(2σN ,又3.0)42(=<<X P ,求)0(>X P .解:)24222()42(σσσ-<-<-=<<X P X P 3.0)0(2(=Φ-Φ=σ,∴8.03.0)0()2(=+Φ=Φσ,∴8.0)2()2(1)0(1)0(=Φ=-Φ-=≤-=>σσX P X P .16.设X ~)4,10(N ,求a ,使得9.0)10(=<-a X P .解:)10()10(a X a P a X P <-<-=<-)22102(a X a P <-<-=)2()2(a a -Φ-Φ=9.01)2(2=-Φ=a,∴95.0)2(=Φa,查标准正态分布表知645.12=a,∴290.3=a .17.设X ~)9,60(N ,求分点1x ,2x ,使得X 分别落在),(1x -∞,),(21x x ,),(2∞x 的概率之比为3:4:5.解:由题知5:4:3)(:)(:)(2211=><<<x X P x X x P x X P ,又1)()()(2211=>+<<+<x X P x X x P x X P ,∴25.041)(1==<x X P ,33.031)(21==<<x X x P ,125)(2=>x X P ,则5833.0127)(1)(22==>-=≤x X P x X P .25.0)360()360360()(111=-Φ=-<-=<x x X P x X P ,查标准正态分布表知03601<-x ,∴03601>--x ,则75.0)360(1)360(11=-Φ-=--Φx x 查标准正态分布表,有7486.0)67.0(=Φ,7517.0)68.0(=Φ,75.02)68.0()67.0(=Φ+Φ,∴675.0268.067.03601=+=--x ,即975.571=x .5833.0360()360360()(222=-Φ=-≤-=≤x x X P x X P ,查标准正态分布表知5833.0)21.0(=Φ,∴21.03602=-x ,即63.602=x .18.某高校入学考试的数学成绩近似服从正态分布)100,65(N ,如果85分以上为“优秀”,问数学成绩为“优秀”的考生大致占总人数的百分之几?解:设X 为考生的数学成绩,则X ~)100,65(N ,于是)85(1)85(≤-=>X P X P )1065851065(1-≤--=X P 0228.09772.01)2(1=-=Φ-=,即数学成绩为“优秀”的考生大致占总人数的2.28%.19.设随机变量X 的分布律为求2X Y =的分布律.解:Y 所有可能的取值为0,1,4,9,则51)0()0(====X P Y P ,307)1()1()1(==+-===X P X P Y P ,51)2()4(=-===X P Y P ,3011)3()9(====X P Y P ,∴Y 的分布律为20.设随机变量X 在)1,0(上服从均匀分布,求:(1)X Y e =的概率密度;(2)X Y ln 2-=的概率密度.解:由题设可知⎩⎨⎧<<=其他.,0,10,1)(x x f ,(1)当0≤y 时,=≤}{y Y ∅,X 2-1-013P5161511513011X 0149P51307513011∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;e 0<<y 时,)e ()()(y P y Y P y F X Y ≤=≤=)(ln )ln (y F y X P X =≤=,此时,yy f y y y F y F y f X XY X 1)(ln 1)(ln )(ln )()(=='⋅'='=;e ≥y 时,1)()(=≤=y Y P y F Y ,0)(=y f Y ;∴⎪⎩⎪⎨⎧<<=其他.,0,e 0,1)(y y y f Y .(2)当0≤y 时,=≤}{y Y ∅,∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;当0>y 时,)e ()ln 2()()(2y Y X P y X P y Y P y F -≥=≤-=≤=)e (1)e (122y X y F X P ---=<-=,此时,222e 21)e ()e ()()(yy y X Y X F y F y f ---='⋅'-='=;∴⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2y y y f yY .21.设X ~)1,0(N ,求:(1)X Y e =的概率密度;(2)122+=X Y 的概率密度;(3)X Y =的概率密度.解:由题知22e 21)(x X xf -=π,+∞<<∞-x ,(1)0≤y 时,=≤=}e {y Y X ∅,∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;0>y 时,)(ln )ln ()e ()()(y F y X P y P y Y P y F X X Y =≤=≤=≤=,此时,2)(ln 2e 21)(ln 1)(ln )(ln )()(y X XY X y f yy y F y F y f -=='⋅'='=π;综上,⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2)(ln 2y y y f y Y π.(2)1<y 时,=≤+=}12{2y X Y ∅,∴0)()(=≤=y Y P y F Y ;1≥y 时,21()12()()(22-≤=≤+=≤=y X P y X P y Y P y F Y )2121(-≤≤--=y X y P 当1=y 时,0)(=y F Y ,故1≤y 时,0)(=y F Y ,0)(=y f Y ;当1>y 时⎰⎰------==210221212d e22d e21)(22y x y y x Y x x y F ππ,此时,41e)1(21)()(---='=y Y Y y y F y f π,综上,⎪⎩⎪⎨⎧≤>-=--.1,0,1,e )1(21)(41y y y y f y Y π.(3)0<y 时,=≤=}{y X Y ∅,∴0)()()(=≤=≤=y X P y Y P y F Y ,0≥y 时,)()()()(y X y P y X P y Y P y F Y ≤≤-=≤=≤=)()(y F y F X X --=,0=y 时,0)(=y F Y ,∴0≤y 时,有0)(=y F Y ,0)(=y f Y ;0>y 时,22e 22)()()()()(y X X Y Y Y yf y f y F y F y f -=-+=-'+'=π,综上,⎪⎩⎪⎨⎧≤>=-.0,0,0,e 22)(22y y y f yY π.22.(1)设随机变量X 的概率密度为)(x f ,+∞<<∞-x ,求3X Y =的概率密度.(2)设随机变量X 的概率密度为⎩⎨⎧>=-其他.,00,e )(x x f x 求2X Y =的概率密度.解:(1)0=y 时,0)()(=≤=y Y P y F Y ,0)(=y f Y ;0≠y 时,)()()()()(333y F y X P y X P y Y P y F X Y =≤=≤=≤=,3233331())(()()(-⋅=''='=y y f y y F y F y f XY Y ;∴⎪⎩⎪⎨⎧=≠=-.0,0,0),(31)(332y y y f y y f Y .(2)由于02≥=X Y ,故当0<y 时,}{y Y ≤是不可能事件,有0)()(=≤=y Y P y F Y ;当0≥y 时,有)()(()()()(2y F y F y X y P y X P y Y P y F X X Y --=≤≤-=≤=≤=;因为当0=y 时,0)0()0()(=--=X X Y F F y F ,所以当0≤y 时,0)(=y F Y .将)(y F Y 关于y 求导数,即得Y 的概率密度为⎪⎩⎪⎨⎧≤>-+=.,;,000)](([21)(y y y f y f y y f X X Y ,⎪⎩⎪⎨⎧≤>+=-.0,0,0),e e (21y y yyy .23.设随机变量X 的概率密度为⎪⎩⎪⎨⎧<<=其他.,0,0,2)(2ππx xx f 求X Y sin =的概率密度.解:由于X 在),0(π内取值,所以X Y sin =的可能取值区间为)1,0(,在Y 的可能取值区间之外,0)(=y f Y ;当10<<y 时,使}{y Y ≤的x 取值范围是),arcsin []arcsin ,0(ππy y - ,于是}arcsin {}arcsin 0{}{ππ<≤-≤<=≤X y y X y Y .故)arcsin ()arcsin 0()()(ππ<≤-+≤<=≤=X y P y X P y Y P y F Y ⎰⎰-+=ππyX y X x x f x x f arcsin arcsin 0d )(d )(⎰⎰-+=ππππyy x xx xarcsin 2arcsin 02d 2d 2,上式两边对y 求导,得22222121)arcsin (21arcsin 2)(yyy yyy f Y -=--+-=ππππ;综上,⎪⎩⎪⎨⎧<<-=其他.,0,10,12)(2y y y f Y π.。
第二章 课后习题及答案

第二章心理辅导的理论基础一、理论测试题(一)单项选择题1.()是根据操作性条件反射原理,强调行为的改变是依据行为后果而定的。
A.强化法B.系统脱敏法C.代币法D.来访者中心疗法2.在对学生进行心理辅导时,常使用的“强化法”属于()。
A.行为改变技术B.认知改变法C.运动改变法D.精神分析法3.在心理辅导的行为演练中,系统脱敏法是由()首创。
A.皮亚杰B.沃尔帕C.艾利斯D.罗杰斯4.心理辅导老师帮李晓明建立焦虑等级,让他想象引起焦虑的情境,然后逐渐减少焦虑等级,直至完全放松,以缓解其考试焦虑,这种方法是()。
A.强化法B.系统脱敏法C.理性一情绪疗法D.来访者中心疗法5.行为塑造法是根据()的操作条件反射研究结果而设计的培育和养成新反应或行为模式的一项行为治疗技术,是操作条件作用法强化原则的有力应用之一。
A.皮亚杰B.斯金纳C.艾利斯D.奥苏贝尔6.()就是运用代币并编制一套相应的激励系统来对符合要求的目标行为的表现进行肯定和奖励。
A.强化法B.理性一情绪疗法C.代币法D.来访者中心疗法7.李老师通过奖励小红花来表扬学生的行为,这种心理辅导方法属于()。
A.系统脱敏法B.代币法C.行为塑造法D.来访者中心疗法8.晓红是韩老师班上的学生,她孤僻、羞涩,当她主动与同学交谈或请教老师时,韩老师就给予肯定或激励。
这种心理辅导方法是()。
A.强化法B.系统脱敏法C.来访者中心法D.理性一情绪疗法9.()不是行为改变的基本方法。
A.强化法B.代币法C.自我控制法D.演练法10.小伟过分害怕狗,通过让他看狗的照片,谈论狗,远看狗到近看狗、摸狗、抱狗,消除对狗的惧怕反应,这是行为训练的()。
A.全身松弛训练B.系统脱敏法C.行为塑造法D.肯定性训练11.当一位胆小的学生敢于主动向教师提问时,教师耐心解答并给予表扬和鼓励。
教师的这种做法属于行为改变方法中的()。
A.强化法B.示范法C.消退法D.行为塑造法12.认知疗法于20世纪六七十年代在()产生。
生物化学教程第二章习题答案(详解)

第二章课后习题答案1.计算赖氨酸的ε-NH3+20%被解离时的溶液PH。
解:pH = pKa + lg20% pKa =pH = + lg20% =2. 计算谷氨酸的γ-COOH三分之二被解离时的溶液pH。
解:pH = pKa + lg((2/3)/(1/3))= pKa =3. 计算下列物质L溶液的pH:(a)亮氨酸盐酸盐;(b)亮氨酸钠盐;(c)等电亮氨酸。
解:a:pH=+ lg(C(H+)/)=b: pH=+lgC(OH+))=c:pH=pI=1/2+=4.计算下列氨基酸的pI值:丙氨酸、半胱氨酸、谷氨酸和精氨酸。
解:pI = 1/2(pKa1+ pKa2)pI(Ala) = 1/2(+)=pI(Cys) = 1/2(+)=pI(Glu) = 1/2(+)=pI(Ala) = 1/2(+)=5. 向1L1mol/L的处于等电点的甘氨酸溶液加入,问所得溶液的pH是多少如果加入NaOH以代替HCl时,pH将是多少解:pH1=pKa1+lg(7/3)=pH2=pKa2+lg(3/7)=6. 计算L的组氨酸溶液在时各种离子形式的浓度(mol/L)。
解:由pH=pK1+lg(His+/ His2+)=pKr+lg(His0/His+)=pK2+lg(His-/ His0)得His2+为×10-6,His+为,His0为×10-47. 说明用含一个结晶水的固体组氨酸盐酸盐(相对分子质量=;咪唑基pKa=)和1mol/L KOH配制的L组氨酸盐缓冲液的方法解:取组氨酸盐酸盐41.92g,加入352ml 1mol/L KOH,用水稀释至1L。
8. L-亮氨酸溶液(3.0g/50ml 6mol/L HCl)在20cm旋光管中测得的旋光度为+º。
计算L-亮氨酸在6mol/L HCl中的比旋。
解:c=50=0.06g/ml l=2dm. +=[a]**2 得:[a]= +º9. 甘氨酸在溶剂A中的溶解度为在溶剂B中的4倍,苯丙氨酸在溶剂A中的溶解度为溶剂B中的两倍。
第二章 课后作业参考答案
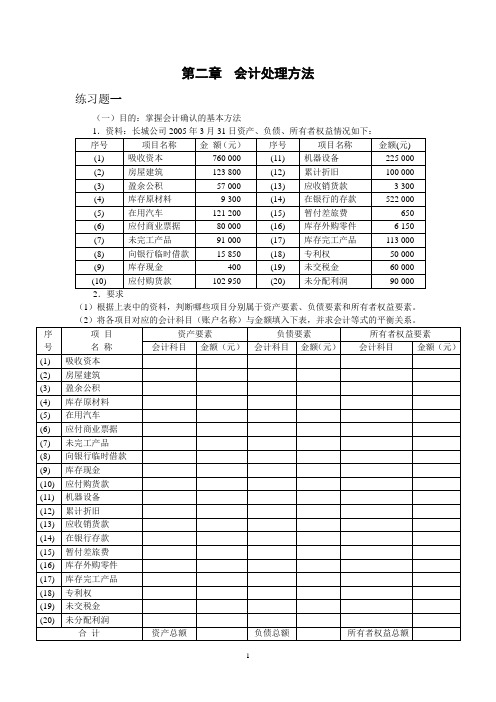
第二章会计处理方法练习题一(一)目的:掌握会计确认的基本方法(1)根据上表中的资料,判断哪些项目分别属于资产要素、负债要素和所有者权益要素。
练习题一参考答案要点(1)资产要素的有:(2);(4);(5);(7);(9);(11);(12);(13);(14);(15);(16);(17);(18) 负债要素的有:(6);(8);(10);(19)所有者权益要素的有:(1);(3);(20)(2)负债表存货项目中。
严格来说,此处是不对的。
因为“生产成本”是费用类账户。
练习题二(二)目的:掌握权责发生制与收付实现制1.资料绿叶公司2005年10月份发生如下经济业务:(1)支付本月的水电费300元。
(2)预付下个月房屋租金2 000元。
(3)支付上月工商部门罚款500元。
(4)销售商品收入20 000元,款项尚未收到。
(5)支付上月购货款38 000元。
(6)采购员报销差旅费2 500元,退回多余现金500元(出差前预借3 000元)。
(7)收到上月销售货款500 000,存入银行。
2.要求分别根据权责发生制和现金收付制,确认和计算本月收入与费用(将结果填入下表)。
练习题二参考答案要点练习题三(三)目的:掌握会计确认的基本方法1.资料上扬公司2005年12月发生如下经济交易与事项:(1)10日,与甲公司签订购货合同,协议购买A材料50万元,约定合同签订之日起10日内预付购货定金10万元。
(2)12日,有一批产品完工验收入库,这批产品的生产成本为20万元。
(3)18日,根据购货合同预付甲公司购货定金10万元。
(4)20日,公司发生失窃事件,丢失现金5万元。
(5)25日,以银行存款预付下年度财产保险费3万元。
(6)28日,以银行存款支付本季度贷款利息费用9万元,其中前两个月已预提6万元。
(7)31日,计算出本月产品销售应缴纳的税金5万元,但尚未实际缴纳。
(8)31日,计算出本月应负担的工资费用15万元,其中管理人员5万元,生产工人10万元,公司每月的工资在下月上旬发放。
机械振动 课后习题和答案 第二章 习题和答案

2.1 弹簧下悬挂一物体,弹簧静伸长为δ。
设将物体向下拉,使弹簧有静伸长3δ,然后无初速度地释放,求此后的运动方程。
解:设物体质量为m ,弹簧刚度为k ,则:mg k δ=,即:n ω==取系统静平衡位置为原点0x =,系统运动方程为: δ⎧+=⎪=⎨⎪=⎩00020mx kx x x (参考教材P14)解得:δω=()2cos n x t t2.2 弹簧不受力时长度为65cm ,下端挂上1kg 物体后弹簧长85cm 。
设用手托住物体使弹簧回到原长后无初速度地释放,试求物体的运动方程、振幅、周期及弹簧力的最大值。
解:由题可知:弹簧的静伸长0.850.650.2()m =-= 所以:9.87(/)0.2n g rad s ω=== 取系统的平衡位置为原点,得到:系统的运动微分方程为:20n x x ω+=其中,初始条件:(0)0.2(0)0x x =-⎧⎨=⎩ (参考教材P14) 所以系统的响应为:()0.2cos ()n x t t m ω=-弹簧力为:()()cos ()k n mg F kx t x t t N ω===-因此:振幅为0.2m 、周期为2()7s π、弹簧力最大值为1N 。
2.3 重物1m 悬挂在刚度为k 的弹簧上并处于静平衡位置,另一重物2m 从高度为h 处自由落到1m 上而无弹跳,如图所示,求其后的运动。
解:取系统的上下运动x 为坐标,向上为正,静平衡位置为原点0x =,则当m 有x 位移时,系统有: 2121()2T E m m x =+ 212U kx =由()0T d E U +=可知:12()0m m x kx ++= 即:12/()n k m m ω=+系统的初始条件为:⎧=⎪⎨=-⎪+⎩2020122m gx k m x gh m m (能量守恒得:221201()2m gh m m x =+) 因此系统的响应为:01()cos sin n n x t A t A t ωω=+其中:ω⎧==⎪⎨==-⎪+⎩200021122n m g A x k x m g ghk A k m m即:ωω=-2()(cos )n n m g x t t t k2.4 一质量为m 、转动惯量为I 的圆柱体作自由纯滚动,圆心受到一弹簧k 约束,如图所示,求系统的固有频率。
2劳动经济学(人大三版)第二章课后参考答案(王松峰 刘娇伟)

劳动经济学第二章课后习题答案一、关键词解释劳动力供给:从性质上说:是指劳动力的供给主体(劳动者个人,在某些情况下可以指家庭)在一定劳动条件下自愿对存在于主体中的劳动力使用权的出让;从量的角度说:是指一个经济体(大至一个国家,小至一个企业,一个雇请了保姆的家庭)在某一段时期中,可以获得的劳动者愿意提供的劳动能力的总和。
劳动力参与率:指劳动范围内的人口参与市场性劳动的比率,是反映就业和劳动人口参与劳动程度的重要指标。
劳动力供给曲线:是指在其他条件不变,市场工资率作为影响劳动力供给的唯一因素的条件下,根据劳动力供给量相对于市场工资率的变动程度绘制而成的曲线劳动力供给弹性:指劳动力供给量变动对工资率变动的反映程度效用理论:效用是指消费者在消费商品或劳务时的满足程度,与此相关的理论就叫效用理论,主要包括基数效用理论和序数效用理论收入约束线:表示个人在时间和劳动能力状况约束下所能消费余暇和获得收入的最大组合线余暇-收入无差异曲线:可以带来一定水平的余暇时间与收入的组合点连接所形成的曲线称为余暇-收入无差异曲线主体均衡:所谓主体均衡,就是在资源约束的条件下余暇和收入的组合能使主体获得最大效用的状态收入效应:收入效应指由商品价格的变动所引起的实际收入水平的变动,进而由由实际收入水平的变动所引起的商品需求量的变动替代效应:因该商品名义价格的变动而导致消费者所购买的商品组合中,该商品与其他商品之间的替代个人劳动力供给曲线:揭示劳动者个人劳动力供给意愿随工资率变动而变动的规律,工资率的上升会导致个人劳动力供给时间的增加,而在此工资率水平之上,工资率的上升反而会导致个人劳动力供给时间的减少。
市场劳动力供给曲线:将一个市场中的个人劳动力供给曲线相加即是市场劳动力供给曲线劳动力的流量:把就业、失业等各种各样的劳动力状况在某个时间点的劳动力的存量向某个方向的流入或流出的量称为劳动力的流量劳动力的流量表:把劳动力人口分为就业、失业、非劳动力三种状态,以观察存量劳动力状况的时间点的变化而形成的劳动力流量,由此而绘制成的表格就是劳动力流量表转移率:从流动量和存储量,到流动的概率,换言之对原本的存量也可以计算流动的变化概率二、问答题1.如何理解劳动力供给的含义?劳动力供给是指在某一特定时间内,在一定工资率水平下,劳动者愿意并且能够提供的劳动力数量深入理解劳动力供给概念,需把握以下三点:个体决策:在市场经济体制下,劳动者是寄寓于其身上的劳动力的法定产权所有者劳动者有充分的自由使用权和处置权,并有凭借直接提供劳务或出租劳动力使用权获得收益的权利主体意愿,劳动力市劳动者的私有财产,劳动者是否愿意提供劳动取决于多种因素,如工资率高低、工作时间长短、个人家庭经济状况等,因此劳动力供给的量和质在很大程度上受到劳动力供给者主观愿望的影响时间要素:包括两层含义:劳动者愿意提供的工作时间、劳动力供给分析的时间2.分析劳动力供给通常有哪些假设(1)劳动力供给主体的目标假设,该假设认为劳动者在作出供给决策时,以追求效用最大化为目标(2)市场环境假设:假定市场是完全竞争状态(3)关于劳动力质量的假设:假定劳动力是同质的3、影响劳动力个人供给的主要因素有哪些?答:一般说来,影响劳动力个人供给的因素包括以下几方面:劳动者受教育时间的长短;工资政策及工资关系;工资水平;个人非劳动收入;居民家庭生产率的变化;社会保障制度;宏观经济状况;其它社会文化、风俗习惯、社会心理等。
第二章课后习题答案

1. 已知某一时期内某商品的需求函数为Q =50-5P ,供给函数为Qs=-10+5p。
(1)求均衡价格Pe和均衡数量Qe,并作出几何图形。
(2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Qd=60-5P。
求出相应的均衡价格Pe 和均衡数量Qe ,并作出几何图形。
(3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Qs=-5+5p。
求出相应的均衡价格Pe 和均衡数量Qe ,并作出几何图形。
(4)利用(1)(2 )(3),说明静态分析和比较静态分析的联系和区别。
(5)利用(1)(2 )(3),说明需求变动和供给变动对均衡价格和均衡数量的影响.解答: (1)将需求函数Qd = 50-5P和供给函数Qs =-10+5P 代入均衡条件Qd = Qs ,有: 50- 5P= -10+5P得: Pe=6以均衡价格Pe =6 代入需求函数Qd =50-5p ,得: Qe=20所以,均衡价格和均衡数量分别为Pe =6 , Qe=20 (图略)(2)将由于消费者收入提高而产生的需求函数Qd=60-5p 和原供给函数Qs=-10+5P, 代入均衡条件Q d= Qs ,有: 60-5P=-10+5P 得Pe=7以均衡价格Pe=7代入Qd方程,得Qe=25所以,均衡价格和均衡数量分别为Pe =7 , Qe=25 (图略)(3) 将原需求函数Qd =50-5p和由于技术水平提高而产生的供给函数Q =-5+5p ,代入均衡条件Qd =Qe ,有: 50-5P=-5+5P得Pe= 5.5以均衡价格Pe= 5.5 代入Qd =50-5p ,得22.5所以,均衡价格和均衡数量分别为Pe=5.5 Qe=22.5(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征.也可以说,静态分析是在一个经济模型中根据所给的外生变量来求内生变量的一种分析方法.以(1)为例,在图中,均衡点 E 就是一个体现了静态分析特征的点.它是在给定的供求力量的相互作用下所达到的一个均衡点.在此,给定的供求力量分别用给定的供给函数Q=-10+5P 和需求函数Q=50-5P表示,均衡点具有的特征是:均衡价格P=6 且当P =6 时,有Q= Q d= Qe =20 ,同时,均衡数量Qe= 20 ,且当Qe=20 时,有Pd=Ps=Pe=6 ,也可以这样来理解静态分析:在外生变量包括需求函数的参数(50,-5) 以及供给函数中的参数(-10,5)给定的条件下,求出的内生变量分别为P= 6 ,Qe =20依此类推,以上所描素的关于静态分析的基本要点,在(2)及其图和(3)及其图中的每一个单独的均衡点上都得到了体现。
第二章远期合约与期货合约课后习题及答案

第二章远期合约与期货合约复习思考题2.1.简述远期合约的构成要素及其与合约损益的关系。
2.2.简述远期合约做多和做空的含义。
2.3.什么是远期汇差?阐明远期汇率与即期汇率的关系。
2.4.什么是远期外汇综合协议(SAFE)?交易者在什么情况下会买入SAFE或卖出SAFE?2.5.请说明远期外汇综合协议和远期利率协议的区别和联系。
2.6.说明远期利率协议的特点。
交易者在什么情况下选择做FRA的多头(买方)和空头(卖方)。
2.7.什么是期货合约,其基本条款包括哪些?2.8.请说明期货交易和远期交易的差异。
2.9.请说明保证金和逐日结算制度是如何使期货交易者免于违约的。
2.10.期货市场的主要功能有哪些?2.11.实物交割和现金结算有什么主要区别?哪些期货合约适宜现金结算?2.12.阐述股指期货的交易特征。
2.13.期货交易的结清方式有哪些?2.14.对比分析退出期货交易和远期交易方式的差异,并分析其背后的原因。
2.15.一家公司签订一份空头期货合约,以每蒲式耳300美分卖出5000蒲式耳小麦。
初始保证金为3000美元,维持保证金为2000美元。
价格如何变化会导致保证金催付?在什么情况下,可以从保证金账户中提取1000美元?2.16.一个投资者买入了两份冷冻橙汁期货合约。
每份合约的合约规模为15000磅。
当前期货价格为每磅170美分;每份期货合约的初始保证金都为6000美元,维持保证金都为4500美元。
价格如何变化会导致保证金催付?在什么情况下,可以从保证金账户中提取1500美元?讨论题2.1.请讨论FXA和ERA在使用中的差异。
2.2.你认为如果在期货合约中没有指明标的物的质量,会发生什么情况?2.3.结合美国次贷危机的实际,分析场外衍生工具交易的优势和劣势。
2.4.请讨论期货结算所的作用。
复习思考题答案2.1.简述远期合约的构成要素及其与合约损益的关系。
答:远期合约包括以下基本构成要素:(1)标的资产。
财务管理课后习题答案(第二章)

思考题1.答题要点:(1)国外传统的定义是:即使在没有风险和没有通货膨胀的条件下,今天1元钱的价值亦大于1年以后1元钱的价值。
股东投资1元钱,就失去了当时使用或消费这1元钱的机会或权利,按时间计算的这种付出的代价或投资收益,就叫做时间价值。
(2)但并不是所有货币都有时间价值,只有把货币作为资本投入生产经营过程才能产生时间价值。
同时,将货币作为资本投入生产过程所获得的价值增加并不全是货币的时间价值,因为货币在生产经营过程中产生的收益不仅包括时间价值,还包括货币资金提供者要求的风险收益和通货膨胀贴水。
(3)时间价值是扣除风险收益和通货膨胀贴水后的真实收益率。
在没有风险和没有通货膨胀的情况下,银行存款利率、贷款利率、各种债券利率、股票的股利率可以看作是时间价值。
2.答题要点:(1)单利是指一定期间内只根据本金计算利息,当期产生的利息在下一期不作为本金,不重复计算利息。
(2)复利就是不仅本金要计算利息,利息也要计算利息,即通常所说的“利滚利”。
复利的概念充分体现了资金时间价值的含义,因为资金可以再投资,而且理性的投资者总是尽可能快地将资金投入到合适的方向,以赚取收益。
3.答题要点:(1)不是,年金是指一定时期内每期相等金额的收付款项。
(2)例如,每月月末发放等额的工资就是一种年金,这一年的现金流量共有12次。
4.答题要点:(1)对投资活动而言,风险是与投资收益的可能性相联系的,因此对风险的衡量,就要从投资收益的可能性入手。
(2)风险与收益成反向变动关系,风险大,预期收益就高;反之,风险小,预期收益少。
5.答题要点:(1)股票风险中能够通过构建投资组合被消除的部分称作可分散风险,也被称作公司特别风险,或非系统风险。
而不能够被消除的部分则称作市场风险,又被称作不可分散风险,或系统风险,或贝塔风险,是分散化之后仍然残留的风险。
(2)二者的区别在于公司特别风险,是由某些随机事件导致的,如个别公司遭受火灾,公司在市场竞争中的失败等。
《基础会计学》第二章课后习题及参考答案

5.在借贷记账法下,有关账户之间形成的应借应贷的相互关系称为账户对应关系。
()第二章会计记账方法6.总分类账户与明细分类账户进行平行登记时的所谓同时登记,确切地说应该是同一会计期间作业一:登记。
()一,单项选择题:7.平行登记的要求中,所谓登记方向一致,是指会计分录中总分类账户和明细分类账户的记账1.下列科目中属于流动资产的是()符号是一致的。
()A预提费用B短期借款C资本公积D应收账款8.采用借贷记账法,每发生一笔经济业务必定要在两个账户中同时登记。
()2.企业全部资产减去全部负债后的净额,就是企业的()四,名词解释A所有者权益B实收资本C资本公积D盈余公积平行登记发生额平衡法余额平衡法3.预付供货单位货款属于企业的一项()五,简答题A资产B负债C收入D费用1.简述借贷复式记账法的内容和特点。
4.经济业务发生后,会计等式的平衡关系()2.简述总账和明细账平行登记的要点及两者数量关系核对的公式。
A可能会受影响B不一定受影响C必然不受影响D必然受影响3.简述借贷记账法的试算平衡。
5.资产与权益的平衡关系是指()六,综合题A一项资产金额与一项权益金额的相等关系B几项资产金额与一项权益金额的相等关系1. 计算题C流动资产合计金额与流动负债金额的相等关系D资产总额与权益总额的相等关系某企业有关会计要素的数据如下:6. 引起资产内部一个项目增加,另一个项目减少,而资产总额不变的经济业务是()负债5000万元;所有者权益8000万元;A用银行存款偿还短期借款B收到投资者投入的机器一台C收到外单位前期欠的货款费用200 万元;利润6000 万元;D 收到国家拨入的特种储备物资要求:计算资产总额和收入总额7. 企业用借款直接偿还应付购货款,属于()2. 某公司设有以下账户:实收资本、本年利润、现金、银行存款、待摊费用、预提费用、原材A 资产项目和权益项目同增B权益项目之间此增彼减C资产项目和权益项目同减料、固定资产、其他应收款、应收账款、应付账款、预收账款、预付账款、其他应付款、材料采D 资产项目之间此增彼减购、累计折旧、管理费用、财务费用、营业费用、主营业务收入、其他业务收入、营业外收入、8. 只有采用权责发生制原则核算的企业,才需要设置()主营业务成本、其他业务支出、应交税金、短期借款、资本公积、制造费用、生产成本、库存商A待摊费用B本年利润C银行存款D库存商品品、产成品9.企业设置会计科目要保持()要求:分析以上账户归属于资产类、权益类、收入成果类和费用成本类的哪一类,并指出各账户A经常变动B永久不变C定期变动D相对稳定性增、减的金额应在借还是贷方,有余额的账户其正常余额的方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.22设F是论域U上的模糊集,R是U×V上的模糊关系,F和R分别为:
求模糊变换FοR。
解:
={0.1∨0.4∨0.6, 0.3∨0.6∨0.3,0.4∨0.6∨0 }
={0.6, 0.6, 0.6}
第6章
6.8设有如下一组推理规则:
r1: IF E1THEN E2(0.6)
r2: IF E2AND E3THEN E4(0.7)
4
S03
1100
12
S04
0111
7
若规定选择概率为100%,选择算法为轮盘赌算法,且依次生成的4个随机数为0.42, 0.16, 0.89, 0.71,请填写上表中的全部内容,并求出经本次选择操作后所得到的新的种群。
解:表格的完整内容为:
编号
个体串
x
适应值
百分比
累计百分比
选中次数
S01
1010
10
( x)(NC(x)→F(x)∧B(x))
(4)不是每个计算机系的学生都喜欢在计算机上编程序。
解:定义谓词
S(x):x是计算机系学生
L(x, pragramming):x喜欢编程序
U(x,computer):x使用计算机
将知识用谓词表示为:
¬( x)(S(x)→L(x, pragramming)∧U(x,computer))
解:
(3)学习班的学员有男、有女、有研究生、有本科生。
解:参例2.14
(4)创新公司在科海大街56号,刘洋是该公司的经理,他32岁、硕士学位。
解:参例2.10
(5)红队与蓝队进行足球比赛,最后以3:2的比分结束。
解:
2.19请把下列命题用一个语义网络表示出来:
(1)树和草都是植物;
解:
(2)树和草都有叶和根;
第2章
1.设有如下语句,请用相应的谓词公式分别把他们表示出来:s
(1)有的人喜欢梅花,有的人喜欢菊花,有的人既喜欢梅花又喜欢菊花。
解:定义谓词d
P(x):x是人
L(x,y):x喜欢y
其中,y的个体域是{梅花,菊花}。
将知识用谓词表示为:
( x )(P(x)→L(x,梅花)∨L(x,菊花)∨L(x,梅花)∧L(x,菊花))
=0.1/u1+0.3/u2+0.5/u3+0.7/u4+1/u5
5.21设有如下两个模糊关系:
请写出R1与R2的合成R1οR2。
解:R(1,1)=(0.3∧0.2)∨(0.7∧0.6)∨(0.2∧0.9)= 0.2∨0.6∨0.2=0.6
R(1,2)=(0.3∧0.8)∨(0.7∧0.4)∨(0.2∧0.1)= 0.3∨0.4∨0.1=0.4
100
32.36
32.36
1
S02
0100
4
16
5.18
37.54
0
S03
1100
12
144
44.60
84.14
2
S04
0111
7
49
15.86
100
1
本次选择后所得到的新的种群为:
S01=1100
S02=1010
S03=0111
S04=1100
5.18设某小组有5个同学,分别为S1,S2,S3,S4,S5。若对每个同学的“学习好”程度打分:
=0/u1+0/u2+0.5/u3+0.3/u4+0/u5
=0.5/u3+0.3/u4
F∪G=(0.9∨0)/u1+(0.7∨0)/u2+(0.5∨0.6)/u3+(0.3∨0.8)/u4+(0∨1)/u5
=0.9/u1+0.7/u2+0.6/u3+0.8/u4+1/u5
﹁F=(1-0.9)/u1+(1-0.7)/u2+(1-0.5)/u3+(1-0.3)/u4+(1-0)/u5
(2)有人每天下午都去打篮球。
解:定义谓词
P(x):x是人
B(x):x打篮球
A(y):y是下午
将知识用谓词表示为:a
( x )( y)(A(y)→B(x)∧P(x))
(3)新型计算机速度又快,存储容量又大。
解:定义谓词
NC(x):x是新型计算机
F(x):x速度快
B(x):x容量大
将知识用谓词表示为:
CF(E4)=0.7×max{0, min{CF(E2), CF(E3)}}
5.19设有论域
U={u1, u2, u3, u4, u5}
并设F、G是U上的两个模糊集,且有
F=0.9/u1+0.7/u2+0.5/u3+0.3/u4
G=0.6/u3+0.8/u4+1/u5
请分别计算F∩G,F∪G,﹁F。
解:F∩G=(0.9∧0)/u1+(0.7∧0)/u2+(0.5∧0.6)/u3+(0.3∧0.8)/u4+(0∧1)/u5
R(2,1)=(1∧0.2)∨(0∧0.6)∨(0.4∧0.9)= 0.2∨0∨0.4=0.4
R(2,2)=(1∧0.8)∨(0∧0.4)∨(0.4(0.5∧0.6)∨(1∧0.9)= 0.2∨0.6∨0.9=0.9
R(3,2)=(0∧0.8)∨(0.5∧0.4)∨(1∧0.1)= 0∨0.4∨0.1=0.4
r3: IF E4THEN H (0.8)
r4: IF E5THEN H (0.9)
且已知CF(E1)=0.5, CF(E3)=0.6, CF(E5)=0.7。求CF(H)=?
解:(1)先由r1求CF(E2)
CF(E2)=0.6×max{0,CF(E1)}
=0.6×max{0,0.5}=0.3
(2)再由r2求CF(E4)
解:
(3)水草是草,且生长在水中;
解:
(4)果树是树,且会结果;
解:
(5)梨树是果树中的一种,它会结梨。
解:
第
5.15对遗传法的选择操作:设种群规模为4,个体采用二进制编码,适应度函数为f(x)=x2,初始种群情况如下表所示:
编号
个体串
x
适应值
百分比
累计百分比
选中次数
S01
1010
10
S02
0100
S1:95 S2:85 S3:80 S4:70 S5:90
这样就确定了一个模糊集F,它表示该小组同学对“学习好”这一模糊概念的隶属程度,请写出该模糊集。
解:对模糊集为F,可表示为:
F=95/S1+85/S2+80/S3+70/S4+90/S5
或
F={95/S1, 85/S2, 80/S3, 70/S4, 90/S5}
(5)凡是喜欢编程序的人都喜欢计算机。
解:定义谓词
P(x):x是人
L(x, y):x喜欢y
将知识用谓词表示为:
( x)(P(x)∧L(x,pragramming)→L(x, computer))
2请对下列命题分别写出它们的语义网络:
(1)每个学生都有一台计算机。
解:
(2)高老师从3月到7月给计算机系学生讲《计算机网络》课。
