第3章习题参考答案
电工与电子技术基础第2版习题参考答案第3章

习题3.1 某三相同步发电机,三相绕组连接成星形时的线电压为10.5kV ,若将它连接成三角形,则线电压是多少?若连接成星形时,B 相绕组的首末端接反了,则3 个线电压的有效值 U AB 、U BC 、U CA 各是多少?解:三相绕组连接成星形时U L =3U P ,线电压为10.5kV ,则每相绕组的电压为6.06kV ,若连接成三角形U L =U P ,则线电压为6.06kV 。
若连接成星形时,B 相绕组的首末端接反了,则B 相相电压的相位与原来的相差1800, 根据相量计算可得U AB =6.06 kV 、U BC =6.06 kV 、U CA =10.5 kV 。
3.2 题3.2 图所示的三相对称电路,线电压U L =380V ,每相负载Z = 6+j8Ω,试求相电压、相电流和线电流,并画出电压和电流的相量图。
题3.2 图解:由题意:负载作星接U l =3U p 因U l =380V ,则U a =U b =U c = = 220 (V )设U a = 220/0°(V )因相电流即线电流,其大小为:.220/0°I A == 22/−53°(A) 6 + j 8.I B = 22/−173ο(A).I C = 22/67°(A) 此时的相量图略。
3.3 有一电源和负载都是星形连接的对称三相电路,已知电源相电压为220V ,负载每相阻抗Z = Ω10 ,试求负载的相电流和线电流。
3 380第3 章三相交流电路习题解答77解:负载的相电压等于电源的相电压:U p = 220(V)U P 220(A)I l = I p = = = 22Z 103.4 已知星形联接的对称三相负载,每相阻抗为40∠25°(Ω);对称三相电源的线电压为380V。
求: 负载相电流,并绘出电压、电流的相量图。
解:UAB =380VZ=40∠25°Ω(1)三相对称电源接入三相对称负载令U A =220∠0°V则相线电流I A =U A /Z=5.5∠-25°VI B =5.5∠-145°VI c =5.5∠95°V(2) 矢量图如图所示。
逻辑第三章习题参考答案(0710)

30
III. 三、2. P94
【原题】 ⒉ 已知“有S不是p”为假
【参考答案】
SP
SOP
0
例S 蕃茄
例P 西红柿
2021/4/14
PS
SP
0
1
美国人
人
SP
1
SP
1
31
III. 三、3. P94
【原题】 ⒊ 已知“有S是P”为真
【参考答案】
SP
SIP
1
例S 蕃茄
2021/4/14
36
III. 四、2. P94
【原题】 ⒉ 这架飞机上的乘客都是去英国旅游的。
【参考答案】
整理:所有乘客是去英国旅游的。SAP为真
SIP:有的乘客是去英国旅游的。 真 SOP:有的乘客不是去英国旅游的。假 SEP:所有乘客不是去英国旅游的。假
【参考答案】
不表达判断
因为是一般疑问句,是有疑而问,无所断定。
2021/4/14
3
III. 一、2. P93
【原题】 ⒉ 没有耕耘,哪来收获?
【参考答案】
间接表达判断:没有耕耘就没有收获。 因为是反诘句。
2021/4/14
第三章练习题
(共一讲)
III. 一、P93 (共 10 小题)
【原题】 一、下列语句是否表达判断?为什么?
【知识点】
语句和判断的关系 何种语句表达判断?何种语句不表达判断?
2021/4/14
2
III. 一、1. P93
【原题】 ⒈ 为什么说社会主义制度有无比的优越性?
2021/4/14
15
III. 二、3. P93
第3章 场效应管及其基本放大电路 参考答案

第 3章 场效应管及其基本放大电路3.1填空题(1)按照结构,场效应管可分为 。
它属于 型器件,其最大的优点是 。
(2)在使用场效应管时,由于结型场效应管结构是对称的,所以 极和 极可互换。
MOS 管中如果衬底在管内不与 极预先接在一起,则 极和 极也可互换。
(3)当场效应管工作于恒流区时,其漏极电流D i 只受电压 的控制,而与电压 几乎无关。
耗尽型D i 的表达式为 ,增强型D i 的表达式为 。
(4)一个结型场效应管的电流方程为2GS D 161mA 4U I=×− ,则该管的DSS I = ,p U = 。
(5)某耗尽型MOS 管的转移曲线如习题3.1.5图所示,由图可知该管的DSS I = ,p U = 。
(6)N 沟道结型场效应管工作于放大状态时,要求GS 0u ≥≥ ,DS u > ;而N 沟道增强型MOS 管工作于放大状态时,要求GS u > ,DS u > 。
(7)耗尽型场效应管可采用 偏压电路,增强型场效应管只能采用 偏置电路。
(8)在共源放大电路中,若源极电阻s R 增大,则该电路的漏极电流D I ,跨导m g ,电压放大倍数 。
(9)源极跟随器的输出电阻与 和 有关。
答案:(1)结型和绝缘栅型,电压控制,输入电阻高。
(2)漏,源,源,漏,源。
(3)GS u ,DS u ,2GS D DSS P 1u i I U =− ,2GS D DO T 1u i I U=−。
(4)16mA ,4V 。
(5)习题3.1.5图4mA ,−3V 。
(6)p U ,GS p u U −,T U ,GS T u U −。
(7)自给,分压式。
(8)减小,减小,减小。
(9)m g ,s R 。
3.2试分别画出习题3.2图所示各输出特性曲线在恒流区所对应的转移特性曲线。
解:3.3在带有源极旁路电容s C 的场效应管放大电路如图3.5.6(a )所示。
若图中的场效应管为N 沟道结型结构,且p 4V U =−,DSS 1mA I =。
数据与计算机通信答案(第3章)

而对于数字彩色电视机,相当不错了。如果不提高数据率,还可以通过降低分辨率或刷新速 率,来换取色彩数的提高,但这也不实用的方法。
已知视频带宽 B=5MHz,所以有 5=P/105,则每行的像素数 P=5x105=525。 然而,通常 CCIR-M/NTSC 制式每行只约有 450 像素,带宽 B=P/105=450/105=4.3MHz (实 际技术指标 4.2Hz) 。 带宽由 4.2MHz 增加到 5MHz 时,水平分辨率约增加 75 像素,增幅 16.7%。 (2)计算垂直分辨率的增幅 由于信号最高频率 fH=5MHz,即最短的信号周期 1/fH=0.2υs。 又因为每个最短周期包含 2 个像素,则有 225 周期/行。那么,每行扫描时间为 0.2υs×225=45υs。加上水平回扫 11υs,每行往返扫描时间为 56υs ,即 56x10-6 s, 假定每屏 V 行,每秒扫描 30 场(帧、屏),则每秒扫描行数为 30V。 因此对于画面刷新,有 30V×56x10-6 = 1s,V = 595 行/屏。目前 NSTL 制式每行只有 525 行。垂直分辨率增加了 70 行,增幅 13.3%。
cos 2 t = cos t cos t = 1 (cos 2t + cos 0) = 1 (cos 2t + 1)
2
2
所以, f (t) = (10 cos t)2 = 100 cos 2 t = 50 + 50 cos 2t
《信息论与编码》第三章部分习题参考答案

第三章习题参考答案第三章习题参考答案3-1解:(1)判断唯一可译码的方法:①先用克劳夫特不等式判定是否满足该不等式;②若满足再利用码树,看码字是否都位于叶子结点上。
如果在叶节点上则一定是唯一可译码,如果不在叶节点上则只能用唯一可译码的定义来判断是不是。
可译码的定义来判断是不是。
其中C1,C2,C3,C6都是唯一可译码。
都是唯一可译码。
对于码C2和C4都满足craft 不等式。
但是不满足码树的条件。
但是不满足码树的条件。
就只能就只能举例来判断。
举例来判断。
对C5:61319225218ki i ---==+´=>å,不满足该不等式。
所以C5不是唯一可译码。
译码。
(2)判断即时码方法:定义:即时码接收端收到一个完整的码字后,就能立即译码。
特点:码集任何一个码不能是其他码的前缀,即时码必定是唯一可译码, 唯一可译码不一定是即时码。
唯一可译码不一定是即时码。
其中C1,C3,C6都是即时码。
都是即时码。
对C2:“0”是“01”的前缀,……,所以C2不是即时码。
不是即时码。
(1) 由平均码长61()i i i K p x k ==å得1236 3 1111712(3456) 241681111712(3456) 2416811152334 24162K bitK bit K bitK bit==´+´+´+++==´+´+´+++==´+´+´´=62111223366()()log () 2 /()266.7%3()294.1%178()294.1%178()280.0%52i i i H U p u p u H U K H U K H U K H U K h h h h ==-=============å比特符号3-7解:(1)信源消息的概率分布呈等比级数,按香农编码方法,其码长集合为自然数数列1, 2, 3, ···, i, ·, i, ····;对应的编码分别为:0, 10, 110, ···, 111…110 ( i 110 ( i –– 1个1), ·1), ····。
中国近代史纲要第三章习题参考答案

第三章习题参考答案第三章辛亥革命与君主专制制度的终结一、单项选择题1.B2.C3.C4.C5.A6.C7.C8.D9.D 10.C11.B 12.B 13.C 14.A 15.B16.B 17.B 18.B 19.D 20.C21.D 22. A 23. C 24. A 25.C26.D 27. D 28.C 29. A 30. B 31. A二、多项选择题1. ABCD2. ABCD3. AB4. ABD5.BCD6. ABCD7. ABD8.ABC9.CD 10. ABD11. ABC 12.BCD 13.BCD 14.ABC 15.ABCD16.ABCD 17.ABC 18.AC三、简答题1.简述资产阶级革命派形成的阶级基础参考答案:19 世纪末20 世纪初,中国民族资本主义得到了初步的发展。
随着民族资本主义企业发展数量的增多和规模的扩大,民族资产阶级及与它相联系的社会力量也有了较大的发展。
民族资产阶级为了冲破帝国主义、封建主义的桎梏,发展资本主义,需要自己政治利益的代言人和经济利益的维护者。
这正是资产阶级革命派形成的阶级基础。
2.简述资产阶级革命派所进行的宣传和组织工作答:历史进入20 世纪,随着一批新兴知识分子的产生,各种宣传革命的书籍报刊纷纷涌现,民主革命思想得到广泛传播。
1903 年,章炳麟发表了《驳康有为论革命书》,反对康有为的保皇观点,强调中国人民完全有能力建立民主共和制度。
邹容创作了《革命军》,阐述在中国进行民主革命的必要性和正义性,号召人民推翻清朝统治,建立“中华共和国”。
陈天华创作了《警世钟》、《猛回头》两本小册子,痛陈帝国主义侵略给中国带来的沉重灾难,揭露清政府已经成了帝国主义统治中国的工具,号召人民推翻清政府。
在资产阶级革命思想的传播过程中,资产阶级革命团体也在各地相继成立。
从1904 年开始,出现了10 多个革命团体,其中重要的有华兴会、科学补习所、光复会等。
这些革命团体的成立为革命思想的传播及革命运动的发展提供了不可缺少的组织力量。
第3章 问题及习题参考答案

Cl 2HCl Cl H ++CH 4Cl CH 3Cl H +++Cl +CH 4CH 3HCl +Cl +CH 3Cl CH 3Cl 2第3章 思考题及习题参考答案思考题3-1用纽曼投影式画出下列化合物的对位交叉和全重叠式构象。
1. 解: 1-氯-2-溴乙烷;2. 解:3-羟基丙酸。
对位交叉式; 全重叠式 对位交叉式; 全重叠式。
思考题3-2利用键能数据的计算,判断下列A 和B 两种甲烷氯代的反应历程,哪个较合理?A.B.解:从图3-7可以看出链传递的第一步反应是反应的速度决定步骤。
根据键能分别计算两个历程的此步反应的焓变:历程A. ∆H = 434.7 一 351.1 = 83.6 kJ ·mol -1,活化能 > 83.6 kJ ·mol -1历程B. ∆H = 434.7 一 430.5 = 4.2 kJ ·mol -1,活化能为16.7 kJ·mol -1答:历程A 的速度决定步骤的活化能必须大于83.6 kJ · mol -1,而历程B 的活化能为16.7 kJ·mol -1,因此,历程B 较为合理。
习题3.1. 在标准状况下37.0g 由甲烷与另一种烷烃两种气态烷烃组成的混合物完全燃烧消耗4.25 molO 2,计算两种可能的混合物的摩尔组成。
解:设气态烷烃混合物的组成为CnHm ,完全燃烧的反应方程式为:++CnHm O 2CO 2H 2O n +m 4n m 2(12n + m)g 4m +n mol 37.0g 4.25 mol 4m +n 4.25×(12n + m) = 37.0× 4.25m - (37.0/4)m = 37.0n - 4.25×12nm = 4.25×12 - 37.0 37.0/4 - 4.25n m = 2.8n m/n = 2.8气体烷烃中:甲烷CH 4的m/n = 4 > 2.8,乙烷C 2H 6的m/n = 3 > 2.8;丙烷C 3H 8的m/n = 2.7 < 2.8,丁烷C 4H 10的m/n = 2.5 < 2.8。
第3章习题答案

练习题:1.单项选择⑴当砼预制桩的设计间距大于4倍桩直径(或边长)时,宜采用的打桩顺序为( A)。
A.逐排打设B.自中间向四周打设C.自四周向中间打设D.逐排打设⑵摩擦桩型的预制桩在沉桩时,主要质量控制指标是(B)。
A.最后贯入度B.设计标高C.垂直度D.平面位置⑶在周围建筑物密集的狭窄场地施工大直径砼灌注桩,较宜采用(A)。
A.钻孔灌注桩B.沉管灌注桩C.人工挖孔灌注桩D.爆扩灌注桩3.填空题:(1)泥浆护壁钻孔灌注桩成孔施工时,泥浆的作用是:(护壁、携砂、排土、降低钻头温度)。
(2)钢筋砼预制桩的打桩顺序一般有:(逐排打设)、(自中间向四周打设)、(有中间向两边打)。
(3)桩锤重量可按那几个因素来选择:(地质条件)、(工程结构)、(桩的类型)。
密集程度及施工条件(4)预制打入桩垂直度偏差应控制在( 100mm )以内。
(5)入土深度控制对摩擦桩应以(设计标高)为主,以(最后贯入度)作为参考。
端承桩应以(最后贯入度)为主。
(6)钻孔灌注桩钻孔时的泥浆循环工艺有(正循环、反循环)两种,其中(反循环)工艺的泥浆上流速度高,携土能力大。
(7)打入桩施工时,当桩间距(当桩中心距小于等于4倍桩长或桩径时)时,一定要确定合理的打桩顺序。
(2)若按施工方法分,预制桩可划分为(打入法)、(静压法)(8)预制桩吊点设计的原则是:(平稳,避免冲击和振动)。
(9)桩架的作用是(导向)、(固定桩的位置)、(承受桩锤重量)。
(10)预制桩接桩的方法有:(焊接法)、(浆锚法)、(法兰接桩)。
(11)打入桩施工时,宜采用的打桩方法:(重锤低击)。
(12)套管成孔灌注桩施工时,为提高桩的质量,提高桩的承载力,经常采用(复打法施工)。
(13)水下浇筑砼经常采用的方法是(导管法)。
(14)砼预制桩应在砼达到设计强度的(75%)后方可起吊,达到设计强度的100%后方可(运输)和(打设)。
(15)沉管灌注桩施工时,常遇问题有:(断桩)、(缩颈)、(吊脚桩)(砼过量)。
第3章《自测题、习题》参考答案

第 3 章 场效应管及其基本放大电路自测题3.1填空题1.按照结构,场效应管可分为 。
它属于 型器件,其最大的优点是 。
2.在使用场效应管时,由于结型场效应管结构是对称的,所以 极和 极可互换。
MOS 管中如果衬底在管内不与 极预先接在一起,则 极和 极也可互换。
3.当场效应管工作于线性区时,其漏极电流D i 只受电压 的控制,而与电压 几乎无关。
耗尽型D i 的表达式为 ,增强型D i 的表达式为 。
4.某耗尽型MOS 管的转移曲线如题3.1.4图所示,由图可知该管的DSS I = ,U P = 。
5.一个结型场效应管的电流方程为2GS D 161(mA)4U I ⎛⎫=⨯- ⎪⎝⎭,则该管的DSS I = , U P = ;当GS 0u =时的m g = 。
6.N 沟道结型场效应管工作于放大状态时,要求GS 0u ≥≥ ,DS u > ;而N 沟道增强型MOS 管工作于放大状态时,要求GS u > ,DS u > 。
7.耗尽型场效应管可采用 偏压电路,增强型场效应管只能采用 偏置电路。
8.在共源放大电路中,若源极电阻s R 增大,则该电路的漏极电流D I ,跨导m g ,电压放大倍数 。
9.源极跟随器的输出电阻与 和 有关。
答案:1.结型和绝缘栅型,电压控制,输入电阻高。
2.漏,源,源,漏,源。
3.GS u ,DS u ,2GS D DSS P 1u i I U ⎛⎫=- ⎪⎝⎭,2GS D DO T 1u i I U ⎛⎫=- ⎪⎝⎭。
4.4mA ,-3V 。
5.16mA ,题3.1.4图4V ,8ms 。
6.p U ,GS P u U -,T U ,GS T u U -。
7.自给,分压式。
8.减小,减小,减小。
9.m g ,s R 。
3.2选择题1.P 沟道结型场效应管中的载流子是 。
A .自由电子;B .空穴;C .电子和空穴;D .带电离子。
2.对于结型场效应管,如果GS P |||U U >,那么管子一定工作于 。
数据库答案 第三章习题参考答案

7. 找出没有使用天津产的零件的工程项目代码。 找出没有使用天津产的零件的工程项目代码。 Select jno from j where not exists (Select * from spj where spj.jno=j.jno and sno in (Select sno from s where city=‘天津’) city=‘天津了供应商 所供应的全部零件的工程号 求至少用了供应商S1所供应的全部零件的工程号 求至少用了供应商 所供应的全部零件的工程号JNO。 。 即查找:不存在这样的零件y,供应商S1供应了 供应了y,而工程x 即查找:不存在这样的零件 ,供应商 供应了 ,而工程 为选用y。 为选用 。 Select distinct jno From spj z Where not exists (select * from spj x where sno=‘S1’ and not exists (select * from spj y where y.pno=x.pno and y.jno=z.jno));
习题三
Select sno from spj Where jno=‘J1’;
第 4题
1.求供应工程 零件的供应商号码 求供应工程J1零件的供应商号码 求供应工程 零件的供应商号码SNO。 。
2.求供应工程 零件 的供应商号码 求供应工程J1零件 的供应商号码SNO。 求供应工程 零件P1的供应商号码 。 Select sno from spj Where jno=‘J1’ and pno=‘P1’;
1
3.求供应工程 零件为红色的供应商号码。 求供应工程J1零件为红色的供应商号码 求供应工程 零件为红色的供应商号码。 Select sno from spj, p Where spj.pno=p.pno and jno=‘J1’ and color=‘红 color=‘红’; 或: Select sno from spj Where jno =‘J1’ and pno in (Select pno from p where color=‘红’ ); color=‘红
第三章习题解答及参考答案

(
)
①
2 式中 m 为整数。令 u = αr ,显然上式是 u 的周期函数,周期为 2π ,故可展开成傅里 ∞ 1 1 + sgn (cos u ) = ∑ Cn e inu 2 2 n = −∞
叶级数:
其中,
Cn =
1 2π
∫
π 2
−π 2
e −inu du =
sin (nπ 2) nπ
②
遂有:
∞ 1 1 sin (nπ 2 ) inαr 2 e + sgn cos αr 2 = ∑ 2 2 nπ n= −∞
②
σ ( f x ,0 ) 2λd i =1− f x = 1− f x f0 σ0 l
l l ≤ λd i f x ≤ (见附图3 - 4(b)) 4 2
2 1 l l σ ( f x ,0 ) = (l − λd i f x ) l − = − λd i l f x 2 2 2
λd ;两个一级分量与中央亮斑 L
附图 3-2
习题[3-2]图示
附图 3-3
归一化强度分布
[3-3]
将面积为 10 mm × 10 mm 的透射物体置于一傅里叶变换透镜的前焦面上作频谱分析。
用波长 λ = 0.5 µ m 的单色平面波垂直照明,要求在频谱面上测得的强度在频率 140 线/mm 以下能准确代表物体的功率谱。并要求频率为 140 线/mm 与 20 线/mm 在频谱面上的间隔为 30mm,问该透镜的焦距和口径各为多少? 解:取面积为10mm ×10mm 的透射物体的对角线方向为 x 轴。因要求在 140 线/mm 以下的 空间频率成分不受到有限孔径的渐晕效应的影响,故透镜的口径 D 应满足条件:
第三章习题参考答案
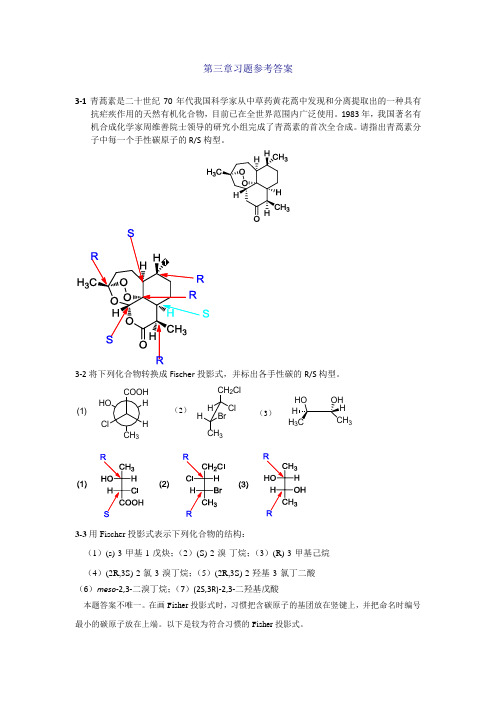
第三章习题参考答案3-1青蒿素是二十世纪70年代我国科学家从中草药黄花蒿中发现和分离提取出的一种具有抗疟疾作用的天然有机化合物,目前已在全世界范围内广泛使用。
1983年,我国著名有机合成化学家周维善院士领导的研究小组完成了青蒿素的首次全合成。
请指出青蒿素分子中每一个手性碳原子的R/S 构型。
3-2将下列化合物转换成Fischer 投影式,并标出各手性碳的R/S 构型。
(2)(3)3BrH3HClCH 2ClH 3H 3(1)3-3用Fischer 投影式表示下列化合物的结构:(1)(s)-3-甲基-1-戊炔;(2)(S)-2-溴-丁烷;(3)(R)-3-甲基己烷 (4)(2R,3S)-2-氯-3-溴丁烷;(5)(2R,3S)-2-羟基-3-氯丁二酸 (6)meso -2,3-二溴丁烷;(7)(2S,3R)-2,3-二羟基戊酸本题答案不唯一。
在画Fisher 投影式时,习惯把含碳原子的基团放在竖键上,并把命名时编号最小的碳原子放在上端。
以下是较为符合习惯的Fisher 投影式。
3-4下列化合物中哪些有手性?(1)、(3)、(5)、(7)、(9)无手性(2)、(4)、(6、)(8)、(10)有手性3-5长尾粉蚧壳虫信息素A是雌性长尾粉蚧壳虫(一种植物害虫)分泌的性激素,其外消旋体目前已被人工合成,并商业化用于农田害虫的控制和诱杀。
最近,化学家通过全合成途径确定了天然长尾粉蚧壳虫信息素的绝对构型(.Chem.2013,78,6281−6284)。
通过全合成方法分别得到了A的2种立体异构体,发现其中的(S)-(+)-异构体具有吸引雄性长尾粉蚧壳虫的活性,而它的对映体(R)-( )-A则无此生物活性。
此结果表明雌性长尾粉蚧壳虫分泌的天然长尾粉蚧壳虫信息素为(S)-A。
商业化使用的外消旋体与纯的(S)-对映体生物活性相似,说明(R)-A对(S)-A的生物活性无抑制作用。
写出(R)-A和(S)-A的结构式。
(R)-A(S)-A3-6山梗烷定是从印度烟叶中分离到的一种化合物,它没有旋光性,也不可被拆分。
电磁场与电磁波第三章习题及参考答案

第3章习题3-1 半径为的薄圆盘上电荷面密度为s ρ,绕其圆弧轴线以角频率旋转形成电流,求电流面密度。
解:圆盘以角频率旋转,圆盘上半径为r 处的速度为r ω,因此电流面密度为ϕωρρˆr v J s s s ==3-2 在铜中,每立方米体积中大约有28105.8⨯个自由电子。
如果铜线的横截面为210cm ,电流为A 1500。
计算 1) 电流密度;2) 电子的平均漂移速度; 解:1)电流密度m A S I J /105.11010150064⨯=⨯==- 2) 电子的平均漂移速度 v J ρ=,3102819/1036.1105.8106.1m C eN ⨯=⨯⨯⨯==-ρs m J v /101.11036.1105.14106-⨯=⨯⨯==ρ 3-3 一宽度为cm 30传输带上电荷均匀分布,以速度s m /20匀速运动,形成的电流,对应的电流强度为A μ50,计算传输带上的电荷面密度。
解:电流面密度为m A L I J S /7.1663.050μ===因为 v J S S ρ= 所以 2/33.8207.166m C v J S S μρ=== 3-4 如果ρ是运动电荷密度,U是运动电荷的平均运动速度,证明:0=∂∂+∇⋅+⋅∇tU U ρρρ证:如果ρ是运动电荷密度,U是运动电荷的平均运动速度,则电流密度为U J ρ=代入电荷守恒定律tJ ∂∂-=⋅∇ρ得0=∂∂+∇⋅+⋅∇t U U ρρρ3-5 由m S /1012.17⨯=σ的铁制作的圆锥台,高为m 2,两端面的半径分别为cm 10和cm 12。
求两端面之间的电阻。
解:用两种方法(1)如题图3.5所示⎰⎰==2122)(tan zz lz dzS dl R ασπσ)11()(tan 1212z z -=ασπ 01.0202.0tan ==α题3.5图m r z .1001.0/1.0tan /11===α,m r z 1201.0/12.0tan /22===αΩ⨯=-⨯⨯⨯=-=--647212107.4)121101(101012.11)11()(tan 1πασπz z R (2)设流过的电流为I ,电流密度为2rI S I J π==电场强度为 2r IJ E πσσ== 电压为 dz z IEdz V z z z z ⎰⎰==21212)tan (σαπ ⎰==2122)(tan zz zdz I V R απσΩ⨯=-6107.4 3-6 在两种媒质分界面上,媒质1的参数为2,/10011==r m S εσ,电流密度的大小为2/50m A ,方向和界面法向的夹角为030;媒质2的参数为4,/1022==r m S εσ。
控制工程基础第三章参考答案

第三章 习题及答案3-1.假设温度计可用11+Ts 传递函数描述其特性,现在用温度计测量盛在容器内的水温。
发现需要min 1时间才能指示出实际水温的98%的数值,试问该温度计指示出实际水温从10%变化到90%所需的时间是多少? 解: 41min, =0.25min T T =1111()=1-e0.1, =ln 0.9t h t t T -=-T21T22()=0.9=1-e ln 0.1t h t t T -=-,210.9ln2.20.55min 0.1r t t t T T =-===2.已知某系统的微分方程为)(3)(2)(3)(t f t f t y t y +'=+'+'',初始条件2)0( , 1)0(='=--y y ,试求:⑴系统的零输入响应y x (t ); ⑵激励f (t )(t )时,系统的零状态响应y f (t )和全响应y (t );⑶激励f (t ) e3t(t )时,系统的零状态响应y f (t )和全响应y (t )。
解:(1) 算子方程为:)()3()()2)(1(t f p t y p p +=++)()e 25e 223()()()( )()e 21e 223()()()( )()e e 2()(2112233)( )2(; 0 ,e 3e 4)( 34221e e )( 2x 2222x 212121221x t t y t y t y t t t h t y t t h p p p p p p H t t y A A A A A A A A t y t t t t t t f f t t t t εεεε------------+=+=+-==-=⇒+-+=+++=-=⇒⎩⎨⎧-==⇒⎩⎨⎧--=+=⇒+=∴*)()e4e 5()()()( )()e e ()(e )()( )3(2x 23t t y t y t y t t t h t y ttt t t f f εεε------=+=-==*3.已知某系统的微分方程为)(3)(')(2)(' 3)(" t f t f t y t y t y +=++,当激励)(t f =)(e 4t t ε-时,系统的全响应)()e 61e 27e 314()(42t t y t t t ε-----=。
概率论与数理统计第三章课后习题及参考答案

概率论与数理统计第三章课后习题及参考答案1.设二维随机变量),(Y X 只能取下列数组中的值:)0,0(,)1,1(-,31,1(-及)0,2(,且取这几组值的概率依次为61,31,121和125,求二维随机变量),(Y X 的联合分布律.解:由二维离散型随机变量分布律的定义知,),(Y X 的联合分布律为2.某高校学生会有8名委员,其中来自理科的2名,来自工科和文科的各3名.现从8名委员中随机地指定3名担任学生会主席.设X ,Y 分别为主席来自理科、工科的人数,求:(1)),(Y X 的联合分布律;(2)X 和Y 的边缘分布律.解:(1)由题意,X 的可能取值为0,1,2,Y 的可能取值为0,1,2,3,则561)0,0(3833====C C Y X P ,569)1,0(381323====C C C Y X P ,569)2,0(382313====C C C Y X P ,561)3,0(3833====C C Y X P ,283)0,1(382312====C C C Y X P ,289)1,1(38131312====C C C C Y X P ,283)2,1(382312====C C C Y X P ,0)3,1(===Y X P ,563)0,2(381322====C C C Y X P ,563)1,2(381322====C C C Y X P ,0)2,2(===Y X P ,0)3,2(===Y X P .),(Y X 的联合分布律为:(2)X 的边缘分布律为X 012P1452815283Y 的边缘分布律为Y 0123P285281528155613.设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其他.,0,42,20),6(),(y x y x k y x f 求:(1)常数k ;(2))3,1(<<Y X P ;(3))5.1(<Y P ;(4))4(≤+Y X P .解:方法1:(1)⎰⎰⎰⎰--==+∞∞-+∞∞-422d d )6(d d ),(1yx y x k y x y x f ⎰--=42202d |)216(y yx x x k k y y k 8d )210(42=-=⎰,∴81=k .(2)⎰⎰∞-∞-=<<31d d ),()3,1(y x y x f Y X P ⎰⎰--=32102d d )216(yx yx x x ⎰--=32102d |)216(81y yx x x 83|)21211(81322=-=y y .(3)),5.1()5.1(+∞<<=<Y X P X P ⎰⎰+∞∞-∞---=5.1d d )6(81yx y x ⎰⎰--=425.10d d )6(81y x y x y yx x x d )216(81422⎰--=3227|)43863(81422=-=y y .(4)⎰⎰≤+=≤+4d d ),()4(y x y x y x f Y X P ⎰⎰---=2042d )6(d 81x y y x x ⎰+-⋅=202d )812(2181x x x 32|)31412(1612032=+-=x x x .方法2:(1)同方法1.(2)20<<x ,42<<y 时,⎰⎰∞-∞-=yxv u v u f y x F d d ),(),(⎰⎰--=y xv u v u 20d d )6(81⎰--=y xv uv u u 202d |)216(81⎰--=y v xv x x 22d )216(81y xv v x xv 222|)21216(81--=)1021216(81222x xy y x xy +---=,其他,0),,(=y x F ,∴⎪⎩⎪⎨⎧<<<<+---=其他.,0,42,20),1021216(81),(222y x x x xy y x xy y x F 83)3,1()3,1(==<<F Y X P .(3))42,5.1(),5.1()5.1(<<<=+∞<<=<Y X P Y X P X P )2,5.1()4,5.1(<<-<<=Y X P Y X P 3227)2,5.1()4,5.1(=-=F F .(4)同方法1.4.设随机变量),(Y X 的概率密度为⎩⎨⎧>>=--其他.,0,0,0,e ),(2y x A y x f y x 求:(1)常数A ;(2)),(Y X 的联合分布函数.解:(1)⎰⎰⎰⎰+∞+∞--+∞∞-+∞∞-==02d d e d d ),(1yx A y x y x f y x ⎰⎰+∞+∞--=002d e d e y x A y x2|)e 21(|)e (020A A y x =-⋅-=∞+-∞+-,∴2=A .(2)0>x ,0>y 时,⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰--=yxv u vu 02d d e 2yv x u 020|)e 21(|)e (2---⋅-=)e 1)(e 1(2y x ----=,其他,0),(=y x F ,∴⎩⎨⎧>>--=--其他.,0,0,0),e 1)(e 1(),(2y x y x F y x .5.设随机变量),(Y X 的概率密度为⎩⎨⎧≤≤≤≤=其他.,0,10,10,),(y x Axy y x f 求:(1)常数A ;(2)),(Y X 的联合分布函数.解:(1)2121d d d d ),(11010⋅⋅===⎰⎰⎰⎰+∞∞-+∞∞-A y y x x A y x y x f ,∴4=A .(2)10≤≤x ,10≤≤y 时,⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰=yxv u uv 0d d 4220202||y x v u yx =⋅=,10≤≤x ,1>y 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4xv u uv 210202||x v u x =⋅=,10≤≤y ,1>x 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4yu v uv 202102||y v u y =⋅=,1>x ,1>y 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=101d d 4v u uv 1||102102=⋅=v u,其他,0),(=y x F ,∴⎪⎪⎪⎩⎪⎪⎪⎨⎧>>≤≤>>≤≤≤≤≤≤=其他.,0,1,1,1,10,1,,1,10,,10,10,),(2222y x y x y y x x y x y x y x F .6.把一枚均匀硬币掷3次,设X 为3次抛掷中正面出现的次数,Y 表示3次抛掷中正面出现次数与反面出现次数之差的绝对值,求:(1)),(Y X 的联合分布律;(2)X 和Y 的边缘分布律.解:由题意知,X 的可能取值为0,1,2,3;Y 的可能取值为1,3.易知0)1,0(===Y X P ,81)3,0(===Y X P ,83)1,1(===Y X P ,0)3,1(===Y X P 83)1,2(===Y X P ,0)3,2(===Y X P ,0)1,3(===Y X P ,81)3,3(===Y X P 故),(Y X 得联合分布律和边缘分布律为:7.在汽车厂,一辆汽车有两道工序是由机器人完成的:一是紧固3只螺栓;二是焊接2处焊点,以X 表示由机器人紧固的螺栓紧固得不牢的数目,以Y 表示由机器人焊接的不良焊点的数目,且),(Y X 具有联合分布律如下表:求:(1)在1=Y 的条件下,X 的条件分布律;(2)在2=X 的条件下,Y 的条件分布律.解:(1)因为)3,3()1,2()1,1()1,0()1(==+==+==+====Y X P Y X P Y X P Y X P Y P 08.0002.0008.001.006.0=+++=,所以43)1()1,0()1|0(=======Y P Y X P Y X P ,81)1()1,1()1|1(=======Y P Y X P Y X P ,101)1()1,2()1|2(=======Y P Y X P Y X P ,401)1()1,3()1|3(=======Y P Y X P Y X P ,故在1=Y 的条件下,X 的条件分布律为X 0123P4381101401(2)因为)2,2()1,2()0,2()2(==+==+====Y X P Y X P Y X P X P 032.0004.0008.002.0=++=,所以85)2()0,2()2,0(=======X P Y X P X Y P ,4)2()1,2()2,1(=======X P Y X P X Y P ,81)2()2,2()2,2(=======X P Y X P X Y P ,故在2=X 的条件下,Y 的分布律为:Y 012P8541818.设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧>>=+-其他.,0,0,0,e ),()2(y x c y x f y x 求:(1)常数c ;(2)X 的边缘概率密度函数;(3))2(<+Y X P ;(4)条件概率密度函数)|(|y x f Y X ,)|(|x y f X Y .解:(1)⎰⎰⎰⎰+∞+∞+-+∞∞-+∞∞-==0)2(d d e d d ),(1yx c y x y x f y x⎰⎰+∞+∞--=002d e d ey x c y x2|)e (|)e 21(002c c y x =-⋅-=∞+-∞+-,∴2=c .(2)0>x 时,⎰+∞∞-=y y x f x f X d ),()(⎰+∞+-=0)2(d e 2y y x x y x 202e 2|)e (e 2-+∞--=-=,0≤x 时,0)(=x f X ,∴⎩⎨⎧≤>=-.0,0,0,e 2)(2x x x f x X ,同理⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y .(3)⎰⎰<+=<+2d d ),()2(y x y x y x f Y X P ⎰⎰---=2202d d e 2xy x yx 422202e e 21d e d e 2-----+-==⎰⎰xy x y x .(4)由条件概率密度公式,得,当0>y 时,有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他.其他.,0,0,e 2,0,0,e e 2)(),()|(22|x x y f y x f y x f xy y x Y Y X ,0≤y 时,0)|(|=y x f Y X ,所以⎩⎨⎧>>=-其他.,0,0,0,e 2)|(2|y x y x f x Y X ;同理,当0>x 时,有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他.其他.,0,0,e ,0,0,2e e 2)(),()|(22|y y x f y x f x y f yx y x X X Y 0≤x 时,0)|(|=x y f X Y ,所以⎩⎨⎧>>=-其他.,0,0,0,e )|(|y x x y f y X Y .9.设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧<<<<=其他.,0,0,10,3),(x y x x y x f求:(1)关于X 、Y 的边缘概率密度函数;(2)条件概率密度函数)|(|y x f Y X ,)|(|x y f X Y .解:(1)10<<x 时,⎰+∞∞-=y y x f x f X d ),()(203d 3x y x x==⎰,其他,0)(=x f X ,∴⎩⎨⎧<<=其他.,0,10,3)(2x x x f X ,密度函数的非零区域为}1,10|),{(}0,10|),{(<<<<=<<<<x y y y x x y x y x ,∴10<<y 时,⎰+∞∞-=x y x f y f Y d ),()()1(23d 321y x x y-==⎰,其他,0)(=y f Y ,∴⎪⎩⎪⎨⎧<<-=其他.,0,10),1(23)(2y y y f Y .(2)当10<<y 时,有⎪⎩⎪⎨⎧<<-=⎪⎪⎩⎪⎪⎨⎧<<-==其他.其他.,0,1,12,0,1,)1(233)(),()|(22|x y y x x y y xy f y x f y x f Y Y X ,其他,0)|(|=y x f Y X ,故⎪⎩⎪⎨⎧<<<<-=其他.,0,10,1,12)|(2|y x y y xy x f Y X .当10<<x 时,有⎪⎩⎪⎨⎧<<=⎪⎩⎪⎨⎧<<==其他.其他.,0,0,1,0,0,33)(),()|(2|x y x x y x x x f y x f x y f X X Y ,其他,0)|(|=x y f X Y ,故⎪⎩⎪⎨⎧<<<<=其他.,0,10,0,1)|(|x x y x x y f X Y .10.设条件密度函数为⎪⎩⎪⎨⎧<<<=其他.,0,10,3)|(32|y x yx y x f Y X Y 的概率密度函数为⎩⎨⎧<<=其他.,0,10,5)(4y y y f Y 求21(>X P .解:⎩⎨⎧<<<==其他.,0,10,15)|()(),(2|y x y x y x f y f y x f Y X Y ,则6447d )(215d d 15d d ),(21(121421211221=-===>⎰⎰⎰⎰⎰>x x x x y y x y x y x f X P xx .11.设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧<<<<+=其他.,0,20,10,3),(2y x xyx y x f 求:(1)),(Y X 的边缘概率密度;(2)X 与Y 是否独立;(3))),((D Y X P ∈,其中D 为曲线22x y =与x y 2=所围区域.解:(1)10<<x 时,x x y xy x y y x f x f X 322d )3(d ),()(222+=+==⎰⎰+∞∞-,其他,0)(=x f X ,∴⎪⎩⎪⎨⎧<<+=其他.,0,10,322)(2x x x x f X ,20<<y 时,⎰+∞∞-=x y x f y f Y d ),()(316)d 3(12+=+=⎰y x xy x ,其他,0)(=y f Y ,∴⎪⎩⎪⎨⎧<<+=其他.,0,20,316)(y y y f Y .(2)),()()(y x f y f x f Y X ≠,∴X 与Y 不独立.(3)}22,10|),{(2x y x x y x D ≤≤<<=,∴⎰⎰+=∈102222d d )3()),((x xx y xy x D Y X P 457d )32238(10543=--=⎰x x x x .12.设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=-其他.,0,0,0,e )1(),(2y x y x y x f x试讨论X ,Y 的独立性.解:当0>x 时,xx x X x yx y y x y y x f x f -∞+-∞+-∞+∞-=+-=+==⎰⎰e |11e d )1(e d ),()(002,当0≤x 时,0)(=x f X ,故⎩⎨⎧≤>=-.0,0,0,e )(x x x x f x X ,同理,可得⎪⎩⎪⎨⎧≤>+=.0,0,0,)1(1)(2y y y y f Y ,因为)()(),(y f x f y x f Y X =,所以X 与Y 相互独立.13.设随机变量),(Y X 在区域}|),{(a y x y x g ≤+=上服从均匀分布,求X 与Y 的边缘概率密度,并判断X 与Y 是否相互独立.解:由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤+=其他.,0,,21),(2a y x a y x f ,当0<<-x a 时,有)(1d 21d ),()(2)(2x a ay a y y x f x f xa x a X +===⎰⎰++-+∞∞-,当a x <≤0时,有)(1d 21d ),()(2)(2x a a y a y y x f x f x a x a X -===⎰⎰---+∞∞-,当a x ≥时,0d ),()(==⎰+∞∞-y y x f x f X ,故⎪⎩⎪⎨⎧≥<-=.a x a x x a a x f X ,0,),(1)(2,同理,由轮换对称性,可得⎪⎩⎪⎨⎧≥<-=.a y a y y a a y f Y ,0,),(1)(2,显然)()(),(y f x f y x f Y X ≠,所以X 与Y 不相互独立.14.设X 和Y 时两个相互独立的随机变量,X 在)1,0(上服从均匀分布,Y 的概率密度为⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2y y y f yY (1)求X 和Y 的联合概率密度;(2)设含有a 的二次方程为022=++Y aX a ,试求a 有实根的概率.解:(1)由题可知X 的概率密度函数为⎩⎨⎧<<=其他.,0,10,1)(x x f X ,因为X 与Y 相互独立,所以),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧><<==-其他.,0,0,10,e 21)()(),(2y x y f x f y x f yY X ,(2)题设方程有实根等价于}|),{(2X Y Y X ≤,记为D ,即}|),{(2X Y Y X D ≤=,设=A {a 有实根},则⎰⎰=∈=Dy x y x f D Y X P A P d d ),()),(()(⎰⎰⎰---==1021002d )e 1(d d e 2122xx y x x y⎰--=102d e12x x ⎰--=12e 21212x x ππππ23413.01)]0()1([21-=Φ-Φ-=.15.设i X ~)4.0,1(b ,4,3,2,1=i ,且1X ,2X ,3X ,4X 相互独立,求行列式4321X X X X X =的分布律.解:由i X ~)4.0,1(b ,4,3,2,1=i ,且1X ,2X ,3X ,4X 相互独立,易知41X X ~)84.0,16.0(b ,32X X ~)84.0,16.0(b .因为1X ,2X ,3X ,4X 相互独立,所以41X X 与32X X 也相互独立,又32414321X X X X X X X X X -==,则X 的所有可能取值为1-,0,1,有)1()0()1,0()1(32413241======-=X X P X X P X X X X P X P 1344.016.084.0=⨯=,)1,1()0,0()0(32413241==+====X X X X P X X X X P X P )1()1()0()0(32413241==+===X X P X X P X X P X X P 7312.016.016.084.084.0=⨯+⨯=,)0()1()0,1()1(32413241=======X X P X X P X X X X P X P 1344.084.016.0=⨯=,故X 的分布律为X 1-01P1344.07312.01344.016.设二维随机变量),(Y X 的概率密度为⎩⎨⎧>>=+-其他.,0,0,0,e 2),()2(y x y x f y x 求Y X Z 2+=的分布函数及概率密度函数.解:0≤z 时,若0≤x ,则0),(=y x f ;若0>x ,则0<-=x z y ,也有0),(=y x f ,即0≤z 时,0),(=y x f ,此时,0d d ),()2()()(2==≤+=≤=⎰⎰≤+zy x Z y x y x f z Y X P z Z P z F .0>z 时,若0≤x ,则0),(=y x f ;只有当z x ≤<0且02>-=xz y 时,0),(≠y x f ,此时,⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 2d d ),()2()()(⎰⎰-+-=zx z y x y x 020)2(d e 2d z z z ----=e e 1.综上⎩⎨⎧≤>--=--.0,0,0,e e 1)(z z z z F z z Z ,所以⎩⎨⎧≤<='=-.0,0,0,e )()(z z z z F z f z Z Z .17.设X ,Y 是相互独立的随机变量,其概率密度分别为⎩⎨⎧≤≤=其他.,0,10,1)(x x f X ,⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y 求Y X Z +=的概率密度.解:0<z 时,若0<x ,则0)(=x f X ;若0≥x ,则0<-=x z y ,0)(=-x z f Y ,即0<z 时,0)()(=-x z f x f Y X ,此时,0d )()()(=-=⎰+∞∞-x x z f x f z f Y X Z .10≤≤z 时,若0<x ,则0)(=x f X ;只有当z x ≤≤0且0>-=x z y 时0)()(≠-x z f x f Y X ,此时,z zx z Y X Z x x x z f x f z f ---+∞∞--==-=⎰⎰e 1d e d )()()(0)(.1>z 时,若0<x ,0)(=x f X ;若1>x ,0)(=x f X ;若10≤≤x ,则0>-=x z y ,此时,0)()(≠-x z f x f Y X ,z x z Y X Z x x x z f x f z f ---+∞∞--==-=⎰⎰e )1e (d e d )()()(1)(.综上,⎪⎩⎪⎨⎧<>-≤≤-=--.0,0,1,e )1e (,10,e 1)(z z z z f z z Z .18.设随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=+-其他.,0,0,0,e)(21),()(y x y x y x f y x (1)X 和Y 是否相互独立?(2)求Y X Z +=的概率密度.解:(1)),()()(y x f y f x f Y X ≠,∴X 与Y 不独立.(2)0≤z 时,若0≤x ,则0)(=x f X ;若0>x ,则0<-=x z y ,0),(=y x f ,此时,0d ),()(=-=⎰+∞∞-x x z x f z f Z .0≥z 时,若0≤x ,则0)(=x f X ;只有当z x <<0且0>-=x z y 时0),(≠y x f ,此时,⎰+∞∞--=x x z x f z f Z d ),()(⎰+-+=zy x x y x 0)(d e )(21⎰-=z z x z 0d e 21z z -=e 212,所以⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2z z z z f zZ .19.设X 和Y 时相互独立的随机变量,它们都服从正态分布),0(2σN .证明:随机变量22Y X Z +=具有概率密度函数⎪⎩⎪⎨⎧<≥=-.0,0,0,e )(2222z z z z f z Z σσ.解:因为X 与Y 相互独立,均服从正态分布),0(2σN ,所以其联合密度函数为2222)(2e 121),(σσπy x y xf +-⋅=,(+∞<<∞-y x ,)当0≥z 时,有⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 22d d ),()()()(22⎰⎰≤++-⋅=zy x y x y x 22222d e 1212)(2σσπ⎰⎰-⋅=πσθσπ2022d ed 12122zr r r ⎰-=zr r r 022d e122σσ,此时,2222e)(σσz Z z z f -=;当0<z 时,=≤+}{22z Y X ∅,所以0)()()(22=≤+=≤=z Y X P z Z P z F Z ,此时,0)(=z f Z ,综上,⎪⎩⎪⎨⎧<≥=-.0,0,0,e )(2222z z z z f z Z σσ.20.设),(Y X 在矩形区域}10,10|),{(≤≤≤≤=y x Y X G 上服从均匀分布,求},min{Y X Z =的概率密度.解:由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤≤≤≤=其他.,0,20,10,21),(y x y x f ,易证,X ~]1,0[U ,Y ~]2,0[U ,且X 与Y 相互独立,⎪⎩⎪⎨⎧≥<≤<=.1,1,10,,0,0)(x x x x x F X ,⎪⎪⎩⎪⎪⎨⎧≥<≤<=.2,1,20,2,0,0)(y y yy y F Y ,可得)](1)][(1[1)(z F z F z F Y X Z ---=)()()()(z F z F z F z F Y X Y X -+=⎪⎪⎩⎪⎪⎨⎧≥<≤-<=.1,1,10,223,0,02z z z z z ,求导,得⎪⎩⎪⎨⎧<<-=其他.,0,10,23)(z z z f Z .21.设随机变量),(Y X 的概率密度为⎩⎨⎧+∞<<<<=+-其他.,0,0,10,e ),()(y x b y x f y x (1)试确定常数b ;(2)求边缘概率密度)(x f X 及)(y f Y ;(3)求函数},max{Y X U =的分布函数.解:(1)⎰⎰⎰⎰+∞+-+∞∞-+∞∞-==01)(d d e d d ),(1yx b y x y x f y x ⎰⎰+∞--=10d e d e y x b y x)e 1(|)e(|)e (10102-+∞---=-⋅=b b y x ,∴1e11--=b .(2)10<<x 时,1)(1e1e d e e 11d ),()(--∞++--∞+∞--=-==⎰⎰x y x X y y y x f x f ,其他,0)(=x f X ,∴⎪⎩⎪⎨⎧<<-=--其他.,0,10,e 1e )(1x x f xX ,0>y 时,⎰+∞∞-=x y x f y f Y d ),()(yy x x -+--=-=⎰e d e e 1110)(1,0≤y 时,0)(=y f Y ,∴⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y .(3)0≤x 时,0)(=x F X ,10<<x 时,101e1e 1d e 1e d )()(----∞---=-==⎰⎰xxt xX X t t t f x F ,1≥x 时,1)(=x F X ,∴⎪⎪⎩⎪⎪⎨⎧≥<<--≤=--.1,1,10,e 1e1,0,0)(1x x x x F x X ;0≤y 时,0)(=y F Y ,0>y 时,y yv y Y Y v v v f y F --∞--===⎰⎰e 1d e d )()(0,∴⎩⎨⎧≤>-=-.0,0,0,e 1)(y y y F y Y ,故有)()()(y F x F u F Y X U =⎪⎪⎩⎪⎪⎨⎧≥-<≤--<=---.1,e 1,10,e 1e1,0,01u u u uu .。
第三章离散傅里叶变换及其快速算法习题答案参考

第三章离散傅里叶变换及其快速算法习题答案参考3.1 图P3.1所示的序列是周期为4的周期性序列。
请确定其傅里叶级数的系数。
解:3.2 (1)设为实周期序列,证明的傅里叶级数是共轭对称的,即。
(2)证明当为实偶函数时,也是实偶函数。
证明:(1)(2)因为实函数,故由(1)知有或又因为偶函数,即,所以有3.3 图P3.3所示的是一个实数周期信号。
利用DFS的特性及3.2题的结果,不直接计算其傅里叶级数的系数,确定以下式子是否正确。
(1),对于所有的k;(2),对于所有的k;(3);(4),对所有的k是实函数。
解:(1)正确。
因为一个周期为N=10的周期序列,故也是一个周期为N=10的周期序列。
(2)不正确。
因为一个实数周期序列,由例3.2中的(1)知,是共轭对称的,即应有,这里不一定是实数序列。
(3)正确。
因为在一个周期内正取样值的个数与负取样值的个数相等,所以有(4)不正确。
根据周期序列的移位性质,=对应与周期序列,如图P3.3_1所示,它不是实偶序列。
由题3.2中的(2)知道,不是实偶序列。
3.4 设,,求,并作图表示和。
解:和的图形如图3.4_1所示:3.5 在图P3.5中表示了两个周期序列和,两者的周期都为6,计算这两个序列的周期卷积,并图表示。
解:图P3.5_1所示的是计算这两个序列的周期卷积的过程,可以看出,是延时1的结果,即。
3.5 计算下列序列的N点DFT:(1)(2)(3)(4)解:(1)(2)(3)(4)3.7 图P3.7表示的是一个有限长序列,画出和的图形。
(1)(2)解:和的图形如图P3.7_1所示:3.8 图P3.8表示一个4点序列。
(1)绘出与的线性卷积结果的图形。
(2)绘出与的4点循环卷积结果的图形。
(3)绘出与的8点循环卷积结果的图形,并将结果与(1)比较,说明线性卷积与循环卷积之间的关系。
解:(1)图P3.8_1(1)所示的是与的线性卷积结果的图形。
(2)图P3.8_1(2)所示的与的4点循环卷积结果的图形。
第3章多组分系统热力学习题参考答案-点评5-16

多组分系统热力学习题参考答案三、习题的主要类型1.计算溶液中由于某组分物质的量改变引起偏摩尔体积的变化以及溶液混合过程中体积的变化。
(例3-2, 例3-4)2.计算从大量或少量等物质量的A 和B 之理想混合物中分离出1mol 纯A 过程的吉布斯自由能。
(例3-6)3.由液体和固体的饱和蒸气压与温度的关系式,计算不可逆相变过程的热力学函数。
(例4-14题)4.用拉乌尔定律和亨利定律计算溶液的气、液组成以及亨利系数 (1) 根据气液平衡计算蒸气分压力。
(例3-7) (2) 根据气液平衡计算亨利系数。
(例3-8) (3) 根据稀溶液气液平衡计算溶质的溶解度。
(例3-9) (4) 计算蒸发过程中,最后一滴液体的组成。
(例3-10) (5) 根据克-克方程和拉乌尔定律,计算气、液组成。
(例3-11题) 5.逸度及活度的应用与计算(1) 气体的逸度和逸度系数的概念和计算。
(例3-5) (2) 由非理想液态混合物应用拉乌尔定律时,其浓度应以活度表示的方法计算活度。
(例3-15题)6.稀溶液依数性的计算。
(例3-12、例3-13题) 7.证明题 (1) 证明物质的摩尔分数、物质的质量摩尔浓度和量浓度三种浓度表示法之间的联系。
(例3-1)(2)证明偏摩尔体积与物质浓度之间的关系。
(例3-3题)四、精选题及其解例3-1 若以x 代表物质的摩尔分数,m 代表质量摩尔浓度,c 代表物质的量浓度。
(1)证明这三种浓度表示法有如下关系B B AB B A B B B A1.0A c M m M x c M c M m M ρ==-++ 式中,ρ为溶液的密度,单位为kg·m -3,A M 、B M 分别为溶剂和溶质的摩尔质量。
(2)证明当浓度很稀时有如下关系B AB B A Ac M x m M ρ==式中,A ρ为纯溶剂的密度。
证:(1)设溶剂为A ,溶质为B ,则溶液的体积(m -3)为:A AB Bn M n M V ρ+=而 B B BBB A A B B A A B B AB A B Bn n x x c V n M n M x M x M M x M x M ρρρ====++-+故 B B B A B B Ac M x c M c M ρ=-+又 B BB B A A A A AB An x x m n M x M M x M ===-所以 B AB B A1.0m M x m M =+(2)当溶液很稀时,A ρρ→,B 0c →,B 0m → 故 B AB B A Ac M x m M ρ==【点评】 该题重点考查以x 代表的物质的摩尔分数、以m 代表的质量摩尔浓度和以c 代表的物质的量浓度的概念定义,以及他们之间的相互关系。
第三章习题参考答案

数据库原理应用教程第三章习题参考答案DB-A/010 第1页共4 页第三章习题答案:一、选择题:1、A2、D3、B4、C5、D6、D7、B8、B9、C 10、C二、填空题1、不能重复(或叫唯一),非空2、m1与m2之积(或:m1×m2)3、dom,F4、关系代数,关系演算5、外键值6、外连接7、省时间,省空间,提高效率8、建立优化语法树的标准格式,形成优化的语法树。
三、计算题:1、解:2、解:(1)检索供应零件给工程J1的供应商编号SNO与零件编号PNO.ΠSNO.PNO(δJNO=’J1’(SPJ))或Π1,2(δ3=’J1’(SPJ))(2)检索供应零件给工程J1,且零件编号为P1的供应商编号SNO.ΠSNO(δjno=’J1’(SPJ))(3)检索使用了编号为P3零件的工程编号和名称。
ΠSNO.JNAME(δPNO=’P3’(J∞SPJ))(4)检索供应零件给工程P1,且零件颜色为红色的供应商名称SNAME和地址SADDR.ΠSNAME.SADDR(δJNO=’J1’^PNO=’红色’(J∞SPJ∞P))(5)检索使用了编号为P3或P5零件的工程编号JNO。
ΠJ NO(δPNO=’P3’VPNO=’P5’(SPJ))(6)检索至少使用了编号为P3零件的工程编号JNO。
ΠJ NO(δ1=6^2=’P3’V7=’P5’(SPJ×SPJ))(7)检索不使用编号为P3零件的工程编号JNO和工程名称JNAME。
ΠJ NO.JNAME(J)- ΠJ NO.JNAME (δPNO=’P3’(J∞SPJ))(8)检索使用了全部零件的工程名称JNAME。
ΠJ NAME(J∞(ΠJ NO.PN0(SPJ)÷ΠPNO(P)))(9)检索使用零件包含编号为S1的供应商所供应的全部零件的工程编号JNO。
ΠJ NO.PNO(SPJ)÷ΠPNO(δSNO=’S1’(SPJ))3、解解决以上问题的关系代数表达式是:ΠSNAME.SADDR(δJNO=’J1’ AND COLOR =’红色’(J∞SPJ∞P))(1)把以上表达式转化成笛卡儿积形式ΠSNAME.SADDR(δJNO=’J1’ AND COLOR =’红色’(ΠL(δS。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PUSH 30H ;61H=24H
PUSH 31H ;62H=10H SP=62H
POP DPL ;DPL=10H
POP DPH ;DPH=24H SP=60H
答:AJMP addr11 为2K字节范围内的无条件转跳指令,把程序的执行转移到指定的地址。SJMP rel是无条件转跳指令,执行时在PC加2后,把指令中补码形式的偏移量值加到PC上,并计算出转向目标地址。转向的目标地址可以在这条指令前128字节到后127字节之间。
LJMP addr16执行这条指令时把指令的第二和第三字节分别装入PC的高位和低位字节中,无条件地转向指定地址。转移的目标地址可以在64K程序存储器地址空间的任何地方,不影响任何标志。
A=25H R0=50H 50H=00H 51H=25H
3-2 访问外部数据存储器和程序存储器可以用哪些指令来实现?举例说明。
答:访问外部数据存储器指令有:
MOVX @DPTR,A MOV DPTR,#0100H MOV @DPTR,A
MOVX A,@DPTR MOV DPTR,#0200H MOV A,@DPTR
LOOP1: ORL C, ACC.0 ;CY=1
JB ACC.2,LOOP2 ;
CLR 00H
LOOP2: MOV P1,A ;P1=01100110B
3-7指令SJMP rel中,设rel=60H,并假设该指令存放在2114H和2115H单元中。当该条指令执行后,程序将跳转到何地址?
答: 2116H+60H=2176H
3-8 简述转移指令AJMP addr11、SJMP rel、 LJMP addr16及JMP @A+DPTR的应用场合。
MOV 55H,A
MOV A,52H
ADDC A,50H
DA A
MOV 56H,C
SJMP $
JMP @A+DPTR 指令的功能是把累加器中8位无符号数与数据指针DPTR中的16位数相加,将结果作为下条指令地址送入PC,利用这条指令能实现程序的散转。
3-9 试分析下列程序段,当程序执行后,位地址00H,01H中的内容将为何值?P1口的8条I/O线为何状态?
CLR C ;CY=0
XCHD A,@R1 ;A=25H 40H=03H
3-5 两个四位BCD码数相加,被加数和加数分别存于50H,51H和52H,53H单元中(千位、百位在低地址中,十位、个位在高地址中),和存放在54H,55H和56H中(56H用来存放最高位的进位),试编写加法程序。
MOV 30H,#00H ;30H=00H
MOV 31H,#0FFH ;31H=0FFH
3-4 设(A)=40H,(R1)=23H,(40H)=05H。执行下列两条指令后,累加器A和R1以及内部RAM中40H单元的内容各为何值?
XCH A,R1 ;A=23H R1=40H
MOV A,#66H ;A=66H
JC LOOP1
CPL C ;CY=1
SETB 01H ;20H.1=1
SJMP $
20H.0=0 20H.1=1 P1=66H
3-10 查指令表,写出下列两条指令的机器码,并比较一下机器码中操作数排列次序的特点。
MOV 58H,80H
85(80)(58) 直接寻址字节送直接寻址字节: 汇编时源操作数在目标操作数之前。
MOV 58H,#80H
75(58)(80) 立即数送直接寻址字节: 汇编时目标操作数在原操作数之前。
第3章习题参考答案
3-1 设内部RAM中59H单元的内容为50H,写出当执行下列程序段后寄存器A,R0和内部RAM中50H,51H单元的内容为何值?
MOV A,59H ;A=50H
MOV R0,A ;R0=50H
END
3-6 设(A)=01010101B,(R5)=10101010B,分别写出执行下列指令后结果。
ANL A , R5 ; 00000000B
ORL A , R5 ; 11111111B
XRL A , R5 ; 11111111B
ORG 0000H
LJMP START
ORG 0100H
START: MOV A,53H
ADD A,51H
DA A
MOV A,#00H ;A=00H
MOV @R0,A ;50H=00H
MOV A,#25H ;A=25H
MOV 51H,A ;51H=25H
MOV 52H,#70H ;52H=70H
MOVX A,@Ri MOVX A,@R0
MOVX @Ri,A MOVX @R1,A
访问程序存储器指令有:
MOVC A,@A+PC
MOVC A,@A+DPTR
3-3 设堆栈指针SP中的内容为60H,内部RAM中30H和31H单元的内容分别为24H和10H,执行下列程序段后,61H,62H,30H,31H,DPTR及SP中的内容将有何变化?
