静定梁的弯矩

剪力与弯矩的计算方法

§7-2剪力与弯矩一、剪力和弯矩根据作用在梁上的已知载荷，求出静定梁的支座反力以后，梁横截面上的内力可利用前面讲过的“截面法”来求解，如图7-8a 所示简支梁在外力作用下处于平衡状态，现在讨论距A 支座距离为x 的m m -截面上的内力。

图7-8简支梁指定截面的剪力、弯矩计算根据截面法计算内力的基本步骤“切、代、平”，计算梁的内力的步骤为：①、首先根据静力平衡方程求支座反力Ay F 和By F ，为推导计算的一般过程，暂且用Ay F 和By F 代替。

②、用截面假想沿m m -处把梁切开为左、右两段，如图7-8b、7-8c 所示，取左段梁为脱离体，因梁原来处于平衡状态，所以被截取的左段梁也同样保持平衡状态。

从图7-8b 中可看到，左段梁上有一向上的支座反力Ay F 、向下的已知力1P 作用，要使左段梁不发生竖向移动，则在m m -截面上必定存在一个竖直方向的内力S F 与之平衡；同时，Ay F 、1P 对m m -截面形心O 点有一个力矩，会引起左段梁转动，为了使其不发生转动，在m m -截面上必须有一个力偶矩M 与之平衡，才能保持左段梁的平衡。

S F 和M 即为梁横截面上的内力，其中内力S F 使横截面有被剪开的趋势，称为剪力；力偶矩M 将使梁发生弯曲变形，称为弯矩。

由于外载荷的作用线垂直于梁的轴线，所以轴力为零，通常不予考虑。

剪力S F 和弯矩M 的大小可由左段梁的静力平衡方程来求解。

由0=∑Y 得：10Ay S F P F --=，得1S Ay F F P =-由0o M =∑得：()01=+-+-M a x P x F Ay 得()a x P x F M Ay --=1如图7-8c 所示，如果取右段梁为脱离体，同样可求得m m -截面的剪力S F 和弯矩M 。

根据作用力与反作用力原理，右段梁在m m -截面上的剪力S F 和弯矩M 与左段梁在m m -截面上的剪力S F 和弯矩M 应大小相等，方向相反。

单跨超静定梁的杆端弯矩和杆端剪力

多余未知力X1求得后，即可由静力平衡条件求得其余的约束反力和内力。最后弯矩图也可以利用已经绘出的基本结构的M1图和MP图由叠加原理按下
M=M1X1+MP 也就是将M1图的竖标乘以X1倍，再与MP图中的
MA=MAX1+MAP=l×3/8ql-1/2ql2 =-1/8ql2 (上侧受拉)
最后内力图如图19.9
b
Δ3=δ31X1+δ32X2+δ33X3+Δ3P=0 式(b)就是由位移条件所建立的求解X1、X2和X3
对于n次超静定结构有n个多余约束，也就是有n 个多余未知力x1，x2，…，xn，且在n个多余约束处有n个已知的位移条件，故可建立n个方程，例如原结构在荷载作用下各多余约束处的位移为零时，有
19 力法
本章提要
本章主要介绍超静定结构的计算方法——力法。介绍如何选择力法的基本结构、建立力法典型方程，以求出超静定结构的内力图。重点掌握力法的基本原理、基本结构的选择方法和力法解超静定结构的三方面因素。同时对一些特殊结构，如：对称结构、两铰拱等也作了基本的介绍。
本章内容
19.1 超静定结构概述 19.2 力法原理 19.3 力法的典型方程 19.4 力法应用举例 19.5 利用对称性简化计算 19.6 支座移动时超静定结构的计算
② 作剪力图根据已求出的杆端弯矩和荷载，画AB 梁的受力图如图19.12所示。由∑MA=0得
1 2ql11 2ql211 2ql2+Q B Agl0
所以QBA=-ql/2 由∑Y=0
QAB－ql－QBA=0 QAB=ql+QBA=ql－ql/2=ql/2 因为AB梁受到均匀分布荷载，剪力图应为斜直线，如图19.11(h)所示。

土木工程力学(本)练习答案(电大考试专用)

土木工程力学（本）综合练习题及解析一、判断题将判断结果填入括弧，以√表示正确，以×表示错误。

1．基本附属型结构力的传递顺序是：从附属部分到基本部分。

（） 2．结构由于弱阻尼影响自振频率会变小。

（） 3．当AB 杆件刚度系数i S AB 3 时，杆件的B 端为固定支座。

（）4．温度变化时静定结构中的杆件截面发生变形。

（）5．图（a ）对称结构受对称荷载作用，利用对称性可简化为图（b ）来计算。

（）（a ）（b ） 6．结构的自振频率与干扰力无关。

（）7．位移法的基本结构不是唯一的。

（）8．由于支座位移超静定结构产生的内力与刚度的绝对值有关。

（） 9．实际桁架结构的杆件只有轴力产生。

（） 10．结构的自振频率与结构中某杆件的刚度有关。

()11．图示为刚架的虚设力状态，按此力状态及位移计算公式可求出A 处的竖向位移。

（）A12．图示结构的超静定次数是n=2。

（）13．结构的自振频率与结构所受的外荷载大小相关。

（）14．根据静力平衡条件对静定结构进行受力分析，结果是唯一正确的结果。

（）15．桁架中的零杆是多余的，应该去掉。

（）16．在力矩分配法中，当远端为固定支座时，其传递系数为1。

（） 17．在温度变化与支座位移因素作用下，静定结构有内力和位移产生。

（） 18．在结构动力计算中，振动体系的质点数目与振动自由度不一定相等。

（） 19．图示结构A 截面剪力影响线在B 处的竖标为0。

（）l20．在结点荷载作用下，桁架结构中的杆件内力不一定只有轴力。

（）二、单项选择题在所列备选项中，选1项正确的或最好的作为答案，将选项号填入各题的括号中。

1．用位移法计算图示各结构，基本未知量是两个的结构为（） A BCD2．用力法计算超静定结构时，其基本未知量为（） A 杆端弯矩 B 结点角位移 C 结点线位移 D 多余未知力 3．图示结构杆件BA 的B 端转动刚度BA S 为（） A 2 B 3C 4D 6ABCm3m3i = 1i = 24．用力矩分配法计算结构得到一个收敛的结果，是因为（）A 分配系数小于1B 分配节点之间的传递系数小于1C 结点上有外力矩作用D A 和B 同时满足 5．反映结构动力特性的重要物理参数是（）A 质点的质量B 自振频率C 振幅D 干扰力的大小6．用力矩分配法计算超静定结构时，刚结点的不平衡力矩等于（）A 外力矩B 附加刚臂中的约束反力矩C 杆端固端弯矩D 杆端传递弯矩 7．影响线的纵坐标是（）A 固定荷载的数值B 移动荷载的数值C 不同截面的某一量值D 指定截面的某一量值 8．受弯杆件截面内力有（）A 弯矩B 剪力C 轴力D A 、B 、C9．不考虑杆件的轴向变形，竖向杆件的EI =常数。

土木工程力学(本)综合习题

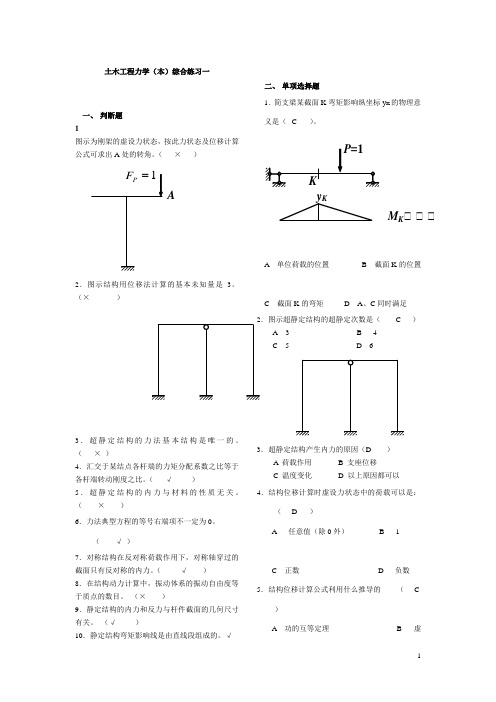
土木工程力学（本）综合练习一一、判断题1图示为刚架的虚设力状态，按此力状态及位移计算公式可求出A处的转角。

（×）A2．图示结构用位移法计算的基本未知量是3。

（×）3．超静定结构的力法基本结构是唯一的。

（×）4．汇交于某结点各杆端的力矩分配系数之比等于各杆端转动刚度之比。

（√）5．超静定结构的内力与材料的性质无关。

（×）6．力法典型方程的等号右端项不一定为0。

（√）7．对称结构在反对称荷载作用下，对称轴穿过的截面只有反对称的内力。

（√）8．在结构动力计算中，振动体系的振动自由度等于质点的数目。

（×）9．静定结构的内力和反力与杆件截面的几何尺寸有关。

（√）10．静定结构弯矩影响线是由直线段组成的。

√二、单项选择题1．简支梁某截面K弯矩影响纵坐标y K的物理意义是（ C ）。

M K影影影A 单位荷载的位置 B 截面K的位置C 截面K的弯矩D A、C同时满足C ）A 3B 4C 5D 63．超静定结构产生内力的原因（D ）A 荷载作用B 支座位移C 温度变化D 以上原因都可以4．结构位移计算时虚设力状态中的荷载可以是：（ D ）A 任意值（除0外）B 1C 正数D 负数5．结构位移计算公式利用什么推导的（C ）A 功的互等定理B 虚位移原理C 虚功原理D 反力互等定理6．用位移法计算超静定结构时，独立的结点角位移数等于（ D ）A 铰结点数B 刚结点数C 多余约束数D 不确定7．在图示结构中，使体系自振频率ω减小，可以（ C ）A 减小PF B 减小mC 减小EID 减小ll m t8．求图示结构AB两点的相对线位移，虚设力状态为图（ A ）ABM=1M=1A B C D1=F9．与杆件的传递弯矩有关的是（D ）A 分配弯矩B 传递系数C 分配系数D 结点位移10．用位移法解超静定结构其基本未知量的数目等于（A ）A 独立的结点位移数目B 刚结点数目C 线位移数目 D超静定次数三、作图题1.作图示静定梁的弯矩图。

电大《土木工程力学》本历届试题及答案

1.用位移法计算图示各结构，基本未知量是两个的结构为（A ）。

2. 用力法计算超静定结构时，基本未知量是（D 多余未知力）。

3. 图示结构杆件BA 的B 端转动刚度BA S 为（ B 3 ）。

4. 用力矩分配法计算结构得到一个收敛的结果，是因为（ D ）。

A. 分配系数小于1B. 分配结点之间传递系数小于1C. 结点上有外力矩作用D. A 和B 同时满足5. 反映结构动力特性的重要物理参数是（ B 自振频率）。

6. 用力矩分配法计算超静定结构时，刚结点的不平衡力矩等于（ B 附加刚臂中的约束反力矩）。

7. 影响线的纵坐标是（ D 指定截面的某一量值）。

8. 受弯杆件截面内力有（ D 弯矩剪力轴力）。

9. 不考虑杆件的轴向变形，竖向杆件的 E I = 常数。

下图所示体系的振动自由度为（ A 1 ）。

10. 力法典型方程是（ B 多余约束处的位移协调条件）。

三、（10分）21.作图示静定结构的弯矩图。

四、（16分）22.用力法计算图示结构并作弯矩图，EI=常数。

解：典型方程011111=∆+=∆P x δ五、（14分）23.用位移法计算图示刚架，列出典型方程，求出系数项及自由项。

解：典型方程01111=+∆P F k1.图示对称结构作用反对荷载，EI=常数，对称轴穿过的AB 杆件内力满足（D 0,0,0===N Q F F M ）2.机动法作静定梁弯矩影响线应用的原理是( C 刚体虚功原理 )。

3．结构不考虑阻尼时的自振频率为ω，考虑阻尼时的自振频率为D ω，则( C D ωω )4．图示结构中，除横梁外，各杆件EI=常数。

不考虑杆件的轴向变形，则体系振动的自由度数为(A 1)。

5．位移法典型方程是根据( D 附加约束的平衡条件 )列出的。

6．图示a 、b 两体系的自振频率a ω与b ω的关系为( B b a ωω )。

7．图示对称结构作用反对称荷载，杆件EI 为常量，利用对称性简化后的一半结构为（ A ）。

第3章静定梁

上一张下一张主页退出
城乡建设学院
Urban and Rural Development college
§3-2 简支斜梁的计算
§3-2 简支斜梁的计算
上一张下一张主页
退出
城乡建设学院
Urban and Rural Development college
§3-2 简支斜梁的计算
1.斜梁承受竖向均布荷载时的两种表示方法
M B 0,VA
上一张下一张主页
退出
城乡建设学院
Urban and Rural Development college
§3-1 静定单跨梁的计算
2.
作剪力图
-
QAD QDA 18kN QDE 18 8 10 kN
QE QDE 10 kN
QF 6kN
上一张下一张主页退出
城乡建设学院
Urban and Rural Development college
本章小结
本章基本内容是静定单跨梁和多跨梁的支座反力、内力的计算及内力图的绘制。
（1）计算步骤。（2）截面内力有弯矩、剪力、轴力，应注意其定义及正负号规定。（3）计算截面内力的基本方法是截面法。（4）绘制弯矩图的基本方法是分段叠加法。（5）内力图的纵坐标垂直于杆轴线画。
城乡建设学院
Urban and Rural Development college
§3-1 静定单跨梁的计算
不同教材中内力分量的两种表达形式:
Q
N
Q’
N’
城乡建设学院
Urban and Rural Development college
§3-1 静定单跨梁的计算

梁的弯曲分析

连续梁的超静定结构问题
连续梁的刚度分析—三弯方程
L1
01
2
3
Ln n-2 n-1
n
n+1
Mn-1 n-1
Mn
Mn
n
Mn+1 n+1
连续梁的刚度分析
在对连续梁做出了结构上的分解简化以后，利用应变的几何变化，以及莫尔积分和力法计算后，可以得到连续梁的三湾方程：连续梁三弯方程的个数等于其超静定的次数。
变形几何关系在纯弯曲梁中取一微段dx。变形前互相平行相距dx的两个横截面变形后会形成一个角度为θ的夹角，OO代表中性层，其弯曲后曲率半径为ρ，则设距离中性层y的纤维长度bb变为b1b1
则线段的应变为：
物理与静力学关系当应力不超过比例极限时，由胡克定律可知，距中性轴为y处的正应力为：
如图所示悬臂梁抗弯刚度为EI，在自由端受到一集中载荷作用，
试求梁的剪力，弯矩方程，挠曲线方程和斜度，并确定其最
大挠度和最大转角。
解：
F
L
R
固定端支反力R=F
x
根据截面法易求出剪力和弯矩方程分别为：
Fs=F；M=F*x；最大M=Fl；
挠曲线的近似微分方程为：
积分后得到：
梁弯曲变形—挠度和斜度的计算—例子
当在固定端即x=L时有，斜度i=0，挠度w=0；将此条件带入到上述两个方程中得到： C=-(FL^2)/2,D=(FL^3)/3 将C和D两个带入挠度和斜度方程得到：
式中为最大抗弯应力，等于最大弯矩和梁高h/2乘积除以二次矩I的值。
梁的优化设计—提高刚度
梁的优化设计—提高刚度
等强梁的概念
T
T
弯曲在包含杆件轴线的纵向平面内，作用大小相等、方向相

马不停蹄总结静定结构专题1——斜梁弯矩

力学分析专题：斜梁弯矩分析1.斜梁受力的来龙去脉斜梁属于静定结构中理解难度相对较大的一种结构，其根本原因在于，对简支梁以及荷载分布理解不够深刻，很多人搞不清楚斜梁的荷载分布，在其具体的受力分析中，哪些是不变量，哪些是变化量，斜梁分析的核心问题，就是在变化中找不变！首先我们对斜梁有一个直观的认识：思考：（a）、（b）、（c）在实际工程中分别对应何种荷载类型？弯矩分析：在分析斜梁之前，首先分析一下简支梁：其分析步骤为：1、求支座反力；2、假定最大弯矩截面距支座的位置；3、列出弯矩对距离的函数，求导确定位置；4、代入数据，求出最大弯矩。

按正常的力学思维方式，所有的梁内力，都应该按照上述的步骤进行分析，但是，由于其身份的特殊性和重要性，我们很多人只记住了M=(ql^2)/8,而忽略了这个弯矩的来源，其造成的直接影响，就是，斜梁的三种弯矩一对比：瞬间懵逼的节奏！卖了这么多关子，我们开始进入正题这个是上面的（a）请看图中列出的算式，再和简支梁的进行对比，可以发现：对于l0的跨度，荷载q的分布，其弯矩计算方法，和跨度为l0，荷载为q的简支梁，列出的弯矩表达式是完全一样的！这就是“不变”。

这个结果完全可信，因为我们是经过了严密的推导得出的结论，而且，因为这个结果可以和简支梁的计算结果相统一，其计算结果，也是可以和简支梁的计算结果一样，应该被记住的：投影长度为l0的斜梁，在沿投影分布荷载作用q下，最大弯矩为M=(ql0^2)/8。

这个原理以及分析方法，就是我们前面提到的，在变化中找不变，变化的是形式，不变的是具体的力学分析和基本荷载分布与弯矩的对应关系，只要将二者统一，就可以直接抓住问题的“七寸”，又快又准的将其拿下。

从上面的结果出发，我们分析（b）对于这个问题，因为已经知道斜梁沿投影分布时候弯矩的算法，这就可以作为我们的一个“不变量”，抓住了这个关键，问题也就迎刃而解，既然都是均布荷载，那么也应该在均布荷载的范畴内，再找到一个“不变量”统一在一起：均布值×分布长度=总重：q’l0=ql(l0为投影长度，l为实际长度)这样的结论，就可以得出：q’=ql/l0=q/(l0/l)=q/cosα(α为构件倾斜角度)此时，弯矩的最大值即为：M=(q’l0^2)/8=(ql^2)/[8(cosα)^2]此处多说一句，因为弯矩的矢量方向在平面外（具体不用深究，左右手法则一两句话说不清，对结构分析也不必掌握），这使得弯矩有个特点：对于平面内的一根梁，取截面的时候，只要形心位置确定，弯矩最大值就是一定的，与截面的朝向无关，在算剪力的时候，就与此有着明显的不同，需要认真体会其中的奥妙。

快速巧解材料力学静定梁的约束力及剪力弯矩图

快速巧解材料力学静定梁的约束力及剪力弯矩图作者：张圣光来源：《价值工程》2014年第09期摘要：材料力学是高等院校工科必修的一门专业基础课。

在机械、土木、采矿等领域有着广泛的应用。

本文以数学、理论力学为基础，总结出求约束力的“四大原理”以及剪力弯矩图画法的“三看一算”口诀，并形成规律，避免了繁琐的平衡方程，在工程及教学应用上的运算速度都得到了提高。

Abstract： Materials mechanics is a required professional basic course for engineering colleges and universities， and it has been widely used to mechanical， civil， mining and other fields. Based on mathematics and theoretical mechanics， this paper summarizes "four principles" for solving the binding force as well as the "three seeing and one calculating" formula for drawing shear bending moment diagram， forming the law， avoiding the tedious balance equation， and the improving the operation speed in engineering and teaching application.关键词：约束力；弯矩；剪力Key words： binding force；bending moment；shear中图分类号：[O341] 文献标识码：A 文章编号：1006-4311（2014）09-0240-020 引言计算约束反力是画剪力弯矩图的基础，一旦求错就导致后面的解体都出错，笔者根据自己的解题经验总结出了“四大原理”，避免用理论力学解题时的繁琐，方便快捷。

材料力学试卷及答案7套

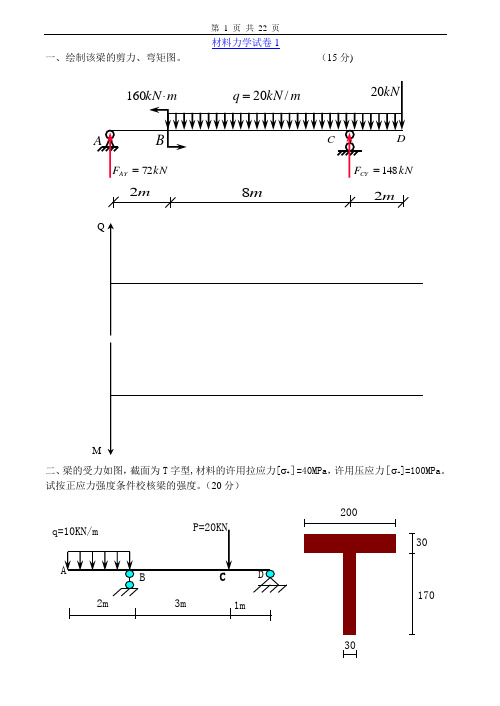
材料力学试卷1一、绘制该梁的剪力、弯矩图。

（15分)二、梁的受力如图，截面为T 字型,材料的许用拉应力[σ+］=40MPa ，许用压应力［σ-]=100MPa 。

试按正应力强度条件校核梁的强度。

（20分）m8m2m230170302002m3m1mM三、求图示单元体的主应力及其方位，画出主单元体和应力圆。

（15分）30四、图示偏心受压柱,已知截面为矩形，荷载的作用位置在A点，试计算截面上的最大压应力并标出其在截面上的位置，画出截面核心的形状.（15分)五、结构用低碳钢A 3制成，A 端固定,B 、C 为球型铰支，求：允许荷载［P ］。

已知:E=205GPa ，σs =275MPa ，σcr =338—1。

12λ,，λp =90，λs =50，强度安全系数n=2,稳定安全系数n st =3，AB 梁为N 016工字钢,I z ＝1130cm 4，W z ＝141cm 3，BC 杆为圆形截面，直径d=60mm 。

（20分）六、结构如图所示.已知各杆的EI 相同，不考虑剪力和轴力的影响,试求:D 截面的线位移和角位移.（15分)材料力学2一、回答下列各题（共4题，每题4分，共16分）1、已知低碳钢拉伸试件，标距mm l 1000=，直径mm d 10=，拉断后标距的长度变为mm l 1251=，断口处的直径为mm d 0.61=，试计算其延伸率和断面收缩率。

2、试画出图示截面弯曲中心的位置。

3、梁弯曲剪应力的计算公式zzQS =τ，若要计算图示矩形截面A 点的剪应力，试计算z S 。

aa4/h4、试定性画出图示截面截面核心的形状（不用计算）。

二、绘制该梁的剪力、弯矩图.（15分) 三、图示木梁的右端由钢拉杆支承.已知梁的横截面为边长等于0.20m 的正方形，q=4OKN/m,弹性模量E 1＝10GPa ；钢拉杆的横截面面积A 2＝250mm 2，弹性模量E 2=210GPa .试求拉杆的伸F sM矩形圆形矩形截面中间挖掉圆形圆形截面中间挖掉正方形四、砖砌烟窗高m h 30=,底截面m m -的外径m d 31=，内径m d 22=,自重kN P 20001=,受m kN q /1=的风力作用。

梁的内力剪力弯矩方程剪力弯矩图

q=0 FS M q >0 q<0 当q<0,
(3)若某截面处FS=0
dF S dx
q(x)
dM dx
FS
d M dx
2
2
q(x)
则该截面上M取极值：当q>0, M取到极小值当q<0, M取到极大值（4）集中力F作用处，FS突变，跳跃值为F，M有尖点； q>0 q<0
集中力偶M作用处，M突变，跳跃值为M， FS不受影响。 F M
例题
例题 2
2qa
A
§9 变形体静力学概述及一般杆件内力分析
qa2 q
B C
解： 1.求约束力
FB q 2 a a 2 qa 3 a qa 2a 7 2 qa ( )
2
D
a
3 2 qa
FB a
a
a 2

FD
F D 4 qa
7 2
qa
1 2
qa ( )
D
FD
FD
F Ax 1 2 2 ( kN )( )
A
FAx
FAy
2m
F Ay 5 3 2 kN ( )
例题
例题 4
5kN B
§9 变形体静力学概述及一般杆件内力分析
4kN· m C
2.作内力图 D 3kN 轴力图： AB段 F N 2 kN
1m
1m
(F S )
1 qa
2
2.作内力图
1 2 qa
M
7 2
1 4 qa
2
B
2 qa
2
2qa (M)
qa
8

单跨超静定梁的杆端弯矩和杆端剪力

δ11X1+δ12X2+…+δ1nXn+Δ1P=0 ……
δi1X1+δi2X2+…+δinXn+ΔiP=0 ……
δn1X1+δn2X2+…+δnnXn+ΔnP=0 式(19.2)为力法方程的一般形式，常称为力法典型方程。
其物理意义是：基本结构在全部多余未知力和已知荷载作用下，沿着每个多余未知力方向的位移，应与原结构相应的位移相等。
移Δ1必须为零，也就是说基本结构在已知荷载与多
余未知力X1共同作用下；在拆除约束处沿多余未知
力X1作用方向产生的位移应与原结构在X1方向的位
Δ1=0
(a)
这就是基本结构应满足的变形谐调条件，又称位移条件
若用Δ1P和Δ11分别表示荷载q和多余未知力X1单独作用下基本结构在X1作用处沿X1方向产生的位移，则由叠加原理根据位移条件可得下列方程
超静定结构中多余约束的数目称为超静定次数。判断超静定次数可以用去掉多余约束使原结构变成静定结构的方法进行。去掉多余约束的方式一般有
(1) 去掉一根支座链杆或切断一根链杆等于去掉一个约束，图19.3
(2) 去掉一个铰支座或拆去联结两刚片的单铰等于去掉两个约束，图19.4
(3) 将固定端支座改成铰支座，或将刚性联结改成单铰联结，等于去掉一个约束，图19.5。
Δ1=Δ11+Δ1P=0 (b) 若X1=1时在X1方向产生的位移为δ11，则有 Δ11=δ11X1，于是(b)
δ11X1+Δ1P=0 (19.1) 这就是求解多余未知力的补充方程，称为力法方程。
为了计算δ11和Δ1P，分别作基本结构在荷载q作用下的弯矩图MP(图19.8(a))和在单位力X1=1作用下的单位弯矩图M1(图19.8(b))

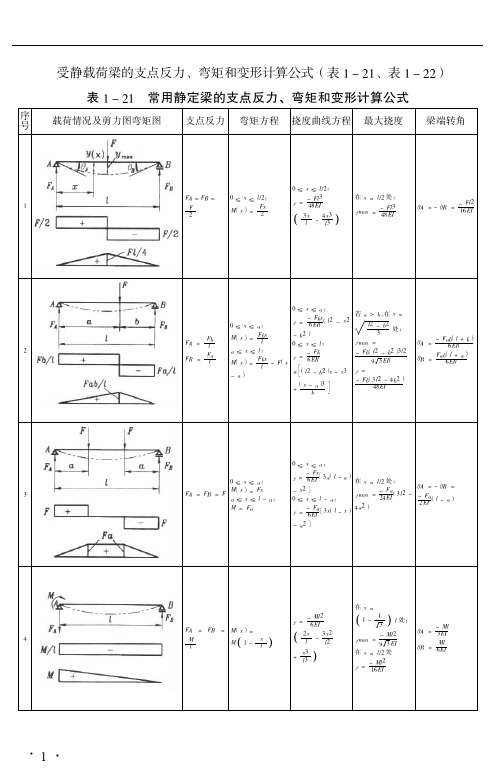
静载荷梁的受力,力矩,变形计算公式整理总结

&）［ %$
!（ %$ # & *$ ）,& 处：
’$()* "
!,
"
%#($)（% & *$
.
# & *$ #（ % # &）$ ］
& +$ # %$ ）
# $（ %$ # & *$ ）&,$
+!& ()%
/
!" " !# "
-% $
$（ &）"
-$&（ % #
’ &）
.
"
# $0
(-&（)
)&
&& ）
#
$ %&$
在 & " %,$ 处：
’()*()
!"
" #!#
"
# -%& $0 ()
1
!"
"
-- % %
!#
"
-- % &
$（ &）"
( ) -- %& %
’#
&$ %$
’"
# -- %0 &%- ()
2
( ) /& %
#
’-&$ %$
.
&&! %!
在 & " -3!’+ % 处： ’()* " # -3--%!$ -- %&
"# ’
),]
在 # # .0++) ’ 处：
$&’(

简支梁和连续梁的弯矩

简支梁和连续梁的弯矩简支梁和连续梁都是土木工程中常用的结构构件，用于承载和传递荷载，其弯矩分布是结构设计中需要考虑的重要参数。

下面将分别介绍简支梁和连续梁的弯矩计算相关内容。

1. 简支梁的弯矩计算：简支梁是指两端支座处受到约束，不能转动的梁，其弯矩计算可以通过应变能定理或矩形法等方法进行。

1.1 应变能定理方法：该方法基于能量原理，根据梁的弹性形变能和外力的功的平衡关系进行计算。

简支梁的最大正弯矩Mmax和最大剪力Vmax可以通过强度学分析计算得到。

用弯矩分布图表示，从梁的一端开始逐段计算，考虑不同段的梁长、梁高、截面转动等参数，可得到各段的弯矩分布。

1.2 矩形法等方法：该方法将梁截面的应变转化为应力，结合截面形状和材料性质，可以通过材料力学的相关公式计算出不同截面形状的梁的弯矩。

常见的矩形法有：直矩形法、威特拉斯法、钢筋均布法等，通过计算梁截面的面积和应力的分布，得到不同截面形状的弯矩。

2. 连续梁的弯矩计算：在横跨较大跨度时，常会使用连续梁来代替简支梁，以减小支座反力和降低结构的变形。

连续梁是指有两个或两个以上的支座的梁，支座之间可以相互转动。

2.1 弹性力学法：连续梁的弯矩计算可以通过弹性力学的原理和基本方程进行，主要有：静定连续梁的力学基本方程、静定超静定连续梁的自由度数等。

根据结构的支座条件、受力情况和边界条件，可以建立相应的方程组求解，得到连续梁各个截面的弯矩、剪力、反力等。

2.2 曲率影响线法：该方法基于连续梁的几何特性和支座反力的分布，通过绘制曲率影响线和弯矩影响线等图形，计算连续梁的弯矩。

在绘制过程中，需考虑连续梁的跨度、支座位置、曲线形状等因素，通过坐标轴的运算和图形的叠加，可以得到连续梁中各个截面的弯矩分布。

总结：简支梁和连续梁的弯矩计算是土木工程中非常重要的问题，关系到结构的安全性和合理性。

弯矩的计算可以通过应变能定理、矩形法和弹性力学法等方法进行。

在实际工程中，根据不同的结构形式、荷载情况和设计要求，可以选择合适的方法进行计算和分析。

静定梁的内力—单跨静定梁的内力计算(建筑力学)

MO 0 : M FA x 0
B FB
F
lx
c
FQ FA
M FA x
与横截面相切的内力，称为剪力FQ , 常用单位为N或kN 。
作用在外力作用平面内（纵向对称平面
B
内）的内力偶，其力偶矩称为弯矩M，
FB 常用单位为
N m或 k N m 。
注：不论是左段还是右段隔离体计算出的内力应该是同一截面上的内力，在大小、性质上应该是相同的结果。
MB 0
FA 4 4 2 21 0 FA 2kN
（2）计算各截面上的剪力
FQ1 FQ2 FQ3 = 2kN FQ4 2+6=4kN FQ4 2 2=4kN
4kN m 2kN/m
12 3
Aபைடு நூலகம்
B4 C
FA
2m
FB
2m
2m
（2）计算各截面上的弯矩
M1 2 2 4kN m（上部受拉） M2 2 2 4 0
M1
qa
a 2
Fa
0
M1
qa
a 2
Fa
4
2
2 2
5
2
18kN
m
（上部受拉）
应用举例
[例2] 如图所示简支梁，已知：F1=F2=30kN, 求1-1横截面上的剪力和弯矩。
F1 1
A
1
FA 1m 1m
2m
F2 B
2m FB
F1 1 M1
1 FA 1m 1m FQ1
M11
F2
1 FS1 2m
2m FB
（2）代替留下一部分（脱离体），并以内力代替弃去部分对保留部分的作用。
（3）平衡对脱离体建立静力平衡方程，求解未知力。注意：取出的梁段上保留作用于该段上的所有外力（包括荷载和支座反力），在截开的截面上画出未知的剪力和弯矩时，剪力和弯矩均假设为正向。

结构力学静定结构——梁

A
q B

L Mk
q FNk FQk
A
FYA x
k
q
M F YA
0 0 k
F
0 Qk
§3-2 斜梁
d、画内力图
2
B
A qLcosα 2
＋
qL 2
弯矩图 qL sinα
＋
B
－
2 B
A
qLcosα 2
－
剪力图
A qL sinα 2
轴力图
§3-3 多跨静定梁
1）多跨静定梁(statically determinate multi-span beam) 的组成由若干根梁用铰联接后跨越几个相连跨度的静定结构——称为多跨静定梁，如图所示：
第3章静定结构内力计算
主要内容
§3-1 梁的内力计算回顾 §3-2 斜梁 §3-3 多跨静定梁 §3-4 静定刚架 §3-5 桁架 §3-6 组合结构 §3-7 三铰拱
§3-1 梁的内力计算回顾
首先回顾一下梁的内力计算。 1、计算方法
利用力的平衡原理，对每个隔离体可建立三个平衡方程：
FX 0, FY 0,
Fp q(x) M
y
p(x)
dx
x
dFQ dFN dM FQ , q( x ) , p( x ) dx dx dx
M FN
q(x)
M+dM
dx
FQ
FN+d FN P(x) F ＋dF Q Q
§3-1 梁的内力计算回顾
无何载区段均布荷载区段
↓↓↓↓↓↓
集中力作用处发生突变
集中力偶作用处
A C 26 E 30 8 8 G
2
弯矩图