第八章 热力学第一定律
热力学第一定律总结

298 K时,H2(g)的∆cHmө = -285.83 kJ·mol-1, H2S(g)和 SO2(g)的∆fHmө分别为-20.63 kJ·mol-1和-296.83 kJ·mol-1。 求下列反应在498 K时的∆rUmө。已知水在373 K时的摩 尔蒸发焓∆vapHm (H2O, 373 K) = 40.668 kJ·mol-1. 2H2S (g) + 3O2 (g) = 2SO2 (g) + 2H2O(g)
其中,T2的值由理想气体绝热方程式(pVγ=C)求得。
3、Q的计算 、 的计算
• Q = ∆U – W • 如恒容,Q = ∆U • 如恒压,Q = ∆H
1. 绝热密闭体系里,以下过程的ΔU不等于零的是: A) 非理想气体混合 B) 白磷自燃 C) 乙醚挥发 D) 以上均为0 2.“爆竹声中一岁除,春风送暖入屠苏”。我国 春节有放鞭炮的习俗。在爆竹爆炸的过程中,以 下热力学量的符号表示正确的是(忽略点火时火柴 传递给引线的少量热量) ( ) A) Q<0,W<0,ΔU<0 B) Q<0,W=0,ΔU<0 C) Q=0,W<0,ΔU<0 D) Q=0,W=0,ΔU=0
nN2CV, m(N2)(T-T1) + nCuCV,误二: ∆U =∆UN2 + ∆UCu = 0
nN2CV, m(N2)*(T-T1) + nCuCV, m(Cu)*(T-T2) = 0
正确解法:
∆U =∆UN2 + ∆UCu = ∆UN2 + ∆HCu = 0 nN2CV, m(N2)*(T-T1) + nCuCp, m(Cu)*(T-T2) = 0
• 求火焰最高温度: Qp = 0, ΔH = 0 求火焰最高温度: • 求爆炸最高温度、最高压力:QV = 0, W = 0 求爆炸最高温度、最高压力: =0
热力学第一定律

23
本章学习要求
• 掌握能量、热力系统储存能、热力学能、热量和功量 的概念,理解热量和功量是过程量而非状态参数。 • 理解热力学第一定律的实质能量守恒定律。 • 掌握稳定流动能量方程,能熟练运用稳定流动能量方 程对简单的工程问题进行能量交换的分析和计算。 • 掌握膨胀功、轴功、流动功和技术功的概念、计算及 它们之间的关系。 • 理解焓的定义式及其物理意义。 • 了解常用热工设备主要交换的能量及稳定流动能量方 程的简化形式。
2. 宏观位能: Ep ,单位为 J 或 kJ
Ep mgz
5
热力系总储存能:E ,单位为 J 或 kJ
E U Ek Ep
比储存能:e ,单位为 J/kg 或 kJ /kg
1 2 e u ek ep u cf gz 2
6
内动能-温度 热力学能 (内能U、u) 外储存能 内位能-比体积
∴流动功是一种特殊的功,其数值取决于
控制体进、出口界面上工质的热力状态。
14
根据热力学第一定律, 有 :
1 2 1 2 u1 cf 1 gz1 p1v1 q u2 cf 2 gz2 p2v2 ws 0 2 2
令 upv h,由于u、p、v都是状态参数,所以h也是 状态参数,称为比焓。
对一切热力系统和热力过程,有:
进入系统的能量-离开系统的能量 = 系统储存能量的变化
8
二、闭口热力系的能量方程
如图: Q=△U+W 对微元过程: Q QdUW 或 qduw 即: 热力系获得热量= 增加的热力学能+膨胀做功 对于可逆过程 : qdupdv 或
ΔU
W
qu pdv
第八章热力学定律

第八章热力学定律本章学习提要1.理解热力学第一定律,知道热力学第一定律反映了系统内能的变化和系统通过做功及传热过程与外界交换的能量之间的关系。
初步会用热力学第一定律分析理想气体的一些过程,以及生活和生产中的实际问题。
2.知道热力学第二定律的表述。
知道熵是描写系统无序程度的物理量。
热力学的两个基本定律是能量守恒定律和热力学第一定律。
热力学第二定律表述了热力学过程的不可逆性,即孤立系统自发地朝着热力学平衡方向——最大熵状态——演化。
这两个定律都是通过对自然界和生活、生产实际的观察、思考、分析、实验而得到的,这也是我们学习这两条基本定律应采取的方法。
人类的进步是与对蕴藏在物质内部能量的认识和利用密切相关的。
热力学定律为更好地设计和制造热机、更好地开发和利用能源指明了方向。
随着生产和科学实践的发展,人们逐步领悟到有效利用能源的意义,懂得遵循科学规律的重要性,从而更自觉地抵制违背科学规律的行为。
A 热力学第一定律一、学习要求理解热力学第一定律。
初步会用热力学第一定律分析理想气体的一些过程,以及生活和生产中的实际问题。
我们应聚焦于热力学第一定律的构建过程,理解它既包括内能的转换,也遵循能量守恒定律。
这一定律是通过对自然界以及生活和生产实际的深入观察、思考、分析和实验而得出的自然界中最基本、最普遍的定律之一。
通过学习热力学第一定律,我们能体会到它在科学史上的重要地位,并感受到它对技术进步和社会发展的巨大影响。
二、要点辨析1.热力学第一定律的含义和表式热力学第一定律涉及到能量的转化和能量守恒两个方面。
内能是物质内部大量微观粒子无序热运动所具有的能量形式。
一个物质系统的内能变化是由它与外部环境进行能量交换的结果,而这种能量交换可以通过两种方式实现:做功和热传递。
热力学第一定律揭示了系统内能变化(ΔU)与系统与外部环境交换的功(W)和热量(Q)之间的定量关系。
ΔU=Q+W。
2.应用热力学第一定律解题时,要注意各物理量正、负号的含义当热力学第一定律表示为ΔU=Q+W时,ΔU为正值,表示系统内能增加;负值表示系统内能减小。
热力学第一定律

m1 m2 m
ECV 0
热流科学与工程系
稳定系统的能量分析: 进入系统的能量:
1 Q E1 p1V1 Q (U1 m1c12 m1 gz1 ) p1V1 2 离开系统的能量: 1 2 E2 p2V2 Wsh (U 2 m2c2 m2 gz2 ) p2V2 Wsh 2
燃气轮机装置如图所示。已知在截面1处 h1=286 kJ/kg的燃 料与空气的混合物以 20 m/s 的速度进入燃烧室,在定压下燃烧, 相当于从外界获得热量q=879 kJ/kg。燃烧后的燃气在喷管中绝 热膨胀到 3, h3=502kJ/kg.流速增加到 c3 。然后燃气推动叶轮 转动作功。若燃气推动叶轮时热力状态不变,只是流速降低。 离开燃气轮机的速度 c4 =150 m/s.试求: (1) 燃气在喷管出口的流速c3 ;
若过程可逆
q h vdp
1
2
q dh vdp Q dH Vdp
Q H Vdp
1
2
热流科学与工程系
3、一般开口系统的能量方程
在dτ间内 进入系统的能量:
Q dE1 p1dV1
离开系统的能量:
dE2 p2 dV2 Wsh
系统能量的增加: dEsy,CV 代入能量方程, 整理后得
对于一个循环
Q U pdV
1
2
q u pdv
1
2
Q dU W
由于 dU 0 所以
Qnet dQ dW Wnet qnet dq dq qnet
热流科学与工程系
2、开口系统的能量方程式
(1)、稳定流动系统的能量方程 稳定流动: 流动过程中开口系内部的状态参数(热力学参数和动 力学参数)不随时间变化的流动称为稳定流动。
大学物理答案8.第八章

⼤学物理答案8.第⼋章第⼋章热⼒学第⼀和第⼆定律思考题8-13 强光照射物体,可以使物体的温度上升,导致物体内能的改变。
试问这⼀过程属于热量传递还是⼴义的做功。
8-14 储⽓瓶中的⼆氧化碳急速喷出,瓶⼝处会出现固态的⼆氧化碳----⼲冰。
为什么?8-15 ⽇常⽣活中有“摩擦⽣热”的提法,从物理上讲正确的表述是什么?8-16 有⼈说:只有温度改变时,才有吸热或放热现象。
这种说法正确吗?试举例说明之。
8-17 微元dW、dQ和dU与具体微元过程有关吗?微元dQT呢?8-18 参考§8.4关于开尔⽂表述与克劳修斯表述等价性的证明,试⽤反证法证明卡诺循环与克劳修斯表述的等价性。
8-19 等温膨胀过程的熵变⼤于零,有⼈说这表明此过程是不可逆的过程。
这种说法正确吗?8-20 基于克劳修斯表述证明两条绝热线不可能相交。
8-21 定义状态量焓H=U+pV。
对准静态且只有压强做功的过程,证明dH=Tds+Vdp,并说明该量在等压过程中的物理意义。
8-22报载,⼀⼩孩在夏季午睡时,由于长时间压着⼀个⼀次性打⽕机,导致打⽕机破裂,其⽪肤轻度冻伤。
试思考其中的物理原因。
8-23 ⼀般来说,物体吸热(放热)温度上升(下降),其热容量为正值。
但是对于⾃引⼒系统,热容量可能取负值。
试以第七章例7.3为例说明之。
习题8-1 某⼀定量氧⽓原处于压强P1=120atm 、体积V1=1.0L 、温度t1=27摄⽒度的状态,经(1)绝热膨胀,(2)等温膨胀,(3)⾃由膨胀,体积增⾄V2=5.0L 。
求这三个过程中⽓体对外做功及末状态压⼒值。
解:112120, 1.0,300 5.0p atm V l T K V l====氧⽓的775225p vC R R C γ=== (1)绝热膨胀:111611122212() 1.2810a V p V p V p p P V ---===? 1412[1()] 1.44101V pVW J V γγ-=-=?- (2)等温过程:111611122212() 1.2810a V p V p V p p P V ---=∴==? 1412[1()] 1.44101V pVW J V γγ-=-=?- (3)⾃由膨胀,T 不变 622.4310a p P =? W=08-2 将418.6J 的热量传给标准态下的5.00×10-3kg 的氢⽓[Cv,m=20.331J/(mol.k)] (1) 若体积不变,这热量变为什么?氢⽓的温度变为多少? (2) 若温度不变,这热量变为什么?氢⽓的压强及体积变为多少? (3) 若压强不变,这热量变为什么?氢⽓的温度和体积变为多少?解:(1)V 不变5131416.8, 1.01310,273.15 510Q W U Q J P Pa T K M Kg-?=+?∴?==?==?50, 8.05522M QW Q U R T T KM R µµ?=?=?=∴?== 273.158.05281.2()T K ∴=+=(2)T 不变12211123111111 0, 1.0775.610QMRT V VMU Q W RT Ln e V V MRT MPV RT V m P µµµµ-===∴===∴==?223112225.610 1.0776.0310() 9.4110 ( )PV V m P Pa V --∴=??=?==? (3)P 不变22321212221211111 , 5.85(),72273.15 5.7279.0()5.7210P MQQ C T T K M R T K V V T MRTT MRT V V m T T T PT P µµµµ??===∴=+======?1125()121.6 299.02M W P V V J U R T J µ=-=?== 计算结果Q U W ?≠?+是因为Cp 和Cv 近似取值,若取实验值20.331,28.646v p C C ==可得:25.845,279.0,297.1T K T K U J ?==?=8-3有20.0L 的氢⽓,温度为27摄⽒度,压强为P=1.25105pa 。
第八章第二节 热力学定律及能量守恒 气体

发器中制冷剂汽化吸收箱体内的热量,
经过冷凝器时制冷剂_______. A.热量可以自发地从冰箱内传到冰 箱外
B.电冰箱的制冷系统能够不断地把 冰箱内的热量传到外界,是因为其消 耗了电能 C.电冰箱的工作原理不违反热力学 第一定律 D.电冰箱的工作原理违反热力学第 一定律
二、能量守恒定律 能量既不会凭空产生,也不会凭空消 失,它只能从一种形式转化为别的形 式,或者从一个物体转移到别的物体, 在转化或转移的过程中,其总量不变.
三、气体的状态参量 1.温度 (1)宏观上:表示物体的______程度. 冷热 (2)微观上:表示气体分子无规则热运
激烈 动的______程度.
C.若气体的温度随时间不断升高, 其压强也一定不断增大 D.气体温度每升高1 K所吸收的热量 与气体经历的过程有关 E.当气体温度升高时,气体的内能 一定增大
解析:选ADE.一定质量的理想气体, pV =C,p、V不变,则T不变,分 T 子平均动能不变,又理想气体分子势 能为零,故气体内能不变,A项正确; 理想气体内能不变,则温度T不变,由 pV =C知,p及V可以变化,故状态 T 可以变化, B项错误;
于所有分子动能的和,内能增加,气 体分子的平均动能增加,温度升高, 选项A正确. 二、对热力学第二定律的理解 1.在热力学第二定律的表述中,“自 发地”、“不产生其他影响”的涵义
(1)“自发地”指明了热传递等热力学 宏观现象的方向性,不需要借助外界 提供能量的帮助. (2)“不产生其他影响”的涵义是发生 的热力学宏观过程只在本系统内完成, 对周围环境不产生热力学方面的影响. 如吸热、放热、做功等.
两类永动机第一类永动机第二类永动机不消耗能量却可以源源不断地对外做功的机器从单一热源吸热全部用来对外做功而不引起其他变化的机器违背能量守恒定律不可能实现违背热力学第二定律不可能实二能量守恒定律能量既不会凭空产生也不会凭空消失它只能从一种形式转化为别的形式或者从一个物体转移到别的物体在转化或转移的过程中其总量不变
第八章 热力学第一定律1

i2 2 , i i 1
R 1 T1 T2 p1V1 p2V2 A 1 1
V 1 p1V1 1 1 1 V2
1
气体的摩尔定压热容为:
C p ,m 1 dQ 1 dE p dV dT p dT p dT p
i E RT , pV RT 2
C p,m
i RR 2
Qp C p,m T2 T1 C p,mT
QV CV ,m T2 T1 CV ,mT
热力学第一定律为: dQV dE 理想气体内能:
i E RT 2
i E RT CV , m T 2
i E RT CV , m T 2
p
2 ( p ,V , T ) 2 2 1
V
( p1 ,V , T1 )
p p1
p2
V T 1 ( p1, 1, )
p p1
2
V2
1 ( p1, 1, ) V T
( p2 , 2 ,T ) V
A
V1
p2
( p2 , 2 ,T ) V
A
V1
2
V2
o
V
o
V
QT
E
A
QT
E
A
等温膨胀,从外界吸热,等温压缩,气体对外界放热
例题8.1
气体等温过程:vmol的理想气体在保持温度T不变 的情况下,体积从V1经过准静态过程变化到V2。求 这一等温过程中气体对外做的功和它从外界吸收的 热。 解: pV=vRT 代入(9)式:
间为1s。内燃机的压缩时间0.01s。均可视这一过程为准静 态过程 • 3 准静态过程的表示方法:p-V图(p-T图、V-T图) a 曲线上的每一个点都是一个 准静态过程 b 非平衡态不能用一定的状态 参量描述,即不能表示为状态 图中的一条线!
热力学第一定律

H
T2 T1
nCp,mdT
nCp,m (T2
T1)
?J
25
6. 10mol、300K,101.325 kPa的双原子理想气体, 在恒外压506.625kPa的压力下绝热压缩至平衡, 求此过程的终态温度及W、Q、ΔU、ΔH。
解:
n=10mol, pg
p1 =101.325 kPa T1 =300K
r
H
m
(298.15K
)
f
H
m
(C2
H
5OH
,
l
)
B
c
H
m
(
B,298.15K
)
[c
H
m
(C2
H
5OH
,
l
)
2
cH m(C Nhomakorabea石墨)
3
c
H
m
(
H
2
,
g
)
1
/
2
c
H
m
(O2
,
g
)]
?
kJ
mol-1
c
H
m
(石墨)
f
H
m
(CO2
n=10mol,pg
δQ=0
p2 = 506.625kpa
p外=506.625kpa T2 =?
26
解:
n=10mol, pg
p1 =101.325 kPa T1 =300K
n=10mol,pg
δQ=0
第8章热力学第一定律2(循环修定)

a
Q1
d
T1 T2
T1
b
V2 V3 V1 V4
V3 ln Q2 T2 V4 1 1 Q1 T1 ln V2 V1
第八章 热力学第一定律
P2 P4
A
Q2
P3
T2
V2
c
O V1 V4
V
V3
T2 1 T1
西南大学 大学基础物理学
讨论 (1)要完成循环,必须有高温热源和低温热源。
Q2
V0 图8–15 奥托循环
V V
TeV TbV
1 1
TdV0 TcV0
1
1
西南大学 大学基础物理学
TeV TbV
1 1
TdV0 TcV0
1
(Te Tb )V 1 (Td Tc )V0 1
1
1
Te Tb V0 Td Tc V
V0 Te Tb Q2 1 1 1 Q1 Td Tc V
1
1
1 V V 0
1
1
1
r : 压缩比
效率决定于压缩比。
r 1 可见,奥托循环的
第八章 热力学第一定律
西南大学 大学基础物理学
§8.6 卡诺循环 1824 年法国的年青工程师卡诺对热机的最大可能 效率问题进行理论研究提出的一个理想循环 — 卡诺循 环, 它给出了热机效率的理论极限值。 该循环: 以理想气体为工作物质 由两个准静态等温过程和两个 准静态绝热过程所组成。 工质在两个恒定的高、低温热源 之间工作。
一种。内燃机是燃料在汽缸内燃烧,产生高温高压气
体,推动活塞并输出动力的机械。1872年,德国工程 师奥托(N.A.Otto,1832–1891)研制成功了第一台 四冲程活塞式煤气内燃机。 1883 年,德国人戴姆勒 ( G.Daimler , 1834–1900 )成功地制造出了第一台
热力学第一定律总结

热一定律总结一、 通用公式ΔU = Q + W绝热: Q = 0,ΔU = W 恒容(W ’=0):W = 0,ΔU = Q V恒压(W ’=0):W =—p ΔV =-Δ(pV ),ΔU = Q —Δ(pV ) → ΔH = Q p 恒容+绝热(W '=0) :ΔU = 0 恒压+绝热(W ’=0) :ΔH = 0焓的定义式:H = U + pV → ΔH = ΔU + Δ(pV )典型例题:3.11思考题第3题,第4题。
二、 理想气体的单纯pVT 变化恒温:ΔU = ΔH = 0变温:或或 如恒容,ΔU = Q ,否则不一定相等。
如恒压,ΔH = Q ,否则不一定相等. C p , m – C V , m = R双原子理想气体:C p , m = 7R /2, C V , m = 5R /2 单原子理想气体:C p , m = 5R /2, C V , m = 3R /2典型例题:3。
18思考题第2,3,4题书2。
18、2.19三、 凝聚态物质的ΔU 和ΔH 只和温度有关或 典型例题:书2.15四、可逆相变(一定温度T 和对应的p 下的相变,是恒压过程)U ≈ ΔH –ΔnRT (Δn :气体摩尔数的变化量。
如凝聚态物质之间相变,如熔化、凝固、转晶等,则Δn = 0,ΔU ≈ ΔH 。
101.325 kPa 及其对应温度下的相变可以查表。
ΔU = n C V , m d T T 2T 1∫ ΔH = n C p, md T T 2 T1∫ ΔU = nC V , m (T 2-T 1) ΔH = nC p, m (T 2-T 1)ΔU ≈ ΔH = nC p, m d T T 2T 1∫ΔU ≈ ΔH = nC p, m (T 2-T 1)ΔH = Q p = n Δ H m αβ其它温度下的相变要设计状态函数不管是理想气体或凝聚态物质,ΔH 1和ΔH 3均仅为温度的函数,可以直接用C p,m计算。
热力学第一定律

P2V2
ln
V2 V1
7
又 ∵ 等温过程有
V2 P1 V1 P2
有
AT
P1V1 M
ln P1 P2 RT
ln
P2V2 P1
ln
P1 P2
M mol
P2
(3)强调QT=AT
即在等温过程中,系统的热交换不能直接计算,但可用等 温过程中的功值AT来间接计算。
8
※三种过程中气体做的功
等体过程
(1)特征:dT=0, ∴dE=0 热一律为 QT=AT
在等温过程中,理想气体所吸收 的热量全部转化为对外界做功,系 统内能保持不变。
(2)等温过程的功
PI
P1
P2
o
V1
II
V2 V
∵T=C(常数),
P RT 1
V
dAT PdV
AT
V2 RTdV RT ln V2
V V1
V1
P1V1
ln
V2 V1
T1)
M M mol R(T2 T1)
5
C p
C V
R i2R 2
──此即迈耶公式
(3)比热容比:
定义
Cp
Cv
i 2
RR iR
i2 i
2
对理想气体刚性分子有:
单原子分子:
双原子分子:
5 3 7 5
1.67 1.4
*: 经典理论的缺陷
多原子分子:
8 6
1.33
6
3、等温过程
1
符号规定
Q
吸热为正, 放热为负.
系统对外做功为正, A 外界对系统做功为负.
各物理量的单位统一用国际单位制。
热力学第一定律

工质的容 积变化功
膨胀功
工质机械 能的变化
维持工质流 动的流动功
工质对机 器作的功
热能转变成的机械能(由于膨胀而导致1的7 )
技术功:技术上可资利用的功,符号为
联立(2-18)与
,则
(2-19) (2-20)
18
对于可逆过程,
图中的阴影面积,即 对于微元过程,
图中的面积5-1-2-6-5
说明: (1)若dp为负(过程中工质压力降低),技 术功为正,工质对机器作功。如燃气轮机; (2)若dp为正,机器对工质作功,如活塞式 压气机和叶轮式压气机。
对于闭口系统:进入和离开系统的能量只包括热量和作功两项; 对于开口系统:进入和离开系统的能量除热量和作功外,
还有随同物质带进、带出系统的能量(因为有物 质进出分界面)
2
闭口系统的基本能量方程式
取气缸活塞系统中的工质为研究系统,考察其在状态变化过程 中和外界(热源和机器设备)的能量交换。由于过程中没有工 质越过边界,所以这是一个闭口系统。
的平均值为该截面的流速;
8
一、开口系统能量方程
开口系统内既有质量变化,又有能量变化,控 制体内应同时满足质量守恒与能量守恒关系。 考察以下开口系统(dτ)
9
➢ 从1-1’界面进入控制体流体的质量为 m1 ➢ 从2-2’界面进入控制体流体的质量为 m2
➢ 系统从外界吸热 Q ,对机器设备作功 Wi
加入系统的能量总和-热力系统输出的能量总和=热力系总储存能的增量
则有:
整理得:
11
考虑到
和
,且
,则上式可以写成
(2-13)
假设流进流出控制容积的工质各有若干股,则上式可写成
(2-14)
热力学第一定律

第1章热力学第一定律1.1 重要概念1.状态函数与过程量这是两类完全不同的物理量。
状态函数是系统的性质,如温度(T),压力(p),体积(V),内能(U),焓(H)和定压热容(C V)等,而过程量是指功(W)和热(Q),它们是过程的属性。
状态函数与过程量主要区别如下:(1)状态函数决定于系统的状态,而过程量取决于过程。
所以状态函数用来描述系统状态,而过程量用于描述过程。
(2)当系统中发生变化时,状态函数的变化只取决于系统的初末状态,而与变化的具体方式(过程)无关。
因而在计算状态函数变化时,若给定过程不能或不易求得,可通过设计途径进行计算,与此相反,过程量则不可以设计途径进行计算,因为对于不同途径,它们的值可能不同。
过程量,即功和热是在系统和环境之间的两种能量传递方式,在系统内部不能讨论功和热。
可见在计算W和Q时,首先要明确系统是什么,其次要搞清过程的特点。
(3)若y代表某个状态函数,任意一个过程的状态函数变为∆Y,功和热为W和Q。
假设该过程在相反方向进行时上述各量分别为∆Y逆、W逆和Q逆,则必有∆ Y=一∆Y逆一般W ≠一W逆Q≠一Q逆2.等温过程环境温度恒定不变的情况下,系统初态和末态温度相同且等于环境温度的过程,即T l=T2=T环=常数所谓等温过程,是指上式中三个等号同时成立的过程。
有人认为等温过程是系统温度始终不变的过程,这是一种误解。
诚然,在某一过程中如果系统温度始终不变,则过程必是等温过程,因为该过程服从上式。
但这并非等温过程的全部,只不过是等温过程的一种特殊情况。
3.等压过程外压(即环境压力)恒定不变的情况下,系统初态和末态的压力相同且等于外压的过程,即p1=p2=p外=常数所谓等压过程,是指式中三个等号同时成立的过程。
有人把等压过程说成是系统压力始终不变的过程,这是一种不全面的理解,因为这只是等压过程的一种特殊情况。
在热力学中会遇到p1=p2的过程,称为初末态压力相等的过程,还会遇到p外=常数的过程,称为恒外压过程,但它们都不是等压过程。
热力学第一定律

热力学第一定律热力学第一定律,也被称为能量守恒定律,是热力学基本定律之一。
它阐述了能量在物理系统中的守恒原理,即能量不会被创造或消灭,只会在不同形式之间转换或传递。
该定律在许多领域都有广泛的应用,包括工程、物理、化学等。
1. 定律的表述热力学第一定律可从不同的角度进行表述,以下是几种常见的表述方式:1.1 内能变化根据热力学第一定律,一个封闭系统内能的变化等于系统所吸收的热量与系统所做的功的代数和。
数学表达式如下:ΔU = Q + W其中,ΔU表示系统内能的变化,Q表示系统吸收的热量,W表示系统所做的功。
1.2 能量守恒根据能量守恒定律,能量既不能被创造也不能被摧毁,只会在不同形式之间传递或转换。
能量的总量在一个封闭系统中保持不变。
2. 系统内能的变化系统内能的变化是热力学第一定律的核心内容之一。
系统内能的变化是由系统吸收或释放的热量以及系统所做的功决定的。
2.1 系统吸收的热量系统吸收的热量指的是系统从外界获得的热能。
当一个热源与系统接触时,能量会以热量的形式从热源传递到系统中。
系统吸收的热量可以引起系统内能的增加。
2.2 系统所做的功系统所做的功指的是系统对外界做的能量转移。
当系统对外界施加力并移动时,能量会以功的形式从系统传递到外界。
系统所做的功可以引起系统内能的减少。
3. 热力学第一定律的应用3.1 工程应用热力学第一定律在工程领域有着广泛的应用。
例如,在能源系统的设计与优化中,需要根据系统的能量转换过程,计算系统的内能变化和热功效率等参数,以提高能源利用效率。
3.2 物理学应用在物理学研究中,热力学第一定律通常用于分析热力学过程中的能量转化。
例如,在热力学循环中,通过计算各个环节的能量转换情况,可以确定工作物质的热效率,从而评估系统的性能。
3.3 化学反应在化学反应中,热力学第一定律对于研究反应的能量变化和平衡状态具有重要意义。
通过计算反应过程中释放或吸收的热量,可以确定反应的放热性或吸热性,并预测反应的发生与否。
大学物理等温过程和绝热过程
pd
Qdef Edf Adef
e
f
Qdf Edf Adf
O
V
图(2)
即 0 Edf Adf
Edf Adf
Qdef Edf Adef Adef Adf 0
所以是放热过程
8.4 理06想_01_气牛顿体相对的性等原理温和伽过利略程变和换 —绝—热力学过程 第八章 热力学第一定律
8.4 理06想_01_气牛顿体相对的性等原理温和伽过利略程变和换 —绝—热力学过程 第八章 热力学第一定律
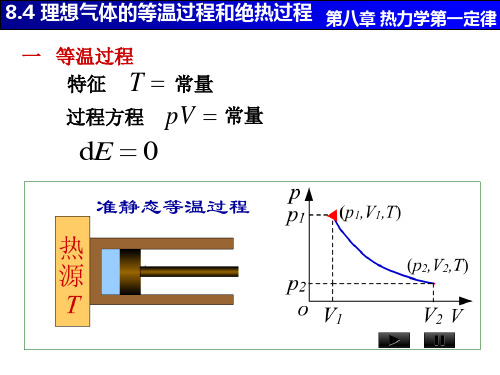
一 等温过程
特征 T 常量
过程方程 pV 常量
dE 0
8.4 理06想_01_气牛顿体相对的性等原理温和伽过利略程变和换 —绝—热力学过程 第八章 热力学第一定律
特征 T 常量 过程方程 pV 常量
p
p2
2 T2
p2' T2' T1 Q 0
p1
2'
T1
T 常量 1
o V2 V2' V1 10 V1 V
3)对等温过程
T2 753K
A12
m M
பைடு நூலகம்
CV ,m (T2
T1)
CV ,m 20.44J mol1 K1
A12 4.70 10 4 J
p'2
p1
(V1 V2
)
1.013106 Pa
V
RT
dV V
1 dT 1 T
p
p1
1( p1,V1,T1)
Q0
p2
o V1
( p2,V2,T2 ) 2
V2 V
绝 V 1T 常量
热 方
pV
常量
程 p 1T 常量
【步步高】高中物理大一轮复习 第八章 第2课时 热力学定律与能量守恒讲义课件 大纲人教版

列说法正确的是 A.气体分子间的作用力增大 B.气体分子的平均速率增大 C.气体分子的平均动能减小 D.气体组成的系统的熵增加
()
(2)若将气泡内的气体视为理想气体,气泡从湖底上升到湖面 的过程中,对外界做了 0.6 J 的功,则此过程中的气泡 ________(填“吸收”或“放出”)的热量是__________J. 气泡到达湖面后,温度上升的过程中,又对外界做了 0.1 J 的功,同时吸收了 0.3 J 的热量,则此过程中,气泡内气体 内能增加了________J. (3)已知气泡内气体的密度为 1.29 kg/m3,平均摩尔质量为 0.029 kg/mol.阿伏加德罗常数 NA=6.02×1023 mol-1,取气体 分子的平均直径为 2×10-10 m,若气泡内的气体能完全变为 液体,请估算液体体积与原来气体体积的比值.(结果保留 一位有效数字)
题型二 热力学第二定律的应用
例2 (2009·四川理综·16)关于热力学定律,下列说法正确的
是
( B)
A.在一定条件下物体的温度可以降到0 K
B.物体从单一热源吸收的热量可全部用于做功
C.吸收了热量的物体,其内能一定增加
D.压缩气体总能使气体的温度升高
解析 0 K只能接近而不能到达,A错;根据热力学第二定
(3)设气体体积为V0,液体体积为V1 气体分子数n=ρMVm0olNA,V1=nπ6d3(或V1=nd3) 则VV10=6Mρmolπd3NA(或VV10=Mρmold3NA) 代入数据解得VV10=1×10-4(9×10-5~2×10-4都算对)
答案 (1)D (2)吸收 0.6 0.2 (3)1×10-4
解析 (1)将空气压缩装入气瓶的过程中,空气温度不变, 所以内能不变,潜水员背着气瓶潜入海底的过程中,放出
热力学第一定律

热力学第一定律 公式 解释 备注1V V U T T U U TV d d d ⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=系统的热力学能U 可看做温度T 和体积V 的函数,可写作全微分。
热力学能是状态性质,故用U d 以表示它是全微分。
2(微分式)W Q U δδ+=d (积分式)W Q U +=∆ 系统的热力学能变化量U ∆等于系统与环境交换的热Q 和功W 之和。
热和功不是状态性质,故用Q δ和W δ而不是Q d 和W d 以表示它们不是全微分。
规定,系统得到热或得到功时Q 和W 为正,反之系统失去热或对外做功时Q 和W 为负。
3 (微分式)外V p W d -=δ 体积功等于气体膨胀或压缩时抵抗外压所做的功。
负号是因为规定系统对外做功时W 为负。
推导:气体抵抗外压外p 膨胀,使得截面积为A 的理想活塞移动了l d ,可以求出膨胀所做的功为dV p Adl p dl F W 外外外-=-=-=δ。
(向真空膨胀)0=W(恒外压膨胀)外V p W ∆-=(定温定压可逆相变)V p W ∆-= (理气等温可逆膨胀)⎪⎪⎭⎫⎝⎛-=12V V nRT W ln推导:向真空膨胀,0=外p 。
等温可逆膨胀时,内压p 恒比外压外p 大p d ,()⎰⎰--=-=2121d d d V V V V V p p V p W 外,忽略二阶小量V p d d ,并将理想气体方程V nRT p =带入得⎪⎪⎭⎫ ⎝⎛-=-=⎰1221d V V nRT V V nRTW VV ln 。
4 U Q V ∆=恒容过程的热等于热力学能变。
V Q 是状态函数。
推导:V p Q W Q U d d -=+=δδδ,定容条件下0d =V ,可得U Q V d =δ,积分后即为U Q V ∆=5H Q P ∆=恒压过程的热等于焓变。
p Q 也是状态函数。
推导:V p Q W Q U d d -=+=δδδ,定压条件下(21p p =)积分,可得()()H H H V p U V p U V p U Q p ∆=-=+-+=∆+∆=12111222,其中焓H 被定义为pV U H def+==。
热力学第一定律

二、膨胀功、可逆过程与最大功在热力学中常见的功的形式有膨胀功、电功、表面功…… ,其中膨胀功最常遇到,因为在状态变化过程中往往伴随着体积的变化。
表1-1 列举各种形式的功的表示方法。
从表中可以看出每一种形式的功都由两个因素所组成:1.所抵抗的“ 力” :如f 、P e 、E 、v 等;2.在抵抗一定的“ 力” 的条件下所产生的“ 位移” :如dl 、dV 、dq 、dA 等。
表1-1 各种形式的功前者属强度性质而后者属容量性质。
习惯上将前者称为“ 广义力” 而后者称为“ 广义位移” 。
广义力的名称系由与机械功中的f 相比拟而得,广义位移的名称则系由与机械功中的dl 相比拟而得。
若以y 表示广义力而以dx 表示广义位移,则广义功可以表示如下:δW = ydx(1-21) 以及W = ∫ δW = ∫ ydx(1-22) 常把膨胀功以外其它各种形式的功如电功、表面功等统称为“ 非膨胀功” 或“ 其它功” ,以δW ' 及W ' 表示。
δW = p e dV + δW '(1-23) 及W = ∫ p e dV + ∫ δW ''(1-24) (一)、膨胀功(体积功)膨胀功是机械功的一种特殊形式。
体系发生物理变化或化学变化时常伴随着体积的变化。
当体系在抵抗外压条件下发生体积变化,则体系将对环境或环境将对体系作功。
这种由于体积变化而产生的机械功称为“ 膨胀功” 。
如图 3 所示,假设在一底面积为A 的圆柱形钢筒中装有气体,作用于钢筒顶部的无摩擦活塞的总外力为f ,则作用于活塞单位面积上的外压p e = f/A 。
若活塞抵抗p e 向上移动了dl 的距离。
按机械功定义,在此元过程中的膨胀功为:δW =- fdl =- (p e A)dl =- p e (Adl)式中Adl = dV ,为此元过程中气体体积的增量,∴δW = - p e dV(1-25)在一体积由V 1 变化至V 2 的状态变化过程中,当途径确定时,过程所作功为各元过程元功δW 的总和:显然,当体系压力p 大于外压p e ,则体系可以发生一膨胀过程,过程中体系对环境做功;反之,若体系压力p 小于外压p e ,则可发生一压缩过程,过程中环境对体系做功。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
pV const V
1 1
T const
p V
const
0 M
推导:对绝热过程,由热力学第一定律
dQ dE dW 0
理想气体
CV ,m dT PdV
M
pV=
M
RT
pdV Vdp=
RdT
CV ,m pdV CV ,mVdp RpdV
在等体过程中,系统对外界不作功,系统吸收的热量 全部用来增加系统的内能。
2、定体摩尔热容 •定义
1mol理想气体在等体过程中,温度伸高1K时所吸收的热 量,称为该物质的定体摩尔热容。
CV , m
QV i R M 2 T
•等体过程的热量公式
QV
M
CV ,m (T2 T1 )
QV 0 QV 0
•过程曲线:
在PV图上是一条双曲线,叫等温线。
系统从外界 吸收的热量, 全部用来对 外作功。
•过程方程:
p1V1 p2V2
•内能、功和热量的变化
WT pdV
V1
V2
V
pV
M
M
V2 WT RT ln V1 M V2 M p1 QT WT RT ln RT ln V1 p2
§8.3 热容 热力学第一定律对理想气体的应用 一、热容
1、物质的热容量 物质温度升高一度所吸收的热量。
2、摩尔热容量
1mol物质温度升高一度所吸收 的热量。 与过程有关 可以 >0 = 0 <0 3、比热容
单位质量的热容称为比热容。
dQ C dT
dQ Cm dT
C 1 dQ c m m dT
四、热力学第一定律
1、内容
系统从外界吸收的热量,一部分使系统的内能增加,另 一部分使系统对外界作功
Q E W ( E2 E1 ) W
对于微小过程
dQ dE dW
2、本质
热力学第一定律是包括热现象在内的能量守恒定律,对 任何物质的任何过程都成立。
3、说明 •符号规定:
考虑
C P ,m-CV ,m=R
C P ,m CV ,m
dV dp V p
d pV 0
pV const
将上式与理想气体的状态方程结合即可得
1 1
V
T const
p V
const
绝热过程计算功的方法
pV p1V1 代入W pdV 得 将绝热方程
在等压过程中,系统吸收的热量一部分用来增加系统 的内能,另一部分使系统对外界作功。
V1
2、定压摩尔热容 •定义
1mol理想气体在等压过程中,温度伸高1K时所吸收的热 量,称为该物质的定体摩尔热容。
C p ,m
i2 R T 2 Qp
3、关于摩尔热容的讨论 •Mayer公式
推导
C P ,m-CV ,m=R
•准静态过程只有在进行的“无限缓慢”的条件下才可能实 现。对于实际过程则要求系统状态发生变化的特征时间远 远大于弛豫时间τ 才可近似看作准静态过程。
说明:
平衡态具有确定的状态参量值, 可用P—V图上的一点来表示这个 平衡态。因而系统的准静态变化 过程可用P—V图上的一条曲线表 示,称之为过程曲线。
二、准静态过程中体积功的计算
系统从初态 P V1 1
末态 P2 V2
P V1 1
P2 V2
df
系统对外作的功
在某一时刻 系统器壁上小面元 ds
对器壁作用力 df Pdsn ˆ
dA df dl df dl Pds dl
P dV ds dl
df
dA P dV
A PdV
工质经一循环 高温热源 T1
Q1
W Q2
W= Q1-Q2
热机效率或循环效率:
表示热机的效能
低温热源 T2
W Q1 Q2 Q2 1 Q1 Q1 Q1
3、制冷机
工作物质作逆循环的机器,称为制 冷机,它是利用功把热量从低温热 源抽到高温热源的机器。
逆循环的特征:
制冷机经历一个逆循环后,由于外界对它 作功,可以把热量由低温热源传递到高温 热源。在一个循环中,外界作功W,从低温 热源吸收热量Q2,向高温热源放出热量Q1。 并且工质回到初态,内能不变。 高温热源 T1
Qp
m
PV
m
C p ,m T E W
m
CV ,m T PV
RT PV
m
RT C p ,m CV ,m R
理想气体的定压摩尔热容比定体摩尔热容大一个恒量R •在等体过程中,气体吸收的热量全部用来增加系统的内能 •等压过程中,气体吸收的热量,一部分用来增加系统的内能, 还有一部分用于气体膨胀时对外界作功 气体升高相同的温度,在等压过程吸收的热量要比在等温过 程中吸收的热量多。
制冷系数:
表示制冷机的效能
Q1
W
Q2
Q2 Q2 e W Q1 Q2
低温热源 T2
三、卡诺循环
法国青年工程师、热力学的创始人之一, 是第一个把热和动力联系起来的人。 他 出色地、创造性地用“理想实验”的思维 方法,提出了最简单、但有重要理论意义 的热机循环——卡诺循环,并假定该循 环在准静态条件下是可逆的,与工质无关, 创造了一部理想的热机(卡诺热机)。卡 诺的目标是揭示热产生动力的真正的、独 立的过程和普遍的规律。1824年卡诺提出 了对热机设计具有普遍指导意义的卡诺定 理,指出了提高热机效率的有效途径,揭 示了热力学的不可逆性,被后人认为是热 力学第二定律的先驱。
三、绝热线和等温线 绝热线
pV const
斜率
dp p dV V
等温线
pV const
斜率
因为 =CP/CV1, 所以绝热线比等温 线更陡
dp p dV V
§8.4 循环过程 一、循环过程
卡诺循环
历史上,热力学理论最初是在研究热机工作过程的基 础上发展起来的。在热机中被用来吸收热量并对外作 功的物质叫工作物质,简称工质。工质往往经历着循 环过程,即经历一系列变化又回到初始状态。
质点系的机械能的增量等于外力和非保守 内力对系统所作的功之和。 2、柯尼希定理 质点系相对于惯性系的总动能等于质心动能和 内动能之和。 如:容器中的气体 3、内能 组成热力学系统的所有分子的 动能和势能的总和
M i E= RT 2
二、热量 1、微观功
例子:加热过程
外界向系统传递热量,系统内能增大:加热水 系统向外界传递热量,系统内能减小。
p1V1 W dV V1 V p1V1 1 1 1 1 1 V1 V2
V2
1 V1 p1V1 1 V 1 2 1 p1V1 p2V2 1
2、非静态过程
在热力学过程的发生时,系统往往由 一个平衡状态经过一系列状态变化后到达 另一平衡态。如果中间状态为非平衡态, 则此过程称非静态过程。
推进活塞压缩汽缸内 的气体时,气体的体 积、密度、温度或压 强都将变化
为从平衡态破坏到新平衡态建立所需 的时间称为弛豫时间。
3、准静态过程
如果一个热力学系统过程在始末两平衡态,可以近似当作平衡 态,则此过程为准静态过程。
沿顺时针方向进行的 循环称为正循环。 沿反时针方向进行的 循环称为逆循环。
p a
b
p a c
b
d
d
c
正循环
V
逆循环
V
2、热机
工作物质作正循 环的机器,称为 热机,它是把热 量持续不断地转 化为功的机器。 T1 Q1 泵
|W| 气缸
T2 Q2
正循环的特征:
一定质量的工质在一次循环过程中 要从高温热源吸热Q1,对外作净功 W,又向低温热源放出热量Q2。并 且工质回到初态,内能不变。
1、定义:
系统经过一系列状态变化以后,又回 到原来状态的过程叫作热力学系统的 循环过程,简称循环。
2、特点:
•若循环的每一阶段都是准静态过程,则此循环可 用P-V图上的一条闭合曲线表示。工质在整个循环 过程中对外作 的净功等于曲线所包围的面积。 •系统经过一个循环以后,系统的内能没有变化
二、热机和制冷机 1、循环过程的分类
dE 0,
RT
四、绝热过程 1、绝热过程
•特点:
系统与外界没有热量交换的过程, Q=0。
•内能和功的变化
E E2 E1
W M
M
CV ,m T2 T1
•特征:
CV ,m T2 T1
在绝热过程中,系统对外界所作的功是由于系统内能 的减少来完成的。2Βιβλιοθήκη 绝热方程•摩尔热容比
C P ,m CV ,m
γ 1.67 CV,m 12.61 12.53 20.47 20.56 21.16 27.8 27.2 63.7 实验值 CP,m 20.95 20.90 28.83 28.88 29.61 36.2 35.2 72.0 γ 1.66 1.67 1.41 1.40 1.40 1.31 1.30 1.13
系统吸收热量
T2 T1 0 T2 T1 0
•气体内能的增量
系统放出热量
E E2 E1
M
CV ,m T2 T1
三、等压过程 1、等压过程
•特点: 理想气体的压强保持不变,p=const •过程曲线: 在PV 图上是一条平行于V 轴的直线,叫等 压线。
