材料结构习题纯晶体的凝固-DZ版
纯金属的凝固习题与答案

纯金属的凝固习题与答案1 说明下列基本概念凝固、结晶、过冷、过冷度、结构起伏、能量起伏、均匀形核、非均匀形核、临界晶核半径、临界晶核形核功、形核率、生长线速度、光滑界面、粗糙界面、动态过冷度、柱状晶、等轴晶、树枝状晶、单晶、非晶态、微晶、液晶。
2 当球状晶核在液相中形成时,系统自由能的变化为σππ23344r G r G V +∆=∆,(1)求临界晶核半径c r ;(2)证明V V c c G A G c ∆-==∆231σ(c V 为临界晶核体积);(3)说明上式的物理意义。
3 试比较均匀形核与非均匀形核的异同点,说明为什么非均匀形核往往比均匀形核更容易进行。
4 何谓动态过冷度?说明动态过冷度与晶体生长的关系。
在单晶制备时控制动态过冷度的意义?5 分析在负温度梯度下,液态金属结晶出树枝晶的过程。
6 在同样的负温度梯下,为什么Pb 结晶出树枝状晶而Si 的结晶界面却是平整的?7 实际生产中怎样控制铸件的晶粒大小?试举例说明。
8 何谓非晶态金属?简述几种制备非晶态金属的方法。
非晶态金属与晶态金属的结构和性能有什么不同。
9 何谓急冷凝固技术?在急冷条件下会得到哪些不同于一般晶体的组织、结构?能获得何种新材料?. 计算当压力增加到500×105Pa 时锡的熔点的变化,已知在105Pa 下,锡的熔点为505K ,熔化热7196J/mol ,摩尔质量为118.8×10-3kg/mol ,固体锡的体积质量7.30×103kg/m 3,熔化时的体积变化为+2.7%。
2. 考虑在一个大气压下液态铝的凝固,对于不同程度的过冷度,即:ΔT=1,10,100和200℃,计算: (a)临界晶核尺寸;(b)半径为r*的团簇个数;(c)从液态转变到固态时,单位体积的自由能变化ΔGv ; (d)从液态转变到固态时,临界尺寸r*处的自由能的变化 ΔGv 。
铝的熔点T m =993K ,单位体积熔化热ΔH f =1.836×109J/m 3,固液界面自由能γsc =93J/m 2,原子体积V 0=1.66×10-29m 3。
纯金属的凝固习题与答案

纯金属的凝固习题与答案1 说明下列基本概念凝固、结晶、过冷、过冷度、结构起伏、能量起伏、均匀形核、非均匀形核、临界晶核半径、临界晶核形核功、形核率、生长线速度、光滑界面、粗糙界面、动态过冷度、柱状晶、等轴晶、树枝状晶、单晶、非晶态、微晶、液晶。
2 当球状晶核在液相中形成时,系统自由能的变化为σππ23344r G r G V +∆=∆,(1)求临界晶核半径c r ;(2)证明V V c c G A G c ∆-==∆231σ(c V 为临界晶核体积);(3)说明上式的物理意义。
3 试比较均匀形核与非均匀形核的异同点,说明为什么非均匀形核往往比均匀形核更容易进行。
4 何谓动态过冷度?说明动态过冷度与晶体生长的关系。
在单晶制备时控制动态过冷度的意义?5 分析在负温度梯度下,液态金属结晶出树枝晶的过程。
6 在同样的负温度梯下,为什么Pb 结晶出树枝状晶而Si 的结晶界面却是平整的?7 实际生产中怎样控制铸件的晶粒大小?试举例说明。
8 何谓非晶态金属?简述几种制备非晶态金属的方法。
非晶态金属与晶态金属的结构和性能有什么不同。
9 何谓急冷凝固技术?在急冷条件下会得到哪些不同于一般晶体的组织、结构?能获得何种新材料?. 计算当压力增加到500×105Pa 时锡的熔点的变化,已知在105Pa 下,锡的熔点为505K ,熔化热7196J/mol ,摩尔质量为118.8×10-3kg/mol ,固体锡的体积质量7.30×103kg/m 3,熔化时的体积变化为+2.7%。
2. 考虑在一个大气压下液态铝的凝固,对于不同程度的过冷度,即:ΔT=1,10,100和200℃,计算: (a)临界晶核尺寸;(b)半径为r*的团簇个数;(c)从液态转变到固态时,单位体积的自由能变化ΔGv ; (d)从液态转变到固态时,临界尺寸r*处的自由能的变化 ΔGv 。
铝的熔点T m =993K ,单位体积熔化热ΔH f =1.836×109J/m 3,固液界面自由能γsc =93J/m 2,原子体积V 0=1.66×10-29m 3。
材料科学基础-作业参考答案与解析
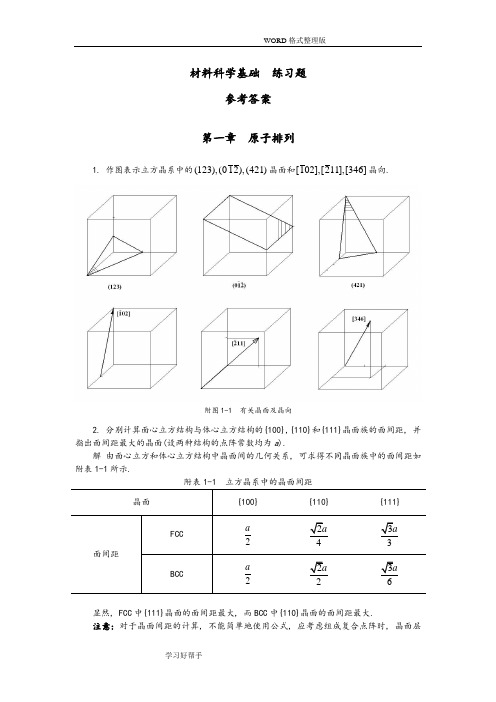
材料科学基础练习题参考答案第一章原子排列1. 作图表示立方晶系中的(123),(012),(421)晶面和[102],[211],[346]晶向.附图1-1 有关晶面及晶向2. 分别计算面心立方结构与体心立方结构的{100},{110}和{111}晶面族的面间距, 并指出面间距最大的晶面(设两种结构的点阵常数均为a).解由面心立方和体心立方结构中晶面间的几何关系, 可求得不同晶面族中的面间距如附表1-1所示.附表1-1 立方晶系中的晶面间距晶面{100} {110} {111}面间距FCC2a24a33aBCC2a22a36a显然, FCC中{111}晶面的面间距最大, 而BCC中{110}晶面的面间距最大.注意:对于晶面间距的计算, 不能简单地使用公式, 应考虑组成复合点阵时, 晶面层数会增加.3. 分别计算fcc和bcc中的{100},{110}和{111}晶面族的原子面密度和<100>,<110>和<111>晶向族的原子线密度, 并指出两种结构的差别. (设两种结构的点阵常数均为a) 解原子的面密度是指单位晶面内的原子数; 原子的线密度是指晶面上单位长度所包含的原子数. 据此可求得原子的面密度和线密度如附表1-2所示.附表1-2 立方晶系中原子的面密度和线密度晶面/晶向{100} {110} {111} <100> <110> <111>面/线密度BCC21a22a233a1a22a233aFCC22a22a2433a1a2a33a可见, 在BCC中, 原子密度最大的晶面为{110}, 原子密度最大的晶向为<111>; 在FCC 中, 原子密度最大的晶面为{111}, 原子密度最大的晶向为<110>.4. 在(0110)晶面上绘出[2113]晶向.解详见附图1-2.附图1-2 六方晶系中的晶向5. 在一个简单立方二维晶体中, 画出一个正刃型位错和一个负刃型位错. 试求:(1) 用柏氏回路求出正、负刃型位错的柏氏矢量.(2) 若将正、负刃型位错反向时, 说明其柏氏矢量是否也随之反向.(3) 具体写出该柏氏矢量的方向和大小.(4) 求出此两位错的柏氏矢量和.解正负刃型位错示意图见附图1-3(a)和附图1-4(a).(1) 正负刃型位错的柏氏矢量见附图1-3(b)和附图1-4(b).(2) 显然, 若正、负刃型位错线反向, 则其柏氏矢量也随之反向.(3) 假设二维平面位于YOZ坐标面, 水平方向为Y轴, 则图示正、负刃型位错方向分别为[010]和[010], 大小均为一个原子间距(即点阵常数a).(4) 上述两位错的柏氏矢量大小相等, 方向相反, 故其矢量和等于0.6. 设图1-72所示立方晶体的滑移面ABCD平行于晶体的上下底面, 该滑移面上有一正方形位错环. 如果位错环的各段分别与滑移面各边平行, 其柏氏矢量b // AB, 试解答:(1) 有人认为“此位错环运动离开晶体后, 滑移面上产生的滑移台阶应为4个b”, 这种说法是否正确? 为什么?(2) 指出位错环上各段位错线的类型, 并画出位错移出晶体后, 晶体的外形、滑移方向和滑移量. (设位错环线的方向为顺时针方向)图1-72 滑移面上的正方形位错环 附图1-5 位错环移出晶体引起的滑移解 (1) 这种看法不正确. 在位错环运动移出晶体后, 滑移面上下两部分晶体相对移动的距离是由其柏氏矢量决定的. 位错环的柏氏矢量为b , 故其相对滑移了一个b 的距离.(2) A ′B ′为右螺型位错, C ′D ′为左螺型位错, B ′C ′为正刃型位错, D ′A ′为负刃型位错. 位错运动移出晶体后滑移方向及滑移量见附图1-5.7. 设面心立方晶体中的(111)晶面为滑移面, 位错滑移后的滑移矢量为[110]2a .(1) 在晶胞中画出此柏氏矢量b 的方向并计算出其大小.(2) 在晶胞中画出引起该滑移的刃型位错和螺型位错的位错线方向, 并写出此二位错线的晶向指数.解 (1) 柏氏矢量等于滑移矢量, 因此柏氏矢量的方向为[110], 大小为2/2a .(2) 刃型位错与柏氏矢量垂直, 螺型位错与柏氏矢量平行, 晶向指数分别为[112]和[110], 详见附图1-6.附图1-6 位错线与其柏氏矢量、滑移矢量8. 若面心立方晶体中有[101]2a b =的单位位错及[121]6a b =的不全位错, 此二位错相遇后产生位错反应.(1) 此反应能否进行? 为什么?(2) 写出合成位错的柏氏矢量, 并说明合成位错的性质.解 (1) 能够进行.因为既满足几何条件:[111]3a b b ==∑∑后前,又满足能量条件: . 22222133b a b a =>=∑∑后前. (2) [111]3a b =合, 该位错为弗兰克不全位错. 9. 已知柏氏矢量的大小为b = 0.25nm, 如果对称倾侧晶界的取向差θ = 1° 和10°, 求晶界上位错之间的距离. 从计算结果可得到什么结论?解 根据bD θ≈, 得到θ = 1°,10° 时, D ≈14.3nm, 1.43nm. 由此可知, θ = 10°时位错之间仅隔5~6个原子间距, 位错密度太大, 表明位错模型已经不适用了.第二章 固体中的相结构1. 已知Cd, In, Sn, Sb 等元素在Ag 中的固熔度极限(摩尔分数)分别为0.435, 0.210, 0.130, 0.078; 它们的原子直径分别为0.3042 nm, 0.314 nm, 0.316 nm, 0.3228 nm; Ag 的原子直径为0.2883 nm. 试分析其固熔度极限差异的原因, 并计算它们在固熔度极限时的电子浓度.答: 在原子尺寸因素相近的情况下, 熔质元素在一价贵金属中的固熔度(摩尔分数)受原子价因素的影响较大, 即电子浓度e /a 是决定固熔度(摩尔分数)的一个重要因素, 而且电子浓度存在一个极限值(约为1.4). 电子浓度可用公式A B B B (1)c Z x Z x =-+计算. 式中, Z A , Z B 分别为A, B 组元的价电子数; x B 为B 组元的摩尔分数. 因此, 随着熔质元素价电子数的增加, 极限固熔度会越来越小.Cd, In, Sn, Sb 等元素与Ag 的原子直径相差不超过15%(最小的Cd 为5.5%, 最大的Sb 为11.96%), 满足尺寸相近原则, 这些元素的原子价分别为2, 3, 4, 5价, Ag 为1价, 据此推断它们的固熔度极限越来越小, 实际情况正好反映了这一规律; 根据上面的公式可以计算出它们在固熔度(摩尔分数)极限时的电子浓度分别为1.435, 1.420, 1.390, 1.312.2. 碳可以熔入铁中而形成间隙固熔体, 试分析是α-Fe 还是γ-Fe 能熔入较多的碳. 答: α-Fe 为体心立方结构, 致密度为0.68; γ-Fe 为面心立方结构, 致密度为0.74. 显然, α-Fe 中的间隙总体积高于γ-Fe, 但由于α-Fe 的间隙数量多, 单个间隙半径却较小, 熔入碳原子将会产生较大的畸变, 因此, 碳在γ-Fe 中的固熔度较α-Fe 的大.3. 为什么只有置换固熔体的两个组元之间才能无限互熔, 而间隙固熔体则不能?答: 这是因为形成固熔体时, 熔质原子的熔入会使熔剂结构产生点阵畸变, 从而使体系能量升高. 熔质原子与熔剂原子尺寸相差越大, 点阵畸变的程度也越大, 则畸变能越高, 结构的稳定性越低, 熔解度越小. 一般来说, 间隙固熔体中熔质原子引起的点阵畸变较大,故不能无限互熔, 只能有限熔解.第三章 凝固1. 分析纯金属生长形态与温度梯度的关系.答: 纯金属生长形态是指晶体宏观长大时固-液界面的形貌. 界面形貌取决于界面前沿液相中的温度梯度.(1) 平面状长大: 当液相具有正温度梯度时, 晶体以平直界面方式推移长大. 此时, 界面上任何偶然的、小的凸起深入液相时, 都会使其过冷度减小, 长大速率降低或停止长大, 而被周围部分赶上, 因而能保持平直界面的推移. 长大过程中晶体沿平行温度梯度的方向生长, 或沿散热的反方向生长, 而其它方向的生长则受到限制.(2) 树枝状长大: 当液相具有负温度梯度时, 晶体将以树枝状方式生长. 此时, 界面上偶然的凸起深入液相时, 由于过冷度的增大, 长大速率越来越大; 而它本身生长时又要释放结晶潜热, 不利于近旁的晶体生长, 只能在较远处形成另一凸起. 这就形成了枝晶的一次轴, 在一次轴成长变粗的同时, 由于释放潜热使晶枝侧旁液体中也呈现负温度梯度, 于是在一次轴上又会长出小枝来, 称为二次轴, 在二次轴上又长出三次轴……由此而形成树枝状骨架, 故称为树枝晶(简称枝晶).2. 简述纯金属晶体长大机制及其与固-液界面微观结构的关系.答: 晶体长大机制是指晶体微观长大方式, 即液相原子添加到固相的方式, 它与固-液界面的微观结构有关.(1) 垂直长大方式: 具有粗糙界面的物质, 因界面上约有50% 的原子位置空着, 这些空位都可以接受原子, 故液相原子可以进入空位, 与晶体连接, 界面沿其法线方向垂直推移, 呈连续式长大.(2) 横向(台阶)长大方式: 包括二维晶核台阶长大机制和晶体缺陷台阶长大机制, 具有光滑界面的晶体长大往往采取该方式. 二维晶核模式, 认为其生长主要是利用系统的能量起伏, 使液相原子在界面上通过均匀形核形成一个原子厚度的二维薄层状稳定的原子集团, 然后依靠其周围台阶填充原子, 使二维晶核横向长大, 在该层填满后, 则在新的界面上形成新的二维晶核, 继续填满, 如此反复进行.晶体缺陷方式, 认为晶体生长是利用晶体缺陷存在的永不消失的台阶(如螺型位错的台阶或挛晶的沟槽)长大的.第四章 相图1. 在Al-Mg 合金中, x Mg 为0.15, 计算该合金中镁的w Mg 为多少.解 设Al 的相对原子量为M Al , 镁的相对原子量为M Mg , 按1mol Al-Mg 合金计算, 则镁的质量分数可表示为Mg MgMg Al Al Mg Mg 100%x M w x M x M =⨯+.将x Mg = 0.15, x Al = 0.85, M Mg = 24, M Al = 27代入上式中, 得到w Mg = 13.56%.2. 根据图4-117所示二元共晶相图, 试完成:(1) 分析合金I, II的结晶过程, 并画出冷却曲线.(2) 说明室温下合金I, II的相和组织是什么, 并计算出相和组织组成物的相对量.(3) 如果希望得到共晶组织加上相对量为5%的β初的合金, 求该合金的成分.图4-117 二元共晶相图附图4-1 合金I的冷却曲线附图4-2 合金II的冷却曲线解 (1) 合金I的冷却曲线参见附图4-1, 其结晶过程如下:1以上, 合金处于液相;1~2时, 发生匀晶转变L→α, 即从液相L中析出固熔体α, L和α的成分沿液相线和固相线变化, 达到2时, 凝固过程结束;2时, 为α相;2~3时, 发生脱熔转变, α→βII.合金II的冷却曲线参见附图4-2, 其结晶过程如下:1以上, 处于均匀液相;1~2时, 进行匀晶转变L →β;2时, 两相平衡共存, 0.50.9L β;2~2′ 时, 剩余液相发生共晶转变0.50.20.9L βα+;2~3时, 发生脱熔转变α→βII .(2) 室温下, 合金I 的相组成物为α + β, 组织组成物为α + βII .相组成物相对量计算如下:αβ0.900.20100%82%0.900.050.200.05100%18%0.900.05w w -=⨯=--=⨯=- 组织组成物的相对量与相的一致.室温下, 合金II 的相组成物为α + β, 组织组成物为β初 + (α+β).相组成物相对量计算如下:αβ0.900.80100%12%0.900.050.800.05100%88%0.900.05w w -=⨯=--=⨯=- 组织组成物相对量计算如下:β(α+β)0.800.50100%75%0.900.500.900.80100%25%0.900.50w w -=⨯=--=⨯=-初 (3) 设合金的成分为w B = x , 由题意知该合金为过共晶成分, 于是有β0.50100%5%0.900.50x w -=⨯=-初 所以, x = 0.52, 即该合金的成分为w B = 0.52.3. 计算w C 为0.04的铁碳合金按亚稳态冷却到室温后组织中的珠光体、二次渗碳体和莱氏体的相对量, 并计算组成物珠光体中渗碳体和铁素体及莱氏体中二次渗碳体、共晶渗碳体与共析渗碳体的相对量.解 根据Fe-Fe 3C 相图, w C = 4%的铁碳合金为亚共晶铸铁, 室温下平衡组织为 P + Fe 3C II + L d ′, 其中P 和Fe 3C II 系由初生奥氏体转变而来, 莱氏体则由共晶成分的液相转变而成, 因此莱氏体可由杠杆定律直接计算, 而珠光体和二次渗碳体则可通过两次使用杠杆定律间接计算出来.L d ′ 相对量: d L 4 2.11100%86.3%4.3 2.11w '-=⨯=-. Fe 3C II 相对量: 3II Fe C 4.34 2.110.77100% 3.1%4.3 2.11 6.690.77w --=⨯⨯=--.P 相对量: P 4.34 6.69 2.11100%10.6%4.3 2.11 6.690.77w --=⨯⨯=--. 珠光体中渗碳体和铁素体的相对量的计算则以共析成分点作为支点, 以w C = 0.001%和w C = 6.69%为端点使用杠杆定律计算并与上面计算得到的珠光体相对量级联得到.P 中F 相对量: F P 6.690.77100%9.38%6.690.001w w -=⨯⨯=-. P 中Fe 3C 相对量: 3Fe C 10.6%9.38% 1.22%w =-=.至于莱氏体中共晶渗碳体、二次渗碳体及共析渗碳体的相对量的计算, 也需采取杠杆定律的级联方式, 但必须注意一点, 共晶渗碳体在共晶转变线处计算, 而二次渗碳体及共析渗碳体则在共析转变线处计算.L d ′ 中共晶渗碳体相对量: d Cm L 4.3 2.11100%41.27%6.69 2.11w w '-=⨯⨯=-共晶L d ′ 中二次渗碳体相对量: d Cm L 6.69 4.3 2.110.77100%10.2%6.69 2.11 6.690.77w w '--=⨯⨯⨯=--II L d ′ 中共析渗碳体相对量:d Cm L 6.69 4.3 6.69 2.110.770.0218100% 3.9%6.69 2.11 6.690.77 6.690.0218w w '---=⨯⨯⨯⨯=---共析 4. 根据下列数据绘制Au-V 二元相图. 已知金和钒的熔点分别为1064℃和1920℃. 金与钒可形成中间相β(AuV 3); 钒在金中的固熔体为α, 其室温下的熔解度为w V = 0.19; 金在钒中的固熔体为γ, 其室温下的熔解度为w Au = 0.25. 合金系中有两个包晶转变, 即1400V V V 1522V V V (1) β(0.4)L(0.25)α(0.27)(2) γ(0.52)L(0.345)β(0.45)w w w w w w =+===+==℃℃解 根据已知数据绘制的Au-V 二元相图参见附图4-3.附图4-3 Au-V 二元相图第五章 材料中的扩散1. 设有一条直径为3cm 的厚壁管道, 被厚度为0.001cm 的铁膜隔开, 通过输入氮气以保持在膜片一边氮气浓度为1000 mol/m 3; 膜片另一边氮气浓度为100 mol/m 3. 若氮在铁中700℃时的扩散系数为4×10-7 cm 2 /s, 试计算通过铁膜片的氮原子总数.解 设铁膜片左右两边的氮气浓度分别为c 1, c 2, 则铁膜片处浓度梯度为7421510010009.010 mol /m 110c c c c x x x --∂∆-≈===-⨯∂∆∆⨯ 根据扩散第一定律计算出氮气扩散通量为 722732410(10)(9.010) 3.610 mol/(m s)c J D x---∂=-=-⨯⨯⨯-⨯=⨯∂ 于是, 单位时间通过铁膜片的氮气量为 3-22-63.610(310) 2.5410 mol/s 4J A π-=⨯⨯⨯⨯=⨯最终得到单位时间通过铁膜片的氮原子总数为-62318-1A () 2.5410 6.02102 3.0610 s N J A N =⨯=⨯⨯⨯⨯=⨯第六章 塑性变形1. 铜单晶体拉伸时, 若力轴为 [001] 方向, 临界分切应力为0.64 MPa, 问需要多大的拉伸应力才能使晶体开始塑性变形?解 铜为面心立方金属, 其滑移系为 {111}<110>, 4个 {111} 面构成一个八面体, 详见教材P219中的图6-12.当拉力轴为 [001] 方向时, 所有滑移面与力轴间的夹角相同, 且每个滑移面上的三个滑移方向中有两个与力轴的夹角相同, 另一个为硬取向(λ = 90°). 于是, 取滑移系(111)[101]进行计算.222222222222k s cos 3001111cos 2001(1)01cos cos 60.646 1.57 MPa.m mϕλϕλτσ==++⨯++==++⨯-++=====即至少需要1.57 MPa 的拉伸应力才能使晶体产生塑性变形.2. 什么是滑移、滑移线、滑移带和滑移系? 作图表示α-Fe, Al, Mg 中的最重要滑移系. 那种晶体的塑性最好, 为什么?答: 滑移是晶体在切应力作用下一部分相对于另一部分沿一定的晶面和晶向所作的平行移动; 晶体的滑移是不均匀的, 滑移部分与未滑移部分晶体结构相同. 滑移后在晶体表面留下台阶, 这就是滑移线的本质. 相互平行的一系列滑移线构成所谓滑移带. 晶体发生滑移时, 某一滑移面及其上的一个滑移方向就构成了一个滑移系.附图6-1 三种晶体点阵的主要滑移系α-Fe具有体心立方结构, 主要滑移系可表示为 {110}<111>, 共有6×2 = 12个; Al 具有面心立方结构, 其滑移系可表示为 {111}<110>, 共有4×3 = 12个; Mg具有密排六方结构, 主要滑移系可表示为{0001}1120<>, 共有1×3 = 3个. 晶体的塑性与其滑移系的数量有直接关系, 滑移系越多, 塑性越好; 滑移系数量相同时, 又受滑移方向影响, 滑移方向多者塑性较好, 因此, 对于α-Fe, Al, Mg三种金属, Al的塑性最好, Mg的最差, α-Fe 居中. 三种典型结构晶体的重要滑移系如附图6-1所示.3. 什么是临界分切应力? 影响临界分切应力的主要因素是什么? 单晶体的屈服强度与外力轴方向有关吗? 为什么?答:滑移系开动所需的作用于滑移面上、沿滑移方向的最小分切应力称为临界分切应力.临界分切应力τk的大小主要取决于金属的本性, 与外力无关. 当条件一定时, 各种晶体的临界分切应力各有其定值. 但它是一个组织敏感参数, 金属的纯度、变形速度和温度、金属的加工和热处理状态都对它有很大影响.如前所述, 在一定条件下, 单晶体的临界分切应力保持为定值, 则根据分切应力与外加轴向应力的关系: σs= τk/ m, m为取向因子, 反映了外力轴与滑移系之间的位向关系, 因此, 单晶体的屈服强度与外力轴方向关系密切. m越大, 则屈服强度越小, 越有利于滑移.4. 孪生与滑移主要异同点是什么? 为什么在一般条件下进行塑性变形时锌中容易出现挛晶, 而纯铁中容易出现滑移带?答: 孪生与滑移的异同点如附表6-1所示.附表6-1 晶体滑移与孪生的比较锌为密排六方结构金属, 主要滑移系仅3个, 因此塑性较差, 滑移困难, 往往发生孪生变形, 容易出现挛晶; 纯铁为体心立方结构金属, 滑移系较多, 共有48个, 其中主要滑移系有12个, 因此塑性较好, 往往发生滑移变形, 容易出现滑移带.第七章 回复与再结晶1. 已知锌单晶体的回复激活能为8.37×104J/mol, 将冷变形的锌单晶体在-50 ℃进行回复处理, 如去除加工硬化效应的25% 需要17 d, 问若在5 min 内达到同样效果, 需将温度提高多少摄氏度?解 根据回复动力学, 采用两个不同温度将同一冷变形金属的加工硬化效应回复到同样程度, 回复时间、温度满足下述关系:122111exp t Q t R T T ⎛⎫⎛⎫=-- ⎪ ⎪ ⎪⎝⎭⎝⎭整理后得到221111ln T t R T Q t =+.将41211223 K,/5/(172460),8.3710 J/mol, 8.314 J/(mol K)4896T t t Q R ==⨯⨯==⨯=⋅代入上式得到2274.7 K T =.因此, 需将温度提高21274.722351.7 T T T ∆=-=-=℃.2. 纯铝在553 ℃ 和627 ℃ 等温退火至完成再结晶分别需要40 h 和1 h, 试求此材料的再结晶激活能.解 再结晶速率v 再与温度T 的关系符合阿累尼乌斯(Arrhenius)公式, 即exp()Q v A RT=-再 其中, Q 为再结晶激活能, R 为气体常数.如果在两个不同温度T 1, T 2进行等温退火, 欲产生同样程度的再结晶所需时间分别为t 1, t 2, 则122112122111exp[()]ln(/)t Q t R T T RTT t t Q T T =--⇒=-依题意, 有T 1 = 553 + 273 = 826 K, T 2 = 627 + 273 = 900 K, t 1 = 40 h, t 2 = 1 h, 则58.314826900ln(40/1)3.0810J/mol 900826Q ⨯⨯⨯=⨯-3. 说明金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能特点与主要区别.答: 金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能特点与主要区别详见附表7-1.附表7-1 金属在冷变形、回复、再结晶及晶粒长大各阶段的显微组织、机械性能第八章固态相变。
材料科学基础习题

第1章固体结构1.何谓晶体?晶体与非晶体有何区别?2.已知MgO晶体中Mg2+和O2-在三维空间有规律地相间排列,其晶体结构相当于两套面心立方点阵互相套叠在一起,晶胞常数a=b=c=4.20 ,α=β=γ=90℃,请回答:①画出MgO晶体二维和三维空间的晶体结构图.②从①的图形中抽象出MgO晶体的空间点阵图形.③从②中划分出单位空间格子,计算其结点数.④画出晶胞结构图,指出晶胞中的分子数.3.何谓元素电负性,有何意义?在元素周期表中分布规律如何?4.何谓晶格能,用途?试计算MgO晶格能。
已知:MgO属NaCl型结构,立方面心点阵N0=6.023×1023,e=4.8×10-10静电单位,r =1.32 , r =0.78 ,A=1.74765.画出MgO晶体(立方面心点阵)在(1 0 0)、(1 1 0)、(1 1 1)晶面上的结点和离子排布图.6.立方晶系中①画出下列晶面:(0 0 1)、(1 0)、(1 1 1)②在①所画晶面上分别标出下列晶向:[2 1 0]、[1 1 1]、[1 0 ].7.在立方晶系中给出(1 1 1)面和(1 1 )面交棱的晶棱符号.8.找出正交晶系(斜方)(P点阵)宏观对称型.9.何谓布拉维点阵?举例论证为什么仅有14种?14种布拉维点阵分属的七个晶系名称?点阵常数特点?14种布拉维点阵分为几个类型?结点数计算?10.表示晶体的宏观对称性,其特点?如何表示晶体的微观对称性,其特点?11.划分单位平行六面体应遵循那些原则?何谓晶格常数?12.何谓晶胞、原胞、单位空间格子?13.试举例说明:晶体结构与空间点阵?晶胞与单位空间格子的关系?14.什么叫离子半径?有何实用意义?什么叫离子极化?极化对晶体结构有什么影响?15.解释原子,离子配位数. 根据半径比关系,说明下列离子与O2-配位时的配位数及配位多面体的类型.r =1.32 , r =0.39 ,r =0.57 ,r =0.78 ,r =1.10 .16.胞林规则有几条?其要点是什么?应用胞林规则有何局限性?17.试用胞林规则分析MgO晶体结构.(r =0.78 ,r =1.32 )18.运用胞林规则来解释在氧离子立方密堆体中,对于获得稳定结构各需要何种电价的离子,其中:①所有八面体间隙位置均填满.②所有四面体间隙位置均填满.③填满一半八面体间隙位置.④填满一半四面体间隙位置.19.已知:r =0.78 ,Mg的原子量为24.30,r =1.32计算:①MgO的点阵常数;②MgO的密度.20.画出闪锌矿、萤石晶胞结构在(0 0 1)面上的投影图.21.金红石的晶胞为什么不属于四方体心格子而是四方原始格子呢?而萤石的结构为什么不是立方原始格子而是立方面心格子?22.比较ThO2、TiO2、MgO结构中间隙的大小.23.简单说明下列名词的含义:反萤石结构,反尖晶石结构.24.指出下列化合物的结构类型,并改写成化学式:γ-Ca2[SiO4]、Ca2Al[AlSiO7]、CaMg[Si2O6]、Mg3[Si4O10](OH)2、K[AlSi3O8].25.高岭石、叶腊石和云母具有相似的结构,画出它们的结构草图,说明它们结构的区别及由此而引起的性质上的差异.26.下列物质的结构式,化学组成式写成相应的化学组成式和结构式:a) Al2O3·2SiO2·2H2O; ②2CaO·5MgO·8SiO2·H2O;③CaMg[Si206]; ④Na[AlSi3O8]27.说明高岭石、叶腊石和白云母结构区别及由此引起的性质上差异.28.在层状硅酸盐结构中,八面体层中的Al3+可以取代四面体层中的Si4+、而四面体层中的Si4+从来不会置换八面体层中的Al3+为什么?已知:r =1.40 , r =0.40 ,r =0.53 .29.青石2MgO·2Al2O3·5SiO2具有与绿柱石Be3Al2[Si6O8]类型结构,写出它的结构式,并指出它是由绿柱石进行怎样的离子置换而得来的?30.α—方石英属立方晶系,面心立方点阵,a=7.05 ,请a) 画出晶胞在(0 0 1)面上的投影图,注明各离子相对标高。
《材料科学基础》习题

1
2.固态下完全不互溶的三元共晶相图如图6-2所示,画出过Am、PQ的垂直截面。若三组元的熔点tA>tB>tC,请画出tB <t<tA温度下的水平截面。
3.液相面投影图如图6-3,分析O合金的结晶过程,画出冷却曲线、结晶示意图、注明反应式,并计算室温下组织组成物的相对量。
4.液相面投影图如图6-4,请写出全部四相平衡转变。
4.计算面心立方结构(111)、(110)与(100)面的面密度和面间距。
5.FeAl是电子化合物,具有体心立方点阵,试画出其晶胞,计算电子浓度,画出(112)面原子排列图。
6.合金相VC、Fe3C、CuZn、ZrFe2属于何种类型,并指出其结构特点。
第二章 晶体缺陷
1.铜的空位生成能1.7×10-19J,试计算1000℃时,1cm3铜所包含的空位数,铜的密度8.9g/cm3,相对原子质量63.5,玻尔兹曼常数K=1.38×10-23J/K。
1.何为成份过冷?影响成份过冷的因素有那些?试述区域提纯的原理。
2.简述枝晶偏析形成过程和消除方法。
3.分析0.45%C,1.2%C和2.3%C 的铁碳合金的平衡结晶过程,计算室温下组织组成 物的相对量及两相相对量。
4.根据显微组织分析,一灰口铁内石墨的体积占12%,铁素体的体积占88%,试求该合金的碳含量。
如图2-1所示的位错环,说明各段位错的性质,并指出刃位错多余半原子面的位置。
2.如图2-2,某晶体滑移面上有一个 柏氏矢量为b的位错环,受到均匀切应力τ作用,试分析:
该位错环各段位错的结构类型;
求各段位错所受的力;
在τ的作用下,位错环将如何运动?
在τ的作用下,位错环稳定不动,其最小半径应该多大?
晶体结构与性质练习题

晶体结构与性质练习题晶体是由一定的周期性排列的原子、分子或离子组成的固体物质。
晶体的结构与性质有着密切的联系,不同的晶体结构会导致不同的晶体性质。
为了帮助大家更好地理解晶体结构与性质之间的关系,下面将提供一些练习题,供大家进行学习和思考。
题目一:简单晶体结构1. 以NaCl为例,简述其晶体结构的特点。
2. 请说出以下晶体中的阴离子和阳离子:CaF2、K2SO4、MgO。
3. 解释为什么NaCl和KCl的晶体结构相似,但是它们的性质却有所不同。
题目二:晶体缺陷1. 什么是点缺陷?举例说明。
2. 简述晶体中的位错缺陷以及其对晶体性质的影响。
3. 解释为什么金刚石可以成为优质的宝石。
题目三:晶体的导电性1. 解释为什么金属晶体具有良好的导电性。
2. 什么是半导体晶体?举例说明其应用。
3. 简述离子晶体的导电性及其应用。
题目四:晶体的光学性质1. 什么是吸收谱和荧光谱?它们对于研究晶体结构和性质有何意义?2. 简述偏光现象产生的原因以及其应用。
3. 解释为什么金属外观呈现出不同的颜色。
题目五:晶体的热学性质1. 解释晶体的热膨胀现象及其原理。
2. 简述晶体的热导性质以及其在热散热领域的应用。
3. 解释为什么铁磁性晶体具有自发磁化特性。
题目六:晶体的力学性质1. 解释为什么晶体呈现出不同的硬度。
2. 简述晶体的弹性性质以及其应用。
3. 什么是形状记忆合金?简述其工业应用。
以上是晶体结构与性质练习题,希望能够帮助大家加深对晶体结构与性质之间关系的理解。
通过思考与学习这些问题,相信大家能够更好地掌握晶体学知识,并在实际应用中发挥自己的才能。
祝你们学习进步!。
材料科学基础习题库第章凝固

第三章纯金属的凝固(一) 填空题1.金属结晶两个密切联系的基本过程是和2 在金属学中,通常把金属从液态向固态的转变称为,通常把金属从一种结构的固态向另一种结构的固态的转变称为。
3.当对金属液体进行变质处理时,变质剂的作用是4.铸锭和铸件的区别是。
5.液态金属结晶时,获得细晶粒组织的主要方法是6.金属冷却时的结晶过程是一个热过程。
7.液态金属的结构特点为。
8.如果其他条件相同,则金属模浇注的铸件晶粒比砂模浇注的,高温浇注的铸件晶粒比低温浇注的,采用振动浇注的铸件晶粒比不采用振动的,薄铸件的晶粒比厚铸件。
9.过冷度是。
一般金属结晶时,过冷度越大,则晶粒越。
(二) 判断题1 凡是由液态金属冷却结晶的过程都可分为两个阶段。
即先形核,形核停止以后,便发生长大,使晶粒充满整个容积。
2.凡是由液体凝固成固体的过程都是结晶过程。
3.近代研究表明:液态金属的结构与固态金属比较接近,而与气态相差较远。
( )4.金属由液态转变成固态的过程,是由近程有序排列向远程有序排列转变的过程。
( )5.当纯金属结晶时,形核率随过冷度的增加而不断增加。
( ) 6.在结晶过程中,当晶核成长时,晶核的长大速度随过冷度的增大而增大,但当过冷度很大时,晶核的长大速度则很快减小。
( )7.金属结晶时,冷却速度愈大,则其结晶后的晶粒愈细。
( )8.所有相变的基本过程都是形核和核长大的过程。
( )9.在其它条件相同时,金属模浇注的铸件晶粒比砂模浇注的铸件晶粒更细( )10.在其它条件相同时,高温浇注的铸件晶粒比低温浇注的铸件晶粒更细。
( )11.在其它条件相同时,铸成薄件的晶粒比铸成厚件的晶粒更细。
( )12. 金属的理论结晶温度总是高于实际结晶温度。
( )13.在实际生产条件下,金属凝固时的过冷度都很小(<20℃),其主要原因是由于非均匀形核的结果。
( )14.过冷是结晶的必要条件,无论过冷度大小,均能保证结晶过程得以进行。
( )15.在实际生产中,评定晶粒度方法是在放大100倍条件下,与标准晶粒度级别图作比较,级数越高,晶粒越细。
材料结构习题纯晶体凝固答案

《材料结构》习题:纯晶体的凝固1. 设均匀形核时其晶核为球形,试证明临界形核功ΔG c 与临界晶核体积V c 的关系为:12c c V G V G ∆=-∆ 2. 设非均匀形核时其晶核为球冠形,试证明临界形核功*c G ∆与临界晶核体积*c V 也存在上列关系式。
3. 当临界晶核为球形和小立方体形时,试分别求出各临界晶核中的原子数n 的表达式:n =f (ΔG V , σ,V)式中V 为每个原子的体积。
4. 试说明金属结晶时粗糙型液-固界面的微观结构特点,指出该界面在结晶过程中的作用。
5. 综述金属结晶的热力学条件、动力学条件、能量条件和结构条件。
6. 已知金的熔点Tm 为1063℃,熔化潜热Lm 为12.8kJ/mol ,密度为19.3g/cm3,摩尔质量为197g/mol 。
若液态金在1000℃均匀形核时的临界晶核半径r =43.3×10-10m ,试计算金的液固界面能σ和临界形核功。
7. 根据克拉珀龙方程可以推导出液-固或固-固相变温度与压力的关系式: T V T H P mm m ∆∆∆=∆ 式中,ΔH m 为相变潜热;T m 为相变温度;ΔV m 为摩尔体积变化。
试分别计算:(1) 已知α-F e →γ-Fe 在1大气压下T m =912℃,若外加压力增加到1000大气压时,转变温度应是多少(已知ΔH m =920.5J/mol ,α-F e 的密度为7.57g/cm 3,γ-Fe 的密度为7.63g/cm 3,Fe 的摩尔质量为55.85g/mol )。
(2) 已知纯铁熔化时体积变化为膨胀3%,求10个大气压下的熔点(已知L m =15.2kJ/mol ,T m =1803K ,密度为7.6g/cm 3,摩尔质量为55.85g/mol )。
习题答案1. 证明:设均匀形核时其球形晶核半径为r ,则32232344304802242143232V V V c Vc V c V c c V c c V c V G V G A r G r G r G rr G r G r G G r G r r G V G σππσππσσσπππ∆=∆+=∆+∂∆=⇒∆+∂∆∴=-=-∆∆∴∆=∆-=-∆=-∆令 = 即2.证明:设非均匀形核时其球冠状晶核的曲率半径为r ,高为h ,则系统总表面自由能的增量ΔG S 为S L L W W LW LW G A A A A αααασσσσ∆==+-∑因为晶核周边表面张力应彼此平衡,则cos LW W L αασσσθ=+ 即cos W LW L αασσσθ-=-222(1cos )L A rh r αππθ==-222(sin )(1cos )W A r r απθπθ==-222S 232(1cos )(1cos )cos (23cos cos )L L L G r r r αααπθσπθσθπσθθ∆=---=-+ 球冠的体积 23311(3)(23cos cos )33V r h h r ππθθ=-=-+ 令31()(23cos cos )4f θθθ=-+ **3*24()4()3V S V L G V G G r G f r f απθπσθ∆=∆+∆=∆+则 **2**04()8()0c V c L G r G f r f rαπθπσθ∂∆=⇒∆+∂令 = ****22L c c cL V r G r G αασσ∆∴=-=-∆ 即 ****3**2*3*424()()323c V cc V c c V r G G r G r f r G f ππθπθ⎛⎫∆∴∆=∆-=-∆ ⎪⎝⎭ **3***41()32c c c c V V r f G V G πθ=∴∆=-∆3.解: (1)当临界晶核为球形时,设其半径为r c ,则33333243233323c c c V Vc V r V r G G V n V G V σπσππσ=-∴==-∆∆∴==-∆(2)当晶核为正方形时,设其边长为a ,则326V V G V G A a G a σσ∆=∆+=∆+2403120c V c c VG a G a a r G σσ∂∆=⇒∆+=-∂∆令 =,即 333336464c c c V V V V a n V G V G σσ=∴==-=-∆∆4.答:金属结晶时粗糙型液-固界面的微观结构为粗糙界面。
纯晶体的凝固习题与答案

1. 证明:(1)设均匀形核时其晶核为球形,临界形核功ΔG c 与临界晶核体积V c 的关系为:12c c V G V G ∆=-∆ (2)设均匀形核时其晶核为正方形,临界形核功ΔG c 与临界晶核体积V c 也存在上述关系。
(3)任意形状晶核的临界晶核形核功ΔG c 与临界晶核体积V c 也存在上述关系。
(4)设非均匀形核时其晶核为球冠形,临界形核功*c G ∆与临界晶核体积*c V 也存在上述关系。
2. 综述金属结晶的热力学条件、动力学条件、能量条件和结构条件。
习题答案1. (1)证明:设均匀形核时其球形晶核半径为r ,则322323443048r 02242143232V V V c Vc V c V c c V c c V c V G V G A r G r G r G rr G r G r G G r G r r G V G σππσππσσσπππ∆=∆+=∆+∂∆=⇒∆+∂∆∴=-=-∆∆∴∆=∆-=-∆=-∆令 = 即(4)证明:设非均匀形核时其球冠状晶核的曲率半径为r ,高为h ,则系统总表面自由能的增量ΔG S 为S L L W W LW LW G A A A A αααασσσσ∆==+-∑因为晶核周边表面张力应彼此平衡,则cos LW W L αασσσθ=+ 即cos W LW L αασσσθ-=-222(1cos )L A rh r αππθ==-222(sin )(1cos )W A r r απθπθ==-222S 232(1cos )(1cos )cos (23cos cos )L L L G r r r αααπθσπθσθπσθθ∆=---=-+球冠的体积 23311(3)(23cos cos )33V r h h r ππθθ=-=-+ 令31()(23cos cos )4f θθθ=-+ **3*24()4()3V S V L G V G G r G f r f απθπσθ∆=∆+∆=∆+则 **2**04()8()0c V c L G r G f r f rαπθπσθ∂∆=⇒∆+∂令 = ****22L c c cL V r G r G αασσ∆∴=-=-∆ 即 ****3**2*3*424()()323c V cc V c c V r G G r G r f r G f ππθπθ⎛⎫∆∴∆=∆-=-∆ ⎪⎝⎭ **3***41()32c c c c V V r f G V G πθ=∴∆=-∆2.答:必须同时满足以下四个条件,结晶才能进行。
单组元相图及纯晶体的凝固

自由能随温度变化的示意图
(2) 纯晶体的凝固
在一定温度下,从一相转变为另一相的自由能变化为
GV
LmT Tm
式中,ΔT=Tm-T,是熔点Tm与实际凝固温度T之差。
由上式可知,要使 ΔGv<0,必须使ΔT>0,即 T<Tm,故ΔT称为过冷度。晶 体凝固的热力学条件表明,实际凝固温度应低于熔点Tm,即需要有过冷度。
GS x 1 x x ln x 1 x ln(1 x)
NT kTm 式中,k是玻尔兹曼常数; Tm是熔点;x是界面上被固相原子占据位置的分数;
而 ,其中Lm为熔化热, ,是界面原子的平均配位数;是晶体配位数。
恒小于1。
(2) 纯晶体的凝固
将上式按 GS 与x的关系作图,并改变值,得到一系列曲线,如下图所示。 NT kTm
晶体长大方式和生长递率 晶体的长大方式与上述的界面构造有关,可有连续长大、二维形核、螺型位错 长大等方式。 a.连续长大
对于粗糙界面,由于界面上约有一半的原子位置空着,故液相的原子可以进 入这些位置与晶体结合起来,晶体便连续地向液相中生长,故这种生长方式为 垂直生长。对于大多数金属来说,由于动态过冷度很小,因此其平均生长速率 与过冷度成正比,即
dG= Vdp- SdT。 在等压时,dp=0,故上式简化为:
dG S dT 由于熵恒为正值,所以自由能是随温度增高而减小。
(2) 纯晶体的凝固
纯晶体的液、固两相的自由 能随温度变化规律如.右图所示。 这样,两条斜率不同的曲线必 然相交于一点,该点表示液、 固两相的自由能相等,故两相 处于平衡而共存,此温度即为 理论凝固温度,也就是晶体的 熔点Tm。事实上,在此两相共 存温度,既不能完全结晶,也 不能完全熔化,要发生结晶则 体系必须降至低于Tm温度, 而发生熔化则必须高于Tm。
纯金属的凝固习题与答案

纯金属的凝固习题与答案1 说明下列基本概念凝固、结晶、过冷、过冷度、结构起伏、能量起伏、均匀形核、非均匀形核、临界晶核半径、临界晶核形核功、形核率、生长线速度、光滑界面、粗糙界面、动态过冷度、柱状晶、等轴晶、树枝状晶、单晶、非晶态、微晶、液晶。
2 当球状晶核在液相中形成时,系统自由能的变化为σππ23344r G r G V +∆=∆,(1)求临界晶核半径c r ;(2)证明V V c c G A G c ∆-==∆231σ(c V 为临界晶核体积);(3)说明上式的物理意义。
3 试比较均匀形核与非均匀形核的异同点,说明为什么非均匀形核往往比均匀形核更容易进行。
4 何谓动态过冷度说明动态过冷度与晶体生长的关系。
在单晶制备时控制动态过冷度的意义5 分析在负温度梯度下,液态金属结晶出树枝晶的过程。
6 在同样的负温度梯下,为什么Pb 结晶出树枝状晶而Si 的结晶界面却是平整的7 实际生产中怎样控制铸件的晶粒大小试举例说明。
8 何谓非晶态金属简述几种制备非晶态金属的方法。
非晶态金属与晶态金属的结构和性能有什么不同。
9 何谓急冷凝固技术在急冷条件下会得到哪些不同于一般晶体的组织、结构能获得何种新材料. 计算当压力增加到500×105Pa 时锡的熔点的变化,已知在105Pa 下,锡的熔点为505K ,熔化热7196J/mol ,摩尔质量为×10-3kg/mol ,固体锡的体积质量×103kg/m 3,熔化时的体积变化为+%。
2. 考虑在一个大气压下液态铝的凝固,对于不同程度的过冷度,即:ΔT=1,10,100和200℃,计算: (a)临界晶核尺寸;(b)半径为r*的团簇个数;(c)从液态转变到固态时,单位体积的自由能变化ΔGv ; (d)从液态转变到固态时,临界尺寸r*处的自由能的变化 ΔGv 。
铝的熔点T m =993K ,单位体积熔化热ΔH f =×109J/m 3,固液界面自由能γsc =93J/m 2,原子体积V 0=×10-29m 3。
第四章凝固
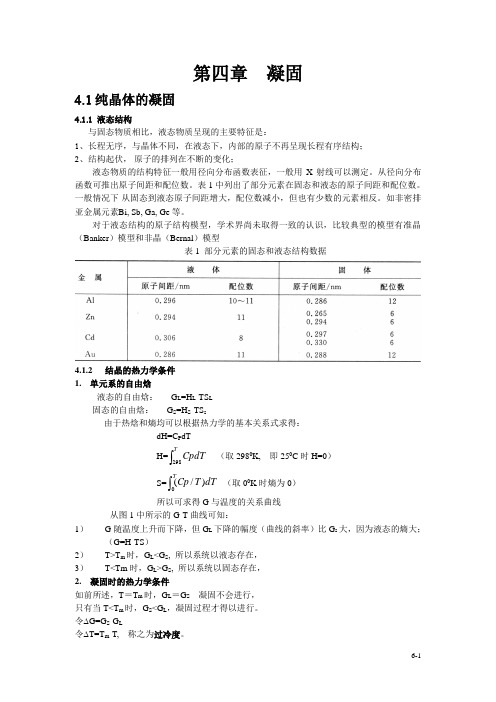
第四章 凝固4.1 纯晶体的凝固4.1.1 液态结构与固态物质相比,液态物质呈现的主要特征是:1、长程无序,与晶体不同,在液态下,内部的原子不再呈现长程有序结构;2、结构起伏, 原子的排列在不断的变化;液态物质的结构特征一般用径向分布函数表征,一般用X 射线可以测定。
从径向分布函数可推出原子间距和配位数。
表1中列出了部分元素在固态和液态的原子间距和配位数。
一般情况下 从固态到液态原子间距增大,配位数减小,但也有少数的元素相反。
如非密排亚金属元素B i, Sb, Ga, Ge 等。
对于液态结构的原子结构模型,学术界尚未取得一致的认识,比较典型的模型有准晶(Banker )模型和非晶(Bernal )模型表1 部分元素的固态和液态结构数据4.1.2结晶的热力学条件1. 单元系的自由焓液态的自由焓: G L =H L -TS L固态的自由焓: G S =H S -TS s由于热焓和熵均可以根据热力学的基本关系式求得:dH=C P dT H=⎰T C pdT 298(取2980K, 即250C 时H=0)S=⎰TdT T Cp 0)/( (取00K 时熵为0)所以可求得G 与温度的关系曲线从图1中所示的G-T 曲线可知:1) G 随温度上升而下降,但G L 下降的幅度(曲线的斜率)比G s 大,因为液态的熵大;(G=H-TS )2) T>T m 时,G L <G S , 所以系统以液态存在, 3)T<Tm 时,G L >G S , 所以系统以固态存在,2. 凝固时的热力学条件如前所述,T =T m 时,G L =G S 凝固不会进行, 只有当T<T m 时,G S <G L ,凝固过程才得以进行。
令∆G=G S -G L令∆T=T m -T, 称之为过冷度。
只有∆T>0,才有∆G<0所以:∆T>0是凝固的热力学条件, ∆G 称之为凝固的驱动力。
∆G 的绝对值越大,凝固的驱动力也就越大。
材料科学基础-单组元相图及纯晶体的凝固.doc

材料科学基础-单组元相图及纯晶体的凝固(总分:110.00,做题时间:90分钟)一、论述题(总题数:11,分数:110.00)1.计算当压力增加到500×105Pa时锡的熔点变化,已知在105Pa下,锡的熔点为505K,熔化热为7196J/mol,摩尔质量为118.8×10-3kg/mol,固体锡的密度为7.30×103kg/m3,熔化时的体积变化为+2.7%。
(分数:10.00)__________________________________________________________________________________________2.根据下列条件建立单元系相图:①组元A在固态有两种结构A1和A2,且密度A2>A1>液体;②A1转变到A2的温度随压力增加而降低;③A1相在低温是稳定相;④固体在其本身的蒸气压1333Pa(10mmHg)下的熔点是8.2℃;⑤在1.013×105Pa(1个大气压)下沸点是90℃;⑥A1,A2和液体在1.013×106Pa(10个大气压)下及40℃时三相共存(假设升温相变△H<0)。
(分数:10.00)__________________________________________________________________________________________3.考虑在1个大气压下液态铝的凝固,对于不同程度的过冷度,即△T=1,10,100和200℃,计算:①临界晶核尺寸;②半径为r*的晶核个数;③从液态转变到固态时,单位体积的自由能变化△G V;④从液态转变到固态时,临界尺寸r*处的自由能的变化△G r*(形核功)。
铝的熔点T m=993K,单位体积熔化热L m=1.836×109J/m3,固液界面比表面能δ=93×10-3J/m2,原子体积V0=1.66×10-29m3。
材料科学基础习题与参考答案

第一章材料的结构一、解释以下基本概念空间点阵、晶格、晶胞、配位数、致密度、共价键、离子键、金属键、组元、合金、相、固溶体、中间相、间隙固溶体、置换固溶体、固溶强化、第二相强化。
二、填空题1、材料的键合方式有四类,分别是(),(),(),()。
2、金属原子的特点是最外层电子数(),且与原子核引力(),因此这些电子极容易脱离原子核的束缚而变成()。
3、我们把原子在物质内部呈()排列的固体物质称为晶体,晶体物质具有以下三个特点,分别是(),(),()。
4、三种常见的金属晶格分别为(),()和()。
5、体心立方晶格中,晶胞原子数为(),原子半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶面为(),晶胞中八面体间隙个数为(),四面体间隙个数为(),具有体心立方晶格的常见金属有()。
6、面心立方晶格中,晶胞原子数为(),原子半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶面为(),晶胞中八面体间隙个数为(),四面体间隙个数为(),具有面心立方晶格的常见金属有()。
7、密排六方晶格中,晶胞原子数为(),原子半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶面为(),具有密排六方晶格的常见金属有()。
8、合金的相结构分为两大类,分别是()和()。
9、固溶体按照溶质原子在晶格中所占的位置分为()和(),按照固溶度分为()和(),按照溶质原子与溶剂原子相对分布分为()和()。
10、影响固溶体结构形式和溶解度的因素主要有()、()、()、()。
11、金属化合物(中间相)分为以下四类,分别是(),(),(),()。
12、金属化合物(中间相)的性能特点是:熔点()、硬度()、脆性(),因此在合金中不作为()相,而是少量存在起到第二相()作用。
13、CuZn、Cu5Zn8、Cu3Sn的电子浓度分别为(),(),()。
14、如果用M表示金属,用X表示非金属,间隙相的分子式可以写成如下四种形式,分别是(),(),(),()。
《材料科学基础》练习题集02

厦门理工学院《材料科学基础》练习题集 02第9章材料的凝固一、名词解释:1、均匀形核:在一定条件下,从液态金属中直接产生,原子呈规则排列的结晶核心。
2、非均匀形核:是液态金属依附在一些未溶颗粒表面或固液界面所形成的晶核。
3、变质处理:在液态金属结晶前,特意加入某些难熔固态颗粒,造成大量可以成为非均匀形核晶核的固态质点,使结晶时的晶核数目大大增加,从而提高了形核率,细化晶粒,这种处理方法即为变质处理。
4、变质剂:在浇注前所加入的难熔杂质称为变质剂。
5、枝晶偏析:实际生产中,合金冷却速度快,原子扩散不充分,使得先结晶出来的固溶体合金含高熔点组元较多,后结晶含低熔点组元较多,这种在晶粒内化学成分不均匀的现象称为枝晶偏析。
6、比重偏析:比重偏析是由组成相与溶液之间的密度差别所引起的。
如果先共晶相与溶液之间的密度差别较大,则在缓慢冷却条件下凝固时,先共晶相便会在液体中上浮或下沉,从而导致结晶后铸件上下部分的化学成分不一致,产生比重偏析。
7、溶质再分配8、成分过冷二、判断题:1、液态金属的结构特点是近程有序,长程无序。
()2、晶粒尺寸和形核率N、线长大速度Vg之间的关系是N/Vg越大,晶粒尺寸越大。
()3、区域提纯技术的理论基础是凝固过程中的溶质再分配。
()4、液-固粗糙界面可描述为微观粗糙、宏观平整。
()5、在结晶过程中,晶核越多,生长速率越慢,则凝固后的晶粒越细小。
()6、在单相固溶体铸锭结晶时,成分过冷越大,越易形成枝晶。
()7、由凝固理论可知,细化晶粒的途径是提高形核率,降低长大速率。
()8、金属-非金属型共晶具有粗糙-光滑型界面,所以它多为树枝状,针状或螺旋状。
()三、选择题:1、纯金属结晶均匀形核,当过冷度 T很小时,形核率低,是因为。
A、原子可动性低,相变驱动力低;B、原子可动性高,相变驱动力低;C、原子可动性低,相变驱动力高;D、原子可动性高,相变驱动力高;2、合金凝固时,出现成分过冷的原因是。
机械工程材料 第三章 材料的凝固.答案

具有共晶成分的合金称共晶合金。在共晶线上,凡
成分位于共晶点以左的合金称亚共晶合金,位于共
晶点以右的合
金称过共晶合
A
金。 凡具有共晶线
成分的合金液
L+
B
C
D
体冷却到共晶
温度时都将发
生共晶反应。
⑵ 合金的结晶过程 ① 含Sn量小于C点合金(Ⅰ合金)的结晶过程
在3点以前为匀晶转变,结晶出单相 固溶体,这种
根据组元数, 分为二元相图、三元相图和多元相图。
Fe-C二元相图
三元相图
一、二元相图的建立
几乎所有的相图都是通过实验得到的,最常用的是 热分析法。
二元相图的建立步骤为:[以Cu-Ni合金(白铜)为例] 1. 配制不同成分的合金,测出各合金的冷却曲线,
找出曲线上的临界点(停歇点或转折点)。 2. 将临界点标在温度-成分坐标中的成分垂线上。 3. 将垂线上相同意义的点连接起来,并标上相应
1、铁的同素异构转变
铁在固态冷却过程中有两次 晶体结构变化,其变化为:
1394℃
912℃
-Fe ⇄ -Fe ⇄ -Fe
-Fe、 -Fe为体心立方结构(BCC),-Fe为面心立方 结构(FCC)。都是铁的同素异构体。
-Fe
-Fe
2、固态转变的特点 ⑴形核一般在某些特定部
相图被两条线分为三 个相区,液相线以上 为液相区L ,固相线以 下为 固溶体区,两 条线之间为两相共存 的两相区(L+ )。
L
液相线 L
+
固相线
Cu
成分(wt%Ni)
Ni
A portion of the copper-nickel phase diagram for which compositions and phase amounts are determined at point B
材料科学基础练习题

第2章固体结构一、填空题1.所谓_______________是指晶体结构中任一原子周围最近邻且___________的原子数;而_______________是指晶体结构中原子体积占总体积的百分比。
面心立方和密排六方结构的致密度均为____________,是纯金属中最密集的结构。
2.组成合金的基本的___________的物质称为组元。
组元可以是金属和非金属元素,也可以是化合物。
固态下所形成的合金相基本上可分为_________和__________两大类。
3.固溶体是以某一组元为溶剂,在其晶体点阵中溶入其他组元原子(溶质原子)所形成的均匀混合的________________,它保持着_____________的晶体结构类型。
4.影响固体溶解度的因素很多,主要取决于四个因素:a._____________,b.__________,c._________________,d.___________________5. fcc结构的密排方向是_______,密排面是______,密排面的堆垛顺序是_______致密度为___________配位数是________________晶胞中原子数为___________,把原子视为刚性球时,若晶体点阵常数为a,原子的半径是____________;bcc结构的密排方向是_______,密排面是_____________致密度为___________配位数是________________ 晶胞中原子数为___________,若晶体点阵常数为a,原子的半径是____________;hcp结构的密排方向是_______,密排面是______,密排面的堆垛顺序是_______,致密度为___________配位数是________________,晶胞中原子数为___________,若晶体点阵常数为a和c,原子的半径是____________。
6.铝晶体属于_____________点阵。
材料科学基础习题及答案

第一章材料的结构一、解释以下基本概念空间点阵、晶格、晶胞、配位数、致密度、共价键、离子键、金属键、组元、合金、相、固溶体、中间相、间隙固溶体、置换固溶体、固溶强化、第二相强化。
二、填空题1、材料的键合方式有四类,分别是(),(),(),()。
2、金属原子的特点是最外层电子数(),且与原子核引力(),因此这些电子极容易脱离原子核的束缚而变成()。
3、我们把原子在物质内部呈()排列的固体物质称为晶体,晶体物质具有以下三个特点,分别是(),(),()。
4、三种常见的金属晶格分别为(),()和()。
5、体心立方晶格中,晶胞原子数为(),原子半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶面为(),晶胞中八面体间隙个数为(),四面体间隙个数为(),具有体心立方晶格的常见金属有()。
6、面心立方晶格中,晶胞原子数为(),原子半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶面为(),晶胞中八面体间隙个数为(),四面体间隙个数为(),具有面心立方晶格的常见金属有()。
7、密排六方晶格中,晶胞原子数为(),原子半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶面为(),具有密排六方晶格的常见金属有()。
8、合金的相结构分为两大类,分别是()和()。
9、固溶体按照溶质原子在晶格中所占的位置分为()和(),按照固溶度分为()和(),按照溶质原子与溶剂原子相对分布分为()和()。
10、影响固溶体结构形式和溶解度的因素主要有()、()、()、()。
11、金属化合物(中间相)分为以下四类,分别是(),(),(),()。
12、金属化合物(中间相)的性能特点是:熔点()、硬度()、脆性(),因此在合金中不作为()相,而是少量存在起到第二相()作用。
13、CuZn、Cu5Zn8、Cu3Sn的电子浓度分别为(),(),()。
14、如果用M表示金属,用X表示非金属,间隙相的分子式可以写成如下四种形式,分别是(),(),(),()。
第04章 纯金属的凝固 重点内容与习题

纯金属均匀形核研究发现,有效形核温度约在 0.2Tm,表明均匀形核所需的过冷度很大。 纯金属在实际凝固中,所需过冷度却很小,其 原因是实际凝固是非均匀(异质)形核。异质 基底通常可有效地降低单位体积的表面能,从 而降低形核功,这种异质基底的催化作用使非 均匀(异质)形核的过冷度仅为0.02Tm。
(1)形核又分为均匀形核与非均匀(异质)形核。 均匀形核 结晶的驱动力 结晶的阻力 临界半径r* 物理意义: 当半径小于r*的晶胚是不稳定的,不能自发长大,最终熔 化而消失,而半径等于或大于r*的晶胚可以自发长大成为晶核。 形核功:临界半径对应的自由能 结晶条件:需要过冷度、结构起伏(出现半径大于r*的晶胚)和能量 起伏 形核率:是一个重要的参数,它涉及到凝固后的晶粒的大小,而晶粒 尺寸对材料的性能有重要影响。形核率受两个因素控制,即形核功 因子核和扩散几率因子。
纯晶体凝固时的生长形态:(2)取决于界面 前沿液体中的温度分布情况。 在正的温度梯度下,光滑界面结构的晶体,其 生长形态呈现台阶状;而粗糙界面的晶体,其 生长形态呈平面状。在负的温度梯度下,粗糙 界面结构的晶体,其生长形态呈树枝状;光滑 界面结构的晶体,其生长形态也呈现树枝状, 只有当α值很大的晶体,其生长形态才呈现平 面状。
重要概念与名词: 凝固,结晶,近程有序,结构起伏,能量起伏 ,过冷度,均匀形核,非均匀形核,晶胚,晶 核,临界晶粒,临界形核功,光滑界面,粗糙 界面,温度梯度,平面状,树枝状,结晶度
作业
1.考虑在一个大气压下液态铝的凝固,对于不同程度 的过冷度,即:ΔT=1,10,100和200℃,计算: (a)临界晶核尺寸; (b)半径为r*的晶核个数; (c) 从液态转变到固态时,单位体积的自由能变化 ΔG*(形核功); (d)从液态转变到固态时,临界尺寸r*处的自由能的 变化 ΔGv。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《材料结构》习题:纯晶体的凝固
1.设均匀形核时其晶核为球形,试证明临界形核功ΔG c 与临界晶核体积V c
的关系为: 12
c c V G V G ∆=-∆ 2.设非均匀形核时其晶核为球冠形,试证明临界形核功*c G ∆与临界晶核体积*c V 的关系为:
12c c V G V G *
*∆=-∆ 3.当临界晶核为球形和小立方体形时,试分别求 出各临界晶核中的原子数n 的表达式:
n =f (ΔG V , σ,V )
式中V 为每个原子的体积。
4.试说明金属结晶时粗糙型液-固界面的微观结构特点,指出该界面在结晶过程中的作用。
5.综述金属结晶的热力学条件、动力学条件、能量条件和结构条件。
6.已知金的熔点T m 为1063℃,熔化潜热L m 为12.8kJ/mol ,密度为19.3g/cm 3
,摩尔质量为197g/mol 。
若液态金在1000℃均匀形核时的临界晶核半径r =43.3×10-10m ,试计算金的液固界面能σ和临界形核功。
7.根据克拉珀龙方程可以推导出液-固或固-固相变温度与压力的关系式:
T V T H P m
m m ∆∆∆=∆ 式中,ΔH m 为相变潜热;T m 为相变温度;ΔV m 为摩尔体积变化。
试分别计算:
(1) 已知α-F e →γ-Fe 在1大气压下T m =912℃,若外加压力增加到1000大气压时,转变温度应是多少(已知ΔH m =920.5J/mol ,α-F e 的密度为7.57g/cm 3,γ-Fe 的密度为7.63g/cm 3,Fe 的摩尔质量为55.85g/mol )。
(2) 已知纯铁熔化时体积变化为膨胀3%,求10个大气压下的熔点(已知L m =15.2kJ/mol ,T m =1803K ,密度为
7.6g/cm 3,摩尔质量为55.85g/mol )。
