数字信号处理之DCT变换公式
DCT算法的相关知识与原理

DCT算法的相关知识与原理DCT(Discrete Cosine Transform,离散余弦变换)是一种基于频域的信号处理技术,广泛应用于图像和音频压缩、数据压缩和信号处理等领域。
其主要原理是将时域的一段信号变换为频域的一组余弦系数,通过保留部分重要系数来减少信号的冗余信息,从而实现信号的压缩和重建。
正变换的具体步骤如下:1.将时域信号分为若干个相同大小的块,并在每个块的边缘上添加一个边界。
2.对每个块进行离散余弦变换,并计算出对应的余弦系数矩阵。
3.对余弦系数矩阵进行量化处理,将其舍入为整数值。
量化矩阵是用于将高频部分的系数舍弃,从而减少冗余信息的重要步骤。
4.保留部分重要的系数,舍弃剩余的系数。
常用的方法是选择一个适当的阈值来判断系数的重要性,将小于阈值的系数置为零。
5.将量化后的系数按照其中一种编码方式进行编码,以便存储和传输。
常用的编码方式包括霍夫曼编码和算术编码等。
逆变换则是正变换的逆过程,用于将频域信号恢复为时域信号。
1.将编码后的系数解码,恢复为量化前的系数。
2.逆量化步骤是将量化后的系数乘以量化矩阵,以恢复出原始大小的系数矩阵。
3.对逆量化后的系数矩阵进行离散余弦逆变换,得到逆变换后的时域信号。
4.去掉边界,得到最终的还原信号。
DCT算法主要应用在图像和音频压缩中。
在图像压缩中,通常将图像分为若干个8x8的图像块,并对每个块进行DCT变换。
由于图像的高频成分较低频成分所占比例较小,因此可以通过量化和舍弃高频系数来减少数据量。
在音频压缩中,也可以将音频信号分帧处理,并使用DCT变换将时域信号转换为频域系数,之后再通过量化和编码来减少数据量。
总之,DCT算法通过将时域信号转换为频域系数,并舍弃冗余信息来实现信号的压缩。
其核心思想是通过保留重要的低频成分来表示原始信号,在不失真的情况下减少信号的体积,并在需要时进行解码和还原。
DCT算法在图像和音频压缩领域有着广泛的应用,是实现高效数据压缩和传输的重要技术。
DCT--离散余弦变换

K. R. Rao and P. Yip, 离散余弦变换 : 算法、优点和应用 (Discrete Cosine Transform: Algorithms, Advantages, Applications) (Academic Press, Boston, 1990).
A. V. Oppenheim, R. W. Schafer, and J. R. Buck, 时间离散信号处理 (Discrete-Time Signal Processing), second edition (Prentice-Hall, New Jersey, 1999).
mhtml:file://C:\Documents%20and%20Settings\Administrator\桌面\FAT3... 2010-10-22
Hale Waihona Puke 反变换DCT-I的反变换是把DCT-I乘以系数
。 DCT-IV的反变换是把DCT-IV乘以系数 。
DCT-II的反变换是把DCT-III乘以系数 ,反之亦然。
离散余弦变换
维基百科,自由的百科全书
离散余弦变换(DCT for Discrete Cosine Transform)是与傅里叶变换相关的一 种变换,它类似于离散傅里叶变换 (DFT for Discrete Fourier Transform),但 是只使用实数。离散余弦变换相当于 一个长度大概是它两倍的离散傅里叶 变换,这个离散傅里叶变换是对一个 实偶函数进行的(因为一个实偶函数的 傅里叶变换仍然是一个实偶函数),在 有些变形里面需要将输入或者输出的 位置移动半个单位(DCT有8种标准类 型,其中4种是常见的)。
和离散傅里叶变换类似,变化前面的归一化系数仅仅是常规而已,改变这个系数并不改变变
DCT变换
DCT变换的全称是离散余弦变换(Discrete Cosine Transform),离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换,这个离散傅里叶变换是对一个实偶函数进行的。
通过数字信号处理的学习我们知道实函数的傅立叶变换获得的频谱大多是复数,而偶函数的傅立叶变换结果是实函数。
以此为基础,使信号函数成为偶函数,去掉频谱函数的虚部,是余弦变换的特点之一。
要实现DCT有多种方法,一种可以采用DSP处理器,但这是牺牲了速度换来设计的灵活;一种是采用ASIC技术,这使得速度较快但灵活性又不好;还有一种就是用FPGA(可编程逻辑器件),利用这项技术既能加快速度又能带来设计的灵活性。
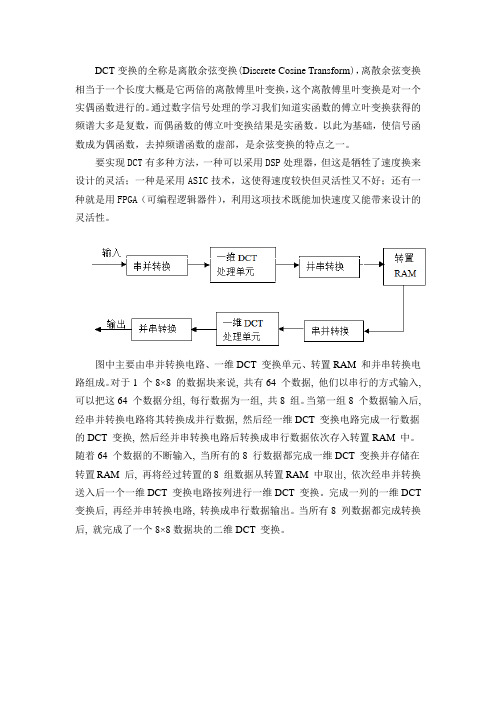
图中主要由串并转换电路、一维DCT 变换单元、转置RAM 和并串转换电路组成。
对于1 个8×8 的数据块来说, 共有64 个数据, 他们以串行的方式输入, 可以把这64 个数据分组, 每行数据为一组, 共8 组。
当第一组8 个数据输入后, 经串并转换电路将其转换成并行数据, 然后经一维DCT 变换电路完成一行数据的DCT 变换, 然后经并串转换电路后转换成串行数据依次存入转置RAM 中。
随着64 个数据的不断输入, 当所有的8 行数据都完成一维DCT 变换并存储在转置RAM 后, 再将经过转置的8 组数据从转置RAM 中取出, 依次经串并转换送入后一个一维DCT 变换电路按列进行一维DCT 变换。
完成一列的一维DCT 变换后, 再经并串转换电路, 转换成串行数据输出。
当所有8 列数据都完成转换后, 就完成了一个8×8数据块的二维DCT 变换。
离散余弦变换(DCT)

离散余弦变换(DCT)DCT变换、DCT反变换、分块DCT变换⼀、引⾔DCT变换的全称是离散余弦变换(Discrete Cosine Transform),主要⽤于将数据或图像的压缩,能够将空域的信号转换到频域上,具有良好的去相关性的性能。
DCT变换本⾝是⽆损的,但是在图像编码等领域给接下来的量化、哈弗曼编码等创造了很好的条件,同时,由于DCT变换时对称的,所以,我们可以在量化编码后利⽤DCT反变换,在接收端恢复原始的图像信息。
DCT变换在当前的图像分析已经压缩领域有着极为⼴⼤的⽤途,我们常见的JPEG静态图像编码以及MJPEG、MPEG动态编码等标准中都使⽤了DCT变换。
⼆、⼀维DCT变换⼀维DCT变换时⼆维DCT变换的基础,所以我们先来讨论下⼀维DCT变换。
⼀维DCT变换共有8种形式,其中最常⽤的是第⼆种形式,由于其运算简单、适⽤范围⼴。
我们在这⾥只讨论这种形式,其表达式如下:其中,f(i)为原始的信号,F(u)是DCT变换后的系数,N为原始信号的点数,c(u)可以认为是⼀个补偿系数,可以使DCT变换矩阵为正交矩阵。
三、⼆维DCT变换⼆维DCT变换其实是在⼀维DCT变换的基础上在做了⼀次DCT变换,其公式如下:由公式我们可以看出,上⾯只讨论了⼆维图像数据为⽅阵的情况,在实际应⽤中,如果不是⽅阵的数据⼀般都是补齐之后再做变换的,重构之后可以去掉补齐的部分,得到原始的图像信息,这个尝试⼀下,应该⽐较容易理解。
另外,由于DCT变换⾼度的对称性,在使⽤Matlab进⾏相关的运算时,我们可以使⽤更简单的矩阵处理⽅式:接下来利⽤Matlab对这个过程进⾏仿真处理:1clear;2clc;3 X=round(rand(4)*100) %产⽣随机矩阵4 A=zeros(4);5for i=0:36for j=0:37if i==08 a=sqrt(1/4);9else10 a=sqrt(2/4);11 end12 A(i+1,j+1)=a*cos(pi*(j+0.5)*i/4);13 end14end15 Y=A*X*A' %DCT变换16 YY=dct2(X) %Matlab⾃带的dct变换运⾏结果为:1 X =23 42 66 68 664 92 4 76 175 79 85 74 716 96 93 39 3789 Y =1011 242.7500 48.4317 -9.7500 23.505212 -12.6428 -54.0659 7.4278 22.795013 -6.2500 10.7158 -19.7500 -38.804614 40.6852 -38.7050 -11.4653 -45.9341151617 YY =1819 242.7500 48.4317 -9.7500 23.505220 -12.6428 -54.0659 7.4278 22.795021 -6.2500 10.7158 -19.7500 -38.804622 40.6852 -38.7050 -11.4653 -45.9341由上⾯的结果我们可以看出,我们采⽤的公式的⽅法和Matlab⾃带的dct变化⽅法结果是⼀致的,所以验证了我们⽅法的正确性。
简单描述离散余弦变换dct基本原理

简单描述离散余弦变换dct基本原理
离散余弦变换(Discrete Cosine Transform,DCT)是一种常用的信号处理方法,它将时序信号或图像转换为频域信号或图像,常见于视频压缩、音频压缩、图像压缩等领域。
DCT 可以将一个长度为N 的实数序列转换为另一个长度为N 的实数序列,这个过程类似于傅里叶变换,但是更适用于实数信号的处理。
DCT 的基本原理是将原始信号表示为余弦函数的线性组合,通过将原始信号转换为一组余弦基函数来实现。
离散余弦变换使用的基函数是从正余弦函数中选取出来的一组奇偶性相同的余弦函数,它们的频率依次递增,形成一个正交基。
这组基函数的选择使得信号的变换能够更好地适应实际情况,因为大多数实际信号都是以相对于它们的平均值为中心的,这与余弦函数的性质非常相似。
DCT 变换的过程可以通过矩阵乘法来实现,这个矩阵称为变换矩阵。
由于DCT 变换的基函数是正交的,所以变换矩阵是一个正交矩阵,它的逆矩阵等于其转置矩阵,因此,DCT 变换是可逆的,可以通过对变换后的频域信号进行逆变换,恢复原始信号。
总之,离散余弦变换在时域和频域之间建立了一种转换关系,它通过将原始信号表示为一组余弦基函数的线性组合来实现。
离散余弦变换是一种常用的信号处理方法,在压缩领域、音频领域、图像领域等方面都有广泛的应用。
dct 变换 原理

dct 变换原理DCT变换原理DCT(Discrete Cosine Transform,离散余弦变换)是一种常用的信号处理技术,广泛应用于图像、音频和视频等领域。
它通过将输入信号分解为一系列余弦函数的加权和来表示,同时保留了原始信号的主要特征。
本文将介绍DCT变换的原理及其应用。
一、DCT变换的原理DCT变换的基本思想是将输入的离散信号分解为一系列具有不同频率的余弦函数的加权和。
DCT变换可以将信号从时域转换到频域,通过分析不同频率分量的能量分布,可以提取信号的主要特征。
DCT 变换的公式如下:X(k) = 2/N * Σ[n=0 to N-1] x(n) * cos(π/N * (n + 0.5) * k)其中,x(n)表示输入信号的离散采样值,N表示采样点数,X(k)表示变换后的频域系数,k表示频域的索引。
DCT变换可以分为一维和二维变换。
一维DCT变换用于处理一维信号,如音频;而二维DCT变换用于处理二维信号,如图像。
二、DCT变换的应用DCT变换在图像、音频和视频等领域有广泛的应用。
以下分别介绍其在这些领域的应用。
1. 图像压缩DCT变换在图像压缩中起到了重要作用。
在JPEG图像压缩中,图像先被分成8x8的图像块,然后对每个图像块进行DCT变换,将图像从时域转换到频域。
通过保留主要的频域系数,可以实现对图像的高效压缩。
2. 音频压缩DCT变换在音频压缩中也有广泛应用。
在MP3音频压缩中,音频信号被分成一系列短时窗口,然后对每个窗口的音频信号进行DCT变换。
通过量化和编码DCT系数,可以实现对音频信号的高比特率压缩。
3. 视频压缩DCT变换在视频压缩中也发挥着重要作用。
在H.264视频编码中,视频帧被分成一系列宏块,然后对每个宏块的亮度和色度分量进行DCT变换。
通过压缩和编码DCT系数,可以实现对视频的高效压缩。
除了压缩应用外,DCT变换还可以用于信号去噪、特征提取、模式识别等领域。
例如,在图像去噪中,通过DCT变换将图像从时域转换到频域,然后滤除高频噪声,最后再通过逆DCT变换将图像恢复到时域。
javadct_DCT(离散余弦变换)算法原理和源码

javadct_DCT(离散余弦变换)算法原理和源码离散余弦变换(Discrete Cosine Transform,简称DCT)是一种常用的信号处理技术,广泛应用于图像和音频压缩领域。
DCT将输入的离散信号转换为一组系数,这些系数代表了信号的频域特征。
在压缩领域中,DCT可将信号从时域转换为频域,通过舍弃一些高频系数实现信号的压缩。
DCT算法的原理基于傅里叶变换(Fourier Transform)的思想,将时域信号转换为频域信号。
然而,与傅里叶变换相比,DCT更适合处理实数信号,因为它只使用实数运算,而不需要复数运算。
DCT算法的一般步骤如下:1.将输入的离散信号分为若干个块,每个块包含N个采样点。
2.对每个块进行预处理,例如减去均值。
3.对每个块进行DCT变换。
4.根据需要舍弃一些高频系数。
5.对经过舍弃的系数进行逆DCT变换,恢复原始信号。
下面是一个简单的离散余弦变换的Python实现:```pythonimport numpy as npdef dct_transform(signal):N = len(signal)dct_coef = np.zeros(N)for k in range(N):sum = 0for n in range(N):sum += signal[n] * np.cos((np.pi/N)*(n+0.5)*k)dct_coef[k] = sumreturn dct_coefdef idct_transform(dct_coef):N = len(dct_coef)signal = np.zeros(N)for n in range(N):sum = 0for k in range(N):sum += dct_coef[k] * np.cos((np.pi/N)*(n+0.5)*k)signal[n] = sum / Nreturn signal```以上是一个简单的DCT变换和逆变换的实现,其中`dct_transform`函数接受输入信号并返回DCT系数,`idct_transform`函数接受DCT系数并返回恢复的原始信号。
Chen快速DCT实现

Chen的快速DCT算法一、原始DCT变换原理1、一维DCT变换定义对于离散函数f(j),j=0,1…,N-1,(N=2m,m≥2)一维离散余弦变换(1-D DCT)定义为:F(k)=2c(k)N ∑f(j)cos[(2j+1)kπ2N]N−1j=0;K=0,1,…,N-1其逆变换公式(1-D IDCT)为:f(j)=∑F(k)cos[(2j+1)kπ2N ]N−1k=0; (1)j=0,1,…,N-1其中:c(k)=√2 当k=01 ,当k≠0通过直接计算,当N=8时,利用公式(4-1)进行DCT变化需要64次乘法和56次加法运算。
2、二维DCT变换定义一维离散余弦变换的定义可推广到二维的情形,对于离散函数f(i,j),i=0,1,…,N-1;j=0,1,…,M-1, 二维离散余弦变换(2-D DCT)定义为:F(u,v)=√MN∑f(i,j)M−1j=0cos[(2i+1)uπ2N]N−1i=0cos[(2j+1)vπ2N]; (2)u=0,1,…N-1;v=0,1,…,M-1,其中:c(u),c(v)=√2 当u,v=01 ,其他取N=M=8时,利用公式(4-3)进行直接计算需要4096次乘法和3584次加法,通常利用DCT的可分解的性质,先进行8行一维DCT变换,在进行8列一维DCT变换,可将计算量减少为直接计算的1/4,需要1024次乘法和896次加法。
二、Chen的快速DCT原理离散余弦变换(DCT for Discrete Cosine Transform)是与傅立叶变换相关的一种变换,它类似于离散傅立叶变换(DFT for Discrete Fourier Transform),但是只使用实数。
离散余弦变换相当于一个长度大概是它两倍的离散傅立叶变换,这个离散傅立叶变换是对一个实偶函数进行的(因为一个实偶函数的傅立叶变换仍然是一个实偶函数),在有些变形里面需要将输入或者输出的位置移动半个单位(DCT有8种标准类型,其中4种是常见的)。
离散余弦变换_DCT_.

ELECTRONICS QUALITY
·2007第12期·
小知识
离散余弦变换(DCT)
离散余弦变换(D C T )是N. A h m e d 等人在1974年提出的正交变换方法。
它常被认为是对语音和图像信号进行变换的最佳方法。
由于近年来数字信号处理芯片(D S P )的发展,加上专用集成电路设计上的优势,这就牢固地确立离散余弦变换(D C T )在目前图像编码中的重要地位,成为H. 261、J P E G 、M P E G 等国际上公用的编码标准的重要环节。
在视频压缩中,最常用的变换方法是D C T , D C T 被认为是性能接近K -L 变换的准最佳变换,变换编码的主要特点有:
(1)在变换域里视频图像要比空间域里简单。
(2)视频图像的相关性明显下降,信号的能量主要集中在少数几个变换系数上,采用量化和熵编码可有效地压缩其数据。
(3)具有较强的抗干扰能力,传输过程中的误码对图像质量的影响远小于预测编码。
通常, 对高质量的图像,D M C P 要求信道误码率,而变换编码仅要求信道误码率。
HEVC变换部分总结

HEVC变换部分总结1、介绍DCT1.1、DCT矩阵的推导4*4 DCT变换公式:,将上式分解进行先列变换:再行变换:将矩阵A中的系数乘以(根据公式:,,此时m=2),再根据变换矩阵设计原则取近似数,就得到变换系数矩阵。
尺寸为8*8、16*16、32*32的变换系数矩阵类似。
1.2 、DCT矩阵的性质一维DCT变换的系数公式:(1)基向量为标准正交基,变换矩阵为正交矩阵。
即:for,for(2)DCT矩阵系数之间存在三角函数关系。
(3)尺寸为的DCT矩阵中包含了尺寸为的DCT矩阵。
(4)尺寸为的DCT矩阵可用个元素表示。
比如:4*4可用64、83、36表示,8*8可用64、89、83、75、50、36、18表示。
除了64*64系数矩阵,其余尺寸都可用第一列元素表示(第一列元素中64出现两次)。
(5)偶数行是中心对称的,奇数行是中心反对称的。
1.3、DCT矩阵的设计设计固定的DCT矩阵是为了防止不同的生产商制作的编码器和译码器不同而产生误差。
因为1.2小节提到的第4,5,6条DCT矩阵性质在实现算法的过程中可以减少大量计算量,所以必须严格保持,其他性质尽可能达到。
同时,也要考虑到运算中矩阵系数的比特深度带来的运算消耗。
总结DCT矩阵设计的原则:(1)尽可能的让基向量为标准正交基。
(2)DCT矩阵保持对称性和反对称性。
(3)小尺寸的DCT矩阵嵌套在大尺寸的DCT矩阵中。
(4)8bit表示变换矩阵系数。
(5)变换后移位前不超过32bit,移位后不超过16bit。
(实验表明,如果用18bit或者20bit表示只会减少0.5%的BD-rate)(6)尺寸为的DCT矩阵可用个元素表示。
1.4、DCT的作用DCT 将原始图像信息块转换成代表不同频率分量的系数集,这有两个优点:其一,信号常将其能量的大部分集中于频率域的一个小范围内,这样一来,描述不重要的分量只需要很少的比特数;其二,频率域分解映射了人类视觉系统的处理过程,并允许后继的量化过程满足其灵敏度的要求。
dct 变换 原理

dct 变换原理DCT变换原理DCT(Discrete Cosine Transform,离散余弦变换)是一种将时域信号转换为频域信号的数学变换方法。
它在数字信号处理领域被广泛应用,尤其在图像和音频压缩中起到了重要的作用。
本文将介绍DCT变换的原理及其应用。
1. DCT变换原理DCT变换是一种将一个N维实数序列转换为N维实数序列的线性变换。
它将时域上的信号分解为一组基函数的系数,这些基函数是余弦函数的线性组合。
DCT变换的基本思想是利用信号的局部平稳性,将信号分解为不同频率的分量,从而实现信号的压缩和重构。
2. DCT变换的公式DCT变换的公式如下所示:X(k) = ∑[n=0 to N-1] x(n) * cos[(π/N)*(n+0.5)*k]其中,x(n)是原始信号的时域序列,X(k)是DCT变换后的频域序列,N是信号的长度,k是频域的索引。
3. DCT变换的性质DCT变换具有以下几个重要的性质:- 对称性:DCT变换是对称的,即X(k) = X(N-k),其中k为频域的索引。
- 能量集中性:原始信号的大部分能量集中在低频分量上,而高频分量上的能量较小。
- 无损压缩:DCT变换可以实现无损压缩,即将信号从时域转换到频域后再转换回时域时不会有信息损失。
4. DCT变换的应用DCT变换在图像和音频压缩中得到了广泛应用。
以图像压缩为例,DCT变换可以将图像分解为一组亮度和颜色分量的系数。
由于图像的亮度分量在低频区域具有较高的能量集中度,而颜色分量在高频区域具有较高的能量集中度,因此可以通过去除高频系数来实现图像的压缩。
同样,DCT变换也可以应用于音频压缩中,将音频信号分解为一组频率分量的系数。
5. DCT变换的优点DCT变换具有以下几个优点:- 能量集中性:DCT变换将信号的大部分能量集中在低频分量上,可以通过丢弃高频分量来实现信号的压缩。
- 低复杂度:DCT变换的计算复杂度相对较低,可以快速实现。
DCT变换的原理及算法
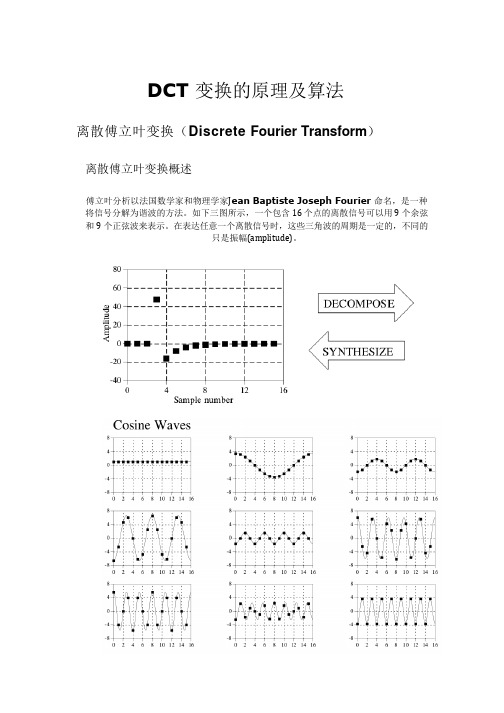
DCT 变换的原理及算法离散傅立叶变换(Discrete Fourier Transform)离散傅立叶变换概述傅立叶分析以法国数学家和物理学家J ean Baptiste Joseph Fourier 命名,是一种将信号分解为谐波的方法。
如下三图所示,一个包含16 个点的离散信号可以用9个余弦和9个正弦波来表示。
在表达任意一个离散信号时,这些三角波的周期是一定的,不同的只是振幅(amplitude)。
图1-1 离散信号与对应的三角波信号可以是连续的或离散的,同时也可以是周期性的或非周期性的,根据信号的这两个特点,傅立叶变换可以分为四种类型:傅立叶变换(F o u r i e r T r a n sfo r m),处理非周期性的连续信号(A p e r i o d i c-C o n t i nu o u s)。
傅立叶序列(Fourier Series) ,处理周期性的连续信号(P eriodic-C o n t i nu o u s)。
离散时间域傅立叶变换(Di sc r e t e T i m e F o u r i e r T r a n sfo r m),处理非周期性的离散信号(A p e r i o d i c-Di sc r e t e)。
离散傅立叶变换(Discrete Fourier Transform) ,处理周期性的离散信号(Periodic-Discrete)。
计算机只能处理离散的和有限长度的信号,因此只有离散傅立叶变换(D F T)能在计算机中以算法实现。
图1-2 四种不同类型的傅立叶分析实数离散傅立叶变换(R eal DFT)的格式和表示如图1-3所示,离散傅立叶变换将包含N个点的输入波转为两个包含N/2+1个点的输出波。
输入波常被称作时间域,因为信号的波形基本上都是随时间变化,输出波常被称作频率域。
时间域与频率域中存储的信息是一样的,只是表现方式不一样。
将时间域转为频率域的过程叫离散傅立叶变换(D F T),将频率域转换为时间域的过程叫反变换(ID F T)。
2_2---DCT变换

DCT离散余弦变换求N个数的离散余弦变换,就是把这N个数延拓成2N的序列,再向右平移1 /2个单位,如果下图所示,这2N个元素的序列是基于原点对称的。
求这个元素为2N的序列的DFT变换,就是所求的元素为N的序列的DCT变换。
因为偶对称实数序列的DFT变换是实偶的函数,DCT变换后的表示比较简单。
DCT的优点:1 它变换的形式简单,相比于DFT会减少一半的计算;2 它具有能量集中性,图片经过DCT变换后,有用信息主要集中于低频部分,基于这个原理,可以对图像进行压缩。
一维离散余弦变换的推导推导N点长实序列的DCT,首先来定义一个新的长度为2N的序列:可看作是将周期为N的序列x[m]做一个周期延拓成一个周期为2N的序列。
如图1中第一张图。
再来看图1中第一张图是关于x = -1/2对称的,要让他关于x = 0对称需要将其向右平移1/2个单位,得到x’[m] = x’[m – 1/2]就是关于x = 0对称的周期序列了(如图1中第二张图)。
然后求这个2N序列的DFT:就是DCT-2型离散余弦变换.从上面的过程也可以直接看出,离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换.变换后的x[n]是以2N为周期,偶对称的序列: X[N+n] = X[N+n-2N] = X[n-N] = x[N-n]定义变换矩阵C[n,m]:求一下矩阵的DCT离散余弦就换方法一:直接对这个矩阵进行DCT变换,如下程序程序如下所示:pic=imread('e:\test.jpg');pic=rgb2gray(pic);imshow(pic);a=dct2(pic);figure(2);imshow(log(a),[]);colormap(jet);colorbar;方法二:要求矩阵A的DCT变换,其中A是一个N*N的矩阵。
先利用dctmtx(x);这个函数求出DCT变换矩阵B,则DCT(A)=B*A*B’;这是求DCT变换矩阵的第二种方法。
离散余弦变换;dct

离散余弦变换;dct离散余弦变换(Discrete Cosine Transform,DCT)是一种广泛应用于数字信号处理领域的数学变换,可以将一个长度为N的信号(比如音频、图像等)转换为一组N个离散余弦函数的系数。
DCT的应用很广泛,比如JPEG、H.264等压缩算法都使用了DCT,具有较好的压缩性能和鲁棒性。
下面我们就来看一看DCT的一些基本概念和原理。
一、离散余弦变换的定义离散余弦变换的定义可以用下面的公式表示:$ X_k = \sum_{n=0}^{N-1} x_n \cos \left[ \frac{\pi}{N} \left( n +\frac{1}{2} \right) k \right] $其中,x(n)是原始的离散信号,X(k)是它的DCT系数,N是信号的长度,k为DCT系数的下标,它的范围是0~N-1。
二、离散余弦变换的性质DCT具有诸多良好的性质,包括:1. 对称性:DCT在奇偶性、中心对称等方面具有较强的对称性,这有利于算法的实现和计算速度的提高。
2. 能量集中性:DCT可以将信号的能量分为前面的几个系数,这些系数包含了大部分信号的信息,后面的系数则可以舍弃,从而达到压缩和降噪的目的。
3. 可逆性:DCT是一种可逆变换,可以通过逆变换将DCT系数还原为原始信号。
三、离散余弦变换的种类DCT的种类比较多,常用的有DCT-I、DCT-II、DCT-III和DCT-IV等,它们的定义和公式略有不同。
其中,DCT-II是应用最广泛的一种,在JPEG和其他压缩算法中大量应用。
四、离散余弦变换的应用DCT的应用非常广泛,比如:1. 图像和视频压缩:JPEG、H.264等压缩算法都使用了DCT,能够将信号压缩到很小的数据量。
2. 语音信号处理:DCT可以将语音信号转换为频域表示,对于语音的噪声消除、识别和压缩等方面具有重要应用。
3. 数字水印:DCT可以将数字水印嵌入到信号的某些DCT系数中,从而实现数字版权保护、信息隐藏等应用。
傅立叶变换(FFT)离散余弦变换(DCT)

0
0
N
在频域中,原点平移到(u0,v0)时,其对应的f(x,y) 要乘上一个正的指数项 ej2π(u0xv0y)
fx ,y e x j2p u 0x v 0y F u u,v v
N
0
0
也就是说,当空域中f(x,y)产生移动时,在频域中只发 生相移,而傅立叶变换的幅值不变
|F (u ,v )|
22
即,如果将图像频谱的原点从起点(0,0)移到图像中 心点(N/2,N/2),只要f(x,y)乘上(-1)(x+y)因子进行傅 立叶变换即可
平移
(3)周期性和共轭对程性
周期性可表示为
Fu,vFuN,vFu,vNFum,vN nN
f(x,y)f(xm,N yn)N m ,n0,1,2,
共轭对称性可表示为
原点对
平移x
折
对于图像二维函数的卷积,则
nm
z(i,j) f(k,l)g(ik,jl) k1l1
相关
2个函数的相关定义为
N 1
z(x)f(x)g(x) f*(i)g(xi)di i0
其中f*(i)为f(i)的复共轭
一维连续傅立叶变换
定义及基本概念
设f(x)为x的函数,如果f(x)满足下面的狄里赫莱条件:
例:求如图所示的函数的傅立叶谱 f(x,y) A
y f(x,y)函数 x
f(x,y) 0 A
0xX ,0yY xX ,x0 ,yY ,y0
其傅立叶变换为:
XY
F(u,v) f (x, y)ej2π(uxvy)dxdy Aej2π(uxvy)dxdy
00
X
A
0
e
Y
j 2π u xdx
0
DCT变换原理解析

DCT变换原理解析DCT(离散余弦变换)是一种常用的信号处理技术,广泛应用在图像压缩、声音处理以及数据压缩等领域。
DCT的主要原理是将时间域上的离散信号转换到频域上,通过对频域上的分量进行压缩和重构,实现对信号的高效编码和解码。
DCT的原理基于离散余弦函数的性质,它是一组正交基函数。
正交函数具有较好的表示性能,可以将信号按不同频率的分量进行分解。
DCT将信号表示为一系列余弦函数的加权和,具有较好的能量集中性,能够将信号主要能量集中在较少的系数上,实现信号的压缩。
DCT的计算过程可以分为以下几个步骤:1.分块:将输入信号分成多个重叠或不重叠的块,每个块包含一定数量的采样点。
分块可以提高计算效率,并能够处理较大的信号。
2.窗函数:对每个块进行加窗处理,常用的窗函数有矩形窗、汉宁窗等。
窗函数的作用是减小边界效应,并将信号限定在特定的时间范围内。
3.应用DCT变换:对每个分块的信号应用DCT变换,得到对应的频域系数。
DCT变换将时域的离散信号转换为频域上的离散余弦系数。
4.量化:对每个分块的频域系数进行量化操作,将其映射到离散的数值上。
量化可以减少数据量,通过减少系数的精度来实现信号的压缩。
5.压缩:对量化后的系数进行编码压缩,常用的压缩算法包括哈夫曼编码、熵编码等。
压缩算法根据系数的统计特性,对系数进行编码,使得较常出现的系数用较短的编码表示,较不常出现的系数用较长的编码表示。
6.解码和重构:对压缩后的数据进行解码和重构,恢复原始信号。
解码过程是编码的逆操作,通过解码算法将压缩数据转换为频域系数。
然后将频域系数应用DCT的逆变换,得到恢复后的时域信号。
总结来说,DCT变换的原理是将时域上的离散信号转换为频域上的离散余弦系数,通过对系数进行量化和编码压缩,实现对信号的高效表示和压缩。
DCT变换具有较好的能量集中性,能够将信号主要能量集中在少量的系数上,实现信号的稀疏表示,从而减少数据量,提高信号的传输和存储效率。
dct工作原理

dct工作原理
DCT(离散余弦变换)是一种广泛应用于图像与音频压缩领域的数学变换方法。
其工作原理基于信号的时域与频域之间的转换。
DCT的工作原理分为以下几个步骤:
1. 分块:将原始信号分成若干个小块,通常为8x8像素的图像块或者音频信号的样本块。
这样的分块方式可以更好地集中信号的频域特征。
2. 对每个块进行预处理:对每个块进行零均值处理,使块中心移到原点,减小直流分量的影响。
3. DCT变换:对每个块应用离散余弦变换公式,将每个块从时域表示转换为频域表示。
离散余弦变换可以将信号表示为一组频率系数的加权和,得到的频谱表示了信号中不同频率成分的分布情况。
4. 频率量化:对DCT变换得到的频谱系数进行量化,将其量化为离散的数值表示。
这一步骤是压缩的关键,可以减小数据量并提高压缩比,但也会引入一定的信息损失。
通常采用变化的量化步长,将更多的比特用于较重要的频谱系数。
5. 反量化:将量化后的频谱系数恢复为原始的频谱系数,以便进行后续的反变换。
6. 反变换:对反量化后的频谱系数应用逆离散余弦变换公式,将频域表示转换回时域表示。
这一步骤可以将信号恢复为与原始信号相似的形态。
7. 重组:对各个块进行重组,将分块压缩得到的数据按一定的规则重新排列,以便于储存或传输。
通过以上的步骤,DCT能够将信号从时域压缩为频域,从而减小信号的冗余信息,实现信号的高效压缩和传输。
它被广泛应用于图像、音频和视频压缩标准中,如JPEG、MPEG等。
dct算法

1. DCT算法:DCT变换的全称是离散余弦变换(Discrete Cosine Transform),离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换,这个离散傅里叶变换是对一个实偶函数进行的。
通过数字信号处理的学习我们知道实函数的傅立叶变换获得的频谱大多是复数,而偶函数的傅立叶变换结果是实函数。
以此为基础,使信号函数成为偶函数,去掉频谱函数的虚部,是余弦变换的特点之一。
它可以将将一组光强数据转换成频率数据,以便得知强度变化的情形。
若对高频的数据做些修饰,再转回原来形式的数据时,显然与原始数据有些差异,但是人类的眼睛却是不容易辨认出来。
压缩时,将原始图像数据分成8*8数据单元矩阵,例如亮度值的第一个矩阵内。
2.DCT产生的工程背景:视频信号的频谱线在0-6MHz范围内,而且1幅视频图像内包含的大多数为低频频谱线,只在占图像区域比例很低的图像边缘的视频信号中才含有高频的谱线。
因此,在视频信号数字处理时,可根据频谱因素分配比特数:对包含信息量大的低频谱区域分配较多的比特数,对包含信息量低的高频谱区域分配较少的比特数,而图像质量并没有可察觉的损伤,达到码率压缩的目的。
然而,这一切要在低熵(Entropy)值的情况下,才能达到有效的编码。
能否对一串数据进行有效的编码,取决于每个数据出现的概率。
每个数据出现的概率差别大,就表明熵值低,可以对该串数据进行高效编码。
反之,出现的概率差别小,熵值高,则不能进行高效编码。
视频信号的数字化是在规定的取样频率下由A/D转换器对视频电平转换而来的,每个像素的视频信号幅度随着每层的时间而周期性地变化。
每个像素的平均信息量的总和为总平均信息量,即熵值。
由于每个视频电平发生几乎具有相等的概率,所以视频信号的熵值很高。
熵值是一个定义码率压缩率的参数,视频图像的压缩率依赖于视频信号的熵值,在多数情况下视频信号为高熵值,要进行高效编码,就要将高熵值变为低熵值。
怎样变成低熵值呢?这就需要分析视频频谱的特点。
数字信号处理常用公式(不惧怕繁琐的推导)

数字信号处理常⽤公式(不惧怕繁琐的推导)数学信号处理基本公式1、傅⾥叶变换定义连续正变换:X j ω = x t e ?j ωt dt ∞∞ 连续反变换:x t =12π X j ω e j ωt d ω∞∞ 离散正变换:21()(),0,1,,1N jnk NNN n X k x n WW ek N π--====-∑离散反变换:2101()(),0,1,,1N j nkNNN n x n X k W W en N N π---====-∑2、傅⾥叶变换性质线性:[])]([)]([))()((t g F t f F t g t f F βαβα+=+ 位移:)]([)]([00t f F et t f F t j ω-=-; )]([)]([1010ωωωωF F e F F t j --=-.尺度:设)]([)(t f f F =ω, )(||1)]([aF a at f F ω=. 微分:)]([)]('[t f F j t f F ω=,要求0)(lim =∞→t f t)]([)()]([)(t f F j t f F n n ω=,要求()lim ()0(1,2,1)k t f t k n →+∞==-积分:)]([1])([t f F j dt t f F tω=∞-,要求lim ()0t t f t dt -∞→+∞=?帕塞⽡尔等式:()221()()2f t dt F d ωωπ+∞+∞-∞-∞=,)]([)(t f f F =ω频率位移:若()ωj e X n x ?)(,则()()00)(ωωω-?j nj e X n x e时间共轭:若()ωj e X n x ?)(,则(),)(**ωj e X n x -? 频率共轭:若()ωj eX n x ?)(,则()ωj e X n x **)(?-序列卷积:若)()()(n y n x n w *=,则)()()(z Y z X z W = 序列乘积:若)()()(n y n x n w =,则++---< =y x y x c R R z R R dv v v z Y v X j z W 1)(21)(π输⼊)cos()(?ω+=n A n x ,则输出响应为:()()[])()(2)(?ωω?ωω+--++=n j j n j j e e H e e H An y输⼊12()()()x n x n x n =+,则输出响应为:()()()()()2j j n j j n Ay n H e e H e e ωω?ωω?+--+??=+?3、傅⽴叶级数满⾜狄利克雷条件的周期函数可由三⾓函数的线性组合表⽰:()f t 的周期为1T ,112T πω=其中:()00011t T t a f t dt T +=?;()()010112cos t T n t a f t n t dt T ω+=?;()()01 112sin t T n t b f t n t dt T ω+=?指数形式的付⾥叶级数表⽰:0111()[()sin()](5)n n n f t a a cos n n b n n ωω∞==++-----∑由欧拉公式:1111()()2jn t jn t cos n n e e ωωω-=+;1111sin()()2jn t jn t n n e e j ωωω-=+ 4、随机信号定义4.1均值、⽅差离散均值:{}x kk kE X xp µ==∑ 连续均值:{}()x E X xp x dx µ∞-∞==离散⽅差:222{||}||X X k X k k E X x p σµµ=-=-∑ 连续⽅差:222{||}||()X X X E X x p x dx σµµ∞-∞=-=4.2相关函数的定义互相关: ()()()xy n r m x n y n m ∞=-∞=+∑ ⾃相关: ()()()xxn rm x n x n m ∞=-∞=+∑有限点⾃相关函数估计值为:11()()()N N N n r m x n x n m N -∧==+∑平稳随机过程的互相关函数: ()[()()]xy r m E x n y n m *=+ ⾃相关: ()[()()]xx r m E x n x n m =+()()()()()()()()()011112121110111cos sin cos 2sin 2cos sin .................cos sin ..n n n n n f t a a t b t a t b t a n t b n t a a n t b n t ωωωωωωωω∞==++++++++=++∑(1)4.3功率谱⾃功率谱:()()j j mX xm P e r m eωω∞-=-∞=∑ 互功率谱:()()j j m XY xym P e rm e ωω∞-=-∞=注意:功率信号的⾃相关函数与其功率谱是⼀对傅⾥叶变换:P x e j ω = r x e ?j ωm ∞m=?∞5、三⾓函数变换sin(A+B) = sinAcosB+cosAsinB ;sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB ;cos(A-B) = cosAcosB+sinAsinBtanA tanB tan(A+B) =1-tanAtanB +;tanA tanBtan(A-B) =1tanAtanB -+cotAcotB-1cot(A+B) =cotB cotA +;cotAcotB 1cot(A-B) =cotB cotA +-倍⾓公式22tanA tan2A =1tan A-;sin2A=2sinA cosA ;Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 三倍⾓公式sin3A = 3sinA-4(sinA)3;cos3A = 4(cosA)3-3cosAa a tan3a = tana tan(+a)tan(-a)33和差化积sina+sinb=2sincos 22a b a b +-;sina-sinb=2cos sin 22a b a b+- cosa+cosb = 2cos cos 22a b a b +-;cosa-cosb = -2sin sin 22a b a b+-sin()tana+tanb=cos cos a b a b+积化和差1sinasinb =[cos(a+b)-cos(a-b)]2-, 1cosacosb =[cos(a+b)+cos(a-b)]21 sinacosb =[sin(a+b)+sin(a-b)]2,1cosasinb =[sin(a+b)-sin(a-b)]2诱导公式:sin(-a) = -sina;cos(-a) = cosa;sin(-a) = cos a;cos(-a) = sina 22ππsin(+a) = cos a;cos(+a) = -sina 22ππsin(-a) = sina,cos(-a) = -cosa ππsin(+a) = -sina;cos(+a) = -cosa ππ22a a a a1+sin(a) =(sin +cos );1-sina=(sin -cos )2222函数展开成幂级数:+++''+'+===-+=+-++-''+-=∞→++nn n n n n n n n x n f x f x f f x f x R x f x x n f R x x n x f x x x f x x x f x f !)0(!2)0()0()0()(00lim )(,)()!1()()(!)()(!2)())(()()(2010)1(00)(20000时即为麦克劳林公式:充要条件是:可以展开成泰勒级数的余项:函数展开成泰勒级数:ξ⼀些函数展开成幂级数:)()!12()1(!5!3sin )11(!)1()1(!2)1(1)1(121532+∞<<-∞+--+-+-=<<-++--++-++=+--x n xx x x x x x n n m m m x m m mx x n n nm 欧拉公式:-=+=+=--2sin 2cos sin cos ixix ixix ixe e x e e x x i x e 或。
