初中数学将军饮马问题的六种常见题型汇总

将军饮马问题的11个模型及例题

将军饮马问题的11个模型及例题将军饮马问题是一个经典的逻辑问题，涉及到将军如何用有限数量的马和酒到达目的地。

本文将介绍将军饮马问题的11个模型及相应的例题。

1. 直线模型将军与目的地之间没有障碍物，可以直线前进。

此时，将军只需将马拉到目的地即可。

例题1：将军与目的地之间距离为10公里，马的速度为每小时5公里，将军能否在2小时内到达目的地？2. 单个障碍物模型在将军与目的地之间存在一个障碍物，将军可以绕过该障碍物。

例题2：将军与目的地之间距离为15公里，马的速度为每小时4公里，障碍物位于距离将军起点5公里处，将军能否在3小时内到达目的地？3. 多个障碍物模型在将军与目的地之间存在多个障碍物，将军需要逐一绕过这些障碍物。

例题3：将军与目的地之间距离为20公里，马的速度为每小时6公里，障碍物位于距离将军起点分别为5公里、10公里和15公里的位置，将军能否在4小时内到达目的地？4. 跳跃模型将军可以让马跳过障碍物，从而直接到达目的地。

例题4：将军与目的地之间距离为12公里，马的速度为每小时8公里，将军在距离起点6公里处设置一个障碍物，将军能否在2小时内到达目的地？5. 限时模型将军需要在规定的时间内到达目的地。

例题5：将军与目的地之间距离为30公里，马的速度为每小时10公里，将军需要在3小时内到达目的地，是否可能？6. 守备模型目标地点有守备军，将军需要巧妙规避守备军。

例题6：将军与目的地之间距离为25公里，马的速度为每小时7公里，目的地有一支守备军位于距离目标地点10公里处，将军能否在4小时内到达目的地？7. 短平快模型将军不借助马匹，直接徒步走到目的地。

例题7：将军与目的地之间距离为8公里，将军的步行速度为每小时2公里，将军能否在4小时内到达目的地？8. 时间窗模型将军只能在规定时间范围内到达目的地。

例题8：将军与目的地之间距离为18公里，马的速度为每小时6公里，将军需要在3小时到4小时之间到达目的地，是否可能？9. 兵变模型将军需要利用敌军马匹达到目的地。

初中数学之将军饮马的6种模型(培优)

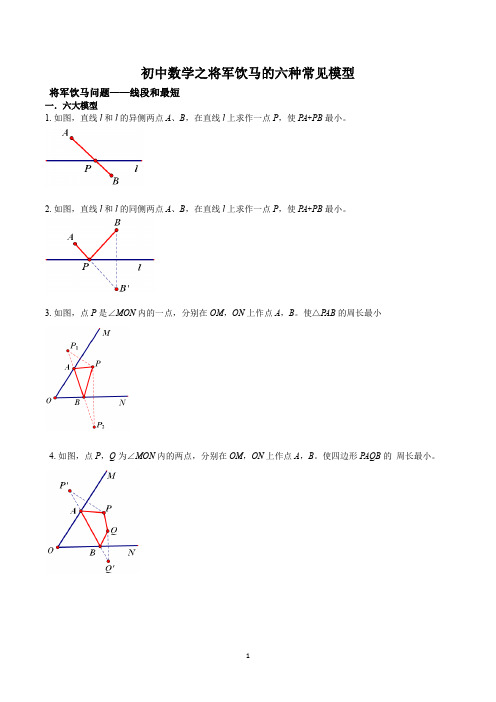
初中数学之将军饮马的六种常见模型将军饮马问题——线段和最短一．六大模型1.如图，直线l和l的异侧两点A、B，在直线l上求作一点P，使P A+PB最小。

2.如图，直线l和l的同侧两点A、B，在直线l上求作一点P，使P A+PB最小。

3.如图，点P是∠MON内的一点，分别在OM，ON上作点A，B。

使△P AB的周长最小4.如图，点P，Q为∠MON内的两点，分别在OM，ON上作点A，B。

使四边形P AQB的周长最小。

5.如图，点A是∠MON外的一点，在射线ON上作点P，使P A与点P到射线OM的距离之和最小6. .如图，点A是∠MON内的一点，在射线ON上作点P，使P A与点P到射线OM的距离之和最小二、常见题目类型一、三角形1．如图，在等边△ABC中，AB= 6，AD⊥BC，E是AC上的一点，M是AD上的一点，AE=2，求EM+EC 的最小值解：∵点C关于直线AD的对称点是点B，∴连接BE，交AD于点M，则ME+MD最小，过点B作BH⊥AC于点H，则EH = AH–AE = 3–2 = 1，BH=在直角△BHE中，BE2．如图，在锐角△ABC中，AB =BAC＝45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是____．解：作点B关于AD的对称点B'，过点B'作B'E⊥AB于点E，交AD于点F，则线段B'E长就是BM＋ＭＮ的最小值在等腰Rt△AEB'中，根据勾股定理得到，B'E = 43．如图，△ABC中，AB=2，∠BAC=30°，若在AC、AB上各取一点M、N，使BM+MN的值最小，则这个最小值解：作AB关于AC的对称线段AB'，过点B'作B'N⊥AB，垂足为N，交AC于点M，则B'N= MB'+MN = MB+MN. B'N的长就是MB+MN的最小值，则∠B'AN = 2∠BAC= 60°，AB' = AB = 2，∠ANB'= 90°，∠B' = 30°。

将军饮马五大模型七类题型(解析版)-初中数学

将军饮马五大模型七类题型(模型梳理与题型分类讲解)第一部分【知识点归纳】【理论依据】路径最短、线段和最小、线段差最大、周长最小等一系列最值问题。

【方法原理】1.两点之间，线段最短；2.三角形两边之和大于第三边，两边之差小于第三边；3.中垂线上的点到线段两端点的距离相等；4.垂线段最短.【基本模型】【模型一：两定交点型】如图1，直线l和l的异侧两点A.B，在直线l上求作一点P，使P A+PB最小；图1【模型二：两定一动型】如图2，直线l和l的同侧两点A.B，在直线l上求作一点P，使P A+PB最小(同侧转化为异侧)；图2【模型三：一定两动型】如图3，点P是∠MON内的一点，分别在OM，ON上作点A，B。

使△P AB 的周长最小。

图3【模型四：两定两动型】如图4，点P，Q为∠MON内的两点，分别在OM，ON上作点A，B。

使四边形P AQB的周长最小。

图4【模型五：一定两动(垂线段最短)型】如图5，点A是∠MON外的一点，在射线ON上作点P，使P A 与点P到射线OM的距离之和最小。

图5【模型六：一定两动，找(作)对称点转化型】如图6，点A是∠MON内的一点，在射线ON上作点P，使P A与点P到射线OM的距离之和最小。

图6【题型目录】【题型1】两定一动型.......................................................3;【题型2】一定两动(两点之间线段最短)型...................................6;【题型3】一定两动(垂线段最短)型.........................................9；【题型4】两定两动型.......................................................12;【题型5】一定两动(等线段)转化型.........................................14;【题型6】直通中考.........................................................18;【题型7】拓展延伸.........................................................21;第二部分【题型展示与方法点拨】【题型1】两定一动型；1.(23-24八年级上·河北廊坊·期中)如图，在△ABC中，∠BAC=90°，AB=12，AC=16，BC=20，将△ABC沿射线BM折叠，使点A与BC边上的点D重合．(1)线段CD的长是；(2)若点E是射线BM上一动点，则△CDE周长的最小值是．【答案】824【分析】本题主要考查了的折叠的性质、两点之间线段最短，熟练掌握折叠的性质是解此题的关键．(1)由折叠的性质可得BD=AB=12，再由CD=BC-BD进行计算即可得到答案；(2)设BM与AC的交点为点F，连接AE，由折叠的性质可得：DF=AF，DE=AE，∠BDF=∠BAF，再根据两点之间线段最短可得当点E与点F重合时，AE+CE取最小值，最小值为AC，由此即可得到答案．解：(1)由折叠的性质可得：BD=AB=12，∴CD=BC-BD=20-12=8，故答案为：8；(2)如图，设BM与AC的交点为点F，连接AE，由折叠的性质可得：DF=AF，DE=AE，∠BDF=∠BAF，由(1)得：CD=8，∴△CDE的周长=CD+DE+CE=8+AE+CE，要是△CDE的周长最小，只需AE+CE最小，由两点之间线段最短可知，当点E与点F重合时，AE+CE取最小值，最小值为AC，∴△CDE的周长=8+AC=8+16=24，故答案为：24．2.(22-23八年级上·广西南宁·期末)如图，点E在等边△ABC的边BC上，BE=4，射线CD⊥BC，垂足为点C，点P是射线CD上一动点，点F是线段AB上一动点，当EP+FP的值最小时，BF=5，则AB 的长为．【答案】7【分析】本题考查最短路径问题、等边三角形的性质、含30度角的直角三角形的性质，熟练掌握利用轴对称性质求最短距离的方法是解答的关键．作点E 关于射线CD 的对称点E ，过E 作E F ⊥AB 于F ，交射线CD 于P ，连接PE ，此时EP +FP 的值最小，利用等边三角形的性质和三角形的内角和定理求得∠E =90°-∠B =30°，然后利用含30度角的直角三角形的性质求得BE =2BF =10，进而求得CE =3即可求解．解：作点E 关于射线CD 的对称点E ，过E 作E F ⊥AB 于F ，交射线CD 于P ，连接PE ，如图，则E P =EP ，∴EP +FP =E P +FP =E F ，此时EP +FP 的值最小，则BF =5，∵△ABC 是等边三角形，∴∠B =60°，AB =BC ，在Rt △BFE 中，∠E =90°-∠B =30°，∴BE =2BF =10，∵BE =4，CE =CE ，∴2CE +4=10，∴CE =3，∴AB =BC =3+4=7，故答案为：7．3.(23-24八年级下·河南郑州·阶段练习)如图，在△ABC 中，AB =AC ．在AB 、AC 上分别截取AP 、AQ ，使AP =AQ ．再分别以点P ，Q 为圆心，以大于12PQ 的长为半径作弧，两弧在∠BAC 内交于点R ，作射线AR ，交BC 于点D ．已知BC =5，AD =6．若点M 、N 分别是线段AD 和线段AB 上的动点，则BM +MN 的最小值为．【答案】6013【分析】本题考查作图-复杂作图，角平分线的定义，等腰三角形的性质等知识，解题关键是读懂图形信息，灵活运用所学知识解决问题，属于中考常考题型．过点B 作BH ⊥AC 于点H ，交AD 于点M ，根据等腰三角形的性质和勾股定理求出AC ，然后根据S ΔABC =12⋅BC ⋅AD =12⋅AC ⋅BH ，可得BH =6013．作点H 关于解：如图，过点B 作BH ⊥AC 于点H ，交AD 于点M ，由作图可知，AD 平分∠BAC ，∵AB =AC ，∴AD ⊥BC ，∴BD =CD =12BC =52，∵AD =6．∴AC =AD 2+DC 2=62+52 2=132，∵S ΔABC =12⋅BC ⋅AD =12⋅AC ⋅BH ，∴5×6=132BH ，∴BH =6013．∵AB =AC ，AD ⊥BC ，作点H 关于AD 的对称点交AB 于点N ，连接M N ，当M 与M 重合时，此时BM +MN 最小，∴M H =M N ，∴BH =BM +M H =BM +M N ，则BM +MN 的最小值为6013．故答案为：6013【题型2】一定两动(两点之间线段最短)型；4.(23-24七年级下·陕西西安·期末)如图，在锐角△ABC 中，∠ABC =30°，AC =4，△ABC 的面积为5，P 为△ABC 内部一点，分别作点P 关于AB ，BC ，AC 的对称点P 1，P 2，P 3，连接P 1P 2，PP 3，则2P 1P 2+PP 3的最小值为．【答案】5【分析】首先由△ABC 的面积为5，12AC ⋅BM =5，求出BM =52，然后由∠ABC =30°和对称构造正三角形，将P 1P 2转化成BP ，将2P 1P 2+PP 3提取系数2，最终转化成垂线段最短．解：设PP3与AC 交于点Q ，则PQ =12PP 3，连接BP 、BQ 、BP 1、BP 2，作BM ⊥AC ，垂足为M ，AC =4，△ABC 的面积为5，∴12AC ⋅BM =5，即12×4BM =5∴BM =5，根据对称性得BP=BP1=BP2，∠ABP=∠ABP1，∠CBP=∠CBP2，∴∠P1BP2=2∠ABC=60°，∴△P1BP2是正三角形，∴P1P2=BP1=BP，∴2P1P2+PP3=2P1P2+12PP3=2(BP+PQ)≥2BQ≥2BM=5，故答案为：5．【点拨】本题考查了轴对称、正三角形、三角形面积、垂线段最短等知识，解题的关键是将P1P2转化成BP，将2P1P2+PP3提取系数2，最终转化成垂线段最短．形式上易与胡不归混淆．5.(23-24八年级上·北京海淀·期中)如图，已知∠MON=30°，在∠MON的内部有一点P，A为OM上一动点，B为ON上一动点，OP=a，当△P AB的周长最小时，∠APB=度，△P AB的周长的最小值是．【答案】120a【分析】分别作出点P关于OM，ON两条射线的对称点，连接两个对称点的线段与OM，ON的交点即为所确定的点；连接OP，OP ，OP ，由轴对称的性质得：OP=OP =OP =a，∠P OA=∠POA，∠P OB=∠POB，证得△P OP 是等边三角形，即可得到结论．解：①分别作点P关于OM，ON的对称点P ，P ；连接P ，P ，分别交OM，ON于点A、点B，则此时△P AB的周长最小．连接OP，OP ，OP ，由轴对称的性质得：OP=OP =OP =a，∠P OA=∠POA，∠P OB=∠POB，∵∠MON=30°，∴∠P OP =2∠MON=60°，∴△P OP 是等边三角形，∴P P =OP=a，∠AP O=∠APO，∠BP O=∠BPO，∴∠APB=∠AP O+∠BP O=120°，∴△P AB的周长=P P =a，故答案为：120，a．【点拨】此题主要考查了轴对称-最短路径问题，解决本题的关键是理解要求周长最小问题可归结为求线段最短问题，通常是作已知点关于所求点所在直线的对称点．6.(22-23八年级上·新疆乌鲁木齐·期末)如图，已知∠AOB的大小为α，P是∠AOB内部的一个定点，且OP=5，点E、F分别是OA、OB上的动点，若△PEF周长的最小值等于5，则α=()A.30°B.45°C.60°D.90°【答案】A【分析】设点P关于OA的对称点为C，关于OB的对称点为D，当点E、F在CD上时，△PEF的周长为PE+ EF+FP=CD，此时周长最小，根据CD=5可求出α的度数．解：如图，作点P关于OA的对称点C，关于OB的对称点D，连接CD，交OA于E，OB于F．此时，△PEF 的周长最小．连接OC，OD，PE，PF．∵点P与点C关于OA对称，∴OA垂直平分PC，∴∠COA=∠AOP，PE=CE，OC=OP，同理，可得∠DOB=∠BOP，PF=DF，OD=OP．∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB=α，OC=OD=OP=5，∴∠COD=2α．又∵△PEF的周长为：PE+EF+FP=CE+EF+FD=CD=5，∴OC=OD=CD=5，∴△COD是等边三角形，∴2α=60°，∴α=30°．故选：A．【点拨】此题主要考查了最短路径问题，本题找到点E和F的位置是解题的关键．要使△PEF的周长最小，通常是把三边的和转化为一条线段，运用三角形三边关系解决．【题型3】一定两动型(垂线段最短)；7.(2024八年级上·全国·专题练习)如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，AD是∠BAC的平分线，若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是()A.2.4B.3C.4D.5【答案】A【分析】本题考查了轴对称最短路径问题，角平分线定义，勾股定理，作点Q关于AD的对称点Q ，连接PQ ，股定理求出AB 的长，再利用三角形面积求出CH 的长即可得到结果．解：如图，作点Q 关于AD 的对称点Q ，连接PQ ，CQ ，过点C 作CH ⊥AB 于点H ，∵AD 是△ABC 的角平分线，Q 与Q 关于AD 对称，∴点Q 在AB 上，PC +PQ =PC +PQ ≥CH ，∵AC =3，BC =4，∴AB =AC 2+BC 2=5，12⋅AC ⋅BC =12⋅AB ⋅CH 即12×3×4=12×5×CH ，∴CH =2.4，∴CP +PQ ≥2.4，∴PC +PQ 的最小值为2.4，故选：A ．8.(23-24七年级下·广东深圳·期末)如图，在等腰三角形ABC 中，AB =AC ，AD ⊥BC ，点D 为垂足，E 、F 分别是AD 、AB 上的动点．若AB =6，△ABC 的面积为12，则BE +EF 的最小值是()A.2B.4C.6D.8【答案】B 【分析】本题考查等腰三角形的性质，轴对称-最短路线问题，垂线段最短．解此题的关键是正确作出辅助线．作点F 关于AD 的对称点M ，连接BM 、EM ，过点B 作BN ⊥AC 于点N ，从而可确定BE +EF ≥BM ，即BM 最小时，BE +EF 最小．再根据垂线段最短可知BN 的长即为BM 最小时，最后根据三角形面积公式求出BN 的长即可．解：如图，作点F 关于AD 的对称点M ，连接BM 、EM ，过点B 作BN ⊥AC 于点N ，∴EF =EM ，∴BE +EF =BE +EM ≥BM ，∴BM 最小时，BE +EF 最小．当BM ⊥AC 时BM 最小，即为BN 的长，∵S △ABC =12AC ⋅BN =12，AB =AC =6，∴BN =2×12÷6=4，∴BE +EF 的最小值是4．故选B ．9.(23-24八年级·江苏·假期作业)如图，在△ABC 中，AB =AC =10,BC =12,AD =8，AD 是∠BAC 的平分线．若P ，Q 分别是AD 和AC 上的动点，则PC +PQ 的最小值是．【答案】9.6【分析】本题考查了轴对称--最短路线问题、等腰三角形的性质以及三角形的面积，线段垂直平分线的性质．连接PB ，PQ ，根据线段垂直平分线的性质可得BP =CP ，从而得到当点B ，P ，Q 三点共线时，PC +PQ 取得最小值，最小值为BQ 的长，且当BQ ⊥AC 时，BQ 最小，再由S △ABC =12BC ⋅AD =12AC ⋅BQ ，求出BQ 的长，即可．解：如图，连接PB ，PQ ，∵AB =AC ，AD 是∠BAC 的平分线，∴AD 垂直平分BC ，∴BP =CP ，∴PC +PQ =PB +PQ ≥PQ ，∴当点B ，P ，Q 三点共线时，PC +PQ 取得最小值，最小值为BQ 的长，且当BQ ⊥AC 时，BQ 最小，∵S △ABC =12BC ⋅AD =12AC ⋅BQ ，∴12×12×8=12×10BQ ，∴BQ =9.6．故答案为：9.6【题型4】两定两动型；10.(22-23八年级上·湖北武汉·期末)如图，∠AOB =20°，M ，N 分别是边OA ，OB 上的定点，P ，Q 分别是边OB ，OA 上的动点，记∠OPM =α，∠OQN =β，当MP +PQ +QN 最小时，则关于α，β的数量关系正确的是()A.β-α=30°B.β+α=210°C.β-2α=30°D.β+α=200°【答案】D 【分析】如图，作M 关于OB 的对称点M ，N 关于OA 的对称点N ，连接M N 交OA 于Q ，交OB 于P ，则MP +PQ +QN 最小，易知∠OPM =∠OPM ′=∠NPQ ，∠OQP =∠AQN ′=∠AQN ，∠OQN =180°-20°-∠ONQ ，∠OPM =∠NPQ =20°+∠OQP ，∠OQP =∠AQN =20°+∠ONQ ，由此即可解决问题．PQ +QN 最小，解:由轴对称的性质得∠OPM =∠OPM ′=∠NPQ ，∠OQP =∠AQN ′=∠AQN ，∠OQN =180°-20°-∠ONQ ，∠OPM =∠NPQ =20°+∠OQP ，∠OQP =∠AQN =20°+∠ONQ ，∴α+β=180°-20°-∠ONQ +20°+20°+∠ONQ =200°．故选：D ．【点拨】本题考查轴对称-最短问题、三角形的内角和定理．三角形的外角的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．【变式】(20-21八年级上·天津·期末)如图，∠AOB =25°，点M ，N 分别是边OA ，OB 上的定点，点P ，Q 分别是边OB ，OA 上的动点，记∠MPQ =α，∠PQN =β，当MP +PQ +QN 的值最小时，β-α的大小=_______(度)．【答案】50【分析】本题主要考查最短路径问题、轴对称的性质，三角形外角的性质，作M 关于OB 的对称点M ，N 关于OA 的对称点N ，连接M N ，交OB 于点P ，交OA 于点Q ，连接MP ，QN ，可知此时MP +PQ +QN 最小，此时∠OPM =∠OPM =QPN ，∠OQP =∠AQN =∠AQN ，再根据三角形外角的性质和平角的定义即可得出结论．解：作M 关于OB 的对称点M ，N 关于OA 的对称点N ，连接M N ，交OB 于点P ，交OA 于点Q ，连接MP ，QN ，如图所示．根据两点之间，线段最短，可知此时MP +PQ +QN 最小，即MP +PQ +QN =M N ，∴∠OPM =∠OPM =QPN ，∠OQP =∠AQN =∠AQN ，∵∠MPQ =α，∠PQN =β，∴∠QPN =12180°-α ，∠OQP =12180°-β ，∵∠QPN =∠AOB +∠OQP ，∠AOB =25°,∴12180°-α =25°+12180°-β ，∴β-α=50°，故答案为：50．【题型5】一定两动(等线段)转化型；11.(23-24九年级下·广西南宁·开学考试)如图，△ABC 是等边三角形，AB =4．过点A 作AD ⊥BC 于点D ，点P 是直线AD 上一点，以CP 为边，在CP 的下方作等边△CPQ ，连接DQ ，则DQ 的最小值为．【答案】1【分析】连接BQ ，先证△ACP ≌△BCQ (SAS )，则可得∠CBQ =∠CAP =30°，由此可知Q 点在过B 点且与BC 成30°角的直线上运动．根据垂线段最短可知，当DQ ⊥BQ 时，DQ 最小，求出DQ 的值即可．本题主要考查了等边三角形的性质，全等三角形的判定和性质，以及垂线段最短．熟练掌握以上知识，找出Q 点的运动轨迹是解题的关键．解：连接BQ ，∵△ABC 和△CPQ 都是等边三角形，∴AC =BC ，PC =QC ，∠ACB =∠PCQ =60°，∴∠ACB -∠PCB =∠PCQ -∠PCB ，即∠ACP =∠BCQ ，∴△ACP ≌△BCQ (SAS )，∴∠CBQ =∠CAP ，∵△ABC 是等边三角形，AB =4，∴BC =AB =4，∠BAC =60°，∵AD ⊥BC ，∴BD =DC =12BC =2，∠CAP =12∠BAC =30°，∴∠CBQ =30°，∴Q 点在过B 点且与BC 成30°角的直线上运动．当DQ ⊥BQ 时，DQ 最小，此时DQ =12BD =1，∴DQ 的最小值为1．故答案为：1．12.(23-24八年级下·湖北武汉·阶段练习)如图，在Rt △ABC 中，∠BAC =90°，AC =6，BC =10，D 、E 分别是AB 、BC 上的动点，且CE =BD ，连接AE 、CD ，则AE +CD 的最小值为．【答案】234【分析】本题主要考查了全等三角形的判定及性质，勾股定理，两点之间，线段最短，过点C 作CN ∥AB 且使CN =BC ，连接EN ，AN ，证明△CEN ≌△BDC SAS ，得EN =DC 进而可得AE +CD =AE +EN ，再由两点之间线段最短可得：AE +EN ≥AN ，所以当点E 在AN 上时，AE +EN 有最小值,即AE +CD 有最小值为AN ，利用勾股定理计算即可，熟练掌握相关知识点是解题的关键．解：过点C 作CN ∥AB 且使CN =BC ，连接EN ，AN ，∵CN ∥AB ，∴∠ECN =∠ABC ，∠ACN =180°-∠BAC =90°，在△CEN 和△BDC 中，EC =BD∠ECN =∠DBC CN =BC，∴△CEN ≌△BDC SAS ，∴EN =DC ，∴AE +CD =AE +EN ，由两点之间线段最短可得：AE +EN ≥AN ，所以当点E 在AN 上时，AE +EN 有最小值,即AE +CD 有最小值为AN ，∵AC =6，BC =CN =10，∴Rt △ACN 中，AN =AC 2+CN 2=62+102=234，∴AE +CD 最小值为：234，故答案为：234．13.(2024·安徽合肥·二模)如图，△ABC 和△ADE 都是等腰三角形，且∠BAC =∠DAE =120°，AB =8，O 是AC 的中点，若点D 在直线BC 上运动，连接OE ，则在点D 运动过程中，OE 的最小值为()A.42B.433C.32D.2【答案】D 【分析】设AB 的中点为Q ，连接DQ ，过点Q 作QH ⊥BC 于H ，证△AQD 和△AOE 全等得QD =OE ，因此当QD 为最小时，OE 为最小，根据“垂线段最短”得QD ≥QH ，故点D 与点H 重合时，QD 为最小，最小值为QH 的长，然后在Rt △BQH 中求出QH 的长即可．解：设AB 的中点为Q ，连接DQ ，过点Q 作QH⊥BC 于H ，如下图所示：∵△ABC 和△ADE 都是等腰三角形，且∠BAC =∠DAE =120°，∴AB =AC ，AD =AE ，∠QAD +∠DAC =∠DAC +∠OAE =120°，∴∠QAD =∠OAE ，∵点Q 是AB 的中点，点O 是AC 的中点，AB =AC ，∴AQ =AO ，在△AQD 和△AOE 中，AQ =AO∠QAD =∠OAE AD =AE，∴△AQD ≌△AOE (SAS )，∴QD =OE ，∴当QD 为最小时，OE 为最小，∵点Q 为AB 的中点，AB =8，点D 在直线BC 上运动，∴根据“垂线段最短”得：QD ≥QH ，∴当点D 与点H 重合时，QD 为最小，最小值为QH 的长，在△ABC 中，AB =AC =8，∠BAC =120°，∴∠B =∠C =12(180°-∠BAC )=30°，在Rt △BQH 中，∠B =30°，BQ =12AB =4，∴QH =12BQ =2，∴QD 的最小值为2，即OE 的最小值为2.故选：D ．【点拨】此题主要考查了等腰三角形的性质，直角三角形的性质，全等三角形的判定和性质，垂线段的性质，熟练掌握等腰三角形的性质，直角三角形的性质，全等三角形的判定和性质，理解垂线段最短是解决问题的关键，难点是正确地作出辅助线构造全等三角形和直角三角形．第三部分【中考链接与拓展延伸】【题型6】直通中考14.(2023·辽宁锦州·中考真题)如图，在Rt △ABC 中，∠ACB =90°，∠ABC =30°，AC =4，按下列步骤作图：①在AC 和AB 上分别截取AD 、AE ，使AD =AE ．②分别以点D 和点E 为圆心，以大于12DE 的长为半径作弧，两弧在∠BAC 内交于点M ．③作射线AM 交BC 于点F ．若点P 是线段AF 上的一个动点，连接CP ，则CP +12AP 的最小值是．【答案】23【分析】过点P 作PQ ⊥AB 于点Q ，过点C 作CH ⊥AB 于点H ，先利用角平分线和三角形的内角和定理求出∠BAF =30°，然后利用含30°的直角三角的性质得出PQ =12AP ，则CP +12AP =CP +PQ ≥CH ，当C 、P 、Q 三点共线，且与AB 垂直时，CP +12AP 最小，CP +12AP 最小值为CH ，利用含30°的直角三角的性质和勾股定理求出AB ，BC ，最后利用等面积法求解即可．解：过点P 作PQ ⊥AB 于点Q ，过点C 作CH ⊥AB 于点H ，由题意知：AF 平分∠BAC ，∵∠ACB =90°，∠ABC =30°，∴∠BAC =60°，∴∠BAF =12∠BAC =30°，∴PQ =12AP ，∴CP +12AP =CP +PQ ≥CH ，∴当C 、P 、Q 三点共线，且与AB 垂直时，CP +12AP 最小，CP +12AP 最小值为CH ，∵∠ACB =90°，∠ABC =30°，AC =4，∴AB =2AC =8，∴BC =AB 2-AC 2=43，∵S △ABC =12AC ⋅BC =12AB ⋅CH ，∴CH =AC ⋅BC AB =4×438=23，1故答案为：23．【点拨】本题考查了尺规作图-作角平分线，含30°的直角三角形的性质，勾股定理等知识，注意掌握利用等积法求三角形的高或点的线的距离的方法．15.(2020·新疆·中考真题)如图，在△ABC 中，∠A =90°,∠B =60°,AB =4，若D 是BC 边上的动点，则2AD+DC 的最小值为．【答案】12【分析】过点C 作射线CE ，使∠BCE =30°，再过动点D 作DF ⊥CE ，垂足为点F ，连接AD ，在Rt △DFC 中，∠DCF =30°，DF =12DC ，2AD +DC =2AD +12DC =2(AD +DF )当A ，D ，F 在同一直线上，即AF ⊥CE 时，AD +DF 的值最小，最小值等于垂线段AF 的长．解：过点C 作射线CE ，使∠BCE =30°，再过动点D 作DF ⊥CE ，垂足为点F ，连接AD ，如图所示：在Rt △DFC 中，∠DCF =30°，∴DF =12DC ，∵2AD +DC =2AD +12DC =2(AD +DF )，∴当A ，D ，F 在同一直线上，即AF ⊥CE 时，AD +DF 的值最小，最小值等于垂线段AF 的长，此时，∠B =∠ADB =60°，∴△ABD 是等边三角形，∴AD =BD =AB =4，在Rt △ABC 中，∠A =90°，∠B =60°，AB =4，∴BC =8，∴DC =4，∴DF =12DC =2，∴AF =AD +DF =4+2=6，∴2(AD +DF )=2AF =12，∴2AD +DC 的最小值为12，故答案为：12．【点拨】本题考查垂线段最短、等边三角形的判定和性质，含30度的直角三角形等知识，解题的关键是学会添加辅助线，构造数学模型，学会用转化的思想思考问题，属于中考填空题中的压轴题．【题型7】拓展延伸16.(2024·辽宁葫芦岛·二模)在△ABC 中，∠ABC =60°，BC =4，AC =5，点D ，E 在AB ，AC 边上，且AD=CE ，则CD +BE 的最小值是．【答案】61【分析】本题考查两点之间线段最短、勾股定理，全等三角形的性质和判定等知识，学会构造全等三角形解决问题是解题的关键．如图作CK∥AB，使得CK=CA．作BG⊥KC交KC的延长线于G．首先证明EK=CD，可得CD+BE =EK+EB≥BK，推出CD+BE的最小值为BK的长．解：如图作CK∥AB，使得CK=CA．作BG⊥KC交KC的延长线于G．∵CK∥AB，∴∠KCE=∠A，∵CK=CA，CE=AD，∴△CKE≌△CAD SAS，∴CD=KE，∵CD+BE=EK+EB≥BK，∴CD+BE的最小值为BK的长，∵KG∥AB，∴∠GCB=∠ABC=60°，∴∠CBG=90°-∠GCB=30°，在Rt△BCG中，∵∠G=90°，BC=4，∴CG=12BC=2，BG=BC2-CG2=23，∴GK=KC+CG=AC+CG=5+2=7，在Rt△KBG中，BK=GK2+BG2=72+(23)2=61．故答案为：61．17.(23-24八年级上·湖北武汉·阶段练习)如图，等腰△ABC中，∠BAC=100°，BD平分∠ABC，点N为BD上一点，点M为BC上一点，且BN=MC，若当AM+AN的最小值为4时，AB的长度是．【答案】4【分析】由等腰△ABC中，∠BAC=100°，可得∠ABC=∠ACB=180°-∠BAC2=40°，由BD平分∠ABC，可得∠ABD=12∠ABC=20°，如图，作∠BCE=∠ABD=20°，使CE=AB，连接EM，则∠ACE=∠ACB+E三点共线时，AM+AN最小，即AE=4，证明△ACE是等边三角形，则AC=AE=4，进而可求AB．解：∵等腰△ABC中，∠BAC=100°，=40°，∴∠ABC=∠ACB=180°-∠BAC2∵BD平分∠ABC，∠ABC=20°，∴∠ABD=12如图，作∠BCE=∠ABD=20°，使CE=AB，连接EM，∴∠ACE=∠ACB+∠BCE=60°，∵CE=AB，∠BCE=∠ABD，MC=BN，∴△CEM≌△BAN SAS，∴ME=AN，CE=AB，∴AM+AN=AM+ME，∴当A、M、E三点共线时，AM+AN最小，即AE=4，∵CE=AC，∠ACE=60°，∴△ACE是等边三角形，∴AC=AE=4，∴AB=4，故答案为：4．【点拨】本题考查了等腰三角形的性质，角平分线，全等三角形的判定与性质，等边三角形的判定与性质等知识．熟练掌握等腰三角形的性质，角平分线，全等三角形的判定与性质，等边三角形的判定与性质是解题的关键．。

(完整版)将军饮马问题的11个模型及例题

理由：AP+PQ≧AQ，当且仅当A、P、Q三点共线时，
AP+PQ取得最小值AQ，根据垂线段最短，当
AQ⊥ON时，AQ最小.
2. 已知：如图，A为锐角∠MON内一定点；
要求：在射线OM上找一点P，在射线ON上找一点Q，使
AP+PQ的值最小.
解：作点A关于OM的对称点A′，过点A′作AQ⊥ON
于点Q，A′Q交OM于点P，此时AP+PQ最小；
点到l的距离不相等）
要求：在直线l上找一点P，使︱PA-PB︱的值最大
解：作点B关于直Байду номын сангаасl的对称点B´，连接B´A并延长交
于点P，点P即为所求；
理由：根据对称的性质知l为线段BB´的中垂线，由中垂
线的性质得：PB=PB´，要使︱PA-PB︱最大，则需
︱PA-PB´︱值最大，从而转化为模型3.
典型例题1-1
∴PM=OE= ，∵OE=OE′，∴PM=OE′，PM∥OE′，
(a为定值)的线段PQ在l上移动（P在Q左边）
要求：确定PQ的位置，使得AP+PQ+QB最小
分析：PQ为定值，只需AP+QB的值最小，可通过平移，
使P、Q“接头”，转化为基本模型
解：将点A沿着平行于l的方向，向右移至A´，使
AA´=PQ=a,连接A´B交直线l于点Q，在l上截取
PQ=a（P在Q左边），则线段PQ即为所求，此时
AP+PQ+QB的最小值为A´B+PQ，即A´B+a
理由：易知四边形APQA´为平行四边形，则PA=QA´，
当A´、Q、B三点共线时，QA´+QB最小，即PA+QB
最小，又PQ长为定值此时PA+PQ+QB值最小.

中考复习：“将军饮马”类题型大全

“将军饮马”类题型大全一．求线段和最值1（一）两定一动型例1：如图，AM⊥EF，BN⊥EF，垂足为M、N，MN＝12m，AM＝5m，BN＝4m， P是EF 上任意一点，则PA＋PB的最小值是______m．分析：这是最基本的将军饮马问题，A，B是定点，P是动点，属于两定一动将军饮马型，根据常见的“定点定线作对称”，可作点A关于EF的对称点A’，根据两点之间，线段最短，连接A’B，此时A’P＋PB即为A’B，最短．而要求A’B，则需要构造直角三角形，利用勾股定理解决．解答：作点A关于EF的对称点A’，过点A’作A’C⊥BN的延长线于C．易知A’M＝AM＝NC＝5m，BC＝9m，A’C＝MN＝12m，在Rt△A’BC中，A’B＝15m，即PA＋PB的最小值是15m．变式：如图，在边长为2的正三角形ABC中，E，F，G为各边中点，P为线段EF上一动点，则△BPG周长的最小值为_________．分析：考虑到BG为定值是1，则△BPG的周长最小转化为求BP＋PG的最小值，又是两定一动的将军饮马型，考虑作点G关于EF的对称点，这里有些同学可能看不出来到底是哪个点，我们不妨连接AG，则AG⊥BC，再连接EG，根据“直角三角形斜边中线等于斜边的一半”，可得AE＝EG，则点A就是点G关于EF的对称点．最后计算周长时，别忘了加上BG的长度．解答：连接AG，易知PG＝PA，BP＋PG＝BP＋PA，当B，P，A三点共线时，BP＋PG＝BA，此时最短，BA＝2，BG＝1，即△BPG周长最短为3.2（二）一定两动型例2：如图，在△ABC中，AB＝AC＝5，D为BC中点，AD＝5，P为AD上任意一点，E 为AC上任意一点，求PC＋PE的最小值．分析：这里的点C是定点，P，E是动点，属于一定两动的将军饮马模型，由于△ABC 是等腰三角形，AD是BC中线，则AD垂直平分BC，点C关于AD的对称点是点B，PC＋PE＝PB＋PE，显然当B，P，E三点共线时，BE更短．但此时还不是最短，根据“垂线段最短” 只有当BE⊥AC时，BE最短．求BE时，用面积法即可．解答：作BE⊥AC交于点E，交AD于点P，易知AD⊥BC，BD＝3，BC＝6，则AD·BC＝BE·AC，4×6＝BE·5，BE＝4.8变式：如图，BD平分∠ABC，E，F分别为线段BC，BD上的动点，AB＝8，△ABC的周长为20，求EF＋CF的最小值________．分析：这里的点C是定点，F，E是动点，属于一定两动的将军饮马模型，我们习惯于“定点定线作对称”，但这题这样做，会出现问题．因为点C的对称点C’必然在AB上，但由于BC长度未知，BC’长度也未知，则C’相对的也是不确定点，因此我们这里可以尝试作动点E关于BD的对称点．解答：如图，作点E关于BD的对称点E’，连接E’F，则EF＋CF＝E’F＋CF，当E’，F，C三点共线时，E’F＋CF＝E’C，此时较短．过点C作CE’’⊥AB于E’’，当点E’ 与点E’’重合时，E’’C最短，E’’C为AB边上的高，E’’C＝5.（三）两定两动型例3：如图，∠AOB＝30°，OC＝5，OD＝12，点E，F分别是射线OA，OB上的动点，求CF＋EF＋DE的最小值.分析：这里的点C，点D是定点，F，E是动点，属于两定两动的将军饮马模型，依旧可以用“定点定线作对称”来考虑．作点C关于OB的对称点，点D关于OA的对称点．解答：作点C关于OB的对称点C’，点D关于OA的对称点D’，连接C’D’． CF＋EF＋DE＝C’F＋ EF＋D’E，当C’，F， E，D’四点共线时，CF＋EF＋DE＝C’D’最短．易知∠D’OC’＝90°，OD’＝12，OC’＝5，C’D’＝13，CF＋EF＋DE最小值为13．变式：（原创题）如图，斯诺克比赛桌面AB宽1.78m，白球E距AD边0.22m，距CD 边1.4m，有一颗红球F紧贴BC边，且距离CD边0.1m，若要使白球E经过边AD，DC，两次反弹击中红球F，求白球E运动路线的总长度．分析：本题中，点E和点F是定点，两次反弹的点虽然未知，但我们可以根据前几题的经验作出，即分别作点E关于AD边的对称点E’，作点F关于CD边的对称点F’，即可画出白球E的运动路线，化归为两定两动将军饮马型．解答：作点E关于AD边的对称点E’，作点F关于CD边的对称点F’，连接E’F’，交AD于点G，交CD于点H，则运动路线长为EG＋GH＋HF长度之和，即E’F’长，延长E’E交BC于N，交AD于M，易知E’M＝EM＝0.22m，E’N＝1.78＋0.22＝2m，NF’＝NC＋CF’＝1.4＋0.1＝1.5m，则Rt△E’NF’中，E’F’＝2.5m，即白球运动路线的总长度为2.5m．小结：以上求线段和最值问题，几乎都可以归结为“两定一动”“一定两动”“两定两动”类的将军饮马型问题，基本方法还是“定点定线作对称”，利用“两点之间线段最短”“垂线段最短”的2条重要性质，将线段和转化为直角三角形的斜边，或者一边上的高，借助勾股定理，或者面积法来求解．当然，有时候，我们也需学会灵活变通，定点对称行不通时，尝试作动点对称．（二）求角度例1:P为∠AOB内一定点，M，N分别为射线OA，OB上一点，当△PMN周长最小时，∠MPN＝80°．（1）∠AOB＝_____°（2）求证：OP平分∠MPN分析：这又是一定两动型将军饮马问题，我们应该先将M，N的位置找到，再来思考∠AOB 的度数，显然作点P关于OA的对称点P’，关于OB的对称点P’’，连接P’P’’，其与OA交点即为M，OB交点即为N，如下图，易知∠DPC与∠AOB互补，则求出∠DPC的度数即可．解答：（1）法1：如图，∠1＋∠2＝100°，∠1＝∠P’＋∠3＝2∠3，∠2＝∠P’’＋∠4＝2∠4，则∠3＋∠4＝50°，∠DPC＝130°，∠AOB＝50°．再分析：考虑到第二小问要证明OP平分∠MPN，我们就连接OP，则要证∠5＝∠6，显然很困难，这时候，考虑到对称性，我们再连接OP’，OP’’，则∠5＝∠7，∠6＝∠8，问题迎刃而解．解答：（1）法2：易知OP’＝OP’’，∠7＋∠8＝∠5＋∠6＝80°，∠P’OP’’＝100°，由对称性知，∠9＝∠11，∠10＝∠12，∠AOB＝∠9＋∠10＝50°（2）由OP’＝OP’’，∠P’OP’’＝100°知，∠7＝∠8＝40°，∠5＝∠6＝40°，OP平分∠MPN．变式：如图，在五边形ABCDE中，∠BAE＝136°，∠B＝∠E＝90°，在BC、DE上分别找一点M、N，使得△AMN的周长最小时，则∠AMN＋∠ANM的度数为________．分析：这又是典型的一定两动型将军饮马问题，必然是作A点关于BC、DE的对称点A′、A″，连接A′A″，与BC、DE的交点即为△AMN周长最小时M、N的位置．解答：如图，∵∠BAE＝136°，∴∠MA′A＋∠NA″A＝44°由对称性知，∠MAA′＝∠MA′A，∠NAA″＝∠NA″A，∠AMN＋∠ANM＝2∠MA′A＋2∠NA″A＝88°思考题：1.（2017·安顺）如图所示，正方形ABCD的边长为6，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为_______．2.（2017·安徽改编）如图，在矩形ABCD中，AB=4，AD=3．P为矩形ABCD内一点，若矩形ABCD面积为△PAB面积的4倍，则点P到A，B两点距离之和PA+PB 的最小值为________．。

初中将军饮马问题总结--学生版

初中涉及将军饮马问题题型总结题型一：将军饮马之单动点1.三角形中的将军饮马【真题链接1.】（2017•天津）如图，在ABC∆中，AB AC=，AD、CE是ABC∆的两条中线，P是AD上一个动点，则下列线段的长度等于BP EP+最小值的是()A．BC B．CE C．AD D．AC【真题链接2.】（2020•天津一模）如图，ABC∆是等边三角形，2AB=，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，则PE PC+的最小值为()A．1 B．2 CD．BB如图，在ABC ∆中，AB AC =，4BC =，面积是16，AC 的垂直平分线EF 分别交AC ，AB 边于E ，F 点，若点D 为BC 边的中点，点M 为线段EF 上一动点，则CDM ∆周长的最小值为( )A ．6B ．8C ．10D ．12【真题链接4.】（2019•陕西）如图，在正方形ABCD 中，8AB =，AC 与BD 交于点O ，N 是AO 的中点，点M 在BC 边上，且6BM =．P 为对角线BD 上一点，则PM PN −的最大值为．A如图，在ABC ∆中，3AB =，4AC =，5BC =，EF 是BC 的垂直平分线．点P 是EF 上的动点，则||PA PB −的最大值为．2. 菱形、矩形、正方形中的将军饮马【真题链接6】（2019春•息县期末）如图，在菱形ABCD 中，6AB =，60ABC ∠=°，M 为AD 中点，P 为对角线BD 上一动点，连接PA 和PM ，则PA PM +的最小值是．【真题链接7】（2019春•息县期末）（2016•龙岩）如图，在周长为12的菱形ABCD 中，1AE =，2AF =，若P 为对角线BD 上一动点，则EP FP +的最小值为( )A ．1B ．2C ．3D ．4BB【真题链接8】（2019•西藏）如图，在矩形ABCD 中，6AB =，3AD =，动点P 满足13PAB ABCD S S ∆=矩形，则点P 到A 、B两点距离之和PA PB +的最小值为( )A． B．C．D【真题链接9】（2020•恩施州）如图，正方形ABCD 的边长为4，点E 在AB 上且1BE =，F 为对角线AC 上一动点，则BFE ∆周长的最小值为( )A ．5B ．6C ．7D ．8如图，已知正方形ABCD的边长为4，点E是边AB的中点，点P是对角线BD上的动点，则AP PE+的最小值是．3.圆中的将军饮马【真题链接11】（2020•河南）如图，在扇形BOC中，60BOC∠=°，OD平分BOC∠交 BC于点D，点E为半径OB上一动点．若2OB=，则阴影部分周长的最小值为．【真题链接12】（2020•潍坊）如图，在Rt AOB∆中，90AOB∠=°，3OA=，4OB=，以点O为圆心，2为半径的圆与OB 交于点C，过点C作CD OB⊥交AB于点D，点P是边OA上的动点．当PC PD+最小时，OP的长为()A．12B．34C．1 D．32如图，AB 为O 的直径，BC 、CD 是O 的切线，切点分别为点B 、D ，点E 为线段OB 上的一个动点，连接OD ，CE ，DE，已知AB =2BC =，当CE DE +的值最小时，则CEDE的值为( )A ．910B ．23CD4. 一次函数中的将军饮马【真题链接14】（2019•聊城）如图，在Rt ABO ∆中，90OBA ∠=°，(4,4)A ，点C 在边AB 上，且13AC CB =，点D 为OB 的中点，点P 为边OA 上的动点，当点P 在OA 上移动时，使四边形PDBC 周长最小的点P 的坐标为( )A ．(2,2)B ．5(2，5)2C ．8(3，8)3D ．(3,3)A如图，直线1y x =+与抛物线245y x x =−+交于A ，B 两点，点P 是y 轴上的一个动点，当PAB ∆的周长最小时，PAB S ∆= ．题型二：将军饮马之双动点【真题链接16】（2019•营口）如图，ABC ∆为等边三角形，边长为6，AD BC ⊥，垂足为点D ，点E 和点F 分别是线段AD 和AB 上的两个动点，连接CE ，EF ，则CE EF +的最小值为．B如图，在Rt ABC ∆中，90ACB ∠=°，6AC =，8BC =，AD 平分CAB ∠交BC 于D 点，E ，F 分别是AD ，AC 上的动点，则CE EF +的最小值为( )A ．403B ．154C ．245D ．6【真题链接18】（2020•内江）如图，在矩形ABCD 中，10BC =，30ABD ∠=°，若点M 、N 分别是线段DB 、AB 上的两个动点，则AM MN +的最小值为．【真题链接19】（2017•呼伦贝尔）如图，在Rt ABC ∆中，90C ∠=°，3AC =，4BC =，D 、E 分别是AB 、BC 边上的动点，则AE DE +的最小值为( )A ．485B ．245C ．5D ．125A在平面直角坐标系中的位置如图所示，且60AOB ∠=°，在AOB ∠内有一点(4,3)P ，M ，N 分别是OA ，OB 边上的动点，连接PM ，PN ，MN ，则PMN ∆周长的最小值是．【真题链接21】（2020春•历下区期末）如图，点P 是AOB ∠内任意一点，8OP =，M 、N 分别是射线OA 和OB 上的动点，若PMN ∆周长的最小值为8，则AOB ∠= ．【真题链接22】（2019•灞桥区校级三模）如图，点(4,2)A ，点(1,6)B 在第一象限，点D 、C 分别是x 轴、y 轴上动点，则四边形ABCD 的周长最小值是．xOA题型三：将军饮马之三动点【真题链接23】（2019•兴安盟）如图，ABC ∆中，3AC BC ==，2AB =，将它沿AB 翻折得到ABD ∆，点P 、E 、F 分别为线段AB 、AD 、DB 上的动点，则PE PF +的最小值是( )AB ．223CD【真题链接24】（2020•江阴市模拟）在ABC ∆中，60A ∠=°，75C ∠=°，8AB =，D 、E 、F 分别在AB 、BC 、CA 上，则DEF ∆的周长最小值是．BABA题型四：将军饮马之平移型【真题链接25】（2020•邗江区二模）如图，菱形ABCD 的的边长为6，60ABC ∠=°，对角线BD 上有两个动点E 、F （点E 在点F 的左侧），若2EF =，则AE CF +的最小值为( )A．B．C ．6 D ．8【真题链接26】（2020•荆门）在平面直角坐标系中，长为2的线段CD （点D 在点C 右侧）在x 轴上移动，(0,2)A ，(0,4)B ，连接AC ，BD ，则AC BD +的最小值为( )A． B．C． D．B【真题链接27】（2020•黑龙江）如图，在边长为4的正方形ABCD 中，将ABD ∆沿射线BD 平移，得到EGF ∆，连接EC 、GC ．求EC GC +的最小值为．PS1：将军饮马知识点总结可以到我的百度文库店铺搜寻“几何最值之将军饮马(知识点总结)” PS2：此文档没有答案，答案可以去我的百度文库店铺搜寻，解析版。

【中考数学】最全“将军饮马”类问题（类型大全+分类汇编）总复习

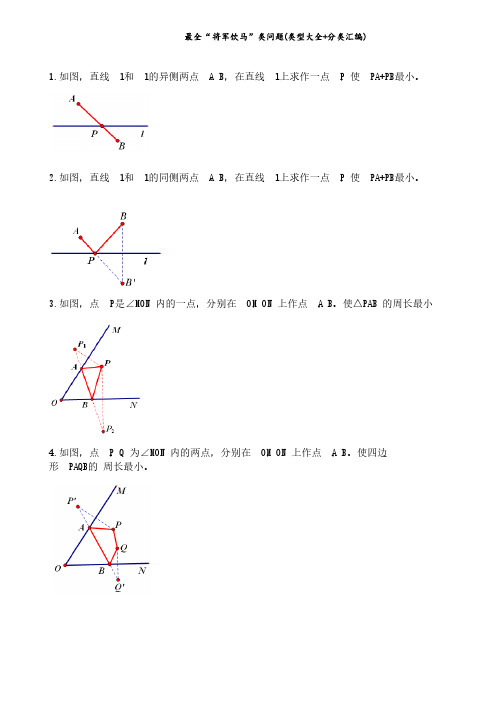
最全“将军饮马”类问题(类型大全+分类汇编)1.1.如图，直线如图，直线如图，直线 l l 和 l 的异侧两点的异侧两点的异侧两点 A A 、B ，在直线，在直线 l l 上求作一点上求作一点上求作一点 P P ，使，使，使 PA+PB PA+PB 最小。

最小。

2.2.如图，直线如图，直线如图，直线 l l 和 l 的同侧两点的同侧两点的同侧两点 A A 、B ，在直线，在直线 l l 上求作一点上求作一点上求作一点 P P ，使，使，使 PA+PB PA+PB 最小。

最小。

3.3.如图，点如图，点如图，点 P P 是∠是∠是∠MON MON 内的一点，分别在内的一点，分别在 OM OM ，ON 上作点上作点 A A ，B 。

使△。

使△PAB PAB 的周长最小的周长最小4.4.如图，点如图，点如图，点 P P ，Q 为∠为∠MON MON 内的两点，分别在内的两点，分别在 OM OM ，ON 上作点上作点 A A ，B 。

使四边形 PAQB 的周长最小。

周长最小。

5.5.如图，点如图，点如图，点 A A 是∠是∠是∠MON MON 外的一点，在射线外的一点，在射线 OM OM 上作点上作点上作点 P P ，使，使，使 PA PA 与点与点与点 P P 到射线到射线到射线 ON ON 的距离的距离之和最小之和最小6. .如图，点如图，点如图，点 A A 是∠是∠是∠MON MON 内的一点，在射线内的一点，在射线 OM OM 上作点上作点上作点 P P ，使，使，使 PA PA 与点与点与点 P P 到射线到射线到射线 ON ON 的距的距离之和最小离之和最小EMME HM30°二、常见题型三角形问题1．如图，在等边△如图，在等边△ABC ABC ABC 中，中，中，AB = 6AB = 6AB = 6，，AD AD⊥⊥BC BC，，E E 是是 AC AC 上的一点，上的一点，上的一点，M M M 是是 AD AD 上的一点，若上的一点，若上的一点，若 AE = 2 AE = 2 AE = 2，求，求，求 EM+EC EM+EC EM+EC 的最小值的最小值 A解：∵点解：∵点 C C C 关于直线关于直线关于直线 AD AD AD 的对称点是点的对称点是点的对称点是点 B B B，，A∴连接∴连接 BE BE BE，交，交，交 AD AD AD 于点于点于点 M M M，则，则，则 ME+MD ME+MD 最小，过点过点 B B B 作作 BH BH⊥⊥AC AC 于点于点于点 H H H，，则 EH = AH EH = AH –– AE = 3 AE = 3 –– 2 = 1，BH = BC2 - CH2 = 62 - 32 = 3 3在直角△在直角△BHE BHE BHE 中，中，中，BE = BE = BH2 + HE2B=(3 3)2 + 12 = 2 7DCBDC2．如图，在锐角△如图，在锐角△ABC ABC ABC 中，中，中，AB = 4 2AB = 4 2AB = 4 2，∠，∠，∠BAC BAC BAC＝45°，∠＝45°，∠＝45°，∠BAC BAC BAC 的平分线交的平分线交的平分线交 BC BC BC 于点于点于点 D D D，，M 、N N 分别是分别是分别是 AD AD AD 和和 AB AB 上的动点，上的动点，则 BM+MN BM+MN 的最小值是的最小值是．解：作点解：作点 B B B 关于关于关于 AD AD AD 的对称点的对称点 B'B'，，过点过点 B' B' B'作作 B'E B'E⊥⊥AB AB 于点于点 E ，交，交 AD AD AD 于点于点于点 F F F，，则线段则线段 B'E B'E B'E 的长就是的长就是的长就是 BM BM BM＋ＭＮ的最小值＋ＭＮ的最小值在等腰等腰 Rt Rt Rt△△AEB'AEB'中，中，根据勾股定理得到，根据勾股定理得到，B'E B'E = 4CB'M FDAN EB3．如图，△如图，△ABC ABC ABC 中，中，中，AB=2AB=2AB=2，∠BAC=30°，若在，∠BAC=30°，若在，∠BAC=30°，若在 AC AC AC、、AB AB 上各取一点上各取一点上各取一点 M M M、、N ，使，使 BM+MN BM+MN BM+MN 的值最小，则这个最小值的值最小，则这个最小值C解：作解：作 AB AB AB 关于关于关于 AC AC AC 的对称线段的对称线段 AB'AB'，，过点过点 B' B' B'作作 B'N B'N⊥⊥AB AB，垂足为，垂足为，垂足为 N N N，交，交，交 AC AC AC 于点于点 M ，则 B'N = MB'+MN = MB+MN B'N B'N 的长就是的长就是的长就是 MB+MN MB+MN MB+MN 的最小值的最小值则∠则∠B'AN = 2B'AN = 2B'AN = 2∠∠BAC= 60BAC= 60°，°，°，AB' = AB = 2AB' = AB = 2AB' = AB = 2，， ∠ANB'= 90ANB'= 90°，∠°，∠°，∠B' = 30B' = 30B' = 30°。

中考数学动点问题之将军饮马问题

中考数学“将军饮马”类题型大全一．求线段和最值1（一）两定一动型例1：如图，AM⊥EF，BN⊥EF，垂足为M、N，MN＝12m，AM＝5m，BN＝4m，P是EF上任意一点，则PA＋PB的最小值是______m．分析：这是最基本的将军饮马问题，A，B是定点，P是动点，属于两定一动将军饮马型，根据常见的“定点定线作对称”，可作点A关于EF的对称点A’，根据两点之间，线段最短，连接A’B，此时A’P＋PB即为A’B，最短．而要求A’B，则需要构造直角三角形，利用勾股定理解决．解答：作点A关于EF的对称点A’，过点A’作A’C⊥BN的延长线于C．易知A’M＝AM＝NC＝5m，BC＝9m，A’C＝MN＝12m，在Rt⊥A’BC中，A’B＝15m，即PA＋PB的最小值是15m．变式：如图，在边长为2的正三角形ABC中，E，F，G为各边中点，P为线段EF上一动点，则⊥BPG周长的最小值为_________．分析：考虑到BG为定值是1，则⊥BPG的周长最小转化为求BP＋PG的最小值，又是两定一动的将军饮马型，考虑作点G关于EF的对称点，这里有些同学可能看不出来到底是哪个点，我们不妨连接AG，则AG⊥BC，再连接EG，根据“直角三角形斜边中线等于斜边的一半”，可得AE＝EG，则点A就是点G关于EF的对称点．最后计算周长时，别忘了加上BG的长度．解答：连接AG，易知PG＝PA，BP＋PG＝BP＋PA，当B，P，A三点共线时，BP＋PG＝BA，此时最短，BA＝2，BG＝1，即⊥BPG周长最短为3.2（二）一定两动型例2：如图，在⊥ABC中，AB＝AC＝5，D为BC中点，AD＝5，P为AD上任意一点，E为AC 上任意一点，求PC＋PE的最小值．分析：这里的点C是定点，P，E是动点，属于一定两动的将军饮马模型，由于⊥ABC是等腰三角形，AD是BC中线，则AD垂直平分BC，点C关于AD的对称点是点B，PC＋PE＝PB＋PE，显然当B，P，E三点共线时，BE更短．但此时还不是最短，根据“垂线段最短” 只有当BE⊥AC时，BE最短．求BE时，用面积法即可．解答：作BE⊥AC交于点E，交AD于点P，易知AD⊥BC，BD＝3，BC＝6，则AD·BC＝BE·AC，4×6＝BE·5，BE＝4.8变式：如图，BD平分⊥ABC，E，F分别为线段BC，BD上的动点，AB＝8，⊥ABC的周长为20，求EF＋CF的最小值________．分析：这里的点C是定点，F，E是动点，属于一定两动的将军饮马模型，我们习惯于“定点定线作对称”，但这题这样做，会出现问题．因为点C的对称点C’必然在AB上，但由于BC长度未知，BC’长度也未知，则C’相对的也是不确定点，因此我们这里可以尝试作动点E关于BD的对称点．解答：如图，作点E关于BD的对称点E’，连接E’F，则EF＋CF＝E’F＋CF，当E’，F，C三点共线时，E’F＋CF＝E’C，此时较短．过点C作CE’’⊥AB于E’’，当点E’ 与点E’’重合时，E’’C最短，E’’C为AB边上的高，E’’C＝5.（三）两定两动型例3：如图，⊥AOB＝30°，OC＝5，OD＝12，点E，F分别是射线OA，OB上的动点，求CF＋EF＋DE的最小值.分析：这里的点C，点D是定点，F，E是动点，属于两定两动的将军饮马模型，依旧可以用“定点定线作对称”来考虑．作点C关于OB的对称点，点D关于OA的对称点．解答：作点C关于OB的对称点C’，点D关于OA的对称点D’，连接C’D’．CF＋EF＋DE＝C’F＋EF＋D’E，当C’，F，E，D’四点共线时，CF＋EF＋DE＝C’D’最短．易知⊥D’OC’＝90°，OD’＝12，OC’＝5，C’D’＝13，CF＋EF＋DE最小值为13．变式：（原创题）如图，斯诺克比赛桌面AB宽1.78m，白球E距AD边0.22m，距CD边1.4m，有一颗红球F紧贴BC边，且距离CD边0.1m，若要使白球E经过边AD，DC，两次反弹击中红球F，求白球E运动路线的总长度．本题中，点E和点F是定点，两次反弹的点虽然未知，但我们可以根据前几题的经验作出，即分别作点E关于AD边的对称点E’，作点F关于CD边的对称点F’，即可画出白球E的运动路线，化归为两定两动将军饮马型．解答：作点E关于AD边的对称点E’，作点F关于CD边的对称点F’，连接E’F’，交AD于点G，交CD于点H，则运动路线长为EG＋GH＋HF长度之和，即E’F’长，延长E’E交BC于N，交AD于M，易知E’M＝EM＝0.22m，E’N＝1.78＋0.22＝2m，NF’＝NC＋CF’＝1.4＋0.1＝1.5m，则Rt⊥E’NF’中，E’F’＝2.5m，即白球运动路线的总长度为2.5m．小结：以上求线段和最值问题，几乎都可以归结为“两定一动”“一定两动”“两定两动”类的将军饮马型问题，基本方法还是“定点定线作对称”，利用“两点之间线段最短”“垂线段最短”的2条重要性质，将线段和转化为直角三角形的斜边，或者一边上的高，借助勾股定理，或者面积法来求解．当然，有时候，我们也需学会灵活变通，定点对称行不通时，尝试作动点对称．（二）求角度例1:P为⊥AOB内一定点，M，N分别为射线OA，OB上一点，当⊥PMN周长最小时，⊥MPN ＝80°．（1）⊥AOB＝_____°（2）求证：OP平分⊥MPN分析：这又是一定两动型将军饮马问题，我们应该先将M，N的位置找到，再来思考⊥AOB的度数，显然作点P关于OA的对称点P’，关于OB的对称点P’’，连接P’P’’，其与OA交点即为M，OB交点即为N，如下图，易知⊥DPC与⊥AOB互补，则求出⊥DPC的度数即可．（1）法1：如图，⊥1＋⊥2＝100°，⊥1＝⊥P’＋⊥3＝2⊥3，⊥2＝⊥P’’＋⊥4＝2⊥4，则⊥3＋⊥4＝50°，⊥DPC ＝130°，⊥AOB＝50°．再分析：考虑到第二小问要证明OP平分⊥MPN，我们就连接OP，则要证⊥5＝⊥6，显然很困难，这时候，考虑到对称性，我们再连接OP’，OP’’，则⊥5＝⊥7，⊥6＝⊥8，问题迎刃而解．解答：（1）法2：易知OP’＝OP’’，⊥7＋⊥8＝⊥5＋⊥6＝80°，⊥P’OP’’＝100°，由对称性知，⊥9＝⊥11，⊥10＝⊥12，⊥AOB＝⊥9＋⊥10＝50°（2）由OP’＝OP’’，⊥P’OP’’＝100°知，⊥7＝⊥8＝40°，⊥5＝⊥6＝40°，OP平分⊥MPN．变式：如图，在五边形ABCDE中，⊥BAE＝136°，⊥B＝⊥E＝90°，在BC、DE上分别找一点M、N，使得⊥AMN的周长最小时，则⊥AMN＋⊥ANM的度数为________．分析：这又是典型的一定两动型将军饮马问题，必然是作A点关于BC、DE的对称点A′、A″，连接A′A″，与BC、DE的交点即为⊥AMN周长最小时M、N的位置．解答：如图，⊥⊥BAE＝136°，⊥⊥MA′A＋⊥NA″A＝44°由对称性知，⊥MAA′＝⊥MA′A，⊥NAA″＝⊥NA″A，⊥AMN＋⊥ANM＝2⊥MA′A＋2⊥NA″A＝88°思考题：1.如图所示，正方形ABCD的边长为6，⊥ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为_______．2.如图，在矩形ABCD中，AB=4，AD=3．P为矩形ABCD内一点，若矩形ABCD面积为⊥PAB 面积的4倍，则点P到A，B两点距离之和PA+PB的最小值为________．。

中考数学复习：“将军饮马”类题型大全

中考数学复习：“将军饮马”类题型大全一、求线段和最值1.两定一动型例1：在图中，AM⊥EF，BN⊥EF，垂足为M、N，MN＝12m，AM＝5m，BN＝4m，P是EF上任意一点，则PA＋PB的最小值是多少？分析：这是最基本的将军饮马问题，A，B是定点，P是动点，属于两定一动将军饮马型。

根据常见的“定点定线作对称”，可作点A关于EF的对称点A’，根据两点之间，线段最短，连接A’B，此时A’P＋PB即为A’B，最短。

而要求A’B，则需要构造直角三角形，利用勾股定理解决。

解答：作点A关于EF的对称点A’，过点A’作A’C⊥BN的延长线于C。

易知A’M＝AM＝NC＝5m，BC＝9m，A’C＝MN＝12m，在Rt△A’BC中，A’B＝15m，即PA＋PB的最小值是15m。

变式：在边长为2的正三角形ABC中，E，F，G为各边中点，P为线段EF上一动点，则△BPG周长的最小值为多少？分析：考虑到BG为定值是1，则△BPG的周长最小转化为求BP＋PG的最小值，又是两定一动的将军饮马型，考虑作点G关于EF的对称点，这里有些同学可能看不出来到底是哪个点，我们不妨连接AG，则AG⊥BC，再连接EG，根据“直角三角形斜边中线等于斜边的一半”，可得AE＝EG，则点A就是点G关于EF的对称点。

最后计算周长时，别忘了加上BG的长度。

解答：连接AG，易知PG＝PA，BP＋PG＝BP＋PA，当B，P，A三点共线时，BP＋PG＝BA，此时最短，BA＝2，BG＝1，即△BPG周长最短为3.2.一定两动型例2：在△ABC中，AB＝AC＝5，D为BC中点，AD＝5，P为AD上任意一点，E为AC上任意一点，求PC＋PE的最小值。

分析：这里的点C是定点，P，E是动点，属于一定两动的将军饮马模型。

由于△ABC是等腰三角形，AD是BC中线，则AD垂直平分BC，点C关于AD的对称点是点B，PC＋PE＝PB＋PE，显然当B，P，E三点共线时，BE更短。

将军饮马题型总结

将军饮马题型总结将军饮马问题=轴对称问题=最短距离问题（轴对称是工具，最短距离是题眼）。

所谓轴对称是工具，即这类问题最常用的做法就是作轴对称。

而最短距离是题眼，也就意味着归类这类的题目的理由。

比如题目经常会出现线段a+b 这样的条件或者问题。

一旦出现可以快速联想到将军问题，然后利用轴对称解题。

将军饮马最常见的三大模型1. 如图，在直线异侧两个点A 和B ，在直线上求一点P 。

使得PA+PB 最短（题眼）。

一般做法：作点A （B ）关于直线的对称点，连接A ’B ，A ’B 与直线交点即为所求点。

A’B即为最短距离理由：A ’为A 的对称点，所以无论P 在直线任何位置都能得到AP=A ’P 。

所以PA+PB=PA ’+PB 。

这样问题就化成了求A ’到B 的最短距离，直接相连就可以了。

2. 如图，在∠OAB 内有一点P ，在OA 和OB 各找一个点M 、N ，使得△PMN 周长最短（题眼）。

一般做法：作点P 关于OA 和OB 的对称点P1、P2。

连接P1P2。

P1P2与OA 、OB 的交点即为所求点。

P1P2即为最短周长。

理由：对称过后，PM=P1M ，PN=P2N 。

所以PM+PN+MN=P1M+P2N+MN 。

所以问题就化成了求P1到P2的最短距离，直接相连就可以了。

B3.如图，在∠OAB内有两点P、Q，在OAPMNQ周长最短（题眼）。

一般做法：题目中PQ距离固定。

所以只是求PM+MN+QN的最短距离。

最终P’Q’+PQ即为所求最短周长。

M、N即为所求的点。

理由：作完对称后，由于P’M=PM，Q’N=QN，所以PM+MN+QN=P’M+MN+Q’N。

所以就化成了求P’到Q’的最短距离，所以相连即可。

常见问题1.怎么对称，作谁的对称？2.对称完以后和谁连接？3.所求点怎么确定？首先明白几个概念，动点、定点、对称点。

动点一般就是题目中的所求点，即那个不定的点。

定点即为题目中固定的点。

对称的点，作图所得的点，需要连线的点。

中学数学 “将军饮马”类问题 (含答案)

最全“将军饮马”类问题(类型大全+分类汇编)1.如图，直线 l 和 l 的异侧两点 A、B，在直线 l 上求作一点 P，使 PA+PB 最小。

2.如图，直线 l 和 l 的同侧两点 A、B，在直线 l 上求作一点 P，使 PA+PB 最小。

3.如图，点 P 是∠MON 内的一点，分别在 OM，ON 上作点 A，B。

使△PAB 的周长最小4.如图，点 P，Q 为∠MON 内的两点，分别在 OM，ON 上作点 A，B。

使四边形 PAQB 的周长最小。

5.如图，点 A 是∠MON 外的一点，在射线 OM 上作点 P，使 PA 与点 P 到射线 ON 的距离之和最小6. .如图，点 A 是∠MON 内的一点，在射线 OM 上作点 P，使 PA 与点 P 到射线 ON 的距离之和最小E MMEHM30°二、常见题型三角形问题1．如图，在等边△ABC 中，AB = 6，AD⊥BC，E 是 AC 上的一点，M 是 AD 上的一点，若 AE = 2，求 EM+EC 的最小值A解：∵点 C 关于直线 AD 的对称点是点 B，A∴连接 BE，交 AD 于点 M，则 ME+MD 最小，过点 B 作 BH⊥AC 于点 H，则 EH = AH – AE = 3 – 2 = 1，BH = BC2 - CH2 = 62 - 32 = 3 3在直角△BHE 中，BE = BH2 + HE2 B= (3 3)2 + 12 = 2 7D C B D C2．如图，在锐角△ABC 中，AB = 4 2，∠BAC＝45°，∠BAC 的平分线交 BC 于点 D，M、N 分别是 AD 和 AB 上的动点，则 BM+MN 的最小值是．解：作点 B 关于 AD 的对称点B'，过点 B'作 B'E⊥AB 于点E，交 AD 于点 F，则线段 B'E 的长就是 BM＋ＭＮ的最小值在等腰 Rt△AEB'中，根据勾股定理得到，B'E = 4CB'M F D A N E B3．如图，△ABC 中，AB=2，∠BAC=30°，若在 AC、AB 上各取一点 M、N，使 BM+MN 的值最小，则这个最小值C 解：作 AB 关于 AC 的对称线段AB'，过点 B'作 B'N⊥AB，垂足为 N，交 AC 于点M，则 B'N = MB'+MN = MB+MNB'N 的长就是 MB+MN 的最小值则∠B'AN = 2∠BAC= 60°，AB' = AB = 2，∠ANB'= 90°，∠B' = 30°。

将军饮马等8类常见最值问题(原卷版)

将军饮马等8类常见最值问题题型一两定一动型（线段和差最值问题）题型二双动点最值问题（两次对称）题型三动线段问题：造桥选址（构造平行四边形）题型四垂线段最短题型五相对运动平移型将军饮马题型六通过瓜豆得出轨迹后将军饮马题型七化斜为直，斜大于直题型八构造二次函数模型求最值一、单动点问题【问题1】在直线l 上求一点P ，使PA ＋PB 最小问题解决：连接AB ，与l 交点即为P ，两点之间线段最短PA ＋PB 最小值为AB【问题2】在直线l 上求一点P ，使PA ＋PB 最小lA l问题解决：作B 关于l 的对称点B '⇒PB ＝PB '，则PA ＋PB ＝PA ＋PB '，当A ，P ，B '共线时取最小，原理：两点之间线段最短，即PA ＋PB 最小值为AB '【问题3】在直线l 上求一点P ，使|PA －PB |最大问题解决：连接AB ，当A ，B ，P 共线时取最大原理：三角形两边之和大于第三边，在△AB 'P 中，|PA －PB '|≤AB '【问题4】在直线l 上求一点P ，使|PA －PB |最大问题解决：作B 关于直线l 的对称点B '⇒PB ＝PB '，|PA －PB |＝|PA －PB '| 原理：三角形两边之和大于第三边，连接AB '，在△AB 'P 中|PA －PB '|≤AB 'llllll二、双动点问题（作两次对称）【问题5】在直线1l ，2l 上分别求点M ，N ，使△PMN 周长最小问题解决：分别作点P 关于两直线的对称点P ’和P ''，PM ＝P 'M ，PN ＝P ''N ，原理：两点之间线段最短，P '，P ''，与两直线交点即为M ，N ，则AM ＋MN ＋PN 的最小值为线段P 'P ''的长【问题6】P ，Q 为定点，在直线1l ，2l 上分别求点M ，N ，使四边形PQMN 周长最小问题解决：分别作点P ，Q 关于直线1l ，2l 的对称点P ’和Q '，PM ＝P 'M ，QN ＝Q 'N原理：两点之间线段最短，连接P 'Q '，与两直线交点即为M ，N ，则PM ＋MN ＋QN 的最小值为线段P 'Q '的长，周长最小值为P 'Q '＋PQl 1l 1l 1l 1【问题7】A ，B 分别为1l ，2l 上的定点，M ，N 分别为1l ，2l 上的动点，求AN MN BM ＋＋最小值问题解决：分别作A ，B 关于1l ，2l 的对称点'A ，'B ，则'AN A N ＝，'BM B M ＝，''A B 即所求原理：两点之间距离最短，A '，N ，M ，B '共线时取最小，则AN ＋MN ＋BM ＝A 'N ＋MN ＋B 'M ≤A 'B '三、动线段问题（造桥选址）【问题8】直线m ∥n ，在m ，n 上分别求点M ，N ，使MN ⊥m ，且AM ＋MN ＋BN 的最小值问题解决：将点B 向上平移MN 的长度单位得B '，连接B 'M ，当AB 'M 共线时有最小值原理：通过构造平行四边形转换成普通将军饮马，AM ＋MN ＋BN ＝AM ＋MN ＋B 'M ≤AB '＋MNl 2l 2n mn m【问题9】在直线l 上求两点M ，N (M 在左）且MN ＝a ，求AM MN BN ＋＋的最小值问题解决：将B 点向左移动a 个单位长度，再作B '关于直线l 的对称点B ''，当''AB M 共线有最小值原理：通过平移构造平行四边''''BB MN BN B M B M ⇒＝＝，''''AM MN BN AM MN B M AB ≤＋＋＝＋＋四、垂线段最短【问题10】在直线1l ，2l 上分别求点A ，B ，使PB ＋AB 最小问题解决：作P 关于2l 的对称点'P ，作1'P A l ⊥于A ，交2l 于B ，'P A 即所求原理：点到直线，垂线段最短，''PB AB P B AB P A ≤＋＝＋lll1l 1五、相对运动，平移型将军饮马【问题11】在直线l 上求两点M ，N (M 在左）且MN ＝a ，求AM ＋AN 的最小值问题解决：相对运动或构造平行四边形策略一：相对运动思想过点A 作MN 的平行线，相对MN ，点A 在该平行线上运动，则可转化为普通饮马问题策略二：构造平行四边形等量代换，同问题9.六、瓜豆轨迹，手拉手藏轨【问题12】如图，点P 在直线BC 上运动，将点P 绕定点A 逆时针旋转90°，得到点Q ，求Q 点轨迹？问题解决：当AP 与AQ 夹角固定且AP :AQ 为定值的话，P 、Q 轨迹是同一种图形．当确定轨迹是线段的时候，可以任取两个时刻的Q 点的位置，连线即可，比如Q 点的起始位置和终点位置，连接即得Q 点轨迹线段．llA''Q 2Q 1ABC原理：由手拉手可知12ABC AQ Q △≌△，故21CB AQ Q A =∠∠,故Q 点轨迹为直线七、化斜为直，斜大于直【问题13】已知：AD 是Rt ABC △斜边上的高（1）求ADBC的最大值；（2）若2AD =，求BC 的最大值问题解决：取BC 中点M ，（1）则12AD AM BC BC ≤=；（2）224BC AM AD =≤= 八、构造二次函数求最值这类问题一般无法通过纯几何方法来解决或几何方法比较复杂，需要通过面积法或者构造全等、相似建立等量关系，将待求的线段或图形的面积用含有自变量的式子来表示，一般是一个二次函数或者换元后是一个二次函数，然后通过配方得到最值．当然，配方的目的是为了避开基本不等式这个超纲的知识点，如果是选择题或填空题，你可以直接用基本不等式来秒杀，不需要配方．【问题14】正方形ABCD 的边长为6，点Q 在边CD 上，且3CD CQ =，P 是边BC 上一动点，连接PQ ，过点P 作EP PQ ⊥交AB 边于点E ，设BP 的长为x ，则线段BE 长度的最大值为 .问题解决：根据题意，作出图形，根据两个三角形相似的判定得到∽△△PCQ EBP ，进而根据相似比得到()219322BE x =−−+，利用二次函数求最值方法求解即可得到答案【详解】易知∽△△PCQ EBP ∴，QC PCBP BE ∴=， 3CD CQ =，6CD =，∴2QC =，26x x BE−∴=， ∴()()()()221119663062222BE x x x x x x =−=−−=−−+≤≤，BB102−< ，∴()219322BE x =−−+在3x =时有最大值，最大值为92题型一两定一动型（线段和差最值问题）2．透明圆柱形容器（容器厚度忽略不计）的高为12cm ，底面周长为10cm ，在容器内壁离底部3cm的点B 处有一饭粒，此时一只蚂蚁正好在容器外壁且离容器上沿3cm 的点A 处．求蚂蚁吃到饭点C 的坐标为（1，0），且∠AOB =30°点P 为斜边OB 上的一个动点，则P A +PC 的最小值为（）4．如图，点A ，B 在直线MN 的同侧，A 到MN 的距离8AC =，B 到MN 的距离5BD =，已知4CD =，5．如图，在矩形ABCD 中，AB ＝3，BC ＝5．动点P 满足S △PBC ＝S 矩形ABCD ．则点P 到B ，C 两点距离之和PB+PC 的最小值为。

将军饮马问题例题

将军饮马问题例题将军饮马问题是一个经典的数学谜题，题目如下：【题目】有一座1000级的楼梯，上面站着一位将军和他的马。

将军说：“我每次可以上1级、2级或者3级楼梯，而我的马每次只能上2级或者3级楼梯。

我们两个必须同时到达楼顶。

问，将军和马分别需要多少次才能到达楼顶，并且楼梯的哪些级别才能让他们同时到达楼顶？”【解答】假设将军上x次楼梯，马上y次楼梯。

1. 如果将军上1级楼梯，则马上y次楼梯，剩下的楼梯有999-x-2y级，将剩余楼梯由马上。

2. 如果将军上2级楼梯，则马上y次楼梯，剩下的楼梯有998-x-2y级，将剩余楼梯由马上。

3. 如果将军上3级楼梯，则马上y次楼梯，剩下的楼梯有997-x-2y级，将剩余楼梯由马上。

根据题意，将军和马必须同时到达楼顶，所以剩余的楼梯必须是2的倍数。

而剩余楼梯有999-x-2y、998-x-2y、997-x-2y三种情况，这些数分别除以2后的余数只能是0、1或者2。

又考虑到将军和马上楼梯的次数必须是整数，所以只需考虑将军和马都上奇数次楼梯的情况。

假设将军上奇数次楼梯x=2n+1，马上奇数次楼梯y=2m+1，代入上述条件，有：1. 剩下楼梯为999-(2n+1)-2(2m+1)=998-(2n+2m)-4=2(499-n-m)-4，是2的倍数；2. 剩下楼梯为998-(2n+1)-2(2m+1)=997-(2n+2m)-4=2(498-n-m)-3，不是2的倍数；3. 剩下楼梯为997-(2n+1)-2(2m+1)=996-(2n+2m)-4=2(498-n-m)-2，是2的倍数。

所以，将军和马必须同时走的是第3种情况，即将军和马都上奇数次楼梯。

最终答案是将军和马各上398次楼梯，并且将军和马会同时站在2、4、6、...、996、998共有499级楼梯上。

(完整word版)中考复习：“将军饮马”类题型大全

“将军饮马”类题型大全一．求线段和最值1（一）两定一动型例1：如图，AM⊥EF，BN⊥EF，垂足为M、N，MN＝12m，AM＝5m，BN＝4m， P是EF 上任意一点，则PA＋PB的最小值是______m．分析：这是最基本的将军饮马问题，A，B是定点，P是动点，属于两定一动将军饮马型，根据常见的“定点定线作对称”，可作点A关于EF的对称点A’，根据两点之间，线段最短，连接A’B，此时A’P＋PB即为A’B，最短．而要求A’B，则需要构造直角三角形，利用勾股定理解决．解答：作点A关于EF的对称点A’，过点A’作A’C⊥BN的延长线于C．易知A’M＝AM＝NC＝5m，BC＝9m，A’C＝MN＝12m，在Rt△A’BC中，A’B＝15m，即PA＋PB的最小值是15m．变式：如图，在边长为2的正三角形ABC中，E，F，G为各边中点，P为线段EF上一动点，则△BPG周长的最小值为_________．分析：考虑到BG为定值是1，则△BPG的周长最小转化为求BP＋PG的最小值，又是两定一动的将军饮马型，考虑作点G关于EF的对称点，这里有些同学可能看不出来到底是哪个点，我们不妨连接AG，则AG⊥BC，再连接EG，根据“直角三角形斜边中线等于斜边的一半”，可得AE＝EG，则点A就是点G关于EF的对称点．最后计算周长时，别忘了加上BG的长度．解答：连接AG，易知PG＝PA，BP＋PG＝BP＋PA，当B，P，A三点共线时，BP＋PG＝BA，此时最短，BA＝2，BG＝1，即△BPG周长最短为3.2（二）一定两动型例2：如图，在△ABC中，AB＝AC＝5，D为BC中点，AD＝5，P为AD上任意一点，E 为AC上任意一点，求PC＋PE的最小值．分析：这里的点C是定点，P，E是动点，属于一定两动的将军饮马模型，由于△ABC 是等腰三角形，AD是BC中线，则AD垂直平分BC，点C关于AD的对称点是点B，PC＋PE＝PB＋PE，显然当B，P，E三点共线时，BE更短．但此时还不是最短，根据“垂线段最短” 只有当BE⊥AC时，BE最短．求BE时，用面积法即可．解答：作BE⊥AC交于点E，交AD于点P，易知AD⊥BC，BD＝3，BC＝6，则AD·BC＝BE·AC，4×6＝BE·5，BE＝4.8变式：如图，BD平分∠ABC，E，F分别为线段BC，BD上的动点，AB＝8，△ABC的周长为20，求EF＋CF的最小值________．分析：这里的点C是定点，F，E是动点，属于一定两动的将军饮马模型，我们习惯于“定点定线作对称”，但这题这样做，会出现问题．因为点C的对称点C’必然在AB上，但由于BC长度未知，BC’长度也未知，则C’相对的也是不确定点，因此我们这里可以尝试作动点E关于BD的对称点．解答：如图，作点E关于BD的对称点E’，连接E’F，则EF＋CF＝E’F＋CF，当E’，F，C三点共线时，E’F＋CF＝E’C，此时较短．过点C作CE’’⊥AB于E’’，当点E’ 与点E’’重合时，E’’C最短，E’’C为AB边上的高，E’’C＝5.（三）两定两动型例3：如图，∠AOB＝30°，OC＝5，OD＝12，点E，F分别是射线OA，OB上的动点，求CF＋EF＋DE的最小值.分析：这里的点C，点D是定点，F，E是动点，属于两定两动的将军饮马模型，依旧可以用“定点定线作对称”来考虑．作点C关于OB的对称点，点D关于OA的对称点．解答：作点C关于OB的对称点C’，点D关于OA的对称点D’，连接C’D’． CF＋EF＋DE＝C’F＋ EF＋D’E，当C’，F， E，D’四点共线时，CF＋EF＋DE＝C’D’最短．易知∠D’OC’＝90°，OD’＝12，OC’＝5，C’D’＝13，CF＋EF＋DE最小值为13．变式：（原创题）如图，斯诺克比赛桌面AB宽1.78m，白球E距AD边0.22m，距CD 边1.4m，有一颗红球F紧贴BC边，且距离CD边0.1m，若要使白球E经过边AD，DC，两次反弹击中红球F，求白球E运动路线的总长度．分析：本题中，点E和点F是定点，两次反弹的点虽然未知，但我们可以根据前几题的经验作出，即分别作点E关于AD边的对称点E’，作点F关于CD边的对称点F’，即可画出白球E的运动路线，化归为两定两动将军饮马型．解答：作点E关于AD边的对称点E’，作点F关于CD边的对称点F’，连接E’F’，交AD于点G，交CD于点H，则运动路线长为EG＋GH＋HF长度之和，即E’F’长，延长E’E交BC于N，交AD于M，易知E’M＝EM＝0.22m，E’N＝1.78＋0.22＝2m，NF’＝NC＋CF’＝1.4＋0.1＝1.5m，则Rt△E’NF’中，E’F’＝2.5m，即白球运动路线的总长度为2.5m．小结：以上求线段和最值问题，几乎都可以归结为“两定一动”“一定两动”“两定两动”类的将军饮马型问题，基本方法还是“定点定线作对称”，利用“两点之间线段最短”“垂线段最短”的2条重要性质，将线段和转化为直角三角形的斜边，或者一边上的高，借助勾股定理，或者面积法来求解．当然，有时候，我们也需学会灵活变通，定点对称行不通时，尝试作动点对称．（二）求角度例1:P为∠AOB内一定点，M，N分别为射线OA，OB上一点，当△PMN周长最小时，∠MPN＝80°．（1）∠AOB＝_____°（2）求证：OP平分∠MPN分析：这又是一定两动型将军饮马问题，我们应该先将M，N的位置找到，再来思考∠AOB 的度数，显然作点P关于OA的对称点P’，关于OB的对称点P’’，连接P’P’’，其与OA交点即为M，OB交点即为N，如下图，易知∠DPC与∠AOB互补，则求出∠DPC的度数即可．解答：（1）法1：如图，∠1＋∠2＝100°，∠1＝∠P’＋∠3＝2∠3，∠2＝∠P’’＋∠4＝2∠4，则∠3＋∠4＝50°，∠DPC＝130°，∠AOB＝50°．再分析：考虑到第二小问要证明OP平分∠MPN，我们就连接OP，则要证∠5＝∠6，显然很困难，这时候，考虑到对称性，我们再连接OP’，OP’’，则∠5＝∠7，∠6＝∠8，问题迎刃而解．解答：（1）法2：易知OP’＝OP’’，∠7＋∠8＝∠5＋∠6＝80°，∠P’OP’’＝100°，由对称性知，∠9＝∠11，∠10＝∠12，∠AOB＝∠9＋∠10＝50°（2）由OP’＝OP’’，∠P’OP’’＝100°知，∠7＝∠8＝40°，∠5＝∠6＝40°，OP平分∠MPN．变式：如图，在五边形ABCDE中，∠BAE＝136°，∠B＝∠E＝90°，在BC、DE上分别找一点M、N，使得△AMN的周长最小时，则∠AMN＋∠ANM的度数为________．分析：这又是典型的一定两动型将军饮马问题，必然是作A点关于BC、DE的对称点A′、A″，连接A′A″，与BC、DE的交点即为△AMN周长最小时M、N的位置．解答：如图，∵∠BAE＝136°，∴∠MA′A＋∠NA″A＝44°由对称性知，∠MAA′＝∠MA′A，∠NAA″＝∠NA″A，∠AMN＋∠ANM＝2∠MA′A＋2∠NA″A＝88°思考题：1.（2017·安顺）如图所示，正方形ABCD的边长为6，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为_______．2.（2017·安徽改编）如图，在矩形ABCD中，AB=4，AD=3．P为矩形ABCD内一点，若矩形ABCD面积为△PAB面积的4倍，则点P到A，B两点距离之和PA+PB 的最小值为________．。

初中将军饮马问题题型总结(全)

初中将军饮马问题题型总结(全)题型一：将军饮马之单动点1.三角形中的将军饮马题目描述：在等腰三角形ABC中，AB=AC，AD、CE是三角形ABC的两条中线，P是AD上的一个动点，则下列线段的长度等于BP+EP最小值的是()解析：连接PC，由于AB=AC，BD=CD，AD垂直于BC，所以PB=PC。

因此，PB+PE=PC+PE，PE+PC>CE，当P、C、E共线时，PB+PE的值最小，最小值为CE的长度，故选B．2.等边三角形中的将军饮马题目描述：在等边三角形ABC中，AB=2，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，则PE+PC的最小值为()解析：连接BE交AD于点P'，AD、BE分别是等边三角形ABC边BC、AC的垂直平分线，P'B=P'C，P'E+P'C=P'E+P'B=BE。

根据两点之间线段最短，点P在点P'时，PE+PC有最小值，最小值即为BE的长。

因此，BE=BC/2-CE/2=3，所以P'E+P'C的最小值为3，故选C．3.等腰三角形中的将军饮马题目描述：在等腰三角形ABC中，AB=AC，BC=4，面积是16，AC的垂直平分线EF分别交AC、AB边于E、F点，若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为()解析：连接AD、AM，由于△ABC是等腰三角形，点D是BC边的中点，AD垂直于BC，所以S△ABC=1/2×4×AD=16，解得AD=8.EF是线段AC的垂直平分线，所以点C关于直线EF的对称点为点A，MA=MC，AD=AM+MD，因此AD的长为CM+MD的最小值。

且AC6，BM3，因为BM AD，故BM AC，所以BM是AC的中线，故CM3。

又因为AC是菱形的对角线，所以AC平分DAB，即DAM30。

又因为AM MD，所以ADM75。