初二数学思维导图
初二数学-八年级数学-因式分解的思维导图知识点结构图
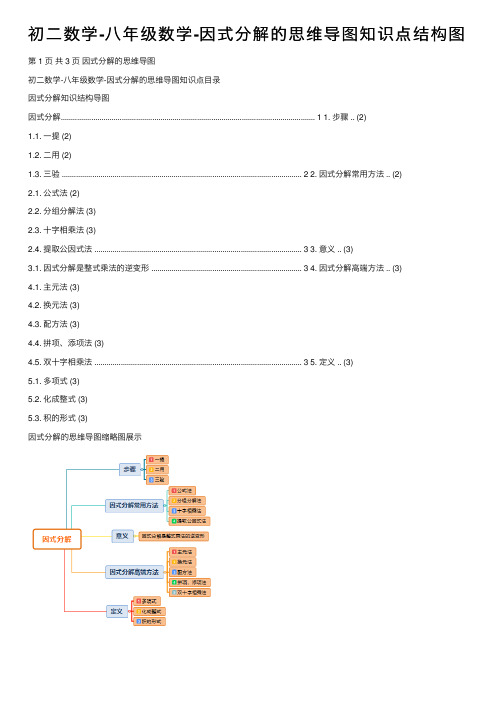
初二数学 -八年级Hale Waihona Puke 学 -因式分解的思维导图知识点结构图
第 1 页 共 3 页 因式分解的思维导图 初二数学-八年级数学-因式分解的思维导图知识点目录 因式分解知识结构导图 因式分解............................................................................................................................. 1 1. 步骤 .. (2) 1.1. 一提 (2) 1.2. 二用 (2) 1.3. 三验 ...................................................................................................................... 2 2. 因式分解常用方法 .. (2) 2.1. 公式法 (2) 2.2. 分组分解法 (3) 2.3. 十字相乘法 (3) 2.4. 提取公因式法 ...................................................................................................... 3 3. 意义 .. (3) 3.1. 因式分解是整式乘法的逆变形 .......................................................................... 3 4. 因式分解高端方法 .. (3) 4.1. 主元法 (3) 4.2. 换元法 (3) 4.3. 配方法 (3) 4.4. 拼项、添项法 (3) 4.5. 双十字相乘法 ...................................................................................................... 3 5. 定义 .. (3) 5.1. 多项式 (3) 5.2. 化成整式 (3) 5.3. 积的形式 (3) 因式分解的思维导图缩略图展示
八年级数学的思维导图

八年级数学的思维导图:全等三角形:二次根式:实数:相似图形因式分解1. 因式分把一个多项式化为几个整式的积的形式,叫做把这个多项式因式分解;注意:因式分解与乘法是相反的两个转化.2.因式分解的方法:常用提取公因式法、公式法、分组分解法、十字相乘法.3.公因式的确定:系数的最大公约数相同因式的最低次幂.注意公式:a+b=b+a; a-b=-(b-a); (a-b)2=(b-a)2; (a-b)3=-(b-a)3.4.因式分解的公式:(1)平方差公式: a2-b2=(a+ b)(a- b);(2)完全平方公式: a2+2ab+b2=(a+b)2, a2-2ab+b2=(a-b)2.5.因式分解的注意事项:(1)选择因式分解方法的一般次序是:一提取、二公式、三分组、四十字;(2)使用因式分解公式时要特别注意公式中的字母都具有整体性;(3)因式分解的最后结果要求分解到每一个因式都不能分解为止;(4)因式分解的最后结果要求每一个因式的首项符号为正;(5)因式分解的最后结果要求加以整理;(6)因式分解的最后结果要求相同因式写成乘方的形式.6.因式分解的解题技巧:(1)换位整理,加括号或去括号整理;(2)提负号;(3)全变号;(4)换元;(5)配方;(6)把相同的式子看作整体;(7)灵活分组;(8)提取分数系数;(9)展开部分括号或全部括号;(10)拆项或补项.7.完全平方式:能化为(m+n)2的多项式叫完全平方式;对于二次三项式x2+px+q, 有 x2+px+q是完全平方式 .分式1.分式:一般地,用A、B表示两个整式,AB就可以表示为的形式,如果B中含有字母,式子叫做分式.2.有理式:整式与分式统称有理式;即 .3.对于分式的两个重要判断:(1)若分式的分母为零,则分式无意义,反之有意义;(2)若分式的分子为零,而分母不为零,则分式的值为零;注意:若分式的分子为零,而分母也为零,则分式无意义.4.分式的基本性质与应用:(1)若分式的分子与分母都乘以(或除以)同一个不为零的整式,分式的值不变;(2)注意:在分式中,分子、分母、分式本身的符号,改变其中任何两个,分式的值不变;即(3)繁分式化简时,采用分子分母同乘小分母的最小公倍数的方法,比较简单.5.分式的约分:把一个分式的分子与分母的公因式约去,叫做分式的约分;注意:分式约分前经常需要先因式分解.6.最简分式:一个分式的分子与分母没有公因式,这个分式叫做最简分式;注意:分式计算的最后结果要求化为最简分式.7.分式的乘除法法则: .8.分式的乘方: .9.负整指数计算法则:(1)公式: a0=1(a0), a-n= (a0);(2)正整指数的运算法则都可用于负整指数计算;(3)公式: , ;(4)公式: (-1)-2=1, (-1)-3=-1.。
人教版 八年级上册数学 章节思维导图集 图片版
你现在的努力要对得起别人对你的好!
Math 实验室-1-人教版八年级数学上册章节思维导图
共5章
人教版八年级数学上册教材目录
第11章三角形的思维导图
11.1与三角形有关的线段
11.2与三角形有关的角
11.3多边形及其内角和
第12章全等三角形的思维导图
12.1全等三角形
12.2三角形全等的判定
12.3角的平分线的性质
第13章轴对称的思维导图
13.1轴对称
13.2画轴对称图形
13.3等腰三角形
13.4课题学习最短路径问题
第14章整式的乘法与因式分解的思维导图
14.1整式的乘法
14.2乘法公式
14.3因式分解
第15章分式的思维导图
15.1分式
15.2分式的运算
15.3
分式方程。
八年级上册数学人教版思维导图

第十一章 三角形与三角形有关的线段与三角形有关的角多边形及其内角和相关概念三角形的定义三角形的分类三角形的三边关系①三条线段②不在同一直线上③首位顺次相接按角分类锐角三角形直角三角形钝角三角形按边分类三边都不相等的三角形等腰三角形底和腰不相等的等腰三角形等边三角形(特殊的等腰三角形)三角形两边的和大于第三边三角形两边的差小于第三边三角形的三条重要线段(高,中线,角平分线)相同点都是线段都有三条,且交于一点交点位置高线锐角三角形→三角形内部直角三角形→直角顶点钝角三角形→三角形外部 中线(交点叫做三角形的重心)角平分线位于三角形内部性质三角形的高线→直角三角形或90°的角 三角形的中线→所分的两个三角形面积相等(所分两个三角形等底同高)三角形的角平分线→相等的角或成2倍关系的角三角形的稳定性 三角形具有稳定性,而其他多边形都不具有稳定性 三角形内角和定理:三角形三个内角的和等于180° 三角形的外角:三角形的外角等于与它不相邻的两个内角的和直角三角形性质:直角三角形的两个锐角互余判定有一个角是直角的三角形是直角三角形有两个角互余的三角形是直角三角形 概念:在平面内,由一些线段首位顺次相接组成的封闭图形叫做多边形多边形的内角和多边形的外角和各条边都相等的多边形叫做正多边形边形的内角和等于正边形的每一个内角为多边形的外角和等于360°(与边数无关)正边形的每一个外角为多边形的对角线边形的对角线的条数为第十三章轴对称轴对称用坐标表示轴对称有关概念线段的垂直平分线轴对称图形的有关性质轴对称图形:把一个平面图形沿着一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形成轴对称:把一个图形沿着一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称定义:经过线段中点并且垂直于这条线段的直线性质判定:与线段两个端点距离相等的点在这条线段的垂直平分线上对应线段相等,对应角相等对称轴垂直平分连接对应点的线段关于x轴对称的两个点的坐标特征:横坐标相等,纵坐标互为相反数关于y轴对称的两个点的坐标特征:横坐标互为相反数,纵坐标相等等腰三角形等腰三角形性质轴对称图形→有一条对称轴等边对等角→在同一个三角形中证明角相等三线合一顶角平分线底边上的高底边上的中线相互重合判定定义:两边相等等角对等边→也是证明线段相等的方法等边三角形性质轴对称图形→三条对称轴三线合一→三条三线合一的线三条边都相等三个内角都相等,并且每一个角都等于60°判定三条边相等的三角形→已知三边关系用此方法三个角都相等的三角形→已知三个内角的关系用此方法有一个角是60°的等腰三角形→已知两边相等时可找一个60°的角用此方法含30°角的直角三角形的性质:在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半应用“已知一条直线及其同侧的两点,在直线上确定一点,使它到这两个已知点的距离之和最小”的问题,这类问题一般都是首先作出其中一个点关于直线的对称点,然后连接另一点和对称点,借助两点之间线段最短解决问题线段垂直平分线垂直且平分该线段线段垂直平分线上任意一点到该线段两端点的距离相等三角形三条边的垂直平分线相交于一点,这一点到三个顶点的距离相等与线段两个端点距离相等的点在这条线段的垂直平分线上第十四章整式的乘法与因式分解幂的运算法则同底数幂的乘法法则:都是正整数推广:均为正整数逆用:都是正整数幂的乘方法则:都是正整数推广:都是正整数逆用:都是正整数积的乘方法则:都是正整数推广:都是正整数)逆用:都是正整数同底数幂的除法法则:都是正整数并且推广:都是正整数并且逆用:都是正整数并且零指数幂整式的乘、除法法则单项式乘单项式单项式乘多项式多项式乘多项式单项式除以单项式多项式除以单项式乘法公式平方差公式完全平方公式添括号因式分解提取公因式公式法系数×系数→积的系数同底数幂×同底数幂→积的幂只在一个单项式里含有的字母→连同指数作为积的一个因式法则:单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加公式表示:m(a+b-c)=ma+mb+m(-c)=ma+mb-m c法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加公式表示:(a+b)(m-n)=am+a(-n)+bm+b(-n)=a m-an+bm-bn被除式系数÷除式系数→商的系数被除式同底数幂÷除式同底数幂→商中的幂只在被除式里含有的字母→连同指数作为商的一个因式法则:多项式除以单项式,先把这个多项式的每一项除以单项式,再把所得的商相加公式表示:(am+bm-cm)÷m=am÷m+bm÷m+(-c m)÷m=a+b+(-c)=a+b-c括号前“+”→括到括号里的各项都不变符号括号前“-”→括到括号里的各项都改变符号m a+mb+mc→m(a+b+c)公因式的确定方法系数→多项式中各项系数的最大公因数字母→多项式中各项中都含有的相同字母相同字母的次数→多项式中各项中相同字母的最低次幂第十五章分式分式的有关概念分式的基本性质分式方程分式的运算分式的定义分式有意义的条件分式值为零的条件基本性质约分和通分分式的乘法分式的除法分式的乘方分式的加减分式的混合运算分式方程的定义分式方程的解法分式方程的应用一般地如果表示两个整式并且中含有字母那么式子叫做分式分式无意义→B=0分式有意义→B≠0A=0B≠0缺一不可分式的式子与分母乘(或除以)同一个不等于0的整式,分式的值不变式子表示其中是整式分式的通分→确定最简公分母分式的约分→确定分子和分母的公因式最简公分母的确定方法系数→各分母系数的最小公倍数字母→各分母中含有的所有字母相同字母的次数→各分母中相同字母的最高次幂不等于不等于法则:是正整数逆用是正整数)同分母相加减:异分母相加减:无括号:乘方→乘除→加减有括号:小括号→中括号→大括号结果为最简形式负整数指数幂科学记数法绝对值小于1的数→为原数第个不为零的数字前面所有零的个数包括小数点前面的零分母中含有未知数的方程是分式方程,判断一个方程是否为分式方程关键看分母中是否含有未知数去分母→方程两边同乘最简公分母,把分式方程化为整式方程解整式方程检验→将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解使原分式方程的解;否则,就是原分式方程的增根,原分式方程无解审→审清题意,弄清已知量和未知量找→找出等量关系设→设未知数列→列分式方程解→解这个方程验→既要检验所求的解使分式方程的解,又要检验求得的解是否符合实际意义答→写出答案。
八年级上册数学第十三章 轴对称思维导图 脑图
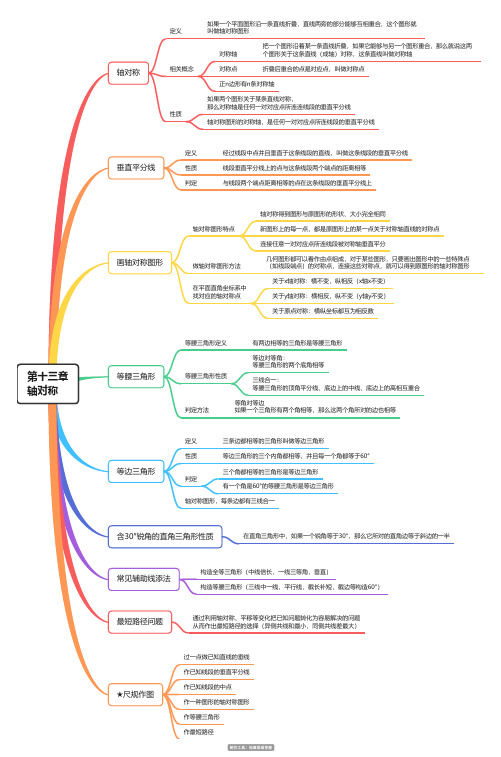
第十三章轴对称轴对称定义如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形相关概念对称轴把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做对称轴对称点折叠后重合的点是对应点,叫做对称点正n边形有n条对称轴性质如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连连线段的垂直平分线轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线垂直平分线定义经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线性质线段垂直平分线上的点与这条线段两个端点的距离相等判定与线段两个端点距离相等的点在这条线段的垂直平分线上画轴对称图形轴对称图形特点轴对称得到图形与原图形的形状、大小完全相同新图形上的每一点,都是原图形上的某一点关于对称轴直线的对称点连接任意一对对应点所连线段被对称轴垂直平分做轴对称图形方法几何图形都可以看作由点组成,对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形在平面直角坐标系中找对应的轴对称点关于x轴对称:横不变,纵相反(x轴x不变)关于y轴对称:横相反,纵不变(y轴y不变)关于原点对称:横纵坐标都互为相反数等腰三角形等腰三角形定义有两边相等的三角形是等腰三角形等腰三角形性质等边对等角:等腰三角形的两个底角相等三线合一:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合判定方法等角对等边如果一个三角形有两个角相等,那么这两个角所对的边也相等等边三角形定义三条边都相等的三角形叫做等边三角形性质等边三角形的三个内角都相等,并且每一个角都等于60°判定三个角都相等的三角形是等边三角形有一个角是60°的等腰三角形是等边三角形轴对称图形,每条边都有三线合一含30°锐角的直角三角形性质在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半常见辅助线添法构造全等三角形(中线倍长,一线三等角,垂直)构造等腰三角形(三线中一线,平行线,截长补短,截边等构造60°)最短路径问题通过利用轴对称、平移等变化把已知问题转化为容易解决的问题从而作出最短路径的选择(异侧共线和最小,同侧共线差最大)★尺规作图过一点做已知直线的垂线作已知线段的垂直平分线作已知线段的中点作一种图形的轴对称图形作等腰三角形作最短路径。
八年级上册数学第14章思维导图

八年级上册数学第14章思维导图1. 引言数学是一门让人们锻炼思维的学科,而思维导图则是一种帮助我们整理、梳理思路的工具。
在八年级上册数学的第14章中,我们将学习使用思维导图来解决各种数学问题。
2. 思维导图的定义思维导图是一种以中心主题为核心,通过分支思维展开的图形结构。
它可以帮助我们更好地组织和理清思路,发现问题的关联性和隐含规律。
3. 思维导图的作用思维导图在数学学习中有着重要的作用,它可以帮助我们:- 整理和梳理知识点 - 分析和解决问题 - 建立知识框架4. 思维导图的制作步骤制作思维导图的步骤如下: 1. 根据主题确定中心思想,并将其写在中心节点上。
2. 再根据主题确定一级分支,将其写在中心节点的周围。
3. 对于每个一级分支,进一步确定二级分支,并写在一级分支的周围。
4. 如此类推,逐级展开分支,直到思维导图中的所有内容都被覆盖到。
5. 思维导图的设计要点制作思维导图时需要注意以下几个设计要点: - 标题要明确简洁,突出主题。
- 结点之间要有一定的关联性,分支之间的连接要清晰。
- 结点和分支的字体大小要适中,不同级别的结点可以使用不同的字体大小来区分。
- 可以使用不同的颜色、形状和图标来标记重要内容或特点。
6. 思维导图在数学学习中的应用思维导图在数学学习中有很广泛的应用,特别是在解决问题时: - 在解决复杂的数学问题时,可以使用思维导图将问题进行拆解,找到解决问题的关键步骤和方法。
- 在学习概念和定理时,可以使用思维导图将相关的内容整理出来,帮助记忆和理解。
- 在学习数学思维方法和解题技巧时,可以使用思维导图将各种方法和技巧整合起来,形成一个完整的思维体系。
7. 总结通过学习并使用思维导图,我们可以更好地整理和梳理数学知识,提高问题解决能力。
思维导图是一种简单实用的工具,帮助我们理清思路,深入思考问题。
在以后的数学学习中,我们可以随时运用思维导图的方法,将复杂的问题化繁为简,提高学习的效果和速度。
2020人教版八上数学思维导图(史上最新最全)

整章内容预览,梳理知识脉络,学习记忆好帮手,复习补漏好工具 目录
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十一章 三角形
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十二章 全等三角形
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十三章 轴对称
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
第十四章 整式的公众号“数学资料库”,更多优质内容免费领。
第十五章 分式
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
精心原创,谢绝盗图 关注公众号“数学资料库”,更多优质内容免费领。
初中数学各章节知识图解思维导图

最简公分母
子积为子母积为母
化除法为乘法
注:分子、 分母为多 项式时先 分解因式
同类项
合并 同类项
系数 相加 字母 不变
通分
约分
不改变 分式的值
应用
解法
因式分解
除法
乘法
加减
定义
性质
运算
加减
乘除
系数
次数
数字因数
字母指数和
意义
次数
项
最高项的次数
每个单项式
升降幂排列
一次函数与反比例函数
动
圆
四边形
四 边 形 与 圆
梯形
平行四边形
性质
性质
菱形
①
②
④
③
④
等腰
直角
辅助线
平移两腰
平移对角线
作高线
延长两腰
利用腰中点 割补成--- 全等三角形、 平行四边形
性质
判定
边
角
对角线
对边平行且相等
对角相等邻角互补
对角线 互相平分
性质
判定
判定
判定
矩形
一个直角
对角线相等
一组邻边相等
镶嵌
定义
条件
概念
性质
判定
特例
定 义
表 示 方 法
要 素
等 边 对 等 角
三 线 合 一
等 角 对 等 边
等 边 三 角 形
勾股定理
锐角三角函数
定理
逆定理
应用
证明
内容
文字.符号图形
已知两边求第三边
弦图 毕达哥拉斯苏菲尔德
应用
证明
初中数学八年级上册思维导图

初中数学八年级上册思维导图一、数的开方1. 平方根:如果一个正数x的平方等于a,那么x是a的平方根,记作x=√a。
正数a的平方根有两个,它们互为相反数,分别记作√a和√a。
0的平方根是0。
2. 立方根:如果一个数x的立方等于a,那么x是a的立方根,记作x=³√a。
立方根只有一个。
3. 算术平方根:正数a的正的平方根,记作√a,称为a的算术平方根。
4. 立方根的性质:①正数的立方根是正数;②负数的立方根是负数;③0的立方根是0。
二、实数1. 实数的概念:实数包括有理数和无理数。
有理数是可以表示为两个整数比的数,无理数是不能表示为两个整数比的数。
2. 实数的分类:①正实数;②负实数;③零。
3. 实数的运算:实数的加减乘除运算与有理数的运算类似,但需要注意无理数的运算。
三、二次根式1. 二次根式的概念:形如√a的式子,其中a≥0,称为二次根式。
2. 二次根式的性质:①√a²=a(a≥0);②(√a)²=a(a≥0);③√ab=√a√b(a≥0,b≥0);④√a²+b²=√a²+√b²(a≥0,b≥0)。
3. 二次根式的运算:二次根式的加减乘除运算与有理数的运算类似,但需要注意无理数的运算。
四、一元二次方程1. 一元二次方程的概念:形如ax²+bx+c=0(a≠0)的方程,称为一元二次方程。
2. 一元二次方程的解法:①配方法;②求根公式法;③因式分解法。
3. 一元二次方程的根的判别式:判别式△=b²4ac,当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根。
五、不等式1. 不等式的概念:表示不相等关系的式子称为不等式。
2. 不等式的性质:①两边同时加上或减去同一个数,不等号方向不变;②两边同时乘以或除以同一个正数,不等号方向不变;③两边同时乘以或除以同一个负数,不等号方向改变。
数学八年级上册第一章思维导图
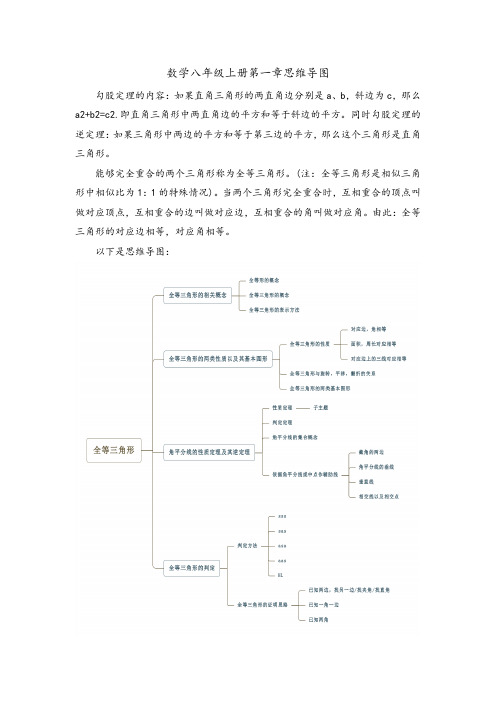
数学八年级上册第一章思维导图
勾股定理的内容:如果直角三角形的两直角边分别是a、b,斜边为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方。
同时勾股定理的逆定理:如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
能够完全重合的两个三角形称为全等三角形。
(注:全等三角形是相似三角形中相似比为1:1的特殊情况)。
当两个三角形完全重合时,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角。
由此:全等三角形的对应边相等,对应角相等。
以下是思维导图:
全等三角形的判定定理:
⑴边边边:三边对应相等的两个三角形全等。
⑵边角边:两边和它们的夹角对应相等的两个三角形全等。
⑶角边角:两角和它们的夹边对应相等的两个三角形全等。
⑷角角边:两角和其中一个角的对边对应相等的两个三角形全等。
⑸斜边、直角边:斜边和一条直角边对应相等的两个直角三角形全等
1、其中三角形全等是条件,结论是对应角、对应边相等。
而全等的判定却刚好相反。
2、利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键。
在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便。
3、当图中出现两个以上等边三角形时,应首先考虑用SAS找全等三角形。
4、用在实际中,一般我们用全等三角形测相等的距离。
以及相等的角,可以用于工业和军事。
数学八年级思维导图上册

数学八年级思维导图上册数学八年级思维导图上册
一、有理数
1. 有理数的定义
2. 有理数的四则运算
3. 有理数的大小比较
4. 有理数的绝对值
5. 有理数的加减法运算规律
二、代数式与方程式
1. 代数式的概念
2. 代数式的加减乘除
3. 代数式的因式分解
4. 简单一元一次方程式的解法
5. 一元一次方程式的应用
三、平面图形
1. 平面图形的基本概念
2. 三角形的性质及分类
3. 四边形的性质及分类
4. 正多边形的性质及分类
5. 平行线与平面图形的性质
四、函数
1. 函数的定义
2. 常见函数及其图像
3. 函数的性质及变化规律
4. 函数的概念拓展
5. 函数的图像及其在实际问题中的应用
五、统计与概率
1. 统计中的基本概念及统计图
2. 概率的基本概念及概率模型
3. 事件的概念及其运算
4. 概率的应用
5. 统计与概率在实际问题中的应用
六、三角函数
1. 角度制与弧度制
2. 常见三角函数及其性质
3. 三角函数的等式和恒等式
4. 三角函数的运用及其在实际问题中的应用
5. 三角函数的图像和周期性
七、空间图形
1. 空间图形的基本概念及表示方法
2. 立体图形的计算
3. 空间直角坐标系及其应用
4. 空间几何中的关系与定理
5. 空间几何在实际问题中的应用
总结:
数学八年级思维导图上册内容涵盖了初中阶段最重要的数学知识点,包括有理数、代数式与方程式、平面图形、函数、统计与概率、三角函数以及空间图形等方面,是初中数学学习的重要参考资料。
八年级数学思维导图

八年级数学思维导图
第十一章三角形
有关概念三角形的定义顶点、边、内角及其表示方法三角形三边的关系两边之和大于第三边(指任意两边)与三角形有关的线段三角形的高
三条重要线段三角形的中线三角形的角平分线三角形内角和定理三角形三个内角的和等于180°三角形与三角形有关的角三角形的外角及其性质三角形的外角三角形外角的性质多边形
多边形的有关概念内角、外角、对角线凸多边形
多边形及其内角和正多边形
多边形的内角和n边形的内角和等于(n-2)x 180°多边形的外角和n边形的外角和等于360°第十二章全等三角形
全等三角形的对应边相等全等三角形的性质
全等形
全等三角形的对应角相等边边边SSS一般三角形边角边SAS
特殊的全等形
角边角ASA三角形全等的判定角角边AASSSS,SAS,ASA,AAS直角三角形HL只适用于直角三角形全等三角形
应用全等三角形解决实际问题
互逆定理角中分线的性子角中分线的性子与判定角中分线的判定第十三章轴对称第十四章整式的乘法与因式分化第十五章分式第十六章二次根式
满意以下两个特点的二次根式,
叫最简二次根式.
(1)被开方数不含分母,分母
中不含二次根式;
(2)被开方数中不含开得尽方的因数或因式.
最简二次根式
二次根式
的乘法
二次根式
的除法
(a≥0,b>0)
二次根式
的夹杂运算。
八年级数学的思维导图

八年级数学的思维导图:全等三角形:二次根式:实数:相似图形因式分解1、因式分把一个多项式化为几个整式的积的形式,叫做把这个多项式因式分解;注意:因式分解与乘法是相反的两个转化。
2、因式分解的方法:常用提取公因式法、公式法、分组分解法、十字相乘法。
3、公因式的确定:系数的最大公约数相同因式的最低次幂。
注意公式:a+b=b+a;a-b=-(b-a);(a-b)2=(b-a)2;(a-b)3=-(b-a)3、4、因式分解的公式:(1)平方差公式:a2-b2=(a+b)(a-b);(2)完全平方公式:a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2、5、因式分解的注意事项:(1)选择因式分解方法的一般次序是:一提取、二公式、三分组、四十字;(2)使用因式分解公式时要特别注意公式中的字母都具有整体性;(3)因式分解的最后结果要求分解到每一个因式都不能分解为止;(4)因式分解的最后结果要求每一个因式的首项符号为正;(5)因式分解的最后结果要求加以整理;(6)因式分解的最后结果要求相同因式写成乘方的形式。
6。
因式分解的解题技巧:(1)换位整理,加括号或去括号整理;(2)提负号;(3)全变号;(4)换元;(5)配方;(6)把相同的式子看作整体;(7)灵活分组;(8)提取分数系数;(9)展开部分括号或全部括号;(10)拆项或补项。
7。
完全平方式:能化为(m+n)2的多项式叫完全平方式;对于二次三项式2+p+q,有2+p+q是完全平方式。
分式1、分式:一般地,用A、B表示两个整式,AB就可以表示为的形式,如果B中含有字母,式子叫做分式。
2、有理式:整式与分式统称有理式;即。
3、对于分式的两个重要判断:(1)若分式的分母为零,则分式无意义,反之有意义;(2)若分式的分子为零,而分母不为零,则分式的值为零;注意:若分式的分子为零,而分母也为零,则分式无意义。
4、分式的基本性质与应用:(1)若分式的分子与分母都乘以(或除以)同一个不为零的整式,分式的值不变;(2)注意:在分式中,分子、分母、分式本身的符号,改变其中任何两个,分式的值不变;即(3)繁分式化简时,采用分子分母同乘小分母的最小公倍数的方法,比较简单。
