机械设计基础课后答案(杨可桢)50781
机械设计基础课后答案(杨可桢)

图8.11
解:〔1〕求质心偏移实际就是求静平衡时的平衡向静,因此可以按照静平衡条件考虑这个
问题。
先求出各不平衡质径积的大小:
方向沿着各自的向径指向外面。
用作图法求解,取,作图8.11〔a〕所示。
由静平衡条件得:
,偏移的方由图量得,那么质心偏移的距离为向就是平衡质
径积的方向,与水平夹角为。
(2〕求左右支反力实际上就是求动平衡时在左右支点所在平面所需要的平衡力。
先把
不平衡质量在两支承所在平面上分解。
左支承:;
右支承:;
那么在两个支承所在平面上的质径积的大小分别为:
左支承:;
右支承:;
方向沿着各自的向径指向外面。
用作图法求解,取,作图8.11〔b〕〔c〕所示。
由动平衡条件得:
左支承:,量得,
那么支反力大小为
右支承:,量得,
那么支反力大小为
8-7
图8.13
解:〔1〕先把不平衡质量在两平衡基面Ⅰ和Ⅱ上分解。
基面Ⅰ:
基面Ⅱ:。
机械设计基础(第五版)_杨可桢主编_课后习题答案之欧阳文创编

机械设计基础(第五版)课后习题答案(完整版)时间:2021.03.12 创作:欧阳文杨可竺、程光蕴、李仲生主编1-1至1-4解机构运动简图如下图所示。
图 1.11 题1-1解图图1.12 题1-2解图图 1.13 题1-3解图图1.14 题1-4解图1-5 解1-6 解1-7 解1-8 解1-9 解1-10 解1-11 解1-12 解1-13解该导杆机构的全部瞬心如图所示,构件 1、3的角速比为:1-14解该正切机构的全部瞬心如图所示,构件 3的速度为:,方向垂直向上。
1-15解要求轮 1与轮2的角速度之比,首先确定轮1、轮2和机架4三个构件的三个瞬心,即,和,如图所示。
则:,轮2与轮1的转向相反。
1-16解( 1)图a中的构件组合的自由度为:自由度为零,为一刚性桁架,所以构件之间不能产生相对运动。
( 2)图b中的 CD 杆是虚约束,去掉与否不影响机构的运动。
故图 b中机构的自由度为:所以构件之间能产生相对运动。
题 2-1答 : a ),且最短杆为机架,因此是双曲柄机构。
b ),且最短杆的邻边为机架,因此是曲柄摇杆机构。
c ),不满足杆长条件,因此是双摇杆机构。
d ),且最短杆的对边为机架,因此是双摇杆机构。
题 2-2解 : 要想成为转动导杆机构,则要求与均为周转副。
( 1 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在中,直角边小于斜边,故有:(极限情况取等号);在中,直角边小于斜边,故有:(极限情况取等号)。
综合这二者,要求即可。
( 2 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在位置时,从线段来看,要能绕过点要求:(极限情况取等号);在位置时,因为导杆是无限长的,故没有过多条件限制。
( 3 )综合( 1 )、( 2 )两点可知,图示偏置导杆机构成为转动导杆机构的条件是:题 2-3 见图 2.16 。
图 2.16题 2-4解 : ( 1 )由公式,并带入已知数据列方程有:因此空回行程所需时间;( 2 )因为曲柄空回行程用时,转过的角度为,因此其转速为:转 / 分钟题 2-5解 : ( 1 )由题意踏板在水平位置上下摆动,就是曲柄摇杆机构中摇杆的极限位置,此时曲柄与连杆处于两次共线位置。
机械设计基础(第五版)_杨可桢主编_课后习题答案之欧阳育创编

机械设计基础(第五版)课后习题答案(完整版)时间:2021.02.04 创作:欧阳育杨可竺、程光蕴、李仲生主编1-1至1-4解机构运动简图如下图所示。
图 1.11 题1-1解图图1.12 题1-2解图图 1.13 题1-3解图图1.14 题1-4解图1-5 解1-6 解1-7 解1-8 解1-9 解1-10 解1-11 解1-12 解1-13解该导杆机构的全部瞬心如图所示,构件1、3的角速比为:1-14解该正切机构的全部瞬心如图所示,构件3的速度为:,方向垂直向上。
1-15解要求轮 1与轮2的角速度之比,首先确定轮1、轮2和机架4三个构件的三个瞬心,即,和,如图所示。
则:,轮2与轮1的转向相反。
1-16解( 1)图a中的构件组合的自由度为:自由度为零,为一刚性桁架,所以构件之间不能产生相对运动。
(2)图b中的CD 杆是虚约束,去掉与否不影响机构的运动。
故图 b中机构的自由度为:所以构件之间能产生相对运动。
题 2-1答 : a ),且最短杆为机架,因此是双曲柄机构。
b ),且最短杆的邻边为机架,因此是曲柄摇杆机构。
c ),不满足杆长条件,因此是双摇杆机构。
d ),且最短杆的对边为机架,因此是双摇杆机构。
题2-2解: 要想成为转动导杆机构,则要求与均为周转副。
( 1 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在中,直角边小于斜边,故有:(极限情况取等号);在中,直角边小于斜边,故有:(极限情况取等号)。
综合这二者,要求即可。
( 2 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在位置时,从线段来看,要能绕过点要求:(极限情况取等号);在位置时,因为导杆是无限长的,故没有过多条件限制。
( 3 )综合( 1 )、( 2 )两点可知,图示偏置导杆机构成为转动导杆机构的条件是:题 2-3 见图 2.16 。
图 2.16题2-4解: (1 )由公式,并带入已知数据列方程有:因此空回行程所需时间;( 2 )因为曲柄空回行程用时,转过的角度为,因此其转速为:转 / 分钟题 2-5解: (1 )由题意踏板在水平位置上下摆动,就是曲柄摇杆机构中摇杆的极限位置,此时曲柄与连杆处于两次共线位置。
杨可桢《机械设计基础》课后习题及详解(平面机构的自由度和速度分析)【圣才出品】
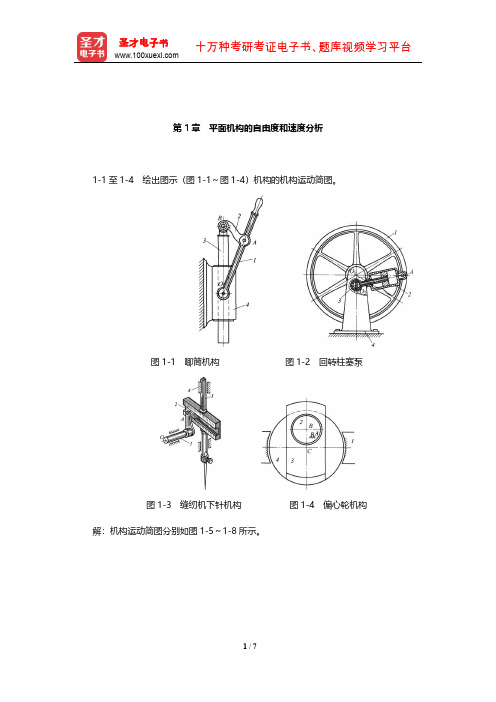
第1章平面机构的自由度和速度分析1-1至1-4 绘出图示(图1-1~图1-4)机构的机构运动简图。
图1-1 唧筒机构图1-2 回转柱塞泵图1-3 缝纫机下针机构图1-4 偏心轮机构解:机构运动简图分别如图1-5~1-8所示。
1-5至1-12 指出(图1-9~图1-16)机构运动简图中的复合铰链、局部自由度和虚约束,计算各机构的自由度。
图1-9 平炉渣口堵塞机构图1-10 锯木机机构图1-11 加药泵加药机构图1-12 测量仪表机构图1-13 缝纫机送布机构图1-14 冲压机构图1-15 差动轮系 图1-16 机械手解:图1-9 滚子处为局部自由度,。
图1-10 滚子处为局部自由度,。
图1-11。
图1-12。
图1-13 滚子处为局部自由度,。
图1-14 滚子处为局部自由度,右方三杆铰接处为复合铰链,下方两导程槽之一为虚约束,。
图1-15 最下方齿轮与机架,杆组成复合铰链,。
图1-16 3233233L H F n P P =--=⨯-⨯=。
1-13 求出图1-17导杆机构的全部瞬心和构件1、3的角速比。
图1-17 导杆机构解:该导杆机构的全部瞬心如图1-18所示。
由1141333413P P P P ωω=可得,杆件1、3的角速度比:3413131413P P P P ωω=。
1-14 求出图1-19正切机构的全部瞬心。
设1ω=10 rad /s ,求构件3的速度3ν。
图1-19 正切机构解:该正切机构的全部瞬心如图1-20所示。
由114133P P v ω=可得,构件3的速度:311413102002000v P P ω==⨯=。
1-15 图1-21所示为摩擦行星传动机构,设行星轮2与构件1、4保持纯滚动接触,图试用瞬心法求轮1与轮2的角速比1ω/2ω。
图1-21 摩擦行星传动机构解:确定轮1、轮2和机架4三个构件的三个瞬心121424P P P 、、,如图1-22所示。
由于在行星轮2和构件1的瞬心12P 处,有12v v =,即11222r r ωω=⋅ 因此,轮1和轮2的角速比12212r r ωω=。
机械设计基础课后答案(杨可桢)

1-1至1-4解机构运动简图如下图所示。
图1.11 题1-1解图图1.12 题1-2解图图1.13 题1-3解图图1.14 题1-4解图1-5 解1-6 解1-7 解1-8 解1-9 解1-10 解1-11 解1-12 解1-13解该导杆机构的全部瞬心如图所示,构件1、3的角速比为:1-14解该正切机构的全部瞬心如图所示,构件3的速度为:,方向垂直向上。
1-15解要求轮1与轮2的角速度之比,首先确定轮1、轮2和机架4三个构件的三个瞬心,即,和,如图所示。
则:,轮2与轮1的转向相反。
1-16解(1)图a中的构件组合的自由度为:自由度为零,为一刚性桁架,所以构件之间不能产生相对运动。
(2)图b中的CD 杆是虚约束,去掉与否不影响机构的运动。
故图b中机构的自由度为:所以构件之间能产生相对运动。
题2-1答: a ),且最短杆为机架,因此是双曲柄机构。
b ),且最短杆的邻边为机架,因此是曲柄摇杆机构。
c ),不满足杆长条件,因此是双摇杆机构。
d ),且最短杆的对边为机架,因此是双摇杆机构。
题2-2解: 要想成为转动导杆机构,则要求与均为周转副。
(1 )当为周转副时,要求能通过两次与机架共线的位置。
见图2-15 中位置和。
在中,直角边小于斜边,故有:(极限情况取等号);在中,直角边小于斜边,故有:(极限情况取等号)。
综合这二者,要求即可。
(2 )当为周转副时,要求能通过两次与机架共线的位置。
见图2-15 中位置和。
在位置时,从线段来看,要能绕过点要求:(极限情况取等号);在位置时,因为导杆是无限长的,故没有过多条件限制。
(3 )综合(1 )、(2 )两点可知,图示偏置导杆机构成为转动导杆机构的条件是:题2-3 见图2.16 。
图2.16题2-4解: (1 )由公式,并带入已知数据列方程有:因此空回行程所需时间;(2 )因为曲柄空回行程用时,转过的角度为,因此其转速为:转/ 分钟题2-5解: (1 )由题意踏板在水平位置上下摆动,就是曲柄摇杆机构中摇杆的极限位置,此时曲柄与连杆处于两次共线位置。
机械设计基础(第五版)_杨可桢主编_课后习题答案.

0°≤ ≤ 150°
(2)回程:等加速段 0°≤ ≤60 °
等减速段
60°≤ ≤120 °
为了计算从动件速度和加速度,设 。计算各分点的位移、速度以及加速度值如下:
总转角
0°
15°
30°
45°
60°
75°
90°
105°
位移(mm)
0
0.734
2.865
6.183
10.365
15
19.635
, 。
题2-13证明:见图2.25。在 上任取一点 ,下面求证 点的运动轨迹为一椭圆。见图
可知 点将 分为两部分,其中 , 。
又由图可知 , ,二式平方相加得
可见 点的运动轨迹为一椭圆。
3-1解
图3.10题3-1解图
如图3.10所示,以O为圆心作圆并与导路相切,此即为偏距圆。过B点作偏距圆的下切线,此线为
当凸轮转角 在0≤ ≤ 过程中,从动件按简谐运动规律上升h=30mm。根据教材(3-7)式可
得:
0≤ ≤
0≤ ≤
当凸轮转角 在 ≤ ≤ 过程中,从动件远休。
S 2 =50 ≤ ≤
≤ ≤
当凸轮转角 在 ≤ ≤ 过程中,从动件按等加速度运动规律下降到升程的一半。根据
教材(3-5)式可得:
≤ ≤
≤ ≤
当凸轮转角 在 ≤ ≤ 过程中,从动件按等减速度运动规律下降到起始位置。根
(2)因为曲柄空回行程用时 ,
转过的角度为 ,
因此其转速为: 转/分钟
题2-5
解:(1)由题意踏板 在水平位置上下摆动 ,就是曲柄摇杆机构中摇杆的极限位置,此时
曲柄与连杆处于两次共线位置。取适当比例图尺,作出两次极限位置 和 (见图
机械设计基础(第五版)课后习题答案(完整版)_杨可竺、程光蕴、李仲生主编_高等教育出版社
1-1至1-4解机构运动简图如下图所示。
图 1.11 题1-1解图图1.12 题1-2解图图1.13 题1-3解图图1.14 题1-4解图1-5 解1-6 解1-7 解1-8 解1-9 解1-10 解1-11 解1-12 解1-13解该导杆机构的全部瞬心如图所示,构件1、3的角速比为:1-14解该正切机构的全部瞬心如图所示,构件3的速度为:,方向垂直向上。
1-15解要求轮1与轮2的角速度之比,首先确定轮1、轮2和机架4三个构件的三个瞬心,即,和,如图所示。
则:,轮2与轮1的转向相反。
1-16解(1)图a中的构件组合的自由度为:自由度为零,为一刚性桁架,所以构件之间不能产生相对运动。
(2)图b中的CD 杆是虚约束,去掉与否不影响机构的运动。
故图b中机构的自由度为:所以构件之间能产生相对运动。
题2-1答: a ),且最短杆为机架,因此是双曲柄机构。
b ),且最短杆的邻边为机架,因此是曲柄摇杆机构。
c ),不满足杆长条件,因此是双摇杆机构。
d ),且最短杆的对边为机架,因此是双摇杆机构。
题2-2解: 要想成为转动导杆机构,则要求与均为周转副。
( 1 )当为周转副时,要求能通过两次与机架共线的位置。
见图2-15 中位置和。
在中,直角边小于斜边,故有:(极限情况取等号);在中,直角边小于斜边,故有:(极限情况取等号)。
综合这二者,要求即可。
( 2 )当为周转副时,要求能通过两次与机架共线的位置。
见图2-15 中位置和。
在位置时,从线段来看,要能绕过点要求:(极限情况取等号);在位置时,因为导杆是无限长的,故没有过多条件限制。
( 3 )综合(1 )、(2 )两点可知,图示偏置导杆机构成为转动导杆机构的条件是:题2-3 见图 2.16 。
图 2.16题2-4解: (1 )由公式,并带入已知数据列方程有:因此空回行程所需时间;( 2 )因为曲柄空回行程用时,转过的角度为,因此其转速为:转/ 分钟题2-5解: (1 )由题意踏板在水平位置上下摆动,就是曲柄摇杆机构中摇杆的极限位置,此时曲柄与连杆处于两次共线位置。
机械设计基础(第五版)课后习题答案(整理版)要点
机械设计基础(第五版)课后习题答案(完整版) 杨可竺、程光蕴、李仲生主编高等教育出版社1-1至1-4解机构运动简图如下图所示。
图 1.11 题1-1解图图1.12 题1-2解图图1.13 题1-3解图图1.14 题1-4解图 1-5 解1-6 解1-7 解1-8 解1-9 解1-10 解1-11 解1-12 解1-13解该导杆机构的全部瞬心如图所示,构件 1、3的角速比为:1-14解该正切机构的全部瞬心如图所示,构件 3的速度为:向垂直向上。
,方1-15解要求轮 1与轮2的角速度之比,首先确定轮1、轮2和机架4三个构件的三个瞬心,即,和,如图所示。
则:,轮2与轮1的转向相反。
1-16解( 1)图a中的构件组合的自由度为:自由度为零,为一刚性桁架,所以构件之间不能产生相对运动。
( 2)图b中的 CD 杆是虚约束,去掉与否不影响机构的运动。
故图 b中机构的自由度为:所以构件之间能产生相对运动。
4.5课后习题详解4-1解分度圆直径齿顶高齿根高顶隙中心距齿顶圆直径齿根圆直径基圆直径齿距齿厚、齿槽宽4-2解由分度圆直径4-3解由可得模数得4-4解分度圆半径分度圆上渐开线齿廓的曲率半径分度圆上渐开线齿廓的压力角基圆半径基圆上渐开线齿廓的曲率半径为 0;压力角为。
齿顶圆半径齿顶圆上渐开线齿廓的曲率半径齿顶圆上渐开线齿廓的压力角4-5解正常齿制渐开线标准直齿圆柱齿轮的齿根圆直径:基圆直径假定故当齿数于齿根圆。
则解得,基圆小时,正常齿制渐开线标准直齿圆柱齿轮的基圆大于齿根圆;齿数4-6解中心距内齿轮分度圆直径内齿轮齿顶圆直径内齿轮齿根圆直径正好在刀具 4-7 证明用齿条刀具加工标准渐开线直齿圆柱齿轮,不发生根切的临界位置是极限点的顶线上。
此时有关系:正常齿制标准齿轮、,代入上式短齿制标准齿轮、,代入上式图 4.7 题4-7解图4-8证明如图所示,、两点为卡脚与渐开线齿廓的切点,则线段。
即为渐开线的法线。
根据渐开线的特性:渐开线的法线必与基圆相切,切点为再根据渐开线的特性:发生线沿基圆滚过的长度,等于基圆上被滚过的弧长,可知:AC对于任一渐开线齿轮,基圆齿厚与基圆齿距均为定值,卡尺的位置不影响测量结果。
机械设计基础(杨可桢)习题答案

1 8、n 6, PL 8, PH 1, F 3n (2PL PH ) 1 1 9、n 4, PL 4, PH 2, F 3n (2PL PH ) 2 1 10、n 9, PL 12, PH 2, F 3n (2PL PH ) 1
5-3.图示轮系。已知各轮齿 数.试作:
①写出该轮系类型; ②用齿数表示轮系传动比iH3
iH 3
。
注意五章的习题
2020/10/13
• 六、分析题
6-1
注意斜齿轮锥齿轮蜗轮蜗杆的受力,例如习 题11-7,11-9,11-15
2020/10/13
6-2
2020/10/13
答案 答案
• 6-2或者考其它类型的题。
4 3、由da mz 2h*am 27mm
m 5mm
4 4、解 db dk cosk
分度圆曲 压率 力半 角径
200
r sin
mz 2
sin
200
5 40 sin 2
200
34.20m m
基圆曲 压率 力半 角径 bb
00 0m
m
齿顶圆
由d
b
da
cosa则a
arccos
2
ism
1 i1s
• i1m
60
imH
1 i1m
• i1H
12
5 4、i H13 n1 nH n3 nH
1 i1H
Z2Z3 Z1Z2
3
i1H
4
n1 nH
1 H
当手柄转过 900时,H转过22.50
5 5、iH13
n1 nH n3 nH
机械设计基础(杨可桢)习题答案

Just for reference Li Chengbing
2020/10/13
1-1
1-2
n 3, pL 4, pH 0
n 3, pL 4, pH 0
F 3n 2 pL pH 1
41.5
即z 41,基圆大于齿根圆
2)、同理,z 41,基圆小于齿根圆
4.6
分度圆直径 d mz 4 20 80mm 内齿轮 齿顶圆直径 da mz 2h*am 88mm
齿根圆直径 d f m(z 2h*a 2c*) 70mm
外齿轮分度圆直径 d外 mz 240mm
中心距 d外 d内 80mm 22
2 2、lAB e lBC
2 4、K
1800 1800
300 300
1.4
1)、设空回行程需t秒,t 7 5 1.4
2)、一转所需的时间是7 5 12秒,一分钟
曲柄转5转。
2020/10/13
4 2、由a
m 2
(
第四章
z1 z2 )得m
2a z1 z2
4mm
d1 mZ1 80mm d2 mZ2 240mm
mzcos 200 mz 2h*am
26.500
曲率半径 a
da 2
sin a
46.85m m
2020/10/13
4.5
d f db
(z 2h*a
d cos
2c*)m
mz cos
正常齿制标准齿轮h*a
1,c*
0.25
1)、当mz cos
(z
2h*a
2c*)m,则z
杨可桢《机械设计基础》课后习题及详解(机械运转速度波动的调节)【圣才出品】

又平均角速度:
;速度不平均系数:
故飞轮转动惯量:
。
7-6 何谓周期性速度波动?何谓非周期性速度波动?它们各用何种装置进行调节? 经过调节之后主轴能否获得匀速转动?
解:周期性速度波动:机械有规律的,周期性的速度变化;非周期性速度波动:系统速 度波动是随机的、不规则的,没有一定的周期。
调节方法:周期性速度波动的调节方法是增加等效构件的质量或转动惯量,使等效构件 的角加速度α减小,从而使机器的运转趋于平衡,通常用安装飞轮来实现;对非周期性速度 波动的调节是设法使驱动力矩和阻力矩恢复平衡关系,常用调速器来调节非周期性速度波动。
的精确性。
解:由公式
,代入数值
可得,飞轮安装在
电机轴上时的转动惯量
。
7-4 已知某轧钢机的原动机功率等于常数,P′=2600 HP(马力),钢材通过轧辊时消 耗的功率为常数,P″=4000 HP,钢材通过轧辊的时间 t″=5 s,主轴平均转速 n=80 r/
min,机械运转速度不均匀系数 =0.1,求:(1)安装在主轴上的飞轮的转动惯量;(2)
的飞轮的转动惯量。
图 7-1
解:根据题意做出能量指示图,如图 7-2 所示,由图可知该机械系统的最大盈亏功:
Amax 520 190 390 720N m
平均角速度
,机械运转速度不均匀系数
。
由公式
可得,飞轮的转动惯量:
。
图 7-2
1/6
圣才电子书 十万种考研考证电子书、题库视频学习平台
经调节后只能使主轴的波动速度减小,不能使其获得匀速转动。
7-7 某机组主轴上作用的驱动力矩 M′为常数,它的一个运动循环中阻力矩 M″的变化
如图 7-6 所示。今给定 m=25 rad/s,δ=0.04,采用平均直径 Dm=0.5 m 的带轮辐
机械设计基础(第五版)_杨可桢主编_课后习题答案之欧阳科创编

机械设计基础(第五版)课后习题答案(完整版)时间:2021.02.05 创作:欧阳科杨可竺、程光蕴、李仲生主编1-1至1-4解机构运动简图如下图所示。
图1.11 题1-1解图图1.12 题1-2解图图1.13 题1-3解图图1.14 题1-4解图1-5 解1-6 解1-7 解1-8 解1-9 解1-10 解1-11 解1-12 解1-13解该导杆机构的全部瞬心如图所示,构件1、3的角速比为:1-14解该正切机构的全部瞬心如图所示,构件3的速度为:,方向垂直向上。
1-15解要求轮1与轮2的角速度之比,首先确定轮1、轮2和机架4三个构件的三个瞬心,即,和,如图所示。
则:,轮2与轮1的转向相反。
1-16解( 1)图a中的构件组合的自由度为:自由度为零,为一刚性桁架,所以构件之间不能产生相对运动。
( 2)图b中的 CD 杆是虚约束,去掉与否不影响机构的运动。
故图 b 中机构的自由度为:所以构件之间能产生相对运动。
题 2-1答 : a ),且最短杆为机架,因此是双曲柄机构。
b ),且最短杆的邻边为机架,因此是曲柄摇杆机构。
c ),不满足杆长条件,因此是双摇杆机构。
d ),且最短杆的对边为机架,因此是双摇杆机构。
题 2-2解 : 要想成为转动导杆机构,则要求与均为周转副。
(1 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在中,直角边小于斜边,故有:(极限情况取等号);在中,直角边小于斜边,故有:(极限情况取等号)。
综合这二者,要求即可。
(2 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在位置时,从线段来看,要能绕过点要求:(极限情况取等号);在位置时,因为导杆是无限长的,故没有过多条件限制。
( 3 )综合(1 )、( 2 )两点可知,图示偏置导杆机构成为转动导杆机构的条件是:题 2-3 见图 2.16 。
图 2.16题 2-4解 : ( 1 )由公式,并带入已知数据列方程有:因此空回行程所需时间;( 2 )因为曲柄空回行程用时,转过的角度为,因此其转速为:转 / 分钟题 2-5解 : ( 1 )由题意踏板在水平位置上下摆动,就是曲柄摇杆机构中摇杆的极限位置,此时曲柄与连杆处于两次共线位置。
机械设计基础课外习题-杨可祯

螺栓
轴 F× F 轴
D
解: F 2 T 6D
29.451040.143KN 6220
②、所需轴向预紧力Fa
Fa
cF mf
1.20.1430.858KN 0.2
13、图所示一凸缘联轴器,用6个普通螺栓将两半联轴器相联,螺栓中心圆 直径D=220mm,被联轴的转速n=960r/min,传递的功率P = 9.5kw。联轴器接
C、拉扭复合
D、承载面积
(8)受轴向载荷的紧螺栓联接,为保证被连接件不出现缝隙,
剩余预紧压力FR
B
A、应小于零;
B、应大于零;
C、应等于零
(9)、平键联接中,侧面 是工作面;楔形键联接中,上下面是 工作面;平键联接中,导向平键 用于动联接。
(10)提高螺栓联接强度有哪些主要措施?
①、降低螺栓总拉伸载荷的变化范围;
(1)、螺纹的公称直径是指螺纹的 大径 径,螺纹的升角是 指螺纹 中径 径处的升角。
(2)、三角形螺纹主要用于联接 ,而矩形、梯形和锯齿形螺 纹主要用于传动 。
(3)、受轴工作向载荷的紧螺栓所受的总拉力是 Qa = FE+FR F0+∆Fb
(4)、联接承受横向工作载荷,当采用普通螺栓通孔联接时,横
向载荷靠被连接件接触面间摩擦力来平衡;当采用铰制孔螺栓链接时,
横向载荷靠
螺栓杆本身 来平衡。
(5)、双头螺栓的两被联接件之一是 通 孔,另一是 盲孔 孔。
(6)、相同大径的普通螺纹细牙比粗牙有 B
。
A、较小的承载能力;
B、 好的自锁性;
C、承载面积小
(7)紧螺栓联接强度公式σ =1.3Q/(πD21/4) [σ]中,系数1.3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-1至1-4解机构运动简图如下图所示。
图 1.11 题1-1解图图1.12 题1-2解图图1.13 题1-3解图图1.14 题1-4解图1-5 解1-6 解1-7 解1-8 解1-9 解1-10 解1-11 解1-12 解1-13解该导杆机构的全部瞬心如图所示,构件 1、3的角速比为:1-14解该正切机构的全部瞬心如图所示,构件 3的速度为:,方向垂直向上。
1-15解要求轮 1与轮2的角速度之比,首先确定轮1、轮2和机架4三个构件的三个瞬心,即,和,如图所示。
则:,轮2与轮1的转向相反。
1-16解( 1)图a中的构件组合的自由度为:自由度为零,为一刚性桁架,所以构件之间不能产生相对运动。
( 2)图b中的 CD 杆是虚约束,去掉与否不影响机构的运动。
故图 b中机构的自由度为:所以构件之间能产生相对运动。
题 2-1答 : a ),且最短杆为机架,因此是双曲柄机构。
b ),且最短杆的邻边为机架,因此是曲柄摇杆机构。
c ),不满足杆长条件,因此是双摇杆机构。
d ),且最短杆的对边为机架,因此是双摇杆机构。
题 2-2解 : 要想成为转动导杆机构,则要求与均为周转副。
( 1 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在中,直角边小于斜边,故有:(极限情况取等号);在中,直角边小于斜边,故有:(极限情况取等号)。
综合这二者,要求即可。
( 2 )当为周转副时,要求能通过两次与机架共线的位置。
见图 2-15 中位置和。
在位置时,从线段来看,要能绕过点要求:(极限情况取等号);在位置时,因为导杆是无限长的,故没有过多条件限制。
( 3 )综合( 1 )、( 2 )两点可知,图示偏置导杆机构成为转动导杆机构的条件是:题 2-3 见图 2.16 。
图 2.16题 2-4解 : ( 1 )由公式,并带入已知数据列方程有:因此空回行程所需时间;( 2 )因为曲柄空回行程用时,转过的角度为,因此其转速为:转 / 分钟题 2-5解 : ( 1 )由题意踏板在水平位置上下摆动,就是曲柄摇杆机构中摇杆的极限位置,此时曲柄与连杆处于两次共线位置。
取适当比例图尺,作出两次极限位置和(见图2.17 )。
由图量得:,。
解得:由已知和上步求解可知:,,,( 2 )因最小传动角位于曲柄与机架两次共线位置,因此取和代入公式( 2-3 )计算可得:或:代入公式( 2-3 )′,可知题 2-6解:因为本题属于设计题,只要步骤正确,答案不唯一。
这里给出基本的作图步骤,不给出具体数值答案。
作图步骤如下(见图 2.18 ):( 1 )求,;并确定比例尺。
( 2 )作,。
(即摇杆的两极限位置)( 3 )以为底作直角三角形,,。
( 4 )作的外接圆,在圆上取点即可。
在图上量取,和机架长度。
则曲柄长度,摇杆长度。
在得到具体各杆数据之后,代入公式( 2 — 3 )和( 2-3 )′求最小传动角,能满足即可。
图 2.18题 2-7图 2.19解 : 作图步骤如下(见图 2.19 ):( 1 )求,;并确定比例尺。
( 2 )作,顶角,。
( 3 )作的外接圆,则圆周上任一点都可能成为曲柄中心。
( 4 )作一水平线,于相距,交圆周于点。
( 5 )由图量得,。
解得:曲柄长度:连杆长度:题 2-8解 : 见图 2.20 ,作图步骤如下:( 1 )。
( 2 )取,选定,作和,。
( 3 )定另一机架位置:角平分线,。
( 4 ),。
杆即是曲柄,由图量得曲柄长度:题 2-9解:见图 2.21 ,作图步骤如下:( 1 )求,,由此可知该机构没有急回特性。
( 2 )选定比例尺,作,。
(即摇杆的两极限位置)( 3 )做,与交于点。
( 4 )在图上量取,和机架长度。
曲柄长度:连杆长度:题 2-10解 : 见图 2.22 。
这是已知两个活动铰链两对位置设计四杆机构,可以用圆心法。
连接,,作图 2.22 的中垂线与交于点。
然后连接,,作的中垂线与交于点。
图中画出了一个位置。
从图中量取各杆的长度,得到:,,题 2-11解 : ( 1 )以为中心,设连架杆长度为,根据作出,,。
( 2 )取连杆长度,以,,为圆心,作弧。
( 3 )另作以点为中心,、,的另一连架杆的几个位置,并作出不同半径的许多同心圆弧。
( 4 )进行试凑,最后得到结果如下:,,,。
机构运动简图如图 2.23 。
题 2-12解 : 将已知条件代入公式( 2-10 )可得到方程组:联立求解得到:,,。
将该解代入公式( 2-8 )求解得到:,,,。
又因为实际,因此每个杆件应放大的比例尺为:,故每个杆件的实际长度是:,,,。
题 2-13证明 : 见图 2.25 。
在上任取一点,下面求证点的运动轨迹为一椭圆。
见图可知点将分为两部分,其中,。
又由图可知,,二式平方相加得可见点的运动轨迹为一椭圆。
3-1解图 3.10 题3-1解图如图 3.10所示,以O为圆心作圆并与导路相切,此即为偏距圆。
过B点作偏距圆的下切线,此线为凸轮与从动件在B点接触时,导路的方向线。
推程运动角如图所示。
3-2解图 3.12 题3-2解图如图 3.12所示,以O为圆心作圆并与导路相切,此即为偏距圆。
过D点作偏距圆的下切线,此线为凸轮与从动件在D点接触时,导路的方向线。
凸轮与从动件在D点接触时的压力角如图所示。
3-3解:从动件在推程及回程段运动规律的位移、速度以及加速度方程分别为:( 1)推程:0°≤ ≤ 150°( 2)回程:等加速段0°≤ ≤60 °等减速段60°≤ ≤120 °为了计算从动件速度和加速度,设。
计算各分点的位移、速度以及加速度值如下:总转角0° 15° 30° 45° 60° 75° 90° 105° 位移 (mm) 00.734 2.865 6.183 10.365 15 19.635 23.817 速度0 19.416 36.931 50.832 59.757 62.832 59.757 50.832(mm/s)加速度65.797 62.577 53.231 38.675 20.333 0 -20.333 -38.675(mm/s2 )总转角120° 135° 150° 165° 180° 195° 210° 225° 位移 (mm) 27.135 29.266 30 30 30 29.066 26.250 21.563速度36.932 19.416 0 0 0 -25 -50 -75(mm/s)加速度-53.231 -62.577 -65.797 0 -83.333 -83.333 -83.333 -83.333 (mm/s2 )总转角240° 255° 270° 285° 300° 315° 330° 345° 位移 (mm) 15 8.438 3.75 0.938 0 0 0 0速度-100 -75 -50 -25 0 0 0 0(mm/s)加速度-83.333 -83.333 83.333 83.333 83.333 0 0 0 (mm/s2 )根据上表作图如下(注:为了图形大小协调,将位移曲线沿纵轴放大了 5倍。
):图 3-13 题3-3解图3-4 解:图 3-14 题3-4图根据 3-3题解作图如图3-15所示。
根据(3.1)式可知,取最大,同时s 2 取最小时,凸轮机构的压力角最大。
从图3-15可知,这点可能在推程段的开始处或在推程的中点处。
由图量得在推程的开始处凸轮机构的压力角最大,此时<[ ]=30° 。
图 3-15 题3-4解图3-5解:( 1)计算从动件的位移并对凸轮转角求导当凸轮转角在0≤ ≤ 过程中,从动件按简谐运动规律上升 h=30mm。
根据教材(3-7)式可得:0≤ ≤0≤ ≤当凸轮转角在≤ ≤ 过程中,从动件远休。
S 2 =50 ≤ ≤≤ ≤当凸轮转角在≤ ≤ 过程中,从动件按等加速度运动规律下降到升程的一半。
根据教材(3-5)式可得:≤ ≤≤ ≤当凸轮转角在≤ ≤ 过程中,从动件按等减速度运动规律下降到起始位置。
根据教材(3-6)式可得:≤ ≤≤ ≤当凸轮转角在≤ ≤ 过程中,从动件近休。
S 2 =50 ≤ ≤≤ ≤( 2)计算凸轮的理论轮廓和实际轮廓本题的计算简图及坐标系如图 3-16所示,由图可知,凸轮理论轮廓上B点(即滚子中心)的直角坐标为图 3-16式中。
由图 3-16可知,凸轮实际轮廓的方程即B ′ 点的坐标方程式为因为所以故由上述公式可得理论轮廓曲线和实际轮廓的直角坐标,计算结果如下表,凸轮廓线如图3-17所示。
x′ y′ x′ y′0° 49.301 8.333 180° -79.223 -8.88510° 47.421 16.843 190° -76.070 -22.42120° 44.668 25.185 200° -69.858 -34.84030° 40.943 33.381 210° -60.965 -45.36940° 36.089 41.370 220° -49.964 -53.35650° 29.934 48.985 230° -37.588 -58.31260° 22.347 55.943 240° -24.684 -59.94970° 13.284 61.868 250° -12.409 -59.00280° 2.829 66.326 260° -1.394 -56.56690° -8.778 68.871 270° 8.392 -53.041100° -21.139 69.110 280° 17.074 -48.740110° -33.714 66.760 290° 24.833 -43.870120° -45.862 61.695 300° 31.867 -38.529130° -56.895 53.985 310° 38.074 -32.410140° -66.151 43.904 320° 43.123 -25.306150° -73.052 31.917 330° 46.862 -17.433160° -77.484 18.746 340° 49.178 -9.031170° -79.562 5.007 350° 49.999 -0.354180° -79.223 -8.885 360° 49.301 8.333图 3-17 题3-5解图3-6 解:图 3-18 题3-6图从动件在推程及回程段运动规律的角位移方程为:1.推程:0°≤ ≤ 150°2.回程:0°≤ ≤120 °计算各分点的位移值如下:总转角(°)0 15 30 45 60 75 90 105角位移(°)0 0.367 1.432 3.092 5.182 7.5 9.818 11.908总转角(°)120 135 150 165 180 195 210 225角位移(°)13.56814.633 15 15 15 14.429 12.803 0.370总转角(°)240 255 270 285 300 315 330 345 角位移(°)7.5 4.630 2.197 0.571 0 0 0 0 根据上表作图如下:图 3-19 题3-6解图3-7解:从动件在推程及回程段运动规律的位移方程为: 1.推程: 0°≤ ≤ 120° 2.回程: 0°≤ ≤120 °计算各分点的位移值如下:总转角( °) 0153045607590105位移( mm ) 00.761 2.929 6.173 10 13.827 17.071 19.239总转角( °)120 135150 165 180 195 210225 位移( mm ) 20 20 2019.239 17.07113.827 106.173 总转角( °)240 255270 285 300 315330 345 位移( mm ) 2.9290.761 0图 3-20 题3-7解图4.5课后习题详解4-1解分度圆直径齿顶高齿根高顶隙中心距齿顶圆直径齿根圆直径基圆直径齿距齿厚、齿槽宽4-2解由可得模数分度圆直径4-3解由得4-4解分度圆半径分度圆上渐开线齿廓的曲率半径分度圆上渐开线齿廓的压力角基圆半径基圆上渐开线齿廓的曲率半径为 0;压力角为。
