(完整版)高中常见数学模型案例
高二数学中常见的实际问题数学建模解析

高二数学中常见的实际问题数学建模解析数学建模是将数学方法和技巧应用于实际问题的过程,通过建立数学模型来解决问题。
在高二数学学习中,我们经常遇到一些实际问题,这些问题需要我们通过数学建模来解析和求解。
本文将介绍高二数学中常见的实际问题,并给出相应的数学建模解析。
一、汽车加速问题在实际生活中,我们经常会遇到汽车加速问题。
假设一个汽车从静止开始加速,我们希望得到汽车的加速度函数和速度函数。
解析:设汽车在时间t时刻的加速度为a(t),速度为v(t),位移为s(t)。
根据牛顿第二定律可以得到汽车的运动方程:m*a(t) = F(t),其中m为汽车的质量,F(t)为汽车受到的合力。
通过解这个微分方程,我们可以得到汽车的加速度函数a(t),再次积分得到速度函数v(t)和位移函数s(t)。
二、投影问题投影问题是高二数学中比较常见的一类实际问题。
给定一个物体的运动轨迹和初速度,我们希望求解物体的运动方程和运动性质。
解析:设物体的运动轨迹为y=f(x),初速度为v0。
根据物体在x和y方向上的运动分量可以得到物体的运动方程:x(t) = v0 * t,y(t) = f(v0 * t),其中t为时间。
通过对物体的运动方程进行微分和积分,我们可以求解出物体的速度、加速度、位移等运动性质,从而了解物体的运动规律。
三、最优化问题最优化问题是高二数学中的重要内容,也是实际生活中经常遇到的问题。
给定一个约束条件,我们希望求解出使某一目标函数值达到最小或最大的变量取值。
解析:设目标函数为f(x),约束条件为g(x)=0。
对目标函数f(x)进行求导并令导数为零,可以解得使目标函数达到最小或最大的变量取值。
通过最优化问题的解析,我们可以确定最优解,并对实际问题进行优化设计。
四、概率问题概率问题在高二数学中也是常见的实际问题。
给定一些事件的概率和条件,我们希望求解出与事件相相关的概率或输赢的概率。
解析:根据事件的概率规律和条件概率可以得到事件的概率分布和相应的求解公式。
高中教育数学必修第二册湘教版《6.2 数学建模案例1 烧开水问题》教学课件

检验与改进 1.取旋钮39°的位置,烧一壶开水,记录所得实际用气量是不是 0.121 8 m3.如果基本吻合,就可以依此作结论了.如果相差太大,特 别是当用气量大于0.121 8 m3时,最小值点就肯定不是39°,说明上 述三组数据取得不好,可以换另外的点重新计算,然后再检验,直到
结果与实际比较接近就可以了. 实际上,如果我们取(18,0.130),(36,0.122),(54,0.139),求出
评价与推广 该模型建立过程中的假设条件太强.该模型只考虑通过改变阀门位 置来达到节约燃气用量的目的,有一定的局限性,实际过程中也可以 考虑通过控制阀门大小,每次只烧半壶水,分两次完成烧水的方法来 实现节约燃气用量的目的.阀门位置改变时,燃气量的变化与阀门本 身设计也有关,而在该模型中没有讨论.
2.在选好的五个位置上,分别记录烧开一壶水所需的时间和所用的 燃气量,得到了几组实验数据,如下表:
位置项目
18° 36° 54° 72° 90°
开始时燃气 读表数/m3
9.080 8.958 8.819 8.670 8.498
水开时燃气 读表数/m3
9.210 9.080 8.958 8.819 8.670
1.给定燃气灶和一只水壶,选择燃气灶旋钮的五个位置(当然多选 一些更好,这里由于是粗略地寻找一个最佳位置,故只选择五个位置, 在要求精度较高的情况下,可以探究更多的位置).因为关闭时,燃 气旋钮的位置为竖直方向,我们把这个位置定为0°,燃气开到最大 时,旋钮转了90°.为了方便计算,将0°~90°五等分,如图,分别 以18°,36°,54°,72°,90°来确定五个位置(其他位置选取方 法,同学们可以自己进行尝试).
所需燃气量 /m3 0.130 0.122 0.139 0.149 0.172
高中数学建模案例精选

高中数学建模案例精选In the realm of high school mathematics, modeling serves as a bridge between theoretical concepts and practical applications. This approach encourages students to apply mathematical principles to real-world scenarios, fostering a deeper understanding of the subject. One such case study involves the optimization of a shipping route.在高中数学领域,建模是连接理论概念与实际应用的桥梁。
这种方法鼓励学生将数学原理应用于现实世界的场景中,从而加深对学科的理解。
其中一个案例研究就是优化运输路线。
Imagine a shipping company that needs to transport goods from point A to point B. The company has multiple routes to choose from, each with different costs and travel times. The objective is to find the most efficient route that minimizes overall cost while considering factors like fuel consumption, tolls, and the value of time.设想一家运输公司需要从点A运输货物到点B。
公司有多个路线可供选择,每条路线的成本和旅行时间都不同。
目标是找到最高效的路线,以最小化整体成本,同时考虑燃料消耗、过路费和时间的价值。
高中数学建模的教学案例

高中数学建模的教学案例高中数学建模是一门富有挑战性和创造性的学科,旨在培养学生的逻辑思维能力、问题解决能力以及数学建模的应用能力。
为了帮助学生更好地理解和应用数学建模,以下是一个教学案例,通过实际问题引导学生进行数学建模的步骤和方法。
案例背景:某小区的居民数逐年增加,导致小区配套的市政建设不足。
为了解决该问题,物业公司统计了小区每户居民的用水量,并希望通过数学建模来预测未来几年的整体用水量,以供决策参考。
1. 问题分析首先,学生需要分析问题的背景和目标。
他们可以思考以下几个问题:- 该问题的关键因素是什么?- 什么样的数据对解决问题有帮助?- 可以借助哪些数学方法和模型来解决问题?2. 数据收集学生需要搜集相关的数据,可以通过访谈物业公司负责人、查阅相关资料等方式获取所需数据。
在这个案例中,学生需要收集每年小区的居民数量和每户居民的用水量数据。
3. 数据处理和分析接下来,学生可以使用合适的数学方法和模型来处理和分析数据。
在这个案例中,学生可以使用线性回归模型来分析用水量和居民数量之间的关系。
他们可以通过计算回归方程,预测未来几年的整体用水量。
4. 模型建立和验证学生需要建立数学模型,并验证模型的有效性。
在这个案例中,学生可以以小区的居民数量作为自变量,以每户居民的用水量作为因变量,建立线性回归模型。
然后,他们可以将该模型应用于其他小区的数据,观察预测结果和实际结果的差异,以验证模型的准确性。
5. 结果与讨论最后,学生需要对结果进行总结和讨论。
他们可以回答以下问题:- 预测结果与实际情况是否一致?- 模型的优缺点是什么?- 如何改进模型的准确性和实用性?通过以上的教学案例,学生可以在实际问题中学习和应用数学建模的方法和步骤。
这种教学方法可以培养学生的实际应用能力和创造力,并提高他们对数学建模的兴趣和理解。
总结:高中数学建模的教学案例是一个有效的教学方法,可以提高学生的数学能力和创造力。
通过引导学生在实际问题中进行数学建模的步骤和方法,可以培养他们的问题解决和应用能力。
高中数学二轮复习关于三角函数解题中常用数学模型构造

二轮复习关于三角函数解题中常用数学模型构造构造数学模型是一种比较重要、灵活的思维方式,它没有固定的模式。
在解题中要想用好它,需要有敏锐的观察、丰富的联想、灵活的构思、创造性的思维等能力。
应用好构造思想解题的关键有二:一是要有明确的方向,即为什么目的而构造;二是弄清条件的本质特点和背景,以便重新进行逻辑组合。
常用的有构造命题、构造表达式、构造几何体等,本文拟就通过介绍几种解三角函数的具体问题,对构造的各种思维方式作一些探讨。
1 构造直角三角形例1 设x ∈[4π,2π],求证:cscx -ctgx ≥2-1 思路分析:由2、1联想等腰直角三角形,不仿构造一个等腰直角三角形来研究。
作Rt ⊿ABC ,令∠C=900,AC=1,在AC上取一点D ,记∠CDB=x ,则BD=cscx ,CD=ctgx ,AD=1-ctgx ,利用AD+DB≥AB=2,可得cscx -ctgx ≥2-1,等号仅在x =4π时成立。
2 构造单位圆例 2若0<β<α<2π,求证:α-β<tg α-tg β 思路分析:构造单位圆,借助三角函数线与三角函数式的关系,把数的比较转化为几何图形面积的比较。
作单位圆O ,AP 1=β,AP 2=α,∴ P 1P 2=α-β,AT 1=tg β,AT 2=tg α,S ⊿AT O =21tg α,S ⊿AP O =21tg β,由于S 扇形OAP=21α,S 扇形OAP =21β。
∴S 扇形OP P =21(α-β),S ⊿OT T=21tg α-21tg β。
则S ⊿OT T>S 扇形OP P即 21(α-β)<21(tg α-tg β) 所以 α-β<tg α-tg β3 构造函数表达式例3已知x 、y ∈[-4π,4π],a ∈R ,且⎩⎨⎧=++=-+0cos sin 402sin 33a y y y a x x ,求cos (x+2y )思路分析:由x 3+sinx 与2(4y 3+sinycosy ),这两部分形式完全类似,由此可构造函数形式。
【高中数学】函数模型及其应用

函数模型及其应用一、基础知识1.常见的8种函数模型(1)正比例函数模型:f(x)=kx(k为常数,k≠0);(2)反比例函数模型:f(x)=kx(k为常数,k≠0);(3)一次函数模型:f(x)=kx+b(k,b为常数,k≠0);(4)二次函数模型:f(x)=ax2+bx+c(a,b,c为常数,a≠0);(5)指数函数模型:f(x)=ab x+c(a,b,c为常数,a≠0,b>0,b≠1);(6)对数函数模型:f(x)=m log a x+n(m,n,a为常数,m≠0,a>0,a≠1);(7)幂函数模型:f(x)=ax n+b(a,b,n为常数,a≠0,n≠1);(8)“对勾”函数模型:y=x+ax(a>0).(1)形如f(x)=x+ax(a>0)的函数模型称为“对勾”函数模型,“对勾”函数的性质:①该函数在(-∞,-a]和[a,+∞)上单调递增,在[-a,0)和(0,a]上单调递减.②当x>0时,x=a时取最小值2a,当x<0时,x=-a时取最大值-2a.(2)函数f(x)=xa+bx(a>0,b>0,x>0)在区间(0,ab]内单调递减,在区间[ab,+∞)内单调递增.2.三种函数模型的性质函数性质y=a x(a>1)y=log a x(a>1)y=x n(n>0)在(0,+∞)上的增减性单调递增单调递增单调递增增长速度越来越快越来越慢相对平稳图象的变化随x的增大,逐渐表现为与y轴平行随x的增大,逐渐表现为与x轴平行随n值变化而各有不同值的比较存在一个x0,当x>x0时,有log a x<x n<a x幂函数模型y=x n(n>0)可以描述增长幅度不同的变化,当n,值较小(n≤1)时,增长较慢;当n值较大(n>1)时,增长较快.考点一二次函数、分段函数模型[典例]国庆期间,某旅行社组团去风景区旅游,若每团人数在30或30以下,飞机票每张收费900元;若每团人数多于30,则给予优惠:每多1人,机票每张减少10元,直到达到规定人数75为止.每团乘飞机,旅行社需付给航空公司包机费15000元.(1)写出飞机票的价格关于人数的函数;(2)每团人数为多少时,旅行社可获得最大利润?[解](1)设每团人数为x,由题意得0<x≤75(x∈N*),飞机票价格为y元,则y ,0<x≤30,-10(x-30),30<x≤75,即y,0<x≤30,200-10x,30<x≤75.(2)设旅行社获利S元,则Sx-15000,0<x≤30,200x-10x2-15000,30<x≤75,即Sx-15000,0<x≤30,10(x-60)2+21000,30<x≤75.因为S=900x-15000在区间(0,30]上为增函数,故当x=30时,S取最大值12000.又S=-10(x-60)2+21000,x∈(30,75],所以当x=60时,S取得最大值21000.故当x=60时,旅行社可获得最大利润.[解题技法]二次函数、分段函数模型解决实际问题的策略(1)在建立二次函数模型解决实际问题中的最值问题时,一定要注意自变量的取值范围,需根据函数图象的对称轴与函数定义域在坐标系中对应区间之间的位置关系讨论求解.(2)对于分段函数模型的最值问题,应该先求出每一段上的最值,然后比较大小.(3)在利用基本不等式求解最值时,一定要检验等号成立的条件,也可以利用函数单调性求解最值.[题组训练]1.某市家庭煤气的使用量x(m3)和煤气费f(x)(元)满足关系f(x),0<x≤A,+B(x-A),x>A.已知某家庭2018年前三个月的煤气费如表:月份用气量煤气费一月份4m34元二月份25m314元三月份35m 319元若四月份该家庭使用了20m 3的煤气,则其煤气费为()A .11.5元B .11元C .10.5元D .10元解析:选A根据题意可知f (4)=C =4,f (25)=C +B (25-A )=14,f (35)=C +B (35-A )=19,解得A =5,B =12,C =4,所以f (x ),0<x ≤5,+12(x -5),x >5,所以f (20)=4+12×(20-5)=11.5.2.A ,B 两城相距100km ,在两城之间距A 城x (km)处建一核电站给A ,B 两城供电,为保证城市安全,核电站距城市距离不得小于10km.已知供电费用等于供电距离(km)的平方与供电量(亿度)之积的0.25倍,若A 城供电量为每月20亿度,B 城供电量为每月10亿度.(1)求x 的取值范围;(2)把月供电总费用y 表示成x 的函数;(3)核电站建在距A 城多远,才能使月供电总费用y 最少?解:(1)由题意知x 的取值范围为[10,90].(2)y =5x 2+52(100-x )2(10≤x ≤90).(3)因为y =5x 2+52(100-x )2=152x 2-500x +25000+500003,所以当x =1003y min =500003.故核电站建在距A 城1003km 处,能使月供电总费用y 最少.考点二指数函数、对数函数模型[典例]某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量y (微克)与时间t (小时)之间近似满足如图所示的曲线.(1)写出第一次服药后y 与t 之间的函数关系式y =f (t );(2)据进一步测定,每毫升血液中含药量不少于0.25微克时治疗疾病有效,求服药一次后治疗疾病有效的时间.[解](1)由题图,设y 0≤t ≤1,a,t >1,当t =1时,由y =4,得k =4,由-a =4,得a =3.所以y 0≤t ≤1,-3,t >1.(2)由y ≥0.25≤t ≤1,t ≥0.253≥0.25,解得116≤t ≤5.故服药一次后治疗疾病有效的时间是5-116=7916(小时).[解题技法]1.掌握2种函数模型的应用技巧(1)与指数函数、对数函数模型有关的实际问题,在求解时,要先学会合理选择模型,在三类模型中,指数函数模型是增长速度越来越快(底数大于1)的一类函数模型,与增长率、银行利率有关的问题都属于指数函数模型.(2)在解决指数函数、对数函数模型问题时,一般先需要通过待定系数法确定函数解析式,再借助函数的图象求解最值问题,必要时可借助导数.2.建立函数模型解应用问题的4步骤(1)审题:弄清题意,分清条件和结论,理顺数量关系,初步选择模型.(2)建模:将文字语言转化为数学语言,利用数学知识建立相应的数学模型.(3)求模:求解数学模型,得出数学结论.(4)还原:将利用数学知识和方法得出的结论,还原到实际问题中.[题组训练]1.某位股民购进某支股票,在接下来的交易时间内,他的这支股票先经历了n 次涨停(每次上涨10%),又经历了n 次跌停(每次下跌10%),则该股民这支股票的盈亏情况(不考虑其他费用)为()A.略有盈利B.略有亏损C.没有盈利也没有亏损D.无法判断盈亏情况解析:选B设该股民购进这支股票的价格为a元,则经历n次涨停后的价格为a(1+10%)n=a×1.1n元,经历n次跌停后的价格为a×1.1n×(1-10%)n=a×1.1n×0.9n=a×(1.1×0.9)n=0.99n·a<a,故该股民这支股票略有亏损.2.声强级Y(单位:分贝)由公式Y=10lg I为声强(单位:W/m2).(1)平常人交谈时的声强约为10-6W/m2,求其声强级.(2)一般常人能听到的最低声强级是0分贝,求能听到的最低声强为多少?解:(1)当声强为10-6W/m2时,由公式Y=得Y=10lg106=60(分贝).(2)当Y=0时,由公式Y=得0.∴I10-12=1,即I=10-12W/m2,则最低声强为10-12W/m2.[课时跟踪检测]1.(2018·福州期末)某商场销售A型商品.已知该商品的进价是每件3元,且销售单价与日均销售量的关系如下表所示:销售单价/元45678910日均销售量/件400360320280240200160请根据以上数据分析,要使该商品的日均销售利润最大,则此商品的定价(单位:元/件)应为()A.4B.5.5C.8.5D.10解析:选C由数据分析可知,当单价为4元时销售量为400件,单价每增加1元,销售量就减少40件.设定价为x 元/件时,日均销售利润为y 元,则y =(x -3)·[400-(x -4)·40]=-+1210,故当x =172=8.5时,该商品的日均销售利润最大,故选C.2.(2019·绵阳诊断)某单位为鼓励职工节约用水,作出如下规定:每位职工每月用水不超过10立方米的,按每立方米3元收费;用水超过10立方米的,超过的部分按每立方米5元收费.某职工某月的水费为55元,则该职工这个月实际用水为()A .13立方米B .14立方米C .15立方米D .16立方米解析:选C 设该职工某月的实际用水为x 立方米时,水费为y 元,由题意得y =x ,0≤x ≤10,+5(x -10),x >10,即y x ,0≤x ≤10,x -20,x >10.易知该职工这个月的实际用水量超过10立方米,所以5x -20=55,解得x =15.3.利民工厂某产品的年产量在150吨至250吨之间,年生产的总成本y (万元)与年产量x (吨)之间的关系可近似地表示为y =x 210-30x +4000,则每吨的成本最低时的年产量为()A .240吨B .200吨C .180吨D .160吨解析:选B 依题意,得每吨的成本为y x =x 10+4000x -30,则yx≥2x 10·4000x-30=10,当且仅当x 10=4000x,即x =200时取等号,因此,当每吨成本最低时,年产量为200吨.4.某工厂产生的废气经过过滤后排放,排放时污染物的含量不得超过1%.已知在过滤过程中废气中的污染物数量P (单位:毫克/升)与过滤时间t (单位:时)之间的函数关系为P =P 0e -kt (k ,P 0均为正常数).如果在前5个小时的过滤过程中污染物被排除了90%,那么排放前至少还需要过滤的时间是()A.12小时 B.59小时C .5小时D .10小时解析:选C 由题意,前5个小时消除了90%的污染物.∵P =P 0e -kt ,∴(1-90%)P 0=P 0e -5k,∴0.1=e-5k,即-5k =ln 0.1,∴k =-15ln 0.1.由1%P 0=P 0e -kt ,即0.01=e -kt ,得-kt =ln 0.01,=ln 0.01,∴t =10.∴排放前至少还需要过滤的时间为t -5=5(时).5.(2019·蚌埠模拟)某种动物的繁殖数量y (单位:只)与时间x (单位:年)的关系式为y =a log 2(x +1),若这种动物第1年有100只,则到第7年它们发展到________只.解析:由题意,得100=a log 2(1+1),解得a =100,所以y =100log 2(x +1),当x =7时,y =100log 2(7+1)=300,故到第7年它们发展到300只.答案:3006.某人根据经验绘制了从12月21日至1月8日自己种植的西红柿的销售量y (千克)随时间x (天)变化的函数图象如图所示,则此人在12月26日大约卖出了西红柿________千克.解析:前10天满足一次函数关系,设为y =kx +b ,将点(1,10)和点(10,30)代入函数解析=k +b ,=10k +b ,解得k =209,b =709,所以y =209x +709,则当x =6时,y =1909.答案:19097.候鸟每年都要随季节的变化进行大规模的迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v (单位:m/s)与其耗氧量Q 之间的关系为:v =a +b log 3Q10(其中a ,b 是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1m/s.(1)求出a ,b 的值;(2)若这种鸟类为赶路程,飞行的速度不能低于2m/s ,求其耗氧量至少要多少个单位?解:(1)由题意可知,当这种鸟类静止时,它的速度为0m/s ,此时耗氧量为30个单位,故有a +b log 33010=0,即a +b =0.当耗氧量为90个单位时,速度为1m/s ,故a +b log 39010=1,整理得a +2b =1.+b =0,+2b =1,=-1,=1.(2)由(1)知,v =a +b log 3Q 10=-1+log 3Q10.所以要使飞行速度不低于2m/s ,则有v ≥2,所以-1+log 3Q10≥2,即log 3Q 10≥3,解得Q10≥27,即Q ≥270.所以若这种鸟类为赶路程,飞行的速度不能低于2m/s ,则其耗氧量至少要270个单位.8.据气象中心观察和预测:发生于沿海M 地的台风一直向正南方向移动,其移动速度v (单位:km/h)与时间t (单位:h)的函数图象如图所示,过线段OC 上一点T (t,0)作横轴的垂线l ,梯形OABC 在直线l 左侧部分的面积为时间t 内台风所经过的路程s (单位:km).(1)当t =4时,求s 的值;(2)将s 随t 变化的规律用数学关系式表示出来;(3)若N 城位于M 地正南方向,且距M 地650km ,试判断这场台风是否会侵袭到N 城,如果会,在台风发生后多长时间它将侵袭到N 城?如果不会,请说明理由.解:(1)由图象可知,直线OA 的方程是v =3t (0≤t ≤10),直线BC 的方程是v =-2t +70(20<t ≤35).当t =4时,v =12,所以s =12×4×12=24.(2)当0≤t ≤10时,s =12×t ×3t =32t 2;当10<t ≤20时,s =12×10×30+(t -10)×30=30t -150;当20<t ≤35时,s =150+300+12×(t -20)×(-2t +70+30)=-t 2+70t -550.综上可知,s 随t 变化的规律是s2,t ∈[0,10],t -150,t ∈(10,20],t 2+70t -550,t ∈(20,35].(3)当t ∈[0,10]时,s max =32×102=150<650,当t ∈(10,20]时,s max =30×20-150=450<650,当t ∈(20,35]时,令-t 2+70t -550=650,解得t =30或t =40(舍去),即在台风发生30小时后将侵袭到N 城.。
快解高中数学143模型

快解高中数学143模型数学模型在现实生活中扮演着重要的角色,能够帮助人们理解和解决各种实际问题。
在高中数学教学中,143模型被广泛地应用于各类数学题目的解决过程中。
本文将以实际案例为依据,通过快速解析高中数学143模型,帮助读者更好地理解和掌握该模型的应用。
案例一:图形的变换假设有一辆卡车,长为8m,宽为2m,高为3m,在运输过程中,将其放入一船箱中,该箱的尺寸为10m×3m×5m,问是否能够容纳?解析:这个问题可以转化为求箱子的体积是否大于卡车的体积。
我们可以先计算卡车的体积,即8m × 2m × 3m = 48m³。
接下来计算箱子的体积,即10m × 3m × 5m =150m³。
由此可知,箱子的体积大于卡车的体积,因此可以容纳卡车。
案例二:数列的求和已知数列{an}的通项公式为an = 3n² + 2n + 1,试求该数列的前n项和。
解析:对于此类数列,我们可以利用143模型中的求和公式来求解。
首先,我们要明确该数列的首项和公差,通过观察可以得知,a₁ = 6,d = 4。
接下来,我们可以利用求和公式Sₙ = (a₁ + aₙ) * n/2来计算前n项和。
将已知的数值代入公式中,得到Sₙ = (6 + (3n² + 2n + 1)) * n/2。
化简后,得到Sₙ = (3n³ + 5n² + 3n)/2。
案例三:函数的应用某人在市场上购买一个商品,它的价格随销量的增加而变动。
已知当销量为10时,该商品的价格为100元,当销量为30时,价格为200元。
问当销量为20时,商品的价格是多少?解析:这个问题可以通过函数的应用来解决。
假设动态函数f(x)表示商品的价格,其中x表示销量。
根据已知信息,我们可以列出两个点的坐标:(10, 100)和(30, 200)。
利用两点式求出直线的方程为f(x) = 6x - 40,其中x表示销量,f(x)表示价格。
(完整版)高中常见数学模型案例

高中常见数学模型案例中华人民共和国教育部2003年4月制定的普通高中《数学课程标准》中明确指出:数学探究、数学建模、数学文化是贯穿于整个高中数学课程的重要内容”,数学建模是数学学习的一种新的方式,它为学生提供了自主学习的空间,有助于学生体验数学在解决问题中的价值和作用,体验数学与日常生活和其他学科的联系,体验综合运用知识和方法解决实际问题的过程,增强应用意识;有助于激发学生学习数学的兴趣,发展学生的创新意识和实践能力。
”教材中常见模型有如下几种:一、函数模型用函数的观点解决实际问题是中学数学中最重要的、最常用的方法。
函数模型与方法在处理实际问题中的广泛运用,两个变量或几个变量,凡能找到它们之间的联系,并用数学形式表示出来,建立起一个函数关系(数学模型),然后运用函数的有关知识去解决实际问题,这些都属于函数模型的范畴。
1、正比例、反比例函数问题例1:某商人购货,进价已按原价a扣去25%,他希望对货物订一新价,以便按新价让利销售后仍可获得售价25%的纯利,则此商人经营者中货物的件数x与按新价让利总额y 之间的函数关系是_____________ 。
分析:欲求货物数x与按新价让利总额y之间的函数关系式,关键是要弄清原价、进价、新价之间的关系。
若设新价为b,则售价为b( 1 -20%),因为原价为a,所以进价为a (1 - 25%)5 解:依题意,有b(1 0.2) a(1 0.25) b(1 0.2)0.25 化简得b a,所以45 ay 0.2bx a 0.2 x,即y x, x N4 42、一次函数问题例2:某人开汽车以60km/h的速度从A地到150km远处的B地,在B地停留1h后,再以50km/h 的速度返回A地,把汽车离开A地的路x ( km)表示为时间t ( h)的函数,并画出函数的图像。
分析:根据路程=速度X时间,可得出路程x和时间t得函数关系式x (t);同样,可列出v(t)的关系式。
(完整word版)高中数学的八个有趣模型——搞定空间几何体的外接球与内切球

八个幽默模型——搞定空间几何体的外接球与内切球种类一、墙角模型(三条线两个垂直,不找球心的地址即可求出球半径)PPPPO 2ccccACbCba CbBCab AAaBBaBA图1图2 图3 图 4方法:找三条两两垂直的线段,直接用公式(2R)2a 2b 2c 2 ,即 2R a 2 b 2 c 2 ,求出 R例 1 (1)已知各极点都在同一球面上的正四棱柱的高为4 ,体积为 16,则这个球的表面积是(C)A . 16B. 20C. 24D . 32( 2)若三棱锥的三个侧面两垂直,且侧棱长均为 3 ,则其外接球的表面积是9解:( 1) V a 2 h 16 , a 2, 4R 2 a 2 a 2h 24 416 24 , S 24 ,选 C ;( 2) 4R 23 3 3 9, S4 R 29( 3)在正三棱锥 S ABC 中, M 、 N 分别是棱 SC 、BC 的中点,且 AM MN , 若侧棱 SA2 3 , 则正三棱锥 SABC 外接球的表面积是。
36解:引理: 正三棱锥的对棱互垂直 。
证明以下:如图( 3)-1 ,取 AB , BC 的中点 D , E ,连接 AE, CD , AE ,CD 交于 H ,连接 SH ,则 H 是底面正三角形 ABC 的中心, SH 平面 ABC , SH AB ,AC BC , AD BD , CDAB , AB 平面 SCD ,AB SC ,同理: BC SA , ACSB ,即正三棱锥的对棱互垂直,本题图如图( 3) -2 ,AM MN , SB// MN ,SACAM SB , AC SB , SB 平面 SAC ,SB SA SB SC ,SB SA , BC SA,,DHEB(3) 题-1SA 平面 SBC ,SA SC ,S故三棱锥 SABC 的三棱条侧棱两两互相垂直,M(2R) 2( 23)2 ( 2 3)2( 2 3)2 36 ,即 4R 236 ,AC正三棱锥 S ABC 外接球的表面积是 36NB( 4)在周围体S ABC 中,SA平面 ABC ,BAC120, SA AC2, AB1, 则该周围体的外接球的表面积为(D) A.11 B.71040 C. D .333( 5)若是三棱锥的三个侧面两两垂直,它们的面积分别为 6 、 4 、,那么它的外接球的表面积是( 6)已知某几何体的三视图以下列图,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为解析:( 4)在ABC 中,BC2AC2AB 22AB BC cos1207 ,BC7 ,ABC 的外接球直径为2r BC7 2 7,BAC33sin2(2R) 2( 2r ) 2SA2(27)2440, S40,选 D333( 5)三条侧棱两两生直,设三条侧棱长分别为a, b, c( a, b, c R),则ab12bc8,abc24 ,a3, b4, c 2 ,( 2R)2a2b2c229 , S 4 R229 ,ac6( 6)(2 )2a2b2c23, R233R, R24PV4R34333,3382A C种类二、垂面模型(一条直线垂直于一个平面)B1.题设:如图 5,PA平面 ABC解题步骤:第一步:将ABC 画在小圆面上, A 为小圆直径的一个端点,作小圆的直径AD ,连接 PD ,则 PD 必过球心 O ;PO第二步: O1为ABC 的外心,所以OO1平面 ABC ,算出小圆O1的半CA O1D径 O1D r (三角形的外接圆直径算法:利用正弦定理,得Ba b c1PA ;图 5 2r ), OO1sin A sin B sin C2第三步:利用勾股定理求三棱锥的外接球半径:①(2R)2PA 2(2r )22R PA2(2r )2;2.题设: 如图 6,7,8, P 的射影是 ABC 的外心 三棱锥 P ABC 的三条侧棱相等三棱锥 PABC 的底面 ABC 在圆锥的底上,极点 P 点也是圆锥的极点PPPPOOO OCCCCAO 1DAA O 1O 1O 1BABBB图 6 图 7-1图 7-2图 8PPPAAAO 2BCO 2CO 2DBDBOOO图8-1 图8-2 图8-3解题步骤:第一步:确定球心 O 的地址,取ABC 的外心 O 1 ,则 P,O, O 1 三点共线;第二步:先算出小圆 O 1 的半径 AO 1 r ,再算出棱锥的高 PO 1h (也是圆锥的高) ;第三步:勾股定理:OA 2O 1 A 2 O 1O 2R 2( h R) 2 r 2 ,解出 R方法二: 小圆直径参加构造大圆。
高中物理数学模型应用案例分享

高中物理数学模型应用案例分享概述在高中物理学习中,数学模型的应用十分重要。
通过运用数学方法和工具,我们可以解决一系列与物理相关的问题。
本文将分享一些高中物理领域常见的数学模型应用案例,展示它们的实际意义和解决问题的能力。
1. 简谐振动模型简谐振动是高中物理课程中经常涉及到的一个重要概念。
例如,弹簧振子、单摆等都可以使用简谐振动模型进行分析。
应用案例:弹簧振子考虑一个质量为m的弹簧振子,已知其劲度系数为k,并受到外力F(t)作用。
我们可以建立以下方程来描述其运动:m * x'' + k * x = F(t)其中x表示位移,x''表示加速度。
通过求解上述微分方程,我们可以确定该弹簧振子在外力作用下的运动规律。
2. 牛顿第二定律模型牛顿第二定律是经典力学中最基本也是最重要的定律之一。
它描述了一个物体所受合力在大小和方向上与物体的加速度成正比。
在高中物理学习中,我们经常利用牛顿第二定律建立力学模型。
应用案例:匀变速直线运动考虑一个沿直线运动的自由落体,已知其质量为m,受到重力作用。
根据牛顿第二定律,我们可以得到以下方程:m * a = -mg其中a表示加速度,g表示重力加速度。
通过求解上述方程,我们可以确定自由落体在重力作用下的运动规律。
3. 热传导模型热传导是研究物质内部温度分布和传播过程的一门学科,在高中物理学习中也有广泛应用。
应用案例:热扩散问题考虑一个长条形杆体,在不同端温度已知的情况下,我们希望推导出杆体内部温度分布。
通过应用热传导方程:∂T/∂t = k * ∂²T/∂x²其中T表示温度,t表示时间,k表示热扩散系数。
通过求解上述偏微分方程,并满足边界条件,可以得到杆体内部温度随时间的变化情况。
4. 电路模型在高中物理中,我们学习了许多关于电路的知识。
通过建立电路模型,我们可以分析电流、电势差、电阻等各种参数之间的关系。
应用案例:串联和并联电阻考虑一个由两个电阻R1和R2串联或并联组成的电路,已知电源提供的电压为V。
高中数学:零点区间的寻找技巧和常见模型

零点区间的寻找技巧方法一:直接放缩法。
成功关键:在目标区间上找到一个合适的逼近函数.【示例】证明:当10a e<<时,()ln f x x ax =-有两个零点. 分析:极值点为1x a=(大于e ),11ln 10f a a ⎛⎫=-> ⎪⎝⎭,所以需要在左右两侧各找一个函数值小于零的点.因为ln 1x x ≤-,要使得ln 0x ax -<,只需要10x ax --≤,即11x a ≤-,考虑到10a e<<,所以11,11e a e ⎛⎫∈ ⎪--⎝⎭,所以左侧可取:()10f a =-<,111ln 1011111a a f a a a a a ⎛⎫=-<--= ⎪-----⎝⎭;另一方面:因为)ln 1x x <>或)ln 1x x ≤>,要使得ln 0x ax -<0ax -≤,即21x a ≥,所以右侧可取:2211111ln 0f a a a a a a a⎛⎫⎛⎫=-≤--=-< ⎪ ⎪⎝⎭⎝⎭.方法二:在特定条件下进行放缩。
成功关键:找到的点一定要在特定的条件下.【示例】已知2a <,()()()22112x f x x x e ax x =+--++,试找一个00x >使得()00f x >. 分析:因为1x e x ≥+,要利用它来放缩,还需要考虑因式21x x +-的正负. 要使得()()()221120x f x x x e ax x =+--++>,只需()()()2221011120x x x x x ax x ⎧+->⎪⎨+-+-++≥⎪⎩,即()2013x x a ⎧<<⎪⎨⎪+≤-⎩,因此取01x ⎫⎪=⎬⎪⎪⎩⎭即可使得()00f x >.或写得好看一点,取{}01x =-也能符合要求.方法三:目测。
成功关键:数感与大胆.【示例】证明:当a e >时,()xf x e ax =-有两个零点.分析:极值点为ln x a =(大于1),()()l n 1l n 0f a a a =-<,所以需要在左右两侧各找一个函数值大于零的点.左侧,自变量越小,成功的可能性越高,则可找:1110af e a ⎛⎫=-> ⎪⎝⎭,()010f =>,()110f a e -=+>.右侧,自变量越大,成功的可能性越高,则可找:()()2ln 2ln 2ln 2ln 0a f a e a a a a a =-=->,()20a f a e a =->.方法四:分而治之。
模型1公切线模型(高中数学模型大归纳)
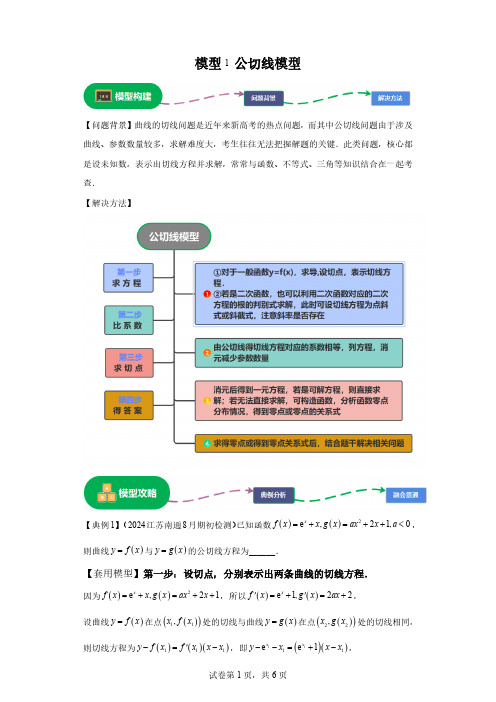
模型1 公切线模型【问题背景】曲线的切线问题是近年来新高考的热点问题,而其中公切线问题由于涉及曲线、参数数量较多,求解难度大,考生往往无法把握解题的关键.此类问题,核心都是设未知数,表示出切线方程并求解,常常与函数、不等式、三角等知识结合在一起考查.【解决方法】【典例1】(2024江苏南通8月期初检测)已知函数()()2e ,21,0xf x xg x ax x a =+=++<,则曲线()y f x =与()y g x =的公切线方程为______.【套用模型】第一步:设切点,分别表示出两条曲线的切线方程.因为()()2e ,21xf x xg x ax x =+=++,所以()()e 1,22x f x g x ax ''=+=+,设曲线()y f x =在点()()11,x f x 处的切线与曲线()y g x =在点()()22,x g x 处的切线相同,则切线方程为()()()111y f x f x x x '-=-,即()()1111e e 1x xy x x x --=+-,整理得()1111e 1e e x x xy x x =+-+.又切线方程也可表示为()()()222y g x g x x x '-=-,即()()222222122y ax x ax x x ---=+-,整理得()222221y ax x ax =+-+.第二步:得出关于切线方程系数的方程.所以1112212e 122,e e 1,x x x ax x ax ⎧+=+⎨-+=-+⎩消去2x ,整理得()11121e 4e 42e 410x x x ax a a -+--+=.【点技巧】合理消元,若消去1x ,则会产生对数,求解复杂,应该消去2x ,由12e 122x ax +=+,得12e 12x x a-=第三步:构造函数,利用函数的单调性求解切点坐标.令()()2e 4e 42e 410,0x x xm x ax a a a =-+--+=<,则()()()22e 4e 4e 42e 2e e 21x x x x x xm x a ax a ax =--+-=--'.令()e 21,0xx ax a ϕ=--<,因为a<0,所以函数21y ax =--在R 上单调递增,又函数e x y =在R 上单调递增,所以()x ϕ在R 上单调递增.又()00ϕ=,所以当(),0x ∈-∞时,()0x ϕ<;当()0,x ∈+∞时,()0x ϕ>.又e 0x >,所以当(),0x ∈-∞时,()0m x '<,当()0,x ∈+∞时,()0m x '>,所以()m x 在(),0∞-上单调递减,在()0,∞+上单调递增,所以()()00m x m ≥=,因此函数()y m x =只有一个零点,即关于1x 的方程()11121e 4e 42e 410x x x ax a a -+--+=只有一个解10x =.【破瓶颈】此方程无法直接求解,构造函数,应用导数分析函数单调性,求得零点10x =第四步:求得公切线方程.由10x =得切线方程为21y x =+,所以公切线方程为21y x =+.【典例2】(双空题 2024江苏基地大联考第一次质量监测)已知直线l 与曲线1e x y -=和()ln 1y x =+都相切,请写出符合条件的两条直线l 的方程:______,______.【套用模型】第一步:设切点,分别表示出曲线1e x y -=和()ln 1y x =+的切线方程.设直线l 与曲线1e x y -=和()ln 1y x =+分别切于点()()()111222,e ,,ln 1,1x x x x x -+>-,由()()111e e ,ln 11x x x x --''⎡⎤=+=⎣⎦+可得切线方程分别为()()()111112221e e ,ln 11x x y x x y x x x x --=-+=-+++,即()111111212221e e e ,ln 111x x x x y x x y x x x x ---=-+=-++++.第二步:得出关于切线方程系数的方程.因此1121e1x x -=+,则()121ln 1x x -=-+,又()11112122e e ln 11x x x x x x ----+=+++,所以()()1111212222211ee ln 11ln 1111x x x x x x x x x ---⎡⎤-+=+-⋅+=++⎣⎦+++.【指点迷津】根据曲线1e x y -=和()ln 1y x =+的公切线斜率相等,可得()121ln 1x x -=-+,根据两个切线方程的对应系数相等列方程,化简整理求解第三步:化简求切点横坐标.化简得()2221ln 101x x x ⎡⎤-+⋅=⎣⎦+,解得20x =或2e 1x =-.第四步:求得两条切线方程.当20x =时,11x =,切线方程为y x =;当2e 1x =-时,10x =,切线方程为11e ey x =+.【典例3】(2024安徽合肥一中9月模拟)曲线e x y =与ln y x =的两条公共切线的斜率分别为()1212,k k k k <,设两切线的夹角为02πθθ⎛⎫<< ⎪⎝⎭,则21tan k k θ=-______.【套用模型】第一步:设切点横坐标,分别表示出曲线e x y =与ln y x =的两条公共切线的方程.设两条公切线与曲线e x y =相切的两个切点横坐标分别为13,x x ,与曲线ln y x =相切的两个切点横坐标分别为24,x x ,其中1432x x x x <<<,则1230,1,0x x x <>>且341,01x x ≠<<.由()()1ee ,ln xxx x''==,可得31122411e ,e x x k k x x ====.斜率为1k 的切线方程为()111e e x xy x x -=-,也可以表示为()2221ln y x x x x -=-;斜率为2k 的切线方程为()333e e x xy x x -=-,也可以表示为()4441ln y x x x x -=-.第二步:得出关于切线方程系数的方程.所以()112121e ,e 1ln 1,x x x x x ⎧=⎪⎨⎪-=-⎩整理得1111e 1x x x +=-,同理得3331e 1x x x +=-.【会类比】3x 与1x 的“地位”一样,得到1x 的关系式,可同理得到3x 的关系式第三步:构造函数,利用函数的单调性得切点横坐标的关系式.因此13,x x 是方程1e 1xx x +=-的根,又111e e 11xx x x x x ---+===+--,所以若x 是方程1e 1xx x +=-的根,则x -也是方程1e 1xx x +=-的根.设()()12e e 1111xx x f x x x x +=-=--≠--,易知()()22e 01xf x x -'=+>,则()f x 在()(),1,1,-∞+∞上单调递增,()()()22111320,10,50,2e 30,e 3e2f f f f ⎛⎫-=-<-=>=<=-> ⎪⎝⎭于是函数()f x 在()32,1,,22⎛⎫-- ⎪⎝⎭上各有一个零点,即方程1e 1xx x +=-有两个不等根,则130x x +=,即3112e e 1x xk k =⋅=.【扫清障碍】函数()f x 无法求出零点,但可分析得到130x x +=,进而可得121k k =第四步:求代数式的值.令斜率为12,k k 的切线倾斜角分别为12,αα,则21θαα=-,()212121212112tan tan tan tan 1tan tan 12k k k k k k ααθαααα---=-===++,所以21tan 12k k θ=-.(2024·安徽·高三校联考阶段练习)1.已知函数()222x ef x e x =+,()3lng x x =,若直线l 与曲线()y f x =及()y g x =均相切,且切点相同,求公切线l 的方程为 .(2024·山东青岛·高三山东省青岛第一中学校考期中)2.若曲线()21:C f x x a =+和曲线()2:4ln 2C g x x x =-存在有公共切点的公切线,则该公切线的方程为 .(2024·福建厦门·统考模拟预测)3.已知函数()()2ln ,f x mx x g x x mx =+=-,若曲线()y f x =与曲线()y g x =存在公切线,则实数m 的最大值为 .(2024·江苏南通·高三统考期末)4.已知直线l 与曲线2e x y -=和ln y x =都相切,请写出符合条件的两条直线l 的方程: , .(2024·高三上·江苏泰州·期中)5.若曲线e x y =在点()00,e x A x 00x >处的切线也是曲线ln y x =的切线,则004xx +e 的最小值为 .(2024·黑龙江哈尔滨·哈尔滨三中校考模拟预测)6.曲线ln y m x =+过点()2,0-的切线也是曲线e x y =的切线,则m =;若此公切线恒在函数()212e 31e e x f x a x x ⎛⎫=-+-+- ⎪⎝⎭的图象上方,则a 的取值范围是.(2024·广东·校联考模拟预测)7.曲线e x y =与ln y x =的公共切线的条数为 .(2024·广东深圳·深圳外国语学校二模)8.已知曲线()()1:ln 21C f x x =-在点()11,M x y 处的切线与曲线()212:e x C g x -=相切于点()22,N x y ,则下列结论正确的是()A .函数()()21h x x g x =-有2个零点B .函数()()()3e 2m x f x xg x =-在1,12⎛⎫⎪⎝⎭上单调递增C .()21121g x x =-D .211201x x +=-(2024·河南安阳·校联考一模)9.已知函数222e ()e x f x x=+,()3eln g x x =,其中e 为自然对数的底数.(1)讨论函数()f x 的单调性.(2)试判断曲线()y f x =与()y g x =是否存在公共点并且在公共点处有公切线.若存在,求出公切线l 的方程;若不存在,请说明理由.(2024·全国·模拟预测)10.如果有且仅有两条不同的直线与函数()(),f x g x 的图象均相切,那么称这两个函数()(),f x g x 为“L 函数组”.(1)判断函数2e x y -=与ln y x =是否为“L 函数组”,其中e 为自然对数的底数,并说明理由;(2)已知函数()2ln f x x =+与()g x =“L 函数组”,求实数a 的取值范围.参考答案:1.3y x e=.【分析】由条件可知()()()()0000f x g x f x g x ''⎧=⎪⎨=⎪⎩,求得切点后,再求切线方程.【详解】设切点为()00,x y ,由()()()()0000f x g x f x g x ''⎧=⎪⎨=⎪⎩,得200200220023ln 43x ex e x x e ex x ⎧+=⎪⎪⎨⎪-=⎪⎩ 解得0x e =,003ln 3y x ==,故切线方程为()33y x e e -=-,即3y x e=.故答案为:3y x e=2.24y x =-【分析】先分别求出()f x 和()g x 的导数,然后设公共切点的坐标为0(x ,0)y ,根据题意有00()()f x g x ''=,00()()f x g x =,代入相应表达式列出方程组,解出0x 与a 的值,计算出切线斜率和公切线的切点坐标,即可得到切线的方程.【详解】()2f x x a =+,()4ln 2g x x x =-,则有()2f x x '=,4()2g x x'=-.设公共切点的坐标为0(x ,0)y ,则00()2f x x '=,004()2g x x '=-,200()f x x a =+,000()4ln 2g x x x =-.根据题意,有00200004224ln 20x x x a x x x ⎧=-⎪⎪⎪+=-⎨⎪>⎪⎪⎩,解得013x a =⎧⎨=-⎩.∴公切线的切点坐标为(1,2)-,切线斜率为2.∴公切线的方程为22(1)y x +=-,即24y x =-.故答案为:24y x =-3.12##0.5【分析】根据导数的几何意义,利用斜率等于切点处的导数,和切线相同即可判断.【详解】()()1,2f x m g x x m x ''=+=-,假设两曲线在同一点()00,x y 处相切,则002000012ln m x m x mx x x mx⎧+=-⎪⎨⎪+=-⎩,可得2001ln x x -=,即200ln 10x x +-=,因为函数2ln 1y x x =+-单调递增,且1x =时0y =,所以01x =,则12m =,此时两曲线在11,2⎛⎫⎪⎝⎭处相切,根据曲线的变化趋势,若12m >,则两曲线相交于两点,不存在公切线,如图,所以m 的最大值为12.故答案为:12.4.1y x =-1ey x=【分析】设出切点,利用切点求解切线方程,联立方程即可求解切点处的值,代入即可求解切线方程【详解】2e x y -'=,1y x'=,设直线与曲线2e x y -=和ln y x =相切于点()()2112,,,x y y x ,则所以切线方程分别为()()112212221e e ,ln x x y x x y x x x x --=-+=-+,因此1221e ,x x -=则122ln x x -=-,又112212e e 1ln x x x x ---+=-+,将122ln x x -=-代入可得()()1112221111e e 12+1e 10+10x x x x x x x ----+=-+-⇒--=⇒-=或12e 10x --=12e 10x --=,解得11x =或12x =,将其代入()11221e e x x y x x --=-+中,因此当11x =时,切线方程为1ey x =,当12x =时,切线方程为1y x =-,故答案为:1y x =-,1ey x =5.5+【分析】由两条曲线的公切线斜率分别等于各曲线上切点处的导数值,以及各曲线上切点分别满足切线方程来列方程组,得到0x 与0e x 满足的关系式,将原式中的0e x 替换,再利用基本不等式求最小值即可.【详解】曲线e x y =在点A 处的切线可写作000()xxy x x =-+e e 设该切线在曲线ln y x =上的切点为(,ln )t t ,则有000ln e ()e 1e x x x t t x t⎧=-+⎪⎨=⎪⎩,消去t 得0001e 1x x x +=-则0000000112441)44(511x x x x x x x ++=+=-+≥+++--e 当且仅当00421)1(x x --=,即01x =时取得该最小值.故答案为:5+6.2e2e a <-【分析】根据导数的几何意义可求出m ;将此公切线恒在函数()212e 31e e xf x a x x ⎛⎫=-+-+- ⎪⎝⎭的图象上方,转化为231e xx x a ++<恒成立,再构造函数231()e xx x g x ++=,利用导数求出最小值即可得解.【详解】由ln y m x =+得1y x'=,设曲线ln y m x =+过点()2,0-的切线的切点为00(,ln )x m x +,则切线的斜率为01x ,切线方程为0001ln ()y m x x x x --=-,由于该切线过点(2,0)-,所以002ln 1m x x --=--,设该切线与曲线e x y =切于11(,)x y ,因为e x y =,所以e x y '=,所以该切线的斜率为1e x ,所以切线方程为111e e ()x xy x x -=-,将(2,0)-代入得1110e e (2)x x x -=--,得11x =-,所以1011e e x x ==,所以0e x =,所以ln e=m --21e--,所以2e m =.由以上可知该公切线方程为11(1)e e y x -=+,即12e e y x =+,若此公切线恒在函数()212e 31e e x f x a x x ⎛⎫=-+-+- ⎪⎝⎭的图象上方,则21212e (3)1e e e e x x a x x +>-+-+-,即231e xx x a ++<恒成立,令231()e xx x g x ++=,则()22(23)e (31)e ()e x x x x x x g x +⋅-++⋅'=22e x x x --+=,令()0g x '>,得220x x --+>,得2<<1x -,令()0g x '<,得220x x --+>,得<2x -或1x >,所以()g x 在(,2)-∞-上单调递减,在(2,1)-上单调递增,在(1,)+∞上单调递减,因为0x >时,()0g x >,所以当2x =-时,()g x 取得最小值2(2)e g -=-.所以2e a <-.【点睛】关键点点睛:求解第二个空时,转化为不等式恒成立,利用导数求解是解题关键.7.2【分析】设公切线关于两函数图像的切点为()()1122,e ,,l n xx x x ,则公切线方程为:()()1112221e e l n x x y x x x x x x =-+=-+,则()112121e e 1ln 1x x x x x ⎧=⎪⇒⎨⎪-=-⎩()222110l n xx x ---=,则公切线条数为()()1ln 1h x x x x =---零点个数.【详解】设公切线关于两函数图像的切点为()()1122,e ,,l n xx x x ,则公切线方程为:()()1112221eel n x x y x x x x x x =-+=-+,则()112121e e 1ln 1x x x x x ⎧=⎪⎨⎪-=-⎩,注意到121e xx =,21ln x x =-,则由()112e 1ln 1xx x -=-,可得()22222221110l n l n l n x x x x x x x +=-⇒---=.则公切线条数为方程()222110l n x x x ---=的根的个数,即函数()()1ln 1h x x x x =---的零点个数.()1ln h x x x '=-,令()1l n p x x x =-,则()2110p x x x'=+>,得()()h x p x '=在()0,∞+上单调递增.因()()111010,e eh h ''=-<=->,则()01,e x ∃∈,使得()00010l n h x x x '=-=.则()h x 在()00,x 上单调递减,在()0,x +∞上单调递增,故()()()0000001110m i n l n h x h x x x x x x ==---=--<,又注意到()()2222321110e e e e h ---=---=->,()()222221130e e e e h =---=->,则()()223040e ,,,e x x x x -∃∈∃∈,使得()()340h x h x ==,得()h x 有2个零点,即公共切线的条数为2.故答案为:2【点睛】关键点点睛:本题涉及研究两函数公切线条数,难度较大.本题关键为将求公切线条数转化为求相关函数零点个数,又由题2x 有范围,故选择消掉1x ,构造与2x 有关的方程与函数.8.BCD【分析】利用导数说明函数的单调性,结合零点存在性定理判断A ,利用导数判断函数的单调性,即可说明B ,利用导数的几何意义表示出切线方程,即可得到方程组,从而判断C 、D.【详解】对于A :()()()()22221111e21e x x h x x g x h x x x x ---'=+⇒=-=,当0x >时,()()0,h x h x '>单调递增,当10x -<<时,()()0,h x h x '>单调递减,当1x <-时,()()0,h x h x '>单调递增,函数()h x 的极大值为()31e 10h --=-<,极小值为()010h =-<,因此当1x <-时,()0h x <,当10x -<<时,()0h x <,又()1e 10h =->,所以()()010h h <,则()h x 在()0,1上存在零点,因此函数()h x 只有一个零点,故A 不正确;对于B :()()()()2133e eln 21e 22x m x f x xg x x x -=-=--,则()()213e21e 21x m x x x -'=-+-,令()()2121e x H x x -=-+,1,12x ⎛⎫∈ ⎪⎝⎭,则()()2143e0x H x x -'=-+<,所以()H x 在1,12⎛⎫ ⎪⎝⎭上单调递减,又3e 21y x =-在1,12⎛⎫⎪⎝⎭上单调递减,当1,12x ⎛⎫∈ ⎪⎝⎭时,函数()m x '单调递减,所以当1,12x ⎛⎫∈ ⎪⎝⎭时,()()10m x m ''>=,所以函数()()()3e 2m x f x xg x =-在1,12⎛⎫⎪⎝⎭上单调递增,故B 正确;对于C :()()()2ln 2121f x x f x x '=-⇒=-,因此曲线()()1:ln 21C f x x =-在点()11,M x y 处的切线方程为:()()()1111111222ln 21ln 21212121x xy x x x y x x x x --=-⇒=+-----,由()()2121e2e x x g x g x --'=⇒=,因此曲线()212:ex C g x -=相切方程为:()22222212121212122e 2e 2e e 2e x x x x x y x x y x x ------=-⇒=+-,因为曲线()()1:ln 21C f x x =-在点()11,M x y 处的切线与曲线()212:e x C g x -=相切于点()22,N x y ,所以()()2222222121112121212111121211212e e212122ln 21e 2e ln 21e 2e 2121x x x x x x x x x x x x x x x x ------⎧⎧==⎪⎪--⎪⎪⇒⎨⎨⎪⎪--=---=-⎪⎪--⎩⎩,因此()221211e21x g x x -==-,故C 正确;对于D :由上可知:()222211212111211e 212ln 21e 2e 21x x x x x x x x ---⎧=⎪-⎪⎨⎪--=-⎪-⎩,因此有()22212111212ln 21e 2e 21x x x x x x ----=--()22112111221ln e 212121x x x x x x --⇒-=----12211122121212121x x x x x x ⇒-+-=----()122212112210211201x x x x x x x ⇒-+=⇒-=-⇒+=-,故D 正确,故选:BCD【点睛】关键点睛:涉及公切线问题,一般是利用导数的几何意义表示出切线方程,根据两切线相同得到方程组,从而整理得到()222211212111211e 212ln 21e 2e 21x x x x x x x x ---⎧=⎪-⎪⎨⎪--=-⎪-⎩.9.(1)()f x 在(),0∞-上单调递减,在⎛ ⎝上单调递减,在⎫∞⎪⎭上单调递增.(2)存在,3y x=【分析】(1)求出函数的定义域与导函数,再解关于导函数的不等式,即可求出函数的单调区间;(2)假设曲线()y f x =与()y g x =存在公共点且在公共点处有公切线,且切点横坐标为00x >,即可得到()()()()0000f x g x f x g x ''⎧=⎪⎨=⎪⎩,则有3230043e e 0x x --=,构造函数()32343e e h x x x =--,()0,x ∈+∞,利用导数说明函数的单调性,即可知方程()00h x =在()0,∞+上有唯一实数根0e x =,即可得到切点横坐标,再根据导数的几何意义计算可得.【详解】(1)解:因为222e ()e x f x x=+定义域为{}|0x x ≠,所以()233224e 4e e e x x f x x x -'=-=,令()0f x '=,解得x =当x <0x ≠时,()0f x '<;当x ()0f x '>,所以()f x 在(),0∞-上单调递减,在⎛ ⎝上单调递减,在⎫+∞⎪⎭上单调递增.(2)解:由()3eln g x x =定义域为()0,∞+,3e ()g x x'=,假设曲线()y f x =与()y g x =存在公共点且在公共点处有公切线,且切点横坐标为00x >,则()()()()0000f x g x f x g x ''⎧=⎪⎨=⎪⎩,即2200020200e 23eln 4e 3e e x x x x x x ⎧+=⎪⎪⎨⎪-=⎪⎩,其中202004e 3e e x x x -=即3230043e e 0x x --=,记()32343e e h x x x =--,()0,x ∈+∞,则()()()32e 2e h x x x '=+-,所以当e02x <<时()0h x '<,当e 2x >时()0h x '>,所以()h x 在e 02⎛⎫⎪⎝⎭,上单调递减,在e ,2⎛⎫+∞ ⎪⎝⎭上单调递增,又()30e h =-,3e 2e 2h ⎛⎫=- ⎪⎝⎭,()e 0h =,故方程()00h x =在()0,∞+上有唯一实数根0e x =,经验证0e x =也满足22000e 23eln x x x +=,于是()()003e f x g x ==,()()003f x g x ''==,所以曲线()y f x =与()y g x =的公切线l 的方程为()3e 3e y x -=-,即3y x =.10.(1)它们为“L 函数组”,理由见解析(2)()0,2【分析】(1)设出切点,得到两函数的切线方程,根据斜率相等得到1221ex x -=,代入两切线方程,对照系数得到()()1211e 10x x --+-=,解得11x =或12x =,求出两条切线方程,得到答案;(2)设出切点,得到两切线方程,求出0a >,再联立1ln 1y x t t y ⎧=++⎪⎨⎪=⎩,转化为方程有两个正数根,构造()4ln 4t g t t+=,求导得到其单调性,极值最值情况,数形结合得到答案.【详解】(1)函数2e x y -=和ln y x =是“L 函数组”,理由如下:设直线与曲线2e x y -=和ln y x =相切于点()()1122,,,x y x y ,2e x y -'=,1y x'=,则切线方程分别为()()112212221ee ,ln x x y x x y x x x x --=-+=-+.因此1221ex x -=,则122ln x x -=-.故()()11221112222111e e x x x x y x x x x x x x x ---=-+=-+=+,()()()2221122211ln 21xy x x x x x x x x x x =-+=---=+-,由于两切线为同一直线,故11211x x x -=-,即()112110x x x ---=,又1221e x x -=,故()()1211e 10x x --+-=,解得11x =或12x =,当11x =时,切线方程为1ey x =,当12x =时,切线方程为1y x =-,因此切线方程为1ey x =或1y x =-.因为有且仅有两条不同的直线与函数2e x y -=和ln y x =的图象均相切,所以它们为“L 函数组”.(2)因为函数()2ln f x x =+与()g x =“L 函数组”,所以它们的图象有且仅有两条公切线.由()2ln f x x =+,得()1f x x'=,设切点坐标为(),2ln t t +,0t >,则切线方程为()12ln y x t t t=-++,()g x '=(,m,则切线方程为)y x m -=-,由题意得1t =0t >,所以0a >.联立1ln 1y x t t y ⎧=++⎪⎨⎪=⎩,所以ln 0x t t t -+=.由判别式22Δ4ln 40a t t t t =--=,可得24ln 4t a t+=.依题意,关于实数t 的方程224ln 40a t t t t --=恰有两个不同的正数解.令()4ln 4t g t t+=,则()2244ln 44ln t tg t t t ---==',故当()0,1t ∈时,()0g t '>,所以()g t 单调递增;当()1,t ∞∈+时,()0g t '<,所以()g t 单调递减,所以()()max 14g t g ==.又10e g ⎛⎫= ⎪⎝⎭,当x →+∞时,()0g x +→;所以204a <<.又0a >,所以02a <<,实数a 的取值范围是()0,2.【点睛】当已知切点坐标为()00,x y 时,根据导函数的几何意义可得到切线的斜率,再利用()()()000y f x f x x x '-=-求出切线方程;当不知道切点坐标时,要设出切点坐标,结合切点既在函数图象上,又在切线方程上,列出等式,进行求解.。
高中数学立体几何之外接球与内切球问题常见模型归纳(完整版)
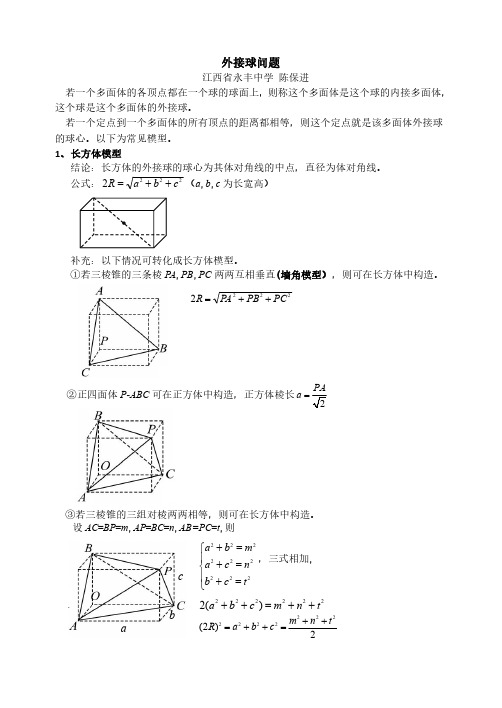
外接球问题江西省永丰中学陈保进若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
若一个定点到一个多面体的所有顶点的距离都相等,则这个定点就是该多面体外接球的球心。
以下为常见模型。
1、长方体模型结论:长方体的外接球的球心为其体对角线的中点,直径为体对角线。
公式:2222c b a R ++=(a ,b ,c 为长宽高)补充:以下情况可转化成长方体模型。
①若三棱锥的三条棱PA ,PB ,PC 两两互相垂直(墙角模型),则可在长方体中构造。
2222PC PB P A R ++=②正四面体P -ABC 可在正方体中构造,正方体棱长2=PA a ③若三棱锥的三组对棱两两相等,则可在长方体中构造。
设AC =BP =m ,AP =BC =n ,AB=PC =t ,则⎪⎩⎪⎨⎧=+=+=+222222222t c b n c a m b a ,三式相加,222222)(2t n m c b a ++=++2)2(2222222t n m c b a R ++=++=abc2、直三棱柱模型结论:直三棱柱外接球的球心是上、下底面外心连线的中点,222()2hR r =+r 为底面三角形外接圆的半径,可用正弦定理求,h 为直三棱柱的高。
补充:有一条侧棱垂直底面的三棱锥可补成直三棱柱,如图P -ABC 中,PA ⊥平面ABC ,则可补成直三棱柱PB 1C 1-ABC ,外接球半径公式同上。
提醒:底面具有外接圆的直棱柱才有外接球,比如正棱柱,且球心在上、下底面外心连线的中点,底面无外接圆的直棱柱,以及所有斜棱柱均无外接球。
3、共斜边模型四面体D-ABC 中,DC AD ⊥,BC AB ⊥,AC 为公共的斜边,O 为AC 的中点,则O 为四面体D-ABC 外接球的球心。
4、正棱锥模型外接球的球心在正棱锥的高所在直线上,如图正三棱锥A-BCD 中,作AO 1⊥平面BCD ,则易得BO 1=CO 1=DO 1,所以O 1为△BCD 的外心,设O 为其外接球球心,半径为R ,则BO =AO =R ,设AO 1=h ,BO 1=r ,则由BO 2=BO 12+OO 12,得R 2=r 2+(h-R )2。
高中数学数学建模案例

高中数学数学建模案例在高中数学课程中,数学建模是一个重要的部分。
它通过数学模型来解决实际生活中的问题,培养学生的数学思维和解决问题的能力。
下面我将给大家介绍一个高中数学数学建模的案例。
目标:优化校园电费的管理问题陈述:某高中校园有多个教学楼和宿舍楼,每个建筑都有独立的电费计量表。
校方希望通过合理的电费管理来节约能源和降低费用支出,同时保证校园的正常运行。
解决方案:1. 数据收集和分析:首先,校方需要收集校园各个建筑的用电量数据和相应的费用数据。
这些数据可以通过系统监测或者人员抄表的方式收集。
然后,校方需要对数据进行分析,找出电费支出的主要因素和影响因素。
2. 建立数学模型:然后,校方可以根据数据分析的结果和实际情况,建立数学模型来描述校园的电费管理问题。
这个模型可以包括以下几个方面的因素: - 建筑的用电规模:每个建筑的用电规模不同,可以通过建筑的面积、人员数量等来估计。
- 用电设备和使用模式:不同的教室、实验室和宿舍楼都有不同的用电设备和使用模式,需要对其进行分类和分析。
- 电费计价规则:校方可以根据实际情况来确定电费的计价规则,例如按照用电量或者按照峰谷分时段计费等。
3. 模型求解和优化:校方可以使用数学软件或者编程工具来求解和优化建立的数学模型。
通过模型的求解,可以得到一些关键的结论和优化建议,例如: - 不同建筑的用电量和费用占比;- 用电量较大的建筑和使用模式;- 节约用电的策略和措施;- 改进计费规则的建议等。
4. 实施和监测:最后,校方需要根据模型的结果和建议,进行实施和监测。
可以通过相关培训和教育来提高师生对节约用电的意识,同时可以安装电表监测系统来实时监测用电情况,及时调整和改进管理策略。
结论:通过数学建模,校园电费管理可以得到优化,节约能源和降低费用支出。
同时,这个案例也展示了数学建模在实际问题中的应用和重要性。
总结:数学建模是高中数学课程中的一个重要组成部分,通过建立数学模型解决实际问题,培养学生的数学思维和解决问题的能力。
高一数函数模型的应用实例【共44张PPT】

分段函数模型
某市居民自来水收费标准如下:每户每月用水不 超过4吨时每吨为1.80元,当用水超过4吨时,超过部分每吨为 3.00元,某月甲、乙两用户共交水费y元,已知甲、乙两用户该 月用水量分别为5x,3x吨.
(1)求y关于x的函数; (2)若甲、乙两用户该月共交水费26.40元,分别求出甲、 乙两用户该月的用水量和水费.
(5) 指 数 函 数 模 型 : f(x) = __a__·_b_x_+__c__(a , b , c 为 常 数 , a≠0,b>0,b≠1);
(6)对数函数模型:f(x)=____m__lo_g_a_x_+__n_____(m,n,a为常 数,m≠0,a>0,a≠1);
(7)幂函数模型:f(x)=_____a_x_n+__b_(a,b,n为常数,a≠0, n≠1).
3x+1 600(0≤x≤2 000,x∈N*).
2.借助已知对数值求解实际问题的关键是什么?
5元,若普通车存车数为x辆次,存车费总收入为y元,则y关于x的函数关系式是( )
付费 y =4×1.80+3.5×3.00=17.70(元). (3)分段函数的值域求法为:逐段求函数值的范围,最后再下结论(关键词:值域). 1
1.某林场计划第一年造林10 000亩,以后每年比前一年多
造林20%,则第四年造林( )
A.14 400亩
B.172 800亩
C.20 736亩
D.17 280亩
解析: 设年份为x,造林亩数为y,则y=10 000×(1+
20%)x-1,
∴x=4时,y=17 280.故选D.
答案: D
2.据调查,某自行车存车处在某星期日的存车量为2 000 辆次,其中变速车存车费是每辆一次0.8元,普通车存车费是每 辆一次0.5元,若普通车存车数为x辆次,存车费总收入为y元, 则y关于x的函数关系式是( )
高中数学建模案例

高中数学建模案例数学建模是一门综合性强、应用范围广的学科,其在高中数学教学中也占据着重要的地位。
通过数学建模,可以帮助学生将数学知识与实际问题相结合,提高学生的综合运用能力和解决问题的能力。
本文将以高中数学建模案例为例,介绍数学建模的基本流程和方法。
首先,数学建模的基本流程包括问题的建模、模型的建立、模型的求解和模型的验证。
在问题的建模阶段,需要对实际问题进行分析,确定问题的具体要求和条件。
在模型的建立阶段,需要根据问题的特点选择合适的数学模型,建立数学模型,并进行合理的假设和简化。
在模型的求解阶段,需要运用数学知识和方法对建立的数学模型进行求解。
在模型的验证阶段,需要对求解结果进行分析和验证,确保模型的合理性和可靠性。
其次,数学建模的方法包括数学分析方法、数值计算方法和模拟实验方法。
在数学分析方法中,需要运用微积分、线性代数、概率统计等数学知识对问题进行分析和建模。
在数值计算方法中,需要利用计算机编程和数值计算方法对复杂的数学模型进行求解。
在模拟实验方法中,需要通过实际数据的收集和实验的设计,对数学模型进行验证和修正。
最后,我们以一个高中数学建模案例来具体说明数学建模的应用过程。
假设某地区的人口增长率为每年1.5%,现有人口为100万,请问经过多少年,该地区的人口将达到200万?首先,我们可以利用指数增长模型来建立数学模型,假设人口增长率为r,经过t年后的人口数量为N(t),则有N(t)=N(0)(1+r)^t。
然后,我们可以利用对数函数的性质,求解出t的值,即t=ln(2)/ln(1+r)≈46.4年。
最后,我们可以通过实际数据的收集和对结果的分析,验证我们的模型和求解结果的合理性。
通过上述案例,我们可以看到数学建模在高中数学教学中的重要性和应用价值。
通过数学建模,不仅可以帮助学生提高数学运用能力和解决问题的能力,还可以培养学生的创新意识和实践能力。
因此,数学建模应该成为高中数学教学中的重要内容,引导学生通过数学建模来解决实际问题,提高数学知识的实际运用能力。
高中数学建模生活案例

高中数学建模生活案例
从数学建模的内涵看,数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养.数学建模过程主要包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题.
从数学建模的学科价值看,数学建模素养是学生在数学建模活动中形成的,它集理解问题、提出问题、分析问题和解决问题于一身,是最具有综合性的数学素养.数学模型素养搭建了数学与外部世界联系的桥梁,是数学应用的重要形式.数学建模是应用数学解决实际问题的基本手段,也是推动数学发展的动力.
从数学建模的教育价值看,通过高中数学课程的学习,学生能有意识地用数学语言表达现实世界,发现和提出问题,感悟数学与现实之间的关联;学会用数学模型解决实际问题,积累数学实践的经验;认识数学模型在科学、社会、工程技术诸多领域的作用,提升实践能力,增强创新意识和科学精神.。
高中物理数学模型教案

高中物理数学模型教案概述在高中物理教学中,数学模型是一个重要的工具。
使用数学语言和思维,可以帮助学生更好地理解物理概念和问题,并解决实际的物理应用题。
本教案将介绍几个常见的高中物理数学模型,并给出相关例题和解答。
一、速度-时间图像1. 基本概念速度-时间图像是描述物体运动状态的图像之一,横坐标表示时间,纵坐标表示速度。
直线代表匀速运动,曲线代表变速运动。
### 2. 相关公式和计算方法 -(Δx表示位移变化量,Δt表示时间变化量) - 瞬时速度:平均速度:v avg=ΔxΔt(表示某一瞬间的速度)v=dxdt3. 例题分析:已知某辆汽车在0~10s内做匀加速运动,其加速度为2m/s²。
根据其速度-时间图像求该车10秒内所走过的总位移。
#### 解答:根据匀加速直线运动的规律可知,由于加速度为常数,所以速度-时间图像为一条斜线。
速度随时间的变化可以用v=at表示,其中v为速度,a为加速度。
因此在10秒内,车辆的瞬时速度将从0增加到20m/s(由v=at=2×10=20得到)。
根据速度-时间图像下方的面积等于位移的原理,所以总位移等于速度变化曲线下方面积的和。
根据几何知识可计算出总位移为100m(即1×20×10=100)。
2二、动量守恒定律1. 基本概念动量守恒定律是描述物体碰撞过程中动量守恒的规律。
当系统受到外力作用时,系统总动量可能发生变化;但在没有外力作用下,系统总动量保持不变。
###2. 相关公式和计算方法 - 动量:p =mv (其中p 表示动量,m 表示物体质量,v 表示物体速度) - 动量守恒定律:对于一个孤立系统,在碰撞前后系统总动量保持不变。
###3. 例题分析: 有一个质量为1kg 的小球以4m/s 的速度向右运动,与一个质量为2kg 的小球以2m/s 的速度向左运动发生碰撞,求碰撞后两个小球的速度。
#### 解答: 根据动量守恒定律可知,在碰撞前后系统总动量保持不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中常见数学模型案例
中华人民共和国教育部2003年4月制定的普通高中《数学课程标准》中明确指出:“数学探究、数学建模、数学文化是贯穿于整个高中数学课程的重要内容”,“数学建模是数学学习的一种新的方式,它为学生提供了自主学习的空间,有助于学生体验数学在解决问题中的价值和作用,体验数学与日常生活和其他学科的联系,体验综合运用知识和方法解决实际问题的过程,增强应用意识;有助于激发学生学习数学的兴趣,发展学生的创新意识和实践能力。
”教材中常见模型有如下几种:
一、函数模型
用函数的观点解决实际问题是中学数学中最重要的、最常用的方法。
函数模型与方法在处理实际问题中的广泛运用,两个变量或几个变量,凡能找到它们之间的联系,并用数学形式表示出来,建立起一个函数关系(数学模型),然后运用函数的有关知识去解决实际问题,这些都属于函数模型的范畴。
1、正比例、反比例函数问题
例1:某商人购货,进价已按原价a 扣去25%,他希望对货物订一新价,以便按新价让利销售后仍可获得售价25%的纯利,则此商人经营者中货物的件数x 与按新价让利总额y 之间的函数关系是___________。
分析:欲求货物数x 与按新价让利总额y 之间的函数关系式,关键是要弄清原价、进价、新价之间的关系。
若设新价为b ,则售价为b (1-20%),因为原价为a ,所以进价为a (1-25%) 解:依题意,有25.0)2.01()25.01()2.01(⋅-=---b a b 化简得a b 45=,所以x a bx y ⋅⋅==2.0452.0,即+∈=N x x a y ,4
2、一次函数问题
例2:某人开汽车以60km/h 的速度从A 地到150km 远处的B 地,在B 地停留1h 后,再以50km/h 的速度返回A 地,把汽车离开A 地的路x (km )表示为时间t (h )的函数,并画出函数的图像。
分析:根据路程=速度×时间,可得出路程x 和时间t 得函数关系式x (t );同样,可列出v(t)的关系式。
要注意v(t)是一个矢量,从B 地返回时速度为负值,重点应注意如何画这两个函数的图像,要知道这两个函数所反映的变化关系是不一样的。
解:汽车离开A 地的距离x km 与时间t h 之间的关系式是:⎪⎩
⎪⎨⎧∈--∈∈=]5.6,5.3(),5.3(50150]5.3,5.2(,150]5.2,0[,60t t t t t x ,图略。
速度vkm/h 与时间t h 的函数关系式是:⎪⎩
⎪⎨⎧∈-∈∈=)5.6,5.3[,50)5.3,5.2[,0)5.2,0[,60t t t v ,图略。
3、二次函数问题
例3:有L 米长的钢材,要做成如图所示的窗架,上半部分为半圆,下半部分为六个全等小矩形组成的矩形,试问小矩形的长、宽比为多少时,窗所通过的光线最多,并具体标出窗框面积的最大值。
解:设小矩形长为x ,宽为y ,则由图形条件可得:l y x x =++911π
∴x l y )11(9π+-=
要使窗所通过的光线最多,即要窗框面积最大,则:
)44(32)442(644])11([322622
222
2ππππππ+++-+-=+-+=+=l l x x lx x xy x s ∴当π
+=442l x 时,)44(9)22(9)11(πππ+-=+-=l x l y 即:π
-=2218y x 此时窗框面积S 有最大值)44(322m ax π+=l s 。
可见,一般的设自变量为x ,函数为y ,并用x 表示各相关量,然后根据问题已知条件,运用已掌握的数学知识、物理知识及其它相关知识建立函数关系式,将实际问题转化为数学问题,实现问题的数学化,也就是建立数学模型。
二、数列模型
数列模型有增长率问题和银行中的储蓄与贷款问题。
在高一年级教材中就有这类数学问题,下面以一个例题来分析银行中的数学建模问题。
例4:某银行设立了教育助学贷款,其中规定一年期以上贷款月均等额还本付息,如果贷款10000元,两年还清,月利率为0.4575%,那么每月应还多少钱呢?
分析与假设:按照规定,偿还贷款既要偿还本金,还要支付利息。
在上述问题中,到贷款两年(即24个月)付清时,10000元贷款的本金与它的利息之和是多少呢?引导学生通过填表来回答:
通过对例子的分析,与学生交流使学生认识到:到期偿还贷款的含义即各月所付款连同到贷款付清时所生利息之和,等于贷款本金及到贷款付清时的利息之和,计算每月应付款额。
2423004575.110000004575.1004575.1⨯=+++x x x Λ
可以发现,上述等式是一个关于x 的一次方程,且等号左边括号内是一个首项为1,公比为1.004575的等比数列的前24项的和,于是:
2424
004575.110000004575
.11004575.11⨯=--⋅x 即2424004575.11)004575.11(004575.110000--⨯⨯=x 解之得91.440≈x
提出问题:如果采用上述分期付款方式贷款a 元,m 个月将款全部付清,月利率为r ,那么每月付款款额的计算公式是什么?
显然问题转化为建立关于x 的方程。
设采用分期付款方式贷a 元,m 个月将款全部付清,月利率为r ,每月付款x 元,那么: 把右边求和,得r
r x r a m m ]1)1[()1(-+=+, 所以:1
)1()1(-++=m m
r r ar x 万元。
三、初等概率模型
古典概率不仅要求基本实践的出现具有等可能性,而且要求样本空间为有限集,但实际问题中却经常会碰到无限样本空间的情形,对于无限样本空间的情形,常可转化为几何概率来解决。
例5:将n 个球随机地放入n 个盒子中去,求每个盒子恰有一个球的概率。
分析与求解:因为每一个球都可以放进n 个盒子中的任一个盒子,共有n 种不同的放法,n 个球放进n 个盒子就有n ×n ×…×n=n
n 种不同的放法,而每种放法就是样本空间中的一个元素,所以样本空间中元素的总数为n n 个。
现在来求每个盒子恰有一个球时,球的不同放法的种数。
第一个球可以放进n 个盒子之一,有n 种放法;第二个球只能放进余下的(n-1)个盒子之一,有(n-1)种放法,…,最后一个球只可以放进唯一余下的盒子,所以n 个球放进n 个盒子中要使每个盒子中都恰有一个球,共有!n 种不同的放法,因而所求得概率为: n n
n
A A P =)(。
几何概率所描述的随机试验满足:试验的样本空间是一个可度量的几何区域(这个区域可以是一维、二维甚至n 维);试验中每个基本事件发生的可能性都一样,即样本点落入某一个可度量的子集A 的可能性与A 的几何测度成正比,而与A 的形状及位置无关。
如下面的例子“会面问题”是几何概率的典型例子。
例7:两位网友相约见面,约定在下午4:00到5:00之间在某一街角相会,他们约好当其中一人先到后,一定要等另一人20分钟,若另一人仍不到则离去,试问这两位朋友能相遇的概率为多少?(假定他们到达约定地点的时间是随机的,且都在约定的一小时内) 解:以x 、y 分别表示两人到达的时刻,则两人相遇必须满足下列条件:∣x -y ∣≤20,两人到达时刻的所有可能结果可用边长为60的正方形区域上的任意点(x ,y )表示,该正方()()
()()122(1)11...11m m m a r x rx r x r x r x --+=+++++++++
形上的所有点的集合构成了样本空间。
如下图的阴影部分(满足不等式∣x -y ∣≤20的点的集合)表示“两人能相遇”这一事件的概率应等于图中阴影部分的面积与正方形的面积之比。
9536002000)(===大小
S S A P 。
通过这一段的研究,笔者有如下心得:
(1)在数学教学中和对学生数学学习的指导中,应重视介绍数学知识的来龙去脉。
(2)在数学教学和课外活动中,要鼓励支持学生“面对实际问题时,能主动尝试着以数学的角度运用所学知识和方法寻求解决问题的策略”。
开阔学生的数学视野,使他们了解数学的应用价值。
