Theta图的Merrifield-Simmons指数和Hosoya指数
一类三圈图关于 Merrifield-Simmons 指标和Hosoya 指标的排序

一类三圈图关于 Merrifield-Simmons 指标和Hosoya 指标的排序柴文丽;田文文【摘要】文章研究了一类三圈图Tm, k, rn, p, q的Merrifield-Simmons指标和Hosoya指标,根据CP上两接点u和v之间的距离,给出了该类三圈图关于这两种指标的排序。
%The Merrifield-Simmons index and Hosoya index of the class of tricyclic graphs were inves-tigated according to the distance between and on.Their orderings with respect to these two indices had been obtained.【期刊名称】《西北民族大学学报(自然科学版)》【年(卷),期】2015(036)004【总页数】5页(P1-5)【关键词】三圈图;Merrifield-Simmons指标;Hosoya指标;排序【作者】柴文丽;田文文【作者单位】西北民族大学美术学院,甘肃兰州 730030;西北民族大学数学与计算机科学学院,甘肃兰州 730030【正文语种】中文【中图分类】O157.5Merrifield-Simmons指标是在1989年由美国化学家Richard E.Merrifield和Howard E.Simmons在文献[3]中引入的化学拓扑指标,它表示图G中所有独立集的数目,记为σ(G),该指标与物质的沸点有着密切的联系.Hosoya指标是由日本化学家Haruo Hosoya于1971年在文献[2]中提出并进行研究的.它表示图G 中所有匹配的数目,记为μ(G).该指标与物质的沸点、熵、化学键的计算和化学结构等有着密切的联系.这两个拓扑指标在结构化学中有着重要的意义,它们常常被用来描述有机化合物的物理化学特征与药理特征,且有着较为广泛的应用,相关的应用参见文献[3~5].文献[6~9]中确定了双圈图中最大和最小的Merrifield-Simmons指标和Hosoya指标,并刻画了相应的极图.文献[10]中研究了一类特殊双圈图的两种指标的排序.文献[11~13]中研究了三圈图中最大和最小的Merrifield-Simmons指标和Hosoya指标,并刻画了相应的极图.文献[14]中研究了给定悬挂顶点的树关于Merrifield-Simmons指标和Hosoya指标的排序.本文主要研究了一类特殊三圈图关于Merrifield-Simmons指标和Hosoya指标的排序问题.设G=(V,E)是一个简单的连通图,它的点集和边集分别为V(G)和E(G).令e和x分别为图G的一条边和一个顶点,我们用G-{e}表示图G删去边e得到的图,用G-{x}表示图G删去顶点x(及关联的边)得到的图.用NG(v)表示G中点v的邻点集,且NG[v]={v}∪NG(v).令fn表示第n个Fibonacci数,定义为f0=0,f1=1,满足fn=fn-1+fn-2,n≥2,其中(φn-(-φ)-n).令ln表示第n个Lucas数,定义为l0=2,l1=1,满足ln=ln-1+ln-2,n≥2,其中ln=φn+(-φ)-n,而φ文中未加说明的符号及术语参见文献[1].图表示一类具有n个顶点的特殊三圈图,它由三个圈CP,Cq,Cm和一条路Pr构成,其中Cp和Cq被一条路Pr连接,Pr和Cm与Cp的交点分别为u和v,且d(u,v)=k,如图1所示.引理1[4] 设G是一个简单的连通图,对任意的u,v∈V(G),uv∈E(G),则σ(G)=σ(G-{v})+σ(G-NG[v]);σ(G)=σ(G-{uv})-σ(G-(NG[u]∪NG[v])).引理2[4] 设G是一个简单的连通图,对任意的v∈V(G),uv∈E(G),则μ(G){v,x}).引理3[4] 若G1,G2,…,Gk是图G的连通分支,则引理4[4] 对于n阶的路Pn,有σ(Pn)=fn+2;μ(Pn)=fn+1.引理5[4] 对于n阶的圈Cn,有σ(Cn)=fn+1+fn-1;μ(Cn)=fn+1+fn-1.引理6[15] 对于正整数m≥n,有).由引理1~5可得以下结论:引理7 对于如图2所示的图H,有1) σ(H)=fm+2fn+2·(fq+1fr+fq-1fr-1)+fm+1fn+1·(fq+1fr-1+fq-1fr-2);2) μ(H)= (fq+1+fq-1)(fm+1fn+1fr+fm+1fnfr-1+fmfn+1fr-1)+fq·(fm+1fn+1fr-1+fm+1fnfn-2+fmfn+1fr-2).该类三圈图关于Merrifield-Simmons指标和Hosoya指标的排序,我们将得出以下结论:定理1 设为如图1所示的图.令,且,则有).证明如图1所示,由引理1及引理7可知(fq+1fr-1+fq-1fr-2)(fm+1fkfp-k+fm-1fk-1fp-k-1).(fq+1fr-1+fq-1fr-2)(fm+1fk+1fp-k-1+fm-1fkfp-k-2).所以,由引理6可知-fkfp-k)]+(fq+1fr-1+fq-1fr-2)[fm+1·(fk+1fp-k-1-fkfp-k)+fm-1·(fkfp-k-2-fk-1fp-k-1)]+(fq+1fr-1+fq-1fr-2)[fm+1·(lp-2k+lp-2k-2)+fm+1·(-lp-2k-lp-2k-2)]}而fm·(-fq+1fr-2-fq-1fr-3)<0.故当k为偶数时,有;当k为奇数时,有).下面比较)与)的大小关系.因为+(fq+1fr-1+fq-1fr-2)(fm+1fk+2fp-k-2+fm-1fk+1fp-k-3),所以由引理6可知-fkfp-k)]+(fq+1fr-1+fq-1fr-2)[fm+1·(fk+2fp-k-2-fkfp-k)+fm-1·(fk+1fp-k-3-fk-1fp-k-1)]+(fq+1fr-1+fq-1fr-2)[fm+1·(lp-2k-lp-2k-4)+fm+1·(lp-2k-4-lp-2k)]}而fm·(lp-2k-4-lp-2k)(fq+1fr-2+fq-1fr-3)<0,故当k为偶数时,有;当k为奇数时,有).综上所述,对,有).定理2 设为如图1所示的图.令,且,则有).证明由引理2及引理7可知fm·(fkfp-k-1fr+fkfp-k-2fr-1+2fk-1fp-k-1fr-1+fk-1fp-kfr+fk-2fp-kfr-1)]+fq·[(fm+1+fm-1)(fkfp-kfr-1+fkfp-k-1fr-2+fk-1fp-kfr-2)+fm(fkfp-k-1fr-1+ fkfp-k-2fr-2+2fk-1fp-k-1fr-2+fk-1fp-kfr-1+fk-2fp-kfr-2)].+fm·(fk+1fp-k-2fr+fk+1fp-k-3fr-1+2fkfp-k-2fr-1+fkfp-k-1fr+fk-1fp-k-1fr-1)]fq·[(fm+1+fm-1)(fk+1fp-k-1fr-1+fk+1fp-k-2fr-2+fkfp-k-1fr-2)+fm·(fk+1fp-k-2fr-1+fk+1fp-k-3fr-2+2fkfp-k-2fr-2+fkfp-k-1fr-1+fk-1fp-k-1fr-2)].所以,由引理6可知-fk-1fp-kfr-1)+fm·(fk+1fp-k-2fr+fk+1fp-k-3fr-1+fkfp-k-2fr-1-fk-1fp-k-1fr-1-fk-1fp-kfr-fk-2fp-kfr-1)]+fq·[(fm+1+fm-1)(fk+1fp-k-1fr-1+fk+1fp-k-2fr-2-fkfp-kfr-1-fk-1fp-kfr-2)+fm·(fk+1fp-k-2fr-1+fk+1fp-k-3fr-2+fkfp-k-2fr-2-fk-1fp-k-1fr-2-fk-1fp-kfr-1-fk-2fp-kfr-2)]).[fr-1·(fq+1+fq-1)(fm+1+fm-1)+fr-2fm·(fq+1+fq-1)+fr-2fq·(fm+1+fm-1)+fr-3fqfm]}.又因(lp-2k+lp-2k+2)-(lp-2k+lp-2k-2)>0,(fm+1+fm-1)(fq+1fr+fq-1fr+fqfr-1)-[fr-1·(fq+1+ fq-1)(fm+1+fm-1)+fr-2fm·(fq+1+ fq-1)+fr-2fq·(fm+1+fm-1)+fr-3fqfm]=2fm-1fr-2·(fq+1+ fq-1)+2fm-1fr-3fq>0, 所以(fm+1+fm-1)(fq+1fr+fq-1fr+fqfr-1)(lp-2k+lp-2k+2)-(lp-2k+lp-2k-2)[fr-1·(fq+1+ fq-1)(fm+1+fm-1)+fr-2fm·(fq+1+ fq-1)+fr-2fq·(fm+1+fm-1)+fr-3fqfm]>0.故当k为偶数时,有;当k为奇数时,有).下面比较)与)的大小关系.因为+fm·(fk+2fp-k-3fr+fk+2fp-k-4fr-1+2fk+1fp-k-3fr-1+fk+1fp-k-2fr+fkfp-k-2fr-1)]+fq·[(fm+1+fm-1)(fk+2fp-k-2fr-1+fk+2fp-k-3fr-2+fk+1fp-k-2fr-2)+fm·(fk+2fp-k-3fr-1+fk+2fp-k-4fr-2+2fk+1fp-k-3fr-2+fk+1fp-k-2fr-1+fkfp-k-2fr-2)].所以由引理6可知(fk+2fp-k-3+fk+1fp-k-2-fkfp-k-1-fk-1fp-k)·fr-1+fmfr·(fk+2fp-k-3+fk+1fp-k-2-fkfp-k-1-fk-1fp-k)+fmfr-1·(fk+2fp-k-4+2fk+1fp-k-3-2fk-1fp-k-1-fk-2fp-k)]+fq·[(fm+1+fm-1)(fk+2fp-k-2-fkfp-k)·fr-1+(fm+1+fm-1)(fk+2fp-k-3+fk+1fp-k-2-fkfp-k-1-fk-1fp-k)·fr-2+fmfr-1·(fk+2fp-k-3+fk+1fp-k-2-fkfp-k-1-fk-1fp-k)+fmfr-2·(fk+2fp-k-4+2fk+1fp-k-3-2fk-1fp-k-1-fk-2fp-k)]-fqfr-3fm](lp-2k-1+lp-2k-3)].而2fm-1fr-2·(fq+1+ fq-1)+2fqfm-1fr-3>0.故当k为偶数时,有;当k为奇数时,有).综上所述,对,有).通过观察可知,该类特殊三圈图关于Merrifield-Simmons指标和Hosoya指标的排序恰好相反.[1] Bondy J A,Murty U S R.Graph theory with applications[M].New York:The Macmillan Press,1976.[2] Hosoya H.Topological index[J].Bull Chem Soc Japan,1971,44:2332-2339.[3] Merrfield R E,Simmons H E.Topological Methods inChemistry[M].New York:Wiley,1989.[4] Gutman I,Polansky O E.Mathematical Concepts in OrganicChemistry[M].Berlin:Spring-er,1986.[5] Gutman I,Cyvin S J.Introduction to the Theory of Benzenoid Hydrocarbons[M].Berlin:Springer,1989.[6] Deng H Y,Chen S B,Zhang J.The Merrifield-Simmons index in-graphs[J].Journal of Mathematical Chemistry,2008,43(1):75-91.[7] Deng H Y.The smallest Merrifield-Simmons index of -graphs[J].Math Comput Model,2009,49(1-2):320-326.[8] Deng H Y.The smallest Hosoya index in -graphs[J].Journal of Mathematical Chemistry,2008,43(1):119-133.[9] Xu Kexiang,Gutman I.The Greatest Hosoya Index of Bicyclic Graphs with Given Maximum Degree[J].MATCH Commun Math ComputChem,2011,66(3):795-824.[10] 周旭冉,王力工.一类双圈图的两种指标的排序[J].山东大学学报(理学版),2011,46(11):44-47.[11] Zhu Zhongxun,Li Shuchao,Tan Liansheng.Tricyclic graphs with maximum Merrifield-Simmons index[J].Discrete Applied Mathematics,2010,158(3):204-212.[12] Dolati A,Haghighat M,Golalizadeh S,Safari M.The Smallest Hosoya index of Connected Tricyclic Graphs[J].MATCH Commun Math Comput Chem,2011,65(1):57-70.[13] Zhu Zhongxun,Yu Qigang.The number of independent sets of tricyclic graphs[J].Applied Mathematics Letters,2012,25(10):1327-1334.[14] Xuezheng Lv,Yan Yan,Aimei Yu,Jingjing Zhang.Ordering strees with given pendent vertices with respect to Merrifield-Simmons indicesand Hosoya indices[J].Journal of Mathemati-cal Chemistry,2010,47:11-20.[15] Stephan G Wagner.Extremal trees with respect to Hosoya index and Merrifield-Simmons index[J].MATCH Commun Math Comput Chem,2007,57(1):221-233.。
泰尔指数的大小

泰尔指数的大小泰尔指数是一种统计学上的分布曲线,是通过描述一个随机变量X的概率分布,用来反映该随机变量分布密集的程度。
由于概率分布常用无偏估计或者称作无偏向估计,也可简称为无偏估计或者无偏。
按照统计学的定义,如果一个概率分布有f个参数,其中第i个参数i为该参数服从的分布。
那么,这样的概率分布被称为参数可决系统或者参数可决空间。
而对于概率分布的参数估计问题,相应地也存在多种可行的方法,比如使用最大似然估计( MLE)、贝叶斯估计( BI)等。
通过搜索引擎的使用,我们还可以进行相应分析。
但是,从古至今的很多文献都没有给出一个合适的定义,这也让广大读者迷茫。
现在我们再来看看泰尔指数和贝塔系数。
泰尔指数又叫做哈尔指数或者哈尔-洛德指数,是描述一个随机变量概率分布密集程度的一个数值。
是某一随机变量取值X0时,用其后取X的平均值,除以X0得到的商。
是x-->,用f(x)/f(x0)。
这样的分布式样与x1, x2的数值密集程度无关,所以泰尔指数是独立于两个变量的,而且是完全依赖于随机变量的。
从上面两个例子,我们可以看出贝塔系数不同于泰尔指数。
它是指一个随机变量的数值密集度。
也就是一个随机变量y的值域。
当贝塔系数越大,说明一个随机变量越集中;泰尔指数的值与z无关。
以前我曾经认为在生活中只要遇到了高分就是最好的,但是,慢慢地我发现这是错误的。
人们更注重的是自己想要什么,并不会盲目崇拜高分数,更何况在学习的道路上,不可能永远处在优势。
在期末考试中,能得到一个高分固然是令人高兴的事情,但是真正重要的是得到了多少个高分,即在每次考试中得到多少个高分才算优秀?如果把一个人的成绩按照100分为满分计算,那么高分的总和为100分。
低分的总和则为0分,零分的总和则为负100分。
那么请问,谁是最终的赢家?所以,现在我觉得把评价的标准多元化,对于我们的成长才是有利的。
回到语文教学上来,虽然评价标准也很重要,但是绝对不是最主要的因素。
ace 指数、chao 指数、shannon 指数、simpson 指数等多种评估指数。

ace 指数、chao 指数、shannon 指数、simpson 指数等多种评估指数。
生物多样性评估生物多样性是指地球上生命体的多种形式、基因组成、物种和生态系统的丰富性。
评估生物多样性可以帮助我们更好地了解生态系统的状态和变化,同时加强对生物多样性的保护和管理。
以下是一些常用的生物多样性评估指数。
1. Ace指数Ace指数(Abundance-based Coverage Estimator)是衡量样本覆盖率的指标,它可以根据样本中物种的个体数和种类丰富度等信息来计算样本中未被观察到的物种数。
Ace指数常用于评估生态系统中物种的多样性和稳定性。
2. Chao指数Chao指数是一种基于样本中物种个体丰度分布的多样性估计指数,它可以根据物种种类数和每种物种的个体数来计算样本中物种的总个体数。
Chao指数可以用来预测未被发现的物种数量和物种丰度的分布情况。
3. Shannon指数Shannon指数是衡量生态系统中物种丰富度和均匀度的指标。
它考虑了各物种在样本中的相对丰度,越多的物种相对丰度分布均匀越高,Shannon指数也就越高。
4. Simpson指数Simpson指数是另一种测量生态系统中物种多样性的指标。
它考虑了物种的丰度和物种的数目,有时被称为优势度指数,因为它更加关注的是样本中最多个体数的物种。
5. Jaccard指数Jaccard指数可以用来评估两个生态系统之间的相似度。
它根据两个生态系统共有的物种和独特的物种数量来计算它们之间的相似度。
6. Bray–Curtis指数Bray–Curtis指数也可以用来评估两个生态系统之间的相似度,但它不仅考虑物种是否存在,还考虑物种的相对数量。
总结这些生物多样性指标常被用于评估生态系统和群落的物种多样性和均匀度。
单独使用这些指标可能会遗漏某些重要的信息,因此,在评估生态系统多样性时,需要综合考虑各项指标以形成全面的视角。
数学应用典型案例模型1马尔萨斯人口增长(指数增长)模型

xc e hx
C
其中 C 为任意常数,可由初始条件确定。
捕食----被捕食模型有着广泛的应用。当一个包含两个群体的系统中,只要
两个群体相互依存、相互制约,均可用捕食----被捕食模型来描述。例如,鲨鱼
与食用鱼、寄生虫与其宿主、害虫与其天敌、肿瘤细胞与正常细胞等都可用该模
型来描述。下图表明了狐狸----野兔(数量)随着时间 t 所发生的周而复始的变
化,正是这种变化维持着该系统的生态平衡。
在狐狸----野兔生态系统中,生态系统的平衡点就是使 dx 0, dy 0 的点。 dt dt
即
a byx 0 c hxy 0
(3-2)
只求非零解,可知平衡点为: x c , y a 。也就是说,当野兔数量保持在 c ,
设人类生存空间及可利用资源(食物、水、空气)等环境因素所能容纳的最 大人口容量为 K(称为饱和系数).人口数量 N(t)的增长速率不仅与现有人口 数量成正比,而且还与人口尚未实现的部分(相对最大容量 K 而言)所占比例 K N 成比例,比例系数为固有增长率 r.于是,修改后的模型为
K
dN
hb
h
狐狸数量保持在 a 时,就能维持狐狸----野兔生态系统的平衡。 b
图 3-2
例 狐狸----野兔模型为
dx dt
0.03x
0.001xy
dy dt
0.9 y 0.002xy
(3-3)
试问:狐狸、野兔的数目各为多少时,该系统才达到平衡?
解:由 dx 0 ,得 y狐狸 0.03 3(0 只);
模型 3 捕食——被捕食模型 所用知识:微分方程组 内容介绍:
三元素链的Merrifield-Simmons指标和Hosoya指标

确定 . 如 图 1所示 :
△ △ : △ △
图 l 三 元 素 链 ,
语参 见 文献 [ 1 ] .
Me r r i f i e l d — S i mmo n s指 标 是 在 1 9 8 9年 由 以 下几 个
第2 7卷 第 2期
2 O 1 3年 3 月
甘 肃联 合 大 学 学报 ( 自然科 学版 )
J o u r n a l o f Ga n s u I . i a n h e Un i v e r s i t y( Na t u r a l S c i e n c e s )
引理 .
Me r r i f i e l d和 S i mmo n s 在文献E 2 3中 引 入 的化 学
拓扑 指标 , 它 表示 图 G的所 有独 立集 的数 目, 记 为 ( G) , 该 指 标 与 物 质 的 沸 点 有 着 密 切 的 联 系.
Ho s o y a指标 是 由 日本 化 学家 Ho s o y a于 1 9 7 1 年
( i ) d ( G ) 一I I a ( G ) ;
=
1
定义 1 设L , L , …, L 为 个正 三 角形序 列, 则 称该 三 角形序 列 为三 元素 链 , 记 为 , 如果
收 稿 日期 : 2 0 1 2 — 1 1 — 2 0 .
( i i ) ( G ) 一1 1 7 t  ̄ ( G k ) .
点、 熵、 化 学 键 的 计 算 和 化 学 结 构 等 有 着 密 切 的 联
( i ) ( G)一 ( G一 “ ) +d ( G— Nf E u ] ) ;
( i i ) ( G)一 ( G 一 删 )+ ( G 一 “一 ) .
极值五角链的Merrifield-Simmons指标和Hosoya指标研究

立 集 数 的极 端 情 形 , 并 得 出 了相 应 的极 图 . 本 文
主要通过递推的方法给出了这两类极值五角链
[ 收稿 日期 ] 2 0 1 3 — 0 3 — 1 2
[ 基金项 目] 西北 民族 大学 中央高 校科研 专项 资金 资助研 究 生项 目( Y C X 1 3 1 6 0 ) ; 中 央高校 基 本科 研业 务 费专项 资 金项 目
m O l l S 在 文献 [ 3 ] 中引入 的化 学拓 扑 指标 , 它 表 示 图 G中所有 独立 集 的数 目, 记 为 ( G ). 该 指标
去边 e得 到 的图 , 用 G— 表 示 图 G删去 顶 点 ( 及 关联 的 边 ) 得到的图. 若A ( G ), 对 任 意 的两个顶 点 u , ∈ A, 都有 t t V譬 E( G), 则称 A
2 0 1 3年 9月
重 庆 文 理 学 院 学 报
J o ur n a l o f C h o n g q i n g Un i v e r s i t y o f Ar t s a n d S c i e n c e s
S e p.,2 0 1 3 V0 1 . 3 2 No . 5
( Z Y Z 2 0 1 2 0 7 7) .
[ 作者简介] 田文文 ( 1 9 8 7 一) , 男, 甘肃天水人 , 硕士 , 主要从事 图论与组合优化方面的研究.
28
见 文献 [ 1 ] . 定义 1 设 C , C : , …, C 为 个 正 五边形 序 列, 则 称该 五边 形 序列 为 五角 链 , 记 为 每一个 五边形 至 多 与两个 五边 形相 邻 . , 如 果
[ 中图分类号 ] O 1 5 7 . 5 [ 文献标志码 ] A [ 文章编号] 1 6 7 3 — 8 0 0 4 ( 2 0 1 3 ) 0 5~ 0 0 2 8 — 0 4
ace 指数、chao 指数、shannon 指数、simpson 指数等多种评估指数。

ace 指数、chao 指数、shannon 指数、simpson 指数等多种评估指数。
评估指数是一种用于评价和度量某种特定现象或情况的指标。
在不同领域中,常用的评估指数有很多种,其中包括ACE指数、CHAO指数、Shannon指数和Simpson指数等。
1. ACE指数(Abundance-based Coverage Estimator):ACE指数是一种用于估计未观测到的物种丰富度的一种指标。
它基于统计模型,通过对已观测到的物种丰富度进行推断,来估计未观测到的物种数量。
一般来说,ACE指数越高,表示物种丰富度越大。
2. CHAO指数:CHAO指数也是一种用于估计未观测到的物种丰富度的指标。
它是在ACE指数的基础上发展而来的,通过对已观测到的物种数量和种群中每个物种的存在次数进行计算,来估计未观测到的物种数量。
与ACE指数类似,CHAO指数越高,表示物种丰富度越大。
3. Shannon指数:Shannon指数是用于衡量生物群落物种多样性的一种指标。
它综合了物种丰富度和物种均匀度两个方面,通过计算各物种的丰富度和相对丰度的乘积,并进行加权求和,来反映物种多样性的程度。
Shannon指数越高,表示物种多样性越丰富。
4. Simpson指数:Simpson指数也是用于衡量生物群落物种多样性的一种指标。
它与Shannon指数类似,也综合考虑了物种丰富度和物种均匀度,但是更加注重物种均匀度的影响。
Simpson指数的计算基于物种相对丰度,其值越小表示物种多样性越高。
这些评估指数在生态学、生物多样性研究以及社会科学等领域中得到广泛应用。
它们可以帮助人们更全面地了解生态系统的结构和功能,并提供参考依据用于保护和管理生物资源。
此外,这些评估指数还可以用于统计学分析、生物多样性评估、物种丰富度预测等方面,为科学研究和实践提供有力支持。
总结起来,ACE指数、CHAO指数、Shannon指数和Simpson指数等评估指数都在不同领域中发挥着重要作用,它们可以帮助人们评估和度量特定现象或情况,并提供决策支持和科学依据。
ace 指数、chao 指数、shannon 指数、simpson 指数等多种评估指数。

ace 指数、chao 指数、shannon 指数、simpson 指数等多种评估指数。
评估指数是用于评估和度量某个领域或系统的多样性、均匀性或复杂性的工具。
这些指数提供了一种量化多样性或均匀性的方式,可以帮助研究人员、生态学家、经济学家等更好地理解和比较不同系统的特征。
下面将介绍几种常用的评估指数:1. ACE指数(Abundance-based Coverage Estimator)是用于评估生物多样性的一种非参数方法。
该指数基于给定样本中物种的数量和频率来预测其完全样本覆盖的结果。
ACE指数通过对物种的出现次数进行统计分析,估计未观测到的物种丰富度。
2. Chao指数(Chao1)是一种用于评估物种丰富度的非参数方法。
该指数基于已经观测到的物种数量和样本中物种的频率,估计未观测到的物种丰富度。
Chao指数可以理解为总的物种数目,包括已观测到的和未观测到的物种。
3. Shannon指数(Shannon index)是用于评估物种多样性的一种常用指数。
该指数基于不同物种的丰富度和均匀度对样本的多样性进行统计分析。
Shannon指数考虑了物种的数量和相对丰度,因此可以比较物种多样性较高的样本和物种多样性较低的样本。
4. Simpson指数(Simpson index)也是用于评估物种多样性的一种常用指数。
Simpson指数计算了同一物种在样本中出现的概率的平方和,并用1减去该值来反映物种的均匀度。
Simpson指数越接近1,表示物种均匀度越高,越接近0,表示物种均匀度越低。
这些指数可以帮助我们了解不同系统或领域的多样性、均匀性或复杂性。
例如,在生态学研究中,这些指数可以用于比较不同生态系统的物种多样性或评估物种灭绝的风险;在经济学研究中,这些指数可以用于评估市场竞争的程度或企业创新的能力。
需要注意的是,以上介绍的只是一小部分评估指数,并且在不同领域有不同的应用和变种。
此外,评估指数的选择应该根据具体研究目的和数据特点来确定,并且需要结合其他统计方法和领域专家的意见进行综合分析。
一类双圈图的Merrifield-Simmons指标和Hosoya指标序列

湖 南 文 理 学 院 学 报 ( 然 科 学 版) 自
J u n f n nUn v r i f t a d S i c ( t r l c n e d t n o r a o a ie s yo Ars n c n eNau a i c io ) l Hu t e S e E i
1 一
÷ [ ( )】 其中 ( √) . 表 一一 , =1 5 2 用 + / 示第
45
n个 L cs ,满 足 =2 厶 =1 +:L + 一并 ua 数 , , l 1
Ⅳ ( : UE ( ). GV 川 V G ) ) E
引理 4 [ 设 G是 一个 图 , U 是 G 的一条边 , ' V
是 研 究 给 定 图类 的 指 标 和 指 标 的 极 值及 大 小 排 序 .文献 [,】 1 中确 定 了 n 顶 点 的树 中 ,星 图 5 个
引 理5
= 【+一一 一, f ÷ ( ) ,( ) 1 】m .
J
1
证明 由 = [ ( 】 = 一 】 ÷ 一一 和 【 (
排序.
关 键 词 : 双 圈 图 ;Mer edSmmo s 标 ;Hoo a 标 ; r f l—i i i n指 sy 指
2 )个 顶 点 星 图 1
+ 的 中 心 与 双 中双 圈 的公 共 顶 点 相 重 合 得 到 的 n阶 双
文献标识码 : A
中图分类号 :O 17 5. 6
圈连通 图.为方便 , 别用 ( , ) z , ) 分 和 ( 表 示 盯 Q( , )和 z Q( , ) ; 分 别 用 ( , , ( ) ( )
)和 z , , ( +)表 示 G Q C , , ((k
一类特殊三圈图关于Merrifield-Simmons指标和Hosoya指标的排序

一类特殊三圈图关于Merrifield-Simmons指标和Hosoya指标的排序田文文;田双亮【期刊名称】《宁夏大学学报(自然科学版)》【年(卷),期】2014(000)003【摘要】研究了一类三圈图Tk 的Merrifield-Simmons指标和 Hosoya指标,根据Cq 上2接点u和v之间的距离,给出了该类三圈图关于这2种指标的排序。
%The Merrifield-Simmons index and Hosoya index of a class of tricyclic graphs Tk is investigated. According to the distance between u and v on Cq ,their orderings with respect to these two indices are obtained.【总页数】4页(P212-215)【作者】田文文;田双亮【作者单位】西北民族大学数学与计算机科学学院,甘肃兰州 730030;西北民族大学数学与计算机科学学院,甘肃兰州 730030【正文语种】中文【中图分类】O157.5【相关文献】1.一类特殊单圈图关于Merrifield-Simmons指标和Hosoya指标的排序 [J], 王燕凤;马宁;2.一类特殊双圈图关于Merrifield-Simmons指标和Hosoya指标的排序 [J], 张静;田文文;田双亮3.一类特殊单圈图关于Merrifield-Simmons指标和Hosoya指标的排序 [J], 王燕凤;马宁4.一类三圈图关于 Merrifield-Simmons 指标和Hosoya 指标的排序 [J], 柴文丽;田文文5.一类特殊(n,n+1)-图关于Merrifield-Simmons指标和Hosoya指标的排序 [J], 尚娅璇;因版权原因,仅展示原文概要,查看原文内容请购买。
莫兰指数以及泰尔指数

莫兰指数与泰尔指数深度分析一、引言在经济学和社会学中,空间计量经济学是一个关键的研究领域,它研究的是地理空间如何影响经济和社会现象。
其中,两个重要的空间计量经济学指数是莫兰指数(Moran's I)和泰尔指数(Theil Index)。
本文档将深入探讨这两个指数的定义、计算方法、应用以及限制。
二、莫兰指数1. 定义:莫兰指数是用于测量空间自相关性的一种方法,由法国统计学家Anselin Moran 于1950年提出。
它衡量的是观察值之间的相似性或差异性,如果观察值相似,则莫兰指数接近1;如果观察值差异大,则莫兰指数接近-1。
2. 计算方法:莫兰指数的计算公式为:I = n/(n-1) * Σ(xi - x¯)(yi - y¯) / Σ(xi - x¯)²,其中,xi和yi是观察值,x¯和y¯是观察值的平均值。
3. 应用:莫兰指数广泛应用于空间自相关性分析,如城市发展、疾病传播、犯罪率等领域。
通过莫兰指数,我们可以识别出哪些区域具有相似的特征,哪些区域存在显著的差异。
4. 限制:莫兰指数假设数据是正态分布的,且空间权重矩阵是恒定的。
然而,这些假设在实际应用中往往难以满足。
此外,莫兰指数只能测量全局的空间自相关性,不能测量局部的空间自相关性。
三、泰尔指数1. 定义:泰尔指数是一种衡量收入或财富不平等的指标,由泰尔(Theil)于1967年提出。
它的计算基于熵的概念,可以分解为三个部分:总体不平等、组内不平等和组间不平等。
2. 计算方法:泰尔指数的计算公式为:T = (p1 - p2) / (p1 + p2),其中,pi是第i组的收入或财富份额。
3. 应用:泰尔指数广泛应用于经济和社会研究,如收入分配、贫困分析、教育不平等等领域。
通过泰尔指数,我们可以了解收入或财富的分配情况,评估社会公平性。
4. 限制:泰尔指数假设数据是单调的,即每个人的收入或财富都是唯一的。
关于Hosoya指标和Merrifield-Simmons指标的k色极图

关 于 Hoo a指 标 和 Merf l-i sy ri e Smmo s 标 的 id n 指 色 极 图
许 克 祥
( 京 航 空 航 天 大 学理 学 院 , 南 江苏 南 京 2 0 1 ) 10 6
摘要: 图的 H sy 指标定义为图中包含空边集在内的对集总数. ooa 图的Me i l S m n 指标定义为图中包含空点集 rf d i os ri - m e
最先 引 人 开 始 , s y Hoo a指 标 已引 起 了很 多 学 者 的注 意. 而且 Ho o a指标 在 研 究 某 些 碳水 化 合 物 的分 子 sy 结 构与 物 理 、 学 性 质 的关 系 时 起 了 重 要 的 作 用. 化
Mer il Smmo s指 标 在 1 8 ried i f — n 9 9年 由 Mer il ried和 f
指标 , 并确 定 了 ( ) Mer il-i 七的 riedSmmo s指 标 的 f n 值. 最后证 明 了 k一2 3时 ,中 Hoo a , sy 指标 最小 和
Mer i dSmmo s指标最 大 的图是 Kl 1 ) ri e — i fl n (一 .
上 的应用 的研究 却 少 得 多. 文献 [ ] 3 中已 经证 明 Me— r
在 内 的点 独 立 集 总 数 . 虑 点 数 为 的 k色 连 通 图 的 集 合 G , 明 了 T rn图 ( ) 考 证 uf i 是 ,中 Hoo a指 标 最 大 且 sy Mer e — imo s 标 最 小 的图 , 确 定 了 k= 2 3时 . Hoo a指标 最小 且 Mer e -i mo s 标 最 大 的 图. r f l Sm n 指 i d i 还 , 中 sy ri l Sm n 指 i f d
棒棒糖图的Merrifield—Simmons和Hosoya指数

万一电子能 、分子 的沸点 【 等 有密 切 的关 系 ,一 4 】
些 图 的 Mer edSmmo s r f l.i n 指数 与 Hoo a i i sy 指数 已 经 被研究 了 ,文献 【] 5 中确 定了 n 顶点具有 最 大 个
顶 点 称 为 茎 ,茎 与 它 叶 子 所 连 的 边 称 为 悬 挂
边 . io ac Fb nc i数…: ,1 1 2 3 5 8 3 . 0 , , , , , ,1 … ,
定 义 为 F 0 = , Ff =1, 且 n 2 时 , () 0 1 ) , = ( 一 ) F n + ( 一 ) {} x }
集 ,G 的独 立集 的数 目记 为 i 1 ( ,在 理论化 学上 G i 称 为 图 G 的 Mer e .i ( G) r f l Smmo s指 数或 O一 i d i n -
指数【 3 】 .. 图 G的 匹配是 指 G中 的边子 集 M ,在 中
一
一
一
一
-
一
一
一
一
-
●————— —_.
.
‘
k 。
=0
n2 / 的整数部 分 ,m G,) ( k 表示 G 中 k匹配数 ,很
显然 m( 0 =1 G,) ,m( , =m ,由 Hoo a指数 的 G1 ) sy 定 义可 知 当 k>I / 】 , m G k :0. n 2时 ( .1
指数 和 Hooa指数 的极 值 问题 , sy 并且 对
了排 序 .
按照
Mer e —i n 指数 和 Hooa指数分别 进行 rf l Smmos i d i sy
何集 合的一个 独立集 . G) ,( 表示包 含顶点 x的独 立 集之集 , , G 表 示不 包含顶 点 x的独 立集 之 ()
赫斯特指数计算

赫斯特指数计算赫斯特指数(Herfindahl Index),又称赫斯特-奥林达指数(Herfindahl-Hirschman Index,简称HHI),是衡量一个行业市场集中度的常用指标。
它通过计算市场上各个参与者的市场份额的平方和来衡量市场的竞争程度。
赫斯特指数的数值范围在0到1之间,数值越高表示市场集中度越高,竞争程度越低。
赫斯特指数的计算公式如下:HHI = (s1^2 + s2^2 + ... + sn^2)其中,s1、s2、...、sn分别表示参与者的市场份额。
赫斯特指数的应用非常广泛,特别是在反垄断政策和市场监管中扮演着重要的角色。
通过计算赫斯特指数可以判断市场是否存在垄断行为,进而采取相应的监管措施。
赫斯特指数的数值解释如下:- 当赫斯特指数为0时,表示市场完全竞争,不存在市场集中度。
- 当赫斯特指数接近1时,表示市场高度集中,存在垄断或寡头垄断的情况。
- 当赫斯特指数大于1时,表示市场集中度较低,存在一些大型企业,但整体竞争程度仍然较高。
赫斯特指数的计算可以通过市场份额数据来进行。
例如,某个市场有4个参与者,他们的市场份额分别为30%、20%、25%和25%。
那么赫斯特指数的计算如下:HHI = (0.3^2 + 0.2^2 + 0.25^2 + 0.25^2) = 0.175赫斯特指数的数值可以帮助政府、监管机构和企业判断市场的竞争程度,从而制定相应的政策和策略。
当赫斯特指数较高时,可能意味着市场存在垄断行为,需要采取措施来促进竞争,保护消费者利益。
而当赫斯特指数较低时,市场竞争程度较高,政府和企业可以采取一些措施来进一步推动市场发展,提高效率。
然而,赫斯特指数也存在一些局限性。
首先,它只能反映市场参与者的市场份额,而不能全面反映市场竞争的各个方面。
其次,赫斯特指数无法考虑到市场参与者的行为和策略,以及市场的动态变化。
因此,在使用赫斯特指数进行市场分析时,需要综合考虑其他因素,如市场结构、市场规模、市场需求等。
具有极小Hosoya指数的含圈共轭图

具有极小 Ho so ya 指数的含圈共轭图
孙志荣
( 安徽大学数学科学学院 , 安徽 合肥 230039)
摘要 : 图 G = ( V ( G) , E ( G) ) 为简单连通共轭图 , 即含有完备匹配的图 , 其顶点集为 V ( G) , 边集为 E
( G) . <n, m 表示含有 n ( n ≥ 8) 个顶点 m ( n ≤m ≤n + n
孙志荣 : 具有极小 Ho soya 指数的含圈共轭图
第1期
引理 3 若 ( X , Y ) 是一个二部图 G 的二部划分 , | E ( G) | = p , 且满足 | X | ≥ 2, | Y | ≥ 2. 则 这个二部图至少有 p - 2 个 2 2匹配 . 证明 G 是二部图 , 所以 G 没有奇圈 . 如果二部图 G 可以分成边不交的两部分 G1 和 G2 , 即 G 是不连通的 , 设 | E ( G1 ) | = a , | E ( G2 ) | = b , 则 a + b = p. 按照从 G1 中选择一条边 , 从 G2 中选择一条边的方法组成 2 2匹配 . 根据引理 1 , 则至 少可以选出 ab ≥p - 1 个 2 2匹配 . 若 G 是连通的 , 即不能分成边不交的两部分 , 且二部划分 | X | ≥2 , | Y | ≥ 2 , 则在 G 中存在边 ν ( ) ( ν ) ( ) ( ν ) ν之外 , 与 u 关联 u , 满足 d u ≥ 2, d ≥ 2 . 设 d u = k1 , d = k2 . 由于 G 不含奇圈 , 除了边 u 的 k1 - 1 条边和与ν关联的 k 2 - 1 条边无公共顶点 . 设与 u 关联的边集为 E1 , 与ν关联的边集为 E2 , 则 | ν| = k1 - 1 , | E2 - u ν| = k2 - 1 . 首先边 u ν可与 p - 1 - ( k1 - 1 ) - ( k2 - 1 ) 条边组成 p + 1 - k1 E1 - u ν和 E2 - u ν中各取一边的选法至少有 ( k1 - 1) ( k2 - 1) ≥k1 + k2 - 3 个 2 2 - k2 个 2 2匹配 . 按照从 E1 - u 匹配 , 所以图 G 至少有 p + 1 - k1 - k2 + k1 + k2 - 3 = p - 2 个 2 2匹配 . 证毕
【国家自然科学基金】_匹配数_基金支持热词逐年推荐_【万方软件创新助手】_20140802
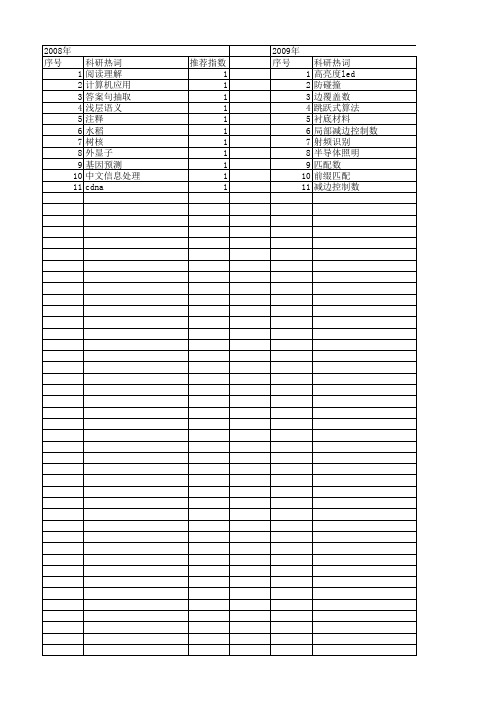
推荐指数 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
科研热词 树 匹配 零阶广义randi(c)指标 邻接矩阵 边割 谱半径 语义规则 自适应支持加权 肝移植 线性递推式 第二个最大特征值 查准率 最小特征值 最大稳定极值区域 最大匹配数 感染 巨细胞病毒 宽基线图像 完美匹配 匹配数 仿射传递 交错路 二分图 web服务发现 sift shape index hla配型 hamilton圈 3d人耳识别
2008年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 阅读理解 计算机应用 答案句抽取 浅层语义 注释 水稻 树核 外显子 基因预测 中文信息处理 cdna
推荐指数 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 高亮度led 防碰撞 边覆盖数 跳跃式算法 衬底材料 局部减边控制数 射频识别 半导体照明 匹配数 前缀匹配 减边控制数
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 完美匹配 线性递推式 棋盘 递推式 视觉感知 特征方程 恰可识别差异(jnd) 尺度空间 图 六面体 六角系统 信息量
推荐指数 6 5 4 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
一类树的Hosoya指标序列苏连存

Value Engineering 0引言在分子结构分析研究中,一个分子的拓扑结构可以用一个图来表示。
图的拓扑指标是描述化合物分子拓扑结构图的一个重要指标,实验研究结果表明,许多拓扑指标都与分子的某些物理化学性质密切相关,而不同的分子拓扑指标反映该分子的不同性能。
其中Hosoya 指标是较为重要的拓扑指标之一。
在数学方面的特征被研究的比较透彻(参见文献[1,2,3,4,5,6,7]),它是由H.Hosoya 在1971年提出(Topological index.A newly proposed quantity charactering the topological nature of satu rated hydrocarbons.Bull.chem.Soc.Jpn;44:2332-2339,1971)(参见文献[1])。
当今组合化学在制药和分子合成领域起着重要的作用,一个中心问题是研究限定区间上的某一指标的所有图和给定图族的最值。
Guyman 证明了路P n 具有最大的Hosoya 指标,星图S n 有最小的Hosoya 指标(参见文献[8,9]),C.Ye 刻画了具有第三小Hosoya 指标的m-匹配树(参见文献[4]),S.G.Wagner 刻画了具有最大Hosoya 指标的的四叶树(参见文献[10]),C.Ye 刻画了具有n 个顶点和直径至少为d 的树集T n,d 中取得最小、第二小Hosoya 指标的树(参见文献[11]),Y.Hao 描述了无圈图中具有最小值和第二小值的Hosoya 指标的极值图(参见文献[3])。
本文刻画了一类四叶树的Hosoya 指标序列。
1预备知识———————————————————————作者简介:苏连存(1977-),女,青海互助人,讲师,硕士,研究方向为图论。
一类树的Hosoya 指标序列The Sequence of Hosoya Index for Some Kind of Trees苏连存Su Liancun(青海大学基础部,西宁810016)(Department of Basic Research ,Qinghai University ,Xining 810016,China )摘要:许多拓扑指标都与分子的某些物理化学性质密切相关,而不同的分子拓扑指标反映该分子的不同性能。
特殊树的冠积的merrifield-simmons指标和hosoya指标

大度或连通度时关于 M -S 指标和 H 指标的极值图ꎬ文[10 - 11] 研究了一些运算图的 M - S 指标和 H 指
标的计数问题. 受这些文献的启发ꎬ本文研究特殊树与任意图的冠积的 M - S 指标和 H 指标的计数
Hosoya 指标是由日本化学家 Haruo Hosoya 于 1971 年在文献[1] 中提出并研究ꎬ表示图 G 中所有匹
配的数目ꎬ简称 H 指标ꎬ记为 μ( G) . Merrifield ̄Simmons 指标是 1989 年美国化学家 Richard E. Merrifield
和 Howard E. Simmons 在文献[2] 中引入的化学拓扑指标ꎬ表示图 G 中所有独立集的数目ꎬ简称 M - S 指
示由图 G 的每个顶点分别与图 H 的一个拷贝的所有顶点相连接得到的图. 如图 1 所示的双星图与任意
图 H 的冠积记为 S2n Hꎬ如图 2 所示的毛毛虫树与任意图 H 的冠积记为 M n H.
引理 1 [13]
设 G 是一个简单连通图ꎬ对任意的 uꎬv ∈ V( G) ꎬe = uv ∈ E( G) ꎬ则
引理 2 [13]
设 G 是一个简单连通图ꎬ对任意的 uꎬv ∈ V( G) ꎬe = uv ∈ E( G) ꎬ则
1) μ( G) = μ( G - e) + μ( G - u - v) ꎻ 2) μ( G) = μ( G - v) +
引理 3 [13]
1) σ( G) =
第一作者简介:索郎王青(1994—) ꎬ男ꎬ藏族ꎬ四川阿坝人ꎬ硕士研究生ꎬ研究方向为图论与组合数学. E-mail:suolwq@ 163. com
一类特殊(n,n+1)-图关于Merrifield-Simmons指标和Hosoya指标的排序

v 的邻点集,即
NG (v)= {u|uv ∈ E},
则点v 的闭邻集为
NG [v]= {v}∪ NG (v).
d(u,v)表示顶点u 与顶点v 之间的距离,fn 表示
第n 个 Fibonacci数,满足:
fn =fn-1 +fn-2,
其中f0 =0,f1 =1,n ≥ 2,ln 表 示 第n 个 Lucas
们常常被用来描述有机化合物的物理化学特征与
药 理 特 征 ,且 有 着 较 为 广 泛 的 应 用 ,相 关 的 应 用 参
见文献[1,3G4].文献[5G7]中 确 定 了 双 圈 图 的 最
大和最 小 的 MerrifieldGSimmons指 标 和 Hosoya
指标;文 献 [8]中 确 定 了 给 定 最 大 度 的 双 圈 图 的
31
引理1[3] 设 G 是一个 简 单 的 连 通 图,对 任
意的u,v ∈V(G),uv ∈ E(G),有 (i)σ(G)=σ(G -v)+σ(G -NG [v]); (ii)σ(G)=σ(G -uv)-σ(G - (NG [u]∪
NG [v])). 引理2[3] 设 G 是一个 简 单 的 连 通 图,对 任
究
了
一
类
特
殊
(n,n+1)G图
Gm ,k n,p,q
的
MerrifieldGSimmons指 标 和
Hosoya指 标,并 给 出 了 该 类 图 关 于 这 两 种
指标的排序.
关 键 词 :(n,n+1)G图 ;MerrifieldGSimmons指 标 ;Hosoya指 标 ;排 序
中 图 分 类 号 :O157.5 文 献 标 志 码 :A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Theta图的Merrifield-Simmons指数和Hosoya指数
发表时间:2012-06-28T14:45:26.093Z 来源:《时代报告(学术版)》2012年5月(上)供稿作者:万花[导读] 理论化学上,称为图G的Merrifield-Simmons指数,称为图G的Hosoya指数[2-4]。
万花青海师范大学数学系青海西宁 810008 中图分类号院O157.6 文献标识码院A 摘要:两个顶点间由三条边相连,分别剖分此多重图的三条边a次、b次、c次所得到的图称为Theta图,即,这里 ,顶点数为。
刻画了的Merrifield-Simmons指数和Hosoya指数,给出了其按内部路路长变化的序关系,在a分别为奇、偶数时给出了Theta图的Merrifield-Simmons 指数和Hosoya指数的极大(极小)值,以及对应的极图。
关键词:Merrifield-Simmons指数;Hosoya指数;Theat图 1 引言
本文仅考虑有限无向图(环和重边不被允许),对任意点,表示图G中所有与点 v相邻的顶点集。
若,表示删除图G中E 的顶点集后所得子图。
,则表示删去图G中的边集所得子图。
当
我们用来代替。
图G的独立集是指图G的顶点集的一个子集,中任意两个不同的顶点都不相邻,则成是V的一个独立集。
空集为任何集
合的一个独立集。
表示独立集的数目,类似的,图G的一个边子集,中每两条边均不相邻,则 E是G的匹配,Z(G) 表
示图G所有匹配数目之和,,指G中k匹配数目,有。
且时。
理论化学上,称为图G的Merrifield-Simmons指数,称为图G的Hosoya指数[2-4]。
Merrifield-Simmons指数和Hosoya指数是被研究的比较多的拓扑指数,其中一个重要的研究课题就是研究这两个图指标的极值问题,并已有一些重要结果,关于这方面的结论可参见综述文献[1] n阶图是指这样的一类图:
本文研究的是的Merrifield-Simmons指数和Hosoya指数,给出了其按内部路路长变化的序关系,在a分别为奇、偶数时给出了Theta图的Merrifield-Simmons指数和Hosoya指数的极大(极小)值,以及对应的极图。
2 主要结论及证明
参考文献:
[1] J. A. Bondy and U. S. R. Murty, Graph Theory with Application[M]. North-Holland, Amsterdam, 1976.
[2] R. E. Merrifield and H. E. Sinnons, Topological Methods in Chemistry[M]. New York:John Wiely\&Sons, 1989.
[3] H. Hosoya, Topological index, a newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons[J]. Bull. Chem. Soc. Japan., 1971,44:2322-2339.
[4] I. Cutman and O. E. Polansky, Mathematical Concepts in Organic Chemistry[M]. Berlin:Springer,1986.
[5] S. Wagner and I. Cutman, Maxima and minima of the Hosoya index and the Merrifield-Simmons index:A survey of results and techniques[J]. Acta Applicandae Mathematicae, 2010,112(3):323-346.
[6] H. Prodinger and R.F.Tichy, Fibonacci numbers of graphs[J]. Fibonacci Quart., 1982, 20(1):16-21.。
