(完整word版)RS编译码原理
RS编码原理及其在移动多媒体广播中的应用.

VIDEO ENGINEERINGNo.S1Vol.342010(Sum No.3411RS 码概述RS 码是以组为单位进行校正的分组校正码,适用于多进制,具有较强的纠正突发误码的能力。
在(n ,k RS 码中,输入信号被分为每组k 个符号,每个符号m bit ,每组km bit 。
纠正t 个符号错误的RS 码的参数如表1所示。
数字电视数据流的信道编码中,采用了(204,188,t =8的RS 码,即一个数据包的长度为204byte ,其中信息位188byte ,监督位16byte ,纠错能力为8byte ,即这种RS 码总共能纠正204byte 中发生的8byte 有误码的差错字节,不论每个字节中发生1位误码还是8位全误码。
2伽罗华域伽罗华域是由2m个符号及相应的加法、乘法运算组成的域,记为GF (2m ,在这个域中,任何运算的结果仍是这个域中的元素。
本原多项式指能除尽x w+1且w =2m-1的m 次既约多项式,对不同的m ,都对应一个本原多项式,从本原多项式就可以得到GF (2m域的所有元素。
GF (23域的加法和乘法运算分别如表2、表3所示,GF (23域元素对应的二进制表示如表4所示。
其中a 是GF (2m 域的本原元素,也是本原多项式的根,伽罗华域的计算方法是以本原多项式的根为前提的模二加和模二乘运算。
RS 码的所有元素均定义在GF (2m 域,其运算方式遵循伽罗华域内的运算法则。
文章编号:1002-8692(2010S1-0015-03RS 编码原理及其在移动多媒体广播中的应用杨凤霞1,王亚男2(1.中国传媒大学信息工程学院,北京100024;2.国家广电总局广播科学研究院信息技术研究所,北京100053【摘要】结合RS 码编码框图,通过公式详细地解释了RS 码的编码、纠错原理,同时介绍了移动多媒体广播(CMMB 技术中RS编码原理在其信道编码上的应用。
【关键词】伽罗华域;RS 码;编码原理;纠错原理;CMMB 【中图分类号】TN911.22【文献标识码】APrinciples of RS Coding and Its Applications in CMMBYANG Feng-xia 1,WANG Ya-nan 2(1.School of Information Engineering,Communication University of China,Beijing 100024,China ;rmation Technology Research Institute,Academy of Broadcasting Science,Beijing 100053,China【Abstract 】In this paper,principles of RS coding and error correcting are explained in detail through formulas combined with thediagram.Application of RS in channel coding of CMMB technology is also introduced.【Key words 】Galois fields;RS code;coding principle;error correcting principle;CMMB·实用设计·参数符号数/个比特数/bit码长≤2m -1≤(2m -1m信息段k km 监督段n-k =2t (n-k m 最小码距2t +1(2t +1m表1纠正t 个符号错误的RS 码的参数1a a 2a 3a 4a 5a 610a 3a 6a a 5a 4a 2a a 30a 41a 2a 6a 5a 2a 6a 40a 5a a 31a 3a 1a 50a 6a 2a 4a 4a 5a 2a a 601a 3a 5a 4a 6a 3a 210a a 6a 2a 51a 4a 3a 0表2GF (23域内的加法计算1a a 2a 3a 4a 5a 611a a 2a 3a 4a 5a 6a a a 2a 3a 4a 5a 61a 2a 2a 3a 4a 5a 61a a 3a 3a 4a 5a 61a a 2a 4a 4a 5a 61a a 2a 3a 5a 5a 61a a 2a 3a 4a 6a 61aa 2a 3a 4a 5表3GF (23域内的乘法计算GF (23元素二进制表示a 0100a 1010a 2001a 3110a 4011a 5111a 6101表4GF (23域元素的二进制表示152010年第34卷第S1期(总第341期3RS 码编码原理设信息组为A 1,A 2,…,当生成多项式的根为a 时,RS 码可表示为A 1+A 2+…+A n +Q 0+Q 1=0aA 1+a 2A 2+…+a nA n +a n+1Q 0+a n+2Q 1=(1编码的关键是产生监督码元,下面结合RS (7,5码的编码框图(如图1,通过运算具体阐述一下RS 码的监督符号的生成过程。
RS纠错编码原理及其实现方法

RS 纠错编码原理 ―及其实现方法
陈文礼
January 08 于郑州
If you have any suggestion or criticism . please email to ciciendi@
参数 n 为码长一般 n = 2m −1,k 为信息码元个数。 例如 m=4, 码长 n=15,信息码元长度为 9 GF(24)的本原多项式可以根据指令 >>rsgenpoly(15,9) 得到: ans = GF(2^4) array. Primitive polynomial = D^4+D+1 (19 decimal)
即
7
g 0h0 = −1 g 0h1 + g1h0 = 0
Zhengzhou Oriole Xinda Electronic Information Co.,Ltd.
g 0 hi + g1hi−1 + + g h n−k i−(n−k ) = 0
g 0 hn−1 + g1hn−2 + g n−k hk = 1
例如 c =(1,1,0,0,0) r =(1,0,0,0,1) e =(1+1,1+0,0+0,0+0,0+1)=(0,1,0,0,1)
从而可以看出从左端起第 2 位和第 5 位是错误的。
2、校验矩阵概念 码长为 n,信息数为 k,监督数为 r。
这样的一组码形式为: c = m1, m2 ,...mk , p1, p2 ,... pr
1
0
...
0)
h1k 1
h2k 0
RS编译码

一.RS 码RS 码是有限域GF (p^m )上,码长为n=p^m-1的本原BCH 码,它是多进制的BCH 码。
RS 码不但可以纠正随机错误、突发错误以及二者的组合,而且可以用来构造其它码类。
在计算机中数据是以二进制的形式存在,所以p 通常取值为2。
RS 码的参数:符号取自GF(2^m),纠t 个错的RS(n,k)码的定义如下: 符号大小m .表示符号比特数为m 位。
码块总长度为n 个符号,其中信息长度k 个符号,校验位长度K=n —k 个符号。
RS 码的纠错能力是出码块中的冗余数据校验码的长度K 决定的。
在码块中的错误位置事先并不知道的情况下,RS(n ,k)码可以纠正t=K /2个错误符号。
显然t 值越大,RS 码的纠错能力越强,但与之相对应的是更复杂的算法,更长的运算时间,更低效的数据传输率。
RS 码既可以纠随机错又可以纠突发错。
但RS 码中采用符号这一特性使得它特别适用于产生突发错的场合。
因为不论一个符号中错了多少位,在RS 解码过程中。
它只会被认为是产生了一个符号错。
一个可以纠t 个符号的RS 码,它至少可以纠一个(t-1)m+1个连续比特组成的突发错,而当随机错恰好都不在同一个符号中时只能纠正t 个比特的随机错。
二.RS 码编码对于GF(2^m)来说,若域中非零元素a 的级是2^m-1,则将a 称为本原域元素。
设符号取自GF(2^m),纠t 个错的RS(n,k)码,它的最小距离d=2t+1,则由本原域元素a 的2t 个连续根 ,0αm ,α120-+t m 作为g(x)的根来构造生成多项式g(x)=(x+αm 0)(x+α10+m ))(012αm t x +-+通常情况下取通常取m 0 = 0或m 0 = 1只要将信息码多项式m(x)=m m x m x k k 0111+++-- 乘以x k n -次,然后以g(x)为模,求出余式q(x)便可以得到系统码。
q (x )= m(x) x k n -modg(x)=q q x q x k n k n 0111+++---- C(x)= m(x) x k n -+ q (x )例 构造能纠正2个错误,码长为15符号的RS 码n=15,t=2可得m=4,k=11,d=5.因此RS 码为(15,11)码,生成多项式为g(x)=(x+α)(x+α2)(x+α3)(x+α4) =αααα103263134++++x x x x假设待发送的信息码组为m(x)=x x m x x ααα963102)(++=则编码后的码组多项式为C(x)= m(x) x k n -+ m(x) x k n -modg(x)=ααααα133359103142+++++x x x x x编码的实现:1)首先构造有限域,RS 码的性质和运算法则均定义在Galois 域上,Galois 域是能进行加减乘除运算的有限个元素的封闭集合,它的加减运算符合结合律、交换律和分配律。
RS码简介与编译码算法综述

计算βi
PGZ译码算法
——算法总结
∗
PGZ译码算法
——算法总结
∗
BM译码算法
——引入 1965年E.R.Berlekamp提出了由伴随式求σ(x)的 迭代译码算法,极大地加快了求σ(x)的速度, 实现时比较简单,且易于用计算机完成译码, 因而从工程上解决了BCH码的译码问题。1969 年J.L.Massey指出,迭代译码算法与序列的最 短线性移位寄存器的综合之间的关系,并进 行了简化,自此以后把这种算法成为BM迭代 译码算法。
RS编码
——编码器设计
最小距离为d的本原RS码的生成多项式为 g(x)=(x-α)(x-α2)(x-α3)…(x-αd-2) 信息元多项式为 m(x)=m0+m1x+m2x2+…+mk-1xk-1 编码器主要有三种类型: 1.基于乘法形式的编码器 2.基于除法形式的编码器 3.基于校验多项式形式的编码器
背景知识
——线性分组码
分组:将码字分为许用码字和禁用码字 两组 线性:许用码字的线性组合还是许用码 字
∗
BCH码
——引入 BCH码是一类最重要的循环码,能纠正多个随 机错误,它是1959年由Bose、Chaudhuri及 Hocquenghem各自独立发现的线性循环码, 人们以他们的名字字头命名为BCH码。 BCH码打破了一般线性分组码先编码再验证性 能的模式,能够根据实际纠错需求进行编码。
BCH码
——定义
∗
BCH码
——有限域
∗
∗
∗
BCH码
——设计准则
RS码
——引入 RS编码起源于1960年MIT Lincoln实验室的S. Reed和G. Solomon在Journal of the Society for Industrial and Applied Mathematics上发表的 一篇论文:Polynomial Codes over Certain Finite Fields(某些有限域上的多项式码)。经历 了数十年的发展,RS码成为了研究最详尽, 分析最透彻,应用最广泛,研究成果最多的 码类之一。
RS码简介与编译码算法综述

BM译码算法
——算法基础
BM译码算法
——算法原理
BM译码算法
——迭代的具体实现
j -1 0 1 2 3a 4 5 6 1 1 1+αx 1+α11x 1+α8x+α8x2 1+α6x+αx2 1+α6x+αx2 1+α6x+αx2 0 1 1 1+α6x 1+α10x 1+α11x+α5x2 1+α11x+α5x2 1+α11x+α5x2 0 0 1 1 2 2 2
E(x)
计算S2t
计算βi
PGZ译码算法
——算法总结
PGZ译码算法
——算法总结
BM译码算法
——引入
1965年E.R.Berlekamp提出了由伴随式求σ(x)的 迭代译码算法,极大地加快了求σ(x)的速度, 实现时比较简单,且易于用计算机完成译码, 因而从工程上解决了BCH码的译码问题。1969 年J.L.Massey指出,迭代译码算法与序列的最 短线性移位寄存器的综合之间的关系,并进 行了简化,自此以后把这种算法成为BM迭代 译码算法。
RS码简介
熊竹林
背景知识
RS码是一种BCH码 BCH码是一种循环码 循环码是一种线性分组码 线性分组码是一种信道编码
背景知识
——信道编码
信道的非理想性 传输差错 香农告诉我们要纠错必须增加冗余 信道编码就是一门增加冗余的学问 亡羊补牢:反馈重传 未雨绸缪:前向纠错 线性分组码就是前向纠错码的一种
RS编码
——编码器设计
最小距离为d的本原RS码的生成多项式为 g(x)=(x-α)(x-α2)(x-α3)…(x-αd-2) 信息元多项式为 m(x)=m0+m1x+m2x2+…+mk-1xk-1 编码器主要有三种类型: 1.基于乘法形式的编码器 2.基于除法形式的编码器 3.基于校验多项式形式的编码器
rs(255,239) 编译码原理

rs(255,239) 编译码原理1. 什么是rs(255,239)编码?RS(Reed-Solomon)编码是一种纠错码,可用于在数据传输过程中检测和纠正错误。
RS(255,239)编码是一种RS编码,其参数为255和239,表示在255个符号中添加16个纠错符号,以实现对239个数据符号的纠错。
2. RS(255,239)编码的编码过程在RS(255,239)编码中,数据被视为一个多项式,并进行编码。
编码的过程如下:1)将239个数据符号转换为一个多项式,如:D(x) = d<sub>0</sub> + d<sub>1</sub>x + d<sub>2</sub>x<sup>2</sup> + ... +d<sub>238</sub>x<sup>238</sup>2)计算出一个16次的多项式E(x),表示16个纠错符号的值。
3)将D(x)和E(x)相加得到一个多项式T(x)。
4)将T(x)除以一个特定的多项式G(x),得到商式Q(x)和余数R(x)。
5)将Q(x)和R(x)组合成一个新的多项式C(x),即:C(x) = Q(x)G(x) + R(x)。
6)将C(x)中的每个系数转换为一个8位二进制数,得到255个符号。
3. RS(255,239)编码的解码过程在RS(255,239)编码中,解码的过程如下:1)将接收到的255个符号转换为一个多项式R(x)。
2)计算出一个16次的多项式S(x),表示接收到的16个纠错符号的值。
3)将R(x)和S(x)相加得到一个多项式E(x)。
4)计算E(x)的根,得到错误位置的信息。
5)使用错误位置的信息和接收到的符号,计算出错误的数据符号的值。
6)将错误的数据符号的值替换为正确的值。
4. RS(255,239)编码的优点RS(255,239)编码具有以下优点:1)能够检测和纠正多个错误,即使在高噪声环境下也能工作。
rs技术原理

rs技术原理RS技术是一种纠错编码技术,RS是Reed-Solomon的缩写,由Irving S. Reed和Gustave Solomon于1960年代初发明。
它可以在数据传输过程中检测和纠正错误,广泛应用于数字通信、光盘、磁盘等领域。
一、概述RS技术是一种块编码技术,它将数据分成若干个块进行编码。
每个块包含k个数据符号和n-k个校验符号,总共有n个符号。
当接收方接收到这些符号时,可以使用校验符号来检测和纠正错误。
二、编码过程1.数据分块首先将要传输的数据按照固定的长度分成若干个块,每个块包含k个数据符号。
2.生成多项式然后生成一个n次多项式:g(x) = (x-a1)(x-a2)...(x-an+k)其中a1,a2,...,an+k是不同的元素。
这里需要满足n+k<=GF(q),其中q为一个素数幂次。
3.计算校验符号将生成的多项式g(x)除以x-a1,x-a2,...,x-an得到余数:r(x) = g(x) mod (x-a1)(x-a2)...(x-an)这里r(x)是一个(n-k-1)次多项式,它的系数就是n-k个校验符号。
4.计算编码符号将数据符号和校验符号组合起来,得到n个编码符号:c(x) = (m1,m2,...,mk,r1,r2,...,rn-k)其中m1,m2,...,mk是k个数据符号,r1,r2,...,rn-k是n-k个校验符号。
三、解码过程1.接收数据接收方接收到n个编码符号。
2.计算伴随式首先计算伴随式:A(x) = det(M(x))其中M(x)是一个(n-k)×(n-k)的矩阵,每个元素都是一个多项式。
M(x)的第i行第j列的元素为x^(i+j-2),其中i,j=1,2,...,n-k。
3.计算误差定位多项式然后计算误差定位多项式:Λ(x) = x^(n-1)B(1/x)其中B(x)=A(αx)/A'(αx),α为一个非零元素。
Λ(x)的根就是错误位置。
RS编码rs(204,188)设计原理

11.9.2 RS(204, 188)译码器的设计RS码在通信系统、数字电视和计算机存储系统中应用很广泛。
例如,DVB(数字电视)标准中信道编/解码采用RS(204, 188);ATM网络中使用RS(128, 124)作为前向纠错编码(Forward Error Correcting, FEC)。
本节将以DVB标准中定义的RS(204, 188)译码器为例,详细介绍基于改进的BM迭代算法、pipeline结构的译码的所有技术细节。
考虑到译码器的可扩展性、可维护性,实例中尽可能地使用参数化、模块化的设计。
读者可在实例代码基础上作很小的改动,就能实现不同需要的RS译码器。
1. 应用背景在数字通信、数字电视中,信道编码的使用提高了数据传输的质量。
虽然增加了传输带宽,但信道编码减小了数据传输出现误码的概率,同时也减小了所需要的信噪比(signal-to-noise rate)。
在大多数应用中,将RS码与卷积码级联使用进行纠错。
在自信源至接收的过程中,数字电视信号的编码包括信源编码、信道编码及加密。
信道编码又称做前向纠错编码,其目的是提高信息传送或传输的可靠性,当传输差错在一定范围内,接收机都能将误码纠正过来。
必须指出,信道编码并非指信号经上变频发送出去后,在传输信道中(有线、卫星或地面)进行编码,而是指经过编码后便匹配信道传输和减少差错。
因此,自信源编码后的所有编码包括能量随机化扰码、卷积、交织、Reed-Solomon编码等都可划为信道编码。
典型的数字电视信道编码如图11-73所示。
为信息位,t为能纠正误码的最大的码位,且RS外码编码的特点是纠正与本组有关的误码,尤其对纠正突发性的误码最有效。
通常,n、k、t分别为204、188和8。
如图11-74所示为"EN 300 429"有线数字电视(DVB-C)标准规定的发送端(Cable Head-end)框图,其中包括了数据帧结构(Framing structure)、信道编码及调制。
RS编译码原理

1.除法电路实现的RS 系统典型编码算法设)2(m GF 域上的待编码的信息矢量为),...,,(021m m m k k --,可用多项式表示为如下的形式:012211...)(m x m x m x m x m k k k k ++++=---- (1-1) 首先确定)2(m GF 上的一个本原域元素α,构成生成多项式: ))...()(()(121000-++---=t m m m x x x x g ααα(1-2)其中,t 为设计的纠错符号个数,0m 为任意非负整数 。
把)(2x m x t 除以)(x g ,所得余式是一个次数小于等于12-t 次多项式)(x r ,计算式如下:))(mod()()(2x g x m x x r t ≡ (1-3) 于是)()()(2x r x m x x C t -=能被)(x g 整除,故是一个码多项式。
这样的RS 码字中,信息集中在码字的高k 位,称这种码为系统RS 码。
系统RS 码编码可采用k n -级除法电路来实现,电路结构如图1.1所示。
图1.1 系统RS 码的编码电路图编码器工作过程如下:(1)寄存器1210,....,,-t D D D 的初始状态全为0,门开,开关置于2,然后进行移位。
送入信息序列的系数,高次位系数先进入电路,它一方面经开关输出,一方面自动乘以tkn x x 2=-后进入)(x g 除法电路;(2)k 次移位后,信息元全部进入电路,完成了除法运算,此时寄存器中保留了余式的系有限域乘法 有限域加法12门数,即校验元;(3)此时,门关、开关置于1;再经过k n -次移位后,寄存器中校验元全部输出,与原先的k 位信息元组成了一个码长为n 的码字;(4)门开,开关置2,送入第二组信息组重复上述过程。
此编码算法满足大多数应用,若无法满足速率的要求,可以参考脉动RS 编码算法,这里不做介绍。
2.RS 译码算法上述已得到一个码长为n ,信息序列长度k ,校验元为k n -的RS 码,为了对此RS 码进行译码,我们需要使用与二进制BCH 码译码相同的三个步骤;此外们还需要计算错误数值的第四个步骤。
(完整word版)RS编译码原理

RБайду номын сангаас编码器的结构
RS码的基本思想就是选择一个合适的生成多项式g(x),并且使得对每个信息段计算得到的码字多项式都是g(x)的倍式,即使得码字多项式除以g(x)的余式为0。这样,如果接收到的码字多项式除以g(x)的余式不是0,则知道接收码字的余式存在错误;而且通过进一步可以纠正最多t=(n-k)/2个错误。
一个RS码有以下几个参数:
码长:n=2^m-1个符号或者m(2m-1)比特
信息段:k个符号或者mk个比特
监督段:2t=n-k个符号2mt=m(n-k)个比特
最小码距:dmin=n-k+1个符号或者mdmin=m(n-k+1)
例如,对RS(204,188)码来说,源数据被分割为188个符号为一组,经过编码变换后,成为204个符号长度的码字。长度为16个符号的监督为可以纠正码字中出现的最多8个符号错误。
1
RS码(Reed-solomon codes)一种低速率的前向纠错的信道编码,是一类具有强纠错能力的多进制BCH码,在线性分组码中,它的纠错能力和编码效率是最高的。相比于其他线性分组码而言,在同样的效率下,RS的纠错能力是特别强的,特别是在短的中等码长下,其性能接近于理论值,它不但可以纠正随机错误,突发错误及两者的结合,而且可以用来构造其他码型,如级联码。
RS码生成多项式一般按照如下公式选择,即
g(x)=(x-a)(x-a2)(x-a3)···(x-a2t-1)(x-a2t)
式中,ai是GF(2m)中的一个元素。如果用d(x)表示信息段多项式,则可以按照如下方法构造码字多项式c(x)。首先计算商式h(x)和余式r(x),得
xn-kd(x)/ g(x)= h(x) g(x)+ r(x)
rs编译码原理流程

rs编译码原理流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!Rust 编译器流程。
1. 词法分析:Rust 编译器将源代码解析为一系列称为词素的符号,包括标识符、关键字、标点符号和数字。
RS码译码算法及其实现的研究

RS码译码算法及其实现的研究RS码译码算法及其实现的研究摘要:纠错编码在信息传输中起到了至关重要的作用,其中纠错码是最常用的一种编码方式。
RS码作为一种具有高纠错能力的纠错码,被广泛应用于存储介质、数字通信和数据传输等领域。
本文将详细介绍RS码的编码和译码原理,以及RS 码译码算法的研究进展和实现方法。
一、引言在现代通信系统中,由于信道和介质的不完美性,信息传输过程中常常伴随着噪声和错误,导致数据传输错误率的增加。
为了提高数据传输的可靠性和冗余性,人们引入了纠错码,用于在数据传输过程中对错误进行修正。
二、RS码的原理RS码全称为Reed-Solomon码,是一种基于有限域的纠错码。
RS码利用了有限域GF(q)上的多项式编码理论,通过在数据流中引入冗余位进行编码和译码,从而实现错误的检测和纠正。
1. 编码原理RS码的编码原理是将信息数据流进行多项式编码,然后再添加纠错码,生成一个较长的编码后数据流进行传输。
具体编码流程如下:(1)将n个信息符号划分为m个长度为t的子串,其中m = n / t,t为RS码的最小距离;(2)将每个子串看作一个特定的数字,代入t-1次幂相乘的多项式中;(3)将每个子串多项式求模,得到t-1阶多项式;(4)在多项式后方添加r个纠错码位,使整个编码构成一个长度为t+r的新多项式;(5)重复以上步骤,直到对所有信息子串进行编码处理。
2. 译码原理RS码的译码原理是利用多项式除法实现。
译码时,首先接收到一个由编码器生成的编码后数据流,然后通过解码器进行解码,恢复原始信息数据流。
具体译码流程如下:(1)通过接收到的数据流计算相应的符号多项式;(2)使用Berlekamp-Massey算法,计算出多项式的最小生成多项式,从而确定修正多项式;(3)对错误位置进行定位,然后使用Forney算法计算纠错多项式;(4)使用译码器获得纠正后的数据流。
三、RS码的译码算法研究进展1. 经典的译码算法目前,根据实际应用需求,已经提出了许多RS码译码算法。
龚政辉-RS码及其编译码算法

RS码及其编译码算法指导教员:雷 菁姓 名:龚 政 辉第一章 引言本文介绍符号取自)GF里的里德-所罗门码(Reed-Solomon(qCode,以下简称RS码)。
RS码是非二进制BCH码的一个最常用的子类,而BCH码是大家所熟悉的。
虽然RS码属于BCH码,但是它却是由Reed和Solomon于1960年采用完全不同的方法独立构造出来的。
RS码的最小距离等于它的奇偶校验符号数加一。
RS码在纠正随机符号错误和随机突发错误方面非常有效,因此被广泛应用于通信和数据存储系统中以便进行差错控制,应用领域涵盖从深空通讯到高密度磁盘等多方面。
以RS码作为外码,简单二进制码作为内码的级联方式在降低译码复杂度的同时,能够提供很高的数据可靠性。
但与二进制BCH码不同,RS码的译码需要同时确定符号错误的的位置和取值,所以它的译码更为复杂而编码算法是大体一致的。
第二章 循环纠错码的基本理论2.1 有限域(Galoias 域)基本概念及相关结论有限域(Galoias 域)就是域中元素的个数是有限的,元素的个数称为域的阶。
q 阶有限域,用()GF q 表示。
如果q 为一个素数,则集合{}0,1,2,,1q − 在模q 加法和乘法下,构成一个q 阶有限域()GF q 。
有限域在编码理论中具有重要的地位,下面给出Galoias 域的几个基本概念和相关结论。
定义1 在域()GF q 中,满足0ne =的最小正整数n 称为域的特征,e 为域的单位。
定义2以q 为特征的域是()m GF q ,1,2,m =…,称()GF q 是()m GF q 的基域,()m GF q 为()GF q 的扩域。
域中一切非零元素的特征都等于域的特征,且域的特征一定为素数。
非零元素构成的乘法群的阶定义为域中该元素的级。
若α为域()GF q 中的n 级元素,则称α为n 次单位原根。
若某一元素α的级为1q −,则称α为本原域元素。
域的特征表明了域中加法运算的循环性,而域的级则表明了域中乘法运算的循环性。
RS(16,12)缩短码编译码原理及性能

2012年第02期,第45卷 通 信 技 术 Vol.45,No.02,2012 总第242期 Communications Technology No.242,Totally(16,12)RS缩短码编译码原理及性能分析赵 旸, 耿相铭(上海交通大学 电子信息与电气工程学院,上海 200240)【摘 要】在各类数字通信系统以及计算机存储和运算系统经常利用差错控制编码降低误码率,提高通信质量,满足对数据传输通道可靠性的要求。
RS码是一种性能优良的前向纠错码,具有同时纠正随机错误和突发错误的能力,它的构造特点决定了其非常适合于纠正突发性错误。
文中在阐述RS系统码编译码原理的基础上,提出了(16,12)RS缩短码的编译码方法,利用MATLAB对(16,12)RS缩短码在高斯信道和瑞利信道条件下的纠错能力进行仿真,并分析其纠错性能。
【关键词】里德-所罗门码(RS码);缩短码;编译码;瑞利信道;MATLAB仿真【中图分类号】TN918 【文献标识码】A 【文章编号】1002-0802(2012)02-0049-04 Encoding and Decoding Algorithm for(16,12)RS Shortened Codesand Its Performance AnalysisZHAO Yang, GENG Xiang-ming(SEIEE, Shanghai Jiaotong University, Shanghai 200240)【Abstract】In various digital communication systems and computer storage and computing systems, the error control coding is often used to reduce bit or symbol error rate, and thus to improve communication quality and meet the reliability requirements of data transmission. RS code, as an excellent forward error correction code, has the capability to correct both random error and burst error, and its structured characteristics feature its suitability for correcting burst errors. Based on description of the RS system code’s encoding and decoding principles, this paper proposes(16,12)RS shortened code’s encoding and decoding method. And with MATLAB the(16,12)RS shortened code’s error correction capability in the AWGN and Rayleigh fading channel conditions is simulated.【Key words】Reed-Solomon code; shortened code; encoding & decoding algorithm; Reyleigh fading channel; MATLAB simulation0 引言里德-所罗门码(RS码)是性能优良的多进制BCH码,相比于其他线性分组码,在同样的编码效率下,RS码具有较强的纠错能力,特别是在短的中等码长下,其性能很接近于理论值,不但可以纠正随机错误、突发错误及两者的结合,而且可以用来构造其他码类,如RS码和卷积码构成的级联码已经被用在深空通信的下行链路中,因此RS码在数字存储和通信系统中获得了广泛应用,例如用于CD ROM-、DVD和陆地数字传输中定义在8(2)GF上的缩短RS码。
RS纠错编码原理

RS 基本概念GF (2)域域在RS 编码理论中起着至关重要的作用。
简单点说域GF (2m )有2m (设2m = q )个符号 a 0, a 1, a 2, a m-1的和来表示。
除0、1外其余所有元素由本原多项式Rx )生成。
本原多项式的特性是尸茂)得到的余式等于0。
在纠错编码运算过程中,加、减、乘和除的运算是在伽罗华域中进行 在GF 域上的加、减、乘、除运算定义如下(GF (24 )为例):1、 力口、减运算均定义为元素的二进制表示方式进行异或运算。
如: a 8+a 10,先查表,将其化为二进制表示方式得 0101+0111,经过异或运算得 0010,再查表得a 1,即:a 8+a 10= a 1。
减运算与加运算相同,即: a 8-a 10= a 1。
2、 乘运算定义为元素的指数相加后进行模15运算后所得的新元素,但若有一个元素7137135为 0,则相乘结果为 0。
如:a *a , (7+13)mod 15=5,即 a *a = a 。
3、 除运算定义为元素的指数相减后进行模15运算后所得的新元素(指数为正数)。
若被除数为 0,则结果为 0。
如:a 5/a 9, (5-9)mod 15=11 ,即 a 5/a 9= a 11。
F 面以一个较简单例子说明域的构造。
GF 24)的所有元素例:m=4,本原多项式 p (x )=x 4 +x+1求GF 24)的所有元素: 因为a 为p (x )的根得到:-4 + '-■ +1 =0或〉4 =〉+1 (根据运算规则)丿元糸 多项式表示二进制表示 十八进制表示0 0 0000 0 0 a1 0001 1 1 aa 0010 2 2a 2a 0100 4 3 a3 a1000 8 4a a+1 0011 3 5a a +a mod p(a) 0110 6 6aa 3+a 2 mod p(a)1100C且具有以下性质:域中的每个元素都可以用符号(n, k)RS在介绍之前需要说明一些符号。
RS编码——精选推荐

RS编码RS 码是⼀类纠错能⼒很强的多进制BCH 码,由于采⽤了q 进制,所以它是多进制调制时的⾃然和⽅便的编码⼿段。
因为RS 码能够纠正t 个q 位⼆进制码,即可以纠正≤q 位⼆进制错误(当然,对于 q 位⼆进制码中分散的单个错误也能被纠正),所以适合于在衰落信道中使⽤,以克服突发性差错。
另外RS 码也被应⽤在计算机存储系统中,以克服这系统中存在的差错串。
RS编码过程:(1)得到RS码的⽣成多项式g(x)(2)⽤信息码多项式 m(x)除以⽣成多项式 g(x),所得余式 r(x)为监督码多项式,将监督码多项式r(x)置于信息码多项式之后,形成RS 码。
GF(2m)域中计算,码字长度:n=2m-1,纠错能⼒:t=(n-k)/2matlab相应函数:1)rsgenpoly:Generator polynomial of Reed-Solomon codegenpoly = rsgenpoly(n,k,prim_poly)genpoly = rsgenpoly(n,k,prim_poly) returns the narrow-sense generator polynomial of a Reed-Solomon code with codeword length n and message length k. The codeword length n must have the form 2m-1 for some integer m, and n-k must be an even integer. The output genpoly is a Galois row vector that represents the coefficients of the generator polynomial in order of descending powers. The narrow-sense generator polynomial is (X - A1)(X - A2)...(X - A2t) where A is a root of the default primitive polynomial for the field GF(n+1) and t is the code's error-correction capability, (n-k)/2. prim_poly is an integer whose binary representation indicates the coefficients of the primitive polynomial. To use the default primitive polynomial GF(n+1), set prim_poly to [].If prim_poly specifies the primitive polynomial for GF(n+1) that has A as a root. The examples below create Galois row vectors that represent generator polynomials for a [7,3] Reed-Solomon code. The vectors g and g2 both represent the narrow-sense generator polynomial, but with respect to different primitive elements A. More specifically, g2 is defined such that A is a root of the primitive polynomial D3 + D2 + 1 for GF(8), not of the default primitive polynomial D3 + D + 1. The vector g3 represents the generator polynomial (X - A3)(X - A4)(X - A5)(X - A6), where A is a root of D3 + D2 + 1 in GF(8).2)primpolyFinding Primitive PolynomialsYou can use the primpoly function to find primitive polynomials for GF(2^m) and the isprimitive function to determine whether a polynomial is primitive for GF(2^m). The code below illustrates.m = 4;allprimpolys = primpoly(m,'all') % All primitive polys for GF(16)i1 = isprimitive(25) % Can 25 be the prim_poly input in gf(...)?function [alpha_to,index_of]=gen_galois()clcm=8;n=2^m-1;p=de2bi(285);%p=[101001];alpha_to=zeros(1,2^m);mask=1;alpha_to(m+1)=0;for i=1:malpha_to(i)=mask;if(p(i)~=0)alpha_to(m+1)=bitxor(alpha_to(m+1),mask);endmask=mask*2;endmask=alpha_to(m);for i=m+2:nif(alpha_to(i-1)>=mask)alpha_to(i)=bitxor(alpha_to(m+1),bitxor(alpha_to(i-1),mask)*2);elsealpha_to(i)=alpha_to(i-1)*2;endendalpha_to(2^m)=0;index_of=zeros(1,2^m);for i=1:2^m-1index_of(alpha_to(i))=i-1;enda=3;b=27;y=rs_mul(a,b,m,alpha_to,index_of)ya=rs_add(a,b,m)function y=rs_mul(a,b,m,alpha_to,index_of) if a*b==0y=0;elsea1=index_of(a);b1=index_of(b);c=mod((a1+b1),(2^m-1));y=alpha_to(c+1);endfunction y=rs_add(a,b,m)a1=de2bi(a,m);b1=de2bi(b,m);y1=bitxor(a1,b1);y=bi2de(y1);。
RS码编码算法
RS 码编码算法一.RS 编码对于能够纠正t 个错误的RS (n,k,d )码,具有如下特征:1) 码长:12n m -=符号或)12(m m -比特2) 信息码元数:t 2n k -=或mk 比特;3) 监督码元数:t 2k n =-符号或)k n (m -比特;4) 最小距离:1k n 1t 2d +-=+=符号或)1k n (m +-比特;最小距离为d 的本原RS 码的生成多项式为)x ()x )(x )(x ()x (g 2d 32-α-α-α-α-=式中的m 是一个任意整数。
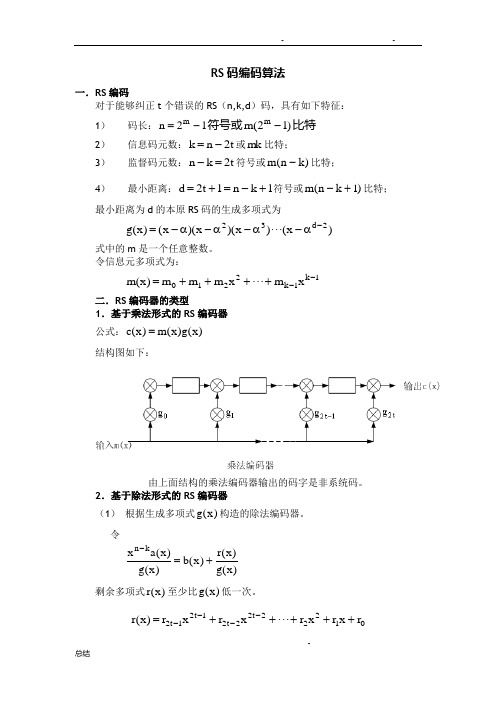
令信息元多项式为:1k 1k 2210x m x m m m )x (m --++++=二.RS 编码器的类型1.基于乘法形式的RS 编码器公式:)x (g )x (m )x (c =结构图如下:由上面结构的乘法编码器输出的码字是非系统码。
2.基于除法形式的RS 编码器(1) 根据生成多项式)x (g 构造的除法编码器。
令)x (g )x(r )x (b )x (g )x (a x k n +=-剩余多项式)x (r 至少比)x (g 低一次。
01222t 22t 21t 21t 2r x r x r x r x r )x (r +++++=----则编程的码多项式为1222n2n1n1nkncxcxcxcxc)x(r)x(ax)x(c+++++=+=-----具体实现如下图:(2)根据校验码多项式)x(h构造的除法编码器设校验多项式为:11k1kkkhxhxhxh)x(h++++=--系统码的多项式为:11kn1knknkn2n2n1n1ncxcxcxcxcxc)x(C+++++++=----------它的前k位系数:kn2n1nc,,c,c---是已知的信息位,而后kn-位系数:12kn1knc,c,,c,c----是需求的校验位。
码多项式必是生成多项式)x(g的背式,所以)x(g)x(q)x(C=1k)x(q,kn)x(g,1n)x(C-≤∂-=∂-≤∂而)x(qx)x(q)1x)(x(q)x(h)x(g)x(q)x(C)x(h nn-=-==由于1k)x(q,kn)x(g,kn)x(g,1n)x(C-≤∂-=∂-=∂-≤∂所以nx)x(q的最低位次数至少为n次,而在)x(C)x(h的乘积中k2n1n x,,x,x--的次数为0。
数字通信中的RS编码

数字通信中的RS编码摘要:由于信道中存在干扰,数字信号在信道中传输的过程中会产生误码。
为了提高通信质量,保证通信的正确性和可靠性,通常采用差错控制的方法来纠正传输过程中的错误。
本文的目的就是重点研究一种信道编码的算法和逻辑电路的实现方法,并在硬件上验证。
RS码是一种典型的纠错码,在线性分组码中,它具有最强的纠错能力,在分析RS编码原理的基础上,介绍RS(15,11)码的编码算法和逻辑电路的实现方法。
关键词:数字通信纠错编码RS码1.引言目前RS码已经成为美国航天局(NASA)和欧洲空间站(ESA)在深空通信级联系统中采用的标准码,此外RS码也是存储器系统的标准用码。
RS码编解码的纯硬件实现比较复杂,EDA技术的出现,使得利用软件开发工具实现硬件电路设计成为现实。
编解码的实现过程都在VHDL环境下完成。
2.RS码的参数及编码设计本章详细讨论RS编码器和解码器的逻辑电路设计以及对设计进行的优化。
RS编解码【2】算法中大量用到多项式求值运算,如伴随式计算,BM算法求解错误位置等,而这些多项式的求解可以使用乘加运算来实现,因而制约RS码编解码器性能的最主要的因素是乘法器和求逆器的设计。
我们首先研究GF(24)有限域的乘法器和求逆器的逻辑电路实现。
2.1 GF(2m)运算“加法”:只需要把它们的矢量表示进行按位异或运算即可。
其程序如下:L xor P;“乘法”:标准基乘法器【4】的原理如下:基于GF(24)域上面的任意两个元素A,B及其乘积C分别可以用多项式表示为:A(x)=a3x3+a2x2+a1x+a0 B(x)=b3x3+b2x2+b1x+b01.将A(x)和B(x)两个多项式按照常规方法相乘,得到一个次数不大于6的多项式Q(x);2.将Q(x)对GF(24)的本原多项式P(x)=x4+x+1求模,得到次数不大于4的多项式,即得到A与B的乘积C(x)。
Q(x)=q6x6+q5x5+q4x4+q3x3+q2x2+q1x+q0其中Q(x)各项的系数如下:q0=a0b0;q1=a1b0+a0b1;q2=a2b0+a1b1+a0b2;q3=a3b0+a2b1+a1b2+a0b3;q4=a 3b1+a2b2+a1b3;q5=a3b2+a2b3;q6=a3b3可以得到化简的计算方法:C(x)=A(x)×B(x)modp(x)=C3x3+C2x2+C1x+C0 其中:C3=q3+q6C2=q2+q5+q6C1=q1+q4+q5C0=q0+q4由上面的分析可以知道,直接利用一个纯组合逻辑电路就可以求解出在有限域上面A(x)和B(x)的乘积的系数。
最新RS码编码及译码 (优选.)

wo最新文件---------------- 仅供参考--------------------已改成-----------word文本--------------------- 方便更改rdRS码的编码和译码算法的实现摘要:RS码是对突发错误具有良好纠错能力的通信信道编码。
本文主要讨论了RS码的编码和译码,主要推导了伽罗华域的生成方法和BM迭代译码算法。
关键词:RS码;伽罗华域;编码;BM译码1 RS码的基本介绍RS码是一类有很强纠错能力的BCH码,也是一类典型的代数几何码[1],是由里德和索罗蒙于1960年构造出来的。
RS码是非二进制BCH码的一个重要子类,是一类最大距离可分组码。
RS码已经被广泛应用于通信和存储系统中,以进行差错控制。
的q进制的BCH码是q进制BCH码中最重要的一个子类。
这一子类的编码被称为里德—所罗门(Reed-Solomon,RS)码。
令α为GF(q)中的本原元。
符号取自GF(q)、纠正t个错误的RS码,其生成多项式g(x)以α,,…,为其全部的根。
由于是GF(q)中的元素,因此其最小多项式(x)即为。
因此,得到+其中GF(q),由于α,,…,是-1的根,因此-1能够被g(X)整除。
所以,g(X)将生成恰好具有2t个奇偶校验符号、长度为n = q – 1的q 进制循环码[2]。
符号取自GF(q)、纠正t个错误的RS码具有如下参数:分组长度:n = q - 1奇偶校验符号数: n – k = 2t维数: k = q – 1 – 2t最小距离: = 2t + 1于是,我们看到RS码具有如下特性:(1)码的长度比码字母表的大小少1;(2)最小距离比奇偶校验符号数多1。
最小距离比奇偶校验符号数多1的编码称为极大最小距离可分(Maximum Distance Separable,MDS)码。
2 伽罗华域元素和二进制代码表的生成伽罗华域是以q=为元素的有限域,p为素数,m为正整数。
其特征是域中各元素可以用基本元素及其表达式来表示,并且域中各元素经过域内运算,其结果仍为域内元素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
RS编码器的结构
RS码的基本思想就是选择一个合适的生成多项式g(x),并且使得对每个信息段计算得到的码字多项式都是g(x)的倍式,即使得码字多项式除以g(x)的余式为0。这样,如果接收到的码字多项式除以g(x)的余式不是0,则知道接收码字的余式存在错误;而且通过进一步可以纠正最多t=(n-k)/2个错误。
以RS(7,3)码为例介绍RS码的编码过程。RS(7,3)码利用3个信息符号得到长度为7的编码,码元符号取自GF(23).即m=3。域GF(23)的本原多项式为a3+a+1,RS码的生成多项式为g(x)=x4+3x3+x2+2Байду номын сангаас+3。假如输入符号为[4 0 6],则信息多项式d(x)=4x2+6。生成码字的过程如下:
RS码生成多项式一般按照如下公式选择,即
g(x)=(x-a)(x-a2)(x-a3)···(x-a2t-1)(x-a2t)
式中,ai是GF(2m)中的一个元素。如果用d(x)表示信息段多项式,则可以按照如下方法构造码字多项式c(x)。首先计算商式h(x)和余式r(x),得
xn-kd(x)/ g(x)= h(x) g(x)+ r(x)
(4)生成的码字即为[4 0 6 4 2 2 0].
1.2
RS码的译码算法是从BCH码的译码算法演变而来的。与编码算法相比,译码算法比较复杂,需要的运算量也比较大。其中,比较有代表性的算法是Berlekamp-Messay算法(简称BM算法)和Euclid算法。在这两种算法的基础上,后来又派生出了一些修正算法或陕速算法。
RS码的译码可以按照下面的步骤来进行:
1.由接收多项式计算伴随式;
2.用BM算法或Euclid算法,由伴随式,求出错误位置多项式;
3.用Chien搜索法求伴随式的根,其倒数为错误位置数;
4.计算错误值;
5.接收多项式减去错误多项式,完成纠错。
如图所示
RS译码器原理框图
译码最关键和最复杂的一个步骤是求出错位置多项式,求取关键方程组的常用算法Berlekamp-Massey算法、Euclid算法。以下是BM的算法流程
(1)由于码元符号取自域GF(23),所以一个符号可以由3比特表示,x4d(x)的二进制比特表示为[100 000 110 000 000 000 000];
(2)g(x)的二进制比特表示为[001 011 001 010 011];
(3)计算xn-kd(x)/ g(x)得到的余式r(x)的二进制比特表示为[100 010 010 000],因此校验位为[4 2 2 0];
取余式r(x)作为校验字,然后令
c(x)=xn-kd(x)+r(x)
即将信息位放置于码字的前半部分,监督位码字放在后半部分,则
c(x)/g(x)= xn-kd(x)/ g(x)+r(x)/g(x)
=h(x)g(x)+r(x)+r(x)= h(x)g(x)
因此,码字多项式c(x),必可以被生成多项式g(x)整除。如果在接收端检测不到余式为0,则可判断接收到的码字有错误。由于这种RS能纠正t个m进制的错误码字,所以,RS码特别适用于突发错误的信道
一个RS码有以下几个参数:
码长:n=2^m-1个符号或者m(2m-1)比特
信息段:k个符号或者mk个比特
监督段:2t=n-k个符号2mt=m(n-k)个比特
最小码距:dmin=n-k+1个符号或者mdmin=m(n-k+1)
例如,对RS(204,188)码来说,源数据被分割为188个符号为一组,经过编码变换后,成为204个符号长度的码字。长度为16个符号的监督为可以纠正码字中出现的最多8个符号错误。
1
RS码(Reed-solomon codes)一种低速率的前向纠错的信道编码,是一类具有强纠错能力的多进制BCH码,在线性分组码中,它的纠错能力和编码效率是最高的。相比于其他线性分组码而言,在同样的效率下,RS的纠错能力是特别强的,特别是在短的中等码长下,其性能接近于理论值,它不但可以纠正随机错误,突发错误及两者的结合,而且可以用来构造其他码型,如级联码。
其编码过程首先在多个点上对这些多项式求冗余,然后将其传输或者存储。对多项式的这种超出必要值的采样使得多项式超定(过限定)。当接收器正确的收到足够的点后,它就可以恢复原来的多项式,即使接收到的多项式上有很多点被噪声干扰失真。
1.1
RS码是一类纠错能力很强的特殊的非二进制BCH码。对于任选正整数S可构造一个相应的码长为n=qS-1的q进制BCH码,而q作为某个素数的幂。当S=1,q>2时所建立的码长n=q-1的q进制BCH码,称它为RS码。当q=2m(m>1),其码元符号取自于GF(2m)的二进制RS码可用来纠正突发差错,它是最常用的RS码。
