2007年天津高考物理试题及标准答案
2007年全国统一高考物理试卷(ⅱ)及解析

第 2 页(共 13 页)
A.
B.
C.
D.
二、实验题
9.(17 分)(1)在做“用单摆测定重力加速度”的实验中,有人提出以下几点建议:
A、适当加长摆线
B、质量相同,体积不同的摆球,应选用体积较大的
C、单摆偏离平衡位置的角度不能太大
D、单摆偏离平衡位置时开始计时,经过一次全振动后停止计时,用此时间间隔作为单摆
【解答】解:在物体下落的过程中,只有重力对物体做功,故机械能守恒
第 6 页(共 13 页)
故有 mgh=
解得 v= 所以在相同的高度,两物体的速度大小相同,即速率相同. 由于 a 的路程小于 b 的路程.故 ta<tb,即 a 比 b 先到达 s. 又到达 s 点时 a 的速度竖直向下,而 b 的速度水平向左. 故两物体的动量不相等. 故选 A. 【点评】两物体运动的路程关系:sb>sa,但在相同的高度速率相同,这是本题的突破 口.所以挖掘出隐含条件是解题的关键. 4.(3 分) 【考点】光的偏振. 【分析】根据光的现象,只要光的振动方向不与偏振片的狭逢垂直,都能有光通过偏振 片. 【解答】解:A、太阳光包含垂直传播方向向各个方向振动的光,当太阳光照射 P 时能在 P 的另一侧观察到偏振光,故 A 正确; B、沿竖直方向振动的光能通过偏振片,故 B 正确; C、沿水平方向振动的光不能通过偏振片,因为它们已经相互垂直.故 C 是错误的; D、沿与竖直方向成 45°角振动的光也能通过偏振片,故 D 正确; 故选:ABD 【点评】D 选项容易漏选,其实题中另一侧能观察到光即可.
采用的测量电路图如图所示,实验步骤如下:a.断开 S1 和 S2,将 R 调到最大;b.合上
S1,调节 R 使 满偏;c.合上 S2,调节 R1 使 半偏,此时可认为的 的内阻 rg=R1.试 问:
2007年---2012年高考物理(新课标)真题解析

2007年普通高等学校招生全国统一考试(新课标)二、选择题:本题包括8小题,每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对得6分,选对但不全得3分,有选错的得0分14、天文学家发现了某恒星有一颗行星在圆形轨道上绕其运动,并测出了行星的轨道半径和运行周期。
由此可推算出A .行星的质量B .行星的半径C .恒星的质量D .恒星的半径 15、下列说法正确的是A .行星的运动和地球上物体的运动遵循不同的规律B .物体在转弯时一定受到力的作用C .月球绕地球运动时受到地球的引力和向心力的作用D .物体沿光滑斜面下滑时受到重力、斜面的支持力和下滑力的作用16、甲乙两辆汽车在平直的公路上沿同一方向作直线运动,t =0时刻同时经过公路旁的同一个路标。
在描述两车运动的v -t 图中(如图),直线a 、b 分别描述了甲乙两车在0-20 s 的运动情况。
关于两车之间的位置关系,下列说法正确的是 A .在0-10 s 内两车逐渐靠近 B .在10-20 s 内两车逐渐远离 C .在5-15 s 内两车的位移相等 D .在t =10 s 时两车在公路上相遇17、一正弦交流电的电压随时间变化的规律如图所示。
由图可知A .该交流电的电压瞬时值的表达式为u =100sin(25t)VB .该交流电的频率为25 HzC.该交流电的电压的有效值为D .若将该交流电压加在阻值R =100 Ω的电阻两端,则电阻消耗的功率时50 W18、两个质量相同的小球用不可伸长的细线连结,置于场强为E 的匀强电场中,小球1和小球2均带正电,电量分别为q 1和q 2(q 1>q 2)。
将细线拉直并使之与电场方向平行,如图所示。
若将两小球同时从静止状态释放,则释放后细线中的张力T 为(不计重力及两小球间的库仑力)A .121()2T q q E =- B .12()T q q E =-C .121()2T q q E =+ D .12()T q q E =+19、在如图所示的电路中,E 为电源电动势,r 为电源内阻,R 1和R 3均为定值电阻,R 2为滑动变阻器。
2007年普通高等学校招生全国统一考试(天津卷)

绝密★启用前2007年普通高等学校招生全国统一考试(天津卷)文科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共300分,考试用时150分钟。
第Ⅰ卷1至8页,第Ⅱ卷9至16页。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上,并在规定位置粘贴考试用条形码。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在试卷上的无效。
3.本卷共35题,每题4分,共140分。
在每题列出的四个选项中,只有一项是最符合题目要求的。
读图1回答1~2题。
图11.甲、乙两图所示大洲的人口特点是A.城市人口若悬河B.生育率较低C.人口平均密度大D.老龄化程度高2.李明同学发现乙、丙、丁三图所示现象有因果联系,地理老师认为有道理。
此因果顺序应该是A.乙→丙→丁B.丙→丁→乙C.丙→乙→丁D.丁→丙→乙读图2和图3,回答3~5题。
3.图2所示季节,一位俄罗斯专家在e地看到日落正西方,之后1小时下列各地发生的现象是A.a——日光直射B.b——夕阳西下C.c——旭日东升D.d——午阳低垂4.在之后的两个月中,下列变化规律符合实际的是A.a地白昼逐渐变长B.a、c两地气温都在下降C.b地牧草日益茂盛D.c、d两地河流水位升高5.俄罗斯专家发现图3中标示的某种地理事物与实际分布不符..。
它是图4显示了2001年至2005年格陵兰岛某冰川末端不断消融后退的“足迹”。
读图4回答6~7题。
6.据图中M、N两点量算,此期间该冰川末端年平均后退的距离约为A.0.4 kmB.0.5kmC.1.2kmD.1.5km7.若全球冰川大规模融化,可能产生的影响有A.极地高压增强B.沿海平原扩大C.陆地淡水减少D.植被类型增多图5是喜马拉雅山区某交通不便谷地中的景观图。
读图回答8~9题。
8.图中地质构造形成并出露地表的主要原因是岩层A.受挤压,经侵蚀B.受挤压,经风化C.受张力,经搬运D.受张力,经沉积9.形成图中乡村聚落最基本的环境条件应该是A.地质灾害少B.土地可以耕牧C.河湖密度大D.旅游资源丰富景假,某地理小组在图6(冀东某地等高线地形图)所示地区野外考察。
2007年高考物理试题全集含答案(2020082790257)

)
16.如图所示,质量为 m 的活塞将一定质量的气体封闭在气缸内,活塞与气缸之间无
摩擦。 a 态是气缸放在冰水混合物中气体达到的平衡状态,
b 态是气缸从容器中移出后,在
室温( 270C)中达到的平衡状态。气体从 a 态变化到 b 态的过程中大气压强保持不变。 若忽
略气体分子之间的势能,下列说法正确的是(
体在 3 秒末的速率,则这四个速率中最大的是(
)
A 、 v1
B 、 v2
C、 v3
D 、 v4
19 .用大量具有一定能力的电子轰击大量处于基态的氢原子,
线。调高电子的能力在此进行观测,发现光谱线的数目比原来增加了
观测到了一定数目的光谱 5 条。用△ n 表示两侧
观测中最高激发态的量子数 n 之差, E 表示调高后电子的能量。 根据氢原子的能级图可以判
撞。在平衡位置附近存在垂直于纸面的磁场。 已知由于磁场的阻尼作用, 金属球将于再次碰
撞前停在最低点处。求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于
450。
25.两屏幕荧光屏互相垂直放置,在两屏内分别去垂直于两屏交线的直线为
x 和 y 轴,
交点 O 为原点,如图所示。在 y>0, 0<x<a 的区域有垂直于纸面向内的匀强磁场,在
断,△ n 和 E 的可能值为(
)
A 、△ n=1, 13.22 eV < E<13.32 eV
B、△ n=2, 13.22 eV < E<13.32 eV
C、△ n=1, 12.75 eV < E<13.06 eV
D、△ n=2, 12.75 eV < E<13.06 Ev
20.a、b、c、d 是匀强电场中的四个点,它们正好是一个矩形的四个顶点。电场线与矩
2007年天津高考物理试题及答案

2007年天津高考物理试题及答案2007年普通高等学校招生全国统一考试(天津卷)物理部分本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分,共300分,考试用时150分钟。
第Ⅰ卷1至5页,第Ⅱ卷6至16页。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上,并在规定位置粘贴考试用条形码。
2.每小题选出答案后,用铅笔把答题卡上对应题目的标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在试卷上的无效。
3.本卷共21题,每题6分,共126分。
在每题列出的四个选项中,只有一项是最符合题目要求的。
以下数据可供解题时参考:相对原子质量:H 1 Li 7 C 12 O 16S 32 Fe 56 Cu 64 Zn 6514.下列说法正确的是A.电路中交变电流的频率为0.25 HzB.通过电阻的电流为2AC.电阻消耗的电功率为2.5 WD.用交流电压表测得电阻两端的电压是5 V12.我国绕月探测工程的预先研究和工程实施已取得重要进展。
设地球、月球的质量分别为m 1、m 2,半径分别为R 1、R 2,人造地球卫星的第一宇宙速度为v ,对应的环绕周期为T ,则环绕月球表面附近圆轨道飞行的探测器的速度和周期分别为 A.v R m R m 2112,T R m R m 312321 B. v R m R m 1221,T R m R m 321312 C.v R m R m 2112,T R m R m 321312 D. v R m R m 1221,T R m R m 31232118.右图为氢原子能级的示意图,现有大量的氢原子处于n =4的激发态,当向低能级跃迁时辐射出若干不同频率的光。
关于这些光下列说法正确的是A.最容易表现出衍射现象的光是由n=4能级跃迁到n=1能级产生的B.频率最小的光是由n=2能级跃迁到n=1能级产生的C.这些氢原子总共可辐射出3种不同频率的光D.用n=2能级跃迁到n=1能级辐射出的光照射逸出功为6.34eV的金属铂能发生光电效应19.如图所示,在x轴上方存在着垂直于纸面向里、磁感应强度为B的匀强磁场,一个不计重力的带电粒子从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成120°角,若粒子穿过y轴正半轴后在磁场中到x轴的最大距离为a,则该粒子的比荷和所带电荷的正负是A.aB v 23,正电荷B. aB v 2,正电荷 C.aB v 23,负电荷 D. aB v2,负电荷 20.A 、B 两装置,均由一支一端封闭、一端开口且带有玻璃泡的管状容器和水银槽组成,除玻璃泡在管上的位置不同外,其他条件都相同。
普通高等学校招生全国统一考试(天津卷)理综试卷

高中物理学习材料金戈铁骑整理制作2007年普通高等学校招生全国统一考试(天津卷)理综试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分,共300分,考试用时150分钟。
第Ⅰ卷1至5页,第Ⅱ卷6至16页。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上,并在规定位置粘贴考试用条形码。
2.每小题选出答案后,用铅笔把答题卡上对应题目的标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在试卷上的无效。
3.本卷共21题,每题6分,共126分。
在每题列出的四个选项中,只有一项是最符合题目要求的。
以下数据可供解题时参考:相对原子质量:H 1 Li 7 C 12 O 16 S 32 Fe 56 Cu 64 Zn 651.下列关于细胞基因复制与表达的叙述,正确的是A.一种密码子可以编码多种氨基酸B.基因的内含子能翻译成多肽C.编码区增加一个碱基对,只会改变肽链上的一个氨基酸D.DNA分子经过复制后,子代DNA分子中(C+T)/(A+G)=12.下列关于动物新陈代谢的叙述,不正确...的是A.在正常情况下,肝脏细胞可以将多余的脂肪合成为脂蛋白B.当血糖含量升高时,肌肉细胞可以将葡萄糖合成为糖元C.糖类分解时可以产生与必需氨基酸相对应的中间产物D.氨基酸脱氧基产生的不含氮部分可以合成为脂肪3.下列叙述正确的是A.当病毒侵入人体后,只有细胞免疫发挥防御作用B.大肠杆菌在葡萄糖和乳糖为碳源的培养基上,只有葡萄糖耗尽才能利用乳糖C.大水分供应充足的大田中,只有通风透光才能提高光能利用率D.当甲状腺激素含量偏高时,只有反馈抑制下丘脑活动才能使激素含量恢复正常4.下图表示玉米种子的形成和萌发过程。
据图分析正确的叙述是A.①与③细胞的基因型可能不同B.①结构由胚芽、胚轴、胚要和胚柄四部分构成C.②结构会出现在所有被子植物的成熟种子中D.④过程的初期需要添加必需矿质元素5.利用细胞工程方法,以SARS病毒核衣壳蛋白为抗原制备出单质克隆抗体。
[实用参考]2007年(理)天津卷
![[实用参考]2007年(理)天津卷](https://img.taocdn.com/s3/m/a67bc20a0722192e4536f69f.png)
20GG 年(理)天津卷第Ⅰ卷一、选择题:本题考查基本知识和基本运算.每小题5分,满分50分. 1.C 2.B 3.A 4.D 5.C6.D7.B8.B9.A10.A一、选择题:在每小题列出的四个选项中,只有一项是符合题目要求的.1.i 是虚数单位,32i 1i=-( )A.1i + B.1i -+ C.1i -D.1i -- 2.设变量x y ,满足约束条件1133x y x y x y ⎧--⎪+⎨⎪-<⎩,,.≥≥则目标函数4z x y =+的最大值为( )A.4 B.11 C.12 D.143.“2π3θ=”是“πtan 2cos 2θθ⎛⎫=+ ⎪⎝⎭”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件D.既不充分也不必要条件4.设双曲线22221(00)x y a b a b-=>>,24y x =的准线重合,则此双曲线的方程为( )A.2211224x y -= B.2214896x y -=C.222133x y -= D.22136x y -= 5.函数2log 2)(0)y x =>的反函数是( ) A.142(2)x x y x +=-> B.142(1)x x y x +=-> C.242(2)x x y x +=->D.242(1)x x y x +=->6.设a b ,为两条直线,αβ,为两个平面,下列四个命题中,正确的命题是( ) A.若a b ,与α所成的角相等,则a b ∥;B.若a b αβ,∥∥,αβ∥,则a b ∥ C.若a b a b αβ⊂⊂,,∥,则αβ∥D.若a b αβ⊥⊥,,αβ⊥,则a b ⊥7.在R 上定义的函数()f x 是偶函数,且()(2)f x f x =-,若()f x 在区间[12],上是减函数,则()f x ( )A.在区间[21]--,上是增函数,在区间[34],上是增函数 B.在区间[21]--,上是增函数,在区间[34],上是减函数C.在区间[21]--,上是减函数,在区间[34],上是增函数D.在区间[21]--,上是减函数,在区间[34],上是减函数8.设等差数列{}n a 的公差d 不为0,19a d =.若k a 是1a 与2k a 的等比中项,则k =( ) A.2B.4C.6D.89.设a b c ,,均为正数,且122log aa =,121log 2bb ⎛⎫= ⎪⎝⎭,21log 2cc ⎛⎫= ⎪⎝⎭.则( )A.a b c << B.c b a << C.c a b << D.b a c << 10.设两个向量22(2cos )λλα=+-,a 和sin 2m m α⎛⎫=+ ⎪⎝⎭,b ,其中m λα,,为实数.若2=a b ,中央电视台m λ的取值范围是( )A.B.[48],C. D.第Ⅱ卷二、填空题:本题考查基本知识和基本运算.每小题4分,满分24分. 11.212.14π13.314.30x y +=15.83-16.390二、填空题:本大题共6小题,每小题4分,共24分,把答案填在题中横线上.11.若621x ax ⎛⎫+ ⎪⎝⎭的二项展开式中2x 的系数为52,则a = (用数字作答).12.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 .13.设等差数列{}n a 的公差d 是2,前n 项的和为n S ,则22lim n n na n S →∞-= . 14.已知两圆2210x y +=和22(1)(3)20x y -+-=相交于A B ,两点,则直线AB 的方程是 .15.如图,在ABC △中,12021BAC AB AC ∠===,,°,AB DCD 是边BC 上一点,2DC BD =,则AD BC =· .16.如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有 种(用数字作答). 三、解答题:本大题共6小题,共76分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)已知函数()2cos (sin cos )1f x x x x x =-+∈R ,.(Ⅰ)求函数()f x 的最小正周期;(Ⅱ)求函数()f x 在区间π3π84⎡⎤⎢⎥⎣⎦,上的最小值和最大值.17.本小题考查三角函数中的诱导公式、特殊角三角函数值、两角差公式、倍角公式、函数sin()y A x ωϕ=+的性质等基础知识,考查基本运算能力.满分12分.(Ⅰ)解:π()2cos (sin cos )1sin 2cos 224f x x x x x x x ⎛⎫=-+=-=- ⎪⎝⎭.因此,函数()f x 的最小正周期为π.(Ⅱ)解法一:因为π()24f x x ⎛⎫=- ⎪⎝⎭在区间π3π88⎡⎤⎢⎥⎣⎦,上为增函数,在区间3π3π84⎡⎤⎢⎥⎣⎦,上为减函数,又π08f ⎛⎫= ⎪⎝⎭,3π8f ⎛⎫= ⎪⎝⎭,3π3πππ14244f ⎛⎫⎛⎫=-==- ⎪ ⎪⎝⎭⎝⎭,故函数()f x 在区间π3π84⎡⎤⎢⎥⎣⎦,1-.解法二:作函数π()24f x x ⎛⎫=- ⎪⎝⎭在长度为一个周期的区间π9π84⎡⎤⎢⎥⎣⎦,上的图象如下:由图象得函数()f x 在区 间π3π84⎡⎤⎢⎥⎣⎦,上的最大值为,最小值为3π14f ⎛⎫=- ⎪⎝⎭.x18.(本小题满分12分)已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.(Ⅰ)求取出的4个球均为黑球的概率;(Ⅱ)求取出的4个球中恰有1个红球的概率;(Ⅲ)设ξ为取出的4个球中红球的个数,求ξ的分布列和数学期望. 18.本小题主要考查互斥事件、相互独立事件、离散型随机变量的分布列和数学期望等基础知识,考查运用概率知识解决实际问题的能力.满分12分. (Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件A ,“从乙盒内取出的2个球均为黑球”为事件B .由于事件A B ,相互独立,且23241()2C P A C ==,24262()5C P B C ==. 故取出的4个球均为黑球的概率为121()()()255P AB P A P B ==⨯=··. (Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件C ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件D .由于事件C D ,互斥,且21132422464()15C C C P C C C ==··,123422461()5C C PD C C ==·. 故取出的4个球中恰有1个红球的概率为417()()()15515P C D P C P D +=+=+=.(Ⅲ)解:ξ可能的取值为0123,,,.由(Ⅰ),(Ⅱ)得1(0)5P ξ==,7(1)15P ξ==,13224611(3)30C P C C ξ===·.从而3(2)1(0)(1)(3)10P P P P ξξξξ==-=-=-==. ξ的分布列为ξ的数学期望17317012351510306E ξ=⨯+⨯+⨯+⨯=.19.(本小题满分12分)如图,在四棱锥P ABCD-中,PA ⊥底面A B C ,60AB AD AC CD ABC ⊥⊥∠=,,°,PA AB BC ==,E 是PC 的中点.(Ⅰ)证明CD AE ⊥; (Ⅱ)证明PD ⊥平面ABE ; (Ⅲ)求二面角A PD C --的大小.19.本小题考查直线与直线垂直、直线与平面垂直、二面角等基础知识,考查空间想象能力、运算能力和推理论证能力.满分12分. (Ⅰ)证明:在四棱锥P ABCD -中,因PA ⊥底面ABCD ,CD ⊂平面ABCD ,故PA CD ⊥.AC CD PAAC A ⊥=,∵,CD ⊥∴平面PAC .而AE ⊂平面PAC ,CD AE ⊥∴.(Ⅱ)证明:由PA AB BC ==,60ABC ∠=°,可得AC PA =.E ∵是PC 的中点,AE PC ⊥∴.由(Ⅰ)知,AE CD ⊥,且PC CD C =,所以AE ⊥平面PCD . 而PD ⊂平面PCD ,AE PD ⊥∴.PA ⊥∵底面ABCD PD ,在底面ABCD 内的射影是AD ,AB AD ⊥,AB PD ⊥∴.又AB AE A =∵,综上得PD ⊥平面ABE .(Ⅲ)解法一:过点A 作AM PD ⊥,垂足为M ,连结EM .则(Ⅱ)知,AE ⊥平面PCD ,AM 在平面PCD 内的射影是EM ,则EM PD ⊥.因此AME ∠是二面角A PD C --的平面角. 由已知,得30CAD ∠=°.设AC a =,可得332PA a AD PD AE a ====,,,. 在ADP Rt △中,AM PD ⊥∵,AM PD PAAD =∴··, ABCDPEACDPEM则7aPA ADAM aPD===·.在AEMRt△中,sin4AEAMEAM==所以二面角A-arcsin4.解法二:由题设PA⊥底面ABCD,PA⊂平面PAD,则平面PAD⊥平面ACD,交线为AD.过点C作CF AD⊥,垂足为F,故CF⊥平面PAD.过点F作FM PD⊥,垂足为M,连结CM,故CM PD⊥.因此CMP∠是二面角A PD C--的平面角.由已知,可得30CAD∠=°,设AC a=,可得13326PA a AD PD a CF a FD a=====,,,,.FMD PAD∵△∽△,FD=.于是,14FD PAFM aPD===·.在CMFRt△中,1tanaCMFFM==所以二面角A PD C--的大小是.20.(本小题满分12分)已知函数2221()()1ax af x xx-+=∈+R,其中a∈R.(Ⅰ)当1a=时,求曲线()y f x=在点(2(2))f,处的切线方程;(Ⅱ)当0a≠时,求函数()f x的单调区间与极值.20.本小题考查导数的几何意义,两个函数的和、差、积、商的导数,利用导数研究函数的单调性和极值等基础知识,考查运算能力及分类讨论的思想方法.满分12分.(Ⅰ)解:当1a=时,22()1xf xx=+,4(2)5f=,又2222222(1)2222()(1)(1)x x x xf xx x+--'==++·,6(2)25f'=-.所以,曲线()y f x=在点(2(2))f,处的切线方程为46(2)525y x-=--,即62320x y+-=.(Ⅱ)解:2222222(1)2(21)2()(1)()(1)(1)a x x ax a x a axf xx x+--+--+'==++.由于0a≠,以下分两种情况讨论.ABCDPEFM(1)当0a >时,令()0f x '=,得到11x a=-,2x a =.当x 变化时,()()f x f x ',的变化情况如下表:所以()f x 在区间1a ⎛⎫-- ⎪⎝⎭,∞,()a +,∞内为减函数,在区间1a a ⎛⎫- ⎪⎝⎭,内为增函数. 函数()f x 在11x a =-处取得极小值1f a ⎛⎫- ⎪⎝⎭,且21f a a ⎛⎫-=- ⎪⎝⎭,函数()f x 在21x a=处取得极大值()f a ,且()1f a =.(2)当0a <时,令()0f x '=,得到121x a x a==-,,当x 变化时,()()f x f x ',的所以()f x 在区间()a -,∞,1a ⎛⎫- ⎪⎝⎭,+∞内为增函数,在区间1a a ⎛⎫- ⎪⎝⎭,内为减函数.函数()f x 在1x a =处取得极大值()f a ,且()1f a =. 函数()f x 在21x a=-处取得极小值1f a ⎛⎫- ⎪⎝⎭,且21f a a ⎛⎫-=- ⎪⎝⎭. 21.(本小题满分14分)在数列{}n a 中,1112(2)2()n n n n a a a n λλλ+*+==++-∈N ,,其中0λ>.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)求数列{}n a 的前n 项和n S ; (Ⅲ)证明存在k *∈N ,使得11n k n ka aa a ++≤对任意n *∈N 均成立. 21.本小题以数列的递推关系式为载体,主要考查等比数列的前n 项和公式、数列求和、不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.满分14分. (Ⅰ)解法一:22222(2)22a λλλλ=++-=+,2232333(2)(2)222a λλλλλ=+++-=+, 3343444(22)(2)232a λλλλλ=+++-=+.由此可猜想出数列{}n a 的通项公式为(1)2n n n a n λ=-+.以下用数学归纳法证明. (1)当1n =时,12a =,等式成立.(2)假设当n k =时等式成立,即(1)2k k k a k λ=-+,那么111(2)2k k k a a λλλ++=++-11(1)222k k k k k k λλλλλ++=-+++-11[(1)1]2k k k λ++=+-+.这就是说,当1n k =+时等式也成立.根据(1)和(2)可知,等式(1)2n n n a n λ=-+对任何n *∈N 都成立.解法二:由11(2)2()n n n n a a n λλλ+*+=++-∈N ,0λ>,可得111221n nn nn n a a λλλλ+++⎛⎫⎛⎫-=-+ ⎪ ⎪⎝⎭⎝⎭,所以2n n n a λλ⎧⎫⎪⎪⎛⎫-⎨⎬ ⎪⎝⎭⎪⎪⎩⎭为等差数列,其公差为1,首项为0,故21n n n a n λλ⎛⎫-=- ⎪⎝⎭,所以数列{}n a 的通项公式为(1)2n n n a n λ=-+.(Ⅱ)解:设234123(2)(1)n n n T n n λλλλλ-=++++-+-, ①345123(2)(1)n n n T n n λλλλλλ+=++++-+- ②当1λ≠时,①式减去②式,得212311(1)(1)(1)1n nn n n T n n λλλλλλλλλ+++--=+++--=---, 21121222(1)(1)(1)1(1)n n n n n n n n T λλλλλλλλλ++++----+=-=---. 这时数列{}n a 的前n 项和21212(1)22(1)n n n n n n S λλλλ+++--+=+--. 当1λ=时,(1)2n n n T -=.这时数列{}n a 的前n 项和1(1)222n n n n S +-=+-. (Ⅲ)证明:通过分析,推测数列1n n a a +⎧⎫⎨⎬⎩⎭的第一项21aa 最大,下面证明:21214,22n n a a n a a λ++<=≥. ③ 由0λ>知0n a >,要使③式成立,只要212(4)(2)n n a a n λ+<+≥, 因为222(4)(4)(1)(1)2n n n a n λλλλ+=+-++124(1)424(1)2n n n n n n λλλ++>-+⨯=-+·1212222n n n n a n λ++++=,≥≥.所以③式成立.因此,存在1k =,使得1121n k n k a a aa a a ++=≤对任意n *∈N 均成立. 22.(本小题满分14分)设椭圆22221(0)x ya b a b+=>>的左、右焦点分别为12F F A ,,是椭圆上的一点,212AF F F ⊥,原点O 到直线1AF 的距离为113OF .(Ⅰ)证明a =;(Ⅱ)设12Q Q ,为椭圆上的两个动点,12OQ OQ ⊥,过原点O 作直线12Q Q 的垂线OD ,垂足为D ,求点D 的轨迹方程.22.本小题主要考查椭圆的标准方程和几何性质、直线方程、求曲线的方程等基础知识,考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力.满分14分.(Ⅰ)证法一:由题设212AF F F ⊥及1(0)F c -,,2(0)F c ,,不妨设点()A c y ,,其中0y >.由于点A 在椭圆上,有22221c y a b +=,即222221a b y a b -+=. 解得2by a =,从而得到2b Ac a ⎛⎫ ⎪⎝⎭,.直线1AF 的方程为2()2by x c ac=+,整理得2220b x acy b c -+=. 由题设,原点O 到直线1AF 的距离为113OF2,将222c a b =-代入上式并化简得222a b =,即a 证法二:同证法一,得到点A 的坐标为2b c a ⎛⎫⎪⎝⎭,.过点O 作1OB AF ⊥,垂足为B ,易知1F BO △∽12F F A △,故211BO F AOF F A=. 由椭圆定义得122AF AF a +=,又113BO OF =,所以2212132F AF A F A a F A ==-, 解得22a F A =,而22b F A a =,得22b a a =,即a=(Ⅱ)解法一:设点D 的坐标为00()x y ,.当00y ≠时,由12OD QQ ⊥知,直线12Q Q 的斜率为0程为0000()x y x x y y =--+,或y kx m =+,其中00x k y =-,200x m y y =+.点111222()()Q x y Q x y ,,,的坐标满足方程组22222y kx m x y b =+⎧⎨+=⎩,. 将①式代入②式,得2222()2x kx m b ++=,整理得2222(12)4220k x kmx m b +++-=,于是122412km x x k +=-+,21222212m bx x k-=+. 由①式得2212121212()()()y y kx m kx m k x x km x x k =++=+++2222222222242121212m b km m b k k km m k k k---=++=+++··. 由12OQ OQ ⊥知12120x x y y +=.将③式和④式代入得22222322012m b b k k --=+, 22232(1)m b k =+.将200000x x k m y y y =-=+,代入上式,整理得2220023x y b +=. 当00y =时,直线12Q Q 的方程为0x x =,111222()()Q x y Q x y ,,,的坐标满足方程组022222x x x y b =⎧⎨+=⎩,.所以120x x x ==,12y =,. 由12OQ OQ ⊥知12120x x y y +=,即200202x -=,解得22023x b =. 这时,点D 的坐标仍满足2220023x y b +=.综上,点D 的轨迹方程为 22223x y b +=.解法二:设点D 的坐标为00()x y ,,直线OD 的方程为000y x x y -=,由12OD QQ ⊥,垂足为D ,可知直线12Q Q 的方程为220000x x y y x y +=+.记2200m x y =+(显然0m ≠),点111222()()Q x y Q x y ,,,的坐标满足方程组 0022222x x y y m x y b +=⎧⎪⎨+=⎪⎩, ①. ②由①式得00y y m x x =-. ③ 由②式得22222200022y x y y y b +=. ④将③式代入④式得222220002()2y x m x x y b +-=.整理得2222220000(2)4220x y x mx x m b y +-+-=,于是222122200222m b y x x x y -=+. ⑤ 由①式得00x x m y y =-. ⑥由②式得22222200022x x x y x b +=. ⑦将⑥式代入⑦式得22222000()22m y y x y x b -+=,。
2007年普通高等学校招生全国统一考试理科综合试卷及答案-天津卷

2007年普通高等学校招生全国统一考试(天津卷)理科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分,共300分,考试用时150分钟。
第Ⅰ卷1至5页,第Ⅱ卷6至16页。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上,并在规定位置粘贴考试用条形码。
2.每小题选出答案后,用铅笔把答题卡上对应题目的标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在试卷上的无效。
3.本卷共21题,每题6分,共126分。
在每题列出的四个选项中,只有一项是最符合题目要求的。
以下数据可供解题时参考:相对原子质量:H 1 Li 7 C 12 O 16 S 32 Fe 56 Cu 64 Zn 651.下列关于细胞基因复制与表达的叙述,正确的是A.一种密码子可以编码多种氨基酸B.基因的内含子能翻译成多肽C.编码区增加一个碱基对,只会改变肽链上的一个氨基酸D.DNA分子经过复制后,子代DNA分子中(C+T)/(A+G)=12.下列关于动物新陈代谢的叙述,不正确的是A.在正常情况下,肝脏细胞可以将多余的脂肪合成为脂蛋白B.当血糖含量升高时,肌肉细胞可以将葡萄糖合成为糖元C.糖类分解时可以产生与必需氨基酸相对应的中间产物D.氨基酸脱氧基产生的不含氮部分可以合成为脂肪3.下列叙述正确的是A.当病毒侵入人体后,只有细胞免疫发挥防御作用B.大肠杆菌在葡萄糖和乳糖为碳源的培养基上,只有葡萄糖耗尽才能利用乳糖C.大水分供应充足的大田中,只有通风透光才能提高光能利用率D.当甲状腺激素含量偏高时,只有反馈抑制下丘脑活动才能使激素含量恢复正常4.下图表示玉米种子的形成和萌发过程。
据图分析正确的叙述是A.①与③细胞的基因型可能不同B.①结构由胚芽、胚轴、胚要和胚柄四部分构成C.②结构会出现在所有被子植物的成熟种子中D.④过程的初期需要添加必需矿质元素5.利用细胞工程方法,以SARS病毒核衣壳蛋白为抗原制备出单质克隆抗体。
2007年高考理科综合试题及参考答案(天津卷)

2007年普通高等学校招生全国统一考试(天津卷)理科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分,共300分,考试用时150分钟。
第Ⅰ卷1至5页,第Ⅱ卷6至16页。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上,并在规定位置粘贴考试用条形码。
2.每小题选出答案后,用铅笔把答题卡上对应题目的标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在试卷上的无效。
3.本卷共21题,每题6分,共126分。
在每题列出的四个选项中,只有一项是最符合题目要求的。
以下数据可供解题时参考:相对原子质量:H 1 Li 7 C 12 O 16 S 32 Fe 56 Cu 64 Zn 651.下列关于细胞基因复制与表达的叙述,正确的是A.一种密码子可以编码多种氨基酸B.基因的内含子能翻译成多肽C.编码区增加一个碱基对,只会改变肽链上的一个氨基酸D.DNA分子经过复制后,子代DNA分子中(C+T)/(A+G)=12.下列关于动物新陈代谢的叙述,不正确的是A.在正常情况下,肝脏细胞可以将多余的脂肪合成为脂蛋白B.当血糖含量升高时,肌肉细胞可以将葡萄糖合成为糖元C.糖类分解时可以产生与必需氨基酸相对应的中间产物D.氨基酸脱氧基产生的不含氮部分可以合成为脂肪3.下列叙述正确的是A.当病毒侵入人体后,只有细胞免疫发挥防御作用B.大肠杆菌在葡萄糖和乳糖为碳源的培养基上,只有葡萄糖耗尽才能利用乳糖C.大水分供应充足的大田中,只有通风透光才能提高光能利用率D.当甲状腺激素含量偏高时,只有反馈抑制下丘脑活动才能使激素含量恢复正常4.下图表示玉米种子的形成和萌发过程。
据图分析正确的叙述是A.①与③细胞的基因型可能不同B.①结构由胚芽、胚轴、胚要和胚柄四部分构成C.②结构会出现在所有被子植物的成熟种子中D.④过程的初期需要添加必需矿质元素5.利用细胞工程方法,以SARS病毒核衣壳蛋白为抗原制备出单质克隆抗体。
2007年普通高等学校招生全国统一考试数学卷(天津.理)含答案

2007年普通高等学校招生全国统一考试(天津卷)数学理第Ⅰ卷一、选择题:在每小题列出的四个选项中,只有一项是符合题目要求的.1.i 是虚数单位,32i 1i=-( ) A.1i +B. 1i -+C.1i -D.1i --2.设变量x y ,满足约束条件1133x y x y x y ⎧--⎪+⎨⎪-<⎩,,.≥≥则目标函数4z x y =+的最大值为( ) A.4B.11C.12D.143.“2π3θ=”是“πtan 2cos 2θθ⎛⎫=+ ⎪⎝⎭”的( ) A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.设双曲线22221(00)x y a b a b-=>>,,且它的一条准线与抛物线24y x =的准线重合,则此双曲线的方程为( )A.2211224x y -=B.2214896x y -= C.222133x y -=D.22136x y -= 5.函数2log 2)(0)y x =>的反函数是( ) A.142(2)xx y x +=-> B.142(1)x x y x +=-> C.242(2)x x y x +=->D.242(1)xx y x +=->6.设a b ,为两条直线,αβ,为两个平面,下列四个命题中,正确的命题是( ) A.若a b ,与α所成的角相等,则a b ∥ B.若a b αβ,∥∥,αβ∥,则a b ∥ C.若a b a b αβ⊂⊂,,∥,则αβ∥D.若a b αβ⊥⊥,,αβ⊥,则a b ⊥7.在R 上定义的函数()f x 是偶函数,且()(2)f x f x =-,若()f x 在区间[12],上是减函数,则()f x ( )A.在区间[21]--,上是增函数,在区间[34],上是增函数 B.在区间[21]--,上是增函数,在区间[34],上是减函数 C.在区间[21]--,上是减函数,在区间[34],上是增函数 D.在区间[21]--,上是减函数,在区间[34],上是减函数8.设等差数列{}n a 的公差d 不为0,19a d =.若k a 是1a 与2k a 的等比中项,则k =( ) A.2B.4C.6D.89.设a b c ,,均为正数,且122log a a =,121log 2bb ⎛⎫= ⎪⎝⎭,21log 2cc ⎛⎫= ⎪⎝⎭.则( )A.a b c <<B.c b a <<C.c a b <<D.b a c <<10.设两个向量22(2cos )λλα=+-,a 和sin 2m m α⎛⎫=+ ⎪⎝⎭,b ,其中m λα,,为实数.若2=a b ,中央电视台mλ的取值范围是( ) A.B.[48],C.D.2007年普通高等学校招生全国统一考试(天津卷)数学(理工类)第Ⅱ卷注意事项:1.答案前将密封线内的项目填写清楚.2.用钢笔或圆珠笔直接答在试卷上. 3.本卷共12小题,共100分.二、填空题:本大题共6小题,每小题4分,共24分,把答案填在题中横线上.11.若621x ax ⎛⎫+ ⎪⎝⎭的二项展开式中2x 的系数为52,则a = (用数字作答).12.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 .13.设等差数列{}n a 的公差d 是2,前n 项的和为n S ,则22lim n n na n S →∞-= .14.已知两圆2210x y +=和22(1)(3)20x y -+-=相交于A B ,两点,则直线AB 的方程是 . D 是边BC15.如图,在ABC △中,12021BAC AB AC ∠===,,°,上一点,2DC BD =,则ADBC =· . 16.如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有 种(用数字作答).三、解答题:本大题共6小题,共76分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分) 已知函数()2cos (sin cos )1f x x x x x =-+∈R ,. (Ⅰ)求函数()f x 的最小正周期;(Ⅱ)求函数()f x 在区间π3π84⎡⎤⎢⎥⎣⎦,上的最小值和最大值.18.(本小题满分12分)已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.(Ⅰ)求取出的4个球均为黑球的概率;(Ⅱ)求取出的4个球中恰有1个红球的概率;(Ⅲ)设ξ为取出的4个球中红球的个数,求ξ的分布列和数学期望.19.(本小题满分12分)如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,60AB ADAC CD ABC ⊥⊥∠=,,°,PA AB BC ==,E 是PC 的中点. (Ⅰ)证明CD AE ⊥;(Ⅱ)证明PD ⊥平面ABE ; (Ⅲ)求二面角A PD C --的大小.ABDCABCDPE20.(本小题满分12分)已知函数2221()()1ax a f x x x -+=∈+R ,其中a ∈R . (Ⅰ)当1a =时,求曲线()y f x =在点(2(2))f ,处的切线方程; (Ⅱ)当0a ≠时,求函数()f x 的单调区间与极值. 21.(本小题满分14分)在数列{}n a 中,1112(2)2()n n n n a a a n λλλ+*+==++-∈N ,,其中0λ>.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列{}n a 的前n 项和n S ; (Ⅲ)证明存在k *∈N ,使得11n k n ka aa a ++≤对任意n *∈N 均成立. 22.(本小题满分14分)设椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12F F A ,,是椭圆上的一点,212AF F F ⊥,原点O 到直线1AF 的距离为113OF .(Ⅰ)证明a =;(Ⅱ)设12Q Q ,为椭圆上的两个动点,12OQ OQ ⊥,过原点O 作直线12Q Q 的垂线OD ,垂足为D ,求点D 的轨迹方程.2007年普通高等学校招生全国统一考试(天津卷)数学(理工类)参考解答一、选择题:本题考查基本知识和基本运算.每小题5分,满分50分. 1.C 2.B 3.A 4.D 5.C 6.D 7.B 8.B 9.A 10.A二、填空题:本题考查基本知识和基本运算.每小题4分,满分24分. 11.212.14π 13.314.30x y +=15.83-16.390三、解答题17.本小题考查三角函数中的诱导公式、特殊角三角函数值、两角差公式、倍角公式、函数sin()y A x ωϕ=+的性质等基础知识,考查基本运算能力.满分12分.(Ⅰ)解:π()2cos (sin cos )1sin 2cos 224f x x x x x x x ⎛⎫=-+=-=- ⎪⎝⎭.因此,函数()f x 的最小正周期为π.(Ⅱ)解法一:因为π()24f x x ⎛⎫=- ⎪⎝⎭在区间π3π88⎡⎤⎢⎥⎣⎦,上为增函数,在区间3π3π84⎡⎤⎢⎥⎣⎦,上为减函数,又π08f ⎛⎫=⎪⎝⎭,3π8f ⎛⎫= ⎪⎝⎭3π3πππ14244f ⎛⎫⎛⎫=-==- ⎪ ⎪⎝⎭⎝⎭,故函数()f x 在区间π3π84⎡⎤⎢⎥⎣⎦,,最小值为1-.解法二:作函数π()24f x x ⎛⎫=- ⎪⎝⎭在长度为一个周期的区间π9π84⎡⎤⎢⎥⎣⎦,上的图象如下:间π3π84⎡⎤⎢⎥⎣⎦,上的最大值为由图象得函数()f x在区,最小值为3π14f ⎛⎫=- ⎪⎝⎭.18.本小题主要考查互斥事件、相互独立事件、离散型随机变量的分布列和数学期望等基础知识,考查运用概率知识解决实际问题的能力.满分12分.(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件A ,“从乙盒内取出的2个球均为黑球”为事件B .由于事件AB ,相互独立,且23241()2C P A C ==,24262()5C P B C ==. 故取出的4个球均为黑球的概率为121()()()255P A B P A P B ==⨯=··. (Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件C ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件D .由于事件C D ,互斥,且21132422464()15C C C P C C C ==··,123422461()5C C PD C C ==·. 故取出的4个球中恰有1个红球的概率为417()()()15515P C D P C P D +=+=+=. (Ⅲ)解:ξ可能的取值为0123,,,.由(Ⅰ),(Ⅱ)得1(0)5P ξ==,7(1)15P ξ==,13224611(3)30C P C C ξ===·.从而3(2)1(0)(1)(3)10P P P P ξξξξ==-=-=-==.ξ的分布列为xξ的数学期望1012351510306E ξ=⨯+⨯+⨯+⨯=.19.本小题考查直线与直线垂直、直线与平面垂直、二面角等基础知识,考查空间想象能力、运算能力和推理论证能力.满分12分.(Ⅰ)证明:在四棱锥P ABCD -中,因PA ⊥底面ABCD ,CD ⊂平面ABCD ,故PA CD ⊥. AC CD PA AC A ⊥=,∵,CD ⊥∴平面PAC .而AE ⊂平面PAC ,CD AE ⊥∴.(Ⅱ)证明:由PA AB BC ==,60ABC ∠=°,可得AC PA =. E ∵是PC 的中点,AE PC ⊥∴.由(Ⅰ)知,AE CD ⊥,且PC CD C =,所以AE ⊥平面PCD .而PD ⊂平面PCD ,AE PD ⊥∴.PA ⊥∵底面ABCD PD ,在底面ABCD 内的射影是AD ,AB AD ⊥,AB PD ⊥∴. 又AB AE A =∵,综上得PD ⊥平面ABE .(Ⅲ)解法一:过点A 作AM PD ⊥,垂足为M ,连结EM .则(Ⅱ)知,AE ⊥平面PCD ,AM 在平面PCD 内的射影是EM ,则EM PD ⊥. 因此AME ∠是二面角A PD C --的平面角. 由已知,得30CAD ∠=°.设AC a =, 可得332PA a AD a PD a AE a ====,,,. 在ADP Rt △中,AM PD ⊥∵,AM PD PA AD =∴··,则7a PA AD AM a PD===·. 在AEM Rt △中,sin AE AME AM == 所以二面角A PD C --的大小是arcsin4. 解法二:由题设PA ⊥底面ABCD ,PA ⊂平面PAD ,则平面PAD ⊥平面ACD ,交线为AD .过点C 作CF AD ⊥,垂足为F ,故CF ⊥平面PAD .过点F 作FM PD ⊥,垂足为M ,连结CM ,故CM PD ⊥.因此CMP ∠是二面角A PD C --的平面角. 由已知,可得30CAD ∠=°,设AC a =, 可得12PA a AD PD CF a FD =====,,,,. FMD PAD ∵△∽△,FM FDPA PD=∴. PABCDPEM于是,14aFD PAFM aPD===··.在CMFRt△中,1tan14aCFCMFFM===所以二面角A PD C--的大小是arctan.20.本小题考查导数的几何意义,两个函数的和、差、积、商的导数,利用导数研究函数的单调性和极值等基础知识,考查运算能力及分类讨论的思想方法.满分12分.(Ⅰ)解:当1a=时,22()1xf xx=+,4(2)5f=,又2222222(1)2222()(1)(1)x x x xf xx x+--'==++·,6(2)25f'=-.所以,曲线()y f x=在点(2(2))f,处的切线方程为46(2)525y x-=--,即62320x y+-=.(Ⅱ)解:2222222(1)2(21)2()(1)()(1)(1)a x x ax a x a axf xx x+--+--+'==++.由于0a≠,以下分两种情况讨论.(1)当0a>时,令()0f x'=,得到11x=-,2x a=.当x变化时,()()f x f x',的变化情况如下表:所以()f x在区间1a⎛⎫--⎪⎝⎭,∞,()a+,∞内为减函数,在区间1aa⎛⎫-⎪⎝⎭,内为增函数.函数()f x在11xa=-处取得极小值1fa⎛⎫-⎪⎝⎭,且21f aa⎛⎫-=-⎪⎝⎭,函数()f x在21xa=处取得极大值()f a,且()1f a=.(2)当0a<时,令()0f x'=,得到121x a xa==-,,当x变化时,()()f x f x',的变化情况如下表:所以()f x 在区间()a -,∞,1a ⎛⎫- ⎪⎝⎭,+∞内为增函数,在区间1a a ⎛⎫- ⎪⎝⎭,内为减函数. 函数()f x 在1x a =处取得极大值()f a ,且()1f a =. 函数()f x 在21x a=-处取得极小值1f a ⎛⎫- ⎪⎝⎭,且21f a a ⎛⎫-=- ⎪⎝⎭. 21.本小题以数列的递推关系式为载体,主要考查等比数列的前n 项和公式、数列求和、不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.满分14分.(Ⅰ)解法一:22222(2)22a λλλλ=++-=+,2232333(2)(2)222a λλλλλ=+++-=+, 3343444(22)(2)232a λλλλλ=+++-=+.由此可猜想出数列{}n a 的通项公式为(1)2n nn a n λ=-+.以下用数学归纳法证明.(1)当1n =时,12a =,等式成立.(2)假设当n k =时等式成立,即(1)2k kk a k λ=-+, 那么111(2)2k kk a a λλλ++=++-11(1)222k k k k k k λλλλλ++=-+++-11[(1)1]2k k k λ++=+-+.这就是说,当1n k =+时等式也成立.根据(1)和(2)可知,等式(1)2n n n a n λ=-+对任何n *∈N 都成立.解法二:由11(2)2()n n n n a a n λλλ+*+=++-∈N ,0λ>,可得111221n nn nn n a a λλλλ+++⎛⎫⎛⎫-=-+ ⎪⎪⎝⎭⎝⎭,所以2nn n a λλ⎧⎫⎪⎪⎛⎫-⎨⎬ ⎪⎝⎭⎪⎪⎩⎭为等差数列,其公差为1,首项为0,故21n n n a n λλ⎛⎫-=- ⎪⎝⎭,所以数列{}n a 的通项公式为(1)2n nn a n λ=-+. (Ⅱ)解:设234123(2)(1)n n n T n n λλλλλ-=++++-+-, ①345123(2)(1)n n n T n n λλλλλλ+=++++-+- ②当1λ≠时,①式减去②式, 得212311(1)(1)(1)1n n n n n T n n λλλλλλλλλ+++--=+++--=---,21121222(1)(1)(1)1(1)n n n n n n n n T λλλλλλλλλ++++----+=-=---.这时数列{}n a 的前n 项和21212(1)22(1)n n n n n n S λλλλ+++--+=+--. 当1λ=时,(1)2n n n T -=.这时数列{}n a 的前n 项和1(1)222n n n n S +-=+-. (Ⅲ)证明:通过分析,推测数列1n n a a +⎧⎫⎨⎬⎩⎭的第一项21a a 最大,下面证明:21214,22n n a a n a a λ++<=≥. ③ 由0λ>知0n a >,要使③式成立,只要212(4)(2)n n a a n λ+<+≥, 因为222(4)(4)(1)(1)2n nn a n λλλλ+=+-++124(1)424(1)2n n n n n n λλλ++>-+⨯=-+·1212222n n n n a n λ++++=,≥≥.所以③式成立. 因此,存在1k =,使得1121n k n k a a aa a a ++=≤对任意n *∈N 均成立. 22.本小题主要考查椭圆的标准方程和几何性质、直线方程、求曲线的方程等基础知识,考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力.满分14分.(Ⅰ)证法一:由题设212AF F F ⊥及1(0)F c -,,2(0)F c ,,不妨设点()A c y ,,其中0y >.由于点A 在椭圆上,有22221c y a b +=,即222221a b y a b-+=. 解得2b y a =,从而得到2b Ac a ⎛⎫ ⎪⎝⎭,.直线1AF 的方程为2()2b y x c ac=+,整理得2220b x acy b c -+=. 由题设,原点O 到直线1AF 的距离为113OF,即23c =,将222c a b =-代入上式并化简得222a b =,即a =.证法二:同证法一,得到点A 的坐标为2b c a ⎛⎫⎪⎝⎭,.过点O 作1OB AF ⊥,垂足为B ,易知1F BO △∽12F F A △,故211BO F AOF F A=. 由椭圆定义得122AF AF a +=,又113BO OF =, 所以2212132F AF A F A a F A==-, 解得22aF A =,而22b F A a =,得22b a a =,即a =.(Ⅱ)解法一:设点D 的坐标为00()x y ,.当00y ≠时,由12OD Q Q ⊥知,直线12Q Q 的斜率为0x y -,所以直线12Q Q 的方程为0000()x y x x y y =--+,或y kx m =+,其中00x k y =-,200x m y y =+.点111222()()Q x y Q x y ,,,的坐标满足方程组22222y kx m x y b =+⎧⎨+=⎩,.将①式代入②式,得2222()2x kx m b ++=, 整理得2222(12)4220k x kmx m b +++-=,于是122412kmx x k+=-+,21222212m b x x k -=+. 由①式得2212121212()()()y y kx m kx m k x x km x x k =++=+++2222222222242121212m b km m b k k km m k k k---=++=+++··. 由12OQ OQ ⊥知12120x x y y +=.将③式和④式代入得22222322012m b b k k --=+, 22232(1)m b k =+.将200000x x k m y y y =-=+,代入上式,整理得2220023x y b +=.当00y =时,直线12Q Q 的方程为0x x =,111222()()Q x y Q x y ,,,的坐标满足方程组022222x x x y b =⎧⎨+=⎩,.所以120x x x ==,12y =,. 由12OQ OQ ⊥知12120x x y y +=,即2220202b x x --=, 解得22023x b =. 这时,点D 的坐标仍满足2220023x y b +=. 综上,点D 的轨迹方程为 22223x y b +=.解法二:设点D 的坐标为00()x y ,,直线OD 的方程为000y x x y -=,由12OD Q Q ⊥,垂足为D ,可知直线12Q Q 的方程为220000x x y y x y +=+.记2200m x y =+(显然0m ≠),点111222()()Q x y Q x y ,,,的坐标满足方程组0022222x x y y m x y b +=⎧⎪⎨+=⎪⎩, ①. ② 由①式得00y y m x x =-. ③由②式得22222200022y x y y y b +=. ④ 将③式代入④式得222220002()2y x m x x y b +-=. 整理得2222220000(2)4220x y x mx x m b y +-+-=,于是222122200222m b y x x x y -=+. ⑤ 由①式得00x x m y y =-. ⑥由②式得22222200022x x x y x b +=. ⑦ 将⑥式代入⑦式得22222000()22m y y x y x b -+=, 整理得2222220000(2)220x y y my y m b x +-+-=,于是22212220022m b x y y x y -=+. ⑧ 由12OQ OQ ⊥知12120x x y y +=.将⑤式和⑧式代入得2222220022220000222022m b y m b x x y x y --+=++, 22220032()0m b x y -+=.将2200m x y =+代入上式,得2220023x y b +=. 所以,点D 的轨迹方程为22223x y b +=.。
2007年全国统一高考物理试卷(全国卷Ⅰ)及解析.docx
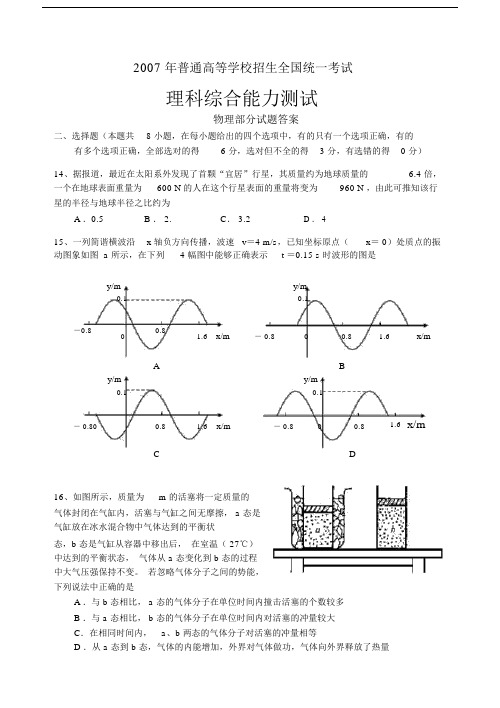
2007 年普通高等学校招生全国统一考试理科综合能力测试物理部分试题答案二、选择题(本题共8 小题,在每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得 6 分,选对但不全的得 3 分,有选错的得0 分)14、据报道,最近在太阳系外发现了首颗“宜居”行星,其质量约为地球质量的 6.4 倍,一个在地球表面重量为600 N 的人在这个行星表面的重量将变为960 N ,由此可推知该行星的半径与地球半径之比约为A .0.5B . 2.C. 3.2 D . 415、一列简谐横波沿x 轴负方向传播,波速 v=4 m/s,已知坐标原点(x= 0)处质点的振动图象如图 a 所示,在下列 4 幅图中能够正确表示t =0.15 s 时波形的图是y/m y/m0.10.1-0.800.81.6x/m- 0.800.8 1.6x/my/m A By/m0.10.1- 0.800.8 1.6x/m- 0.800.8 1.6 x/mC D16、如图所示,质量为m 的活塞将一定质量的气体封闭在气缸内,活塞与气缸之间无摩擦, a 态是气缸放在冰水混合物中气体达到的平衡状态,b 态是气缸从容器中移出后,在室温( 27℃)中达到的平衡状态,气体从 a 态变化到 b 态的过程中大气压强保持不变。
若忽略气体分子之间的势能,下列说法中正确的是A .与 b 态相比, a 态的气体分子在单位时间内撞击活塞的个数较多B .与 a 态相比, b 态的气体分子在单位时间内对活塞的冲量较大C.在相同时间内,a、b 两态的气体分子对活塞的冲量相等D .从 a 态到 b 态,气体的内能增加,外界对气体做功,气体向外界释放了热量17、从桌面上有一倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示,有一半径为 r 的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合。
2007年高考天津理科综合物理部分

一、单项选择题(本大题23小题,每小题3分,共69分).1.国际单位制中规定,力学量所选用的基本量是A.长度、力、时间B.长度、质量、时间C.长度、力、质量、时间D.速度、加速度、力2.关于物体做匀变速直线运动,下列说法中正确的是A.每一秒内速度的变化量相等B.速度保持不变C.加速度随时间均匀变化D.位移随时间均匀变化3.甲、乙两车在同一地点同时做直线运动,其v-t图象如图所示,则A.它们的初速度均为零B.甲的加速度大于乙的加速度C.t1时刻,甲的速度大于乙的速度D.0~t1时间内,甲的位移大于乙的位移4.关于惯性,下列说法正确的是A.物体质量越大,惯性越大B.物体速度越大,惯性越大C.只有静止的物体才有惯性D.只有做匀速直线运动的物体才有惯性5.如图所示的四个图中,M、N两方形木块处于静止状态,它们相互之间一定没有弹力......作用的是6.在力的合成中,合力与分力的大小关系是A.合力一定大于每一个分力B.合力一定至少大于其中一个分力C.合力可能比两个分力都小,也可能比两个分力都大D.合力一定随两个分力夹角的增大而增大7.利用如图所示的装置探究加速度与力、质量的关系,下列说法中正确的是A.保持小车所受拉力不变,只改变小车的质量,就可以探究加速度与力、质量的关系B.保持小车质量不变,只改变小车的拉力,就可以探究加速度与力、质量之间的关系C.先保持小车所受拉力不变,研究加速度与力的关系;再保持小车质量不变,研究加速度与质量的关系,最后归纳出加速度与力、质量的关系D.先保持小车质量不变,研究加速度与力的关系;再保持小车受力不变,研究加速度与质量的关系,最后归纳出加速度与力、质量的关系tv 甲乙t18.图中的四幅图展示了某同学做引体向上运动前的四种抓杠姿势,其中手臂受力最小......的是A B C D9.一船以恒定的速率渡河,水速恒定(小于船速).要使船垂直河岸到达对岸,则A .船应垂直河岸航行B .船的航行方向应偏向上游一侧C .船不可能沿直线到达对岸D .河的宽度一定时,船垂直到对岸的时间是任意的10.下列情况中的物体,能看作质点的是A .太空中绕地球运行的卫星B .正在闯线的百米赛跑运动员C .匀速行驶着的汽车的车轮D .正在跃过横杆的跳高运动员11.以10m/s 的初速度从10m 高的塔上水平抛出一个石子。
2007物理高考真题(全国卷)

2007年普通高等学校招生全国统一考试(全国卷Ⅱ)理科综合能力测试物理部分详细解答(贵州、黑龙江、吉林、云南、甘肃、新疆、内蒙古、青海、西藏等省用)二、选择题(本题共8小题。
在每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全选对的得6分,选对但不全的得3分,有选错的得0分)14.对一定质量的气体,下列说法正确的是A.在体积缓慢不断增大的过程中,气体一定对外界做功B.在压强不断增大有过程中,外界对气体一定做功C.在体积不断被压缩的过程中,内能一定增加D.在与外界没有发生热量交换的过程中,内能一定不变【答案】ApV 【分析】当气体增大时,气体对外界做功,当气体减小时,外界对气体做功;故A选正确;根据T=常数,p增大时,V不一定变化,故B选项错;在V减小的过程中,可能向外界放热,根据ΔE =W+Q可知,内能不一定增大,故C选项错误;Q=0的过程中,W不一定为0,故D选项错误。
【高考考点】热力学第一定律、气体压强、体积、温度三者的关系【易错点】ΔE=W+Q的符号【备考提示】热学部分虽然不是重点中,但在全国高考理综物理部分每年必考一道选择题,而且题目相对较容易。
但这部分知识较多,应注意全面掌握基础知识。
15.一列横波在x轴上传播,在x=0与x=1cm的两点的振动图线分别如图中实线与虚线所示。
由此可以得出ArrayA.波长一定是4cmB.波的周期一定是4sC.波的振幅一定是2cmD.波的传播速度一定是1cm/s【答案】BC【分析】根据振动图象两个最大值的横坐标之差为振动周期,故T=4s,B选项正确;QOPS从图象可看出振幅A =2cm ,C 选项正确;根据题中所给的振动图象无法得到波长(或波速),也就无法根据λ=Tv算出波速(或波长),故A 、D 选项错误。
【高考考点】机械振动和机械波【易错点】容易混淆振动图象和波动图象。
【备考提示】机械振动和机械波是每年必考的知识点,应加强理解质点的振动过程、振动图象、波的形成过程及波的图象,弄清振动图象和波动图象的区别和联系。
C112.2007年理综天津卷

0 1 2 3 4 5 6 7 8 9 0
游标尺
5
1
2
漏掉末位有效数字“ 不给分 不给分) (漏掉末位有效数字“0”不给分)
2007年天津理综卷 年天津理综卷22(2) 年天津理综卷 22⑵.某学生用打点计时器研究小车的匀变速直线运动。 某学生用打点计时器研究小车的匀变速直线运动。 ⑵ 某学生用打点计时器研究小车的匀变速直线运动 他将打点计时器接到频率为50 Hz的交流电源上 , 实 的交流电源上, 他将打点计时器接到频率为 的交流电源上 验时得到一条纸带。 验时得到一条纸带。他在纸带上便于测量的地方选取 第一个计时点,在这点下标明A 第六个点下标明B 第一个计时点,在这点下标明 ,第六个点下标明 , 第十一个点下标明C 第十六个点下标明D 第十一个点下标明 ,第十六个点下标明 ,第二十 一个点下标明E 测量时发现B点已模糊不清 点已模糊不清, 一个点下标明 。 测量时发现 点已模糊不清 , 于是 他测得AC长为 长为14.56 cm ,CD长为 长为11.15cm ,DE长为 他测得 长为 长为 长为 13.73 cm , 则 打 C 点 时 小 车 的 瞬 时 速 度 大 小 为 0.986 ________m/s ,小车运动的加速度大小为 2.58 m/s2 , AB的距离应为 5.99 cm 。(保留三位有效数字) 保留三位有效数字) 的距离应为
A
B
C
D
2007年天津理综卷 年天津理综卷23 年天津理综卷 23. ( 16分 ) 如图所示 , 水平光滑地面上停放着一 . 分 如图所示, 辆小车, 左侧靠在竖直墙壁上, 辆小车 , 左侧靠在竖直墙壁上 , 小车的四分之一圆 弧轨道AB是光滑的 在最低点B与水平轨道 相切, 是光滑的, 与水平轨道BC相切 弧轨道 是光滑的 , 在最低点 与水平轨道 相切 , BC的长度是圆弧半径的 倍 , 整个轨道处于同一竖 的长度是圆弧半径的10倍 的长度是圆弧半径的 直平面内。可视为质点的物块从A点正上方某处无初 直平面内。可视为质点的物块从 点正上方某处无初 速下落, 恰好落入小车圆弧轨道滑动, 然后沿水平 速下落 , 恰好落入小车圆弧轨道滑动 , 轨道滑行至轨道末端C处恰好没有滑出 处恰好没有滑出。 轨道滑行至轨道末端 处恰好没有滑出。已知物块到 达圆弧轨道最低点B时对轨道的压力是物块重力的 时对轨道的压力是物块重力的9 达圆弧轨道最低点 时对轨道的压力是物块重力的 小车的质量是物块的3倍 倍, 小车的质量是物块的 倍, 不考虑空气阻力和物 块落人圆弧轨道时的能量损失。 块落人圆弧轨道时的能量损失。求 物块开始下落的位置距水平轨道BC的竖直高度是 ⑴.物块开始下落的位置距水平轨道 的竖直高度是 物块开始下落的位置距水平轨道 圆弧半径的几倍; 圆弧半径的几倍; 物块与水平轨道BC ⑵.物块与水平轨道 物块与水平轨道 A 间的动摩擦因数μ。 C B
2007年普通高等学校招生全国统一考试(天津卷)

2007年普通高等学校招生全国统一考试(天津卷)数 学(理工类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至10页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上,并在规定位置粘贴考试用条形码。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在试卷上的无效。
3.本卷共10小题,每小题5分,共50分。
参考公式:·如果事件A B ,互斥,那么球的表面积公式()()()P A B P A P B +=+24πS R =·如果事件A B ,相互独立,那么其中R 表示球的半径()()()P A B P A P B =··一、选择题:在每小题列出的四个选项中,只有一项是符合题目要求的。
1.i 是虚数单位,32i 1i=-( ) A .1i +B . 1i -+C .1i -D .1i --2.设变量x y ,满足约束条件1133x y x y x y ⎧--⎪+⎨⎪-<⎩,,.≥≥则目标函数4z x y =+的最大值为( )A .4B .11C .12D .14 3.“2π3θ=”是“πtan 2cos 2θθ⎛⎫=+ ⎪⎝⎭”的( ) A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件4.设双曲线22221(00)x y a b a b-=>>,的离心率为,且它的一条准线与抛物线24y x =的准线重合,则此双曲线的方程为( )A .2211224x y -=B .2214896x y -= C .222133x y -=D .22136x y -=5.函数2log 2)(0)y x =>的反函数是( )A .142(2)xx y x +=->B .142(1)x x y x +=-> C .242(2)x x y x +=->D .242(1)x x y x +=->6.设a b ,为两条直线,αβ,为两个平面,下列四个命题中,正确的命题是( )A .若a b ,与α所成的角相等,则a b ∥B .若a b αβ,∥∥,αβ∥,则a b ∥C .若a b a b αβ⊂⊂,,∥,则αβ∥D .若a b αβ⊥⊥,,αβ⊥,则a b ⊥7.在R 上定义的函数()f x 是偶函数,且()(2)f x f x =-,若()f x 在区间[12],上是减函数,则()f x ( )A .在区间[21]--,上是增函数,在区间[34],上是增函数B .在区间[21]--,上是增函数,在区间[34],上是减函数C .在区间[21]--,上是减函数,在区间[34],上是增函数D .在区间[21]--,上是减函数,在区间[34],上是减函数8.设等差数列{}n a 的公差d 不为0,19a d =.若k a 是1a 与2k a 的等比中项,则k =( ) A .2 B .4 C .6D .89.设a b c ,,均为正数,且122log aa =,121log 2b b ⎛⎫= ⎪⎝⎭,21log 2cc ⎛⎫= ⎪⎝⎭.则( )A .a b c <<B .c b a <<C .c a b <<D .b a c <<10.设两个向量22(2cos )λλα=+-,a 和sin 2m m α⎛⎫=+ ⎪⎝⎭,b ,其中m λα,,为实数.若2=a b ,则mλ的取值范围是( ) A .[-6,1] B .[48],C .(-6,1]D .[-1,6]第Ⅱ卷注意事项:1.答案前将密封线内的项目填写清楚. 2.用钢笔或圆珠笔直接答在试卷上. 3.本卷共12小题,共100分.二、填空题:本大题共6小题,每小题4分,共24分,把答案填在题中横线上.11.若621x ax ⎛⎫+ ⎪⎝⎭的二项展开式中2x 的系数为52,则a = (用数字作答)12.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 .13.设等差数列{}n a 的公差d 是2,前n 项的和为n S ,则22lim n n na n S →∞-= .14.已知两圆2210x y +=和22(1)(3)20x y -+-=相交于A B ,两点,则直线AB 的方程是 .15.如图,在ABC △中,12021BAC AB AC ∠===,,°,D 是边BC 上一点,2DC BD =,则AD BC =· .16.如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有 种(用数字作答).三、解答题:本大题共6小题,共76分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知函数()2cos (sin cos )1f x x x x x =-+∈R ,. (Ⅰ)求函数()f x 的最小正周期;(Ⅱ)求函数()f x 在区间π3π84⎡⎤⎢⎥⎣⎦,上的最小值和最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007年普通高等学校招生全国统一考试(天津卷)
物理部分
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷两部分,共300分,考试用时150分钟。
第Ⅰ卷1至5页,第Ⅱ卷6至16页。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!
第Ⅰ卷
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上,并在规定位置粘贴考试用条形码。
2.每小题选出答案后,用铅笔把答题卡上对应题目的标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在试卷上的无效。
3.本卷共21题,每题6分,共126分。
在每题列出的四个选项中,只有一项是最符合题目要求的。
以下数据可供解题时参考:
相对原子质量:H1ﻩLi7 ﻩC12ﻩO 16 ﻩS 32 ﻩFe 56 Cu 64 Zn65
14.下列说法正确的是
A.用三棱镜观察太阳光谱是利用光的干涉现象
B.在光导纤维束内传送图象是利用光的全反射现象
C.用标准平面检查光学平面的平整程度是利用光的偏振现象
D.电视机遥控器是利用发出紫外线脉冲信号来换频道的
15.如图所示,物体A静止在光滑的水平面上,A的左边固定有轻质弹簧,与A质量相等的物体B以速度v向A运动并与弹簧发生碰撞,A、B始终沿同一直线运动,则A、B组成的系统动能损失最大的时刻是
A.A开始运动时
B.A的速度等于v时
C.B的速度等于零时
D.A和B的速度相等时
16.将阻值为5Ω的电阻接到内阻不计的交流电源上,电源电动势随时间变化的规律如图所示。
下列说法正确的是
A.电路中交变电流的频率为0.25Hz
B.通过电阻的电流为2A
C.电阻消耗的电功率为2.5 W
D.用交流电压表测得电阻两端的电压是5V
12.我国绕月探测工程的预先研究和工程实施已取得重要进展。
设地球、月球的质量分
别为m 1、m 2,半径分别为R 1、R2,人造地球卫星的第一宇宙速度为v ,对应的环绕周期为T,则环绕月球表面附近圆轨道飞行的探测器的速度和周期分别为
A .v R m R m 21
12,T R m R m 312321 ﻩﻩ B. v R m R m 1221,T R m R m 32
1312 C. v
R m R m 2112,T R m R m 3213
12 ﻩﻩﻩﻩ D. v R m R m 1221,T R m R m 3
12321 18.右图为氢原子能级的示意图,现有大量的氢原子处于n =4的激发态,当向低能级跃迁时辐射出若干不同频率的光。
关于这些光下列说法正确的是
A.最容易表现出衍射现象的光是由n =4能级跃迁到n =1能级产生的
B.频率最小的光是由n =2能级跃迁到n =1能级产生的
C.这些氢原子总共可辐射出3种不同频率的光
D.用n =2能级跃迁到n =1能级辐射出的光照射逸出功为6.34eV 的金属铂能发生光电效应
19.如图所示,在x 轴上方存在着垂直于纸面向里、磁感应强度为B 的匀强磁场,一个不计重力的带电粒子从坐标原点O 处以速度v 进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x 轴正方向成120°角,若粒子穿过y 轴正半轴后在磁场中到x 轴的最大距离为a ,则该粒子的比荷和所带电荷的正负是
A .
aB v 23,正电荷ﻩﻩﻩ ﻩ B. aB v 2,正电荷 C. aB v 23,负电荷ﻩ ﻩ ﻩﻩ D. aB
v 2,负电荷 20.A 、B 两装置,均由一支一端封闭、一端开口且带有玻璃泡的管状容器和水银槽组成,除玻璃泡在管上的位置不同外,其他条件都相同。
将两管抽成真空后,开口向下竖起插入水银槽中(插入过程没有空气进入管内),水银柱上升至图示位置停止。
假设这一过程水银与外界没有热交换,则下列说法正确的是。
