电路原理第五版第七章基本题
大学电路习题解答第7章
第七章(一阶电路)习题解答一、选择题1.由于线性电路具有叠加性,所以 C 。
A .电路的全响应与激励成正比;B .响应的暂态分量与激励成正比;C .电路的零状态响应与激励成正比;D .初始值与激励成正比2.动态电路在换路后出现过渡过程的原因是 A 。
A . 储能元件中的能量不能跃变;B . 电路的结构或参数发生变化;C . 电路有独立电源存在;D . 电路中有开关元件存在3.图7—1所示电路中的时间常数为 C 。
A .212121)(C C C C R R ++; B .21212C C C C R +;C .)(212C C R +;D .))((2121C C R R ++解:图7—1中1C 和2C 并联的等效电容为21C C +,而将两个电容摘除后,余下一端口电路的戴维南等效电阻为2R ,所以此电路的时间常数为)(212C C R +。
4.图7—2所示电路中,换路后时间常数最大的电路是 A 。
解:图7—2(A )、(B )、(C )、(D )所示四个电路中的等效电感eq L 分别为M L L 221++、21L L +、M L L 221-+和M L L 221++。
0>t 时,将图6—2(A )、(B )、(C )、(D )中的电感摘除后所得一端口电路的戴维南等效电阻eq R 分别为2R 、2R 、2R 和21R R +。
由于RL 电路的时间常数等于eqeq R L ,所以图7—2(A )所示电路的时间常数最大。
5.RC 一阶电路的全响应)e610(10tc u --=V ,若初始状态不变而输入增加一倍,则全响应c u 变为 D 。
A .t10e1220--; B .t10e620--;C .t10e1210--; D.t10e1620--解:由求解一阶电路的三要素法 τtc c c c u u u u -+∞-+∞=e)]()0([)( 可知在原电路中10)(=∞c u V ,4)0(=+c u V 。
电路原理第五版 第七章考研题
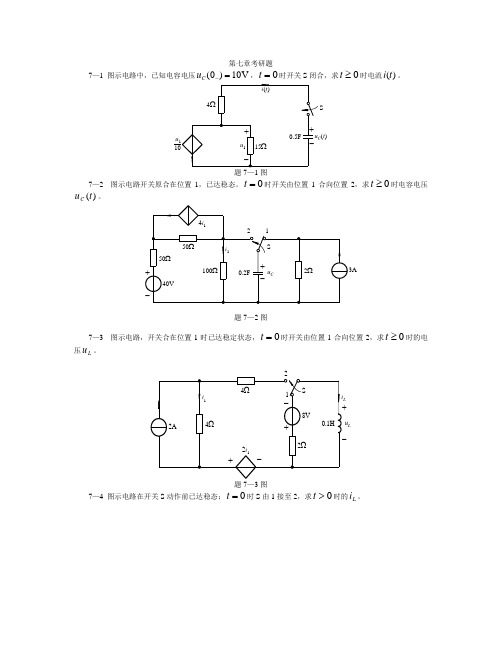
第七章考研题7—1 图示电路中,已知电容电压(0)10V C u -=,0=t时开关S 闭合,求0≥t 时电流)(t i 。
+-+-S0.5Fi (t )u 14Ω15Ωu C (t )u 110题7—1图7—2 图示电路开关原合在位置1,已达稳态。
0=t时开关由位置1合向位置2,求0≥t时电容电压)(t u C 。
+-+-0.2FS123Ai 14i 140V50Ω50Ω100ΩuC 2Ω题7—2图7—3 图示电路,开关合在位置1时已达稳定状态,0=t 时开关由位置1合向位置2,求0≥t 时的电压L u 。
+-+-+-2AS 28V0.1H1i 12i 14Ω4Ω2Ωu Li L题7—3图7—4 图示电路在开关S 动作前已达稳态;0=t时S 由1接至2,求0>t 时的L i 。
+-+-6V4V12S 2Ω0.2Fi L 1H(t = 0)题7—4图7—5 图示电路中,已知S 10()i t ε=A ,Ω=11R ,Ω=22R ,F μ1=C ,(0)2V C u -=,25.0=g S 。
求全响应)(1t i 、)(t i C 、)(t u C 。
+-+-i Si 1R 1u 1R 2gu 1i Cu CC题7—5图7—6 电路如图所示,当:(1)S()A i t δ=,0)0(=-C u ;(2)S ()A i t δ=,(0)1V C u -=;(3)S 3(2)A i t δ=-,(0)2V C u -=时,试求响应)(t u C 。
+-i S1k Ω2k Ω3 F u Cμ题7—6图7—7 图示电路中,S1()V u t ε=,S25()V u t ε=,试求电路响应)(t i L 。
+-+-u S1u S21Ω2Ω3Ωi L4H题7—7图7—8 图示电路中,电源S[50()2()]V u t t εδ=+,求0>t 时电感支路的电流)(t i 。
+-u S10Ω10Ωi0.1H题7—8图7—9 图示电路中,5S G =,0.25H L =,1F C =。
电路(第5版)第七章习题答案

t
U S (1 e
t
)
=
零输入响应
+
零状态响应
uC (0 ) U 0
根据经典法推导的结果:
t
S (t =0)
i R
+ uR C
+ US _
RC
_
+ u _ C
uC U S (U 0 U S )e
uC ( t ) uC () [uC (0 ) uC ()] e
可得一阶电路微分方程解的通用表达式:
t
RC
f (t ) f () [ f (0 ) f ()] e
t
【7-5】 图中开关S在位置1已久,t=0时合向位置2,求换路后的 i(t) 和 uL(t). 1W i 1H 1 解:三要素法 uL S 2
初始值:
10V 10 i (0 ) i (0 ) 2 A 5
4 i1
50W 50W 100W
150i1 50 5i1 40 i1 0.1 A
i1
uOC
uOC 100i1 10V
40V
4 i1
50W 50W 100W
4 i1 i1
uOC
50W 50W 100W
i1
i SC
40V
40V
uOC 10 V, i SC
i
4W
4W
稳态值: 时间常数: 所以:
i 0
L 1 s R 8
i ( t ) i ( 0 )e
t 2e源自 tAdi 8 t uL ( t ) L 16e A dt
第五版物理化学第七章习题答案

第七章电化学7.1用铂电极电解溶液。
通过的电流为20 A,经过15 min后,问:(1)在阴极上能析出多少质量的?(2) 在的27 ØC,100 kPa下的?解:电极反应为电极反应的反应进度为因此:7.2在电路中串联着两个电量计,一为氢电量计,另一为银电量计。
当电路中通电1 h后,在氢电量计中收集到19 ØC、99.19 kPa的;在银电量计中沉积。
用两个电量计的数据计算电路中通过的电流为多少。
解:两个电量计的阴极反应分别为电量计中电极反应的反应进度为对银电量计对氢电量计7.3用银电极电解溶液。
通电一定时间后,测知在阴极上析出的,并知阴极区溶液中的总量减少了。
求溶液中的和。
解:解该类问题主要依据电极区的物料守恒(溶液是电中性的)。
显然阴极区溶液中的总量的改变等于阴极析出银的量与从阳极迁移来的银的量之差:7.4用银电极电解水溶液。
电解前每溶液中含。
阳极溶解下来的银与溶液中的反应生成,其反应可表示为总反应为通电一定时间后,测得银电量计中沉积了,并测知阳极区溶液重,其中含。
试计算溶液中的和。
解:先计算是方便的。
注意到电解前后阳极区中水的量不变,量的改变为该量由两部分组成(1)与阳极溶解的生成,(2)从阴极迁移到阳极7.5用铜电极电解水溶液。
电解前每溶液中含。
通电一定时间后,测得银电量计中析出,并测知阳极区溶液重,其中含。
试计算溶液中的和。
解:同7.4。
电解前后量的改变从铜电极溶解的的量为从阳极区迁移出去的的量为因此,7.6在一个细管中,于的溶液的上面放入的溶液,使它们之间有一个明显的界面。
令的电流直上而下通过该管,界面不断向下移动,并且一直是很清晰的。
以后,界面在管内向下移动的距离相当于的溶液在管中所占的长度。
计算在实验温度25 ØC下,溶液中的和。
解:此为用界面移动法测量离子迁移数7.7已知25 ØC时溶液的电导率为。
一电导池中充以此溶液,在25 ØC时测得其电阻为。
电路第五版课件及课后答案第七章

L
i k未动作前,电路处于稳定状态: i = 0 , uL = 0 未动作前,电路处于稳定状态: 未动作前 US/R
US k接通电源后很长时间,电路达到新的稳定 接通电源后很长时间, 接通电源后很长时间 状态,电感视为短路: 状态,电感视为短路: uL= 0, i=Us /R uL 有一过渡期 t1 t 0
∆w p= ∆t
∆t ⇒0
p ⇒∞
返 回 上 页 下 页
2. 动态电路的方程
电路 例 RC电路 应用KVL和电容的 和电容的VCR得: 应用 和电容的 得
(t >0) + Us -
R i + uC –
C
Ri + uC = uS(t) duC i =C dt
若以电流为变量: 若以电流为变量:
duC RC +uC = uS(t) dt dt 1 Ri + ∫idt = uS(t) C
前一个稳定状态 新的稳定状态 US k接通电源后很长时间,电容充电完毕,电路 接通电源后很长时间, 接通电源后很长时间 电容充电完毕, R
?
i i = 0 , u有一过渡期 C= Us t
返 回
0
t1
过渡状态
上 页
下 页
电感电路 + Us (t = 0) R i + k uL – + Us (t →∞) R i + uL –
本章重点
首页
重点 1.动态电路方程的建立及初始条件的确定; 1.动态电路方程的建立及初始条件的确定; 动态电路方程的建立及初始条件的确定 2.一阶和二阶电路的零输入响应、 2.一阶和二阶电路的零输入响应、零状态响 一阶和二阶电路的零输入响应 应和全响应的概念及求解; 应和全响应的概念及求解; 3.一阶和二阶电路的阶跃响应概念及求 3.一阶和二阶电路的阶跃响应概念及求 解。
《电路》第五版 课件 第7章

c
全解
uc = uc′ + uc′′ = U s + Ae
由初始条件u 确定积分常数A 由初始条件 c(0+)=U0确定积分常数
uc (0+ ) = A + U s = U 0
∴ A = U0 − U s
− 1 t RC
uc (t ) = U s + (U 0 − U s )e
强制分量 稳态分量) (稳态分量)
1 t = iL (0− ) + ∫ u (ξ )dξ L 0−
Ψ=LiL
ψ = ψ (0− ) + ∫ u (ξ )dξ
0−
t
当u(ξ) 为有限值时 iL(0+)=iL(0-) Ψ(0+)=Ψ(0-)
∫0
0+
−
u (ξ )dξ → 0
磁链守恒
换路定理
uc(0+)=uc(0-) q(0+)=q(0-) iL(0+)=iL(0-) Ψ(0+)=Ψ(0-)
t
uc(0-)
换路定理
t =0+等 等 效电路
uc(0+)
ic(0+)
(1)由t=0-电路求uc(0-) 电路求 (1)由 电路 uc(0-)=8V ic(0-)=0≠ic(0+) (2)由 电阻(2)由换路定理
电路
uc(0+)=uc(0-)=8V
电阻 (0 ) ic + 电路
电路求 (3)由 (3)由t=0+电路求ic(0+)
思考题: 思考题:含有两个储能元件的电路
求iC(0+)和uL(0+) 和
电路原理 第五版 第五版 第七章(3)

2
P + 200P + 20000 = 0
2
P= -100 ± j100
∴i = 1 + Ae
(4)定常数 定常数
−100t
sin(100t +ϕ)
ϕ = 45o A = 2
1 + Asinϕ = 2 ← iL (0+ ) + 100Acosϕ −100Asinϕ = 0 ← uL(0 )
(3)
uc = Ae−25t sin(139t +θ ) uc (0+ ) = 25 Asinθ = 25 139cosθ − 25sinθ = − 5 duc c = −5 10−4 dt 0 A = 355 ,θ = 176
uc 355 25 0
uc = 355e−25t sin(139t +1760 )V
U0 A= sin β
ω,ω0,δ间的关系 间的关系: 间的关系
ω ,β = arctg δ
ω0
ω β δ
ω sin β = ω0
ω0 −δ t uc = U0e sin(ωt + β ) ω
ω0 A = U0 ω
ω0 uc是其振幅以± U0为包线依指数衰减的正 弦函数。 弦函数。 ω
t=0时 uc=U0 时
t t=0+ ic=0 , t=∞ i c=0 ∞ ic>0 t = tm 时ic 最大 0< t < tm i 增加 uL>0 增加, i 减小 uL <0 减小,
duc − U0 p1t p2t ic = −C (e − e ) = dt L(P − P ) 2 1
《电工技术基础》第七章试题

【电子技术根底】第七章试题一、填空题1、U、V、W是三相交流发电机的三个绕组,它们的电阻不计,每相产生的感应电动势可表示为:e U=311sin314tv,e V=311sin〔314t-120o〕V,e W=311sin(314t+120o)V,负载由三只相同的灯泡接成星形,假设能正常发光,可知,灯泡的额定电压是V2、三相对称负载作星形连接时,U Y= U1,I Y= I Y,此时电流为。
3、三相对称负载作三角形连接时,UΔΦ= U1,且IΔ1= IΔΦ,各线电流比相应的相电流度。
4、工厂中一般动力电源电压为V,照明电源电压为V、V以下的电压称为平安电压。
5、触电对人体的伤害度与、、、以及等因素有关。
6、三相三线制电源供电时,在中线不直接接地的电力网中,应将电器设备的金属外壳用连接起来,叫做保护措施。
7、有一对称三相负载接成星形,每相负载的阻抗为22欧,功率因数为0。
8,测出负载中的电流为10A,那么三相电路的有功功率为,如果保持电源线电压不变,负载改为三角形连接,那么三相电路的有功功率为。
8、三相交流电是三个、、的单相交流电按一定方式供电。
9、习惯上三相交流电的相序为。
10、在三相四线制中,零线也叫地线,常用色或色线来表示,三相火线常用、、三色表示。
11、三相四线制供电系统,可传送V和V两种电压,该供电系统用符号“〞表示。
12、在三相四线制中,线电压分别超前相应的相电压度。
13、当三相负载对称时,三相功率的计算式为。
14、发电机是利用原理制成的,它是其他形式的能转换为电能的设备。
15、电动机按使用电源相数不同分为和,在电动机中,鼠笼式电动机结构简单,价格低廉,运行可靠,使用极为广泛。
16、鼠笼式电动机主要由和两局部组成,前者由和组成,后者由、、和组成。
17、电动机定子绕组是由假设干线圈组成的三相绕组,每组绕组有两个引出线端,分别叫首端和尾端,三个首端分别用、、表示,三个尾端分别用、、表示。
18、旋转磁场的转速计算公式为。
《电路原理》第7-13、16章作业答案
12-6题12-6图所示对称三相电路中, ,三相电动机吸收的功率为1.4kW,其功率因数 (滞后), 。求 和电源端的功率因数 。
题12-6图
第十三章“非正弦周期电流电路和信号的频谱”练习题
13-7已知一RLC串联电路的端口电压和电流为
试求:(1)R、L、C的值;(2)3的值;(3)电路消耗的功率。
13-9题13-9图所示电路中 为非正弦周期电压,其中含有 和 的谐波分量。如果要求在输出电压 中不含这两个谐波分量,问L、C应为多少?
题13-9图
第十六章“二端口网络”练习题
16-1求题16-1图所示二端口的Y参数、Z参数和T参数矩阵。(注意:两图中任选一个)
(a)(b)
题16-1图
16-5求题16-5图所示二端口的混合(H)参数矩阵。(注意:两图中任选一个)
题10-21图
第十一章“电路的频率响应”练习题
11-6求题11-6图所示电路在哪些频率时短路或开路?(注意:四图中任选两个)
(a)(b)(c)(d)
题11-6图
11-7RLC串联电路中, , , ,电源 。求电路的谐振频率 、谐振时的电容电压 和通带BW。
11-10RLC并联谐振时, , , ,求R、L和C。
题9-19图
9-25把三个负载并联接到220V正弦电源上,各负载取用的功率和电流分别为: , (感性); , (感性); , (容性)。求题9-25图中表A、W的读数和电路的功率因数。
邱关源《电路》(第5版)笔记和课后习题(含考研真题)详解

解: (1)图1-14(a)所示 电压源u、i参考方向非关联,发出功率:
电阻元件吸收功率:
电流源u、i参考方向关联,吸收功率:
图1-14
(2)图1-14(b)所示
电阻元件吸收功率:
电流源u、i参考方向非关联,发出功率: 电压源u、i参考方向非关联,发出功率:
目 录
8.2 课后习题详解 8.3 名校考研真题详解 第9章 正弦稳态电路的分析 9.1 复习笔记 9.2 课后习题详解 9.3 名校考研真题详解 第10章 含有耦合电感的电路 10.1 复习笔记 10.2 课后习题详解 10.3 名校考研真题详解 第11章 电路的频率响应 11.1 复习笔记 11.2 课后习题详解 11.3 名校考研真题详解 第12章 三相电路 12.1 复习笔记 12.2 课后习题详解 12.3 名校考研真题详解 第13章 非正弦周期电流电路和信号的频谱 13.1 复习笔记 13.2 课后习题详解 13.3 名校考研真题详解 第14章 线性动态电路的复频域分析 14.1 复习笔记 14.2 课后习题详解 14.3 名校考研真题详解 第15章 电路方程的矩阵形式 15.1 复习笔记 15.2 课后习题详解 15.3 名校考研真题详解 第16章 二端口网络 16.1 复习笔记
图1-11
解: 根据关联参考方向、功率吸收和发出的相关概念可得:
图1-11(a),对于NA ,u、i的参考方向非关联,乘积ui对NA 意味着发出功率;对于NB ,u,i的参考方向关 联,乘积ui对NB 意味着吸收功率。
图1-11(b),对于NA ,u、i的参考方向关联,乘积ui对NA 意味着吸收功率;对于NB ,u,i的参考方向关 联,乘积ui对NB 意味着发出功率。
电路原理第五版第七章基本题

电路原理第五版第七章基本题(总5页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第七章基本题7—1 图(a )、(b )所示电路中开关S 在0=t时动作,试求电路在+=0t 时刻电压、电流的初始值。
+--++-+-+-(a)(b)10V5V12S 10Ωi CC 2Fu C 10V5Ω12S 5Ωi L L 1Hu L(t = 0)(t = 0)题7—1图7—2 图示各电路中开关S 在0=t时动作,试求各电路在+=0t 时刻的电压、电流。
已知图(d )中的π()100sin V 3e t t ω⎛⎫=+ ⎪⎝⎭,(0)20V C u -=。
(a ) (b )题7—2图7—3 电路如图所示,开关未动作前电路已达稳态,0=t时开关S 打开。
求)0(+C u 、(0)L i +、+0d d tu C 、+0d d ti L 、+0d d ti R 。
+-+-+-12V6ΩΩSi Ri C u C 241F0.1Hu L i L3Ω题7—3图7—4 开关S 原在位置1已久,0=t时合向位置2,求)(t u C 和)(t i 。
Ω题7—4图7—5 图中开关S 在位置1已久,0=t时合向位置2,求换路后的)(t i 和)(t u L 。
题7—5图7—6 图示电路开关原合在位置1,0=t时开关由位置1合向位置2,求0≥t 时电感电压)(t u L 。
2Ω6u题7—6图7—7 图示电路中,若0=t时开关S 打开,求C u 和电流源发出的功率。
C题7—7图7—8 图示电路中开关S 闭合前,电容电压C u 为零。
在0=t时S 闭合,求0>t 时的)(t u C 和)(t i C 。
C题7—8图7—9 图示电路中开关S 打开前已处稳定状态。
0=t 开关S 打开,求0≥t 时的)(t u L 和电压源发出的功率。
+-u L题7—9图7—10 图示电路中开关闭合前电容无初始储能,0=t时开关S 闭合,求0≥t 时的电容电压)(t u C 。
(完整版)电路原理课后习题答案
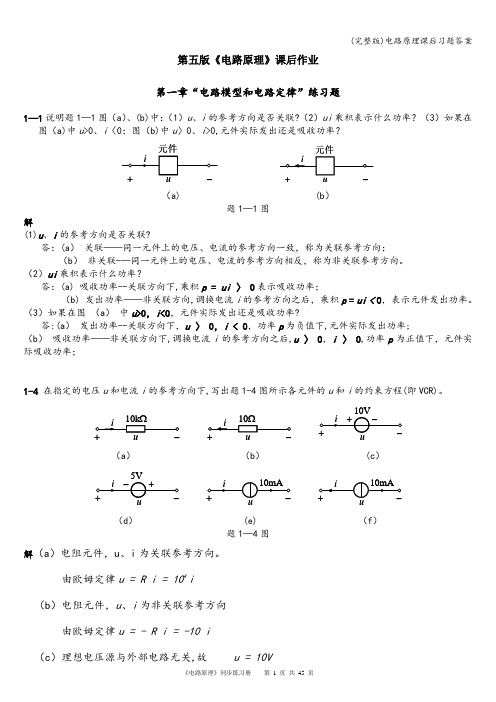
因此, 时,电路的初始条件为
t〉0后,电路的方程为
设 的解为
式中 为方程的特解,满足
根据特征方程的根
可知,电路处于衰减震荡过程,,因此,对应齐次方程的通解为
式中 。由初始条件可得
解得
故电容电压
电流
7-29RC电路中电容C原未充电,所加 的波形如题7—29图所示,其中 , 。求电容电压 ,并把 :(1)用分段形式写出;(2)用一个表达式写出。
题4-17图
解:首先求出 以左部分的等效电路.断开 ,设 如题解4-17图(a)所示,并把受控电流源等效为受控电压源。由KVL可得
故开路电压
把端口短路,如题解图(b)所示应用网孔电流法求短路电流 ,网孔方程为
解得
故一端口电路的等效电阻
画出戴维宁等效电路,接上待求支路 ,如题解图(c)所示,由最大功率传输定理知 时其上获得最大功率。 获得的最大功率为
(a)(b)
题3—1图
解:(1)每个元件作为一条支路处理时,图(a)和(b)所示电路的图分别为题解3-1图(a1)和(b1)。
图(a1)中节点数 ,支路数
图(b1)中节点数 ,支路数
(2)电压源和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理时,图(a)和图(b)所示电路的图分别为题解图(a2)和(b2)。
电容电流
t=2 ms时
电容的储能为
7—20题7—20图所示电路,开关合在位置1时已达稳定状态,t=0时开关由位置1合向位置2,求t0时的电压 .
题7-20图
解:
用加压求流法求等效电阻
7-26题7—26图所示电路在开关S动作前已达稳态;t=0时S由1接至2,求t0时的 .
题7-26图
解:由图可知,t>0时
电路原理课后习题答案-2

解:画出电源分别作用的分电路图
对(a)图应用结点电压法有
解得:
对(b)图,应用电阻串并联化简方法,可得:
所以,由叠加定理得原电路的 为
4-5应用叠加定理,按下列步骤求解题4-5图中 。(1)将受控源参与叠加,画出三个分电路,第三分电路中受控源电压为 , 并非分响应,而为未知总响应;(2)求出三个分电路的分响应 、 、 , 中包含未知量 ;(3)利用 解出 。
题4-17图
解:首先求出 以左部分的等效电路。断开 ,设如题解4-17图(a)所示,并把受控电流源等效为受控电压源。由KVL可得 故开路电压
把端口短路,如题解图(b)所示应用网孔电流法求短路电流 ,网孔方程为 解得 故一端口电路的等效电阻 画出戴维宁等效电路,接上待求支路 ,如题解图(c)所示,由最大功率传输定理知 时其上获得最大功率。 获得的最大功率为
(a)(b)
题7-29图
解:(1)分段求解。在 区间,RC电路的零状态响应为
时
在 区间,RC的全响应为
时
在 区间,RC的零输入响应为
(3)用阶跃函数表示激励,有
而RC串联电路的单位阶跃响应为
根据电路的线性时不变特性,有
第八章“相量法”练习题
8-7若已知两个同频正弦电压的相量分别为 , ,其频率 。求:(1) 、 的时域形式;(2) 与 的相位差。
因为变换前,△中
所以变换后,
故
(2)变换后的电路如图2-5图(b)所示。
因为变换前,Y中
所以变换后,
故
2-11利用电源的等效变换,求题2-11图所示电路的电流i。
题2-11图
解由题意可将电路等效变
为解2-11图所示。
于是可得 ,
电路原理作业第七章

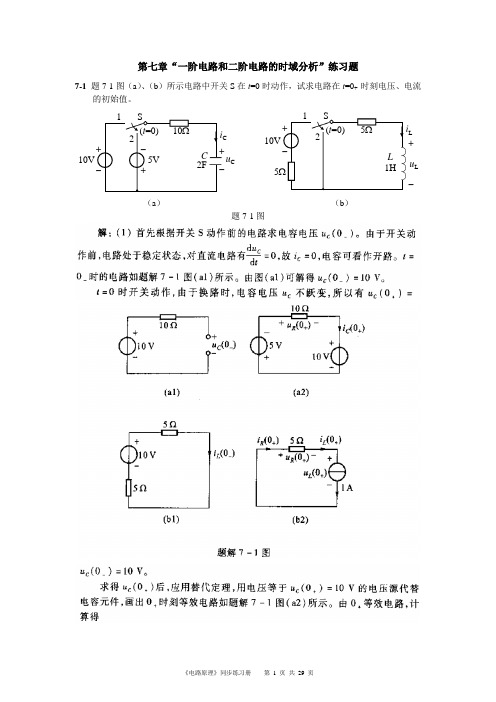
电路原理作业第七章第七章“一阶电路和二阶电路的时域分析”练习题7-1 题7-1图(a )、(b )所示电路中开关S 在t =0时动作,试求电路在t =0+ 时刻电压、电流的初始值。
10Ω10V+-i C 1+-u CC 2F5V -+(t =0)2S5Ω10V+-i L 1+-u LL 1H(t =0)2S 5Ω(a )(b ) 题7-1图解:(a)第一步 求t<0时,即开关S 动作前的电容电压(0)c u -。
由于开关动作前,电路处于稳定状态,对直流电路有cdu dt=,故0c i =,电容看作开路,0t -=时的电路如题解7-1图(a1)所示,可得(0)10c u V -=。
题解7-1图第二步 根据换路时,电容电压cu 不会跃变,所以有(0)(0)10ccu u V +-==应用替代定理, 用电压等于(0)10c u V +=的电压源代替电容元件,画出0+时刻的等效电路如题解7-1图(a2)所示。
第三步 由0+时刻的等效电路,计算得105(0) 1.510c i A ++=-=-(0)10(0)10( 1.5)15Rc ui V++=⨯=⨯-=-换路后,ci 和Ru 发生了跃变。
(b ) 第一步 由t<0时的电路,求(0)Li -的值。
由于t<0时电路处于稳定状态,电感电流L i 为常量,故0Ldi dt=,即0L u =,电感可以看作短路。
0t -=时的电路如图解7-1图(b1)所示,由图可知10(0)155Li A -==+题解7-1图第二步 根据换路时,电感电流Li 不会跃变,所以有 (0)(0)1LLi i A +-==应用替代定理, 用电流等于(0)1Li A +=的电流源代替电感元件,画出0+时刻的等效电路如题解7-1图(b2)所示。
第三步 由0+时刻的等效电路,计算初始值 2(0)(0)5(0)515R L u u i V +++=-=⨯=⨯=(0)(0)1RLi i A ++==显然电路换路后,电感电压2u 发生了跃变。
《电路原理》第7-13、16章作业参考
(b)
(c)
题10-5图
解:(1)首先作出原边等效电路,如解10-5图(a)所示。
解10-5图
其中 (亦可用去耦的方法求输入阻抗)
(2)首先作出并联去耦等效电路,如解10-5图(b)所示。
即
(3)首先作出串联去耦等效电路(反接串连),如解10-5图(b)所示。
其中
10-17如果使100电阻能获得最大功率,试确定题10-17图所示电路中理想变压器的变比n。
=iL( )+〔iL(0+)-iL( )〕e-1/ =1.2+(-4-1.2) e-100s=1.2-5.2 e-100s
=L(diL/ dt)=52 e-100sV
7-26题7-26图所示电路在开关S动作前已达稳态;t=0时S由1接至2,求t0时的 。
题7-26图
解:由图可知,t<0时 因此t=0时电路的初始条件为
9-25把三个负载并联接到220V正弦电源上,各负载取用的功率和电流分别为: , (感性); , (感性); , (容性)。求题9-25图中表A、W的读数和电路的功率因数。
题9-25图
解:表W的读数为P1+P2+P3=19.8KW令 求电流 、 、 、 即有
⑴
⑵
⑶
根据KCL有: = + + =
功率因数
(右) =g (KCL)
= (KVL)右网孔电流方程可以不用列出
结点电压方程为: = +
(2)如题9-17图b所示,设顺时针网孔电流为 (左上)、 (左下)、 (中)
(右)。网孔电流方程为: ,
(2+j8) = (左上)
-(1+j8) =0(左下) (中)
数字电路习题-第七章

第七章 D/A转换器和A/D转换器A/D转换器和D/A转换器是反馈控制系统中,不可缺少的集成电路器件,它在系统中起着“数字至模拟”或“模拟至数字”的桥梁性作用。
本章要求学生理解D/A转换器和A/D转换器的工作原理,掌握他们的主要性能指标和使用方法。
第一节 基本知识、重点与难点一、基本知识(一)D/A转换器和A/D转换器的基本原理D/A转换器和A/D转换器的主要技术参数有转换速度、转换精度、抗干扰能力等。
在选用D/A转换器和A/D转换器时,一般根据这几个性能指标综合考虑。
分辨率和转换误差影响D/A转换器的精度,转换时间影响转换器的转换速度。
A/D转换器是将模拟量转换成数字量,转换过程包括采样、保持、量化和编码4个步骤。
D/A转换器是将数字量转换成模拟量,它通过电阻网络、模拟开关和运算放大器将数字量转换成电流,再用加法器将各有效支路电流相加并转换成电压。
(二)D/A转换器1.权电阻网络权电阻网络由一组电阻组成,其中每个权电阻的阻值与该电阻所对应的权位成反比。
使流过每个接到基准电源U REF上电阻的电流和对应的权值成正比。
权电阻网络D/A转换器的优点是电路结构简单,所用元器件数量较少。
但当二进制数位较多时,权电阻值种类多,且阻值分散,使得转换精度较低。
2.R-2R网络R-2R网络D/A转换器中各支路的电流直接流入运算放大器的反相端,它们之间不存在传输误差,因而提高了转换速度,减小了动态过程中在输出端可能出现的尖峰脉冲。
由于只采用了R和2R两种阻值,因此能比较容易保证电阻网络的精度,也容易集成化。
3.集成D/A转换器目前市场集成D/A转换器的芯片种类较多,可根据电路系统要求的技术参数,参考数据手册,综合考虑选用集成D/A转换器。
(三)A/D转换器1.并行比较型A/D转换器并行比较型A/D转换器是高速A/D转换器,其转换不需要反复,在所有种类A/D转换器中转换速度最快。
然而这种A/D转换器的缺点是分辨率低,比较器的数量也随着数字量的增加而增加。
电路原理第五版
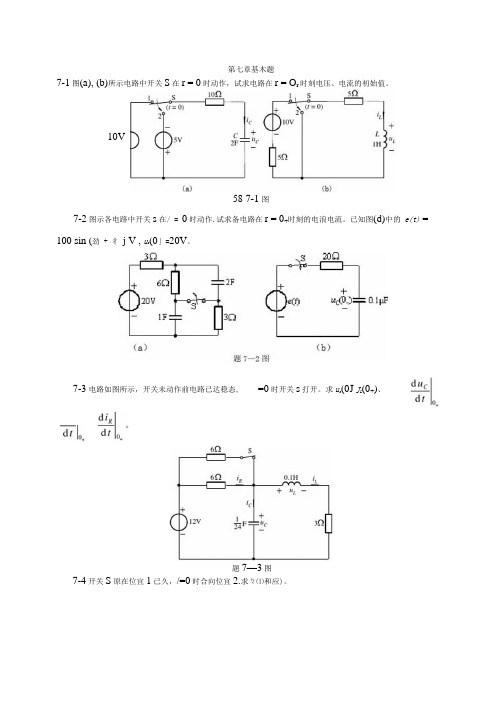
第七章基木题7-1图(a), (b)所示电路中开关S在r = 0时动作,试求电路在r = O r时刻电压、电流的初始值。
10V58 7-1 图7-2图示各电路中开关s在/ = 0时动作.试求备电路在r = 0+时刻的电浪电流。
已知图(d)中的e(t) = 100 sin (劲 + 彳j V , u c(0」=20V。
7-3电路如图所示,开关未动作前电路已达稳态, =0时开关s打开。
求u c(0J J L(0+)、題7—3图7-4开关S原在位宜1已久,/=0时合向位宜2.求々⑴和应)。
題7—6图7-7图示电路中.若/=0时开关S 打开,求I 々和电流源发出的功率。
題7—7图图示电路中开关S 闭合前•电容电压铁•为零。
在7=0时S 闭合.求/>0时的“(・(/)和7—5 7— 6 图中开关S 在位宜1已久.『=0时合向位宜2,求换路后的“/)和叫(/)。
7—8 求/>0时电感电压U L (t ) o題7—8图7-9图示电路中开关S打开前已处稳定状态。
/ = 0开关S打开,求/>0时的%⑴和电压源发出的功率。
7-10图示电路中开关闭合前电容无初始储能,7=0时开关$闭合・求/二0时的电容电J^lt c(t)o7—11 图示电路中e(t) = yjl 220cos(314r+ 30 )V , 7=0 时合上开关s。
求:u c.7—12图示电路中.电容原先已充电.仪・(0」=6V. R = 2.5Q. L = 0.25H. C = 0・25F。
试求:(1)开关闭合后的仇・(/)、,(/):(2)使电路在临界阻尼下放电.为z和c不变时,电阻斤应为何值?7-13图示电路在开关s打开之前已达稳态:/=0时,开关s打开•求/>0时的5Q0.5H7-14电路如图所示,7=0时开关s闭合,设w c(0.) = 0, /(0_) = 0, L = 1H. C = lpF・ i/ = 100Vo 若(1〉电阻/? = 3kP: (2) /? = 2kQ: (3) /? = 200Q.试分别求在上述电阻值时电路中的电流f和电圧%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章基本题
7—1 图(a )、(b )所示电路中开关S 在0=t
时动作,试求电路在+=0t 时刻电压、电流的初始值。
+
--+
+-
+
-+
-
(a)
(b)
10V
5V
1
2S
10Ω
i C
C 2F
u C 10V
5Ω
1
2
S 5Ω
i L L 1H
u L
(t = 0)
(t = 0)
题7—1图
7—2 图示各电路中开关S 在0=t
时动作,试求各电路在+=0t 时刻的电压、电流。
已知图(d )中的
π()100sin V 3e t t ω⎛
⎫=+ ⎪⎝
⎭,(0)20V C u -=。
(a ) (b )
题7—2图
7—3 电路如图所示,开关未动作前电路已达稳态,0=t
时开关S 打开。
求)0(+C u 、(0)L i +、+
0d d t
u
C 、
+
0d d t
i L 、
+
0d d t
i R 。
+
-
+-
+
-12V
6Ω
6Ω
S
i R
i C u C 241F
0.1H
u L i L
3Ω
题7—3图
7—4 开关S 原在位置1已久,0=t
时合向位置2,求)(t u C 和)(t i 。
Ω
题7—4图
7—5 图中开关S 在位置1已久,0=t
时合向位置2,求换路后的)(t i 和)(t u L 。
题7—5图
7—6 图示电路开关原合在位置1,0=t
时开关由位置1合向位置2,求0≥t 时电感电压)(t u L 。
6u
题7—6图
7—7 图示电路中,若0=t
时开关S 打开,求C u 和电流源发出的功率。
C
题7—7图
7—8 图示电路中开关S 闭合前,电容电压C u 为零。
在0=t
时S 闭合,求0>t 时的)(t u C 和)(t i C 。
C
题7—8图
7—9 图示电路中开关S 打开前已处稳定状态。
0=t 开关S 打开,求0≥t 时的)(t u L 和电压源发出的
功率。
+
-u L
题7—9图
7—10 图示电路中开关闭合前电容无初始储能,0=t
时开关S 闭合,求0≥t 时的电容电压)(t u C 。
u C
题7—10图
7—11 图示电路中()
30)V e t t =+,0=t
时合上开关S 。
求:C u 。
μ
题7—11图
7—12 图示电路中,电容原先已充电,(0)
6V C u -=,Ω=5.2R ,0.25H L =,0.25F C =。
试求:
(1)开关闭合后的)(t u C 、)(t i ;
(2)使电路在临界阻尼下放电,当L 和C 不变时,电阻R 应为何值
C
题7—12图
7—13 图示电路在开关S 打开之前已达稳态;0=t
时,开关S 打开,求0>t 时的C u 。
Ω
0.5H
题7—13图
7—14 电路如图所示,0=t
时开关S 闭合,设0)0(=-C u ,0)0(=-i ,1H L =,F μ1=C ,
100V U =。
若(1)电阻k Ω3=R ;(2)k Ω2=R ;(3)Ω200=R ,试分别求在上述电阻值时电路中的电流i 和电压C u 。
C
题7—14图
7—15 图(a )所示电路中的电压)(t u 的波形如图(b )所示,试求电流)(t i 。
(a)
(b)
u /V
2
1
O 1t /s
题7—15图
7—16 图示电路中,0)
0(=-C u ,Ω=k 31R ,Ω=k 62R ,F μ5.2=C ,试求电路的冲激响应C i 、
1i 和C u 。
R R 2
题7—16图
7—17 图示电路中0)
0(=-L i ,Ω=61R ,Ω=42R ,100mH L =。
求冲激响应L i 和L u 。
题7—17 图。
