八年级下数学难题精选含答案
初二数学经典难题(带答案及解析)
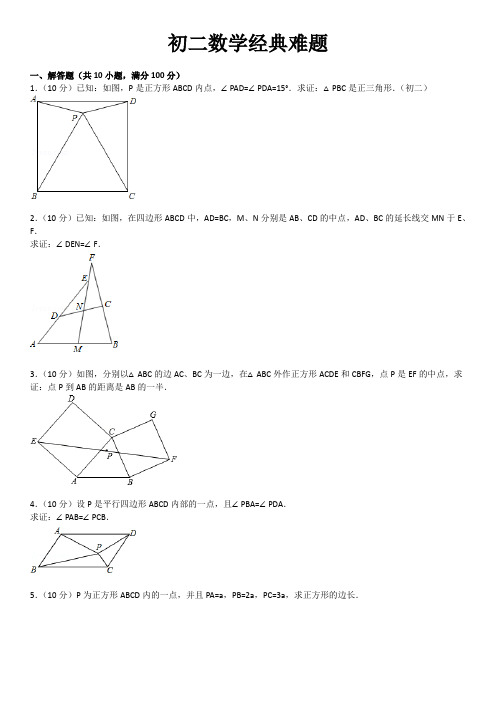
初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
初二数学好题难题集锦含答案

八年级下册数学难题精选分式:一:如果abc=1,求证11++a ab +11++b bc +11++c ac =1二:已知a 1+b 1=)(29b a +,则a b +ba等于多少?三:一个圆柱形容器的容积为V 立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水。
向容器中注满水的全过程共用时间t 分。
求两根水管各自注水的速度。
四:联系实际编拟一道关于分式方程2288+=xx 的应用题。
要求表述完整,条件充分并写出解答过程。
五:已知M =222y x xy -、N =2222yx y x -+,用“+”或“-”连结M 、N,有三种不同的形式,M+N 、M-N 、N-M ,请你任取其中一种进行计算,并简求值,其中x :y=5:2。
反比例函数:一:一张边长为16cm 正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“E ”图案如图1所示.小矩形的长x (cm )与宽y (cm )之间的函数关系如图2所示:(1)求y 与x 之间的函数关系式; (2)“E ”图案的面积是多少?(3)如果小矩形的长是6≤x ≤12cm ,求小矩形宽的范围.二:是一个反比例函数图象的一部分,点(110)A,,(101)B,是它的两个端点.(1)求此函数的解析式,并写出自变量x的取值范围;(2)请你举出一个能用本题的函数关系描述的生活实例.三:如图,⊙A和⊙B都与x轴和y轴相切,圆心A和圆心B都在反比例函数1yx的图象上,则图中阴影部分的面积等于 .四:如图11,已知正比例函数和反比例函数的图像都经过点M(-2,1),且P(1,-2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图12,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的OPCQ周长的最小值.五:如图,在平面直角坐标系中,直线AB 与Y 轴和X 轴分别交于点A 、点8,与反比例函数y 一罟在第一象限的图象交于点c(1,6)、点D(3,x).过点C 作CE 上y 轴于E ,过点D 作DF 上X 轴于F . (1)求m ,n 的值;(2)求直线AB 的函数解析式;勾股定理:一:清朝康熙皇帝是我国历史上对数学很有兴趣的帝王.近日,•西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,•设其面积为S ,则第一步:6S=m ;第二步:m =k ;第三步:分别用3、4、5乘以k ,得三边长”.(1)当面积S 等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.二:一张等腰三角形纸片,底边长l5cm,底边上的高长22.5cm.现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )A.第4张 B.第5张 C.第6张 D.第7张三:如图,甲、乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的A处目测得点A与甲、乙楼顶B C、刚好在同一直线上,且A与B相距350米,若小明的身高忽略不计,则乙楼的高度是米.20乙CBA甲1020四:恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷()A 和世界级自然保护区星斗山()B 位于笔直的沪渝高速公路X 同侧,50km AB A =,、B 到直线X 的距离分别为10km 和40km ,要在沪渝高速公路旁修建一服务区P ,向A 、B 两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(AP 与直线X 垂直,垂足为P ),P 到A 、B 的距离之和1S PA PB =+,图(2)是方案二的示意图(点A 关于直线X 的对称点是A ',连接BA '交直线X 于点P ),P 到A 、B 的距离之和2S PA PB =+. (1)求1S 、2S ,并比较它们的大小; (2)请你说明2S PA PB =+的值为最小;(3)拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,B 到直线Y 的距离为30km ,请你在X 旁和Y 旁各修建一服务区P 、Q ,使P 、A 、B 、Q 组成的四边形的周长最小.并求出这个最小值.P图(1)图(3)图(2)五:已知:如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,DE ⊥AC 于点F ,交BC 于点G ,交AB 的延长线于点E ,且AE AC =. (1)求证:BG FG =;(2)若2AD DC ==,求AB 的长. 四边形:一:如图,△ACD 、△ABE 、△BCF 均为直线BC 同侧的等边三角形. (1) 当AB ≠AC 时,证明四边形ADFE 为平行四边形;(2) 当AB = AC 时,顺次连结A 、D 、F 、E 四点所构成的图形有哪几类?直接写出构成图形的类型和相应的条件.DCEB GAFEFDABC二:如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF。
浙教版初中数学八年级下册第一单元《二次根式》(困难)(含答案解析)

浙教版初中数学八年级下册第一单元《二次根式》(困难)(含答案解析)考试范围:第一单元; 考试时间:120分钟;总分:120分,第I卷(选择题)一、选择题(本大题共12小题,共36.0分。
在每小题列出的选项中,选出符合题目的一项)1. 在实数范围内,√x−1有意义,则x的取值范围是( )A. x≥1B. x≤1C. x>1D. x<12. 设等式√a(x−a)+√a(y−a)=√x−a−√a−y在实数范围内成立,其中a、x、y是两两不同的实数,则3x 2+xy−y2x2−xy+y2的值是( )A. 3B. 13C. 2 D. 533. 设x、y、z是两两不等的实数,且满足下列等式:√x3(y−x)3+√x3(z−x)3=√y−x−√x−z,则x3+y3+z3−3xyz的值是( )A. 0B. 1C. 3D. 条件不足,无法计算4. 化简二次根式√−8a3的结果为( )A. −2a√−2aB. 2a√2aC. 2a√−2aD. −2a√2a5. 如果a+√a2−6a+9=3成立,那么实数a的取值范围是( )A. a≤0B. a≤3C. a≥−3D. a≥36. 如图为直线l:y=mx+n(m,n为常数且m≠0)的图象,化简√n2−|m−n|的结果为( )A. −mB. mC. m−2nD. 2n−m7. a,b,c为有理数,且等式a+b√2+c√3=√5+2√6成立,则2a+999b+1001c的值是( )A. 1999B. 2000D. 不能确定8. a,b,c为有理数,且等式a+b√2+c√3=√5+2√6成立,则2a+999b+1001c的值是( )A. 1999B. 2000C. 2001D. 不能确定9. 如图,在长方形ABCD中,AB=6,BC=10,其内部有边长为a的正方形AEFG与边长为b的正方形HIJK,两个正方形的重合部分也为正方形,且面积为5,若S2=4S1,则正方形AEFG与正方形HIJK的面积之和为( )A. 20B. 25C. 492D. 81410. 已知x=√2021−√2020,则x6−2√2020x5−x4+x3−2√2021x2+2x−√2021的值为( )A. 0B. 1C. √2020D. √202111. 下列根式中为最简二次根式的是( )B. √a2+b2C. √12D. √3a312. 二次根式:①√9−x2;②√(a+b)(a−b);③√a2−2a+1;④√1;⑤√0.75中最简x二次根式是( )A. ①②B. ③④⑤C. ②③D. 只有④第II卷(非选择题)二、填空题(本大题共4小题,共12.0分)13. 若√4−a有意义,则a的取值范围为.a+214. 已知a<b,化简二次根式√−2a2b的结果是______.15. 实数a、b、c在数轴上的位置如图所示,化简下列代数式的值√a2−√(c−a+b)2+|b+3=______.c|−√b33=___________16. 若x<0,则√x2−√x3三、解答题(本大题共10小题,共80.0分。
(完整版)初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
初二数学经典难题(带答案及解析)

初二数学经典难题(带答案及解析)初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ 周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD 对角线AC上一动点(P与A、C不重合),点E在线段BC 上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD 边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC 和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
八下数学试题难题及答案

八下数学试题难题及答案一、选择题(每题3分,共30分)1. 若a、b、c是三角形的三边长,则下列不等式中正确的是()。
A. a + b > cB. a + b = cC. a + b < cD. a + b ≤ c答案:A2. 计算下列算式的结果:\(\sqrt{4} + \sqrt{9} - \sqrt{16}\) 的值是()。
A. 1B. 2C. 3D. 4答案:C3. 一个数的平方是9,这个数是()。
A. 3B. -3C. 3或-3D. 0答案:C4. 一个数的立方是-8,这个数是()。
A. 2B. -2C. 1D. -1答案:B5. 计算下列算式的值:\((-2)^3\) 的结果是()。
A. -8B. 8C. -2D. 2答案:A6. 一个等腰三角形的两边长分别为3和5,那么它的周长是()。
A. 8B. 11C. 13D. 16答案:C7. 一个数的绝对值是5,这个数是()。
A. 5B. -5C. 5或-5D. 0答案:C8. 计算下列算式的值:\((-3)^2\) 的结果是()。
A. 9B. -9C. 3D. -3答案:A9. 一个数的相反数是-7,那么这个数是()。
A. 7B. -7C. 0D. 14答案:A10. 计算下列算式的值:\(\frac{1}{2} + \frac{1}{3}\) 的结果是()。
A. \(\frac{1}{5}\)B. \(\frac{5}{6}\)C. \(\frac{3}{5}\)D. \(\frac{1}{6}\)答案:B二、填空题(每题4分,共20分)1. 一个数的平方根是4,那么这个数是______。
答案:162. 一个数的立方根是-2,那么这个数是______。
答案:-83. 一个数的绝对值是7,那么这个数可以是______。
答案:7或-74. 一个等腰三角形的两边长分别为4和6,那么它的周长是______。
答案:14或165. 计算下列算式的值:\(\frac{3}{4} - \frac{1}{2}\) 的结果是______。
八年级数学经典难题(答案 解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.GM=BCADMG=BC3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.PQ=(PQ=PQ=5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.PE=2PE==2CF=EF=CE===即正方形的边长为6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.解之得:经检验得:∴小口径水管速度为立方米7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.Y=上的一点,所以,所以正比例函数解析式为x,|OB×m|所以有,)=))﹣OP=(=28.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值..BE PF=x﹣xx xx x=()<时,9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.y=的图象上,﹣=12=,即PE=CE10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.xx与双曲线在双曲线××=×)))。
初二数学经典难题(带答案与解析)
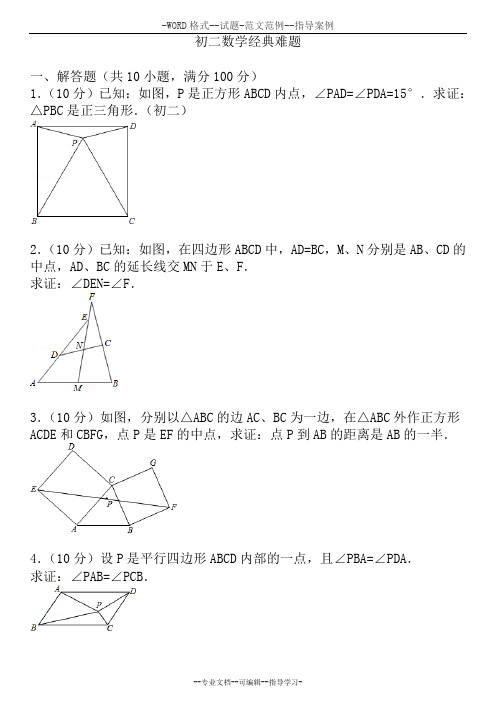
-WORD格式--试题-范文范例--指导案例初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ 与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
数学八年级试卷难题及答案

一、选择题(每题5分,共25分)1. 已知函数f(x) = 2x - 3,若f(a) = 1,则a的值为:A. 2B. 3C. 4D. 5答案:A解析:由f(a) = 2a - 3 = 1,得2a = 4,a = 2。
因此,选项A正确。
2. 在等腰三角形ABC中,底边AB = AC,顶角A的度数为:A. 45°B. 60°C. 90°D. 120°答案:D解析:等腰三角形的底角相等,顶角等于底角之和的一半。
因此,顶角A的度数为180° - 2×(底角/2) = 180° - 2×(90°/2) = 180° - 90° = 90°。
选项D 正确。
3. 已知一元二次方程x^2 - 5x + 6 = 0,其解为:A. x = 2, x = 3B. x = 2, x = 4C. x = 3, x = 4D. x = 2, x = -3答案:A解析:使用因式分解法解方程,得(x - 2)(x - 3) = 0,解得x = 2或x = 3。
因此,选项A正确。
4. 在直角坐标系中,点P(3, 4)关于y轴的对称点为:A. (3, -4)B. (-3, 4)C. (-3, -4)D. (3, 4)答案:B解析:点P(3, 4)关于y轴的对称点横坐标取相反数,纵坐标不变,即(-3, 4)。
因此,选项B正确。
5. 下列函数中,是反比例函数的是:A. y = x^2B. y = 2x + 1C. y = 1/xD. y = x^3答案:C解析:反比例函数的一般形式为y = k/x(k ≠ 0)。
选项C符合这一形式,因此是反比例函数。
二、填空题(每题5分,共25分)6. 已知等腰三角形底边AB = 8cm,腰AC = 10cm,则高CD的长度为______cm。
答案:6cm解析:由等腰三角形的性质,高CD将底边AB平分,即AD = DB = 4cm。
(完整版)初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
八年级下数学难题精选含答案

m =k;第三步:分别用 3、4、5
(1)当面积 S 等于 150 时,请用康熙的“积求勾股法”求出这个直角三角形的
三边长;
(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.
二:一张等腰三角形纸片,底边长 l5cm,底边上的高长 22.5cm.现沿底边 依次从下往上裁剪宽度均为 3cm 的矩形纸条,如图所示.已知剪得的纸条中有 一张是正方形,则这张正方形纸条是( )
DE,连接 BD.点 P 从点 E 出发沿射线 ED 运动,过点 P 作 PQ∥BD 交直线 BE
于点 Q.
(1) 当点 P 在线段 ED 上时(如图 1),求证:BE=PD+
3 PQ;
3
(2)若 BC=6,设 PQ 长为 x,以 P、Q、D 三点为顶点所构成的三角形面
积为 y,求 y 与 x 的函数关系式(不要求写出自变量 x 的取值范围);
由勾股定理可得 OQ2 = n2 + 4 = (n- 2)2 + 4 ,
n2
n
所以当 (n- 2)2 = 0 即 n- 2 = 0时, OQ2 有最小值 4,
n
n
又因为 OQ 为正值,所以 OQ 与 OQ2 同时取得最小值,
所以 OQ 有最小值 2. 由勾股定理得 OP= 5 ,所以平行四边形 OPCQ周长的最小值是
A.第 4 张 B.第 5 张 C.第 6 张 D.第 7 张
三:如图,甲、乙两楼相距 20 米,甲楼高 20 米,小明站在距甲楼 10 米的 A 处
目测得点 A 与甲、乙楼顶 B、C 刚好在同一直线上,且 A 与 B 相距 50 米,若小 3
明的身高忽略不计,则乙楼的高度是
米.
四:恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的
八年级数学经典难题(答案 解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.GM=BCADMG=BC3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.PQ=(PQ=PQ=5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.PE=2PE==2CF=EF=CE===即正方形的边长为6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.解之得:经检验得:∴小口径水管速度为立方米7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.Y=上的一点,所以,所以正比例函数解析式为x,|OB×m|所以有,)=))﹣OP=(=28.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值..BE PF=x﹣xx xx x=()<时,9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.y=的图象上,﹣=12=,即PE=CE10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.xx与双曲线在双曲线××=×)))。
八年级下数学难题精选含答案

(2)判断四边形ABDF是怎样的四边形,并说明理由。
(3)若AB=6,BD=2DC,求四边形ABEF的面积。
三:如图,在△ABC中,∠A、∠B的平分线交于点D,DE∥AC交BC于点E,DF∥BC交AC于点F.
(1)点D是△ABC的________心;
(1)当面积S等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;
(2)你能证明“积求勾股法”的正确性吗?请写出证明过程.
二:一张等腰三角形纸片,底边长l5cm,底边上的高长22.5cm.现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
三:如图,甲、乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的 处目测得点 与甲、乙楼顶 刚好在同一直线上,且A与B相距 米,若小明的身高忽略不计,则乙楼的高度是米.
四:恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷 和世界级自然保护区星斗山 位于笔直的沪渝高速公路 同侧, 、 到直线 的距离分别为 和 ,要在沪渝高速公路旁修建一服务区 ,向 、 两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图( 与直线 垂直,垂足为 ), 到 、 的距离之和 ,图(2)是方案二的示意图(点 关于直线 的对称点是 ,连接 交直线 于点 ), 到 、 的距离之和 .
分式:
1、解:原式= + +
= + +
=ห้องสมุดไป่ตู้
=1
2、解: + =
=
2( ) =9
初二数学八年级各种经典难题例题(含答案)非常经典

1已知一个等腰三角形二内角的度数之比为1:4,则那个等腰三角形顶角的度数为()之阳早格格创做A .20 B .120 C .20或者120 D .36 1.一个凸多边形的每一个内角皆等于150°,则那个凸多边形所有对付角线的条数总同有( )A .42条B .54条C .66条D .78条 3、若曲线11y k x =+与24y k x =-的接面正在x 轴上,那么k k 等于()(竞赛)1 正真数,x y 谦脚1xy =,那么44114x y +的最小值为:( ) (A)12 (B)58 (C)1 (D)2(竞赛)正在△ABC 中,若∠A >∠B ,则边少a 与c 的大小闭系是( )A 、a >cB 、c >aC 、a >1/2cD 、c >1/2a16.如图,曲线y=kx+6与x 轴y 轴分别接于面E ,F.面E 的坐标为(-8,0),面A 的坐标为(-6,0).(1)供k 的值;(2)若面P(x ,y)是第二象限内的曲线上的一个动面,当面P 疏通历程中,试写出△OPA 的里积S 与x的函数闭系式,并写出自变量x的与值范畴;(3)商量:当P 疏通到什么位子时,△OPA 的里积为827,并道明缘由.6、已知,如图,△ABC 中,∠BAC=90°,AB=AC,D 为AC 上一面,且∠BDC=124°,延少BA 到面E ,使AE=AD,BD 的延少线接CE 于面F ,供∠E 的度数.7.正圆形ABCD 的边少为4,将此正圆形置于仄里曲角坐标系中,使AB 边降正在X 轴的正半轴上,且A 面的坐标是(1,0).①曲线y=43x-83通过面C ,且与x 轴接与面E ,供四边形AECD 的里积;②若曲线l 通过面E 且将正圆形ABCD 分成里积相等的二部分供曲线l 的剖析式,③若曲线1l 通过面F ⎪⎭⎫ ⎝⎛-0.23且与曲线y=3x 仄止,将②中曲线l 沿着y 轴进与仄移32个单位接x 轴于面M ,接曲线1l 于面N ,供NMF ∆的里积.(竞赛奥数)如图,正在△ABC 中,已知∠C=60°,AC >BC ,又△ABC′、△BCA′、△CAB′皆是△ABC 形中的等边三角形,而面D 正在AC 上,且BC=DC(1)道明:△C′BD ≌△B′DC ;(2)道明:△AC′D ≌△DB′A ;9.已知如图,曲线343y x =-+x 轴相接于面A ,与曲线3y x=相接于面P .①供面P 的坐标. ②请推断OPA ∆的形状并道明缘由.③动面E 从本面O 出收,以每秒1个单位的速度沿着O→P→A 的门路背面A 匀速疏通(E 没有与面O 、A 沉合),过面E 分别做EF ⊥x 轴于F ,EB ⊥y 轴于B .设疏通t 秒时,矩形EBOF 与△OPA 沉叠部分的里积为S .供: S 与t 之间的函数闭系式.16多边形内角战公式等于(n - 2)×180根据题意即(n - 2)×180=150n,供得n=12, 多边形的对付角线的条数公式等于 n(n-3)/2戴进个多边形所有对付角线的条数同有54条果为二曲线接面正在x 轴上,则k1战k2必定没有为0,且接面处x=-1/k1=4/k2,所以k1:k2=-1:41/x^4+1/4y^4=(y^4+x^4)/x^4y^4果为xy=1所以x^4y^4=1所以本式=y^4+x^4果为(x^2-y^2)^2>0且(x^2-y^2)^2=y^4+x^4-x^2y^2大于或者等于0所以y^4+x^4大于或者等于x^2y^2 即1所以y^4+x^4的最小值为1竞赛解:正在△ABC中,∵∠A>∠B,∴a>b,∵a+b>c,∴2a>a+b>c,∴a>12c.故选C.1、y=kx+6过面E(-8,0)则-8K+6=0K=3/42、果面E(-8,0)则OE=8曲线剖析式Y=3X/4+6当X=0时,Y=6,则面F(0,6)果面A(0,6),则A、F沉合OA=6设面P(X,Y)则面P对付于Y轴的下为|X|当P正在第二象限时,|X|=-XS=OA×|X|/2=-6X/2=-3X3、S=3|X|当S=278时278=±3XX1=278/3,X2=-278/3Y1=3X1/4+6=3/4×278/3+6=151/2Y2=3X2/4+6=-3/4×278/3+6=-127/2面P1(278/3,151/2),P2(-278/3,-127/2)6解:正在△ABD战△ACE中,∵AB=AC,∠DAB=∠CAE=90°AD=AE,∴△ABD≌△ACE(SAS),∴∠E=∠ADB.∵∠ADB=180°-∠BDC=180°-124°=56°,∴∠E=56°.7(1)由题意知边少已经报告,易供四边形的里积;(2)由第一问供出E面的坐标,设出F面,根据曲线l通过面E且将正圆形ABCD分成里积相等的二部分,本来是二个曲角梯形,根据梯形里积公式,可供出F面坐标,进而解出曲线l的剖析式.解:(1)由已知条件正圆形ABCD的边少是4,∴四边形ABCD的里积为:4×4=16;(2)由第一问知曲线y=4/3x-8/3与x轴接于面E,∴E(2,0),设F(m,4),曲线l通过面E且将正圆形ABCD分成里积相等的二部分,由图知是二个曲角梯形,∴S梯形AEFD=S梯形EBCF= 1/2(DF+AE)•AE= 1/2(FC+EB)∴m=4,∵F(4,4),E(2,0),∴曲线l的剖析式为:y=2x-4竞赛奥数(1) 先证△ABC≌△C1BD:∵AB=C1B, ∠ABC=∠C1BD (果为皆是60°+∠ABD), BD=BC. (SAS)(得出:∠C1DB=∠C=60°)再证:△ABC≌△B1DC:∵AC=B1C, ∠C=∠B1CA=60°, BC=DC.(SAS)∴△C1BD≌△B1DC(得出:B1C=C1D)(2) ∵B1C=C1D,B1C=AB1,∴AB1=C1D∠C1DB=60°,∠BDC=60°,∴∠ADC1=60°=∠B1ADAD是公同边∴△AC1D≌△DB1A (SAS)(3) S△B1CA > S△ABC1 > S△ABC > S△BCA1y=-(3^½)x+4*(3^½)与x轴相接于A,即x=4,y=0,则A面坐标为:(4,0)又与y=(3^½)x相接于P,则联列解得:x=2,y=2*(3^½)即P面坐标为:(2,2*(3^½))|OP|={2²+[2*(3^½)]²}^½=4|AP|={(2-4)²+[2*(3^½)]²}^½=4而|OA|=4所以△OAP为等边三角形。
(完整版)初二数学八年级各种经典难题例题(含答案)非常经典

1 已知一个等腰三角形两内角的度数之比为1: 4 ,则这个等腰三角形顶角的度数为( )A . 20B .120C . 20 或120D . 361.一个凸多边形的每一个内角都等于 150°,则这个凸多边形所有对角线的条数总共有( )A .42 条B .54 条C .66 条D .78 条3、若直线 y = k x +1 与 y = k x - 4 的交点在 x 轴上,那么 k 1 等于() 1 2 2A .4 B. - 4 C. 1 41 1 D. - 1 4 (竞赛)1 正实数 x , y 满足 xy = 1,那么 x 4 + 4 y 4的最小值为:( ) 15(A) (B) (C)1 (D) 2 8(竞赛)在△ABC 中,若∠A >∠B ,则边长 a 与 c 的大小关系是()A 、a >cB 、c >aC 、a >1/2cD 、c >1/2a16. 如图,直线 y=kx+6 与 x 轴 y 轴分别交于点 E ,F.点 E的坐标为(-8,0),点 A 的坐标为(-6,0).(1)求 k 的值;(2) 若点 P(x ,y)是第二象限内的直线上的一个动点,当点 P 运动过程中,试写出△OPA 的面积 S 与 x 的函数关系式,并写出自变量 x 的取值范围;27(3) 探究:当 P 运动到什么位置时,△OPA 的面积为 ,并说明理由.8 2k⎝ ⎭ 6、已知,如图,△ABC 中,∠BAC=90°,AB=AC,D 为 AC 上一点,且∠BDC=124°,延长 BA 到点 E ,使 AE=AD,BD 的延长线交 CE 于点 F ,求∠E 的度数。
7.正方形 ABCD 的边长为 4,将此正方形置于平面直角坐标系中,使 AB 边落在 X 轴的正半轴上,且 A 点的坐标是(1,0)。
4 8 ①直线 y=3x-3经过点 C ,且与 x 轴交与点 E ,求四边形 AECD 的面积;②若直线l 经过点 E 且将正方形 ABCD 分成面积相等的两部分求直线l 的解析式, ③若直线l 经过点 F ⎛- 3 .0⎫ 且与直线 y=3x 平行,将②中直线l 沿着 y 轴向上平移 2 个单位1 2 ⎪ 3交 x 轴于点 M ,交直线l 1 于点 N ,求∆NMF 的面积.(竞赛奥数)如图,在△ABC 中,已知∠C=60°,AC>BC,又△ABC′、△BCA′、△CAB′都是△ABC 形外的等边三角形,而点D 在AC 上,且BC=DC(1)证明:△C′BD≌△B′DC;(2)证明:△AC′D≌△DB′A;3x + 4 与x 轴相交于点A,与直线y = 3x 相交于点P.9.已知如图,直线y =-3①求点P 的坐标.②请判断∆OPA 的形状并说明理由.③动点E 从原点O 出发,以每秒1 个单位的速度沿着O→P→A 的路线向点A 匀速运动(E 不与点O、A 重合),过点E 分别作EF⊥x 轴于F,EB⊥y 轴于B.设运动t 秒时,矩形EBOF 与△OPA 重叠部分的面积为S.求:S 与t 之间的函数关系式.yPEBO F A x16多边形内角和公式等于(n -2)×180根据题意即(n -2)×180=150n,求得n=12,多边形的对角线的条数公式等于 n(n-3)/2 带入 n=12,则这个多边形所有对角线的条数共有 54 条因为两直线交点在x 轴上,则k1 和k2 必然不为0,且交点处x=-1/k1=4/k2,所以k1:k2=-1:41/x^4+1/4y^4=(y^4+x^4)/x^4y^4因为xy=1所以x^4y^4=1所以原式=y^4+x^4因为(x^2-y^2)^2>0且(x^2-y^2)^2=y^4+x^4-x^2y^2 大于或等于0所以y^4+x^4 大于或等于x^2y^2 即1所以 y^4+x^4 的最小值为 1竞赛解:在△ABC 中,∵∠A>∠B,∴a>b,∵a+b>c,∴2a>a+b>c,∴a>12c.故选C.1、y=kx+6 过点E(-8,0)则-8K+6=0K=3/42、因点E(-8,0)则OE=8直线解析式Y=3X/4+6当X=0 时,Y=6,则点F(0,6)因点A(0,6),则A、F 重合OA=6设点P(X,Y)则点P 对于Y 轴的高为|X|当P 在第二象限时,|X|=-XS=OA×|X|/2=-6X/2=-3X3、S=3|X|当S=278 时278=±3XX1=278/3,X2=-278/3 Y1=3X1/4+6=3/4×278/3+6=151/2 Y2=3X2/4+6=-3/4×278/3+6=-127/2点 P1(278/3,151/2),P2(-278/3,-127/2)6解:在△ABD 和△ACE 中,∵AB=AC,∠DAB=∠CAE=90°AD=AE,∴△ABD≌△ACE(SAS),∴∠E=∠ADB.∵∠ADB=180°-∠BDC=180°-124°=56°,∴∠E=56°.7(1)由题意知边长已经告诉,易求四边形的面积;(2)由第一问求出E 点的坐标,设出F 点,根据直线l 经过点E 且将正方形ABCD 分成面积相等的两部分,其实是两个直角梯形,根据梯形面积公式,可求出F 点坐标,从而解出直线l 的解析式.解:(1)由已知条件正方形ABCD 的边长是4,∴四边形ABCD 的面积为:4×4=16;(2)由第一问知直线y=4/3x-8/3 与x 轴交于点E,∴E(2,0),设F(m,4),直线l 经过点E 且将正方形ABCD 分成面积相等的两部分,由图知是两个直角梯形,∴S 梯形AEFD=S 梯形EBCF= 1/2(DF+AE)•AE= 1/2(FC+EB)∴m=4,∵F(4,4),E(2,0),∴直线 l 的解析式为:y=2x-4竞赛奥数(1) 先证△ABC≌△C1BD:∵AB=C1B, ∠ABC=∠C1BD (因为都是60°+∠ABD), BD=BC。
初二数学经典难题(带答案及解析)
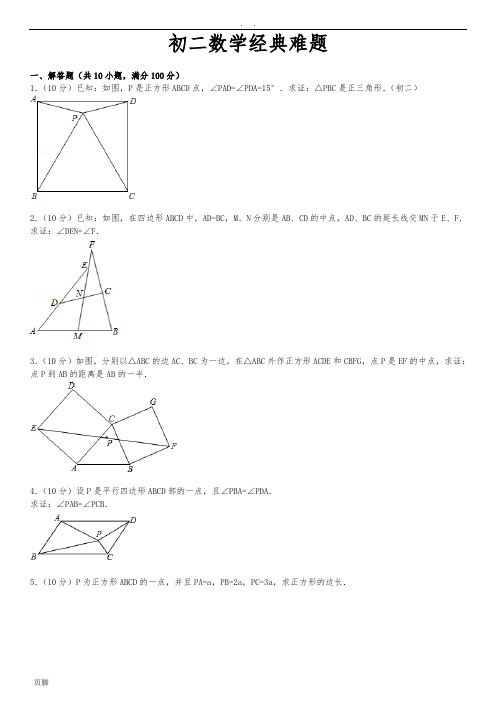
. .初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC 上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学难题精选分式:一:如果abc=1,求证:11++a ab +11++b bc +11++c ac =1二:已知a 1+b 1=)(29b a +,则a b +b a等于多少反比例函数:一:一张边长为16cm 正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“E ”图案如图1所示.小矩形的长x (cm )与宽y (cm )之间的函数关系如图2所示:(1)求y 与x 之间的函数关系式; (2)“E ”图案的面积是多少(3)如果小矩形的长是6≤x ≤12cm ,求小矩形宽的范围.二:如图,是一个反比例函数图象的一部分,点(110)A ,,(101)B ,是它的两个端点.(1)求此函数的解析式,并写出自变量x 的取值范围; (2)请你举出一个能用本题的函数关系描述的生活实例.三:如图,已知正比例函数和反比例函数的图像都经过点M (-2,1),且P (1,-2)为双曲线上的一点,Q 为坐标平面上一动点,PA 垂直于x 轴,QB 垂直于y 轴,垂足分别是A 、B .1111ABOy(1)写出正比例函数和反比例函数的关系式;(2)当点Q 在直线MO 上运动时,直线MO 上是否存在这样的点Q ,使得△OBQ 与△OAP 面积相等如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图,当点Q 在第一象限中的双曲线上运动时,作以OP 、OQ 为邻边的平行四边形OPCQ ,求平行四边形OPCQ 周长的最小值.四:如图,在平面直角坐标系中,直线AB 与Y 轴和X 轴分别交于点A 、点B 与反比例函数在第一象限的图象交于点c(1,6)、点D(3,x).过点C 作CE ⊥y 轴于E ,过点D 作DF ⊥X 轴于F .(1)求m ,n 的值; (2)求直线AB 的函数解析式;xyBA OMQP图xyBCA OMPQ勾股定理:一:清朝康熙皇帝是我国历史上对数学很有兴趣的帝王.近日,•西安发现了他的数学专著,其中有一文《积求勾股法》,它对“三边长为3、4、5的整数倍的直角三角形,已知面积求边长”这一问题提出了解法:“若所设者为积数(面积),以积率六除之,平方开之得数,再以勾股弦各率乘之,即得勾股弦之数”.用现在的数学语言表述是:“若直角三角形的三边长分别为3、4、5的整数倍,•设其面积为S ,则第一步:6S=m ;第二步:m =k ;第三步:分别用3、4、5乘以k ,得三边长”.(1)当面积S 等于150时,请用康熙的“积求勾股法”求出这个直角三角形的三边长;(2)你能证明“积求勾股法”的正确性吗请写出证明过程.二:一张等腰三角形纸片,底边长l5cm ,底边上的高长22.5cm .现沿底边依次从下往上裁剪宽度均为3cm 的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )A .第4张B .第5张C .第6张D .第7张三:如图,甲、乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的A 处目测得点A 与甲、乙楼顶BC 、刚好在同一直线上,且A 与B 相距350米,若小明的身高忽略不计,则乙楼的高度是 米.四:恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世.著名的恩施大峡谷()A 和世界级自然保护区星斗山()B 位于笔直的沪渝高速公路X 同侧,50km AB A =,、B 到直线X 的距离分别为10km 和40km ,要在沪渝高速公路旁修建一服务区P ,向A 、B 两景区运送游客.小民设计了两种方案,图(1)是方案一的示意图(AP 与直线X 垂直,垂足为P ),P 到A 、B 的距离之和1S PA PB =+,图(2)是方案二的示意图(点A 关于直线X 的对称点是A ',连接BA '交直线X 于点P ),P 到A 、B 的距离之和2S PA PB =+.(1)求1S 、2S ,并比较它们的大小; (2)请你说明2S PA PB =+的值为最小;(3)拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直,建立如图(3)所示的直角坐标系,B 到直线Y 的距离为30km ,请你在X 旁和Y 旁各修建一服务区P 、Q ,使P 、A 、B 、Q 组成的四边形的周长最小.并求出这个最小值.米五:已知:如图,在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,DE ⊥AC 于点F ,交BC 于点G ,交AB 的延长线于点E ,且AE AC =. (1)求证:BG FG =;(2)若2AD DC ==,求AB 的长.四边形:一:如图,△ACD 、△ABE 、△BCF 均为直线BC 同侧的等边三角形. (1) 当AB ≠AC 时,证明四边形ADFE 为平行四边形;(2) 当AB = AC 时,顺次连结A 、D 、F 、E 四点所构成的图形有哪几类直接写出构成图形的类型和相应的条件.图(1)图(3)图(2)DCEB GAF EFDA二:如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF。
(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明。
(2)判断四边形ABDF是怎样的四边形,并说明理由。
(3)若AB=6,BD=2DC,求四边形ABEF的面积。
三:如图,在△ABC中,∠A、∠B的平分线交于点D,DE∥AC交BC于点E,DF∥BC交AC于点F.(1)点D是△ABC的________心;(2)求证:四边形DECF为菱形.四:在矩形ABCD中,点E是AD边上一点,连接BE,且∠ABE=30°,BE =DE,连接BD.点P从点E出发沿射线ED运动,过点P作PQ∥BD交直线BE于点Q.3PQ;(1) 当点P在线段ED上时(如图1),求证:BE=PD+3(2)若 BC=6,设PQ长为x,以P、Q、D三点为顶点所构成的三角形面积为y,求y与 x的函数关系式(不要求写出自变量x的取值范围);(3)在②的条件下,当点P运动到线段ED的中点时,连接QC,过点P作PF⊥QC,垂足为F,PF交对角线BD于点G(如图2),求线段PG的长。
五:如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形分别画出它们的示意图...,并写出它们的周长.六:已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF ⊥ED.求证:AE平分∠BAD.(第23题)七:如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10.(1)当折痕的另一端F 在AB 边上时,如图(1).求△EFG 的面积.(2)当折痕的另一端F 在AD 边上时,如图(2).证明四边形BGEF 为菱形,并求出折痕GF 的长.HA BCD EF G图(2)ABCDE FG H (A)(B)ABCDE F G图(1)分式:1、解:原式=11++a ab +a ab abc a +++ababc bc a ab ++2=11++a ab +a ab a ++1+aba ab++1=11++++a ab a ab=1 2、解:a 1+b 1=)(29b a + ab b a +=)(29b a + 2(b a +)2=9ab 22a +4ab +22b =9ab 2(22b a +)=5abab b a 22+=25a b +b a =25反比例函数1、解:(1)设函数关系式为xky =∵函数图象经过(10,2) ∴102k = ∴k =20, ∴xy 20= (2)∵xy 20=∴xy =20, ∴2162022162=⨯-=-=xy S S E 正 (3)当x =6时,310620==y 当x =12时,351220==y ∴小矩形的长是6≤x ≤12cm ,小矩形宽的范围为cm y 31035≤≤2、解:(1)设ky x=,(110)A ,在图象上,101k∴=,即11010k =⨯=, 10y x∴=,其中110x ≤≤; (2)答案不唯一.例如:小明家离学校10km ,每天以km/h v 的速度去上学,那么小明从家去学校所需的时间10t v=. 3、 解:(1)设正比例函数解析式为y kx =,将点M (2-,1-)坐标代入得12k,所以正比例函数解析式为12y x 同样可得,反比例函数解析式为2y x(2)当点Q 在直线DO 上运动时,设点Q 的坐标为1()2Q m m ,,于是,2m 41m m 212121=••==BQ OB SOBQ △而,()SOAP 12121=-=△ 所以有,2114m ,解得2m =±所以点Q 的坐标为1(21)Q ,和2(21)Q , (3)因为四边形OPCQ 是平行四边形,所以OP =CQ ,OQ =PC ,而点P (1-,2-)是定点,所以OP 的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ 的最小值.因为点Q 在第一象限中双曲线上,所以可设点Q 的坐标为2()Q n n ,,由勾股定理可得222242()4OQ n nn n,所以当22()0nn即20nn 时,2OQ 有最小值4,又因为OQ 为正值,所以OQ 与2OQ 同时取得最小值, 所以OQ 有最小值2.由勾股定理得OP =5,所以平行四边形OPCQ 周长的最小值是2()2(52)254OPOQ勾股定理1、解:(1)当S=150时,==, 所以三边长分别为:3×5=15,4×5=20,5×5=25; (2)证明:三边为3、4、5的整数倍, 设为k 倍,则三边为3k ,4k ,5k ,• 而三角形为直角三角形且3k 、4k 为直角边. 其面积S=12(3k )·(4k )=6k 2,所以k 2=6S ,, 即将面积除以6,然后开方,即可得到倍数. 2、答案:C 3、答案:40米 4、解:⑴:图(1)中过B 作BC ⊥AP,垂足为C,则PC =40,又AP =10, ∴AC =30在Rt △ABC 中,AB =50 AC =30 ∴BC =40 ∴ BP =24022=+BC CP S 1=10240+⑵:图(2)中,过B 作BC ⊥AA ′垂足为C ,则A ′C =50,又BC =40∴BA'=4110504022=+ 由轴对称知:PA =PA' ∴S 2=BA'=4110 ∴1S ﹥2S(2)如 图(2),在公路上任找一点M,连接MA,MB,MA',由轴对称知MA =MA' ∴MB+MA =MB+MA'﹥A'B ∴S 2=BA'为最小(3)过A 作关于X 轴的对称点A', 过B 作关于Y连接A'B',交X 轴于点P, 交Y 轴于点Q,则P,Q 即为所求 过A'、 B'分别作X 轴、Y 轴的平行线交于点G, A'B'=5505010022=+ ∴所求四边形的周长为55050+5、解:(1)证明:90ABC DE AC ∠=°,⊥于点F ,ABC AFE ∴∠=∠.AC AE EAF CAB =∠=∠,,ABC AFE ∴△≌△AB AF ∴=. 连接AG , AG =AG,AB =AF ,Rt Rt ABG AFG ∴△≌△.DCBGAFBG FG ∴=.(2)解:∵AD =DC,DF ⊥AC ,1122AF AC AE ∴==. 30E ∴∠=°. 30FAD E ∴∠=∠=°,3AF ∴=. 3AB AF ∴==.四边形1、解:(1) ∵△ABE 、△BCF 为等边三角形,∴AB = BE = AE ,BC = CF = FB ,∠ABE = ∠CBF = 60°. ∴∠FBE = ∠CBA . ∴△FBE ≌△CBA . ∴EF = AC .又∵△ADC 为等边三角形, ∴CD = AD = AC . ∴EF = AD. 同理可得AE = DF .∴四边形AEFD 是平行四边形.(2) 构成的图形有两类,一类是菱形,一类是线段.当图形为菱形时,∠ BAC ≠60°(或A 与F 不重合、△ABC 不为正三角形) 当图形为线段时,∠BAC = 60°(或A 与F 重合、△ABC 为正三角形). 2、解:(1)(选证一)BDE FEC ≅,,,60ABC CD CE BD AE EDC DE EC CDE DEC ∴∠=∴=∴=∠=∠=0是等边三角形,BC=AC,ACB=60是等边三角形 0120,,BDE FEC EF AE BD FE BDE FEC ∴∠=∠==∴=∴≅(选证二)BCE FDC ≅ 证明:0,,60ABC BC AC ACB ∴=∠=是等边三角形0,60,,,CD CE EDC BCE FDC DE CEEF AE EF DE AE CE FD AC BC BCE FDC=∴∴∠=∠===∴+=+∴==∴≅是等边三角形(选证三)ABE ACF ≅ 证明:0,,60ABC AB AC ACB BAC ∴=∠=∠=是等边三角形0,,,60CD CE EDC AEF CED EF AE AEF AE AF EAF ABE ACF=∴∴∠=∠=∴∴=∠=∴≅0是等边三角形=60是等边三角形 (2)四边形ABDF 是平行四边形。
