等边三角形PPT课件-精
合集下载
《等边三角形》课件PPT1
将两个含30°角的同样的三角尺如图摆放在一起. 4m, ∠A=30°.
例 2.已 知 ： 如 图 ， △ ABC 中 ， AB ＝ AC， ∠ A ＝ 在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.
你会用学过的方法证明吗?
120°，DE垂直平分AB于D，交BC于E点． 如图:△ABC是等边三角形，AD⊥BC，DE⊥AB，若AB=8cm， 求证：CE＝2BE. 如图，已知△ABC 是等边三角形，D、E 分别是
Ｂ Ｃ 30° Ａ
2.如图:△ABC是等边三角形，
A
AD⊥BC，DE⊥AB，若AB=8cm，
BD=＿＿＿，BE=_______.
E
B DC
【典例分析】
例1.已知,如图是屋架设计图的一部分，点D是斜 梁 AB 的 中 点 ， 立 柱 BC,DE 垂 直 于 横 梁 AC ， AB=7.4m, ∠A=30°.立柱BC，DE要多长.
AB
你会用学过的方法证明吗?
【归纳】
定理:在直角三角形中，如果一个锐角等于30°, 那么它所对的直角边等于斜边的一半.
应用格式：
B
在△ABC中,∵∠ACB=90°,∠A=30°.
∴BC=
1 2
AB.
A 300
C
这是一个判定两条线段成倍半关系的根据之一.
【比一比】看 谁 算 得 快
1.如图：在Rt△ABC中 ∠A=30°,AB+BC=12cm， 则AB=_____cm.
2.等边三角形的判定：
（1）三边相等的三角形是等边三角形. （2）三个内角都相等的三角形是等边三角形. （3）有一个角是60 °的等腰三角形是等边三角形.
【探究】
将两个含30°角的同样的三角尺如图摆放在 一起.你能借助这个图形，找到Rt△ABC的直角边 BC与斜边AB之间的数量关系吗?
《等边三角形》课件
∴∠A=∠B=∠C（等边对等角）.
∵∠A+∠B+∠C=180°，
B
C
∴∠A=∠B=∠C=60°.
等边三角形的性质：等边三角形的三个内角都相等，
并且每一个角都等于60°. A
几何语言：如图，在△ABC中，
∵AB=BC=AC，
∴∠A=∠B=∠C=60°.
B
C
把等腰三角形的性质应用到等边三角形，能得到等边
三角形的什么性质？
等腰三角形的性质2：等腰三角形的顶角平分线、底边
上的中线、底边上的高互相重合.
A
等边三角形每条边上的中线、高
和所对角的平分线相互重合.
B
C
把等腰三角形的性质应用于等边三角形，能得到等边
三角形的什么性质？
等腰三角形是轴对称图形，对称轴是顶角平分线（底边
上的中线、底边上的高）所在的直线. A 等边三角形是轴对称图形， 它有三条对称轴.
∴∠ABC=∠ACB=60°，∴∠DBE=
1 2
∠ABC=30°.
∵DE=DB， ∴∠E=∠DBE=30°.
∵∠ACB=∠CDE+∠E, ∴∠CDE=∠ACB-∠E=30°.
∴∠CDE=∠E. ∴CD=CE.
∵等边三角形ABC的边长为3，点D是AC的中点，
∴CE=CD=
3 2
.
随堂练习
1.如图，已知△ABC是等边三角形，点 B，C，D，E在同一直线上，且CG=CD， DF=DE，则∠E=（ A ） A.15° B.20° C.25° D.30°
△ABC为 等边三角形
∠ACB=60°
CG=CD ∠CGD=∠CDG
∠CDG=30 ° 同理，∠E=15 °
2.如图，在等边三角形ABC中，D，E
等边三角形优秀PPT课件
04
等边三角形在生活中的应用
建筑领域应用
建筑设计
等边三角形在建筑设计中常被用作基本的几何形状，创造出 独特而稳定的结构。例如，在穹顶、尖顶和拱门等建筑元素 中，等边三角形能够提供均匀的支撑力，并赋予建筑物动感 和美感。
结构设计
等边三角形的稳定性使其在建筑结构设计中具有优势。工程 师经常利用等边三角形的特性来构建桥梁、塔楼和其他需要 坚固支撑的建筑结构。
等边三角形的判定
关键知识点总结
01பைடு நூலகம்
若三角形三边长度相等，则它是 等边三角形。
02
若三角形有两个内角为60°，则它 是等边三角形。
易错难点剖析
1 2
与等腰三角形的混淆
学生容易将等边三角形与等腰三角形混淆。等腰 三角形有两边长度相等，而等边三角形三边长度 均相等。
角度计算错误
在等边三角形中，每个内角都是60°。学生在计 算角度时可能会出错，导致后续问题无法解决。
性质总结
性质一
等边三角形的三个内角 均为60°。
性质二
等边三角形的任意一边 上的中线、高线和角平 分线互相重合（三线合
一）。
性质三
等边三角形是轴对称图 形，它有三条对称轴， 分别是三条边的垂直平
分线。
性质四
等边三角形在平面内绕 其重心旋转120°后，能 够和原来的图形重合。
02
等边三角形判定方法
周长计算公式推导
等边三角形周长公式
P = 3a，其中a为等边三角形的边长。
公式推导
等边三角形的三条边长度相等，因此周长为3倍的边长，即P = 3a。
典型例题解析
例题1
解析
例题2
解析
已知等边三角形的边长为5cm ，求其面积和周长。
课件《等边三角形》优质PPT课件_人教版1
以AD为一边，作等边三角形ADE，则DE与AC垂直吗？请说明理由。 ⒈ 三个角都相等的三角形是等边三角形.
∴ ∠A=∠B=∠C(在同一个三角形中等边对等角)
∴BC=CA（等角对等边）
1、如图，在等边三角形ABC中AD⊥BC于D。
三边相等的三角形是等边三角形.
有一个角是60°的等腰三角形是等边三角形.
已知:等边△ABC中, BD是AC边上的高,E是BC延长线上一点,且DB=DE,求∠ E的度数.
(2) △DEF为等边三角形吗?为什么?
探究：如图,等边三角形ABC,以下三种方法分别得到的三角形ADE都是等边三角形吗？为什么？
等腰三角形 （2）∠ADE=60°，D，E分别在边AB，AC上
∴ ∠A=∠B=∠C(在同一个三角形中等边对等角)
0
A
(1)求∠BEC的度数.
已知： ⊿ABC中，AB=AC， ∠B=600。
求证：AB=AC=BC ∵ ∠ A=∠B（已知）
等边三角形的判定方法:
∴ ∠B=∠C （等边对等角）
证明： ⊿ABC中 有一个是60°的等腰三角形是等边三角形。
∠APB＝60°AP＝BP＝200cm,他们 等边三角形的内角都相等,且等于60 °
想想看，等边三角形
A
有什么性质？
B
C
⑴三边之间 AB＿＝AC＿＝BC
⑵三角之间 ∠A＿＝∠B＿＝∠C
探索星空：探究性质一
1、等边三角形的三个内角都相等，并且每一
个角都等于60°.
A
∵ AB=AC=BC
∴ ∠A=∠B=∠C(在同一
B
C
个三角形中等边对等角)
∵ ∠A+∠B+∠C=180° ∴ ∠A=∠B=∠C=60°
∴ ∠A=∠B=∠C(在同一个三角形中等边对等角)
∴BC=CA（等角对等边）
1、如图，在等边三角形ABC中AD⊥BC于D。
三边相等的三角形是等边三角形.
有一个角是60°的等腰三角形是等边三角形.
已知:等边△ABC中, BD是AC边上的高,E是BC延长线上一点,且DB=DE,求∠ E的度数.
(2) △DEF为等边三角形吗?为什么?
探究：如图,等边三角形ABC,以下三种方法分别得到的三角形ADE都是等边三角形吗？为什么？
等腰三角形 （2）∠ADE=60°，D，E分别在边AB，AC上
∴ ∠A=∠B=∠C(在同一个三角形中等边对等角)
0
A
(1)求∠BEC的度数.
已知： ⊿ABC中，AB=AC， ∠B=600。
求证：AB=AC=BC ∵ ∠ A=∠B（已知）
等边三角形的判定方法:
∴ ∠B=∠C （等边对等角）
证明： ⊿ABC中 有一个是60°的等腰三角形是等边三角形。
∠APB＝60°AP＝BP＝200cm,他们 等边三角形的内角都相等,且等于60 °
想想看，等边三角形
A
有什么性质？
B
C
⑴三边之间 AB＿＝AC＿＝BC
⑵三角之间 ∠A＿＝∠B＿＝∠C
探索星空：探究性质一
1、等边三角形的三个内角都相等，并且每一
个角都等于60°.
A
∵ AB=AC=BC
∴ ∠A=∠B=∠C(在同一
B
C
个三角形中等边对等角)
∵ ∠A+∠B+∠C=180° ∴ ∠A=∠B=∠C=60°
等边三角形的性质及判定ppt课件
避雷器施工方案避雷器施工方案一、施工准备1.安排专业电力施工人员，进行施工前培训，确保施工人员了解避雷器的安装要求和技术要求。
2.检查和确保所有施工所需的材料和设备齐全。
3.提前与施工现场相关部门进行沟通和协调，确保施工过程中不会受到其他工程的影响。
4.制定详细的施工方案和时间表，确保施工进度和质量。
二、施工步骤1.确定避雷器的安装位置，根据建筑物的结构和用途选择合适的位置。
2.准备施工区域，清理杂物和尘土，保持施工现场整洁。
3.安装避雷器支架，根据避雷器的尺寸和重量选择合适的支架，并按照安装说明进行固定。
4.安装避雷器导引线，将导引线安装在避雷器和接地装置之间，确保导引线的长度和质量符合要求。
5.连接避雷器和接地装置，使用合适的导线将避雷器与接地装置相连，确保连接牢固。
6.进行接地测试，使用测试仪器对避雷器和接地装置进行测试，确保接地电阻符合要求。
三、施工注意事项1.施工过程中要注意安全，佩戴好安全帽、防护眼镜等安全装备，确保施工人员的人身安全。
2.施工过程中要严格按照安装说明和施工方案进行操作，不得随意更改安装位置和方法。
3.避雷器施工完成后，要对避雷器进行检查和测试，确保安装质量和安全可靠性。
4.施工现场要保持干燥和整洁，防止杂物堆放或者其他物体碰撞避雷器，影响其使用寿命和效果。
5.施工完成后，要将施工现场清理干净，并将有关材料和设备整理妥当，妥善保管起来。
四、质量验收施工完成后，由相关部门进行质量验收并出具质量验收报告，确保避雷器的施工和安装质量符合相关规定和要求。
总结：避雷器的施工是一项技术活，需要专业的电力施工人员进行操作。
在施工过程中要严格按照施工方案和安装说明进行操作，注意安全和质量，确保避雷器安装的可靠性和持久性。
施工完成后要进行质量验收，确保避雷器施工的合格率和安全性。
同时，施工过程中要保持施工现场的整洁和安全，避免因杂物堆放或者其他原因影响避雷器的使用寿命和效果。
等边三角形(课件)-八年级数学上册(人教版)
证明：在△ABC 中，∵ ∠C =90°，
A
∠A =30°, ∴ ∠B =60°．
延长BC 到D，使BD =AB，连接AD，
则△ABD 是等边三角形．
又∵AC⊥BD, ∴BC = 1 BD．
2
∴BC = 1 AB．
2
B
C
证明方法： 倍长法
D
证法2
证明： 在BA上截取BE=BC，连接EC.
∵ ∠B= 60° ，BE=BC.
三个角都相等的三角 形是等边三角形
有一角是60°的等腰 三角形是等边三角形
例2 如图,在等边三角形ABC中，DE∥BC,
求证：△ADE是等边三角形.
证明：∵ △ABC是等边三角形， ∴ ∠A= ∠B= ∠C. ∵ DE//BC, ∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
证明： 三个角都相等的三角形是等边三角形.
已知：如图，∠A=∠B=∠C.
A
求证：AB=AC=BC.
证明： ∵ ∠A= ∠B,
∴ AC=BC. ∵ ∠B=∠C,
Bபைடு நூலகம்
C
∴ AB=AC.
∴AB=AC=BC.
证明： 有一个角是60°的等腰三角形是等边三角形.
已知： 若AB=AC ,∠A= 60°.
A
求证： AB=AC=BC.
从而△ABD是一个等边三角形. 再由AC⊥BD, 可得BC=CD=你 法还 证12 能 明AB用吗. 其？他方 性质：
B
C
D
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等 于斜边的一半.
证法1
已知：如图，在Rt△ABC 中，∠C =90°，∠A =30°.
《等边三角形》轴对称PPT课件
（2）求∠BFD的度数．
（1）证明：∵△ABC为等边三角形， ∴∠BAC=∠C=60°，AB=CA，即∠BAE=∠C=60°， 在△ABE和△CAD中， ∴△ABE≌△CAD（SAS）． （2）解：∵∠BFD=∠ABE+∠BAD， 又∵△ABE≌△CAD， ∴∠ABE=∠CAD． ∴∠BFD=∠CAD+∠BAD=∠BAC=60°．
2.如图，等边三角形ABC的三条角平分线交于点O，DE∥BC，则这个图形中的等腰
三角形共有（ ）
A. 4个 C. 6个
B. 5个 D. 7个
D
A
DOE
B
C
课堂检测
3.在等边△ABC中，BD平分∠ABC，BD=BF，则∠CDF的度数是（ ）
A．10° B．15° B
C．20°
D．25°
4.如图,△ABC和△ADE都是等边三角形，已知
∴AC＝MC，CN＝CB， ∠ACM＝∠BCN＝60°.
∴∠ACN＝∠MCB. ∴△ACN≌△MCB(SAS)． ∴AN＝BM.
图①
课堂检测
(2)△CEF是等边三角形． 证明：∵∠ACE＝∠FCM=60°，
∴∠ECF=60°. ∵△ACN≌△MCB， ∴∠CAE＝∠CMB. ∵AC＝MC， ∴△ACE≌△MCF(ASA)， ∴CE＝CF.
变式训练上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说
明理由.
证明： ∵ △ABC是等边三角形， ∴ ∠A= ∠B= ∠C. ∵ AD=AE, ∴ ∠ADE= ∠B, ∠ AED= ∠C. ∴ ∠A= ∠ADE= ∠ AED. ∴ △ADE是等边三角形.
A
D
E
B
C
探究新知
（1）证明：∵△ABC为等边三角形， ∴∠BAC=∠C=60°，AB=CA，即∠BAE=∠C=60°， 在△ABE和△CAD中， ∴△ABE≌△CAD（SAS）． （2）解：∵∠BFD=∠ABE+∠BAD， 又∵△ABE≌△CAD， ∴∠ABE=∠CAD． ∴∠BFD=∠CAD+∠BAD=∠BAC=60°．
2.如图，等边三角形ABC的三条角平分线交于点O，DE∥BC，则这个图形中的等腰
三角形共有（ ）
A. 4个 C. 6个
B. 5个 D. 7个
D
A
DOE
B
C
课堂检测
3.在等边△ABC中，BD平分∠ABC，BD=BF，则∠CDF的度数是（ ）
A．10° B．15° B
C．20°
D．25°
4.如图,△ABC和△ADE都是等边三角形，已知
∴AC＝MC，CN＝CB， ∠ACM＝∠BCN＝60°.
∴∠ACN＝∠MCB. ∴△ACN≌△MCB(SAS)． ∴AN＝BM.
图①
课堂检测
(2)△CEF是等边三角形． 证明：∵∠ACE＝∠FCM=60°，
∴∠ECF=60°. ∵△ACN≌△MCB， ∴∠CAE＝∠CMB. ∵AC＝MC， ∴△ACE≌△MCF(ASA)， ∴CE＝CF.
变式训练上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说
明理由.
证明： ∵ △ABC是等边三角形， ∴ ∠A= ∠B= ∠C. ∵ AD=AE, ∴ ∠ADE= ∠B, ∠ AED= ∠C. ∴ ∠A= ∠ADE= ∠ AED. ∴ △ADE是等边三角形.
A
D
E
B
C
探究新知
等边三角形课件共14张PPT
2
你能用一句话来
A
描述你的结论吗？
B
C
D
定理
在直角三角形中,如果一个锐角等于30° 那么它所对的直角边等于斜边的一半。
数学式:
A
30°
∵∴B∠CA＝C12B=ARBt ∠ ,∠A＝30°
C ┓ B 你还能用其它方法证明吗?
“在直角三角形中,如果一个锐角等于30° 那么它所对的直角边等于斜边的一半。”
C D
B
E
A
5、 如图，在△ABC中， ∠ACB= 90°，
∠B= 15°，AB的垂直平分线分别交BC、AB 于D、E。求证：DB=2AC
小结：
❖ 等边三角形的性质: 三边相等,三个角都是600,”三线合一”,三条对 称轴. ❖ 等边三角形的判定: 定义:有三边相等的三角形是等边三角形. 定理:有一个角是600的等腰三角形是等边三角形. 定理:三个角都相等的三角形是等边三角形. ❖ 特殊的直角三角形的性质: 定理:在直角三角形中, 如果有一个锐角等于300, 那么它所对的直角边等于斜边的一半. 定理:在直角三角形中, 如果一条直角边等于斜 边的一半,那么它所对的锐角等于300.
C D
B
E
A
4、 如图，上午9时，一条渔船从A出发，
以12海里/时的速度向正北航行，11时到达
B处，从A、B两处望小岛C，测得
∠NAC=150内有暗礁，问该渔船继续向正北
航行有无触礁的危险？
N
C
D
B
A
4、如图，在△ABC中， AB=AC， ∠BAC= 120°，AC的垂直平分线EF交AC 于点E，交BC于点F。求证：BF=2CF。
练习： 已知:等腰三角形的底角为150,腰长为2a. 求:腰上的高.
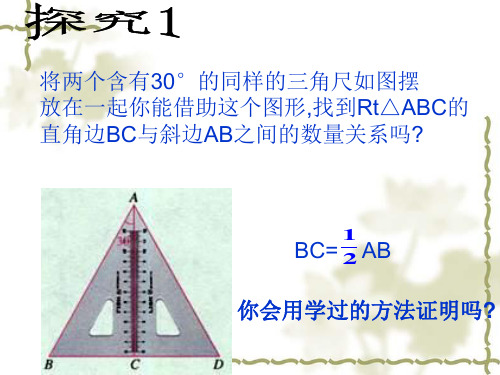
你能用一句话来
A
描述你的结论吗？
B
C
D
定理
在直角三角形中,如果一个锐角等于30° 那么它所对的直角边等于斜边的一半。
数学式:
A
30°
∵∴B∠CA＝C12B=ARBt ∠ ,∠A＝30°
C ┓ B 你还能用其它方法证明吗?
“在直角三角形中,如果一个锐角等于30° 那么它所对的直角边等于斜边的一半。”
C D
B
E
A
5、 如图，在△ABC中， ∠ACB= 90°，
∠B= 15°，AB的垂直平分线分别交BC、AB 于D、E。求证：DB=2AC
小结：
❖ 等边三角形的性质: 三边相等,三个角都是600,”三线合一”,三条对 称轴. ❖ 等边三角形的判定: 定义:有三边相等的三角形是等边三角形. 定理:有一个角是600的等腰三角形是等边三角形. 定理:三个角都相等的三角形是等边三角形. ❖ 特殊的直角三角形的性质: 定理:在直角三角形中, 如果有一个锐角等于300, 那么它所对的直角边等于斜边的一半. 定理:在直角三角形中, 如果一条直角边等于斜 边的一半,那么它所对的锐角等于300.
C D
B
E
A
4、 如图，上午9时，一条渔船从A出发，
以12海里/时的速度向正北航行，11时到达
B处，从A、B两处望小岛C，测得
∠NAC=150内有暗礁，问该渔船继续向正北
航行有无触礁的危险？
N
C
D
B
A
4、如图，在△ABC中， AB=AC， ∠BAC= 120°，AC的垂直平分线EF交AC 于点E，交BC于点F。求证：BF=2CF。
练习： 已知:等腰三角形的底角为150,腰长为2a. 求:腰上的高.
等边三角形PPT课件
回头看了一眼，朝独自跪在那里的人最后投去悲哀的一瞥。因为挨了四鞭，那人的背还在火辣辣的痛，他的膝盖也跪疼了。不过，这个老人会带着尊严死去，或至少是抱着这样的想法死去。 （节选自《偷书贼》第七章P265～267，略有删改） 致中国读者的信 亲爱的中国读者： ? 谢谢您阅读了这
本《偷书贼》。 ? 我小时候长听故事。我的爸爸妈妈经常在厨房里，把他们小时候的故事告诉我的哥哥、两个姐姐和我，我听了非常着迷，坐在椅子上动都不动。他们提到整个城市被大火笼罩，炸弹掉在他们家附近，还有童年时期建立的坚强友谊，连战火、时间都无法摧毁的坚强友谊。 ? 其中有
所以∠B=600
2
从而∠B=300
B
C
6
逆定理
在直角三角形中锐角是30°。
A
∵ AC⊥BC ， BC= 1AB
2
∴ ∠A= 30°
B
C
2021/4/8
7
例1 如图，是屋架设计图的一部分，点D是斜梁
AB的中点，立柱BC、DE垂直于横梁AC，AB=7.4 m ∠A= 30°,立柱BC、DE要多长？
；单创:/c/7radcKIT9fA
；
本文以小红包为线索，两次设置悬念，把小说情节推向高潮；小说的结尾安排巧妙，出人意料却又在情理之中，引人入胜． 【点评】本题考查对文本、故事情节的理解分析能力和对句子含义、作者感情的理解分析能力．其中第（2）题是重点题目，学生解答时，在理解文章内容主旨的基础上，结合
2
如图，将两个含30°角的三角尺摆放在一起。 你能借助这个图形，找到Rt △ABC的直角 边BC与斜边AB之间的数量关系吗？
A
另证：在BA上截取BE=BC，连接EC
30 ° 30 °
则△BCE是等边三角形，所以
《等边三角形》PPT优质课件
∴∠DBE= 1 ∠ABC=30°.
2
∵DE=DB，∴∠E=∠DBE=30°.
B
D CE
∵∠ACB=∠CDE+∠E,∴∠CDE=∠ACB-∠E=30°.
探索新知
知识点1 等边三角形的性质 【变式】如图，等边三角形ABC的边长为3，点D是AC的中点，点E在BC 的延长线上，若DE=DB，求CE的长.
知识点1 等边三角形的性质
A
BC边上的中线,高和所对角的平分线“三线合一”.
AB边上的中线,高和所对角的平分线“三线合一”.
B
C AC边上的中线,高和所对角的平分线“三线合一”.
等边三角形每条边上的中线、高和所对角的平分线相互重 合，即“三线合一”.
探索新知
知识点1 等边三角形的性质
思考3 把等腰三角形的对称性用于等边三角形，能得到什么结 论？
知识点1 等边三角形的性质
图形 性边 质角
三线 合一
等腰三角形
两条边相等 两个底角相等
底边上的中线、高和顶角 的平分线互相重合
对称 性
1条对称轴
等边三角形
三条边都相等 三个角都相等， 且都是60º 每一边上的中线、高和这一边 所对的角的平分线互相重合
3条对称轴
探索新知
知识点1 等边三角形的性质 例1 如图，△ABC是等边三角形，BD平分∠ABC，延长BC到点E，使 得CE=CD．求证：BD=DE．
有一个角是60°的等腰 三角形是等边三角形.
探索新知
知识点2 等边三角形的判定
例2 如图，△ABC是等边三角形，DE∥BC，分别交AB，AC于点D，E.
求证：△ADE是等边三角形.
证明：∵△ABC是等边三角形，∴∠A=∠B=∠C.
等边三角形PPT课件
②得出300 角所对的直角边与斜边之间的数量关系，说明理由.
第34页/共50页
• 探究2
操 作探 究
①当将两个同样大小的三角板（含30 °和60 °的角）摆在一起，
新得到的三角形是特殊的三角形吗？请说明理由；
②得出300 角所对的直角边与斜边之间的数量关系，说明理由.
第35页/共50页
验证：我们可以用两个同样大小的三角尺
二、 等边三角形的判定
1．三个边都相等的三角形是等边三角形； 2．三个角都相等的三角形是等边三角形； 3．有一个内角等于60 °的等腰三角形是等边三角形．
第31页/共50页
• 探究1
操 作探 究
用直尺量一量含30°角的直角三角板的最短直角边(即300 角所
对的直角边)与斜边，记录下数据，你有什么发现？
第14页/共50页
（3）等边三角形各边上中线,高
A
和所对角的平分线都三线合一. D
E
O
（4）等边三角形是轴对称 B F C
图形，有三条对称轴.
A
B
C
第15页/共50页
△ABC是等边三角形,D为AC的中点,延长BC到 E,使CE=CD, 求证:BD=DE A
证明：∵ △ABC是等边三角形
∴ AB=AC=BC，
B
C
第25页/共50页
1.三边都相等的三角形是等边三角形.（定义）
A ∵AB=BC=AC
一般三角形
∴△ABC是等边三角形 等边三角形
B
C
2. 三个角都相等的三角形是 ∵ ∠A= ∠ B= ∠ C
等边三角形.
A
∴△ABC是等边三角形
等腰三角形
等边三角形
B
等边三角形-PPT课件
图形，有三条对称轴.
B
C
请同学们认真快速的完成： 讲学稿中练一练（1）
1、已知等边△ABC中，AB=3cm则△ABC 的周长为___9_c_m___
2、用一个5倍的放大镜照等边三角形 △ABC，则∠A=__6_0_°___
3、△ABC是等边三角形，则∠A的外角= ____1__2_0° 4、等边三角形两条高相交所成的钝角 的度数是_1_2__0_°__
？
细心观察，探索等边三角形性质
结合等腰三角形的性质，你能填出等边三角形对应 的结论吗？
图形
等腰 三角形
等边 三角形
边
两边相等 （定义）
三边相等 （定义）
角
轴对称图形
两底角相等 （等边对等角）
是（三线合一） 一条对称轴
相等
是（三线合一）
每个角都等于60° 三条对称轴
细心观察，探索等边三角形性质
对“等边三角形的三个内角都相等，并且每一个角 都等于60°”这一结论进行证明.
∵ DE∥BC，
∴ ∠B =∠ADE，∠C =∠AED． D
E
∴ ∠A=∠ADE =∠AED．
∴ △ADE 是等边三角形．
B
C
动脑思考，变式训练
变式： △ABC 是等边三角形，若点D、E 在边AB、 AC 的延长线上，且 DE∥BC，结论还成立吗？
证明：∵ △ABC 是等边三角形，
∴ ∠A =∠ABC =∠ACB =60°． A
思考1 一个三角形的满足什么条件是等边三角形？到的这两个命题进行证明.
一般三角形
等边三角形
等腰三角形
满足什么条件的三角 形是等腰三角形?
方法一：从边看
有两边相等的三角形是 等腰三角形（定义）