电磁学课后习题答案
大学物理电磁学课后作业答案(清华大学出版社)

1
I A
2
O
I2 I C
B1
大小:B1
0 I1
2R
2 2
0 I
2R
2
2 2
方向: ⊙
I2在圆心处产生
B2
大小:B2
0 I2
2R
2
0 I 2 2R 2 2
方向:
B1 B2 0 ∴圆心处的总磁感应强度为0.
8.5解:
d
(1)所求磁感应强度方向:⊙ I1 大小为
l I2
dB dt
L 2
R2 L2 / 4 dB dt
方向:a →b(可由楞次定律判断),b端电势高。
∴整个带电直线在P点的场强大小为
E
dE
L/ 2 L/ 2
dx 4 0 ( r
x
)2
L 4 0 ( r 2
L2
/
4)
方向沿X轴正向。
1.11解(弥补法):
设电荷线密度为,缝隙宽为d. 先补上 d ,构成完整的圆 环,
其在圆心处的场强为 EO1 0.
o
R●
E0 d
再补上 - d ,可视作点电荷,
∴所求磁通量为
21
0 I1l
ln r1 r2 r1
2.2 106Wb
8.28解:
(1)
Id
0 S板
dE dt
0R2
dE dt
8.85 1012 0.052 1.0 1012 7.0 102 A
(2) 以极板边缘线作为安培回路L,则
B dl
0 Id
B
0 Id 2R
B 2 0 I 4.0 105T 2 d / 2
O
x x+dx
电磁学课后习题-答案

第五章 静 电 场5 -9 若电荷Q 均匀地分布在长为L 的细棒上.求证:(1) 在棒的延长线,且离棒中心为r 处的电场强度为2204π1L r QεE -=(2) 在棒的垂直平分线上,离棒为r 处的电场强度为2204π21Lr r QεE +=若棒为无限长(即L →∞),试将结果与无限长均匀带电直线的电场强度相比较.分析 这是计算连续分布电荷的电场强度.此时棒的长度不能忽略,因而不能将棒当作点电荷处理.但带电细棒上的电荷可看作均匀分布在一维的长直线上.如图所示,在长直线上任意取一线元d x ,其电荷为d q =Q d x /L ,它在点P 的电场强度为r r q εe E 20d π41d '=整个带电体在点P 的电场强度⎰=E E d接着针对具体问题来处理这个矢量积分.(1) 若点P 在棒的延长线上,带电棒上各电荷元在点P 的电场强度方向相同,⎰=LE i E d(2) 若点P 在棒的垂直平分线上,如图(A )所示,则电场强度E 沿x 轴方向的分量因对称性叠加为零,因此,点P 的电场强度就是⎰⎰==Ly E αE j j E d sin d证 (1) 延长线上一点P 的电场强度⎰'=L r πεE 202,利用几何关系 r ′=r -x 统一积分变量,则()220022204π12/12/1π4d π41L r QεL r L r L εQ x r L x Q εE L/-L/P -=⎥⎦⎤⎢⎣⎡+--=-=⎰电场强度的方向沿x 轴.(2) 根据以上分析,中垂线上一点P 的电场强度E 的方向沿y 轴,大小为E r εqαE L d π4d sin 2⎰'=利用几何关系 sin α=r /r ′,22x r r +=' 统一积分变量,则()2203/22222041π2d π41L r r εQ rx L xrQ εE L/-L/+=+=⎰当棒长L →∞时,若棒单位长度所带电荷λ为常量,则P 点电场强度rελL r L Q r εE l 0220π2 /41/π21lim=+=∞→此结果与无限长带电直线周围的电场强度分布相同[图(B )].这说明只要满足r 2/L 2 <<1,带电长直细棒可视为无限长带电直线.5 -14 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行,试计算通过此半球面的电场强度通量.分析 方法1:由电场强度通量的定义,对半球面S 求积分,即⎰⋅=SS d s E Φ方法2:作半径为R 的平面S ′与半球面S 一起可构成闭合曲面,由于闭合面内无电荷,由高斯定理∑⎰==⋅0d 0q εSS E 这表明穿过闭合曲面的净通量为零,穿入平面S ′的电场强度通量在数值上等于穿出半球面S 的电场强度通量.因而⎰⎰'⋅-=⋅=S SS E S E Φd d解1 由于闭合曲面内无电荷分布,根据高斯定理,有⎰⎰'⋅-=⋅=S SS E S E Φd d依照约定取闭合曲面的外法线方向为面元d S 的方向,E R πR E 22πcos π=⋅⋅-=Φ解2 取球坐标系,电场强度矢量和面元在球坐标系中可表示为①()r θθθE e e e E sin sin cos sin cos ++=r θθR e S d d sin d 2=ER θθER θθER SS2ππ2222πdsin d sin dd sin sin d ===⋅=⎰⎰⎰⎰S E Φ5 -17 设在半径为R 的球体内,其电荷为球对称分布,电荷体密度为()()R r ρkr ρ>=≤≤=0R r 0k 为一常量.试分别用高斯定理和电场叠加原理求电场强度E 与r 的函数关系.分析 通常有两种处理方法:(1) 利用高斯定理求球内外的电场分布.由题意知电荷呈球对称分布,因而电场分布也是球对称,选择与带电球体同心的球面为高斯面,在球面上电场强度大小为常量,且方向垂直于球面,因而有2S π4d r E ⋅=⋅⎰S E根据高斯定理⎰⎰=⋅V ρεd 1d 0S E ,可解得电场强度的分布. (2) 利用带电球壳电场叠加的方法求球内外的电场分布.将带电球分割成无数个同心带电球壳,球壳带电荷为r r ρq ''⋅=d π4d 2,每个带电球壳在壳内激发的电场0d =E ,而在球壳外激发的电场rrεqe E 20π4d d =由电场叠加可解得带电球体内外的电场分布()()()()R r r r Rr>=≤≤=⎰⎰d R r 0d 0E E E E解1 因电荷分布和电场分布均为球对称,球面上各点电场强度的大小为常量,由高斯定理⎰⎰=⋅V ρεd 1d 0S E 得球体内(0≤r ≤R ) ()40202πd π41π4r εk r r kr εr r E r ==⎰()r εkr r e E 024=球体外(r >R )()400202πd π41π4r εk r r kr εr r E R ==⎰ ()r εkR r e E 024=解2 将带电球分割成球壳,球壳带电r r r k V ρq '''==d π4d d 2由上述分析,球体内(0≤r ≤R )()r r rεkr r r r r k εr e e E 0222004d π4π41=''⋅'=⎰ 球体外(r >R )()r r Rr εkR r r r πr k πεr e e E 20222004d 441=''⋅'=⎰5 -20 一个内外半径分别为R 1 和R 2 的均匀带电球壳,总电荷为Q 1 ,球壳外同心罩一个半径为R 3 的均匀带电球面,球面带电荷为Q 2 .求电场分布.电场强度是否为离球心距离r 的连续函数? 试分析.分析 以球心O 为原点,球心至场点的距离r 为半径,作同心球面为高斯面.由于电荷呈球对称分布,电场强度也为球对称分布,高斯面上电场强度沿径矢方向,且大小相等.因而24d rπE ⋅=⎰S E .在确定高斯面内的电荷∑q 后,利用高斯定理∑⎰=0/d εq S E 即可求出电场强度的分布.解 取半径为r 的同心球面为高斯面,由上述分析∑=⋅02/π4εq r Er <R 1 ,该高斯面内无电荷,0=∑q ,故01=E R 1 <r <R 2 ,高斯面内电荷()31323131R R R r Q q --=∑ 故 ()()23132031312π4r R R εR r Q E --= R 2 <r <R 3 ,高斯面内电荷为Q 1 ,故2013π4r εQ E =r >R 3 ,高斯面内电荷为Q 1 +Q 2 ,故20214π4rεQ Q E +=电场强度的方向均沿径矢方向,各区域的电场强度分布曲线如图(B )所示.在带电球面的两侧,电场强度的左右极限不同,电场强度不连续,而在紧贴r =R 3 的带电球面两侧,电场强度的跃变量230234π4ΔεσR εQ E E E ==-=这一跃变是将带电球面的厚度抽象为零的必然结果,且具有普遍性.实际带电球面应是有一定厚度的球壳,壳层内外的电场强度也是连续变化的,本题中带电球壳内外的电场,在球壳的厚度变小时,E 的变化就变陡,最后当厚度趋于零时,E 的变化成为一跃变.5 -21 两个带有等量异号电荷的无限长同轴圆柱面,半径分别为R 1 和R 2 >R 1 ),单位长度上的电荷为λ.求离轴线为r 处的电场强度:(1) r <R 1 ,(2) R 1 <r <R 2 ,(3) r >R 2 .分析 电荷分布在无限长同轴圆柱面上,电场强度也必定沿轴对称分布,取同轴圆柱面为高斯面,只有侧面的电场强度通量不为零,且⎰⋅=rL E d π2S E ,求出不同半径高斯面内的电荷∑q .即可解得各区域电场的分布.解 作同轴圆柱面为高斯面,根据高斯定理∑=⋅0/π2εq rL Er <R 1 ,0=∑q01=E在带电面附近,电场强度大小不连续,电场强度有一跃变 R 1 <r <R 2 ,L λq =∑rελE 02π2=r >R 2,0=∑q03=E在带电面附近,电场强度大小不连续,电场强度有一跃变00π2π2ΔεσrL εL λr ελE ===这与5 -20 题分析讨论的结果一致.5 -22 如图所示,有三个点电荷Q 1 、Q 2 、Q 3 沿一条直线等间距分布且Q 1 =Q 3 =Q .已知其中任一点电荷所受合力均为零,求在固定Q 1 、Q 3 的情况下,将Q 2从点O 移到无穷远处外力所作的功.分析 由库仑力的定义,根据Q 1 、Q 3 所受合力为零可求得Q 2 .外力作功W ′应等于电场力作功W 的负值,即W ′=-W .求电场力作功的方法有两种:(1)根据功的定义,电场力作的功为l E d 02⎰∞=Q W其中E 是点电荷Q 1 、Q 3 产生的合电场强度. (2) 根据电场力作功与电势能差的关系,有()0202V Q V V Q W =-=∞其中V 0 是Q 1 、Q 3 在点O 产生的电势(取无穷远处为零电势). 解1 由题意Q 1 所受的合力为零()02π4π420312021=+d εQ Q d εQ Q 解得 Q Q Q 414132-=-=由点电荷电场的叠加,Q 1 、Q 3 激发的电场在y 轴上任意一点的电场强度为()22031π2yd εQ E E E yy y +=+=将Q 2 从点O 沿y 轴移到无穷远处,(沿其他路径所作的功相同,请想一想为什么?)外力所作的功为()dεQ y y d εQ Q Q W y 022/322002π8d π241d =+⋅⎥⎦⎤⎢⎣⎡--=⋅-='⎰⎰∞∞l E 解2 与解1相同,在任一点电荷所受合力均为零时Q Q 412-=,并由电势的叠加得Q 1 、Q 3 在点O 的电势dεQd εQ d εQ V 003010π2π4π4=+=将Q 2 从点O 推到无穷远处的过程中,外力作功dεQ V Q W 0202π8=-=' 比较上述两种方法,显然用功与电势能变化的关系来求解较为简洁.这是因为在许多实际问题中直接求电场分布困难较大,而求电势分布要简单得多. 5 -23 已知均匀带电长直线附近的电场强度近似为r rελe E 0π2=为电荷线密度.(1)求在r =r 1 和r =r 2 两点间的电势差;(2)在点电荷的电场中,我们曾取r →∞处的电势为零,求均匀带电长直线附近的电势时,能否这样取? 试说明. 解 (1) 由于电场力作功与路径无关,若沿径向积分,则有12012ln π2d 21r r ελU r r =⋅=⎰r E (2) 不能.严格地讲,电场强度r e rελE 0π2=只适用于无限长的均匀带电直线,而此时电荷分布在无限空间,r →∞处的电势应与直线上的电势相等.5 -27 两个同心球面的半径分别为R 1 和R 2 ,各自带有电荷Q 1 和Q 2 .求:(1) 各区域电势分布,并画出分布曲线;(2) 两球面间的电势差为多少?分析 通常可采用两种方法(1) 由于电荷均匀分布在球面上,电场分布也具有球对称性,因此,可根据电势与电场强度的积分关系求电势.取同心球面为高斯面,借助高斯定理可求得各区域的电场强度分布,再由⎰∞⋅=pp V l E d 可求得电势分布.(2) 利用电势叠加原理求电势.一个均匀带电的球面,在球面外产生的电势为rεQV 0π4=在球面内电场强度为零,电势处处相等,等于球面的电势RεQV 0π4=其中R 是球面的半径.根据上述分析,利用电势叠加原理,将两个球面在各区域产生的电势叠加,可求得电势的分布.解1 (1) 由高斯定理可求得电场分布()()()22021321201211π4π40R r r εQ Q R r R r εQ R r r r >+=<<=<=e E e E E 由电势⎰∞⋅=rV l E d 可求得各区域的电势分布.当r ≤R 1 时,有20210120212113211π4π4π411π40d d d 2211R εQ R εQ R εQ Q R R εQ V R R R R r+=++⎥⎦⎤⎢⎣⎡-+=⋅+⋅+⋅=⎰⎰⎰∞lE l E l E当R 1 ≤r ≤R 2 时,有202012021201322π4π4π411π4d d 22R εQ r εQ R εQ Q R r εQ V R R r+=++⎥⎦⎤⎢⎣⎡-=⋅+⋅=⎰⎰∞lE l E当r ≥R 2 时,有rεQ Q V r02133π4d +=⋅=⎰∞l E(2) 两个球面间的电势差⎪⎪⎭⎫⎝⎛-=⋅=⎰210121211π4d 21R R εQ U R R l E 解2 (1) 由各球面电势的叠加计算电势分布.若该点位于两个球面内,即r ≤R 1 ,则2021011π4π4R εQ R εQ V +=若该点位于两个球面之间,即R 1 ≤r ≤R 2 ,则202012π4π4R εQ r εQ V +=若该点位于两个球面之外,即r ≥R 2 ,则rεQ Q V 0213π4+=(2) 两个球面间的电势差()2011012112π4π42R εQ R εQ V V U R r -=-== 第六章 静电场中的导体与电介质6 -1 将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,则导体B 的电势将( )(A ) 升高 (B ) 降低 (C ) 不会发生变化 (D ) 无法确定分析与解 不带电的导体B 相对无穷远处为零电势。
电磁学第二版习题答案

电磁学-第二版-习题答案第二版《电磁学》的习题答案:1. 第一章:电荷和电场习题1:假设有两个电荷,一个带正电量Q1,另一个带负电量Q2,在他们之间的距离为r1。
如果将Q1的电荷减小到原来的一半,同时将Q2的电荷加倍,并将它们之间的距离改为r2,那么这两个电荷之间的相互作用力是怎样改变的?解答:根据库伦定律,两个电荷之间的相互作用力正比于它们的电荷量乘积,反比于它们之间的距离的平方。
即F∝(Q1Q2)/r^2。
根据题目,Q1变为原来的一半,Q2变为原来的两倍,r由r1变为r2。
代入上述关系式,可得新的相互作用力F'为:F'∝((Q1/2)*(Q2*2))/(r2^2)。
化简上式,可得F'∝(Q1Q2)/(r2^2)。
由上式可知,新的相互作用力与原来相互作用力相等。
即新旧相互作用力大小相同。
习题2:有一组平行板电容器,两板之间的距离为d,电容的电极面积为A。
当电容器充满理想电介质时,电容器的电容是原来的多少倍?解答:当电容器充满理想电介质时,电容的电容量由电容公式C=εA/d得到。
其中,ε为电介质的相对介电常数。
而当电容器未充满电介质时,电容的电容量为C0=ε0A/d。
其中,ε0为真空的介电常数。
所以,电容器充满电介质时,电容与未充满时的电容C0比较,即C/C0=ε/ε0。
所以,电容器电容是原来的ε/ε0倍。
2. 第二章:电荷的连续分布习题1:在距离线段中点为R的的P点,取出一个长度为l的小线段,小线段的位置如何改变时,该小线段对P点电势的贡献较大?解答:根据电场电势公式,P点电势由该小线段的电荷贡献决定。
即V=k(q/R),其中k为电场常量,q为该小线段的电荷量,R为该小线段到P点的距离。
所以,小线段对P点电势的贡献较大的情况是,当该小线段长度l较大且该小线段离P点的距离R较小的时候,即小线段越靠近P点且长度越大,对P点电势的贡献越大。
习题2:线电荷的线密度为λ,长度为L,P点到线电荷的距离为d。
电磁学习题答案

I=
ε1 − ε 2
2R
=
8−4 = 0.5( A) 2× 4
U AB = −ε 1 + IR = −8 + 0.5 × 4 = −6(V )
U CD = U AB = −6(V )
(3)
1 1 1 U O1B = − ε 1 + IR = U AB = −3(V ) 2 2 2 1 U O2 B = U CD = −3(V ) 2
由于 Q ∝ f 2 ,所以频率增加一倍时,热量增加到原来的 4 倍。
1-5
6. 解:连接 OM 和 ON,回路 OMNO 的电动势为 dΦ dB 1 S = −k ⋅ πR 2 εi = − m = − dt dt 2 反时针方向。 MN 中的电动势等于回路 OMNO 的电动势,即。 1 ε i = −k ⋅ πR 2 2 方向 M→N。 M
N S I 0 ⋅ 2πf l R 30 π × 0.004 2 = 4π × 10 −7 × × × 25 × 2π × 10 5 −3 0.2 5 × 10 = 29.7( A) I m = µ0
(2)
Q = I 2R = (
(3)
Im 2
)2 R = (
29.7 2
) 2 × 5 × 10 −3 = 2.2( J )
1. 解:通过线圈 ACD 的磁通量为
Φ m = ∫ dΦ m = ∫ B ⋅ dS
S S
C
=∫
a + cos 30° l
a
µ0 I [a + cos 30°l − r ] ⋅ 2tg 30° ⋅ dr 2πr
3
r
l dr
D
υ
v
a+ l µ I 3 3 2 − µ0 I 3 l) ⋅ = 0 (a + ln a π π 3 2 3
电磁学习题答案

电磁学习题答案第一、二章静电场(一)填空题0111 引,引,引,不受静电0211 带电小球不是点电荷,库仑定律不适用0322 小0423 1∶50522 q=Q/20622 小0721 移到大地,不会移动0821 不会改变0911 同号等量1023 物质在引力场中1111 电力线的方向是电场的方向,即正电荷受力的方向而不是运动方向和轨迹1211 空过高斯曲面的电通量,电场E1311 不一定为零,必为零1423 不会成立这时 ∮E·dS=∫1/4π0q/rn1/ε0qrn-21522 能,不能1621 q/(6ε),在体内时不变,体外为零1723 恒为零,恒为一定值,由定值变为零1823 1/4πε4Qa21924 5/22022 2q/(4πεR2)2122 不能,能2222 能,不能2322 无限远或大地,整机外壳,并不一定相等2422 零,常数,2524 g,gh,mgh2611 -q2724 4.0×106N/C,02824 7.1×10-5C·m-22923 16∶253024 6.9×10-19J 、3112 升高3222 有,有,无,有3322 均匀分布,仍然为均匀3422 相等3523 rA ∶rB3624 2md/(et 2),2md 2/t 2 3722 1∶53824 EM <EN3923 W0/εr4024 600V(二)选择题0132 (B) 0222 (C) 0322 (B) 0422 (B)0523 (D) 0622 (A) 0724 (D) 0824 (D)0924 (D) 1023 (B) 1122 (B) 1222 (B)1321 (C) 1421 (C) 1521 (C) 1622 (C)1724 (D) 1834 (D) 1921 (D) 2022 (A)2123 (C) 2224 (C) 2322 (B) 2424 (CD)2523 (C) 2624 (D) 2724 (C) 2824 (C)2923 (C) 3034 (C) 3122 (A) 3222 (C)3322 (A) 3422 (B) 3523 (C) 3624 (C) 3734BF,D,AC 3824 (D) 3924 (C) 4024 (A)第三章稳恒电流(一)填空题0111 非保守力非静电场0211 非静电力将单位正电荷在电源内部由负极移到正极所作的功0322 不一定相同,不同,相同0423 x=l/2(1±n-4)0532 e2/(4πr0621 2nevS0721 2I/30821 l/2和l/20922 60V1034 92.5V1121 1159kW1223 1∶3,1∶1,3∶161333 并,2.71424 U3>U2>U1,相等,相等1534 闭路式,因为开路式当开关在触点间跨越时可能烧坏表头1622 灯泡点亮时电阻变大1722 零,增大,R>r时将减小,R<r时将增大,R=r时功率最大1822 新旧电池的电动势变化不大而内阻变化很大,故输出功率大大减小 1922 nε,nr2022 ε,r/n(二)选择题0122 (B) 0223 (C) 0321 (C) 0423 (C) 0522 (C) 0621 (B) 0722 (D) 0823 (B) 0922 (A) 1033 (D) 1134 (C) 1234 (B)1334 (A) 1424 (D) 1534 (B) 1622 (D)1723 (B) 1823 (C) 1923 (C) 2023 (B)第四、五章稳恒磁场(一)填空题0111 在与x轴的两个相交点处B=0,在与y轴相交的两点处B=μ0/4πidR2,但分别沿k和-k方向0211 μI/2R0312 μI0411 沿x方向0511 因引力而靠近0612 一方面朝两环电流方向相同的方位转动,同时相互平动靠近0711 电场或磁场,磁场,电场0811 相等0922 μ0I/(2π)1022 2μ0I/(πa)1121 零,μI/2πR (1+π/4),零1224 弱1311 零1411 μ0nI,μ0nI1512 能,不能1623 μ0Ir2πr2 μI/2πr ,零1722 无源有旋1821 μev/4πr21922 靠近导线平移,转动且平移靠近导线,转动且平移靠近导线2024 零2122 零,不一定为零2234 大,不变2324 右2424 ne(IB/b)2523 2mEk/(qr)2623 以半径R=mv2/(qvB)作圆周运动;以较小的半径反方向作圆周运动 2722 收缩变短2823 自上而下俯视为逆时针2932 向下偏移3024 vBd,上边为正极板,下边为负极板3122 B和M都与外磁场B0同方向,B和M都与外磁场B反方向3234 磁化的铁钉与磁场间的相互作用能(磁势能),铁钉接近磁铁时磁势能减小而转化为铁钉动能3322 弹簧伸长,插入部分变长,瞬间上升而随即又伸长插入螺线管中 3422 相同电流,不变3522 加一个反向磁场,或敲击震动磁铁,或加热使温度升高到居里点以上3622 加一块衔铁将两极闭合,将两条磁铁的异性磁极靠在一起3721 南,指向地面3821 抗磁质,顺磁质3921 ②,①4034 下降,下降,上升,上升,上升,吸住(二)选择题0121 (D) 1124 (A) 2121 (C) 3121 (B)0222 (D) 1223 (C) 2221 (B) 3234 (B)0324 (B) 1334 (BC) 2322 (C) 3323 (D)0421 (D) 1433 (D) 2422 (A) 3424 (C)0522 (D) 1522 (B) 2522 (A) 3534 (B)0634 (B) 1623 (AB) 2622 (D) 3622 (B)0723 (C) 1724 (D) 2724 (C) 3722 (A)0822 (BD) 1823 (B) 2833 (C) 3821 (A)0922 (B) 1923 (C)(B) 2933 (B) 3922 (B)1021 (D) 2023 (C) 3032 (A) 4033 (BCDA)第六章电磁感应(一)填空题0111 先加速最后以一恒速度0211 一个反抗拉力0322 垂直导线而远离0422 受到较大阻力而很快停下来,受到的阻力减小而好久才能停住 0523 变化的B在薄片上产生涡电流,由椤次定律知,涡流磁场总是阻碍原磁场变化,而具屏蔽作用0621 0,Blv,bωl 2/2,00721 0.1,a→d→c→b→a0834 右0921 增大1022 ωBR2/21122 0.05T1222 电能1323 ε/Bl1422 产生电流而不运动1523 μ0N21a2/2R,μ0N22a2/2R,μN1N2a2/2R1621 使二线圈的半径基本相等,同轴紧套在一起1721 两线圈互相垂直放置1821 同轴顺向紧密连接1921 先将电阻丝折成双线再绕在绝缘筒上而使电流相反 2021 交流电源,减少,焦耳热(二)选择题0121 (B) 0632 (AD) 1124 (D) 1623 (C) 0223 (D) 0732 (BD) 1223 (D) 1723 (D)0323 (A) 0824 (C) 1323 (D) 1823 (C)0421 (A) 0934 (C) 1423 (C) 1924 (D)0534 (C) 1021 (B) 1523 (D) 2024 (B)第七章电磁场和电磁波(一)填空题0111 涡旋电场和位移电流0211 变化的电场,电位移通量的变化率dφD/dt0312 位移电流产生于变化的电场且无焦耳热,而传导电流产生于电荷的运动且有焦耳热0422 是横波,S=E×H,E和H同位相、同周期变化,εE=μH2, v=(εμ)-1/2等0533 独立客观存在,有能量动量,有粒子性,与实物粒子可相互转换等 0622 传导,位移,传导0722 变化的电场和变化的磁场0833 不会产生,仍不产生0922 发射电磁波必须是高频的开放型振荡电路1033 实验规律中直接归纳,积分形式通过数学推演1121 3×1018 ,5. 09×1014 , 2.19×108 ,1.07×106Hz1221 2.0×108 m/s1321 7.0×10-2A1421 3.33×10-12T1522 3.95×1026W1623 1.74×10-2V/m, 5.8×10-11T1724 2.68×102W/m21824 3m,108Hz,2.0×10-9cos〔2π×108(t-x/c)〕1924 4.3×10-13~3.9×10-10F2023 1.6×10-5W/m2(二)选择题0121 (AC) 0322 (AC) 0522 (C) 0721 (D)0222 (AD) 0422 (AD) 0621 (D) 0821 (D)0924 (D) 1223 (A) 1524 (C) 1824 (D)1024 (A) 1323 (C) 1622 (C) 1924 (B)1123 (B) 1422 (C) 1723 (B) 2034 (D)。
电磁学习题答案1-3章

第一章 习题一1、电量Q 相同的四个点电荷置于正方形的四个顶点上,0点为正方形中心,欲使每个顶点的电荷所受电场力为零,则应在0点放置一个电量q =-(1+2√2)Q/4 的点电荷。
2、在点电荷系的电场中,任一点的电场强度等于各点电荷单独在该点产生场强的矢量和,这称为电场强度叠加原理。
3、一点电荷电场中某点受到的电场力很大,则该点的电场强度E :( C )(A)一定很大 (B)一定很小 (C)可能大也可能小4、两个电量均为+q 的点电荷相距为2a ,O 为其连线的中点,求在其中垂线上场强具有极大值的点与O 点的距离R 。
解法一:22020214141aR qπεr q πεE E +=== 21E E E+=,θE θE θE E cos 2cos cos 121=+=2222042a R R a R q πε++=()2/32202a R R πεq +=E 有极值的条件是:()0222/522220=+-=a R R a πεq dR dE 即 0222=-R a ,解得极值点的位置为:a R 22=∵ ()2/722220223223a R a R πεqR dR E d +-=,而 0398402/222<-==aπεqdR E d a R ∴ 中垂线上场强具有极大值的点与O 点的距离为a R 22= 且 ()202/3220m a x 332/2/2aπεq a a a πεq E =+=解法二:θaq πεr q πεE E 2202021sin 4141===,21E E E +=+qθE θE θE E cos 2cos cos 121=+=θθaq πεcos sin 21220=)cos (cos 21320θθaq πε-=E 有极值的条件是:0)sin 3sin 2(2320=-=θθaπεq θd dE E 有极值时的θ满足:31cos 32sin 1cos 0sin 2211====θ,θ;θ,θ )cos 7cos 9(2)cos sin 9cos 2(232022022θθa πεq θθθa πεq θd E d -=-= 0)cos 7cos 9(22011320221>=-==a πεq θθa πεq θd E d θθ 032)cos 7cos 9(22022320222<-=-==aπεq θθa πεq θd E d θθ 可见 θ = θ2时,E 有极大值。
电磁学课后部分习题答案解析

电磁学课后部分习题答案解析1.2.2 两个同号点电荷所带电荷量之和为Q.在两者距离一定的前提下,他们带电荷量各为多少时相互作用力最大?解答:设一个点电荷的电荷量为1q q =,另一个点电荷的电荷量为()2q Q q =-,两者距离为r,则由库仑定律求得两个电电荷之间的作用力为()204q Q q F rπε-=令力F 对电荷量q 的一阶导数为零,即()2004Q q qdF dq r πε--== 得122Qq q == 即取 122Qq q ==时力F 为极值,而222202204Q q d Fdq rπε==-<故当 122Qq q ==时,F 取最大值 1.2.6 两个电荷量相等的同性点电荷相距为2a ,在两者连线的中垂面上置一试探点电荷0q , 求0q 受力最大的点的轨迹.解答:如图(a)所示,设有两个电荷量为q 的点电荷 ,坐标分别为(-a ,0,0)和(a ,0,0),试探点电荷0q 置于二者连线的中垂面Oyz 上坐标为(0,y,z).r y j zk =+ 为原点O 至试探点电荷0q 的失径,距离为r = ,如图(b)所示.根据对称性, 所受合力的方向与失径r 平行或反平行.其大小为()003222222sin 2q q q qrF k k r a r a α==++ 求上式的级值,去F 对r 的一阶导数并令其为零,的方程 ()22230r r a -++=求得22ar =求二阶导数并带入22ar =,得()272222022120a r d Fa kqq r a rdr -==-+<说明此时F 取极大值因此,0q 受力最大的点的轨迹是在中垂面上的圆心坐标为(0,0,0)半径为2a的圆. 1.3.6 附图中均匀带电圆环的半径为R,总电荷量为q (1)求数轴线上离环心O 为x 处的场强E (2) 轴线上何处场强最大?其值是多少? (3)大致画出E-x 曲线.解答:设圆环的带电线密度为 2q Rηπ=如图(a)所示,圆环一小段dl 到轴上一点P 的距离为r ,即有dq dl η=,cos xrα=,该小段对P 点产生的场强大小为 22dqdl dE kk r r η== 根据对称性,P 点场强仅有x 分量, d E 在x 轴的分量大小为()3222cos x xdldE dE kRxηα==+()()()33322222222200224x xRxqx E dE kR RxR xR xηηπεπε====+++⎰P 点场强为()322204qx E iR xπε=+(2)应求dE dx并令其值为0,求得当22R x =,E 取极值,而2220R x d E dx =<,根据对称性,位于轴上22R x =±点的场强取最大值,其值为 2063E i Rπε=±(3)如图(b )所示。
电磁学第三章课后习题答案

电磁学第三章课后习题答案电磁学第三章课后习题答案电磁学是物理学中的重要分支,研究电荷和电流之间相互作用的规律。
在电磁学的学习过程中,习题是巩固知识和提高能力的重要途径。
本文将为大家提供电磁学第三章的课后习题答案,希望能对大家的学习有所帮助。
1. 一个导线的长度为l,电流为I,如图所示。
求导线两端的电势差。
答案:根据欧姆定律,电势差等于电流乘以电阻。
而导线的电阻可以通过电阻率乘以长度除以横截面积来计算。
所以,导线两端的电势差为V = I × (ρl/A)。
2. 一个导线的电阻为R,电流为I,如图所示。
求导线两端的电势差。
答案:根据欧姆定律,电势差等于电流乘以电阻。
所以,导线两端的电势差为V = I × R。
3. 一个导线的电阻为R,电流为I,导线的长度为l,电阻率为ρ,横截面积为A。
求导线两端的电势差。
答案:根据欧姆定律,电势差等于电流乘以电阻。
而导线的电阻可以通过电阻率乘以长度除以横截面积来计算。
所以,导线两端的电势差为V = I × R = I × (ρl/A)。
4. 在一个电路中,有一个电阻为R1的电阻器和一个电阻为R2的电阻器连接在一起,电流为I。
求两个电阻器上的电势差。
答案:根据欧姆定律,电势差等于电流乘以电阻。
所以,第一个电阻器上的电势差为V1 = I × R1,第二个电阻器上的电势差为V2 = I × R2。
5. 在一个电路中,有一个电阻为R1的电阻器和一个电阻为R2的电阻器连接在一起,电阻器之间的电势差为V。
求电流的大小。
答案:根据欧姆定律,电势差等于电流乘以电阻。
所以,V = I × (R1 + R2)。
解方程可得电流的大小为I = V / (R1 + R2)。
6. 一个电路中有两个电阻器,电阻分别为R1和R2,电流为I。
求电路中的总电阻。
答案:电路中的总电阻可以通过电阻器的并联和串联来计算。
如果电阻器是串联的,总电阻等于各个电阻器的电阻之和,即R = R1 + R2。
《电磁学》梁灿彬课后答案

300
−
1 2
eE m
t2
=
0
解之得: t = 2mv0 sin 300 eE
所以在原来高度时水平射程为:
x = v0 cos 300 t =
3mv02 2eE
1.3.4 电子的电荷受罪先是由密立根通过油滴实验测出的,密立根设计的实验装置如附图所示。 一个很小的带电油滴在电场 E 内,调节 E 使作用在油滴上的电场力与油滴的重量平衡,如果油滴
f
= 2k
qq′ (a2 + r2)
r (a2 + r2 )
=
2kqq′r
(a2
+
r2
)3 2
又∵ df = 0 dr
即:
2kqq′
⎡ ⎢ ⎢ ⎢
(a2
+
r2
)3 2
− r × 3 (a2 2
(a2 + r2 )3
+
r
2
)1 2
i 2r
⎤ ⎥ ⎥ ⎥
=
0
⎣
⎦
∴
(a2
+
r 2 )32
− 3r 2 (a2
答案:无外场时,对球外而言是正确的。
1.5 附图中 A 和 B 为两个均匀点电体,S 为与 A 同心的球面,试问: (1)S 面的通量与 B 的位置及电荷是否有关? (2)S 面上某点的电场强度与 B 的位置及电荷是否有关? (3)可否用高斯定理求出 S 面上一点的场强?为什么?
答案:(1)无关 (2) 有关 (3)不能(导体球)、可以(介质球)。 场强叠加原理应用到有导体的问题时,要注意,带电导体单独存在时,有一种电荷分布,它
∫∫ (3)
s1
《电磁学》梁灿彬课后部分答案
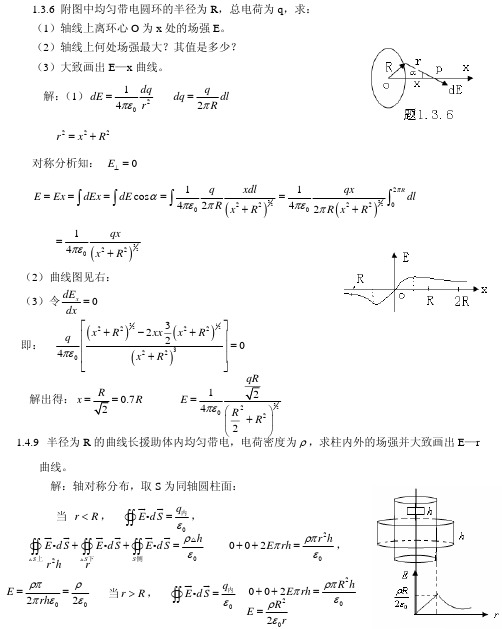
B
=
μ0 μ rH
=
μ0μrN L
I
(2) 线圆电流 I0 产生的磁场为 B0
∫ ∑ L B0 ⋅ dl = μ0 Ii
B0 ⋅l = μ0 NI ,
B0
=
μ0 N l
I
磁化电流在匀质中产生的磁场为 B′
B′
=
B−
B0
=
μ0μr N l
I
−
μ0 N l
I
=
μ0 N I l
(ur
− 1)
7.6.1 解: 圆电流圆心处 代入数据得:
1.3.6 附图中均匀带电圆环的半径为 R,总电荷为 q,求: (1)轴线上离环心 O 为 x 处的场强 E。 (2)轴线上何处场强最大?其值是多少? (3)大致画出 E—x 曲线。
解:(1) dE
=
1 4πε 0
dq r2
dq = q dl 2π R
r2 = x2 + R2
对称分析知: E⊥ = 0
曲线。 解:轴对称分布,取 S 为同轴圆柱面:
当 r<R,
∫∫
Eid
S
=
q内 ε0
,
∫∫ ∫∫ ∫∫ Eid S + Eid S + Eid S = ρ h
S上 r2h
Sr下
S侧
ε0
0 + 0 + 2Eπ rh = ρπ r2h , ε0
E = ρπ = ρ 2π rhε0 2ε0
当r > R,
∫∫
解:(1)解法一:在两电容器中,
C1
=
ε0s d1
, C2
=
d
ε0s −t −
d1
电磁学习题解答

b
l
两平面之间为
I
B
1 2
0
j
1 2
0
j
0
j
0
I b
a
I
两平面之间的磁通量为
B
B
S
0
I b
la
LI
故有 L 0la
b
电磁感应习题课
【例4】如图所示( t=0 时刻),一无限长直导线与一矩形 线圈共面,直导线中通有电流 I=I0e-kt ( I0、k 为正常数), 矩形线圈以速度 v 向右作平动,求任一时刻 t 矩形线圈中 的感应电动势。
oI
2R
磁 偶
3)轴线以外的磁场较复杂, 极
可定性给出磁感应线,
子S
P.
B
x
N
定电义流:与磁B偶线极仍矩服从P右m手 螺IS旋n 关系。S n与I的方向 N
若有N匝线圈,总磁矩为 : Pm NISn Npm
4) x >>R时:
B
o IR2
2x3
o IS 2x 3
比较:E
成右手关系
即:
B
o Pm 2x3
o
i
c
与P点到平板的距离无关。
i
i
dB
... .
dl
....
dl
.
. B oi B0 B 0i
•
×
0 0i 0
×
a
B
b
25
例9. 求通电螺绕环的磁场分布。已知环管轴线的半径
为R,环上均匀密绕N匝线圈,设通有电流I。
解:由于电流对称分布,与环共轴
R
的圆周上,各点B大小相等,
R1
方向沿圆周切线方向。
电磁学课后习题答案
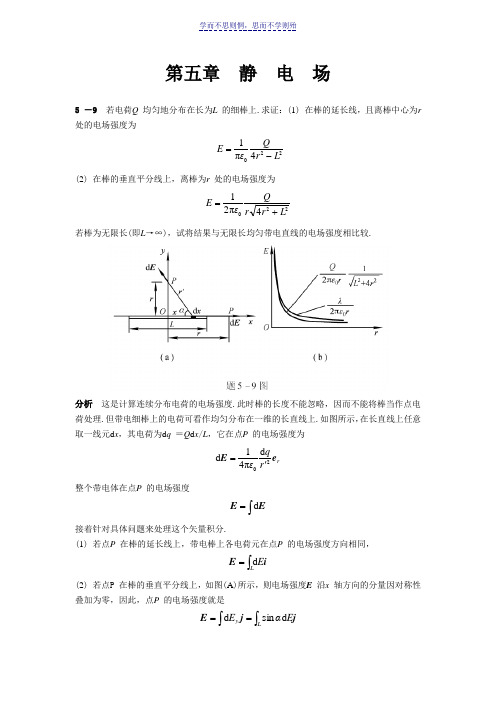
第五章 静 电 场5 -9 若电荷Q 均匀地分布在长为L 的细棒上.求证:(1) 在棒的延长线,且离棒中心为r 处的电场强度为2204π1L r QεE -=(2) 在棒的垂直平分线上,离棒为r 处的电场强度为2204π21Lr r QεE +=若棒为无限长(即L →∞),试将结果与无限长均匀带电直线的电场强度相比较.分析 这是计算连续分布电荷的电场强度.此时棒的长度不能忽略,因而不能将棒当作点电荷处理.但带电细棒上的电荷可看作均匀分布在一维的长直线上.如图所示,在长直线上任意取一线元d x ,其电荷为d q =Q d x /L ,它在点P 的电场强度为r r q εe E 20d π41d '=整个带电体在点P 的电场强度⎰=E E d接着针对具体问题来处理这个矢量积分.(1) 若点P 在棒的延长线上,带电棒上各电荷元在点P 的电场强度方向相同,⎰=LE i E d(2) 若点P 在棒的垂直平分线上,如图(A )所示,则电场强度E 沿x 轴方向的分量因对称性叠加为零,因此,点P 的电场强度就是⎰⎰==Ly E αE j j E d sin d证 (1) 延长线上一点P 的电场强度⎰'=L r πεE 202,利用几何关系 r ′=r -x 统一积分变量,则()220022204π12/12/1π4d π41L r QεL r L r L εQ x r L x Q εE L/-L/P -=⎥⎦⎤⎢⎣⎡+--=-=⎰电场强度的方向沿x 轴.(2) 根据以上分析,中垂线上一点P 的电场强度E 的方向沿y 轴,大小为E r εqαE L d π4d sin 2⎰'=利用几何关系 sin α=r /r ′,22x r r +=' 统一积分变量,则()2203/22222041π2d π41L r r εQ rx L xrQ εE L/-L/+=+=⎰当棒长L →∞时,若棒单位长度所带电荷λ为常量,则P 点电场强度rελL r L Q r εE l 0220π2 /41/π21lim=+=∞→此结果与无限长带电直线周围的电场强度分布相同[图(B )].这说明只要满足r 2/L 2 <<1,带电长直细棒可视为无限长带电直线.5 -14 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行,试计算通过此半球面的电场强度通量.分析 方法1:由电场强度通量的定义,对半球面S 求积分,即⎰⋅=SS d s E Φ方法2:作半径为R 的平面S ′与半球面S 一起可构成闭合曲面,由于闭合面内无电荷,由高斯定理∑⎰==⋅0d 0q εSS E 这表明穿过闭合曲面的净通量为零,穿入平面S ′的电场强度通量在数值上等于穿出半球面S 的电场强度通量.因而⎰⎰'⋅-=⋅=S SS E S E Φd d解1 由于闭合曲面内无电荷分布,根据高斯定理,有⎰⎰'⋅-=⋅=S SS E S E Φd d依照约定取闭合曲面的外法线方向为面元d S 的方向,E R πR E 22πcos π=⋅⋅-=Φ解2 取球坐标系,电场强度矢量和面元在球坐标系中可表示为①()r θθθE e e e E sin sin cos sin cos ++=r θθR e S d d sin d 2=ER θθER θθER SS2ππ2222πdsin d sin dd sin sin d ===⋅=⎰⎰⎰⎰S E Φ5 -17 设在半径为R 的球体内,其电荷为球对称分布,电荷体密度为()()R r ρkr ρ>=≤≤=0R r 0k 为一常量.试分别用高斯定理和电场叠加原理求电场强度E 与r 的函数关系.分析 通常有两种处理方法:(1) 利用高斯定理求球内外的电场分布.由题意知电荷呈球对称分布,因而电场分布也是球对称,选择与带电球体同心的球面为高斯面,在球面上电场强度大小为常量,且方向垂直于球面,因而有2S π4d r E ⋅=⋅⎰S E根据高斯定理⎰⎰=⋅V ρεd 1d 0S E ,可解得电场强度的分布. (2) 利用带电球壳电场叠加的方法求球内外的电场分布.将带电球分割成无数个同心带电球壳,球壳带电荷为r r ρq ''⋅=d π4d 2,每个带电球壳在壳内激发的电场0d =E ,而在球壳外激发的电场rrεqe E 20π4d d =由电场叠加可解得带电球体内外的电场分布()()()()R r r r Rr>=≤≤=⎰⎰d R r 0d 0E E E E解1 因电荷分布和电场分布均为球对称,球面上各点电场强度的大小为常量,由高斯定理⎰⎰=⋅V ρεd 1d 0S E 得球体内(0≤r ≤R ) ()40202πd π41π4r εk r r kr εr r E r ==⎰()r εkr r e E 024=球体外(r >R )()400202πd π41π4r εk r r kr εr r E R ==⎰ ()r εkR r e E 024=解2 将带电球分割成球壳,球壳带电r r r k V ρq '''==d π4d d 2由上述分析,球体内(0≤r ≤R )()r r rεkr r r r r k εr e e E 0222004d π4π41=''⋅'=⎰ 球体外(r >R )()r r Rr εkR r r r πr k πεr e e E 20222004d 441=''⋅'=⎰5 -20 一个内外半径分别为R 1 和R 2 的均匀带电球壳,总电荷为Q 1 ,球壳外同心罩一个半径为R 3 的均匀带电球面,球面带电荷为Q 2 .求电场分布.电场强度是否为离球心距离r 的连续函数? 试分析.分析 以球心O 为原点,球心至场点的距离r 为半径,作同心球面为高斯面.由于电荷呈球对称分布,电场强度也为球对称分布,高斯面上电场强度沿径矢方向,且大小相等.因而24d rπE ⋅=⎰S E .在确定高斯面内的电荷∑q 后,利用高斯定理∑⎰=0/d εq S E 即可求出电场强度的分布.解 取半径为r 的同心球面为高斯面,由上述分析∑=⋅02/π4εq r Er <R 1 ,该高斯面内无电荷,0=∑q ,故01=E R 1 <r <R 2 ,高斯面内电荷()31323131R R R r Q q --=∑ 故 ()()23132031312π4r R R εR r Q E --= R 2 <r <R 3 ,高斯面内电荷为Q 1 ,故2013π4r εQ E =r >R 3 ,高斯面内电荷为Q 1 +Q 2 ,故20214π4rεQ Q E +=电场强度的方向均沿径矢方向,各区域的电场强度分布曲线如图(B )所示.在带电球面的两侧,电场强度的左右极限不同,电场强度不连续,而在紧贴r =R 3 的带电球面两侧,电场强度的跃变量230234π4ΔεσR εQ E E E ==-=这一跃变是将带电球面的厚度抽象为零的必然结果,且具有普遍性.实际带电球面应是有一定厚度的球壳,壳层内外的电场强度也是连续变化的,本题中带电球壳内外的电场,在球壳的厚度变小时,E 的变化就变陡,最后当厚度趋于零时,E 的变化成为一跃变.5 -21 两个带有等量异号电荷的无限长同轴圆柱面,半径分别为R 1 和R 2 >R 1 ),单位长度上的电荷为λ.求离轴线为r 处的电场强度:(1) r <R 1 ,(2) R 1 <r <R 2 ,(3) r >R 2 .分析 电荷分布在无限长同轴圆柱面上,电场强度也必定沿轴对称分布,取同轴圆柱面为高斯面,只有侧面的电场强度通量不为零,且⎰⋅=rL E d π2S E ,求出不同半径高斯面内的电荷∑q .即可解得各区域电场的分布.解 作同轴圆柱面为高斯面,根据高斯定理∑=⋅0/π2εq rL Er <R 1 ,0=∑q01=E在带电面附近,电场强度大小不连续,电场强度有一跃变 R 1 <r <R 2 ,L λq =∑rελE 02π2=r >R 2,0=∑q03=E在带电面附近,电场强度大小不连续,电场强度有一跃变00π2π2ΔεσrL εL λr ελE ===这与5 -20 题分析讨论的结果一致.5 -22 如图所示,有三个点电荷Q 1 、Q 2 、Q 3 沿一条直线等间距分布且Q 1 =Q 3 =Q .已知其中任一点电荷所受合力均为零,求在固定Q 1 、Q 3 的情况下,将Q 2从点O 移到无穷远处外力所作的功.分析 由库仑力的定义,根据Q 1 、Q 3 所受合力为零可求得Q 2 .外力作功W ′应等于电场力作功W 的负值,即W ′=-W .求电场力作功的方法有两种:(1)根据功的定义,电场力作的功为l E d 02⎰∞=Q W其中E 是点电荷Q 1 、Q 3 产生的合电场强度. (2) 根据电场力作功与电势能差的关系,有()0202V Q V V Q W =-=∞其中V 0 是Q 1 、Q 3 在点O 产生的电势(取无穷远处为零电势). 解1 由题意Q 1 所受的合力为零()02π4π420312021=+d εQ Q d εQ Q 解得 Q Q Q 414132-=-=由点电荷电场的叠加,Q 1 、Q 3 激发的电场在y 轴上任意一点的电场强度为()22031π2yd εQ E E E yy y +=+=将Q 2 从点O 沿y 轴移到无穷远处,(沿其他路径所作的功相同,请想一想为什么?)外力所作的功为()dεQ y y d εQ Q Q W y 022/322002π8d π241d =+⋅⎥⎦⎤⎢⎣⎡--=⋅-='⎰⎰∞∞l E 解2 与解1相同,在任一点电荷所受合力均为零时Q Q 412-=,并由电势的叠加得Q 1 、Q 3 在点O 的电势dεQd εQ d εQ V 003010π2π4π4=+=将Q 2 从点O 推到无穷远处的过程中,外力作功dεQ V Q W 0202π8=-=' 比较上述两种方法,显然用功与电势能变化的关系来求解较为简洁.这是因为在许多实际问题中直接求电场分布困难较大,而求电势分布要简单得多. 5 -23 已知均匀带电长直线附近的电场强度近似为r rελe E 0π2=为电荷线密度.(1)求在r =r 1 和r =r 2 两点间的电势差;(2)在点电荷的电场中,我们曾取r →∞处的电势为零,求均匀带电长直线附近的电势时,能否这样取? 试说明. 解 (1) 由于电场力作功与路径无关,若沿径向积分,则有12012ln π2d 21r r ελU r r =⋅=⎰r E (2) 不能.严格地讲,电场强度r e rελE 0π2=只适用于无限长的均匀带电直线,而此时电荷分布在无限空间,r →∞处的电势应与直线上的电势相等.5 -27 两个同心球面的半径分别为R 1 和R 2 ,各自带有电荷Q 1 和Q 2 .求:(1) 各区域电势分布,并画出分布曲线;(2) 两球面间的电势差为多少?分析 通常可采用两种方法(1) 由于电荷均匀分布在球面上,电场分布也具有球对称性,因此,可根据电势与电场强度的积分关系求电势.取同心球面为高斯面,借助高斯定理可求得各区域的电场强度分布,再由⎰∞⋅=pp V l E d 可求得电势分布.(2) 利用电势叠加原理求电势.一个均匀带电的球面,在球面外产生的电势为rεQV 0π4=在球面内电场强度为零,电势处处相等,等于球面的电势RεQV 0π4=其中R 是球面的半径.根据上述分析,利用电势叠加原理,将两个球面在各区域产生的电势叠加,可求得电势的分布.解1 (1) 由高斯定理可求得电场分布()()()22021321201211π4π40R r r εQ Q R r R r εQ R r r r >+=<<=<=e E e E E 由电势⎰∞⋅=rV l E d 可求得各区域的电势分布.当r ≤R 1 时,有20210120212113211π4π4π411π40d d d 2211R εQ R εQ R εQ Q R R εQ V R R R R r+=++⎥⎦⎤⎢⎣⎡-+=⋅+⋅+⋅=⎰⎰⎰∞lE l E l E当R 1 ≤r ≤R 2 时,有202012021201322π4π4π411π4d d 22R εQ r εQ R εQ Q R r εQ V R R r+=++⎥⎦⎤⎢⎣⎡-=⋅+⋅=⎰⎰∞lE l E当r ≥R 2 时,有rεQ Q V r02133π4d +=⋅=⎰∞l E(2) 两个球面间的电势差⎪⎪⎭⎫⎝⎛-=⋅=⎰210121211π4d 21R R εQ U R R l E 解2 (1) 由各球面电势的叠加计算电势分布.若该点位于两个球面内,即r ≤R 1 ,则2021011π4π4R εQ R εQ V +=若该点位于两个球面之间,即R 1 ≤r ≤R 2 ,则202012π4π4R εQ r εQ V +=若该点位于两个球面之外,即r ≥R 2 ,则rεQ Q V 0213π4+=(2) 两个球面间的电势差()2011012112π4π42R εQ R εQ V V U R r -=-== 第六章 静电场中的导体与电介质6 -1 将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,则导体B 的电势将( )(A ) 升高 (B ) 降低 (C ) 不会发生变化 (D ) 无法确定分析与解 不带电的导体B 相对无穷远处为零电势。
电磁学第二版课后习题答案

电磁学第二版课后习题答案电磁学是物理学中的重要分支,研究电荷和电流的相互作用以及电磁场的产生和传播。
对于学习电磁学的学生来说,课后习题是巩固知识和提高能力的重要途径。
本文将对《电磁学第二版》课后习题进行一些解答和讨论,帮助读者更好地理解电磁学的概念和应用。
第一章:电荷和电场1. 问题:两个等量的正电荷之间的相互作用力是多少?答案:根据库仑定律,两个等量的正电荷之间的相互作用力等于它们之间的电荷量的平方乘以一个常数k,即F = kq1q2/r^2。
2. 问题:电场是什么?如何计算电场强度?答案:电场是指电荷周围的一种物理量,它描述了电荷对其他电荷的作用力。
电场强度E可以通过电场力F除以测试电荷q得到,即E = F/q。
第二章:静电场1. 问题:什么是电势能?如何计算电势能?答案:电势能是指电荷在电场中由于位置变化而具有的能量。
电势能可以通过电荷q乘以电势差V得到,即U = qV。
2. 问题:什么是电势差?如何计算电势差?答案:电势差是指单位正电荷从一个点移动到另一个点时所做的功。
电势差可以通过电场力F乘以移动距离d得到,即V = Fd。
第三章:电流和电阻1. 问题:什么是电流?如何计算电流?答案:电流是指单位时间内通过导体横截面的电荷量。
电流可以通过电荷量Q除以时间t得到,即I = Q/t。
2. 问题:什么是电阻?如何计算电阻?答案:电阻是指导体中电流流动受到的阻碍程度。
电阻可以通过电压V除以电流I得到,即R = V/I。
第四章:电路和电源1. 问题:什么是电路?如何计算电路中的电流和电压?答案:电路是指由电源、导线和电器元件组成的路径,用于电流的传输和电能的转换。
电路中的电流可以通过欧姆定律计算,即I = V/R,其中V为电压,R 为电阻。
2. 问题:什么是直流电源?什么是交流电源?答案:直流电源是指电流方向保持不变的电源,如电池。
交流电源是指电流方向周期性变化的电源,如交流发电机。
通过以上的解答和讨论,我们对电磁学的基本概念和计算方法有了更深入的了解。
电磁学习题答案

第一章 静电场一、选择题(每题三分)1) 将一个试验电荷Q (正电荷)放在带有正电荷的大导体附近P 点处,测得它所受力为F ,若考虑到电量Q 不是足够小,则:()A 、F/Q 比P 点处原先的场强数值大 C 、F/Q 等于原先P 点处场强的数值B 、F/Q 比P 点处原先的场强数值小 D 、F/Q 与P 点处场强数值关系无法确定 答案(B )·P+Q2) 图中所示为一沿X 轴放置的无限长分段均匀带电直线,电荷线密度分别为+λ(X<0)和一个-λ(X>0),则OXY 坐标平面上点(0,a )处的场强E为( )A 、0B 、a 2i 0πελC 、a i 0πελD 、a 4)j i (0πε+λ3) 图中所示曲线表示球对称或轴对称静电场的某一物理量随径向距离r 变化的关系,请指出该曲线可描述下面那方面内容(E 为电场强度的大小,U 为静电势)()A 、半径为R 的无限长均匀带电圆柱体电场的E-r 关系 C 、半径为R 的均匀带正电球体电场的U-r 关系B 、半径为R 的无限长均匀带电圆柱面电场的E-r 关系 D 、半径为R 的均匀带正电球面电场的U-r 关系答案(B )4) 有两个点电荷电量都是+q ,相距2a,今以左边的点电荷为球心,以a为半径作一球形高斯面,在球面上取两块相等的小面积1S 和 2S 的电场强度通量分别为1ϕ和 2ϕ,通过整个球面的电场强度通量为3ϕ,则()5) 已知一高斯面所包围的体积内电量代数和0=∑iq ,则可肯定()A 、高斯面上各点场强均为零 C 、穿过整个高斯面的电通量为零B 、穿过高斯面上每一面元的电通量为零 D 、以上说法都不对 答案(C ) 6) 两个同心带电球面,半径分别为)(,b a b a R R R R <,所带电量分别为b a Q Q ,。
设某点与球心相距r,当b a R r R <<时,该点的电场强度的大小为() A 、2ba 0rQ Q 41+∙πε B 、2ba 0rQ Q 41-∙πε C 、)R Q r Q (412bb 2a 0+∙πε D 、2a 0r Q 41∙πε 答案(D )7) 如图所示,一个带电量为q 的点电荷位于立方体的A 角上,则通过侧面abcd 的电场强度通量为() A 、6q ε B 、12qε C 、24q ε D 、048qε 答案(C )8) 半径为R 的均匀带电球面,若其电荷密度为σ,则在距离球面R 处的电场强度为()A 、0εσ B 、02εσC 、04εσD 、8εσ答案(C )9) 高斯定理⎰⎰ερ=∙vs dV S d E ()A 、适用于任何静电场 C 、只适用于具有球对称性,轴对称性和平面对称性的静电场B 、只适用于真空中的静电场 D 、只适用于虽然不具有(C)中所述的对称性,但可以找到合适的高斯面的静电场 答案(B ) 10) 关于高斯定理的理解正确的是()A 、 如果高斯面上处处E为零,则该面内必无电荷 C 、如果高斯面内有许多电荷,则通过高斯面的电通量必不为零B 、 如果高斯面内无电荷,则高斯面上处处E为零 D 、如果高斯面的电通量为零,则高斯面内电荷代数和必为零 答案(D )11) 如图两同心的均匀带电球面,内球面半径为1R ,电量1Q ,外球面半径为2R ,电量2Q ,则在内球面内距离球心为r 处的P 点场强大小E 为() A 、2021r 4Q Q πε+ B 、+πε2101R 4Q 2202R 4Q πε C 、201r 4Q πε D 、0 答案(D)12)若均匀电场的场强为E,其方向平行于半径为R 的半球面的轴,则通过此半球面的电通量Φ为()13) 下列说法正确的是()A 、 闭合曲面上各点场强为零时,面内必没有电荷 C 、闭合曲面的电通量为零时,面上各点场强必为零B 、 闭合曲面内总电量为零时,面上各点场强必为零 D 、通过闭合曲面的电通量仅决定于面内电荷 答案(D )14) 在空间有一非均匀电场,其电力线分布如图,在电场中作一半径为R 的闭合球面S ,已知通过球面上某一面元S ∆的电场线通量为,则通过该球面其余部分的电场强度通量为()A 、e ∆Φ-B 、e S r ∆Φ⋅∆24π C 、e SSr ∆Φ⋅∆∆-24π D 、0 答案(15) 在电荷为q +的电场中,若取图中点P 处为电势零点,则M 点的电势为()16)下列说法正确的是()A 、 带正电的物体的电势一定是正的 C 、带负电的物体的电势一定是负的B 、 电势等于零的物体一定不带电 D 、物体电势的正负总相对电势参考点而言的 答案(D )17) 在点电荷q 的电场中,选取以q 为中心,R 为半径的球面上一点P 处作电势零点,则与点电荷q 距离为r 的P ‘点电势为()A 、r 4q 0πε B 、)R 1r 1(4q 0-πε C 、)R r (4q 0-πε D 、)R1r 1(4q 0-πε-答案(B )18) 半径为R 的均匀带电球面,总电量为Q ,设无穷远处的电势为零,则球内距球心为r 的P 强度和 电势为() A 、E=0, U=r 4Q 0πε B 、 E=0, U=R 4Q 0πε C 、E=2r 4Q0πε. U=r 4Q 0πε D 、E=2r 4Q0πε答案(B )19) 有N 个电量为q 布,比较在这两种情况下在通过圆心O 并垂直与圆心的Z 轴上任意点P 的 场强与电势,则有() A 、场强相等,电势相等B 、场强不相等,电势不相等C 、场强分量z E 相等,电势相等D 、场强分量z E 相等,电势不相等答案(C )20)在边长为a 正方体中心处放置一电量为Q 的点电荷,设无穷远处为电势零点,则在一个侧面的中心处的电势为()A 、a 4Q 0πε B 、R 2Q 0πε C 、R Q 0πε D 、R22Q0πε答案(B )21)如图两个同心的均匀带电球面,内球面半径为1R ,电量1Q ,外球面半径为2R ,电量2Q ,则在内球面内距离球心为r 处的P 点的电势U 为()A 、r4Q Q 021πε+ B 、101R 4Q πε+202R 4Q πε C 、0 D 、101R 4Q πε 答案(B )22) 真空中一半径为R 的球面均匀带电为Q ,,在球心处有一带电量为q 的点电荷,如图设无穷远处为电势零点,则在球内离球心O 距离A 、E R 2π B 、E R 22π C 、E R 221π D 、E R 22πE 、22ERπ 答案(A )A 、a 4q 0πε B 、a8q 0πε C 、a 4q 0πε-D 、a8q0πε- 答案(D )为r的P 点处的电势为()A 、r4Q 0πε B、)R Q r q (410+πε C 、r 4q Q 0πε+ D 、)RqQ r q (410-+πε 答案(B )23)当带电球面上总的带电量不变,而电荷的分布作任意改变时,这些电荷在球心出产生的电场强度E和电势U 将()A 、E 不变,U 不变 B 、E 不变,U 改变 C 、E 改变 ,U 不变 D 、E改变,U 也改变 答案(C )24) 真空中有一电量为Q 的点电荷,在与它相距为r 的A 点处有一检验电荷q,现使检验电荷q 从A 点沿半圆弧轨道运动到B 点,如图则电场场力做功为()A 、q 2r r 4Q 220⋅π⋅πεB 、rq 2r 4Q 20⋅πεC 、rq r 4Q20π⋅πε D 、0 答案(D )25) 两块面积为S 的金属板A 和B 彼此平行放置,板间距离为d (d 远远小于板的线度),设A 板带电量1q , B 板带电量2q ,则A,B 板间的电势差为() A 、S2q q 021ε+ B 、d S 4q q 021⋅ε+ C 、d S 2q q 021⋅ε- D 、d S4q q 021⋅ε- 答案(C )26) 图中实线为某电场中电力线,虚线表示等势(位)面,由图可以看出() A 、c E >>b a E E c U >>b a U U C 、c E >>b a E E c U <<b a U UB 、c E <<b aE E c U <<b a U U D 、c E <<b a E E c U >>b a U U 答案(A )27) 面积为S 的空气平行板电容器,极板上分别带电量为q ±,若不考虑边缘效应,则两极板间的相互作用力为()A 、S q 02ε- B 、S 2q 02ε- C 、202S 2q ε D 、202S q ε 答案(B )28)长直细线均匀带电。
电磁学第一章习题答案

第一章 静电场习题答案1-1 氢原子由一个质子(即氢原子核)和一个电子组成。
根据经典模型,在正常状态下,电子绕核作圆周运动,轨道半径是5.29×10-11m 。
已知质子质量m p =1.67×10-27kg ,电子质量m e =9.11×10-31kg ,电荷分别为±e=±1.60×10-19C ,万有引力常量G=6.67×10-11N.m 2/kg 2。
(1)求电子所受质子的库仑力和引力;(2)库仑力是万有引力的多少倍?(3)求电子的速度。
答:(1)设电子所受的库仑力为F ,根据库仑定律,其大小()()N r q q F 8211219922101023.81029.51060.11099.841---⨯=⨯⨯⨯⨯=⋅=πε设电子所受的万有引力为f ,根据万有引力定律,其大小()N r mM G f 4721127311121063.31029.51067.11011.91067.6-----⨯=⨯⨯⨯⨯⨯⨯=⋅= (2)394781027.21063.31023.8⨯=⨯⨯=--f F (3)设电子绕核做圆周运动的速度为v ,因为F f <<,所以可认为向心力就是库仑力F ,根据Rv m F 2=向得s m m RF v /1019.21011.91029.51023.8631118⨯=⨯⨯⨯⨯==---向 1-3 答:(1)它们之间的库仑力为()()N r q q F 4.14100.41060.11099.84121521992210=⨯⨯⨯⨯=⋅=--πε(2)每个质子所受的重力为:N Mg P 26271064.18.91067.1--⨯=⨯⨯==2626108.81064.14.14⨯=⨯=-P F 所以P F >> 1-5 答:设油滴的电量为q ,它受的电场力和重力分别为F 和P ,由F =P ,即mg Eq =,得()C E mg q 19563361002.81092.18.91010851.01064.114.334---⨯=⨯⨯⨯⨯⨯⨯⨯⨯== 考虑到电荷的正负,C q 191002.8-⨯-=1-7 根据经典理论,在正常状态下,氢原子中电子绕核做圆周运动,其轨道半径为m 111029.5-⨯,已知质子电荷为C e 191060.1-⨯=,求电子所在处原子核(即质子)的电场强度。
电磁学课后答案

【习题1.2解】924331329(243)54(9)(243)236335x y z x y z x y z x y z x y z x y z x y z x y z A B e e e e e e e e e A B e e e e e e e e e A B e e e e e e A B +=--+-+=-+=----+=---∙=--∙-+=+-=⨯()()-()(9)(243)19124331514xy z x y z x y z x y ze e e e e e e e e e e e =--⨯-+=---=--+【习题 1.3解】 已知,38,x y z x y z A e be ce B e e e =++=-++(1)要使A B ⊥,则须散度 0A B =所以从 1380AB b c =-++=可得:381b c +=即只要满足3b+8c=1就可以使向量错误!未找到引用源。
和向量错误!未找到引用源。
垂直。
(2)要使A B ,则须旋度 0A B ⨯=所以从1(83)(8)(3)0138xy zx y z e e e A B b c b c e c e b e ⨯==--+++=- 可得 b=-3,c=-8 【习题1.4解】 已知129x y z A e e e =++,x yB ae be =+,因为B A ⊥,所以应有0A B ∙=即()()1291290xy z x y ee e ae be a b ++∙+=+= ⑴又因为 1B =; 所以221a b +=; ⑵由⑴,⑵ 解得 34,55a b =±=【习题1.6解】已知矢量场222()()(2)x y z A axz x e by xy e z z cxz xyz e =++++-+- 若 A 是一个无源场 ,则应有 div A =0 即: div A =0y x zA A A A x y z∂∂∂∇⋅=++=∂∂∂ 因为 2x A axz x =+ 2y A by xy =+ 22z A z z cxz xyz =-+- 所以有div A =az+2x+b+2xy+1-2z+cx-2xy =x(2+c)+z(a-2)+b+1=0 得 a=2, b= -1, c= - 2【习题1.9解】 已知 222(2)(2)(22)x yz A y x z e x yz e x z y z e=++-+-+ 所以()()1144(22)0xyzy yx x z z x y z x yzx y z A A A A A A rot A A x y z y z z x x y A A A xz xz y y e e ee e e e e e ∂∂⎛⎫⎛⎫∂∂∂∂∂∂∂⎛⎫=∇⨯==-+-+- ⎪ ⎪ ⎪∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭-++-+-=由于场A的旋度处处等于0,所以矢量场A 为无旋场。
电磁学(赵凯华 陈熙谋 ) 第二版 课后答案1

电磁学(赵凯华陈熙谋 ) 第二版课后答案1电磁学(赵凯华-陈熙谋-)--第二版-课后答案1第一章静电场§1.1静电的基本现象和基本规律计算题:1、真空中两个点电荷q1=1.0×10-10c,q2=1.0×10-11c,距离100mm,谋q1受到的力。
解:f?q1q2?10?9.0?10n(排斥力)24??0r12、真空中两个点电荷q与q,相距5.0mm,吸引力为40达因。
已知q=1.2×10-6c,求q。
求解:1超过因=克厘米/秒=10-5牛顿4??0r2fqqf??q93?10?13c24??0rq13、为了得到一库仑电量大小的概念,试计算两个都是一库仑的点电荷在真空中相距一米时的相互作用力和距离一千米时的相互作用力。
q1q2?9.0?109n(当r?1m)相当于90万吨物体的重量解:f34??0r29.0?10n(当r?1000m)相当于900kg物体的重量?14、氢原子由一个质子(即氢原子核)和一个电子组成。
根据经典模型,在正常状态下,电子拖核作圆周运动,轨道半径就是r=5.29×10-11m。
未知质子质量m=1.67×10-27kg,电子质量m=9.11×10-31kg。
电荷分别为e=±1.6×10-19c,万有引力常数g=6.67×10-11nm2/kg2。
(1)谋电子难以承受的库仑力;(2)库仑力就是万有引力的多少倍?(3)谋电子的速度。
e2?8(1)fe??8.22?10n(吸引力)4??0r21(2)fg?g解:m1m2?3.63?10?47n(吸引力)?fe/fg?2.26?10392re2?2.19?106m/s4??0mr1v21e2(3)m??v?2r4??0r由此可知,在原子范围内,与库仑力相比,万有引力完全可以略去不计5、卢瑟福实验证明:当两个原子核之间的距离小到10-15米时,它们之间的排斥力仍遵守库仑定律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章静电场5 -9若电荷Q均匀地分布在长为L的细棒上.求证:(1) 在棒的延长线,且离棒中心为r处的电场强度为224π1LrQεE-=(2) 在棒的垂直平分线上,离棒为r处的电场强度为2204π21LrrQεE+=若棒为无限长(即L→∞),试将结果与无限长均匀带电直线的电场强度相比较.分析这是计算连续分布电荷的电场强度.此时棒的长度不能忽略,因而不能将棒当作点电荷处理.但带电细棒上的电荷可看作均匀分布在一维的长直线上.如图所示,在长直线上任意取一线元d x,其电荷为d q=Q d x/L,它在点P 的电场强度为rrqεeE2dπ41d'=整个带电体在点P的电场强度⎰=EE d接着针对具体问题来处理这个矢量积分.(1) 若点P 在棒的延长线上,带电棒上各电荷元在点P的电场强度方向相同,⎰=L E iE d(2) 若点P 在棒的垂直平分线上,如图(A)所示,则电场强度E沿x轴方向的分量因对称性叠加为零,因此,点P的电场强度就是⎰⎰==LyEαE jjE dsind证 (1) 延长线上一点P 的电场强度⎰'=L r πεE 202,利用几何关系 r ′=r -x 统一积分变量,则()220022204π12/12/1π4d π41L r QεL r L r L εQ x r L x Q εE L/-L/P -=⎥⎦⎤⎢⎣⎡+--=-=⎰电场强度的方向沿x 轴.(2) 根据以上分析,中垂线上一点P 的电场强度E 的方向沿y 轴,大小为E r εqαE L d π4d sin 2⎰'=利用几何关系 sin α=r /r ′,22x r r +=' 统一积分变量,则()2203/22222041π2d π41Lr rεQrx L xrQ εE L/-L/+=+=⎰当棒长L →∞时,若棒单位长度所带电荷λ为常量,则P 点电场强度rελL r L Q r εE l 0220π2 /41/π21lim=+=∞→此结果与无限长带电直线周围的电场强度分布相同[图(B)].这说明只要满足r 2/L 2 <<1,带电长直细棒可视为无限长带电直线.5 -14 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行,试计算通过此半球面的电场强度通量.分析 方法1:由电场强度通量的定义,对半球面S 求积分,即⎰⋅=SS d s E Φ方法2:作半径为R 的平面S ′与半球面S 一起可构成闭合曲面,由于闭合面内无电荷,由高斯定理∑⎰==⋅0d 0q εSS E 这表明穿过闭合曲面的净通量为零,穿入平面S ′的电场强度通量在数值上等于穿出半球面S 的电场强度通量.因而⎰⎰'⋅-=⋅=S SS E S E Φd d解1 由于闭合曲面内无电荷分布,根据高斯定理,有⎰⎰'⋅-=⋅=S SS E S E Φd d依照约定取闭合曲面的外法线方向为面元d S 的方向,E R πR E 22πcos π=⋅⋅-=Φ解2 取球坐标系,电场强度矢量和面元在球坐标系中可表示为①()r θθθE e e e E sin sin cos sin cos ++=r θθR e S d d sin d 2=ER θθER θθER SS2ππ2222πdsin d sin dd sin sin d ===⋅=⎰⎰⎰⎰S E Φ5 -17 设在半径为R 的球体内,其电荷为球对称分布,电荷体密度为()()R r ρkr ρ>=≤≤= 0R r 0k 为一常量.试分别用高斯定理和电场叠加原理求电场强度E 与r 的函数关系.分析 通常有两种处理方法:(1) 利用高斯定理求球内外的电场分布.由题意知电荷呈球对称分布,因而电场分布也是球对称,选择与带电球体同心的球面为高斯面,在球面上电场强度大小为常量,且方向垂直于球面,因而有2S π4d r E ⋅=⋅⎰S E根据高斯定理⎰⎰=⋅V ρεd 1d 0S E ,可解得电场强度的分布. (2) 利用带电球壳电场叠加的方法求球内外的电场分布.将带电球分割成无数个同心带电球壳,球壳带电荷为r r ρq ''⋅=d π4d 2,每个带电球壳在壳内激发的电场0d =E ,而在球壳外激发的电场rrεqe E 20π4d d =由电场叠加可解得带电球体内外的电场分布()()()()R r r r Rr>=≤≤=⎰⎰d R r 0d 0E E E E解1 因电荷分布和电场分布均为球对称,球面上各点电场强度的大小为常量,由高斯定理⎰⎰=⋅V ρεd 1d 0S E 得球体内(0≤r ≤R ) ()4202πd π41π4r εk r r kr εr r E r==⎰()r εkr r e E 024=球体外(r >R )()4202πd π41π4r εk r r kr εr r E R==⎰()r εkR r e E 024=解2 将带电球分割成球壳,球壳带电r r r k V ρq '''==d π4d d 2由上述分析,球体内(0≤r ≤R )()r r rεkr r r r r k εr e e E 0222004d π4π41=''⋅'=⎰ 球体外(r >R )()r r Rr εkR r r r πr k πεr e e E 20222004d 441=''⋅'=⎰5 -20 一个内外半径分别为R 1 和R 2 的均匀带电球壳,总电荷为Q 1 ,球壳外同心罩一个半径为R 3 的均匀带电球面,球面带电荷为Q 2 .求电场分布.电场强度是否为离球心距离r 的连续函数 试分析.分析 以球心O 为原点,球心至场点的距离r 为半径,作同心球面为高斯面.由于电荷呈球对称分布,电场强度也为球对称分布,高斯面上电场强度沿径矢方向,且大小相等.因而24d rπE ⋅=⎰S E .在确定高斯面内的电荷∑q 后,利用高斯定理∑⎰=0/d εq S E 即可求出电场强度的分布.解 取半径为r 的同心球面为高斯面,由上述分析∑=⋅02/π4εq r Er <R 1 ,该高斯面内无电荷,0=∑q ,故01=E R 1 <r <R 2 ,高斯面内电荷()31323131R R R r Q q --=∑ 故 ()()23132031312π4r R R εR r Q E --= R 2 <r <R 3 ,高斯面内电荷为Q 1 ,故2013π4r εQ E =r >R 3 ,高斯面内电荷为Q 1 +Q 2 ,故20214π4r εQ Q E +=电场强度的方向均沿径矢方向,各区域的电场强度分布曲线如图(B)所示.在带电球面的两侧,电场强度的左右极限不同,电场强度不连续,而在紧贴r =R 3 的带电球面两侧,电场强度的跃变量230234π4ΔεσR εQ E E E ==-=这一跃变是将带电球面的厚度抽象为零的必然结果,且具有普遍性.实际带电球面应是有一定厚度的球壳,壳层内外的电场强度也是连续变化的,本题中带电球壳内外的电场,在球壳的厚度变小时,E 的变化就变陡,最后当厚度趋于零时,E 的变化成为一跃变.5 -21 两个带有等量异号电荷的无限长同轴圆柱面,半径分别为R 1 和R 2 >R 1 ),单位长度上的电荷为λ.求离轴线为r 处的电场强度:(1) r <R 1 ,(2) R 1 <r <R 2 ,(3) r >R 2 .分析 电荷分布在无限长同轴圆柱面上,电场强度也必定沿轴对称分布,取同轴圆柱面为高斯面,只有侧面的电场强度通量不为零,且⎰⋅=rL E d π2S E ,求出不同半径高斯面内的电荷∑q .即可解得各区域电场的分布.解 作同轴圆柱面为高斯面,根据高斯定理∑=⋅0/π2εq rL Er <R 1 ,0=∑q01=E在带电面附近,电场强度大小不连续,电场强度有一跃变 R 1 <r <R 2 ,L λq =∑rελE 02π2=r >R 2,0=∑q03=E在带电面附近,电场强度大小不连续,电场强度有一跃变00π2π2ΔεσrL εL λr ελE ===这与5 -20 题分析讨论的结果一致.5 -22 如图所示,有三个点电荷Q 1 、Q 2 、Q 3 沿一条直线等间距分布且Q 1 =Q 3 =Q .已知其中任一点电荷所受合力均为零,求在固定Q 1 、Q 3 的情况下,将Q 2从点O 移到无穷远处外力所作的功.分析 由库仑力的定义,根据Q 1 、Q 3 所受合力为零可求得Q 2 .外力作功W ′应等于电场力作功W 的负值,即W ′=-W .求电场力作功的方法有两种:(1)根据功的定义,电场力作的功为l E d 02⎰∞=Q W其中E 是点电荷Q 1 、Q 3 产生的合电场强度. (2) 根据电场力作功与电势能差的关系,有()0202V Q V V Q W =-=∞其中V 0 是Q 1 、Q 3 在点O 产生的电势(取无穷远处为零电势). 解1 由题意Q 1 所受的合力为零()02π4π420312021=+d εQ Q d εQ Q 解得 Q Q Q 414132-=-=由点电荷电场的叠加,Q 1 、Q 3 激发的电场在y 轴上任意一点的电场强度为()2/322031π2yd εQ E E E yy y +=+=将Q 2 从点O 沿y 轴移到无穷远处,(沿其他路径所作的功相同,请想一想为什么)外力所作的功为()d εQ y y d εQ Q Q W y 022/322002π8d π241d =+⋅⎥⎦⎤⎢⎣⎡--=⋅-='⎰⎰∞∞l E 解2 与解1相同,在任一点电荷所受合力均为零时Q Q 412-=,并由电势 的叠加得Q 1 、Q 3 在点O 的电势dεQd εQ d εQ V 003010π2π4π4=+=将Q 2 从点O 推到无穷远处的过程中,外力作功dεQ V Q W 0202π8=-=' 比较上述两种方法,显然用功与电势能变化的关系来求解较为简洁.这是因为在许多实际问题中直接求电场分布困难较大,而求电势分布要简单得多. 5 -23 已知均匀带电长直线附近的电场强度近似为r rελe E 0π2=为电荷线密度.(1)求在r =r 1 和r =r 2 两点间的电势差;(2)在点电荷的电场中,我们曾取r →∞处的电势为零,求均匀带电长直线附近的电势时,能否这样取 试说明. 解 (1) 由于电场力作功与路径无关,若沿径向积分,则有12012ln π2d 21r r ελU r r =⋅=⎰r E (2) 不能.严格地讲,电场强度r e rελE 0π2=只适用于无限长的均匀带电直线,而此时电荷分布在无限空间,r →∞处的电势应与直线上的电势相等.5 -27 两个同心球面的半径分别为R 1 和R 2 ,各自带有电荷Q 1 和Q 2 .求:(1) 各区域电势分布,并画出分布曲线;(2) 两球面间的电势差为多少分析 通常可采用两种方法(1) 由于电荷均匀分布在球面上,电场分布也具有球对称性,因此,可根据电势与电场强度的积分关系求电势.取同心球面为高斯面,借助高斯定理可求得各区域的电场强度分布,再由⎰∞⋅=pp V l E d 可求得电势分布.(2) 利用电势叠加原理求电势.一个均匀带电的球面,在球面外产生的电势为rεQV 0π4=在球面内电场强度为零,电势处处相等,等于球面的电势RεQV 0π4=其中R 是球面的半径.根据上述分析,利用电势叠加原理,将两个球面在各区域产生的电势叠加,可求得电势的分布.解1 (1) 由高斯定理可求得电场分布()()()22021321201211 π4 π40R r rεQ Q R r R rεQ R r r r>+=<<=<=e E e E E 由电势⎰∞⋅=rV l E d 可求得各区域的电势分布.当r ≤R 1 时,有20210120212113211π4π4π411π40d d d 2211R εQ R εQ R εQ Q R R εQ V R R R R r+=++⎥⎦⎤⎢⎣⎡-+=⋅+⋅+⋅=⎰⎰⎰∞lE l E l E当R 1 ≤r ≤R 2 时,有202012021201322π4π4π411π4d d 22R εQ r εQ R εQ Q R r εQ V R R r+=++⎥⎦⎤⎢⎣⎡-=⋅+⋅=⎰⎰∞lE l E当r ≥R 2 时,有rεQ Q V r02133π4d +=⋅=⎰∞l E(2) 两个球面间的电势差⎪⎪⎭⎫⎝⎛-=⋅=⎰210121211π4d 21R R εQ U R R l E 解2 (1) 由各球面电势的叠加计算电势分布.若该点位于两个球面内,即r ≤R 1 ,则2021011π4π4R εQ R εQ V +=若该点位于两个球面之间,即R 1 ≤r ≤R 2 ,则202012π4π4R εQ r εQ V +=若该点位于两个球面之外,即r ≥R 2 ,则rεQ Q V 0213π4+=(2) 两个球面间的电势差()2011012112π4π42R εQ R εQ V V U R r -=-==第六章 静电场中的导体与电介质6 -1 将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,则导体B 的电势将( )(A ) 升高 (B ) 降低 (C ) 不会发生变化 (D ) 无法确定分析与解 不带电的导体B 相对无穷远处为零电势。
