(完整版)新北师大初三三角函数知识点总结及中考真题汇总有答案
【初中要点】北师大版九年级数学三角函数的计算知识点

张小只初中知识库张小只爱学习北师大版初三数学三角函数的计算知识点本文为学生介绍的是初三数学三角函数的计算,主要包括了幂级数、泰勒展开式、实用幂级数、三角函数恒等变形公式、课后习题与解析等内容,具体内容请阅读:三角函数知识点公式定理记忆口诀三角函数是函数,象限符号坐标注。
函数图象单位圆,周期奇偶增减现。
幂级数c0+c1x+c2x2+...+cnxn+...=∑cnxn (n=0..∞)c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=∑cn(x-a)n (n=0..∞)它们的各项都是正整数幂的幂函数, 其中c0,c1,c2,.....及a都是常数, 这种级数称为幂级数.泰勒展开式(幂级数展开法)f(x)=f(a)+f’(a)/1!*(x-a)+f’’(a)/2!*(x-a)2+...f(n)(a)/n!*(x-a)n+...实用幂级数ex = 1+x+x2/2!+x3/3!+...+xn/n!+...ln(1+x)= x-x2/3+x3/3-...(-1)k-1*xk/k+... (|x|小于1)sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞)cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞)arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|小于1)arccos x = π - (x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... )(|x|小于1)arctan x = x - x /3 + x /5 - ... (x≤1)sinh x = x+x3/3!+x5/5!+...(-1)k-1*x2k-1/(2k-1)!+... (-∞)。
(完整版)新北师大初三三角函数知识点总结及中考真题汇总有答案
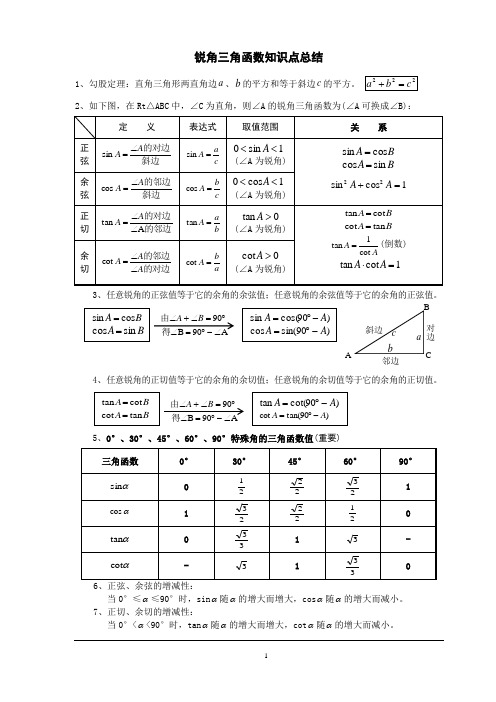
锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)6、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、余切的增减性:当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小。
A 90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边 C A90B 90∠-︒=∠︒=∠+∠得由B A8、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)9、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即hi l=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。
(完整版)新北师大九年级数学下册知识点总结

新北师大版九年级数学下册知识点总结第一章直角三角形边的关系一•锐角三角函数 1.正切:定义:在Rt △ ABC 中,锐角/A 的对边与邻边的比叫做/A的正切,记作tanA ,① tanA 是一个完整的符号,它表示/A的正切,记号里习惯省去角的符号“/”;② tanA 没有单位,它表示一个比值,即直角三角形中/A 的对边与邻边的比;③ tanA 不表示"tan ”乘以"A ”;④ 初中阶段,我们只学习直角三角形中,/A是锐角的正切;⑤ tanA 的值越大,梯子越陡,ZA 越大;ZA 越大,梯子越陡,tanA 的值越大。
2. 正弦:定义:在Rt △ ABC 中,锐角/A 的对边与斜边的比叫做/A 的正弦,记作sinA ,即sin AA的对边................................... """■ 斜边3. 余弦:定义:在Rt △ ABC 中,锐角/A 的邻边与斜边的比叫做/A 的余弦,记作cosA ,即cosA A的邻边 .............................. ■■■■■斜边之变化三•三角函数的计算1. 仰角:当从低处观测高处的目标时,视线与水平线所成的锐角称为 仰角2. 俯角:当从高处观测低处的目标时,视线与水平线所成的锐角称为 俯角值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大 < sin a< 1, 0< cos a< 1。
4. 坡度:如图2,坡面与水平面的夹角叫做坡角坡角的正切称为坡度i tan Al5. 方位角:从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角...。
如图3,OA OB OC 的方位角分别为 45 °、135 °、225 °。
6. 方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角.。
九年级三角函数知识点整理

九年级三角函数知识点整理三角函数是数学中一个重要的概念,特别是在处理角度、弧度、三角形和圆等方面。
以下是九年级三角函数知识点整理:1. 锐角三角函数的定义:锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
正弦(sin):等于对边比斜边,即sinA=a/c。
余弦(cos):等于邻边比斜边,即cosA=b/c。
正切(tan):等于对边比邻边,即tanA=a/b。
余切(cot):等于邻边比对边,即cotA=b/a。
正割(sec):等于斜边比邻边,即secA=c/b。
余割(csc):等于斜边比对边,即cscA=c/a。
2. 特殊角的三角函数值:对于一些特定的角度,三角函数有特定的值。
例如,当角度为30°、45°和60°时,正弦、余弦和正切的值分别是1/2、√2/2、√3/3等。
3. 互余角的关系:sin(π-α)=cosα,cos(π-α)=sinα,tan(π-α)=cotα,cot(π-α)=tanα。
4. 平方关系:sin^2(α)+cos^2(α)=1,tan^2(α)+1=sec^2(α),cot^2(α)+1=csc^2(α)。
5. 积的关系:sinα=tanα·cosα,cosα=cotα·sinα。
6. 诱导公式:对于角度的和差、倍角等运算,可以通过诱导公式简化计算。
例如,sin(A+B)和cos(A+B)可以通过诱导公式转化为sinAcosB+cosAsinB 和cosAcosB-sinAsinB。
7. 图像与性质:正弦、余弦和正切的图像是周期函数,具有对称性。
例如,正弦函数在y轴两侧对称,余弦函数在x轴上对称。
此外,三角函数的最大值和最小值以及对应的x值也是重要的知识点。
8. 应用:三角函数在日常生活和科学研究中有着广泛的应用。
例如,在测量、航海、工程、物理和数学等领域中,经常需要用到三角函数的知识。
九年级《三角函数》知识点、经典例题

九年级《三角函数》知识点、例题、中考真题1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A(∠A 为锐角)B A cot tan = B A tan cot =AA cot 1tan =(倒数) 1cot tan =⋅A A余切 的对边的邻边A A A ∠∠=cot a bA =cot 0cot >A(∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan 0 33 1 3 - αcot-3133 06、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、余切的增减性:当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小。
)90cot(tan A A -︒=)90tan(cot A A -︒= B A cot tan = B A tan cot =)90cos(sin A A -︒=)90sin(cos A A -︒=B A cos sin =BA sin cos =A 90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba cA90B 90∠-︒=∠︒=∠+∠得由B A8、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
初中三角函数知识点总结及典型习题含答案)

初中三角函数知识点总结及典型习题含答案)初三下学期锐角三角函数知识点总结及典型题1.勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方,即a^2+b^2=c^2.2.在直角三角形ABC中,若∠C为直角,则∠A的三角函数为:正弦函数sinA=对边a/斜边c,取值范围为[0,1]。
余弦函数cosA=邻边b/斜边c,取值范围为[0,1]。
正切函数tanA=对边a/邻边b,取值范围为R(实数集)。
3.任意锐角的正弦值等于其余角的余弦值,余弦值等于其余角的正弦值,即sinA=cosB,cosA=sinB,其中A+B=90°。
4.特殊角的三角函数值:30°:sin30°=1/2,cos30°=√3/2,tan30°=1/√3.45°:sin45°=cos45°=√2/2,tan45°=1.60°:sin60°=√3/2,cos60°=1/2,tan60°=√3.6.正弦、余弦的增减性:当0°≤A≤90°时,XXX随A的增大而增大,cosA随A的增大而减小。
7.正切的增减性:当0°<A<90°时,XXX随A的增大而增大。
8.解直角三角形的方法:已知边和角(其中必有一边)→求所有未知的边和角。
依据:①边的关系:a^2+b^2=c^2;②角的关系:A+B=90°;③三角函数的定义。
9.应用举例:仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
坡度:坡面的铅直高度h和水平宽度l的比,用i=h/l表示。
方位角:从某点的指北方向按顺时针转到目标方向的水平角。
方向角:指北或指南方向线与目标方向线所成的小于90°的水平角。
例1:在直角三角形ABC中,已知∠C=90°,sinA=3/5,求XXX的值。
三角函数中考知识点归纳

三角函数中考知识点归纳三角函数是数学中的一个重要分支,它在中考数学中占有一席之地。
以下是对三角函数中考知识点的归纳:基础概念- 三角函数是直角三角形中,锐角的正弦、余弦和正切函数的简称。
- 正弦(sin):直角三角形中,锐角的对边与斜边的比值。
- 余弦(cos):直角三角形中,锐角的邻边与斜边的比值。
- 正切(tan):直角三角形中,锐角的对边与邻边的比值。
三角函数的图像与性质- 三角函数的周期性:正弦和余弦函数的周期为2π,正切函数的周期为π。
- 三角函数的奇偶性:正弦函数和正切函数是奇函数,余弦函数是偶函数。
- 三角函数的单调性:在每个周期内,正弦函数和余弦函数都有单调递增和递减的区间。
特殊角的三角函数值- 30°、45°、60°角的正弦、余弦和正切值是中考中常见的考点。
- 例如:sin30° = 1/2,cos30° = √3/2,tan30° = √3/3;sin45° = cos45° = √2/2,tan45° = 1;sin60° = √3/2,cos60° = 1/2,tan60° = √3。
三角函数的变换- 函数的平移:将三角函数图像沿x轴或y轴平移。
- 函数的伸缩:改变三角函数图像的振幅或周期。
三角函数的应用- 三角函数在解决实际问题中的应用,如测量、建筑、物理等领域。
- 利用三角函数解决直角三角形问题,如利用三角函数求边长、角度等。
解题技巧- 熟练掌握三角函数的基本公式和性质,能够快速解决相关问题。
- 学会利用图形辅助解题,如通过画图来理解三角函数的性质。
- 掌握特殊角的三角函数值,能够快速计算和应用。
结束语:三角函数在中考数学中是一个重要的知识点,掌握好这些基础知识和解题技巧,可以帮助学生在考试中取得更好的成绩。
希望以上的归纳能够帮助学生更好地理解和运用三角函数。
初三数学三角函数知识点整理

初三数学三角函数知识点整理
三角函数知识:
(一)基本概念:
1. 三角函数:三角函数是一类变化比较复杂的可以描述出来的函数,它们可以用来描述各种具有特殊的几何关系的函数关系。
2. 周期性特征:三角函数都具有周期性的特征,正弦函数的周期长度为2π,余弦、正切函数的周期有π。
3. 区间形态特征:三角函数的话,一个比较方便的办法是先分析函数图像的区间变化形态,分析一下函数的一般变化规律,进而猜测出变化规律。
(二)三角函数求值
1. 小角度求值法:小角度求值法是把角极限值和角转换为弧度来进行求解,这种方法的优点是可以把角的大小任意进行变量,从而实现任意角度的三角函数求值。
2. 单位圆三角等价:单位圆三角等价是把圆上的位置用三角函数来表示,其中圆心为(0,0),半径为1。
3. 唯一方程法:唯一方程法就是把三角函数问题变成一般代数方程来求解,这样就可以利用代数方法解决三角函数问题了。
(三)三角函数运算
1. 三角函数对数:三角函数对数可以得到两个三角函数的乘积,除法
或求幂的值。
2. 三角形关系:三角形关系是指把一个等腰三角形的一条边的长度按照给定的一定比例缩放得到另外两边的长度。
3. 余弦定理:余弦定理是指任意一个三角形的两边的长度乘积等于它的最短的三条边的三次方再乘以一个特别的常数。
北师大版2020九年级数学《三角函数及解直角三角形》知识点总结

【文库独家】复习《三角函数及解直角三角形》在是三角形ABC中,∠C=90°,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA。
(2)锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA。
(3)锐角A的对边与邻边的比叫做∠A的正切,记作tanA。
(4)锐角A的邻边与对边的比叫做∠A的余切,记作cotA。
锐角A的正弦、余弦、正切、余切都叫做∠A的三角函数。
注意:(1)正弦、余弦、正切、余切都是在直角三角形中给出的,要避免应用时对任意的三角形随便套用定义;(2)sinA不是sin与A的乘积,是三角形函数记号,是一个整体。
“sinA”表示一个比值,其他三个三角函数记号也是一样的;(3)锐角三角函数值与三角形三边长短无关,只与锐角的大小有关。
(1)平方关系:sin²α+cos²α=1α为锐角,即同一锐角的正弦和余弦的平方和等于1;(2)倒数关系:tanα·cotα=1α为锐角,即同一锐角的正切与余切的积为1,互为倒数;(3)商的关系:tanα=,cotα=,α为锐角,即同一锐角的正弦与余弦的商等于正切,同一锐角的余弦与正弦的商等于余切。
注意:(1)这些关系式都是恒等式,正反均可运用,同时还要注意它们的变形,如:︳sinA︳=1-︳cos²A︳,︳cosA︳=1-sin²A;(2)sin²α是(sinα)²的简写,读作“sinα”的平方;不能将sin²α写成sinα²,前者是α的正弦值的平方,后者表示α²的正弦值。
特殊角有0°、30°、45°、60°、90°,它们的三角函数值如下表:注意:记忆特殊角的三角函数值,可用下述方法:0°、30°、45°、60°、90°的正弦值分别是它们的余弦值分别是30°、45°、60°的正切值分别是它们的余切值分别是若∠A+∠B=90°则sinA=cos(90°-A)=cosB任意锐角的正弦值等于它的余角的余弦值cosA=sin(90°-A)=sinB任意锐角的余弦值等于它的余角的正弦值tanA=cot(90°-A)=cotB任意锐角的正切值等于它的余角的余切值cotA=tan(90°-A)=tanB任意锐角的余切值等于它的余角的正切值用计算器求已知锐角的三角函数值和由三角函数值求对应的锐角是必须掌握的。
三角函数知识点归纳总结初三

三角函数知识点归纳总结初三三角函数是数学中重要的一部分,在初三阶段的学习过程中,三角函数的知识点是较为集中的。
以下是三角函数知识点归纳总结:一、正弦函数和余弦函数正弦函数和余弦函数的定义域是任意实数x,值域是x不等于0的情况下,正弦函数是x,余弦函数是π-x。
正弦函数的周期是2π,正弦函数的最大值在x=0处取得。
余弦函数的周期也是2π,但余弦函数的最大值在x=π/2处取得。
二、正切函数正切函数的定义域是任意实数x和y,值域是x不等于0且y不等于0的情况下,正切函数是x,y。
正切函数的周期性是2π/2,即正切函数的值在两个周期之间循环。
在极坐标系中,正切函数的值可以通过对x取极值来表示。
三、三角函数的图像正弦函数和余弦函数的图像呈“S”形,当x=0时,y取最大值,当y=0时,x取最小值。
正切函数的图像呈“E”形,在x=0处取得最大值,在y=0处取得最小值。
四、三角函数的应用正弦函数和余弦函数在解直角三角形、立体几何、平面向量等方面有广泛的应用。
正切函数在解直角三角形应用最为广泛,可以用于计算角、边的关系。
五、三角函数的公式正弦函数和余弦函数的公式如下:正弦函数:sinθ=√(1-cos2θ)sinθ=2cos2θ-1cosθ=2(1-cos2θ)/√(1-cos2θ)sin2θ=2cos2θ=1-cos2θ余弦函数:cosθ=√(1-sin2θ)cosθ=2sin2θ-1cosθ=2(1-sin2θ)/√(1-sin2θ)cos2θ=2sin2θ=1-sin2θ六、三角函数的解题方法正弦函数和余弦函数的解题方法较多,一般可以通过求导、化简、代入等方法求解。
正切函数的解题方法较多,可以通过直接计算、求导、化简等方法求解。
以上是三角函数的知识点归纳总结,希望能有所帮助。
在后续的学习中,可以多练习,加深对三角函数的理解和掌握。
北师大版九年级数学(下)全书知识总结

(2) 的值越大,梯子越陡。
(3) 的值越小,梯子越陡。
3、导出公式
(1) ; 。
(2) 。
(3) .
要点诠释:
(1)公式成立的条件是
(2)锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.
1.230°、45°、60°角的三角函数值
要点一、1.2 30°、45°、60°角的三角函数值
利用三角函数的定义,可求出30°、45°、60°角的各三角函数值,归纳如下:
锐角
30°
45°
1
60°
要点诠释:
(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若 ,则锐角 .
(3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.
(4)由锐角三角函数的定义知:
当角度在0°<∠A<90°间变化时, , ,tanA>0.
要点二、梯子的倾斜程度与梯子的关系
1、坡度:坡面的铅直高度 与水平宽度 的比称为坡度(或坡比),用字母 表示。设坡角为 ,则坡度 = = ,如图,坡度通常写成 的形式.
顶点坐标
对称轴
函数变化
最大(小)值
y=ax2
a>0
向上
(0,0)
y轴
x>0时,y随x增大而增大;
x<0时,y随x增大而减小.
当x=0时,
y最小=0
y=ax2
a<0
向下
(0,0)
y轴
x>0时,y随x增大而减小;
三角函数的应用(1个知识点4种题型1个易错点1种中考考法)(解析版)-初中数学北师大版9年级上册

专题04三角函数的应用(1个知识点4种题型1个易错点1种中考考法)【目录】倍速学习四种方法【方法一】脉络梳理法知识点1.解直角三角形的应用(重点、难点)【方法二】实例探索法题型1.方向角问题题型2.坡度、坡角问题题型3.方案决策问题题型4.一题多解——求建筑物的高【方法三】差异对比法易错点:对俯角的意义理解错误【方法四】仿真实战法考法.解直角三角形的应用-坡角问题【方法四】成果评定法【学习目标】1.进一步体会三角函数在解决实际问题中的作用。
2.能够把实际问题转化数学问题,能够借助计算器进行有关s'j函数的计算,并能够进一步对结果的意义进行说明,提高解决实际问题的能力。
3.能利用解直角三角形的有关知识,解决测量、航海、工程技术等生活中的实际问题。
重难点:把实际问题转化为直角三角形问题,通过解直角三角形形达到求解的目的。
【倍速学习四种方法】【方法一】脉络梳理法知识点1.解直角三角形的应用(重点、难点)1.水平线:水平面上的直线以及和水平面平行的直线.2.铅垂线:垂直于水平面的直线,我们通常称为铅垂线.3.在测量时,如图,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,视线在水平线下方的角叫做俯角.4.如图,坡面的铅垂高度(h )和水平宽度(l )的比叫做坡面的坡度(或坡比),记作i ,即h i l=.坡度通常写成1:m 的形式,如i =1︰1.5.5.坡面与水平面的夹角叫做坡角,记作α.坡度i 与坡角α之间的关系:h i tan lα==.知识延伸※1.方向角:以观测者的位置为中心,将正北或正南方向作为起始方向,旋转到目标的方向线所成的小于90°的角,通常表达成北(南)偏东(西)*度.若正好为45°,则表示为西(东)南(北)方向.2.方位角:从标准方向的北端起,顺时针方向到直线的水平角称为该直线的方位角.方位角θ的取值范围为0360θ≤< .【例1】.(2023秋•成都期中)如图,一座古塔座落在小山上(塔顶记作点A ,其正下方水平面上的点记作点)B ,小李站在附近的水平地面上,他想知道自己到古塔的水平距离,便利用无人机进行测量,但由于某些原因,无人机无法直接飞到塔顶进行测量,因此他先控制无人机从脚底(记为点)C 出发向右上方(与地面成45︒,点A ,B ,C ,O 在同一平面)的方向匀速飞行4秒到达空中O 点处,再调整飞行方向,继续匀速飞行8秒到达塔顶,已知无人机的速度为5米/秒,75AOC ∠=︒,(求小李到古塔的水平距离即BC 的长.(结果精确到1m 1.41≈ 1.73)≈【分析】过点O作OD BC⊥,交BC的延长线于点D,过点O作OE AB⊥,垂足为E,根据题意可得:40AO=米,20OC=米,OE BD=,//OE BD,从而可得45EOC OCD∠=∠=︒,进而可得30AOE∠=︒,然后在Rt OCD∆中,利用锐角三角函数的定义求出CD的长,再在Rt AOE∆中,利用锐角三角函数的定义求出OE的长,从而求出BD的长,最后利用线段的和差关系进行计算,即可解答.【解答】解:过点O作OD BC⊥,交BC的延长线于点D,过点O作OE AB⊥,垂足为E,由题意得:8540AO=⨯=(米),4520OC=⨯=(米),OE BD=,//OE BD,45EOC OCD∴∠=∠=︒,75AOC∠=︒,30AOE AOC EOC∴∠=∠-∠=︒,在Rt OCD∆中,2cos452022CD OC=⋅︒=⨯=),在Rt AOE∆中,3cos304032OE AO=⋅︒=⨯=(米),3OE BD∴==),310221BC BD CD∴=-=-≈(米),∴小李到古塔的水平距离即BC的长约为21米.【点评】本题考查了解直角三角形的应用-仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.【例2】.(2023秋•盘州市期中)某超市利用一个带斜坡的平台装卸货物,其纵断面ACFE如图所示.AE为台面,AC垂直于地面,AB表示平台前方的斜坡.斜坡的坡角ABC∠为43︒,坡长AB为2m.为保障安全,又便于装卸货物,决定减小斜坡AB的坡角,AD是改造后的斜坡(D在直线BC上),坡角ADC∠为31︒.求斜坡AD底端D与平台AC的距离CD.(结果精确到0.1)m【参考数据:sin430.68︒=,cos430.73︒=,tan430.93︒=;sin310.52︒=,cos310.86︒=,tan310.60︒=】【分析】首先在Rt ABC∆中,求出AC的长,再在Rt ADC∆,由tanACADCCD∠=,即可求出CD的长.【解答】解:在Rt ABC∆中,sinAC ABCAB∠=,sin4320.68 1.36() AC AB m∴=⋅︒=⨯=,在Rt ADC∆中,tanAC ADCCD ∠=,∴1.362.3()tan310.60ACCD m ==≈︒,∴斜坡AD底端D与平台AC的距离CD约为2.3m.【点评】本题考查了解直角三角形的应用,解答本题的关键是利用三角函数知识解直角三角形.【例3】.(2023秋•九龙坡区校级月考)如图,海岸边上有三个观测站A,B,C,观测站B在观测站A的东北方向,观测站C在观测站B的正东方向,观测站B,C之间的距离为30海里.某天,观测站A,B,C同时收到一艘轮船在D处发出的求救信号,经分析,D在观测站C的南偏东15︒方向,在观测站B的东南方向,在观测站A的正东方向.(1)求CD的长度.(结果精确到个位)(2)目前只有观测站A与B配备了搜救艇,搜救艇航速为30海里/时.收到求救信号后,因观测站B的搜救艇在检修,接到任务后不能马上出发,需30分钟后才能出发,而且必须先去C处,才能再去D处(在C 处停留时间可忽略不计);而观测站A的搜救艇接到任务后可马上出发,并直接到达D处.请问哪一个观测站的搜救艇可以更快到达D 1.414≈ 1.732)≈【分析】(1)过点C 作CE BD ⊥于点E ,利用方向角的意义,等腰直角三角形的性质和含30︒角的直角三角形的性质解答即可;(2)过点B 作BF AD ⊥于点F ,利用(1)的结论和等腰直角三角形的判定与性质求得AD 的长度,通过比较两个搜救艇到达D 处所需的时间解答即可.【解答】解:(1)由题意得://AD BC ,45CBD ∠=︒,9015105BCD ∠=︒+︒=︒,30BC =海里.过点C 作CE BD ⊥于点E ,如图,则CBE ∆为等腰直角三角形,45BCE ∴∠=︒,21522BE CE ===(海里),60DCE BCD BCE ∴∠=∠-∠=︒,30CDE ∴∠=︒,2242CD CE ∴==≈(海里);(2)观测站A 的搜救艇可以更快到达D 处.理由:由(1)知:152BE =海里,22156DE CD CE =-=(海里),(152156)BD BE DE ∴=+=海里.过点B 作BF AD ⊥于点F ,由题意得:45NAB BAD ∠=∠=︒,//BF AN ,45ABF ∴∠=︒,45DAF ∠=︒ ,90ABD ∴∠=︒,ABD ∴∆为等腰直角三角形,23030382AD BD ∴==+≈(海里).∴观测站A 的搜救艇到达D 处需要8230 2.73÷=(小时). 观测站B 的搜救艇到达D 处需要:1(3042)300.5 2.4 2.92++÷=+=(小时),∴观测站A 的搜救艇可以更快到达D 处.【点评】本题主要考查了解直角三角形的应用,方向角,直角三角形的边角关系定理,特殊角的三角函数值,利用已知条件恰当的添加辅助线,构造直角三角形是解题的关键.【方法二】实例探索法题型1.方向角问题1.(2023•高碑店市模拟)如图为东西流向且河岸平行的一段河道,点A ,B 分别为两岸上一点,且点B 在点A 正北方向,由点A 向正东方向走a 米到达点C ,此时测得点B 在点C 的北偏西55︒方向上,则河宽AB 的长为()A .tan 55a ︒米B .cos55a ︒米C .tan 35a ︒米D .tan 55a ︒米【分析】连接AB ,BC ,根据三角函数的定义即可得到结论.【解答】解:连接AB ,BC ,由题意得,90BAC ∠=︒,55ABC ∠=︒,AC a =米,tan tan 55AC ABC AB ∴∠=︒=,tan 55tan 55AC a AB ∴==︒︒,【点评】本题考查了解直角三角形的应用-方向角问题,熟练掌握三角函数的定义是解题的关键.2.(2023•金东区二模)如图,小明在C 处看到西北方向上有一凉亭A ,北偏东35︒的方向上有一棵大树B ,已知凉亭A 在大树B 的正西方向,若50BC =米,则AB 的长等于()米.A .5050sin 35cos35-︒︒B .5050sin 35cos35+︒︒C .50(cos35sin 35)︒-︒D .50(cos35sin 35)︒+︒【分析】过点C 作CD AB ⊥,垂足为D ,先在Rt BCD ∆中,利用锐角三角函数的定义求出BD ,CD 的长,然后在Rt ADC ∆中,利用锐角三角函数的定义求出AD 的长,从而利用线段的和差关系进行计算,即可解答.【解答】解:过点C 作CD AB ⊥,垂足为D ,在Rt BCD ∆中,35BCD ∠=︒,50BC =米,sin 3550sin 35BD BC ∴=⋅︒≈︒(米),cos 4550cos 35CD BC =⋅︒=︒(米),在Rt ADC ∆中,45ACD ∠=︒,tan 4550cos 35AD CD CD ∴=⋅︒==︒(米),50cos3550sin 3550(cos35sin 35)AB AD BD ∴=+=︒+︒=︒+︒米,【点评】本题考查了解直角三角形的应用-方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.3.(2023秋•徐汇区期末)如图,一段东西向的限速公路MN 长500米,在此公路的南面有一监测点P ,从监测点P 观察,限速公路MN 的端点M 在监测点P 的北偏西60︒方向,端点N 在监测点P 的东北方向,那么监测点P 到限速公路MN 的距离是米(结果保留根号).【分析】过点P 作PA MN ⊥于点A ,则90PAM PAN ∠=∠=︒,设PA x =米,证PAN ∆是等腰直角三角形,得NA PA x ==米,再由锐角三角函数定义得MA =米,然后由MA NA MN +=,求出250x =-,即可得出结论.【解答】解:如图,过点P 作PA MN ⊥于点A ,则90PAM PAN ∠=∠=︒,设PA x =米,由题意可知,60MPA ∠=︒,45NPA ∠=︒,PAN ∴∆是等腰直角三角形,NA PA x ∴==米,tan tan 60MAMPA PA∠==︒= ,MA ∴==(米),500MA NA MN +== ,∴500x +=,解得:250x =-,即监测点P 到限速公路MN 的距离是250)-米,故答案为:250)-.【点评】本题考查了解直角三角形的应用—方向角问题,正确作出辅助线构造直角三角形是解题的关键.4.(2023春•沙坪坝区校级期中)在公园里,同一平面内的五处景点的道路分布如图所示,经测量,点D 、E 均在点C 的正北方向且600CE =米,点B 在点C 的正西方向,且BC =点B 在点A 的南偏东60︒方向且400AB =米,点D 在点A 1.414≈, 1.732≈ 2.449)≈.(1)求道路AD 的长度(精确到个位);(2)若甲从A 点出发沿A —D —E 的路径去点E ,与此同时乙从点B 出发,沿B —A —E 的路径去点E ,其速度为40米/分钟.若两人同时到达点E ,请比较谁的速度更快?快多少?(精确到十分位)【分析】(1)过点A 作AF CB ⊥,交CB 的延长线于点F ,过点A 作AG DC ⊥,垂足为G ,根据题意可得:AF CG =,AG CF =,然后在Rt AFB ∆中,利用锐角三角函数的定义求出AF ,BF 的长,从而求出CF 的长,再在Rt ADG ∆中,利用锐角三角函数的定义求出AD 的长,即可解答;(2)利用(1)的结论可求出EG 的长,再在Rt AGE ∆中,利用勾股定理可求出AE 的长,然后在Rt ADG ∆中,利用锐角三角函数的定义求出DG 的长,从而求出甲和乙的路程,最后进行计算即可解答.【解答】解:(1)过点A 作AF CB ⊥,交CB 的延长线于点F ,过点A 作AG DC ⊥,垂足为G ,由题意得:AF CG =,AG CF =,在Rt AFB ∆中,60BAF ∠=︒,400AB =米,∴1cos604002002AF AB=⋅︒=⨯=(米),sin60400BF AB=⋅︒=⨯(米),200CG AF∴==米,BC=∴CF BF BC=+=+=(米),∴AG CF==米,在Rt ADG∆中,904545DAG∠=︒-︒=︒,∴980cos45AGAD==︒(米),∴道路AD的长度约为980米;(2)600CE=米,200CG=米,400EG CE CG∴=-=(米),在Rt AGE∆中,AG=米,∴800AE=(米),在Rt ADG∆中,45DAG∠=︒,∴tan45DG AG=⋅︒=),∴甲的路程400)AD DE AD DG EG=+=+-=米,乙的路程4008001200AB AE=+=+=(米),乙的速度为40米/分钟,∴乙所用的时间12003040==(分钟),∴甲所用的时间也是30分钟,∴甲的速度42.4=≈(米/分钟),42.440 2.4∴-=(米/分钟),∴若两人同时到达点E,甲的速度更快,快2.4米/分钟.【点评】本题考查了解直角三角形的应用-方向角问题,勾股定理的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.5.(2023秋•沙坪坝区校级月考)如图,五边形ABCDE 是某公园的游览步道,把公园的五个景点连接起来,为方便游览,增设了步道AC .经勘测,90BAE ∠=︒,景点C 在景点A 的东北方向,且在景点B 的南偏东60︒方向的800米处,景点D 在景点C 的正南方向500米处,150AED ∠=︒ 1.414≈ 1.732)≈(1)求景点A 与景点E 的距离;(结果精确到1米)(2)甲、乙两人同时从景点A 出发,选择相反的路线依次游览其余四个景点,最后回到景点A ,两人在各景点处停留时间忽略不计.其中甲的游览路线是A B C D E A →→→→→,甲游览的平均速度是100米/分,乙游览的平均速度是80米/分.请通过计算说明在游览过程中,甲、乙谁先到达景点C ?【分析】(1)延长AE ,CD 交于点G ,连接AC ,过点C 作CF AB ⊥于点F ,利用含30︒角的直角三角形的性质,等腰直角三角形的性质解答即可;(2)利用(1)的结论分别计算出甲,乙两人的走的路程,再计算出到达点C 的时间即可.【解答】解:(1)延长AE ,CD 交于点G ,连接AC ,过点C 作CF AB ⊥于点F ,如图,由题意得:800BC =米,500CD =米,60ABC ∠=︒,景点C 在景点A 的东北方向,45BAC CAG ∴∠=∠=︒.在Rt BFC ∆中,60B ∠=︒ ,30BCF ∴∠=︒,400BF ∴=(米),CF ==(米).90AFC ∠=︒ ,45BAC ∠=︒,AF FC ∴==),AC ∴==),45CAG ∠=︒ ,90G ∠=︒,2AG GC AC ∴===(米),500)DG CG CD ∴=-=米,150AED ∠=︒ ,30DEG ∴∠=︒,21000)DE DG ∴==米,(1200EG ∴==-米,1200359AE AG EG ∴=-=-≈(米).答:景点A 与景点E 的距离359米.(2)乙先到达景点C ,理由:由(1)知:4008001893AB AF BF =+=++≈(米),35910005001245AE DE CD ++=++=(米),∴甲到达点C 所有的时间为189310018.93÷=(分),乙到达点C 所有的时间为12458015.56÷≈(分),18.9315.56> ,∴乙先到达景点C .【点评】本题主要考查了直角三角形的应用,含30︒角的直角三角形的性质,等腰直角三角形的性质,勾股定理,方向角,近似数和有效数字,恰当的构造直角三角形是解题的关键.6.(2023秋•九龙坡区校级期中)如图,五边形ABCDE 是一个公园沿湖的健身步道(步道可以骑行),BD 是仅能步行的跨湖小桥.经勘测,点B 在点A 的正北方935米处,点E 在点A 的正东方,点D 在点B 的北偏东74︒,且在点E 的正北方,90C ∠=︒,800BC =米,600CD =米.(参考数据:sin 740.96︒≈,cos 740.27︒≈,tan 74 3.55)︒≈(1)求AE 的长度(结果精确到1米);(2)小明和爸爸在健身步道锻炼,小明以200米/分的速度从点A 出发沿路线A B C D E A →→→→→的方向骑行,爸爸以150米/分的速度从点B 出发沿路线B D E A →→→的方向跑步前行.两人约定同时出发,那么小明和爸爸谁先到达A 点?请说明理由.【分析】(1)过点B 作BF DE ⊥,垂足为F ,根据垂直定义可得90BFE BFD ∠=∠=︒,再根据题意可得:74GBD ∠=︒,90A E ∠=∠=︒,从而可得四边形ABFE 是矩形,进而可得AB FE =,AE BF =,//AB EF ,然后利用平行线的性质可得74GBD BDF ∠=∠=︒,在Rt BCD ∆中,利用勾股定理求出BD 的长,再在Rt BFD ∆中,利用锐角三角函数的定义求出BF 的长,即可解答;(2)在Rt BFD ∆中,利用锐角三角函数的定义求出DF 的长,从而求出DE 的长,然后进行计算,比较即可解答,【解答】解:(1)如图:过点B 作BF DE ⊥,垂足为F ,90BFE BFD ∴∠=∠=︒,由题意得:74GBD ∠=︒,90A E ∠=∠=︒,∴四边形ABFE 是矩形,935AB FE ∴==米,AE BF =,//AB EF ,74GBD BDF ∴∠=∠=︒,90C ∠=︒ ,800BC =米,600CD =米1000BD ∴===(米),在Rt BFD ∆中,sin 7410000.96960BF BD =⋅︒≈⨯=(米),960BF AE ∴==米,AE ∴的长度约为960米;(2)爸爸先到达A 点,理由:在Rt BFD ∆中,74BDF ∠=︒,1000BD =米,cos 7410000.27270DF BD ∴=⋅︒≈⨯=(米),935EF = 米,9352701205DE DF EF ∴=+=+=(米),∴小明从点A 出发沿路线A B C D E A →→→→→的方向骑行需要的时间450022.5200200AB BC CD DE AE ++++===(分钟),爸爸从点B 出发沿路线B D E A →→→的方向跑步前行需要的时间316521.1150150BD DE EA ++===(分钟),21.1 分钟22.5<分钟,∴爸爸先到达A 点.【点评】本题考查了解直角三角形的应用-方向角问题,矩形的判定与性质,勾股定理的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.7.(2023秋•沙坪坝区校级月考)如图,小明家A 和商店C 都在地铁站D 的正西方向,小亮家B 在地铁站的西北方,且在小明家北偏东15︒方向.一天,小明和小亮相约去地铁站坐地铁,小明到离家4千米的商店C 时,小亮家B 恰在商店C 的北偏西30︒方向. 1.41≈, 2.45)≈(1)求小明和小亮家的距离(保留根号);(2)小明从商店出发继续前往地铁站,此时小亮也从家出发乘坐公交车沿BD 方向前往地铁站,其中小明的步行速度为每小时8千米,公交车的行驶速度为每小时25千米,谁先到达地铁站呢?请说明理由.【分析】(1)过点A 作AE BC ⊥,垂足为E ,根据题意可得:75BAC ∠=︒,60BCA ∠=︒,从而利用三角形内角和定理可得45ABC ∠=︒,然后在Rt AEC ∆中,利用锐角三角函数的定义求出AE 和CE 的长,再在Rt ABE ∆中,利用锐角三角函数的定义求出AB 的长,即可解答;(2)过点B 作BF AC ⊥,垂足为F ,在Rt ABE ∆中,利用锐角三角函数的定义求出BE 的长,从而求出BC 的长,然后在Rt BCF ∆中,利用锐角三角函数的定义求出BF 和CF 的长,再在Rt BFD ∆中,利用锐角三角函数的定义求出DF 和BD 的长,从而求出CD 的长,最后进行计算即可解答.【解答】解:(1)过点A 作AE BC ⊥,垂足为E,由题意得:901575BAC ∠=︒-︒=︒,903060BCA ∠=︒-︒=︒,18045ABC BAC BCA ∴∠=︒-∠-∠=︒,在Rt AEC ∆中,4AC =千米,1cos 60422CE AC ∴=⋅︒=⨯=(千米),3sin 60432AE AC =⋅︒=⨯=(千米),在Rt ABE ∆中,2326sin 4522AE AB ===︒,∴小明和小亮家的距离为26千米;(2)小明先到达地铁站,理由:过点B 作BF AC ⊥,垂足为F,在Rt ABE ∆中,45ABE ∠=︒,AE =千米,tan 45AE BE ∴==︒,2CE =千米,(2BC BE CE ∴=+=+千米,在Rt BCF ∆中,60BCF ∠=︒,sin 60(2(32BF BC ∴=⋅︒=+⨯=+千米,1cos 60(2(12CF BC =⋅︒=+⨯=千米,在Rt BFD ∆中,904545BDF ∠=︒-︒=︒,(3tan 45BF DF ∴==︒千米,sin 45BF BD ==︒千米,3(12CD DF CF ∴=-=++=(千米), 小明的步行速度为每小时8千米,公交车的行驶速度为每小时25千米,∴小明到达地铁站需要的时间210.2584===(小时),小亮到达地铁站需要的时间0.27=(小时),0.25 小时0.27<小时,∴小明先到达地铁站.【点评】本题考查了解直角三角形的应用-方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.题型 2.坡度、坡角问题8.(2023•秦都区校级模拟)菏泽某超市计划更换安全性更高的手扶电梯,如图,把电梯坡面的坡角由原来的37︒减至30︒,已知原电梯坡面AB 的长为8米,更换后的电梯坡面为AD ,点B 延伸至点D ,求BD 的长.(结果精确到0.1米.参考数据:sin 370.60︒≈,cos 370.80︒≈,tan 370.75︒≈,3 1.73)≈【分析】根据正弦的定义求出AC ,根据余弦的定义求出BC ,根据正切的定义求出CD ,结合图形计算,得到答案.【解答】解:在Rt ABC ∆中,8AB =米,37ABC ∠=︒,则sin 80.60 4.8AC AB ABC =⋅∠≈⨯=(米),cos 80.80 6.40BC AB ABC =⋅∠≈⨯=(米),在Rt ADC ∆中,30ADC ∠=︒,则 4.88.30tan tan 3033AC CD ADC ===≈∠︒(米),8.30 6.40 1.9BD CD BC ∴=-=-≈(米),答:BD 的长约为1.9米.【点评】本题考查的是解直角三角形的应用—坡度坡角问题,掌握锐角三角函数的定义是解题的关键.题型3.方案决策问题9.(2023秋•大东区期末)如图1是某越野车的侧面示意图,折线段ABC 表示车后盖,已知1AB m =,0.6BC m =,123ABC ∠=︒,该车的高度 1.7AO m =.如图2,打开后备箱,车后盖ABC 落在AB C ''处,AB '与水平面的夹角27B AD '∠=︒.(1)求打开后备箱后,车后盖最高点B '到地面l 的距离;(2)若小明爸爸的身高为1.83m ,他从打开的车后盖C 处经过,有没有碰头的危险请说明理由.(结果精确到0.01m ,参考数据:sin 270.454︒≈,cos 270.891︒≈,tan 270.510︒≈3 1.732)≈【分析】(1)过点B E AD '⊥于E ,根据正弦的定义求出B E ',进而求出车后盖最高点B '到地面l 的距离;(2)过点C '作C F B E '⊥'于点F ,根据题意求出60C B F ∠''=︒,根据余弦的定义求出B F ',再求出点C '到地面l 的距离,比较大小证明结论.【解答】解:(1)如图2,过点B E AD '⊥于E ,在Rt △AB E '中,1AB AB m '==,27B AD ∠'=︒,sin B E B AE AB '∠'=',sin 1sin 270.454()B E AB B AE m ∴'='⋅∠'=⨯︒≈,∴点B '到地面l 的距离为:0.454 1.7 2.154 2.15()m +=≈,答:车后盖最高点B '到地面l 的距离约为2.15m ;(2)没有碰头的危险,理由如下:如图2,过点C '作C F B E '⊥'于点F ,在Rt △AB E '中,27B AD ∠'=︒,则902763AB E ∠'=︒-︒=︒,123AB C ABC ∠'=∠=︒ ,60C B F ∴∠''=︒,0.6B C BC m ''== ,1cos 0.60.3()2B F BC C B F m ∴'=''⋅∠''=⨯=,∴点C '到地面l 的距离为:2.150.3 1.85()m -=,1.85 1.8> ,∴没有碰头的危险.【点评】本题考查的是解直角三角形的应用-坡度坡角问题,正确作出辅助线、熟记锐角三角函数的定义是解题的关键.题型4.一题多解——求建筑物的高10.(2023秋•长春期末)在综合与实践活动中,要利用测角仪测量塔的高度.如图,塔AB 前有一座高为3m 的观景台DE ,已知30DCE ∠=︒,点E 、C 、A 在同一条水平直线上.某学习小组在观景台C 处测得塔顶部B 的仰角为45︒,在观景台D 处测得塔顶部B 的仰角为27︒.求塔AB 的高度.【参考数据:tan 270.5︒=,3 1.7=】.【分析】根据题意可得:DE EC ⊥,然后在Rt DEC ∆中,利用含30度角的直角三角形的性质得333CE DE m ==,过点D 作DF AB ⊥,垂足为F ,设AB h =m ,根据题意得:(33)DF EA h m ==,3DE FA m ==,则(3)BF h m =-,然后在Rt BDF ∆中,利用锐角三角函数的定义求出BF 的长,从而列出关于h 的方程,进行计算即可解答.【解答】解:由题意得:DE EC ⊥,在Rt DEC ∆中,30DCE ∠=︒,90DEC ∠=︒,3DE m =,∴333CE DE m ==,BA EA ⊥ ,在Rt ABC ∆中,45BCA ∠=︒,AB h =m ,tan 45AB AC h m ∴==︒,∴)AE EC AC h m =+=,过点D 作DF AB ⊥于点F ,由题意得:3DE FA m ==,)DF EA h m ==,AB h = m ,(3)BF AB AF h m ∴=-=-,在Rt BDF ∆中,27BDF ∠=︒,tan 270.5(33)BF DF h m ∴=⋅︒=+,∴3)h h -=,∴611.1h =+=,11.1AB m ∴=,∴塔AB 的高度约为11.1m .【点评】本题考查解直角三角形的应用-仰角俯角,熟练掌握直角三角形中的边角关系是解题的关键.11.(2023秋•闵行区月考)如图,AB ,CD 表示两栋建筑,小明想利用建筑CD 玻璃幕墙的反射作用来测建筑AB 的高度,首先他在建筑AB 的底部A 处用测角仪测得其顶部B 在建筑CD 玻璃幕墙上的反射点E 的仰角为α,然后他沿AC 前进了10米到达点F 处,再用测角仪测得建筑AB 的顶部B 在建筑CD 玻璃幕墙上的反射点G 的仰角为β,已知1tan 3α=,1sin 3β=,测角仪置于水平高度1.5米的M 、N 处.试求建筑AB 的高度.【分析】延长BE .BG 分别交MN 的延长线于M ',N ',MM '于CD 相交于H ,设NH xm =,则(10)MH x m =+,(210)N M x m '=+,(220)MM x m '=+,在Rt △MM B '中,1tan (210)3BM MM x α='=+ ,在Rt △MN B '中,tan BM MN β=' ,根据1sin 3β=求得2tan 4β=,于是得到210)4BM x =+,列方程解得30235x =+,于是得到1[2(30235)20] 1.5(20231.5)3AB m =⨯+++=+.【解答】解:延长BE .BG 分别交MN 的延长线于M ',N ',MM '于CD 相交于H ,设NH xm =,则(10)MH x m =+,(210)N M x m '=+,(220)MM x m '=+,在Rt △MM B '中,1tan (220)3BM MM x α='=+ ,在Rt △MN B '中,tan BM MN β=' ,1sin 3β=,22cos 3β∴=,2tan 4β∴=,210)BM x ∴=+,∴12(220)10)34x x +=+,解得:30235x =,1[2(30235)20] 1.5(20231.5)3AB m ∴=⨯+++=+.答:建筑AB 的高度为(20231.5)m .【点评】本题考查了解直角三角形的应用-仰角俯角,解答本题的关键是根据仰角构造直角三角形,利用三角函数的知识求解.【方法三】差异对比法易错点:对俯角的意义理解错误12.(2023秋•诸城市期中)如图,数学兴趣小组用无人机测量一幢楼AB 的高度.小亮站立在距离楼底部94米的D 点处,操控无人机从地面F 点,竖直起飞到正上方60米E 点处时,测得楼AB 的顶端A 的俯角为30︒,小亮的眼睛点C 看无人机的仰角为45︒(点B 、F 、D 三点在同一直线上).求楼AB 的高度.(参考数据:小亮的眼睛距离地面1.7米,3 1.7)≈【分析】过点C 作CG EF ⊥,垂足为G ,延长BA 交HE 于点I ,根据题意可得:BI EH ⊥, 1.7GF CD ==米,CG DF =,EI BF =,60EF IB ==米,94BD =米,从而可得58.3EG =米,然后在Rt EGC ∆中,利用锐角三角函数的定义求出CG 的长,从而求出IE 的长,再在Rt AIE ∆中,利用锐角三角函数的定义求出AI 的长,最后利用线段的和差关系进行计算,即可解答.【解答】解:如图:过点C 作CG EF ⊥,垂足为G ,延长BA 交HE 于点I ,由题意得:BI EH ⊥, 1.7GF CD ==米,CG DF =,EI BF =,60EF IB ==米,94BD =米,60 1.758.3EG EF FG ∴=-=-=(米),在Rt EGC ∆中,45ECG ∠=︒,58.3tan 45EG CG ∴==︒(米),58.3CG DF ∴==米,9458.335.7IE BF BD DF ∴==-=-=(米),在Rt AIE ∆中,30AEI ∠=︒,tan 3035.7AI IE ∴=⋅︒=⨯(米),6039.77AB IB IA ∴=-=-≈(米),∴楼AB 的高度约为39.77米.【点评】本题考查了解直角三角形的应用-仰角俯角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.【方法四】仿真实战法考法.解直角三角形的应用-坡角问题1.(2023•淄博)如图,与斜坡CE 垂直的太阳光线照射立柱AB (与水平地面BF 垂直)形成的影子,一部分落在地面上,另一部分落在斜坡上.若2BC =米,8.48CD =米,斜坡的坡角32ECF ∠=︒,则立柱AB 的高为米(结果精确到0.1米).科学计算器按键顺序计算结果(已取近似值)0.5300.8480.625【分析】延长AD 交BF 于点H ,根据余弦的定义求出CH ,进而求出BH ,再根据正切的定义计算,得到答案.【解答】解:如图,延长AD 交BF 于点H ,在Rt CDH ∆中,8.48CD =米,32DCH ∠=︒,cos CD DCH CH ∠=,8.4810cos 0.848CD CH DCH ∴=≈=∠(米),10212BH CH BC ∴=+=+=(米),90CDH ∠=︒ ,32DCH ∠=︒,903258DHC ∴∠=︒-︒=︒,AB BF ⊥ ,905832BAH ∴∠=︒-︒=︒,在Rt ABH ∆中,tan BH BAH AB ∠=,1219.2tan 0.625BH AB BAH ∴=≈=∠(米),故答案为:19.2.【点评】本题考查的是解直角三角形的应用-坡度坡角问题,熟记锐角三角函数的定义是解题的关键.2.(2023•十堰)如图所示,有一天桥高AB 为5米,BC 是通向天桥的斜坡,45ACB ∠=︒,市政部门启动“陡改缓”工程,决定将斜坡的底端C 延伸到D 处,使30D ∠=︒,则CD 的长度约为()(参考数据:1.414≈ 1.732)≈A .1.59米B .2.07米C .3.55米D .3.66米【分析】由90BAC ∠=︒,45ACB ∠=︒,得45ABC ACB ∠=∠=︒,则5AC AB ==米,由90BAD ∠=︒,30D ∠=︒,得60ABD ∠=︒,则tan 603AD AB =︒=,所以3AD AB =,则3 3.66CD AD AC AB AC =-=-≈米,于是得到问题的答案.【解答】解:在Rt ABC ∆中,90BAC ∠=︒,45ACB ∠=︒,45ABC ACB ∴∠=∠=︒,5AC AB ∴==米,在Rt ABD ∆中,90BAD ∠=︒,30D ∠=︒,60ABD ∴∠=︒,∴tan tan 603AD ABD AB=∠=︒=,3AD AB ∴=,3 1.73255 3.66CD AD AC AB AC ∴=-=-≈⨯-≈(米),CD ∴的长度约为3.66米,故选:D .【点评】此题重点考查直角三角形的两个锐角互余、等腰直角三角形的判定、锐角三角函数与解直角三角形等知识,推导出3AD AB =是解题的关键.3.(2023•深圳)爬坡时坡面与水平面夹角为α,则每爬1m 耗能(1.025cos )J α-,若某人爬了1000m ,该坡角为30︒,则他耗能()(参考数据:3 1.732≈,2 1.414)≈A .58J B .159J C .1025J D .1732J【分析】根据题意可得:他耗能1000(1.025cos30)=⨯-︒,进行计算即可解答.【解答】解:由题意得:某人爬了1000m ,该坡角为30︒,则他耗能1000(1.025cos30)1000(1.025159()J =⨯-︒=⨯-≈,故选:B .【点评】本题考查了解直角三角形的应用-坡度坡角问题,准确熟练地进行计算是解题的关键.4.(2023•辽宁)暑假期间,小明与小亮相约到某旅游风景区登山.需要登顶600m 高的山峰,由山底A 处先步行300m 到达B 处,再由B 处乘坐登山缆车到达山顶D 处.已知点A ,B ,D ,E ,F 在同一平面内,山坡AB 的坡角为30︒,缆车行驶路线BD 与水平面的夹角为53︒(换乘登山缆车的时间忽略不计).(1)求登山缆车上升的高度DE ;(2)若步行速度为30/m min ,登山缆车的速度为60/m min ,求从山底A 处到达山顶D 处大约需要多少分钟(结果精确到0.1)min .(参考数据:sin 530.80︒≈,cos 530.60︒≈,tan 53 1.33)︒≈【分析】(1)根据直角三角形的边角关系求出BM ,进而求出DE 即可;(2)利用直角三角形的边角关系,求出BD 的长,再根据速度、路程、时间的关系进行计算即可.【解答】解:(1)如图,过点B 作BM AF ⊥于点M ,由题意可知,30A ∠=︒,53DBE ∠=︒,600DF m =,300AB m =,在Rt ABM ∆中,30A ∠=︒,300AB m =,11502BM AB m EF ∴===,600150450()DE DF EF m ∴=-=-=,答:登山缆车上升的高度DE 为450m ;(2)在Rt BDE ∆中,53DBE ∠=︒,450DE m =,sin DE BD DBE∴=∠4500.80≈562.5()m =,∴需要的时间t t t =+步行缆车300562.53060=+19.4()min ≈,答:从山底A 处到达山顶D 处大约需要19.4分钟.【点评】本题考查解直角三角形的应用,掌握直角三角形的边角关系是正确解答的前提.5.(2023•大庆)某风景区观景缆车路线如图所示,缆车从点A 出发,途经点B 后到达山顶P ,其中400AB =米,200BP =米,且AB 段的运行路线与水平方向的夹角为15︒,BP 段的运行路线与水平方向的夹角为30︒,求垂直高度PC .(结果精确到1米,参考数据:sin150.259︒≈,cos150.966︒≈,tan150.268)︒≈【分析】过点B 作BD PC ⊥,垂足为D ,过点B 作BE AC ⊥,垂足为E ,根据题意可得:CD BE =,然后分别在Rt ABE ∆和Rt BDP ∆中,利用锐角三角函数的定义求出BE 和DP 的长,从而利用线段的和差关系进行计算,即可解答.【解答】解:过点B 作BD PC ⊥,垂足为D ,过点B 作BE AC ⊥,垂足为E ,由题意得:CD BE =,在Rt ABE ∆中,15A ∠=︒,400AB =米,sin154000.259103.6BE AB ∴=⋅︒≈⨯=(米),103.6CD BE ∴==米,在Rt BDP ∆中,30PBD ∠=︒,200BP =米,11002DP BP ∴==(米),204PC PD DC ∴=+≈(米),∴垂直高度PC 约为204米.【点评】本题考查了解直角三角形的应用-坡度坡角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.【方法五】成果评定法一、单选题A .10tan 40⋅︒米B 【答案】A 【分析】本题主要考查解直角三角形,熟练掌握三角函数的定义是解题的关键.【详解】解:∵ABC 为直角三角形,A .170m【答案】D 【分析】本题主要考查了解直角三角形的实际应用,矩形的性质与判定,过点四边形ABED 是矩形,得到可求出答案.【详解】解:如图所示,过点由题意得AB CD AD ∥,∴AB AD ⊥,又∵BE CD ⊥,∴四边形ABED 是矩形,∴10m DE AB AD ==,在Rt EBC 中,tan α=∴105m CE =,∴115m CD DE CE =+=故选D .4.(2023上·四川资阳则AC的长是()A.53米B【答案】A【分析】本题考查了坡比计算,熟练掌握定义是解题的关键.【详解】∵堤高5BC=米,迎水坡∴:5:1:==BC AC AC解得53AC=(米),故选A.5.(2023上·山西长治·九年级校联考期末)该支架三个脚长度相同且与地面夹角相同.如图∠脚AB的长为2米,BA.2tan70︒米B.2sin【答案】B【分析】本此题主要考查了解直角三角形的应用,直接利用锐角三角函数关系得出。
北师大版初三数学下册中考专题复习——三角函数及应用

中考考前专题复习——三角函数及应用一、教材剖析1、本节内容属于北师大版九年级数学下册第一章的内容,位于本册书的第 19 页至 21 页(包含练习题)。
2、本章“直角三角形的边角关系”属于三角学,主要内容包含:锐角三角函数(正弦、余弦和正切),解直角三角形以及三角函数法在解有关的综合题中的运用(意识)。
解直角三角形在实质中间有着宽泛的应用,锐角三角函数为解直角三角形供给了有效的工具.相像三角形的知识是学习锐角三角函数的直接基础,勾股定理等内容也是解直角三角形时常常使用的数学结论,所以本章与“勾股定理” 和“相像”两章有着亲密关系。
锐角三角函数是本套教科书中独一出现过的初等超越函数,出现过的其余函数(一次函数、二次函数等)都是代数函数。
锐角三角函数的一个突出特色是看法的产生和应用都与图形分不开 .锐角三角函数拥有鲜亮的几何意义,其自变量是角,函数值是直角三角形中边长的比值。
学习本章不单能够使学生对函数看法的认识更全面,并且能够对用变化和对应的看法议论几何图形问题的方法认识得更深入 .。
3、本节内容属于三角学内容的一部分,是在直角三角形三角函数知识教授以后的简单运用。
是《数学课程标准》中“图形与几何”领域的“图形变化” 中的重要内容。
主要研究解利用三角函数解决实质问题.掌握锐角三角函数的看法和解直角三角形的方法,是学习三角函数和解斜三角形的重要准备。
二、学生知识情况剖析学生已经学习了直角三角形中量与量之间的三个关系:边与边的关系(勾股定理);角与角的关系(直角三角形两锐角互余);边与角的关系(正弦、余弦、正切)。
并能够利用这三个关系,在直角三角形中进行一些简单计算,并且能依据生活中的一些情形,用所学知识解决一些简单的实质问题。
在整个学习过程中学生已经经历了好多合作学习的过程,拥有了必定的合作学习的经验,具备了必定的合作与沟通的能力。
并对用数学有相当的兴趣和踊跃性.可是学生研究和解决问题的能力毕竟有限,尚待增强.本节课主假如在学生原有认知能力的基础上,进一步学惯用锐角三角函数解决实质问题,经历把实质问题转变成数学识题的过程,成立相应的数学模型,以提升应用数学知识解决实质问题的能力。
新北师大九年级数学下册知识点总结

图1九年级数学下册知识点总结第一章 直角三角形边的关系一.锐角三角函数 1.正切:定义:在Rt△ABC 中,锐角∠A 的对边与邻边的比叫做∠A 的正切..,记作tanA, 即的邻边的对边A A A ∠∠=tan ;①tanA 是一个完整的符号,它表示∠A 的正切,记号里习惯省去角的符号“∠”;②tanA 没有单位,它表示一个比值,即直角三角形中∠A 的对边与邻边的比; ③tanA 不表示“tan”乘以“A”;④初中阶段,我们只学习直角三角形中,∠A 是锐角的正切;⑤tanA 的值越大,梯子越陡,∠A 越大;∠A 越大,梯子越陡,tanA 的值越大. 2.正弦..: 定义:在Rt△ABC 中,锐角∠A 的对边与斜边的比叫做∠A 的正弦,记作sinA,即斜边的对边A A ∠=sin ;3.余弦:定义:在Rt△ABC 中,锐角∠A 的邻边与斜边的比叫做∠A 的余弦,记作cosA,即斜边的邻边A A ∠=cos ;锐角A 的正弦、余弦和正切都是∠A 的三角函数当锐角A 变化时,相应的正弦、余弦和正切之也随之变化. 二.特殊角的三角函数值30 o 45 o 60 o图2hi=h:lBC图3 图4三.三角函数的计算1. 仰角:当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角..2. 俯角:当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角..3.规律:利用特殊角的三角函数值表,可以看出,1当角度在0°~90°间变化时,正弦值、正切值随着角度的增大或减小而增大或减小;余弦值随着角度的增大或减小而减小或增大.20≤sin α≤1,0≤cos α≤1.4.坡度:如图2,坡面与水平面的夹角叫做坡角坡角的正切称为坡度........... 或坡比...用字母i 表示,即A lhi tan ==5.方位角:从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角....如图3,OA 、OB 、OC 的方位角分别为45°、135°、225°.6.方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角....如图4,OA 、OB 、OC 、OD 的方向角分别是;北偏东30°,南偏东45°东南方向、南偏西为60°,北偏西60°. 7.同角的三角函数间的关系:①互余关系sinA=cos90°-A 、cosA=sin90°-A②平方关系:③商数关系:8.解直角三角形:在直角三角形中,除直角外,一共有五个元素,即三条边和二sin α 21 22 23 cos α 23 22 21 tan α33 13个锐角.由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形须知一条边. 9.直角三角形变焦关系:在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别为a 、b 、c,则有 1三边之间的关系:a 2+b 2=c 2; 2两锐角的关系:∠A +∠B=90°; 3边与角之间的关系:;cot ,tan ,cos ,sin a bA b aA c bA c aA ====;cot ,tan ,cos ,sin baB abB caB cbB ====4面积公式:c ch ab 2121S ==∆h c 为C 边上的高;5直角三角形的内切圆半径2cb a r -+=6直角三角形的外接圆半径c R 21=10.三角函数的应用 教材第18页 11.利用三角函数测高 教材第22页第二章 二次函数1.概念:一般地,若两个变量x,y 之间对应关系可以表示成c bx ax y ++=2a 、b 、c 是常数,a ≠0的形式,则称y 是x 的二次函数.....自变量x 的取值范围是全体实数.在写二次函数的关系式时,一定要寻找两个变量之间的等量关系,列出相应的函数关系式,并确定自变量的取值范围.........2. 图像性质:1二次函数y =ax 2的图象:是一条顶点在原点且y 轴对称的抛物..线..)0(2≠=a ax y 是二次函数c bx ax y ++=2的特例,此时常数b=c=0.2抛物线的描述:开口方向、对称性、y 随x 的变化情况、抛物线的最高或最低点、抛物线与x 轴的交点. ①函数的取值范围是全体实数;②抛物线的顶点在0,0,对称轴是y 轴或称直线x =0.③当a >0时,抛物线开口向上,并且向上方无限伸展.当a <0时,抛物线开口向下,并且向下方无限伸展. ④函数的增减性:A 、当a >0时⎩⎨⎧≥≤.,0;,0增大而增大随时增大而减小随时x y x x y x B 、当a <0时⎩⎨⎧≥≤.,0;,0增大而减小随时增大而增大随时x y x x y x ⑤当|a |越大,抛物线开口越小;当|a |越小,抛物线的开口越大.⑥最大值或最小值:当a >0,且x =0时函数有最小值,最小值是0;当a <0,且x =0时函数有最大值,最大值是0.3二次函数c ax y +=2的图象:是一条顶点在y 轴上且与y 轴对称的抛物线,二次函数c ax y +=2的图象中,a 的符号决定抛物线的开口方向,|a|决定抛物线的开口程度大小,c 决定抛物线的顶点位置,即抛物线位置的高低. 4二次函数c bx ax y ++=2的图象:是以直线abx 2-=为对称轴,顶点坐标为ab 2-,a b ac 442-的抛物线.开口方向和大小由a 来决定|a|的越大,抛物线的开口程度越小,越靠近对称轴y 轴,y 随x 增长或下降速度越快;|a|的越小,抛物线的开口程度越大,越远离对称轴y 轴,y 随x 增长或下降速度越慢.5二次函数c bx ax y ++=2的图象与y =ax 2的图象的关系:c bx ax y ++=2的图象可以由y =ax 2的图象平移得到:利用顶点坐标 6二次函数k h x a y +-=2)(的图象:是以直线x=h 为对称轴,顶点坐标为h,k 的抛物线.开口方向和大小由a 来决定 7二次函数c bx ax y ++=2的性质:二次函数c bx ax y ++=2配方成ab ac a b x a y 44)2(22-++=则抛物线的①对称轴:x=ab2- ②顶点坐标:ab 2-,a b ac 442-③增减性:若a>0,当x<ab 2-时,y 随x 的增大而减小.....;当x>ab2-时,y 随x 的增大而增大.......若a<0,则当x<ab 2-时,y 随x 的增大而增大.....;当x>ab2-时,y 随x 的增大而减小.......④最值:若a>0,则当x=a b2-时,a b ac y 442-=最小;若a<0,则当x=ab2-时,ab ac y 442-=最大3.确定二次函数的表达式:待定系数法 1一般式:c bx ax y ++=2 2顶点式:k h x a y +-=2)( 2交点式:y=ax-x 1x-x 24.二次函数的应用:教材第46页 几何方面教材第48页 应用题5.二次函数与一元二次方程1二次函数c bx ax y ++=2的图象抛物线与x 轴的两个交点的横坐标x 1,x 2是对应一二次方程02=++c bx ax 的两个实数根2抛物线与x 轴的交点情况可以由对应的一元二次方程的根的判别式判定: ac b 42->0 <===> 抛物线与x 轴有2个交点; ac b 42-=0 <===> 抛物线与x 轴有1个交点; ac b 42-<0 <===> 抛物线与x 轴有0个交点无交点;3当ac b 42->0时,设抛物线与x 轴的两个交点为A 、B,则这两个点之间的距离:化简后即为:)04(||4||22>--=ac b a ac b AB 这就是抛物线与x 轴的两交点之间的距离公式.第三章 圆1.圆的定义:描述性定义:在一个平面内,线段OA 绕它固定的一个端点O 旋转一周,另一个端点A 随之旋转所形成的圆形叫做圆.;固定的端点O 叫做圆心..;线段OA 叫做半径..;以点O 为圆心的圆,记作⊙O,读作“圆O ” 集合性定义:圆是平面内到定点距离等于定长的点的集合.其中定点叫做圆心..,定长叫做圆的半径....,圆心定圆的位置,半径定圆的大小,圆心和半径确定的圆叫做定圆... 对圆的定义的理解:①圆是一条封闭曲线,不是圆面;②圆由两个条件唯一确定:一是圆心即定点,二是半径即定长.2.点与圆的位置关系及其数量特征:如果圆的半径为r,点到圆心的距离为d,则①点在圆上 <===> d=r;②点在圆内 <===> d<r;③点在圆外 <===> d>r.其中点在圆上的数量特征是重点,它可用来证明若干个点共圆,方法就是证明这几个点与一个定点、的距离相等.3. 圆的对称性:1 与圆相关的概念:①弦和直径:弦:连接圆上任意两点的线段叫做弦.. 直径:经过圆心的弦叫做直径...②弧、半圆、优弧、劣弧:弧:圆上任意两点间的部分叫做圆弧..,简称弧.,用符号“⌒”表示,以CD为端点的弧记为“”,读作“圆弧CD”或“弧CD”.半圆:直径的两个端点分圆成两条弧,每一条弧叫做半圆...优弧:大于半圆的弧叫做优弧...为了区别优弧和劣弧,优弧用三个...劣弧:小于半圆的弧叫做劣弧字母表示.③弓形:弦及所对的弧组成的图形叫做弓形...④同心圆:圆心相同,半径不等的两个圆叫做同心圆....⑤等圆:能够完全重合的两个圆叫做等圆,半径相等的两个圆是等圆.⑥等弧:在同圆或等圆中,能够互相重合的弧叫做等弧...⑦圆心角:顶点在圆心的角叫做圆心角....⑧弦心距:从圆心到弦的距离叫做弦心距....2. 圆是轴对称图形,直径所在的直线是它的对称轴,圆有无数条对称轴.圆是中心对称图形,对称中心为圆心.定理:在同圆或等圆中,相等的圆心角所对的弧相等、所对的弦相等、所对的弦心距相等.推论: 在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.4.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.推论:平分一般弦不是直径的直径垂直于弦,并且平分弦所对的两条弧.说明:根据垂径定理与推论可知对于一个圆和一条直线来说,如果具备:①过圆心;②垂直于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧.上述五个条件中的任何两个条件都可推出其他三个结论.5.圆周角和圆心角的关系:1圆周角::顶点在圆上,并且两边都与圆相交的角,叫做圆周角.2圆周角定理:圆周角的度数等于它所对弧上的的圆心角度数的一半.推论1: 同弧或等弧所对的圆周角相等.推论2:直径所对的圆周角是直角;90°的圆周角所对的弦是直径;3圆内接四边形:若四边形的四个顶点都在同一个圆上,这个四边形叫做圆内接四边形.圆内接四边形的性质: 圆内接四边形的对角互补;6 确定圆的条件:1理解确定一个圆必备两个条件:圆心和半径,圆心决定圆的位置,半径决定圆的大小. 经过一点可以作无数个圆,经过两点也可以作无数个圆,其圆心在这个两点线段的垂直平分线上.2经过三点作圆要分两种情况:经过同一直线上的三点不能作圆.经过不在同一直线上的三点,能且仅能作一个圆.定理: 不在同一直线上的三个点确定一个圆.尺规作图教材第85页7.三角形的外接圆、三角形的外心.1三角形的外接圆: 经过一个三角形三个顶点的圆叫做这个三角形的外接圆. 2三角形的外心: 三角形外接圆的圆心叫做这个三角形的外心.3三角形的外心的性质:三角形外心到三顶点的距离相等.8.直线与圆的位置关系1相交: 直线与圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线.2相切: 直线和圆有惟一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,惟一的公共点做切点.3相离: 直线和圆没有公共点时,叫做直线和圆相离.4直线与圆的位置关系的数量特征:设⊙O的半径为r,圆心O到直线的距离为d;①d<r <===> 直线L和⊙O相交.②d=r <===> 直线L和⊙O 相切.③d>r <===> 直线L 和⊙O 相离.5切线的判定定理: 经过半径的外端并且垂直于半径的直线是圆的切线. 切线的性质定理:圆的切线垂直于过切点的半径. 推论1 经过圆心且垂直于切线的直线必经过切点. 推论2 经过切点且垂直于切线的直线必经过圆心.分析性质定理及两个推论的条件和结论间的关系,可得如下结论: 如果一条直线具备下列三个条件中的任意两个,就可推出第三个. ①垂直于切线; ②过切点; ③过圆心. 6三角形的内切圆、内心.和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心.三角形内心的性质:三角形的内心到三边的距离相等. 三角形的内切圆作法尺规作图教材第92页9切线长定理:过圆外一点所画的圆的两条切线长想等,圆外切四边形对边相等,直角三角形内切圆半径公式. 10.圆内接正多边形1定义:顶点都在同一圆上的正多边形叫做圆内接正多边形,这个圆叫做该正多边形的外接圆. 2中心角、边心距: 11.弧长及扇形的面积 1 弧长公式: 弧长180Rn l π=R 表示圆的半径, n 表示弧所对的圆心角的度数2扇形定义:一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形. 3 扇形的面积公式:扇形的面积3602R n S π=扇形R 表示圆的半径, n 表示弧所对的圆心角的度数扇形的面积S 扇形=LR /212.与圆有关的辅助线1如圆中有弦的条件,常作弦心距,或过弦的一端作半径为辅助线.圆心向弦作垂线2如圆中有直径的条件,可作出直径上的圆周角.直径添线成直角3若条件交代了某点是切点时,连结圆心和切点是最常用的辅助线.切点圆心要相连。
九年级数学三角函数全章知识点整理

一、角度与弧度制度量1.角度的定义与表示方法:度、分、秒2.角度的换算:度与弧度的换算3.弧度制度量的定义与表示方法4.弧度与角度之间的换算二、三角函数的定义与基本性质1.正弦函数:定义、图像、性质(周期性、奇偶性、单调性)2.余弦函数:定义、图像、性质(周期性、奇偶性、单调性)3.正切函数:定义、图像、性质(周期性、奇偶性、单调性)4.函数值的范围与周期性5.三角函数的基本关系式和恒等式6.正弦、余弦的诱导公式和和差公式7.三角函数的同角关系式三、常用角的三角函数值1.0度、30度、45度、60度和90度的三角函数值2.零点的三角函数值3.常用角的三角函数值的对称性四、图像与性质1.角度对应的弧度的图像与性质2.角度对应的三角函数图像与性质3.三角函数的周期性、奇偶性和对称性4.幅度与峰值五、三角函数的性质与变换1. 函数y=A*sin(Bx+C)+D和y=A*cos(Bx+C)+D的基本性质和变换2.三角函数的峰值、最小值和最大值3.三角函数图像的平移、伸缩、翻转等变换4.三角函数的同位角恒等式与诱导公式的应用5.反三角函数的性质与定义六、三角函数的应用1.正弦定理与余弦定理:直角三角形、任意三角形的应用2.解三角形的基本步骤和技巧3.短边与短边之间的关系(余弦定理)4.弧度与扇形面积、扇形弧长的关系5.三角函数在测量、工程设计等方面的应用七、用三角函数解直角三角形1.斜边和斜边所对应的角的关系2.已知两边求角度3.已知两边求第三边4.解一般直角三角形问题的基本步骤八、平面向量与复数1.平面向量的定义、表示方法和性质2.平面向量的共线与平行3.向量在平面内的平移九、极坐标与复数1.平面极坐标系的定义与性质2.复数的定义与基本性质3.复数运算:加法、减法、乘法、除法4.复数的共轭、模和辐角5.复数的指数形式与三角形式以上为九年级数学三角函数全章的知识点整理,其中包括角度与弧度制度量、三角函数的定义与基本性质、常用角的三角函数值、图像与性质、三角函数的性质与变换、三角函数的应用、用三角函数解直角三角形、平面向量与复数、极坐标与复数等内容,共计1200字以上。
(word完整版)新北师大九年级数学下册知识点总结,推荐文档

图1新北师大版九年级数学下册知识点总结第一章 直角三角形边的关系一.锐角三角函数 1.正切:定义:在Rt△ABC 中,锐角∠A 的对边与邻边的比叫做∠A 的正切..,记作tanA , 即的邻边的对边A A A ∠∠=tan ;①tanA 是一个完整的符号,它表示∠A 的正切,记号里习惯省去角的符号“∠”; ②tanA 没有单位,它表示一个比值,即直角三角形中∠A 的对边与邻边的比; ③tanA 不表示“tan”乘以“A”;④初中阶段,我们只学习直角三角形中,∠A 是锐角的正切;⑤tanA 的值越大,梯子越陡,∠A 越大;∠A 越大,梯子越陡,tanA 的值越大。
2.正弦..: 定义:在Rt△ABC 中,锐角∠A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即斜边的对边A A ∠=sin ;3.余弦:定义:在Rt△ABC 中,锐角∠A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即斜边的邻边A A ∠=cos ;锐角A 的正弦、余弦和正切都是∠A 的三角函数当锐角A 变化时,相应的正弦、余弦和正切之也随之变化。
二.特殊角的三角函数值三.三角函数的计算1. 仰角:当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角..2. 俯角:当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角..3.规律:利用特殊角的三角函数值表,可以看出,(1)当角度在0°~90°间变化时,正弦值、正切值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大(或减小)而减小(或增大)。
(2)0≤sin α≤1,0≤cos α≤1。
4.坡度:如图2,坡面与水平面的夹角叫做坡角坡角的正切称为坡度........... (或坡比..)。
用字母i 表示,即A lhi tan ==5.方位角:从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角...。
如图3,OA 、OB 、OC 的方位角分别为45°、135°、225°。
新北师大九年级数学下册知识点总结

图 1图 3图4新北师大版九年级数学下册知识点总结第一章 直角三角形边的关系一.锐角三角函数 1.正切:定义:在Rt△ABC 中,锐角∠A 的对边与邻边的比叫做∠A 的正切..,记作tanA , 即的邻边的对边A A A ∠∠=tan ;①tanA 是一个完整的符号,它表示∠A 的正切,记号里习惯省去角的符号“∠”; ②tanA 没有单位,它表示一个比值,即直角三角形中∠A 的对边与邻边的比; ③tanA 不表示“tan”乘以“A”;④初中阶段,我们只学习直角三角形中,∠A 是锐角的正切;⑤tanA 的值越大,梯子越陡,∠A 越大;∠A 越大,梯子越陡,tanA 的值越大。
2.正弦..: 定义:在Rt△ABC 中,锐角∠A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即斜边的对边A A ∠=sin ;3.余弦:定义:在Rt△ABC 中,锐角∠A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即斜边的邻边A A ∠=cos ;锐角A 的正弦、余弦和正切都是∠A 的三角函数当锐角A 变化时,相应的正弦、余弦和正切之也随之变化。
二.特殊角的三角函数值三.三角函数的计算1. 仰角:当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角..2. 俯角:当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角..3.规律:利用特殊角的三角函数值表,可以看出,(1)当角度在0°~90°间变化时,正弦值、正切值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大(或减小)而减小(或增大)。
(2)0≤sin α≤1,0≤cos α≤1。
4.坡度:如图2,坡面与水平面的夹角叫做坡角坡角的正切称为坡度........... (或坡比..)。
用字母i 表示,即A lhi tan == 5.方位角:从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角...。
如图3,OA 、OB 、OC 的方位角分别为45°、135°、225°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)6、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、余切的增减性:当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小。
A 90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边 C A90B 90∠-︒=∠︒=∠+∠得由B A8、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)9、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即hi l=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。
:i h l =hlα要点一:锐角三角函数的基本概念 一、选择题1.(2009·漳州中考)三角形在方格纸中的位置如图所示,则tan α的值是( )A .35B .43 C .34 D .45 【解析】选C. tan α43==角的邻边角的对边αα. 2.(2008·威海中考)在△ABC 中,∠C =90°,tan A =13,则sin B =( )A .1010 B .23C .34D .31010【解析】选D. 31tan ==AB BC A ,设BC=k,则AC=3k,由勾股定理得,10)3(2222k k k BC AC AB =+=+=310sin AC B AB == 3.(2009·齐齐哈尔中考)如图,O ⊙是ABC △的外接圆,AD 是O ⊙的直径,若O ⊙的半径为32,2AC =,则sin B 的值是( )A .23 B .32 C .34 D .43【解析】选A.连接CD,由O ⊙的半径为32.得AD=3. sin B =.32sin ==AD AC D 4.(2009·湖州中考)如图,在Rt ABC △中,ACB ∠=Rt ∠,1BC =,2AB =,则下列结论正确的是( )A.3sin2A=B.1tan2A=C.3cos2B=D.tan3B=【解析】选D在直角三角形ABC中,1BC=,2AB=,所以AC=3;所以1sin2A=,3cos A=,3tan A=;3sin B=,1cos2B=,tan3B=;5.(2008·温州中考)如图,在Rt ABC△中,CD是斜边AB上的中线,已知2CD=,3AC=,则sin B的值是()A.23B.32C.34D.43【解析】选C.由CD是Rt ABC△斜边AB上的中线,得AB=2CD=4.∴sin B43==ABAC6.(2007·泰安中考)如图,在ABC△中,90ACB∠=o,CD AB⊥于D,若3AC= 32AB=tan BCD∠的值为()(A2(B)22(C)63(D)33答案:B二、填空题ACBD7.(2009·梧州中考)在△ABC中,∠C=90°, BC=6 cm,53sin=A,则AB的长是 cm.【解析】,536sin===ABABBCA解得AB=10cm答案:108.(2009·孝感中考)如图,角α的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则sinα=.【解析】因为P(3,4),所以OP=5,所以4sin5α=;答案:45;9.(2009·庆阳中考)如图,菱形ABCD的边长为10cm,DE⊥AB,3sin5A=,则这个菱形的面积= cm2.【解析】.5310sin===DEADDEA解得DE=6cm.∴10660=⨯=⨯=LINGS AB DE cm2.答案:60三、解答题10.(2009·河北中考) 如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD = 24 m,OE⊥CD于点E.已测得sin∠DOE =1213.(1)求半径OD;AOBEC D(2)根据需要,水面要以每小时0.5 m的速度下降,则经过多长时间才能将水排干?【解析】(1)∵OE⊥CD于点E,CD=24(m),∴ED =12CD=12(m).在Rt△DOE中,∵sin∠DOE =EDOD =12 13,∴OD =13(m).(2)OE5(m)∴将水排干需:5÷0.5=10(小时).11.(2009·綦江中考)如图,在矩形ABCD中,E是BC边上的点,AE BC=,DF AE⊥,垂足为F,连接DE.(1)求证:ABE△DFA≌△;(2)如果10AD AB=,=6,求sin EDF∠的值.【解析】(1)在矩形ABCD中,90BC AD AD BC B=∠=,∥,°DAF AEB∴∠=∠DF AE AE BC⊥=Q,90AFD B∴∠=∠°=AE AD=ABE DFA∴△≌△.(2)由(1)知ABE DFA△≌△6AB DF∴==在直角ADF△中,8AF===2EF AE AF AD AF∴=-=-=在直角DFE △中,222262210DE DF EF =+=+= 210sin 10210EF EDF DE ∴∠===. 12.(2008·宁夏中考)如图,在△ABC 中,∠C =90°,sin A =54,AB =15,求△ABC 的周长和tan A 的值.【解析】在Rt △ABC 中, ∠C =90°, AB =15A sin =AB BC =54, ∴ 12=BC 912152222=-=-=BC AB AC∴周长为36,BC 124tan A .AC 93=== 13.(2008·肇庆中考)在Rt △ABC 中,∠C = 90°,a =3 ,c =5,求sin A 和tan A 的值.【解析】在Rt △ABC 中,c =5,a =3. ∴ 22a c b -=2235-=4=∴ 53sin ==c a A 43tan ==b a A .14.(2007·芜湖中考)如图,在△ABC 中,AD 是BC 上的高,tan cos B DAC =∠,(1) 求证:AC=BD ; (2)若12sin 13C =,BC =12,求AD 的长.【解析】(1)∵AD 是BC 上的高,∴AD ⊥BC . ∴∠ADB =90°,∠ADC =90°. 在Rt △ABD 和Rt △ADC 中, ∵tan B =AD BD ,cos DAC ∠=ADAC又已知tan cos B DAC =∠∴AD BD =AD AC.∴AC=BD . (2)在Rt △ADC 中, 12sin 13C =,故可设AD =12k ,AC =13k .22DC AC AD 5kAD AD BD 13ktan B cos DAC BC 13k 5k 122k ,AD 8.3∴=-====∠∴=+=∴== 要点二、特殊角的三角函数值 一、选择题1.(2009·钦州中考)sin30°的值为( )A .3 B .2 C .12D .3 答案:C2.(2009·长春中考).菱形OABC 在平面直角坐标系中的位置如图所示,452AOC OC ∠==°,,则点B 的坐标为( )A .2,B .2),C .211),D .(121),答案:C3.(2009·定西中考)某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为( )A .8米B .83C 83D 43米答案:C4.(2008·宿迁中考)已知α为锐角,且23)10sin(=︒-α,则α等于( ) A.︒50 B.︒60C.︒70 D.︒80 答案:C5.(2008·毕节中考) A (cos60°,-tan30°)关于原点对称的点A 1的坐标是( )A .1323⎛⎫- ⎪ ⎪⎝⎭,B .3323⎛⎫- ⎪ ⎪⎝⎭,C .1323⎛⎫-- ⎪ ⎪⎝⎭,D .1322⎛⎫- ⎪ ⎪⎝⎭, 答案:A6.(2007·襄樊中考)计算:2cos 45tan 60cos30+o o o g等于( ) (A )1 (B )2 (C )2 (D )3 答案:C二、填空7. (2009·荆门中考)104cos30sin 60(2)(20092008)-︒︒+---=______.【解析】104cos30sin 60(2)(20092008)-︒︒+---3314()1213()1232=⋅⋅+--=+--= 答案:238.(2009·百色中考)如图,在一次数学课外活动中,测得电线杆底部B 与钢缆固定点C 的距离为4米,钢缆与地面的夹角为60º,则这条钢缆在电线杆上的固定点A 到地面的距离AB 是 米.(结果保留根号).答案:439.(2008·江西中考)计算:(1)1sin 60cos302-=o o g . 【解析】1sin 60cos302-=o o g .412143212323=-=-⨯ 答案:1410.(2007·济宁中考)计算sin 60tan 45cos30︒-︒︒的值是 。
