理论力学课后习题答案_第5章__点的复合运动分析)
理论力学课后答案第五章(周衍柏)上课讲义

理论力学课后答案第五章(周衍柏)第五章思考题5.1虚功原理中的“虚功”二字作何解释?用虚功原理理解平衡问题,有何优点和缺点?5.2 为什么在拉格朗日方程中,a θ不包含约束反作用力?又广义坐标与广义力的含义如何?我们根据什么关系由一个量的量纲定出另一个量的量纲?5.3广义动量a p 和广义速度a q 是不是只相差一个乘数m ?为什么a p 比a q 更富有意义?5.4既然a q T ∂∂是广义动量,那么根据动量定理,⎪⎪⎭⎫ ⎝⎛∂∂αq T dt d 是否应等于广义力a θ?为什么在拉格朗日方程()14.3.5式中多出了aq T ∂∂项?你能说出它的物理意义和所代表的物理量吗?5.5为什么在拉格朗日方程只适用于完整系?如为不完整系,能否由式()13.3.5得出式()14.3.5?5.6平衡位置附近的小振动的性质,由什么来决定?为什么22s 个常数只有2s 个是独立的?5.7什么叫简正坐标?怎样去找?它的数目和力学体系的自由度之间有何关系又每一简正坐标将作怎样的运动?5.8多自由度力学体系如果还有阻尼力,那么它们在平衡位置附近的运动和无阻尼时有何不同?能否列出它们的微分方程?5.9 dL 和L d 有何区别?a q L ∂∂和aq L ∂∂有何区别? 5.10哈密顿正则方程能适用于不完整系吗?为什么?能适用于非保守系吗?为什么?5.11哈密顿函数在什么情况下是整数?在什么情况下是总能量?试祥加讨论,有无是总能量而不为常数的情况?5.12何谓泊松括号与泊松定理?泊松定理在实际上的功用如何?5.13哈密顿原理是用什么方法运动规律的?为什么变分符号δ可置于积分号内也可移到积分号外?又全变分符号∆能否这样?5.14正则变换的目的及功用何在?又正则变换的关键何在?5.15哈密顿-雅可比理论的目的何在?试简述次理论解题时所应用的步骤.5.16正则方程()15.5.5与()10.10.5及()11.10.5之间关系如何?我们能否用一正则变换由前者得出后者?5.17在研究机械运动的力学中,刘维定理能否发挥作用?何故?5.18分析力学学完后,请把本章中的方程和原理与牛顿运动定律相比较,并加以评价.第五章思考题解答5.1 答:作.用于质点上的力在任意虚位移中做的功即为虚功,而虚位移是假想的、符合约束的、无限小的.即时位置变更,故虚功也是假想的、符合约束的、无限小的.且与过程无关的功,它与真实的功完全是两回事.从∑⋅=iii r F W δδ可知:虚功与选用的坐标系无关,这正是虚功与过程无关的反映;虚功对各虚位移中的功是线性迭加,虚功对应于虚位移的一次变分.在虚功的计算中应注意:在任意虚过程中假定隔离保持不变,这是虚位移无限小性的结果.虚功原理给出受约束质点系的平衡条件,比静力学给出的刚体平衡条件有更普遍的意义;再者,考虑到非惯性系中惯性力的虚功,利用虚功原理还可解决动力学问题,这是刚体力学的平衡条件无法比拟的;另外,利用虚功原理解理想约束下的质点系的平衡问题时,由于约束反力自动消去,可简便地球的平衡条件;最后又有广义坐标和广义力的引入得到广义虚位移原理,使之在非纯力学体系也能应用,增加了其普适性及使用过程中的灵活性.由于虚功方程中不含约束反力.故不能求出约束反力,这是虚功原理的缺点.但利用虚功原理并不是不能求出约束反力,一般如下两种方法:当刚体受到的主动力为已知时,解除某约束或某一方向的约束代之以约束反力;再者,利用拉格朗日方程未定乘数法,景观比较麻烦,但能同时求出平衡条件和约束反力.5.2 答 因拉格朗日方程是从虚功原理推出的,而徐公原理只适用于具有理想约束的力学体系虚功方程中不含约束反力,故拉格朗日方程也只适用于具有理想约束下的力学体系,αθ不含约束力;再者拉格朗日方程是从力学体系动能改变的观点讨论体系的运动,而约束反作用力不能改变体系的动能,故αθ不含约束反作用力,最后,几何约束下的力学体系其广义坐标数等于体系的自由度数,而几何约束限制力学体系的自由运动,使其自由度减小,这表明约束反作用力不对应有独立的广义坐标,故αθ不含约束反作用力.这里讨论的是完整系的拉格朗日方程,对受有几何约束的力学体系既非完整系,则必须借助拉格朗日未定乘数法对拉格朗日方程进行修正.广义坐标市确定质点或质点系完整的独立坐标,它不一定是长度,可以是角度或其他物理量,如面积、体积、电极化强度、磁化强度等.显然广义坐标不一定是长度的量纲.在完整约束下,广义坐标数等于力学体系的自由度数;广义力明威力实际上不一定有力的量纲可以是力也可以是力矩或其他物理量,如压强、场强等等,广义力还可以理解为;若让广义力对应的广义坐标作单位值的改变,且其余广义坐标不变,则广义力的数值等于外力的功由W q r F s i ni i δδθδααα==⋅∑∑==11 知,ααδθq 有功的量纲,据此关系已知其中一个量的量纲则可得到另一个量的量纲.若αq 是长度,则αθ一定是力,若αθ是力矩,则αq 一定是角度,若αq 是体积,则αθ一定是压强等.5.3 答 αp 与αq 不一定只相差一个常数m ,这要由问题的性质、坐标系的选取形式及广义坐标的选用而定。
理论力学答案第5章点的复合运动分析
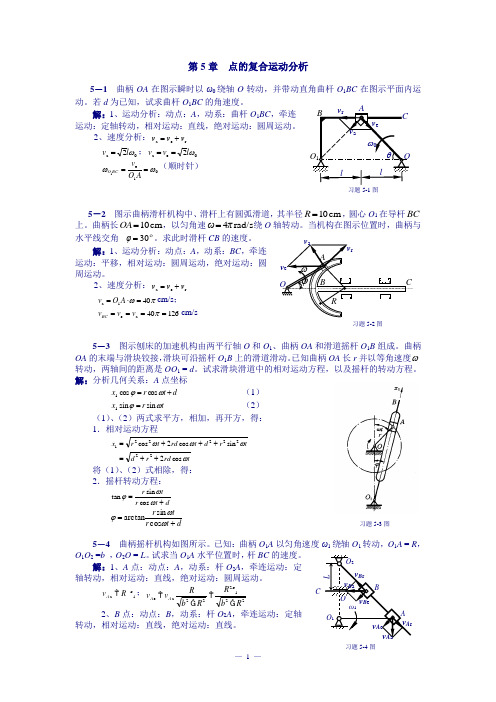
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v +=πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将(1)、(2)式相除,得: 2.摇杆转动方程: dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5-4 曲柄摇杆机构如图所示。
《理论力学》武清玺第五章_点的运动_习题全解

第五章 点的运动 习题全解[习题5-1] 一点按2123+-=t t x 的规律沿直线动动(其中t 要s 计,x 以m 计).试求:(1)最初s 3内的位移;(2)改变动动方向的时刻和所在位置;(3)最初s 3内经过的路程;(4)s t 3=时的速度和加速度;(5)点在哪段时间作加速度,哪段时间作减速运动. 解:(1)求最初s 3内的位移.m x 220120)0(3=+⨯-= m x 723123)3(3-=+⨯-=)(927)0()3(m x x x -=--=-=∆ (动点的位移为9m,位移的方向为负x 方向). (2)求改变动动方向的时刻和所在位置. 改变方向时,动点的速度为零.即: 01232=-==t dtdxv , 亦即:当s t 2=时,动点改变运动方向.此时动点所在的位置为: )(1422122)2(3m x -=+⨯-= (3)求最初s 3内经过的路程.)(23716|)14(7||214|)3~2()2~0()3~0(m S S S =+=---+--=+= (4)求s t 3=时的速度和加速度1232-==t dt dx v )/(151233)3(2s m dt dx v =-⨯== t dtdv a 6== )/(1836)3(2s m a =⨯=(5)求动点在哪段时间作加速度,哪段时间作减速运动.若v 与a 同号,则动点作加速运动; 若v 与a 异号,则动点作减速运动.即: 同号时有:0)2)(2(18)4(18)6)(123(22>+-=-=-=t t t t t t t va0)2)(2(>+-t t t20<<t .即当s t 20<<时,动点作加速动动.Oxy图题25-异号时有:0)2)(2(<+-t t t2>t即当s t 2>时,动点作减速运动.[习题5-2] 已知图示机构中,l AB OA ==,a AC DM CM ===,求出t ωϕ=时,点M 的动动方程和轨迹方程。
理论力学课后答案5

CD veAB vrAB ve vrCD
将上式向 v2 方向投影,有: CD veAB cos vrAB sin ve 由此得到
即:
课
答
CD ve veAB cos v2 v1cos sin sin
案
网
CD va ve vrCD
va (veAB ) 2 (vrAB ) 2
5.8 如图所示,摇杆机构的滑杆 AB 以等速 v 向上运动。摇杆长 OC a ,距离 π OD l 。求当 时点 C 的速度的大小。 4
魏 魏 魏
后
泳 泳 泳
ww
涛 涛 涛
m
案
ve va cos 45
ve v lOA 2l av vC a 2l
课
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
w.
kh
da
w.
co
我在沙滩上写上你的名字,却被浪花带走了;我在云上写上你的名字,却被风儿带走了;于是我在理论力 学的习题答案上写上我的名字.
5.2 斗挖掘机的链速 v1 16 m min ,斗间的距离 l 0.8m ,在垂直于图形平面的 方向上的斗宽为 b 0.4m 。问挖掘机沿斜坡纵向应以多大的速度 v2 行走,才能使 斗在挖土时不留下挖痕和空白
魏 魏 魏
后
泳 泳 泳
ww
涛 涛 涛
m
课
答
解: 显然,相对运动轨迹为圆,轨迹方程为 x y ( 1) 2 ( ) 2 1 40 40 从动坐标系 Oxy 向定坐标系的变换矩阵为 cos sin sin cos 所以,相对坐标为 ( x, y) 的动点 M 的绝对坐标为 x cos sin x 4 cos 40 cos t cos 40 sin t sin y sin cos y 40 sin 40 sin t sin 40 sin t sin 注意到 t ,由此可得 x 40(cos t 1) y 40 sin t 绝对运动轨迹为圆,轨迹方程为 x y ( 1) 2 ( ) 2 1 40 40
理论力学课后答案第五章

第五章思考题5.1虚功原理中的“虚功”二字作何解释?用虚功原理理解平衡问题,有何优点和缺点?5.2 为什么在拉格朗日方程中,a θ不包含约束反作用力?又广义坐标与广义力的含义如何?我们根据什么关系由一个量的量纲定出另一个量的量纲?5.3广义动量a p 和广义速度a q &是不是只相差一个乘数m ?为什么a p 比aq &更富有意义? 5.4既然aq T &∂∂是广义动量,那么根据动量定理,⎪⎪⎭⎫ ⎝⎛∂∂αq T dt d &是否应等于广义力a θ?为什么在拉格朗日方程()14.3.5式中多出了a q T ∂∂项?你能说出它的物理意义和所代表的物理量吗?5.5为什么在拉格朗日方程只适用于完整系?如为不完整系,能否由式()13.3.5得出式()14.3.5?5.6平衡位置附近的小振动的性质,由什么来决定?为什么22s 个常数只有2s 个是独立的?5.7什么叫简正坐标?怎样去找?它的数目和力学体系的自由度之间有何关系又每一简正坐标将作怎样的运动?5.8多自由度力学体系如果还有阻尼力,那么它们在平衡位置附近的运动和无阻尼时有何不同?能否列出它们的微分方程?5.9 dL 和L d 有何区别?a q L ∂∂和aq L ∂∂有何区别? 5.10哈密顿正则方程能适用于不完整系吗?为什么?能适用于非保守系吗?为什么?5.11哈密顿函数在什么情况下是整数?在什么情况下是总能量?试祥加讨论,有无是总能量而不为常数的情况?5.12何谓泊松括号与泊松定理?泊松定理在实际上的功用如何?5.13哈密顿原理是用什么方法运动规律的?为什么变分符号δ可置于积分号内也可移到积分号外?又全变分符号∆能否这样?5.14正则变换的目的及功用何在?又正则变换的关键何在?5.15哈密顿-雅可比理论的目的何在?试简述次理论解题时所应用的步骤.5.16正则方程()15.5.5与()10.10.5及()11.10.5之间关系如何?我们能否用一正则变换由前者得出后者?5.17在研究机械运动的力学中,刘维定理能否发挥作用?何故?5.18分析力学学完后,请把本章中的方程和原理与牛顿运动定律相比较,并加以评价.第五章思考题解答5.1 答:作.用于质点上的力在任意虚位移中做的功即为虚功,而虚位移是假想的、符合约束的、无限小的.即时位置变更,故虚功也是假想的、符合约束的、无限小的.且与过程无关的功,它与真实的功完全是两回事.从∑⋅=ii i r F W ρρδδ可知:虚功与选用的坐标系无关,这正是虚功与过程无关的反映;虚功对各虚位移中的功是线性迭加,虚功对应于虚位移的一次变分.在虚功的计算中应注意:在任意虚过程中假定隔离保持不变,这是虚位移无限小性的结果.虚功原理给出受约束质点系的平衡条件,比静力学给出的刚体平衡条件有更普遍的意义;再者,考虑到非惯性系中惯性力的虚功,利用虚功原理还可解决动力学问题,这是刚体力学的平衡条件无法比拟的;另外,利用虚功原理解理想约束下的质点系的平衡问题时,由于约束反力自动消去,可简便地球的平衡条件;最后又有广义坐标和广义力的引入得到广义虚位移原理,使之在非纯力学体系也能应用,增加了其普适性及使用过程中的灵活性.由于虚功方程中不含约束反力.故不能求出约束反力,这是虚功原理的缺点.但利用虚功原理并不是不能求出约束反力,一般如下两种方法:当刚体受到的主动力为已知时,解除某约束或某一方向的约束代之以约束反力;再者,利用拉格朗日方程未定乘数法,景观比较麻烦,但能同时求出平衡条件和约束反力.5.2 答 因拉格朗日方程是从虚功原理推出的,而徐公原理只适用于具有理想约束的力学体系虚功方程中不含约束反力,故拉格朗日方程也只适用于具有理想约束下的力学体系,αθ不含约束力;再者拉格朗日方程是从力学体系动能改变的观点讨论体系的运动,而约束反作用力不能改变体系的动能,故αθ不含约束反作用力,最后,几何约束下的力学体系其广义坐标数等于体系的自由度数,而几何约束限制力学体系的自由运动,使其自由度减小,这表明约束反作用力不对应有独立的广义坐标,故αθ不含约束反作用力.这里讨论的是完整系的拉格朗日方程,对受有几何约束的力学体系既非完整系,则必须借助拉格朗日未定乘数法对拉格朗日方程进行修正.广义坐标市确定质点或质点系完整的独立坐标,它不一定是长度,可以是角度或其他物理量,如面积、体积、电极化强度、磁化强度等.显然广义坐标不一定是长度的量纲.在完整约束下,广义坐标数等于力学体系的自由度数;广义力明威力实际上不一定有力的量纲可以是力也可以是力矩或其他物理量,如压强、场强等等,广义力还可以理解为;若让广义力对应的广义坐标作单位值的改变,且其余广义坐标不变,则广义力的数值等于外力的功由W q r F s i ni i δδθδααα==⋅∑∑==11ρρ知,ααδθq 有功的量纲,据此关系已知其中一个量的量纲则可得到另一个量的量纲.若αq 是长度,则αθ一定是力,若αθ是力矩,则αq 一定是角度,若αq 是体积,则αθ一定是压强等.5.3 答 αp 与αq &不一定只相差一个常数m ,这要由问题的性质、坐标系的选取形式及广义坐标的选用而定。
哈尔滨工业大学 第七版 理论力学 第5章 课后习题答案

第5章 摩 擦5-1 如图5-1a 所示,置于V 型槽中的棒料上作用1力偶,力偶矩m N 15⋅=M 时,刚好能转动此棒料。
已知棒料重力N 400=P ,直径m 25.0=D ,不计滚动摩阻。
求棒料与V 形槽间的静摩擦因数f s 。
(a)(b)图5-1解 圆柱体为研究对象,受力如图5-1b 所示,F s1,F s2为临界最大摩擦力。
0=∑x F ,045cos 2s 1N =°−+P F F (1) 0=∑y F ,045sin 1s 2N =°−−P F F (2) 0=∑O M ,0222s 1s =−+M DF D F(3)临界状态摩擦定律:1N s 1s F f F =(4) 2N s 2s F f F =(5)以上5式联立,化得 0145cos s2s =+°−MPDf f 代入所给数据得01714.4s 2s =+−f f 方程有2根:442.4s1=f (不合理), 223.0s2=f (是解)故棒料与V 形槽间的摩擦因数223.0s =f5-2 梯子AB 靠在墙上,其重力为N 200=P,如图5-2a 所示。
梯长为l ,并与水平面交角°=60θ。
已知接触面间的静摩擦因数均为0.25。
今有1重力为650 N 的人沿梯向上爬,问人所能达到的最高点C 到点A 的距离s 应为多少?AN F As F(a)(b)图5-2解 梯子为研究对象,受力如图5-2b 所示,刚刚要滑动时,A ,B 处都达最大静摩擦力。
人重力N 650=W ,平衡方程: 0=∑x F , 0s N =−A B F F (1) 0=∑y F , 0s N =−−+W P F F B A(2)0=∑A M ,060cos 60sin 60cos 60cos 2s N =°−°−°+°l F l F Ws lPB B (3) 临界补充方程:A s A F f F N s = (4)B s B F f F N s =(5)联立以上5式,解得 N 80012sN =++=f WP F A ,N 200s =A F N 200)(12s N =++=W P f f F sB ,N 50s =B F l PF f W l s B 456.02)3[(N s =−+=5-3 2根相同的匀质杆AB 和BC ,在端点B 用光滑铰链连接,A ,C 端放在不光滑的水平面上,如图5-3a 所示。
清华大学版理论力学课后习题答案大全-----第5章点的复合运动分析
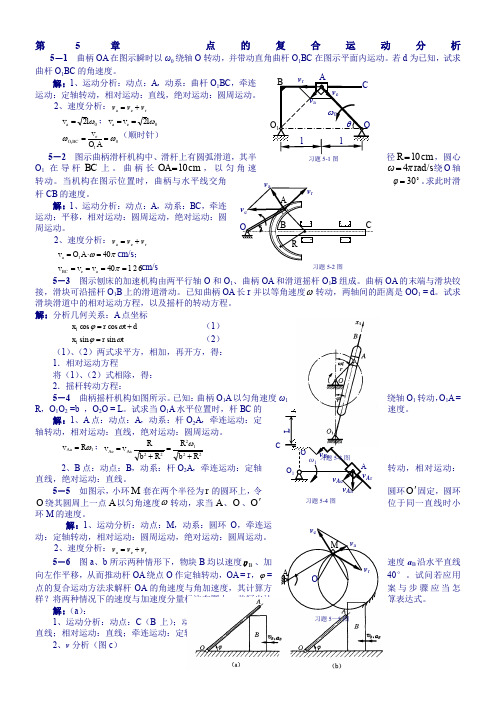
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴30=φ。
求此时滑转动。
当机构在图示位置时,曲柄与水平线交角杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v += πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程 将(1)、(2)式相除,得: 2.摇杆转动方程:5-4 曲柄摇杆机构如图所示。
已知:曲柄O 1A 以匀角速度ω1绕轴O 1转动,O 1A = R ,O 1O 2 =b ,O 2O = L 。
试求当O 1A 水平位置时,杆BC 的速度。
解:1、A 点:动点:A ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
理论力学(周衍柏)习题答案,第五章

第五章习题解答5.1解如题5.1.1图杆受理想约束,在满足题意的约束条件下杆的位置可由杆与水平方向夹角所唯一确定。
杆的自由度为1,由平衡条件:即mg y =0①变换方程y=2rcos sin-= rsin2②故③代回①式即因在约束下是任意的,要使上式成立必须有:rcos2-=0④又由于cos=故cos2=代回④式得5.2解如题5.2.1图三球受理想约束,球的位置可以由确定,自由度数为1,故。
得由虚功原理故①因在约束条件下是任意的,要使上式成立,必须故②又由得:③由②③可得5.3解如题5.3.1图,在相距2a的两钉处约束反力垂直于虚位移,为理想约束。
去掉绳代之以力T,且视为主动力后采用虚功原理,一确定便可确定ABCD的位置。
因此自由度数为1。
选为广义坐。
由虚功原理:w①又取变分得代入①式得:化简得②设因在约束条件下任意,欲使上式成立,须有:由此得5.4解自由度,质点位置为。
由①由已知得故②约束方程③联立②③可求得或又由于故或5.5解如题5.5.1图按题意仅重力作用,为保守系。
因为已知,故可认为自由度为1.选广义坐标,在球面坐标系中,质点的动能:由于所以又由于故取Ox为零势,体系势能为:故力学体系的拉氏函数为:5.6解如题5.6.1图.平面运动,一个自由度.选广义坐标为,广义速度因未定体系受力类型,由一般形式的拉格朗日方程①在广义力代入①得:②在极坐标系下:③故将以上各式代入②式得5.7解如题5.7.1图又由于所以①取坐标原点为零势面②拉氏函数③代入保守系拉格朗日方程得代入保守系拉格朗日方程得5.8解:如图5.8.1图.(1)由于细管以匀角速转动,因此=可以认为质点的自由度为1.(2)取广义坐标.(3)根据极坐标系中的动能取初始水平面为零势能面,势能:拉氏函数①(4),代入拉氏方程得:(5)先求齐次方程的解.②特解为故①式的通解为③在时:④⑤联立④⑤得将代回式③可得方程的解为:5.9解如题5.9.1图.(1)按题意为保守力系,质点被约束在圆锥面内运动,故自有度数为2. (2)选广义坐标,.(3)在柱坐标系中:以面为零势能面,则:拉氏函数-①(4)因为不显含,所以为循环坐标,即常数②对另一广义坐标代入保守系拉氏方程③有得④所以此质点的运动微分方程为(为常数)所以5.10解如题5.10.1图.(1)体系自由度数为2.(2)选广义坐标(3)质点的速度劈的速度故体系动能以面为零势面,体系势能:其中为劈势能.拉氏函数①(4)代入拉格郎日方程得:②代入拉格郎日方程得③联立②,③得5.11 解如题5.11.1图(1)本系统内虽有摩擦力,但不做功,故仍是保守系中有约束的平面平行运动,自由度(2)选取广义坐标(3)根据刚体力学其中绕质心转动惯量选为零势面,体系势能:其中C为常数.拉氏函数(4)代入保守系拉氏方程得:对于物体,有5.12解如题5.12.1图.(1)棒作平面运动,一个约束,故自由度. (2)选广义坐标(3)力学体系的动能根据运动合成又故设为绕质心的回转半径,代入①得动能②(4)由③(其中)则④因为、在约束条件下任意且独立,要使上式成立,必须:⑤(5)代入一般形式的拉氏方程得:⑥又代入一般形式的拉氏方程得:⑦⑥、⑦两式为运动微分方程(6)若摆动角很小,则,代入式得:,代入⑥⑦式得:⑧又故代入⑧式得:(因为角很小,故可略去项)5.13解如题5.13.1图(1)由于曲柄长度固定,自由度.(2)选广义坐标,受一力矩,重力忽略,故可利用基本形式拉格朗日方程:①(3)系统动能②(4)由定义式③(5)代入①得:得5.14.解如题5.14.1图.(1)因体系作平面平行运动,一个约束方程:(2)体系自由度,选广义坐标.虽有摩擦,但不做功,为保守体系(3)体系动能:轮平动动能轮质心转动动能轮质心动能轮绕质心转动动能.①以地面为零势面,体系势能则保守系的拉氏函数②(1)因为不显含,得知为循环坐标.故=常数③开始时:则代入得又时,所以5.15解如题5.15.1图(1)本系统作平面平行运动,干限制在球壳内运动,自由度;选广义坐标,体系摩擦力不做功,为保守力系,故可用保守系拉氏方程证明①(2)体系动能=球壳质心动能+球壳转动动能+杆质心动能+杆绕中心转动动能②其中代入②得以地面为零势面,则势能:(其中为常数)(3)因为是循环坐标,故常熟③而代入①式得④联立③、④可得(先由③式两边求导,再与④式联立)⑤⑤试乘并积分得:又由于当5.16解如题图5.16.1.(1)由已知条件可得系统自由度.(2)取广义坐标.(3)根据刚体力学,体系动能:①又将以上各式代入①式得:设原点为零势能点,所以体系势能体系的拉氏函数②(1)因为体系只有重力势能做工,因而为保守系,故可采用③代入③式得即(5)解方程得5.17解如题5.17.1图(1)由题设知系统动能①取轴为势能零点,系统势能拉氏函数②(2)体系只有重力做功,为保守系,故可采用保守系拉氏方程.代入拉氏方程得:又代入上式得即③同理又代入上式得④令代入③④式得:欲使有非零解,则须有解得周期5.18解如题5.18.1图(1)系统自由度(2)取广义坐标广义速度(3)因为是微震动,体系动能:以为势能零点,体系势能拉氏函数(4)即①同理②同理③设代入①②③式得欲使有非零解,必须解之又故可得周期5.19解如题5.19.1图(1)体系自由度(2)取广义坐标广义速度(3)体系动能体系势能体系的拉氏函数(4)体系中只有弹力做功,体系为保守系,可用①将以上各式代入①式得:②先求齐次方程③设代入③式得要使有非零,必须即又故通解为:其中又存在特解有②③式可得式中及为积分常数。
清华理论力学课后答案5

第五章点的合成运动习题解答5-1在图a 、b 所示的两种机构中,已知20021==a O O mm ,31=ωrad/s 。
求图示位置时杆A O 2的角速度。
解:(1)取杆A O 1上的A 点为动点,杆A O 2为动系。
1a ωa v =,由r e a v v v +=作速度平行四边形(如题5-1图a 所示),得a v v 1a e 2330cos ω==�,rad/s 5.1212e 2===ωωA O v ,(逆时针)(2)取滑块A 为动点,杆A O 1为动系,1e ωa v =,由r e a v v v +=作速度平行四边形(如题5-1图b 所示),得1ea 3230cos ωa v v ==�,rad/s 23212a 2===ωωA O v .(逆时针)5-2图示曲柄滑道机构中,杆BC 为水平,杆DE 保持铅直。
曲柄长10.OA =m ,并以匀角速度20=ωrad/s 绕O 轴转动,通过滑块A 使杆BC 作往复运动。
求当曲柄水平线的交角分别为0=ϕ、�30、�90时杆BC 的速度。
解:取滑块A 为动点,动系为BCE 杆。
m/s 2OA a =⋅=ϕ̇v .由r e a v v v +=得ϕsin a e v v =当�0=ϕ时,0e =v ;当�30=ϕ时,m/s 1e =v ;当90=ϕ时,m/s 2e =v .5-3图示曲柄滑道机构中,曲柄长r OA =,并以匀角速度ω饶O 轴转动。
装在水平杆上的滑槽DE 与水平线成�60角。
求当曲柄与水平线交角0=ϕ、�30、�60时,杆BC 的速度。
解:取滑块A 为动点,动系为杆BC ,ωωr v =⋅=OA a .作速度矢量图如图示。
题5-2图(a)(b)题5-1图课后答案网ww w.kh da w .c o m题5-3图由正弦定理)30-sin()60-sin(180ea ���ϕv v =,解得)30-sin(32-e �ϕω⋅=r v .当�0=ϕ时,e v r =;当30o ϕ=时,0=e v ;当60o ϕ=时,e v r =(向右).5-4如图所示,瓦特离心调速器以角速度ω绕铅垂轴转动。
理论力学简明教程第五章答案

第五张 刚体力学平动中见彼此,转动中见分高低.运动美会让你感受到制造的乐趣.走过这遭,或许会有曾经沧海难为水的感叹.别忘了,坐标变换将为你迷津救渡,同时亦会略显身手.【要点分析与总结】1 刚体的运动(1)刚体内的任一点的速度、加速度(A 为基点)A r υυω'=+⨯()()A d r a a r dtωωω'⨯'=++⨯⨯ (2)刚体内的瞬心S :()21s A A r r ωυω=+⨯〈析〉ω为基点转动的矢量和,12ωωω=++A r r r '=+dr dtυ=*A A A dr dr d r r r dt dt dt υωυω''''=+=++⨯=+⨯ ()A d r d d a dt dt dtωυυ'⨯==++()r ωω'⨯⨯ 值得注意的是:有转动时r '与r ω'⨯的微分,引入了r ω'⨯与()r ωω'⨯⨯项。
2 刚体的动量,角动量,动能 (1)动量:c P m υ=(2)角动量: x x xx xy xz i i i y yxyy yz y zx zyzz z z L J J J L r m L J J J J J J J L ωυωωω⎛⎫⎛⎫⎛⎫-- ⎪ ⎪⎪=⨯===-- ⎪ ⎪ ⎪ ⎪ ⎪⎪--⎝⎭⎝⎭⎝⎭∑式中:转动惯量()()()222222xx yy zz J y z dmJ z x dm J x y dm ⎧=+⎪⎪=+⎨⎪=+⎪⎩⎰⎰⎰惯量积xx yy zz J xydm J yzdm J zxdm ⎧=⎪⎪=⎨⎪=⎪⎩⎰⎰⎰且c c cL r m L υ'=⨯+* l e 方向(以l 为轴)的转动惯量:(),,l l J e J e J ααβγβγ⎛⎫ ⎪== ⎪ ⎪⎝⎭222222xx yy zz yz zx xy J J J J J J αβγβγγααβ=++---(,,αβγ别离为l e 与,,x y z 轴夹角的余弦) * 惯量主轴惯量主轴能够是对称轴或对称面的法线若X 轴为惯量主轴,那么含X 的惯量积为0,即: 0==xy xz J J 若,,x y z 轴均为惯量主轴,那么:xx yy zz L J i J j J k =++ 〈析〉成立的坐标轴轴应尽可能的是惯量主轴,如此会降低解题繁度。
理论力学第五章习题答案
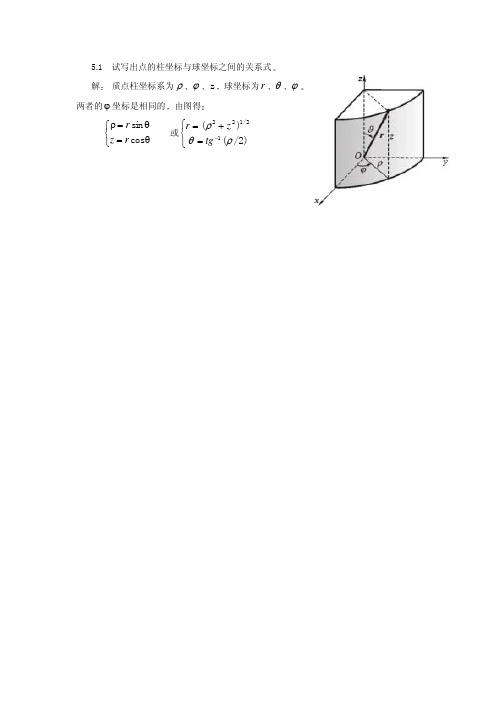
& = ak sin kt y
得
积分得 s = 4a (1 − cos
kt ) 2
5.3
根据下列点在极坐标系中的轨迹方程
试写出点的直角坐标轨迹方程
式中 p
e 均为正的常数
1
ρ=
p 1 + e cos ϕ p 1 − e cos ϕ p 1 − cos ϕ
e <1
2
ρ=
e >1
3 解
ρ=
直角坐标与极坐标有以下关系:
与 前 题 相 比 仅
e 差 一 符 号
→ (1 − e 2 ) x 2 + y 2 − 2 pex − p 2 = 0
3
ρ=பைடு நூலகம்
p 1 − cos ϕ
与 前 题 相 比
只 要 令 前 题 中 e =1 即 可
→ y 2 − 2 px − p 2 = 0
5.4 加速度 解
试以直角坐标及其导数表示 x = a ( kt − sin kt ) 切向加速度 法向加速度以及轨迹的曲率半径
sin γ = Rω / v
则由式 (**) 得 ρ = v / Rω = R / sin γ
2
2
2
5.8
如图所示
飞机 P 在任一时刻的经度为 ψ (t )
纬度为 λ (t )
高度为 h(t )
其在
地心坐标系中的球坐标运动方程为
r = R + h(t )
其中 R 是地球半径
θ = π / 2 − λ (t )
5.1 解
试写出点的柱坐标与球坐标之间的关系式 质点柱坐标系为 ρ
ϕ
z 球坐标为 r θ
ϕ
两者的 ϕ 坐标是相同的
理论力学课后习题部分答案

B
A FAC FBA
P
(l)
(l1)
(l2)
(l3)
图 1-1
1-2 画出下列每个标注字符的物体的受力图。题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
(a)
B
FN1
C
FN 2
P2 P1
FAy
A
FAx
(a2)
(b)
FN1
A
P1
FN
(b2)
C
FN′
P2
(a1)
B
FN1
FN 2
FN
P1
F Ay
FCy
FAx (f2)
C FC′x
FC′y F2
FBy
FBx B (f3)
FAy A FAx
FB
C B
(g)
FAy
FAx A
D FT C FCx
(g2)
FB
B
F1
FB′ B
FAy
A
FAx
(h)
(h1)
P (g1)
FC′y
FT
C
FC′x
P (g3)
D
FCy
FB
F2
C FCx
B
(h2)
A FAx
FAy
FCy
D FAy
A
FAx
(k3)
6
FB
F1
FB′
B B
FD D
(l) FD′ D
A FA
(l1) F2
C
FC (l2)
F1
D
F2
B
A
E
FE
FA
(l3) 或
F1
FB′
理论力学课后习题答案解析第5章点的复合运动分析)

第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v +=0a 2ωl v =;0e a 2ωl v v ==1e1ωω==AO v BCO (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v += πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将(1)、(2)式相除,得: 2.摇杆转动方程: dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5-4 曲柄摇杆机构如图所示。
《理论力学》课后习题解答(赫桐生版)
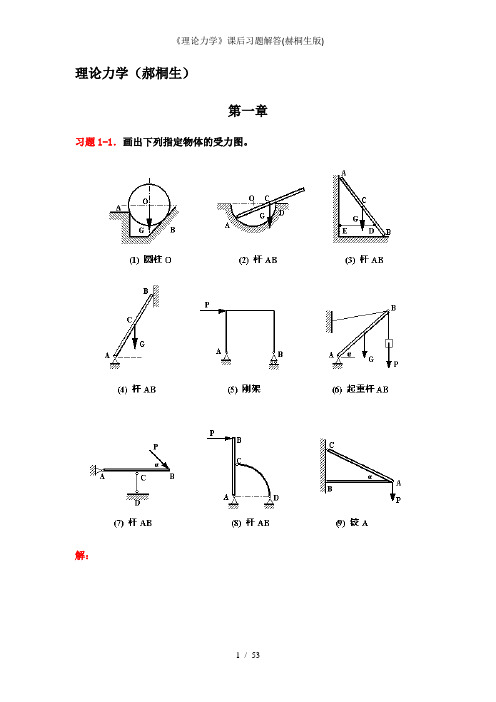
理论力学(郝桐生)第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
理论力学运动学习题及详解
y f 2 (t ) z f 3 (t )
2 2
a x x a y y a z z
2 2 2
v vx v y vz
2
a ax a y az
方向均由相应的方向余弦确定。
第2章 运动学练习
二.基本公式 自然法(轨迹已知时)
运动方程 速度
ae 5 2 0 r 4
5 2a r0 4
B
aC 0
O2
3销钉C固定在AB杆,在滑槽O2D中运动,该瞬时O1A与AB水平,O2D
铅直,且O1A=AC=CB=O2C=r,ω0=常数,求
AB、O2 D、 AB、O2 D .
D
n aCA
(2)加速度分析
AB 0
a 常量, an 0
,点做何种运动( B)。
B.匀变速曲线运动 D.匀变速直线运动
(3)已知点的运动方程为 x 2t 2 4, y 3t 2 3 ,其轨迹方程为(
B)
A.3x 4 y 36 0, C.2 x 2 y 24 0,
第2章 运动学练习
B.3x 2 y 18 0 D.2 x 4 y 36 0
1.选择题:
【练习题】
(4). 如图所示平面机构中,O1A=O2B= r, O1O2 =AB, O1A以匀角速度绕垂直于图 面的O1轴转动,图示瞬时,C点的速度为:( D )
A.
B. C.
Vc 0
Vc r a
2 2
水平向右
O1 A
O2
Vc r0 D. Vc r0
铅直向上 水平向右
2.刚体运动学
基本运动 平面运动
理论力学课后习题参考答案第5章
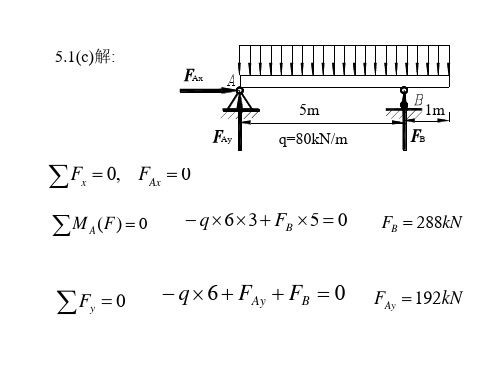
40kNm D 2m
FD
F
y
0
FA FB FD Q2 0 FA 15kN
5.24a解: 对于BC梁:
M
B
(F ) 0
q 6 3 FC 4 0
FC 18kN
整体:
FAx 0
y
F
M
0
(F ) 0
FAy FC q 6 0
M F 0 :
x
FA AD Q ED Gl cos 0
1 FA a sin 60 100 a sin 60 30 3.5cos 30 0 3 FA 12.3kN
M
y
(F) 0
FB BD FC CD G l sin 0
a a FB FC 30 3.5sin 30 0 2 2
(a)
F
z
0, FB FC FA Q G 0
FB FC 12.3 100 30 0 (b)
联立求解(a)(b)两式得:
FB 48.3kN FC 69.4kN
5.23(b) 题解:
5.16解
z
,, z
5 cm 0
M
M
z
(F ) 0
F2 0
z,
0m 0c 1
z, y ,4 5 y 6 x , 3
(F ) 0
1
2
F4 0
x
M
z ,,
(F ) 0
F6 0
z
,, z
5 cm 0
M
x,
(F ) 0
F 50 F1 50 0
理论力学参考答案第5章

理论力学参考答案第5章第5章摩擦· ·47· 47·第5章摩擦一、是非题正确的在括号内打“√”、错误的打“×” 1静滑动摩擦力与最大静滑动摩擦力是相等的。
× 2最大静摩擦力的方向总是与相对滑动趋势的方向相反。
√ 3摩擦定律中的正压力即法向约束反力是指接触面处物体的重力。
× 4当物体静止在支撑面上时支撑面全约束反力与法线间的偏角不小于摩擦角。
× 5斜面自锁的条件是斜面的倾角小于斜面间的摩擦角。
√ 二、填空题1当物体处于平衡时静滑动摩擦力增大是有一定限度的它只能在0≤Fs≤Fsmax范围内变化而动摩擦力应该是不改变的。
2静滑动摩擦力等于最大静滑动摩擦力时物体的平衡状态称为临界平衡状态。
3对于作用于物体上的主动力若其合力的作用线在摩擦角以内则不论这个力有多大物体一定保持平衡这种现象称为自锁现象。
4当摩擦力达到最大值时支撑面全约束反力与法线间的夹角为摩擦角。
5重量为G的均质细杆AB与墙面的摩擦系数为0.6f如图5.12所示则摩擦力为0。
6物块B重2kNP物块A重5kNQ在B上作用一水平力F如图5.13所示。
当系A之绳与水平成30角B与水平面间的静滑动摩擦系数s102f.物块A与B之间的静滑动摩擦系数s2025f.要将物块B拉出时所需水平力F的最小值为2.37kN。
A CB G A B F 图5.12 图5.13 ·48·理论力学·48·三、选择题1如图5.14所示重量为P的物块静止在倾角为的斜面上已知摩擦系数为sfsF为摩擦力则sF的表达式为B 临界时sF的表达式为 A 。
A sscosFfP B ssinFP C sscosFfP D ssinFP NF P sF 图5.14 2重量为G的物块放置在粗糙的水平面上物块与水平面间的静摩擦系数为sf今在物块上作用水平推力P 后物块仍处于静止状态如图5.15所示那么水平面的全约束反力大小为C 。
理论力学-5-点的复合运动分析

5.1 点的合成运动的基本概念
三种运动与三种速度和加速度
动点相对于动系的运动,称为 动点的相对运动(relative)。动 点刀尖上P点的相对运动是在工件 圆柱面上的螺旋线(相对轨迹)运 动。 动点相对于动系的运动速度和 加速度,分别称为动点的相对速度 和相对加速度,分别用符号vr和ar 表示。
具体方法:在有的机构中,一个构件上总有一个点被另一个构件所约束。 这时,以被约束的点作为动点,在约束动点的构件上建立动系,相对运动 轨迹便是约束构件的轮廓线或者约束动点的轨道。
(3) 应用速度合成定理时,可利用速度平行四边形中的几何关系解出 未知数。也可以采用投影法:即等式左右两边同时对某一轴进行投 影,投影的结果相等。
5.1 点的合成运动的基本概念
三种运动与三种速度和加速度
动系相对于定系的运动, 称为牵连运动。图中,牵连 运动为绕Oy ' 轴的定轴转动。
5.1 点的合成运动的基本概念
三种运动与三种速度和加速度
动系上每一瞬时与动点相重 合的那一点,称为瞬时重合点,又 称为牵连点。由于动点相对于动 系是运动的,因此,在不同的瞬 时,牵连点是动系上的不同点。 动系上牵连点相对定系的运 动速度和加速度,分别称为为动 点的牵连速度和牵连加速度,分 别用符号ve和ae表示。
第5章 点的复合运动分析 5.1 点的合成运动的基本概念 5.2 点的速度合成定理 5.3 牵连运动为平移时点的加速度合成定理 5.4 牵连运动为转动时点的加速度合成定理 科氏加速度 5.5 结论与讨论
第5章 点的复合运动分析
5.1 点的合成运动的基本概念
5.1 点的合成运动的基本概念
vr
q
ve OA
3 2 3e va ve tan q OA 3 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e1ωω==AO v BCO (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v += πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1=(2)习题5-1图(1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将(1)、(2)式相除,得: 2.摇杆转动方程: dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5-4 曲柄摇杆机构如图所示。
已知:曲柄O 1A 以匀角速度ω1绕轴O 1转动,O 1A = R ,O 1O 2 =b ,O 2O = L 。
试求当O 1A 水平位置时,杆BC 的速度。
解:1、A 点:动点:A ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
1a ωR v A =;221222ae R b R R b R vv A A +=+=ω2、B 点:动点:B ,动系:杆O 2A ,牵连运动:定轴转动,相对运动:直线,绝对运动:直线。
221222ee R b b LR AO B O v v A B +==ω21222ea b LR b R b v v v B B BC ω=+==5-5 如图示,小环M 套在两个半径为r 的圆环上,令圆环O '固定,圆环O 绕其圆周上一点A 以匀角速度ω转动,求当A 、O 、O '位于同一直线时小环M 的速度。
解:1、运动分析:动点:M ,动系:圆环O ,牵连运动:定轴转动,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v +=ωr v 3e =ωr v v v M =︒==30tan e a5-6 图a 、b 所示两种情形下,物块B 均以速度B υ、加速度a B 沿水平直线向左作平移,从而推动杆OA 绕点O 作定轴转动,OA = r ,ϕ= 40°。
试问若应用点的复合运动方法C 习题5-4图Av Av 习题5—5图(d)r(f)(e)υr求解杆OA 的角速度与角加速度,其计算方案与步骤应当怎样?将两种情况下的速度与加速度分量标注在图上,并写出计算表达式。
解:(a ):1、运动分析:动点:C (B 上);动系:OA ;绝对运动:直线;相对运动:直线;牵连运动:定轴转动。
2、v 分析(图c ) r e v v v +=B (1)ϕsin e B v v = OCv OC v B OA ϕωsin e ==(2) ϕcos r B v v =3、a 分析(图d )C r t en ea a a a a +++=B (3)(3)向a C 向投影,得 C t esin a a a B +-=-ϕ其中OCv v a B OA ϕω2sin 22r C ==C t esin a a a B +=ϕOCa OAt e =α (b ):1、运动分析:动点:A (OA 上);动系:B ;绝对运动:圆周运动;相对运动:直线;牵连运动:平移。
2、v 分析(图e ) r e a v v v +=ϕsin a B vv =ϕωsin a r v OA v BOA ==3、a 分析(图f )r e ta n a a a a a +=+上式向a e 向投影,得 e t a n a sin cos a a a =+ϕϕϕ222a na sin r v r v a B ==ϕϕsin /)cos (n at aa a a B -=ra OA a OA ta t a ==α习题5—6图aυ15Ca 5-7 图示圆环绕O 点以角速度ω= 4 rad/s 、角加速度α= 2 rad/s 2转动。
圆环上的套管A 在图示瞬时相对圆环有速度5m/s ,速度数值的增长率8m/s 2。
试求套管A 的绝对速度和加速度。
解:1、运动分析:动点:A ,动系:圆环,牵连运动:定轴转动,相对运动:圆周运动,绝对运动:平面曲线。
2、速度:(图a )︒⨯=︒=15cos 2215cos 2r OA︒=⨯︒=⋅=15cos 16415cos 4e ωOA v 5r =v m/s3.2015cos 2r e 2r 2e a =︒++=v v v v v m/s3、加速度:(图b )C t r n r t e n e n a t a a a a a a a a ++++=+︒-︒+︒+=15sin 15cos 15cos t r C n r n e n a a a a a a (1) ︒+︒+︒+=15sin 15sin 15cos n r C t r t e t a a a a a a (2 ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧︒=⋅===⨯⨯====︒=⨯︒=⋅=15cos 884054222515cos 64415cos 4t e tr r C 22r n r22n eαωωOA a a v a r v a OA a 代入(1)46.11015sin 815cos 5.116n a=︒-︒=a m/s 2代入(2)04.2915sin 5.5215cos 16t a =︒+︒=a m/s 2114)()(2t a 2n a a =+=a a a m/s 25-8 图示偏心凸轮的偏心距OC = e ,轮半径r =e 3。
凸轮以匀角速0ω绕O 轴转动。
设某瞬时OC 与CA 成直角。
试求此瞬时从动杆AB 的速度和加速度。
解:1.动点:A (AB 上),动系:轮O ,绝对运动:直线,相对运动:圆周,牵连运动:定轴转动。
2.r e a v v v +=(图a ) 0e 2ωe v =,0e a 33230tan ωe v v =︒=(↑),0a r 3342ωe v v == 3.C t r n r e a a a a a a +++=(图b )习题5—7图习题5—8图向n r a 投影,得C n r e a 30cos 30cos a a a a -+︒=︒︒-+=cos30C n r e a a a a a )23(322r 02r 2e v ev e ωω-+=)33423316(322002020ωωωωe e e -+==292ωe (↓)5-9 如图所示机构,O 1A =O 2B =r =10cm ,O 1O 2 =AB =20cm 。
在图示位置时,O 1A 杆的角速度ω=1 rad/s ,角加速度α=0.5rad /s 2,O l A 与EF 两杆位于同一水平线上。
EF 杆的E 端与三角形板BCD 的BD 边相接触。
求图示瞬时EF 杆的加速度。
解:1.运动分析:动点:E (EF 上),动系:轮BCD ,绝对运动:直线,相对运动:直线,牵连运动平移。
2.加速度分析:t ener a a a a a ++=沿BC 垂直方向投影:︒-︒=︒30cos 30sin 30cos n et ea a a a11.7103530tan n et ea -=-=-︒=a a a cm/s25-10 摇杆OC 绕O 轴往复摆动,通过套在其上的套筒A 带动铅直杆AB 上下运动。
已知l = 30cm ,当θ = 30° 时,ω = 2 rad/s ,α = 3 rad/s 2,转向如图所示,试求机构在图示位置t r a习题5—9图CC时,杆AB 的速度和加速度。
解:1.运动分析:动点:A ,动系:杆OC ,绝对运动:直线,相对运动:直线,牵连运动:定轴转动。
2.速度分析(图a ) r e a v v v +=3120cos e =⋅=θωl v cm/s 80cos e a ===θvv v ABcm/s4030tan e r =︒=v v cm/s3.加速度分析(图b ):C t e n e r a a a a a a +++= 沿a C 方向投影:t e C a 30cos a a a -=︒76.64)30cos 2(32r a =︒-==lv a a AB αωcm/s25-11 如图所示圆盘上C 点铰接一个套筒,套在摇杆AB 上,从而带动摇杆运动。
已知:R =0.2m ,h = 0.4m ,在图示位置时 ︒=60θ,ω0=4rad/s ,20s rad/2=α。
试求该瞬时,摇杆AB 的角速度和角加速度。
解:1.运动分析:动点:C ,动系:杆AB ,绝对运动:圆周运动,相对运动:直线,牵连运动:定轴转动。
2.速度分析(图a ) r e a v v v +=8.00a ==R v ωm/s0e =v0=AB ω3.加速度分析(图b ) t e r n a t a a a a a +=+沿na a 方向投影:2.320t e n a ===R a a ωm/s 2 ;2t e rad/s 24.932.02.3sin ===θαh a AB (逆时针)5-12 在图示机构中,已知O 1A = OB = r = 250mm ,且AB = O 1O ;连杆O 1A 以匀角速度ω = 2 rad/s 绕轴O 1转动,当φ = 60° 时,摆杆CE 处于铅垂位置,且CD = 500mm 。
求此时摆杆CE 的角速度和角加速度。
习题5-11图(a )习题16-13图(a)(b)解:1.运动分析:动点:D ,动系:杆CE ,绝对运动:圆周运动,相对运动:直线,牵连运动:定轴转动。
