小升初数学冲刺---较复杂的行程问题
小升初数学冲刺名校-----行程问题作业(含答案)

行程问题作业(含答案)1.甲、乙两地相距480千米,一辆货车从甲地开往乙地,当行了全程的16时,一辆客车从乙地开往甲地,经过5小时两车相遇,已知客车和货车的速度比是7:9,客车每小时行多少米?480*(1-1/6)=400(千米)400÷5=80(千米/小时)……客车和货车的速度和80÷(1+7/9)=45(千米/小时)……客车45*7/9=35(千米/小时)……货车2.甲、乙两地相距690千米,一列快车和一列慢车同时从两地相对开出,3小时相遇。
已知两车的速度比是12:11,两列火车每小时各行多少千米?速度和690/3=230km/h速度共12+11=23份;每份230/23=10km/h 所以快车速度10*12=120km/h慢车速度10*11=110km/h3.甲、乙两车同时从A、B两地相对开出,当甲行了全程的13时,乙车行了16千米;当甲车到达B地时,乙车行了全程的45。
A、B 两地相距多少千米?当甲车行了全程的1/3时,乙车行了16千米,当甲到达B地时,即甲走了3倍的1/3,此时乙车走了16千米的3倍,即48千米。
同时这也是全程的4/5。
因此全程是 48/(4/5)=60千米综合算式:16*3/(4/5)=60千米4.客车从甲地,货车从乙地同时相对开出5小时后,客车距乙地还有全程的16,货车距甲地还有142千米。
已知客车比货车每小时多行12千米,甲、乙两地间的路程是多少千米?12*5=60(千米)……5小时中,客车比货车多行60千米。
再用(142-60)÷1/6=492(千米)答:甲乙两地间的路程是492千米。
5.乐乐放学回家需走10分钟,晶晶放学回家需走14分钟。
已知晶晶回家的路程比乐乐的路程多16,乐乐每分钟比晶晶多走12米,那么晶晶回家的路程是多少米?解:设晶每分钟走x米,乐每分钟走(x+12)米14x=10*(x+12)*(1+1/6)化简得12x=10x+1202x=120x=60 x+12=72所以晶晶每分钟走60米,走了14分钟,(乐乐每分钟走72米,走了10分钟,共720米)路程为60*14=840米12÷【1/10÷(1+1/6)-1/14】=12÷【3/35-1/14】=12÷1/70=840米6.甲、乙两辆汽车同时从A、B两站相对开出,第一次相遇离A站有90千米,然后各自按原速继续行驶,分别到达对方出发站后立即沿原路返回,第二次相遇时离A站的距离占AB两站间全长的65%,AB两站间的路程长多少千米?90*3/(1-65%+1)=200千米注:第二次相遇走了3个全程,1个全程甲走90,3个走了90*3=270,走了全程的1-65%+17.甲、乙两车同时从A、B两地出发,相对而行,甲每小时行45千米,乙每小时行55千米,如果甲每小时增加15千米,乙每小时增加5千米,则相遇时间可提前41小时,A、B两地的路程是多少千米?1/4÷【1/(45+55)-1/(45+15+55+5)】=1/4÷【1/100-1/120】=1/4÷1/600=150千米解设原来的相遇时间是x小时(45+55)x=(45+55+15+5)×(x-1/4)100x=120x-3020x=30x=1.5A、B两地的路程是:(45+55)×1.5=150千米算式:(15+5+45+55)×1/4=30千米原来相遇时间:30÷(15+5)=1.5小时A、B两地的路程是:(45+55)×1.5=150千米。
小升初较难必考数学题

小升初较难必考数学题一、工程问题1. 一项工程,甲队单独做需要10天完成,乙队单独做需要15天完成。
两队合作3天后,剩下的工程由乙队单独完成,还需要多少天?解析:- 把这项工程的工作量看作单位“1”。
- 根据工作效率 = 工作量÷工作时间,甲队的工作效率为1÷10=(1)/(10),乙队的工作效率为1÷15=(1)/(15)。
- 两队合作3天的工作量为((1)/(10)+(1)/(15))×3。
- 先计算括号内的值:(1)/(10)+(1)/(15)=(3 + 2)/(30)=(1)/(6)。
- 再乘以3得到(1)/(6)×3=(1)/(2)。
- 剩下的工作量为1-(1)/(2)=(1)/(2)。
- 乙队单独完成剩下工程需要的时间为(1)/(2)÷(1)/(15)=(1)/(2)×15 = 7.5(天)2. 修一条路,甲、乙两队合作8天完成。
如果甲队单独修12天可以完成。
实际上先由乙队修了若干天后,再由甲队继续修,全部完成时共用了15天。
求甲、乙两队各修了多少天?解析:- 设乙队的工作效率为x。
- 因为甲、乙两队合作的工作效率为(1)/(8),甲队单独的工作效率为(1)/(12),则x=(1)/(8)-(1)/(12)=(3 - 2)/(24)=(1)/(24)。
- 设甲队修了y天,则乙队修了(15 - y)天。
- 根据工作量 = 工作效率×工作时间,可得到方程(1)/(12)y+(1)/(24)(15 - y)=1。
- 去括号得(1)/(12)y+(15)/(24)-(1)/(24)y = 1。
- 移项合并同类项得((1)/(12)-(1)/(24))y=1-(15)/(24)。
- 即(1)/(24)y=(9)/(24),解得y = 9。
- 所以甲队修了9天,乙队修了15 - 9=6天。
二、行程问题1. 甲、乙两车分别从A、B两地同时相向而行,速度比是5:3。
小升初数学行程问题必考题型

小升初数学行程问题必考题型摘要:一、小升初数学行程问题概述1.行程问题的基本概念2.行程问题的常见题型二、小升初数学行程问题必考题型及解析1.火车过桥问题a.基本公式b.例题解析2.相遇问题a.基本公式b.例题解析3.追及问题a.基本公式b.例题解析4.环形运动问题a.基本公式b.例题解析5.流水行船问题a.基本公式b.例题解析正文:小升初数学行程问题必考题型一、小升初数学行程问题概述行程问题一直是小升初数学考试中的重点和难点,主要涉及物体在运动过程中的速度、时间和路程等关系。
解决行程问题的关键是理解并熟练运用速度、时间和路程之间的关系。
二、小升初数学行程问题必考题型及解析1.火车过桥问题火车过桥问题是一种典型的行程问题,需要考虑火车的长度、速度和桥的长度等因素。
基本公式为:路程=速度×时间。
例题解析:一列长240 米的火车以每秒30 米的速度过一座桥,从车头上桥到车尾离桥用了1 分钟,求这座桥有多长?解答:火车速度乘以时间得到的是火车走的路程,即30×60=1800 米。
因为火车的长度为240 米,所以桥的长度为1800-240=1560 米。
2.相遇问题相遇问题是指两个物体在运动过程中,在某一点相遇的问题。
基本公式为:路程和=速度和×时间。
例题解析:甲、乙两辆汽车同时分别从A,B 两站相对开出,第一次相遇时离A 站有90 千米,然后各自按原速继续行驶,分别到达对方出发站后立即沿原路返回。
第二次相遇时离A 站的距离占A,B 两站间全长的65%。
求A,B 两站间的路程长。
解答:第一次相遇时,甲乙合行了一个AB 两地之间的距离,且甲行了90 千米;第二次相遇时,甲乙合行了三个AB 两地之间的距离,则甲行了90×3=270 千米。
又知第一二次相遇时距离A 站的距离占全程的65%,则全程为270÷65%=415 千米。
3.追及问题追及问题是指一个物体在运动过程中,另一个物体在某一时刻开始追赶它,求追及的时间和距离。
小升初--行程问题--专项讲解及试题

行程问题一【知识点导航】行程问题从运动形式上分可以分为五大类:二【典例解析】1. 直线上的相遇与追及只要涉及到速度和、路程和的问题就应该用第一个公式,即使题目的背景是追及;而只要涉及到速度差、路程差的问题就应该用第二个公式,即使题目的背景是相遇。
【例1】甲、乙两辆汽车同时从东西两地相向开出,甲每小时行56千米,乙每小时行48千米,两车在离两地中点32千米处相遇。
问:东西两地间的距离是多少千米?(某重点中学2007年小升初考题)【解析】本题表面上看是一个典型的相遇问题,其实里面暗藏了路程差的关系,就在条件"两车在离两地中点32千米处相遇"这句话中。
【变式】大客车和小轿车同地、同方向开出,大客车每小时行60千米,小轿车每小时行84千米,大客车出发2小时后小轿车才出发,几小时后小轿车追上大客车?【例2】两名游泳运动员在长为30米的游泳池里来回游泳,甲的速度是每秒游1米,乙的速度是每秒游0.6米,他们同时分别从游泳池的两端出发,来回共游了5分钟。
如果不计转向的时间,那么在这段时间内两人共相遇多少次?(某重点中学2006年小升初考题)【解析】相遇次数与两人的路程和有关.如下图所示【变式】甲、乙两车同时从A、B两站相对开出,第一次相遇离A站有90千米,然后各自按原速继续行驶,分别到达对方出发站后立即沿原路返回。
第二次相遇时离A站的距离占AB两站全长的65%。
求AB两站的距离。
2.火车过人、过桥与错车问题在火车问题中,速度和时间并没有什么需要特殊处理的地方,特殊的地方是路程。
因为此时的路程不仅与火车前进的距离有关,还与火车长、隧道长、桥长这些物体长度相关。
就拿火车过桥来说,如果题目考察的是火车过桥的整个过程,那么就应该从"车头上桥"开始到"车尾下桥"结束,对应的路程就等于"车长桥长";如果题目考察的是火车停留在桥上的过程,那就应该从"车尾上桥"到"车头下桥"结束。
小升初数学冲刺举一反三例题及解析:行程问题通用版3

小升初数学冲刺专题:行程问题(三)专题简析:很多稍复杂的应用题,运用算术方法解答有一定困难,列方程解答就比较容易。
列方程解答行程问题的优点是可以使未知道的数直接参加运算,列方程时能充分利用我们熟悉的数量关系。
因此,对于一些较复杂的行程问题,我们可以用题中已知的条件和所设的未知数,根据自己最熟悉的等量关系列出方程,方便解题。
例1A、B两地相距259千米,甲车从A地开往B地,每小时行38千米;半小时后,乙车从B地开往A地,每小时行42千米。
乙车开出几小时后和甲车相遇?分析我们可以设乙车开出后X小时和甲车相遇。
相遇时,甲车共行了38×(X+0.5)千米,乙车共行了42X千米,用两车行的路程和是259千米来列出方程,最后求出解。
解:设乙车开出X小时和甲车相遇。
38×(X+0.5)+42X=259解得X=3即:乙车开出3小时后和甲车相遇。
练习一1,甲、乙两地相距658千米,客车从甲地开出,每小时行58千米。
1小时后,货车从乙地开出,每小时行62千米。
货车开出几小时后与客车相遇?2,小军和小明分别从相距1860米的两处相向出发,小军出发5分钟后小明才出发。
已知小军每分钟行120米,小明骑车每分钟行300米。
求小军出发几分钟后与小明相遇?3,甲、乙两地相距446千米,快、慢两车同时从甲、乙两地相对开出,快车每小时行68千米,慢车每小时行35千米。
中途慢车因修车停留半小时,求共经过几小时两车在途中相遇。
例2一辆汽车从甲地开往乙地,平均每小时行20千米。
到乙地后又以每小时30千米的速度返回甲地,往返一次共用7.5小时。
求甲、乙两地间的路程。
分析如果设汽车从甲地开往乙地时用了X小时,则返回时用了(7.5-X)小时,由于往、返的路程是一样的,我们可以通过这个等量关系列出方程,求出X值,就可以计算出甲、乙两地间的路程。
解:设去时用X小时,则返回时用(7.5-X)小时。
20X=30(7.5-X)解得X=4.520×4.5=90(千米)即:甲、乙两地间的路程是90千米。
小升初奥数难点之行程问题

小升初奥数难点之行程问题在小学竞赛阶段,很多孩子谈行程色变。
为何行程问题难住了我们?原因是过程过于复杂和动态。
解决问题的总方针就是动中找静。
化动态为静态,化复杂为简单,化抽象为具体,化陌生情境为熟悉情境是我们解决行程问题的不二法门。
很多竞赛资料上处理行程问题的时候都是以画线段图为主来解题的。
对于完全依赖线段图的做法我是不赞成的。
孩子年级小对于动态的东西本难以理解,如多次相遇问题两次以内还好,当次数多于3的时候画图都画不清楚的。
我认为解决行程问题就需要2大理念,一是整体的思想,二是抓住运动过程中的不变的静止的量。
一般的辅导资料解题就是过于纠结于局部,使得孩子们做题缺乏大局观,往往被繁杂的细节转昏了头。
接下来我谈谈如何解决行程问题。
任何复杂的问题都是一些列简单的问题组成的,难题做不出实际上就是对于基础知识点没吃透。
行程问题最基本的关系就是速度时间=路程;路程速度=时间;路程时间=速度。
这3个关系很简单,可是它蕴含的内含并不简单。
解决难题需要我们对简单模型的深刻认识而不是简单的套公式。
将行程大方向分类就是相遇问题和追及问题。
当然简单的一人行程问题可以看为相遇问题。
可以认为1个人从A到B,另外一人从B到A速度为0,当然就是在B相遇。
我们先从简单的相遇问题谈起。
例:甲乙两人同时从AB两地分别出发相向而行6分钟相遇。
甲的速度是60米每分钟,乙是50米每分钟。
求AB的路程?这个题很容易(50+60) 6=660米。
很多孩子上来就套相遇路程=速度和乘以相遇时间。
这个题不是最关键的,关键是题目后面的思考和内涵。
开始我谈了把一人行程变为2人的一分为二的方法,这里为什么不能合二为一呢?实际上可以把两人看为1人以110米的速度出发6分钟到达终点来思考。
相遇问题实际上可以把2人看为1人,把两人的速度和看为对应那人的速度。
接下来我说下第二层思考。
就是这个过程的整体是AB的路程,局部是甲走的路程与乙走的路程。
为何我这里强调整体呢?很多行程问题的不变量就是两地路程。
小升初数学讲义之——行程问题

小升初——行程问题行程问题(一)行程问题是小学、初中的重难点,行程问题关系复杂,而多数小学生的分析能力还未能达到理想的水平。
体会相遇、追及问题的特点,并灵活运用列方程、比例等方法解行程问题,训练假设法、守恒等数学思维。
行程问题的三个基本量是距离、速度和时间。
其互逆关系可用乘、除法计算,方法简单,但应注意行驶方向的变化,按所行方向的不同可分为三种:(1)相遇问题;(2)相离问题;(3)追及问题。
行程问题的主要数量关系是:距离=速度×时间。
它大致分为以下三种情况:(1)相向而行:相遇时间=距离÷速度和(2)相背而行:相背距离=速度和×时间。
(3)同向而行:速度慢的在前,快的在后。
追及时间=追及距离÷速度差在环形跑道上,速度快的在前,慢的在后。
追及距离=速度差×时间。
解决行程问题时,要注意充分利用图示把题中的情节形象地表示出来,有助于分析数量关系,有助于迅速地找到解题思路。
1.一辆客车和一辆货车同时分别从A、B两城相对开出,客车每小时行9 5千米,货车每小时行8 5千米,相遇时客车比货车多行了3 0千米,求A、B两城相距多少千米?2.甲、乙二人在同一条公路上,他们相距100米,二人同时出发,朝各自的方向前进,甲的速度为每分钟100米,乙的速度为每分钟80米,问:经过多长时间两人相距200米?3.ABCD是一个边长为6米的正方形模拟跑道,甲玩具车从A出发顺时针行进,速度是每秒5厘米,乙玩具车从CD的中点出发逆时针行进,结果两车第二次相遇恰好是在B点,求乙车每秒走多少厘米?4.小明去学校,去时速度为15千米/小时,返回时速度为10千米/小时,那么平均速度为多少?5.已知甲车速度为每小时90千米,乙车速度为每小时60千米,甲乙两车分别从A,B两地同时出发相向而行,在途经C地时乙车比甲车早到10分钟;第二天甲乙分别从B,A两地出发同时返回原来出发地,在途经C地时甲车比乙车早到1个半小时,那么AB距离时多少?6.甲、乙、丙三人步行的速度分别是:每分钟甲走90米,乙走75米,丙走60米。
广州小升初-复杂的行程问题

1、多次相遇问题; 2、环形行程问题; 3、运用比例、方程等解复杂的题。
典型例题解析
1 典型的相遇问题
【例 1】(★★)甲、乙两人沿 400 米环形跑道练习跑步,两人同时从跑道的同一 地点向相反方向跑去。相遇后甲比原来速度增加 2 米/秒,乙比原来速度减少 2 米/秒,结果都用 24 秒同时回到原地。求甲原来的速度?
家庭作业
1、大货车和小小轿 车出发后 4 小时后追上了大货车.如果小轿车每小时多行 5 千米,那么出发后 3 小 时就追上了大货车.问:小轿车实际上每小时行多少千米?
2、小强骑自行车从家到学校去,平常只用 20 分钟。由于途中有 2 千米正在修路, 只好推车步行,步行速度只有骑车的 1/3,结果用了 36 分钟才到学校。小强家到 学校有多少千米?
相遇问题:速度和×相遇时间=相遇路程;
课 堂 教 追及问题:速度差×追及时间=路程差;
公式需牢记 做题有信心!
教学
学
流水问题:关键是抓住水速对追及和相遇的时间不产生影响;
过内
程 容 顺水速度=船速+水速 逆水速度=船速-水速
静水速度=(顺水速度+逆水速度)÷2 水速=(顺水速度-逆水速度)÷2 (也就是顺水速度、逆水速度、船速、水速 4 个量中只要有 2 个就可求另外 2 个) 其他问题:利用相应知识解决,比如和差分倍和盈亏;
5、一列长 225 米的慢车以每秒 17 米的速度行驶,一列长 140 米的快车以每秒 22 米的速度在后面追赶,求快车从追上到追过慢车需要多长时间?
6、一列长 150 米的列车以每秒 22 米的速度行驶,有一个扳道工人以每秒 3 米的 速度迎面走来,那么,火车从工人身旁驶过需要多少时间?
7、一列火车穿越一条长 2000 米的隧道用了 88 秒,以同样的速度通过一条长 1250 米的大桥用了 58 秒。求这列火车的车速和车身长度各是多少?
小学数学小升初行程问题总结及答案详解

行程问题经典题型1、甲、乙两地相距6千米,某人从甲地步行去乙地,前一半时间平均每分钟行80米,后一半时间平均每分钟行70米。
问他走后一半路程用了多少分钟?2、甲、乙两辆汽车同时从东西两地相向开出,甲每小时行56千米,乙每小时行48千米,两车在离两地中点32千米处相遇。
问:东西两地的距离是多少千米?3、李华步行以每小时4千米的速度从学校出发到20.4千米外的冬令营报到.0.5小时后,营地老师闻讯前往迎接,每小时比李华多走1.2千米。
又过了1。
5小时,张明从学校骑车去营地报到。
结果3人同时在途中某地相遇。
问:骑车人每小时行驶多少千米?4 小轿车的速度比面包车速度每小时快6千米,小轿车和面包车同时从学校开出,沿着同一路线行驶,小轿车比面包车早10分钟到达城门,当面包车到达城门时,小轿车已离城门9千米,问学校到城门的距离是多少千米?5 小张从家到公园,原打算每分种走50米。
为了提早10分钟到,他把速度加快,每分钟走75米.问家到公园多远?6、上午8点8分,小明骑自行车从家里出发,8分钟后,爸爸骑摩托车去追他,在离家4千米的地方追上了他。
然后爸爸立即回家,到家后又立刻回头去追小明,再追上小明的时候,离家恰好是8千米,这时是几点几分?“相遇问题”,常常要考虑两人的速度和.7、小张从甲地到乙地步行需要36分钟,小王骑自行车从乙地到甲地需要12分钟。
他们同时出发,几分钟后两人相遇?8、小张从甲地到乙地,每小时步行5千米,小王从乙地到甲地,每小时步行4千米。
两人同时出发,然后在离甲、乙两地的中点1千米的地方相遇,求甲、乙两地间的距离.9、一列长100米的火车过一座桥,火车的速度是25米/秒,它过桥一共用了10秒,那么桥的长度是多少?10、甲骑摩托车,乙骑自行车,同时从相距126千米的A、B两城出发、相向而行。
3小时后,在离两城中点处24千米的地方,甲、乙二人相遇。
求甲、乙二人的速度各是多少?11、客轮行了全程的3\7时,货轮行全程的多少? 3/7×7/10=3/10 2.甲乙两码头相距多少千米?12、A、B两城相距240千米,一辆汽车计划用6小时从A城开到B城,汽车行驶了一半路程,因故障在中途停留了30分钟,如果按原计划到达B城,汽车在后半段路程时速度应加快多少?13、两码头相距231千米,轮船顺水行驶这段路程需要11小时,逆水每小时少行10千米,问行驶这段路程逆水比顺水需要多用几小时?14、一辆汽车从甲地出发到300千米外的乙地去,在一开始的120千米内平均速度为每小时40千米,要想使这辆车从甲地到乙地的平均速度为每小时50千米,剩下的路程应以什么速度行驶?15、骑自行车从甲地到乙地,以每小时10千米的速度行驶,下午1时到;以每小时15千米的速度行驶,下午1时到;以每小时15千米的速度行进,上午11时到;如果希望中午12时到,应以怎样的速度行进?16、一辆公共汽车和一辆小轿车同时从相距299千米的两地相向而行,公共汽车每小时行 40千米,小轿车每小时行52千米,问:几小时后两车第一次相距69千米?再过多少时间两车再次相距69千米?17、一列客车与一列货车同时同地反向而行,货车比客车每小时快6千米,3小时后,两车相距342千米,求两车速度.18、甲、乙两车同时从A、B两地相向而行,它们相遇时距A、B两地中心处8千米,已知甲车速度是乙车的1.2倍,求A、B两地距离。
2023年小升初数学行程问题doc

行程问题(一)1、如图,客车和货车同时从A点出发向两个不同的方向行驶,4小时后在C点相遇,已知BC相距18千米,货车与客车的速度比为6:7,相遇时货车行了多少千米?2、一个人从县城骑车去乡办厂。
他从县城骑车出发,用30分钟时间行完了一半路程,这时,他加快了速度,每分钟比本来多行50米,又骑了20分钟后,他从路旁的里程标志牌上知道,必须再骑2千米才干赶到乡办厂,求县城到乡办厂之间的总路程。
3、甲乙两人往返于AB,第一次距离A90米处相遇,第二次距离A 65%处相遇求AB的距离?4、从甲地到乙地有上坡和下坡,上坡和下坡时速分别为20千米和35千米。
甲到乙要9小时,乙到甲7.5小时,求甲乙路程?5、一客车和货车从AB中点反向而行,4小时后客车到了A,货车离B尚有60千米。
客车速度比货车快40%,求AB的路程?6、一辆客车和一辆货车同时从AB 出发相向而行,11小时后客车行了全程的89,货车只行了一半的路程多176千米,客车时速比货车快12千米,求AB 的路程?7、有甲乙丙三辆车,各以一定速度从A 到B ,乙比丙晚出发10分钟,40分钟后追上丙,甲比乙晚出发20分钟,1小时40分钟追上丙,甲出发多久后追上乙?8、甲乙两船静水速度相同。
甲船和一木筏从A 顺流而下。
乙同时从B 逆流而上。
4小时后甲和木筏相距100千米。
甲乙相遇6小时后,乙与木筏相遇。
求AB 的距离?9、小时乘车从A 到B ,计划5.5小时到。
有段36千米路由于堵车,速度只有计划的34,于是晚到了12分钟,求AB 距离?10、一辆车从甲地开往乙地,假如把车速提高14,可比原定期间早1小时到达,假如以本来速度行驶120千米后,再将速度提高百分之二十,可以提前20分钟到达乙地,求甲乙两地相距多少千米?11、小明和小李上山和下山的速度分别为20,30米每分。
小明从山脚出发,小李从山顶同时出发上下山往返。
小明到山顶后休息30分钟后返回,两人距离山顶480米处第二次相遇,求山的高度?12、甲乙两车同时从AB的中点C出发反向而行。
小升初数学冲刺-----行程问题(含答案)

小升初数学冲刺-----行程问题1、甲、乙两架飞机同时从一个机场起飞,向同一方向飞行,甲机每小时行300千米,乙机每小时行340千米,飞行4小时后它们相隔多少千米?这时候甲机提高速度用2小时追上乙机,甲机每小时要飞行多少千米?解析:①4小时后相差多少千米:1604)300340(=⨯-(千米).②甲机提高速度后每小时飞行多少千米:4203402160=+÷(千米).2、两地相距900米,甲、乙二人同时、同地向同一方向行走,甲每分钟走80米,乙每分钟走100米,当乙到达目标后,立即返回,与甲相遇,从出发到相遇共经过多少分钟?解析:甲、乙二人开始是同向行走,乙走得快,先到达目标.当乙返回时运动的方向变成了同时相对而行,把相同方向行走时乙用的时间和返回时相对而行的时间相加,就是共同经过的时乙到达目标时所用时间:9100900=÷(分钟),甲9分钟走的路程:720980=⨯(米),甲距目标还有:180720900=-(米),相遇时间:1)80100(180=+÷(分钟),共用时间:1019=+(分钟).3、甲、乙二人分别从东、西两镇同时出发相向而行.出发2小时后,两人相距54千米;出发5小时后,两人还相距27千米.问出发多少小时后两人相遇?解析:根据2小时后相距54千米,5小时后相距27千米,可以求出甲、乙二人3小时行的路程和为)2754(-千米,即可求出两人的速度和:9)25()2754(=-÷-(千米),根据相遇问题的解题规律;相隔距离÷速度和=相遇时间,可以求出行27千米需要:89275=÷+(小时).4、甲乙两座城市相距530千米,货车和客车从两城同时出发,相向而行.货车每小时行50千米,客车每小时行70千米.客车在行驶中因故耽误1小时,然后继续向前行驶与货车相遇.问相遇时客车、货车各行驶多少千米?解析:因为客车在行驶中耽误1小时,而货车没有停止继续前行,也就是说,货车比客车多走1小时.如果从总路程中把货车单独行驶1小时的路程减去,然后根据余下的就是客车和货车共同走过的.再求出货车和客车每小时所走的速度和,就可以求出相遇时间.然后根据路程=速度×时间,可以分别求出客车和货车在相遇时各自行驶的路程.解:相遇时间:4)7050()50530(=+÷-(小时)相遇时客车行驶的路程:280470=⨯(千米)相遇时货车行驶的路程:250)14(50=+⨯(千米).5、两车同时从甲乙两地相对开出,甲车每小时行48千米,乙车每小时行54千米,相遇时两车离中点36千米,甲乙两地相距多少公里?解:甲乙两车的速度比=48:54=8:9那么相遇时甲车行了全程的8/17所以甲乙距离=36/(1/2-8/17)=36/(1/34)=1224千米6、客货两车从甲地到乙地客车出发,30分钟后货车才出发,结果货车比客车早到1小时,如果甲乙两地相距360km,客车速度是货车的3/4.货车和客车行驶的速度分别是多少?解:若同时出发客车比货车晚到1小时30分=1.5小时客车和货车的速度比=3:4时间比=4:3所以客车行驶全程的时间=1.5/(1-3/4)=6小时所以客车速度=360/6=60千米/小时货车速度=60/(3/4)=80千米/小时7、甲乙两车同时从A、B两地相对开出,4小时后相遇,相遇后甲车在开3小时到达B地。
小升初行程问题例题及答案

小升初行程问题例题及答案小升初行程问题例题及答案【第一篇:流水行船求时间】某河有相距45千米的上下两港,每天定时有甲乙两船速相同的客轮分别从两港同时出发相向而行,这天甲船从上港出发掉下一物,此物浮于水面顺水漂下,4分钟后与甲船相距1千米,预计乙船出发后几小时可与此物相遇。
【解】:物体漂流的速度与水流速度相同,所以甲船与物体的速度差即为甲船本身的船速(水速作用抵消),甲的船速为1÷1/15=15千米/小时;乙船与物体是个相遇问题,速度和正好为乙本身的船速,所以相遇时间为:45÷15=3小时【拓展】甲轮船和自漂水流测试仪同时从上游的A站顺水向下游的B站驶去,与此同时乙轮船自B站出发逆水向A站驶来。
7.2时后乙轮船与自漂水流测试仪相遇。
已知甲轮船与自漂水流测试仪2.5时后相距31.25千米,甲、乙两船航速相等,求A,B两站的距离。
【解】:因为测试仪的漂流速度与水流速度相同,所以若水不流动,则7.2时后乙船到达A站,2.5时后甲船距A站31.25千米。
由此求出甲、乙船的航速为31.25÷2.5=12.5(千米/时)。
A,B两站相距12.5×7.2=90(千米)。
【第二篇:流水行船求船速】江上有甲、乙两码头,相距15千米,甲码头在乙码头的上游,一艘货船和一艘游船同时从甲码头和乙码头出发向下游行驶,5小时后货船追上游船。
又行驶了1小时,货船上有一物品落入江中(该物品可以浮在水面上),6分钟后货船上的人发现了,便掉转船头去找,找到时恰好又和游船相遇。
则游船在静水中的速度为每小时多少千米?【解】:此题可以分为几个阶段来考虑。
第一个阶段是一个追及问题。
在货舱追上游船的过程中,两者的追及距离是15千米,共用了5小时,故两者的速度差是15÷5=3千米。
由于两者都是顺水航行,故在静水中两者的速度差也是3千米。
在紧接着的1个小时中,货船开始领先游船,两者最后相距3*1=3千米。
小学思维数学复杂的行程问题-带详解

÷30 10 5= ( 行程综合问题教学目标1. 运用各种方法解决行程内综合问题。
2. 发现一些综合问题中,行程与其它模块的联系,并解决奥数综合问题。
知识精讲行程问题是奥数中的一个难点,内容多而杂。
而在行程问题中,还有一些尤其复杂的综合问题。
它们大致可以分为两类:一、 行程内综合,把行程问题中的一些零散的知识点综合在一道题目中,这就是一道行程内综合题目。
例如把环形跑道和猎狗追兔结合在一起,把流水行船和发车间隔结合起来等等。
二、 学科内综合,这种问题就不只是行程问题了,把行程问题和其它知识模块里的思想方法结合在一起,这种综合性题目的难度也很大,比如行程与策略综合等等。
本讲内容主要就是针对这种综合性题目。
虽然题目难度偏大,但是这种题目在杯赛和小升初试题中是 很受“偏爱”的。
所以很重要。
模块一、行程内综合【例 1】 邮递员早晨 7 时出发送一份邮件到对面山里,从邮局开始要走 12 千米上坡路,8 千米下坡路。
他上坡时每小时走 4 千米,下坡时每小时走 5 千米,到达目的地停留 1 小时以后,又从原路返 回,邮递员什么时候可以回到邮局?【考点】变速问题与走停问题 【难度】2 星 【题型】解答【解析】法一:先求出去的时间,再求出返回的时间,最后转化为时刻。
①邮递员到达对面山里需时间:12÷4+8÷5=4.6(小时);②邮递员返回到邮局共用时间:8÷4+12÷5+1+4.6 =2+2.4+1+4.6 = l 0(小时)③ 邮递员回到邮局时的时刻是:7+10-12=5(时).邮递员是下午 5 时回到邮局的。
法二:从整体上考虑,邮递员走了(12+8)千米的上坡路,走了(12+8)千米的下坡路,所以共 用时间为:(12+8)÷4+(12+8)÷5+1=10(小时),邮递员是下午 7+10-12=5(时) 回到邮局的。
【答案】5 时【例 2】 小红上山时每走 30 分钟休息 10 分钟,下山时每走 30 分钟休息 5 分钟.已知小红下山的速度是上山速度的1.5 倍,如果上山用了 3 小时 50 分,那么下山用了多少时间?【考点】变速问题与走停问题 【难度】2 星 【题型】解答【解析】上山用了 3 小时 50 分,即 60 ⨯ 3 + 50 = 230 (分),由 230 ( + ) 30,得到上山休息了 5 次,走了 230 - 10⨯ 5= 180 分 ) .因为下山的速度是上山的 1.5 倍,所以下山走了 180 ÷1.5 = 120 (分).由120 ÷30 =4 知,下山途中休息了 3 次,所以下山共用120 + 5 ⨯ 3 = 135 (分) = 2 小时 15 分.【答案】 2 小时 15 分【例 3】 已知猫跑 5 步的路程与狗跑 3 步的路程相同;猫跑 7 步的路程与兔跑 5 步的路程相同.而猫跑3 步的时间与狗跑 5 步的时间相同;猫跑 5 步的时间与兔跑 7 步的时间相同,猫、狗、兔沿着 周长为 300 米的圆形跑道,同时同向同地出发.问当它们出发后第一次相遇时各跑了多少路程?【考点】环形跑道与猎狗追兔 【难度】5 星 【题型】解答 【解析】方法一:由题意,猫与狗的速度之比为9: 25 ,猫与兔的速度之比为 25: 49 .米,兔跑 米. 狗追上猫一圈需 300 ÷ - 1⎪ = 单位时间, 兔追上猫一圈需 300 ÷ - 1⎪ = 单位时间. 猫、狗、兔再次相遇的时间,应既是 的整数倍,又是 的整数倍.与 的最小公倍数等于两个分数中,分子的最小公倍数除以分母的最大公约数,即 ⎡ 675 625 ⎤ ⎡⎣675,625 ] (4,2 )⎢ 4 2 ⎥⎦ 此时,猫跑了 8437.5 米,狗跑了 8437.5 ⨯ 25 = 23437.5 米,兔跑了 8437.5 ⨯ = 16537.5 米.⎝ 35 21 25 ⎭ [35,21,25 ] 3 ⨯ 5 ⨯ 5 ⨯ 7 ,, , ⎪ =即设猫的速度为 15 ÷ = 225 ,那么狗的速度为 ÷ = 625 ,则兔的速度为÷ = 441 . 而 ⎢ , ⎣ 4 18 ⎥⎦ (4,18) 2 = ⨯ 225 = 8437.5 米,狗跑了⨯ 625 = 23437.5 米,兔跑了 ⨯ 441 = 16537.5 米. 路程之和等于 400 米,24V +24(V +2 )=400 易得 V = 7 米/秒【答案】 7 米/秒设单位时间内猫跑 1 米,则狗跑25 499 25⎛ 25 ⎫ 675 ⎝ 9 ⎭ 4⎛ 49 ⎫ 625 ⎝ 25 ⎭ 2675 6254 2675 6254 2⎣, = = 16875 = 8437.5 . 2上式表明,经过 8437.5 个单位时间,猫、狗、兔第一次相遇.499 25方法二:根据题意,猫跑 35 步的路程与狗跑 21 步的路程、兔跑 25 步的路程相等;而猫跑 15 步 的时间与狗跑 25 步、兔跑 21 步的时间相同.所以猫、狗、兔的速度比为 15 : 25 : 21,它们的最大公约数为35 21 25⎛ 15 25 21 ⎫ (15,25,21 )1 =1 25 135 3 ⨯ 5 ⨯ 5 ⨯ 7 21 3 ⨯ 5 ⨯ 5 ⨯ 721 125 3 ⨯ 5 ⨯ 5 ⨯ 7于是狗每跑 300 ÷ (625 - 225) = 34 单位时追上猫;兔每跑 300 ÷ (441 - 225) = 2518 单位时追上猫.⎡ 3 25 ⎤ [3,25 ] 75 75 = ,所以猫、狗、兔跑了 单位时,三者相遇. 2猫跑了75275 752 2【答案】16537.5 米【例 4】 甲、乙两人沿 400 米环形跑道练习跑步,两人同时从跑道的同一地点向相反方向跑去。
(完整版)小升初行程问题

(完整版)⼩升初⾏程问题⾏程问题考点⼀:⼀般⾏程问题公式,速度×时间=路程路程÷时间=速度路程÷速度=时间考点⼆:相遇问题公式,速度和×相遇时间=相遇路程相遇路程÷相遇时间=速度和相遇路程÷速度和=相遇时间考点三:追及问题公式,速度差×追及时间=追及距离追及距离÷追及时间=速度差追及距离÷速度差=追及时间考点四:⽕车过桥公式:⽕车速度×过桥时间=车长+桥长考点五:流⽔⾏船公式,顺⽔速度=船速+⽔速逆⽔速度=船速-⽔速船速=(顺⽔速度+逆⽔速度)÷2 ⽔速=(顺⽔速度-逆⽔速度)÷2 顺⽔速度=逆⽔速度+⽔速×2 逆⽔速度=顺⽔速-⽔速×2考点六:环形⾏程问题公式,封闭环形上的相遇问题,利⽤关系式:环形周长÷速度和=相遇时间封闭环形上的追及问题,利⽤关系:环形周长÷速度差=追及时间【例1】甲⼄⼆⼈同时从两地出发,相向⽽⾏。
⾛完全程,甲需要60分钟,⼄需要40分钟。
出发后5分钟,甲因忘带东西⽽返回出发点,取东西⼜耽误了5分钟。
甲再次出发,多长时间后两⼈相遇?【例2】两列⽕车从甲、⼄两地相向⽽⾏,慢车从甲地到⼄地需要8⼩时,⽐快车从⼄地到甲地多⽤31的时间。
如果两车同时开出,那么相遇时快车⽐慢车多⾏40千⽶。
求甲、⼄两地的距离。
【例3】⼀艘轮船顺流航⾏120千⽶,逆流航⾏80千⽶共⽤了16⼩时,逆流航⾏120千⽶也⽤了16⼩时。
求⽔流速度。
【例4】已知某铁路长1000⽶,⼀列⽕车从桥上通过,测得⽕车从开始上桥到完全下桥共⽤了120秒,整列⽕车完全在桥上的时间为80秒,求⽕车的速度和长度。
【例5】甲⼄⼆⼈在操场的400⽶跑到上练习竞⾛,两⼈同时出发,出发时甲在⼄的后⾯,出发后6分钟甲第⼀次追上⼄,22分钟时甲第⼆次追上⼄。
假设两⼈的速度都保持不变,问:出发时甲在⼄⾝后多少⽶?【例6】甲⼄两车分别从A 、B 两地同时出发,在A 、B 之间不断往返⾏驶。
小升初行程问题专项讲解及试题

小升初行程问题专项讲解及试题小升初是每个孩子都要面临的重要转折点,对于家长来说,不仅要关注孩子的学习情况,还要与孩子一起规划好小升初的行程。
本文将针对小升初行程问题进行专项讲解,并附上相应的试题,帮助家长更好地理解和规划孩子的行程。
一、选择适当的时间段小升初行程应该选择在孩子有足够时间准备的情况下进行。
通常来说,小升初的考试时间集中在每年的5月至6月左右,因此,为了给孩子留出充分的备考时间,一般建议将行程安排在3月至4月进行,这样孩子可以有大约两个月的时间进行系统的复习和冲刺。
试题:1. 小升初的考试时间通常集中在每年的哪个月份?2. 为什么建议将行程安排在3月至4月进行?二、选定目标学校在规划小升初行程时,首先要考虑的是目标学校。
不同的学校要求不同的考试科目、内容和方式,因此,家长需要提前了解目标学校的招生政策,明确所需备考内容。
此外,还应考虑学校的地理位置、校风教育理念等因素,以便更好地适应和适合孩子的学习环境。
试题:1. 规划小升初行程时,首先要考虑的是什么?2. 为什么需要提前了解目标学校的招生政策?三、合理安排学习时间小升初是一项需要紧张备考的考试,因此,合理安排学习时间是非常重要的。
家长可以制定学习计划,根据孩子的实际情况制定每天的学习任务和时间安排,确保孩子有足够的时间进行各科目的学习和复习。
同时,也要注意合理安排孩子的休息时间,保证他们有足够的精力和注意力来面对考试。
试题:1. 为什么合理安排学习时间在小升初备考中十分重要?2. 家长可以通过什么方式来合理安排学习时间?四、备考复习策略除了合理安排学习时间外,备考复习策略也是小升初行程中不可忽视的一部分。
备考策略包括学科知识的系统复习、做题技巧的训练以及模拟考试的实施等。
家长可以根据孩子的特点和优势来制定相应的策略,帮助他们更好地备考和应对考试。
试题:1. 备考复习策略包括哪些方面?2. 家长应该如何制定适合孩子的备考复习策略?五、合理安排休息和放松在小升初行程中,除了紧张备考和复习外,家长还需要合理安排孩子的休息和放松时间。
小升初数学冲刺名校拓展——第16节特殊行程问题
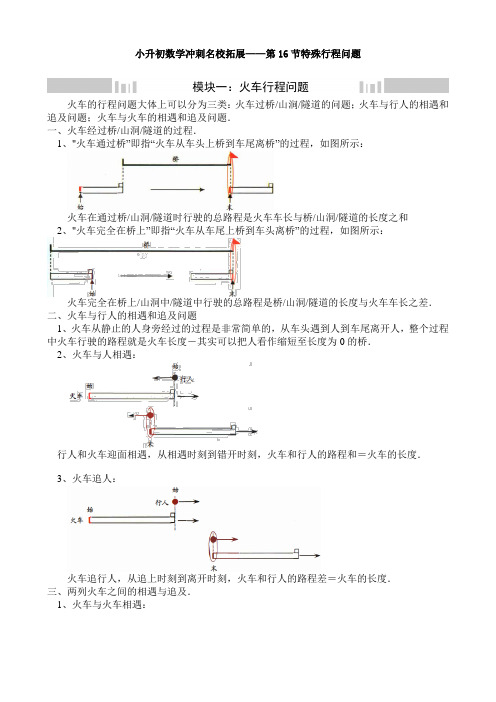
小升初数学冲刺名校拓展——第16节特殊行程问题模块一:火车行程问题火车的行程问题大体上可以分为三类:火车过桥/山涧/隧道的问题;火车与行人的相遇和追及问题;火车与火车的相遇和追及问题.一、火车经过桥/山洞/隧道的过程.1、"火车通过桥”即指“火车从车头上桥到车尾离桥”的过程,如图所示:火车在通过桥/山洞/隧道时行驶的总路程是火车车长与桥/山洞/隧道的长度之和2、"火车完全在桥上”即指“火车从车尾上桥到车头离桥”的过程,如图所示:火车完全在桥上/山洞中/隧道中行驶的总路程是桥/山洞/隧道的长度与火车车长之差.二、火车与行人的相遇和追及问题1、火车从静止的人身旁经过的过程是非常简单的,从车头遇到人到车尾离开人,整个过程中火车行驶的路程就是火车长度-其实可以把人看作缩短至长度为0的桥.2、火车与人相遇:行人和火车迎面相遇,从相遇时刻到错开时刻,火车和行人的路程和=火车的长度.3、火车追人:火车追行人,从追上时刻到离开时刻,火车和行人的路程差=火车的长度.三、两列火车之间的相遇与追及.1、火车与火车相遇:火车和火车相遇,从相遇时刻到错开时刻,两列火车的路程和=两列火车车长之和.2、火车追火车:火车追火车,从追上时刻到离开时刻,两列火车的路程差=两列火车车长之和.【例1】火车进山洞燧道,从车头进入到车尾进人洞口,共用a分钟,又当车头开始进入洞口直到车尾出洞口,共用b分钟,且:8:3b a ,又知山洞隧道长是300米,那么火车车长为多少米?【例2】甲乙两列火车在平行的轨道上相向而行,两车从车头相遇到车尾相离共用4 秒。
甲车长135米,速度是每秒行48 米,乙车每秒行52 米,乙车车长多少米?1.一列火车以每分钟600米的速度通过一座220米的大桥,如果火车全长20米,那么从车头上桥到车尾离开桥,共需分钟。
2.两列火车相向而行,客车每小时行80 千米,货车每小时行55千米,两车相遇错过时,客车上的旅客从看见货车的车头到车尾经过10秒钟,货车的全长是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小升初数学冲刺---较复杂的行程问题
基础达标
1.一辆客车和一辆货车同时从两地相对开出,客车每小时行60千米,货车每小时行52千米,经过3.5小时两车相遇。
求两地之间的距离。
2.两列火车相对行驶,在两地间的中点相遇,甲车每小时行76千米,相遇是行了5小时。
乙车每小时行95千米,他比甲车迟出发了几小时?
3.甲、乙二人在一个长400米的环形跑道上从同一点,同时反向而行,甲每分钟走45米,乙每分钟走35米。
多少分钟后两人第一次相遇?
4.同一条公路上依次排列着A、B、C、D四个车站,B、C两站相距32千米,从B站开出一辆客车,开向A站,每小时行48千米,同时从C站开出一辆货车开向D站,每小时行45千米。
经过2小时后,两车相距多少千米?
5.兄妹两人由家到学校,妹妹步行每分钟走45米,哥哥骑车每分钟行195米。
妹妹走20分钟后,哥哥骑车离家,几分钟后追上妹妹?
6.客、货车两车分别从甲、乙两地同时出发相向而行,如果两车都按原定速度行驶,那么4小时相遇;现在两车都比原计划每小时少走15千米,结果5小时相遇。
甲乙两地相距多少千米?
能力达标
1.甲、乙两车同时从两地相向而行,甲每小时行83千米,乙每小时95千米,两车在距中点24千米处相遇。
求两地间的距离。
2.甲、乙两人骑自行车同时从东、西两地相向而行,经过8小时相遇。
如果甲每小时少行1千米,乙每小时多行3千米,这样经过7小时就能相遇。
东、西两地相距是多少千米?
3.甲、乙两车同时从A、B两地相对开出,40分钟后相遇。
相遇后以原速继续前进,乙车又经过5分钟到达A,B两地之间的中点。
甲车行完全程共需要多少分钟?
4.甲、乙两人骑自行车同时从A、B两地相向而行。
第一次两车在距B地7千米处相遇。
相遇后,两车继续向前行驶,当两车到达目的地后立即返回,返回时在距离A地4千米处相遇。
A,B两地相距多少千米?
5.甲、乙、丙三个小分队都从A地到B地进行野外训练,上午6时,甲、乙两个小队一起从A地出发,甲队每小时行5千米,乙队每小时行4千米,丙队上午8时才从A地出发,傍晚6时甲、丙两队同时到达B地。
那么丙队追上乙队的时间是上午几时?
6.王明从A城步行到B城,同时刘洋从B城骑车到A城,1.2小时后两人相遇。
相遇后继续前进,刘洋到A城立即返回,在第一次相遇后45分钟又追上了王明,两人再继续前进,当刘洋到达B城后立即返回。
两人第二次相遇后多长时间第三次相遇?
趣题荟萃
1.快、慢两车同时从同一地点出发,沿同一公路追赶前面的一个骑车人。
两车分别用了6分钟、10分钟追上骑车人。
已知快车每分钟行400米,慢车每分钟行320米。
骑车人每分钟行多少米?
2.两辆汽车同时从东、西两站相对开出,第一次在离东站45千米的地方相遇,之后两车继续以原来的速度前进,各自到站后都立即返回,又在距中点东侧9千米处相遇。
两站相距多少千米?
3.甲、乙二人同时从某地出发驾车行驶,甲每天行100千米,乙第一天行70千米,以后每天比前一天多行3千米。
乙出发后第几天追上甲?。
