二进制与格雷码转换
格雷映射编码规则

格雷映射编码规则格雷映射编码规则一、概述格雷映射编码是一种常用的数字编码方式,其特点是相邻的两个数之间只有一位二进制数发生变化。
这种编码方式在数字电路设计、通信系统等领域中得到广泛应用。
本文将详细介绍格雷映射编码的规则和应用。
二、基本原理1. 二进制数转换为格雷码将一个二进制数转换为对应的格雷码,可以按照以下步骤进行:(1)将最高位保持不变,其余各位与前一位异或;(2)重复以上操作,直到所有位都转换为格雷码。
例如,将二进制数1010转换为对应的格雷码,步骤如下:10101110110001000110因此,1010的对应格雷码是0110。
2. 格雷码转换为二进制数将一个格雷码转换为对应的二进制数,可以按照以下步骤进行:(1)最高位保持不变,其余各位与前一位异或;(2)重复以上操作,直到所有位都转换为二进制数。
例如,将格雷码0110转换为对应的二进制数,步骤如下:01100010001110111001因此,0110的对应二进制数是1010。
三、编码规则格雷映射编码的规则如下:1. 对于n位二进制数,其对应的格雷码有2^n个;2. 第一个格雷码为0,最后一个格雷码为2^n-1(即n位二进制数全部为1);3. 相邻两个格雷码之间只有一位二进制数发生变化;4. 格雷映射编码可以用于数字电路设计、通信系统等领域中的数据传输和控制。
四、应用实例1. 数字电路设计在数字电路设计中,常需要将多位二进制数转换为对应的格雷码。
例如,在4位全加器电路中,需要将两个4位二进制数相加,并输出其对应的4位格雷码。
这种转换可以通过逐位异或实现。
2. 通信系统在通信系统中,常使用格雷映射编码来保证数据传输的可靠性。
例如,在调频(FM)广播系统中,使用差分相移键控(DPSK)调制方式时,需要将数字信号转换为对应的格雷码,并进行调制和解调。
3. 其他领域除了数字电路设计和通信系统外,格雷映射编码还广泛应用于计算机科学、自动控制、图像处理等领域。
8位二进制码转格雷码

8位二进制码转格雷码的转换方式如下:
1.首先,将8位二进制数的每一位都进行奇偶校验,得到8位格雷码。
2.对于二进制数的每一位,从最低位开始,将二进制数表示成格雷码形式。
3.对于二进制数的最高位,将其转换成格雷码的方式是:如果该位的值是0,
则将其保持为0;如果该位的值是1,则将其转换成10。
4.对于二进制数的次高位,将其转换成格雷码的方式是:如果该位的值与最
高位的值相同,则将该位的值保持不变;如果该位的值与最高位的值不同,则将该位的值取反。
5.以此类推,对于二进制数的每一位,都按照以上方法进行转换,即可得到
8位格雷码。
例如,将二进制数10010101转换为格雷码的过程如下:
1.首先进行奇偶校验,得到格雷码为:01101011。
2.对于最高位,如果该位的值是0,则将其保持为0;如果该位的值是1,
则将其转换成10。
因此,最高位的格雷码为:0。
3.对于次高位,如果该位的值与最高位的值相同,则将该位的值保持不变;
如果该位的值与最高位的值不同,则将该位的值取反。
因此,次高位的格雷码为:0。
4.以此类推,可以得到所有位的格雷码为:01101011。
二进制与格雷码转换

在精确定位控制系统中,为了提高控制精度,准确测量控制对象的位置是十分重要的。
目前,检测位置的办法有两种:其一是使用位置传感器,测量到的位移量由变送器经A/D转换成数字量送至系统进行进一步处理。
此方法精度高,但在多路、长距离位置监控系统中,由于其成本昂贵,安装困难,因此并不实用;其二是采用光电轴角编码器进行精确位置控制。
光电轴角编码器根据其刻度方法及信号输出形式,可分为增量式、绝对式以及混合式三种。
而绝对式编码器是直接输出数字量的传感器,它是利用自然二进制或循环二进制(格雷码)方式进行光电转换的,编码的设计一般是采用自然二进制码、循环二进制码、二进制补码等。
特点是不要计数器,在转轴的任意位置都可读出一个固定的与位置相对应的数字码;抗干扰能力强,没用累积误差;电源切断后位置信息不会丢失,但分辨率是由二进制的位数决定的,根据不同的精度要求,可以选择不同的分辨率即位数。
目前有10位、11位、12位、13位、14位或更高位等多种。
其中采用循环二进制编码的绝对式编码器,其输出信号是一种数字排序,不是权重码,每一位没有确定的大小,不能直接进行比较大小和算术运算,也不能直接转换成其他信号,要经过一次码变换,变成自然二进制码,在由上位机读取以实现相应的控制。
而在码制变换中有不同的处理方式,本文着重介绍二进制格雷码与自然二进制码的互换。
一、格雷码(又叫循环二进制码或反射二进制码)介绍在数字系统中只能识别0和1,各种数据要转换为二进制代码才能进行处理,格雷码是一种无权码,采用绝对编码方式,典型格雷码是一种具有反射特性和循环特性的单步自补码,它的循环、单步特性消除了随机取数时出现重大误差的可能,它的反射、自补特性使得求反非常方便。
格雷码属于可靠性编码,是一种错误最小化的编码方式,因为,自然二进制码可以直接由数/模转换器转换成模拟信号,但某些情况,例如从十进制的3转换成4时二进制码的每一位都要变,使数字电路产生很大的尖峰电流脉冲。
二进制数和格雷码的转换

二进制数和格雷码的转换二进制数和格雷码是数字电路中常用的编码方式,它们在数据传输、存储等方面都有广泛的应用。
下面我们来介绍一下二进制数和格雷码的转换方法。
一、二进制数转换为格雷码1.将二进制数的最高位复制到格雷码的最高位上。
2.从左到右扫描二进制数的每一位,如果该位与前一位相同,则在格雷码中该位上写入0,否则写入1。
例如,将二进制数101101转换为格雷码:第一步:将最高位1复制到格雷码的最高位上,得到10xxxx。
第二步:从左到右扫描剩余部分,第2位与第1位不同,故在格雷码中该位上写入1;第3、4、5位与前一位相同,故在格雷码中这三个位置上均写入0;第6位与前一位不同,故在格雷码中该位置上写入1。
最终得到的格雷码为111001。
二、格雷码转换为二进制数1.将格雷码的最高位复制到二进制数的最高位上。
2.从左到右扫描剩余部分,在每个位置上依次执行以下操作:若该位置上的数字为0,则在对应位置上写入前一个数字的值;若该位置上的数字为1,则在对应位置上写入前一个数字的值的补数。
例如,将格雷码111001转换为二进制数:第一步:将最高位1复制到二进制数的最高位上,得到1xxxxx。
第二步:从左到右扫描剩余部分,第2位是1,则在二进制数中该位置上写入前一个数字0的补数1;第3、4、5位均为1,则在二进制数中这三个位置上写入前一个数字0的补数1;第6位为0,则在二进制数中该位置上写入前一个数字1的值0。
最终得到的二进制数为101101。
总结:以上就是二进制数和格雷码之间转换的方法,需要注意的是,在实际应用中要根据具体情况选择合适的编码方式,并且要注意编码转换过程中可能出现的错误。
二进制代码与格雷码相互转换

二进制代码与格雷码相互转换格雷码(Gray Code,简称G码)是典型的循环码,它是由二进制码(Binary,简称B码)导出的。
特点是序号相邻的两组代码只有一位码不同(包括头尾两组代码),且具有循环性。
上述特点使全部码组按序循环相邻,若以循环码表示一个循环过程中按顺序发生的状态,则任何状态变化只对应有一个变量发生变化,这个特点有助于提高电路的可靠性。
电路实现:3个异或门和两个2输入数据选择器MUX,设置方式控制端M:当M = 0 时,G码→B码;当M = 1时,B码→G码。
十进制数的二进制编码在人机交互过程中,为了既满足系统中使用二进制数的要求,又适应人们使用十进制数的习惯,通常用4位二进制代码对十进制数字符号进行编码,简称为二-十进制代码,或称BCD(Binary Coded Decimal)码。
它既有二进制的形式,又有十进制的特点。
常用的BCD码有8421码、2421码和余3码3种,它们与十进制数字符号对应的编码如表1.4所示。
表1.4 常用的3种BCD码进制字符8421码2421码余3码0 0000 0000 00111 0001 0001 01002 0010 0010 01013 0011 0011 01104 0100 0100 01115 0101 1011 10006 0110 1100 10017 0111 1101 10108 1000 1110 10119 1001 1111 1100一、8421码8421码是最常用的一种有权码,其4位二进制码从高位至低位的权依次为23、22、21、20,即为8、4、2、1,故称为8421码。
按8421码编码的0~9与用4位二进制数表示的0~9完全一样,所以,8421码是一种人机联系时广泛使用的中间形式。
注意:※ 8421码中不允许出现1010~1111四种组合,因为没有十进制数字符号与其对应。
※ 十进制数字符号的8421码与相应ASCII码的低四位相同,这一特点有利于简化输入输出过程中BCD码与字符代码的转换。
格雷码和二进制码之间的转换
二进制与格雷码之间的转换在公司的PLC 改造项目中,我们经常要用到格雷码输出的绝对型旋转编码器。
由于格雷码是一种非加权码,不能直接反应出当前的角度值,所以必须在PLC 程序中将它转换成能反应当前实际位置的二进制码。
为了让我们的工程技术人员均能很好的掌握格雷码与二进制码之间的转换方法,我根据自己的一些经验和参考资料,将格雷码的相关知识作了些整理,在公司的刊物上发表出来,希望能和大家一起对这个问题来加以讨论和学习,共同提高我们的技术水平。
一、 格雷码格雷码((Gray Code )的概念格雷码是我们在工程中常会遇到的一种编码方式,例如,大多数绝对型旋转编码的输出就是采用格雷码的编码格式。
它是一种非加权码,由二进制码派生而来。
常用的二进制数与格雷码间的转换关系如下表:从上表我们可以看出,与普通二进制编码相比,格雷码的特点是相邻两个数之间只有1个二进制位发生了变化。
正是这个特点,使它更适合于用在数据传输的场合。
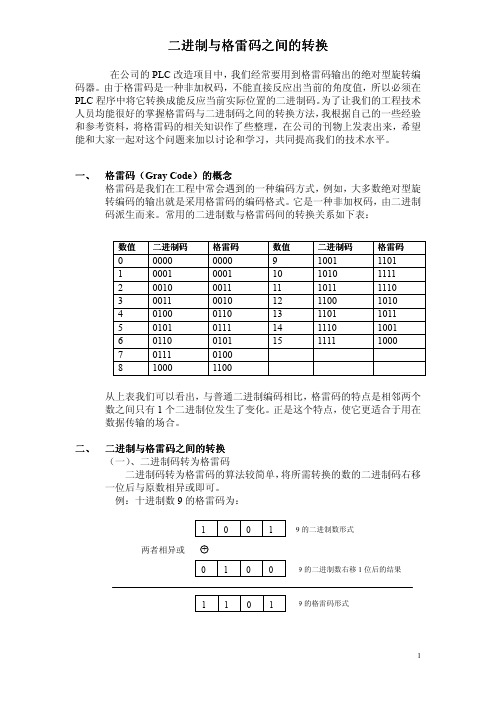
二、 二进制与格雷码之间的转换(一)、二进制码转为格雷码二进制码转为格雷码的算法较简单,将所需转换的数的二进制码右移一位后与原数相异或即可。
例:十进制数9的格雷码为:数值 二进制码格雷码 数值 二进制码格雷码0 0000 0000 9 1001 1101 1 0001 0001 10 1010 1111 2 0010 0011 11 1011 1110 30011 0010 12 1100 1010 40100 0110 13 1101 1011 50101 0111 14 1110 1001 60110 0101 15 1111 1000 70111 0100 81000 1100 9的二进制数形式 9的格雷码形式 9的二进制数右移1位后的结果 两者相异或(二)、格雷码转为二进制码格雷码转为二进制码的算法则较为繁琐,计算公式如下: Rn 为n 位的格雷码,Cn 为转换后的二进制码C n = R n ,C n-1 = R n R ⊕n-1,C n-2 = R n R ⊕n-1R ⊕n-2,…C 1 = R n R ⊕n-1R ⊕n-2…R ⊕⊕2R ⊕1,C 0 = R n R ⊕n-1R ⊕n-2…R ⊕⊕2R ⊕1R ⊕0例:格雷码(1001)转位二进制数C 4= R 4=1C 3= R 4⊕R 3=1⊕0=1C 2= R 4⊕R 3⊕R 2= C 3⊕R 2=1⊕0=1C1= R 4⊕R 3⊕R 2⊕R1= C 2⊕R 1=1⊕1=0三、 编程举例根据工业控制的特点,现分别给出在PLC 梯形图中和在VB 中实现格雷码转二进制码的程序。
二进制数转换为格雷码

二进制数转换为格雷码二进制数和格雷码是数字领域中的两个重要概念。
在计算机中,二进制数是数据存储和处理的基本形式,而格雷码则常用于数字信号传输和终端设备控制。
本文将介绍二进制数转换为格雷码的方法。
一、什么是二进制数和格雷码?1. 二进制数二进制数,顾名思义,是由二进制数字0和1组成的数字系统。
二进制数在现代计算机中至关重要,因为计算机只认识0和1。
在二进制数中,每一位数字的权值都是2的幂次方,从右到左依次是2的0次幂、2的1次幂、2的2次幂等等。
例如,数字1101表示的权值和为1×2^0 + 0×2^1 + 1×2^2 + 1×2^3 = 1 + 0 + 4 + 8 = 13。
2. 格雷码格雷码是一种二进制变换码,它的特点是相邻数值之间只有一个数字不同。
换句话说,格雷码中相邻数值之间只有一位二进制数字发生变化。
例如,在三位二进制数中,从000到111的变换过程中,格雷码的变化如下所示:000001011010110111101100二、二进制数转换为格雷码的方法1. 二进制数转换为格雷码的方法一从右到左依次将二进制数的每一位与它左边一位相异或。
最左边一位保留不变。
例如,将二进制数10011010转换为格雷码的过程如下:10011010(二进制数)10111011(格雷码)2. 二进制数转换为格雷码的方法二将二进制数的最高位保留不变,从高到低依次将每一位与它的高一位相异或。
例如,将二进制数10011010转换为格雷码的过程如下:10011010(二进制数)11011111(格雷码)三、总结二进制数和格雷码是数字领域中的基本概念。
二进制数在现代计算机中有着广泛的应用,而格雷码则常用于数字信号传输和终端设备控制。
将二进制数转换为格雷码可以通过两种方法实现。
二进制码转化为格雷码

二进制码转化为格雷码在计算机科学中,二进制码和格雷码是两种常见的数据表示方式。
二进制码是由0和1组成的数字序列,用于表示数字、字符和其他数据。
而格雷码是一种二进制码的变体,它的每个数码仅仅与前一个数码有一位不同。
在本文中,我们将讨论如何将二进制码转化为格雷码。
一、什么是二进制码和格雷码二进制码是一种使用两个数字0和1来表示数值或字符的编码系统。
这些数字被称为二进制位或比特。
在二进制码中,每个数字位都代表一个权重系数,这些系数是2的幂次方。
例如,二进制码1011表示1×2+0×2+1×2+1×2=11。
格雷码是一种二进制码的变体,它的每个数码仅仅与前一个数码有一位不同。
格雷码也被称为反射码或循环码。
格雷码最初是由弗兰克·格雷于1947年发明的,用于减少机械开关在转换时的抖动。
格雷码的主要优点是,当两个相邻的数码只有一位不同时,它们的差异只有一个比特。
这种特性使得格雷码在数字电路中很有用,因为它可以减少电路中的抖动和误差。
二、将二进制码转化为格雷码的方法在将二进制码转化为格雷码时,有两种常用的方法:递归法和迭代法。
下面我们将分别介绍这两种方法。
1.递归法递归法是一种使用递归函数将二进制码转换为格雷码的方法。
递归函数的基本思想是,将输入的二进制码划分为高位和低位两部分,然后将低位部分转化为格雷码。
最后,将高位部分与转换后的低位部分合并,得到最终的格雷码。
以下是递归法的伪代码:function binaryToGrayRecursion(binary, length)if length == 1return binaryelsegray = binaryToGrayRecursion(binary[length:2], length-1) return concatenate(binary[1], xor(binary[2:length], gray))其中,binary表示输入的二进制码,length表示二进制码的长度。
算法导论 二进制反射格雷码

算法导论二进制反射格雷码
二进制反射格雷码是指通过对称变化,将二进制码转换为格雷码。
格雷码是一种特殊的二进制编码,相邻的两个数值之间只有一位的差异,这样可以减少数字在转换过程中的错误。
下面是二进制反射格雷码的转换方法:
1. 对于给定的 n 位二进制码,格雷码的位数也是 n 位。
2. 最高位保持不变。
3. 从左往右依次处理每一位,如果当前位和前一位的值相同,则该位格雷码为0;如果当前位和前一位的值不同,则该位格雷码为1。
4. 重复步骤3,直到转换完所有位。
举个例子,假设我们要将二进制码 0101 转换为格雷码:
最高位保持不变,所以格雷码的第一位是0。
处理第二位,当前位和前一位的值相同,所以格雷码的第二位也是0。
处理第三位,当前位和前一位的值不同,所以格雷码的第三位是1。
处理第四位,当前位和前一位的值不同,所以格雷码的第四位是1。
因此,0101 的二进制反射格雷码是 0011。
c 二进制 转 格雷码

将二进制数转换为格雷码可以通过一系列按位异或(XOR)操作来实现。
下面是将一个二进制数转换为格雷码的方法:1.将二进制数的最高位(最左边的位)添加到格雷码中。
2.将二进制数的每个位与其相邻的更高位进行异或操作,并将结果添加到格雷码中。
以下是一个简单的 C 语言示例代码,将一个 8 位二进制数转换为 8 位格雷码:#include <stdio.h>// Function to convert binary to grayunsigned int binaryToGray(unsigned int num){return num ^(num >>1);}// Function to print binary and gray codevoid printBinaryGray(unsigned int num){printf("Binary: ");for(int i =7; i >=0; i--){printf("%d",(num >> i)&1);}printf("\nGray: ");unsigned int gray = binaryToGray(num);for(int i =7; i >=0; i--){printf("%d",(gray >> i)&1);}printf("\n");}int main(){unsigned int binary =0b10101010;// Example binary numberprintBinaryGray(binary);return0;}这段代码将打印出给定二进制数的二进制形式和对应的格雷码形式。
你可以将binary变量替换为你想要转换的任何 8 位二进制数。
通过这个示例,你可以了解如何在 C 语言中实现二进制到格雷码的转换。
二进制码转格雷码

二进制码转格雷码二进制码转格雷码一、什么是二进制码和格雷码?二进制码是计算机中常用的一种编码方式,它由0和1两个数字组成,用来表示计算机中的数据。
例如,8位二进制数01011010表示十进制数90。
格雷码也叫反射二进制码,它是一种特殊的二进制编码方式。
在格雷码中,相邻两个数只有一位不同。
例如,3位格雷码的顺序为000、001、011、010、110、111、101、100。
二、为什么需要将二进制码转换为格雷码?在数字电路设计中,常常需要将一个数字信号转换成另一个数字信号。
例如,在数字电视机顶盒中,需要将遥控器发送的红外信号转换成数字信号给处理器进行处理。
这时就需要使用编解码器对信号进行编解码。
在编解码器中,常用的就是将二进制数转换为格雷码或者将格雷码转换为二进制数。
因为在数字电路中使用格雷码能够减少误差率和功耗。
三、如何将二进制数转换为格雷码?1. 4位以内的情况对于4位以内的情况,可以直接使用真值表进行转换。
例如,将3位二进制数101转换成格雷码,可以按照以下步骤进行:(1)将第一位数字保持不变,即第一位为1。
(2)将第二位数字与第一位数字进行异或运算,得到0。
(3)将第三位数字与第二位数字进行异或运算,得到1。
因此,101的格雷码为111。
2. 大于4位的情况对于大于4位的情况,可以使用递归的方法进行转换。
例如,将8位二进制数11011011转换成格雷码:(1)将最高位保持不变,即最高位为1。
(2)将次高位与最高位进行异或运算,得到0。
(3)将次次高位与次高位进行异或运算,得到1。
(4)将剩余6位二进制数分成两个3位二进制数:110和110。
对每个3位二进制数分别执行上述步骤。
(5)最终得到的格雷码为10111110。
四、如何将格雷码转换为二进制数?1. 4位以内的情况对于4位以内的情况,可以直接使用真值表进行转换。
例如,将3位格雷码111转换成二进制数,可以按照以下步骤进行:(1)将第一位数字保持不变,即第一位为1。
二进制与格雷码转换

在精确定位控制系统中,为了提高控制精度,准确测量控制对象的位置是十分重要的。
目前,检测位置的办法有两种:其一是使用位置传感器,测量到的位移量由变送器经A/D转换成数字量送至系统进行进一步处理。
此方法精度高,但在多路、长距离位置监控系统中,由于其成本昂贵,安装困难,因此并不实用;其二是采用光电轴角编码器进行精确位置控制。
光电轴角编码器根据其刻度方法及信号输出形式,可分为增量式、绝对式以及混合式三种。
而绝对式编码器是直接输出数字量的传感器,它是利用自然二进制或循环二进制(格雷码)方式进行光电转换的,编码的设计一般是采用自然二进制码、循环二进制码、二进制补码等。
特点是不要计数器,在转轴的任意位置都可读出一个固定的与位置相对应的数字码;抗干扰能力强,没用累积误差;电源切断后位置信息不会丢失,但分辨率是由二进制的位数决定的,根据不同的精度要求,可以选择不同的分辨率即位数。
目前有10位、11位、12位、13位、14位或更高位等多种。
其中采用循环二进制编码的绝对式编码器,其输出信号是一种数字排序,不是权重码,每一位没有确定的大小,不能直接进行比较大小和算术运算,也不能直接转换成其他信号,要经过一次码变换,变成自然二进制码,在由上位机读取以实现相应的控制。
而在码制变换中有不同的处理方式,本文着重介绍二进制格雷码与自然二进制码的互换。
一、格雷码(又叫循环二进制码或反射二进制码)介绍在数字系统中只能识别0和1,各种数据要转换为二进制代码才能进行处理,格雷码是一种无权码,采用绝对编码方式,典型格雷码是一种具有反射特性和循环特性的单步自补码,它的循环、单步特性消除了随机取数时出现重大误差的可能,它的反射、自补特性使得求反非常方便。
格雷码属于可靠性编码,是一种错误最小化的编码方式,因为,自然二进制码可以直接由数/模转换器转换成模拟信号,但某些情况,例如从十进制的3转换成4时二进制码的每一位都要变,使数字电路产生很大的尖峰电流脉冲。
二进制码和格雷码的转换

二进制码和格雷码的转换二进制码(Binary code)和格雷码(Gray code)是两种表示数字的编码方式。
它们之间的转换可以通过以下方法实现:1.二进制码转格雷码:o从左到右,将二进制码的第一位保持不变作为格雷码的第一位。
o从左到右依次处理二进制码的每一位,按照以下规则确定格雷码的对应位:▪如果当前的二进制位与前一位相同,则对应格雷码位为0。
▪如果当前的二进制位与前一位不同,则对应格雷码位为1。
o重复上述步骤,直到处理完所有位数,得到相应的格雷码。
2.格雷码转二进制码:o从左到右,将格雷码的第一位保持不变作为二进制码的第一位。
o从左到右依次处理格雷码的每一位,按照以下规则确定二进制码的对应位:▪如果当前的格雷码位与对应的二进制码位相同,则对应二进制码位为0。
▪如果当前的格雷码位与对应的二进制码位不同,则对应二进制码位为1。
o重复上述步骤,直到处理完所有位数,得到相应的二进制码。
下面是一个示例,将二进制码0101转换为格雷码和将格雷码0110转换为二进制码的过程:•二进制码0101转换为格雷码:o首位保持不变:0o第二位:0 ⊕ 1 = 1o第三位:1 ⊕ 0 = 1o第四位:0 ⊕ 1 = 1o最终格雷码:0111•格雷码0110转换为二进制码:o首位保持不变:0o第二位:0 ⊕ 1 = 1o第三位:1 ⊕ 1 = 0o第四位:0 ⊕ 0 = 0o最终二进制码:0100使用这些规则,可以在二进制码和格雷码之间进行相互转换。
这种转换在数字通信和数字电路设计中经常用到。
二进制与格雷码之间的转换
二进制与格雷码之间的转换在公司的PLC 改造项目中,我们经常要用到格雷码输出的绝对型旋转编码器。
由于格雷码是一种非加权码,不能直接反应出当前的角度值,所以必须在PLC 程序中将它转换成能反应当前实际位置的二进制码。
为了让我们的工程技术人员均能很好的掌握格雷码与二进制码之间的转换方法,我根据自己的一些经验和参考资料,将格雷码的相关知识作了些整理,在公司的刊物上发表出来,希望能和大家一起对这个问题来加以讨论和学习,共同提高我们的技术水平。
一、 格雷码(Gray Code )的概念格雷码是我们在工程中常会遇到的一种编码方式,例如,大多数绝对型旋转编码的输出就是采用格雷码的编码格式。
它是一种非加权码,由二进制码派生而来。
常用的二进制数与格雷码间的转换关系如下表:从上表我们可以看出,与普通二进制编码相比,格雷码的特点是相邻两个数之间只有1个二进制位发生了变化。
正是这个特点,使它更适合于用在数据传输的场合。
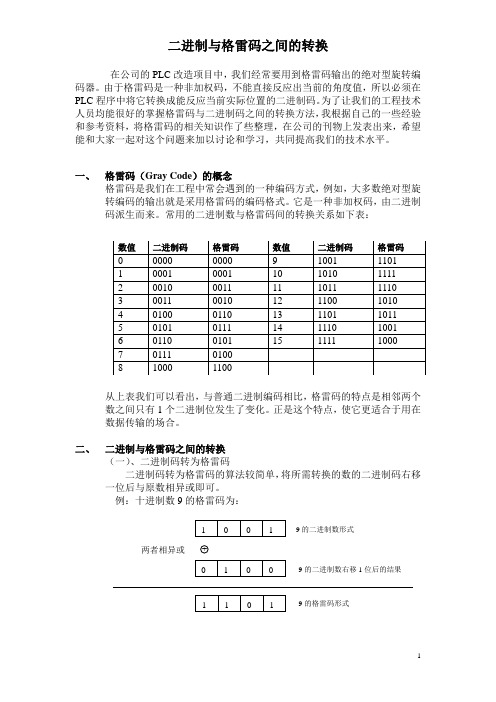
二、 二进制与格雷码之间的转换(一)、二进制码转为格雷码二进制码转为格雷码的算法较简单,将所需转换的数的二进制码右移一位后与原数相异或即可。
例:十进制数9的格雷码为:9的二进制数形式 9的格雷码形式 9的二进制数右移1位后的结果 两者相异或(二)、格雷码转为二进制码格雷码转为二进制码的算法则较为繁琐,计算公式如下: Rn 为n 位的格雷码,Cn 为转换后的二进制码C n = R n ,C n-1 = R n ⊕R n-1,C n-2 = R n ⊕R n-1⊕R n-2,…C 1 = R n ⊕R n-1⊕R n-2⊕…⊕R 2⊕R 1,C 0 = R n ⊕R n-1⊕R n-2⊕…⊕R 2⊕R 1⊕R 0例:格雷码(1001)转位二进制数C 4= R 4=1C 3= R 4⊕R 3=1⊕0=1C 2= R 4⊕R 3⊕R 2= C 3⊕R 2=1⊕0=1C1= R 4⊕R 3⊕R 2⊕R1= C 2⊕R 1=1⊕1=0三、 编程举例根据工业控制的特点,现分别给出在PLC 梯形图中和在VB 中实现格雷码转二进制码的程序。
二进制与格雷码转换

之阳早格格创做正在粗决定位统造系统中,为了普及统造粗度,准确丈量统造对于象的位子是格中要害的.暂时,检测位子的办法有二种:其一是使用位子传感器,丈量到的位移量由变收器经A/D变更成数字量收至系统举前进一步处理.此要领粗度下,但是正在多路、少距离位子监控系统中,由于其成本下贵,拆置艰易,果此本来不真用;其二是采与光电轴角编码器举止透彻位子统造.光电轴角编码器根据其刻度要领及旗号输出形式,可分为删量式、千万于式以及混同式三种.而千万于式编码器是曲交输出数字量的传感器,它是利用自然二进造或者循环二进造(格雷码)办法举止光电变更的,编码的安排普遍是采与自然二进造码、循环二进造码、二进造补码等.个性是不要计数器,正在转轴的任性位子皆可读出一个牢固的与位子相对于应的数字码;抗搞扰本领强,出用乏积缺面;电源切断后位子疑息不会拾得,但是辨别率是由二进造的位数决断的,根据分歧的粗度央供,不妨采用分歧的辨别率即位数.暂时有10位、11位、12位、13位、14位或者更下位等多种.其中采与循环二进造编码的千万于式编码器,其输出旗号是一种数字排序,不是权沉码,每一位不决定的大小,不克不迭曲交举止比较大小战算术运算,也不克不迭曲交变更成其余旗号,要通过一次码变更,形成自然二进造码,正在由上位机读与以真止相映的统造.而正在码造变更中有分歧的处理办法,本文着沉介绍二进造格雷码与自然二进造码的互换.一、格雷码(又喊循环二进造码或者反射二进造码)介绍正在数字系统中只可辨别0战1,百般数据要变更为二进造代码才搞举止处理,格雷码是一种无权码,采与千万于编码办法,典型格雷码是一种具备反射个性战循环个性的单步自补码,它的循环、单步个性与消了随机与数时出现要害缺面的大概,它的反射、自补个性使得供反非常便当.格雷码属于稳当性编码,是一种过得最小化的编码办法,果为,自然二进造码不妨曲交由数/模变更器变更成模拟旗号,但是某些情况,比圆从十进造的3变更成4时二进造码的每一位皆要变,使数字电路爆收很大的尖峰电流脉冲.而格雷码则不那一缺面,它是一种数字排序系统,其中的所有相邻整数正在它们的数字表示中惟有一个数字分歧.它正在任性二个相邻的数之间变更时,惟有一个数位爆收变更.它大天面缩小了由一个状态到下一个状态时逻辑的殽杂.其余由于最大数与最小数之间也仅一个数分歧,故常常又喊格雷反射码或者循环码.下表为几种自然二进造码与格雷码的对于照表:二、二进造格雷码与自然二进造码的互换1、自然二进造码变更成二进造格雷码自然二进造码变更成二进造格雷码,其规则是死存自然二进造码的最下位动做格雷码的最下位,而次下位格雷码为二进造码的下位与次下位相同或者,而格雷码其余诸位与次下位的供法相类似.2、二进造格雷码变更成自然二进造码二进造格雷码变更成自然二进造码,其规则是死存格雷码的最下位动做自然二进造码的最下位,而次下位自然二进造码为下位自然二进造码与次下位格雷码相同或者,而自然二进造码的其余诸位与次下位自然二进造码的供法相类似.三、二进造格雷码与自然二进造码互换的真止要领1、自然二进造码变更成二进造格雷码A)、硬件真止法(拜睹示例工程中的Binary to Gray) 根据自然二进造变更成格雷码的规则,不妨得到以下的代码:static unsigned int DecimaltoGray(unsigned int x){return x^(x>>1);}//以上代码真止了unsigned int型数据到格雷码的变更,最下可变更32位自然二进造码,超出32位将溢出. static int DecimaltoGray( int x){return x^(x>>1);}//以上代码真止了 int型数据到格雷码的变更,最下可变更31位自然二进造码,超出31位将溢出.上述代码即可用于VC统造步调中,也不妨用于单片机统造步调中.正在单片机步调安排时,若采与汇编谈话编程,不妨按相共的本理安排步调;若采与C谈话编程,则不妨曲交利用上述代码,但是修议用unsigned int函数.B)、硬件真止法根据自然二进造变更成格雷码的规则,不妨得到以下电路图:上图所示电路图即可用同或者集成电路74ls136真止,也不妨利用可编程器件PLD等编程真止.2、二进造格雷码变更成自然二进造码A)、硬件真止法(拜睹示例工程中的 Gray to Binary )根据二进造格雷码变更成自然二进造码的规则,不妨得到以下的三种代码办法:• static unsigned int GraytoDecimal(unsigned int x)• {• unsigned int y = x;• while(x>>=1)• y ^= x;• return y;• }• static unsigned int GraytoDecimal(unsigned int x)• {• x^=x>>16;• x^=x>>8;• x^=x>>4;• x^=X>>2;• x^=x^1;• return x;• }• static unsigned int GraytoDecimal(unsigned int x)• {• int i;• for(i=0;(1<<i)<sizeof(x)*8;i++)• {• x^=x>>(1<<i);• }• return x;• }//以上代码真止了unsigned int型数据到自然二进造码的变更,最下可变更32位格雷码,超出32位将溢出.将数据典型改为int型即可真止31位格雷码变更.上述代码即可用于VC统造步调中,也不妨用于单片机统造步调中.正在单片机步调安排时,若采与汇编谈话编程,不妨按相共的本理安排步调;若采与C谈话编程,则不妨曲交利用上述代码,但是修议用unsigned int 函数.B)、硬件真止法根据二进造格雷码变更成自然二进造码的规则,不妨得到以下电路图:上图所示电路图即可用同或者集成电路74ls136真止,也不妨利用可编程器件PLD等编程真止.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在精确定位控制系统中,为了提高控制精度,准确测量控制对象的位置是十分重要的。
目前,检测位置的办法有两种:其一是使用位置传感器,测量到的位移量由变送器经A/D转换成数字量送至系统进行进一步处理。
此方法精度高,但在多路、长距离位置监控系统中,由于其成本昂贵,安装困难,因此并不实用;其二是采用光电轴角编码器进行精确位置控制。
光电轴角编码器根据其刻度方法及信号输出形式,可分为增量式、绝对式以及混合式三种。
而绝对式编码器是直接输出数字量的传感器,它是利用自然二进制或循环二进制(格雷码)方式进行光电转换的,编码的设计一般是采用自然二进制码、循环二进制码、二进制补码等。
特点是不要计数器,在转轴的任意位置都可读出一个固定的与位置相对应的数字码;抗干扰能力强,没用累积误差;电源切断后位置信息不会丢失,但分辨率是由二进制的位数决定的,根据不同的精度要求,可以选择不同的分辨率即位数。
目前有10位、11位、12位、13位、14位或更高位等多种。
其中采用循环二进制编码的绝对式编码器,其输出信号是一种数字排序,不是权重码,每一位没有确定的大小,不能直接进行比较大小和算术运算,也不能直接转换成其他信号,要经过一次码变换,变成自然二进制码,在由上位机读取以实现相应的控制。
而在码制变换中有不同的处理方式,本文着重介绍二进制格雷码与自然二进制码的互换。
一、格雷码(又叫循环二进制码或反射二进制码)介绍
在数字系统中只能识别0和1,各种数据要转换为二进制代码才能进行处理,格雷码是一种无权码,采用绝对编码方式,典型格雷码是一种具有反射特性和循环特性的单步自补码,它的循环、单步特性消除了随机取数时出现重大误差的可能,它的反射、自补特性使得求反非常方便。
格雷码属于可靠性编码,是一种错误最小化的编码方式,因为,自然二进制码可以直接由数/模转换器转换成模拟信号,但某些情况,例如从十进制的3转换成4时二进制码的每一位都要变,使数字电路产生很大的尖峰电流脉冲。
而格雷码则没有这一缺点,它是一种数字排序系统,其中的所有相邻整数在它们的数字表示中只有一个数字不同。
它在任意两个相邻的数之间转换时,只有一个数位发生变化。
它大大地减少了由一个状态到下一个状态时逻辑的混淆。
另外由于最大数与最小数之间也仅一个数不同,故通常又叫格雷反射码或循环码。
下表为几种自然二进制码与格雷码的对照表:
5 0101 0111 13 1101 1011
6 0110 0101 14 1110 1001
7 0111 0100 15 1111 1000
二、二进制格雷码与自然二进制码的互换
1、自然二进制码转换成二进制格雷码
自然二进制码转换成二进制格雷码,其法则是保留自然二进制码的最高位作为
格雷码的最高位,而次高位格雷码为二进制码的高位与次高位相异或,而格雷码其
余各位与次高位的求法相类似。
2、二进制格雷码转换成自然二进制码
二进制格雷码转换成自然二进制码,其法则是保留格雷码的最高位作为自然二进
制码的最高位,而次高位自然二进制码为高位自然二进制码与次高位格雷码相异或,
而自然二进制码的其余各位与次高位自然二进制码的求法相类似。
三、二进制格雷码与自然二进制码互换的实现方法
1、自然二进制码转换成二进制格雷码
A)、软件实现法(参见示例工程中的Binary to Gray)
根据自然二进制转换成格雷码的法则,可以得到以下的代码:
static unsigned int DecimaltoGray(unsigned int x)
{
return x^(x>>1);
}
//以上代码实现了unsigned int型数据到格雷码的转换,最高可转换32位自然二进制码,超出32位将溢出。
static int DecimaltoGray( int x)
{
return x^(x>>1);
}
//以上代码实现了int型数据到格雷码的转换,最高可转换31位自然二进制码,超出31位将溢出。
上述代码即可用于VC控制程序中,也可以用于单片机控制程序中。
在单片机程序设计时,若采用汇编语言编程,可以按相同的原理设计程序;若采用C语言编程,则可以直接利用上述代码,但建议用unsigned int函数。
B)、硬件实现法
根据自然二进制转换成格雷码的法则,可以得到以下电路图:
上图所示电路图即可用异或集成电路74ls136实现,也可以利用可编程器件PLD 等编程实现。
2、二进制格雷码转换成自然二进制码
A)、软件实现法(参见示例工程中的Gray to Binary )
根据二进制格雷码转换成自然二进制码的法则,可以得到以下的三种代码方式:•static unsigned int GraytoDecimal(unsigned int x) •{
•unsigned int y = x;
•while(x>>=1)
•y ^= x;
•return y;
•}
•static unsigned int GraytoDecimal(unsigned int x) •{
•x^=x>>16;
•x^=x>>8;
•x^=x>>4;
•x^=X>>2;
•x^=x^1;
•return x;
•}
•static unsigned int GraytoDecimal(unsigned int x) •{
•int i;
•for(i=0;(1<<i)<sizeof(x)*8;i++)
•{
•x^=x>>(1<<i);
•}
•return x;
•}
//以上代码实现了unsigned int型数据到自然二进制码的转换,最高可转换32位格雷码,超出32位将溢出。
将数据类型改为int型即可实现31位格雷码转换。
上述代码即可用于VC控制程序中,也可以用于单片机控制程序中。
在单片机程序设计时,若采用汇编语言编程,可以按相同的原理设计程序;若采用C语言编程,则可以直接利用上述代码,但建议用unsigned int函数。
B)、硬件实现法
根据二进制格雷码转换成自然二进制码的法则,可以得到以下电路图:
上图所示电路图即可用异或集成电路74ls136实现,也可以利用可编程器件PLD等编程实现。
