最新高考理科数学大题专项训练:选做题
2023年高考全国甲卷理科数学+答案解析
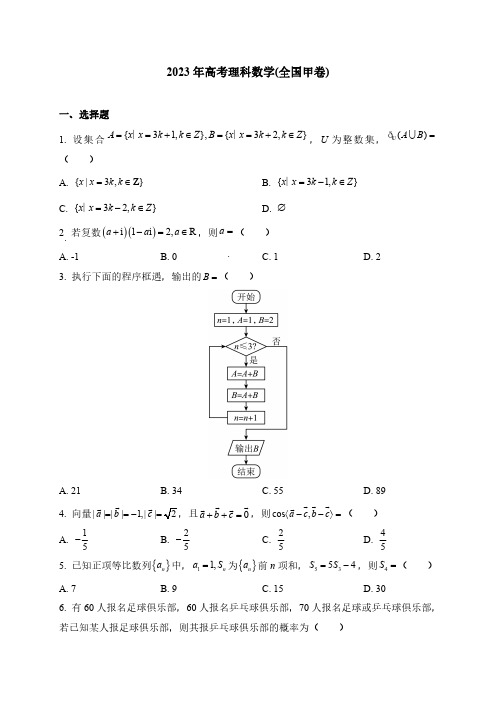
2023年高考理科数学(全国甲卷)一、选择题1.设集合{31,},{32,}A x x k k Z B x x k k Z ==+∈==+∈∣∣,U 为整数集,()A B =U ð()A.{|3,}x x k k =∈ZB.{31,}x x k k Z =-∈∣C.{32,}xx k k Z =-∈∣ D.∅2.若复数()()i 1i 2,R a a a +-=∈,则=a ()A.-1 B.0·C.1D.23.执行下面的程序框遇,输出的B =()A.21B.34C.55D.894.向量||||1,||a b c ==-=,且0a b c ++=,则cos ,a c b c 〈--〉= ()A.15-B.25-C.25D.455.已知正项等比数列{}n a 中,11,n a S =为{}n a 前n 项和,5354S S =-,则4S =()A.7B.9C.15D.306.有60人报名足球俱乐部,60人报名乒乓球俱乐部,70人报名足球或乒乓球俱乐部,若已知某人报足球俱乐部,则其报乒乓球俱乐部的概率为()A.0.8B.0.4C.0.2D.0.17.“22sin sin 1αβ+=”是“sin cos 0αβ+=”的()A.充分条件但不是必要条件B.必要条件但不是充分条件C.充要条件D.既不是充分条件也不是必要条件8.已知双曲线22221(0,0)x y a b a b-=>>的离心率为,其中一条渐近线与圆22(2)(3)1x y -+-=交于A ,B 两点,则||AB =()A.15B.5C.5D.59.有五名志愿者参加社区服务,共服务星期六、星期天两天,每天从中任选两人参加服务,则恰有1人连续参加两天服务的选择种数为()A.120B.60C.40D.3010.已知()f x 为函数πcos 26y x ⎛⎫=+ ⎪⎝⎭向左平移π6个单位所得函数,则() y f x =与1122y x =-的交点个数为()A.1B.2C.3D.411.在四棱锥P ABCD -中,底面ABCD 为正方形,4,3,45AB PC PD PCA ===∠=︒,则PBC 的面积为()A.B.C. D.12.己知椭圆22196x y +=,12,F F 为两个焦点,O 为原点,P 为椭圆上一点,123cos 5F PF ∠=,则||PO =()A.25B.302C.35D.352二、填空题13.若2π(1)sin 2y x ax x ⎛⎫=-+++ ⎪⎝⎭为偶函数,则=a ________.14.设x ,y 满足约束条件2333231x y x y x y -+≤⎧⎪-≤⎨⎪+≥⎩,设32z x y =+,则z 的最大值为____________.15.在正方体1111ABCD A B C D -中,E ,F 分别为CD ,11A B 的中点,则以EF 为直径的球面与正方体每条棱的交点总数为____________.16.在ABC 中,2AB =,60,BAC BC ∠=︒=,D 为BC 上一点,AD 为BAC ∠的平分线,则AD =_________.三、解答题17.已知数列{}n a 中,21a =,设n S 为{}n a 前n 项和,2n n S na =.(1)求{}n a 的通项公式;(2)求数列12n n a +⎧⎫⎨⎬⎩⎭的前n 项和n T .18.在三棱柱111ABC A B C -中,12AA =,1A C ⊥底面ABC ,90ACB ∠=︒,1A 到平面11BCC B 的距离为1.(1)求证:1AC A C =;(2)若直线1AA 与1BB 距离为2,求1AB 与平面11BCC B 所成角的正弦值.19.为探究某药物对小鼠的生长抑制作用,将40只小鼠均分为两组,分别为对照组(不加药物)和实验组(加药物).(1)设其中两只小鼠中对照组小鼠数目为X ,求X 的分布列和数学期望;(2)测得40只小鼠体重如下(单位:g ):(已按从小到大排好)对照组:17.318.420.120.421.523.224.624.825.025.426.126.326.426.526.827.027.427.527.628.3实验组:5.46.66.86.97.88.29.410.010.411.214.417.319.220.223.623.824.525.125.226.0(i )求40只小鼠体重的中位数m ,并完成下面2×2列联表:m<m≥对照组实验组(ii )根据2×2列联表,能否有95%的把握认为药物对小鼠生长有抑制作用.参考数据:k 0.100.050.010()20P k k ≥ 2.7063.8416.63520.设抛物线2:2(0)C y px p =>,直线 2 10x y -+=与C 交于A ,B 两点,且||AB =.(1)求p ;(2)设C 的焦点为F ,M ,N 为C 上两点,0MF NF ⋅=,求MNF 面积的最小值.21.已知3sin π(),0,cos 2x f x ax x x ⎛⎫=-∈ ⎪⎝⎭(1)若8a =,讨论()f x 的单调性;(2)若()sin 2f x x <恒成立,求a 的取值范围.四、选做题22.已知(2,1)P ,直线2cos :1sin x t l y t αα=+⎧⎨=+⎩(t 为参数),l 与x 轴,y 轴正半轴交于A ,B 两点,||||4PA PB ⋅=.(1)求α的值;(2)以原点为极点,x 轴正半轴为极轴建立极坐标系,求l 的极坐标方程.23.已知()2||, 0 f x x a a a =-->.(1)解不等式()f x x<(2)若()y f x =与坐标轴围成的面积为2,求a .2023年高考理科数学(全国甲卷)答案解析一、选择题1.A 因为整数集{}{}{}|3,|31,|32,x x k k x x k k x x k k ==∈=+∈=+∈Z Z Z Z ,U Z =,所以,(){}|3,U A B x x k k ==∈Z ð.故选:A .2.C因为()()()22i 1i i i 21i 2a a a a a a a +-=-++=+-=,所以22210a a =⎧⎨-=⎩,解得:1a =.故选:C.3.B当1n =时,判断框条件满足,第一次执行循环体,123A =+=,325B =+=,112n =+=;当2n =时,判断框条件满足,第二次执行循环体,358A =+=,8513B =+=,213n =+=;当3n =时,判断框条件满足,第三次执行循环体,81321A =+=,211334B =+=,314n =+=;当4n =时,判断框条件不满足,跳出循环体,输出34B =.故选:B.4.D 因为0a b c ++= ,所以a b c +=-r r r ,即2222a b a b c ++⋅= ,即1122a b ++⋅=rr ,所以0a b ⋅=.如图,设,,OA a OB b OC c === ,由题知,1,OA OB OC OAB === 是等腰直角三角形,AB 边上的高22,22OD AD ==,所以23222CD CO OD =+=+=,1tan ,cos 3AD ACD ACD CD ∠==∠=,2cos ,cos cos 22cos 1a cbc ACB ACD ACD 〈--〉=∠=∠=∠-24215=⨯-=.故选:D.5.C由题知()23421514q q q q q q ++++=++-,即34244q q q q +=+,即32440q q q +--=,即(2)(1)(2)0q q q -++=.由题知0q >,所以2q =.所以4124815S =+++=.故选:C.6.A 报名两个俱乐部的人数为50607040+-=,记“某人报足球俱乐部”为事件A ,记“某人报兵乓球俱乐部”为事件B ,则505404(),()707707P A P AB ====,所以4()7()0.85()7P AB P BA P A ===∣.故选:A .7.B当22sin sin 1αβ+=时,例如π,02αβ==但sin cos 0αβ+≠,即22sin sin 1αβ+=推不出sin cos 0αβ+=;当sin cos 0αβ+=时,2222sin sin (cos )sin 1αβββ+=-+=,即sin cos 0αβ+=能推出22sin sin 1αβ+=.综上可知,22sin sin 1αβ+=是sin cos 0αβ+=成立的必要不充分条件.故选:B8.D 由e =,则222222215c a b b a a a +==+=,解得2ba=,所以双曲线的一条渐近线不妨取2y x =,则圆心(2,3)到渐近线的距离55d ==,所以弦长45||5AB ===.故选:D 9.B记五名志愿者为,,,,a b c d e ,假设a 连续参加了两天社区服务,再从剩余的4人抽取2人各参加星期六与星期天的社区服务,共有24A 12=种方法,同理:,,,b c d e 连续参加了两天社区服务,也各有12种方法,所以恰有1人连续参加了两天社区服务的选择种数有51260⨯=种.故选:B.10.C因为πcos 26y x ⎛⎫=+ ⎪⎝⎭向左平移π6个单位所得函数为πππcos 2cos 2sin 2662y x x x ⎡⎤⎛⎫⎛⎫=++=+=- ⎪ ⎢⎥⎝⎭⎝⎭⎣⎦,所以()sin 2f x x =-,而1122y x =-显然过10,2⎛⎫- ⎪⎝⎭与()1,0两点,作出()f x 与1122y x =-的部分大致图像如下,考虑3π3π7π2,2,2222x x x =-==,即3π3π7π,,444x x x =-==处()f x 与1122y x =-的大小关系,当3π4x =-时,3π3πsin 142f ⎛⎫⎛⎫-=--=- ⎪ ⎪⎝⎭⎝⎭,13π1π4284312y +⎛⎫=⨯--=-<- ⎪⎝⎭;当3π4x =时,3π3πsin 142f ⎛⎫=-= ⎪⎝⎭,13π13π412428y -=⨯-=<;当7π4x =时,7π7πsin 142f ⎛⎫=-= ⎪⎝⎭,17π17π412428y -=⨯-=>;所以由图可知,()f x 与1122y x =-的交点个数为3.故选:C.11.C 法一:连结,AC BD 交于O ,连结PO ,则O 为,AC BD 的中点,如图,因为底面ABCD 为正方形,4AB =,所以AC BD ==DO CO ==,又3PC PD ==,PO OP =,所以PDO PCO ≅ ,则PDO PCO ∠=∠,又3PC PD ==,AC BD ==PDB PCA ≅ ,则PA PB =,在PAC △中,3,45PC AC PCA ==∠=︒,则由余弦定理可得22222cos 32923172PA AC PC AC PC PCA =+-⋅∠=+-⨯⨯=,故PA =,则PB =,故在PBC 中,43,P PB C C B ===,所以222916171cos 22343PC BC PB PCB PC BC +-+-∠===⋅⨯⨯,又0πPCB <∠<,所以22sin 3PCB ∠=,所以PBC的面积为1122sin 34223S PC BC PCB =⋅∠=⨯⨯⨯=法二:连结,AC BD 交于O ,连结PO ,则O 为,AC BD的中点,如图,因为底面ABCD 为正方形,4AB =,所以AC BD ==在PAC △中,3,45PC PCA =∠=︒,则由余弦定理可得2222cos 32923172PA AC PC AC PC PCA =+-⋅∠=+-⨯⨯=,故PA =,所以22217cos 217PA PC AC APC PA PC +-∠==-⋅,则17cos 3317PA PC PA PC APC ⎛⎫⋅=∠=⨯-=- ⎪ ⎪⎝⎭,不妨记,PB m BPD θ=∠=,因为()()1122PO PA PC PB PD =+=+ ,所以()()22PA PCPB PD +=+ ,即222222PA PC PA PC PB PD PB PD ++⋅=++⋅ ,则()217923923cos m m θ++⨯-=++⨯⨯,整理得26cos 110m m θ+-=①,又在PBD △中,2222cos BD PB PD PB PD BPD =+-⋅∠,即23296cos m m θ=+-,则26cos 230m m θ--=②,两式相加得22340m -=,故PB m ==故在PBC 中,43,P PB C C B ===,所以222916171cos 22343PC BC PB PCB PC BC +-+-∠===⋅⨯⨯,又0πPCB <∠<,所以22sin 3PCB ∠=,所以PBC 的面积为11sin 34223S PC BC PCB =⋅∠=⨯⨯⨯=故选:C.12.B方法一:设12π2,02F PF θθ∠=<<,所以122212tan tan 2PF F F PF S b b θ∠== ,由22212222cos sin 1tan 3cos cos 2cos +sin 1tan 5F PF θθθθθθθ--∠====+,解得:1tan 2θ=,由椭圆方程可知,222229,6,3a b c a b ===-=,所以,12121116222PF F p p S F F y y =⨯⨯=⨯=⨯ ,解得:23p y =,即2399162p x ⎛⎫=⨯-= ⎪⎝⎭,因此302OP ==.故选:B .方法二:因为1226PF PF a +==①,222121212122PF PF PF PF F PF F F +-∠=,即2212126125PF PF PF PF +-=②,联立①②,解得:22121215,212PF PF PF PF =+=,而()1212PO PF PF =+ ,所以1212OP PO PF PF ==+ ,即1213022PO PF PF =+=.故选:B .方法三:因为1226PF PF a +==①,222121212122PF PF PF PF F PF F F +-∠=,即2212126125PF PF PF PF +-=②,联立①②,解得:221221PF PF +=,由中线定理可知,()()222212122242OP F F PF PF +=+=,易知12F F=,解得:302OP =.故选:B .二、填空题13.【答案】2【解析】因为()()()22π1sin 1cos 2y f x x ax x x ax x ⎛⎫==-+++=-++ ⎪⎝⎭为偶函数,定义域为R ,所以ππ22f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭,即22ππππππ222222s a a ⎛⎫⎛⎫⎛⎫-+=-+ ⎪ -⎪ ⎪⎝⎭⎝⎭--⎝+⎭,则22πππ2π1212a -⎛⎫⎛⎫=+- ⎪⎪⎭⎝⎭= ⎝,故2a =,此时()()2212cos 1cos f x x x x x x =-++=++,所以()()()()221cos s 1co f x x x x x f x -=-++++-==,又定义域为R ,故()f x 为偶函数,所以2a =.故答案为:2.14.【答案】15【解析】作出可行域,如图,由图可知,当目标函数322z y x =-+过点A 时,z 有最大值,由233323x y x y -+=⎧⎨-=⎩可得33x y =⎧⎨=⎩,即(3,3)A ,所以max 332315z =⨯+⨯=.故答案为:1515.【答案】12【解析】设正方体棱长为2,EF 中点为O ,取AB ,1BB 中点,G M ,侧面11BB C C 的中心为N ,连接,,,,FG EG OM ON MN ,如图,由题意可知,O 为球心,在正方体中,2222222EF FG EG =++=,即2R =,则球心O 到1BB的距离为OM ==,所以球O 与棱1BB 相切,球面与棱1BB 只有1个交点,同理,根据正方体的对称性知,其余各棱和球面也只有1个交点,所以以EF 为直径的球面与正方体每条棱的交点总数为12.故答案为:1216.【答案】2【解析】如图所示:记,,AB c AC b BC a ===,方法一:由余弦定理可得,22222cos 606b b +-⨯⨯⨯= ,因为0b >,解得:1b =由ABC ABD ACD S S S =+ 可得,1112sin 602sin 30sin 30222b AD AD b ⨯⨯⨯=⨯⨯⨯+⨯⨯⨯ ,解得:13212AD b +===+.故答案为:2.方法二:由余弦定理可得,22222cos 606b b +-⨯⨯⨯= ,因为0b >,解得:1b =由正弦定理可得,62sin 60sin sin b B C==,解得:62sin 4B =,2sin 2C =,因为1>>45C = ,180604575B =--= ,又30BAD ∠=o ,所以75ADB ∠= ,即2AD AB ==.故答案为:2.三、解答题17.【答案】(1)1n a n =-(2)()1222nn T n ⎛⎫=-+ ⎪⎝⎭【解析】(1)因为2n n S na =,当1n =时,112a a =,即10a =;当3n =时,()33213a a +=,即32a =,当2n ≥时,()1121n n S n a --=-,所以()()11221n n n n n S S a na n a ---==--,化简得:()()121n n n a n a --=-,当3n ≥时,131122n n a a an n -====-- ,即1n a n =-,当1,2,3n =时都满足上式,所以()*1N n a n n =-∈.(2)因为122n n n a n +=,所以12311111232222nn T n ⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯+⨯++⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ ,2311111112(1)22222nn n T n n +⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯++-⨯+⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,两式相减得,123111111111222222111222211n n nn n n n T ++⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎡⎤⎛⎫⨯-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦+-⎝=-⎭⨯-⨯ ,11122nn ⎛⎫⎛⎫=-+⎪⎪⎝⎭⎝⎭,即()1222nn T n ⎛⎫=-+ ⎪⎝⎭,*N n ∈.18.【答案】(1)证明见解析(2)13【解析】(1)如图,1AC ⊥ 底面ABC ,BC ⊂面ABC ,1A C BC ∴⊥,又BC AC ⊥,1,A C AC ⊂平面11ACC A ,1AC AC C ⋂=,BC ∴⊥平面ACC 1A 1,又BC ⊂平面11BCC B ,∴平面11ACC A ⊥平面11BCC B ,过1A 作11A O CC ⊥交1CC 于O ,又平面11ACC A 平面111BCC B CC =,1A O ⊂平面11ACC A ,1A O ∴⊥平面11BCC B 1A 到平面11BCC B 的距离为1,11∴=A O ,在11Rt A CC △中,111112,AC AC CC AA ⊥==,设CO x =,则12C O x =-,11111,,AOC AOC ACC △△△为直角三角形,且12CC =,22211CO A O A C +=,2221111A O OC C A +=,2221111A C A C C C +=,2211(2)4x x ∴+++-=,解得1x =,111AC A C A C ∴===1AC AC ∴=(2)111,,AC A C BC A C BC AC =⊥⊥ ,1Rt Rt ACB ACB ∴△≌△1BA BA ∴=,过B 作1BD AA ⊥,交1AA 于D ,则D 为1AA 中点,由直线1AA 与1BB 距离为2,所以2BD =11A D = ,2BD =,1A B AB ∴==,在Rt ABC △,BC ∴==,延长AC ,使AC CM =,连接1C M ,由1111,CM A C CM A C =∥知四边形11A CMC 为平行四边形,11C M A C ∴∥,1C M ∴⊥平面ABC ,又AM ⊂平面ABC ,1C M AM∴⊥则在1Rt AC M △中,112,AM AC C M AC ==,1AC ∴=,在11Rt AB C △中,1AC =,11B C BC ==1AB ∴==又A 到平面11BCC B 距离也为1,所以1AB 与平面11BCC B1313=.19.【答案】(1)分布列见解析,()1E X =(2)(i )23.4m =;列联表见解析,(ii )能【解析】(1)依题意,X 的可能取值为0,1,2,则022020240C C 19(0)C 78P X ===,120224010C C 20(1)C 39P X ===,202020240C C 19(2)C 78P X ===,X12P197820391978所以X 的分布列为:故192019()0121783978E X =⨯+⨯+⨯=.(2)(i )依题意,可知这40只小鼠体重的中位数是将两组数据合在一起,从小到大排后第20位与第21位数据的平均数,由于原数据已经排好,所以我们只需要观察对照组第一排数据与实验组第二排数据即可,可得第11位数据为14.4,后续依次为17.3,17.3,18.4,19.2,20.1,20.2,20.4,21.5,23.2,23.6, ,故第20位为23.2,第21位数据为23.6,所以23.223.623.42m +==,故列联表为:m<m ≥合计对照组61420实验组14620合计202040(ii )由(i )可得,240(661414) 6.400 3.84120202020K ⨯⨯-⨯==>⨯⨯⨯,所以能有95%的把握认为药物对小鼠生长有抑制作用.20.【答案】(1)2p =(2)12-【解析】(1)设()(),,,A A B B A x y B x y ,由22102x y y px-+=⎧⎨=⎩可得,2420y py p -+=,所以4,2A B A B y y p y y p +==,所以A B AB y ==-==,即2260p p --=,因为0p >,解得:2p =.(2)因为()1,0F ,显然直线MN 的斜率不可能为零,设直线MN :x my n =+,()()1122,,,M x y N x y ,由24y x x my n ⎧=⎨=+⎩可得,2440y my n --=,所以,12124,4y y m y y n +==-,22161600m n m n ∆=+>⇒+>,因为0MF NF ⋅=,所以()()1212110x x y y --+=,即()()1212110my n my n y y +-+-+=,亦即()()()()2212121110m y y m n y y n ++-++-=,将12124,4y y m y y n +==-代入得,22461m n n =-+,()()22410m n n +=->,所以1n ≠,且2610n n -+≥,解得3n ≥+或3n ≤-.设点F 到直线MN 的距离为d,所以d =12MN y y ==-=1==-,所以MNF的面积()2111122S MN d n =⨯⨯=-=-,而3n ≥+或3n≤-,所以,当3n =-时,MNF的面积(2min 212S =-=-21.【答案】(1)答案见解析.(2)(,3]-∞【解析】(1)326cos cos 3sin cos sin ()cos x x x x xf x a x'+=-22244cos 3sin 32cos cos cos x x x a a x x+-=-=-令2cos x t =,则(0,1)t ∈则2223223()()t at t f x g t a t t '-+-==-=当222823(21)(43)8,()()t t t t a f x g t t t '+--+====当10,2t ⎛⎫∈ ⎪⎝⎭,即ππ,,()042x f x '⎛⎫∈< ⎪⎝⎭.当1,12t ⎛⎫∈ ⎪⎝⎭,即π0,,()04x f x '⎛⎫∈> ⎪⎝⎭.所以()f x 在π0,4⎛⎫ ⎪⎝⎭上单调递增,在ππ,42⎛⎫⎪⎝⎭上单调递减(2)设()()sin 2g x f x x=-()22222323()()2cos 2()22cos 12(21)24at t g x f x x g t x t a t t t t''+-=-=--=-=+-+-设223()24t a t t tϕ=+-+-322333264262(1)(22+3)()40t t t t t t t t t tϕ'--+-+=--+==->所以()(1)3t a ϕϕ<=-.1︒若(,3]a ∈-∞,()()30g x t a ϕ'=<-≤即()g x 在0,2π⎛⎫⎪⎝⎭上单调递减,所以()(0)0g x g <=.所以当(,3],()sin 2a f x x ∈-∞<,符合题意.2︒若(3,)a ∈+∞当22231110,333t t t t ⎛⎫→-=--+→-∞ ⎪⎝⎭,所以()t ϕ→-∞.(1)30a ϕ=->.所以0(0,1)t ∃∈,使得()00t ϕ=,即00,2x π⎛⎫∃∈ ⎪⎝⎭,使得()00g x '=.当()0,1,()0t t t ϕ∈>,即当()00,,()0,()x x g x g x '∈>单调递增.所以当()00,,()(0)0x x g x g ∈>=,不合题意.综上,a 的取值范围为(,3]-∞.四、选做题22.【答案】(1)3π4(2)cos sin 30ραρα+-=【解析】(1)因为l 与x 轴,y 轴正半轴交于,A B 两点,所以ππ2α<<,令0x =,12cos t α=-,令0y =,21sin t α=-,所以21244sin cos sin 2PA PB t t ααα====,所以sin 21α=±,即π2π2k α=+,解得π1π,42k k α=+∈Z ,因为ππ2α<<,所以3π4α=.(2)由(1)可知,直线l 的斜率为tan 1α=-,且过点()2,1,所以直线l 的普通方程为:()12y x -=--,即30x y +-=,由cos ,sin x y ραρα==可得直线l 的极坐标方程为cos sin 30ραρα+-=.23.【答案】(1),33a a ⎛⎫ ⎪⎝⎭(2)263【解析】(1)若x a ≤,则()22f x a x a x =--<,即3x a >,解得3a x >,即3a x a <≤,若x a >,则()22f x x a a x =--<,解得3x a <,即3a x a <<,综上,不等式的解集为,33a a ⎛⎫ ⎪⎝⎭.(2)2,()23,x a x a f x x a x a -+≤⎧=⎨->⎩.画出()f x 的草图,则()f x 与坐标轴围成ADO △与ABCABC 的高为3,(0,),,0,,022a a a D a A B ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,所以||=AB a 所以21132224OAD ABC S S OA a AB a a +=⋅+⋅== ,解得263a =。
(完整word版)高考理科数学小题训练.docx

高三理科数学选择、填空训练题(1)一.选择题:本大题共12 小题,每小题 5 分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
( 1)若复数z 满足iz 1 2i ,其中 i 为虚数单位,则在复平面上复数z 对应的点的坐标为()( A )( 2, 1)(B)(2,1)(C)(2,1)(D)(2, 1)( 2)已知全集U R ,集合A x 0 2x 1 , B x log3 x 0 ,则A I C U B()( A)x x 0(B)x x 0(C)x 0 x 1(D)x x1( 3)如图,在正方形ABCD 中,点 E 是 DC 的中点,点 F 是 BC 的一个三等分点,那么 EF =()( A )1AB1AD( B)23( C)1 uuur1 uuur( D)AB AD321 uuur1 uuurAB AD421 uuur2 uuurAB AD23( 4)已知a n为等比数列, a4a7 2 , a5a68 ,则 a1 a10()( A)7( B)7( C)5( D)5( 5)已知随机变量服从正态分布 N (1,1),若 P(3) 0.977 ,则 P( 13)()( A)0.683( B)0.853( C)0.954( D)0.977( 6)已知双曲线x2y21(a0,b 0) 的一个焦点到一条渐近线的距离为2a2b2c (c为双曲线的半焦3距),则双曲线的离心率为()( A)7( B)3 7(C)3 7( D)3 7 327( 7)设S n是等差数列{ a n}的前n项和,若a69S11=()a5,则S911( A)1( B)1( C)2(D)1 2( 8)如图给出了计算1 1 1 1 24 L L的值的程序框图,660其中①②分别是()( A ) i 30 , n n 2 ( B ) i 30 , n n 2 ( C ) i30 , n n 2( D ) i30 , n n 1( 9 )已知函数 f ( x) sin( x )( 0,0) 的最小正周期是,将函数f (x) 图象向左平移个单位长度后所得的函数图象过点P(0,1) ,则函数3 f ( x) sin( x) ()( A )在区间 [, ] 6 3( C )在区间 [, ]3 6上单调递减 (B )在区间上单调递减 ( D )在区间[, ] 上单调递增 6 3[, ] 上单调递增 3 61 n( 10) 若 x 6的展开式中含有常数项,则 n的最小值等于 ()x x( A ) 3( B ) 4 ( C ) 5 ( D ) 6( 11)一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几3何体的()1 13正视图 ( A )外接球的半径为(B )表面积为73 13( C )体积为3( D )外接球的表面积为 4俯视图( 12)已知定义在R 上的函数 y f ( x) 满足:函数 yf (x 1) 的图象关于直线 x 1 对称,且当x (,0),f (x) xf '( x)0 成立 ( f '( x) 是函数 f ( x) 的导函数 ), 若 a(sin 1) f (sin 1) ,22b (ln2) f (ln 2) ,c 2 f (log 211) ,则 a, b, c 的大小关系是()4( A ) a b c( B ) b a c( C ) c a b( D ) a c b二.填空题:本大题共4小题,每小题5分。
新高考数学题型试卷

新高考数学题型试卷一、选择题(每题5分,共8小题)1. 设集合A = {xx^2-3x + 2 = 0},B={xx^2-ax + a - 1 = 0},若A∩ B = B,则a的值为()- A. 2.- B. 3.- C. 2或3。
- D. 1或2或3。
解析:- 先求解集合A,对于方程x^2-3x + 2 = 0,因式分解得(x - 1)(x - 2)=0,解得x = 1或x = 2,所以A={1,2}。
- 对于集合B,方程x^2-ax + a - 1 = 0可化为(x - 1)[x-(a - 1)] = 0,解得x = 1或x=a - 1,所以B={1,a - 1}。
- 因为A∩ B = B,所以B⊆ A。
- 当a-1 = 1时,a = 2;当a - 1=2时,a = 3。
所以a的值为2或3,答案选C。
2. 复数z=(1 + i)/(1 - i)的共轭复数是()- A. i- B. -i- C. 1 - i- D. 1 + i解析:- 先化简z=(1 + i)/(1 - i),分子分母同时乘以1 + i,得到z=frac{(1 + i)^2}{(1 - i)(1 + i)}=frac{1 + 2i+i^2}{2}=(2i)/(2)=i。
- 复数i的共轭复数是-i,所以答案选B。
3. 已知向量→a=(1,2),→b=(x,1),若→a⊥→b,则x的值为()- A. - 2.- B. 2.- C. -(1)/(2)- D. (1)/(2)解析:- 因为→a⊥→b,根据向量垂直的性质→a·→b=0。
- 又→a=(1,2),→b=(x,1),则→a·→b=1× x+2×1 = 0,即x + 2 = 0,解得x=-2,答案选A。
4. 在等差数列{a_n}中,a_3=5,a_7=13,则a_11的值为()- A. 21.- B. 22.- C. 23.- D. 24.解析:- 根据等差数列的性质:若m,n,p,q∈ N^+,且m + n=p + q,则a_m+a_n=a_p+a_q。
高考全国卷数学理科试题及答案详解

2021年普通高等学校招生全国统一考试数学(全国新课标卷II)第一卷一、选择题:本大题共12小题,每题5分,在每题给出的四个选项中,只有一项为哪一项符合题目要求的. 1.(2021课标全国Ⅱ,理1)集合M ={x |(x -1)2<4,x ∈R },N ={-1,0,1,2,3},那么M ∩N =( ).A .{0,1,2}B .{-1,0,1,2}C .{-1,0,2,3}D .{0,1,2,3}2.(2021课标全国Ⅱ,理2)设复数z 满足(1-i)z =2i ,那么z =( ).A .-1+iB .-1-IC .1+iD .1-i3.(2021课标全国Ⅱ,理3)等比数列{a n }的前n 项与为S n .S 3=a 2+10a 1,a 5=9,那么a 1=( ).A .13B .13-C .19D .19-4.(2021课标全国Ⅱ,理4)m ,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l ⊥m ,l ⊥n ,l α,l β,那么( ).A .α∥β且l ∥αB .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l5.(2021课标全国Ⅱ,理5)(1+ax )(1+x )5的展开式中x 2的系数为5,那么a =( ).A .-4B .-3C .-2D .-16.(2021课标全国Ⅱ,理6)执行下面的程序框图,如果输入的N =10,那么输出的S =( ).A .1111+2310+++B .1111+2!3!10!+++C .1111+2311+++ D .1111+2!3!11!+++7.(2021课标全国Ⅱ,理7)一个四面体的顶点在空间直角坐标系O -xyz 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,那么得到的正视图可以为( ).8.(2021课标全国Ⅱ,理8)设a =log 36,b =log 510,c =log 714,那么( ).A .c >b >aB .b >c >aC .a >c >bD .a >b >c 9.(2021课标全国Ⅱ,理9)a >0,x ,y 满足约束条件1,3,3.x x y y a x ≥⎧⎪+≤⎨⎪≥(-)⎩假设z =2x+y 的最小值为1,那么a =( ).A .14B .12 C .1 D .210.(2021课标全国Ⅱ,理10)函数f (x )=x 3+ax 2+bx +c ,以下结论中错误的选项是( ).A .∃x0∈R ,f(x0)=0B .函数y =f(x)的图像是中心对称图形C .假设x0是f(x)的极小值点,那么f(x)在区间(-∞,x0)单调递减D .假设x0是f(x)的极值点,那么f′(x0)=011.(2021课标全国Ⅱ,理11)设抛物线C :y 2=2px (p >0)的焦点为F ,点M 在C 上,|MF |=5,假设以MF 为直径的圆过点(0,2),那么C 的方程为( ).A .y2=4x 或y2=8xB .y2=2x 或y2=8xC .y2=4x 或y2=16xD .y2=2x 或y2=16x12.(2021课标全国Ⅱ,理12)点A (-1,0),B (1,0),C (0,1),直线y =ax +b (a >0)将△ABC 分割为面积相等的两局部,那么b 的取值范围是( ).A .(0,1) B.112⎛⎫ ⎪ ⎪⎝⎭ C.113⎛⎤- ⎥ ⎝⎦ D .11,32⎡⎫⎪⎢⎣⎭ 第二卷本卷包括必考题与选考题两局部,第13题~第21题为必考题,每个试题考生都必须做答。
2024年高考真题分类专项(解析几何)(学生版)

2024年高考真题分类专项(解析几何)一、单选题1.(2024年北京高考数学真题)圆22260x y x y +-+=的圆心到直线20x y -+=的距离为( )A B .2C .3D .2.(2024年天津高考数学真题)双曲线22221()00a x y a b b >-=>,的左、右焦点分别为12.F F P、是双曲线右支上一点,且直线2PF 的斜率为2.12PF F △是面积为8的直角三角形,则双曲线的方程为( )A .22182y x -=B .22184x y -=C .22128x y -=D .22148x y -=3.(2024年新课标全国Ⅱ卷数学真题)已知曲线C :2216x y +=(0y >),从C 上任意一点P 向x 轴作垂线段PP ',P '为垂足,则线段PP '的中点M 的轨迹方程为( ) A .221164x y +=(0y >)B .221168x y +=(0y >)C .221164y x +=(0y >)D .221168y x +=(0y >)4.(2024年高考全国甲卷数学(文)真题)已知直线20ax by a b +-+=与圆2241=0C x y y ++-:交于,A B 两点,则AB 的最小值为( )A .2B .3C .4D .65.(2024年高考全国甲卷数学(理)真题)已知双曲线的两个焦点分别为()()0,4,0,4-,点()6,4-在该双曲线上,则该双曲线的离心率为( )A.4 B .3C .2D6.(2024年高考全国甲卷数学(理)真题)已知b 是,a c 的等差中项,直线0ax by c 与圆22410x y y ++-=交于,A B 两点,则AB 的最小值为( ) A .1B .2C .4D.二、多选题7.(2024年新课标全国Ⅱ卷数学真题)抛物线C :24y x =的准线为l ,P 为C 上的动点,过P 作22:(4)1A x y +-=⊙的一条切线,Q 为切点,过P 作l 的垂线,垂足为B ,则( ) A .l 与A 相切B .当P ,A ,B三点共线时,||PQ = C .当||2PB =时,PA AB ⊥D .满足||||PA PB =的点P 有且仅有2个8.(2024年新课标全国Ⅱ卷数学真题)设计一条美丽的丝带,其造型可以看作图中的曲线C 的一部分.已知C 过坐标原点O .且C 上的点满足:横坐标大于2-,到点(2,0)F 的距离与到定直线(0)x a a =<的距离之积为4,则( )A .2a =- B.点在C 上C .C 在第一象限的点的纵坐标的最大值为1D .当点()00,x y 在C 上时,0042y x ≤+三、填空题9.(2024年上海夏季高考数学真题)已知抛物线24y x =上有一点P 到准线的距离为9,那么点P 到x 轴的距离为 .10.(2024年北京高考数学真题)抛物线216y x =的焦点坐标为 .11.(2024年北京高考数学真题)若直线()3y k x =-与双曲线2214x y -=只有一个公共点,则k 的一个取值为 .12.(2024年天津高考数学真题)圆22(1)25-+=x y 的圆心与抛物线22(0)y px p =>的焦点F 重合,A 为两曲线的交点,则原点到直线AF 的距离为 .13.(2024年新课标全国Ⅱ卷数学真题)设双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点分别为12F F 、,过2F 作平行于y 轴的直线交C 于A ,B 两点,若1||13,||10F A AB ==,则C 的离心率为 .四、解答题14.(2024年上海夏季高考数学真题(网络回忆版))已知双曲线222Γ:1,(0),y x b b-=>左右顶点分别为12,A A ,过点()2,0M -的直线l 交双曲线Γ于,P Q 两点. (1)若离心率2e =时,求b 的值.(2)若2b MA P =△为等腰三角形时,且点P 在第一象限,求点P 的坐标. (3)连接OQ 并延长,交双曲线Γ于点R ,若121A R A P ⋅=,求b 的取值范围.15.(2024年北京高考数学真题)已知椭圆E :()222210x y a b a b +=>>,以椭圆E 的焦点和短轴端点为顶点的四边形是边长为2的正方形.过点()(0,t t >且斜率存在的直线与椭圆E 交于不同的两点,A B ,过点A 和()0,1C 的直线AC 与椭圆E 的另一个交点为D . (1)求椭圆E 的方程及离心率; (2)若直线BD 的斜率为0,求t 的值.16.(2024年天津高考数学真题)已知椭圆22221(0)x y a b a b+=>>椭圆的离心率12e =.左顶点为A ,下顶点为B C ,是线段OB 的中点,其中ABC S △. (1)求椭圆方程.(2)过点30,2⎛⎫- ⎪⎝⎭的动直线与椭圆有两个交点P Q ,.在y 轴上是否存在点T 使得0TP TQ ⋅≤.若存在求出这个T 点纵坐标的取值范围,若不存在请说明理由.17.(2024年新课标全国Ⅱ卷数学真题)已知(0,3)A 和33,2P ⎛⎫ ⎪⎝⎭为椭圆2222:1(0)x y C a b a b+=>>上两点.(1)求C 的离心率;(2)若过P 的直线l 交C 于另一点B ,且ABP 的面积为9,求l 的方程.18.(2024年高考全国甲卷数学(理)真题)已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ,点31,2M ⎛⎫⎪⎝⎭在C 上,且MF x ⊥轴.(1)求C 的方程;(2)过点()4,0P 的直线交C 于,A B 两点,N 为线段FP 的中点,直线NB 交直线MF 于点Q ,证明:AQ y ⊥轴.。
2024全国卷理科数学高考真题

2024年一般高等学校招生全国统一考试理科数学留意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设z=:—+2i,则|z|=1+1A.0B.—C.1D.、/22.已知集合A=(x|x2-x-2>0},贝=A.(x|-l<x<2}B.(x|-l<x<2}C.(x|x<-l}.(x|x>2}D.(x|x<-l}_(x|x>2}3.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入改变状况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:建设前经济收入构成比例建设后经济收入构成比例则下面结论中不正确的是A.新农村建设后,种植收入削减B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入及第三产业收入的总和超过了经济收入的一半4.记&为等差数列{%}的前〃项和.若3S.=S2+S4,%=2,贝胞=A.—12B.-10C・10D.125.设函数了⑴=r+(o_1K+"若/*3)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为A.y=-2x B・y= C.y=2xD."x6.在AABC中,AD为BC边上的中线,E为AD的中点,则E8=311331 A.—AB—AC B.—AB—AC C.—AB h—AC44444413一D.-AB+-AC447.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为8,则在此圆柱侧面上,从肱到N的路径中,最短路径的长度为A.2面「B.2^5C.3D.28.设抛物线Q jMx的焦点为R过点(-2,0)且斜率为甘的直线及。
高考理科数学解答题专题训练(七)选做题

大题专项练(七) 选做题A 组 基础通关1.(2019辽宁沈阳东北育才学校八模)已知函数f (x )=|x-1|+|x+1|. (1)求f (x )≥3的解集;(2)记函数f (x )的最小值为M ,若a>0,b>0,且a+2b=M ,求1a+2b的最小值.由f (x )≥3,得{x ≤-1,-(x -1)-(x +1)≥3或{-1<x ≤1,-(x -1)+(x +1)≥3或{x >1,(x -1)+(x +1)≥3,即{x ≤-1,x ≤-32或{-1<x ≤1,2≥3或{x >1,x ≥32. 解得x ≤-32或x ≥32,∴不等式f (x )≥3的解集为-∞,-32∪32,+∞.(2)∵f (x )=|x-1|+|x+1|≥|(x-1)-(x+1)|=2,∴f (x )的最小值M=2,∴a+2b=2, ∵a>0,b>0,∴1a +2b =(1a +2b )·a+2b 2=125+2ba +2ab ≥125+2√2b a ·2ab =92,当且仅当2ba =2ab 即a=b=23时等号成立,∴1+2的最小值为9.2.(2019江西赣州5月适应性考试)已知函数f (x )=|x+1|+2|x-1|. (1)求不等式f (x )≤4的解集;(2)若函数y=f (x )图象的最低点为(m ,n ),正数a ,b 满足ma+nb=4,求2a +1b的取值范围.当x ≤-1时,f (x )=-3x+1≤4,得x ≥-1,所以x=-1,当-1<x<1时,f (x )=-x+3≤4,得x ≥-1,所以-1<x<1,当x ≥1时,f (x )=3x-1≤4,得x ≤53,所以1≤x ≤53,综上,-1≤x ≤53,不等式f (x )≤4的解集为[1,53].(2)由f (x )={-3x +1(x ≤-1),-x +3(-1<x <1),3x -1(x ≥1)的图象最低点为(1,2),即m=1,n=2,所以a+2b=4,因为a>0,b>0,所以2a +1b =14(a+2b )(2a +1b )=144+4b a +a b ≥14(4+2√4)=2, 当且仅当a=2b=2时等号成立,所以2a+1b的取值范围为[2,+∞).3.(2019河北石家庄一模)已知函数f (x )=√2|x -3|-|x |-m 的定义域为R ; (1)求实数m 的取值范围;(2)设实数t 为m 的最大值,若实数a ,b ,c 满足a 2+b 2+c 2=t 2,求1a 2+1+1b 2+2+1c 2+3的最小值.由题意可知2|x-3|-|x|≥m 恒成立,令g (x )=2|x-3|-|x|,去绝对值号,可得g (x )=2|x-3|-|x|={x -6(x ≥3),6-3x (0<x <3),6-x (x ≤0),画图可知g (x )的最小值为-3,所以实数m 的取值范围为m ≤-3;(2)由(1)可知a 2+b 2+c 2=9,所以a 2+1+b 2+2+c 2+3=15,1a 2+1+1b 2+2+1c 2+3=(1a 2+1+1b 2+2+1c 2+3)·(a 2+1+b 2+2+c 2+3)15=3+b 2+2a 2+1+a 2+1b 2+2+c 2+3a 2+1+a 2+1c 2+3+c 2+3b 2+2+b 2+2c 2+315≥915=35,当且仅当a 2+1=b 2+2=c 2+3=5,即a 2=4,b 2=3,c 2=2时等号成立, 所以1a 2+1+1b 2+2+1c 2+3的最小值为35.4.(2019河南十所名校高三毕业班阶段性测试)在平面直角坐标系xOy 中,直线l 的参数方程为{x =a +√22t ,y =√22t(t 为参数).以坐标原点为极点,x 轴正半轴为极轴建立极坐标系.曲线C 的极坐标方程为ρ2=85-3cos2θ,直线l 与曲线C 交于A ,B 两点.(1)求曲线C 的直角坐标方程;(2)若线段AB 的长度为4√25,求实数a 的值.由ρ2=85-3cos2θ,得ρ2(5-6cos 2θ+3)=8,化简得4ρ2-3ρ2cos 2θ=4.因为x=ρcos θ,y=ρsin θ,所以方程可化为4(x 2+y 2)-3x 2=4,整理得x 2+4y 2=4,即x 24+y 2=1.(2)由直线l 的参数方程{x =a +√22t ,y =√22t 可得其普通方程为x-y-a=0.联立{x 2+4y 2=4,x -y -a =0可得5x 2-8ax+4a 2-4=0.因为直线l 与曲线C 有两个交点,所以Δ=64a 2-4×5×(4a 2-4)=80-16a 2>0,得-√5<a<√5.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=8a ,x 1x 2=4a 2-4.|AB|=√2|x 1-x 2|=√2√(x 1+x 2)2-4x 1x 2=4√25√5-a 2.由4√2√5-a 2=4√2,解得a=±2.5.在平面直角坐标系xOy 中,已知曲线M 的参数方程为{x =1+cosφ,y =1+sinφ(φ为参数),过原点O 且倾斜角为α的直线l 交M 于A 、B 两点.以O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求l 和M 的极坐标方程;(2)当α∈0,π4时,求|OA|+|OB|的取值范围.由题意可得,直线l 的极坐标方程为θ=α(ρ∈R ).曲线M 的普通方程为(x-1)2+(y-1)2=1, 因为x=ρcos θ,y=ρsin θ,x 2+y 2=ρ2,所以M 的极坐标方程为ρ2-2(cos θ+sin θ)ρ+1=0. (2)设A (ρ1,α),B (ρ2,α),且ρ1、ρ2均为正数, 将θ=α代入ρ2-2(cos θ+sin θ)ρ+1=0, 得ρ2-2(cos α+sin α)ρ+1=0,当α∈0,π4时,Δ=4sin 2α>0,所以ρ1+ρ2=2(cos α+sin α),根据极坐标的几何意义,|OA|,|OB|分别是点A ,B 的极径.从而|OA|+|OB|=ρ1+ρ2=2(cos α+sin α)=2√2sin α+π4.当α∈0,π4时,α+π4∈π4,π2,故|OA|+|OB|的取值范围是(2,2√2].6.(2019陕西西安八校高三4月联考)已知曲线C 1:{x =-4+cost ,y =3+sint (t 为参数),C 2:{x =√3cosθ,y =sinθ(θ为参数).(1)将C 1,C 2的方程化为普通方程,并说明它们分别表示什么曲线;(2)若C 1上的点P 对应的参数为t=π2,Q 为C 2上的动点,求PQ 中点M 到直线C 3:{x =3+t ,y =-2+t (t 为参数)距离的最小值.C 1:(x+4)2+(y-3)2=1,C 2:x 23+y 2=1.C 1为圆心是(-4,3),半径是1的圆,C 2为中心是坐标原点,焦点在x 轴上,长半轴长是√3,短半轴长是1的椭圆.(2)当t=π2时,P (-4,4),Q (√3cos θ,sin θ),故M -2+√32cos θ,2+12sin θ,C 3为直线x-y-5=0,M 到C 3的距离d=|√32cosθ-12sinθ-9|√2=√22sin θ-π3+9,从而当sin θ-π3=-1时,d 取得最小值4√2.B 组 能力提升7.(2019全国Ⅲ,理23)[选修4—5:不等式选讲] 设x ,y ,z ∈R ,且x+y+z=1.(1)求(x-1)2+(y+1)2+(z+1)2的最小值;(2)若(x-2)2+(y-1)2+(z-a )2≥13成立,证明:a ≤-3或a ≥-1.[(x-1)+(y+1)+(z+1)]2=(x-1)2+(y+1)2+(z+1)2+2[(x-1)(y+1)+(y+1)(z+1)+(z+1)(x-1)] ≤3[(x-1)2+(y+1)2+(z+1)2],故由已知得(x-1)2+(y+1)2+(z+1)2≥43,当且仅当x=5,y=-1,z=-1时等号成立.所以(x-1)2+(y+1)2+(z+1)2的最小值为43.[(x-2)+(y-1)+(z-a)]2=(x-2)2+(y-1)2+(z-a)2+2[(x-2)(y-1)+(y-1)(z-a)+(z-a)(x-2)]≤3[(x-2)2+(y-1)2+(z-a)2],故由已知得(x-2)2+(y-1)2+(z-a)2≥(2+a)23, 当且仅当x=4-a,y=1-a,z=2a-2时等号成立.因此(x-2)2+(y-1)2+(z-a)2的最小值为(2+a)23.由题设知(2+a)23≥13,解得a≤-3或a≥-1.。
2020版高考数学大二轮培优理科通用版大题专项练:(七) 选做题

������
当 α∈ 0,4 时,Δ=4sin 2α>0,
所以 ρ1+ρ2=2(cos α+sin α),根据极坐标的几何意义,|OA|,|OB|分别是点 A,B 的极径.
������
从而|OA|+|OB|=ρ1+ρ2=2(cos α+sin α)=2 2sin α+4 .
������
������ ������,������
∵a>0,b>0,
( ) 1
∴������
+
2 ������
=
1 ������
+
2 ������
·������
+ 2������ 2
=
1 2
2������
5+ ������
+
2������ ������
1
≥2
5+2
2������ 2������
������ · ������
9
=2,
2������
当且仅当 ������
离的最小值.
������2
解(1)C1:(x+4)2+(y-3)2=1,C2: 3 +y2=1.
C1 为圆心是(-4,3),半径是 1 的圆, C2 为中心是坐标原点,焦点在 x 轴上,长半轴长是 3,短半轴长是 1 的椭圆.
������
3
1
(2)当 t=2时,P(-4,4),Q( 3cos θ,sin θ),故 M -2+ 2 cos θ,2+2sin θ ,
≤3[(x-2)2+(y-1)2+(z-a)2],
2023年高考-数学(理科)考试备考题库附带答案9

2023年高考-数学(理科)考试备考题库附带答案第1卷一.全考点押密题库(共50题)1.(单项选择题)(每题 5.00 分) 已知A,B 是球 O 的球面上两点,∠AOB = 90° ,C为该球面上的动点。
若三棱锥 O - ABC 体积的最大值为36,则球 O 的表面积为A. 36πB. 64πC. 144πD. 256π正确答案:C,2.(填空题)(每题 5.00 分) 已知圆锥的顶点为S,母线SA,SB所成角的余弦值为7/8,SA与圆锥底面所成角为45°.若△SAB的面积为5√15,则该圆锥的侧面积为.正确答案:40√2π,3.(单项选择题)(每题 5.00 分) 记SN.为等差数列αN}的前n项和.若3S3=S2+S4,α=2,则α5= {A. -12B. -10C. 10D. 12正确答案:B,4.(填空题)(每题5.00 分) 已知函数f(x)=2sinx+sin2x,则f(x)的最小值是_______?正确答案:-3√3/2,5.(单项选择题)(每题 5.00 分) 双曲线x2/α2-y2/b2=1(α>0,b>0)的离心率为√3,则其渐近线方程为A. y=±√2xB. y=±√3xC. y=±√2/2xD. y=±√3/2x正确答案:A,6.(单项选择题)(每题 5.00 分) 已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为A. 3√3/4B. 2√3/3C. 3√2/4D. √3/2正确答案:A,7.(单项选择题)(每题 5.00 分) 已知集合A=x∣x2-x-2>0},则CRA={A. x∣-12}{D. {x∣x≦-1}∪{x∣x≧2}正确答案:B,8.(单项选择题)(每题 5.00 分) 在△ABC中,cos C/2=√5/5,BC=1,AC=5,则AB=A. 4√2B. √30C. √29D. 2√5正确答案:A,9.(填空题)(每题 5.00 分) 某髙科技企业生产产品 A 和产品 B 需要甲、乙两种新型材料。
届高三理科数学六大专题训练题含详解

5高三数学(理科)专题训练 A. —B. -C. —D.—6.下列关系式中正确的是()《三角函数、三角包等变换与解三角形》A. sinllsin168C. sin11sin1687.在锐角cos10 sin168sin 11 cos10sin168 cos10cos10 sin11ABC中,角A,B.D.1 . 选择题为三角形的一个内角,边长分别为a,b.若2asinB角A等于()B所对的J3b,则tan A.1212c13B,()VC。
沪2.函数y sin x和函数增函数的区间是()12有cosx者B是A . - B. - C. - D.8.已知函数f (x) Acos( x )(A则f(x)是奇函数”是“0, 0,R),A. [2k. [2k ,2k Lk2— ](k2](k Z)BZ)C. [2k ,2ka](k Z)D.[2k -,2k25 3.已知sin(一2 ](kZ)2A .充分不必要条件B .必要不充分条件C.充分必要条件D .既不充分也不必要条件二、填空题9.已知扇形AOB的周长是6cm,该扇形中心角是1弧度,则该扇形面积是.1,那么510.设sin2 sincos A.() 2 B. 54.在图中,1C.51D. 25 5tan2 的值是11.在锐角ABC中,BC 1, BA、B是单位圆。
上的AC2 A,则小匕的值等于cosA点,C是圆与x轴正半轴的交点,A点的坐标为(3,4),5 5且AOB是正三角形.则cos COB的值为(),AC的取值范围为12.函数 f(x) si 的最大传A.C. 4 3、3103 4 310B.D.4 3.3103 4 . 310-2 sin cos(x )三、解答题山13.已知函数f(x) 3sin( x )( 0,- -)5,将函数y 3cosx sin x(x R)的图象向左平移m(m 0)个长度单位后,所得到的图象关于y轴对称,则m的最小值是() 的图象关于直线x —对称,且3图象上相邻两个最高点的距离为⑴求和的值;3 / ,求⑵右 f (—) 2 cos( ,)的值. 14 .已知向量, 1、।a (cosx, -), b2x R,设函数f (x)(1)求f (x)的最小正周期; (2)求f (x)在[0,—]上的最大值和2最小值.■ ---(3sin x, a b.15 .已知函数f (x) Asin(x —), x R,且 4f(- ) 3. 12 2(1)求A 的值;3⑵若 f( ) f()二, 2 求 f(3).416 .已知函数f (x) 3 sin xcos x Q x R,且函数f (x)的最小正周期为.(1)求的值和函数f(x)的单调增区问;(2)在ABC 中,角A,B,C 所对的边分 别是a,b,c,又A 4f (一 一) —, b 2, ABC 的面积 2 3 5等于3,求边长a 的值. 17 .已知函数x x xf (x) 2 sin - cos - . 3 cos -4 4 2(1)求函数f(x)的最小正周期及 最值;(2)令g(x) f (x 3),判断函数 g(x)的奇偶性,并说明理由.18 .在ABC 中,内角A 、B 、C 所对的边分别为a 、b 、c 已知a b, c 3,(1)求角C 的大小;4(2)若sin A —,求 ABC 的面积.5(",1cos2 x,2高三数学(理科)专题训练数列一、选择题1.数列\;’275,2.虎,/1,,的一个通项公式是()A. a n J3n 3B. a n J3n 1C. a n J3n 1D. % Cn 32.已知等差数列⑶}中,a? a9 16冏1,则a12的值是()A. 15B. 30C. 31D. 643.等比数列⑶}中,a〔a9 64, a3 a? 20,则an 的值是()A. 1B. 64C. 1 或64D. 1 或324. ABC的三边a,b, c既成等差数列又成等比数列,则此三角形是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等边三角形5.已知数列{a n}满足二、填空题9.在等差数列{a n}中,a〔a3 a5 12, a3 a4 a5 8,则通项a n 1 a n a n 1(n 2), a1 记S n a1 a2 a3结论正确的是()1, a2 3, a n,则下列A. a2014C. a2014 a20143,S2014a20141,S20141 ,S2053, S20'514142B.2D.6.如果在等差数列{a n}中,a3 a4 a5 12,那么a〔a2 a?()A. 14B. 21C. 28D. 357.数列{a n}中,a11,a2 2 3,a3 4 5 6,a47 那么a10 ()A. 495B. 505C. 550D. 5958.各项均为实数的等比数列{a n}的前n项和为S n,若S10 10, S30 70,贝US40 ()A. 150B. 200C. 150 或200D. 400 或50 a n .10.设等比数列{a n}的前n项和为S n,若"I 3,则S9 .11.设平面内有n条直线(n 2),其中任意两条直线都相交且交点不同;若用f(n)表示这n条直线把平面分成的区域个数,则f (2) , f(3) , f(4) .当n 4 时,f (n) .12.已知数列{a n}的通项公式为n 1a n log2----------(n N*).设其刖n 项n 2和为S n,则使S n 5成立的最小自然数n是.三、解答题13.等差数列{a n}的前n项和为S n,a123,公差d为整数,且第6 项为正,从第7项起变为负.(1)求d的值;(2)求S n的最大值;(3)当S n是正数时,求n的最大化14.设a1,d为实数,首项为诩、公差为d的等差数列{a n}的前n项和为S n,满足&S6 15 0.⑴若S5 5,求S6及为;(2)求d的取值范围.[0,5.,已知数歹{a n}的首项a1 a,S n是,薮列{a n}的前n项和,且满足S2 3n2a n S21,a n 0,(1)若数列{a n}是等差数列,求a 的值;(2)确定a的取值集合M,使a M时,数列{a n}是递增数列.16 .已知{a n }为递增的等比数列,且⑶自0}{ 10, 6, 2,0,1,3,4,16}.(1)求数列{a n }的通项公式; (2)是否存在等差数列{b n },使得对一切n N *都成立?若存在, 求出bn ;若不存在,说明理由.17 .等差数列{a n }各项均为正整数,a 1 3,前n 项和为S n ,等比数列 {b n }中,b 1 1,且b 2s 2 64, {b a n } 是公比为64的等比数列.(1)求 a n 与 b n ;1 113 (2)证明:-——3S 1 S 2S n 418.已知数列{a n }, S n 为其前n 项的 和,S n n a n 9, n N *.(1)证明数列{a n }不是等比数列;(2)令b n a n 1,求数列{b n }的通项公式b n ;(3)已知用数列{b n }可以构造新数 列.例如:{sin b n },…,请写出用数列{b n }构造 出的新数列{P n }的通项公式,使数 列{P n }满足以下两个条件,并说明 理由.①数列{ P n }为等差数列;②数列a 〔b na 2b n 1a 3b n 2a nb 12n{3b n }, {2b n1}, {b :}, {,}, {2b n },{P n}的前n项和有最大值.高三数学(理科)专题训练三<概率〉一、选择题1 .对满足A B的非空集合A、B有下列四个命题:其中正确命题的个数为()①若任取x A,则x B是必然事件②若x A,则x B是不可能事件③若任取x B,则x A是随机事件④若x B,则x A是必然事件A. 4B. 3C. 2D. 12.从1, 2,…,9中任取两个数,其中在下列事件中,是对立事件的是()①恰有一个是偶数和恰有一个是奇数②至少有一个是奇数和两个都是奇数③至少有一个是奇数和两个都是偶数④至少有一个奇数和至少有一个偶数A.①B.②④C.③D.①③3.如图所示,设D是图中边长为4 的正方形区域,E是D内函数y x2图象下方的点构成的区域,向D中随机投一点,则该点落入E中的概率为()A. 1B. 1C. -D. 12 3 4 54.投掷一枚均匀硬币和一枚均匀骰子各一次,记硬币正面向上”为事件A,骰子向上的点数是3”为内任取A. 1B. 1C. -D. 2 3 36.已知随机变量服从正态分布N(0, 2),若P( 2) 0.023, WJP( 2 2)的值为()7.把半径为2的圆分成相等的四弧,再将四弧围成星形放在半径为2的圆内,现在往该圆内任投8.某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布~N(80,102),则下列命题中不正确的是()事件B,则事件A、件发生的概率是()B中至少有一A. —B. -C.12 2172D-5.如图所示,圆C内切于扇形AOB, AOB 一,若在扇形AOB3点,则该点在圆C内的概率为()点,此点落在星形内2 2 *2 1 2 ,()4 2 c 4 1A . — 1B . — C.——A.该市这次考试的数学平均成绩为80分B.分数在120分以上的人数与分数在60分以下的人数相同C.分数在110分以上的人数与分数在50分以下的人数相同D.该市这次考试的数学成绩标准差为10二、填空题9.盒子里共有大小相同的三只白球、一只黑球,若从中随机摸出两只球,则它们颜色不同的概率是. 10.在集合{x|x —,n 1,2,3, ,10}中任取6 1个元素,所取元素恰好满足方1一程cosx -的概率是.211.在区间[3,3]上随机取一个数x,使得|x 1 | |x 2| 1成立的概率为.12.在一次教师联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目,若选到男教师的概率为旦,则参20 加联欢会的教师共有 _______ 人.13.已知三、解答题14.袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,已知得到红球的概率是1,得到黑球或黄球的概率是—,3 12得到黄球或绿球的概率也是-,12试求得到黑球、黄球、绿球的概率分别是多少?15.某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别是2和3.现安排甲组研发新产品A,3 5乙组研发新产品B.设甲、乙两组的研发相互独立.(1)求至少有一种新产品研发成功的概率;(2)若新产品A研发成功,预计企业可获利润120万元;若新产品B研发成功,预计企业可获得利润100万元.求该企业可获利润的分布列和数学期望.16.一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示:将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立. (1)求在未来连续3天里,有连续2 大的日销售量都不低于100个且另一大的日销售量低于50个的概率;(2)用X表示在未来3天里日销售量2{(x, y)|x y 6,x Qy 0}, A {(x, y)|x 4, y 0,x y 0}. 若向区域上随机投一点P,则P落入区域A的概率是.不低于100个的天数,求随机变量X 的分布列,期望E(X)及方差D(X).17设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0605050.4,各人是否需使用设备相互独立.(1)求同一工作日至少3人需使用设备的概率;(2) X表示同一工作日需使用设备的人数,求X的数学期望.18乒乓球台面被球网分成甲、乙两部分.如图,甲上有两个不相交的区域A,B,乙被划分为两个不相交的区域C,D .某次测试要求队员接到落点在甲上的来球后向乙回球.规定:回球一次,落点在C上记3分,落点在1分,其它情况记0分,落点D上记1在C上的概率为—,在D上的概率为 5 3.假设共有两次来球且落在A, B上 5 各一次,小明的两次回球互不影响. 求:(I )小明两次回球的落点中恰有一次的落点在乙上的概率;(II )两次回球结束后,小明得分之和的分布列与数学期望.高三数学(理科)专题训练四《立体几何初步》一、选择题1.已知ABC的三个顶点为A(3,3,2)、B(4, 3,7)、C(0,5,1), 则BC边上的中线长为()A. 5B. 4C. 3D. 22.如图所示,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A. 6B. 9C. 12D. 183. 一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可能是()A.球B.三棱锥C.正方体D.圆柱4.已知m、n表示两条不同直线,表示平面,下列说法中正确的是()A .若m// , n〃,则m// nB.若m// ,m n,,则nC.若m , m n,,贝U n〃D.若m , n ,,则m n5.已知一个几何体的三视图如图所示(单位:cm),则该几何体的体积为()A. 10 cm3B. 20 cm3c 10 3 20 3C. ---- c m D . ---- cm6.已知过球面上A,B,C三点的截面和球心的距离等于球半径的一半,且AB BC CA 2,则球的半径是()7.用a,b,c表示三条不同的直线,表示平面,给出下列命题:其中正确的命题是()①若a // b,b // c,则a // c;②若 a b,b c,贝U a c;③若a// ,b//,则a//b;④若a ,b ,则a//b.A.①②B.②③C.①④D.③④8. 一个圆锥和一个半球有公共底A.3B. 4C. - D. 45 5二、填空题9.已知三棱柱ABC顶点都在球。
2023年江西省高考理科数学真题及参考答案精选全文

2023年江西省高考理科数学真题及参考答案一、选择题1.设5212ii iz +++=,则=z ()A .i 21-B .i21+C .i -2D .i+22.设集合R U =,集合{}1<=x x M ,{}21<<-=x x N ,则{}=≥2x x ()A .()N M C U ⋃B .MC N U ⋃C .()N M C U ⋂D .NC M U ⋃3.如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则该零件的表面积为()A .24B .26C .28D .304.已知()1-=ax xe xe xf 是偶函数,则=a ()A .2-B .1-C .1D .25.设O 为平面坐标系的坐标原点,在区域(){}41,22≤+≤y x y x 内随机取一点,记该点为A ,则直线OA 的倾斜角不大于4π的概率为()A .81B .61C .41D .216.已知函数()()ϕω+=x x f sin 在区间⎪⎭⎫⎝⎛326ππ,单调递增,直线6π=x 和32π=x 为函数()x f y =的图象的两条对称轴,则=⎪⎭⎫⎝⎛-125πf ()A .23-B .21-C .21D .237.甲乙两位同学从6种课外读物中各自选读2种,则这两人选读的课外读物中恰有1种相同的选法共有()A .30种B .60种C .120种D .240种8.已知圆锥PO 的底面半径为3,O 为底面圆心,PB P A ,为圆锥的母线,︒=∠120AOB ,若P AB ∆的面积等于439,则该圆锥的体积为()A .πB .π6C .π3D .π639.已知ABC ∆为等腰直角三角形,AB 为斜边,ABD ∆为等边三角形,若二面角D AB C --为150°,则直线CD 与平面ABC 所成角的正切值为()A .51B .52C .53D .5210.已知等差数列{}n a 的公差为32π,集合{}*∈=N n a S n cos ,若{}b a S ,=,则=ab ()A .1-B .21-C .0D .2111.已知B A ,是双曲线1922=-y x 上两点,则可以作为B A ,中点的是()A .()1,1B .()2,1-C .()3,1D .()4,1-12.已知圆122=+y x O :,2=OP ,过点P 作直线1l 与圆O 相切于点A ,作直线2l 交圆O 于C B ,两点,BC 中点为D ,则PD P A ⋅的最大值为()A .221+B .2221+C .21+D .22+二、填空题13.已知点()51,A 在抛物线px y C 22=:上,则A 到C 的准线的距离为.14.若y x ,满足约束条件⎪⎩⎪⎨⎧≥+≤+-≤-739213y x y x y x ,则y x z -=2的最大值为.15.已知{}n a 为等比数列,63542a a a a a =,8109-=a a ,则=7a .16.已知()()xxa a x f ++=1,()1,0∈a ,若()x f 在()∞+,0为增函数,则实数a 的取值范围为.三、解答题(一)必做题17.某厂为比较甲乙两种工艺对橡胶产品伸缩率处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为i i y x ,()10,2,1 =i ,试验结果如下试验序号i 12345678910伸缩率i x 545533551522575544541568596548伸缩率iy 536527543530560533522550576536记i i i y x z -=()10,2,1 =i ,记1021,z z z 的样本平均数为z ,样本方差为2s ,(1)求z ,2s ;(2)判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高(如果1022s z ≥,则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高,否则不认为有显著提高).18.在ABC ∆中,︒=∠120BAC ,2=AB ,1=AC .(1)求ABC ∠sin ;(2)若D 为BC 上一点,且︒=∠90BAD ,求ADC ∆的面积.19.如图,在三棱锥ABC P -中,BC AB ⊥,2=AB ,22=BC ,6==PC PB ,BC AP BP ,,的中点分别为O E D ,,,DO AD 5=,点F 在AC 上,AO BF ⊥.(1)证明:EF ∥平面ADO ;(2)证明:平面ADO ⊥平面BEF ;(3)求二面角C AO D --的正弦值.20.已知椭圆C :()012222>>=+b a bx a y 的离心率为35,点()02,-A 在C 上.(1)求C 的方程;(2)过点()3,2-的直线交曲线C 于Q P ,两点,直线AQ AP ,交y 轴于N M ,两点,求证:线段MN 中点为定点.21.已知函数()()1ln 1+⎪⎭⎫⎝⎛+=x a x x f .(1)当1-=a 时,求曲线()x f 在()()1,1f 的切线方程;(2)是否存在实数b a ,使得曲线⎪⎭⎫⎝⎛=x f y 1关于直线b x =对称,若存在,求出b a ,的值;如果不存在,请说明理由;(3)若()x f 在()∞+,0存在极值,求a 的取值范围.(二)选做题【选修4-4】22.在直角坐标系xOy 中,以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线1C 的极坐标方程为⎪⎭⎫ ⎝⎛≤≤=24sin 2πθπθρ,曲线2C :⎩⎨⎧==ααsin 2cos 2y x (α为参数,παπ<<2).(1)写出1C 的直角坐标方程;(2)若直线m x y +=既与1C 没有公共点,也与2C 没有公共点,求m 的取值范围.【选修4-5】23.已知()22-+=x x x f .(1)求不等式()x x f -≤6的解集;(2)在直角坐标系xOy 中,求不等式组()⎩⎨⎧≤-+≤06y x yx f 所确定的平面区域的面积.参考答案一、选择题123456789101112BADDCDCBCBDA1.解:()i i ii i i i i i i z 21112211212252-=--=+=+-+=+++=,则i z 21+=2.解:由题意可得{}2<=⋃x x N M ,则()=⋃N M C U {}2≥x x .3.解:如图所示,在长方体1111D C B A ABCD -中,2==BC AB ,31=AA ,点K J I H ,,,为所在棱上靠近点1111,,,A D C B 的三等分点,N M L O ,,,为所在棱的中点,则三视图所对应的几何体为长方体1111D C B A ABCD -去掉长方体11LMHB ONIC -之后所得的几何体,该几何体的表面积和原来的长方体的表面积相比少2个边长为1的正方体.4.解:∵()1-=ax xe xe xf 是偶函数,则()()=--x f x f ()()[]01111=--=-------axx a x ax x axx e e e x e e x e xe ,又∵x 不恒为0,可得()01=--xa xee ,则()x a x 1-=,∴2=a .5.解:∵区域(){}41,22≤+≤y x y x 表示以()00,O 为圆心,外圆半径2=R ,内圆半径1=r 的圆环,则直线OA 的倾斜角不大于4π的部分如阴影所示,在第一象限对应的圆心角4π=∠MON ,结合对称性可得所求概率为41242=⨯=ππp .6.解:∵()()ϕω+=x x f sin 在区间⎪⎭⎫⎝⎛326ππ,单调递增,∴26322πππ=-=T ,且0>ω,则π=T ,22==Tπω.当6π=x 时,()x f 取得最小值,则Z k k ∈-=+⋅,2262ππϕπ,则Z k k ∈-=,652ππϕ,不妨取0=k 则()⎪⎭⎫ ⎝⎛-=652sin πx x f ,则2335sin 125=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-ππf .7.解:有1本相同的读物,共有16C 种情况,然后两人各自的另外一种读物相当于在剩余的5种读物里,选出两种进行排列,共有25A 种,根据分布乘法公式则共有⋅16C 12025=A 种.8.解:在AOB ∆中,︒=∠120AOB ,而3==OB OA ,取AC 中点C ,连接PC OC ,,有AB OC ⊥,AB PC ⊥,如图,︒=∠30ABO ,23=OC ,32==BC AB ,由P AB ∆的面积为439得439321=⨯⨯PC ,解得233=PC ,于是6232332222=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=-=OC PC PO ,∴圆锥的体积()πππ663313122=⨯⨯=⨯⨯=PO OA V .9.解:取AB 的中点E ,连接DE CE ,,∵ABC ∆为等腰直角三角形,AB 为斜边,则有AB CE ⊥,又ABD ∆为等边三角形,则AB DE ⊥,从而CED ∠为二面角DAB C --的平面角,即︒=∠150CED ,显然E DE CE =⋂,⊂DE CE ,平面CDE ,又⊂AB 平面ABC ,因此平面CDE ⊥平面ABC ,显然平面CDE ∩平面CE ABC =,直线⊂CD 平面CDE ,则直线CD 在平面ABC 内的射影为直线CE ,从而DCE ∠为直线CD 与平面ABC 所成的角,令2=AB ,则1=CE ,3=DE,在CDE ∆中,由余弦定理得:72331231cos 222=⎪⎪⎭⎫⎝⎛-⨯⨯⨯-+=∠⋅-+=CED DE CE DE CE CD ,由正弦定理得CEDCDDCE DE ∠=∠sin sin ,即7237150sin 3sin =︒=∠DCE ,显然DCE ∠是锐角,7257231sin 1cos 22=⎪⎪⎭⎫ ⎝⎛-=∠-=∠DCE DCE ,∴直线CD 与平面ABC 所成角的正切值为53.10.解:依题意,等差数列{}n a 中,()⎪⎭⎫⎝⎛-+=⋅-+=323232111πππa n n a a n ,显然函数==n a y cos ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+3232cos 1ππa n 的周期为3,而*∈N n ,即n a cos 最多有3个不同取值,又{}{}b a Nn a n ,cos =∈*,而在321cos ,cos ,cos a a a 中,321cos cos cos a a a ≠=或321cos cos cos a a a =≠,于是有⎪⎭⎫ ⎝⎛+=32cos cos πθθ,即有Z k k ∈=⎪⎭⎫ ⎝⎛++,232ππθθ,解得Z k k ∈-=,3ππθ213cos cos cos 3cos 343cos 3cos 2-=-=⎪⎭⎫ ⎝⎛--=⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=ππππππππππk k k k k ab 11.解:由对称性只需考虑()1,1,()2,1,()3,1,()4,1即可,注意到()3,1在渐近线上,()1,1,()2,1在渐近线一侧,()4,1在渐近线的另一侧.下证明()4,1点可以作为AB 的中点.设直线AB 的斜率为k ,显然k 存在.设()41+-=x k y l AB :,直线与双曲线联立()⎪⎩⎪⎨⎧=-+-=194122y x x k y ,整理得()()()094429222=------k x k k xk ,只需满足⎩⎨⎧>∆=+0221x x ,∴()29422=--k k k ,解得49=k ,此时满足0>∆.12.解:如图所示,1=OA ,2=OP ,则由题意可知:︒=∠45APO ,由勾股定理可得122=-=OA OP P A ,当点D A ,位于直线PO 异侧时,设40παα≤≤=∠,OPC ,则:⎪⎭⎫ ⎝⎛+⨯=⎪⎭⎫ ⎝⎛+⋅=⋅4cos cos 214cos πααπαPD P A αααααααα2sin 2122cos 1cos sin cos sin 22cos 22cos 22-+=-=⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--=42sin 2221πα∵40πα≤≤,则4424ππαπ≤-≤-,∴当442ππα-=-时,PD P A ⋅有最大值1.当点D A ,位于直线PO 同侧时,设40παα≤≤=∠,OPC ,则:⎪⎭⎫ ⎝⎛-⨯=⎪⎭⎫ ⎝⎛-⋅=⋅4cos cos 214cos πααπαPD P A αααααααα2sin 2122cos 1cos sin cos sin 22cos 22cos 22++=+=⎪⎪⎭⎫ ⎝⎛+=⎪⎭⎫⎝⎛++=42sin 2221πα∵40πα≤≤,则2424ππαπ≤+≤,∴当242ππα=+时,PD P A ⋅有最大值为221+.二、填空题13.49;14.8;15.2-;16.⎪⎪⎭⎫⎢⎣⎡-1,21513.解:由题意可得:()1252⨯=p ,则52=p ,∴抛物线的方程为x y 52=,准线方程为45-=x ,点A 到C 的准线的距离为49451=⎪⎭⎫ ⎝⎛--.14.作出可行域如下图所示,∵y x z -=2,∴z x y -=2,联立有⎩⎨⎧=+-=-9213y x y x ,解得⎩⎨⎧==25y x 设()2,5A ,显然平移直线x y 2=使其经过点A 此时截距z -最小,则z 最大,代入得8=z .15.解:设{}n a 的公比为()0≠q q ,则q a q a a a a a a 5263542⋅==,显然0≠n a ,则24q a =,即231q q a =,则11=q a ,∵8109-=a a ,则89181-=⋅q a q a ,则()()3351528-=-==q q,则23-=q ,则25517-==⋅=q q q a a .16.⎪⎪⎭⎫⎢⎣⎡-1,215解析:()()()a a a a x f xx+++='1ln 1ln ,由()x f 在()∞+,0为增函数可知()∞+∈,0x 时,()0≥'x f 恒成立,只需()0min ≥'x f ,而()()()01ln 1ln 22>+++=''a a a a x f xx,∴()()()01ln ln 0≥++='>'a a f x f ,又∵()1,0∈a ,∴⎪⎪⎭⎫⎢⎣⎡-∈1,215a .三、解答题(一)必做题17.解:(1)∵i i i y x z -=()10,2,1 =i ,∴9536545111=-=-=y x z ;62=z ;83=z ;84-=z ;155=z ;116=z ;197=z ;188=z ;209=z ;1210=z .()()[]1112201819111588691011011021=++++++-+++⨯=++=z z z z ∵()∑=-=1012101i i z z s ,将各对应值代入计算可得612=s (2)由(1)知:11=z ,612=s,∴5122106121061210222=⨯==s ,121112==z ,∴1022s z ≥∴甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高18.解:(1)根据题意,由余弦定理可得:72112212cos 222222=⎪⎭⎫ ⎝⎛-⨯⨯⨯-+=∠⋅-+=BAC AC AB AC AB BC ∴7=BC 由正弦定理ABC AC A BC ∠=∠sin sin ,即ABC∠=sin 1237,解得1421sin =∠ABC .(2)由三角形面积公式可得430sin 2190sin 21=︒⨯⨯⨯︒⨯⨯⨯=∆∆AD AC AD AB S S ACDABD ,则103120sin 12215151=⎪⎭⎫⎝⎛︒⨯⨯⨯⨯==∆∆ABC ACD S S .19.解:(1)连接OF OE ,,设tAC AF =,则()BC t BA t AF BA BF +-=+=1,BC BA AO 21+-=,AO BF ⊥,则()[]()()0414********=+-=+-=⎪⎭⎫⎝⎛+-⋅+-=⋅t t BC t BA t BC BA BC t BA t AO BF 解得21=t ,则F 为AC 的中点,由F O E D ,,,分别为AC BC P A PB ,,,的中点,于是AB OF AB DE AB DE 2121∥,,∥=,即OF DE OF DE =,∥,则四边形ODEF 为平行四边形,DO EF DO EF =,∥,又⊄EF 平面ADO ,⊂DO 平面ADO ,∴EF ∥平面ADO .(2)由(1)可知EF ∥OD ,则266==DO AO ,,得2305==DO AD ,因此215222==+AD AO OD ,则AO OD ⊥,有AO EF ⊥,又BF AO ⊥,F EF BF =⋂,⊂EF BF ,平面BEF ,则有AO ⊥平面BEF ,又⊂AO 平面ADO ,∴平面ADO ⊥平面BEF .(3)过点O 作BF OH ∥交AC 于点H ,设G BE AD =⋂,由BF AO ⊥得AO HO ⊥,且AH FH 31=,又由(2)知,AO OD ⊥,则DOH ∠为二面角C AO D --平面角,∵E D ,分别为P A PB ,的中点,因此G 为P AB ∆的重心,即有,31,31BE GE AD DG ==又AH FH 31=,即有GF DH 23=,622642622215234cos 2⨯⨯-+=⨯⨯-+=∠P A ABD ,解得14=P A ,同理得26=BE ,于是3222==+BF EF BE ,即有EF BE ⊥,则35262631222=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⨯=GF ,从而315=GF ,21531523=⨯=DH ,在DOH ∆中,215,262321====DH OD BF OH ,于是22221sin ,22232624154346cos 2=⎪⎪⎭⎫ ⎝⎛--=∠-=⨯⨯-+=∠DOH DOH .∴二面角C AO D --的正弦值为22.20.解:(1)由题意可得⎪⎪⎪⎩⎪⎪⎪⎨⎧==+==352222a c e c b a b ,解得⎪⎩⎪⎨⎧===523c b a ,∴椭圆的方程为14922=+x y。
2024年新高考新题型数学选填压轴好题汇编08(解析版)

2024年新高考新题型数学选填压轴好题汇编08一、单选题1(2024·广东湛江·二模)已知函数f x =2x -1 -a ,g x =x 2-4x +2-a ,则()A.当g x 有2个零点时,f x 只有1个零点B.当g x 有3个零点时,f x 有2个零点C.当f x 有2个零点时,g x 有2个零点D.当f x 有2个零点时,g x 有4个零点【答案】D【解析】两个函数的零点个数转化为图象与y =a 的图象的公共点的个数,作出y =2x -1 ,y =x 2-4x +2的大致图象,如图所示.由图可知,当g x 有2个零点时,f x 无零点或只有1个零点;当g x 有3个零点时,f x 只有1个零点;当f x 有2个零点时,g x 有4个零点.故选:D2(2024·甘肃定西·一模)在四棱锥P -ABCD 中,底面ABCD 为矩形,PA ⊥底面ABCD ,∠ABD =60°,PB ,PC 与底面ABCD 所成的角分别为α,β,且α+β=45°,则PAAB =()A.17-22B.15-32C.15-22D.17-32【答案】D【解析】如图,设AB =a ,PA =b ,因为在矩形ABCD 中,∠ABD =60°,所以AC =BD =2a ,因为PA ⊥底面ABCD ,所以∠PBA ,∠PCA 分别是PB ,PC 与底面ABCD 所成的角,即α=∠PBA ,β=∠PCA ,所以tan α=tan ∠PBA =b a ,tan β=tan ∠PCA =b2a.因为α+β=45°,所以tan (α+β)=tan α+tan β1-tan αtan β=ba+b2a 1-b a ⋅b 2a =1,解得b a =17-32(负根舍去),所以PAAB =17-32.故选:D .3(2024·高三·江西·开学考试)如图,已知圆O 的半径为2,弦长AB =2,C 为圆O 上一动点,则AC ⋅BC的取值范围为()A.0,4B.5-43,5+43C.6-43,6+43D.7-43,7+43【答案】C【解析】取AB 的中点D ,连接CD 、OD ,则AC ⋅BC =AD +DC ⋅BD +DC =AD ⋅BD +AD +BD ⋅DC +DC 2=DC 2-1,又OD =22-12=3,所以CD min =2-3,CD max =2+3,即2-3≤CD ≤2+3,所以AC ⋅BC min =6-43,AC ⋅BC max =6+43.故AC ⋅BC的取值范围为6-43,6+43 .故选:C4(2024·高三·江苏·期末)已知直线l 与椭圆x 29+y 23=1在第二象限交于A ,B 两点,l 与x 轴,y 轴分别交于M ,N 两点(M ,N 在椭圆外),若AM =BN ,则l 的倾斜角是()A.π6B.π3C.π4D.5π12【答案】A【解析】设l :y =kx +b (k >0,b >0),设A x 1,y 1 ,B x 2,y 2 ,联立y =kx +bx 29+y 23=1,得3k 2+1 x 2+6kbx +3b 2-9=0,由题意知Δ=36k 2b 2-43k 2+1 3b 2-9 =129k 2+3-b 2 >0,所以x 1+x 2=-6kb 3k 2+1,x 1x 2=3b 2-93k 2+1,设AB 的中点为E ,连接OE ,因为AM =BN ,所以AM +AE =BE +BN ,得EM =EN ,又因为N -bk,0 ,M 0,b ,所以E 也是MN 的中点,所以E 的横坐标为x E =x 1+x 22=-b k 2,从而得-6kb 3k 2+1=-b k ,因为A ,B 交在第二象限k >0,解得k =33,设直线l 倾斜角为θ,得tan θ=33,得θ=π6,故A 正确.故选:A .5(2024·湖南娄底·一模)已知圆内接四边形ABCD 中,AD =2,∠ADB =π4,BD 是圆的直径,AC ⋅BD=2,则∠ADC =()A.5π12B.π2C.7π12D.2π3【答案】C【解析】因为AC ⋅BD =2,所以AD +DC ⋅BD =2,易知BD =4,结合图形,AD ·BD =2×4×22=4,∠BCD =90°,则4-DC 2=2,故DC = 2.又BD 是圆的直径,AD =2,∠ADB =π4,所以BD =22,所以在直角三角形BCD 中可得∠BDC =π3,故∠ADC =7π12.故选:C .6(2024·湖南娄底·一模)若直线ex -4y +e ln4=0是指数函数y =a x (a >0且a ≠1)图象的一条切线,则底数a =()A.2或12B.eC.eD.e 或e【答案】D【解析】设切点坐标为x 0,f x 0 ,对函数y =a x ,求导得y =a x ln a ,切线方程ex -4y +e ln4=0化成斜截式为y =e 4x +e ln44,由题设知e4=a x 0ln a >0a x 0=ex 0+e ln44,显然ln a >0,即a >1,由a x 0=e 4ln a ,得e 4ln a =ex 0+e ln44,即1ln a=x 0+ln4,即1=x 0⋅ln a +ln a ln4=ln a x 0+ln4ln a =ln a x⋅4ln a ,即e =a x 0⋅4ln a =e4ln a ⋅4ln a ,化简得4ln a =4ln a ,令ln a =t >0,即4t =4t ,利用指数函数与一次函数的性质,可知t =1或12,即ln a =1或12,解得a =e 或 e.故选:D .7(2024·河北沧州·一模)过点P 1,2 作圆O :x 2+y 2=10相互垂直的两条弦AB 与CD ,则四边形ACBD 的面积的最大值为()A.66B.215C.96D.15【答案】D【解析】如图所示:OP =5,记OM =m ,ON =n ,则m 2+n 2=5,AC =210-m 2,BD =210-n 2,S ACBD =12AC ⋅BD =210-m 2⋅10-n 2≤2×10-m 2+10-n 22=15,当且仅当10-m 2=10-n 2,即m =n =102时,取等号.所以四边形ACBD 的面积的最大值为15.故选:D8(2024·湖南·一模)若不等式e x -1-mx -2n -3≥0对∀x ∈R 恒成立,其中m ≠0,则nm的取值范围为()A.-∞,-ln3e 2B.ln3e 2,+∞ C.-e ,-ln3e 2D.ln3e 2,e 【答案】A【解析】令e x -1-mx -2n -3=0,即e x -1=mx +2n +3,当m <0时,由函数y =e x -1与y =mx +2n +3的图象可知,两函数图象有一个交点,记为x 0,y 0 ,则当x <x 0时,e x -1<mx +2n +3,即e x -1-mx -2n -3<0,不满足题意;当m >0时,令f x =e x -1-mx -2n -3,则f x =e x -1-m ,令f x =0,则x =ln m +1,因为f x =e x -1-m 单调递增,所以当x <ln m +1时,f x <0,f x 单调递减,当x >ln m +1时,f x >0,f x 单调递增,所以x =ln m +1时,f x 有最小值f ln m +1 =-m ln m -2n -3,又e x -1-mx -2n -3≥0对∀x ∈R 恒成立,所以-m ln m -2n -3≥0,即2n ≤-m ln m -3,所以2n m ≤-ln m -3m,当且仅当2n =-m ln m -3时等号成立.令g m =-ln m -3m ,则g m =-1m +3m 2=3-mm 2,当0<m <3时,g m >0,g m 单调递增,当m >3时,g m <0,g m 单调递减,所以当m =3时,g max m =-ln3-1=-ln3e ,所以2n m ≤-ln3e ,即n m ≤-ln3e 2,当且仅当m =3,n ≤-3ln3e 2时等号成立,所以n m 的取值范围为-∞,-ln3e 2 .故选:A9(2024·湖南·模拟预测)如图所示,面积为π的扇形OMN 中,M ,N 分别在x ,y 轴上,点P 在弧MN 上(点P 与点M ,N 不重合),分别在点P ,N 作扇形OMN 所在圆的切线l 1,l 2,且l 1与l 2交于点Q ,其中l 1与x 轴交于点R ,则NQ +QR 的最小值为()A.4B.23C.6D.2【答案】B【解析】解析:因为扇形OMN 的面积为π,即14πOP 2=π,所以OP =2,设∠POM =θ,则在Rt △OPR 中,PR =2tan θ,连接OQ ,根据切线的性质知QN =QP ,∠NOQ =12∠NOP =π4-θ2,则在Rt △NOQ 中,NQ =2tan π4-θ2,所以NQ +QR =PR +2NQ =2tan θ+4tan π4-θ2 ,θ∈0,π2,令α=π4-θ2,则θ=π2-2α,且α∈0,π4,所以原式=2tan π2-2α +4tan α=2tan2α+4tan α=1-tan 2αtan α+4tan α=3tan α+1tan α≥21tan α⋅3tan α=23,当且仅当3tan α=1tan α,即tan α=33时,等号成立,又α∈0,π4 ,所以α=π6=θ=∠POM 时,NQ +QR 取得最小值,为23,故选:B10(2024·陕西商洛·模拟预测)设a =sin0.2,b =0.16,c =12ln 32,则()A.a >c >bB.b >a >cC.c >b >aD.c >a >b【答案】D【解析】设f x =sin x -x -x 2 ,x ∈0,0.2 ,f x =cos x -1+2x ,设g x =f x ,g x =-sin x +2>0,所以g x ≥g 0 =0,所以函数f x 在0,0.2 上单调递增,所以f 0.2 =sin0.2-0.2-0.22 =sin0.2-0.16>f 0 =0,即a >b .根据已知得c =12ln 32=12ln 1.20.8=12ln 1+0.21-0.2,可设h x =12ln 1+x -ln 1-x -sin x ,x ∈ 0,0.2 ,则h x =1211+x +11-x -cos x =11-x 2-cos x >0,所以函数h x 在0,0.2 上单调递增,所以h 0.2 >h 0 =0,即c >a .综上,c >a >b .故选:D .11(2024·河南信阳·模拟预测)已知数列a n 的前n 项和为S n ,S 1=1,S 2=3,且32a n +1是2a n ,a n +2的等差中项,则使得ni =1i a i>509128成立的最小的n 的值为()A.8B.9C.10D.11【答案】D 【解析】∵32a n +1是2a n ,a n +2的等差中项,∴a n +2=3a n +1-2a n ,故a n +2-a n +1=2a n +1-a n ,而a 2-a 1=S 2-2S 1=1≠0,∴a n +2-an +1a n +1-a n=2,故数列a n +1-a n 是首项为1,公比为2的等比数列,则a n +1-a n =2n -1,∴a n =a n -a n -1 +a n -1-a n -2 +⋯+a 2-a 1 +a 1=2n -2+2n -1+⋯+20+1=1-2n -11-2+1=2n -1,记T n =ni =1i a i,则T n =120+221+⋯+n2n -1,2T n =12-1+220+⋯+n2n -2,两式相减可得,T n =12-1+120+121+⋯+12n -2-n 2n -1=21-12 n1-12-n 2n -1=4-2+n 2n -1,即ni =1i a i=4-2+n 2n -1,令4-2+n 2n -1>509128,即2+n 2n -1<3128,设f x =2+x 2x -1x >0 ,则fx =2x -1-2+x ⋅2x -1⋅ln22x -1 2=1-2+x ⋅ln22x -1,∵x >0,∴f x <0,∴f x 在0,+∞ 单调递减,∴2+n 2n -1 是递减数列,∵当n =10时,2+n 2n -1=2+10210-1=3128,∴当n >10时,ni =1i a i >509128,∴使得ni =1i a i>509128成立的最小的n 的值为11.故选:D .12(2024·全国·模拟预测)若关于x 的不等式a (ln x +ln a )≤2e 2x 在(0,+∞)上恒成立,则实数a 的取值范围为()A.(0,e ]B.0,e 2C.(0,e ]D.(0,2e ]【答案】D【解析】依题意得,ax ln ax ≤2xe 2x ,故eln axln ax ≤2xe 2x ,令f x =xe x ,x ∈R ,则f x =x +1 e x ,令f x =0可得x =-1,所以x ∈-∞,-1 时,f x <0,则f x 在-∞,-1 上单调递减,x ∈-1,+∞ 时,f x >0,则f x 在-1,+∞ 上单调递增;且当x <0时,f x <0,当x >0时,f x >0;则由f ln ax ≤f 2x x >0 ,得ln ax ≤2x ,则a ≤e 2xx 令g x =e 2xx ,x ∈0,+∞ ,则g x =2x -1 e 2xx2,故当x ∈0,12 时,g x <0,g x 单调递减,当x ∈12,+∞ 时,g x >0,g x 单调递增,故g x min =g 12=2e ,则a ≤2e ,则实数a 的取值范围为a ∈0,2e .故选:D .13(2024·湖南岳阳·二模)设a =log 23,b =log 35,c =log 58,则()A.a >b >cB.b >a >cC.b >c >aD.c >a >b【答案】A【解析】因为32>23,所以log 232>log 223,即2log 23>3,所以log 23>32,即a >32;因为52<33,所以log 352<log 333,即2log 35<3,所以log 35<32,即b <32;因为82<53,所以log 582<log 553,即2log 58<3,所以log 58<32,即c <32;又因为b -c =log 35-log 58=1log 53-log 58=1-log 53⋅log 58log 53,且2log 53⋅log 58<log 53+log 58=log 524<log 525=2,所以log 53⋅log 58<1,所以b -c >0,所以b >c ;综上所述,a >b >c .故选:A .14(2024·湖南岳阳·二模)已知点A x 1,y 1 ,B x 2,y 2 是圆x 2+y 2=16上的两点,若∠AOB =π2,则x 1+y 1-2 +x 2+y 2-2 的最大值为()A.16B.12C.8D.4【答案】B【解析】因为A (x 1,y 1)、B (x 2,y 2)在圆x 2+y 2=16上,∠AOB =π2,因为|OA |=|OB |=4,则△AOB 是等腰直角三角形,|x 1+y 1-2|+|x 2+y 2-2|表示A 、B 到直线x +y -2=0的距离之和的2倍,原点O 到直线x +y -2=0的距离为d =22=2,如图所示:AC ⊥CD ,BD ⊥CD ,E 是AB 的中点,作EF ⊥CD 于F ,且OE ⊥AB ,|AC |+|BD |=2|EF |,OE =12AB =22,EF ≤OE +d =32,当且仅当O ,E ,F 三点共线,且E ,F 在O 的两侧时等号成立,又EF =12BD +AC ,故BD +AC 的最大值为62|x 1+y 1-2|+|x 2+y 2-2|的最大值为22×32=12.故选:B .15(2024·湖南·二模)2024年春节期间,某单位需要安排甲、乙、丙等五人值班,每天安排1人值班,其中正月初一、二值班的人员只安排一天,正月初三到初八值班人员安排两天,其中甲因有其他事务,若安排两天则两天不能连排,其他人员可以任意安排,则不同排法一共有()A.792种 B.1440种 C.1728种 D.1800种【答案】B【解析】当甲安排在初一或初二时,再安排一人在初二或初一,则有C 12C 14种排法,再利用平均分组分配法将初三到初八分配给剩下的3人,有C 26C 24C 22种排法,所以一共有C 12C 14C 26C 24C 22=720种排法;当甲不安排在初一或初二时,安排两人在初一或初二,有A 24种排法,不考虑甲两天不能连排的情况,有C 26C 24C 22种排法,其中甲两天连排的排法有5C 24C 22种,故初三到初八的值班安排有C 26C 24C 22-5C 24C 22种排法,所以一共有A 24C 26C 24C 22-5C 24C 22 =720种排法;综上可知共有720+720=1440种不同排法.故选:B .16(2024·湖南·二模)已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别是F 1,F 2,O 为坐标原点,以F 1F 2为直径的圆与双曲线C 交于点P ,且OP 在OF 1 上的投影向量为35OF 1,则双曲线C 的离心率为()A.2 B.3C.4D.5【答案】D【解析】不妨设点P 在第二象限,如图,因为OP 在OF 1 上的投影向量为35OF 1 ,则P -35c ,y 0 ,又PO 2=r 2=c 2,所以y 20=c 2--35c 2=1625c 2,又P 在双曲线上,∴9c 225a 2-16c 225b2=1,则25a 2b 2+16a 2c 2-9b 2c 2=0,即25a 2c 2-a 2 +16a 2c 2-9c 2-a 2 c 2=0,整理得9c 2-5a 2 c 2-5a 2 =0,所以9e 2-5 e 2-5 =0,解得e 2=5或e 2=59(舍去),∴e = 5.故选:D .17(2024·湖南·二模)在△ABC 中,角A ,B ,C 所对边分别为a ,b ,c ,且a 2-b 2+c 2+2ac =0,若cos A -C =7210,α∈π4,π2 ,cos α+A cos α+C cos 2α=25,则tan α的值为()A.1 B.2C.4D.2或4【答案】C【解析】由余弦定理得cos B =a 2+c 2-b 22ac =-22⇒B =3π4,A +C =π4,即cos A -C =7210cos A +C =22⇒cos A cos C =325sin A sin C =210,cos α+A cos α+C cos 2α=cos 2αcos A cos C +sin 2αsin A sin Ccos 2α--sin αcos αsin A cos C +sin C cos A cos 2α=325cos 2α+210sin 2α-22sin αcos αcos 2α=325+210tan 2α-22tan α=25,所以tan 2α-5tan α+4=0⇒tan α=1或tan α=4,又α∈π4,π2,所以tan α=4.故选:C18(2024·湖南常德·三模)设有甲、乙两箱数量相同的产品,甲箱中产品的合格率为90%,乙箱中产品的合格率为80%.从两箱产品中任取一件,经检验不合格,放回原箱后在该箱中再随机取一件产品,则该件产品合格的概率为()A.56B.67C.78D.1720【答案】A【解析】设事件B 1表示任选一件产品,来自于甲箱,事件B 2表示任选一件产品,来自于乙箱,事件A 从两箱产品中任取一件,恰好不合格,P A =P A |B 1 P B 1 +P A |B 2 P B 2 =0.1×0.5+0.2×0.5=0.15又P B 1|A =P AB 1 P A =P A |B 1 P B 1 P A=0.1×0.50.15=13P B 2|A =P AB 2 P A =P A |B 2 P B 2 P A=0.2×0.50.15=23,经检验不合格,放回原箱后在该箱中再随机取一件产品,则该件产品合格的概率为13×910+23×810=56.故选:A .19(2024·湖南·模拟预测)有一枚质地均匀点数为1到4的特制骰子,投掷时得到每种点数的概率均等,现在进行三次独立投掷,记X 为得到最大点数与最小点数之差,则X 的数学期望E X =()A.2116B.32C.74D.158【答案】D【解析】X 的所有可能取值为0,1,2,3,记三次得到的数组成数组a ,b ,c ,满足X =0的数组有:1,1,1 ,2,2,2 ,3,3,3 ,4,4,4 ,共4个,所以P X =0 =443=116,满足X =1的数组有:1,1,2 ,1,2,1 ,2,1,1 ,2,2,3 ,2,3,2 ,3,2,2 ,3,3,4 ,3,4,3 ,4,3,3 ,2,2,1 ,2,1,2 ,1,2,2 ,3,3,2 ,3,2,3 ,2,3,3 ,4,4,3 ,4,3,4 ,3,4,4 ,共18个,所以P X =1 =1843=932,满足X =2的数组有:1,1,3 ,1,3,1 ,3,1,1 ,2,2,4 ,2,4,2 ,4,2,2 ,3,3,1 ,3,1,3 ,1,3,3 ,4,4,2 ,4,2,4 ,2,4,4 ,1,2,3 ,1,3,2 ,2,1,3 ,2,3,1 ,3,1,2 ,3,2,1 ,4,2,3 ,4,3,2 ,2,4,3 ,2,3,4 ,3,4,2 ,3,2,4 ,共24个,所以P X =2 =2443=38,满足X =3的数组有:1,2,4 ,1,3,4 ,1,4,4 ,1,4,1 ,1,4,2 ,1,4,3 ,1,1,4 ,2,1,4 ,3,1,4 ,4,1,1 ,4,2,1 ,4,3,1 ,4,1,2 ,4,1,3 ,4,1,4 ,2,4,1 ,3,4,1 ,4,4,1 ,共18个,所以P X =3 =1843=932,所以X 的数学期望E X =0×116+1×932+2×38+3×932=158.故选:D .20(2024·湖南·模拟预测)已知函数f x 满足f x +8 =f x ,f x +f 8-x =0,当x ∈0,4 时,f x =ln 1+sin π4x ,则函数F x =f 3x -f x 在0,8 内的零点个数为()A.3B.4C.5D.6【答案】C【解析】根据题意,函数f x 的周期为8,图象关于点4,0 对称,又f 38-x +f 3x =f 8-3x +f 3x =-f 3x +f 3x =0,所以函数y =f 3x 的图象也关于点4,0 对称,由x ∈0,4 ,f x =ln 1+sin π4x ,∴fx =π4cos π4x 1+sin π4x ,∵0≤π4x <π,sin π4x ≥0,令f x >0,解得0≤x <2,令f x <0,解得2<x <4,所以函数f x 在0,2 上单调递增,在2,4 上单调递减,f 2 =ln2,f 0 =f 4 =0,在同一个坐标系中,作出函数y =f 3x 与y =f x 的图象,如图,由图可得,函数y =f 3x 与y =f x 在0,4 上有两个交点,因为函数y =f 3x 与y =f x 图象均关于点4,0 对称,所以函数y =f 3x 与y =f x 在4,8 上有两个交点,又f 12 =f 4 =0,所以函数F x =f 3x -f x 在0,8 内的零点个数为5.故选:C .21(2024·高三·江苏镇江·开学考试)某校在校庆期间举办羽毛球比赛,某班派出甲、乙两名单打主力,为了提高两位主力的能力,体育老师安排了为期一周的对抗训练,比赛规则如下:甲、乙两人每轮分别与体育老师打2局,当两人获胜局数不少于3局时,则认为这轮训练过关;否则不过关.若甲、乙两人每局获胜的概率分别为p 1,p 2,且满足p 1+p 2=43,每局之间相互独立.记甲、乙在n 轮训练中训练过关的轮数为X ,若E X =16,则从期望的角度来看,甲、乙两人训练的轮数至少为()A.27 B.24 C.32 D.28【答案】A【解析】设每一轮训练过关的概率为p ,则p =p 21p 22+p 21×C 12×p 2×1-p 2 +p 22×C 12×p 1×1-p 1=-3p 21p 22+2p 1p 2p 1+p 2 =-3p 21p 22+2p 1p 2×43=-3p 21p 22+83p 1p 2,0<p 1p 2≤p 1+p 22 2=49,当且仅当p 1=p 2=23时等号成立.函数y =-3x 2+83x 的开口向上,对称轴为x =49,所以0<-3p 21p 22+83p 1p 2≤-3⋅49 2+83⋅49=1627,依题意,X ∼B n ,p ,则E X =n -3p 21p 22+83p 1p 2=16,n =16-3p 21p 22+83p 1p 2≥161627=27,所以至少需要27轮.故选:A22(2024·河南·模拟预测)已知圆O 为△ABC 的外接圆,∠BAC =60°,BC =23,则OB ⋅OC=()A.2B.-2C.4D.-4【答案】B【解析】如图,圆O 的直径为2R =BC sin ∠BAC=2332=4,故OB =OC =R =2,∠BOC =2∠BAC =120°,故OB ⋅OC =OB OC cos120°=2×2×-12=-2.故选:B .二、多选题23(2024·广东湛江·二模)已知函数f x 的定义域为R ,f x 不恒为零,且f x +y +f x -y =2f x f y ,则()A.f 0 =1B.f x 为偶函数C.f x 在x =0处取得极小值D.若f a =0,则f (x )=f (x +4a )【答案】ABD【解析】对于选项A ,令x =y =0,得2f 0 =2f 0 2,解得f 0 =0或f 0 =1,当f 0 =0时,令y =0,则2f x =2f x f 0 ,则f x =0,这与f x 不恒为零矛盾,所以f 0 =1,故选项A 正确,对于选项B ,令x =0,则f 0+y +f 0-y =2f y f 0 ,即f y =f -y ,即f x 为偶函数,所以选项B 正确,对于选项C ,取f x =cos x ,满足题意,此时x =0不是f x 的极小值点,所以选项C 错误,对于选项D ,令y =a ,得f x +a +f x -a =2f x f a ,若f a =0,则f x +a =-f x -a ,则f x =-f x +2a ,则f x +4a =-f x +2a =f x ,所以选项D 正确,故选:ABD .24(2024·甘肃定西·一模)下列命题为真命题的是()A.x 2-4x -8-x +4+x -1 的最小值是2B.x 2-4x -8-x +4+x -1 的最小值是5C.x 2-4x -8-x +4+x 2-2x -4-x +2的最小值是2D.x 2-4x -8-x +4+x 2-2x -4-x +2的最小值是3【答案】BC【解析】设A (0,2),B (-1,1),F (-1,0),P (x ,-4x ),易知点P 的轨迹是抛物线y 2=-4x 的上半部分,抛物线y 2=-4x 的准线为直线x =1,P 到准线的距离d =|x -1|,F 为抛物线y 2=-4x 的焦点,对于AB ,x 2-4x -8-x +4+|x -1|=x 2+(-4x -2)2+d =|PA |+d =|PA |+|PF |≥|AF |=5,所以x 2-4x -8-x +4+|x -1|的最小值为5,故A 错误,B 正确;对于CD ,x 2-4x -8-x +4+x 2-2x -4-x +2=x 2+(-4x -2)2+(x +1)2+(-4x -1)2=|PA |+|PB |≥|AB |=2,所以x 2-4x -8-x +4+x 2-2x -4-x +2的最小值是2,故C 正确,D 错误.故选:BC .25(2024·高二·福建福州·期末)任取一个正整数,若是奇数,就将该数乘3再加上1;若是偶数,就将该数除以2.反复进行上述两种运算,经过有限次步骤后,必进入循环圈1→4→2→1.这就是数学史上著名的“冰雹猜想”(又称“角谷猜想”).比如取正整数m =8,根据上述运算法则得出8→4→2→1→4→2→1.猜想的递推关系如下:已知数列a n 满足a 1=5,a n +1=a n2,a n 为偶数3a n+1,a n为奇数 ,设数列a n的前n 项和为S n ,则下列结论正确的是()A.a3=8B.a 5=2C.S 10=49D.S 300=722【答案】ABD【解析】因为数列a n 满足a 1=5,a n +1=a n2,a n 为偶数3a n+1,a n为奇数 ,所以a 2=3×5+1=16,a 3=162=8,a 4=82=4,a 5=42=2,a 6=22=1,a 7=3×1+1=4,a 8=42=2,a 9=22=1,a 10=3×1+1=4,所以S 10=5+16+8+4+2+1+4+2+1+4=47,所以AB 正确,C 错误,因为数列a n 中从第4项起以4,2,1循环,而(300-3)÷3=99,所以S 300=(5+16+8)+99×(4+2+1)=722,所以D 正确,故选:ABD26(2024·高三·江西·期末)在棱长为2的正方体ABCD -A 1B 1C 1D 1中,点M ,N ,P 分别是线段C 1D 1,线段C 1C ,线段A 1B 上的动点,且MC 1=NC 1≠0.则下列说法正确的有()A.MN ⊥ABB.直线MN 与AP 所成的最大角为90°C.三棱锥M -DPC 的体积为定值D.当四棱锥P -D 1DBB 1体积最大时,该四棱锥的外接球表面积为12π【答案】BCD【解析】对于A ,由MC 1=NC 1≠0,可得D 1C ⎳MN ,因为AB ⎳D 1C 1,所以MN 与AB 不垂直,因此A 不正确;对于B ,因为D 1C ⎳A 1B ,所以MN ⎳A 1B ,因此直线MN 与AP 所成的角就是直线A 1B 与AP 所成的角,当P 为A 1B 中点时,此时AP ⊥A 1B ,直线A 1B 与AP 所成的角最大为90°,因此B 正确:对于C ,由于平面ABB 1A 1⎳平面DCC 1D 1,AP ⊂平面ABB 1A 1,所以V M -DPC =V P -DMC =V P -D 1DC =V A -D 1DC =13×12×2×2×2=43为定值,C 正确:对于D ,VP -BDD 1B 1=2V P -BDD 1=2V D 1-PBD ,由于P 为A 1B 上的点,故D 1到平面A 1BD 的距离为定值,所以D 1到平面PBD 的距离为定值,要使V D 1-PBD 最大,只需要S △PBD 最大,故当P 为A 1点时,四棱锥P -D 1DBB 1体积最大,该四棱锥的外接球即正方体ABCD -A 1B 1C 1D 1的外接球,直径为BD 1=23,所以r =3,故其表面积为12π,因此D 正确.故选:BCD .27(2024·湖南娄底·一模)对于事件A 与事件B ,若A ∪B 发生的概率是0.72,事件B 发生的概率是事件A 发生的概率的2倍,下列说法正确的是()A.若事件A 与事件B 互斥,则事件A 发生的概率为0.36B.P B ∣A =2P A ∣BC.事件A 发生的概率的范围为0.24,0.36D.若事件A 发生的概率是0.3,则事件A 与事件B 相互独立【答案】BCD【解析】对于A ,若事件A 与事件B 互斥,则P A ∪B =P A +P B =3P A =0.72,所以P A =0.24,A ,故A 错误;对于B ,P B |A =P AB P A ,P A |B =P AB P B =P AB 2P A=12P B |A ,故B 正确;对于C ,P A ∪B =P A +P B -P AB =3P A -P AB =0.72,P A =0.24+P AB3,若事件A 与事件B 互斥,则P AB =0,此时P A 取到最小值为0.24,若P A ⊆P B ,此时P AB =P A ,P A 取到最大值为0.36,故C 正确;对于D ,P A =0.3,则P B =0.6,由P A ∪B =P A +P B -P AB ,得P AB =0.3+0.6-0.72=0.18=P A ⋅P B ,则事件A 与事件B 相互独立,故D 正确.故选:BCD .28(2024·湖南娄底·一模)已知函数f x 的定义域和值域均为x ∣x ≠0,x ∈R ,对于任意非零实数x ,y ,x +y ≠0,函数f x 满足:f x +y f x +f y =f x f y ,且f x 在-∞,0 上单调递减,f 1 =1,则下列结论错误的是()A.f 12=2B.2023i =1f12i=22023-2C.f x 在定义域内单调递减 D.f x 为奇函数【答案】BC【解析】对于A ,令x =y =12,则2f 1 f 12=f 12 2,因f 12≠0,故得f 12=2f (1)=2,故A 正确;对于B ,由f x +y f x +f y =f x f y ,令y =x ,则f (2x )=[f (x )]22f (x )=12f (x ),则f12i =f 2×12i +1 =12f 12i +1 ,即f 12i +1 =2f 12i,故f 12i是以f 12 =2为首项,2为公比的等比数列,于是2023i =1f 12i=21-22023 1-2=22024-2,故B 错误;对于D ,由题意,函数f x 的定义域为-∞,0 ∪0,+∞ ,关于原点对称,令y =-2x ,则f -x =f x f -2xf x +f -2x①,把x ,y 都取成-x ,可得f -2x =f -x f -x 2f -x =f -x2②,将②式代入①式,可得f -x =f xf -x2f x +f -x2,化简可得f -x =-f x ,即f x 为奇函数,故D 正确;对于C ,∵f x 在-∞,0 上单调递减,函数为奇函数,可得f x 在0,+∞ 上单调递减,但是不能判断f x 在定义域上的单调性,例如f x =1x,故C 错误.故选:BC .29(2024·高三·湖南长沙·阶段练习)设a ,b 为两个正数,定义a ,b 的算术平均数为A a ,b =a +b2,几何平均数为G a ,b =ab ,则有:G a ,b ≤A a ,b ,这是我们熟知的基本不等式.上个世纪五十年代,美国数学家D .H .Lehmer 提出了“Lehmer 均值”,即L p a ,b =a p +bp a p -1+bp -1,其中p 为有理数.下列关系正确的是()A.L 0.5a ,b ≤A a ,b B.L 0a ,b ≥G a ,b C.L 2a ,b ≥L 1a ,b D.L n +1a ,b ≤L n a ,b【答案】AC【解析】对于A 选项,L 0.5a ,b =a +b 1a+1b=ab ≤a +b2=A a ,b ,当且仅当a =b 时,等号成立,故A 正确;对于B 选项,L 0a ,b =21a +1b =2ab a +b ≤2ab2ab =ab =G a ,b ,当且仅当a =b 时,等号成立,故B 错误;对于C 选项,L 2a ,b =a 2+b 2a +b =a 2+b 2+a 2+b 22a +b ≥a 2+b 2+2ab 2a +b =(a +b )22a +b =a +b 2=L 1a ,b ,当且仅当a =b 时,等号成立,故C 正确;对于D 选项,当n =1时,由C 可知,L 2a ,b ≥a +b2=L 1a ,b ,故D 错误.故选:AC .30(2024·广东广州·模拟预测)如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,已知M ,N ,P 分别是棱C 1D 1,AA 1,BC 的中点,Q 为平面PMN 上的动点,且直线QB 1与直线DB 1的夹角为30°,则()A.DB 1⊥平面PMNB.平面PMN 截正方体所得的截面面积为33C.点Q 的轨迹长度为πD.能放入由平面PMN 分割该正方体所成的两个空间几何体内部(厚度忽略不计)的球的半径的最大值为3-32【答案】ABD【解析】A 选项,以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x ,y ,z 轴,建立空间直角坐标系,P 1,2,0 ,M 0,1,2 ,N 2,0,1 ,D 0,0,0 ,B 12,2,2 ,故DB 1 =2,2,2 ,PM =-1,-1,2 ,PN=1,-2,1 .设平面PMN 的法向量为m=x ,y ,z ,则m ⋅PM=x ,y ,z ⋅-1,-1,2 =-x -y +2z =0m ⋅PN=x ,y ,z ⋅1,-2,1 =x -2y +z =0,令z =1得,x =y =1,故m=1,1,1 ,因为DB 1 =2m ,故DB 1⊥平面PMN ,A 正确;B 选项,取A 1D 1,AB ,CC 1的中点E ,F ,Q ,连接MQ ,ME ,EN ,NF ,FP ,PQ ,EP ,A 1B ,CD 1,因为M ,N ,P 分别是棱C 1D 1,AA 1,BC 的中点,所以NF ⎳A 1B ,MQ ⎳CD 1,又CD 1⎳EP ⎳A 1B ,所以NF ⎳MQ ⎳EP ,所以平面PMN 截正方体所得的截面为正六边形FPQMEN ,其中边长为2,故面积为6×34×2 2=33,B 正确;C 选项,Q 为平面PMN 上的动点,直线QB 1与直线DB 1的夹角为30°,又DB 1⊥平面PMN ,设垂足为S ,以S 为圆心,r =33B 1S 为半径作圆,即为点Q 的轨迹,其中B 1D =B 1D =4+4+4=23,由对称性可知,B 1S =12B 1D =3,故半径r =33×3=1,故点Q 的轨迹长度为2π,C 错误;D 选项,因为M ,N ,P 分别是棱C 1D 1,AA 1,BC 的中点,所以平面PMN 分割该正方体所成的两个空间几何体对称,不妨求能放入含有顶点D 的空间几何体的球的半径最大值,该球与平面PMN 切与点S ,与平面ADD 1A 1,平面ADCB ,平面DCC 1D 1相切,由对称性可知,球心在B 1D 上,设球心为R t ,t ,t ,则半径为t ,S 1,1,1 ,故RS =t ,即31-t =t ,解得t =3-32,故球的半径的最大值为3-32,D 正确.故选:ABD31(2024·湖南·模拟预测)如图,在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别为BC ,CC 1的中点,则下列结论正确的是()A.直线A1B与EF所成的角的大小为60°B.直线AD1⎳平面DEFC.平面DEF⊥平面BCC1B1D.四面体D-EFC外接球的体积与正方体ABCD-A1B1C1D1的体积之比为6π8【答案】ABD【解析】解析:对于A:连接BC1,C1A1,如图,由正方体的结构特征知,BC1=A1C1,=A1B即△A1BC1为正三角形.又因为E,F分别为BC,CC1的中点,则EF∥BC1,因此直线A1B与EF所成的角即为直线A1B与BC1所成的角,即∠A1BC1或其补角,又∠A1BC1=60°,所以直线A1B与EF所成的角的大小为60°,A正确;对于B:因为EF∥BC1,所以AD1∥EF,AD1⊄平面DEF,EF⊂平面DEF,故直线AD1⎳平面DEF,B正确;对于C:取EF的中点为M,连接DM,显然DE=DF,EF的中点为M,则DM⊥EF,假设平面DEF⊥平面BCC1B1,而平面DEF∩平面BCC1B1=EF,于是DM⊥平面BCC1B1,又DC⊥平面BCC1B1,则DM∥DC,与DM∩DC=D矛盾,C错误;对于D:不妨设正方体的棱长为2a,则正方体的体积为V1=8a3,又因为四面体C-DEF的三条侧棱CE,CF,CD两两垂直,则它的外接球即为以CE,CF,CD为棱的长方体的外接球,于是球的直径2R=a2+a2+(2a)2=6a,体积为V 2=43πR 3=43π×62a 3=6πa 3,于是V 2:V 1=6π8,D 正确,故选:ABD .32(2024·湖南·模拟预测)玻璃缸中装有2个黑球和4个白球,现从中先后无放回地取2个球.记“第一次取得黑球”为A 1,“第一次取得白球”为A 2,“第二次取得黑球”为B 1,“第二次取得白球”为B 2,则()A.P A 1B 1 =P A 2B 2B.P A 1B 2 =P A 2B 1C.P B 1 A 1 +P B 2 A 1 =1D.P B 2 A 1 +P B 1 A 2 >1【答案】BCD【解析】对A ,由题意,第一次取得黑球的概率P A 1 =C 12C 16=13,第一次取得白球的概率P A 2 =C 14C 16=23,第一次取得黑球、第二次取得黑球的概率P A 1B 1 =C 12C 11C 16C 15=115,第一次取得白球、第二次取得白球的概率P A 2B 2 =C 14C 13C 16C 15=25,则P A 1B 1 ≠P A 2B 2 ,所以A 错误;对B ,第一次取得黑球、第二次取得白球的概率P A 1B 2 =C 12C 14C 16C 15=415,第一次取得白球、第二次取得黑球的概率P A 2B 1 =C 14C 12C 16C 15=415,则P A 1B 2 =P A 2B 1 ,所以B 正确;对C ,由P B 1 A 1 =P A 1B 1 P A 1 =11513=15,P B 2 A 1 =P A 1B 2 P A 1=41513=45,得P B 1 A 1 +P B 2 A 1 =1,所以C 正确;对D ,由P B 1 A 2 =P A 2B 1 P A 2=41523=25,得P B 2 A 1 +P B 1 A 2 =65>1,所以D 正确.故选:BCD .33(2024·河南信阳·模拟预测)已知函数f x =sin ωx +φ ω>0 ,则()A.若ω=3,φ=π3,则将函数f x 的图象向右平移5π18个单位后关于y 轴对称B.若φ=π3,函数f x 在π6,π3 上有最小值,无最大值,且f π6 =f π3,则ω=5C.若直线x =π4为函数f x 图象的一条对称轴,5π3,0 为函数f x 图象的一个对称中心,且f x 在π4,5π6 上单调递减,则ω的最大值为1817D.若f x =12在x ∈π4,3π4 上至少有2个解,至多有3个解,则ω∈4,163 【答案】ACD【解析】对于A :若ω=3,φ=π3,则f x =sin 3x +π3 ,将函数f x 的图象向右平移5π18个单位后得g x=sin3x-5π6+π3=sin 3x-π2=-cos3x,其图象关于y轴对称,故A正确;对于B:依题意,当x=π6+π32=π4时,f x 有最小值,所以sinωπ4+π3=-1,所以ωπ4+π3=2kπ+3π2k∈Z,所以ω=8k+143k∈Z,因为f x 在区间π6,π3上有最小值,无最大值,所以π3-π4≤πω,即ω≤12,令k=0,得ω=143,故B错误;对于C:依题意有ωπ4+φ=2k1π+π2k1∈Z5ωπ3+φ=k2πk2∈ZT2=πω≥5π6-π4=7π12,则ω=617或1817,故C正确;对于D:因为f x =12,则ωx+φ=2kπ+π6k∈Z或ωx+φ=2kπ+5π6k∈Z,则x=-φ+2kπω+π6ωk∈Z或x=-φ+2kπω+5π6ωk∈Z,则需要上述相邻三个根的距离不超过π2,相邻四个根(距离较小的四个)的距离超过π2,即2πω≤π28π3ω>π2,解得ω∈4,163,故D正确;故选:ACD.34(2024·河南信阳·模拟预测)已知抛物线C:y2=2px p>0的焦点为F,点M,N在抛物线C上,则()A.若M,N,F三点共线,且MFNF=34,则直线MN的倾斜角的余弦值为±37B.若M,N,F三点共线,且直线MN的倾斜角为45°,则△OMN的面积为22p2C.若点A4,4在抛物线C上,且M,N异于点A,AM⊥AN,则点M,N到直线y=-4的距离之积为定值D.若点A2,2在抛物线C上,且M,N异于点A,k AM+k AN=0,其中k AM>1,则sin∠FMN-sin∠FNM≤255【答案】BCD【解析】对A,设抛物线C:y2=2px,设直线MN:x=ty+p2t≠0,设M x1,y1,N x2,y2,联立y2=2pxx=ty+p2 ,则y2-2pty-p2=0,y1+y2=2pt,y1y2=-p2,由于MFNF=34,可得y1y2=-34,代入上式得:14y2=2pt,-34y22=-p2,解得:t2=148,且直线MN的斜率为1t,设直线MN的倾斜角为α,则tan2α=48,且sin2α+cos2α=1,tanα=sinαcosα,则cos 2α=149,解得cos α=±17,故A 错误;对B ,设抛物线C :y 2=2px ,且直线MN 的倾斜角为45°,设直线MN :x =y +p2,设M x 1,y 1 ,N x 2,y 2 ,联立y 2=2pxx =y +p 2,则y 2-2py -p 2=0,y 1+y 2=2p ,y 1y 2=-p 2,S △OMN =12×p 2×|y 2-y 1|=p 4×(2p )2-4(-p 2)=22p 2,故B 正确;对C ,由于点A 4,4 在抛物线C 上,此时抛物线C :y 2=4x ,设M x 1,y 1 ,N x 2,y 2 ,设直线AM :x -4=t y -4 t ≠0 ,联立y 2=4x x -4=t y -4则y 2-4ty +16t -1 =0,解得y 1=4(舍去,此时M ,A 重合)或y 1=4t -4,则点M 到直线y =-4的距离为y 1+4 =4t ,同理可得,因为AM ⊥AN ,则N 到直线y =-4的距离为4⋅1-t =4t,故所求距离之积为4t ⋅4t=16,故C 正确;对D ,由于点A 2,2 在抛物线C 上,此时抛物线C :y 2=2x ,设直线AM :y -2=k x -2 ,与抛物线方程联立可得ky 2-2y +4-4k =0,则y M ⋅2=4-4k k ,则y M =2-2k k ,用-k 替换可得y N =-2+2kk ,则k MN =y M -y N x M -x N =y M -y N y 2M 2-y 2N 2=2y M +y N =-12,则M 21-k 2k 2,2-2k k ,N 21+k 2k2,-2+2kk,故直线MN :y -2-2k k =-12x -21-k 2k 2 ,即y =-12x +1k 2-1,则点F 到直线MN 的距离d =12-2-2k 2k25=5k 2-425k 2k >1 ,而sin ∠FMN -sin ∠FNM =d 1FM -1FN即sin ∠FMN -sin ∠FNM =d1x M +12-1x N +12=d x M -x N x M x N +12x M +x N +14,sin ∠FMN -sin ∠FNM =5k 2-425k 2⋅32k 325k 4-24k 2+16,得sin ∠FMN -sin ∠FNM =165⋅5k -4k 25k 2-24+16k 2=165⋅5k -4k5k -4k 2+16,令t =5k -4k>1,故sin ∠FMN -sin ∠FNM =165⋅t t 2+16=165⋅1t +16t,sin ∠FMN -sin ∠FNM ≤165⋅12t ⋅16t=165⋅18=255,当且仅当t =4时等号成立,故D 正确;故选:BCD .35(2024·湖南岳阳·二模)已知函数f x 的定义域为R ,对任意x ,y ∈R 都有2f x +y 2 fx -y2=f x +f y ,且f 1 =-1,则下列说法正确的是()A.f -1 =1B.f x +12为奇函数C.f x -f 2-x =0 D.f 1 +f 2 +f 3 +⋅⋅⋅+f 2025 =-1【答案】BCD【解析】令x =y =1,则2f 1 f 0 =f 1 +f 1 =2f 1 ,所以f 0 =1,令x =-1,y =1,则2f 0 f -1 =f -1 +f 1 =2f -1 ,∴f -1 =f 1 =-1,故A 错误;要证f x +12 为奇函数,只需证f x +12 +f 12-x =0,即f x +f 1-x =0,令x =1,y =0,则2f 12 f 12 =f 1 +f 0 =0,∴f 12 =0,令y =1-x ,则2f 12 f 2x -12=f x +f 1-x =0,所以成立,故B 正确;令y =-x ,则2f 0 f x =f x +f -x =2f x ,∴f x =f -x ,所以f x 为偶函数,由B 可知,f 1-x =-f x ,所以f 1-x =-f x =-f -x ,则有f 2-x =-f 1-x =f x ,故C 正确;由C 可知f 2-x =f x ,又f x 为偶函数,所以f 2-x =f -x ,则f x 周期为2,f 1 =-1,f 2 =f 0 =1,所以f 1 +f 2 +f 3 +⋅⋅⋅+f 2025 =1012×0-1=-1,故D 正确.故选:BCD36(2024·高三·山东菏泽·阶段练习)如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为2,点M 为BC 的中点,点P 为正方形A 1B 1C 1D 1内(包含边界)的动点,则()A.满足MP ⎳平面A 1BD 的点P 的轨迹为线段B.若MP =22,则动点P 的轨迹长度为π3C.直线AB 与直线MP 所成角的范围为π6,π2D.满足MP ⊥AM 的点P 的轨迹长度为52【答案】AD【解析】对于A ,如图所示,取棱BB 1,A 1B 1,A 1D 1,D 1D ,DC 的中点分别为E ,F ,G ,H ,I ,连接EF 、FG 、GH 、HI 、IM 、ME ,根据正方体的特征易知EM ⎳A 1D ⎳GH ,EF ⎳A 1B ⎳HI ,GF ⎳BD ⎳MI ,则E ,F ,G ,H ,I ,M 共面,且BD ⎳平面EFGHIM ,BA 1⎳平面EFGHIM ,又BD ,BA 1⊂平面BDA 1且相交于B ,故平面BDA 1⎳平面EFGHIM ,所以满足MP ⎳平面A 1BD 的点P 的轨迹为线段FG ,故A 正确;对于B ,设M 到上底面的投影为N ,易知MN =2,而MP =22,所以NP =2,即P 在以N 为圆心,半径为2的圆上,且P 在正方形A 1B 1C 1D 1内,如图所示,即JK上,易知∠JNK =π3,所以JK 的长度为2π3,故B 错误;对于C ,如图所示建立空间直角坐标系,取AD 的中点Q ,连接MQ ,作PL ⊥MQ ,设P x ,y ,2 x ,y ∈0,2 ,则L 1,y ,0 ,M 1,2,0 ,易知直线AB 与直线MP 所成角为∠PMQ ,显然当P 为B 1C 1的中点时,此时∠PMQ =π2,y =2,当y ≠2时,tan ∠PMQ =PL LM=x -1 2+42-y ,易知x -12+4≥2,2-y ∈0,2 ,若∠PMQ 最小,则需x =1,y =0,此时∠PMQ =π4,故C 错误;对于D ,取CS =14DC ,RC 1=14D 1C 1,可知RN ⎳SM ,RN =SM ,即R 、N 、M 、S 共面,在底面正方形中易知CS CM =12=BMAB,∠ABM =∠SCM ,则△SCM ∼△MBA ⇒∠AMS =90°,结合正方体的性质可知MN ⊥底面ABCD ,AM ⊆底面ABCD ,所以AM ⊥MN ,而MN ∩SM =M ,MN 、SM ⊆平面RNMS ,所以AM ⊥平面RNMS ,故P 在线段RN 上运动,易知RN =12+122=52,故D 正确.故选:AD37(2024·湖南·二模)已知f x =3sin ωx 2cos ωx 2+cos 2ωx 2-12,ω>0,下列结论正确的是()A.若f x 的最小正周期为π,则ω=2B.若f x 的图象向左平移π3个单位长度后得到的图象关于y 轴对称,则ωmin =1C.若f x 在0,2π 上恰有4个极值点,则ω的取值范围为53,136D.存在ω,使得f x 在-π6,π4上单调递减【答案】ABC【解析】由f x =3sinωx 2cos ωx 2+cos 2ωx 2-12=32sin ωx +12cos ωx =sin ωx +π6,对于A ,若f x 的最小正周期为π,则T =2πω⇒ω=2,故A 正确;对于B ,若f x 的图象向左平移π3个单位长度后得y =sin ωx +π3 +π6 =sin ωx +π3ω+π6 ,其图象关于纵轴对称,则有π3ω+π6=π2+k πk ∈Z ⇒ω=1+3k ,显然ωmin =1,故B 正确;对于C ,x ∈0,2π ⇒ωx +π6∈π6,2ωπ+π6,根据题意有7π2<2ωπ+π6≤9π2⇒ω∈53,136 ,故C 正确;对于D ,x ∈-π6,π4 ⇒ωx +π6∈-ωπ6+π6,ωπ4+π6,显然ωπ4+π6>π6,-ωπ6+π6<π6,即该区间为包含π6的连续区间,根据正弦函数的单调性可知:该区间不可能单调递减,故D 错误.故选:ABC38(2024·湖南·二模)已知函数f x ,g x 的定义域均为R ,g x +1 +f 1-x =1,f x +1 -g x +2 =1,且y =f x 的图像关于直线x =1对称,则以下说法正确的是()A.f x 和g x 均为奇函数B.∀x ∈R ,f x =f x +4C.∀x ∈R ,g x =g x +2D.g -32=0【答案】BCD【解析】对于B ,由f (x +1)-g (x +2)=1,得f (x )-g (x +1)=1,又g (x +1)+f (1-x )=1,∴f (x )+f (1-x )=2,∵y =f (x )的图象关于直线x =1对称,∴f (1-x )=f (1+x ),∴f (x )+f (1+x )=2,∴f (x +2)+f (1+x )=2,∴f (x )=f (x +2),则f x 是周期函数,且周期为T =2,所以f (x )=f (x +4),故B 正确;对于A ,∵y =f (x )的图象关于直线x =1对称,∴f (-x )=f (2+x ),∴f (x )=f (-x ),∴f (x )是偶函数,若f (x )为奇函数,则f (x )=0恒成立,不满足f (x )+f (1+x )=2,故A 错误;对于C ,由f (x +1)-g (x +2)=1,得g (x )+f (2-x )=1,∴g (x )+f (x )=1,∴g (2+x )+f (2+x )=1,因为f (x )=f (x +2),则g (x +2)=g (x ),所以g (x )是周期函数,且周期为T =2,则g x =g x +2 ,故C 正确;对于D ,由f (x )+f (1-x )=2,得f 12=1,又f (x )=f (x +2),∴f -32 =1,由g (x )+f (x )=1,得g -32 +f -32 =1,∴g -32=0,故D 正确.故选:BCD .39(2024·湖南常德·三模)若函数f (x )=2x sin x -10<x <π2的零点为x 1,函数g (x )=2xcos x -10<x <π2 的零点为x 2,则()A.x 1x 2>π2 B.x 1+x 2<3π4C.cos (x 1+x 2)<0D.cos x 1-sin x 2<0【答案】BCD【解析】令f x =0得sin x =12x,令g x =0得cos x =12x,在同一直角坐标系中作出y =sin x ,x ∈0,π2 ,y =cos x ,x ∈0,π2 ,y =12x,x ∈0,π2的函数图象,。
高三数学:2024年新高考新题型数学选填压轴好题汇编04(解析版)

2024年新高考新题型数学选填压轴好题汇编04一、单选题1(2024·广东·一模)已知集合A=-12,-13,12,13,2,3,若a,b,c∈A且互不相等,则使得指数函数y =a x,对数函数y=log b x,幂函数y=x c中至少有两个函数在(0,+∞)上单调递增的有序数对(a,b,c)的个数是()A.16B.24C.32D.48【答案】B【解析】若y=a x和y=log b x在(0,+∞)上单调递增,y=x c在(0,+∞)上单调递减,则有A22⋅C12=4个;若y=a x和y=x c在(0,+∞)上单调递增,y=log b x在(0,+∞)上单调递减,则有C12⋅C12⋅C12=8个;若y=log b x和y=x c在(0,+∞)上单调递增,y=a x在(0,+∞)上单调递减,则有C12⋅C12⋅C12=8个;若y=a x、y=log b x和y=x c在(0,+∞)上单调递增,则有A22⋅C12=4个;综上所述:共有4+8+8+4=24个.故选:B.2(2024·广东江门·一模)物理学家本·福特提出的定律:在b进制的大量随机数据中,以n开头的数出现的概率为P b n =log b n+1n.应用此定律可以检测某些经济数据、选举数据是否存在造假或错误.若80n=kP10(n)=log4811+log25k∈N*,则k的值为()A.7B.8C.9D.10【答案】C【解析】80n=k P10(n)=P10(k)+P10(k+1)+⋯+P10(80)=lg k+1k +lg k+2k+1+⋯+lg8180=lg81k,而log4811+log25=lg81lg41+lg5lg2=4lg32lg21+lg5lg2=2lg3=lg9,故k=9.故选:C.3(2024·广东·模拟预测)在正三棱锥A-BCD中,△BCD的边长为6,侧棱长为8,E是AB的中点,则异面直线CE与BD所成角的余弦值为()A.33468B.3434C.21717D.1734【答案】A【解析】依题意,记BC的中点为F,连接DF,记正△BCD的中心为O,连接AO,因为在正三棱锥A-BCD中,AO⊥底面BCD,在正△BCD中,DF⊥BC,在平面BCD中过F点作z轴⊥底面BCD,则AO⎳z轴,以F点为原点,建立空间直角坐标系,如图,因为在正三棱锥A-BCD中,△BCD的边长为6,侧棱长为8,所以DF=32CD=32×6=33,2DF=23,AO=AD2-OD2=64-12=213,故B -3,0,0 ,C 3,0,0 ,D 0,33,0 ,O 0,3,0 ,A 0,3,213 ,则E -32,32,13 ,CE =-92,32,13 ,BD =3,33,0 ,所以cos CE ,BD =CE ⋅BDCE BD =-92×3+32×33-92 2+32 2+13×9+27=-33468,则异面直线CE 与BD 所成角的余弦值为33468.故选:A .4(2024·天津滨海新·一模)已知抛物线C 1:y 2=2px p >0 的焦点为F ,准线与x 轴的交点为E ,线段EF 被双曲线C 2:x 2a 2-y 2b2=1(a >0,b >0)顶点三等分,且两曲线C 1,C 2的交点连线过曲线C 1的焦点F ,则双曲线C 2的离心率为()A.2B.322C.113D.222【答案】D【解析】求得抛物线的焦点和准线,可得EF 的长度,由题意可得p =6a ,求出两曲线交点坐标,代入双曲线方程可得a ,b 的关系,利用离心率公式可求得结果.抛物线y 2=2px 的焦点为F p 2,0 ,准线方程为x =-p2,E -p2,0 ,|EF |=p ,因为线段EF 被双曲线C 2:x 2a 2-y 2b2=1(a >0,b >0)顶点三等分,所以2a =p 3,即p =6a ,因为两曲线C 1,C 2的交点连线过曲线C 1的焦点F ,所以两个交点为p 2,p 、p2,-p ,将p 2,p 代入双曲线x 2a 2-y 2b 2=1得p 24a 2-p 2b2=1,所以36a 24a 2-36a 2b 2=1,所以9-36a 2b 2=1,所以b 2a2=92,所以双曲线C 2的离心率e =c a =c 2a 2=a 2+b 2a 2=1+b 2a2=1+92=222.故选:D5(2024·湖南·二模)已知函数f x =sin ωx +3cos ωx ,若沿x 轴方向平移f x 的图象,总能保证平移后的曲线与直线y =1在区间0,π 上至少有2个交点,至多有3个交点,则正实数ω的取值范围为()A.2,83B.2,103C.103,4 D.2,4【答案】A【解析】由f x =sin ωx +3cos ωx 可得:f x =2sin ωx +π3,若沿x 轴方向平移,考虑其任意性,不妨设得到的函数g x =2sin ωx +φ .令g x =1,即sin ωx +φ =12,x ∈[0,π],取z =ωx +φ,则z ∈[φ,ωπ+φ].依题意知,sin z =12在φ,ωπ+φ 上至少有2解,至多有3解,则须使区间[φ,ωπ+φ]的长度在2π到8π3之间,即2π≤ωπ<8π3,解得2≤ω<83.6(2024·湖南·二模)过点P -1,0 的动直线与圆C :(x -a )2+(y -2)2=4(a >0)交于A ,B 两点,在线段AB 上取一点Q ,使得1PA +1PB =2PQ ,已知线段PQ 的最小值为2,则a 的值为()A.1B.2C.3D.4【答案】A【解析】圆心C a ,2 ,半径为2,则圆C 与x 轴相切,设切点为M a ,0 ,则PM =a +1,则|PM |2=PA PB =(a +1)2,设AB 的中点为D ,连接CD ,则CD ⊥AB ,令圆心C 到直线AB 的距离为d ,则0≤d <2,|PA |+|PB |=|PD |-|AD |+|PD |+|AD |=2|PD |,由1PA +1PB =2PQ ,得PQ =2PA PB PA +PB =(a +1)2|PC |2-d 2=(a +1)2(a +1)2+4-d 2,因此(a +1)2(a +1)2+4-0≤PQ <(a +1)2(a +1)2+4-4,而PQ 的最小值为2,所以a +12a +1 2+4=2,则a =1.故选:A7(2024·高三·浙江宁波·阶段练习)如图1,水平放置的直三棱柱容器ABC -A 1B 1C 1中,AC ⊥AB ,AB =AC =2,现往内灌进一些水,水深为2.将容器底面的一边AB 固定于地面上,再将容器倾斜,当倾斜到某一位置时,水面形状恰好为三角形A 1B 1C ,如图2,则容器的高h 为()A.3B.4C.42D.6【答案】A【解析】在图1中水的体积V =12×2×2×2=4,在图2中水的体积V =VABC -A 1B 1C 1-V C -A 1B 1C 1=12×2×2×h -13×12×2×2×h =43h ,4h =4⇒h =3.8(2024·江西·高考真题)已知F 1、F 2是椭圆的两个焦点,满足MF 1 ⋅MF 2=0的点M 总在椭圆内部,则椭圆离心率的取值范围是A.(0,1) B.0,12C.0,22D.22,1 【答案】C【解析】设椭圆的半长轴、半短轴、半焦距分别为a ,b ,c .因为MF 1 ·MF 2=0所以点M 的轨迹为以原点为圆心,半径为c 的圆.与因为点M 在椭圆的内部,所以c <a ,c <b ,所以c 2<b 2=a 2-c 2,所以2c 2<a 2∴e 2=c 2a2<12,所以e ∈0,22,故选C .9(2024·高二·湖北鄂州·阶段练习)已知双曲线x 2a 2-y 2b2=1a >0,b >0 的焦距为2c ,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.设A ,B 到双曲线的同一条渐近线的距离分别为d 1和d 2,且d 1-d 2 ≤c ,则双曲线的离心率的取值范围为()A.1,233B.233,+∞ C.1,2D.2,+∞【答案】C【解析】由题意可知,直线AB 经过双曲线的右焦点,且垂直于x 轴,不妨设A c ,y 0 ,代入椭圆方程c 2a 2-y 02b2=1,又c 2=a 2+b 2,所以y 0=b 2a ,所以A c ,b 2a ,B c ,-b 2a,任取双曲线的一条渐近线为直线bx +ay =0,由点到直线的距离公式可得点A 到渐近线的距离d 1=bc +b 2a 2+b2=bc +b 2c ,点B 到渐近线的距离d 2=bc -b 2a 2+b 2=bc -b 2c ,所以d 1-d 2 =bc +b 2c -bc -b 2c =2b 2c=2b 2c,因为d 1-d 2 ≤c ,所以2b 2c≤c ,因c >0,所以2b 2≤c 2,即2c 2-a 2 ≤c 2,所以c 2≤2a 2,所以c 2a 2≤2,因为双曲线离心率c a >1,所以1<ca≤2,所以双曲线的离心率的取值范围为1,2 .故选:C .10(2024·高二·广东深圳·期末)已知抛物线C :y 2=2px p >0 的焦点为F ,斜率为k 的直线l 经过点F ,并且与抛物线C 交于A 、B 两点,与y 轴交于点M ,与抛物线的准线交于点N ,若AF =2MN,则k =()A.3B.2C.±2D.±3【答案】D【解析】当A 在第一象限时,设准线与x 轴的交点为P ,过A 作准线的垂线,垂足为A ,因为OM ∥PN ,且O 为PF 的中点,所以OM 为三角形PFN 的中位线,即FM =MN ,所以AF =2MN =FN ,又根据抛物线的定义AF =AA ,所以AN =2AF =2AA ,所以在直角三角形AA N 中,∠A AN =60°,所以∠AFx =60°,此时k =3,根据对称性,当A 在第四象限时,k =-3,故选:D .11(2024·湖北·一模)设直线l :x +y -1=0,一束光线从原点O 出发沿射线y =kx x ≥0 向直线l 射出,经l 反射后与x 轴交于点M ,再次经x 轴反射后与y 轴交于点N .若MN =136,则k 的值为()A.32B.23C.12D.2【答案】B【解析】如图,设点O 关于直线l 的对称点为A x 1,y 1 ,则x 12+y12-1=0y 1x 1×-1 =-1得x 1=1y 1=1 ,即A 1,1 ,由题意知y =kx x ≥0 与直线l 不平行,故k ≠-1,由y =kx x +y -1=0 ,得x =1k +1y =k k +1,即P 1k +1,k k +1 ,故直线AP 的斜率为k AP =kk +1-11k +1-1=1k ,直线AP 的直线方程为:y -1=1kx -1 ,令y =0得x =1-k ,故M 1-k ,0 ,令x =0得y =1-1k ,故由对称性可得N 0,1k-1 ,由MN =136得(1-k )2+1k -1 2=1336,即k +1k 2-2k +1k =1336,解得k +1k=136,得k =23或k =32,若k =32,则第二次反射后光线不会与y 轴相交,故不符合条件.故k =23,故选:B 12(2024·湖北·二模)能被3个半径为1的圆形纸片完全覆盖的最大的圆的半径是()A.263B.62C.233D.33+12【答案】C【解析】要求出被完全覆盖的最大的圆的半径,由圆的对称性知只需考虑三个圆的圆心构成等边三角形的情况,设三个半径为1的圆的圆心分别为O 1,O 2,O 3,设被覆盖的圆的圆心为O ,如图,设OO 1=OO 2=OO 3=x ,则O 1H =3x 2,OH =x 2,OA =OH +HA =x 2+1-32x 2=12(x +4-3x 2),又OC =OO 3+O 3C =x +1>OA ,因此圆O 的最大半径为OA ,令f (x )=12(x +4-3x 2),求导得f(x )=4-3x 2-3x 24-3x 2,由f (x )=0,得x =33,当0<x <33时,f (x )>0,当33<x <233时,f (x )<0,因此f (x )在0,33上单调递增,在33,233 上单调递减,f (x )max =f 33 =233,所以被完全覆盖的最大的圆的半径为233,此时O 1O 2=O 2O 3=O 3O 1=1,即圆O 1、圆O 2、圆O 3中的任一圆均经过另外两圆的圆心.故选:C13(2024·高三·浙江嘉兴·期末)已知正实数a ,b ,c 满足a 2-b =2ln ab>0,7b -2b =a +4 c ,则()A.0<c <b <1<aB.0<b <c <1<aC.0<c <b <a <1D.0<b <c <a <1【答案】A【解析】因a >0,b >0,由ln a b >0可得:ab >1,则a >b .由a 2-b =2lnab 化简得:a 2-2ln a =b -2ln b ,分别设函数f x =x 2-2ln x ,g x =x -2ln x .由f(x )=2x 2-1 x,(x >0),则当0<x <1时,f (x )<0,当x >1时,f (x )>0,则f x 在0,1 上递减,在1,+∞ 上递增,故f x min =f 1 =1.又g x =x -2x,(x >0),则当0<x <2时,g (x )<0,当x >2时,g (x )>0,则g x 在0,2 上递减;在2,+∞ 上递增,故g x min =g 2 =2-2ln2.由f x -g x =x 2-x =x x -1 ,则0<x <1时,f x <g x ;x =1时,f x =g x ;x >1时,f x >g x .函数f x 与g x 的图象如图.令f a =f b =k .由于a >b ,则0<b <1,1<a ,排除C ,D ;由于a >1,7b-2b=a +4c>5c,则7b -2b >5c -b .令h x =75 x -25x,其在R 上单调递增.由于0<b <1,则0=h (0)<h b <h (1)=1,则有5c -b <1,即c -b <0得c <b .综上,0<c <b <1<a .故选:A .14(2024·高二·北京西城·期末)在直角坐标系xOy 内,圆C :(x -2)2+(y -2)2=1,若直线l :x +y +m =0绕原点O 顺时针旋转90°后与圆C 存在公共点,则实数m 的取值范围是()A.-2,2B.-4-2,-4+2C.-2-2,-2+2D.-2+2,2+2【答案】A【解析】连接OP ,设∠POx =θ(即以x 轴正方向为始边,OP 为终边的角),由题意对于直线l :x +y +m =0上任意一点P x ,y ,存在a =x 2+y 2,θ∈R ,使得P a cos θ,a sin θ ,则直线l :x +y +m =0绕原点O 顺时针旋转90°后,点P a cos θ,a sin θ 对应点为P 1a cos θ-π2 ,a sin θ-π2 ,即P 1a sin θ,-a cos θ ,因为P a cos θ,a sin θ 在直线l :x +y +m =0上,所以满足a cos θ+a sin θ+m =0设x 1=a sin θ,y 1=-a cos θ,所以-y 1+x 1+m =0,即P 1a sin θ,-a cos θ 所在直线方程为l 1:x -y +m =0,而圆C :(x -2)2+(y -2)2=1的圆心,半径分别为2,2 ,r =1,若直线l :x +y +m =0绕原点O 顺时针旋转90°后与圆C 存在公共点,所以圆心C 2,2 到直线l 1:x -y +m =0的距离d =m2≤r =1,解得-2≤m ≤ 2.故选:A .15(2024·山东青岛·一模)已知A (-2,0),B (2,0),设点P 是圆x 2+y 2=1上的点,若动点Q 满足:QP⋅PB =0,QP =λQA |QA |+QB|QB |,则Q 的轨迹方程为()A.x 2-y 23=1B.x 23-y 2=1C.x 25+y 2=1D.x 26+y 22=1【答案】A【解析】由QP ⋅PB=0,可得QP ⊥PB ,而QP =λQA QA +QBQB,可知点P 在∠BQA 的平分线上.圆x 2+y 2=1,圆心为原点O ,半径r =1,连接AQ ,延长BP 交AQ 于点C ,连接OP ,因为∠PQB =∠PQC 且PQ ⊥BC ,所以QB =QC ,且P 为BC 中点,OP ∥AC ,OP =1AC因此,QA -QB =QA -QC =AC =2OP =2,点Q 在以A 、B 为焦点的双曲线上,设双曲线方程为x 2a 2-y 2b2=1a >0,b >0 ,可知c =2,a 2+b 2=c 2=4,由2a =QA -QB =2,得a =1,故b 2=3,双曲线方程为x 2-y 23=1.故选:A .16(2024·山东青岛·一模)∀x ∈R ,f (x )+f (x +3)=1-f (x )f (x +3),f (-1)=0,则f (2024)的值为()A.2B.1C.0D.-1【答案】B【解析】由题意知∀x ∈R ,f (x )+f (x +3)=1-f (x )f (x +3),f (-1)=0,令x =-1,则f (-1)+f (2)=1-f (-1)f (2),∴f (2)=1显然f (x )=-1时,-1+f (x +3)=1+f (x +3)不成立,故f (x )≠-1,故f (x +3)=1-f (x )1+f (x ),则f (x +6)=1-1-f (x )1+f (x )1+1-f (x )1+f (x )=f (x ),即6为函数f (x )的周期,则f (2024)=f (337×6+2)=f (2)=1,故选:B17(2024·山东聊城·一模)已知P 是圆C :x 2+y 2=1外的动点,过点P 作圆C 的两条切线,设两切点分别为A ,B ,当PA ⋅PB的值最小时,点P 到圆心C 的距离为()A.42 B.32 C.2 D.2【答案】A【解析】设P x ,y ,则OP =x 2+y 2,则PA ⋅PB =PO +OA PO +OB =PO 2+PO ⋅OA +OB +OA ⋅OB ,OA ⋅OB =OA ⋅OBcos ∠AOB =cos ∠AOB =cos2∠POA =2cos 2∠POA -1=2×OA2OP2-1=2x 2+y 2-1,PO ⋅OA =PO ⋅OB =PO ⋅OA cos 180°-∠POA =-PO ⋅OAcos ∠POA=-PO ⋅OA ⋅OA OP=-1,故PA ⋅PB =x 2+y 2-2+2x 2+y2-1≥2x 2+y 2 ⋅2x 2+y 2-3=22-3,当且仅当x 2+y 2=2x 2+y2,即x 2+y 2=2时,等号成立,故当PA ⋅PB的值最小时,点P 到圆心C 的距离为42.故选:A .18(2024·山东聊城·一模)在三棱柱ABC -A 1B 1C 1中,点D 在棱BB 1上,且△ADC 1所在的平面将三棱柱ABC -A 1B 1C 1分割成体积相等的两部分,点M 在棱A 1C 1上,且A 1M =2MC 1,点N 在直线BB 1上,若MN ⎳平面ADC 1,则BB 1NB 1=()【答案】D【解析】如图,连接AB 1,则V A -A 1B 1C 1=13V ABC -A 1B 1C1,又△ADC 1所在的平面将三棱柱ABC -A 1B 1C 1分割成体积相等的两部分,所以V A -DB 1C 1=12V ABC -A 1B 1C 1-13V ABC -A 1B 1C 1=16V ABC -A 1B 1C1,即VA -DB 1C 1=12V A -A 1B 1C1,即V C 1-ADB 1=12V C 1-AA 1B1,设C 1到平面ABB 1A 1的距离为d ,则V C 1-ADB 1=13S △ADB 1⋅d ,V C 1-AA 1B 1=13S △AA 1B1⋅d ,所以S △ADB 1=12S △AA 1B 1=12S △ABB 1,所以D 为BB 1的中点,在AA 1上取点E ,使得A 1E =2AE ,连接EN 、EM ,因为A 1M =2MC 1,所以EM ⎳AC 1,又EM ⊄平面ADC 1,AC 1⊂平面ADC 1,所以EM ⎳平面ADC 1,又MN ⎳平面ADC 1,EM ∩MN =M ,EM ,MN ⊂平面EMN ,所以平面EMN ⎳平面ADC 1,又平面EMN ∩平面ABB 1A 1=EN ,平面ADC 1∩平面ABB 1A 1=AD ,所以AD ⎳EN ,又AE ⎳ND ,所以四边形ADNE 为平行四边形,所以ND =AE =13AA 1=13BB 1,所以B 1N =B 1D -ND =12BB 1-13BB 1=16BB 1,所以BB 1NB 1=6.故选:D19(2024·山东烟台·一模)在平面直角坐标系xOy 中,点A -1,0 ,B 2,3 ,向量OC =mOA +nOB,且m -n -4=0.若P 为椭圆x 2+y 27=1上一点,则PC 的最小值为()A.4510B.10C.8510D.210【答案】A 【解析】设点C (x ,y ),由A -1,0 ,B 2,3 及OC =mOA +nOB ,得(x ,y )=(-m +2n ,3n ),即x =-m +2ny =3n,而m -n -4=0,消去m ,n 得:3x -y +12=0,设椭圆x 2+y 27=1上的点P (cos θ,7sin θ),θ∈R ,则点P 到直线3x -y +12=0的距离d =|3cos θ-7sin θ+12|32+(-1)2=12-4sin (θ+φ)10,其中锐角φ由tan φ=37确定,当sin (θ+φ)=1时,d min =4510,而PC ≥d ,所以PC 的最小值为4510.故选:A 20(2024·山东济宁·一模)已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过F 1的直线与y 轴相交于M 点,与双曲线C 在第一象限的交点为P ,若F 1M =2MP ,F 1P ⋅F 2P=0,则双曲线C 的离心率为()A.2B.3C.332D.3+1【答案】D【解析】设∠PF 1F 2=θ,θ为锐角,因为F 1M =2MP ,F 1P ⋅F 2P =0,所以PF 1⊥PF 2,PF 1 =32MF 1 ,∴MF 1 =c cos θ,∴|PF 1|=32|MF 1|=3c2cos θ,又|PF 2|=2c sin θ,∴|PF 1|2+|PF 2|2=|F 1F 2|2,∴9c 24cos 2θ+4c 2sin 2θ=4c 2,∴9+16sin 2θcos 2θ=16cos 2θ,∴9+16(1-cos 2θ)cos 2θ=16cos 2θ,∴9-16cos 4θ=0,∴cos 2θ=34,∴cos θ=32(负值舍去),∴θ=30°,∴|PF 1|=32|MF 1|=3c2cos θ=3c ,|PF 2|=2c sin θ=c ,∴双曲线C 的离心率e =2c 2a =|F 1F 2||PF 1|-|PF 2|=2c3c -c=3+1.故选:D .21(2024·山东济宁·一模)设函数f (x )定义域为R ,f (2x -1)为奇函数,f (x -2)为偶函数,当x ∈[0,1]时,f (x )=x 2-1,则f (2023)-f (2024)=()A.-1 B.0C.1D.2【答案】C【解析】因为函数f (x )定义域为R ,f (2x -1)为奇函数,所以f (2x -1)=-f (-2x -1),所以函数f (x )关于点-1,0 中心对称,且f -1 =0,因为f (x -2)为偶函数,所以f (x -2)=f (-x -2),所以函数f (x )关于直线x =-2轴对称,又因为f x =-f -2-x =-f -2+x =--f -4+x ,所以函数f (x )的周期为4,因为当x ∈[0,1]时,f (x )=x 2-1,所以f (2023)=f 4×506-1 =f -1 =0,f (2024)=f 4×506 =f 0 =-1,所以f (2023)-f (2024)=1.故选:C .22(2024·山东淄博·一模)已知F 1,F 2是椭圆和双曲线的公共焦点,P ,Q 是它们的两个公共点,且P ,Q 关于原点对称,∠PF 2Q =2π3,若椭圆的离心率为e 1,双曲线的离心率为e 2,则e 21e 21+1+3e 22e 22+3的最小值是()A.2+33B.1+33C.233D.433【答案】A【解析】如图,设椭圆的长半轴长为a 1,双曲线的实半轴长为a 2,则根据椭圆及双曲线的定义得:PF 1 +PF 2 =2a 1,PF 1 -PF 2 =2a 2,∴PF 1 =a 1+a 2,PF 2 =a 1-a 2,设F 1F 2 =2c ,∠PF 2Q =2π3,根据椭圆与双曲线的对称性知四边形PF 1QF 2为平行四边形,则∠F 1PF 2=π3,则在△PF 1F 2中,由余弦定理得,4c 2=a 1+a 2 2+a 1-a 2 2-2a 1+a 2 a 1-a 2 cosπ3,化简得a 21+3a 22=4c 2,即1e 21+3e 22=4,则e 21e 21+1+3e 22e 22+3=11e 21+1+33e 22+1=11e 21+1+33e 22+1 1e 21+1+3e 22+1×16=16×4+3e 22+11e 21+1+31e 21+1 3e 22+1≥16×4+23e 22+11e 21+1×31e 21+1 3e 22+1=16×4+23 =2+33,当且仅当3e 22+1 2=31e 21+121e 21+3e 22=4,即e 21=33+411<1e 22=38-33=24+9337>1时等号成立,故选:A .23(2024·广东茂名·一模)若α∈π4,3π4 ,6tan π4+α +4cos π4-α =5cos2α,则sin2α=()A.2425B.1225C.725D.15【答案】C 【解析】令t =π4+α,t ∈π2,π ,得α=t -π4,则6tan t +4cos π2-t =5cos 2t -π2,即6tan t +4sin t =5sin2t =10sin t cos t ,整理得5cos t +3 cos t -1 =0,且cos t <0,那么cos t =-35,则sin2α=sin 2t -π2 =-cos2t =1-2cos 2t =725.故选:C .二、多选题24(2024·广东江门·一模)已知曲线E :x x 4+y y8=1,则下列结论正确的是()A.y 随着x 增大而减小B.曲线E 的横坐标取值范围为-2,2C.曲线E 与直线y =-1.4x 相交,且交点在第二象限D.M x 0,y 0 是曲线E 上任意一点,则2x 0+y 0 的取值范围为0,4 【答案】AD【解析】因为曲线E :x x 4+y y8=1,当x ≥0,y ≥0时x 24+y 28=1,则曲线E 为椭圆x 24+y 28=1的一部分;当x >0,y <0时x 24-y 28=1,则曲线E 为双曲线x 24-y 28=1的一部分,且双曲线的渐近线为y =±2x ;当x <0,y >0时y 28-x 24=1,则曲线E 为双曲线y 28-x 24=1的一部分,且双曲线的渐近线为y =±2x ;可得曲线的图形如下所示:由图可知y 随着x 增大而减小,故A 正确;曲线E 的横坐标取值范围为R ,故B 错误;因为-1.4>-2,所以曲线E 与直线y =-1.4x 相交,且交点在第四象限,故C 错误;因为2x 0+y 0 =3×2x 0+y 022+12,即点M x 0,y 0 到直线2x +y =0的距离的3倍,当直线2x +y +c =0与曲线x 24+y 28=1x ≥0,y ≥0 相切时,由x 24+y 28=12x +y +c =0,消去y 整理得4x 2+22cx +c 2-8=0,则Δ=22c 2-16c 2-8 =0,解得c =4(舍去)或c =-4,又2x +y =0与2x +y -4=0的距离d =4 2 2+12=43,所以2x 0+y 0 max =3d =4,所以2x 0+y 0 的取值范围为0,4 ,故D 正确;故选:AD25(2024·广东江门·一模)已知函数f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3(ω>0),则下列结论正确的是()A.若f x 相邻两条对称轴的距离为π2,则ω=2B.当ω=1,x ∈0,π2时,f x 的值域为-3,2 C.当ω=1时,f x 的图象向左平移π6个单位长度得到函数解析式为y =2cos 2x +π6D.若f x 在区间0,π6上有且仅有两个零点,则5≤ω<8【答案】BCD【解析】f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3=sin2ωx cos π3+cos2ωx sin π3+sin2ωx cos π3-cos2ωx sin π3+3cos2ωx=sin2ωx +3cos2ωx =2sin 2ωx +π3,对于A ,若f x 相邻两条对称轴的距离为π2,则T =2×π2=π=2π2ω,故ω=1,A 错误,对于B ,当ω=1,f x =2sin 2x +π3 ,当x ∈0,π2 时,2x +π3∈π3,4π3,则f x 的值域为-3,2 ,B 正确,对于C ,当ω=1,f x =2sin 2x +π3,f x 的图象向左平移π6个单位长度得到函数解析式为f x +π6 =2sin 2x +π6 +π3 =2sin 2x +2π3 =2cos 2x +π6,C 正确,对于D ,当x ∈0,π6 时,2ωx +π3∈π3,2ωπ6+π3,若f x 在区间0,π6 上有且仅有两个零点,则2π≤2ωπ6+π3<3π,解得5≤ω<8,故D 正确,故选:BCD26(2024·广东·一模)已知正方体ABCD -A 1B 1C 1D 1的各个顶点都在表面积为3π的球面上,点P 为该球面上的任意一点,则下列结论正确的是()A.有无数个点P ,使得AP ⎳平面BDC 1B.有无数个点P ,使得AP ⊥平面BDC 1C.若点P ∈平面BCC 1B 1,则四棱锥P -ABCD 的体积的最大值为2+16D.若点P ∈平面BCC 1B 1,则AP +PC 1的最大值为6【答案】ACD【解析】令正方体ABCD -A 1B 1C 1D 1的外接球半径为r ,4πr 2=3π,r =32,则BD 1=3,AB =1,连接AB 1,AD 1,B 1D 1,由四边形ABC 1D 1是该正方体的对角面,得四边形ABC 1D 1是矩形,即有AD 1⎳BC 1,而BC 1⊂平面BDC 1,AD 1⊄平面BDC 1,则AD 1⎳平面BDC 1,同理AB 1⎳平面BDC 1,又AB 1∩AD 1=A ,AB 1,AD 1⊂平面AB 1D 1,因此平面AB 1D 1⎳平面BDC 1,令平面ABD 1截球面所得截面小圆为圆M ,对圆M 上任意一点(除点A 外)均有AP ⎳平面BDC 1,A 正确;对于B ,过A 与平面BDC 1垂直的直线AP 仅有一条,这样的P 点至多一个,B 错误;对于C ,平面BCC 1B 1截球面为圆R ,圆R 的半径为22,则圆R 上的点到底面ABCD 的距离的最大值为2+12,因此四棱锥P -ABCD 的体积的最大值为13×1×2+12=2+16,C 正确;对于D ,显然AB ⊥平面BCC 1B 1,在平面BCC 1B 1内建立平面直角坐标系,如图,令点P 22cos θ,22sin θ,而B -12,-12 ,C 112,12,因此AP =1+22cos θ+122+22sin θ+122=2+22(sin θ+cos θ),PC 1=22cos θ-122+22sin θ-122=1-22(sin θ+cos θ),令22(sin θ+cos θ)=x ,AP +PC 1=2+x +1-x =2+x +1-x 2≤22+x 2+1-x 2 =6,当且仅当x =-12取等号,此时22(sin θ+cos θ)=-12,即sin θ+π4 =-12,因此AP +PC 1的最大值为6,D 正确.故选:ACD27(2024·广东·一模)已知偶函数f (x )的定义域为R ,f 12x +1 为奇函数,且f (x )在0,1 上单调递增,则下列结论正确的是()A.f -32<0 B.f 43>0 C.f (3)<0D.f 20243>0【答案】BD【解析】因为f x 为偶函数,所以f -x =f x ;因为f 12x +1 是R 上的奇函数,所以f 1 =0,且f x +22 的图象是由f x 2 的图象向左平移2个单位得到的,所以f x 2 的图象关于2,0 点对称,进一步得f x 的图象关于点1,0 中心对称,即f 1+x =-f 1-x .所以f x +2 =f 1+1+x =-f 1-1+x =-f -x =-f x ,所以f x +4 =-f x +2 =f x .所以函数f x 是周期函数,且周期为4;又f x 在0,1 上单调递增,所以在0,1 上,有f x <0.所以函数的草图如下:由图可知:f -32 >0,故A 错;f 43>0,故B 对;f 3 =0,故C 错;f 20243=f 674+23 =f 4×168+2+23 =f 2+23>0,故D 对.故选:BD 28(2024·广东·模拟预测)已知函数f x 的定义域为R ,f x -1 是奇函数,f x +1 为偶函数,当-1≤x ≤1时,f x =2x +1-13x +1,则()A.f x 的图象关于直线x =1对称B.f x 的图象关于点-1,0 对称C.f x +6 =f xD.f 2021 =-34【答案】ABD【解析】设g x =f x -1 ,因为g x 是奇函数,所以g -x =f -x -1 =-g x =-f x -1 ,即f -1+x +f -1-x =0,即f x 关于-1,0 对称,B 正确;设h x =f x +1 ,因为h x 为偶函数,所以h -x =h x ,即f -x +1 =f x +1 ,f 1+x =f 1-x ,所以f x 的关于直线x =1对称,A 正确;由f x 关于-1,0 对称可得f x +f -2-x =0,由f x 的关于直线x =1对称,可得f x =f 2-x ,两式联立得f 2-x +f -2-x =0,令x =x +2得:f -x +f -4-x =0,即f x +f x -4 =0,令x =x -4,得f x -4 +f x -8 =0,即f x =f x -8 ,故f x 的周期为8,故f x +8 =f x ,C 错误;因为T =8,所以f 2021 =f 252×8+5 =f 5 =f -3 ,又f -1+x +f -1-x =0,令x =-2得f -3 +f 1 =0,f 1 =22-131+1=34,所以f 2021 =f -3 =-f 1 =-34,故D 正确.故选:ABD29(2024·高二·福建三明·期中)如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,线段B 1D 1上有两个动点E ,F ,且EF =12,则下列结论中正确的是()A.异面直线AE 、BF 所成角为定值B.AC ⊥BFC.△AEF 的面积与△BEF 的面积相等D.三棱锥A -BEF 的体积为定值【答案】BD【解析】则A 1,0,0 ,B 1,1,0 ,设E a ,a ,1 ,则F a +24,a +24,1,其中0≤a ≤1-24,AE =(a -1,a ,1),BF =a +24-1,a +24-1,1 ,cos <AE ,BF >=AE ∙BF|AE |∙|BF |=(2a -1)a +24-1 +1(a -1)2+a 2+1∙2a +24-1 2+1.取a =12时,cos <AE ,BF >=442-122,取a =1-24时,cos <AE ,BF >=29-22,∵442-122≠29-22,∴异面直线AE 、BF 所成角不是定值,故A 错误;由正方体的结构特征可知,DD 1⊥AC ,BD ⊥AC ,又BD ∩DD 1=D ,BD ,DD 1⊂平面BDD 1B 1∴AC ⊥平面BDD 1B 1,又BF ⊂平面BDD 1B 1,则AC ⊥BF ,故B 正确;B 到B 1D 1的距离为BB 1=1,A 到B 1D 1的距离大于上下底面中心的连线,则A 到B 1D 1的距离大于1,∴△AEF 的面积大于△BEF 的面积,故C 错误;∵AC ⊥平面BDD 1B 1,∴A 到平面BDD 1B 1的距离为22,△BEF 的面积为定值,∴三棱锥A -BEF 的体积为定值,故D 正确.故选:BD .30(2024·湖南·二模)如图,点P 是棱长为2的正方体ABCD -A 1B 1C 1D 1的表面上一个动点,F 是线段A 1B 1的中点,则()A.若点P 满足AP ⊥B 1C ,则动点P 的轨迹长度为42B.三棱锥A -PB 1D 1体积的最大值为163C.当直线AP 与AB 所成的角为45°时,点P 的轨迹长度为π+42D.当P 在底面ABCD 上运动,且满足PF ⎳平面B 1CD 1时,线段PF 长度最大值为22【答案】CD【解析】对于A ,易知B 1C ⊥平面ABC 1D 1,A ∈平面ABC 1D 1,故动点P 的轨迹为矩形ABC 1D 1,动点P 的轨迹长度为矩形ABC 1D 1的周长,即为42+4,所以A 错误;对于B ,因为V A -PD 1D 1=V P -AB 1D 1,而等边△AB 1D 1的面积为定值23,要使三棱锥P -AB 1D 1的体积最大,当且仅当点P 到平面AB 1D 1的距离最大,易知点C 是正方体到平面AB 1D 1距离最大的点,所以V A -PB 1D 1max =V C -AB 1D 1,此时三棱锥C -AB 1D 1即为棱长是22的正四面体,其高为h =22 2-262=43,所以V =1×1×22×22×3×43=8,B 错误;对于C :连接AC ,AB 1,以B 为圆心,BB 1为半径画弧B 1C,如图1所示,当点P 在线段AC ,AB 1和弧B 1C上时,直线AP 与AB 所成的角为45°,又AC =AB 2+BC 2=4+4=22,AB 1=AB 2+BB 21=4+4=22,弧B 1C 长度14×π×22=π,故点P 的轨迹长度为π+42,故C 正确;对于D ,取A 1D 1,D 1D ,DC ,CB ,BB 1,AB 的中点分别为Q ,R ,N ,M ,T ,H ,连接QR ,QF ,FT ,TM ,MN ,NR ,FH ,HN ,HM ,如图2所示,因为FT ∥D 1C ,FT ⊄平面D 1B 1C ,D 1C ⊂平面D 1B 1C ,故FT ∥平面D 1B 1C ,TM ∥B 1C ,TM ⊄平面D 1B 1C ,B 1C ⊂平面D 1B 1C ,故TM ∥平面D 1B 1C ;又FT ∩TM =T ,FT ,TM ⊂平面FTM ,故平面FTM ∥平面D 1B 1C ;又QF ∥NM ,QR ∥TM ,RN ∥FT ,故平面FTMNRQ 与平面FTM 是同一个平面.则点P 的轨迹为线段MN :在三角形FNM 中,FN =FH 2+HN 2=4+4=22;FM =FH 2+HM 2=4+2=6;NM =2;则FM 2+MN 2=8=FN 2,故三角形FNM 是以∠FMN 为直角的直角三角形;故FP max =FN =22,故FP 长度的最大值为22,故D 正确.故选:CD .31(2024·湖南·二模)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且c =b 2cos A +1 ,则下列结论正确的有()A.A =2BB.若a =3b ,则△ABC 为直角三角形C.若△ABC 为锐角三角形,1tan B -1tan A 的最小值为1D.若△ABC 为锐角三角形,则c a 的取值范围为22,233【答案】ABD【解析】对于A ,△ABC 中,由正弦定理得sin C =2sin B cos A +sin B ,由sin C =sin A +B ,得sin A cos B -cos A sin B =sin B ,即sin A -B =sin B ,由0<A ,B <π,则sin B >0,故0<A -B <π,所以A -B =B 或A -B +B =π,即A =2B 或A =π(舍去),即A =2B ,A 正确;对于B ,若a =3b ,结合A =2B 和正弦定理知a sin A=3b sin2B =b sin B ,cos B =32,又0<A ,B <π,所以可得A =2B =π3,C =π2,B 正确;πππππ3<1.故1tan B -1tan A=1tan B -1-tan 2B 2tan B =1+tan 2B 2tan B >1,C 错误;对于D ,在锐角△ABC 中,由π6<B <π4,22<cos B <32,c a =sin C sin A=sin3B sin2B =sin2B cos B +cos2B sin B sin2B =2cos B -12cos B ,令cos B =t ∈22,32 ,则c a =f t=2t -12t,易知函数f t =2t -12t 单调递增,所以可得c a ∈22,233,D 正确;故选:ABD .32(2024·高二·广东江门·期末)已知抛物线C :y 2=4x 的焦点为F ,直线l :x =-1,过F 的直线交抛物线C 于A x 1,y 1 ,B x 2,y 2 两点,交直线l 于点M ,MA =λ1AF ,MB =λ2BF,则()A.△ABO 的面积的最大值为2 B.y 1y 2=-4C.x 1x 2=1 D.λ1+λ2=0【答案】BCD【解析】设直线AB :x =my +1,由x =my +1y 2=4x得:y 2-4my -4=0.选项A :S △ABO =12OF ·y 1-y 2 =12y 21+y 22 -4y 1y 2=1216m 2+16≥12×4=2,应是最小值为2,故A 错误;选项B :y 1y 2=-4,故B 正确;选项C :x 1=y 214,x 2=y 224,则x 1x 2=(y 1y 2)216=1,故C 正确;选项D :由MA =λ1AF ,MB =λ2BF ,M -1,-2m,得:y 1+2m =-λ1y 1,y 2+2m=-λ2y 2,∴λ1+λ2=-2-2m 1y 1+1y 2=-2-2m ⋅y 1+y 2y 1y 2=-2-2m ⋅4m-4=0,故D 正确.故选:BCD33(2024·高三·黑龙江哈尔滨·阶段练习)已知函数f x =sin ωx +π4ω>0 在区间0,π 上有且仅有3条对称轴,给出下列四个结论,正确的是()A.f x 在区间0,π 上有且仅有3个不同的零点B.f x 的最小正周期可能是2π3C.ω的取值范围是94,134D.f x 在区间0,π15 上单调递增【答案】BD【解析】由函数f x =sin ωx +π4ω>0 ,令ωx +π4=π2+k π,k ∈Z ,则x =(1+4k )π4ω,k ∈Z ,函数f (x )在区间0,π 上有且仅有3条对称轴,即0≤(1+4k )π4ω≤π有3个整数k 符合,由0≤(1+4k)π4ω≤π,得0≤1+4k4ω≤1⇒0≤1+4k≤4ω,则k=0,1,2,即1+4×2≤4ω<1+4×3,∴9 4≤ω<134,故C错误;对于A,∵x∈(0,π),∴ωx+π4∈π4,ωπ+π4,∴ωπ+π4∈5π2,7π2 ,当ωx+π4∈5π2,3π时,f(x)在区间(0,π)上有且仅有2个不同的零点;当ωx+π4∈3π,7π2时,f(x)在区间(0,π)上有且仅有3个不同的零点,故A错误;对于B,周期T=2πω,由94≤ω<134,则413<1ω≤49,∴8π13<T≤8π9,又2π3∈8π13,8π9,所以f(x)的最小正周期可能是2π3,故B正确;对于D,∵x∈0,π15,∴ωx+π4∈π4,ωπ15+π4,又94≤ω<134,∴ωπ15+π4∈2π5,7π15,又7π15<π2,所以f(x)在区间0,π15上一定单调递增,故D正确.故选:BD.34(2024·高一·辽宁丹东·期中)已知f x 是定义在R上的连续函数,且满足f x+y=f x +f y -2xy,当x>0时,f x >0,设g x =f x +x2()A.若f1 ⋅f-1=-3,则f1 =1 B.g x 是偶函数C.g x 在R上是增函数D.x-1g x >0的解集是-∞,0∪1,+∞【答案】ACD【解析】对选项A:取x=y=0得到f0 =f0 +f0 ,即f0 =0,取x=1,y=-1得到f0 =f1 +f-1+2=0,又f1 ⋅f-1=-3,f1 >0,解得f1 =1,正确;对选项B:取y=-x得到f0 =f x +f-x+2x2,即f x +f-x=-2x2,g x +g-x=f x +x2+f-x+x2=0,函数定义域为R,函数为奇函数,错误;对选项C:设x1<x2,则g x2-g x1=f x2+x22-f x1-x21=f x2-x1+x1+x22-f x1-x21=f x2-x1-2x2-x1x1+x22-x21=f x2-x1-2x2x1+x21+x22=f x2-x1+x1-x22,x>0时,f x >0,故f x2-x1>0,x1-x22>0,故g x2-g x1>0,即g x2>g x1,函数单调递增,正确;对选项D:g0 =f0 +0=0,x-1g x >0,当x>1时,g x >0,则x>0,故x>1;当x=1时,不成立;当x<1时,g x <0,则x<0,故x<0;综上所述:x∈-∞,0∪1,+∞,正确;35(2024·湖北·一模)某数学兴趣小组的同学经研究发现,反比例函数y =1x的图象是双曲线,设其焦点为M ,N ,若P 为其图象上任意一点,则()A.y =-x 是它的一条对称轴B.它的离心率为2C.点2,2 是它的一个焦点D.PM -PN =22【答案】ABD【解析】反比例函数的图象为等轴双曲线,故离心率为2,容易知道y =x 是实轴,y =-x 是虚轴,坐标原点是对称中心,联立实轴方程y =x 与反比例函数表达式y =1x得实轴顶点1,1 ,-1,-1 ,所以a =2,c =2,其中一个焦点坐标应为2,2 而不是2,2 ,由双曲线定义可知PM -PN =2a =22.故选:ABD .36(2024·湖北·一模)已知函数f x =ax 3+bx 2+cx +d 存在两个极值点x 1,x 2x 1<x 2 ,且f x 1 =-x 1,f x 2 =x 2.设f x 的零点个数为m ,方程3a f x 2+2bf x +c =0的实根个数为n ,则()A.当a >0时,n =3B.当a <0时,m +2=nC.mn 一定能被3整除D.m +n 的取值集合为4,5,6,7【答案】AB【解析】由题意可知f x =3ax 2+2bx +c 为二次函数,且x 1,x 2x 1<x 2 为f x 的零点,由f f x =3a f x 2+2bf x +c =0得f x =x 1或f x =x 2,当a >0时,令f x >0,解得x <x 1或x >x 2;令f x <0,解得x 1<x <x 2;可知:f x 在-∞,x 1 ,x 2,+∞ 内单调递增,在x 1,x 2 内单调递减,则x 1为极大值点,x 2为极小值点,若x 1≥0,则-x 1≤0<x 2,因为f x 1 >f x 2 ,即-x 1>x 2,两者相矛盾,故x 1<0,则f x =x 2有2个根,f x =x 1有1个根,可知n =3,若f x 2 =x 2>0,可知m =1,mn =3,m +n =4;若f x 2 =x 2=0,可知m =2,mn =6,m +n =5;若f x 2 =x 2<0,可知m =3,mn =9,m +n =6;故A 正确;当a <0时,令f x >0,解得x 1<x <x 2;令f x <0,解得x <x 1或x >x 2;可知:f x 在x 1,x 2 内单调递增,在内-∞,x 1 ,x 2,+∞ 单调递减,则x 2为极大值点,x 1为极小值点,若x 2≤0,则-x 1>0≥x 2,因为f x 1 <f x 2 ,即-x 1<x 2,两者相矛盾,故x 2>0,若f x =-x >0,即x <0,可知m =1,n =3,mn =3,m +n =4;若f x 1 =-x 1=0,即x 1=0,可知m =2,n =4,mn =8,m +n =6;若f x 1 =-x 1<0,即x 1>0,可知m =3,n =5,mn =15,m +n =8;此时m +2=n ,故B 正确;综上所述:mn 的取值集合为3,6,8,9,15 ,m +n 的取值集合为4,5,6,8 ,故CD 错误;故选:AB .37(2024·湖北·二模)如图,棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 为棱DD 1的中点,F 为正方形C 1CDD 1内一个动点(包括边界),且B 1F ⎳平面A 1BE ,则下列说法正确的有()A.动点F 轨迹的长度为2B.三棱锥B 1-D 1EF 体积的最小值为13C.B 1F 与A 1B 不可能垂直D.当三棱锥B 1-D 1DF 的体积最大时,其外接球的表面积为252π【答案】ABD【解析】对A ,如图,令CC 1中点为M ,CD 1中点为N ,连接MN ,又正方体ABCD -A 1B 1C 1D 1中,E 为棱DD 1的中点,可得B 1M ⎳A 1E ,MN ⎳CD 1⎳BA 1,∴B 1M ⎳平面BA 1E ,MN ⎳平面BA 1E ,又B 1M ∩MN =M ,且B 1M ,MN ⊂平面B 1MN ,∴平面B 1MN ⎳平面BA 1E ,又B 1F ⎳平面A 1BE ,且B 1∈平面B 1MN ,∴B 1F ⊂平面B 1MN ,又F 为正方形C 1CDD 1内一个动点(包括边界),∴F ∈平面B 1MN ∩平面C 1CDD 1,而MN =平面B 1MN ∩平面C 1CDD 1,∴F ∈MN ,即F 的轨迹为线段MN .由棱长为2的正方体得线段MN 的长度为2,故选项A 正确;对B ,由正方体侧棱B 1C 1⊥底面C 1CDD 1,所以三棱锥B 1-D 1EF 体积为V =13B 1C 1⋅S △D 1FE =23S △D 1FE ,所以△D 1FE 面积S △D 1FE 最小时,体积最小,如图,∵F ∈MN ,易得F 在N 处时S △D 1FE 最小,此时S △D 1FE =12ND 1⋅D 1E =12,所以体积最小值为13,故选项B 正确;对C ,当F 为线段MN 中点时,由B 1M =B 1N 可得B 1F ⊥MN ,又CC 1中点为M ,CD 1中点为N ,∴MN ⎳D 1C ,而A 1B ⎳D 1C ,∴B 1F ⊥A 1B ,故选项C 不正确;对D ,如图,当F 在M 处时,三棱锥B 1-D 1DF 的体积最大时,由已知得此时FD =FD 1=FB 1=5,所以F 在底面B 1DD 1的射影为底面外心,DD 1=2,B 1D 1=22,DB 1=23,所以底面B 1DD 1为直角三角形,所以F 在底面B 1DD 1的射影为B 1D 中点,设为O 1,如图,设外接球半径为R ,由R 2=OO 12+O 1B 12=OO 12+3,R +OO 1=FO 1=2,可得外接球半径R =524,外接球的表面积为4πR 2=252π,故选项D 正确.故选:ABD .38(2024·湖北·二模)我们知道,函数y =f (x )的图象关于坐标原点成中心对称图形的充要条件是函数y =f (x )为奇函数.有同学发现可以将其推广为:函数y =f (x )的图象关于点P (a ,b )成中心对称图形的充要条件是函数y =f (x +a )-b 为奇函数.已知函数f (x )=42x +2,则下列结论正确的有()A.函数f (x )的值域为(0,2]B.函数f (x )的图象关于点(1,1)成中心对称图形C.函数f (x )的导函数f (x )的图象关于直线x =1对称D.若函数g (x )满足y =g (x +1)-1为奇函数,且其图象与函数f (x )的图象有2024个交点,记为A i (x i ,y i )(i =1,2,⋯,2024),则2024i =1(x i +y i ) =4048【答案】BCD【解析】对于A ,显然f (x )的定义域为R ,2x >0,则0<42x +2<2,即函数f (x )的值域为(0,2),A 错误;对于B ,令h (x )=f (x +1)-1=42x +1+2-1=22x +1-1=1-2x 1+2x ,h (-x )=1-2-x 1+2-x =2x -12x+1=-h (x ),即函数y =f (x +1)-1是奇函数,因此函数f (x )的图象关于点(1,1)成中心对称图形,B 正确;对于C ,由选项B 知,f (-x +1)-1=-[f (x +1)-1],即f (1-x )+f (1+x )=2,两边求导得-f (1-x )+f (1+x )=0,即f (1-x )=f (1+x ),因此函数f (x )的导函数f (x )的图象关于直线x =1对称,C 正确;对于D ,由函数g (x )满足y =g (x +1)-1为奇函数,得函数g (x )的图象关于点(1,1)成中心对称,由选项B 知,函数g (x )的图象与函数f (x )的图象有2024个交点关于点(1,1)对称,因此2024i =1(x i +y i ) =2024i =1x i +2024i =1y i =1012×2+1012×2=4048,D 正确.故选:BCD。
数学试卷高考创新卷

一、选择题(每题5分,共50分)1. 下列各数中,不是有理数的是()A. √9B. -√16C. πD. 0.252. 已知函数f(x) = x^2 - 4x + 4,那么f(x)的图像是()A. 一个开口向上的抛物线B. 一个开口向下的抛物线C. 一条直线D. 一个圆3. 下列各方程中,无解的是()A. x + 3 = 0B. 2x - 4 = 0C. x^2 - 5x + 6 = 0D. 3x^2 - 2x + 1 = 04. 若a、b是实数,且a + b = 0,则下列等式中正确的是()A. a^2 = b^2B. a^2 = -b^2C. a^2 = 2b^2D. a^2 = b^2 + 15. 下列各函数中,单调递增的是()A. f(x) = x^3B. f(x) = x^2C. f(x) = -xD. f(x) = |x|6. 已知等差数列{an}的公差为2,且a1 + a2 + a3 = 18,则数列{an}的第10项是()A. 26B. 28C. 30D. 327. 若复数z满足|z - 2| = |z + 2|,则复数z的实部是()A. 0B. 2C. -2D. 无法确定8. 下列各三角形中,是等边三角形的是()A. 三边长分别为3,4,5的三角形B. 三边长分别为5,5,5的三角形C. 三边长分别为6,8,10的三角形D. 三边长分别为7,7,12的三角形9. 下列各不等式中,正确的是()A. 2x + 3 > 5B. 2x - 3 < 5C. 2x + 3 ≤ 5D. 2x - 3 ≥ 510. 已知函数f(x) = |x - 1| + |x + 1|,那么f(x)的最小值是()A. 0B. 1C. 2D. 3二、填空题(每题5分,共25分)11. 若函数f(x) = 2x - 3在区间[1, 3]上单调递增,则x的取值范围是______。
12. 若复数z满足|z - 1| = |z + 1|,则复数z的实部是______。
高考数学选做题.pdf

13.已知曲线
C1
的参数方程是
x y
= =
2 3
cos极点,
x
轴的正半轴为极轴建
学海无涯
立极坐标系,曲线 C2 :的极坐标方程是 =2,正方形 ABCD 的顶点都在 C2 上,且 A,B,C,D 依逆时针次
序排列,点 A 的极坐标为(2, ). 3
(Ⅰ)求点 A,B,C,D 的直角坐标;
的正半轴为极轴的极坐标系中,射线
=
3
与曲线 C1 , C2
交于不同于原点的点
A,B
求
AB
16.(本小题满分 10 分)选修 4-4:坐标系与参数方程
在直角坐标系
xOy
中,曲线
C1
:
x y
= =
t t
cos sin
, ,
(t 为参数,且 t 0
),其中 0 ,在以 O 为极点,x
轴正半轴为极轴的极坐标系中,曲线 C2 : = 2sin,C3 : = 2 3 cos.
a + b c + d .(Ⅱ)本小题可借助第一问的结论来证明,但要分必要性与充分性来
证明. 试题解析:
( ) ( ) 2
2
解:(Ⅰ)因为 a + b = a + b + 2 ab, c + d = c + d + 2 cd ,
( ) ( ) 2
2
由题设 a + b = c + d , ab cd ,得 a + b c + d ,因此 a + b c + d .
学海无涯
高考数学选做题 1.(本小题满分 10 分)选修 4-5:不等式选讲
最新理科数学练习题296

最新理科数学练习题单选题(共5道)1、的图象为一条连续不断的曲线,,,且当0<x<1时,的导函数满足:,则在上的最大值为()AaB0C-aD20162、同时具有以下性质:“①最小正周期是,②图象关于直线对称;③在上是增函数”的一个函数是()ABCD3、已知向量=()ABCD4、已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为( )。
ABCD5、若全集,集合,则下图中阴影部分表示的集合是()ABCD多选题(共5道)6、已知函数,若互不相等,且,则的取值范围是()ABCD填空题(本大题共4小题,每小题____分,共____分。
)7、已知函数,若互不相等,且,则的取值范围是()ABCD填空题(本大题共4小题,每小题____分,共____分。
)8、已知函数,若互不相等,且,则的取值范围是()ABCD填空题(本大题共4小题,每小题____分,共____分。
)9、已知函数,若互不相等,且,则的取值范围是()ABCD填空题(本大题共4小题,每小题____分,共____分。
)10、已知函数,若互不相等,且,则的取值范围是()ABCD填空题(本大题共4小题,每小题____分,共____分。
)简答题(共5道)11、已知,,。
(1)若,记,求的值;(2)若,,且∥,求证:。
12、的外心,角A、B、C的对边分别是、、,且满足.(Ⅰ)证明:;(Ⅱ)求的值.13、(1)若,求不等式的解集;(2)当方程恰有两个实数根时,求的值;(3)若对于一切,不等式恒成立,求的取值范围。
14、已知正方体的棱长为.(1)求异面直线与所成角的大小;(2)求四棱锥的体积.15、中,是的中点,,,,,二面角的大小为.(1)证明:平面;(2)求直线与平面所成角的正弦值.书面表达(共5道)16、阅读下面的材料,根据要求写一篇不少于800字的文章。
一家人晚饭后边看电视边聊节目。
