DSP正弦函数计算程序的编写
基于DSP的正弦信号发生器的设计

软件设计
正弦波子程序流程图 :
软件设计
调幅和调相流程图: 调幅和调相流程图:
汇报内容
• • • • • • 背景 正弦波信号发生器的几种实现方法比较 正弦波信号发生器的数字实现 硬件设计 软件设计 结论
结论
文中分析了正弦波的产生原理,并给出了硬 件电路和软件编写流程;设计了一个更好的 实现人机对话的正弦波信号发生器,给出了 显示和键盘的接口电路。该设计改进了传统 的需要用软件界面来输入幅值和频率值的方 法,更方便的实现调节输出波形的幅值和频 率值。
正弦波信号发生的数字实现 产生正弦波的方法有两种:
查表法。 优点:处理速度快;调频调相容易。 不足:要得到较高的精度,存储空间足够大以存放 查找表。 适用:对精度要求不高的场合。 泰勒级数展开法。 优点:需要的存储单元很少;精度高;展开的级数 越多,失真度就越小;调频调相易。 不足:处理速度慢。
正弦波信号发生的数字实现
硬件设计
DSP与LCD显示和键盘连接电路: DSP与LCD显示和键盘连接电路: 显示和键盘连接电路
硬件设计
键盘电路:
汇报内容
• • • • • • 背景 正弦波信号发生器的几种实现方法比较 正弦波信号发生器的数字实现 硬件设计 软件设计 结论
软件设计
主程序流程图: 主程序流程图:
设计采用采用模块化思路来编写,包括主程序、 设计采用采用模块化思路来编写,包括主程序、正 采用模块化思路来编写 弦波产生程序、调幅和调相子程序等功能子程序。 弦波产生程序、调幅和调相子程序等功能子程序。
性差,波形精度不够高且用较多硬件等。
正弦波信号发生器的几种实现方法比较
基于DSP的正弦波信号发生器:
组成:DSP处理芯片、 D/A转换器等。 优点:可程控调幅、调频,调节精度高,实
一个简单的dspC语言例子

一个简单的dsp C语言例子开发平台: CCS集成开发环境通过这个简单的例子, 可以大致了解用C语言开发dsp程序的原理。
程序要求: 用C语言编写产生正弦调幅波信号的源程序;正弦调幅波的公式在离散域中的表示:y(n) = (1 + M*sin(2 * PI * fb / fs * n)) * sin(2 * PI * fa / fs * n);编写文件1.sin_am.c#include<stdio.h>#include<math.h>#define TRUE 1#define pi 3.1415926536int y[500],i;float M;void main(){puts("amplitude modulation sinewave example started.\n");M = 50;for(i = 0; i < 500; i++)y[i]= 0;while(TRUE){for(i = 0; i < 500; i++)y[i]=(int)((1 + M / 100 * sin(i * 2 * pi * 20 / 4000))* sin(i * 2 * pi * 200 / 4000)* 16384);puts("program end");}}2.sin_am_v.asm (reset vector file).title "sin_am_v.asm".sect ".vectors".ref _c_int00RESET:B _c_int00.end..3.sin_am.cmdsin_am.objsin_am_v.obj-m sin_am.map-o sin_am.outMEMORY{PAGE 0:EPROG: origin = 0x1400, len = 0x7c00 VECT: origin = 0xff80, len = 0x80PAGE 1:USERREGS: origin = 0x60, len = 0x1c IDATA: origin = 0x80, len = 0x3000 }SECTIONS{.vectors:>VECT PAGE 0.text:>EPROG PAGE 0.cinit:>EPROG PAGE 0.bss:>IDATA PAGE 1.const:>IDATA PAGE 1.switch:>IDATA PAGE 1.system:>IDATA PAGE 1.stack:>IDATA PAGE 1}"*.cmd"文件说明:链接命令文件是实现对段的存储空间位置的定位, C语言程序中常用已初始化和未初始化段如下:已初始化段包括:.init 存放C程序中的变量的初值和常量, 放在ROM和RAM 中均可, 一般属于PAGE 0.const 存放C程序中的字符常量、浮点常量和用const声明的常量, 放在ROM和RAM中均可, 一般属于PAGE 1.text 存放C程序代码, 放在ROM和RAM中均可, 一般属于PAGE 0.switch 存放C程序中的语句的跳针表, 放在ROM和RAM中均可, 一般属于PAGE 0未初始化段包括:.bss 为C程序中的全局和静态变量保留存储空间, 一般存放于RAM中, 属于PAGE 1.stack 为C程序系统堆栈保留存储空间, 用于保存返回地址、函数间的参数传递、存储局部变量和保存中间结果, 一般存放于RAM中, 属于PAGE 1.sysmem 用于C程序中malloc、calloc和realloc函数动态分配存储空间, 一般存放于RAM中, 属于PAGE 14.vary_M.gelmenuitem "Myfunctions"slider vary_M(0, 100, 10, 1, Amount_of_modulation){M = Amount_of_modulation;}该文件用于调试的时候可随意改变变量M的值, 该文件通过file->load GEL File添加到工程中, 调试的时候可选择GEL->My Functions->vary_M来打开vary_M滑动条组件。
正弦发生器的DSP实现

正弦发生器的DSP实现摘要DSP芯片,也称数字信号处理器,是一种具有特殊结构的微处理器。
DSP芯片的内部采用程序和数据分开的哈佛结构,具有专门的硬件乘法器,广泛采用流水线操作,提供特殊的DSP指令,可以用来快速的实现各种数字信号处理算法电子技能、机械、电声、水声及生物等领域可能经常要用到正弦波,而一般它都由数字集成电路或分立元件构成的信号发生器产生,这里介绍一种用DSP实现的正弦信号发生器,其调幅、调频功能均由软件实现,而且有较好的可扩展性、稳定性,与计算机接口方便。
用DSP设计的正弦信号发生器电路基本,调节方便,误差在万分之一以内,产生的波形失真度较小,而且还有进一步拓展功能,如产生三角波信号、方波信号、直流信号、调制信号等,从而使其能运用到更加广泛的领域中。
关键字:DSP芯片,正弦信号发生器, TMS320C5402, 流程图一、DSP芯片DSP芯片,也称数字信号处理器,是一种具有特殊结构的微处理器。
DSP芯片的内部采用程序和数据分开的哈佛结构,具有专门的硬件乘法器,广泛采用流水线操作,提供特殊的DSP指令,可以用来快速的实现各种数字信号处理算法。
1.DSP芯片主要特点根据数字信号处理的要求,DSP芯片一般具有如下的一些主要特点:(1)在一个指令周期内可完成一次乘法和一次加法。
(2)程序和数据空间分开,可以同时访问指令和数据。
(3)片内具有快速RAM,通常可通过独立的数据总线在两块中同时访问。
(4)具有低开销或无开销循环及跳转的硬件支持。
(5)快速的中断处理和硬件I/O支持。
(6)具有在单周期内操作的多个硬件地址产生器。
(7)可以并行执行多个操作。
(8)支持流水线操作,使取指、译码和执行等操作可以重叠执行。
与通用微处理器相比,DSP芯片的其他通用功能相对较弱些。
2.DSP芯片的分类DSP芯片可以按照下列三种方式进行分类。
(1)按基础特性分这是根据DSP芯片的工作时钟和指令类型来分类的。
如果在某时钟频率范围内的任何时钟频率上,DSP芯片都能正常工作,除计算速度有变化外,没有性能的下降,这类DSP芯片一般称为静态DSP芯片。
正弦波信号发生器的DSP设计

正弦波信号发生器的DSP设计摘要:数字信号处理器(DSP)是在模拟信号变成数字信号以后进行高速实时处理的专用处理器。
DSP芯片以其独特的结构和快速实现各种数字信号处理算法的突出优点,发展十分迅速。
本文介绍了正弦信号产生的典型算法,并结合数字振荡器原理,应用迭代法编程完成了TMS320VC5402 DSP 正弦波信号发生器的设计。
关键词:DSP;正弦振荡;信号发生器正弦信号发生器能输出一个幅度可调、频率可调的正弦信号,特别是低频正弦信号发生器在科学研究及生产实践中均有着广泛应用。
目前,常用的信号发生器绝大部分是由模拟电路构成的。
当这种模拟信号发生器用于低频信号输出时,往往需要的RC值很大,这样不但参数准确度难以保证,而且体积和功耗都很大。
而由数字电路构成的低频信号发生器,虽然其低频性能好,但体积较大,价格较贵。
而借助DSP芯片的运算速度高,系统集成度强的优势设计的这种信号发生器,比以前的任意一种信号发生器速度更快,且实现更加简便。
1正弦波信号的产生方式1.1采样回放法通过对已有的标准正弦信号源进行采样得到数据后直接回放或进行变频变幅处理后回放。
该方法的关键在于合理设计高性能的硬件电路,尽量避免信号处理过程中的波形失真,来确保采样数据的精准性。
同时在数字域处理时,数据的回归点数必须满足Nyquist定理,以免频谱混迭情况的发生。
1.2查表法5402的片内ROM中存有256字的正弦及余弦数据表,可以通过程序直接调用该表中的数据,由D/A回放出正弦波。
通过MATLAB模拟仿真自己生成的正弦数据表,不但可以解决频率单一的问题,还可以增加精度,并改善系统的兼容性。
1.3泰勒级数展开法任一角度的正弦及余弦波都可以展开成泰勒级数,取前五项的近似公式为:其中:α为角度值,ω为其对应的弧度值。
通过变换的α值,且利用弧度与频率之间的关系很容易实现变频处理。
1.4数字正弦振荡器数字正弦波振荡器的系统函数可表示为:对应的是在单位圆上有复共轭极点的二阶振荡器,共扼极点为:P1,2=e±jω0,其离散时域脉冲单位冲击响应响应:h(n)=Asin[(n+1)ω0]·u(n)实际应用中对于给定的冲激信号所产生的正弦信号对应的差分方程为:如果系统无阻尼且稳定,我们不对系统加入冲击信号,改变y(-2)的起始值,从而使系统满足起始条件。
DSP28335生成正弦波的程序

IFR = 0x0000;
InitPieVectTable();
EALLOW; // This is needed to write to EALLOW protected registers
PieVectTable.EPWM1_INT = &epwm1_timer_isr;
ERTM;
{
asm(" NOP");
}
}
void InitEPwm1Example()
{
EPwm1Regs.TBCTL.bit.SYNCOSEL = TB_CTR_ZERO;//zhuyi
EPwm1Regs.TBPRD = PRD; //载波周期=2*1500TBCLK
EPwm1Regs.TBCTL.bit.CLKDIV = TB_DIV2;
EPwm1Regs.CMPCTL.bit.SHDWAMODE = CC_SHADOW; // Load registers every ZERO_PRD
EPwm1Regs.CMPCTL.bit.SHDWBMODE = CC_SHADOW;
//float Q;
#define PWM1_INT_ENABLE 1
#define PWM2_INT_ENABLE 1
#define PWM3_INT_ENABLE 1
void InitEPwm1Example(void);
//void InitEPwm2Example(void);
// cmp2[i]=(Uint16)(EvaRegs.T1PR*0.25*(1+M*sin((2*i)*PI/N+PI*4/3)+1+M*sin((2*i+1)*PI/N+PI*4/3)));
基于DSP的正弦信号发生器的设计

/(/A)低16位→d_xc
sinx
/调/ 用sinx程序
cosx
/调/ 用cosx程序
#d_sinx,DP /D/P←d_sinx
@d_sinx,16,A /A/=sin(x)
@d_cosx
/B/= sin(x)*cos(x)
B,1,*AR6+
/A/R6→2*sin(x)*cos(x)
*AR1+0
方
ST
A,*AR2 /(/ A)左移16位→AR2
||LD *AR4,B /(/ AR4)左移16位→B
MASR
*AR2+,*AR3+,B,A /从/ 累加器A中减去(AR2)
*(AR3)
MPYA
A
/操/ 作数与累加器A中高位相乘
STH
A,*AR2 /(/ A)高16位→AR2
MASR
*AR2-,*AR3+,B,A /从/ 累加器A中减去(AR2)
.text
定//义文本代码段
SSBX
FRCT
/F/RCT=1以清除冗余符号位
STM
#d_coef_c,AR5 /A/R5指向d_coef_c首地址
RPT
#3
重//复下条指令4次
MVPD
#table_c,*AR5+ /把/ table_c中的数复制到中
AR5
STM
#d_coef_c,AR3 /A/R3指向d_coef_c首地址
d_temp_c .usect "cos_vars",1 //为d_temp_c中cos_vars保存1个存储
单元
d_cosx .usect "cos_vars",1 //为d_cosx中cos_vars保存1个存储单
DSP正弦函数计算程序的编写

摘要泰勒级数展开法作为一种数学方法,在科研和平时的数据处理方面应用的很广泛。
尤其是在通信、仪器仪表和工业控制等领域应用更为广泛。
在科技高速发展的今天,对函数的计算不仅要求有很高的精度,还对计算的时间又很高的要求,必须在很短的时间内完成数据的处理,否则根本不能完成大批量数据的实时性计算和处理。
介于DSP芯片运算速度快的特点,用DSP芯片完成这些算法已越来越受到重视。
产生正弦波,分别是查表法和泰勒级数展开法。
查表法应用于精度要求不很高的场合,而泰勒级数展开法是一种比查表法更为有效的方法。
它能精确的计算出一个角度的正弦和余弦值,且占用的储存空间较小,体现了它的优越性。
关键词: DSP 泰勒级数正弦波目录摘要 (I)1、正余弦信号发生器的实现原理 (1)1.1、正弦波信号发生器 (1)2、正弦波的实现 (2)2.1、计算一个角度的正弦值 (2)2.2、计算一个角度的余弦值 (4)3、正弦波的实现 (8)4、链接文件 (10)5、调试结果 (12)总结 (13)参考文献 (14)1、正余弦信号发生器的实现原理1.1、正弦波信号发生器泰勒级数展开法是根据泰勒展开式进行计算来实现正弦信号,它能精确地计算出一个角度的正弦和余弦值,且只需要较小的存储空间。
本次主要用泰勒级数展开法来实现正弦波信号。
正弦函数和余弦函数可以展开成泰勒级数,其表达式:3579sin()3!5!7!9!x x x x x x =-+-+-2468cos()12!4!6!8!x x x x x =-+-+-取泰勒级数的前5项,得近似计算式:35792222sin()3!5!7!9!111123456789(((())))x x x x x x xx x x x =-+-+=----⨯⨯⨯⨯ 24682222cos()12!4!6!8!11112345678((()))x x x x x x xx x =-+-+=----⨯⨯⨯ 递推公式:sin(nx ) = 2cos(x )sin[(n -1)x ]-sin[(n -2)x ] cos(nx ) = 2cos(x )sin[(n -1)x ]-cos[(n -2)x ]由递推公式可以看出,在计算正弦和余弦值时,需要已知cos(x )、sin(n -1)x 、sin(n -2)x 和cos(n -2)x 。
基于DSP的正弦波.上斜波,下斜波,梯形波,方波等波形函数发生器源程序
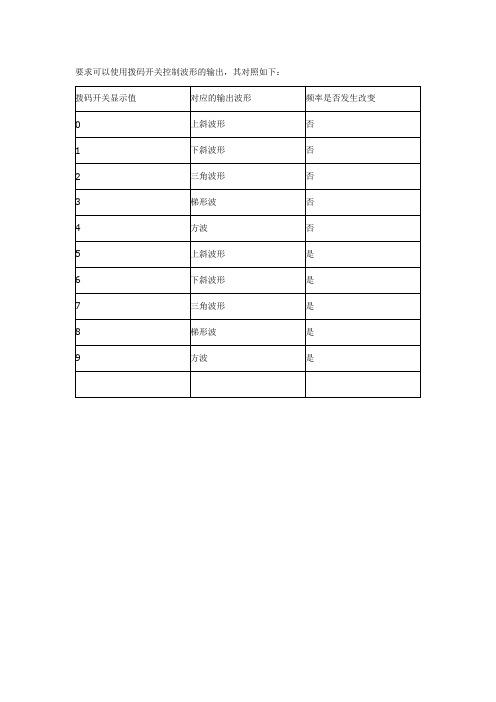
要求可以使用拨码开关控制波形的输出,其对照如下:#include "DSP281x_Device.h" // DSP281x Headerfile Include File #include "DSP281x_Examples.h" // DSP281x Examples Include File #include "f2812a.h"#define DIPS (*(unsigned int *)0xc0001)// Prototype statements for functions found within this file.// interrupt void ISRTimer2(void);void dac_loop(void);typedef unsigned char uint8; /*开始*/typedef unsigned int uint16;typedef unsigned long uint32;uint8 const code ZXB_code[256]={0x80,0x83,0x86,0x89,0x8c,0x8f,0x92,0x95,0x98,0x9c,0x9f,0xa2,0xa5,0xa8,0xab,0xae,0xb0,0xb3,0xb6,0xb9,0xbc,0xbf,0xc1,0xc4,0xc7,0xc9,0xcc,0xce,0xd1,0xd3,0xd5,0xd8,0xda,0xdc,0xde,0xe0,0xe2,0xe4,0xe6,0xe8,0xea,0xec,0xed,0xef,0xf0,0xf2,0xf3,0xf4,0xf6,0xf7,0xf8,0xf9,0xfa,0xfb,0xfc,0xfc,0xfd,0xfe,0xfe,0xff,0xff,0xff,0xff,0xff,0xff,0xff,0xff,0xff,0xff,0xff,0xfe,0xfe,0xfd,0xfc,0xfc,0xfb,0xfa,0xf9,0xf8,0xf7,0xf6,0xf5,0xf3,0xf2,0xf0,0xef,0xed,0xec,0xea,0xe8,0xe6,0xe4,0xe3,0xe1,0xde,0xdc,0xda,0xd8,0xd6,0xd3,0xd1,0xce,0xcc,0xc9,0xc7,0xc4,0xc1,0xbf,0xbc,0xb9,0xb6,0xb4,0xb1,0xae,0xab,0xa8,0xa5,0xa2,0x9f,0x9c,0x99,0x96,0x92,0x8f,0x8c,0x89,0x86,0x83,0x80,0x7d,0x79,0x76,0x73,0x70,0x6d,0x6a,0x67,0x64,0x61,0x5e,0x5b,0x58,0x55,0x52,0x4f,0x4c,0x49,0x46,0x43,0x41,0x3e,0x3b,0x39,0x36,0x33,0x31,0x2e,0x2c,0x2a,0x27,0x25,0x23,0x21,0x1f,0x1d,0x1b,0x19,0x17,0x15,0x14,0x12,0x10,0xf,0xd,0xc,0xb,0x9,0x8,0x7,0x6,0x5,0x4,0x3,0x3,0x2,0x1,0x1,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x1,0x1,0x2,0x3,0x3,0x4,0x5,0x6,0x7,0x8,0x9,0xa,0xc,0xd,0xe,0x10,0x12,0x13,0x15,0x17,0x18,0x1a,0x1c,0x1e,0x20,0x23,0x25,0x27,0x29,0x2c,0x2e,0x30,0x33,0x35,0x38,0x3b,0x3d,0x40,0x43,0x46,0x48,0x4b,0x4e,0x51,0x54,0x57,0x5a,0x5d,0x60,0x63,0x66,0x69,0x6c,0x6f,0x73,0x76,0x79,0x7c};/*结束*/void main(void){InitSysCtrl();dac_loop();}void dac_loop(void){int i,j,m,k;i=0;//m=DIPS&0x0f;for(;;){ m=DIPS&0x0f;if(m==0) //拨码开关值为0,显示上斜波形for(i=0;i<=0xfff;i+=0x10){DA_DA TA_L=i&0xff; //第一通道数据输出量低8位DA_DA TA_H=((i>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x10;j++);}if(m==1) //拨码开关值为1,显示下斜波形for(i=0;i<=0xfff;i-=0x10){DA_DATA_L=i&0xff; //第一通道数据输出量低8位DA_DATA_H=((i>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x10;j++);}if(m==2) //拨码开关值为2,显示三角波形{for(i=0;i<=0xfff;i+=0x10){DA_DATA_L=i&0xff; //第一通道数据输出量低8位DA_DATA_H=((i>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x10;j++);}for(k=0xfff;k>=0;k-=0x10){DA_DA TA_L=k&0xff; //第一通道数据输出量低8位DA_DA TA_H=((k>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x10;j++);}}if(m==3) //拨码开关值为3,显示梯形波{for(i=0;i<=0xfff;i+=0x50){DA_DATA_L=i&0xff; //第一通道数据输出量低8位DA_DATA_H=((i>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x10;j++);}for(i=0;i<=0xfff;i+=0x50){DA_DATA_L=0xff; //第一通道数据输出量低8位DA_DATA_H=0x0f|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x10;j++);}for(i=0xfff;i>=0;i-=0x50){DA_DA TA_L=i&0xff; //第一通道数据输出量低8位DA_DA TA_H=((i>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x10;j++);}for(i=0xfff;i>=0;i-=0x50){DA_DA TA_L=0; //第一通道数据输出量低8位DA_DA TA_H=0|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x10;j++);}}if(m==4) //拨码开关值为4,显示方波{for(i=0;i<=0xfff;i+=0x50){DA_DATA_L=0xff; //第一通道数据输出量低8位DA_DATA_H=0xf|DA_CHN1;//第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x15;j++); //更改频率}for(i=0;i<=0xfff;i+=0x50){DA_DATA_L=0; //第一通道数据输出量低8位DA_DATA_H=0|DA_CHN1; //第一通道da数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x15;j++); //更改频率}}////////if(m==5) //拨码开关值为5,显示更改频率后的上斜波形for(i=0;i<=0xfff;i+=0x10){DA_DA TA_L=i&0xff; //第一通道数据输出量低8位DA_DA TA_H=((i>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x31;j++); //更改频率}if(m==6) //拨码开关值为6,显示更改频率后的下斜波形for(i=0;i<=0xfff;i-=0x10){DA_DATA_L=i&0xff; //第一通道数据输出量低8位DA_DATA_H=((i>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x15;j++); //更改频率}if(m==7) //拨码开关值为7,显示更改频率后的三角波形{for(i=0;i<=0xfff;i+=0x10){DA_DATA_L=i&0xff; //第一通道数据输出量低8位DA_DATA_H=((i>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x31;j++); //更改频率}for(k=0xfff;k>=0;k-=0x10){DA_DA TA_L=k&0xff; //第一通道数据输出量低8位DA_DA TA_H=((k>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x31;j++); //更改频率}}if(m==8) //拨码开关值为8,显示更改频率后的梯形波形{for(i=0;i<=0xfff;i+=0x50){DA_DATA_L=i&0xff; //第一通道数据输出量低8位DA_DATA_H=((i>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x31;j++); //更改频率}for(i=0;i<=0xfff;i+=0x50){DA_DATA_L=0xff; //第一通道数据输出量低8位DA_DATA_H=0x0f|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x31;j++); //更改频率}for(i=0xfff;i>=0;i-=0x50){DA_DA TA_L=i&0xff; //第一通道数据输出量低8位DA_DA TA_H=((i>>8)&0x0f)|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x31;j++); //更改频率}for(i=0xfff;i>=0;i-=0x50){DA_DA TA_L=0; //第一通道数据输出量低8位DA_DA TA_H=0|DA_CHN1; //第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x31;j++) ;//更改频率}}if(m==9) //拨码开关值为9,显示更改频率后的方波{for(i=0;i<=0xfff;i+=0x50){DA_DATA_L=0xff; //第一通道数据输出量低8位DA_DATA_H=0xf|DA_CHN1;//第一通道数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x31;j++); //更改频率}for(i=0;i<=0xfff;i+=0x50){DA_DATA_L=0; //第一通道数据输出量低8位DA_DATA_H=0|DA_CHN1; //第一通道da数据输出量高8位和通道号1DA_CTL=0;for(j=0;j<0x31;j++); //更改频率}}if(m==10) //拨码开关值为10,显示更改频率后的正弦波{uint16 data x;while(1){for(x=0;x<256;x++){DA_DA TA_L =ZXB_code[x]&0xff;DA_DA TA_H=(( ZXB_code[x]>>8)&0x0f)|DA_CHN1;DA_CTL=0;}}}}}。
关于DSP的一些反正切查表算法的编写

关于DSP的一些反正切查表算法的编写一直在拿TMS20F28335做电机控制,也从早前的简单寄存器IO口配置时代过渡到了真正的算法时代,很不适应,起初去查各种书籍,网上搜索各种网站,发现书本上讲的很多都是快速傅里叶啊啥的,找不到很原始的像啥低通滤波器,正弦,正切这些函数的编写。
起初写程序发现,C2000的库里支持啥正弦函数,浮点预算,反正弦函数,开根运算等算法,好兴奋。
用了才知道,太慢了,根本没法用在工程上。
关于三角函数的编写,其实都是利用查表发,查表法大家应该都懂。
这个就不再赘述,怎样去查一个正弦表呢?这里做一个基本的介绍。
首先,你可以自己写一个查表数组,也可以在程序初始化生成一个。
Eg:void SinCOS_TAB(void){unsigned char i;float Theta;for(i=0;i<TAB_Max;i++) // #define TAB_Max 180{Theta = i * Step_Angle; // Step_Angle=1.74532925E-02Sin_tab[i] =sin(Theta); // 生成正弦表数组,利用了库里现成的SIN函数Cos_tab[i] =cos(Theta); // 生成余弦表数组}}为啥我的数组里面只有180个元素呢?一:我的精度要求不高,我是一度一个步进角的,如果你要更高的精度,你可以选择容量更大的数组。
二:我不想因为庞大的浮点数组占据太大的存储空间,所以我利用了奇函数,偶函数的原理再次,就进入正题写查表程序,就我们初中数学所知,正弦函数是奇函数,余弦函数是偶函数,所以我只用了360角度中的一半。
下面为正弦查表程序:/*Refer to the truth that DSP use some SinCos operation will use six or more command* periods , So I look up the pre_generate SINCOS_TAB to speed up the Execution speed*/float SinF(float single){int i=(int)(single*180/pi);float value=0;if(i<0)value = -Sin_tab[i];elsevalue = Sin_tab[i];return value;}看起来应该很简单吧,余弦,正切,余切的编写和上面基本相似。
基于dsp技术的正弦信号发生课程设计
第一章:绪论数字信号处理(Digital Signal Processing,简称DSP)是一门涉及许多学科而又广泛应用于许多领域的新兴学科。
20世纪60年代以来,随着计算机和信息技术的飞速发展,数字信号处理技术应运而生并得到迅速的发展。
数字信号处理是一种通过使用数学技巧执行转换或提取信息,来处理现实信号的方法,这些信号由数字序列表示。
在过去的二十多年时间里,信号处理已经在通信等领域得到极为广泛的应用。
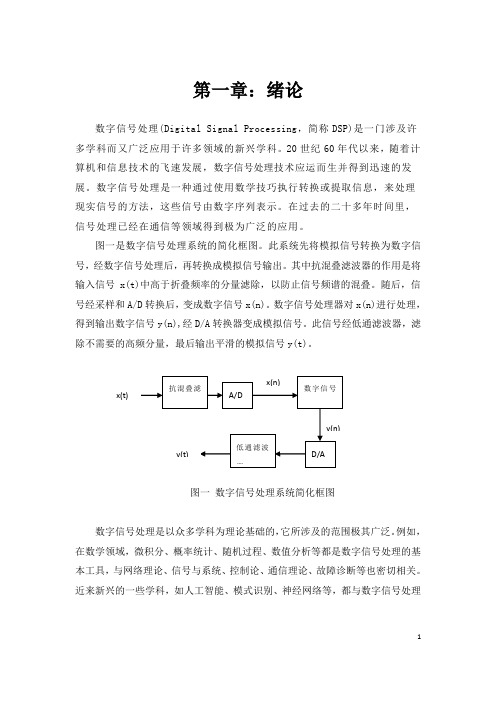
图一是数字信号处理系统的简化框图。
此系统先将模拟信号转换为数字信号,经数字信号处理后,再转换成模拟信号输出。
其中抗混叠滤波器的作用是将输入信号x(t)中高于折叠频率的分量滤除,以防止信号频谱的混叠。
随后,信号经采样和A/D转换后,变成数字信号x(n)。
数字信号处理器对x(n)进行处理,得到输出数字信号y(n),经D/A转换器变成模拟信号。
此信号经低通滤波器,滤除不需要的高频分量,最后输出平滑的模拟信号y(t)。
图一数字信号处理系统简化框图数字信号处理是以众多学科为理论基础的,它所涉及的范围极其广泛。
例如,在数学领域,微积分、概率统计、随机过程、数值分析等都是数字信号处理的基本工具,与网络理论、信号与系统、控制论、通信理论、故障诊断等也密切相关。
近来新兴的一些学科,如人工智能、模式识别、神经网络等,都与数字信号处理密不可分。
可以说,数字信号处理是把许多经典的理论体系作为自己的理论基础,同时又使自己成为一系列新兴学科的理论基础。
第二章:TMS320C54x芯片介绍1.总线结构C54x 包括8 条16 比特宽度的总线,其中:一条程序总线(PB):传送取自程序存储器的指令代码和立即操作数三条数据总线(CB、DB、EB):将内部个单元连接在一起,CB和DB传送读自数据存储器的数据,EB传送写入存储器的数据四条地址总线(PAB CAB DAB EAB):传送执行指令所需的地址2.C P UC54x 的CPU 结构包括:40 比特的ALU ,其输入来自16 比特立即数、16 比特来自数据存储器的数据、暂时存储器、T 中的16 比特数、数据存储器中两个16 比特字、数据存储器中32 比特字、累加器中40 比特字。
dsp正弦信号

实验五 正弦信号发生器一、实验目的1. 掌握利用DSP 产生正弦信号的原理2. 熟悉子程序调用的程序结构以及堆栈的使用3. 掌握CCS 的图形输出操作二、实验设备1. 集成开发环境Code Composer Studio (简称CCS )2. 实验代码Sin.s54、Lab.cmd 和Lab.gel三、实验内容1.阅读理解多项式逼近正弦的文档 2.阅读和理解Sin.s54 3.调试正弦波发生器 4.加入断点,并选取图形观测,利用动画及时更新 5.试利用迭代的方法来实现正弦信号发生器四、实验结果和提示1. 2345sin()= 3.140625 + 0.02026367 - 5.325196 + 0.5446778 + 1.800293x x x x x x x 为第一象限内的弧度值。
因为sin()sin(),sin()sin()x x x x π-=-=-,所以只需将第二,三,四象限内的弧度值转换到第一象限即可计算出相应的正弦函数值。
由于有限精度,规定弧度值从~ππ-,其中π=0x7FFF ,π/2=0x4000,π-=0x8000。
利用级数展开产生正弦波,必须在调用计算子程序之前备份好累加器A 中的当前弧度值,以便计算结束后实现x 增量。
正弦波的频率可以通过增幅的大小来进行控制,如果假定程序循环一次为一个时间单位,则正弦波的周期为65536/步长,频率为周期倒数。
x 自动增长时要注意当x 超过π后必须调整到~ππ-的范围内才能调用计算子程序,即若,2x x x ππ>=-则。
2. 需要使用临时数据时,必须用frame 语句留出所需的空间,使用结束后要将堆栈指针还原以防止堆栈内存泄漏。
要注意的是frame 的下一条指令不能使用直接寻址。
3. 注意事项:利用累加器写乘法寄存器T (stlm )之后的下一条指令不能使用T ;条件转移指令xc 在指令访问阶段判断条件,该条件必须在先于xc 指令的2个指令之前产生;条件转移指令bc 是在指令执行阶段判断条件,不存在这方面的问题。
关于DSP的一些反正切查表算法的编写

关于DSP的一些反正切查表算法的编写一直在拿TMS20F28335做电机控制,也从早前的简单寄存器IO口配置时代过渡到了真正的算法时代,很不适应,起初去查各种书籍,网上搜索各种网站,发现书本上讲的很多都是快速傅里叶啊啥的,找不到很原始的像啥低通滤波器,正弦,正切这些函数的编写。
起初写程序发现,C2000的库里支持啥正弦函数,浮点预算,反正弦函数,开根运算等算法,好兴奋。
用了才知道,太慢了,根本没法用在工程上。
关于三角函数的编写,其实都是利用查表发,查表法大家应该都懂。
这个就不再赘述,怎样去查一个正弦表呢?这里做一个基本的介绍。
首先,你可以自己写一个查表数组,也可以在程序初始化生成一个。
Eg:void SinCOS_TAB(void){unsigned char i;float Theta;for(i=0;i<TAB_Max;i++) // #define TAB_Max 180{Theta = i * Step_Angle; // Step_Angle=1.74532925E-02Sin_tab[i] =sin(Theta); // 生成正弦表数组,利用了库里现成的SIN函数Cos_tab[i] =cos(Theta); // 生成余弦表数组}}为啥我的数组里面只有180个元素呢?一:我的精度要求不高,我是一度一个步进角的,如果你要更高的精度,你可以选择容量更大的数组。
二:我不想因为庞大的浮点数组占据太大的存储空间,所以我利用了奇函数,偶函数的原理再次,就进入正题写查表程序,就我们初中数学所知,正弦函数是奇函数,余弦函数是偶函数,所以我只用了360角度中的一半。
下面为正弦查表程序:/*Refer to the truth that DSP use some SinCos operation will use six or more command* periods , So I look up the pre_generate SINCOS_TAB to speed up the Execution speed*/float SinF(float single){int i=(int)(single*180/pi);float value=0;if(i<0)value = -Sin_tab[i];elsevalue = Sin_tab[i];return value;}看起来应该很简单吧,余弦,正切,余切的编写和上面基本相似。
DSP课程设计--正弦信号发生器的设计

DSP课程设计–正弦信号发生器的设计简介正弦信号发生器是一种常见的电子信号发生器。
在数字信号处理中,正弦信号是非常重要的一种基础信号。
在本次课程设计中,我们将使用MATLAB软件设计一个正弦信号发生器。
设计步骤步骤一:信号采样我们的信号采样频率为fs,即每秒采样多少个点。
首先我们需要设置采样频率。
信号采样频率的选取需要满足采样定理,保证采样信号能够完全还原原信号。
我们使用MATLAB的“fs”命令设置采样频率。
假设我们的采样频率为10KHz,代码为:fs = 10000; % 设置采样频率为10KHz步骤二:生成时域正弦信号根据正弦波方程,我们可以生成时域上的正弦信号:f0 = 1000; % 正弦信号的频率为1kHzA = 1; % 正弦信号的幅度为1Vt = 0:1/fs:1; % 假设信号长度为1秒y = A * sin(2 * pi * f0 * t);代码中,我们生成了一个正弦信号,频率为1kHz,幅度为1V,信号长度为1秒,并将其存放在y变量中。
步骤三:对信号进行FFT变换为了验证我们生成的信号是否正确,我们需要对信号进行FFT变换。
FFT变换可以将一个时域信号转化为频域信号。
我们使用MATLAB的“fft”命令对信号进行FFT变换。
代码如下:Y = fft(y); % 对信号y进行FFT变换,得到频域信号YL = length(y); % 计算信号的长度P2 = abs(Y/L); % 取FFT变换结果的绝对值,然后除以长度LP1 = P2(1:L/2+1);P1(2:end-1) = 2*P1(2:end-1);f = fs*(0:(L/2))/L; % 生成频率坐标轴代码中,我们使用FFT变换对信号y进行变换,并将结果存放在Y变量中。
然后我们根据FFT变换结果,得到频率分量以及对应的幅度分量。
步骤四:绘制频域正弦信号最后,我们使用MATLAB的plot函数绘制频域信号采样结果图。
DSP课程设计 正弦信号的产生

DSP原理及应用课程设计课题:正弦信号发生器的设计班级:通信0802姓名:学号:2008001322课题 正弦信号发生器一、 设计目的学会用ccs 集成开发软件,在开发环境下完成工程项目创建,程序编辑,编译,链接,调试和数据分析。
二、 设计内容用ccs 软件编写程序产生正弦波三、 设计实现正弦波信号发生器已被广泛地应用于通信、仪器仪表和工业控制等领域的信号处理系统中。
通常有两种方法可以产生正弦波,分别为查表法和泰勒级数展开法。
查表法是通过查表的方式来实现正弦波,主要用于对精度要求不很高的场合。
泰勒级数展开法是根据泰勒展开式进行计算来实现正弦信号,它能精确地计算出一个角度的正弦和余弦值,且只需要较小的存储空间。
本次主要用泰勒级数展开法来实现正弦波信号。
产生正弦波的算法正弦函数和余弦函数可以展开成泰勒级数,其表达式:取泰勒级数的前5项,得近似计算式:-+-+-=!9!7!5!3)sin(9753x x x x x x -+-+-=!8!6!4!21)cos(8642x x x x x ))))((((981761541321 !9!7!5!3)sin(22229753⨯-⨯-⨯-⨯-=+-+-=x x x x x x x x x x x )))(((87165143121 !8!6!4!21)cos(22228642⨯-⨯-⨯--=+-+-=x x x x x x x x x递推公式:sin(nx) = 2cos(x)sin[(n-1)x]-sin[(n-2)x]cos(nx) = 2cos(x)sin[(n-1)x]-cos[(n-2)x]由递推公式可以看出,在计算正弦和余弦值时,需要已知cos(x)、sin(n-1)x、sin(n-2)x和cos(n-2)x。
计算一个角度x的正弦值,可利用泰勒级数的展开式,采用子程序的调用方式来实现。
在调用前先在数据存储器d_xs单元中存放x的弧度值,计算结果存放在d_sinx单元中四、设计步骤1、CCS软件的操作:(1)建立工程:点击菜单project-new,在弹出的窗口中输入工程名,后缀是.pjt;(2)建立文件:点击菜单file-new-source file,建立汇编语言文件和链接命令文件;(3)将文件加入工程:点击菜单project-add files to project,选择要加入的文件添加到工程;(4)工程的汇编链接:点击菜单project-rebuild all,若汇编链接成功会生成.out文件;(5)装载可执行程序:点击菜单file-lode program,装载.out文件;(6)执行程序:点击菜单debug-run;(7)观察结果。
DSP正弦函数程序

1 正余弦的泰勒级数展开式正弦函数和余弦函数可以展开的泰勒级数如下:-+-+-=!x !x !x !x x x 9753)sin(9753 (1)-+-+-=!x !x !x !x x 86421)cos(8642 (2)若要计算一个角度x 的正弦和余弦值,可取泰勒级数的前五项进行计算。
!x !x !x !x x x 9753)sin(9753+-+-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=9*817*615*413*212222x x x x x (3) !x !x !x !x x 86421)cos(8642+-+-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=8*716*514*31212222x x x x (4) 由式(3)和(4)可得导出递推公式,即])2sin[(])1sin[()cos(2)sin(x n x n x nx ---= ])2cos[(])1sin[()cos(2)cos(x n x n x nx ---=由递推公式可以看出,在计算正弦和余弦值时,不仅需要已知cos(x),而且需要x n )1sin[(-、x n )2sin[(-和x n )2cos[(-。
2 存储空间分配在正弦函数的计算程序所需要的存储空间有四个已初始化的数据段table_s 与若干个程序段组成的已初始化段和九个存储空间未初始化段,分别为:d_xs 、d_squr_xs 、d_temp_s 、d_sinx 、c_1_s 、d_coef_s(4个存储空间)。
其存储空间分布如下:计算正弦值存储单元分配3流程图4.程序.title "sin.asm".mmregs.def start.ref sin_start,d_xs,d_sinxSTACK: .usect "STACK",10HS tart: STM #STACK+10,SPLD #d_xs,DPST #6487H,d_xsCALL sin_startend: B endsin_start:.def sin_startD_coef_s .usect "coef_s",4.dataTable_s: .word 01C7H.word 030bH.word 0666H.word 1556Hd_xs .usect "sin_vars",1 ;定义未初始化段d_squr_xs .usect "sin_vars",1d_temp_s .usect "sin_vars",1d_sinx .usect "sin_vars",1c_1_s .usect "sin_vars",1.textSSBX FRCT ;设置小数乘法STM #d_coff_s,AR4RPT #3MVPD #table_s,*AR4+ ;c1=1/72,c2=1/42,c3=1/20STM #d_coef_s,AR2STM #d_xs,AR3STM #c_1_s,AR5ST #7FFFH,c_1_sSQUR *AR3+,A ;求x的平方值ST A,*AR3||DL *AR5,B ;B=1MASR *AR3+,*AR2+,B,A ;A=(1-x^2)/72;T = x^2 MPYA A ;A=x^2(1-x^2)/72STH A,*AR3 ; AR3=d_temp_s= x^2(1-x^2)/72MASR *AR3-,*AR2+,B,A ; A = 1-x^2/42(1-x^2/72); T =x^2(1-x^2/72)MPYA *AR3+ ; B = X^2(1-x^2/42(1-x^2/72))ST B,*AR3 ; AR3=d_temp_s=B||DL *AR5,BMASR *AR3-,*AR2+,B,A;A=1-x^2/20(1-x^2/42(1-x^2/7 2)MPYA*AR3+ ;B=(1-x^2/20(1-x^2/42(1-x^2/72))*x^2ST B,*AR3; d_temp_s= B = (1-x^2/20(1-x^2/42(1-x^2/72))*x^2||DL *AR5,BMASR *AR3-,*AR2+,B,A;A=1-x^2/6(1-x^2/20(1-x^2/42(1-x^2/72))*x^2STM #d_xs,AR3MPYA AR3;B=x(1-x^2/6(1-x^2/20(1-x^2/42(1-x^2/72 ))*x^2)STH B, d_sinx ; d_sinx=b 的出结果RET.end。
基于DSP的正弦信号发生器的设计

图1 程序流程图
4、 程序设计
4.1 产生正弦波程序清单sin.asm
.title "sin.asm" //为汇编文件取名为“sin.asm”
.mmregs
/定/ 义存储器映像寄存器
.def
_c_int00
.ref
sinx,d_xs,d_sinx,cosx,d_xc,d_cosx //定义标
号
sin_x: .usect "sin_x",360 //为"sin_x"保留360个存储空间
MPYA
*AR2+ /B/=x^2(1-x^2/30(1-x^2/56))
2(1-x^2/30(1-x^2/56))
||LD *AR4,B //B=1
MASR
*AR2-,*AR3+,B,A //A= 1-x^2/12(1-x^2/30(1-x^2/56))
SFTA
A,-1,A
NEG
A
MPYA
*AR2+ //B=1-x^2/2(1-x^2/12(1-x^2/30(1-x^2/56)))
STM
#d_xc,AR2
/A/R2 指向d_xc首地址
STM
#c_l_c,AR4 /A/R4指向c_l_c首地址
ST
#7FFFh,c_l_c /7/FFFh→c_l_c
SQUR
*AR2+,A
/求/ x的平方存放在累加器A中
ST
A,*AR2
/(/ A)左移16位→AR2
||LD *AR4,B
/(/ AR4)左移16位→B
d_temp_c .usect "cos_vars",1 //为d_temp_c中cos_vars保存1个存储
dsp课程设计正弦

dsp课程设计正弦一、教学目标本章节的教学目标是使学生掌握正弦函数的基本概念、性质和图像,能够运用正弦函数解决实际问题。
具体目标如下:1.知识目标:学生能够准确理解正弦函数的定义,掌握正弦函数的性质,包括周期性、对称性和奇偶性;了解正弦函数的图像特点,能够绘制出正弦函数的图像。
2.技能目标:学生能够运用正弦函数解决简单的三角问题,如求解角度、计算三角函数值等;能够利用正弦函数进行函数图像的变换,如平移、伸缩等。
3.情感态度价值观目标:学生能够积极参与课堂讨论,提出问题并解决问题;通过学习正弦函数,培养对数学的兴趣和好奇心,提高对数学美的欣赏能力。
二、教学内容本章节的教学内容主要包括正弦函数的定义、性质、图像以及应用。
具体安排如下:1.第一课时:正弦函数的定义和性质,包括周期性、对称性和奇偶性。
2.第二课时:正弦函数的图像,包括绘制方法和平移、伸缩等变换。
3.第三课时:正弦函数的应用,包括解决三角问题和实际应用问题。
三、教学方法为了激发学生的学习兴趣和主动性,本章节将采用多种教学方法:1.讲授法:教师通过讲解正弦函数的定义、性质和图像,引导学生理解正弦函数的基本概念。
2.讨论法:学生分组讨论正弦函数的应用问题,培养学生的合作能力和解决问题的能力。
3.案例分析法:教师给出实际应用问题,引导学生运用正弦函数进行解决,提高学生的实际应用能力。
4.实验法:学生进行正弦函数图像的绘制实验,培养学生的实验操作能力和观察能力。
四、教学资源为了支持教学内容和教学方法的实施,丰富学生的学习体验,我们将准备以下教学资源:1.教材:正弦函数的相关内容,包括定义、性质、图像和应用。
2.参考书:提供额外的学习资料,帮助学生深入理解正弦函数的相关知识。
3.多媒体资料:正弦函数的图像动画演示,帮助学生直观地理解正弦函数的图像特点。
4.实验设备:绘图板、尺子等,用于学生进行正弦函数图像的绘制实验。
五、教学评估本章节的评估方式将包括以下几个方面:1.平时表现:通过观察学生在课堂上的参与度、提问回答和小组讨论的表现来评估学生的学习态度和理解程度。
DSP28335生成正弦波的程序

DSP28335⽣成正弦波的程序//产⽣周期变化的正弦波#include "DSP2833x_Device.h" // DSP2833x Headerfile Include File #include "DSP2833x_Examples.h" // DSP2833x Examples Include File #include "IQmathLib.h"#include "qmath.h"#include "math.h"#define N 33#define PI 3.1415925#define PRD 600float M=0.8;int i;//double a[N];//unsigned int n=0;//float Q;#define PWM1_INT_ENABLE 1#define PWM2_INT_ENABLE 1#define PWM3_INT_ENABLE 1void InitEPwm1Example(void);//void InitEPwm2Example(void);//void InitEPwm3Example(void);interrupt void epwm1_timer_isr(void);//interrupt void epwm2_timer_isr(void);//interrupt void epwm3_timer_isr(void);//void InitCmp();//extern Uint16 NN,MM;//Uint16 NN=24,MM=1;//Uint16 n=0;Uint16 cmp1[360],cmp2[360],cmp3[360];Uint32 EPwm1TimerIntCount;Uint32 EPwm2TimerIntCount;Uint32 EPwm3TimerIntCount;void main(void){InitSysCtrl();InitEPwm1Gpio();// InitEPwm2Gpio();// InitEPwm3Gpio();DINT;InitPieCtrl();IER = 0x0000;IFR = 0x0000;InitPieVectTable();EALLOW; // This is needed to write to EALLOW protected registers PieVectTable.EPWM1_INT = &epwm1_timer_isr;// PieVectTable.EPWM2_INT = &epwm2_timer_isr;// PieVectTable.EPWM3_INT = &epwm3_timer_isr;EDIS;EALLOW;SysCtrlRegs.PCLKCR0.bit.TBCLKSYNC = 0; // Stop all the TB clocksEDIS;InitEPwm1Example();// InitEPwm2Example();// InitEPwm3Example();// InitCmp();EALLOW;SysCtrlRegs.PCLKCR0.bit.TBCLKSYNC = 1;EDIS;EPwm1TimerIntCount = 0;EPwm2TimerIntCount = 0;EPwm3TimerIntCount = 0;IER |= M_INT3;PieCtrlRegs.PIEIER3.bit.INTx1 = PWM1_INT_ENABLE;// PieCtrlRegs.PIEIER3.bit.INTx2 = PWM2_INT_ENABLE;// PieCtrlRegs.PIEIER3.bit.INTx3 = PWM3_INT_ENABLE;EINT; // Enable Global interrupt INTMERTM;{asm(" NOP");}}void InitEPwm1Example(){EPwm1Regs.TBCTL.bit.SYNCOSEL = TB_CTR_ZERO;//zhuyiEPwm1Regs.TBPRD = PRD; //载波周期=2*1500TBCLKEPwm1Regs.TBPHS.half.TBPHS = 0x0000; // Phase is 0EPwm1Regs.TBCTL.bit.PRDLD = TB_SHADOW;EPwm1Regs.TBCTR = 0x0000;EPwm1Regs.TBCTL.bit.CTRMODE = TB_COUNT_UPDOWN; // Count up downEPwm1Regs.TBCTL.bit.PHSEN = TB_DISABLE; // Disable phase loadingEPwm1Regs.TBCTL.bit.HSPCLKDIV = TB_DIV2; // Clock ratio to SYSCLKOUTEPwm1Regs.TBCTL.bit.CLKDIV = TB_DIV2;EPwm1Regs.CMPCTL.bit.SHDWAMODE = CC_SHADOW; // Load registers every ZERO_PRD EPwm1Regs.CMPCTL.bit.SHDWBMODE = CC_SHADOW;EPwm1Regs.CMPCTL.bit.LOADAMODE = CC_CTR_ZERO; //??EPwm1Regs.CMPCTL.bit.LOADBMODE = CC_CTR_ZERO;// EPwm1Regs.CMPA.half.CMPA =1000;EPwm1Regs.AQCTLA.bit.CAU = AQ_CLEAR; // Clear PWM1A on CAUEPwm1Regs.AQCTLA.bit.CAD = AQ_SET;EPwm1Regs.AQCTLB.bit.CAU = AQ_SET; // SET PWM1B on CAU,输出互补波形EPwm1Regs.AQCTLB.bit.CAD = AQ_CLEAR;//set dead band//设置中断EPwm1Regs.ETSEL.bit.INTSEL = ET_CTR_PRD; //? Select INT on Zero Prd eventEPwm1Regs.ETSEL.bit.INTEN = PWM1_INT_ENABLE; // Enable INTEPwm1Regs.ETPS.bit.INTPRD = ET_1ST;}/*void InitCmp(){// Uint16 i = 0;if(i{cmp1[i]=(Uint16)(EPwm1Regs.TBPRD*0.25*(1+M*sin((2*i)*PI/N)+1+M*sin((2*i+1)*PI/N)));// cmp2[i]=(Uint16)(EvaRegs.T1PR*0.25*(1+M*sin((2*i)*PI/N+PI*4/3)+1+M*sin((2*i+1)*PI/N+PI*4/3))); // cmp3[i]=(Uint16)(EvaRegs.T1PR*0.25*(1+M*sin((2*i)*PI/N+PI*2/3)+1+M*sin((2*i+1)*PI/N+PI*2/3))); i++;}else{i=0;}}*///⽐较值是按正弦波变化的interrupt void epwm1_timer_isr(void){if(i{// cmp1[i]=(Uint16)(EPwm1Regs.TBPRD*sin((2*i)*PI/N)cmp1[i]=(Uint16)(EPwm1Regs.TBPRD*0.25*(1+M*sin((2*i)*PI/N)+1+M*sin((2*i+1)*PI/N)));// cmp2[i]=(Uint16)(EvaRegs.T1PR*0.25*(1+M*sin((2*i)*PI/N+PI*4/3)+1+M*sin((2*i+1)*PI/N+PI*4/3))); // cmp3[i]=(Uint16)(EvaRegs.T1PR*0.25*(1+M*sin((2*i)*PI/N+PI*2/3)+1+M*sin((2*i+1)*PI/N+PI*2/3))); EPwm1Regs.CMPA.half.CMPA = cmp1[i];i++;}else{i=0;}EPwm1Regs.ETCLR.bit.INT = 1;PieCtrlRegs.PIEACK.all = PIEACK_GROUP3;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
摘要泰勒级数展开法作为一种数学方法,在科研和平时的数据处理方面应用的很广泛。
尤其是在通信、仪器仪表和工业控制等领域应用更为广泛。
在科技高速发展的今天,对函数的计算不仅要求有很高的精度,还对计算的时间又很高的要求,必须在很短的时间内完成数据的处理,否则根本不能完成大批量数据的实时性计算和处理。
介于DSP芯片运算速度快的特点,用DSP芯片完成这些算法已越来越受到重视。
产生正弦波,分别是查表法和泰勒级数展开法。
查表法应用于精度要求不很高的场合,而泰勒级数展开法是一种比查表法更为有效的方法。
它能精确的计算出一个角度的正弦和余弦值,且占用的储存空间较小,体现了它的优越性。
关键词: DSP 泰勒级数正弦波目录摘要 (I)1、正余弦信号发生器的实现原理 (1)1.1、正弦波信号发生器 (1)2、正弦波的实现 (2)2.1、计算一个角度的正弦值 (2)2.2、计算一个角度的余弦值 (4)3、正弦波的实现 (8)4、链接文件 (10)5、调试结果 (12)总结 (13)参考文献 (14)1、正余弦信号发生器的实现原理1.1、正弦波信号发生器泰勒级数展开法是根据泰勒展开式进行计算来实现正弦信号,它能精确地计算出一个角度的正弦和余弦值,且只需要较小的存储空间。
本次主要用泰勒级数展开法来实现正弦波信号。
正弦函数和余弦函数可以展开成泰勒级数,其表达式:3579sin()3!5!7!9!x x x x x x =-+-+-2468cos()12!4!6!8!x x x x x =-+-+-取泰勒级数的前5项,得近似计算式:35792222sin()3!5!7!9!111123456789(((())))x x x x x x xx x x x =-+-+=----⨯⨯⨯⨯ 24682222cos()12!4!6!8!11112345678((()))x x x x x x xx x =-+-+=----⨯⨯⨯ 递推公式:sin(nx ) = 2cos(x )sin[(n -1)x ]-sin[(n -2)x ] cos(nx ) = 2cos(x )sin[(n -1)x ]-cos[(n -2)x ]由递推公式可以看出,在计算正弦和余弦值时,需要已知cos(x )、sin(n -1)x 、sin(n -2)x 和cos(n -2)x 。
2、正弦波的实现2.1、计算一个角度的正弦值计算一个角度x的正弦值,可利用泰勒级数的展开式,采用子程序的调用方式来实现。
在调用前先在数据存储器d_xs单元中存放x的弧度值,计算结果存放在d_sinx单元中。
程序中要用到一些存储单元存放数据和变量,存储单元的分配如下:d_xs:x; d_squr_xs:x2d_temp_s:暂存; d_sinx:计算结果sin xc_1_s:7FFFh (数值1);d_coef_s :泰勒系数存储单元分配图:数据存储器程序存储器表1计算正弦值存储单元分配程序清单sinx.asm:.title “sinx.asm”.mmregs.def start.ref sin_start,d_xs,d_sinxSTACK:.usect “STACK”,10start: STM #STACK+10,SPLD #d_xs,DPST #6487H,d_xsCALL sin_startend: B endsin_start:.def sin_startd_coef_s .usect “coef_s”,4.datatable_s: .word 01C7H ;c1=1/(8*9) .word 030BH ;c2=1/(6*7) .word 0666H ;c3=1/(4*5) .word 1556H ;c4=1/(2*3) d_xs .usect “sin_vars”,1d_squr_xs .usect “sin_vars”,1d_temp_s .usect “sin_vars”,1d_sinx .usect “sin_vars”,1c_1_s .usect “sin_vars”,1.textSSBX FRCTSTM #d_coef_s,AR4RPT #3MVPD #table_s,*AR4+STM #d_coef_s,AR2STM #d_xs,AR3STM #c_1_s,AR5ST #7FFFH,c_1_sSQUR *AR3+,A ;求x的平方值ST A,*AR3 ;x平方值存入(AR3) || LD *AR5,B ;B=1MASR *AR3+,*AR2+,B,A;A=1-x^2/72,T=x^2MPYA A ;A=T*ASTH A,*AR3 ;(d_temp_s) = x^2(1-x^2/72)MASR *AR3-,*AR2+,B,A ;A=1-x^2/42(1-x^2/72);T= x^2(1-x^2/72) MPYA *AR3+ ;B= x^2(1- x^2/42(1- x^2/72))ST B,*AR3 ;(d_temp_s)= x^2(1- x^2/42(1- x^2/72))|| LD *AR5,B ;B=1MASR *AR3-,*AR2,B,A;A=1-x^2/20(1-x^2/42(1-x^2/72)) MPYA *AR3+ ;B=x^2(1-x^2/20(1-x^2/42(1-x^2/72)))ST B,*AR3 ;(d_temp_s) =……|| LD *AR5,B ;B=1MASR *AR3-,*AR2,B,A;A=1-x^2/6(1-x^2/20(1-x^2/42(1-x^2/72))) MPYA d_xs ;B=x(1-x^2/6(1-x^2/20(1-x^2/42(1-x^2/72))))STH B,d_sinx ;sin(theta)RET.end2.2、计算一个角度的余弦值计算余弦值与计算正弦值相同。
存储单元分配图:数据存储器程序存储器表2 计算余弦值存储单元分配程序清单cosx.asm:.title “cosx.asm”.mmregs.def _c_int00.ref cos_start,d_cosxSTACK: .usect “STACK”,10_c_int00:STM # STACK+10,spLD #d_xc,DPST #6487h,d_xcCALL cos_startend: B endcos_start:.def cos_startd_coeff .usect “coef_c”,4.dataTable .word 0249h ; c1=1/(7*8).Word 0444h ; c2=1/(5*6).Word 0aahh ; c3=1/(3*4).word 4000h ; c4=1/2 d_x .usect “cos_vars”,1d_squr_x .usect “cos_vars”,1d_temp .usect “cos_vars”,1d_cosx .usect “cos_vars”,1c_1 .usect “cos_vars”,1.textSSBX FRCTSTM #d_coef_c,AR4Rpt #3MVPD #table_c,*AR4+STM #d_coef_c,AR2STM #d_xc,AR3STM #c_1_c,AR5ST #7FFFH,c_1_cSQUR *AR3+.A ;求x的平方值ST A,*AR3 ;x平方值存入(AR3)|| LD *AR5,B ;B=1MASR *AR3-,*AR2+,B,A ;A=1-x^2/56,T=x^2 MPYA A ;A=T*ASTH A,*AR3 ;(d_temp_c) =x^2(1-x^2/56) MASR *AR-,*AR3+,B,A ;A=1-x^2/30(1-x^2/56);T= x^2(1-x^2/56) MPYA *AR3+ ;B= x^2(1- x^2/30(1- x^2/56))ST B,*AR3 ;(d_temp_s)= x^2(1- x^2/30(1- x^2/56))||LD *AR5,B ;B=1MASR *AR3-,*AR2,B,A;;A=1-x^2/12(1-x^2/30(1-x^2/56)) SFTA A,-1,A ;-1/2NEG AMPYA *AR3+ ;B=-x^2/2(1-x^2/12(1-x^2/30(1-x^2/56))MAR *AR2+RETDADD *AR5,16,B;B=1-x^2/2(1-x^2/12(1-x^2/30(1-x^2/56))STH B,*AR3RET.end3、正弦波的实现利用计算一个角度的正弦值和余弦值程序公式可实现正弦波,步骤如下:第一步:利用sin_start 和cos_start子程序,计算0o~45o(间隔为0.5o)的正弦和余弦值。
第二步:利用sin(2x)=2sin(x)cos(x),计算0-90o的正弦值(间隔为1o).第三步:通过复制,获得0-359o的正弦值。
第四步:将0-359o的正弦值重复从PA口输出,便可得到正弦波。
程序清单sin.asm:.title “sinx_asm”.mmregs.def start.ref d_xs,sinx,d_sinx,d_xc,cosx,d_coxsin_x: .usect “sin_x”,360STACK .usect “STACK”,10k_theta .286 ;theta=pi/360PA0 .set 0Start: .textSTM #STACK+10,SPSTM #0,AR0 ;AR0=x=0STM k_theta,AR1 ;设置增量STM #sin_x,AR7 ;AR7指向sin_xSTM #90,BRC;设置重复次数,计算sin0-sin9RPTB loop-1LDM AR0,ALD #d_xs,DPSTL A,@d_xsSTL A,@d_xcCALL sin_startCALL cos_startLD #d_sinx,DPLD @d_sinx,16,A ;求得sinx加载累加器AMPYA @d_cosx ;计算sinx*cosx,结果存BSTH B,1,*AR7+ ;计算2*sinx*cosx,结果存AR7MAR *AR0+0Loop1: STM #sin_x+89,AR6 ;AR6指向sin_x+89 STM #88,BRC ;设置重复次数,计算sin91至sin197RPTB loop2-1LD *AR6-,ASTL A,*AR7+Loop: STM #179,BRC ;设置重复次数,计算sin180至sin359STM #sin_x,AR6 ;AR6指向sin_xRPTB loop3-1LD *AR6+,ANEG ASTL A,*AR7+Loop3_: STM #sin_x,AR7 ;AR7指向sin_xSTM #1,AR1STM #360,BK ;设置缓冲区长度Loop4: PORTW *AR7+0%,PA0 ;输出正弦值B loop4 ;循环输出,产生正弦波.end4、链接文件链接命令文件是将链接的信息放在一个文件中,这在多次使用同样的链接信息时,可以方便地调用。
