解直角三角形应用题专题练习
解直角三角形应用题专题练习

`解直角三角形应用题专题练习一.解答题(共10 小题)1.( 2015?鄂尔多斯)为响应国家的“节能减排”政策,某厂家开发了一种新式的电动车,如图,它的大灯 A 射出的光辉AB 、AC 与地面 MN 的夹角分别为22°和 31°,AT⊥ MN ,垂足为 T,大灯照亮地面的宽度BC 的长为m.(1)求 BT 的长(不考虑其他因素).(2)一般正常人从发现危险到做出刹车动作的反应时间是,从发现危险到电动车圆满停下所行驶的距离叫做最小安全距离.某人以20km/h 的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是,请判断该车大灯的设计可否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明原因.(参照数据: sin22°≈, tan22°≈, sin31°≈, tan31°≈)2.( 2014?)如图是某商场所下停车场入口的设计图,请依照图中数据计算CE 的长度.(结果保留小数点后两位;参照数据:sin22°, cos22°, tan22°)`3.( 2015?模拟)超速行驶是惹起交通事故的主要原因.上周末,小明和三位同学试一试用自己所学的知识检测车速,如图,观察点设在到万丰路的距离为100 米的点 P 处.这时,一辆小轿车由西向东匀速行驶,测得此车从 A 处行驶到 B 地方用的时间为 4 秒且∠ APO=60 °,∠BPO=45 °.(1)求 A、 B 之间的行程;(2)请判断此车可否高出了万丰路每小时70 千米的限制速度?(参照数据:,).4.( 2015?)如图, A 为某旅游景区的最正确观景点,游客可从 B 处乘坐缆车先到达小观景平台 DE 观景,今后再由 E 处连续乘坐缆车到达 A 处,返程时从 A 处乘坐起落电梯直接到达C 处,已知: AC ⊥BC 于 C,DE∥ BC, BC=110 米, DE=9 米, BD=60 米,α=32 °,β=68°,求AC 的高度.(参照数据: sin32°≈;cos32°≈;tan32°≈;sin68°≈;cos68°≈;tan68°≈)5.( 2013?)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部 CD 是水平的,在的照射下,古塔AB 在斜坡上的影长DE 为 18 米,斜坡顶部的影长 DB 为 6 米,光辉AE 与斜坡的夹角为30°,求古塔的高().6.( 2016?模拟)如图,某人在山坡坡脚 A 处测得电视塔尖点 C 的仰角为 60°,沿山坡向上走到P 处再测得点 C 的仰角为 45°,已知 OA=100 米,山坡坡度(竖直高度与水平宽度的比)i=1 : 2,且 O、 A 、 B 在同一条直线上.求电视塔 OC 的高度以及此人所在地址点 P 的铅直高度.(测倾器高度忽略不计,结果保留根号形式)7.( 2015?义乌市)如图,从地面上的点 A 看一山坡上的电线杆PQ,测得杆顶端点P 的仰角是 45°,向前走 6m 到达 B 点,测得杆顶端点P 和杆底端点Q 的仰角分别是60°和 30°.(1)求∠BPQ 的度数;(2)求该电线杆 PQ 的高度(结果精确到 1m).备用数据:,.8.( 2013?)以以下列图,某工程队准备在山坡(山坡视为直线 l)上修一条路,需要测量山坡的坡度,即 tanα的值.测量员在山坡 P 处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖 C 的仰角为 37°,塔底 B 的仰角为°.已知塔高BC=80 米,塔所在的山高OB=220米,OA=200 米,图中的点 O、B、C、A 、P 在同一平面,求山坡的坡度.(参照数据°≈,°≈;sin37°≈, tan37°≈)9.( 2015?)某海域有 A ,B 两个港口, B 港口在 A 港口北偏西 30°方向上,距 A 港口 60 海里,有一艘船从 A 港口出发,沿东北方向行驶一段距离后,到达位于 B 港口南偏东 75°方向的 C 处,求该船与 B 港口之间的距离即 CB 的长(结果保留根号).10.( 2016?模拟)如图,一条高速公路在城市 A 的东偏北30°方向直线延伸,县城M 在城市 A 东偏北 60°方向上,测试员从 A 沿高速公路前行 4000 米到达 C,测得县城 M 位于 C 的北偏西 60°方向上,现要设计一条从县城 M 进入高速公路的路线,请在高速公路上搜寻连接点N ,使修建到县城 M 的道路最短,试确定 N 点的地址并求出最短路线长.(结果取整数,≈)``解直角三角形应用题专题练习参照答案与试题分析一.解答题(共10 小题)1.( 2015?鄂尔多斯)为响应国家的“节能减排”政策,某厂家开发了一种新式的电动车,如图,它的大灯 A 射出的光辉AB 、AC 与地面 MN 的夹角分别为22°和 31°,AT⊥ MN ,垂足为 T,大灯照亮地面的宽度BC 的长为m.(1)求 BT 的长(不考虑其他因素).(2)一般正常人从发现危险到做出刹车动作的反应时间是,从发现危险到电动车圆满停下所行驶的距离叫做最小安全距离.某人以20km/h 的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是,请判断该车大灯的设计可否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明原因.(参照数据: sin22°≈, tan22°≈, sin31°≈, tan31°≈)【解答】解:( 1)依照题意及图知:∠ACT=31°,∠ ABT=22°∵A T ⊥MN∴∠ ATC=90 °在Rt△ ACT 中,∠ ACT=31 °∴tan31°=可设 AT=3x ,则 CT=5x在Rt△ ABT 中,∠ ABT=22 °∴tan22°=即:解得:∴,∴;`(2),,∴该车大灯的设计不能够满足最小安全距离的要求.2.( 2014?)如图是某商场所下停车场入口的设计图,请依照图中数据计算CE 的长度.(结果保留小数点后两位;参照数据:sin22°, cos22°, tan22°)【解答】解:由已知有:∠ BAE=22 °,∠ ABC=90 °,∠CED= ∠AEC=90 °∴∠ BCE=158 °,∴∠ DCE=22 °,又∵ tan∠ BAE=,∴B D=AB ?tan∠ BAE ,又∵ cos∠ BAE=cos ∠ DCE=,∴CE=CD ?cos∠ BAE=(BD ﹣ BC) ?cos∠BAE=( AB ?tan∠ BAE ﹣ BC) ?cos∠BAE=(10×﹣)×≈( m).3.( 2015?模拟)超速行驶是惹起交通事故的主要原因.上周末,小明和三位同学试一试用自己所学的知识检测车速,如图,观察点设在到万丰路的距离为100 米的点 P 处.这时,一辆小轿车由西向东匀速行驶,测得此车从 A 处行驶到 B 地方用的时间为 4 秒且∠ APO=60 °,∠BPO=45 °.(1)求 A、 B 之间的行程;(2)请判断此车可否高出了万丰路每小时70 千米的限制速度?(参照数据:,).【解答】解:( 1)在 Rt△ BOP 中,∠ BOP=90 °,∵∠ BPO=45 °,OP=100 ,∴O B=OP=100 .`在Rt△ AOP 中,∠ AOP=90 °,∵∠ APO=60 °,∴AO=OP ?tan∠ APO .∴A0=100,AB=100 (﹣ 1)(米);(2)∵此车的速度 ==25 (﹣1)≈25× 米/秒,70 千米 /小时 =≈ 米/秒,18.25 米 /秒< 19.4 米 /秒,∴此车没有高出了万丰路每小时70 千米的限制速度.4.( 2015?)如图, A 为某旅游景区的最正确观景点,游客可从 B 处乘坐缆车先到达小观景平台 DE 观景,今后再由 E 处连续乘坐缆车到达 A 处,返程时从 A 处乘坐起落电梯直接到达C 处,已知: AC ⊥BC 于 C,DE∥ BC, BC=110 米, DE=9 米, BD=60 米,α=32 °,β=68°,求AC 的高度.(参照数据: sin32°≈;cos32°≈;tan32°≈;sin68°≈;cos68°≈;tan68°≈)【解答】解:∵ cos∠ DBF=,∴B F=60 ×0.85=51,FH=DE=9 ,∴E G=HC=110 ﹣ 51﹣9=50,∵tan∠AEG= ,∴A G=50 ×2.48=124 ,∵s in ∠DBF= ,∴D F=60 ×0.53=31.8 ,∴C G=31.8 ,∴A C=AG+CG=124+31.8=155.8 .5.( 2013?)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部 CD 是水平的,在的照射下,古塔AB 在斜坡上的影长DE 为 18 米,斜坡顶部的影长 DB 为 6 米,光辉AE 与斜坡的夹角为30°,求古塔的高().【解答】解:延伸 BD 交 AE 于点 F,作 FG⊥ ED 于点 G,∵斜坡的顶部CD 是水平的,斜坡与地面的夹角为30°,∴∠ FDE= ∠ AED=30 °,∴F D=FE ,∵DE=18 米,∴EG=GD= ED=9 米,在Rt△ FGD 中,DF===6,∴FB= ( 6+6)米,在Rt△ AFB 中,AB=FB ?tan60°=(6+6 )× =(18+6)≈28.2 米,所以古塔的高约为28.2 米.6.( 2016?模拟)如图,某人在山坡坡脚 A 处测得电视塔尖点 C 的仰角为 60°,沿山坡向上走到P 处再测得点 C 的仰角为 45°,已知 OA=100 米,山坡坡度(竖直高度与水平宽度的比)i=1 : 2,且 O、 A 、 B 在同一条直线上.求电视塔 OC 的高度以及此人所在地址点 P 的铅直高度.(测倾器高度忽略不计,结果保留根号形式)【解答】解:作 PE⊥ OB 于点 E,PF⊥ CO 于点 F,在Rt△ AOC 中, AO=100 ,∠CAO=60 °,∴CO=AO ?tan60°=100(米).设PE=x 米,∵t an∠PAB= = ,∴A E=2x .在 Rt△ PCF 中,∠ CPF=45 °, CF=100﹣x,PF=OA+AE=100+2x,∵P F=CF ,∴100+2x=100﹣x,解得 x=(米).答:电视塔OC 高为 100米,点P的铅直高度为(米).`7.( 2015?义乌市)如图,从地面上的点 A 看一山坡上的电线杆PQ,测得杆顶端点P 的仰角是 45°,向前走 6m 到达 B 点,测得杆顶端点P 和杆底端点Q 的仰角分别是60°和 30°.(1)求∠BPQ 的度数;(2)求该电线杆 PQ 的高度(结果精确到 1m).备用数据:,.【解答】解:延伸 PQ 交直线 AB 于点 E,(1)∠ BPQ=90 °﹣ 60°=30 °;(2)设 PE=x 米.在直角△ APE 中,∠ A=45 °,则AE=PE=x 米;∵∠ PBE=60 °∴∠ BPE=30 °在直角△ BPE 中, BE=PE=x 米,∵A B=AE ﹣ BE=6 米,则x﹣ x=6 ,解得: x=9+3.则 BE= ( 3+3)米.在直角△ BEQ 中, QE=BE=( 3+3) =( 3+)米.∴PQ=PE ﹣ QE=9+3 ﹣( 3+) =6+2≈9(米).答:电线杆 PQ 的高度约9 米.8.( 2013?)以以下列图,某工程队准备在山坡(山坡视为直线 l)上修一条路,需要测量山坡的坡度,即 tanα的值.测量员在山坡 P 处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖 C 的仰角为 37°,塔底 B 的仰角为°.已知塔高BC=80 米,塔所在的山高OB=220米,OA=200 米,图中的点 O、B、C、A 、P 在同一平面,求山坡的坡度.(参照数据°≈,°≈;sin37°≈, tan37°≈)【解答】解:如图,过点P 作 PD⊥ OC 于 D , PE⊥ OA 于 E,则四边形ODPE 为矩形.在Rt△ PBD 中,∵ ∠BDP=90 °,∠ BPD=26.6 °,∴BD=PD ?tan∠°;在Rt△ CPD 中,∵ ∠CDP=90 °,∠CPD=37 °,∴CD=PD ?tan∠ CPD=PD ?tan37°;∵CD ﹣ BD=BC ,∴PD ?tan37°﹣°=80,∴0.75PD ﹣ 0.50PD=80 ,解得 PD=320 (米),∴°≈320×0.50=160 (米),∵OB=220米,∴P E=OD=OB ﹣ BD=60 米,∵OE=PD=320 米,∴A E=OE ﹣ OA=320 ﹣ 200=120 (米),∴tanα===0.5 ,∴坡度为 1: 2.9.( 2015?)某海域有A ,B 两个港口, B 港口在 A 港口北偏西30°方向上,距 A 港口 60 海里,有一艘船从 A 港口出发,沿东北方向行驶一段距离后,到达位于 B 港口南偏东75°方向的 C 处,求该船与 B 港口之间的距离即CB 的长(结果保留根号).【解答】解:作 AD ⊥BC 于 D,∵∠ EAB=30 °,AE ∥ BF,∴∠ FBA=30 °,又∠ FBC=75 °,∴∠ ABD=45 °,又 AB=60 ,∴AD=BD=30,∵∠ BAC= ∠ BAE+ ∠CAE=75 °,∠ ABC=45 °,∴∠ C=60°,在 Rt△ ACD 中,∠C=60 °, AD=30,则 tanC=,∴CD==10,∴BC=30+10.故该船与 B 港口之间的距离CB 的长为 30+10 海里.10.( 2016?模拟)如图,一条高速公路在城市 A 的东偏北30°方向直线延伸,县城M 在城市 A 东偏北 60°方向上,测试员从 A 沿高速公路前行 4000 米到达 C,测得县城 M 位于 C 的北偏西 60°方向上,现要设计一条从县城 M 进入高速公路的路线,请在高速公路上搜寻连接点N ,使修建到县城 M 的道路最短,试确定 N 点的地址并求出最短路线长.(结果取整数,≈)`【解答】解:如图,过M 作 MN ⊥ AC 交于 N 点,即 MN 最短,∵∠ EAD=60 °,∠ CAD=30 °,∴∠ CAM=30 °,∴∠ AMN=60 °,又∵ C 处看 M 点为北偏西60°,∴∠ FCM=60 °,∴∠ MCB=30 °,∵∠ EAC=60 °,∴∠ CAD=30 °,∴∠ BCA=30 °,∴∠ MCA= ∠ MCB+ ∠BCA=60 °,∴在 Rt△ AMC 中,∠ AMC=90 °,∠ MAC=30 °,∴MC=AC=2000 ,∠ CMN=30 °,∴NC= MC=1000 ,∵A C=4000 米,∴AN=AC ﹣ NC=4000 ﹣ 1000=3000(米).答:点 N 到 A 市最短路线3000 米.。
(整理)解直角三角形的应用经典题型
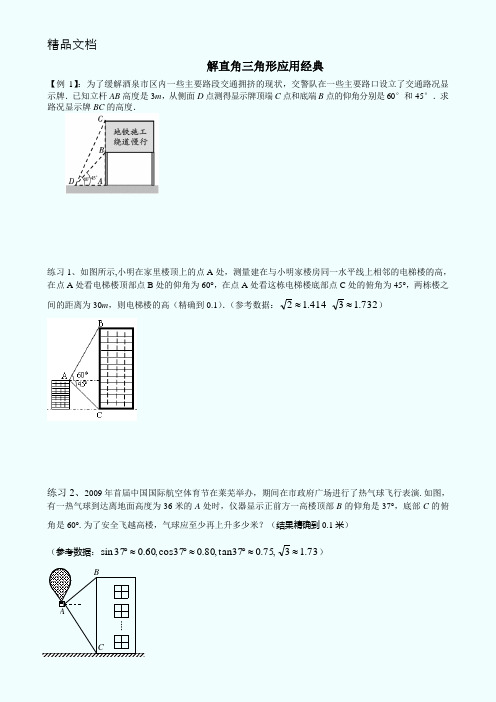
解直角三角形应用经典【例1】:为了缓解酒泉市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌.已知立杆AB 高度是3m ,从侧面D 点测得显示牌顶端C 点和底端B 点的仰角分别是60°和45°.求路况显示牌BC 的高度.练习1、如图所示,小明在家里楼顶上的点A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A 处看电梯楼顶部点B 处的仰角为60°,在点A 处看这栋电梯楼底部点C 处的俯角为45°,两栋楼之间的距离为30m ,则电梯楼的高(精确到0.1).(参考数据:414.12≈732.13≈)练习2、2009年首届中国国际航空体育节在莱芜举办,期间在市政府广场进行了热气球飞行表演.如图,有一热气球到达离地面高度为36米的A 处时,仪器显示正前方一高楼顶部B 的仰角是37°,底部C 的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米) (参考数据:,75.037tan ,80.037cos ,60.037sin ≈︒≈︒≈︒73.13≈)BAC【例2】:在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M 的正西19.5 km 处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A 的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距83km的C处.(1)求该轮船航行的速度;(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.练习:如图,某天然气公司的主输气管道从A市的东偏北30°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市东偏北60°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西60°方向,请你在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,并求AN的长.【例3】:如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60,坡长AB=m320,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=45,求AF的长度(结果精确到1米,参考数据: 414.12≈,732.13≈).NM东北BCAl练习:施工队准备在一段斜坡上铺上台阶方便通行.现测得斜坡上铅垂的两棵树间水平距离AB =4米,斜面距离BC =4.25米,斜坡总长DE =85米. (1)求坡角∠D 的度数(结果精确到1°);(2)若这段斜坡用厚度为17c m 的长方体台阶来铺,需要铺几级台阶?【达标测评】1、如图,一架飞机在空中P 处探测到某高山山顶D 处的俯角为60°,此后飞机以300米/秒的速度沿平行于地面AB 的方向匀速飞行,飞行10秒到山顶D 的正上方C 处,此时测得飞机距地平面的垂直高度为12千米,求这座山的高(精确到0.1千米)2、摩天轮是嘉峪关市的标志性景观之一.某校数学兴趣小组要测量摩天轮的高度.如图,他们在C 处测得摩天轮的最高点A 的仰角为45︒,再往摩天轮的方向前进50 m 至D 处,测得最高点A 的仰角为60︒. 求该兴趣小组测得的摩天轮的高度AB (3 1.732≈, 结果保留整数).17cm(第3题)A BCDEF参考数据 cos20°≈0.94,sin20°≈0.34, sin18°≈0.31,cos18°≈0.95AB12P C D G60AB C D 45°60°3.在一个阳光明媚、清风徐来的周末,小明和小强一起到郊外放风筝﹒他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的C 处(如图).现已知风筝A 的引线(线段AC )长20m ,风筝B 的引线(线段BC )长24m ,在C 处测得风筝A 的仰角为60°,风筝B 的仰角为45°. (1)试通过计算,比较风筝A 与风筝B 谁离地面更高? (2)求风筝A 与风筝B 的水平距离.4. 如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB 长为4米. (1)求新传送带AC 的长度;(2)如果需要在货物着地点C 的左侧留出2米的通道,试判断距离B 点4米的货物MNQP 是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:2≈1.41,3≈1.73,5≈2.24,6≈2.45)AB45° 60°CED。
解直角三角形及其应用练习及答案
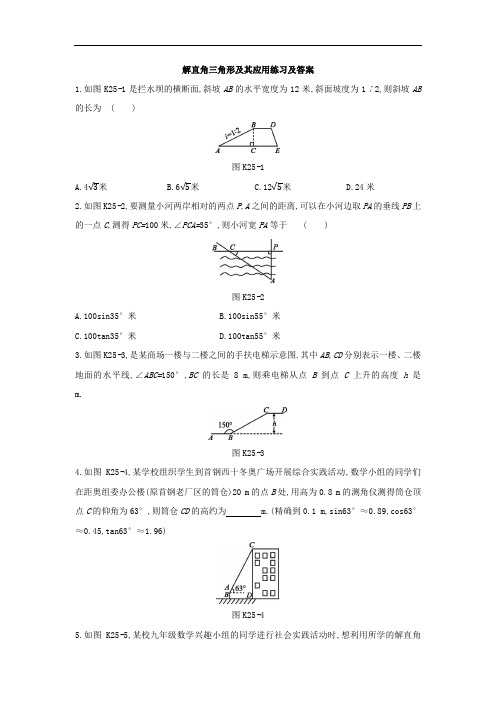
解直角三角形及其应用练习及答案1.如图K25-1是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1∶2,则斜坡AB 的长为()图K25-1A.4√3米B.6√5米C.12√5米D.24米2.如图K25-2,要测量小河两岸相对的两点P,A之间的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于()图K25-2A.100sin35°米B.100sin55°米C.100tan35°米D.100tan55°米3.如图K25-3,是某商场一楼与二楼之间的手扶电梯示意图.其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h是m.图K25-34.如图K25-4,某学校组织学生到首钢西十冬奥广场开展综合实践活动,数学小组的同学们在距奥组委办公楼(原首钢老厂区的筒仓)20 m的点B处,用高为0.8 m的测角仪测得筒仓顶点C的仰角为63°,则筒仓CD的高约为m.(精确到0.1 m,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)图K25-45.如图K25-5,某校九年级数学兴趣小组的同学进行社会实践活动时,想利用所学的解直角三角形的知识测量某塔的高度,他们先在点D用高1.5米的测角仪DA测得塔顶M的仰角为30°,然后沿DF方向前行40 m到达点E处,在E处测得塔顶M的仰角为60°.请根据他们的测量数据求此塔MF的高.(结果精确到0.1米,参考数据:√2≈1.41,√3≈1.73,√6≈2.45)图K25-56.如图K25-6所示,某小组同学为了测量对面楼AB的高度,分工合作,有的组员测得两楼间距离为40米,有的组员在教室窗户处测得楼顶端A的仰角为30°,底端B的俯角为10°,请你根据以上数据,求出楼AB的高度.(精确到0.1米,参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,√2≈1.41,√3≈1.73)图K25-67.2017年5月5日我国自主研发的大型飞机C919成功首飞,如图K25-7给出了一种机翼的示意图,用含有m,n的式子表示AB的长为.图K25-7参考答案1.B [解析] 在Rt △ABC 中,∵i=BC AC =12,AC=12米, ∴BC=6米.根据勾股定理得AB=√AC 2+BC 2=6√5(米).故选B .2.C3.44.40.05.解:由题意:AB=40,CF=1.5,∠MAC=30°,∠MBC=60°, ∴∠AMB=30°,∴∠AMB=∠MAB ,∴AB=MB=40.在Rt △BCM 中,∵∠MCB=90°,∠MBC=60°,∴∠BMC=30°.∴BC=12BM=20.∴MC=2-BC 2=20√3≈34.6,∴MF=MC+CF=36.1.∴塔MF 的高约为36.1米.6.解:过点D 作DE ⊥AB 于点E ,在Rt △ADE 中,∠AED=90°,tan ∠1=AE DE ,∠1=30°, ∴AE=DE ×tan ∠1=40×tan30°=40×√33≈40×1.73×13≈23.1. 在Rt △DEB 中,∠DEB=90°,tan ∠2=BE DE ,∠2=10°, ∴BE=DE ×tan ∠2=40×tan10°≈40×0.18=7.2, ∴AB=AE+BE ≈23.1+7.2=30.3(米).7.m+√33n-n。
九年级数学下册专题28.4 解直角三角形的应用中考真题专项训练(50道)(举一反三)(人教版)

专题28.4 解直角三角形的应用中考真题专项训练(50道)【人教版】考卷信息:本套训练卷共50题,题型针对性较高,覆盖面广,选题有深度,涵盖了解直角三角形的应用中考真题的综合问题的所有类型!一.解答题(共50题)1.(2022·辽宁阜新·中考真题)如图,小文在数学综合实践活动中,利用所学的数学知识测量居民楼的高度AB,在居民楼前方有一斜坡,坡长CD=15m,斜坡的倾斜角为α,cosα= 4.小文在C点处测得楼顶端A的仰角为60°,在D点处测得楼顶端A的仰角为30°(点A,B,5C,D在同一平面内).(1)求C,D两点的高度差;(2)求居民楼的高度AB.(结果精确到1m,参考数据:3≈1.7)使黄河南北“天堑变通途”.已知主塔AB垂直于桥面BC于点B,其中两条斜拉索AD、AC与桥面BC的夹角分别为60°和45°,两固定点D、C之间的距离约为33m,求主塔AB的高度(结果保留整数,参考数据:2≈1.41,3≈1.73)俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5,3≈1.7)【答案】潜艇C离开海平面的下潜深度为308米【分析】过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,分别在Rt三角形ACD中表示出CD和在Rt三角形BCD中表示出BD,从而利用二者之间的关系列出方程求解.根据题意得:∠ACD=30°,∠设AD=x,则BD=BA+AD=1000+在Rt三角形ACD中,CD=在Rt三角形BCD中,BD=CD ∴1000+x=3x⋅tan68°,解得:x=10003⋅tan68°―1=1.7×AB进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东15°方向上,他沿西北方向前进1003米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西60°方向上,(点A、B、C、D在同一平面内)(1)求点D与点A的距离;(2)求隧道AB的长度.(结果保留根号)杆底端有台阶).该小组在C处安置测角仪CD,测得旗杆顶端A的仰角为30°,前进8m 到达E处,安置测角仪EF,测得旗杆顶端A的仰角为45°(点B,E,C在同一直线上),测角仪支架高CD=EF=1.2m,求旗杆顶端A到地面的距离即AB的长度.(结果精确到1m.参考数据:3≈1.7)由题意得:DF=CE=8m,DC=EF=BG=1.2m设AG=x m,在Rt△AFG中,∠AFG=45°,=x(m),∴FG=AGtan45°念“襄樊战役”中牺牲的革命烈士及第一、第二次国内革命战争时期为襄阳的解放事业献身的革命烈士的而兴建的,某校数学兴趣小组利用无人机测量烈士塔的高度.无人机在点A 处测得烈士塔顶部点B 的仰角为45°,烈士塔底部点C 的俯角为61°,无人机与烈士塔的水平距离AD 为10m ,求烈士塔的高度.(结果保留整数.参考数据:sin61°≈0.87,cos61°≈0.48,tan61°≈1.80)善.某市政府为了实现5G 网络全覆盖,2021~2025年拟建设5G 基站3000个,如图,在斜坡CB 上有一建成的5G 基站塔AB ,小明在坡脚C 处测得塔顶A 的仰角为45°,然后他沿坡面CB 行走了50米到达D 处,D 处离地平面的距离为30米且在D 处测得塔顶A 的仰角53°.(点A 、B 、C 、D 、E 均在同一平面内,CE 为地平线)(参考数据:sin53°≈45,cos53°≈35,tan 53°≈43)(1)求坡面CB的坡度;(2)求基站塔AB的高.根据他沿坡面CB行走了50米到达D处,D处离地平面的距离为∴CD=50(米),DM=30(米),根据勾股定理得:CM=CD2―DM2=40(米)∴坡面CB的坡度为;DMCM =3040=34,即坡面CB的坡度比为3:4;船返回舱成功着陆.为弘扬航天精神,某校在教学楼上悬挂了一幅长为8m的励志条幅(即GF=8m).小亮同学想知道条幅的底端F到地面的距离,他的测量过程如下:如图,首先他站在楼前点B处,在点B正上方点A处测得条幅顶端G的仰角为37°,然后向教学楼条幅方向前行12m到达点D处(楼底部点E与点B,D在一条直线上),在点D正上方点C处测得条幅底端F的仰角为45°,若AB,CD均为1.65m(即四边形ABDC为矩形),请你帮助小亮计算条幅底端F到地面的距离FE的长度.(结果精确到0.1m,参考数据:sin37°≈0.60,cos 37°≈0.80,tan37°≈0.75)坡面的坡角由原来的37°减至30°,已知原电梯坡面AB的长为8米,更换后的电梯坡面为AD,点B延伸至点D,求BD的长.(结果精确到0.1米.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0,75,3≈1.73)地面点E处用高1.5m的测角仪DE测得∠ADC=31°,然后沿EB方向向前走3m到达点G 处,在点G处用高1.5m的测角仪FG测得∠AFC=42°.求凉亭AB的高度.(A,C,B三点共线,AB⊥BE,AC⊥CD,CD=BE,BC=DE.结果精确到0.1m)(参考数据:sin 31°≈0.52,cos31°≈0.86,tan31°≈0.60,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)【答案】6.9m【分析】根据题意可得BC=FG=DE=1.5,DF=GE=3,∠ACF=90°,然后设CF=x,则CD=(x+3),先在Rt△ACF中,利用锐角三角函数的定义求出AC的长,再在Rt△ACD中,利用锐角三角函数的定义列出关于x的方程,进行计算即可解答.机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,OA是垂直于工作台的移动基座,AB、BC为机械臂,OA=1m,AB=5m,BC=2m,∠ABC=143°.机械臂端点C到工作台的距离CD=6m.(1)求A、C两点之间的距离;(2)求OD长.(结果精确到0.1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,5≈2.24)【答案】(1)6.7m(2)4.5m【分析】(1)连接AC,过点A作AH⊥BC,交CB的延长线于H,根据锐角三角函数定义和勾股定理即可解决问题.∴OD=AG=4.5m.答:OD的长为4.5m.【点睛】求角的三角画数值或者求线段的长时,我们经常通过观察图形将所求的角成者线段转化到直角三角形中(如果没有直角三角形,设法构造直角三角形),再利用锐角三角画数求解12.(2022·山东日照·中考真题)2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情.如图是某滑雪场的横截面示意图,雪道分为AB,BC两部分,小明同学在C点测得雪道BC的坡度i=1:2.4,在A点测得B点的俯角∠DAB=30°.若雪道AB长为270m,雪道BC 长为260m.(1)求该滑雪场的高度h;(2)据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3,且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.:根据题知坐索道车到达山项,索速车运行的速度是1米/秒,小明要测量莲花山山顶白塔的高度,他在索道A处测得白塔底部B的仰角的为30°,测得白塔顶部C的仰角的为37°.索道车从A 处运行到B处所用时间的为5分钟.(1)索道车从A处运行到B处的距离约为________米;(2)请你利用小明测量的数据,求白塔BC的高度(结果取整数).(参考数据:sin37°≈0.60, cos37°≈0.80,tan37°≈0.75,3≈1.73)的长.(1)如图1所示,将一个测角仪放置在距离灯杆AB底部a米的点D处,测角仪高为b米,从C点测得A点的仰角为α,求灯杆AB的高度.(用含a,b,a的代数式表示)(2)我国古代数学家赵爽利用影子对物体进行测量的方法,在至今仍有借鉴意义图2所示,现将一高度为2米的木杆CG放在灯杆AB前,测得其影长CH为1米,再将木杆沿着BC 方向移动1.8米至DE的位置,此时测得其影长DF为3米,求灯杆AB的高度由题意得BD=a,CD∠B=∠D=∠CEB=90°∴四边形CDBE为矩形,则BE=CD=b,BD=在Rt∆ACE中,tan得AE=CE=CE×tanα15.(2022·湖南郴州·中考真题)如图是某水库大坝的横截面,坝高CD=20m,背水坡BC 的坡度为i1=1:1.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为i2=1:3,求背水坡新起点A与原起点B之间的距离.(参考数据:2≈1.41,3≈1.73.结果精确到0.1m)离,他们借助皮尺、测角仅进行测量,测量结果如下:测量项目测量数据从A处测得路灯顶部P的仰角αα=58°从D处测得路灯顶部P的仰角ββ=31°测角仪到地面的距离AB=DC=1.6m两次测量时测角仪之间的水平距离BC=2m计算路灯顶部到地面的距离PE约为多少米?(结果精确到0.1米.参考数据;cos31°≈0.86,tan31°≈0.60,cos58°≈0.53,tan58°≈1.60)【答案】3.5米【分析】延长DA,交PE于点F,则DF⊥PE,先得到四边形ABCD、CDFE是矩形,然后由解直角三角形求出AF的长度,再求出PF的长度,即可求出答案.【详解】解:如图:延长DA,交PE于点F,则DF⊥PE,∵AB=DC=1.6,AB//DC∴四边形ABCD是平行四边形,∵AB⊥BC,∴四边形ABCD是矩形,同理:四边形CDFE是矩形;∴AD=BC=2,EF=CD=1.6,在直角△PDF中,有PF=DF·tanβ=(AD+AF)·tanβ,在直角△PAF中,有PF=AF·tanα,∴(AD+AF)·tanβ=AF·tanα,即(2+AF)×tan31°=AF×tan58°,∴(2+AF)×0.6=AF×1.6,解得:AF=1.2;∴PF=1.2×1.6≈1.9;∴PE=PF+EF=1.9+1.6=3.5(米);∴路灯顶部到地面的距离PE约为3.5米.【点睛】本题考查了解直角三角形的应用,解直角三角形,矩形的判定和性质,解题的关键是熟练掌握题意,正确的作出辅助线,正确的求出PF的长度.17.(2022·辽宁盘锦·中考真题)如图,小欢从公共汽车站A出发,沿北偏东30°方向走2000米到达东湖公园B处,参观后又从B处沿正南方向行走一段距离,到达位于公共汽车东南方向的图书馆C处.(参考数据:2≈1.414,3≈1.732)(1)求小欢从东湖公园走到图书馆的途中与公共汽车站之间最短的距离;(2)若小欢以100米/分的速度从图书馆C沿CA回到公共汽车站A,那么她在15分钟内能否到达公共汽车站?【答案】(1)小欢从东湖公园走到图书馆的途中与公共汽车站之间最短的距离是1000米(2)小欢15分钟内能到达公共汽车站【分析】(1)过点A作AD⊥C于点D,根据B位于A的北偏东30°方向和AB=2000米可得AD的长度;(2)根据45°角的余弦和AD的长可得AC的长度,再结合小欢的速度可得答案.,∵DC ⊥AM 于点E ,在A 处测得大树底端C 的仰角为15°,沿水平地面前进30米到达B 处,测得大树顶端D 的仰角为53°,测得山坡坡角∠CBM =30°(图中各点均在同一平面内).(1)求斜坡BC 的长;(2)求这棵大树CD 的高度(结果取整数).(参考数据:sin 53°≈45,cos 53°≈35,tan 53°≈43,3≈1.73)【答案】(1)斜坡BC 的长为30米(2)这棵大树CD 的高度约为20米【分析】(1)根据题意可得:∠CAE =15°,AB =30米,根据三角形的外角性质可求出∠ACB =15°,从而得出AB =BC =30米,即可得出答案.(2)在Rt △CBE 中,利用锐角三角函数的定义求出CE ,BE 的长,然后在Rt △DEB 中,利轮航行到A处时,测得码头C在北偏东60°方向上.为了躲避A,C之间的暗礁,这艘货轮调整航向,沿着北偏东30°方向继续航行,当它航行到B处后,又沿着南偏东70°方向航行20海里到达码头C.求货轮从A到B航行的距离(结果精确到0.1海里.参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192).【答案】货轮从A到B航行的距离约为30.6海里.【分析】过B作BD⊥AC于D,在Rt△BCD中,利用正弦函数求得BD=15.32海里,再在Rt△ABD中,利用含30度角的直角三角形的性质即可求解.【详解】解:过B作BD⊥AC于D,由题意可知∠ABE=30°,∠BAC=30°,则∠C=180°-30°-30°-70°=50°,在Rt△BCD中,∠C=50°,BC=20(海里),∴BD= BC sin50°≈20×0.766=15.32(海里),在Rt△ABD中,∠BAD=30°,BD=15.32(海里),∴AB=2BD=30.64≈30.6(海里),答:货轮从A到B航行的距离约为30.6海里.【点睛】本题考查了解直角三角形的应用—方向角问题,正确作出辅助线构造直角三角形是解题的关键.20.(2022·山东青岛·中考真题)如图,AB为东西走向的滨海大道,小宇沿滨海大道参加“低碳生活·绿色出行”健步走公益活动.小宇在点A处时,某艘海上观光船位于小宇北偏东68°的点C处,观光船到滨海大道的距离CB为200米.当小宇沿滨海大道向东步行200米到达点E时,观光船沿北偏西40°的方向航行至点D处,此时,观光船恰好在小宇的正北方向,求观光船从C处航行到D处的距离.(参考数据:sin40°≈0.64,cos40°≈0.77,tan 40°≈0.84,sin68°≈0.93,cos68°≈0.37,tan68°≈2.48)【答案】观光船从C处航行到D处的距离为462.5米【分析】过点C作CF⊥DE于点F,根据题意利用正切函数可得AB=496,由矩形的判定和性质得出CF=BE=296,结合图形利用锐角三角函数解三角形即可.【详解】解:过点C作CF⊥DE于点F,由题意得,∠D=40°,∠ACB=68°,测速仪,如图所示的是该段隧道的截面示意图.测速仪C和测速仪E到路面之间的距离CD=EF=7m,测速仪C和E之间的距离CE=750m,一辆小汽车在水平的公路上由西向东匀速行驶,在测速仪C处测得小汽车在隧道入口A点的俯角为25°,在测速仪E处测得小汽车在B点的俯角为60°,小汽车在隧道中从点A行驶到点B所用的时间为38s(图中所有点都在同一平面内).(1)求A,B两点之间的距离(结果精确到1m);(2)若该隧道限速22m/s,判断小汽车从点A行驶到点B是否超速?通过计算说明理由.(参考数据:3≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,sin65°≈0.9,cos65°≈0.4)天,他们先从基地门口A处向正北方向走了450米,到达菜园B处锄草,再从B处沿正西方向到达果园C处采摘水果,再向南偏东37°方向走了300米,到达手工坊D处进行手工制作,最后从D处回到门口A处,手工坊在基地门口北偏西65°方向上.求菜园与果园之间的距离.(结果保留整数)参考数据:sin65°≈ 0.91,cos65°≈0.42,tan65°≈2.14,sin37°≈ 0.60,cos37°≈ 0.80,tan37°≈0.75的高度,如图,在山坡的坡脚A处测得大楼顶部M的仰角是58°,沿着山坡向上走75米到达B处.在B处测得大楼顶部M的仰角是22°,已知斜坡AB的坡度i=3:4(坡度是指坡面的铅直高度与水平宽度的比)求大楼MN的高度.(图中的点A,B,M,N,C均在同一平面内,N,A,C在同一水平线上,参考数据:tan22°≈0.4,tan58°≈1.6)【详解】分别作BE⊥AC,BF⊥MN,垂足分别为∴∠BEA=∠BFN四边形BENF为矩形,∴BEx,ABE中,分构成如图2,AB是灯杆,CD是灯管支架,灯管支架CD与灯杆间的夹角∠BDC=60°.综合实践小组的同学想知道灯管支架CD的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得AE=3m,EF=8m(A,E,F在同一条直线上).根据以上数据,解答下列问题:(1)求灯管支架底部距地面高度AD的长(结果保留根号);(2)求灯管支架CD的长度(结果精确到0.1m,参考数据:3≈1.73).到某厂房做验证实验.如图,老师在该厂房顶部安装一平面镜MN,MN与墙面AB所成的角∠MNB=118°,厂房高AB= 8 m,房顶AM与水平地面平行,小强在点M的正下方C处从平面镜观察,能看到的水平地面上最远处D到他的距离CD是多少?(结果精确到0.1 m,参考数据:sin34°≈0.56,tan34°≈0.68,tan56°≈1.48)【答案】11.8m【分析】过M点作ME⊥MN交CD于E点,证明四边形ABCM为矩形得到CM=AB=8,∠NMC=180°-∠BNM=62°,利用物理学入射光线与反射光线之间的关系得到∠EMD=∠EMC,且∠CME=90°-∠CMN=28°,进而求出∠CMD=56°,最后在Rt△CMD中由tan∠CMD即可求解.∵C点在M点正下方,∴CM⊥CD,即∠MCD=90°,∵房顶AM与水平地面平行,AB为墙面,∴四边形AMCB为矩形,∴MC=AB=8m,AB∥CM,于2022年3月19日完成首次全货运试飞,很多市民共同见证了这一历史时刻.如图,市民甲在C处看见飞机A的仰角为45°,同时另一市民乙在斜坡CF上的D处看见飞机A的仰角为30°,若斜坡CF的坡比=1:3,铅垂高度DG=30米(点E、G、C、B在同一水平线上).求:(1)两位市民甲、乙之间的距离CD;(2)此时飞机的高度AB,(结果保留根号)【点睛】本题主要考查了解直角三角形的实际应用,矩形的性质与判定,勾股定理,正确理解题意作出辅助线是解题的关键.27.(2022·山西·中考真题)随着科技的发展,无人机已广泛应用于生产和生活,如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测星AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为60m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E 处的俯角为30°,沿水平方向由点O飞行24m到达点F,测得点E处俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC 的长(结果精确到1m.参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,3≈1.73).【答案】58m【分析】延长AB和CD分别与直线OF交于点G和点H,则∠AGO=∠EHO=90°,再根据图形应用三角函数即可求解.【详解】解:延长AB和CD分别与直线OF交于点G和点H,则∠AGO=∠EHO=90°.京举行,我国冬奥选手取得了9块金牌、4块银牌、2块铜牌,为祖国赢得了荣誉,激起了国人对冰雪运动的热情.某地模仿北京首钢大跳台建了一个滑雪大跳台(如图),它由助滑坡道、弧形跳台、着陆坡、终点区四部分组成.图是其示意图,已知:助滑坡道AF=50米,弧形跳台的跨度FG=7米,顶端E到BD的距离为40米,HG∥BC,∠AFH=40°,∠EFG=25°,∠ECB=36°.求此大跳台最高点A距地面BD的距离是多少米(结果保留整数).(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin25°≈0.42,cos 25°≈0.91,tan25°≈0.47,sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)【答案】70【分析】过点E作EN⊥BC,交GF于点M,则四边形HBNM是矩形,可得HB=MN,在Rt∵AF=50,∠AFH=40°,在Rt△AHF中,AH=AF⋅sin∠AFH≈50×0.64=32(米),∵HG∥BC,∴∠EGF=∠ECB∵∠EFG=25°,∠ECB=36°,FG=7米∵FM=EMtan∠EFG,MG=EMtan∠EGF∴EM+EM=7,村旅游的一张靓丽名片.某中学八年级数学兴趣小组参观后,进行了设计伞的实践活动.小文依据黄金分割的美学设计理念,设计了中截面如图所示的伞骨结构(其中DHAH≈0.618):伞柄AH始终平分∠BAC,AB=AC=20cm,当∠BAC=120°时,伞完全打开,此时∠BDC=90°.请问最少需要准备多长的伞柄?(结果保留整数,参考数据:3≈1.732)测量大楼的高度,无人机在空中P处,测得楼CD楼顶D处的俯角为45°,测得楼AB楼顶A 处的俯角为60°.已知楼AB和楼CD之间的距离BC为100米,楼AB的高度为10米,从楼AB 的A处测得楼CD的D处的仰角为30°(点A、B、C、D、P在同一平面内).(1)填空:∠APD=___________度,∠ADC=___________度;(2)求楼CD的高度(结果保留根号);(3)求此时无人机距离地面BC的高度.则∠PFA=∠AED=90°,FG=AB=10(米)∵MN∥AE,∴∠PAF=∠MPA=60°.∵∠ADE=60°,∴∠PAF=∠ADE.∵∠DAE=30°,∴∠PAD=30°.∵∠APD=75°,∴∠ADP=75°.∴∠ADP=∠APD.∴AP=AD.∴△APF≌△DAE(AAS).∴PF=AE=100.∴PG=PF+FG=100+10=110(米)∴无人机距离地面BC的高度为110米.【点睛】此题考查了解直角三角形的应用-——仰角俯角问题的知识.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.31.(2022·四川自贡·中考真题)在东西方向的海岸线上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1h20min,又测得该轮船位于A的北偏东60°,且与A相距83km的C处.(1)求该轮船航行的速度.(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.古洞古部落”享誉巴渠,被誉为“小九寨”.端坐在观音崖旁的一块奇石似一只“啸天犬”,昂首向天,望穿古今.一个周末,某数学兴趣小组的几名同学想测出“啸天犬”上嘴尖与头顶的距离.他们把蹲着的“啸天犬”抽象成四边形ABCD,想法测出了尾部C看头顶B的仰角为40∘,从前脚落地点D看上嘴尖A的仰角刚好60∘,CB=5m,CD=2.7m.景区管理员告诉同学们,上嘴尖到地面的距离是3m.于是,他们很快就算出了AB的长.你也算算?(结果精确到0.1m.参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.2≈1.41,3≈1.73)【点睛】考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.33.(2022·广东广州·中考真题)如图,某无人机于空中A处探测到目标B、D的俯角分别是30°、60°,此时无人机的飞行高度AC为60m,随后无人机从A处继续水平飞行303m到达A′处.(1)求之间的距离(2)求从无人机A′上看目标的俯角的正切值.所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架ACO'后,电脑转到AO'B'位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O'C⊥OA于点C,O'C=12cm.(1)求∠CAO'的度数.(2)显示屏的顶部B'比原来升高了多少?(3)如图4,垫入散热架后,要使显示屏O'B'与水平线的夹角仍保持120°,则显示屏O'B'应绕点O'按顺时针方向旋转多少度?【答案】(1)∠CAO′=30°;(2)(36﹣12)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°.【详解】试题分析:(1)通过解直角三角形即可得到结果;(2)过点B作BD⊥AO交AO的延长线于D,通过解直角三角形求得BD=OBsin∠BOD=24×=12,由C、O′、B′三点共线可得结果;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,求得∠EO′B′=∠FO′A=30°,既是显示屏O′B′应绕点O′按顺时针方向旋转30°.试题解析:(1)∵O′C⊥OA于C,OA=OB=24cm,∴sin∠CAO′=,∴∠CAO′=30°;(2)过点B作BD⊥AO交AO的延长线于D,∵sin∠BOD=,∴BD=OBsin∠BOD,∵∠AOB=120°,∴∠BOD=60°,∴BD=OBsin∠BOD=24×=12,∵O′C⊥OA,∠CAO′=30°,∴∠AO′C=60°,∵∠AO′B′=120°,∴∠AO′B′+∠AO′C=180°,∴O′B′+O′C﹣BD=24+12﹣12=36﹣12,∴显示屏的顶部B′比原来升高了(36﹣12)cm;(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,理由:∵显示屏O′B与水平线的夹角仍保持120°,∴∠EO′F=120°,∴∠FO′A=∠CAO′=30°,∵∠AO′B′=120°,∴∠EO′B′=∠FO′A=30°,∴显示屏O′B′应绕点O′按顺时针方向旋转30°.考点:解直角三角形的应用;旋转的性质.35.(2022·重庆·中考真题)某水库大坝的横截面是如图所示的四边形BACD,其中AB∥CD.瞭望台PC正前方水面上有两艘渔船M、N,观察员在瞭望台顶端P处观测渔船M的俯角α=31°,观测渔船N在俯角β=45°,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.(1)求两渔船M,N之间的距离(结果精确到1米);(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1:0.25.为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为i=1:1.5,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?(参考数据:tan31°≈0.60,sin31°≈0.52)m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos31°≈0.86,tan31°≈0.60)-,在=0.60,解得x=2.5,答:DM和BC的水平距离BM为2.5米.考点:解直角三角形.37.(2022·四川巴中·中考真题)2013年4月20日,四川雅安发生里氏7.0级地震,救援队救援时,利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距4米,探测线与地面的夹角分别为300和600,如图所示,试确定生命所在点C的深度(结果精确到0.1米,参考数据2≈1.41,3≈1.73)BC为63米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF 的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB和CD(均与水平面垂直),再将集热板安装在AD上.为使集热板吸热率更高,公司规定:AD与水平面夹角为θ1,且在水平线上的射影AF为1.4m.现已测量出屋顶斜面与水平面夹角为θ2,并已知tanθ1=1.082,tanθ2 =0.412.如果安装工人确定支架AB高为25cm,求支架CD的高(结果精确到1cm)?【答案】支架DC的高应为119cm.【分析】过A作AE∥BC,则∠EAF=∠CBG=θ2,EC=AB=25cm,再根据锐角三角函数的定义用θ1、θ2表示出DF、EF的值,再根据DC=DE+EC进行解答即可.【详解】解:如图所示,过A作AE∥BC,则∠EAF=∠CBG=θ2,EC=AB=25cm∵Rt△DAF中:∠DAF=θ1,DF=AFtanθ1,Rt△EAF中:∠EAF=θ2,EF=AFtanθ2,∴DE=DF-EF=AF(tanθ1-tanθ2)又∵AF=140cm,tanθ1=1.082,tanθ2=0.412,∴DE=140×(1.082-0.412)=93.8,∴DC=DE+EC=93.8+25=118.8 cm≈119cm.答:支架DC的高应为119cm.【点睛】本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形,利用锐角三角函数的定义进行解答是解答此题的关键.40.(2022·四川泸州·中考真题)如图,海中有两小岛C,D,某渔船在海中的A处测得小岛C位于东北方向,小岛D位于南偏东30°方向,且A,D相距10 nmile.该渔船自西向东航行一段时间后到达点B,此时测得小岛C位于西北方向且与点B相距82nmile.求B,D间的距离(计算过程中的数据不取近似值).根据题意可得,∠BAC=∠在Rt△ABC中,AC=BC=8∴AB=2BC=16(nmile),在Rt△ADE中,AD=10 nmile=∴DE=AD•sin60°=10×32人行步道.经测量,点C在点A的正东方向,AC=200米.点E在点A的正北方向.点B,D在点C的正北方向,BD=100米.点B在点A的北偏东30°,点D在点E的北偏东45°.(1)求步道DE的长度(精确到个位);(2)点D处有直饮水,小红从A出发沿人行步道去取水,可以经过点B到达点D,也可以经过点E到达点D.请计算说明他走哪一条路较近?(参考数据:2≈1.414,3≈1.732)【答案】(1)283米(2)经过点B到达点D较近【分析】(1)过E作BC的垂线,垂足为H,可得四边形ACHE是矩形,从而得到,ACHE是矩形,∴EH=AC=200米,根据题意得:∴DH=EH=200米,∴DE=2EH=30°,在Rt△ABC中,∴AB=2AC∴BC=AB2―BC2=2003(米),+100―200=2003―100(米)B点处的快艇和湖岸A处的救援船接到通知后立刻同时出发前往救援.计划由快艇赶到码头C接该游客,再沿CA方向行驶,与救援船相遇后将该游客转运到救援船上.已知C在A的北偏东30°方向上,B在A的北偏东60°方向上,且B在C的正南方向900米处.(1)求湖岸A与码头C的距离(结果精确到1米,参考数据:3=1.732);(2)救援船的平均速度为150米/分,快艇的平均速度为400米/分,在接到通知后,快艇能否在5分钟内将该游客送上救援船?请说明理由.(接送游客上下船的时间忽略不计)由题意可得:。
解直角三角形应用专题带答案

解直角三角形应用专题带答案解直角三角形应用专题练1.在数学实践活动课上,老师带领同学们到附近的湿地公园测量园内雕塑的高度。
用测角仪在A处测得雕塑顶端点C的仰角为30°,再往雕塑方向前进4米至B处,测得仰角为45°。
求该雕塑的高度(测角仪高度忽略不计,结果不取近似值)。
2.一艘海轮位于灯塔C的北偏东45方向,距离灯塔100海里的A处。
它沿XXX方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处。
求此时船距灯塔的距离(参考数据:√2≈1.414,√3≈1.732,结果取整数)。
3.2018年4月12日,菏泽国际牡丹花会拉开帷幕,XXX用直升机航拍技术全程直播。
在直升机的镜头下,观测曹州牡丹园A处的俯角为30°,B处的俯角为45°。
如果此时直升机镜头C处的高度CD为200米,点A、B、D在同一条直线上,则A、B两点间的距离为多少米?(结果保留根号)4.XXX在某桥附近试飞无人机。
为了测量无人机飞行的高度AD,XXX通过操控器指令无人机测得桥头B、C的俯角分别为∠EAB=60°,∠EAC=30°,且D、B、C在同一水平线上。
已知桥BC=30米,求无人机飞行的高度AD(精确到0.01米,参考数据:√2≈1.414,√3≈1.732)。
5.我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰。
其中山脚A、C两地海拔高度约为1000米,山顶B处的海拔高度约为1400米。
由B处望山脚A处的俯角为30°,由B处望山脚C处的俯角为45°。
若在A、C两地间打通一隧道,求隧道最短为多少米(结果取整数,参考数据√3≈1.732)。
6.随着航母编队的成立,我国海军日益强大。
2018年4月12日,XXX在南海海域隆重举行海上阅兵。
在阅兵之前我军加强了海上巡逻。
巡逻舰在某海域航行到A处时,该舰在观测点P的南偏东45°的方向上,且与观测点P的距离XXX为400海里。
中考数学总复习《解直角三角形及其应用》专项提升练习题(附答案)
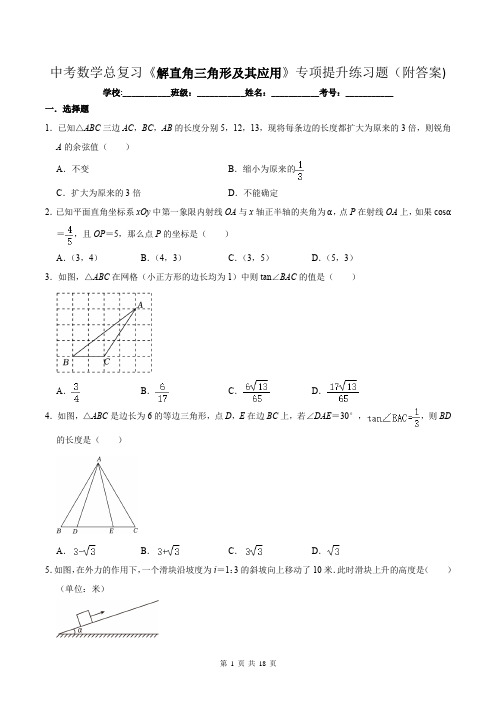
中考数学总复习《解直角三角形及其应用》专项提升练习题(附答案)学校:___________班级:___________姓名:___________考号:___________一.选择题1.已知△ABC三边AC,BC,AB的长度分别5,12,13,现将每条边的长度都扩大为原来的3倍,则锐角A的余弦值()A.不变B.缩小为原来的C.扩大为原来的3倍D.不能确定2.已知平面直角坐标系xOy中第一象限内射线OA与x轴正半轴的夹角为α,点P在射线OA上,如果cosα=,且OP=5,那么点P的坐标是()A.(3,4)B.(4,3)C.(3,5)D.(5,3)3.如图,△ABC在网格(小正方形的边长均为1)中则tan∠BAC的值是()A.B.C.D.4.如图,△ABC是边长为6的等边三角形,点D,E在边BC上,若∠DAE=30°,,则BD 的长度是()A.B.C.D.5.如图,在外力的作用下,一个滑块沿坡度为i=1:3的斜坡向上移动了10米.此时滑块上升的高度是()(单位:米)A.B.C.D.106.如图,沿AB方向架桥BD,以桥两端B、D出发,修公路BC和DC,测得∠ABC=150°,BC=1800m,∠BCD=105°,则公路DC的长为()A.900m B.900m C.900m D.1800m7.如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,测得AB=60cm,∠B=50°,则点A到BC的距离为()A.60sin50°cm B.60cos50°cmC.D.60tan50°cm8.如图,小明为了测量遵义市湘江河的对岸边上B,C两点间的距离,在河的岸边与BC平行的直线EF上点A处测得∠EAB=37°,∠F AC=60°,已知河宽18米,则B,C两点间的距离为()(参考数据:sin37°,cos37°≈,tan37°≈)A.(18+6)米B.(24+10)米C.(24+6)米D.(24+18)米二.填空题9.如图所示,网格中的每个小正方形的边长都是1,△ABC的顶点都在格点处,则∠ABC的正弦值为.10.某人在大厦一层乘坐观光电梯,看到大厦外一棵树上的鸟巢,仰角为30°,到达大厦的第五层后,再看这个鸟巢,俯角为60°,已知大厦的层高均为4m,则这棵树与大厦的距离为m.11.拦水坝的横断面如图所示,迎水坡AB的坡比是,坝高BC=8m,则坡面AB的长度是m.12.一渔船在海上A处测得灯塔C在它的北偏东60°方向,渔船向正东方向航行12海里到达点B处,测得灯塔C在它的北偏东45°方向,若渔船继续向正东方向航行,则渔船与灯塔C的最短距离是海里.13.如图所示,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为150米,则这栋楼的高度为米.14.图1是某种路灯的实物图片,图2是该路灯的平面示意图,MN为立柱的一部分,灯臂AC,支架BC 与立柱MN分别交于A,B两点,灯臂AC与支架BC交于点C,已知∠MAC=60°,∠ACB=15°,AC =40cm,则支架BC的长为cm.(结果精确到1cm,参考数据:≈1.414,≈1.732,≈2.449)三.解答题15.常州天宁寺始建于唐贞观年间,是佛教音乐梵呗的发源地之一,也是常州最大的寺庙.某校数学兴趣小组的同学利用卷尺和自制的测角仪尝试求解天宁寺宝塔的高度.如图所示,平地上一幢建筑物AB与宝塔CD相距56m,在建筑物的顶部分别观测宝塔底部的俯角为45°、宝塔顶部的仰角为60°.求天宁寺宝塔的高度(结果保留根号).16.如图,某住宅小区南,北两栋楼房直立在地面上,且高度相等.为了测量两楼的高度AE、BD和两楼之间的距离AD,小莉在南楼楼底地面A处测得北楼顶部B的仰角为31°,然后她来到南楼离地面12m 高的C处,此时测得B的仰角为20°.求两楼的高度和两楼之间的距离.(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60.)17.如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为75°,测得小区楼房BC顶端点C处的俯角为45°.已知操控者A和小区楼房BC之间的距离为45米,无人机的高度为米.(假定点A,B,C,D都在同一平面内.参考数据:,.计算结果保留根号)(1)求此时小区楼房BC的高度;(2)在(1)条件下,若无人机保持现有高度沿平行于AB的方向,并以5米/秒的速度继续向右匀速飞行.问:经过多少秒时,无人机刚好离开了操控者的视线?18.如图所示,为了知道楼房CP外墙上一广告屏的高度GH是多少,某数学活动小组利用测角仪和米尺等工具进行如下操作:在A处测得∠GDF=30°,在B处测得∠HEF=50°,点A、B、C共线,AC⊥CP 于点C,DF⊥CP于点F,AB为20米,BC=30米,测角仪的高度(AD、BE)为1.3米,根据测量数据,请求出GH的值.(结果精确到0.1米,参考数据:≈1.73,sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)19.如图1,图2分别是网上某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆DE、箱长BC、拉杆AB的长度都相等,即DE=BC=AB,点B、F在线段AC上,点C在DE上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°.请根据以上信息,解决下列问题;(1)求AC的长度(结果保留根号);(2)求拉杆端点A到水平滑杆ED的距离(结果保留到1cm).参考数据:≈1.41,≈1.73,≈2.45.20.如图,海面上有A,B两个小岛,A在B的正东方向,有一艘渔船在点P处,从A处测得渔船在北偏西60°的方向.从B处测得渔船在其东北方向,且测得B,P两点之间的距离为30海里.(1)求小岛A,B之间的距离(结果保留根号);(2)渔船在P处发生故障、在原地等待救援,一艘救援船以每小时45海里的速度从A地出发先沿正西方向前往B点去取修理的材料(将材料装配上船的时间忽略不计),再沿射线BP方向以相同的速度前往P点进行救援.救援船从A点出发的同时,一艘补给船从C点出发,以每小时30海里的速度沿射线CP 方向前往P点,已知A、P,C三点在同一直线上,从B测得C在B的北偏西15°方向,请通过计算说明救援船能否在补给船到达P点后的40分钟之内赶到P点.(参考数据: 1.41,≈1.731,≈2.45)参考答案一.选择题1.解:∵将△ABC三边AC,BC,AB的长度分别5,12,13∴AC2+BC2=52+122=169,AB2=132=169∴AC2+BC2=AB2∴△ABC为直角三角形,即∠C=90°∴cos A==现将每条边的长度都扩大为原来的5倍,则=∴cos A的值不变.故选:A.2.解:过点P作PB⊥x轴于点B∵cosα==∴可假设OB=4,则OP=5∴PB==3∴点P的坐标可能是(4,3)故选:B.3.解:过点C作CD⊥AB,垂足为D.AB===5,BC=2,AC==∵S△ABC=BC•3=3,S△ABC=AB•CD=CD∴CD=.在Rt△ACD中AD====.∴tan∠BAC===.故选:B.4.解:过点A作AH⊥BC于H∵△ABC是等边三角形∴AB=AC=BC=6,∠BAC=60°∵AH⊥BC∴∠BAH=∠BAC=30°∴∠BAD+∠DAH=30°∵∠DAE=30°∴∠BAD+∠EAC=30°∴∠DAH=∠EAC∴tan∠DAH=tan∠EAC=∵BH=AB=3∵AH=AB sin60°=6×=3∴=∴DH=∴BD=BH﹣DH=3﹣故选:A.5.解:如图,设AB=10m,过点B作BC⊥AC于点C由i=1:3,得tanα==∴AC=3BC在Rt△ABC中∵AC2+BC2=AB2∴(3BC)2+BC2=102解得BC=∴滑块上升的高度为:h=.故选:A.6.解:如图,过点C作CE⊥BD,垂足为E∵∠ABC=150°∴∠CBE=180°﹣150°=30°,∠BCE=150°﹣90°=60°又∵∠BCD=105°∴∠DCE=105°﹣60°=45°在R△BCE中∠CBE=30°,BC=1800m∴CE=BC=900(m)在Rt△CDE中∠DCE=45°∴CD=CE=900(m)故选:B.7.解:如图,过点A作AD⊥BC于点D在Rt△ABD中∵sin B=∴AD=sin B•AB=60sin50°即点A到BC的距离为60sin50°cm故选:A.8.解:作AD⊥BC于点D,如图∵BC∥EF∴∠DBA=∠EAB,∠DCA=∠CAF∵∠EAB=37°,∠CAF=60°∴∠DBA=37°,∠DCA=60°∵AD=18米,tan∠DBA=,tan∠DCA=∴=,=解得BD=24米,CD=6米∴BC=BD+CD=(24+6)米故选:C.二.填空题9.解:如图,取BC的中点D,连接AD由网格可得,AC=,AB=∴AB=AC∴AD⊥BCRt△ABD中∵AD=∴sin∠ABC=.故答案为:.10.解:如图,根据题意可知:∠BAC=30°,∠DCB=30°,AB=4×4=16(m)∴∠ADC=90°,设CD=x m∴AD=AD=xm,BD=CD=xm∵AD+BD=AB∴x+x=16∴x=4(m).答:这棵树与大厦的距离为4m.故答案为:4.11.解:∵迎水坡AB的坡比是1:,坝高BC=8m∴==解得AC=8则AB==16(m).故答案为:16.12.解:过点C作CH⊥AB于H.∵∠DAC=60°,∠CBE=45°∴∠CAH=90°﹣∠CAD=30°,∠CBH=90°﹣∠CBE=45°∴∠BCH=90°﹣45°=45°=∠CBH∴BH=CH在Rt△ACH中∠CAH=30°,AH=AB+BH=12+CH,tan30°=∴CH=(12+CH)解得CH=6(+1).答:渔船与灯塔C的最短距离是6(+1)海里.故答案为:6+6.13.解:过点A作AD⊥BC,垂足为D由题意得:AD=150米在Rt△ADB中∠BAD=30°∴BD=AD•tan30°=150×=50(米)在Rt△ADC中∠DAC=60°∴CD=AD•tan60°=150(米)∴BC=BD+CD=200(米)∴这栋楼的高度为200米故答案为:200.14.解:如图2,过C作CD⊥MN于D则∠CDB=90°∵∠CAD=60°,AC=40(cm)∴CD=AC•sin∠CAD=40×sin60°=40×=20(cm)∵∠ACB=15°∴∠CBD=∠CAD﹣∠ACB=60°﹣15°=45°∴BC=CD=×20=20≈20×2.449≈49(cm)故答案为49.三.解答题15.解:如图所示,过点A作AE⊥CD于点E,则四边形AEDB是矩形依题意BD=56,∠EAD=45°,∠CAE=60°∴△ADE是等腰直角三角形∴AE=ED则四边形ABDE是正方形∴AE=BD=56在Rt△ACE中∴答:天宁寺宝塔的高度为()米.16.解:过点C作CF⊥BD,垂足为F由题意得:AC=DF=12m,CF=AD设AD=CF=xm在Rt△ABD中∠BAD=31°∴BD=AD•tan31°≈0.6x(m)在Rt△CFB中∠BCF=20°∴BF=CF•tan20°≈0.36x(m)∴BD=BF+DF=(0.36x+12)m∴0.6x=0.36x+12解得:x=50∴AD=50m,BD=30m∴两楼的高度约为30m,两楼之间的距离约为50m.17.解:(1)过点D作DE⊥AB于点E,过点C作CF⊥DE于点F,如图所示:则四边形BCFE是矩形由题意得:AB=45米,∠DAE=75°,∠DCF=∠FDC=45°∵∠DCF=∠FDC=45°∴CF=DF∵四边形BCFE是矩形∴BE=CF=DF在Rt△ADE中∠AED=90°∴tan∠DAE===2+∴BE=30经检验,BE=30是原方程的解∴EF=DH﹣DF=30+15﹣30=15(米)答:此时小区楼房BC的高度为15米.(2)∵DE=15(2+)米∴AE===15(米)过D点作DG∥AB,交AC的延长线于G,作GH⊥AB于H在Rt△ABC中∠ABC=90°,AB=45米,BC=15米∴tan∠BAC===在Rt△AGH中GH=DE=15(2+)米AH===(30+45)米∴DG=EH=AH﹣AE=(30+45)﹣15=(30+30)米(30+30)÷5=(6+6)(秒)答:经过(6+6)秒时,无人机刚好离开了操控者的视线.18.解:由题意得:EF=BC=30米,DF=AC=AB+BC=50(米)在Rt△EHF中∠HEF=50°∴HF=EF•tan50°≈30×1.19=35.7(米)在Rt△DFG中∠GDF=30°∴FG=DF•tan30°=50×=(米)∴HG=FH﹣FG=35.7﹣≈6.9(米)∴GH的值约为6.9米.19.解:(1)过F作FH⊥DE于H.∴∠FHC=∠FHD=90°.∵∠FDC=30°,DF=30∴,∵∠FCH=45°∴CH=FH=15∴∵CE:CD=1:3∴∵AB=BC=DE∴;(2)过A作AG⊥ED交ED的延长线于G∵∠ACG=45°∴=20×1.41+20×2.45=77.2≈77(cm)答:拉杆端点A到水平滑杆ED的距离为77cm.20.解:(1)过P作PH⊥AB于H,如图:根据已知得:∠PBH=45°,∠P AH=30°,BP=30海里∴∠PBH=∠BPH=45°∴△BPH是等腰直角三角形∴BH=PH===15(海里)在Rt△APH中tan∠P AH=,即tan30°=∴AH=15(海里)∴AB=BH+AH=15+15≈57.9(海里)∴小岛A,B之间的距离约是57.9海里;(2)过P作PG⊥BC于G,如图:由(1)知AB=57.9海里,BP=30海里∴救援船到达P所需时间为≈1.95(小时)由已知可得∠CBP=60°,∠BPC=∠PBA+∠P AB=75°∴∠GPB=90°﹣∠CBP=30°,∠GPC=∠BPC﹣∠GPB=45°在Rt△BPG中cos∠BPG=,即cos30°=∴PG=15∵∠GPC=45°=∠C∴△GPC是等腰直角三角形∴CP=PG=15≈36.75(海里)∴补给船到达P所需时间为36.75÷30=1.23(小时)∵1.95﹣1.23=0.72(小时),0.72×60=43.2(分)∴救援船不能在补给船到达P点后的40分钟之内赶到P点.。
解直角三角形应用题

解直角三角形应用题1、开自驾车人士,将车开到城郊结合部的轨道车站附近停车,转乘轨道交通到市中心).市郊某地正在修建地铁站,拟同步修建地下停车库.如图,是停车库坡道入口的设计图,其中MN 是水平线,MN //AD ,AD ⊥DE ,CF ⊥AB ,垂足分别为D 、F ,坡道AB 的坡度3:1=i ,AD=9米,C 在DE 上,DC=0.5米,CD 是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF 的长,计算该停车库限高多少米.(结果精确到0.1米)(提供可选用的数据:1631073134112...≈≈≈,,)2、我国南水北调中线工程的起点是某水库,按照工程计划,需对原水库大坝进行混凝土培厚加高,使坝高由原来的156米增加到173.2米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE ,背水坡坡角∠BAE=69°,新坝体高为DE ,背水坡坡角∠DCE=60°,求工程完工后背水坡底端水平方向增加的宽度AC .(精确到1米)(参考数据:sin69°≈0.93 ,cos69°≈0.36 ,ta n69°≈2.60 1.732M N第2题图3、为了开发利用海洋资源,需要测量某岛屿两端A 、B 的距离.如图,勘测飞机在距海平面垂直高度为100米的点C 处测得点A 的俯角为60°,然后沿着平行于AB 的方向飞行了500米至D 处,在D 处测得点B 的俯角为45°.求岛屿两端A 、B 的距离.(结果精确到0.1米)说明:①A 、B 、C 、D 在与海平面垂直的同一平面上;②参考数据:414.12732.13≈≈,.4、在数学活动课上,九年级⑴班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:(1)在大树前的平地上选择一点A ,测得由点A 看大树顶端C 的仰角为35︒;(2)在点A 和大树之间选择一点B (A 、B 、D 在同一直线上),测得由点B 看大树顶端C的仰角恰好为45︒;(3)量出A 、B 两点间的距离为4.5米.请你根据以上数据求出大树CD 的高度.(结果精确到0.1米) (参考数据:sin 350.57︒≈,cos350.82︒≈,tan 350.70︒≈)CBA第3题图(第4题图)CDB A回家作业:5、如图是已建设封顶的16层楼房和它的塔吊示意图,吊臂AG 与地面EH 平行,测得A 点到楼顶D 点的距离为5米,每层楼高3.5米,在吊臂上有一点B ,AB =16米,在C 点测得A 点的俯角(∠MCA )为20°, B 点的俯角(∠MCB )为40°,AE 、CH 都垂直于地面,求塔吊的高CH 的长(结果精确到0.1米).(参考数据:34.020sin 0≈,94.020cos 0≈,36.020tan 0≈,64.040sin 0≈,77.040cos 0≈ 84.040tan 0≈)A 第5题DBCGM6、如图,在一笔直的海岸线上有A、B两个观测站,B在A的正东方向,AB=10千米,在某一时刻,从观测站A测得一艘集装箱货船位于北偏西62.6°的C处,同时观测站B测得该集装箱船位于北偏西69.2°方向.问此时该集装箱船与海岸之间距离CH约为多少千米?(最后结果保留整数)(参考数据:sin62.6°≈0.89,cos62.6°≈0.46,tan62.6°≈1.93,sin69.2°≈0.93,cos69.2°≈0.36,tan69.2°≈2.63.)东图。
解直角三角形的应用提高训练

【解直角三角形的应用】一、关于坡度问题、例题1、(2009•深圳)如图,斜坡AC的坡度(坡比)为1:3,AC=10米.坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC的高度.2、2009•山西)有一水库大坝的横截面是梯形ABCD,AD∥BC,EF为水库的水面,点E在DC上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB的长为12米,迎水坡上DE的长为2米,∠BAD=135°,∠ADC=120°,求水深.(精确到0.1米,2≈1.41,3≈1.73例题3、(2009•本溪)如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=4m.(1)求∠CAE的度数;(2)求这棵大树折断前的高度.)(结果精确到个位,参考数据:2≈1.41,3≈1.736 2.4例题7、(2007•江苏)某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为1.6米,现要做一个不锈钢的扶手AB 及两根与FG 垂直且长为l 米的不锈钢架杆AD 和BC (杆子的底端分别为D ,C ),且∠DAB=66.5°. (1)求点D 与点C 的高度差DH ;(2)求所用不锈钢材料的总长度l .(即AD+AB+BC ,结果精确到0.1米) (参考数据:sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)1、2010•通化)如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m ,此时小球距离地面的高度为( )A .5mB 、25 C 、35 D 、1032、(2009•益阳)如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB 为( ) A .5cosα B 、5cos a C .5sinα D 、5sin a3、(2007•宁波)如图,在斜坡的顶部有一铁塔AB ,B 是CD 的中点,CD 是水平的,在阳光的照射下,塔影DE 留在坡面上.已知铁塔底座宽CD=12 m ,塔影长DE=18 m ,小明和小华的身高都是1.6m ,同一时刻,小明站在点E 处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m 和1m ,那么塔高AB 为( ) A .24m B .22m C .20m D .18m4、(2005•黄石)如图,小阳发现电线杆AB 的影子落在土坡的坡面CD 和地面BC 上,量得CD=8米,BC=20米,CD 与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为( ) A .9米 B .28米 C 、73+D 、1423+5、身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300m ,250m ,200m ;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝( )A.甲的最高B.乙的最低C.丙的最低D.乙的最高6、如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为()A.1.8tan80°m B.1.8cos80°m C、1.8sin80?D、1.8tan80?7、如图,将一个Rt△ABC形状的楔子从木桩的底端点P沿水平方向打入木桩底下,使木桩向上运动.已知楔子斜面的倾斜角为15°,若楔子沿水平方向前进6cm(如箭头所示),则木桩上升了()A.6sin15°cm B.6cos15°cm C.6tan15°cm D、6tan15?cm8、2010•鞍山)如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为______m.(结果保留两位有效数字,2≈1.41,3≈1.73)9、(2008•鄂尔多斯)如图,在一个坡角为15°的斜坡上有一棵树,高AB,当太阳光与水平线成60°时,测得该树在斜坡上的树影BC的长为6m,则树高AB= _______m.10、(2007•连云港)如图是一山谷的横断面示意图,宽AA′为15m,用曲尺(两直尺相交成直角)从山谷两侧测量出OA=1m,OB=3m,O′A′=0.5m,O′B′=3m(点A,O,O′A′在同一条水平线上),则该山谷的深h为__________m.11、(2007•湖州)小明发现在教学楼走廊上有一拖把以15°的倾斜角斜靠在栏杆上,严重影响了同学们的行走安全.他自觉地将拖把挪动位置,使其的倾斜角为75°,如果拖把的总长为1.80m,则小明拓宽了行路通道_______m.(结果保留三个有效数字,参考数据:sin15°≈0.26,cos15°≈0.97).12、(2003•陕西)如图梯子AB靠在墙上,梯子的底端A到墙根C的距离为2米,梯子的顶端B到地面的距离为7米,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根C的距离等于3米,同时梯子的顶端B下降至B′,那么BB′①等于1米②大于1米③小于1米.其中正确结论序号是________.二、关于仰角的问题1、(2010•青海)如图,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为150米,且点A、D、B在同一直线上,建筑物A、B间的距离为()A、1503B、1803C、2003D、22032、.(2007•舟山)如图,在高楼前D点测得楼顶的仰角为30°,向高楼前进60米到C点,又测得仰角为45°,则该高楼的高度大约为()A.82米B.163米C.52米D.30米3、.汶川地震后,抢险队派一架直升飞机去A、B两个村庄抢险,飞机在距地面450米上空的P点,测得A村的俯角为30°,B村的俯角为60°(如图)则A,B两个村庄间的距离是()米.A.300 B.900 C、3002D、30034、某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为()(精确到1米,3=1.732).A.585米B.1014米C.805米D.820米5、.(2010•潼南县)如图所示,小明在家里楼顶上的点A处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点C处的俯角为45°,两栋楼之间的距离为30m,则电梯楼的高BC为_______米(精确到0.1).(参考数据:2≈1.414,3≈1.732).例题1、(2011•苏州)如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,巳知该山坡的坡度i(即tan∠ABC)为1:3,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.(1)山坡坡角(即∠ABC)的度数等于度;(2)求A、B两点间的距离(结果精确到0.1米,参考数据:3≈1.732例题2、(2010•包头)如图,线段AB、DC分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,从B点测得D点的仰角α为60°从A点测得D点的仰角β为30°,已知甲建筑物高AB=36米.(1)求乙建筑物的高DC;(2)求甲、乙两建筑物之间的距离BC(结果精确到0.01米).(参考数据:2≈1.414,3≈1.732)例题3、.(2009•烟台)腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据3≈1.732)例题4、.(2009•铁岭)某旅游区有一个景观奇异的望天洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处.在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.(1)求∠ADB的度数;(2)求索道AB的长.(结果保留根号)例题5、.(2009•昆明)如图,AC是我市某大楼的高,在地面上B点处测得楼顶A的仰角为45°,沿BC方向前进18米到达D点,测得tan∠ADC=53.现打算从大楼顶端A点悬挂一幅庆祝建国60周年的大型标语,若标语底端距地面15m,请你计算标语AE的长度应为多少?三、关于方向问题1、(2009•泰安)在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C地南偏西30°方向,则A、C两地的距离为()2、.(2007•临沂)如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1小时后到达C处,C在处测得A的方位角为北偏东20°,则C到A的距离是()3、(2010•深圳)如图所示,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行_______分钟可使渔船到达离灯塔距离最近的位置.4、(2008•威海)如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处东500米的B 处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=_____米.(用根号表示)5、(2011•资阳)在一次机器人测试中,要求机器人从A出发到达B处.如图1,已知点A在O的正西方600cm处,B在O的正北方300cm处,且机器人在射线AO及其右侧(AO下方)区域的速度为20cm/秒,在射线AO的左侧(AO上方)区域的速度为10cm/秒.(1)分别求机器人沿A→O→B路线和沿A→B路线到达B处所用的时间(精确到秒);(2)若∠OCB=45°,求机器人沿A→C→B路线到达B处所用的时间(精确到秒);(3)如图2,作∠OAD=30°,再作BE⊥AD于E,交OA于P.试说明:从A出发到达B处,机器人沿A→P→B路线行进所用时间最短.6、.(2009•中山)如图所示,A、B两城市相距100km,现计划在这两座城市间修建一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据:2≈1.41,3≈1.73≈1.414)7、.(2009•泸州)在某段限速公路BC上(公路视为直线),交通管理部门规定汽车的最高行驶速度不能超过60千米/时(即503米/秒),并在离该公路100米处设置了一个监测点A.在如图所示的直角坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在A的北偏西60°方向上,点C在A的北偏东45°方向上,另外一条高等级公路在y轴上,AO为其中的一段.(1)求点B和点C的坐标;(2)一辆汽车从点B匀速行驶到点C所用的时间是15秒,通过计算,判断该汽车在这段限速路上是否超速?(参考数据:3≈1.73(3)若一辆大货车在限速路上由C处向西行驶,一辆小汽车在高等级公路上由A处向北行驶,设两车同时开出且小汽车的速度是大货车速度的2倍,求两车在匀速行驶过程中的最近距离是多少?8、.(2009•黄冈)如图,在海面上生产了一股强台风,台风中心(记为点M)位于海滨城市(记作点A)的南偏西15°,距离为612千米,且位于临海市(记作点B)正西方向60 3千米处,台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.(1)滨海市、临海市是否会受到此次台风的侵袭请说明理由;(2)若受到此次台风侵袭,该城市受到台风侵袭的持续时间有多少小时?9、(2008•泸州)如图,在气象站台A的正西方向240km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心130km内的地方都要受到其影响.(1)台风中心在移动过程中,与气象台A的最短距离是多少?(2)台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?1:在Rt △ABC 中,∠C=90°a+b=100 ∠B=60°求c 的值2.如图,在四边形ABCD 中,AB=2,CD=1,∠A=60°,∠B=∠D=90°。
(完整word版)解直角三角形的应用中考练习题

解直角三角形的应用练习题一.选择题(共5小题)1.(2012•襄阳)在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为()A.(4+1.6)m B.(12+1.6)m C.(4+1.6)m D.4m2.(2014•随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()D.50米A.100米B.50米C.米3.(2014•衡阳)如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为()A.26米B.28米C.30米D.46米4.(2014•西宁)如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)()A.10.8米B.8.9米C.8.0米D.5.8米5.(2014•临沂)如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为A.20海里B.10海里C.20海里D.30海里()二.填空题6.(2009•仙桃)如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°、35°,则广告牌的高度BC为_________米(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)7.(2009•安徽)长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了_________m.8.(2014•宁波)为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出_________个这样的停车位.(≈1.4)9.(2014•十堰)如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是_________海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)10.(2014•抚顺)如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为_________米.三.解答题(共5小题)11.(2014•南昌)图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.(1)连接CD,EB,猜想它们的位置关系并加以证明;(2)求A,B两点之间的距离(结果取整数,可以使用计算器)(参考数据:≈1.41,≈1.73,≈2.45)12.(2014•铁岭)如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:≈1.41,结果精确到0.1米)13.(2014•抚州)如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.(1)当∠CED=60°时,求C、D两点间的距离;(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1cm)(3)设DG=xcm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1cm)(参考数据≈1.732,可使用科学计算器)14.(2014•宿迁)如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.(1)求FM的长;(2)连接AF,若sin∠FAM=,求AM的长.15.(2014•邵阳)一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)解直角三角形的应用练习题参考答案与试题解析一.选择题(共5小题)1.(2012•襄阳)在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD.如图,已知小明距假山的水平距离BD为12m,他的眼镜距地面的高度为1.6m,李明的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度为()A.(4+1.6)m B.(12+1.6)m C.(4+1.6)m D.4m考点:解直角三角形的应用.分析:根据已知得出AK=BD=12m,再利用tan30°==,进而得出CD的长.解答:解:∵BD=12米,李明的眼睛高AB=1.6米,∠AOE=60°,∴DB=AK,AB=KD=1.6米,∠CAK=30°,∴tan30°==,解得CK=4(米),即CD=CK+DK=4+1.6=(4+1.6)米.故选:A.点评:本题考查的是解直角三角形的应用,根据题意得出tan30°==解答是解答此题的关键.2.(2014•随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()A.100米B.50米C.D.50米米考点:解直角三角形的应用.专题:几何图形问题.分析:过B作BM⊥AD,根据三角形内角与外角的关系可得∠ABC=30°,再根据等角对等边可得BC=AC,然后再计算出∠CBM的度数,进而得到CM长,最后利用勾股定理可得答案.解答:解:过B作BM⊥AD,∵∠BAD=30°,∠BCD=60°,∴∠ABC=30°,∴AC=CB=100米,∵BM⊥AD,∴∠BMC=90°,∴∠CBM=30°,∴CM=BC=50米,∴BM=CM=50米,故选:B.点评:此题主要考查了解直角三角形的应用,关键是证明AC=BC,掌握直角三角形的性质:30°角所对直角边等于斜边的一半.3.(2014•衡阳)如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为()A.26米B.28米C.30米D.46米考点:解直角三角形的应用-坡度坡角问题.专题:几何图形问题.分析:先根据坡比求得AE的长,已知CB=10m,即可求得AD.解答:解:∵坝高12米,斜坡AB的坡度i=1:1.5,∴AE=1.5BE=18米,∵BC=10米,∴AD=2AE+BC=2×18+10=46米,故选:D.点评:此题考查了解直角三角形的应用中的坡度坡角的问题及等腰梯形的性质的掌握情况,将相关的知识点相结合更利于解题.4.(2014•西宁)如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)()A.10.8米B.8.9米C.8.0米D.5.8米考点:解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题.专题:几何图形问题.分析:延长CB交PQ于点D,根据坡度的定义即可求得BD的长,然后在直角△CDA中利用三角函数即可求得CD的长,则BC即可得到.解答:解:延长CB交PQ于点D.∵MN∥PQ,BC⊥MN,∴BC⊥PQ.∵自动扶梯AB的坡度为1:2.4,∴==.设BD=5k米,AD=12k米,则AB=13k米.∵AB=13米,∴k=1,∴BD=5米,AD=12米.在Rt△CDA中,∠CDA=90゜,∠CAD=42°,∴CD=AD•tan∠CAD≈12×0.90≈10.8米,∴BC≈5.8米.故选:D.点评:本题考查仰角和坡度的定义,要求学生能借助仰角构造直角三角形并解直角三角形.5.(2014•临沂)如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为()A.20海里B.10海里C.20海里D.30海里考点:解直角三角形的应用-方向角问题.专题:几何图形问题.分析:如图,根据题意易求△ABC是等腰直角三角形,通过解该直角三角形来求BC的长度.解答:解:如图,∵∠ABE=15°,∠DAB=∠ABE,∴∠DAB=15°,∴∠CAB=∠CAD+∠DAB=90°.又∵∠FCB=60°,∠CBE=∠FCB,∠CBA+∠ABE=∠CBE,∴∠CBA=45°.∴在直角△ABC中,sin∠ABC===,∴BC=20海里.故选:C.点评:本题考查了解直角三角形的应用﹣方向角问题.解题的难点是推知△ABC是等腰直角三角形.二.填空题(共5小题)6.(2009•仙桃)如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°、35°,则广告牌的高度BC为 3.5米(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)考点:解直角三角形的应用-仰角俯角问题.专题:应用题;压轴题.分析:图中有两个直角三角形△ABD、△ACD,可根据两个已知角度,利用正切函数定义,分别求出BD和CD,求差即可.解答:解:根据题意:在Rt△ABD中,有BD=AD•tan52°.在Rt△ADC中,有DC=AD•tan35°.则有BC=BD﹣CD=6(1.28﹣0.70)=3.5(米).点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.7.(2009•安徽)长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了2()m.考点:解直角三角形的应用-坡度坡角问题.专题:压轴题.分析:利用所给角的正弦函数求两次的高度,相减即可.解答:解:由题意知:平滑前梯高为4•sin45°=4•=.平滑后高为4•sin60°=4•=.∴升高了2()m.点评:本题重点考查了三角函数定义的应用.8.(2014•宁波)为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出17个这样的停车位.(≈1.4)考点:解直角三角形的应用.专题:调配问题.分析:如图,根据三角函数可求BC,CE,由BE=BC+CE可求BE,再根据三角函数可求EF,再根据停车位的个数=(56﹣BE)÷EF+1,列式计算即可求解.解答:解:如图,BC=2.2×sin45°=2.2×≈1.54米,CE=5×sin45°=5×≈3.5米,BE=BC+CE≈5.04,EF=2.2÷sin45°=2.2÷≈3.14米,(56﹣5.04)÷3.14+1=50.96÷3.14+1≈16+1=17(个).故这个路段最多可以划出17个这样的停车位.故答案为:17.点评:考查了解直角三角形的应用,主要是三角函数及运算,关键把实际问题转化为数学问题加以计算.9.(2014•十堰)如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是24海里.(结果精确到个位,参考数据:≈1.4,≈1.7,≈2.4)考点:解直角三角形的应用-方向角问题.专题:几何图形问题.分析:作BD⊥AC于点D,在直角△ABD中,利用三角函数求得BD的长,然后在直角△BCD中,利用三角函数即可求得BC的长.解答:解:∠CBA=25°+50°=75°.作BD⊥AC于点D.则∠CAB=(90°﹣70°)+(90°﹣50°)=20°+40°=60°,∠ABD=30°,∴∠CBD=75°﹣30°=45°.在直角△ABD中,BD=AB•sin∠CAB=20×sin60°=20×=10.在直角△BCD中,∠CBD=45°,则BC=BD=10×=10≈10×2.4=24(海里).故答案是:24.点评:本题主要考查了方向角含义,正确求得∠CBD以及∠CAB的度数是解决本题的关键.10.(2014•抚顺)如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为100米.考点:解直角三角形的应用.专题:几何图形问题.分析:过点P作PE⊥AB于点E,先求出∠APE及∠BPE、∠ABP的度数,由锐角三角函数的定义即可得出结论.解答:解:过点P作PE⊥AB于点E,∵∠APC=75°,∠BPD=30°,∴∠APB=75°,∵∠BAP=∠APC=75°,∴∠APB=∠BAP,∴AB=PB=200m,∵∠ABP=30°,∴PE=PB=100m.故答案为:100.点评:本题考查的是解直角三角形的应用,熟知锐角三角函数的定义是解答此题的关键.三.解答题(共5小题)11.(2014•南昌)图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.(1)连接CD,EB,猜想它们的位置关系并加以证明;(2)求A,B两点之间的距离(结果取整数,可以使用计算器)(参考数据:≈1.41,≈1.73,≈2.45)考点:解直角三角形的应用.分析:(1)连接DE.根据菱形的性质和角的和差关系可得∠CDE=∠BED=90°,再根据平行线的判定可得CD,EB的位置关系;(2)根据菱形的性质可得BE,DE,再根据三角函数可得BD,AD,根据AB=BD+AD,即可求解.解答:解:(1)猜想CD∥EB.证明:连接DE.∵中国结挂件是四个相同的菱形,每相邻两个菱形均成30°的夹角,菱形的锐角为60°∴∠CDE=60°÷2×2+30°=90°,∴∠BED=60°÷2×2+30°=90°,∴∠CDE=∠BED,∴CD∥EB.(2)BE=2OE=2×10×cos30°=10cm,同理可得,DE=10cm,则BD=10cm,同理可得,AD=10cm,AB=BD+AD=20≈49cm.答:A,B两点之间的距离大约为49cm.点评:此题考查了解直角三角形的应用,菱形的性质和平行线的判定,主要是三角函数的基本概念及运算,关键是运用数学知识解决实际问题.12.(2014•铁岭)如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:≈1.41,结果精确到0.1米)考点:解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题.分析:根据速度乘以时间得出CE的长度,通过坡度得到∠ECF=30°,作辅助线EF⊥AC,通过平角减去其他角从而得到∠AEF=45°即可求出AE的长度.解答:解:作EF⊥AC,根据题意,CE=18×15=270米,∵tan∠CED=1,∴∠CED=∠DCE=45°,∵∠ECF=90°﹣45°﹣15°=30°,∴EF=CE=135米,∵∠CEF=60°,∠AEB=30°,∴∠AEF=180°﹣45°﹣60°﹣30°=45°,∴AE=135≈190.35米点评:本题考查了解直角三角形的应用,解答本题的关键是作辅助线EF⊥AC,以及坡度和坡角的关系.13.(2014•抚州)如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.(1)当∠CED=60°时,求C、D两点间的距离;(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1cm)(3)设DG=xcm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1cm)(参考数据≈1.732,可使用科学计算器)考点:解直角三角形的应用;菱形的性质.分析:(1)证明△CED是等边三角形,即可求解;(2)分别求得当∠CED是60°和120°,两种情况下AD的长,求差即可;(3)分别求得当∠CED是60°和120°,两种情况下DG的长度,即可求得x的范围.解答:解:(1)连接CD(图1).∵CE=DE,∠CED=60°,∴△CED是等边三角形,∴CD=DE=20cm;(2)根据题意得:AB=BC=CD,当∠CED=60°时,AD=3CD=60cm,当∠CED=120°时,过点E作EH⊥CD于H(图2),则∠CEH=60°,CH=HD.在直角△CHE中,sin∠CEH=,∴CH=20•sin60°=20×=10(cm),∴CD=20cm,∴AD=3×20=60≈103.9(cm).∴103.9﹣60=43.9(cm).即点A向左移动了43.9cm;(3)当∠CED=120°时,∠DEG=60°,∵DE=EG,∴△DEG是等边三角形.∴DG=DE=20cm,当∠CED=60°时(图3),则有∠DEG=120°,过点E作EI⊥DG于点I.∴∠DEI=∠GEI=60°,DI=IG,在直角△DIE中,sin∠DEI=,∴DI=DE•sin∠DEI=20×sin60°=20×=10cm.∴DG=2DI=20≈34.6cm.则x的范围是:20cm≤x≤34.6cm.点评:本题考查了菱形的性质,当菱形的一个角是120°或60°时,连接菱形的较短的对角线,即可把菱形分成两个等边三角形.14.(2014•宿迁)如图是某通道的侧面示意图,已知AB∥CD∥EF,AM∥BC∥DE,AB=CD=EF,∠AMF=90°,∠BAM=30°,AB=6m.(1)求FM的长;(2)连接AF,若sin∠FAM=,求AM的长.考点:解直角三角形的应用-坡度坡角问题.专题:几何图形问题.分析:(1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长线于点H,根据AB∥CD∥EF,AM∥BC∥DE,分别解Rt△ABN、Rt△DCG、Rt△FEH,求出BN、DG、FH的长度,继而可求出FM的长度;(2)在Rt△FAM中,根据sin∠FAM=,求出AF的长度,然后利用勾股定理求出AM的长度.解答:解:(1)分别过点B、D、F作BN⊥AM于点N,DG⊥BC延长线于点G,FH⊥DE延长在Rt△ABN中,∵AB=6m,∠BAM=30°,∴BN=ABsin∠BAN=6×=3m,∵AB∥CD∥EF,AM∥BC∥DE,同理可得:DG=FH=3m,∴FM=FH+DG+BN=9m;(2)在Rt△FAM中,∵FM=9m,sin∠FAM=,∴AF=27m,∴AM==18(m).即AM的长为18m.点评:本题考查了解直角三角形的应用,解答本题的关键是根据坡角构造直角三角形,利用三角函数解直角三角形,注意勾股定理的应用.15.(2014•邵阳)一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)考点:解直角三角形的应用-方向角问题.专题:几何图形问题.分析:过点C作CD⊥AB交AB延长线于D.先解Rt△ACD得出CD=AC=40海里,再解Rt△CBD中,得出BC=≈50,然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间.解答:解:如图,过点C作CD⊥AB交AB延长线于D.在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,∴CD=AC=40海里.在Rt△CBD中,∵∠CDB=90°,∠CBD=90°﹣37°=53°,∴BC=≈=50(海里),∴海警船到大事故船C处所需的时间大约为:50÷40=(小时).点评:本题考查了解直角三角形的应用﹣方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.。
解直角三角形典型应用20例子
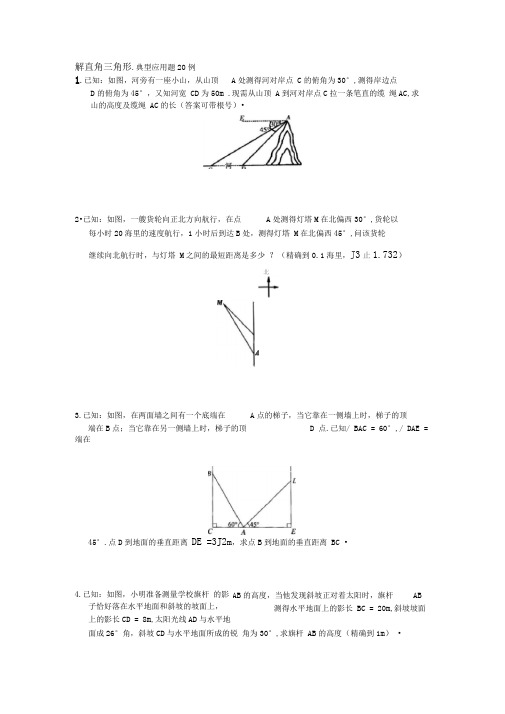
解直角三角形.典型应用题20例1.已知:如图,河旁有一座小山,从山顶 A 处测得河对岸点 C 的俯角为30°,测得岸边点D 的俯角为45°,又知河宽 CD 为50m .现需从山顶 A 到河对岸点C 拉一条笔直的缆 绳AC ,求山的高度及缆绳 AC 的长(答案可带根号)•2•已知:如图,一艘货轮向正北方向航行,在点 A 处测得灯塔M 在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B 处,测得灯塔 M 在北偏西45°,问该货轮 继续向北航行时,与灯塔 M 之间的最短距离是多少 ?(精确到0.1海里,J 3止1.732)3.已知:如图,在两面墙之间有一个底端在端在B 点;当它靠在另一侧墙上时,梯子的顶端在45°.点D 到地面的垂直距离 DE =3J2m ,求点B 到地面的垂直距离 BC •4.已知:如图,小明准备测量学校旗杆 的影子恰好落在水平地面和斜坡的坡面上, 上的影长CD = 8m ,太阳光线AD 与水平地面成26°角,斜坡CD 与水平地面所成的锐 角为30°,求旗杆 AB 的高度(精确到1m ) •A 点的梯子,当它靠在一侧墙上时,梯子的顶D 点.已知/ BAC = 60°,/ DAE=AB 的高度,当他发现斜坡正对着太阳时,旗杆AB测得水平地面上的影长 BC = 20m ,斜坡坡面北A5.已知:如图,在某旅游地一名游客由山脚一个景点B ,再由B 地沿山坡BC 行走320米到达山顶C ,如果在山顶 C 处观测到景点 B 的俯角为60°.求山高CD (精确到0.01米).5.已知:如图,小明准备用如下方法测量路灯的高度:他走到路灯旁的一个地方,竖起一 根2m 长的竹竿,测得竹竿影长为 1m ,他沿着影子的方向,又向远处走出两根竹竿的 长度,他又竖起竹竿,测得影长正好为2m .问路灯高度为多少米 ?运动员从营地A 出发,沿北偏东60°方向走了 500 30°方向走了 500m ,到达目的地 C 点.求IIIA 沿坡角为30°的山坡AB 行走400m ,到达6.已知:如图,在一次越野比赛中,到达B 点,然后再沿北偏西北n(1)A 、C 两地之间的距离;⑵确定目的地C 在营地A 的什么方向?已知:如图,在1998年特大洪水时期,要加固全长为10000m 的河堤.大堤高5m ,坝顶宽4m ,迎水坡和背水坡都是坡度为1 : 1的等腰梯形.现要将大堤加高坡度改为1 : 1.5.已知坝顶宽不变,求大坝横截面面积增加了多少平方米, 多少立方米的土石?(1)BC 的长; ⑵△ ABC 的面积.(1)求AB 的长;a⑵求证:—一si n ot7. 1m ,背水坡完成工程需已知:如图,在△ ABC 中, 9. 已知:如图,在△ ABC 中, AC = b , BC = a ,锐角/ A = Ct ,/ B =P .__b sin P . A拓展、探究、思考AB = c , AC = b ,锐角/ A = Ct .RRt △ ADC 中,/ D = 90°,/ A=a ,/ CBD = P , AB = a.用含a 及P的三10.已知:如图,在角函数的式子表示CD的长.11.已知:△ ABC 中,/ A = 30°, AC = 10,12.已知:四边形 ABCD 的两条对角线 AC 、=a (0 °v a v 90° ),求此四边形的面积. BD 相交于 E 点,AC = a , BD = b , / BEC13 ..已知:如图, 长.(精确到 AB = 52m , / DAB = 430.01m),/ CAB = 40°,求大楼上的避雷针 CD 的□□□□□□□□□ □□口□□口口口口口□□口口□□口口14.已知:如图, 知测角仪AB 的高为在距旗杆 25m 的A 处,用测角仪测得旗杆顶点C 的仰角为30°,已BC =5J2,求 AB 的长.4 1如图,△ ABC 中,AC = 10, si nC=-,si nB=-,求 AB .3如图,在O O 中,/ A =/ C ,求证:AB = CD (利用三角函数证明).如图,P 是矩形ABCD 的CD 边上一点,PE 丄AC 于E , PF 丄BD 于F , AC18.已知:如图,一艘渔船正在港口 A 的正东方向40海里的B 处进行捕鱼作业,突然接到通知,要该船前往C 岛运送一批物资到 A 港,已知C 岛在A 港的北偏东60 ° 方向,且在B 的北偏西45°方向.问该船从B 处出发,以平均每小时20海里的速 度行驶,需要多少时间才能把这批物资送到A 港(精确到1小时)(该船在C 岛停留半个小时"(丁㊁止1.41, J 3 7.73, J 6 止 2.45)15 .已知:16.已知:17.已知:=15, BC = 8,求 PE + PF.C19.已知:如图,直线y = —x+ 12分别交X轴、y轴于A、B点,将△ AOB折叠,使A 点恰好落在0B的中点C处,折痕为DE .(1)求AE 的长及sin / BEC 的值; ⑵求△ CDE 的面积.20..已知:如图,斜坡 PQ 的坡度i = 1 : J 3,在坡面上点0处有一根1m 高且垂直于水平面的水管0A ,顶端A 处有一旋转式喷头向外喷水,水流在各个方向沿相同的 抛物线落下,水流最高点 M 比点A 高出1m ,且在点A 测得点M 的仰角为30°, 以0点为原点,OA 所在直线为 标系•设水喷到斜坡上的最低点为(1) 写出A 点的坐标及直线 PQ 的解析式; (2) 求此抛物线AMC 的解析式;⑶求 I X C — X B I ; ⑷求B 点与C 点间的距离.y 轴,过O 点垂直于OA 的直线为X 轴建立直角坐 B ,最高点为C.。
解直角三角形的应用测试题带答案

解直角三角形的应用测试题 b一、选择题(本大题共10小题,共30.0分)1.小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为()A. 11−sinαB. 11+sinαC. 11−cosαD. 11+cosα2.如图,长4m 的楼梯AB 的倾斜角∠ABD 为60∘,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD 为45∘,则调整后的楼梯AC的长为()A. 2√3mB. 2√6mC. (2√3−2)mD. (2√6−2)m2 3 43.楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要()A. (4+4sinθ)米 2B. 4cosθ米 2 C. (4+4tanθ)米 2 D. (4+4tanθ)米 24.上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处(如图).从A、B两处分别测得小岛M在北偏东45∘和北偏东15∘方向,那么在B处船与小岛M的距离为()A. 20海里B. 20√2海里C. 15√3海里D. 20√3海里5.如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为()A. ℎsinαB. ℎtanαC. ℎcosαD. ℎ−sinα6.如图所示,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30∘,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为60∘,则这个电视塔的高度AB(单位:米)为()A. 60√3B. 61C. 60√3+1D. 1216 7 87.某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西70∘方向航行50千米,第二艘快艇沿南偏西20∘方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是()A. 南偏东25∘,50√2千米B. 北偏西25∘,50√2千米C. 南偏东70∘,100千米D. 北偏西20∘,100千米8.如图,一艘海轮位于灯塔P的南偏东45∘方向,距离灯塔60nmile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30∘方向上的B处,这时,B处与灯塔P的距离为()A. 60√3nmileB. 60√2nmileC. 30√3nmileD. 30√2nmile9.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,则坝底AD的长度为()A. 26米B. 28米C. 30米D. 46米9 10 1110.如图是某水库大坝的横截面示意图,已知AD//BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是()米.A. 7B. 11C. 13D. 20二、填空题(本大题共10小题,共30.0分)11.某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12√3米,∠B=60∘,加固后拦水坝的横断面为梯形ABED,tanE=313√3,则CE的长为________米.12.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30∘,测得底部C的俯角为60∘,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为______ 米.(精确到1米,参考数据:√3≈1.73)12 14 1513.小明沿着坡度i为1:√3的直路向上走了50m,则小明沿垂直方向升高了______ m.14.如图,长4m的楼梯AB的倾斜角∠ABD为60∘,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45∘,则调整后楼梯AC长为______ 米.15.如图,一名滑雪运动员沿着倾斜角为34∘的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了______米.(参考数据:sin34∘≈0.56,cos34∘≈0.83,tan34∘≈0.67)16.如图,为测量某栋楼房AB的高度,在C点测得A点的仰角为30∘,朝楼房AB方向前进10米到达点D,再次测得A点的仰角为60∘,则此楼房的高度为______ 米(结果保留根号).16 17 1817.如图,从热气球C处测得地面A、B两点的俯角分别为30∘、45∘,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是______米(结果保留根号).18.如图,水库堤坝的横断面是梯形,测得BC长为30m ,CD 长为20√5m,斜坡AB的坡比为1:3,斜坡CD的坡比为1:2,则坝底的宽AD为______m.19.如图,某堤坝的斜坡AB的斜角是α,坡度是1:√3,则α=______.20.某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75∘,B处的仰角为30∘.已知无人飞机的飞行速度为3米/秒,则这架无人飞机的飞行高度为(结果保留根号)______ 米.三、计算题(本大题共4小题,共24.0分)21.如图,某数学兴趣小组要测量一栋五层居民楼CD的高度.该楼底层为车库,高2.5米;上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60∘,在B处测得四楼顶部点E的仰角为30∘,AB=14米.求居民楼的高度(精确到0.1米,参考数据:√3≈1.73)22.某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75∘,B处的仰角为30∘.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)23.如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18∘,教学楼底部B的俯角为20∘,量得实验楼与教学楼之间的距离AB=30m.(1)求∠BCD的度数.(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20∘≈0.36,tan18∘≈0.32)24.如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30∘,小红在斜坡下的点C处测得楼顶B的仰角为60∘,在斜坡上的点D处测得楼顶B的仰角为45∘,其中点A、C、E在同一直线上.(1)求斜坡CD的高度DE;(2)求大楼AB的高度(结果保留根号)四、解答题(本大题共2小题,共16.0分)25.如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30∘,测得大楼顶端A的仰角为45∘(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:√2≈1.414,√3≈1.732)26.如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:AB=100米,∠PAB=45∘,∠PBA=30∘.请求出小桥PQ的长.(√2≈1.414,√3≈1.732,结果精确到0.1米)答案和解析【答案】1. A2. B3. D4. B5. A6. C7. B8. B9. D10. C11. 812. 20813. 2514. 2√615. 28016. 5√317. 200(√3+1)18. 13019. 30∘20. 9√3+921. 解:设每层楼高为x米,由题意得:MC′=MC−CC′=2.5−1.5=1米,∴DC′=5x+1,EC′=4x+1,在Rt△DC′A′中,∠DA′C′=60∘,∴C′A′=DC′tan60∘=√33(5x+1),在Rt△EC′B′中,∠EB′C′=30∘,∴C′B′=EC′tan30∘=√3(4x+1),∵A′B′=C′B′−C′A′=AB,∴√3(4x+1)−√33(5x+1)=14,解得:x≈3.17,则居民楼高为5×3.17+2.5≈18.4米.22. 解:如图,作AD⊥BC,BH⊥水平线,由题意得:∠ACH=75∘,∠BCH=30∘,AB//CH,∴∠ABC=30∘,∠ACB=45∘,∵AB=32m,∴AD=CD=16m,BD=AB⋅cos30∘=16√3m,∴BC=CD+BD=(16√3+16)m,则BH=BC⋅sin30∘=(8√3+8)m.23. 解:(1)过点C作CE⊥BD,则有∠DCE=18∘,∠BCE=20∘,∴∠BCD=∠DCE+∠BCE=18∘+20∘=38∘;(2)由题意得:CE=AB=30m,在Rt△CBE中,BE=CE⋅tan20∘≈10.80m,在Rt△CDE中,DE=CD⋅tan18∘≈9.60m,∴教学楼的高BD=BE+DE=10.80+9.60≈20.4m,则教学楼的高约为20.4m.24. 解:(1)在Rt△DCE中,DC=4米,∠DCE=30∘,∠DEC=90∘,∴DE=12DC=2米;(2)过D作DF⊥AB,交AB于点F,∵∠BFD=90∘,∠BDF=45∘,∴∠BFD=45∘,即△BFD为等腰直角三角形,设BF=DF=x米,∵四边形DEAF为矩形,∴AF=DE=2米,即AB=(x+2)米,在Rt△ABC中,∠ABC=30∘,∴BC=ABcos30∘=x+2√32=2x+4√3=√3(2x+4)3米,BD=√2BF=√2x米,DC=4米,∵∠DCE=30∘,∠ACB=60∘,∴∠DCB=90∘,在Rt△BCD中,根据勾股定理得:2x2=(2x+4)23+16,解得:x=4+4√3,则AB=(6+4√3)米.25. 解:如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.则DE=BF=CH=10m,在直角△ADF中,∵AF=80m−10m=70m,∠ADF=45∘,∴DF=AF=70m.在直角△CDE中,∵DE=10m,∠DCE=30∘,∴CE=DEtan30∘=10√33=10√3(m),∴BC=BE−CE=70−10√3≈70−17.32≈52.7(m).答:障碍物B,C两点间的距离约为52.7m.26. 解:设PQ=x米,在直角△PAQ中,tan∠PAQ=x AQ,∴AQ=xtan45∘=x,在直角△PBQ中,tan∠PBQ=x BQ,∴BQ=xtan30∘=√3x,∵AB=100米,∴x+√3x=100,解得:x=50√3−50≈36.6(米).答:小桥PQ的长度约是36.6米.【解析】1. 解:设PA =PB=PB′=x,在RT△PCB′中,,∴x−1x=sinα,∴x−1=xsinα,∴(1−sinα)x=1,∴x=11−sinα.故选:A.设PA=PB=PB′=x,在RT△PCB′中,根据,列出方程即可解决问题.本题考查解直角三角形、三角函数等知识,解题的关键是设未知数列方程,属于中考常考题型.2. 解:在Rt△ABD中,∵sin∠ABD=ADAB,∴AD=4sin60∘=2√3(m),在Rt△ACD中,∵sin∠ACD=ADAC,∴AC=2√3sin45∘=2√6(m).选B.先在Rt△ABD中利用正弦的定义计算出AD,然后在Rt△ACD中利用正弦的定义计算AC即可.本题考查了解直角三角形的应用−坡度坡角:坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=tanα.3. 解:在Rt△ABC中,BC=AC⋅tanθ=4tanθ(米),∴AC+BC=4+4tanθ(米),∴地毯的面积至少需要1×(4+4tanθ)=4+4tanθ(米 2);故选:D.由三角函数表示出BC,得出AC+BC的长度,由矩形的面积即可得出结果.本题考查了解直角三角形的应用、矩形面积的计算;由三角函数表示出BC是解决问题的关键.4. 解:如图,过点B作BN⊥AM于点N.由题意得,AB=40×12=20海里,∠ABM=105∘.作BN⊥AM于点N.在直角三角形ABN中,BN=AB⋅sin45∘=10√2.在直角△BNM中,∠MBN=60∘,则∠M=30∘,所以BM=2BN=20√2(海里).故选B.过点B作BN⊥AM于点N.根据三角函数求BN的长,从而求BM的长.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.5. 解:∵sina=hm,∴m=hsina.故选A.根据三角函数的定义即可求解.本题考查了三角函数的定义,理解定义是关键.6. 【分析】根据题意求出CE的长,根据三角形的外角的性质和等腰三角形的性质求出AE的长,根据正弦的定义计算即可.本题考查的是解直角三角形的应用−仰角俯角问题,理解仰角的概念、熟记锐角三角函数的定义是解题的关键.【解答】解:由题意得,CE=DF=120m,∠EAC=∠AEG−∠ACE=30∘,∴∠EAC=∠ECA,∴AE=DF=120m,∴AG=AE×sin∠AEG=60√3m,∴AB=AG+GB=(60√3+1)m.故选:C.7. 解:∵第一艘快艇沿北偏西70∘方向,第二艘快艇沿南偏西20∘方向,∴∠BOA=90∘,∵BO=AO=50km,∴AB=50√2km,∠B=∠OAB=45∘,∵第二艘快艇沿南偏西20∘方向,∴∠1=∠CAO=20∘,∴∠2=45∘−20∘=25∘,∴第二艘快艇航行的方向和距离分别是:北偏西25∘,50√2千米.故选:B.根据题意得出AO=BO以及∠BOA=90∘,进而得出第二艘快艇航行的方向和距离.此题主要考查了方向角以及勾股定理,正确把握方向角的定义是解题关键.8. 解:如图作PE⊥AB于E.在Rt△PAE中,∵∠PAE=45∘,PA=60nmile,∴PE=AE=√22×60=30√2nmile,在Rt△PBE中,∵∠B=30∘,∴PB=2PE=60√2nmile,故选:B.如图作PE⊥AB于E.在Rt△PAE中,求出PE,在Rt△PBE中,根据PB=2PE即可解决问题.本题考查方向角、直角三角形、锐角三角函数的有关知识.解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.9. 解:∵坝高12米,斜坡AB的坡度i=1:1.5,∴AE=1.5BE=18米,∵BC=10米,∴AD=2AE+BC=2×18+10=46米,故选:D.先根据坡比求得AE的长,已知CB=10m,即可求得AD.此题考查了解直角三角形的应用中的坡度坡角的问题及等腰梯形的性质的掌握情况,将相关的知识点相结合更利于解题.10. 解:过D作DG⊥BC于G,EH⊥BC于H,∴GH=DE=2,∵DG=EH=15,背水坡CD的坡度i=1:0.6,背水坡EF的坡度i=3:4,∴CG=9,HF=20,∴CF=GH+HF−CG=13米,故选C.过D作DG⊥BC于G,EH⊥BC于H,解直角三角形即可得到结论.本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度,难度一般.11. 解:分别过A、D作AF⊥BC,DG⊥BC,垂点分别为F、G,如图所示.∵在Rt△ABF中,AB=12米,∠B=60∘,∴sin∠B=AFAB,∴AF=12×√32=6√3,∴DG=6√3.∵在Rt△DGC中,CD=12√3,DG=6√3米,∴GC=√CD2−DG2=18.∵在Rt△DEG中,tanE=313√3,∴6√3GE =313√3,∴GE=26,∴CE=GE−CG=26−18=8.即CE的长为8米.故答案为8.分别过A、D作下底的垂线,设垂足为F、G.在Rt△ABF中,已知坡面长和坡角的度数,可求得铅直高度AF的值,也就得到了DG的长;在Rt△CDG中,由勾股定理求CG的长,在Rt△DEG中,根据正切函数定义得到GE的长;根据CE=GE−CG即可求解.本题考查的是解直角三角形的应用−坡度坡角问题,锐角三角函数的定义,勾股定理.作辅助线构造直角三角形是解答此类题的一般思路.12. 解:由题意可得:tan30∘=BDAD=BD90=√33,解得:BD=30√3,tan60∘=DCAD=DC90=√3,解得:DC=90√3,故该建筑物的高度为:BC=BD+DC=120√3≈208(m),故答案为:208.分别利用锐角三角函数关系得出BD,DC的长,进而求出该建筑物的高度.此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.13. 解:如图,过点B作BE⊥AC于点E,∵坡度:i=1:√3,∴tan∠A=1:√3=√33,∴∠A=30∘,∵AB=50m,∴BE=12AB=25(m).∴他升高了25m.故答案为:25.首先根据题意画出图形,由坡度为1:√3,可求得坡角∠A=30∘,又由小明沿着坡度为1:√3的山坡向上走了50m,根据直角三角形中,30∘所对的直角边是斜边的一半,即可求得答案.此题考查了坡度坡角问题.此题比较简单,注意能构造直角三角形并用解直角三角形的知识求解是解此题的关键,注意数形结合思想的应用.14. 解:在Rt△ABD中,∵sin∠ABD=ADAB,∴AD=4sin60∘=2√3(m),在Rt△ACD中,∵sin∠ACD=ADAC,∴AC=2√3sin45∘=2√6(m).故答案是:2√6.先在Rt△ABD中利用正弦的定义计算出AD,然后在Rt△ACD中利用正弦的定义计算AC即可.本题考查了解直角三角形的实际应用中的坡度坡角问题,难度不大,注意细心运算即可.15. 解:如图在Rt△ABC中,AC=AB⋅sin34∘=500×0.56≈280m,∴这名滑雪运动员的高度下降了280m.故答案为280如图在Rt△ABC中,AC=AB⋅sin34∘=500×0.56≈280m,可知这名滑雪运动员的高度下降了280m.本题考查解直角三角形、坡度坡角问题、锐角三角函数等知识,解题的关键是熟练掌握锐角三角函数的定义,属于中考常考题型.16. 解:∵在直角三角形ADB中,∠D=30∘,∴ABBD=tan30∘,∴BD=ABtan30∘=√3AB,∵在直角三角形ABC中,∠ACB =60∘,∴BC=ABtan60∘=√33AB,∵CD=10,∴CD=BD−BC=√3AB−√33AB=10,解得:AB=5√3.故答案为:5√3.首先根据题意分析图形;本题涉及到两个直角三角形,应利用其公共边AB及CD=BD−BC=10构造方程关系式,进而可解,即可求出答案.本题考查解直角三角形的应用−仰角俯角问题,要求学生能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形.17. 解:∵从热气球C处测得地面A、B两点的俯角分别为30∘、45∘,∴∠BCD=90∘−45∘=45∘,∠ACD=90∘−30∘=60∘,∵CD⊥AB,CD=200m,∴△BCD是等腰直角三角形,∴BD=CD=200m,在Rt△ACD中,CD=200m,∠ACD=60∘,∴AD=CD⋅tan60∘=200×√3=200√3m,∴AB=AD+BD=200√3+200=200(√3+1)m.故答案为:200(√3+1).先根据从热气球C处测得地面A、B两点的俯角分别为30∘、45∘可求出∠BCD与∠ACD的度数,再由直角三角形的性质求出AD与BD的长,根据AB=AD+BD即可得出结论.本题考查的是解直角三角形的应用−仰角俯角问题,熟知锐角三角函数的定义是解答此题的关键.18. 解:作BE⊥AD于E,CF⊥AD于F,∵斜坡CD的坡比为1:2,即CFDF =12,∴DF=2CF,又CD=20√5m,∴CF=20m,DF=40m,由题意得,四边形BEFC是矩形,∴BE=CF=20m,EF=BC=30m,∵斜坡AB的坡比为1:3,∴BEAE =13,即AE=3BE=60m,∴AD=AE+EF+DF=130m,故答案为:130m.作BE⊥AD于E,CF⊥AD于F,根据坡度的概念分别求出AE、DF,结合图形计算即可.本题考查的是解直角三角形的应用−坡度坡角问题,掌握坡度是坡面的铅直高度h和水平宽度l的比是解题的关键,掌握矩形的判定和性质的应用.19. 解:tanα=1:√3,则α=30∘.故答案是:30∘.根据坡度就是坡角的正切值即可求解.本题主要考查了坡度的定义,理解坡度和坡角的关系是解题的关键.20. 解:如图,作AD⊥BC,BH⊥水平线,由题意得:∠ACH=75∘,∠BCH=30∘,AB//CH,∴∠ABC=30∘,∠ACB=45∘,∵AB=3×12=36m,∴AD=CD=18m,BD=AB⋅cos30∘=18√3m,∴BC=CD+BD=(18√3+18)m,∴BH=BC⋅sin30∘=(9√3+9)m.故答案为:9√3+9.作AD⊥BC,BH⊥水平线,根据题意确定出∠ABC与∠ACB的度数,利用锐角三角函数定义求出AD与BD的长,由CD+BD求出BC的长,即可求出BH的长.此题考查了解直角三角形的应用−仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.21. 设每层楼高为x米,由MC−CC′求出MC′的长,进而表示出DC′与EC′的长,在直角三角形DC′A′中,利用锐角三角函数定义表示出C′A′,同理表示出C′B′,由C′B′−C′A′求出AB的长即可.此题属于解直角三角形的应用−仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.22. 如图,作AD⊥BC,BH⊥水平线,根据题意确定出∠ABC与∠ACB的度数,利用锐角三角函数定义求出AD与BD的长,由CD+BD求出BC的长,即可求出BH的长.此题考查了解直角三角形的应用−仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.23. (1)过点C作CE与BD垂直,根据题意确定出所求角度数即可;(2)在直角三角形CBE中,利用锐角三角函数定义求出BE的长,在直角三角形CDE中,利用锐角三角函数定义求出DE的长,由BE+DE求出BD的长,即为教学楼的高.此题考查了解直角三角形的应用−仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.24. (1)在直角三角形DCE中,利用锐角三角函数定义求出DE的长即可;(2)过D作DF垂直于AB,交AB于点F,可得出三角形BDF为等腰直角三角形,设BF=DF=x,表示出BC,BD,DC,由题意得到三角形BCD为直角三角形,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出AB的长.此题考查了解直角三角形−仰角俯角问题,坡度坡角问题,熟练掌握勾股定理是解本题的关键.25. 如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.通过解直角△AFD得到DF的长度;通过解直角△DCE得到CE的长度,则BC=BE−CE.本题考查了解直角三角形−仰角俯角问题.要求学生能借助仰角构造直角三角形并解直角三角形.26. 设PQ=x米,在直角△PAQ和直角△PBQ中分别利用x表示出AQ和BQ的长,根据AB=AQ+BQ,即可列方程求得x的值.本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数表示出相关线段的长度,难度一般.。
解直角三角形专项练习

解直角三角形的实际应用1.如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走100米至坡顶D处,再从D处沿水平方向继续前行若干米到点E处,在E点测得该建筑物顶端C的仰角为59°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=.根据以上数据,计算出建筑物BC的高度约为多少米。
(结果精确到1.参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)2.如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°、35°,则广告牌的高度BC为多少米。
(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28)3.如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD 为米,点A、D、B在同一水平直线上,则A、B两点间的距离是多少米.(结果保留根号)4.某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为30°;改造后的斜坡式自动扶梯的坡角∠ACB为15°,则改造后的斜坡式自动扶梯AC的长度约为多少米.(结果精确到0.1m,温馨提示:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)5.如图,一艘海轮位于灯塔C的北偏东45方向,距离灯塔60海里的A处,它沿正南方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处,则此时船距灯塔C的距离为多少海里.(结果保留根号)6.如图,从热气球C上测得两建筑物A、B底部的俯角分别为29.5°和45°,如果这时气球的高度CD 为80米,且点A、D、B在同一直线上,求建筑物A、B之间的距离(结果精确到1米).[参考数据:sin29.5°≈0.49,cos29.5°≈0.87,tan29.5°≈0.57]7.如图,某校数学兴趣小组的小明同学为测量位于玉溪大河畔的云铜矿业大厦AB的高度,小明在他家所在的公寓楼顶C处测得大厦顶部A处的仰角为45°,底部B处的俯角为30°.已知公寓高为40m,请你帮助小明计算公寓楼与矿业大厦间的水平距离BD的长度及矿业大厦AB的高度.(结果保留根号)8.热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.9.为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置一个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED),在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米?(结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)10.如图,有一艘渔船在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A、B上的观测点进行观测,从A岛测得渔船在南偏东37°方向C处,B岛在南偏东66°方向,从B岛测得渔船在正西方向,已知两个小岛间的距离是72海里,A岛上维修船的速度为每小时20海里,B岛上维修船的速度为每小时28.8海里,为及时赶到维修,问调度中心应该派遣哪个岛上的维修船?(参考数据:cos37°≈0.8,sin37°≈0.6,sin66°≈0.9,cos66°≈0.4)11.如图,一艘货船在灯塔C的正南方向,距离灯塔257海里的A处遇险,发出求救信号.一艘救生船位于灯塔C的南偏东40°方向上,同时位于A处的北偏东60°方向上的B处,救生船接到求救信号后,立即前往救援.求AB的长.(结果取整数)参考数据:tan40°≈0.84,取1.73.12.如图,一艘货船在灯塔C的北偏西68°方向上的A处遇险,发出求救信号.一艘救生船位于灯塔C 的正西方向距离灯塔350海里的B处,救生船接到求救信号后,立即前往救援.已知货船所在位置点A位于救生船位置点B的北偏东45°方向上,求救生船与货船的距离AB(结果精确到1海里).参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41.13.如图,山顶上有一个信号塔AC,已知信号塔高AC=20米,在山脚下点B处测得塔底C的仰角∠CBD =36.9°,塔顶A的仰角∠ABD=42.0°,求山高CD(点A,C,D在同一条竖直线上).(参考数据:tan36.9°≈0.75,sin36.9°≈0.60,tan42.0°≈0.90.)14.为了完成“综合与实践”作业任务,小明和小华利用周末时间邀约一起去郊外一处空旷平坦的草地上放风筝,小明负责放风筝,小华负责测量相关数据.如图,当小明把风筝放飞到空中点P处时,小华分别在地面的点A、B处测得∠P AB=45°,∠PBA=30°,AB=200米,请你求出风筝的高度PC(点C在点P的正下方,A、B、C在地面的同一条直线上)(参考数据:≈1.414,≈1.732)15.今年,我国“巅峰使命”2022珠峰科考团对珠穆朗玛峰进行综合科学考察,搭建了世界最高海拔的自动气象站,还通过释放气球方式进行了高空探测.某学校兴趣小组开展实践活动,通过观测数据,计算气球升空的高度AB.如图,在平面内,点B,C,D在同一直线上,AB⊥CB,垂足为点B,∠ACB=52°,∠ADB=60°,CD =200m,求AB的高度.(精确到1m)(参考数据:sin52°≈0.79,cos52°≈0.62,tan52°≈1.28,≈1.73)16.如图,学校一幢教学楼AB的顶部竖有一块写有校训的宣传牌AC,小同在M点用测倾器测得宣传牌的底部A点的仰角为31°,他向教学楼前进7米到达N点,测得宣传牌顶部C点的仰角为45°,已知广告牌AC的高度为3米,测倾器DM=EN=1.5米,点B、M、N在同一水平面上,不考虑其他因素,求教学楼AB的高度.(结果保留整数,参考数据sin31°≈0.52,cos31°≈0.86,tan31°≈0.61)17.如图,太阳光照射在办公楼上,办公楼的影子恰好映射到后面的小山包的D处,已知阳光光线与水平线的夹角为49°,小山包坡面CD与水平线的夹角为26.5°,办公楼底部B距离小山包底部C的水平距离BC以及小山包的坡面CD的长均为10米,A、B、C、D均在同一平面上,求办公楼AB的高.(结果精确到0.1米,参考数据:sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15)18.教育部布的《基础教育课程改革纲要》要求每位学生每学年都要参加社会实践活动,某学校组织了一次测量探究活动,如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度1:,AB=10米,AE=21米,求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.41,≈1.73,tan53°≈,cos53°≈0.60)19.本学期小明经过一段时间的学习,想利用所学的数学知识对某小区居民楼AB的高度进行测量.如图,先测得居民楼AB与CD之间的距离BD为31m,后站在F点处测得居民楼CD的顶端C的仰角为45°.居民楼AB的顶端A的仰角为55°.已知居民楼CD的高度为16.7m,小莹的观测点E距地面1.7m.求居民楼AB的高度(精确到1m).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)20.某校开展综合实践活动,测量太阳能路灯电池板离地面的高度,如图,已知测角器的高度为1.6米,在测点A处安置测角器,测得点M的仰角∠MBC=33°,在与A点相距3.5米的测点D处安置测角器,测得点M的仰角∠MEC=45°(点A,D与N在同一条直线上),求电池板离地面的高度MN(结果精确到1米,参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65).21.2022年2月4日,第24届冬季奥林匹克运动会在北京隆重开幕,无人机航拍技术全程直播,如图,在无人机的镜头下,观测冬奥会场地A处的俯角∠ECA=34°,B处的俯角∠ECB=45°,如果此时无人机镜头C处的高度CD为100米,点A,B,D在同一条直线上,求A,B两点间的距离(结果精确到0.1米).(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)22.“为梦想战,决战中考”,如图①是寻乌县第三中学的中考倒计时牌,图②为它的侧面图,图③为它的侧面简意图,已知AB=BC=BD=60cm,∠CBD=30°.(1)如图③A处离地面多高?(2)如图④芳芳站在倒计时牌前的点H处观察倒计时牌(点D、C、H在同一水平线上),测得芳芳的身高GH为158cm,当芳芳的视线恰好落在点B处时(忽略眼睛到头顶的距离)视线俯角为45°,求此时CH的距离.(结果精确到1cm.参考数据:sin15°≈0.256,cos15°≈0.966,tan15°≈0.268,,)23.如图是一种机器零件的侧面示意图,测得∠D=30°,∠A=75°,BD⊥AC于点B,CD=16cm,AB =28cm,AE=25cm,求顶端E到底部CD的距离EF.(结果精确到0.1cm,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,=1.732)24.如图大楼AB的高度为37m,小可为了测量大楼顶部旗杆AC的高度,他从大楼底部B处出发,沿水平地面前行32m到达D处,再沿着斜坡DE走20m到达E处,测得旗杆顶端C的仰角为30°.已知斜坡ED与水平面的夹角∠EDG=37°,图中点A,B,C,D,E,G在同一平面内(结果精确到0.1m)(1)求斜坡ED的铅直高度EG和水平宽度GD.(2)求旗杆的AC高度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)25.图1是一台手机支架,图2是其侧面示意图,AB,BC可分别绕点A,B转动,测得BC=12cm,AB=25cm,∠BAD=60°,∠ABC=50°.(1)在图2中,过点B作BE⊥AD,垂足为E.填空:∠CBE=°;(2)求点C到AD的距离.(结果保留小数点后一位,参考数据:≈1.73,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)第11页共11页。
解直角三角形经典题型应用题

解直角三角形经典题型应用题1. 一个田径运动员越过一根高度为2米的木板,如果他离地面的水平距离是3米,那么他的起跳点距离木板底部的高度是多少?解:设起跳点距离木板底部的高度为x,则根据勾股定理,得到:$x^2 + 3^2 = 2^2$化简得:$x^2 = 2^2 - 3^2 = -5$由于x是高度,因此应该为正数。
但是由于方程无解,因此无法解出起跳点距离木板底部的高度。
这个结果告诉我们,如果要跨越一个木板,距离不能太远,否则就无法起跳!2. 一个人看到一个高楼,测得距离为50米,角度为30度,那么这个高楼的高度是多少?解:设高楼的高度为h,根据三角函数,得到:$tan(30) = \frac{h}{50}$化简得:$h = 50\times tan(30) = 50 \times \frac{1}{\sqrt{3}} \approx28.87$因此,这个高楼的高度约为28.87米。
3. 一个人站在一座桥上,看到一条河流在他的正下方流过,测得桥与河面的垂直距离为20米,角度为45度,那么河宽是多少?解:设河宽为w,根据三角函数,得到:$tan(45) = \frac{w}{20}$化简得:$w = 20\times tan(45) = 20$因此,河宽为20米。
4. 在一个矩形田地中,角A的顶点和角B的底点均在田地边界上,角A的角度为30度,角B的角度为60度,且田地的长宽比为3:2,那么田地的面积是多少?解:假设田地的长为3x,宽为2x,则田地的面积为6x²。
又根据三角函数,得到:$tan(30) = \frac{3x}{y}$$tan(60) = \frac{2x}{y}$化简得:$x = y\times tan(30) = y\cdot\frac{1}{\sqrt{3}}$ $x = y\times tan(60) = y\cdot\sqrt{3}$解得:$y = 6\sqrt{3}$因此,田地的面积为6x² = 1080平方米。
解直角三角形的应用题(经典体例)

BS ABDC A 解直角三角形的应用题(经典体例)1、如图,在山顶上有一电视塔,为了测量山高,在地面上引一条基线EDC ,在M 处用测角仪测得塔顶的仰角为45º,在N 处测得山顶的仰角为30º,仪器高为1.5米,CD=50米,又已知电视塔高为250米,求山高BE (结果保留根号)2、如图,某国侦察机B飞抵我国近海搞侦察活动,我战斗机A奋起拦截,地面雷达C测得:当两机处在同一方向,且在同一高度时,它们的仰角分别为∠DCA=16°,∠DCB=15°,它们与雷达的距离分别为AC=80千米,BC=81千米,求此时两机距离是多少千米?(精确到0.01千米)sin150.26,cos150.97,tan150.27,sin160.28,cos160.96,tan160.29︒≈︒≈︒≈︒≈︒≈︒≈3、A城气象台测得台风中心在A城正西方向300千米的B处,以每小时千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围是受台风影响的区域.(1)A城是否受到这次台风的影响?为什么?(2)如果A城受到台风影响,那么受影响有多长时间?4、如图,已知灯塔S周围15海里范围内有暗礁,一艘轮船以每小时20海里速度向正北方向航行,在A处测得灯塔S在轮船北偏东30°的方向上,1小时后轮船航行到B处,在B处测得灯塔S在船北偏东75°的方向上.(1) 求灯塔S与B的距离;(2) 如果轮船不改变航向,继续向正北航行有无触礁危险?为什么?A B E D C MNF E D C B A 604530D E F C BA EF D C B A 5、浦东机场沿东海岸的拦水坝,拟将背水坡的坝顶加宽2米,坡度由原来的1∶2改成1∶2.5,已知坝高6米,坝长100米. (1) 求加宽部分横断AFEB的面积;(2) 完成这一工程需要多少方材料?6、如图,有一段防洪大堤,其横断面为梯形ABCD,AB∥DC,斜坡AD的坡度为1∶1.2,斜坡BC的坡度为1∶0.8,大堤顶宽DC为6米,为了增强抗洪能力,现将大堤加高,加高部分的横断面为梯形DCEF,EF∥DC,点E、F分别在AD、BC的延长线上.当新大堤顶宽EF为3.8米时,大堤加高了多少米?7、如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着坡角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,求山的高度.8、如图,公路L与正北方向的夹角为60°,甲乙两校分别位于公路边的A、B两点处,在甲校的正东方向千米的C处有一雕塑,乙校在该雕塑的北偏东α的方向上,已知tan α=,求甲乙两校的距离.。
解直角三角形应用题类型大全

P B A 图10北东N M 解直角三角形练习班级 姓名1.我国为了维护队钓鱼岛P 的主权,决定对钓鱼岛进行常态化的立体巡航.在一次巡航中,轮船和飞机的航向相同(AP ∥BD ),当轮船航行到距钓鱼岛20km 的A 处时,飞机在B 处测得轮船的俯角是45°;当轮船航行到C 处时,飞机在轮船正上方的E 处,此时EC=5km .轮船到达钓鱼岛P 时,测得D 处的飞机的仰角为30°.试求飞机的飞行距离BD (结果保留根号).2. (2013•湘西州)钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/小时的速度向正北方向航行,海监船在A 处时,测得钓鱼岛C 在该船的北偏东30°方向上,航行半小时后,该船到达点B 处,发现此时钓鱼岛C 与该船距离最短.(1)请在图中作出该船在点B 处的位置;(2)求钓鱼岛C 到B 处距离(结果保留根号)3.(2013•红河)如图,某山顶上建有手机信号中转塔AB ,在地面D 处测得塔尖的仰角60ADC ∠=,塔底的仰角45BDC ∠=,点D 距塔AB 的距离DC 为100米,求手机信号中转塔AB 的高度(结果保留根号).4。
如图10, 在东西方向的海岸线MN 上有A 、B 两艘船,均收到已触礁搁浅的船P 的求救信号,已知船P 在船A 的北偏东60°方向,船P 在船B 的北偏西45°方向,AP 的距离为30海里.(1) 求船P 到海岸线MN 的距离(精确到0。
1海里); (2) 若船A 、船B 分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P 处.5.(2013•绥化)如图,在△ABC 中,AD ⊥BC 于点D ,AB=8,∠ABD=30°,∠CAD=45°,求BC 的长.BACD60456 如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60º,又从A点测得D点的俯角β为30º,若旗杆底G为BC的中点,求矮建筑物的高CD.7 (2013鞍山)如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜度由45°降为30°,已知原滑滑板AB的长为5米,点D、B、C 在同一水平地面上.求:改善后滑滑板会加长多少?(精确到0.01)(参考数据:=1.414,=1。
中考数学总复习《解直角三角形的应用题》专题测试卷(附答案)

中考数学总复习《解直角三角形的应用题》专题测试卷(附答案)1.如图,小明为了测量学校旗杆CD的高度,在地面离旗杆底部C处22米的A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,求旗杆的高度CD.(结果精确到0.1米)【参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62】2.如图,在一次数学实践活动中,小明同学为了测量学校旗杆EF的高度,在观测点A处观测旗杆顶点E的仰角为45°,接着小明朝旗杆方向前进了7m到达C点,此时,在观测点D处观测旗杆顶点E的仰角为60°.假设小明的身高为1.68m,求旗杆EF的高度.(结果保留一位小数.参考数据:√2≈1.414,√3≈ 1.732)3.如图,在徐州云龙湖旅游景区,点A为“彭城风华”观演场地,点B为“水族展览馆”,点C为“徐州汉画像石艺术馆”.已知∠BAC=60°,∠BCA=45°,AC=1640m.求“彭城风华”观演场地与“水族展览馆”之间的距离AB(精确到1m).(参考数据:√2≈1.41,√3≈1.73)4.大连作为沿海城市,我们常常可以在海边看到有人海钓.小华陪爷爷周末去东港海钓,爷爷将鱼竿AB摆成如图所示.已知AB=2.4m,在有鱼上钩时,鱼竿与地面的夹角∠BAD=45°.此时鱼线被拉直,鱼线BO= 3m.点O恰好位于海面,鱼线BO与海面OH的夹角∠BOH=60°.求海面OH与地面AD之间的距离DH的长.(结果保留一位小数,参考数据:√2=1.414,√3=1.73)5.让运动挥洒汗水,让青春闪耀光芒.重庆某中学倡议全校师生“每天运动一小时,快乐学习每一天”,响应学校号召,小明决定早睡早起,每天步行上学.如图,小明家在A处,学校在C处,从家到学校有两条线路,他可以从点A经过点B到点C,也可以从点A经过点D到点C.经测量,点B在点A的正北方向,AB=300米.点C在点B的北偏东45°;点D在点A的正东方向,点C在点D的北偏东30°方向CD=2900米.(1)求BC的长度(精确到个位);(2)小明每天步行上学都要从点A到点C,路线一;从点A经过点B到点C,路线二;从点A经过点D到点C,请计算说明他走哪一条路线较近?(参考数据:√2≈1.414,√3≈1.732,√6≈2.449)6.拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形BCDE,BC 的长度为60cm,两节可调节的拉杆长度相等,且与BC在同一条直线上.如图1,当拉杆伸出一节(AB)时,AC与地面夹角∠ACG=53°;如图2,当拉杆伸出两节(AM、MB)时,AC与地面夹角∠ACG=37°,两种情况下拉杆把手A点距离地面高度相同.求每节拉杆的长度.(参考数据:sin53°≈45,sin37°≈35,tan53°≈4 3,tan37°≈34)7.某中学凤栖堂前一尊孔子雕像矗立于萋萋芳草间,小刚站在雕像前,自C处测得雕像顶A的仰角为53°,小强站凤栖堂门前的台阶上,自D处测得雕像顶A的仰角为45°,此时,两人的水平距离EC为0.45m,已知凤栖堂门前台阶斜坡CD的坡比为i=1:3.(参考数据:sin53°≈45,cos53°≈35,tan53°≈43)(1)计算台阶DE的高度;(2)求孔子雕像AB的高度.8.如图为某景区平面示意图,C为景区大门,A,B,D分别为三个风景点.经测量,A,B,C在同一直线上,且A,B在C的正北方向,AB=240米,点D在点B的南偏东75∘方向,在点A的东南方向.(参考数据:√2≈1.414,√3≈1.732)(1)求B,D两地的距离;(结果精确到0.1米)(2)大门C在风景点D的南偏西60∘方向,景区管理部门决定重新翻修CD之间的步道,求CD间的距离.9.小明和小玲游览一处景点,如图,两人同时从景区大门A出发,小明沿正东方向步行60米到一处小山B处,再沿着BC前往寺庙C处,在B处测得亭台D在北偏东15°方向上,而寺庙C在B的北偏东30°方向上,小玲沿着A的东北方向上步行一段时间到达亭台D处,再步行至正东方向的寺庙C处.(1)求小山B与亭台D之间的距离;(结果保留根号)(2)若两人步行速度一样,则谁先到达寺庙C处.(结果精确到个位,参考数据:√2≈1.41,√3≈1.73,√6≈2.45)10.研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动,同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的3D扫描仪采集纪念碑的相关数据.数据采集:如图,点A是纪念碑顶部一点,AB的长表示点A到水平地面的距离.航模从纪念碑前水平地面的点M处竖直上升,飞行至距离地面20米的点C处时,测得点A的仰角∠ACD=18.4°;然后沿CN方向继续飞行,飞行方向与水平线的夹角∠NCD=37°,当到达点A正上方的点E处时,测得AE=9米数据应用:已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上.请根据上述数据,计算纪念碑顶部点A到地面的距离AB的长.(结果精确到1米.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin18.4°≈0.32,cos18.4°≈0.95,tan18.4°≈0.33)11.【综合与实践】如图1,光线从空气射入水中会发生折射现象,其中α代表入射角,β代表折射角.学习小组查阅资料了解到,若n=sinαsinβ,则把n称为折射率.(参考数据:sin53°≈45,cos53°≈35,tan53°≈43)【实践操作】如图2,为了进一步研究光的折射现象,学习小组设计了如下实验:将激光笔固定在MN处,光线可沿PD照射到空容器底部B处,将水加至D处,且BF=12cm时,光点移动到C处,此时测得DF=16cm,BC=7cm四边形ABFE是矩形,GH是法线.【问题解决】(1)求入射角∠PDG的度数;(2)请求出光线从空气射入水中的折射率n.12.数学兴趣小组设计了一款含杯盖的奶茶纸杯(如图1),图2为该纸杯的透视效果图,在图3的设计草图中,由AF、线段EF和ED构成的图形为杯盖部分,其中AF、与ED均在以AD为直径的⊙O上,且AF= ED,G为EF的中点,点G是吸管插孔处(忽略插孔直径和吸管直径),由点A,B,C,D构成的图形(杯身部分)为等腰梯形,已知杯壁AB=13.6cm,杯底直径BC=5.8cm,杯壁与直线l的夹角为84°.(1)求杯口半径OD的长;(2)若杯盖顶FE=3.2cm,吸管BH=22cm,当吸管斜插,即吸管的一端与杯底点B重合时,求吸管漏出杯盖部分GH的长.(参考数据:sin84∘≈0.995,cos84∘≈0.105,tan84∘≈9.514,√15.93≈3.99,17.5222≈307.02,√315.43≈17.76,结果精确到0.1cm).13.为了保护小吉的视力,妈妈为他购买了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意图(如图2),测得底座高AB为2cm,∠ABC=150°,支架BC为18cm,面板长DE为24cm,CD为6cm.(厚度忽略不计)(1)求支点C离桌面l的高度:(计算结果保留根号)(2)小吉通过查阅资料,当面板DE绕点C转动时,面板与桌面的夹角α满足30°≤α≤70°时,能保护视力.当α从30°变化到70°的过程中,问面板上端E离桌面l的高度是增加了还是减少了?增加或减少了多少?(精确到0.1cm,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)14.如图,四边形ABCD是某公园的游览步道(步道可以骑行),把四个景点连接起来,为了方便,在景点C的正东方设置了休息区K,其中休息区K在景点A的南偏西30°方向800√2米处,景点A在景点B的北偏东75°方向,景点B和休息区K两地相距400√5米(∠ABK<90°),景点D分别在休息区K、景点A的正东方向和正南方向.(参考数据:√2≈1.41,√5≈2.24,√6≈2.45)(1)求步道AB的长度;(2)周末小明和小宏相约一起去公园游玩,他们在景点C一起向正东出发,不久到达休息区K,他们发现有两条路线到达景点A,于是小宏想比赛看谁先到达景点A.他们分别租了一辆共享单车,两人同时在K点出发,小明选择①K−B−A路线,速度为每分钟320米;小宏选择②K−D−A路线,速度为每分钟240米,其中两人在各个景点停留的时间不计.请你通过计算说明,小明和小宏谁先到达景点A呢?15.某公园里有一座凉亭,亭盖呈圆锥状,如图所示,凉亭的顶点为O,点O在圆锥底面、地面上的正投影分别为点O1,O2,点P为圆锥底面的圆上一点,数据显示,该圆锥的底面半径为2米(即O1P=2米),圆锥底面离地面的高度为3米(即O1O2=3米).(1)若OO1=2米,求圆锥的侧面积;(2)现计划对亭盖的外部进行喷漆作业,需测算亭盖的外部面积(即圆锥的侧面积).因凉亭内堆积建筑材料,导致无法直接测量OO2的高度,工人先在水平地面上选取观测点A,B(A,B,O2在同一直线上),利用测角仪分别测得点O的仰角为α,β,其中tanα=12,tanβ=25,再测得A,B两点间的距离为m米(即AB=MN=m米),已知测角仪的高为1米(即MA=NB=QO2=1米),求亭盖的外部面积(用含m的代数式表示).16.赤水河畔的“美酒河”三个大字,是世界上最大的摩崖石刻汉字.小茜想测量绝壁上“美”字AG的高度,根据平面镜反射原理可推出入射光线与镜面的夹角等于反射光线与镜面的夹角(如图中∠DEC=∠AEB,∠DFC=∠GFB),具体操作如下:将平面镜水平放置于E处,小茜站在C处观测,俯角∠MDE=45°时,恰好通过平面镜看到“美”字顶端A处(CD为小茜眼睛到地面的高度),再将平面镜水平放置于F处观测,俯角∠MDF=36.9°时,恰好通过平面镜看到“美”字底端G处.测得BE=163.3m,CE=1.5m,点C,E,F,B在同一水平线上,点A,G,B在同一铅垂线上.(参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75)(1)CD的高度为__________m,CF的长为__________m;(2)求“美”字AG的高度.17.风能是一种清洁无公害的可再生能源,利用风力发电非常环保.如图1所示,是一种风力发电装置;如图2为简化图,塔座OD建在山坡DF上(坡比i=3:4,DE垂直于水平地面EF,O,D,E三点共线),坡面DF长10m,三个相同长度的风轮叶片OA,OB,OC可绕点O转动,每两个叶片之间的夹角为120°;当叶片静止,OA与OD重合时,在坡底F处向前走25米至点M处,测得点O处的仰角为53°,又向前走23.5米至点N处,测得点A处的仰角为30°(点E,F,M,N在同一水平线上).(1)求叶片OA的长;(2)在图2状态下,当叶片绕点O顺时针转动90°时(如图3),求叶片OC顶端C离水平地面EF的距离.(参考数据:sin53°≈45,cos53°≈35,tan53°≈43,√3≈1.7,结果保留整数)18.贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚A为起点,沿途修建AB,CD两段长度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC为50m.索道AB与AF的夹角为15°,CD与水平线的夹角为45°,A,B 两处的水平距离AE为576m,DF⊥AF,垂足为点F.(图中所有点都在同一平面内,点A,E,F在同一水平线上)(1)求索道AB的长(结果精确到1m);(2)求水平距离AF的长(结果精确到1m).(参考数据:sin15°≈0.26cos15°≈0.97tan15°≈0.27√2≈1.41)19.春天是踏青的好季节小明和小华决定去公园出游踏青.如图已知A为公园入口景点B位于A点东北方向400√2米处景点E位于A点南偏东30°方向景点B在景点E的正北方向景点C既位于景点B正东方向310米处又位于景点D的北偏西37.5°方向.景点F既位于景点E的正东方向又位于景点D的正南方向.DF=400米.(参考数据:√2≈1.41,√3≈1.73,sin37.5°≈35,cos37.5°≈45,tan37.5°≈34)(1)求BE的长;(精确到个位)(2)小明选择了游览路线①:A−B−C−D小明行驶的平均速度是72米/分小明在景点B、C处各停留了10分钟、5分钟.小华选择了游览路线②:A−E−F−D小华行驶的平均速度为96米/分.小华在景点E、F处各停留了9分钟、8分钟.请通过计算说明:小明和小华谁先到达景点D处.20.如图是一种家用健身卷腹机由圆弧形滑轨⌒AB可伸缩支撑杆AC和手柄AD构成.图①是其侧面简化示意图.滑轨⌒AB支撑杆AC与手柄AD在点A处连接其中D A B三点在一条直线上.(1)如图① 固定∠DAC=120°,若BC=30√6cm,AC=60cm,求∠ABC的度数;(2)如图② 固定∠DAC=100°若AC=50cm,∠ABC=30°时圆弧形滑轨AB所在的圆恰好与直线BC 相切于点B求滑轨⌒AB的长度.(结果精确到0.1 参考数据:π取3.14 sin70°≈0.940)参考答案:1.解:由题意得BE⊥CD于EBE=AC=22米∠DBE=32°在Rt△DBE中DE=BE⋅tan∠DBE=22×0.62≈13.64(米)CD=CE+DE=1.5+13.64≈15.14(米)答:旗杆的高CD约为15.14米.2.解:延长AD交EF于点G设EG=x∵AD∥BF,EF⊥BF∵AG⊥EF∵∠B=∠F=∠AGF=90°∵四边形ABFG是矩形∠AGE=90°∵∠EAG=45°∵∠AEG=90°−∠EAG=45°∵AG=EG=x∵AD=7∵DG=x−7∵∠EDG=60°=√3∵tan∠EDG=EGDG=√3∵xx−7∵x=7(3+√3)2∵EG=7(3+√3)2∵GF=AB=1.68∵EF=EG+GF=7(3+√3)2+1.68≈7(3+1.732)2+1.68 =16.562+1.68=18.242≈18.2.故旗杆EF的高度约18.2m.3.解:过B作BH⊥AC于H设AH=xm∵∠BAC=60°∵∠ABH=90°−60°=30°∵AB=2AH=2xm∵tanA=tan60°=BHAH=√3∵BH=√3xm∵∠BCA=45°∠BHC=90°∵△BHC是等腰直角三角形∵CH=BH=√3xm∵AH+CH=√3x+x=AC=1640≈600.7∵x=√3+1∵AB=2x≈1201(m).答:“彭城风华”观演场地与“水族展览馆”之间的距离AB约是1201m.4.解:过点B作BC⊥OH交OH于点C延长AD交BC于点E∵四边形DECH是矩形∵DH=CE.根据题意可知∠BAD=45°,∠BOH=60°在Rt△ABE中AB=2.4m∵sin∠BAE=BEAB即sin45°=BE2.4=1.2×1.41=1.692.解得BE=2.4×√22在Rt△BOC中BO=3m∵sin∠BOC=BCBO即sin60°=BC3=1.5×1.73=2.595解得BC=3×√32∵DH=CE=BC−BE=0.903≈0.9(m).所以海面OH与地面AD之间得距离DH的长0.9m.5.(1)解:过点C作CM⊥AD交AD的延长线于点M过点B作BN⊥AM交AM于点N过点D作DH⊥BN 交BN于点H.由题可知:∠CBN=45°∠A=90°∠CDM=60°.∵四边形ABNM、四边形ABHD、四边形DMNH都是矩形△BCN是等腰直角三角形.在Rt△CMD中∵∠CDM=60°CD=2900米∵DM=12DC=1450米CM=√3DM=1450√3米∵AB=MN=300米∵CN=CM−MN=(1450√3−300)米在Rt△CBN中∠CBN=45°∵CB=√2CN=(1450√6−300√2)米≈3127米答:BC的长度为3127米.(2)解:路线一:AB+BC=(300+1450√6−300√2)米≈3427米∵AM=BN=CN=(1450√3−300)米∵AD=AM−DM=(1450√3−1750)米∵路线二:AD+CD=(1450√3+1150)米≈3361米∵3427<3361∵路线二较近.6.解:如图1 作AF⊥CG垂足为F设AB=xcm则AC=60+x∵sin53°=AFAC =AF60+x∴AF=(60+x)⋅sin53°如图2 作AH⊥CG垂足为H则AC=60+2x∴AH=(60+2x)⋅sin37°∵AF=AH∴(60+x)⋅sin53°=(60+2x)⋅sin37°∴4(60+x)5=3(60+2x)5解得:x=30.答:每节拉杆的长度为30cm.7.(1)解:∵凤栖堂门前台阶斜坡CD的坡比为i=1:3EC为0.45m∵DE EC =13∴DE=EC3=0.15m即台阶DE的高度为0.15m;(2)解:如图所示设AB的对边为MN作DF⊥MN于F∵由题意得四边形NFDE是矩形∵FN=DE=0.15m DF=NE设MN=xm则MF=(x−0.15)m在Rt△MFD中∠MDF=45°∵FD=MF=(x−0.15)m∵NC=NE−EC=(x−0.15)−0.45=(x−0.6)m∵tan53°=MNNC ≈43即xx−0.6=43解得x=2.4经检验x=2.4是原方程的解答:孔子雕像AB的高度约2.4m.8.(1)解:过点B作BP⊥AD于点P由题意知∠BAD=45∘∠CBD=75∘∴∠ADB=30∘∠ABP=45∘=∠A∴BD=2BP AP=BP在Rt△ABP中AB=240米∴AP=BP=AB=120√2(米)sin45∘∴BD=2BP=240√2≈339.4(米).答:B、D两地的距离约为339.4米;(2)解:过点B作BM⊥CD于点M由(1)得BD=2BP=240√2(米)∵∠CDB=180∘−60∘−75∘=45∘∠CBD=75∘∠DCB=60∘∴∠DBM=45∘=∠CDB∴BM=DM在Rt△BDM中BD=240√2sin45∘=BMBD∴BM=DM=BD⋅sin45∘=240√2×√2=240(米)2在Rt△BCM中∠CBM=75∘−45∘=30∘∴CM=BM⋅tan30∘=80√3(米)∴DC=DM+CM=240+80√3(米).9.解:(1)作BE⊥AD于点E由题意知AB=60∠A=45°∠ABD=90°+15°=105°∠CBA=90°+30°=120°在Rt△ABE中在Rt△BDE中ED=√3BE=30√6BD=2BE=60√2∴小山B与亭台D之间的距离60√2米(2)延长AB作DF⊥BA于点F作CG⊥BA于点G则∠CBG=180°−∠CBA=60°由题意知CD∥AB∵四边形CDFG是矩形∵CG=DF,CD=FG.∵AE=30√2ED=30√6∴AD=30√2+30√6在Rt△AFD中DF=AF=√2=30+30√3CG=DF=30+30√3米在Rt△BCG中BG=√3=10√3+30∴CD=FG=AB+BG−AF=60−20√3∴S玲=AD+CD=30√2+30√6+60−20√3≈141.2米S明=AB+BC=60+60+20√3≈154.6米∵141.2<154.6且两人速度一致∴小玲先到.答:小玲先到达寺庙C处.10.解:如图:延长CD交AB于点H则四边形CMBH为矩形∴CM=HB=20在Rt△ACH中∠AHC=90°∠ACH=18.4°∴tan∠ACH=AH CH∴CH=AHtan∠ACH=AHtan18.4°≈AH0.33在Rt△ECH中∠EHC=90°∠ECH=37°∴tan∠ECH=EH CH∴CH=EHtan∠ECH=EHtan37°≈EH0.75设AH=x.∵AE=9∴EH=x+9∴x0.33=x+90.75解得x≈7.1∴AB=AH+HB≈7.1+20=27.1≈27(米).答:点A到地面的距离AB的长约为27米.11.(1)解:如图1 ∵GH∥FB∴∠DBF=∠PDG,∵BF=12cm,DF=16cm,∴tan∠DBF=DFBF=1612=43,∵tan53°≈4 3∴入射角∠PDG约为53°.(2)解:如图2 作DM⊥AB于点T在Rt△BDF中BF=12cm,DF=16cm∴BD=√DF2+BF2=20cm,在Rt△DTC中TC=DF−BC=16−7=9cm,DT=BF=12cm∴CD=√DT2+TC2=√122+92=15cm,∴光线从空气射入水中的折射率∴光线从空气射入水中的折射率n=43.12.(1)解:过点B作BP⊥AD于点D过点C作CQ⊥AD于点Q延长BC到点R ∵四边形BCQP是矩形∵BC=QP BP=CQ∵AB=13.6cm杯底直径BC=5.8cm杯壁与直线l的夹角为84°点A B C D构成的图形(杯身部分)为等腰梯形∵AD∥BC CD=AB=13.6cm QP=BC=5.8cm∵∠A=∠D=∠DCR=84°∵BP=CQ CD=AB∵Rt△ABP≌Rt△DCQ(HL)∵AP=DQ∵AP=DQ=CDcosD=13.6×0.105=1.428(cm)CQ=CDsinD=13.6×0.995=13.532(cm)∵AD=2AP+PQ=DQ=2×1.428+5.8=8.656(cm)AD=4.328≈4.3(cm)∵OD=12故杯口半径OD的长为4.3cm.(2)解:连接GO并延长交BC于点N∵G为EF的中点EF=1.6(cm)∵GO⊥EF,EG=FG=12连接FD∵ AF=ED,∵∠EFD=∠ADF,∵AD∥EF∵GO⊥AD∵ AD∥BC∵GO⊥BC∵NO=13.532(cm)∵GO=√(4.3)2−(1.6)2≈4.0(cm)∵GN≈17.532(cm)∵GB=√(17.532)2+(2.9)2≈17.77(cm)∵GH=BH−GB=22−17.77≈4.2(cm)13.(1)解:过点C作CF⊥l于点F过点B作BM⊥CF于点M∴∠CFA=∠BMC=∠BMF=90°.由题意得:∠BAF=90°∴四边形ABMF为矩形∴MF=AB=2cm∠ABM=90°.∵∠ABC=150°∴∠MBC=60°.∵BC=18cm∴CM=BC⋅sin60°=18×√32=9√3(cm).∴CF=CM+MF=(9√3+2)cm.答:支点C离桌面l的高度为(9√3+2)cm;(2)解:过点C作CN∥l过点E作EH⊥CN于点H∴∠EHC=90°.∵DE=24cm CD=6cm∴CE=18cm.当∠ECH=30°时EH=CE⋅sin30°=18×12=9(cm);当∠ECH=70°时EH=CE⋅sin70°≈18×0.94=16.92(cm);∴16.92−9=7.92≈7.9(cm)∴当α从30°变化到70°的过程中面板上端E离桌面l的高度是增加了增加了约7.9cm.14.(1)解:由题意得∠DAK=30°∠BAD=75°∠D=90°AK=800√2米BK=400√5米∵∠BAK=∠BAD−∠DAK=75°−30°=45°过点K作KH⊥AB于H则∠AHK=∠BHK=90°∵△AHK为等腰直角三角形∵AH=KH=√22AK=√22×800√2=800米∵BH=√BK2−KH2=√(400√5)2−8002=400米∵AB=AH+BH=800+400=1200米;(2)解:∵AK=800√2∠DAK=30°∠D=90°∵DK=12AK=400√2米AD=AK·cos30°=800√2×√32=400√6米∵路线②K−D−A的路程为KD+AD=400√2+400√6≈1544米∵小宏到达景点A的时间为1544÷240≈6.43分钟∵路线①K−B−A的路程为KB+BA=400√5+1200≈2096米∵小明到达景点A的时间为2096÷320≈6.55分钟∵6.43<6.55∵小宏先到达景点A.15.(1)解:由题意得:∠OO1P=90°.∵OO1=2米O1P=2米∴OP=2√2(米).∴圆锥的侧面积=π×2√2×2=4√2π(米2).答:圆锥的侧面积为4√2π平方米;(2)解:由题意得:∠OQM=90°.设OQ长x米.∵tanα=1 2∴MQ=2x米.∵MN=m米∴NQ=(m+2x)米.∵tanβ=2 5∴xm+2x =25.解得:x=2m.∵O1O2=3米QO2=1米∴OO1=2m+1−3=(2m−2)米.∵O1P=2米∠OO1P=90°.∴OP=√22+(2m−2)2=√4m2−8m+8=2√m2−2m+2(米).∴圆锥的侧面积=π×2√m2−2m+2×2=4π√m2−2m+2(米2).答:亭盖的外部面积为4π√m2−2m+2平方米.16.(1)解:∵∠MDE=45°∴∠DEC=45°∵DC⊥BC∴△DCE是等腰直角三角形∴DC=CE=1.5m 在Rt△DCF中∠DFC=36.9°DC=1.5m∴DF=DCsin36.9°=1.50.60=2.5(m)∴CF=√DF2−DC2=√2⋅52−1⋅52=2(m);故答案为:1.52;(2)∵∠DEC=45°∴∠AEB=45°∴∠BAE=45°∴AB=BE=163.3m由题意可知∠MDF=36.9°∴∠GFB=∠DFC=∠MDF=36.9°∵EF=CF−CE=2−1.5=0.5(m)∴BF=163.3−0.5=162.8(m)在Rt△BFG中BG=tan∠GFB⋅BF≈0.75×162.8=122.1(m)∴AG=163.3−122.1=41.2(m)即“美”字的高度AG约为41.2m.17.(1)解:∵DE垂直于水平地面EF∵∠E=90°∵坡比i=3:4∵DE EF =34设DE=3xm则EF=4xm ∵坡面DF长10m∵(3x)2+(4x)2=102解得:x=2(负值舍去)∵DE=6m EF=8m∵MF=25m∵ME=MF+EF=33m由题意得:∠OME=53°=44m∵OE=ME⋅tan53°≈33×43∵MN=23.5m∵NE=ME+MN=56.5m.由题意得:∠N=30°≈32m∵AE=NE⋅tan30°=56.5×√33∵OA=OE−AE=44−32=12m.(2)如图过点C作CH⊥OE于点M CG⊥NE于G∵∠CHE=∠HEG=∠CGE=∠CHO=90°∵四边形HEGC是矩形∵EH=CG∵叶片绕点O顺时针转动90°∵∠AOE=90°∵∠AOC=120°∵∠COH=30°由题意得:OC=OA=12m=6√3m∵OH=OCcos∠COH=12×√32∵CG=HE=OE−OH=44−6√3≈34m.∵叶片OC顶端C离水平地面EF的距离为34m.18.(1)解:在Rt△ABE中∠AEB=90°∠A=15°AE=576m∴AB=AEcosA =576cos15°≈594(m).答:索道AB的长约为594m.(2)延长BC交DF于点G∵BC∥AF DF⊥AF∴DG⊥CG.∵四边形BEFG为矩形.∴EF=BG.∵CD=AB≈594m∠DCG=45°∴CG=CD·cos∠DCG≈594×cos45°=297√2(m).∴AF=AE+EF=AE+BG=AE+BC+CG≈576+50+297√2≈1045(m).答:水平距离AF的长约为1045m19.(1)解:如图所示过点A作AH⊥BE于点H∵∠BAH=45°,AB=400√2米∴AH=BH=√22AB=400米∵∠AEB=30°∴HE=√3AH=400√3米AE=2AH=800米∴BE=400+400√3≈1092(米).∴BE长约1092米.(2)解:小华先到达景点D处理由如下:如图过点C作CN⊥EF于点N过点D作DM⊥BE于点M交CN于点G则四边形BCNE和四边形DFNG都是矩形∴BC=EN BE=CN=(400+400√3)米GN=DF=400米DG=NF∴CG=CN−GN=400√3米∵景点C既位于景点B正东方向310米处又位于景点D的北偏西37.5°方向.∴BC=310(米)∠DCN=37.5°在Rt△CGD中cos∠DCN=CGCD tan∠DCN=DGCG∴CD=CGcos37.5°=400√345≈865(米)DG=CG⋅tan37.5°=400√3×34≈519(米)∴EF=EN+NF=BC+DG≈829(米)∵小明选择了游览路线①:A−B−C−D小明行驶的平均速度是72米/秒.小明在景点B、C处各停留了10分钟、5分钟∴小明的游览时间为400√2+310+86572+10+5≈39(分钟)在Rt△AEH中AH=400米∠EAH=60°∴AE=AHcos60°=40012=800(米)∵小华选择了游览路线②:A−E−F−D小华行驶的平均速度为96米/秒.小华在景点E、F处各停留了9分钟、8分钟∴小华的游览时间为800+829+40096+9+8≈38(分钟)∴小华的游览时间更短先到达景点D处.20.(1)解:如图过点C作CE⊥AB垂足为E∵∠DAC=120°∴∠EAC=180°−∠DAC=60°在Rt△AEC中AC=60cm∴CE=AC⋅sin60°=60×√32=30√3(cm)在Rt△BEC中BC=30√6cm∴sin∠EBC=ECBC=√330√6=√22∴∠ABC=45°∴∠ABC的度数约为45°;(2)解:如图过点A作AF⊥BC垂足为F∵圆弧形滑轨⌒AB所在的圆恰好与直线BC相切于点B ∴过点B作HB⊥BC作AB的垂直平分线MG交HB于点O连接OA∴OB=OA∴圆弧形滑轨⌒AB所在的圆的圆心为O∵∠DAC=100°∠ABC=30°∴∠ACF=∠DAC−∠ABC=100°−30=70°在Rt△AFC中AC=50cm∴AF=AC⋅sin70°≈50×0.940=47(cm)在Rt△AFB中∠ABC=30°∴AB=2AF=2×47=94(cm)∵OB⊥BC∴∠OBC=90°∴∠OBA=∠OBC−∠ABC=60°∴△OBA为等边三角形∴OB=AB=94cm∠BOA=60°∴滑轨⌒AB的长度=60π×94180≈98.4(cm)∴滑轨AB⌒AB的长度约为98.4cm.。
2022年中考解直角三角形的应用专题-含答案

2022年中考解直角三角形的应用专题1.如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,(1)求点E到建筑物AC的距离;.(2)求旗杆AB的高度.(结果精确到0.1米).参考数据:≈1.73,≈1.41.2.某学校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动,如图,她在山坡脚A处测得这座楼房顶B点的仰角为60°,沿山坡向上走到C处再测得B点的仰角为45°,已知OA=200m,山坡的坡度i=,且O、A、D在同一条直线上.求:(1)楼房OB的高度;(2)小红在山坡上走过的距离AC(结果保留根号)3.小明想利用小区附近的楼房来测同一水平线上一棵树的高度.如图,他在同一水平线上选择了一点A,使A与树顶E、楼房顶点D也恰好在一条直线上.小明测得A处的仰角为∠A=30°.已知楼房CD高21米,且与树BE之间的距离BC=30米,求此树的高度约为多少米.(结果保留两个有效数字,≈1.732).4.如图,建筑物BC上有一个旗杆AB,小明和数学兴趣小组的同学计划用学过的知识测量该建筑物的高度,他们制订了测量方案,并利用课余时间完成了实地测量,测量方法如下:在该建筑物底部所在的平地上有一棵小树ED,小明沿CD后退,发现地面上的点F、树顶E、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶E、建筑物顶端B恰好在一条直线上,已知旗杆AB=3米,DE=4米,DF=5米,FG=1.5米,点A、B、C在一条直线上,点C、D、F、G在一条直线上,AC、ED均垂直于CG,根据以上信息,请求出这座建筑物的高BC.5.环球国际金融中心(图中AB所示)是目前上海市的标志性建筑、小明家住在金融中心附近的“祥和”大厦(图中CD所示),小明想利用所学的有关知识测量出环球国际金融中心的高度、他先在自己家的阳台(图中的点Q处)测得金融中心的顶端(点A)的仰角为37°,然后来到楼下,由于附近建筑物影响测量,小明向金融中心方向走了84米,来到另一座高楼的底端(图中的点P处),测得点A的仰角为45°.又点C、P、B在一条直线上,小明家的阳台距地面60米,请你在答题纸上画出示意图,并根据上述信息求出环球国际金融中心(AB)的高度.(备用数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)6.著名的法门寺合十舍利塔由台湾建筑设计大师李祖原设计,呈双手合十状,其恢宏的气势不仅传承佛教建筑的特色,更以现代化的技术融合古今中外建筑之精华周末,小明想用所学的知识来测量该塔的高度.测量方法如下:如图,他先在B处用测倾器AB测得塔顶E的仰角为37°;再从点B沿BF方向走了97米到达D处(即BD=97米),在D处竖立标杆CD,发现水平地面上的点M、标杆的顶端C与塔顶E恰好在一条直线上,已知AB=CD=1.5米,测得DM=1米,点B、M、D、F在同一条直线上,AB⊥BF,CD⊥BF,EF⊥BF,根据测量示意图求该塔的高度EF.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)7.如图是小明同学画出的某同学放风筝的示意图,从地面A处放飞的风筝几分钟后飞至C处,此时,点B与旗杆PQ的顶部点P以及点C恰好在一直线上,PQ⊥AB于点Q.(1)已知旗杆的高为10米,在B处测得旗杆顶部点P的仰角为30°,在A处测得点P的仰角为45°,求A、B之间的距离;(2)此时,在A处测得风筝C的仰角为75°,设绳子AC在空中为一条线段,求AC的长.(结果保留根号)8.为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B 的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行.(1)求点F到直线CE的距离(结果保留根号);(2)若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).9.如图,为了测量楼AB的高度,小明在点C处测得楼AB的顶端A的仰角为30°,又向前走了20米后到达点D,点B、D、C在同一条直线上,并在点D测得楼AB的顶端A的仰角为60°,求楼AB的高.10.如图,为测量一座地标性高楼的高度,小明在A点处测得楼顶D点的仰角为60°,在B点处测得楼顶D点的仰角为30°,A、B、C三点在一条直线上,已知AB=40m,小明的眼睛离地面为1.6m,求楼的高度.11.小军家附近有一棵侧柏,小军和小明计划利用所学过的知识测量侧柏的高度.阳光明媚的周末,小军和小明带着测量工具来到侧柏前.测量方法如下:如图,首先,小军沿侧柏的影子BD移动,当恰好移动到C处时发现小军的影子顶端与侧柏的影子顶端D重合,测得小军身高CE=1.6米,影长CD=2.4米.然后,小军在C处半蹲,小明在BC上竖立高2米的标杆,并沿BC移动,当标杆移动到点H时,小军的眼睛F、标杆顶端G与侧柏顶端A恰好在一条直线上,此时测得小军眼睛到地面的距离CF=1米,HC=1.4米.已知点B、H、C、D在一条直线上,点E、F、C在一条直线上,AB、GH、EC均垂直于BD,请你根据题中提供的相关信息,求出这棵侧柏的高AB.12.如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知BC为4米,且B、C、E三点在同一条直线上.(1)求平房AB的高度;(2)请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计)13.揽月阁是西安唐文化轴的南部重要节点和标志性建筑,与唐大雁塔今古一线、遥相呼应,联袂彰显西安具有历史文化特色的现代化国际大都市风貌.一天下午,小明和小丽来到了揽月阁广场,他们想用所学的知识,测量揽月阁的高度.如图,点A为揽月阁的顶部,点B为揽月阁的底部,小明在点C处放一水平的平面镜,然后沿着BC方向向前走0.5米,到达点D处,这时小明蹲下,恰好在镜子里看到揽月阁的顶端A的像.接下来小明不动,小丽在C处竖起一根可调节高度的测量杆,并调节测量杆的高度,使得测量杆的顶端P、揽月阁的顶端A、小明的眼睛E在一条直线上,此时测得测量杆的高度CF =1.98米.已知小明蹲下时,眼睛到地面的距离DE=1米,点B、C、D在一条直线上,AB⊥BD,CF ⊥BD,DE⊥BD,求揽月阁的高度AB.(平面镜的大小忽略不计)14.如图,某中学操场边有一旗杆A,小明在操场的C处放风筝,风筝飞在图中的D处,在CA的延长线上离小明30米远的E处的小刚发现自己的位置与风筝D和旗杆的顶端B在同一条直线上,小刚在E 处测得旗杆顶点B的仰角为α,且tanα=,小明在C处测得旗杆顶点B的仰角为45°.(1)求旗杆的高度.(2)此时,在C处背向旗杆,测得风筝D的仰角(即∠DCF)为48°,求风筝D离地面的距离.(结果精确到0.1米,其中sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)15.小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,AC的坡度i =1:,且B、C、D三点在同一直线上.(1)求树DE的高度;(2)求食堂MN的高度.16.如图,水库大坝的横断面为四边形ABCD,其中AD∥BC,坝顶BC=10米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°.(1)求坝底AD的长度(结果精确到1米);(2)若坝长100米,求建筑这个大坝需要的土石料(参考数据:)17.如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米.(1)求坡顶与地面的距离BE的长.(2)为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33).18.每逢雨季,天降大雨,山体滑坡灾害时有发生,北峰小学教学楼后面紧邻着一个土坡,坡上面是一块平地,如图所示:AF∥BC,斜坡AB长30米,坡角∠ABC=60°.为了防止滑坡,保障安全,学校决定对该土坡进行改造,经过地质人员勘测,当坡角不超过45°时,可以确保山体不滑坡.(1)求坡顶与地面的距离AD等于多少米?(精确到0.1米)(2)为确保安全,学校计划改造时保持坡脚B不动,坡顶A沿AF削进到E点处,求AE至少是多少米?(精确到0.1米)19.如图:某水坝的横断面为梯形ABCD,坝顶宽BC为6米,坝高BH为20米,斜坡AB的坡度,斜坡CD的坡角为45°.求(1)斜坡AB的坡角;(2)坝底宽AD(精确到1米).(参考数据:,)20.某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,斜坡AB的坡比为i=12:5,为了减缓坡面防山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.(1)求改造前坡顶到地面的距离BE的长;(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确保安全吗?(tan48.8°≈1.14)21.某校九年级数学兴趣小组的同学进行社会实践活动时,象利用所学的解直角三角形的知识测量某大楼高度,如图所示,大楼AB的正前方有一斜坡CD,坡长CD=4米,坡角∠DCE=30°,他们先在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°(1)求斜坡CD的高度DE;(2)求楼AB的高度(结果保留根号).22.如图,一水库大坝的横断面为梯形ABCD,坝顶宽6米,坝高10米,斜坡AB的坡度i1=1:3,斜坡CD的坡度i2=1:1.(1)求斜坡AB的长(结果保留根号);(2)求坝底AD的长度;(3)求斜坡CD的坡角α.23.如图,学校教学楼前方50米A处有一个坡度i=1:的斜坡,为了测学校教学楼MN的高度,小明沿着斜坡向上前进了6米到达点B,在点B处用测角仪测得楼的顶部N的仰角为37°,已知测角仪BC 的高度为1.2米,求教学楼MN的高度.(参考数据:sin37°≈,cos37°≈,tan37°.计算结果保留根号)24.如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了20m到达D处,此时遇到一斜坡,坡度i=1:,沿着斜坡前进40m到达F处测得建筑物顶部的仰角是45°,(坡度i=1:是指坡面的铅直高度FE与水平宽度DE 的比).(1)求斜坡DF的端点F到水平地面AB的距离和斜坡的水平宽度DE分别为多少米?(2)求建筑物BC的高度为多少米?(3)现小亮在建筑物一楼(水平地面上点B处)乘电梯至楼顶(点C),电梯速度为2(+3)m/s,同时小明从测角仪处(点A)出发,骑摩托车至斜坡的端点F处,已知,小明在平地上的车速是上坡车速的两倍,小亮所用时间是小明所用时间的一半,求小明上坡时的车速为多少?然后在水平地面上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:是指坡面的铅直高度FE与水平宽度DE 的比).请你计算出该建筑物BC的高度.(取=1.732,结果精确到0.1m).26.如图,AB是垂直于水平面的建筑物,为测量AB的高度,小红从建筑物底端B出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D在同一平面内),斜坡CD的坡度(或坡比)i=1:2.4,求建筑物AB的高度.(精确到个位)(参考数据:sin=27°≈0.45,cos27°≈0.89,tan27°≈0.51)然后在水平地面上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,请你计算出该建筑物BC的高度.(取=1.732,结果精确到0.1m)28.如图,AB,CD表示两栋建筑,小明想利用建筑CD玻璃幕墙的反射作用来测建筑AB的高度,首先他在建筑AB的底部A处用测角仪测得其顶部B在建筑CD玻璃幕墙上的反射点E的仰角为α,然后他沿AC前进了10米到达点F处,再用测角仪测得建筑AB的顶部B在建筑CD玻璃幕墙上的反射点G 的仰角为β,已知tanα=,sinβ=,测角仪置于水平高度1.5米的M、N处.试求建筑AB的高度.2022年中考解直角三角形的应用专题参考答案与试题解析一.解答题(共28小题)1.如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,(1)求点E到建筑物AC的距离;.(2)求旗杆AB的高度.(结果精确到0.1米).参考数据:≈1.73,≈1.41.【解答】解:(1)∵∠BEC=60°,∠BDE=30°,∴∠DBE=60°﹣30°=30°,∴BE=DE=20,∴CE=BE=10m;∴点E到建筑物AC的距离是10m;(2)在Rt△BEC中,BC=BE•sin60°=20×=10≈17.3(米),∴AB=BC﹣AC=17.3﹣12=5.3(米),答:旗杆AB的高度为5.3米.2.某学校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动,如图,她在山坡脚A处测得这座楼房顶B点的仰角为60°,沿山坡向上走到C处再测得B点的仰角为45°,已知OA=200m,山坡的坡度i=,且O、A、D在同一条直线上.求:(1)楼房OB的高度;(2)小红在山坡上走过的距离AC(结果保留根号)【解答】解:(1)在Rt△ABO中,∠BAO=60°,OA=200m.∵tan60°=,即=,∴OB=OA=200(m).(2)如图,过点C作CE⊥BO于E,CH⊥OD于H.则OE=CH,EC=OH.根据题意,知i==,可设CH=x,AH=x.在Rt△BEC中,∠BCE=45°,∴BE=CE,即OB﹣OE=OA+AH.∴200﹣x=200+x.解得x=200(2﹣).在Rt△ACH中,∵AC2=AH2+CH2,∴AC2=(x)2+x2=4x2.∴AC=2x=2×200(2﹣)=400(2﹣)(m).答:高楼OB的高度为200m,小玲在山坡上走过的距离AC为400(2﹣)m.3.小明想利用小区附近的楼房来测同一水平线上一棵树的高度.如图,他在同一水平线上选择了一点A,使A与树顶E、楼房顶点D也恰好在一条直线上.小明测得A处的仰角为∠A=30°.已知楼房CD高21米,且与树BE之间的距离BC=30米,求此树的高度约为多少米.(结果保留两个有效数字,≈1.732).【解答】解:根据题意可得:AC==21,则AB=AC﹣BC=21﹣30.故树高BE=AB×tan30°=(21﹣30)×tan30°≈3.7(米).4.如图,建筑物BC上有一个旗杆AB,小明和数学兴趣小组的同学计划用学过的知识测量该建筑物的高度,他们制订了测量方案,并利用课余时间完成了实地测量,测量方法如下:在该建筑物底部所在的平地上有一棵小树ED,小明沿CD后退,发现地面上的点F、树顶E、旗杆顶端A恰好在一条直线上,继续后退,发现地面上的点G、树顶E、建筑物顶端B恰好在一条直线上,已知旗杆AB=3米,DE=4米,DF=5米,FG=1.5米,点A、B、C在一条直线上,点C、D、F、G在一条直线上,AC、ED均垂直于CG,根据以上信息,请求出这座建筑物的高BC.【解答】解:由题意可得,∠ACF=∠EDF=90°,∠AFC=∠EFD,∴△ACF∽△EDF,∴,即,∴CD=,由题意可得,∠BCG=∠EDG=90°,∠BGC=∠EGD,∴△BCG∽△EDG,∴,即,∴6.5BC=4(CD+6.5),∴6.5BC=4×,∴BC=14,∴这座建筑物的高BC为14米.5.环球国际金融中心(图中AB所示)是目前上海市的标志性建筑、小明家住在金融中心附近的“祥和”大厦(图中CD所示),小明想利用所学的有关知识测量出环球国际金融中心的高度、他先在自己家的阳台(图中的点Q处)测得金融中心的顶端(点A)的仰角为37°,然后来到楼下,由于附近建筑物影响测量,小明向金融中心方向走了84米,来到另一座高楼的底端(图中的点P处),测得点A的仰角为45°.又点C、P、B在一条直线上,小明家的阳台距地面60米,请你在答题纸上画出示意图,并根据上述信息求出环球国际金融中心(AB)的高度.(备用数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)【解答】解:过点Q作QE⊥AB,交AB于点E.根据题意,得:∠AQE=37°,∠APB=45°,CQ=60,CP=84,设AB=x(米).则AE=(x﹣60),QE=CB=x+84.在Rt△APB中,得:PB=AB=x,在Rt△AQE中,AE=QE•tan37°,即.解得:x=492.答:环球国际金融中心(AB)的高度约为492米.6.著名的法门寺合十舍利塔由台湾建筑设计大师李祖原设计,呈双手合十状,其恢宏的气势不仅传承佛教建筑的特色,更以现代化的技术融合古今中外建筑之精华周末,小明想用所学的知识来测量该塔的高度.测量方法如下:如图,他先在B处用测倾器AB测得塔顶E的仰角为37°;再从点B沿BF方向走了97米到达D处(即BD=97米),在D处竖立标杆CD,发现水平地面上的点M、标杆的顶端C与塔顶E恰好在一条直线上,已知AB=CD=1.5米,测得DM=1米,点B、M、D、F在同一条直线上,AB⊥BF,CD⊥BF,EF⊥BF,根据测量示意图求该塔的高度EF.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)【解答】解:如图,过点C作CH⊥AB于点H,则CH=DF,FH=AB=CD=1.5米,AC=BD=97米,DM=1米,∠EAH=37°,∵CD⊥BD,EF⊥MF,∴CD∥EF,∴△CDM∽△EFM.∴=,∴=,∴EH=1.5CH,在Rt△EAH中,∠EAH=37°,∴tan37°=,∴≈0.75,∴4EH=291+3CH,∴4EH=291+2EH,∴EH=145.5(米),∴EF=EH+HF=145.5+1.5=147(米),答:该塔的高度EF为147米.7.如图是小明同学画出的某同学放风筝的示意图,从地面A处放飞的风筝几分钟后飞至C处,此时,点B与旗杆PQ的顶部点P以及点C恰好在一直线上,PQ⊥AB于点Q.(1)已知旗杆的高为10米,在B处测得旗杆顶部点P的仰角为30°,在A处测得点P的仰角为45°,求A、B之间的距离;(2)此时,在A处测得风筝C的仰角为75°,设绳子AC在空中为一条线段,求AC的长.(结果保留根号)【解答】解:(1)∵PQ⊥AB,∴∠BQP=∠AQP=90°,在RT△BPQ中,∵PQ=10,∠BQP=90°,∠B=30°,∵tan B=,∴=,∴BQ=10,在RT△APQ中,∠AQP=90°,∠P AB=45°,∴APQ=90°﹣∠P AB=45°,AQ=PQ=10,∴AB=BQ+AQ=10+10.答:A、B之间的距离为(10+10)米.(2)如图作AE⊥BC于E.在RT△ABE中,∵∠AEB=90°,∠B=30°,AB=10+10,∴AE=AB=5+5,∵∠CAD=75°,∠B=30°,∴∠C=45°,在RT△CAE中,sin C=,∴=,∴AC=(5+5)=5+5,答:AC的长为(5+5)米.8.为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B 的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行.(1)求点F到直线CE的距离(结果保留根号);(2)若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米,≈1.41,≈1.73).【解答】解:(1)过点F作FG⊥EC于G,依题意知FG∥DE,DF∥GE,∠FGE=90°,∴四边形DEGF是矩形,∴FG=DE,在Rt△CDE中,DE=CE•tan∠DCE=6×tan30o=2(米),∴点F到地面的距离为2米;(2)∵斜坡CF的坡度为i=1:1.5.∴Rt△CFG中,CG=1.5FG=2×1.5=3(米),∴FD=EG=(3+6)(米).在Rt△BCE中,BE=CE•tan∠BCE=6×tan60o=6(米),∴AB=AD+DE﹣BE=3+6+2﹣6=6﹣≈4.3 (米).答:宣传牌的高度约为4.3米.9.如图,为了测量楼AB的高度,小明在点C处测得楼AB的顶端A的仰角为30°,又向前走了20米后到达点D,点B、D、C在同一条直线上,并在点D测得楼AB的顶端A的仰角为60°,求楼AB的高.【解答】解:在Rt△ABC中,设AB=x,则AC=2x,BC==x,则BD=(x﹣20)米,在Rt△ABD中,=tan60°,=,∴x=10.答:楼AB的高为10米.10.如图,为测量一座地标性高楼的高度,小明在A点处测得楼顶D点的仰角为60°,在B点处测得楼顶D点的仰角为30°,A、B、C三点在一条直线上,已知AB=40m,小明的眼睛离地面为1.6m,求楼的高度.【解答】解:在Rt△DEF中,∵∠DFE=60°,∴EF=DE,在Rt△DEG中,∵∠DGE=30°,∴EG=DE,∴GF=EG﹣EF=DE﹣DE=(﹣)DE,又∵GF=AB=40m,∴(﹣)DE=40,解得:DE=60,∴DC=DE+EC=60+1.6=61.6(米),即楼的高度为61.6米.11.小军家附近有一棵侧柏,小军和小明计划利用所学过的知识测量侧柏的高度.阳光明媚的周末,小军和小明带着测量工具来到侧柏前.测量方法如下:如图,首先,小军沿侧柏的影子BD移动,当恰好移动到C处时发现小军的影子顶端与侧柏的影子顶端D重合,测得小军身高CE=1.6米,影长CD=2.4米.然后,小军在C处半蹲,小明在BC上竖立高2米的标杆,并沿BC移动,当标杆移动到点H时,小军的眼睛F、标杆顶端G与侧柏顶端A恰好在一条直线上,此时测得小军眼睛到地面的距离CF=1米,HC=1.4米.已知点B、H、C、D在一条直线上,点E、F、C在一条直线上,AB、GH、EC均垂直于BD,请你根据题中提供的相关信息,求出这棵侧柏的高AB.【解答】解:过F点作FM⊥AB于M,交HG于点N,则MF=BC,NF=HC=1.4,MB=CF=NH=1,NG=HG﹣NH=1,∵∠AMF=∠GNF,∠AFM=∠GFN,∴△AMF∽△GNF,∴,即,∴BC=1.4AB﹣1.4.∵∠ABD=∠ECD,∠ADB=∠EDC,∴△ABD∽△ECD,∴,即,∴3AB=2BC+4.8,∴3AB=2(1.4AB﹣1.4)+4.8,∴AB=10,∴这棵侧柏的高AB为10米.12.如图,某中学数学课题学习小组在“测量物体高度”的活动中,欲测量一棵古树DE的高度,他们在这棵古树的正前方一平房顶A点处测得古树顶端D的仰角为30°,在这棵古树的正前方C处,测得古树顶端D的仰角为60°,在A点处测得C点的俯角为30°.已知BC为4米,且B、C、E三点在同一条直线上.(1)求平房AB的高度;(2)请求出古树DE的高度(根据以上条件求解时测角器的高度忽略不计)【解答】解:(1)在Rt△ABC中,∵BC=4m,∠ACB=30°,∴tan30°=,∴AB=m.(2)在Rt△ACB中,易知AC=2AB=m,在Rt△ACD中,∵∠ACD=90°,∠DAC=60°,∴CD=AC=8,在Rt△CDE中,sin60°=,∴DE=4m.13.揽月阁是西安唐文化轴的南部重要节点和标志性建筑,与唐大雁塔今古一线、遥相呼应,联袂彰显西安具有历史文化特色的现代化国际大都市风貌.一天下午,小明和小丽来到了揽月阁广场,他们想用所学的知识,测量揽月阁的高度.如图,点A为揽月阁的顶部,点B为揽月阁的底部,小明在点C处放一水平的平面镜,然后沿着BC方向向前走0.5米,到达点D处,这时小明蹲下,恰好在镜子里看到揽月阁的顶端A的像.接下来小明不动,小丽在C处竖起一根可调节高度的测量杆,并调节测量杆的高度,使得测量杆的顶端P、揽月阁的顶端A、小明的眼睛E在一条直线上,此时测得测量杆的高度CF =1.98米.已知小明蹲下时,眼睛到地面的距离DE=1米,点B、C、D在一条直线上,AB⊥BD,CF ⊥BD,DE⊥BD,求揽月阁的高度AB.(平面镜的大小忽略不计)【解答】解:延长AE交BC的延长线于H,由题意知∠ACF=∠ECF,∵AB⊥BD,CF⊥BD,DE⊥BD,∴∠BCF=∠DCF=∠ABC=∠EDC=90°,∴∠ACB=∠ECD,∴△ABC∽△EDC,∴=,∵CD=0.5,DE=1,∴=,∴AB=2BC,∵AB⊥BD,CF⊥BD,DE⊥BD,∴ED∥FC∥AB,∴△HFC∽△HAB,△HED∽△HFC,∴=,=,设BC=x,HD=y,则AB=2x,HB=x+y+0.5,HC=y+0.5,,解得:x=49.5,∴AB=99(米)答:揽月阁的高度AB为99米.14.如图,某中学操场边有一旗杆A,小明在操场的C处放风筝,风筝飞在图中的D处,在CA的延长线上离小明30米远的E处的小刚发现自己的位置与风筝D和旗杆的顶端B在同一条直线上,小刚在E 处测得旗杆顶点B的仰角为α,且tanα=,小明在C处测得旗杆顶点B的仰角为45°.(1)求旗杆的高度.(2)此时,在C处背向旗杆,测得风筝D的仰角(即∠DCF)为48°,求风筝D离地面的距离.(结果精确到0.1米,其中sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)【解答】解:(1)在Rt△ABE中,∵tanα==,∴设AB=xm,则AE=2xm,在Rt△ABC中,∠ACB=45°,∴∠ABC=90°﹣∠ACB=45°,∴∠ABC=∠ACB,∴AC=AB=xm,∴EC=AE+AC=30,即:2x+x=30,解得:x=10,答:求得旗杆高度为10米;(2)过D作DG⊥AF于点G,在Rt△DEG中,tanα==,设DG=ym,则EG=2ym,∴CG=2y﹣30,∵tan∠DCG=,∴DG=CG×tan∠DCG,∴y=(2y﹣30)×tan48°,∴y=1.11×(2y﹣30),解得:y≈27.3,答:求得风筝D离地面的距离为27.3米.15.小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,AC的坡度i=1:,且B、C、D三点在同一直线上.(1)求树DE的高度;(2)求食堂MN的高度.【解答】解:(1)如图,设DE=x米,∵AB=DF=2米,∠ACB=30°,∴EF=(x﹣2)米,AC=2AB=4(米),∵∠ECD=60°,∴△ACE是直角三角形,∵AF∥BD,∴∠CAF=30°,∴∠CAE=60°,∠AEC=30°,∴∠ACE=90°,∴AE=2AC=8(米),在Rt△AEF中,∠EAF=30°,∴EF=AE=4(米),即x﹣2=4,解得x=6,即树DE的高度为6米;(2)延长NM交DB延长线于点P,则AM=BP=3米,由(1)知CD=CE=×AC=2(米),BC=2(米),∴PD=BP+BC+CD=(3+2+2)米=(3+4)米,∵∠NDP=45°,且∠NPD=90°,∴NP=PD=(3+4)米,∴NM=NP﹣MP=(3+4﹣2)米=(1+4)米,即食堂MN的高度为(1+4)米.16.如图,水库大坝的横断面为四边形ABCD,其中AD∥BC,坝顶BC=10米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°.(1)求坝底AD的长度(结果精确到1米);(2)若坝长100米,求建筑这个大坝需要的土石料(参考数据:)【解答】解:(1)作BE⊥AD于E,CF⊥AD于F,则四边形BEFC是矩形,∴EF=BC=10米,∵BE=20米,斜坡AB的坡度i=1:2.5,∴AE=50米,∵CF=20米,斜坡CD的坡角为30°,∴DF==20≈35米,∴AD=AE+EF+FD=95米;(2)建筑这个大坝需要的土石料:×(95+10)×20×100=105000米3.17.如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:,且AB=26米.(1)求坡顶与地面的距离BE的长.(2)为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡.学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33).【解答】解:(1)设AE=5x米,∵斜坡AB的坡比为i=1:,∴BE=12x米,由勾股定理得,AE2+BE2=AB2,即(5x)2+(12x)2=262,解得,x=2,∴BE=12x=24(米);(2)过点F作FG⊥AD于G,则四边形FGEB为矩形,∴FG=BE=24米,BF=GE,在Rt△AFG中,∠F AG=53°,∴AG=≈≈18.0(米),由(1)可知,AE=10米,∴BF=GE=AG﹣AE≈8(米),答:BF至少是8米.18.每逢雨季,天降大雨,山体滑坡灾害时有发生,北峰小学教学楼后面紧邻着一个土坡,坡上面是一块平地,如图所示:AF∥BC,斜坡AB长30米,坡角∠ABC=60°.为了防止滑坡,保障安全,学校决定对该土坡进行改造,经过地质人员勘测,当坡角不超过45°时,可以确保山体不滑坡.(1)求坡顶与地面的距离AD等于多少米?(精确到0.1米)(2)为确保安全,学校计划改造时保持坡脚B不动,坡顶A沿AF削进到E点处,求AE至少是多少米?(精确到0.1米)【解答】解:(1)在Rt△ADB中,AB=30m,∠ABC=60°,sin∠ABC=,∴AD=AB•sin∠ABC=30×sin60°≈26.0(m)答:AD等于26.0米;(2)在Rt△ADB中,cos∠ABD=,∴DB=AB•cos∠ABD=30×cos60°=15(m),连接BE、过E作EN⊥BC于N,∵AE∥BC,∴四边形AEND为矩形,NE=AD≈26.0,在Rt△ENB中,由已知∠EBN≤45°,当EBN=45°时,BN=EN=26.0,∴AE=ND=BN﹣BD=11.0(m),答:AE至少是11.0 m.19.如图:某水坝的横断面为梯形ABCD,坝顶宽BC为6米,坝高BH为20米,斜坡AB的坡度,斜坡CD的坡角为45°.求(1)斜坡AB的坡角;(2)坝底宽AD(精确到1米).(参考数据:,)【解答】解:(1)斜坡AB的坡角是∠A,即tan∠A=i.(1分)∵i=1:,∴tan∠A=.(1分)∴∠A=30°.(1分)(2)过点C作CG⊥AD,垂足为点G.由题意可知:BH=CG=20(米),BC=HG=6(米).(2分)。
(整理)解直角三角形的应用经典题型

1解直角三角形应用经典【例1】:为了缓解酒泉市区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌.已知立杆AB 高度是3m ,从侧面D 点测得显示牌顶端C 点和底端B 点的仰角分别是60°和45°.求路况显示牌BC 的高度.练习1、如图所示,小明在家里楼顶上的点A 处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A 处看电梯楼顶部点B 处的仰角为60°,在点A 处看这栋电梯楼底部点C 处的俯角为45°,两栋楼之间的距离为30m ,则电梯楼的高(精确到0.1).(参考数据:414.12≈732.13≈)练习2、2009年首届中国国际航空体育节在莱芜举办,期间在市政府广场进行了热气球飞行表演.如图,有一热气球到达离地面高度为36米的A 处时,仪器显示正前方一高楼顶部B 的仰角是37°,底部C 的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米) (参考数据:,75.037tan ,80.037cos ,60.037sin ≈︒≈︒≈︒73.13≈)2【例2】: 在东西方向的海岸线l 上有一长为1km 的码头MN (如图),在码头西端M 的正西19.5 km 处有一观察站A .某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A 相距40km 的B 处;经过1小时20分钟,又测得该轮船位于A 的北偏东60°,且与A相距的C 处.(1)求该轮船航行的速度;(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN 靠岸?请说明理由.练习:如图,某天然气公司的主输气管道从A 市的东偏北30°方向直线延伸,测绘员在A 处测得要安装天然气的M 小区在A 市东偏北60°方向,测绘员沿主输气管道步行2000米到达C 处,测得小区M 位于C 的北偏西60°方向,请你在主输气管道上寻找支管道连接点N ,使到该小区铺设的管道最短,并求AN 的长.【例3】:如图,水坝的横断面是梯形,背水坡AB 的坡角∠BAD=60,坡长AB=m 320,为加强水坝强度,将坝底从A 处向后水平延伸到F 处,使新的背水坡的坡角∠F=45,求AF 的长度(结果精确到1米,参考数据:414.12≈,732.13≈).东l练习:施工队准备在一段斜坡上铺上台阶方便通行.现测得斜坡上铅垂的两棵树间水平距离AB=4米,斜面距离BC=4.25米,斜坡总长DE=85米.(1)求坡角∠D的度数(结果精确到1°);(2)若这段斜坡用厚度为17c m的长方体台阶来铺,需要铺几级台阶?【达标测评】1、如图,一架飞机在空中P处探测到某高山山顶D处的俯角为60°,此后飞机以300米/秒的速度沿平行于地面AB的方向匀速飞行,飞行10秒到山顶D的正上方C处,此时测得飞机距地平面的垂直高度为12千米,求这座山的高(精确到0.1千米)2、摩天轮是嘉峪关市的标志性景观之一.某校数学兴趣小组要测量摩天轮的高度.如图,他们在C处测得摩天轮的最高点A的仰角为45︒,再往摩天轮的方向前进50 m至D处,测得最高点A的仰角为60︒.求该兴趣小组测得的摩天轮的高度AB1.732≈,结果保留整数).(第3题)A45°60°343.在一个阳光明媚、清风徐来的周末,小明和小强一起到郊外放风筝﹒他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的C 处(如图).现已知风筝A 的引线(线段AC )长20m ,风筝B 的引线(线段BC )长24m ,在C 处测得风筝A 的仰角为60°,风筝B 的仰角为45°. (1)试通过计算,比较风筝A 与风筝B 谁离地面更高? (2)求风筝A 与风筝B 的水平距离.4. 如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB 长为4米. (1)求新传送带AC 的长度;(2)如果需要在货物着地点C 的左侧留出2米的通道,试判断距离B 点4米的货物MNQP 是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:2≈1.41,3≈1.73,5≈2.24,6≈2.45)AB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解直角三角形应用题专题练习一.解答题(共10小题)1.(2015•鄂尔多斯)为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为m.(1)求BT的长(不考虑其他因素).(2)一般正常人从发现危险到做出刹车动作的反应时间是,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.(参考数据:sin22°≈,tan22°≈,sin31°≈,tan31°≈)2.(2014•北海)如图是某超市地下停车场入口的设计图,请根据图中数据计算CE的长度.(结果保留小数点后两位;参考数据:sin22°=,cos22°=,tan22°=)3.(2015•黄石模拟)超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到万丰路的距离为100米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒且∠APO=60°,∠BPO=45°.(1)求A、B之间的路程;(2)请判断此车是否超过了万丰路每小时70千米的限制速度?(参考数据:,).4.(2015•北海)如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈;cos32°≈;tan32°≈;sin68°≈;cos68°≈;tan68°≈)5.(2013•抚顺)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部CD是水平的,在阳光的照射下,古塔AB在斜坡上的影长DE为18米,斜坡顶部的影长DB为6米,光线AE与斜坡的夹角为30°,求古塔的高().6.(2016•贵阳模拟)如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P 的铅直高度.(测倾器高度忽略不计,结果保留根号形式)7.(2015•义乌市)如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.(1)求∠BPQ的度数;(2)求该电线杆PQ的高度(结果精确到1m).备用数据:,.8.(2013•铁岭)如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据°≈,°≈;sin37°≈,tan37°≈)9.(2015•镇江)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).10.(2016•安徽模拟)如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M 在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,≈)解直角三角形应用题专题练习参考答案与试题解析一.解答题(共10小题)1.(2015•鄂尔多斯)为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为m.(1)求BT的长(不考虑其他因素).(2)一般正常人从发现危险到做出刹车动作的反应时间是,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.(参考数据:sin22°≈,tan22°≈,sin31°≈,tan31°≈)【解答】解:(1)根据题意及图知:∠ACT=31°,∠ABT=22°∵AT⊥MN∴∠ATC=90°在Rt△ACT中,∠ACT=31°∴tan31°=可设AT=3x,则CT=5x在Rt△ABT中,∠ABT=22°∴tan22°=即:解得:∴,∴;(2),,∴该车大灯的设计不能满足最小安全距离的要求.2.(2014•北海)如图是某超市地下停车场入口的设计图,请根据图中数据计算CE的长度.(结果保留小数点后两位;参考数据:sin22°=,cos22°=,tan22°=)【解答】解:由已知有:∠BAE=22°,∠ABC=90°,∠CED=∠AEC=90°∴∠BCE=158°,∴∠DCE=22°,又∵tan∠BAE=,∴BD=AB•tan∠BAE,又∵cos∠BAE=cos∠DCE=,∴CE=CD•cos∠BAE=(BD﹣BC)•cos∠BAE=( AB•tan∠BAE﹣BC)•cos∠BAE=(10×﹣)×≈(m).3.(2015•黄石模拟)超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到万丰路的距离为100米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒且∠APO=60°,∠BPO=45°.(1)求A、B之间的路程;(2)请判断此车是否超过了万丰路每小时70千米的限制速度?(参考数据:,).【解答】解:(1)在Rt△BOP中,∠BOP=90°,∵∠BPO=45°,OP=100,∴OB=OP=100.在Rt△AOP中,∠AOP=90°,∵∠APO=60°,∴AO=OP•tan∠APO.∴A0=100,AB=100(﹣1)(米);(2)∵此车的速度==25(﹣1)≈25×=米/秒,70千米/小时=≈米/秒,米/秒<米/秒,∴此车没有超过了万丰路每小时70千米的限制速度.4.(2015•北海)如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈;cos32°≈;tan32°≈;sin68°≈;cos68°≈;tan68°≈)【解答】解:∵cos∠DBF=,∴BF=60×=51,FH=DE=9,∴EG=HC=110﹣51﹣9=50,∵tan∠AEG=,∴AG=50×=124,∵sin∠DBF=,∴DF=60×=,∴CG=,∴AC=AG+CG=124+=.5.(2013•抚顺)在与水平面夹角是30°的斜坡的顶部,有一座竖直的古塔,如图是平面图,斜坡的顶部CD是水平的,在阳光的照射下,古塔AB在斜坡上的影长DE为18米,斜坡顶部的影长DB为6米,光线AE与斜坡的夹角为30°,求古塔的高().【解答】解:延长BD交AE于点F,作FG⊥ED于点G,∵斜坡的顶部CD是水平的,斜坡与地面的夹角为30°,∴∠FDE=∠AED=30°,∴FD=FE,∵DE=18米,∴EG=GD=ED=9米,在Rt△FGD中,DF===6,∴FB=(6+6)米,在Rt△AFB中,AB=FB•tan60°=(6+6)×=(18+6)≈米,所以古塔的高约为米.6.(2016•贵阳模拟)如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P 的铅直高度.(测倾器高度忽略不计,结果保留根号形式)【解答】解:作PE⊥OB于点E,PF⊥CO于点F,在Rt△AOC中,AO=100,∠CAO=60°,∴CO=AO•tan60°=100(米).设PE=x米,∵tan∠PAB==,∴AE=2x.在Rt△PCF中,∠CPF=45°,CF=100﹣x,PF=OA+AE=100+2x,∵PF=CF,∴100+2x=100﹣x,解得x=(米).答:电视塔OC高为100米,点P的铅直高度为(米).7.(2015•义乌市)如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.(1)求∠BPQ的度数;(2)求该电线杆PQ的高度(结果精确到1m).备用数据:,.【解答】解:延长PQ交直线AB于点E,(1)∠BPQ=90°﹣60°=30°;(2)设PE=x米.在直角△APE中,∠A=45°,则AE=PE=x米;∵∠PBE=60°∴∠BPE=30°在直角△BPE中,BE=PE=x米,∵AB=AE﹣BE=6米,则x﹣x=6,解得:x=9+3.则BE=(3+3)米.在直角△BEQ中,QE=BE=(3+3)=(3+)米.∴PQ=PE﹣QE=9+3﹣(3+)=6+2≈9(米).答:电线杆PQ的高度约9米.8.(2013•铁岭)如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据°≈,°≈;sin37°≈,tan37°≈)【解答】解:如图,过点P作PD⊥OC于D,PE⊥OA于E,则四边形ODPE为矩形.在Rt△PBD中,∵∠BDP=90°,∠BPD=°,∴BD=PD•tan∠BPD=PD•°;在Rt△CPD中,∵∠CDP=90°,∠CPD=37°,∴CD=PD•tan∠CPD=PD•tan37°;∵CD﹣BD=BC,∴PD•tan37°﹣PD•°=80,∴﹣=80,解得PD=320(米),∴BD=PD•°≈320×=160(米),∵OB=220米,∴PE=OD=OB﹣BD=60米,∵OE=PD=320米,∴AE=OE﹣OA=320﹣200=120(米),∴tanα===,∴坡度为1:2.9.(2015•镇江)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).【解答】解:作AD⊥BC于D,∵∠EAB=30°,AE∥BF,∴∠FBA=30°,又∠FBC=75°,∴∠ABD=45°,又AB=60,∴AD=BD=30,∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,∴∠C=60°,在Rt△ACD中,∠C=60°,AD=30,则tanC=,∴CD==10,∴BC=30+10.故该船与B港口之间的距离CB的长为30+10海里.10.(2016•安徽模拟)如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M 在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,≈)【解答】解:如图,过M作MN⊥AC交于N点,即MN最短,∵∠EAD=60°,∠CAD=30°,∴∠CAM=30°,∴∠AMN=60°,又∵C处看M点为北偏西60°,∴∠FCM=60°,∴∠MCB=30°,∵∠EAC=60°,∴∠CAD=30°,∴∠BCA=30°,∴∠MCA=∠MCB+∠BCA=60°,∴在Rt△AMC中,∠AMC=90°,∠MAC=30°,∴MC=AC=2000,∠CMN=30°,∴NC=MC=1000,∵AC=4000米,∴AN=AC﹣NC=4000﹣1000=3000(米).答:点N到A市最短路线3000米.。
