转子动平衡检测中不平衡信号幅值与相位的计算方法
转子允许动不平衡量的计算

转子允许动不平衡量的计算允许不平衡量的计算公式 U per=M X G Xnr x x 260Π X 103(g )转子重量M,Kg0.2 0.3 0.2 0.2 平衡精度G ,gmm/kg6.3 2.5 6.3 6.3 转子的校正半径r ,mm20 20 20 20 转子的转速n ,rpm 1000 1000 1000 1000 允许不平衡量,g 0.602 0.358 0.602 0.602 每面的允许不平衡量,g 0.301 0.179 0.301 0.301U per 为允许不平衡量M 代表转子的自身重量,单位是kg ;G 代表转子的平衡精度等级,单位是mm/s ; r 代表转子的校正半径,单位是mm ; n 代表转子的转速,单位是rpm 。
一、动平衡机常用术语1.不平衡量U :转子某平面上不平衡量的量值大小,不涉及不平衡的角度位置。
它等于不平衡质量m 和转子半径r 的乘积。
其单位是gmm 或者gcm ,俗称“矢径积”。
2.不平衡相位:转子某平面上的不平衡质量相对于给定极坐标的角度值。
3.不平衡度e :转子单位质量的不平衡量,单位是gmm/kg 。
在静不平衡时相当于转子的质量偏心距,单位为µm 。
4.初始不平衡量:平衡前转子上存在的不平衡量。
5.许用不平衡量:为保证旋转机械正常工作所允许的转子剩余不平衡量。
该指标用不平衡度表示时,称为许用不平衡度(亦称许用不平衡率)。
6.剩余不平衡量:平衡校正后转子上的剩余不平衡量。
7.校正半径:校正平面上校正质量的质心到转子轴线的距离,一般用mm 表示。
8.校正平面的干扰(相互影响):在给定转子某一校正面上不平衡量的变化引起另一校正平面上的改变(有时称为平面分离影响)9.转子平衡品质:衡量转子平衡优劣程度的指标。
计算公式:G=e perω/1000式中G-转子平衡品质,单位mm/s。
从G0.4-G4000分11级。
eper-转子允许的不平衡率gmm/kg或转子质量偏心距µm。
动平衡不平衡量计算公式

动平衡不平衡量计算公式
1.动态平衡的基本概念
动态平衡是指在自动控制系统中,利用外部输入(例如温度,湿度,压强,速度等)操纵内部参数(例如加热,冷却,调速等),保持系统运行于一个内部稳定状态,并具有良好的自动调节性能的过程或过程群。
当有恒定外部输入加以操纵时,动态平衡又称为自动平衡。
2.动态平衡的计算公式
动态平衡的计算公式是根据系统的输入-输出特性,利用状态反馈控制模型,利用拉普拉斯变换方法求解出系统的具体计算公式:若系统的输入与输出特性满足状态反馈形式:
y=G(s)x
其中,s为复变量,G(s)为传递函数,x为输入,y为输出,则应用Laplace变换,得到系统的动态平衡计算公式:
Y(s)=G(s)X(s)
其中,Y(s)为系统输出复变量,X(s)为系统输入复变量。
3.动态平衡的应用
动态平衡的应用非常广泛,可以用于控制计算机硬件装置、数据处理系统和各种机械系统的自动化控制。
机械手册在动平衡计算公式

机械手册在动平衡计算公式
机械手册动平衡计算公式
1. 转子不平衡力计算公式
•转子不平衡力(U)的计算公式为:U = m * r * ω^2
–U:转子不平衡力,单位为牛顿
–m:转子的不平衡质量,单位为千克
–r:转子不平衡质量与转轴的距离,单位为米
–ω:转轴的角速度,单位为弧度/秒
举例解释:假设一个转子的不平衡质量为10克,不平衡质量与转轴的距离为米,转轴的角速度为100弧度/秒,那么根据上述的计算公式,转子的不平衡力为: U = * * (100^2) = 100牛顿
2. 转子不平衡力矩计算公式
•转子不平衡力矩(M)的计算公式为:M = m * r^2 * ω^2–M:转子不平衡力矩,单位为牛顿·米
–m:转子的不平衡质量,单位为千克
–r:转子不平衡质量与转轴的距离,单位为米
–ω:转轴的角速度,单位为弧度/秒
举例解释:假设一个转子的不平衡质量为10克,不平衡质量与转轴的距离为米,转轴的角速度为100弧度/秒,那么根据上述的计算公式,转子的不平衡力矩为: M = * (^2) * (100^2) = 10牛顿·米3. 转子在平衡质量下的旋转速度计算公式
•转子在平衡质量下的旋转速度(ωb)的计算公式为:ωb = √(G / J)
–ωb:平衡质量下的旋转速度,单位为弧度/秒
–G:转子的刚性系数,单位为牛顿·米/弧度
–J:转子的转动惯量,单位为千克·米^2
举例解释:假设一个转子的刚性系数为200牛顿·米/弧度,转子的转动惯量为千克·米^2,根据上述的计算公式,转子在平衡质量下的旋转速度为:ωb = √(200 / ) ≈ 弧度/秒。
转子允许不平衡量的计算
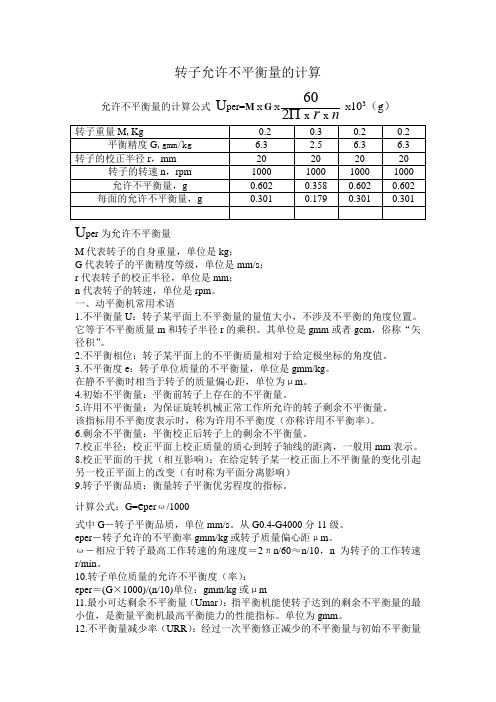
转子允许不平衡量的计算允许不平衡量的计算公式 U per=M X G Xnr x x 260X 103(g )U per 为允许不平衡量M 代表转子的自身重量,单位是kg ;G 代表转子的平衡精度等级,单位是mm/s ; r 代表转子的校正半径,单位是mm ; n 代表转子的转速,单位是rpm 。
一、动平衡机常用术语1.不平衡量U :转子某平面上不平衡量的量值大小,不涉及不平衡的角度位置。
它等于不平衡质量m 和转子半径r 的乘积。
其单位是gmm 或者gcm ,俗称“矢径积”。
2.不平衡相位:转子某平面上的不平衡质量相对于给定极坐标的角度值。
3.不平衡度e :转子单位质量的不平衡量,单位是gmm/kg 。
在静不平衡时相当于转子的质量偏心距,单位为μm 。
4.初始不平衡量:平衡前转子上存在的不平衡量。
5.许用不平衡量:为保证旋转机械正常工作所允许的转子剩余不平衡量。
该指标用不平衡度表示时,称为许用不平衡度(亦称许用不平衡率)。
6.剩余不平衡量:平衡校正后转子上的剩余不平衡量。
7.校正半径:校正平面上校正质量的质心到转子轴线的距离,一般用mm 表示。
8.校正平面的干扰(相互影响):在给定转子某一校正面上不平衡量的变化引起另一校正平面上的改变(有时称为平面分离影响) 9.转子平衡品质:衡量转子平衡优劣程度的指标。
计算公式:G=e per ω/1000式中G -转子平衡品质,单位mm/s 。
从G0.4-G4000分11级。
eper -转子允许的不平衡率gmm/kg 或转子质量偏心距μm 。
ω-相应于转子最高工作转速的角速度=2πn/60≈n/10,n 为转子的工作转速r/min 。
10.转子单位质量的允许不平衡度(率): eper =(G ×1000)/(n/10)单位:gmm/kg 或μm 11.最小可达剩余不平衡量(Umar ):指平衡机能使转子达到的剩余不平衡量的最小值,是衡量平衡机最高平衡能力的性能指标。
三圆幅值法找动平衡原理

三圆幅值法找动平衡原理三圆幅值法是一种常用的动平衡方法,它通过测量转子在不同位置的振动幅值,来确定转子的不平衡质量和相位。
通过调整转子上的补偿质量,使得转子在运转时振动幅值最小,达到动平衡的目的。
三圆幅值法的原理基于以下几个基本概念:1. 不平衡质量:机械转子在运转过程中,由于制造和安装误差,往往会产生不平衡质量。
这些不平衡质量会导致转子产生振动,影响机械设备的正常运行。
因此,找到并消除不平衡质量是动平衡的关键。
2. 振动幅值:振动幅值是指转子在旋转过程中,由于不平衡质量而产生的振动的最大偏移量。
通过测量振动幅值,可以判断转子的不平衡程度和位置。
3. 补偿质量:为了消除转子的不平衡质量,需要在转子上添加或移除一定的质量,以达到平衡状态。
这个补偿质量可以通过计算得到,也可以通过试验方法进行调整。
三圆幅值法的步骤如下:1. 安装传感器:首先需要在转子上安装振动传感器,用于测量转子在不同位置的振动幅值。
传感器通常安装在转子的两端,并与数据采集系统相连。
2. 测量振动幅值:启动转子,使其旋转起来,并记录不同位置的振动幅值。
可以通过数据采集系统实时监测振动信号,并将信号转换为振动幅值。
3. 分析振动幅值:通过分析振动幅值的大小和分布,可以确定转子的不平衡质量和相位。
通常使用三圆图来表示振动幅值的大小和相位关系,从而确定补偿质量的大小和位置。
4. 调整补偿质量:根据分析结果,可以通过在转子上添加或移除一定的补偿质量,来消除不平衡质量。
补偿质量的大小和位置可以根据振动幅值的大小和相位来确定。
5. 重新测量振动幅值:在调整补偿质量后,需要重新测量振动幅值,以确认转子是否达到了动平衡状态。
如果振动幅值仍然较大,可能需要进一步调整补偿质量,直到振动幅值最小。
通过三圆幅值法找动平衡原理,可以有效地消除转子的不平衡质量,降低振动和噪音,提高机械设备的工作效率和寿命。
这种方法在工程实践中得到了广泛应用,特别是对于高速旋转的转子,动平衡更是非常重要。
转子动平衡原理及计算

转子动平衡一、动平衡的定义:不平衡的转子经过测量其不平衡量和不平衡相位,并加以校正消除其不平衡量,使转子在旋转时,不致产生不平衡离心力的平衡工艺叫做动平衡。
二、校正面的选择:平衡校正面必须选择垂直于转子轴线的平面转子外径:D转子长度:L①对于薄盘状转子(L/D≤5),因偶不平面很小,一般只选择一个校正面,称为单面平衡或称静平衡②对于长轴类转子(L/D>5),必须选择两个或者两个以上校正面,称双面平衡或者多面平衡亦称动平衡③对于初始不平衡量很大,旋转时振动过大的转子,应先做单面静平衡,且校正面最好选择在重心所在的平面上,以防偶不平衡量增大;或者选择在重心两侧的两个校正面上校正,或根据要求,选择在靠近重心的平面上校正,然后再做动平衡。
三、校正方法:转子的不平衡是因其中心主惯性轴与旋转轴线不重合而产生的.平衡就是改变转子的质量分布,使其中心主惯性轴与旋转轴线重合而达到平衡的目的.当测量出转子不平衡的量值或相位后,校正的方法有:1、去重法—即在重的一方用钻孔,磨削,錾削,铣削和激光穿孔等方法去除一部分金属。
2、加重法--即在轻的一方用螺钉连接,铆接,焊接,喷镀金属等方法,加上一部分金属。
3、调整法—通过拧入或拧出螺钉以改变校正重量半径,或在槽内调整二个或二个以上配重块位置。
4、热补偿法—通过对转子局部加热来调整工件装配状态。
四、不同类型转子的动平衡注意事项:1.滚动轴承转子的平衡装有滚动轴承的转子,平衡时最好带着滚动轴承一起平衡,从而消除滚动轴承的内环偏心引起的不平衡,带轴承的转子一般在V型支承上进行2.无轴颈的转子的平衡无轴颈的转子必须在工艺轴上进行平衡.由于工艺轴本身的制造误差:径向和轴向跳动.工艺轴本身的不平衡以及转子配合时存在的径向间隙,使转子在平衡时会带来不可避免的误差五、转子不平衡量的计算方法:1、计算转子的允许不平衡度(率)Eper=(G*1000)/(n/10)式中:Eper——允许不平衡度单位μmG——不平衡精度等级一般取6.3n——工作转速单位r/min例如:某工件工作转速1400r/min平衡精度等级取6.3,则Eper=(GX1000)/(n/10)= (6.3X1000)/(1400/10)=45μm2、计算允许残余不平衡量m=(Eper*M)/(r*2)式中:m——允许残余不平衡度单位gM——工件旋转质量单位kgr——工件半径单位mm例如:工件质量20kg,半径60mm双面平衡,故计算每个平衡面的允许的剩余不平衡量为m=(Eper*M)/(r*2)=(45x20)/(60x2)=7.5g3、转子平衡品质——衡量转子平衡优劣程度的指标G=Eper*ω/1000式中:G——转子平衡品质mm/s 从G0.4-G4000分11级;Eper——转子允许的不平衡度g.mm/k 或mm/s或转子质量偏心距μmω——相应于转子最高工作转速的角速度ω=2πn/60≈n/104、最小可达剩余不平衡量(umar)——单位g.m,平衡机能使转子达到的剩余不平衡量的最小值,是衡量平衡机最高平衡能力的性能指标,当该指标用不平衡度表示时,称为最小可达或剩余不平衡度(单位g.mm/kg)5、不平衡量减少率(URR)——经过一次平衡校正所减少的不平衡量与初始不平衡量之比值,他是衡量平衡机效率的性能指标,以百分数表示:URR(%)=(U1-U2)/U1*100式中:U1为初始不平衡量;U2为一次平衡校正后的剩余不平衡量6、校验转子——为校验平衡机性能而设计的刚性转子,其质量、大小、尺寸均为有规定,分立式和卧式两种,立式转子质量为1.1、3.5、11、35、110kg,卧式转子质量为0.5、1.6、5、16、50、160、500kg7、不平衡国偶干扰比——单面平衡机抑制不平衡力偶影响的性能指标。
转子校验动平衡的方法

转子校验动平衡的方法(总6页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除转子校验动平衡的方法经过静平衡校验的转子,在高速下旋转时,往往还会发生振动。
由于所加上或减去的平衡质量快,不一定能和转子原来的不平衡质量恰好在垂直于转轴的同一个平面上,因此转子经过静平衡校验之后,必须再做动平衡校验。
转子校验动平衡是在转动状况下进行的。
对锅炉风机的转子校验动平衡,一般都在现场原设备上,并在工作转速条件下进行。
转子动平衡的状况,通过振动表计测量离转子最近的轴承上的振动间接地表示。
1、校验动平衡的准备工作需满足的条件(1)现场条件。
现场必须整洁、无杂物,能保证人员在异常情况下迅速撤离。
有足够的照明,必须有紧急停机按钮等良好的安全条件。
(2)工具条件。
测振仪器(或闪光测振仪)一套、绘图仪一套、三角板一套、量角器、记录纸、记号笔、刻度盘、天平秤、不同质量的平衡铁块若干、钳工工具及电焊机等。
(3)参数条件。
转子的工作速度、转子的质量、转子的半径。
(4)平衡工作时的假设条件:1)轴承振动只考虑因转子质量不平衡所引起;2)对同一个轴承,不平衡力和引起的振幅成正比关系。
3)转速不变时,轴承的振动和扰动力之间的相位差保持不变。
以上假定在实际中并不都成立,因此在校动平衡过程中会遇到一些困难,特别是由于同一转子上两个轴承的刚性和结构不同,对同一个不平衡力反映的轴承振动可能会有较大的差异。
2、校验动平衡的方法若转子的轴向尺寸不大,如风机、电动机的转子,一般只要在一个平面上加平衡质量,就能消除振动。
用180°和90°两次试加质量平衡法校验平衡的时候,只要有振动表能够测量轴承振幅,就可进行校验平衡工作。
180°试加质量平衡法的两次试加质量所产生的离心力方向相反,对振动的影响亦相反。
在一般情况下,如果第一次试加质量后振动增大,则将试加质量转移180°后,振动必然减小。
转子动平衡检测中不平衡信号幅值与相位的计算方法

2 利用 DF T 获取转子动不平衡信号的幅值
与相位
设振动信号为 x ( t ) ,由于不平衡信号只与基频 成份有关 , 所以我们需对其进行离散傅里叶变换 DF T 。根据采样定理 ( 采样信号的频率大于被采信 号最高频率的 2 倍) ,在一个周期 T 里 ,我们进行等 间隔采样 N 个点 , 采样所得时域序列为 : x ( 0 ) , x ( 1 ) , ……, x ( N - 1) , 则该序列的 DF T 为 : N- 1 2π X ( k ) = ∑x ( n ) exp ( - j k n)
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved.
N
= a1 + b1 i = F1θ 1
其中 a1 = ∑ x ( n ) cos
n=0
N- 1
2πn
N
; b1 = ∑ x ( n ) sin
n=0
N- 1
2πn
N
;幅
2 1/ 2 值 F1 = ( a2 ;信号初相角 θ 1 + b1 ) 1 = arctan ( b1 / a1 ) 。 但是由 DF T 计算出的幅值和相位并不是不平衡信 号的幅值和相位 ,二者有一定的相对数值关系 ,推导 如下 : 设 x ( t ) 代表一个周期为 T 0 的周期性连续时
3 结论
在实际动平衡检测仪的研制与应用过程中 , 采 用此法能够较准确获取转子不平衡信号的幅值和相 位 。相对于采用锁相环硬件的系统 , 本系统具有简 单可靠 、 软硬件易实现的特点 , 在转子动平衡分析中 很具实际意义 。
参考文献
[1 ] 李芳泽 ,刘馥清 ,王正 1 工程振动测试与分析 1 北京 : 高等教育
转子校验动平衡的方法

转子校验动平衡的方法经过静平衡校验的转子,在高速下旋转时,往往还会发生振动。
由于所加上或减去的平衡质量快,不一定能和转子原来的不平衡质量恰好在垂直于转轴的同一个平面上,因此转子经过静平衡校验之后,必须再做动平衡校验。
转子校验动平衡是在转动状况下进行的。
对锅炉风机的转子校验动平衡,一般都在现场原设备上,并在工作转速条件下进行。
转子动平衡的状况,通过振动表计测量离转子最近的轴承上的振动间接地表示。
1、校验动平衡的准备工作需满足的条件(1)现场条件。
现场必须整洁、无杂物,能保证人员在异常情况下迅速撤离。
有足够的照明,必须有紧急停机按钮等良好的安全条件。
(2)工具条件。
测振仪器(或闪光测振仪)一套、绘图仪一套、三角板一套、量角器、记录纸、记号笔、刻度盘、天平秤、不同质量的平衡铁块若干、钳工工具及电焊机等。
(3)参数条件。
转子的工作速度、转子的质量、转子的半径。
(4)平衡工作时的假设条件:1)轴承振动只考虑因转子质量不平衡所引起;2)对同一个轴承,不平衡力和引起的振幅成正比关系。
3)转速不变时,轴承的振动和扰动力之间的相位差保持不变。
以上假定在实际中并不都成立,因此在校动平衡过程中会遇到一些困难,特别是由于同一转子上两个轴承的刚性和结构不同,对同一个不平衡力反映的轴承振动可能会有较大的差异。
2、校验动平衡的方法若转子的轴向尺寸不大,如风机、电动机的转子,一般只要在一个平面上加平衡质量,就能消除振动。
用180°和90°两次试加质量平衡法校验平衡的时候,只要有振动表能够测量轴承振幅,就可进行校验平衡工作。
180°试加质量平衡法的两次试加质量所产生的离心力方向相反,对振动的影响亦相反。
在一般情况下,如果第一次试加质量后振动增大,则将试加质量转移180°后,振动必然减小。
这样便于判别振动是否由质量不平衡引起。
但此法作图后有两个题解,机组可能要多启动一次。
对于90°二次试加质量法,试加质量后,振动值的改变规律不如180°二次加质量法明显,但一般情况下,如果试加质量未超过不平衡质量,其结果只有一个题解。
转子不平衡量的计算

转子不平衡量的计算方法1、计算转子的允许不平衡度Eper=(G×1000)/(n/10)Eqer---允用不平衡度单位μG ---平衡精度等级一般取6.3n----工作转速单位r/min例:某工件工作转速1400r/min平衡精度等级取6.3则Eper=(6.3×1000)/(1400/10)=6300/140=45μ2、计算允许残余不平衡量m=(Eper×M)/(r×2)m------允许残余不平衡量单位gM------工件旋转质量单位kgr------工件半径单位mm例:工件质量20kg半径60mm双面平衡故计算每个平衡面的允许的剩余不平衡量为m=(Eper×M)/(r×2)=45×20/60×2=7.5g不平衡机专用名1、不平衡量――转子某平面上不平衡和量值大小,不涉及不平衡的角位置。
它等于不平衡质量和其质心至转子轴线距离的乘积,不平衡量单位为g.mm或g.cm俗称“重径积”2、不平衡度――转子某平面上的不平衡质相对于给定极坐标的角度值3、不平衡度―――转子单位质量的不平衡量,单位为g.mm/kg,在静不平衡时相当于转子的质量偏心距,单位为微米。
4、初始不平衡量―――平衡前转子上存在的不平衡量。
5、许用不平衡量―――为保证旋转机械正常工作所允许的转子剩余不平衡量该指标用不平衡度表示时,称为许用不平衡度(亦有称许用不平衡率)6、剩余不平衡量―――平衡后转子上剩余的不平衡度。
7、校正半径――――校正平面上校正质量的质心到转子轴线的距离,一般用mm表示。
8、校正平面干扰(相互影响)―――在给定转子某一校正面上不平衡量的变化所引起另一校正平面上平衡机指标值的改变(有时称平面分离影响)。
9、转子平衡品质―――衡量转子平衡优劣程度的指标。
G =Eperω/1000试中G为转子平衡品质,mm/s,从G0 4-G4000分11级,Eper为转子允许的不平衡率g.mm/kg或转子质量偏心距μmω相应于转子最高工作转速的角速度=2Ⅱn/60≈n/1010、转子单位质量的允许残余不平衡度(率)Eper=(G×1000)/(n/10) 单位g.mm/kg或mm/s11、最小可达剩余不平衡量(umar)---单位g.m,平衡机能使转子达到的剩余不平衡量的最小值,是衡量平衡机最高平衡能力的性能指标,当该指标用不平衡度表示时,称为最小可达剩余不平衡度(单位g.mm/kg).12、不平衡量减少率(URR)---经过一次平衡校正所减少的不平衡量与初始不平衡量之比值,它是衡量平衡机效率的性能指标,以百分数表示:URR(%)=(U1-U2)/U1=91-U2/U1)×100式中:U1为初始不平衡量;U2为一次平衡校正后的剩余不平衡量.13、不平衡国偶干扰比---单面平衡机抑制不平衡力偶影响的性能指标。
转子动平衡实验原理与方法

实验原理与方法实验采用的CS-DP-10型动平衡试验机的简图如图1所示。
待平衡的试件1安放在框形摆架的支承滚轮上,摆架的左端与工字形板簧3固结,右端呈悬臂。
电动机4通过皮带带动试件旋转,当试件有不平衡质量存在时,则产生的离心惯性力将使摆架绕工字形板簧做上下周期性的微幅振动,通过百分表5可观察振幅的大小。
1. 转子试件2. 摆架3. 工字形板簧4. 电动机5. 百分表6. 补偿盘7. 差速器8. 蜗杆图1 CS-DP-10型动平衡试验机简图试件的不平衡质量的大小和相位可通过安装在摆架右端的测量系统获得。
这个测量系统由补偿盘6和差速器7组成。
差速器的左端为转动输入端(n1)通过柔性联轴器与试件联接,右端为输出端(n3)与补偿盘联接。
差速器由齿数和模数相同的三个圆锥齿轮和一个蜗轮(转臂H)组成。
当转臂蜗轮不转动时:n3=-n1,即补偿盘的转速n3与试件的转速n1大小相等转向相反;当通过手柄摇动蜗杆8从而带动蜗轮以n H转动时,可得出:n3=2n H-n1,即n3≠-n1,所以摇动蜗杆可改变补偿盘与试件之间的相对角位移。
图2所示为动平衡机工作原理图,试件转动后不平衡质量产生的离心惯性力F =ω2mr,它可分解为垂直分力F y和水平分力F x,由于平衡机的工字形板簧在水平方向(绕y轴)的抗弯刚度很大,所以水平分力F x对摆架的振动影响很小,可忽略不计。
而在垂直方向(绕x轴)的抗弯刚度小,因此在垂直分力产生的力矩M = F y·l =ω2mrlsinφ的作用下,摆架产生周期性上下振动。
1图2 动平衡机工作原理图由动平衡原理可知,任一转子上诸多不平衡质量,都可以用分别处于两个任选平面Ⅰ、Ⅱ内,回转半径分别为r Ⅰ、r Ⅱ,相位角分别为θⅠ、θⅡ,的两个不平衡质量来等效。
只要这两个不平衡质量得到平衡,则该转子即达到动平衡。
找出这两个不平衡质量并相应的加上平衡质量(或减去不平衡质量)就是本试验要解决的问题。
转子允许不平衡量的计算
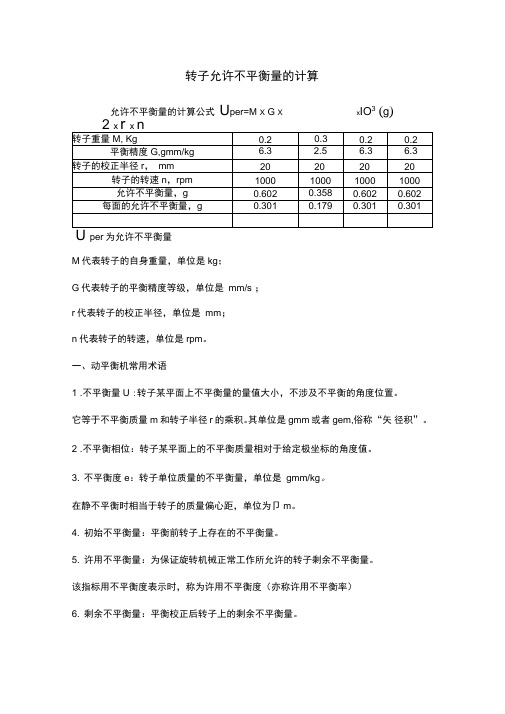
转子允许不平衡量的计算允许不平衡量的计算公式U per=M X G X x IO3(g)per为允许不平衡量M代表转子的自身重量,单位是kg;G代表转子的平衡精度等级,单位是mm/s ;r代表转子的校正半径,单位是mm;n代表转子的转速,单位是rpm。
一、动平衡机常用术语1 .不平衡量U :转子某平面上不平衡量的量值大小,不涉及不平衡的角度位置。
它等于不平衡质量m和转子半径r的乘积。
其单位是gmm或者gem,俗称“矢径积”。
2 .不平衡相位:转子某平面上的不平衡质量相对于给定极坐标的角度值。
3. 不平衡度e:转子单位质量的不平衡量,单位是gmm/kg。
在静不平衡时相当于转子的质量偏心距,单位为卩m。
4. 初始不平衡量:平衡前转子上存在的不平衡量。
5. 许用不平衡量:为保证旋转机械正常工作所允许的转子剩余不平衡量。
该指标用不平衡度表示时,称为许用不平衡度(亦称许用不平衡率)6. 剩余不平衡量:平衡校正后转子上的剩余不平衡量。
7. 校正半径:校正平面上校正质量的质心到转子轴线的距离,一般用mm 表示。
8. 校正平面的干扰(相互影响) :在给定转子某一校正面上不平衡量的变化引起另一校正平面上的改变(有时称为平面分离影响)9. 转子平衡品质:衡量转子平衡优劣程度的指标。
计算公式:G=e pero/1000式中G —转子平衡品质,单位mm/s。
从G0.4-G4000分11级。
eper—转子允许的不平衡率gmm/kg或转子质量偏心距卩m。
①一相应于转子最高工作转速的角速度二2m/60〜n/10 , n为转子的工作转速r/min 。
10. 转子单位质量的允许不平衡度(率) :eper= (G x 1000)/(n/10)单位:gmm/kg 或pm11最小可达剩余不平衡量(Umar):指平衡机能使转子达到的剩余不平衡量的最小值,是衡量平衡机最高平衡能力的性能指标。
单位为gmm。
12不平衡量减少率(URR):经过一次平衡修正减少的不平衡量与初始不平衡量之比值。
幅值误差和相位误差计算公式

幅值误差和相位误差计算公式
幅值误差和相位误差是在信号处理和通信系统中经常使用的两个重要指标,用来评估信号传输过程中的精度和准确性。
幅值误差通常用来衡量信号的幅度在传输过程中发生的变化程度,而相位误差则用来衡量信号的相位在传输中发生的偏移程度。
幅值误差是指信号在传输过程中幅度与原始信号幅度之间的差异。
它可以由绝对误差或相对误差来表示,通常以分贝(dB)为单位。
幅值误差的大小直接影响到信号的准确性和信噪比。
在通信系统中,幅值误差通常会导致信号失真和传输质量下降,因此需要对其进行有效的补偿和校正。
相位误差则是指信号在传输过程中相位与原始信号相位之间的偏移程度。
相位误差通常以角度或弧度来表示,用来衡量信号在传输过程中的相位失真程度。
相位误差的大小会直接影响到信号的相位一致性和时域性能,尤其在需要高精度定时和同步的应用中更为重要。
在实际应用中,幅值误差和相位误差往往是同时存在的,并且相互影响。
因此,在设计和优化信号处理系统时,需要综合考虑两者的影响,以保证信号传输的准确性和稳定性。
通常可以通过校准、补偿和滤波等方法来降低幅值误差和相位误差,从而提高系统的性能和可靠性。
总的来说,幅值误差和相位误差是评估信号处理系统性能的重要指
标,对于保证信号传输的精度和准确性起着至关重要的作用。
在实际应用中,需要根据具体情况综合考虑两者的影响,采取合适的措施来降低误差,从而提高系统的性能和可靠性。
希望本文对读者对幅值误差和相位误差有更深入的了解和认识。
转子允许不平衡量的计算

转子允许不平衡量的计算转子允许不平衡量的计算允许不平衡量的计算公式 Uper=M X G X602xxn3X10(g)Uper为允许不平衡量M代表转子的自身重量,单位是kg;G代表转子的平衡精度等级,单位是mm/s; r代表转子的校正半径,单位是mm; n代表转子的转速,单位是rpm。
一、动平衡机常用术语1.不平衡量U:转子某平面上不平衡量的量值大小,不涉及不平衡的角度位置。
它等于不平衡质量m和转子半径r的乘积。
其单位是gmm或者gcm,俗称“矢径积”。
2.不平衡相位:转子某平面上的不平衡质量相对于给定极坐标的角度值。
3.不平衡度e:转子单位质量的不平衡量,单位是gmm/kg。
在静不平衡时相当于转子的质量偏心距,单位为μm。
4.初始不平衡量:平衡前转子上存在的不平衡量。
5.许用不平衡量:为保证旋转机械正常工作所允许的转子剩余不平衡量。
该指标用不平衡度表示时,称为许用不平衡度(亦称许用不平衡率)。
6.剩余不平衡量:平衡校正后转子上的剩余不平衡量。
7.校正半径:校正平面上校正质量的质心到转子轴线的距离,一般用mm表示。
8.校正平面的干扰(相互影响):在给定转子某一校正面上不平衡量的变化引起另一校正平面上的改变(有时称为平面分离影响)9.转子平衡品质:衡量转子平衡优劣程度的指标。
计算公式:G=eperω/1000式中G-转子平衡品质,单位mm/s。
从G0.4-G4000分11级。
eper-转子允许的不平衡率gmm/kg或转子质量偏心距μm。
ω-相应于转子最高工作转速的角速度=2πn/60≈n/10,n为转子的工作转速r/min。
10.转子单位质量的允许不平衡度(率):eper=(G×1000)/(n/10)单位:gmm/kg或μm 11.最小可达剩余不平衡量(Umar):指平衡机能使转子达到的剩余不平衡量的最小值,是衡量平衡机最高平衡能力的性能指标。
单位为gmm。
12.不平衡量减少率(URR):经过一次平衡修正减少的不平衡量与初始不平衡量。
动平衡校正的计算公式修订版

动平衡校正的计算公式
不平衡量的简化计算公式:
m=9549MG/rXn
M ---- 转子质量单位(kg)
G——精度等级选用
r ------ 校正半径单位(mm)
n------ I】件的匚作转速单位(rpm)
m——不平衡合格量单位(g)
允许不平衡量的计算公式为:
式中mper为允许不平衡量,单位是g;
M代表转子的自身重量,单位是血;
G代表转子的平衡精度等级,单位是mm/s;
r代表转子的校正半径,单位是mm:
n代表转子的转速,单位是rpm。
举例如下:
如一个电机转子的平衡精度要求为G6. 3级,转子的重量为0. 2kg,转子的转速为lOOOrpm,校正半径20mm,
则该转子的允许不平衡量为:
因电机转子一般都是双面校正平衡,故分配到每面的允许不平衡量为0. 3g o
在选择平衡机之前,应先考虑转子所要求的平衡精度。
转子允许不平衡量的计算
允许不平衡量的计算公式为:
式中叫比为允许不平衡量,单位是g;
M代表转子的自身重量,单位是kg;
G代表转子的平衡精度等级,单位是mm/s;
r代表转子的校正半径,单位是mm;
n代表转子的转速,单位是rpmo
举例如下:
如一个电机转子的平衡精度要求为G6. 3级,转子的重量为0. 2kg,转子的转速为lOOOrpm,校正
半径20mm,
则该转子的允许不平衡量为:
因电机转子一般都是双面校正平衡,故分配到每面的允许不平衡量为0. 3go 在选择平衡机之前,应先考虑转子所要求的平衡精度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 振动周期信号整周期采样
111 理论分析
实际的振动信号为一连续信号 , 在实际分析时 无法取无限多个数据 , 所以在进行 DF T 时 , 时域的 截断是必然的 , 会造成频谱产生失真 。另外 ,DF T 计算频谱只限制为基频的整数倍 , 而不可能将频谱 看成连续函数 ,这样在两个离散的谱线之间若有一 个特别重要的频谱分量 , 很容易无法检测出来而被 忽略 。该效应对周期信号尤为严重 , 因为周期信号 的频谱是离散谱 ,如处理不当 ,很多重要谱线不被显 示 。对周期信号进行 DF T 处理时 ,对振动信号进行 整周期采样是解决上述问题有效的措施 。
a 2n + b2n
T 0/ 2 - T 0/ 2 T 0/ 2
其中 a n =
bn =
T∫ 2 T∫
0 0
2
ω0 t d t x ( t ) cos n ω0 t d t x ( t ) sin n
- T0/ 2
N
其中 k = 0 ,1 ,2 …, N - 1 为谐波次数 ; n = 0 , 1 , 2 , …, N - 1 为采样点数 。当 k = 1 时 , X ( 1 ) 为 DF T 的基频分量 。由上式即可知 : N- 1 2π X ( 1 ) = ∑x ( n ) exp ( - j n)
n =0
比较这两式 , 可以看出利用 DF T 的基本定义式 ( 3 ) 计算一个周期信号的傅里叶级数式时 , 频谱的正 常幅度等于 DF T 所求出的频谱分量乘以 1/ N 。 傅里叶级数的三角形式为
∞
x ( t ) = a0 + An =
n =1
∑A
n sin (
ω0 t + φn ) n
间函数 , x ( t ) 可展成傅里叶级数 , 其傅里叶级数的 系数为 X ( jkΩ0 ) , X ( jkΩ0 ) 是离散谱 ,Ω0 为离散频 谱相邻两谱线的角频率间隔 , k 为谐波序号 。二者 有如下关系 : 周期信号的复数傅里叶级数为
∞
x ( t) =
k=- ∞
∑ X ( jkΩ0 ) exp ( jkΩ0 t )
3 结论
在实际动平衡检测仪的研制与应用过程中 , 采 用此法能够较准确获取转子不平衡信号的幅值和相 位 。相对于采用锁相环硬件的系统 , 本系统具有简 单可靠 、 软硬件易实现的特点 , 在转子动平衡分析中 很具实际意义 。
参考文献
[1 ] 李芳泽 ,刘馥清 ,王正 1 工程振动测试与分析 1 北京 : 高等教育
X ( jkΩ0 ) = = T T0
N- 1 n =0
∑x ( n T ) exp ( N- 1 n =0
j nkΩ0 T ) j nkΩ0 T ) ( 2)
1
N
∑x ( n T ) exp ( j N
离散傅里叶变换为
N- 1
X ( k) =
n =0
∑x ( n ) exp ( -
2π
k n)
( 3)
( 1)
式中的傅里叶级数系数为
X ( jkΩ0 ) =
计量技术 20051No 3
1
T0
∫ x ( t ) exp ( 2
T0
T0
出版社 ,1992
jkΩ0 t ) d t
[ 2 ] 程佩青 1 数字信号处理教程 1 北京 : 清华大学出版社 ,1995
2
・ 33 ・
转子动平衡检测中不平衡信号幅值 与相位的计算方法
耿 慧
( 郑州铁路局郑州计量管理所 ,郑州 450052)
摘 要 本文主要论述了在旋转机械的动平衡检测中 ,采用转速脉冲信号触发 A/ D 进行整周期采样 ,然后通 过对采集到的整周期信号进行离散傅里叶变换 ,从而得到不平衡信号的幅值与相位 。 关键词 转子动平衡 ; 离散傅里叶变换 ( DF T) ; 振动信号
4 结束语
从以上对 HL 开关器件的应用结果表明 , 用该 器件组合的经纬仪圆感应同步器测角系统清零电路 的方法是可靠稳定的 。霍尔器件是近年来开发的一 种新的集成元件 ,由于它体积小 、 无触点 、 无火花 、 寿 命长 、 性能可靠 、 抗污染 、 抗干扰强 、 安装方便 、 工作 频率宽等优点 ,所以越来越得到广泛的应用 。
n =0
式中 a n 为常值分量 ; A n 为 n 次谐波的幅值 ;φn 为 相角 ;ω0 为基频 。 比较傅里叶级数的两种展开形式可知 : 复指数 形式的频谱谐波幅值为三角函数形式的频谱幅值的 一半 。于是可知 , 三角函数形式的频谱的正常幅度 等于 DF T 所求出的频谱分量乘以 2/ N ( N 为一周 的采样点数) 。用这种方法可以精确获取周期信号 频谱基频及其整数倍离散点频率处的幅值和相位 。 由以上分析可知 , 不平衡信号 ( 基频信号 ) 的幅 值和初相位可由以下公式求出 : FA = ( 2/ N ) F1 ,θ= θ 1
112 实现方法
首先 ,在旋转体上任意位置处贴反光条确定基 准相位位置 ,当转子转动到基准相位位置时由光电 传感器产生脉冲 , 根据脉冲频率计算出转子稳定旋 转时的转速和转动频率 。原始振动信号的采集一般
・ ・ 32 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved.
计量技术 20051No 3
测量与设备
采用压电加速度传感器 , 由传感器采集到的原始振 动信号经过带通滤波 ( 滤波器中心频率根据转子的 转动频率确定) 、 程控增益放大后形成基频振动信号 并送 A/ D 进行采样 。然后 , 根据采样点数 N 和转 速确定采样频率 , 当转子转到基准相位位置时由光 电传感器产生的脉冲信号触发 A/ D 按照预先设定 的采样频率开始采样 。转子每旋转一周产生一次触 发脉冲信号 ( 相位基准) , 在转子的每一转上就可采 样 N 个点 ,然后取此 N 个点进行离散傅里叶变换 , 就可实现整周期采样 。 令其中 t = n T ( T 为采样间隔 ) , 则有 d t = T , 于是 上式可变为 ,
2 利用 DF T 获取转子动不平衡信号的幅值
与相位
设振动信号为 x ( t ) ,由于不平衡信号只与基频 成份有关 , 所以我们需对其进行离散傅里叶变换 DF T 。根据采样定理 ( 采样信号的频率大于被采信 号最高频率的 2 倍) ,在一个周期 T 里 ,我们进行等 间隔采样 N 个点 , 采样所得时域序列为 : x ( 0 ) , x ( 1 ) , ……, x ( N - 1) , 则该序列的 DF T 为 : N- 1 2π X ( k ) = ∑x ( n ) exp ( - j k n)
© 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved.
测量与设备
这时与门 G2 就得到由 HL 2 上升沿和 HL 1 下降沿组 合± 1° 的脉宽输出 V 12 , 在这 ±1° 范围内只包括一 个周期 T 0 ,MD 遇到周期 T 0 信号 ,就输入一个脉宽 μs 脉 冲 , 作 为 清“0 ” 为5 脉冲,使角度显示全 为 “0” 。 反向转动时 , HL 2 先导通 CP 由低电平上跳为 高电平 , 这时 D 触发器翻转 , 输出 Q 由原来的高电 平下跳低电平 。而后 HL 1 导通 , 使 D 为高电平 , 此 时 CP 已为高电平 ,即 D 触发器不再翻转 ,仍为低电 平 。磁钢全通过 HL 1 HL 2 ,输出 Q 为低电平不变 ,周 期 T 0 和 MD 脉冲被与门 G2 关闭 , R 为 “0 ” , 此电路 反方向转动时不产生清零脉冲 , 保留了正方向产生 清零脉冲 ,这样就保证一点为零 ,此零就是经纬仪工 作的绝对 “0” 点。
0 引言
在旋转机械中 , 由转子质量不平衡引起的有害 振动是影响设备正常工作的主要原因之一 。因此 , 对转子进行动平衡检测是消除这种有害振动的主要 方法 。由质量不平衡引起的强迫振动信号是频率等 于转子转动频率的基频振动信号 。由测振传感器直 接采集到的振动信号一般不是纯粹的正弦信号 , 是 各种频率成份的合成信号 ,其中除了基频信号外 ,可 能还含有其他频率成份的周期信号 , 如何从合成波 形中准确提取转子不平衡信号 ( 基频信号) 的幅值和 相位就成为转子动平衡处理的重要基础 。本文提出 了一种软硬件结合的处理方法 : 首先利用转速脉冲 触发 A/ D 对振动信号进行整周期采样 ,并通过硬件 滤波得到基频振动信号 , 然后对此整周期基频振动 信号进行离散傅里叶变换 ( DF T) 从而得到转子动不 平衡信号的幅值和相位 。
N
= a1 + b1 i = F1θ 1
其中 a1 = ∑ x ( n ) cos
n=0
N- 1
2πn
N
; b1 = ∑ x ( n ) sin
n=0
N- 1
2πn
N
;幅
2 1/ 2 值 F1 = ( a2 ;信号初相角 θ 1 + b1 ) 1 = arctan ( b1 / a1 ) 。 但是由 DF T 计算出的幅值和相位并不是不平衡信 号的幅值和相位 ,二者有一定的相对数值关系 ,推导 如下 : 设 x ( t ) 代表一个周期为 T 0 的周期性连续时
