光学作业题解
第11章光学作业题目讲解 马文蔚第六版

s; n
n
4.88107 m
488nm
Vn
c
51014 Hz
(3)几何路程SC SA AB BC SA d BC 0.111m
cos1
光程 SA 1+AB n+BC1=0.114m
11-14
已知:杨氏干涉实验
n1, n2, ,中央明纹变
• 求解:λ’
• 解:根据题意知牛顿环干涉暗环半径公式
r kR
• 其中k =0,1,2…,k =0,对应牛顿环中心 的暗斑,k=1 和k =4 则对应第一和第四暗环, 由它们之间的间距
r r4 r1 R
• 所以知 r
• 因此,两种波长前后对比
r r • 得到: λ′=546 nm
• 解:根据分析,对应于同一观察点,两 次衍射的光程差相同,由于衍射明纹条
件 bsin 2k 1
2
• 由比较法得
2k1 11 2k2 12
• 将已知条件 2 600 nm,k2 2, k1 3 • 带入上式,得
•
1
2k2 12
2k1 1
•得
k / k 2 / 1 3 / 2
• 显然,第一次重合是λ1 的第3 级明纹与λ2 的 第2级明纹重合,
• 第二次重合是λ1 的第6 级明纹与λ2 的第4级 明纹重合.
• 此时,k=6,k′=4,φ=60°,则光栅常数
d k1/sin 3.05106 m 3.05 μm
2nb 2nx
11-20
• 折射率为1.60的两块标准平面玻璃板之间 形成一个劈形膜(劈尖角θ 很小).用 波长λ=600 nm 的单色光垂直入射,产 生等厚干涉条纹.假如在劈形膜内充满n =1.40 的液体时的相邻明纹间距比劈形 膜内是空气时的间距缩小Δl =0.5 mm, 那么劈尖角θ 应是多少?
应用光学作业题答案

第二题: (1)光线由水中射向空气,求在界面处发生全反射的临界角。
解: 全反射的临界角Im arcsin(n '/ n)
光线由水中射向空气,n’=1,n=1.333
则 Im arc sin(n '/ n)=arc sin(1/1.333)=48.61
(2)光线由玻璃内部射向空气,求发生全反射的临界角。
1 l2
'
-
1 130
=
1 120
l2'=-62.4mm
A”成象于透镜2左侧62.4mm处。
(2)等效光组成象的方法:
解: H’
A
F1
F2’
F1’
F2
f1’=120mm f2’=-120mm d=70mm △= d-f1’- f2’=70mm
f ' f1 ' f2 ' 120 (120) 205.714mm
n0sini1=nsini1’ sini1=0.6552 i1=40.93° 由三角形内角和可求出太阳和幻
日之间的夹角
α=180 °-2×(i1-i1’) =158.14 °
第七题:
为了从坦克内部观察外界目标,需要在坦克上开一个孔,假 定坦克壁厚250mm,孔宽150mm,在孔内装一块折射率 n=1.52的玻璃,厚度与装甲厚度相同,问能看到外界多大的 角度范围?
O’
A’
解:(1)对于在球心的气泡,以O作为 球面顶点,根据符号规则,
O L’A=-200mm,n’=1,n=1.52
由 n ' n n ' n l' l r
1 -1.52 = 1-1.52 l=-200mm -200 l -200
光学第二章习题解答

∆y = y2 − y1 ≈ 2 f ′
λ
b
− f′
λ
b
= f′
λ
b
∆y ⋅ b 0.02 × 0.885 ɺ λ= = = 5900 A f′ 300
(2)波长为 波长为0.1nm的x射线时,相邻最小值间的距离为 射线时, 波长为 的 射线时
′λ 300 × 0.1×10−9 f ∆y = = 0.02 b −6 −4 = 1.5 × 10 m = 1.5 × 10 cm
主焦点
还有次焦点: 还有次焦点:± f ′ /3,
± f ′ /5, ± f ′ / 7⋯
故:光强极大值出现在轴上 1/3m,1/5m,1/7m……1/(2k+1)m等处 , , 等处
2.6 波长为 的点光源波带片成一个像点,该波带 波长为λ的点光源波带片成一个像点 的点光源波带片成一个像点, 个透明奇数半波带(1, , )。另外 有100个透明奇数半波带 ,3,5 ……199)。另外 个透明奇数半波带 )。 100个不透明偶数半波带。比较用波带片换上同样焦 个不透明偶数半波带。 个不透明偶数半波带 距和口径的透镜时像点的强度比I: 距和口径的透镜时像点的强度比 :I0 解:(1) 只有 ) 只有100个透明奇数半波带透过 个透明奇数半波带透过
∵
θ3 < θ 2
∴
二级和三级光谱部分重叠 二级和三级光谱部分重叠
2.14 用波长为 用波长为589nm的单色光照射一衍射光栅, 的单色光照射一衍射光栅 的单色光照射一衍射光栅, 其光谱的中央最大值和第二十级主最大值之间的衍 射角为15 10′。试求该光栅1cm内的缝数是多少? 15° cm内的缝数是多少 射角为15°10′。试求该光栅 cm内的缝数是多少? 解: 由光栅方程 d sin θ = jλ
应用光学习题解答

习题巩固
巩固练习
习题难度:从易到难,逐步提高解题能力 习题类型:覆盖多种题型,包括选择题、填空题、计算题等 习题内容:涉及多个知识点,帮助学生巩固所学内容 习题答案:提供详细的答案解析,帮助学生理解解题思路
练习答案
答案:光在平面镜上的反射遵守光的反射定律。
答案:在应用光学中,透镜的焦距是指平行于主轴的光线通过透镜后汇聚 的点到透镜中心的距离。
题目:应用光学实验操作
解析:通过实验操作,加深对应用光学理论的理解,掌握实验仪器的使用技巧,提高实验操作能力 和数据分析能力。
练习总结
习题巩固:通过 练习题来巩固所 学知识
解题技巧:掌握 解题技巧,提高 解题效率
错题分析:分析 错题原因,避免 重复犯错
举一反三:通过练 习题学会举一反三, 拓展知识面
学科交叉:与其 他学科的知识点 进行交叉融合, 拓宽学生的知识 面和思维方式。
创新实验:设计 一些创新性的实 验,让学生通过 动手实践来加深 对光学的理解。
拓展总结
解题技巧:掌握常用解题方 法,提高解题效率
习题难度:由易到难,逐步 提高解题能力
知识点拓展:通过习题巩固 和拓展所学知识点
举一反三:学会触类旁通, 能够解决类似问题
应用光学习题解析
01
02
习题拓展
习题巩固
03
04
习题解答
光的折射与反射
光的折射:光从一 种介质斜射入另一 种介质时,传播方 向发生改变的现象。
光的反射:光在两 种介质的交界面上 返回原介质的现象。
折射定律:入射角i 、折射角r和介质的 折射率n之间的关 系。
反射定律:入射角i 、反射角i'和介质 的折射率n之间的 关系。
光学作业解
l
2 sin
上面的平玻璃慢慢地向上平移时, 不变化.条纹间隔不 变化.
4.用劈尖干涉法可检测工件表面缺陷,当波长为λ的单色平 行光垂直入射时,若观察到的干涉条纹如图所示(非显微镜图 示),每一条纹弯曲部分的顶点恰好与其左边条纹的直线部分 的连线相切,则工件表面与条纹弯曲处对应的部分 [ C ]
B
θ A
差AB,计算其差值时减掉 了,则条纹间距不变
2.两块长度为10cm 的平玻璃板,一端互相接触,另一端用厚度 为0.004mm的纸片隔开,形成空气劈尖.以波长500.0nm的平 行光垂直照射,观察反射光的等厚干涉条纹,在全部10cm的长 度内呈现多少明条纹? 明条纹
max 2emax
2 2
d sin (n1 n2 )e
3.用波长为λ的单色光垂直照射折射率为n2 的劈尖薄膜(如 图),图中各部分折射率的关系是. n1 n2 n3 观察反射光的 干涉条纹,从劈尖顶开始向右数第五条暗条纹中心所对应的厚 度 e=
n1 n2 n3
暗纹
BC a sin k k
f x1 f tan 1 f sin 1 a f x1 f tan 1 f sin 1 a 2 f a x 条纹宽度: x x1 x1 a
单缝作微小位移不改变衍射图样。选(C) 变窄,不移动
3.(1)在单缝夫琅和费衍射中,垂直入射的光有两种波长 1 = 400.0 nm,2 = 760.0 nm,已知单缝宽度 a = 1.0 10-2 cm,透镜焦距 f = 50cm。求两种光第一级衍射明纹 中心之间的距离。
kmax 16
2
k max
全部光学作业解答Word版
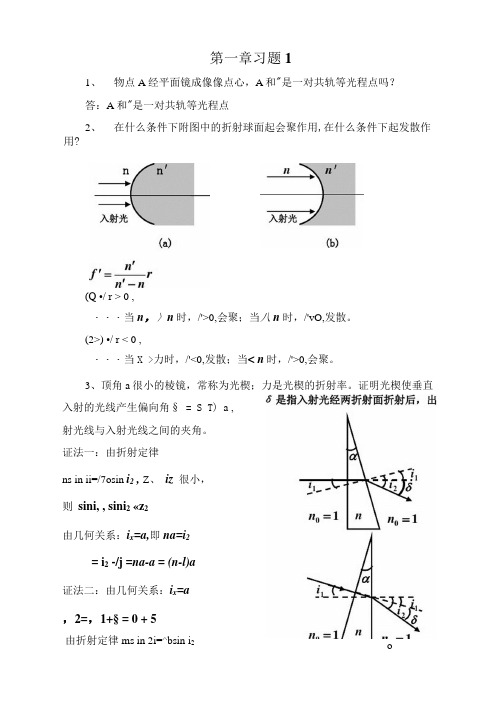
第一章习题11、物点A经平面镜成像像点心,A和"是一对共轨等光程点吗?答:A和"是一对共轨等光程点2、在什么条件下附图中的折射球面起会聚作用,在什么条件下起发散作用?(Q •/ r > 0 ,・・・当n,〉n时,/'>0,会聚;当八n时,/'vO,发散。
(2>) •/ r < 0 ,・・・当X >力时,/'<0,发散;当< n时,/'>0,会聚。
3、顶角a很小的棱镜,常称为光楔;力是光楔的折射率。
证明光楔使垂直入射的光线产生偏向角§ = S T) a ,射光线与入射光线之间的夹角。
证法一:由折射定律ns in ii=/7osin i2 , Z、iz很小,则sini, , sini2 «z2由几何关系:i x=a,即na=i2= i2 -/j =na-a = (n-l)a证法二:由几何关系:i x=a,2=,1+§ = 0 + 5由折射定律ms in 2i=^bsin i2o _V N 很小,sinq =a, sin/2 »i2, 且n0 «1则有na-a + 5, /• 8 = na-a = (n- l)a4>若空气中一均匀球形透明体能将平行光束会聚于其背面顶点上.此透明体的折射率应等于多少?解:设球形透明体的半径为r,其折射率为川已知H =1,p = -g, p' = 2r根据单球面折射成像公式= 得:工=上1 :. n f = 2p p r 2r r5、试证明:一束平行光相继经过几个平行分界面的多层介质折射时,出射光线的方向只与入射光的方向及入射空间和出射空间介质的折射率有关,与中间各层介质无关。
证明:V 坷sinh = //o sin/on2 sini2 = n l smi xn3 sin匚=n2 sin/2ii■g】sinL ijsini—n k sini* sini AU:.n k sini k =n o sin«o即sin/x = (/i0 sini0)/«A,命题成立。
工程光学习题解答

第一章习题1、已知真空中的光速c=3 m/s,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
初中物理光学知识典型例题解析

初中物理光学知识典型例题解析1.用照相机照相时,在拍摄进景和远景时,有什么区别?答:物距均大于二倍焦距(因为照相机常常要得到缩小的实像),像距均在一倍焦距和二倍焦距之间。
由于凸透镜成实像时,物距越远则像距越近,物距越近则像距越小,所以拍摄近景时,物距小,像距较大,成的像也较大,照相机的镜头要往前伸;拍摄远景时,物距大,像距较小,成的像也较小,照相机的镜头要往后缩.2。
凸透镜及其成像规律凸透镜(convex lens)凸透镜是根据光的折射原理制成的。
凸透镜是中央部分较厚的透镜。
凸透镜分为双凸、平凸和凹凸(或正弯月形)等形式,薄凸透镜有会聚作用故又称聚光透镜,较厚的凸透镜则有望远、会聚等作用,这与透镜的厚度有关。
将平行光线(如阳光)平行于轴(凸透镜两个球面的球心的连线称为此透镜的主光轴)射入凸透镜,光在透镜的两面经过两次折射后,集中在轴上的一点,此点叫做凸透镜的焦点(记号为F,英文为:focus),凸透镜在镜的两侧各有一焦点,如为薄透镜时,此两焦点至透镜中心的距离大致相等。
凸透镜之焦距是指焦点到透镜中心的距离,通常以f表示。
凸透镜球面半径越小,焦距(符号为:f,英文为:focal length)越短。
凸透镜可用于放大镜、老花眼及远视的人戴的眼镜、摄影机、电影放映机、显微镜、望远镜的透镜(lens)等。
实验研究凸透镜的成像规律是:当物距在一倍焦距以内时,得到正立、放大的虚像;在一倍焦距到二倍焦距之间时得到倒立、放大的实像;在二倍焦距以外时,得到倒立、缩小的实像。
该实验就是为了研究证实这个规律。
实验中,有下面这个表:物距范围成像性质像距范围u>2f 倒立、缩小、实像、异侧f<v<2fu=2f 倒立、等大、实像、异侧v=2ff<u<2f 倒立、放大、实像、异侧v>2fu=f 不成像u<f 正立、放大、虚像、同侧u<v 这就是为了证实那个规律而设计的表格。
其实,透镜成像满足透镜成像公式:1/u+1/v=1/f物在焦点不成像,二倍焦距倒同样.大于二焦倒立小,焦外二内幻灯放.物体放在焦点内,对侧看见大虚像.像若能够呈屏上,一定倒立是实像.(1)u>f时成实像,u<f成虚像,焦点是实像和虚像的分界点。
光学习题解

第一章光的干涉1.波长为500nm的绿光投射在间距为0.22cm的双缝上,在距离180cm 处的光屏上形成干涉条纹,求两个亮条纹之间的距离。
若改用波长为700nm的红光投射到此双缝上,两个亮纹之间的距离又为多少?算出这两种光第2级亮纹位置的距离。
[解]:(1)双缝干涉产生的亮条纹的条件为===对上式两边取微分,得=令得:==0.409cm.(2) ==0.573cm(3) ==0.327cm2.在扬氏实验装置中,光源波长为640nm,两缝间距为0.4mm,光屏离狭缝的距离为50cm。
试求:(1)光屏上第1亮条纹和中央亮条纹之间的距离;(2)若P点离中央亮条纹的距离为0.1mm,问两束光在P点的相位差是多少?(3)求P点的光强度和中央点的强度之比。
[解]:(1)双缝干涉产生的亮条纹的条件为===令,得:=0.08cm.(2)=(3)如果两束光振动的振幅相等,则有:所以3.把折射率为1.5的玻璃片插入杨氏实验的一束光路中,光屏原来第5级亮条纹所在的位置变为中央亮条纹,试求插入玻璃片的厚度。
已知光波长为6m[解]:当玻璃片未插入时,从和至光屏上点的光程差为当玻璃片插入后从和至光屏上点的光程差为零,点光称差的变化等于插入玻璃片的这束光的光程的变化(4.波长为500nm的单色平行光射在间距为0.2mm的双缝上,通过一个缝的能量为另一个的2倍,在离狭缝50cm的光屏上形成干涉条纹图样。
求干涉条纹间距和条纹的可见度。
[解]:(1)双缝干涉产生的亮条纹的条件为==对上式两边取微分令得:= 1.25m(2) 根据可见度的计算公式=又因为所以=0.945.波长为700nm的光源与菲涅耳双镜的相交棱之间距离为20cm,棱到光屏间的距离L为180cm,若所得干涉条纹中相邻亮条纹的间隔为1mm,求双镜平面之间的的夹角。
[解]:双镜干涉的条纹间距为已知:=6.在题1.6图所示的劳埃镜实验中,光源S到观察屏的距离为1.5m,到劳埃镜面的垂直距离为2mm。
应用光学习题解答

应用光学习题解答一、简答题1、几何光学的基本定律及其内容是什么?答:几何光学的基本定律是直线传播定律、独立传播定律、反射定律和折射定律。
直线传播定律:光线在均匀透明介质中按直线传播。
独立传播定律:不同光源的光在通过介质某点时互不影响。
反射定律:反射光线位于入射面内;反射角等于入射角;折射定律:折射光线位于入射面内;入射角和折射角正弦之比,对两种一定的介质来说,是一个和入射角无关的常数2111sin sin I n I n =。
2、 理想光学系统的基点和基面有哪些?答:理想光学系统的基点包括物方焦点、像方焦点;物方主点、像方主点;物方节点、像方节点。
基面包括:物方焦平面、像方焦平面;物方主平面、像方主平面;物方节平面、像方节平面。
3、什么是光学系统的孔径光阑和视场光阑?答:孔径光阑是限制轴上物点成像光束立体角的光阑。
视场光阑是限制物平面上或物空间中成像范围的光阑。
4、常见非正常眼有哪两种?如何校正常见非正常眼?答:常见非正常眼包括近视眼和远视眼。
近视眼是将其近点校正到明视距离,可以用负透镜进行校正;远视眼是将其远点校正到无限远,可以用正透镜进行校正。
5、光学系统极限分辨角为多大?采取什么途径可以提高极限分辨角? 答:衍射决定的极限分辨角为Dλσ61.0=。
可见其与波长和孔径有关。
减小波长和增大孔径可以提高光学系统的分辨率。
6、什么是共轴光学系统、光学系统物空间、像空间?答:光学系统以一条公共轴线通过系统各表面的曲率中心,该轴线称为光轴,这样的系统称为共轴光学系统。
物体所在的空间称为物空间,像所在的空间称为像空间。
7、如何确定光学系统的视场光阑?答:将系统中除孔径光阑以外的所有光阑对其前面所有的光学零件成像到物空间。
这些像中,孔径对入瞳中心张角最小的一个像所对应的光阑即为光学系统的视场光阑。
8、成像光学系统有哪两种色差?试说明它们的成因?答:有位置色差(或轴向色差)和放大率色差(或垂轴色差)两种。
光学 赵凯华 习题解答

《光学》赵凯华 (钟锡华)习题解答第一章P23—5 (1-4)证一: 对平行平板上下表面分别两次运用折射定律,并考虑到平板上下是同一介质,便可证明最后出射光线与当初入射光线的方向一致。
根据几何关系可得侧向位移量为)cos sin cos (sin 2211 )sin cos cos (sin cos )sin(211221i i i i t i i i i ti i AB X −=−=−=Δ122i折射定律 sini =nsini 在i 2<i 1<<1的条件下, 取小角近似 sini 1≈i 1,cosi 1≈cosi 2≈1于是有 n n X 1−≈Δt i 1证二:)1())sin(11n n t l x ()sin(cos 11t t−=−−=θθθθ=−=θθθθP23—7(1-6)证一:由于光线垂直入射,故光线在第一个界面不发生折射,仅在第二个界面有折射。
如图, 根据折射定律 nsini 2=sini ’2 以及几何关系 i 2=α, 故 nsinα=sini ’2当α很小时, 有sinα≈α,sini ’2≈i ’2 则上式可写成nα=i ’2所以偏向角为αααδ)1(2'2−=−=−=n n i i这个近似公式, 在干涉、衍射、偏振中经常要用到, 我们应当记住。
证二:αααα+δ+⇒δ=)sin(n →sin (当0α时)得出:δα)1(−n=P23—11(1-10)解:设棱镜的折射率为n ,水的折射率为n ’,先求得n=60.15023550sin=+D DD 2sin再由 n=n ’2sin2sin αα+δm 得D25sin 33.160.1sin=+2sin 2′=αδαn nm'132305080.0sin 2D ==+−mδα最后求出此棱镜放在水中的最小偏向角为'411D =m δp23—14(1-13)解 :根据折射定律,得到n 0sin22111sin 1sin θθθ−=n n 21'1cos θ==n 因为光线在玻璃芯和外套的界面上发生全反射的条件为sin122n n ≥θ所以,欲使光线在纤维内发生全反射,1θ必需满足n 0sin2121)(1n n n −1≤θ故数值孔径为 n 0sin221n n −=θ'sin sin i DEF n g =∠n g DEF EDF ∠−=∠D90n n g 21光导纤维的数值孔径反映集光本领,是导光传象的重要性能参数之一。
光学部分习题解答(cai)

2
( 最大高度为 最大高度为 λ 2 = 250 nm) 高度
所以选: 所以选:B
10.(3200)
解 : 原光程为2 ×1d的光程。 放入透明薄片后改变为2nd 所以:光程变为:2nd-2d=2d(n-1)
所以选 所以选:A
11.(3516)
解 : 利用上题的结论得: 2nd-2d=2d(n-1)=λ d=
λ
• 30.(3711)
解 : 同上题解法。 d=N
λ
2
⇒N=
2d
λ
• 31.(3378)
解 : 参看P89公式(11-36) I=I1 +I2 +2 I1I2 cos∆φ,
I=I0 +I0 +2 I0I0 cos∆φ, ∴IMAX = 4 I 0
• 32.(5647)
解 : 参看P92
2 500 × 4 λk ∴e = = = 4 × 103 nm. n − 1 1.5 − 1
2k . ( k = 4)
27.(3179)
解 : 空气中光程差:
δ = s2 p − s1 p =
λ
2
2k
∴ s2 p − s1 p = 3λ
液体中:δ = s2 p − s1 p)n = ( (s2 p − s1 p )n =4λ
∴总光程差 : 2en2
δ总 2en2 4π en2 Q ∆φ = 2π = 2π = λ λ λ
所以选: 所以选:A
(3664)
解 : δ 总 =δ +δ附加
n1 < n2 > n3
∴ δ 总 = 2en2 + λ
δ = 2en2 δ附加 = λ 2 ,Q 只有1个半波损失.
竞赛辅导-光学习题解答

物理竞赛辅导——光学一、干涉 ◆杨氏双缝1、P858-11如图的洛埃镜镜长cm .B 005=,幕与镜的右端相距m .C 005=,点光源高出镜面距离为mm .d 5000=,与镜左端的水平距离cm .A 002=,光波波长nm 600=λ.(1)试求幕上干涉条纹的间距,(2)试问幕上总共能出现多少条干涉条纹。
(3)λ∆有何要求?(1)条纹间距m dCB A x 31004.32-⨯=++=∆λ (2)干涉条纹数()()294.29XH H N m 1093.8BA dC A d C B tg C tg C B H H 1221212≈=∆-=⨯=+⋅-+θ⋅-θ+=-- (3)忽略半波损失,在叠加区最大光程差:2m 1055.2Ad 2A d d 2CB H A d ,tg d 222m ⨯==⋅=+=θ⋅=∆看清全部条纹的条件是:nm 1044.1)(L 822C m -⨯=∆λ≤λ∆∴λ∆λ=≤∆m相干长度2、P859-12间距为d 的双孔1S 和2S 后放置一会聚透镜,透镜后焦平面上放一屏幕。
上述干涉装置正对遥远的双星S 和S ',在幕上观察双星产生的干涉条纹。
当d 从小连续变大时,干涉条纹的反衬度将作周期性变化。
(1)试解释此现象;(2)若星光的平均波长为nm 550,当d 变到mm .02时,条纹第一次变模糊,试求双星的角间距。
(1) 设双星角距离为θ入射光S 在P 点光程差为:P S P S NS 122-+=∆ 入射光S '在P 点光程差为:P S S N P S 112-'-=∆'d 2d2NS 2S N NS 212θ=θ≈='+=∆'-∆∴两套条纹级次差为λθ=λ∆'-∆=∆∴dk 当...3,2,1k =∆∴两套条纹的极大值重合,条纹最清晰 当 (2)5,23,21k =∆∴两套条纹的极大与极小重合,条纹最模糊 当d 从零开始增大时,使21k =∆∴时,条纹第一次出现模糊, 此时θλ=∴2d (2)双星角间距rad 104.10.22105.5d 244--⨯=⨯⨯=λ=θ 3、竞1届:波长为λ的两相干的单色平行光束1、2,分别以入射角ϕθ,入射在屏幕面MN 上,求屏幕上干涉条纹的间距。
光学(难题篇)经典题解版

一、单选题1. 根据分子动理论可知,在使两个分子间的距离由很远(r ≥10-9m)到很难再靠近的过程中,分子间的作用力的大小将( )A .先减小后增大B .先增大后减小C .先增大后减小再增大D .先减小后增大再减小2. 如图甲所示的电路中,变压器为理想变压器,两定值电阻的阻值分别为,,电压表、电流表均为理想电表,当a 、b 两端接入交流电源,交流电的电压随时间变化的规律如图乙所示,电阻和消耗的功率相等,则下列说法正确的是( )A .电压表的示数为27VB .电流表的示数为1.8AC .变压器原副线圈的匝数比为7∶1D .电源的输出功率为64.8W3. “中国载人月球探测工程”计划在2030年前实现中国人首次登陆月球。
设想在地球和月球上有两个倾角相同的山坡,简化为如图所示的足够长的倾角为θ的斜面。
现分别从这两个山坡上以相同大小的速度v 0水平抛出两个完全相同的小球,小球再次落到山坡上时速度大小分别记为v 1、v 2,速度方向与坡面的夹角分别记为θ1、θ2。
已知地球与月球表面重力加速度分别为g 、,不计小球在地球上运动时的空气阻力,以下关系正确的是( )A .θ2>θ1B .θ2<θ1C .v 2<v 1D .v 2=v 14.狄拉克曾经预言,自然界应该存在只有一个磁极的磁单极子,其周围磁感线呈均匀辐射状分布如图甲所示,距离它处的磁感应强度大小为(为常数,其磁场分布与负点电荷的电场如图乙所示分布相似。
现假设磁单极子和负点电荷均固定,有带电小球分别在极和附近做匀速圆周运动。
则关于小球做匀速圆周运动的判断不正确的是( )A .若小球带正电,其运动轨迹平面可在的正上方,如图甲所示B.若小球带负电,其运动轨迹平面可在的正下方,如图乙所示C .若小球带负电,其运动轨迹平面可在的正上方,如图甲所示D .若小球带正电,其运动轨迹平面可在的正下方,如图乙所示5. 如图,某同学将一足球静止摆放在收纳架上。
他估测得足球的直径约为20 cm ,质量约为0. 48 kg ,收纳架两根平行等高的横杆之间的距离d 约为12 cm 。
光学作业题解

光学作业题解5.21 在双缝干涉实验中,两缝间距为0.30mm ,用单色光垂直照射双缝,在离缝1.20m 的屏上测得中央明纹一侧第5条暗纹与另一侧第5条暗纹的距离为22.78mm 。
问所用的波长为多少?是什么颜色的光? 解:(杨氏双缝干涉明暗纹的级数是从0取起,所以两侧第5条暗纹,级数为k=4±)杨氏双缝干涉暗纹位置:(21),0,1,2,2D x k k d λ=±+=2(21)xd k D λ=+由题意,k=4,x=11.39mm ,d=0.3mm ,D=1.20m ,代入上式:33211.39100.310632.7(241) 1.20nmλ--⨯⨯⨯⨯==⨯+⨯是红光。
或:在k=4±的两条暗纹之间有9个x ∆_相邻暗纹间距(明纹一样)Dx d λ∆=33330.301022.7810922.781022.7810632.799 1.2Dd nmdD λλ----⨯⨯⨯=⨯=⨯⨯==⨯是红光。
5.22 在双缝干涉实验装置中,两个缝分别用n1=1.4和n2=1.7的厚度相等的玻璃片遮盖,在光屏上原来的中央明纹处,现在为第5级明纹所占据。
如入射的单色光波长为600nm ,求玻璃片的厚度。
解:两光路光程差:2121()r r n n d δ=-+-在光屏中央210r r -=,现在是第五级明纹:21()5n n d λ-=玻璃片的厚度:9215560010101.7 1.4d mn n λμ-⨯⨯===--5.24 在折射率n 3=1.50的玻璃片上镀一层n 2=1.38的增透膜,可使波长为500nm 的光由空气垂直入射玻璃表面时尽量减少反射,则增透膜的最小厚度为多少?解:增透膜要求反射光相消,且反射光在膜的上下表面都存在半波损失则有22(21),0,1,2,2n e k k λ=+=取k=0,增透膜有最小厚度 92600100.10944 1.38e mn λμ-⨯===⨯5.25 用波长为500nm 的单色光垂直照射到由两块光学玻璃构成的空气劈形膜上。
光学教程习题解

[《光学教程》〔姚启钧〕]习题解答第一章 光的干预1、波长为500nm 的绿光投射在间距d 为0.022cm 的双缝上,在距离180cm 处的光屏上形成干预条纹,求两个亮条纹之间的距离。
假设改用波长为700nm 的红光投射到此双缝上,两个亮纹之间的距离为多少?算出这两种光第2级亮纹位置的距离。
解:1500nm λ= 7011180500100.4090.022r y cm d λ-∆==⨯⨯= 改用2700nm λ= 7022180700100.5730.022r y cm d λ-∆==⨯⨯= 两种光第二级亮纹位置的距离为: 21220.328y y y cm ∆=∆-∆=2、在杨氏实验装置中,光源波长为640nm ,两狭缝间距为0.4mm ,光屏离狭缝的距离为50cm ,试求:⑴光屏上第1亮条纹和中央亮纹之间的距离;⑵假设P 点离中央亮纹为0.1mm 问两束光在P 点的相位差是多少?⑶求P 点的光强度和中央点的强度之比。
解:⑴ 7050640100.080.04r y cm d λ-∆==⨯⨯= ⑵由光程差公式210sin yr r d dr δθ=-== 0224y dr πππϕδλλ∆==⋅=⑶中央点强度:204I A = P 点光强为:221cos4I A π⎛⎫=+ ⎪⎝⎭012(10.8542I I =+=3、把折射率为1.5的玻璃片插入杨氏实验的一束光路中,光屏上原来第5级亮条纹所在的位置变为中央亮条纹,试求插入的玻璃片的厚度。
已知光波长为7610m -⨯解: 1.5n =,设玻璃片的厚度为d由玻璃片引起的附加光程差为:()1n d δ'=- ()15n d λ-= ()7645561061061010.5d m cm n λ---==⨯⨯=⨯=⨯-4、波长为500nm 的单色平行光射在间距为0.2mm 的双缝上。
通过其中一个缝的能量为另一个的2倍,在离狭缝50cm 的光屏上形成干预图样,求干预条纹间距和条纹的可见度。
济南大学大学物理3光学作业题

P57
2. 解:设I0为入射光中自然光的强度,I1、I2分别为穿过P1 和连续穿过P1、P2的强度. (1) 由题意,入射光强为2I0,
1 I 1 2 I 0 0.5 I 0 I 0 cos 2 2
cos2=1 / 2, =45° cos245°) cos2a
得 (2)
max
所以S2到P点的光束比S1到P点的光束相位落后
2π P点合振动振幅的平方为: A A 2 A cos A 2 1分 3
2 2 2
2π 2π r2 r1 3 3 2π
∴ I / Imax = A2 / 4A2 =1 / 4
2分
∵ I∝A2
1分
1
1分 1分
3
k2 e =7.78×10-4 mm 2 n
2分
P53 5. 解:加强, 2ne+ λ /2= k λ , 2分
2ne 4ne 3000 nm 1 2k 1 2k 1 k 2
2分
k = 1, λ 1 = 3000 nm, k = 2, λ 2 = 1000 nm, k = 3, λ 3 = 600 nm, k = 4, λ 4 = 428.6 nm, k = 5, λ 5 = 333.3 nm. 2分 ∴ 在可见光范围内,干涉加强的光的波长是 λ =600 nm 和λ =428.6 nm. 2分
d sin 1
P55 13.8
7.波长为λ=480.0 nm的平行光垂直照射到宽度为a=0.40 mm的单缝上,单缝后透镜的焦距为f=60 cm,当单缝两 边缘点A、B射向P点的两条光线在P点的相位差为π时, P点离透镜焦点O的距离等于____0.36 mm __.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D 光学作业解
5、21 在双缝干涉实验中,两缝间距为0、30mm,用单色光垂直照射双缝,在离缝1、20m 的屏上测得中央明纹一侧第5条暗纹与另一侧第5条暗纹的距离为22、78mm 。
问所用的波长为多少?就是什么颜色的光? 解:(杨氏双缝干涉明暗纹的级数就是从0取起,所以两侧第5条暗纹,级数为k=4±)
杨氏双缝干涉暗纹位置:(21),0,1,2,2D x k k d λ=±+=L
2(21)xd k D
λ=+ 由题意,k=4,x=11、39mm,d=0、3mm,D=1、20m,代入上式:
33
211.39100.310632.7(241) 1.20
nm λ--⨯⨯⨯⨯==⨯+⨯ 就是红光。
或:在k=4±的两条暗纹之间有9个x ∆_相邻暗纹间距(明纹一样) D x d
λ∆= 33330.301022.7810922.781022.7810632.799 1.2D d nm d
D λλ----⨯⨯⨯=⨯=⨯⨯==⨯ 就是红光。
5、22 在双缝干涉实验装置中,两个缝分别用n1=1、4与n2=1、7的厚度相等的玻璃片遮盖,在光屏上原来的中央明纹处,现在为第5级明纹所占据。
如入射的单色光波长为600nm,求玻璃片的厚度。
解:两光路光程差:2121()r r n n d δ=-+-
在光屏中央 210r r -=,现在就是第五级明纹:21()5n n d λ-=
玻璃片的厚度:9
215560010101.7 1.4
d m n n λμ-⨯⨯===-- 5、24 在折射率n 3=1、50的玻璃片上镀一层n 2=1、38的增透膜,可使波长为500nm 的光由空气垂直入射玻璃表面时尽量减少反射,则增透膜的最小厚度为多少?
解:增透膜要求反射光相消,且反射光在膜的上下表面都存在半波损失
则有 22(21),0,1,2,2n e k k λ
=+=L
取k=0,增透膜有最小厚度 9
2600100.10944 1.38e m n λ
μ-⨯===⨯ 5、25 用波长为500nm 的单色光垂直照射到由两块光学玻璃构成的空气劈形膜上。
在观察反射光的干涉现象中,距劈形膜棱边l=1、56cm 的A 处就是从棱边算起的第四条暗纹中心。
(1)求此劈形膜的劈尖角;
(2)改用600nm 的单色光垂直照射到此劈尖上仍观察反射光的干涉条纹,A 处就是明条纹还就是暗条纹? 解:(1)空气劈尖、暗纹条件 2(21),0,1,2,22ne k k λλ+=+=L
空气劈尖n=1,在棱边空气膜厚度e=0处,为k=0的零级暗纹,则第四条暗纹就就是第3级暗纹
对应第3级暗纹,空气膜的厚度 9
4333500100.751022
e cm λ--⨯⨯===⨯ 劈尖角4
430.7510arctan 0.48101.56
e rad l θ--⨯==≈⨯ (2)若改用600nm 的光垂直照射此空气劈尖:
69
920.751030010(2)/3260010e λ
λ---⨯⨯+⨯+==⨯ 光程差就是波长的整数倍,A 处就是明条纹的中心。
(3) 有三条明纹、三条暗纹。
5、32 单缝的宽度b=0、4mm,以波长589nm λ=的单色光垂直照射,设透镜的焦距f=1、0m 。
求:
(1)第一级暗纹距中心的距离,对应单缝可分半波带的数目;
(2)第二级明纹距中心的距离,对应单缝可分半波带的数目。
解:(1)利用半波带法,单缝光程差满足的暗纹条件 sin 2,1,2,32b k
k λθ=±=L 又sin tan x f θθ≈= ,1,2,3,k f x k b λ=±=L
第一级暗纹距中心的距离 913
1589101 1.470.410x mm --⨯⨯⨯==⨯ 第一级暗纹对应单缝可分半波带的数目为2k=2。
(2)同理,单缝光程差满足的明纹条件 sin (21)
,1,2,32b k k λθ=±+=L (21),1,2,3,2f
x k k b λ=±+=L
第二级明纹距中心的距离 923
5891015 3.6820.410x mm --⨯⨯=⨯=⨯⨯ 第二级明纹对应单缝可分半波带的数目:(2k+1)=5、
5、34 一单色平行光垂直入射一单缝,其衍射第三级明纹位置恰与波长为600nm 的单色光垂直入射该缝时衍射的第二级明纹位置重合,试求该单色光的波长。
解:设待求波长为1λ,2600nm λ=
由5、32题可知,单缝明纹位置 (21),1,2,3,2f
x k k b λ=±+=L
两单色光的第三级明纹与第二级明纹位置重合,即 12
33x x λλ= 121232(231)(221)22f f x x b b λλλλ=±⨯+==±⨯+
9
12156001075428.67
nm λλλ-⨯⨯=→== 5、39 波长400nm λ=的平行光,垂直投射到某透射光栅上,测得第三级衍射主极大的衍射角为30°,且第二级明纹不出现。
求:
(1)光栅常数;(2)透光缝的宽度;(3)屏幕上可能出现的全部明纹。
解:(1)由光栅方程 ()sin 0,1,2,3,a b k k θλ+=±=L
400nm λ=,k=3时θ=30° 9
340010()2400sin 0.5
k a b nm λθ-⨯⨯+=== (2)由题意,第二级主极大缺级 'a b k k a
+= 透光缝宽度最小为:当'1
21200a b k a nm a +=== (3)2π
θ=,k 有最大值:max 24006400
a b
k λ+=== 62k π
θ=±=±实际瞧不见,再考虑2,4±±缺级
屏幕上可能出现的全部明纹为0,1,3,5±±±共7条明纹。
