数电习题及答案
数字电路试题及答案

数字电路试题及答案一、选择题(每题10分,共20分)1. 下列数字电路元件中,属于组合逻辑的是A. 集线器B. 隧道二极管C. 寄存器D. D触发器答案:A2. 十进制数 8 的二进制表示形式为A. 1010B. 1110C. 1000D. 1001答案:C3. 十六进制数 B 的二进制表示形式为A. 1010B. 1101C. 1111D. 1011答案:D4. 以下哪个逻辑门的输出是其他逻辑门输出的非A. 与门B. 或门C. 非门D. 异或门答案:C二、填空题(每题10分,共20分)1. 使用 2 输入 AND 门,将 A 和 B 两个开关输入,如果 A 和 B 均为高电平时,输出为________答案:高电平2. 使用 2 输入 OR 门,将 A 和 B 两个开关输入,如果 A 和 B 中有一个或两个为高电平时,输出为________答案:高电平3. 使用 2 输入 XOR 门,将 A 和 B 两个开关输入,如果 A 和 B 中只有一个为高电平时,输出为________答案:高电平4. 使用 2 输入 NAND 门时,输出为低电平的条件是________答案:A 和 B 均为高电平三、简答题(每题20分,共40分)1. 请简述组合逻辑和时序逻辑的区别。
答案:组合逻辑是指电路的输出仅由当前时刻的输入确定,与之前的输入无关。
组合逻辑电路的输出仅取决于输入信号的组合,对于相同的输入,始终保持相同的输出。
而时序逻辑是指电路的输出除了与当前输入有关外,还与之前的输入和输出有关。
时序逻辑电路的输出不仅取决于输入信号的组合,还受到电路之前状态的影响。
2. 请简述二进制和十六进制之间的转换原理。
答案:二进制是一种基于2的数制,只有两个数位 0 和 1。
而十六进制是一种基于16的数制,包含了 0 到 9 的数字和 A 到 F 的六个字母。
进行二进制到十六进制的转换时,将二进制数按照每四位分组,然后将每个四位二进制数转换为相应的十六进制数,最终得到的十六进制数就是对应的表示。
数电试题及答案

数电试题及答案一、选择题(每题5分,共20分)1. 在数字电路中,以下哪个不是基本的逻辑门?A. 与门B. 或门C. 非门D. 异或门答案:D2. 一个触发器可以存储的二进制数是:A. 1位B. 2位C. 3位D. 4位答案:A3. 以下哪个不是组合逻辑电路的特点?A. 无记忆功能B. 输出只依赖于当前输入C. 有记忆功能D. 输出与输入的逻辑关系固定答案:C4. 一个8位二进制计数器的计数范围是:A. 0-7B. 0-15C. 0-255D. 0-511答案:C二、填空题(每题5分,共20分)1. 在数字电路中,最小的可存储单元是______。
答案:触发器2. 一个D触发器的输出Q与输入D的关系是:当时钟脉冲上升沿到来时,Q变为D的______。
答案:值3. 在数字电路中,一个4位的二进制数可以表示的最大十进制数是______。
答案:154. 一个5进制计数器的计数范围是______。
答案:0-4三、简答题(每题10分,共30分)1. 请解释什么是同步电路和异步电路,并说明它们的主要区别。
答案:同步电路是指电路中的所有触发器都由同一个时钟信号控制,从而确保所有触发器在同一时刻更新其状态。
异步电路则没有统一的时钟信号,触发器的状态更新是独立进行的,可能会因为触发器的响应时间不同而导致时序问题。
2. 什么是摩尔斯电码,它在数字通信中有什么应用?答案:摩尔斯电码是一种早期的数字编码系统,通过不同的点(短脉冲)和划(长脉冲)的组合来表示字母、数字和标点符号。
在数字通信中,摩尔斯电码用于无线电通信,因为它可以有效地在嘈杂的信道中传输信息。
3. 解释什么是寄存器,并说明它在计算机系统中的作用。
答案:寄存器是一种高速的存储设备,用于存储指令、数据或地址。
在计算机系统中,寄存器用于快速访问和处理信息,它们是CPU内部的存储单元,用于执行算术和逻辑操作。
四、计算题(每题10分,共30分)1. 假设有一个4位的二进制计数器,起始计数值为0000,每次计数增加1。
数电复习题和答案

数电复习题和答案一、选择题1. 数字电路中最基本的逻辑关系有哪几种?A. 与、或、非B. 与、异或、同或C. 与、或、异或D. 与、或、同或、非答案:D2. 以下哪个不是组合逻辑电路的特点?A. 输出只依赖于当前输入B. 输出与输入有延时C. 没有记忆功能D. 电路结构简单答案:B3. 触发器的主要功能是什么?A. 存储一位二进制信息B. 进行算术运算C. 进行逻辑运算D. 产生时钟信号答案:A二、填空题1. 一个3输入的与门,当输入都为高电平时,输出为________。
答案:高电平2. 一个D触发器的Q端在时钟信号上升沿触发时,其输出Q与输入D的关系是________。
答案:Q=D3. 一个4位二进制计数器在计数到15后,下一个状态是________。
答案:0三、简答题1. 简述什么是布尔代数,并给出一个布尔代数的基本运算规则。
答案:布尔代数是一种数学逻辑代数,用于处理二值逻辑变量的运算。
布尔代数的基本运算规则包括交换律、结合律、分配律、德摩根定律等。
2. 解释什么是时序逻辑电路,并给出一个常见的时序逻辑电路的例子。
答案:时序逻辑电路是一种包含存储元件的数字电路,其输出不仅取决于当前的输入,还取决于电路的历史状态。
常见的时序逻辑电路包括触发器、寄存器和计数器等。
四、计算题1. 给定一个逻辑表达式Y = A + B'C,使用卡诺图化简该表达式。
答案:首先绘制卡诺图,然后圈出最小项,最后写出化简后的表达式。
化简后的表达式为Y = A + B'。
五、分析题1. 描述一个简单的同步计数器的工作原理,并说明其特点。
答案:同步计数器是一种时序逻辑电路,其所有触发器的时钟输入都连接到同一个时钟信号。
工作原理是,每个时钟脉冲触发所有触发器同时更新状态。
其特点是计数速度快,计数精度高,但电路复杂度较高。
六、实验题1. 设计一个3位二进制计数器,并说明其工作原理。
答案:3位二进制计数器可以采用3个D触发器串联实现。
数电考试题及答案

数电考试题及答案一、选择题(每题2分,共20分)1. 在数字电路中,最基本的逻辑关系是:A. 与逻辑B. 或逻辑C. 非逻辑D. 异或逻辑答案:A2. 下列哪个不是数字电路的特点?A. 高速度B. 低功耗C. 高成本D. 可靠性高答案:C3. 一个D触发器具有几个输入端?A. 1B. 2C. 3D. 4答案:B4. 一个完整的数字系统通常包括哪些部分?A. 输入、处理、存储B. 输入、处理、输出C. 输入、存储、输出D. 存储、处理、输出答案:B5. 下列哪个不是组合逻辑电路的特点?A. 输出只依赖于当前输入B. 输出在输入改变后立即改变C. 有记忆功能D. 结构简单答案:C6. 一个4位二进制计数器最多能计数到:A. 15B. 16C. 255D. 1023答案:B7. 在数字电路中,逻辑门的输入端可以连接多少个其他逻辑门的输出端?A. 1个B. 2个C. 3个D. 无限制答案:D8. 一个简单的数字钟电路至少需要几个计数器?A. 1B. 2C. 3D. 4答案:B9. 逻辑门的输出电压通常分为哪两个电平?A. 高电平、低电平B. 正电平、负电平C. 直流电平、交流电平D. 标准电平、非标准电平答案:A10. 下列哪个是数字电路设计中常用的仿真软件?A. MATLABB. AutoCADC. PhotoshopD. SolidWorks答案:A二、填空题(每空2分,共20分)1. 数字电路中最基本的逻辑关系包括______、______和非逻辑。
答案:与逻辑,或逻辑2. 一个3-8译码器有______个输入端,______个输出端。
答案:3,83. 在数字电路中,常用的计数器类型包括二进制计数器、______计数器和______计数器。
答案:十进制,BCD4. 一个8位寄存器可以存储______位二进制数。
答案:85. 触发器的两个稳定状态是______和______。
答案:0,1三、简答题(每题10分,共30分)1. 请简述数字电路与模拟电路的主要区别。
数电考试题及答案

数电考试题及答案一、单项选择题(每题2分,共20分)1. 在数字电路中,最基本的逻辑运算是()。
A. 与运算B. 或运算C. 非运算D. 异或运算2. 一个逻辑门的输入端悬空时,相当于输入()。
A. 0B. 1C. 低电平D. 高电平3. 下列哪个不是组合逻辑电路的特点?()A. 输出只依赖于当前输入B. 输出与输入之间存在时延C. 输出与输入之间没有记忆功能D. 输出与输入之间存在时延4. 在数字电路中,一个触发器可以存储()位二进制信息。
A. 1B. 2C. 4D. 85. 一个4位二进制计数器可以计数的最大值是()。
A. 7B. 15C. 16D. 2556. 下列哪个不是时序逻辑电路的特点?()A. 输出不仅依赖于当前输入,还依赖于电路状态B. 具有记忆功能C. 输出与输入之间存在时延D. 输出只依赖于当前输入7. 在数字电路中,一个D触发器的输出Q与输入D的关系是()。
A. Q=DB. Q=非DC. Q=D的非D. Q=非D的非8. 一个3线-8线译码器可以译码的输入信号有()种。
A. 2B. 4C. 8D. 169. 在数字电路中,一个JK触发器可以工作在()状态。
A. 稳定状态B. 振荡状态C. 稳定状态和振荡状态D. 以上都不是10. 一个8位A/D转换器的量化步长是()。
A. 1/8B. 1/16C. 1/256D. 1/512二、填空题(每题2分,共20分)1. 在数字电路中,逻辑“与”运算的符号是___________。
2. 一个2进制计数器的计数范围是___________。
3. 一个3位二进制数可以表示的最大十进制数是___________。
4. 在数字电路中,逻辑“或”运算的符号是___________。
5. 一个4位二进制数可以表示的最大十进制数是___________。
6. 在数字电路中,逻辑“非”运算的符号是___________。
7. 一个5位二进制数可以表示的最大十进制数是___________。
数电试题及答案

数电试题及答案一、选择题1. 在数字电路中,最基本的逻辑关系有哪几种?A. 与、或、非B. 与、异或、同或C. 与、或、非、异或D. 与、或、非、同或、非门答案:C2. 下列哪个不是数字电路的特点?A. 抗干扰能力强B. 功耗低C. 运算速度快D. 模拟信号处理答案:D3. 逻辑门电路中,"0"和"1"分别代表的电压值是:A. 低电压和高电压B. 高电压和低电压C. 低电压和任意电压D. 任意电压和高电压答案:A二、填空题1. 数字电路是由_______和_______构成的电路。
答案:逻辑门;组合逻辑2. 一个基本的逻辑门至少需要_______个输入端。
答案:13. 一个完整的数字系统通常包括_______、_______和_______。
答案:输入设备;处理单元;输出设备三、简答题1. 请简述数字电路与模拟电路的区别。
答案:数字电路主要处理离散的数字信号,使用二进制逻辑来表示和处理信息,具有抗干扰能力强、功耗低、运算速度快等特点。
而模拟电路处理连续变化的模拟信号,能够模拟自然界的物理量变化,但易受干扰,运算速度相对较慢。
2. 什么是组合逻辑电路?它有哪些特点?答案:组合逻辑电路是由逻辑门组成的电路,其输出只依赖于当前的输入状态,不包含存储元件。
其特点是输出对输入具有即时响应,没有记忆功能,且输出状态的确定性使得电路设计和分析相对简单。
四、计算题1. 给定一个逻辑表达式:Y = A'B + AB',其中A和B是输入变量,Y是输出。
如果A=1,B=0,求Y的值。
答案:将A=1,B=0代入表达式,得到Y = 1'0 + 10' = 0 + 0 = 0。
2. 计算以下逻辑电路的输出Z,当A=1,B=0,C=1时。
逻辑电路表达式:Z = (A + B')(A' + B + C)答案:将A=1,B=0,C=1代入表达式,得到Z = (1 + 0')(1' + 0 + 1) = (1)(1 + 1) = 2,但由于逻辑运算中只考虑0和1,因此Z的实际值为1。
数电考试题及答案大学

数电考试题及答案大学一、选择题(每题3分,共30分)1. 在数字电路中,最基本的逻辑关系不包括以下哪一项?A. 与(AND)B. 或(OR)C. 非(NOT)D. 异或(XOR)答案:D2. 二进制数1011转换为十进制数是多少?A. 8B. 11C. 13D. 15答案:D3. 下列哪个触发器可以实现边沿触发?A. SR触发器B. JK触发器C. D触发器D. T触发器答案:C4. 在CMOS技术中,一个N型MOSFET在其栅极施加()时导通。
A. 低电平B. 高电平C. 任意电平D. 不确定答案:B5. 一个4位二进制计数器的最大计数范围是多少?A. 4B. 8C. 16D. 32答案:C6. 以下哪个是数字电路的优点?A. 高速度B. 低功耗C. 高稳定性D. 所有以上答案:D7. 在数字电路中,逻辑0通常对应于哪个电压范围?A. 0VB. 接近0VC. 接近电源电压D. 任意电压答案:B8. 一个简单的RAM存储单元通常由多少个晶体管组成?A. 4B. 6C. 8D. 16答案:A9. 在数字电路设计中,布尔代数主要用于实现什么?A. 逻辑简化B. 信号放大C. 电源管理D. 时钟分配答案:A10. 以下哪个不是数字电路中的存储元件?A. 触发器B. 寄存器C. 计数器D. 门电路答案:D二、填空题(每题4分,共20分)11. 在数字电路中,一个基本的逻辑门至少需要________个输入端。
答案:212. 一个8位的寄存器可以存储的最大十进制数是________。
答案:25513. 在TTL电路中,逻辑1的最小输出电压是________V。
答案:2.014. CMOS门电路的功耗主要取决于________。
答案:开关频率15. 一个3-8线译码器可以将3位二进制信号转换为________个独立信号。
答案:8三、简答题(每题10分,共30分)16. 解释什么是同步计数器和异步计数器,并说明它们的区别。
数电课后习题及答案

题1.1 完成下面的数值转换:(1)将二进制数转换成等效的十进制数、八进制数、十六进制数。
①(0011101)2②(11011.110)2③(110110111)2解:①(0011101)2 =1×24+ 1×23+ 1×22+ 1×20=(29)10(0011101)2 =(0 011 101)2= (35)8(0011101)2 =(0001 1101)2= (1D)16②(27.75)10,(33.6)8,(1B.C)16;③(439)10,(667)8,(1B7)16;(2)将十进制数转换成等效的二进制数(小数点后取4位)、八进制数及十六进制数。
①(89)②(1800)10③(23.45)1010解得到:①(1011001)2,(131)8,(59)16;②(11100001000) 2,(3410) 8,(708) 16③(10111.0111) 2,(27.31) 8,(17.7) 16;(3)求出下列各式的值。
①(54.2)16=()10 ②(127)8=()16 ③(3AB6)16=()4解①(84.125)10;②(57)16;③(3222312)4;题1.2 写出5位自然二进制码和格雷码。
题1.3 用余3码表示下列各数①(8)10 ②(7)10 ③(3)10解(1)1011;(2)1010;(3)0110题1.4 直接写出下面函数的对偶函数和反函数。
()()Y AB C D E C'=++()()Y AB A C C D E ''=+++ (())Y A B C D E '''=++++()Y A B C A B C '''=++解(1)(())(())(2)()(())()(())(3)(())(())(4)D D D D Y A B C D E C Y A B C D E C Y A B A C C D E Y A B AC C D E Y A BC DE Y A B C D E Y ABC A B C Y A B C A B C'''''''=+++=+++''''''''=+++=+++''''''''''=='''''''=+++=+++,,,,题1.5 证明下面的恒等式相等 ()()()()()()()()AB C B ABC A BC ABC AB B A B A BBC AD A B B D A C C D A C B D B D AB BC ''+=++''++=++=++++'''+++=+1、(AB+C)B=AB+BC=AB ( C+C')+ ( A+A')BC=ABC +ABC'+ABC + A'BC= ABC+ABC'+ A'BC 2、AB'+B+A'B=A+B+A'B=A+B+B=A+B3、左=BC+AD , 对偶式为(B+C)(A+D)=AB+AC+BD+CD 右=(A+B)(B+D) (A+C)(C+D),对偶式为: AB+AC+BD+CD 对偶式相等,推得左=右。
数电考试题及答案

数电考试题及答案一、选择题(每题1分,共10分)1. 数字电路中最基本的逻辑关系是()。
A. 与逻辑B. 或逻辑C. 非逻辑D. 异或逻辑2. 下列哪个不是数字电路的特点?()A. 抗干扰能力强B. 功耗低C. 体积小D. 工作速度慢3. 一个二进制数1011转换为十进制数是()。
A. 10B. 11C. 13D. 154. 在数字电路中,以下哪个不是基本的逻辑门?()A. 与门B. 或门C. 非门D. 放大门5. 触发器的主要用途是()。
A. 放大信号B. 存储信息C. 转换信号D. 滤波6. 一个完整的数字系统包括()。
A. 逻辑电路B. 电源C. 输入设备D. 所有选项7. 以下哪个不是数字电路的分类?()A. 组合逻辑电路B. 时序逻辑电路C. 模拟电路D. 存储电路8. 一个4位二进制计数器最多可以计数到()。
A. 8B. 16C. 32D. 649. 以下哪个是数字电路的优点?()A. 易受干扰B. 集成度高C. 功耗大D. 灵活性差10. 一个简单的数字钟至少需要多少个触发器?()A. 1B. 2C. 4D. 6二、填空题(每空1分,共10分)1. 数字电路中,最基本的逻辑运算包括________、________和________。
2. 一个二进制数1101转换为十进制数是________。
3. 触发器的两个稳定状态是________和________。
4. 一个数字电路系统由________、________和________组成。
5. 一个4位二进制计数器的计数范围是________到________。
三、简答题(每题5分,共20分)1. 简述数字电路与模拟电路的区别。
2. 解释什么是组合逻辑电路和时序逻辑电路。
3. 描述数字电路中的触发器是如何工作的。
4. 什么是数字电路的抗干扰能力?四、计算题(每题10分,共20分)1. 给定一个二进制数101101,转换为十进制数是多少?2. 如果一个数字钟使用4位二进制计数器,计算它的计数周期是多少秒?(假设时钟频率为1Hz)五、综合题(每题15分,共30分)1. 设计一个简单的数字电路,实现两个输入信号A和B的异或逻辑功能。
数电习题及答案
一、时序逻辑电路与组合逻辑电路不同,其电路由 组合逻辑电路 和 存储电路(触发器)两部分组成。
二、描述同步时序电路有三组方程,分别是 驱动方程 、状态方程 和 输出方程 。
三、时序逻辑电路根据触发器的动作特点不同可分为 同步时序逻辑电路和 异步时序逻辑电路 两大类。
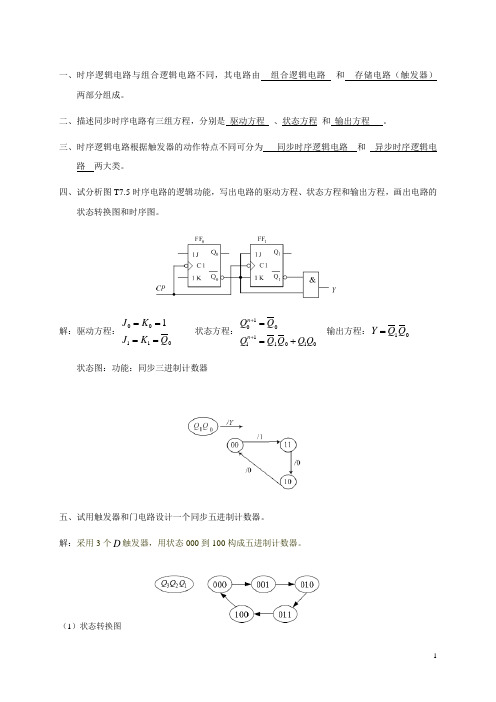
四、试分析图T7.5时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图和时序图。
解:驱动方程:001101J K J K Q ==== 状态方程:100111010n n Q Q QQ Q Q Q ++==+ 输出方程:10Y Q Q =状态图:功能:同步三进制计数器五、试用触发器和门电路设计一个同步五进制计数器。
解:采用3个D 触发器,用状态000到100构成五进制计数器。
(1)状态转换图(2)状态真值表状态转 换顺序 现 态次态进位输出2Q 1Q 0Q12+n Q 11+n Q 1+n Q YS 0 S 1 S 2 S 3 S 40 0 00 0 1 0 1 0 0 1 1 1 0 00 0 1 0 1 0 0 1 1 1 0 0 0 0 00 0 0 0 1(3)求状态方程(4)驱动方程 (5)逻辑图(略)[题7.1] 分析图P7.1所示的时序电路的逻辑功能,写出电路驱动方程、状态转移方程和输出方程,画出状态转换图,并说明时序电路是否具有自启动性。
解:触发器的驱动方程2001021010211J Q K J Q J Q Q K Q K ====⎧⎧⎧⎨⎨⎨==⎩⎩⎩ 触发器的状态方程120011010112210n n n Q Q Q Q Q Q Q Q Q Q Q Q +++==+=⎧⎪⎪⎨⎪⎪⎩输出方程 2Y Q = 状态转换图如图A7.1所示所以该电路的功能是:能自启动的五进制加法计数器。
[题7.3] 试分析图P7.3时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,并检查电路能否自启动。
大学数电测试题及答案

大学数电测试题及答案一、选择题(每题2分,共20分)1. 在数字电路中,最基本的逻辑运算是:A. 与运算B. 或运算C. 非运算D. 异或运算答案:A2. 以下哪个不是数字电路的组成部分?A. 逻辑门B. 触发器C. 电阻D. 电容器答案:C3. 一个基本的RS触发器由几个逻辑门组成?A. 1个B. 2个C. 3个D. 4个答案:B4. 在数字电路中,一个D触发器的输出在时钟脉冲的哪个时刻更新?A. 上升沿B. 下降沿C. 任何时刻D. 时钟脉冲的中间时刻答案:A5. 以下哪个是组合逻辑电路的特点?A. 有记忆功能B. 输出只依赖于当前输入C. 输出依赖于历史输入D. 需要时钟信号答案:B6. 一个4位二进制计数器的最大计数是:A. 8B. 16C. 32D. 64答案:B7. 在数字电路中,一个锁存器与一个触发器的主要区别是什么?A. 锁存器可以保持数据,触发器不能B. 触发器可以保持数据,锁存器不能C. 锁存器和触发器没有区别D. 锁存器需要外部时钟信号,触发器不需要答案:B8. 以下哪个逻辑门可以实现逻辑非运算?A. 与门B. 或门C. 非门D. 异或门答案:C9. 一个典型的二进制加法器可以处理的最大输入是:A. 0和1B. 1和0C. 1和1D. 0和0答案:C10. 在数字电路中,一个寄存器的主要功能是什么?A. 进行算术运算B. 存储数据C. 产生时钟信号D. 转换模拟信号为数字信号答案:B二、填空题(每题2分,共20分)1. 在数字电路中,逻辑“1”通常表示为电压______。
答案:高电平2. 一个完整的数字系统通常包括输入设备、______和输出设备。
答案:处理单元3. 一个8位二进制数可以表示的最大十进制数是______。
答案:2554. 在数字电路中,一个计数器的进位输出通常在计数到______时发生。
答案:最大值5. 一个典型的二进制减法器在减法运算中使用的是______。
数电考试题及答案

数电考试题及答案一、选择题1. 以下哪种数字系统不是使用“0”和“1”来表示数值的?A. 二进制 (B. 十进制C. 八进制D. 十六进制)2. 在逻辑电路中,与门的输出信号只有在________都是高电平时才为高电平。
A. 所有输入端 (B. 任意一个输入端C. 两个输入端D. 没有输入端)3. 下面哪个元器件可以储存数字数据?A. 反相器 (B. 与门C. 键盘D. 线性放大器)4. 在 TTL 逻辑门电路中,晶体管工作在________工作区。
A. 放大 (B. 饱和C. 过饱和D. 切断)5. 在数字系统中,流水线的作用是:A. 加快运算速度 (B. 储存数据C. 降低功耗D. 过滤噪声)二、填空题1. 二进制数101010的十进制表示为________。
2. 用两个2-4译码器可以实现一个________译码器。
3. 用逻辑门实现与非门时,可以将输入端连在一起,通过_______门的输出,再经过一次_______门得到与非门的输出。
4. 在组合逻辑电路中,输出仅和_______有关。
5. 在时序逻辑电路中,输出不仅和_______有关。
三、简答题1. 简述同步计数器和异步计数器的工作原理和区别。
2. 什么是门电路的逻辑功能?简述与门、或门和非门的逻辑功能及其真值表。
3. 解释存储器的读写过程,并简述静态存储器和动态存储器的区别。
4. 请解释卡诺图,并给出一个实际应用的例子。
5. 解释数字系统中的逻辑运算,并给出一个例子说明。
【答案部分】一、选择题1. B2. A3. C4. B5. A二、填空题1. 423. 与门,反相器4. 输入5. 当前状态和输入三、简答题1. 同步计数器在所有触发器的CLK输入端连在一起,采用同步时钟信号驱动,所有触发器的状态同时改变;而异步计数器则不需要同步时钟信号,每个触发器的CLK输入端独立控制。
二者的区别在于输入的控制方式不同。
2. 与门的逻辑功能是只有当所有输入端都为高电平时,输出才为高电平;或门的逻辑功能是只要有一个输入端为高电平,输出就为高电平;非门的逻辑功能是输入端电平取反,即高变低、低变高。
数字电子技术试题及答案

数字电子技术试题及答案一、单项选择题(每题2分,共20分)1. 在数字电路中,最基本的逻辑关系是:A. 与逻辑B. 或逻辑C. 非逻辑D. 异或逻辑2. 下列哪个不是数字电路的特点:A. 抗干扰能力强B. 集成度高C. 功耗高D. 可靠性高3. 一个3输入的与门,当所有输入都为高电平时,输出为:A. 低电平B. 高电平C. 悬空D. 随机状态4. 在数字电路设计中,以下哪个不是常用的逻辑门:A. NAND门B. NOR门C. XOR门D. AND-OR-NOT门5. 一个D触发器的初始状态为0,当输入D=1时,时钟信号上升沿触发后,Q端的输出状态为:A. 0B. 1C. 保持不变D. 翻转6. 在数字电路中,计数器的主要功能是:A. 放大信号B. 存储信息C. 计数和分频D. 逻辑判断7. 下列哪个不是触发器的类型:A. SR触发器B. JK触发器C. D触发器D. 三态触发器8. 在数字电路中,一个4位二进制计数器最多可以计数到:A. 4B. 8C. 16D. 329. 一个简单的数字钟电路至少需要多少个计数器:A. 1B. 2C. 3D. 410. 在数字电路中,以下哪个不是同步计数器的特点:A. 所有触发器的时钟信号同步B. 计数速度快C. 结构复杂D. 计数精度高答案:1-5 B A B B B;6-10 C D C B C二、多项选择题(每题3分,共15分)1. 数字电路中常用的逻辑门包括:A. 与门B. 或门C. 非门D. 异或门E. 同或门2. 下列哪些是数字电路的优点:A. 集成度高B. 功耗低C. 抗干扰能力强D. 易于实现大规模集成E. 易于设计和测试3. 触发器的类型包括:A. SR触发器B. JK触发器C. D触发器D. T触发器E. 三态触发器4. 计数器的计数方式包括:A. 同步计数B. 异步计数C. 双向计数D. 递增计数E. 递减计数5. 以下哪些是数字电路设计中常用的优化方法:A. 逻辑简化B. 门电路优化C. 布局优化D. 时序优化E. 电源管理优化答案:1 ABCDE;2 ABCDE;3 ABCD;4 ABCE;5 ABCDE三、填空题(每空1分,共10分)1. 在数字电路中,最基本的逻辑关系包括______、______和非逻辑。
数字电子技术试题及答案

数字电子技术试题及答案一、选择题(每题2分,共20分)1. 在数字电路中,逻辑“与”门的输出为高电平的条件是:A. 所有输入均为高电平B. 至少有一个输入为高电平C. 所有输入均为低电平D. 至少有一个输入为低电平答案:A2. 下列哪个不是组合逻辑电路的特点?A. 输出只依赖于当前的输入B. 输出与输入之间存在时间延迟C. 没有存储功能D. 电路结构简单答案:B3. 在数字电路中,一个D触发器的初始状态为Q=0,当输入D=1时,触发器的输出Q变为:A. 0B. 1C. 保持不变D. 无法确定答案:B4. 以下哪个不是数字电路中常用的逻辑门?A. 与门B. 或门C. 非门D. 异或门答案:D5. 在数字电路中,一个JK触发器的J=0,K=1时,触发器的状态会发生:A. 保持不变B. 翻转C. 置0D. 置1答案:B6. 下列哪个不是数字电路中的编码方式?A. 二进制编码B. 格雷码C. 十进制编码D. 奇偶校验码答案:C7. 在数字电路中,一个计数器的计数范围是2^n,那么该计数器的位数是:A. nB. n-1C. n+1D. 2n答案:A8. 一个4位的二进制计数器,从0000开始计数,当计数到1111时,下一个状态是:A. 0000B. 1000C. 0001答案:A9. 在数字电路中,一个移位寄存器的移位方向是:A. 左移B. 右移C. 双向移位D. 随机移位答案:C10. 以下哪个不是数字电路中的触发器类型?A. SR触发器B. JK触发器C. D触发器D. 与非门答案:D二、填空题(每题2分,共20分)1. 在数字电路中,一个3输入的或门,当输入为100时,输出为________。
答案:12. 如果一个触发器的Q输出为0,那么它的非Q输出为________。
答案:13. 在数字电路中,一个T触发器的T输入为1时,触发器的状态会________。
答案:翻转4. 在数字电路中,一个同步计数器的计数速度比异步计数器的计数速度________。
数电习题(含答案)

一、选择题1.一位十六进制数可以用 C 位二进制数来表示。
A . 1B . 2C . 4D . 162.十进制数25用8421BCD 码表示为 B 。
A .10 101B .0010 0101C .100101D .101013.以下表达式中符合逻辑运算法则的是 D 。
A.C ·C=C 2B.1+1=10C.0<1D.A+1=14. 当逻辑函数有n 个变量时,共有 D 个变量取值组合?A. nB. 2nC. n 2D. 2n5.F=A B +BD+CDE+A D= A 。
A.D B A + B.D B A )(+ C.))((D B D A ++ D.))((D B D A ++6.逻辑函数F=)(B A A ⊕⊕ = A 。
A.BB.AC.B A ⊕D. B A ⊕7.A+BC= C 。
A .A +B B.A +C C.(A +B )(A +C ) D.B +C8.在何种输入情况下,“与非”运算的结果是逻辑0。
DA .全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是19.在何种输入情况下,“或非”运算的结果是逻辑0。
BCDA .全部输入是0 B.全部输入是1 C.任一输入为0,其他输入为1 D.任一输入为110. N 个触发器可以构成能寄存 B 位二进制数码的寄存器。
A.N -1B.NC.N +1D.2N 11.一个触发器可记录一位二进制代码,它有 C 个稳态。
A.0B.1C.2D.312.存储8位二进制信息要 D 个触发器。
A.2B.3C.4D.813.对于T 触发器,若原态Qn=1,欲使新态Qn+1=1,应使输入T= A 。
A.0B.1C.QD.Q14.对于D 触发器,欲使Q n +1=Q n,应使输入D = C 。
A.0 B.1 C.Q D.Q15.对于J K 触发器,若J =K ,则可完成 C 触发器的逻辑功能。
A.R SB.DC.TD.T ˊ16.为实现将J K 触发器转换为D 触发器,应使 A 。
数电试题及答案

数电试题及答案第一题:选择题1. 二进制数1101对应的十进制数是:a. 9b. 11c. 13d. 15答案:c. 132. 在减法运算电路中使用的补码是为了:a. 简化电路设计b. 提高计算速度c. 实现负数的表示d. 实现浮点数的表示答案:c. 实现负数的表示3. 一个JK触发器在CP=1的时候,J=1,K=0,则在时钟信号下触发器状态将:a. 保持不变b. 清零c. 置1d. 取决于触发器的初始状态答案:a. 保持不变4. 一个带有使能引脚的逻辑门元件,在使能引脚为高电平时,输出始终为:a. 低电平b. 高电平c. 不确定d. 取决于输入信号答案:c. 不确定5. 一个8位寄存器的存储容量是:a. 8个字节b. 64个字节c. 8个位d. 64个位答案:c. 8个位第二题:填空题1. 用JK触发器构成的2位二进制计数器,下一个状态从00到01的时候,J和K的取值分别为______。
答案:J = 1, K = 02. 对于二进制补码,最高位为符号位,0表示正数,1表示负数。
那么10100001的十进制值为_______。
答案:-953. 将十进制数57转换为二进制数,需要______位二进制数来表示。
答案:64. 在门电路中,与门的输出为1当且仅当_______。
答案:所有输入的逻辑值都为1第三题:计算题1. 设有2个8位二进制数A和B,求A和B的和,并将结果转换为十进制。
请给出计算过程和结果。
解答:A = 11001010B = 00111101首先进行二进制加法,从最低位开始逐位相加:1 1 0 0 1 0 1 0 (A)+ 0 0 1 1 1 1 0 1 (B)------------------------1 0 0 0 0 1 1 1 1 (求和结果)将二进制求和结果转换为十进制:10000111 = 135所以A和B的和为135。
2. 设有一个4位二进制数补码操作,求该数的补码。
数电试题及答案

数电试题及答案一、选择题(每题2分,共20分)1. 在数字电路中,最基本的逻辑运算有哪几种?A. 与、或、非B. 与、或、异或C. 与、或、同或D. 与、或、非、异或2. 下列哪个不是数字电路的特点?A. 离散性B. 可编程性C. 模拟性D. 可重复性3. 触发器的主要用途是什么?A. 存储一位二进制信息B. 进行算术运算C. 进行逻辑运算D. 放大信号4. 以下哪个不是组合逻辑电路的特点?A. 输出只依赖于当前输入B. 输出可以延迟于输入C. 没有记忆功能D. 可以进行复杂的逻辑运算5. 以下哪个是同步计数器的特点?A. 所有触发器的时钟输入端连接在一起B. 计数过程可以异步进行C. 计数速度慢D. 计数精度低二、填空题(每空1分,共10分)6. 数字电路中最基本的逻辑门是_________、_________、_________。
7. 一个4位二进制计数器可以表示的最大十进制数是_________。
8. 一个D触发器具有_________个稳定状态。
9. 在数字电路设计中,_________是用于描述电路逻辑功能的图形符号。
10. 一个完整的数字钟电路至少需要_________个计数器。
三、简答题(每题5分,共20分)11. 简述数字电路与模拟电路的主要区别。
12. 解释什么是同步时序逻辑电路,并给出一个常见的同步时序逻辑电路的例子。
13. 说明什么是寄存器,并描述其在数字系统中的作用。
14. 什么是二进制计数器?简述其工作原理。
四、计算题(每题10分,共20分)15. 给定一个由与门、或门和非门组成的电路,输入A=0, B=1, C=0,D=1,请计算输出结果。
16. 设计一个3位二进制计数器,并给出其状态转移图和时序图。
五、设计题(每题15分,共30分)17. 设计一个简单的数字频率计,要求能够测量输入信号的频率,并在七段显示器上显示结果。
18. 设计一个简单的数字电压表,能够测量并显示0-5V范围内的电压值。
数字电路试题及答案

数字电路试题及答案一、单项选择题(每题2分,共10分)1. 在数字电路中,最基本的逻辑门是:A. 与门B. 或门C. 非门D. 异或门答案:C2. 以下哪个不是数字电路的特点?A. 离散性B. 线性C. 确定性D. 可预测性答案:B3. 一个D触发器的输入端是:A. SB. RC. DD. Q答案:C4. 在TTL逻辑门中,高电平的最小值是:A. 0.8VB. 2.0VC. 3.5VD. 5.0V答案:A5. 以下哪个是组合逻辑电路?A. 计数器B. 寄存器C. 译码器D. 触发器答案:C二、填空题(每题2分,共10分)1. 一个标准的二进制数由______和______组成。
答案:0,12. 一个完整的触发器可以存储______位二进制信息。
答案:13. 一个4位二进制计数器可以计数到______。
答案:154. 一个8x3的译码器可以产生______个输出。
答案:85. 在数字电路中,______是最小的可识别信号单位。
答案:位三、简答题(每题5分,共20分)1. 简述数字电路与模拟电路的主要区别。
答案:数字电路处理的是离散信号,具有确定性,而模拟电路处理的是连续信号,具有不确定性。
2. 解释什么是上升沿触发。
答案:上升沿触发是指在时钟信号的上升沿(从低电平变为高电平)时,触发器会根据输入信号更新其状态。
3. 什么是同步电路和异步电路?答案:同步电路是指电路中的各个部分都由同一个时钟信号控制,而异步电路则没有统一的时钟信号,各个部分可以独立工作。
4. 描述一个典型的数字电路设计流程。
答案:数字电路设计流程通常包括需求分析、逻辑设计、电路设计、仿真测试、PCB布局布线、调试和验证。
四、计算题(每题10分,共20分)1. 给定一个逻辑表达式:Y = AB + A'C,请计算当A=0, B=1, C=0时,Y的值。
答案:Y = 0*1 + 0'*0 = 0 + 1 = 12. 一个4位二进制计数器,初始状态为0000,每次计数加1,求经过5次计数后的状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、时序逻辑电路与组合逻辑电路不同,其电路由 组合逻辑电路 和 存储电路(触发器)两部分组成。
二、描述同步时序电路有三组方程,分别是 驱动方程 、状态方程 和 输出方程 。
三、时序逻辑电路根据触发器的动作特点不同可分为 同步时序逻辑电路和 异步时序逻辑电路 两大类。
四、试分析图T7.5时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图和时序图。
解:驱动方程:001101J K J K Q ==== 状态方程:100111010n n Q Q QQ Q Q Q ++==+ 输出方程:10Y Q Q =状态图:功能:同步三进制计数器五、试用触发器和门电路设计一个同步五进制计数器。
解:采用3个D触发器,用状态000到100构成五进制计数器。
(1)状态转换图(2)状态真值表(3)求状态方程(4)驱动方程(5)逻辑图(略)[题7.1] 分析图P7.1所示的时序电路的逻辑功能,写出电路驱动方程、状态转移方程和输出方程,画出状态转换图,并说明时序电路是否具有自启动性。
解:触发器的驱动方程2001021010211J Q K J Q J Q Q K Q K ====⎧⎧⎧⎨⎨⎨==⎩⎩⎩ 触发器的状态方程120 011010112210nnnQ Q QQ Q Q Q QQ Q Q Q+++==+=⎧⎪⎪⎨⎪⎪⎩输出方程2Y Q=状态转换图如图A7.1所示所以该电路的功能是:能自启动的五进制加法计数器。
[题7.3] 试分析图P7.3时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,并检查电路能否自启动。
解:驱动方程输出方程状态方程状态转换图如图 A7.3所示01J X Q=⊕01K=10J X Q=⊕11K=10()Z X Q Q=⊕⋅10000010()nQ J Q K Q X Q Q+=+=⊕11111101()nQ J Q K Q X Q Q+=+=⊕⋅功能:所以该电路是一个可控的3进制计数器。
[题7.5] 分析图P7.5时序电路的功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,并检查电路能否自启动。
解:输出方程1202210,Y SQ Q Y Q Q Q ==驱动方程0011220021011J K J K J Q Q K SQ Q Q SQ Q ==⎧==⎪⎪=⎨⎪=⎪⎩求状态方程100111200112102102120n n n Q Q Q S Q Q Q Q SQ Q Q Q Q Q Q Q Q Q Q +++==+=+⎧⎪⎪+⎨⎪+⎪⎩ 得电路的状态转换表如表A7.5所示表A7.5输 入 现 态次 态输 出 Sn 2Q n1Qn0Q 1|n 2Q + 1n 1Q +1n 0Q + Y 1 Y 20 0 0 0 0 0 0 0 1 1 1 1 1 1 1 10 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 10 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 0 0 0 1 1 1 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1画出电路的状态转换图如图A7.5所示图A7.5逻辑功能:这是一个有两个循环的电路,0S 时实现八进制计数、2Y 为进位输出,1S =时实现六进制计数、1Y 为进位输出。
当1S =时存在2个无效态110、111,但未形成循环,电路能自启动。
[题7.6] 试用JK 触发器和门电路设计一个同步六进制加法计数器。
解:采用3个JK 触发器,用状态000到101构成六进制计数器,设电路的输出为Y 。
根据题意可列电路状态转换表如表A7.6所示状态转 换顺序现 态次态进位输出2Q 1Q 0Q12+n Q 11+n Q 1+n Q YS 0 S 1 S 2 S 3 S 4 S 50 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 10 0 1 0 1 0 0 1 1 1 0 0 1 0 1 0 0 00 0 0 0 0 1由状态表求得电路的次态和输出的卡诺图如图A7.6(a )所示,其中斜线下方是输出端Y 的值,状态101、110、111作无效态处理,用×表示。
由卡诺图得电路的状态方程和输出方程10012101011202102n n n Q Q Q Q Q Q Q Q Q Q Q Q Q Q +++==+=+⎧⎪⎪⎨⎪⎪⎩201Y Q Q Q =由状态方程可得电路的驱动方程00210102201011J K J Q Q J Q Q K Q K Q ==⎧=⎧=⎧⎪⎨⎨⎨==⎪⎩⎩⎩最后设计电路逻辑图如图A7.6(b)[题7.7] 用D 触发器和门电路设计一个十一进制计数器,并检查设计的电路能否自启动。
解:用4个下降沿D 触发器设计,设电路的进位输出为Y ,可列电路的状态转换表如表A7.7表A7.7CP 的顺序 触发器的状态输出3210Q Q Q QY0 10 0 0 0 0 0 0 10 0驱动方程°3321012221010210113001030D Q Q Q Q Q D Q Q Q Q Q Q Q D Q Q Q Q Q D Q Q Q Q ⎧=+⎪=++⎪⎨=+⎪⎪=+⎩ 输出方程31Y Q Q = 电路图略[题7.8] 试用JK 触发器设计一个可控型计数器,其状态转换图如图P7.8所示,0A =,实现8421码六进制计数;1A =,实现循环码六进制计数,并检验电路能否自启动。
解:本例所设计的计数器有一控制变量存在,设计时将控制变量作为一个逻辑变量画入电路的次态卡诺图中。
设电路的进位输出为Y ,根据题意可画出次态卡诺图如图A7.8所示图中上面两行为0M =时的状态及次态的内容,下面两行为1M =的状态及次态的内容。
电路作8421码六进制加法计数器时,110和111为无效状态视为无关项,电路作循环码路进制计数器时,000和100为无效态视为无关项。
电路的驱动方程和输出方程(设计时需用3个JK 触发器)001022100220110221J K J Q Q J A Q Q AQ AQ K Q Q K AQ Q AQ M Q ==⎧⎧⎧==+⎪⎪⎪⎨⎨⎨==⎪⎪⎪+⎩⎩⎩ 201Y Q Q Q =逻辑图略[题7.12] 四相八拍步进电机脉冲分配电路的状态转换图如图P7.12所示。
试用JK 触发器和部分门电路实现之,画出相应的逻辑电路图。
解:用触发器3Q 、2Q 、1Q 、0Q 的状态来表示步进电机四相的状态,根据题意可求得四相八拍脉冲分配电路的驱动方程为00123323232103231021J K Q Q Q J Q Q J Q Q J Q Q K Q K Q K Q ==⎧⎧⎧⎧===⎪⎪⎪⎨⎨⎨⎨===⎪⎪⎪⎩⎩⎩⎩ 逻辑电路图略1.半导体存储器从存、取功能上可以分为 只读 存储器和 随机存取 存储器两大类。
5.半导体存储器中,ROM 属于组合逻辑电路,而RAM 可归属于 时序 逻辑电路。
习题[题11.1] 假设存储器的容量为256ⅹ8位,则地址代码应取几位。
解:8。
一、可以用来暂时存放数据的器件叫 寄存器 。
二、移位寄存器除 寄存数据 功能外,还有 移位 功能。
三、某寄存器由D 触发器构成,有4位代码要存储,此寄存器必须由 4个触发器构成。
四、一个四位二进制加法计数器,由0000状态开始,问经过18个输入脉冲后,此计数器的状态为 0010 。
五、n 级环形计数器的计数长度是 n ,n 级扭环形计数器的计数长度是 2n 。
六、集成计数器的模值是固定的,但可以用 清零 法和 置数法 来改变它们的模值。
七、通过级联方式,把两片4位二进制计数器74161连接成为8位二进制计数器后,其最大模值是 256 ;将3片4位十进制计数器74160连接成12位十进制计数器后,其最大模值是 4096 。
八、设计模值为38的计数器至少需要 6 个触发器 。
[题8.3] 分析图P8.3的计数器电路,画出电路的状态转换图,说明这是多少进制计数器。
十六进制计数器74161的功能表如表8.2.2所示。
解:采用同步预置数法,31LD Q Q 。
计数器起始状态为0011,结束状态为1010,所以该计数器为八进制加法计数器。
状态转换图略。
[题8.4] 分析图P8.4的计数器电路,说明这是多少进制的计数器,并画出电路的状态转换图。
十进制计数器74160的功能表如表8.2.6所示。
解:该计数器采用异步清零法,30D R Q Q =。
计数器起始状态为0000,结束状态为1000(状态1001只是维持瞬间),所以该计数器为九进制加法计数器。
[题8.5] 试用十六进制计数器74161设计十三进制计数器,标出输入、输出端。
可以附加必要的门电路。
74161的功能表如表8.2.2所示。
解:[题8.6] 分析图P8.6的计数器在1M =和0M =时各为几进制计数器,并画出相应的状态转换图。
74161的功能表如表8.2.2所示。
解:该计数器采用同步预置数法,32LD Q Q =。
所以0M =时:起始状态为0010,结束状态为1100,所以该计数器为十一进制加法计数器。
1M =时:起始状态为0100,结束状态为1100,所以该计数器为九进制加法计数器。
状态图略。
[题8.7] 分析图P8.7的计数器在1M =和0M =时各为几进制,并画出相应的状态转换图。
74161的功能表如表8.2.2所示。
解:该计数器采用同步预置数法。
21031LD MQ Q Q MQ Q =+0M =时:起始状态为0000,结束状态为1010,所以该计数器为十一进制加法计数器。
1M =时:起始状态为0000,结束状态为0111,所以该计数器为八进制加法计数器。
状态图略。
[题8.8] 设计一个可控进制的计数器,当输入控制变量1A =时为13进制计数器,0A =时为7进制计数器。
标出计数器的输入端和进位输出端。
解:电路采用同步预置数法。
3221LD AQ Q MQ Q =+电路逻辑图如图A8.8所示[题8.11] 试分析图P8.11计数器电路的分频比(即Y 和CP 的频率比)。
74LS1610的功能表如表8.2.2所示。
解:两片计数器接成并行进位方式,其中第1片74160计数,起始状态为0000,结束状态为1001,为十进制计数器。
第2片74160计数,起始状态为0110,结束状态为1001,为四进制计数器。
