列代数式课件
合集下载
2024年新人教版七年级数学上册 3.1 第2课时 列代数式(课件)

(2)a与b的和的平方是____________;
1
x+5
2
(3)甲数为x,乙数比甲数的一半大5,则乙数是____________.
变式: 下列各项中,列出的代数式错误的是( D )
A.比a与b的积小5的数是ab-5
B.被7除商是a余数是5的数是7a+5
C.x的2倍与y除以3的差是2x-y
3
D.a,b的平方和的一半是 1 a2+b2
提疑惑:你有什么疑惑?
知识点:列代数式(重难点)
1.列代数式的意义:把问题中与数量有关的词语,用含有数字、
字母和运算符号的式子表示出来,就是列代数式.
2.列代数式的关键及注意点:列代数式的关键是抽象出实际问题
中的数量关系.列代数式时,要注意以下几点:
(1)审题,认真分析问题中有关术语的含义.例如,和、差、积、
个句子分成三层:一是 x 与 y 两数的差,二是差的一半,三
是比差的一半小2m.分清层次后很容易得到代数式 1(x-y)-
2
2m.书写过程中,层与层之间要注意适当地添加括号.
5
(4)注意运算的逆向思维.例如,某数与ab的积为5,则该数为
,
ab
问题中出现的是积,而列出的代数式却是商的形式.
注:通过“关键字词”联想代数式中的“运算符号”:
2
【题型二】根据实际问题列代数式
例2:某牧民共有牛羊120只,一只牛每天的食草量是一只羊的4
倍,若一只羊每天需要吃4千克草,设牛有x只,该牧民每天
(12x+480)
需准备_________千克草.
例3:河上游的码头甲与下游的码头乙相距s km,轮船在静水中
的速度为a km/h,水流的速度为b km/h,则轮船从甲到乙往
1
x+5
2
(3)甲数为x,乙数比甲数的一半大5,则乙数是____________.
变式: 下列各项中,列出的代数式错误的是( D )
A.比a与b的积小5的数是ab-5
B.被7除商是a余数是5的数是7a+5
C.x的2倍与y除以3的差是2x-y
3
D.a,b的平方和的一半是 1 a2+b2
提疑惑:你有什么疑惑?
知识点:列代数式(重难点)
1.列代数式的意义:把问题中与数量有关的词语,用含有数字、
字母和运算符号的式子表示出来,就是列代数式.
2.列代数式的关键及注意点:列代数式的关键是抽象出实际问题
中的数量关系.列代数式时,要注意以下几点:
(1)审题,认真分析问题中有关术语的含义.例如,和、差、积、
个句子分成三层:一是 x 与 y 两数的差,二是差的一半,三
是比差的一半小2m.分清层次后很容易得到代数式 1(x-y)-
2
2m.书写过程中,层与层之间要注意适当地添加括号.
5
(4)注意运算的逆向思维.例如,某数与ab的积为5,则该数为
,
ab
问题中出现的是积,而列出的代数式却是商的形式.
注:通过“关键字词”联想代数式中的“运算符号”:
2
【题型二】根据实际问题列代数式
例2:某牧民共有牛羊120只,一只牛每天的食草量是一只羊的4
倍,若一只羊每天需要吃4千克草,设牛有x只,该牧民每天
(12x+480)
需准备_________千克草.
例3:河上游的码头甲与下游的码头乙相距s km,轮船在静水中
的速度为a km/h,水流的速度为b km/h,则轮船从甲到乙往
3.1列代数式(3课时)PPT优质课件

两个人一共花了__(5_m_+2_m)__元,甲比乙多 花了_(5m_–_2m_) _元.
2020/12/9
12
小结:
1. 本节课我们所学的内容是什么? 2. 字母表示什么? 3. 用字母表示数有什么优越性? 4. 你能用字母表示以前所学的运算律和
计算公式吗?
2020/12/9
13
巩固练习:
书 P88练习第1,2题
根据这个关系式,可以由任意给的皮球 的高度,求得相应的弹跳高度。例如, 如果下落高度为200米,那么弹跳高度是 多少呢?
2020/12/9
6
试一试:
1.如果用a、b表示任意两个有理数,那么 加法交换律可以用字母表示为_a_+_b_=_b+_a__,
乘法交换律可以用字母表示为_a_b_=_b_a___.
(3)小强在小学六年中共攒了a元零花钱,上 中学后买文具用去b元,剩下的钱全部存入银
行,则小强可以存款__(__a_–_b__)___元。
(4)某机关原有工作人员 m 人,现精简机构,
减少20%的工作人员,则有_2__0_%__·_m_人被精简。
2020/12/9
20
例2. 结合你的生活经验对下列代数式
作出具体解释:
(1)a–b;
(2) ab
解:(1)今年小明b岁、小明爸爸a岁,小
明比他爸爸小(a–b)岁;
(2)长方形的长为a厘米,宽为b厘米, 长方形的面积是ab平方厘米。
2020/12/9
21
做一做:
下列代数式哪些书写不规范,请改正过来
1. 3x+1
2. mn–3
3. 2y
2. 4. 1b
5. a(b+c) 6. a–
2020/12/9
12
小结:
1. 本节课我们所学的内容是什么? 2. 字母表示什么? 3. 用字母表示数有什么优越性? 4. 你能用字母表示以前所学的运算律和
计算公式吗?
2020/12/9
13
巩固练习:
书 P88练习第1,2题
根据这个关系式,可以由任意给的皮球 的高度,求得相应的弹跳高度。例如, 如果下落高度为200米,那么弹跳高度是 多少呢?
2020/12/9
6
试一试:
1.如果用a、b表示任意两个有理数,那么 加法交换律可以用字母表示为_a_+_b_=_b+_a__,
乘法交换律可以用字母表示为_a_b_=_b_a___.
(3)小强在小学六年中共攒了a元零花钱,上 中学后买文具用去b元,剩下的钱全部存入银
行,则小强可以存款__(__a_–_b__)___元。
(4)某机关原有工作人员 m 人,现精简机构,
减少20%的工作人员,则有_2__0_%__·_m_人被精简。
2020/12/9
20
例2. 结合你的生活经验对下列代数式
作出具体解释:
(1)a–b;
(2) ab
解:(1)今年小明b岁、小明爸爸a岁,小
明比他爸爸小(a–b)岁;
(2)长方形的长为a厘米,宽为b厘米, 长方形的面积是ab平方厘米。
2020/12/9
21
做一做:
下列代数式哪些书写不规范,请改正过来
1. 3x+1
2. mn–3
3. 2y
2. 4. 1b
5. a(b+c) 6. a–
2024年人教版七年级数学上册 3.1 第2课时 列代数式(课件)
甲地到乙地需要行驶 240 h.
v3
汽车加快速度后可以早到
240 v
240 v 3
h.
归纳总结
从上面的例子可以看出,用字母表示数,字母 可以和数一样参与运算,从而可以用代数式把数量 或数量关系简明地表示出来,更具有一般性.
练一练
1. 某停车场的收费标准如下:中型汽车的停车费为 6 元 辆,小型汽车的停车费为 4 元辆,某天停车场内共有 45 辆中小型汽车,其中小型汽车有 a 辆. (1)单项式 4a 表示的实际意义为 a 辆小型汽车的收费 . (2) 这一天停车场共可收缴停车费多少元?
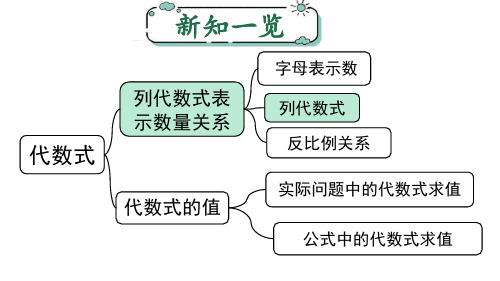
新知一览
代数式
列代数式表 示数量关系
代数式的值
字母表示数 列代数式
反比例关系 实际问题中的代数式求值
公式中的代数式求值
第三章 代数式
3.1 列代数式表示数量关系
第2课时 列代数式
教学目标
1. 学会列代数式及代数式所表示的数量关系. 2. 理解列代数式的方法和技巧. 3. 通过列代数式,培养学生抽象思维能力. 重点:正确地列代数式,并能解释代数式的实际背景
已知父亲身高 a 米,母亲身高 b 米,那么儿子和 女儿的身高有多高?
儿子身高用代数式表示为: a b 1.08
2
女儿身高用代数式表示为: 0.923a b
2
典例精析 例2 甲、乙两地之间公路全长 240 km,汽车从甲地开 往乙地,行驶速度为 v km/h. (1) 汽车从甲地到乙地需要行驶多少小时?
总结 弄清题意中数量关系的运算顺序,正确使用 括号,分出层次,逐步列出代数式.
典例精析 例1 用代数式表示: (1) 购买 2 个单价为 a 元的面包和 3 瓶单价为 b 元的饮 料所需的钱数.
3.1列代数式(3课时)精选教学PPT课件

注意:
(1)在用字母表示数时,字母与字母之间的
乘号,一般省略不写,或者乘号用“•” 表示。
如第一题中的
一般写为 或 • 。
(2)数字与字母相乘,数字一般放在字母的
前面。
(3)上面运算律中,所用到的字母 、 都
是表的字母,它代表我们过去学过的一切数。
问题二:
你能用下面的图来
解释左边3个等式 吗?
由以上规律进一步填空
此刻,我静坐在波光潋滟的水岸,看一 朵花与 风絮语 着情话 。一株 蔷薇, 幽幽一 念,就 葱茏了 一庭落 花深。 我的心 喜便从 檀香木 的光阴 里摇曳 出万种 柔肠。 有这样 的一份 心灵的 悸动, 一见红 了眼, 再见湿 了衣。 我的心 亦随着 一朵花 的绽放 而绽放 ,随着 一个人 的微笑 而暖绒 。
5. a(b+c) 6. a–1b
课堂练习:
教科书第90页练习1,2。
作业:
教科书P93习题3.1第3,4,5题。
§3.1 列 代 数 式
3. 列 代 数 式
复习提问:
1. 书写代数式要注意什么?
答: 书写代数式要注意三点(1)代数式中出现乘号, 通常写作“•”或省略不写;(2)数字与字母相乘, 数字写在字母前面;(3)除法运算写成分数形式。
试一试:
1.如果用a、b表示任意两个有理数,那么 加法交换律可以用字母表示为_a_+_b_=_b+_a__, 乘法交换律可以用字母表示为_a_b_=_b_a___.
2.图中由长方形和正方形拼 成的大正方形的面积等于 __a_²+2_ab_+b.² 我们还可以 这样想,图中大正方形的 边长是___a+_b ,因此它 的面积是___(a_+b_)²_.
列代数式 课件(共26张PPT)

第四章 代数式
4.1 列代数式
浙教版七年级上册数学
温故知新“
5cm
20cm
面积:
20× 5
cm2
数字换成字母
b (cm)
20 (cm)
面积: 20 ×
( cm2 ) 20 ·
( cm2 ) 20 ( cm2 )
a (cm)
b (cm)
2)
×
(
cm
面积:
·
( cm2 )
( + )2
平方结构
(4)2a的立方根。
3
2
开立方结构
例2. 一辆汽车以80km/h的速度行驶,
从A城到B城需t(h)。
如果该车的行驶速度增加v(km/h),
那么从A城到B城需多少时间?
A
80t (km)
B
AB=80t (km)
现在速度:(80+v)km/h,
现在从A城到B城所需时间:
80
,
4
2
2, +180这
样,
由数、表示数的字母和运算符号组成的数学表达式称为代数式
。
这里的运算是指加、减、乘、除、乘方和开方。
单独一个数或者一个字母也称代数式。
例1 用代数式表示:
(1)x的3倍与3的差;
(3x-3)
(2)x的2倍与y的
(2x+
1
y
2
1
的
2
什么结构?
差结构
和;
)
和结构
(3)a与b的和的平方;
4
2
2a
( 3 ) 一 个 五 彩 花 圃 的 形 状 如 图 , 花 圃 的 面 积 为 ______
4.1 列代数式
浙教版七年级上册数学
温故知新“
5cm
20cm
面积:
20× 5
cm2
数字换成字母
b (cm)
20 (cm)
面积: 20 ×
( cm2 ) 20 ·
( cm2 ) 20 ( cm2 )
a (cm)
b (cm)
2)
×
(
cm
面积:
·
( cm2 )
( + )2
平方结构
(4)2a的立方根。
3
2
开立方结构
例2. 一辆汽车以80km/h的速度行驶,
从A城到B城需t(h)。
如果该车的行驶速度增加v(km/h),
那么从A城到B城需多少时间?
A
80t (km)
B
AB=80t (km)
现在速度:(80+v)km/h,
现在从A城到B城所需时间:
80
,
4
2
2, +180这
样,
由数、表示数的字母和运算符号组成的数学表达式称为代数式
。
这里的运算是指加、减、乘、除、乘方和开方。
单独一个数或者一个字母也称代数式。
例1 用代数式表示:
(1)x的3倍与3的差;
(3x-3)
(2)x的2倍与y的
(2x+
1
y
2
1
的
2
什么结构?
差结构
和;
)
和结构
(3)a与b的和的平方;
4
2
2a
( 3 ) 一 个 五 彩 花 圃 的 形 状 如 图 , 花 圃 的 面 积 为 ______
3.1 第1课时 代数式 课件(共19张PPT) 人教版七年级数学上册

略
(p-0.9p)元
不一样.在(1)中,0.9p表示每千克苹果的售价,在(2)中,0.9p表示长为0.9,宽为p的长方形的面积
(3n-10)件;(n-10)件
一定是
1.请同学们指出下列各式中,哪些是代数式,哪些不是代数式? ① 2x-1;②a=1;③S=πR2;④π;⑤
①④是代数式,②③⑤不是代数式
2. 请同学们根据引言和例1、2的作答,试着说一说用字母表示数时有哪些需要注意的地方.
①数与字母相乘或字母与字母相乘时,通常将乘号写作“·”或省略不写;②数与字母相乘时,数写在前;③字母可以像数一样参与运算,相同字母相乘,结果写成幂的形式;④Байду номын сангаас果代数式是带加、减运算且须注明单位的代数式要加括号,后面注明单位;⑤式子中出现除法时一般按分数形式写
A
D
例3:小明每月从零花钱中捐出x元给希望工程,一年下来小明共捐款_______元.变式:如图,某长方形广场的四角各铺设了四分之一圆形的草地,若圆形的半径均为r m, 则草地的面积是_______m2, 空地的面积是__________m2.
【题型二】用代数式表示实际问题中的数量或数量关系
【题型三】代数式的意义及实际意义
D
解:某人以a km/h的速度骑行3 h,以b km/h的速度骑行4 h,所骑行的路程是(3a+4b)km(答案不唯一,合理即可).
1.本节课主要学习了哪些知识?2.本节课你还有哪些疑惑?说一说.
学习了代数式的概念、书写规则,代数式的意义及实际意义
同学们,大家体会到代数式的意义了吗?它能够帮助我们用更加简洁的数学语言表述数量关系,希望同学们课后好好感受.
知识点:代数式的概念及书写(重难点)
注:1.同一个代数式可以表示不同实际问题中的数量或数量关系.2.同一个问题中,相同的字母必须表示相同的量,不同的量必须用不同的字母表示.3.用字母可以表示任意数或式子.4.用字母表示数可以反映事物的规律,更具有一般性.
(p-0.9p)元
不一样.在(1)中,0.9p表示每千克苹果的售价,在(2)中,0.9p表示长为0.9,宽为p的长方形的面积
(3n-10)件;(n-10)件
一定是
1.请同学们指出下列各式中,哪些是代数式,哪些不是代数式? ① 2x-1;②a=1;③S=πR2;④π;⑤
①④是代数式,②③⑤不是代数式
2. 请同学们根据引言和例1、2的作答,试着说一说用字母表示数时有哪些需要注意的地方.
①数与字母相乘或字母与字母相乘时,通常将乘号写作“·”或省略不写;②数与字母相乘时,数写在前;③字母可以像数一样参与运算,相同字母相乘,结果写成幂的形式;④Байду номын сангаас果代数式是带加、减运算且须注明单位的代数式要加括号,后面注明单位;⑤式子中出现除法时一般按分数形式写
A
D
例3:小明每月从零花钱中捐出x元给希望工程,一年下来小明共捐款_______元.变式:如图,某长方形广场的四角各铺设了四分之一圆形的草地,若圆形的半径均为r m, 则草地的面积是_______m2, 空地的面积是__________m2.
【题型二】用代数式表示实际问题中的数量或数量关系
【题型三】代数式的意义及实际意义
D
解:某人以a km/h的速度骑行3 h,以b km/h的速度骑行4 h,所骑行的路程是(3a+4b)km(答案不唯一,合理即可).
1.本节课主要学习了哪些知识?2.本节课你还有哪些疑惑?说一说.
学习了代数式的概念、书写规则,代数式的意义及实际意义
同学们,大家体会到代数式的意义了吗?它能够帮助我们用更加简洁的数学语言表述数量关系,希望同学们课后好好感受.
知识点:代数式的概念及书写(重难点)
注:1.同一个代数式可以表示不同实际问题中的数量或数量关系.2.同一个问题中,相同的字母必须表示相同的量,不同的量必须用不同的字母表示.3.用字母可以表示任意数或式子.4.用字母表示数可以反映事物的规律,更具有一般性.
《列代数式》PPT课件 (公开课获奖)2022年华师大版 (4)

• 让我们再看几个用字母表示数的例子: • 〔1〕 如果用a、b表示任意两个有理数,那么加法交
换律可以用字母表示为:a+b=b+a. • 乘法交换律可以用字母表示为:ab=ba. • 〔2〕 图中由长方形和正方形拼成的大正方形的面积
是多少? • 容易知道: • 正方形①的面积为a2,长方形②和③的面积都为ab
经过多少秒时以C、P、Q为顶点的三角形恰 好与⊿ABC相似? A
A
Q Q
B
P
CB
P
C
如图,△PAC∽△QCB , △PCQ是等边三角形 (1)假设AP=1,BQ=4,求PQ的长. (2)求∠ACB的度数. (3)求证:AC2=AP·AB.
C
AP
Q
B
_________人被精简.
注意 (1)代数式中出现的乘号,通常写作“·”或省略不写,如 6×b 常 写作 6·b 或 6b; (2)数字与字母相乘时,数字写在字母前面,如 6b 一般不写作 b6;
(3)除法运算写成分数形式,如 1÷a 通常写作 1 a 0
a
练习
• 1. 填空: • 〔1〕a千克含盐为10%的盐水中含盐_________千克; • 〔2〕某同学军训期间打靶成绩为10环、8环、8环、7环、
课堂小结 梳理新知
• 1、本节课用字母表示数时应该注意哪些问 题?
• 2、通过本节课的学习你还有哪些收获?
如图,在△ABC中,AB>AC,D为AC边上异于A、C 的一点,过D点作一直线与AB相交于点E,使所得 到的新三角形与原△ABC相似.
问:你能画出符合条件的直线吗?
ห้องสมุดไป่ตู้
A
E
相似三角形的判定方法
解; (1)a2 b2 2ab;(2)ab2 ab2;
人教版七年级上册3.1.1 列代数式表示数量关系 课件(共16张PPT)

高是h cm,用式子表示它的体积;
a2h
(4)用式子表示数n的相反数.
n
归纳:
列式就是把实际问题中与数量有关的语句, 用含有数、字母和运算符号的式子表示出来,也 就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它 们之间的关系,如和、差、积、商及大、小、多、 少、倍、分、倒数、相反数等;
解:去年的产量是 2n 10
1.用代数式表示
(1)某种商品每袋2.8元,在一个月内的销 售量是m 袋,用式子表示在这个月内销售这种商 品的收入.
(2)圆柱体的底面半径、高分别是 r,h, 用式子表示圆柱体的体积.
2 用式子表示:
m
(1)5箱苹果重m kg,每箱重 5 kg ;
(2)一个数比a的2倍小5,则这个数
课后作业
1.课后习题2.1第一题,第二题; 2.完成练习册本课时的习题。
a3
ah 2
a b 2a 4b
字母不仅可以表示数,而且还 可以像数一样进行运算,这是代数 的一个重要特征。
例1(1)苹果原价是每千克p元,按8折优惠 出售,来自式子表示现价;0.8 p
(2)某产品前年的产量是n件,去年的产量是前 年产量的m倍,用式子表示去年的产量;
mn
例1 (3)一个长方体包装盒的长和宽都是a cm,
归纳知识点
上述问题中列出的式子 4a,
a 2,
m 3,
2, d
它们都是用运算符号把数或表示 减、乘、除、乘方、开数的字母 连接起来的式子,我们称这样的 式子为代数式。
1.若正方体的棱长为a,则正方体的体积是多少? 2.若三角形的一边长为a,并且这边上的高为h,则 这个三角形的面积是多少?
3.鸡兔同笼,鸡a只,兔b只,则共有头多少个?脚多少 只?
a2h
(4)用式子表示数n的相反数.
n
归纳:
列式就是把实际问题中与数量有关的语句, 用含有数、字母和运算符号的式子表示出来,也 就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它 们之间的关系,如和、差、积、商及大、小、多、 少、倍、分、倒数、相反数等;
解:去年的产量是 2n 10
1.用代数式表示
(1)某种商品每袋2.8元,在一个月内的销 售量是m 袋,用式子表示在这个月内销售这种商 品的收入.
(2)圆柱体的底面半径、高分别是 r,h, 用式子表示圆柱体的体积.
2 用式子表示:
m
(1)5箱苹果重m kg,每箱重 5 kg ;
(2)一个数比a的2倍小5,则这个数
课后作业
1.课后习题2.1第一题,第二题; 2.完成练习册本课时的习题。
a3
ah 2
a b 2a 4b
字母不仅可以表示数,而且还 可以像数一样进行运算,这是代数 的一个重要特征。
例1(1)苹果原价是每千克p元,按8折优惠 出售,来自式子表示现价;0.8 p
(2)某产品前年的产量是n件,去年的产量是前 年产量的m倍,用式子表示去年的产量;
mn
例1 (3)一个长方体包装盒的长和宽都是a cm,
归纳知识点
上述问题中列出的式子 4a,
a 2,
m 3,
2, d
它们都是用运算符号把数或表示 减、乘、除、乘方、开数的字母 连接起来的式子,我们称这样的 式子为代数式。
1.若正方体的棱长为a,则正方体的体积是多少? 2.若三角形的一边长为a,并且这边上的高为h,则 这个三角形的面积是多少?
3.鸡兔同笼,鸡a只,兔b只,则共有头多少个?脚多少 只?
七年级数学上册列代数式ppt课件全面版

3.将三个边长为a cm的正方体,拼成一个长方体,求这
个长方体的体积.
【解析】a3×3 =3a3 (cm3)
a aa a
a
或a×3a×a
=3a3 (cm3)
a a 3a
通过本节课的学习,同学们应 1.理解列代数式的意义. 2.能用代数式表示简单的数量关系. 3.通过列代数式体会代数式会使问题变得简洁,更具 有一般性.
(3)某数与 2 的和的3倍; 5
(4)某数的倒数与5的差.
【答案】(1) 3 x 1 2
(2)x 10% x
(3)3(x 2 )
(4) 1 5 5 x
【例2】用代数式表示:
(1)a、b两数的平方和减去它们的乘积的2倍;
(2)a、b两数的和的平方减去它们的差的平方;
(3)a、b两数的和与它们的差的乘积;
无知识的人,其生命如同无叶子的树, 缺少勃勃生机.
只要我们坚持了,就没有克服不了的困难。或许,为了将来,为了自己的发展,我们会把一件事情想得非常透彻,对自己越来越严,要求越来越高,对任何机会都不曾错过,其 目的也只不过是不让自己随时陷入逆境与失去那种面对困难不曾屈服的精神。但有时,“千里之行,始于足下。”我们更需要用时间持久的用心去做一件事情,让自己其中那小 小的浅浅的进步,来击破打破突破自己那本以为可以高枕无忧十分舒适的区域,强迫逼迫自己一刻不停的马不停蹄的一直向前走,向前看,向前进。所有的未来,都是靠脚步去 丈量。没有走,怎么知道,不可能;没有去努力,又怎么知道不能实现?幸福都是奋斗出来的。那不如,生活中、工作中,就让这“幸福都是奋斗出来的”完完全全彻彻底底的 渗入我们的心灵,着心、心平气和的去体验、去察觉这一种灵魂深处的安详,侧耳聆听这仅属于我们自己生命最原始最动人的节奏。但,这种聆听,它绝不是仅限于、执着于 “我”,而是观察一种生命状态能够扩展和超脱到什么程度,也就是那“幸福都是奋斗出来的”深处又会是如何?生命不止,奋斗不息!又或者,对于很多优秀的人来说,我们 奋斗了一辈子,拼搏了一辈子,也只是人家的起点。可是,这微不足道的进步,对于我们来说,却是幸福的,也是知足的,因为我们清清楚楚的知道自己需要的是什么,隐隐约 约的感觉到自己的人生正把握在自己手中,并且这一切还是通过我们自己勤勤恳恳努力,去积极争取的!“宝剑锋从磨砺出,梅花香自苦寒来。”当我们坦然接受这人生的终局, 或许,这无所皈依的心灵就有了归宿,这生命中觅寻处那真正的幸福、真正的清香也就从此真正的灿烂了我们的人生。一生有多少属于我们的时光?陌上的花,落了又开了,开 了又落了。无数个岁月就这样在悄无声息的时光里静静的流逝。童年的玩伴,曾经的天真,只能在梦里回味,每回梦醒时分,总是多了很多伤感。不知不觉中,走过了青春年少, 走过了人世间风风雨雨。爱过了,恨过了,哭过了,笑过了,才渐渐明白,酸甜苦辣咸才是人生的真味!生老病死是自然规律。所以,面对生活中经历的一切顺境和逆境都学会 了坦然承受,面对突然而至的灾难多了一份从容和冷静。这世上没有什么不能承受的,只要你有足够的坚强!这世上没有什么不能放下的,只要你有足够的胸襟! 一生有多少 属于我们的时光?当你为今天的落日而感伤流泪的时候,你也将错过了明日的旭日东升;当你为过去的遗憾郁郁寡欢,患得患失的时候,你也将忽略了沿途美丽的风景,淡漠了 对未来美好生活的憧憬。没有十全十美的生活,没有一帆风顺的旅途。波平浪静的人生太乏味,抑郁忧伤的人生少欢乐,风雨过后的彩虹最绚丽,历经磨砺的生命才丰盈而深刻。 见过了各样的人生:有的轻浮,有的踏实;有的喧哗,有的落寞;有的激扬,有的低回。肉体凡胎的我们之所以苦恼或喜悦,大都是缘于生活里的际遇沉浮,走不出个人心里的 藩篱。也许我们能挺得过物质生活的匮乏,却不能抵挡住内心的种种纠结。其实幸福和欢乐大多时候是对人对事对生活的一种态度,一花一世界,一树一菩提,就是一粒小小的 沙子,也有自己精彩的乾坤。如果想到我们终有一天会灰飞烟灭,一切象风一样无影亦无踪,还去争个什么?还去抱怨什么?还要烦恼什么?未曾生我谁是我?生我之时我是谁? 长大成人方是我,合眼朦胧又是谁?一生真的没有多少时光,何必要和生活过不去,和自己过不去呢。你在与不在,太阳每天都会照常升起;你愁与不愁,生活都将要继续。时
3.1-列代数式-课件(共52张)

_________平π方r米2
第五关(500分)
判断题:如果王红用t小时走完的路程为s千米, 那么她的速度为st千米/小时( ) ×
第17页,共52页。
第六关(600分)
选择题:某粮店购进一批大豆,出售时要在进价的基 础上加适当的利润,其出售数量x与售价y的关系(guān xì) 如下表:
数量x 1
如“大”、“小”、“多”、“少”、“和”、“
“倍”、“商”、“倒”数“平方差“、”余数“
”平方“、”立方“、”增加”等等;
第46页,共52页。
(2)正确判断各种数量关系中的运算顺序:
通常是先读的先写,后读的运算后写,并且 正确对待遵循运算顺序(先乘方,后乘除,
最后加减)和运算括号(先括号内,后括 号外;先小括号,再中括号 ,最后大括号)
他最多能买这种钢笔 33支.
第22页,共52页。
我们把像 4a,a2,360(x+y),
2+t,166-5n,-st , 33
代数式 这样 的式子,称为 (zhèyàng)
。
观察以上各式有什么共同特征点?
注 意
单独一个数或一个字母也是代数式。
第23页,共52页。
指出下列各式中哪些(nǎxiē)是代数式,哪些(nǎxiē)不是代数式
2
3
4
…
(千克)
售价y 4+0.6 8+1.2 12+1.8 16+2.4 … (元)
下面用数量x表示售价y的公式中,正确的是( B )
A、y=4x+0.6
C、y=4+0.6x
B、y=(4+0.6)x
D、y=4+0.6+x
第五关(500分)
判断题:如果王红用t小时走完的路程为s千米, 那么她的速度为st千米/小时( ) ×
第17页,共52页。
第六关(600分)
选择题:某粮店购进一批大豆,出售时要在进价的基 础上加适当的利润,其出售数量x与售价y的关系(guān xì) 如下表:
数量x 1
如“大”、“小”、“多”、“少”、“和”、“
“倍”、“商”、“倒”数“平方差“、”余数“
”平方“、”立方“、”增加”等等;
第46页,共52页。
(2)正确判断各种数量关系中的运算顺序:
通常是先读的先写,后读的运算后写,并且 正确对待遵循运算顺序(先乘方,后乘除,
最后加减)和运算括号(先括号内,后括 号外;先小括号,再中括号 ,最后大括号)
他最多能买这种钢笔 33支.
第22页,共52页。
我们把像 4a,a2,360(x+y),
2+t,166-5n,-st , 33
代数式 这样 的式子,称为 (zhèyàng)
。
观察以上各式有什么共同特征点?
注 意
单独一个数或一个字母也是代数式。
第23页,共52页。
指出下列各式中哪些(nǎxiē)是代数式,哪些(nǎxiē)不是代数式
2
3
4
…
(千克)
售价y 4+0.6 8+1.2 12+1.8 16+2.4 … (元)
下面用数量x表示售价y的公式中,正确的是( B )
A、y=4x+0.6
C、y=4+0.6x
B、y=(4+0.6)x
D、y=4+0.6+x
列代数式.课件(共13张PPT)

(3)浓缩原题,分段处理,即在比较复杂的语句中,一般会有 多个“的”字出现.列代数式时,可抓住各个 “的”字将句 子分为几个层次,逐步列出代数式.
1. 用代数式表示数量关系: 易错警示:列代数式的关键是要分析数量关系,
能准确地把文字语言翻译成数学语言. 2. 用代数式表示数、几何关系.
第2章 整式及其加减
复习导入 例题讲解 课堂小结
获取新知 随堂演练
复习导入
问题:代数式的定义是什么?
由数或表示数的字母用运算符号(加、减、乘、除 及乘方等)连接所成的式子,叫做代数式. 单独的一个数或一个字母也是代数式.
思考:你能利列代数式解决实际问题吗?
代数式的 书写要求 有哪些呢?
获取新知
(1)、(2) 小题必须认真 读题,理清运
算顺序.
所以,所有偶数和所有奇数可分别表示为:
2n(n为整数),2n+1(n为整数).
随堂演练
1.用代数式表示: (1) a与b的差的2倍; (2) a与b的2倍的差; (3) a与b、c两数之和的差; (4) a、b两数的差与c的和.
解:(1)2(a-b) . (3)a-(b+c).
【做一做】 某地区夏季高山上的气温从山脚处开始每升高100m
降低0.6℃.如果山脚处的气温为28℃,那么比山脚高300m处 的气温为___2_6_._2_℃____. 一般地,比山脚高x m处的气温
为___2__8-___10_0.6_0_x__℃___.
用代数式表示数量关系
在解决实际问题时,常常先把问题中有关的数 量用代数式表示出来,即列出代数式,使问题变得简 洁,更具一般性.
(2)a-2b. (4)(a-b)+c.
2.用代数式表示: (1) x与y两数的差的平方; (2)比x的平方的5倍少2的数; (3)某商品的原价是a元,提价10%后的价格; (4)比a除以b的商的2倍少4的数.
相关主题
