圆锥曲线知识要点与结论个人总结

合集下载

圆锥曲线知识要点及结论个人总结

《圆锥曲线》知识要点及重要结论一、椭圆1定义平面内到两定点 F 「F 2的距离的和等于常数 2a(2^|F^2)的点P 的轨迹叫做椭圆•若2a = F ,F 2，点P 的轨迹是线段F I F 2・若0 ：：： 2a ：：： F ,F 2，点P 不存在•2 2务与=1(a b 0)，两焦点为 R (_c,0), F 2(c,0). a b2 2=1(a b ■ 0)，两焦点为 F i (0,_c), F 2(0,C ).其中 a 2"2 cla b3几何性质椭圆是轴对称图形，有两条对称轴 .椭圆是中心对称图形，对称中心是椭圆的中心椭圆的顶点有四个，长轴长为2a ，短轴长为2b ，椭圆的焦点在长轴上•2 2若椭圆的标准方程为务•与=1(a b ■ 0)，则- a 空x 空a, -b 曲乞b ； a b2 2若椭圆的标准方程为=1(a b 0)，则-b 辽x 乞b,-a y 乞a .a 2b 2二、双曲线1定义平面内到两定点 F 1, F 2的距离之差的绝对值等于常数 2a(0 ：：： 2a ：：：R F ?)的点的轨迹叫做双曲线.若2^|F 1F 2，点P 的轨迹是两条射线.若2^|F 1F 2，点P 不存在.2 22 标准方程务—£=1(a ■ 0,b0)，两焦点为 F 1(-c,0), F 2(C ,0).a b2 2令…占二“ 0,b 0)，两焦点为 F 1 (0^c ), F 2(0, c ).其中 c 2 二 a 2 b 2. a b3几何性质双曲线是轴对称图形，有两条对称轴；双曲线是中心对称图形，对称中心是双曲线的中心双曲线的顶点有两个 A 1, A 2，实轴长为2a ，虚轴长为2b ，双曲线的焦点在实轴上2 2J 壬-1(a 0,b 0)，则 x 乞-a 或x — a, y R ；a b2-牛=1(a 0,b 0)，则 y — -a 或 y — a, x R .b 22标准方程若双曲线的标准方程为若双曲线的标准方程为2a4渐近线双曲线的渐进线是它的重要几何特征，每一双曲线都对应确定双曲线的渐进线, 组渐进线却对应无数条双曲线 .2 2 2 2与双曲线笃-与 "(a 0,b ■ 0)共渐进线的双曲线可表示为笃-笃二a ba b定要“消元后的方程的二次项系数=0”和“ .0”同时成5等轴双曲线：实轴长等于虚轴长的双曲线叫做等轴双曲线2 2 2 2等轴双曲线的标准方程为笃一爲=1(a . 0)或爲-笃=1(a .0).a aa a等轴双曲线的渐近线方程为 y= x .6共轭双曲线：实轴为虚轴，虚轴为实轴的双曲线互为共轭双曲线2 2 2 2如：笃-Xr =1(a 0,b - 0)的共轭双曲线为 Xr =1(a 0,b - 0)，它们的焦点到 a b b ax 禾廿y = _ a三、抛物线1定义平面内与一个定点 F 和一条定直线l(F 不在I 上)的距离相等的点的轨迹叫做抛物线•定点F 叫做抛物线的焦点，定直线 I 叫做抛物线的准线• 2标准方程(1) y 2=2px(p>0)，焦点为(#,0)，准线方程为x =—号，抛物线张口向右.⑵ y 2- -2px(p0)，焦点为(-号,0)，准线方程为x =号，抛物线张口向左•⑶x 2=2py(p0)，焦点为硝) ，准线方程为y = 一号，抛物线张口向上.⑷X 2 = -2 py (p 0)，焦点为 (0,诗) ，准线方程为y 二号，抛物线张口向下. 其中p 表示焦点到准线的距离. 3几何性质2 2 双曲线x y2-.2ab2 2yx 2.2 a b=1( a 0, b 0)有两条渐近线y=1( a 0, b 0)有两条渐近线y a a x 和yx .即b b 2 2 x y=02■ 2ab22yx2.2ab但对于同直线与双曲线有两个交点的条件,原点的距离相等，因而在以原点为圆心,..a 2 b 2为半径的圆上•且它们的渐近线都是双曲线抛物线是轴对称图形，有一条对称轴.若方程为『=2px(p .0)或y = _2px(p ■ 0),则对称轴是x 轴，若方程为x 2 =2py(p . 0)或x 2 =_2py(p 0)，则对称轴是y 轴.若抛物线方程为 2y = 2 px( p . 0)，则 x _ 0, y R . 若抛物线方程为 2y - -2 px( p - 0)，则 x _ 0, y R . 若抛物线方程为 x = 2 py( p . 0)，则 y _ 0,x R .若抛物线方程为 x = -2py (p 0)，则 y _ 0, x R .圆锥曲线的一些重要结论【几个重要结论】2 21已知椭圆笃•与 "(a b 0)的两焦点为Fj-cQEgO)，P(x 0,y 0)为椭圆上一a b点，则 PF 」=J(x ° +c)2 +y ； = J(x ° +c)2 +b 2(1 —爭)ms 丿丿cx 0 cx 0因为一a 乞 x 0 乞 a ， -c 0 _ c,0 ：：： a -c 0a c ，aa所以 PF^-cx°+a .同理，PF 2 =2a — PF,| =a —绝.aa2 2已知双曲线务-占-1(a 0,b 0)的左、右焦点分别为Fj-cQ), F 2(C ,0) ,P(x 0,y 0)为a b双曲线上一点，则PF 1， PF 2 = 也—aaa2 22椭圆 J 七=1(a b 0)的两焦点为F I ,F 2，P 为椭圆上一点，若• F 1PF 2 7，则 a bb 2 sin ： ’ 2 丄 b tan 1 cos ： 2解：根据椭圆的定义可得 PR + PF 2 =2a ①c X 。

圆锥曲线知识要点及结论个人总结

圆锥曲线知识要点及结论个人总结《圆锥曲线》知识要点及重要结论一、椭圆1定义平面内到两定点F 1,F 2的距离的和等于常数2a(2a • F I F 2)的点P 的轨迹叫做椭圆.若2a =日F ?，点 P 的轨迹是线段RF 2.若0 2a 证，点P 不存在.2 2 ____________________________________________2标准方程笃書l(a b O)，两焦点为a bF !(-C ,0),F 2(C ,0).3几何性质椭圆是轴对称图形，有两条对称轴•椭圆是中心对称图形，对称中心是椭圆的中心•椭圆的顶点有四个，长轴长为2a ，短轴长为2b ，椭圆的焦点在长轴上•、亠 2 2若椭圆的标准方程为与占"(a b • 0)，贝Va b-a三a, —b 三 y ；、 , 2 2若椭圆的标准方程为占討"(a b • 0)，贝Va b-b _x_b, -a -y - a.二、双曲线2 2 ______________________________________■y r £ =1(a b 0)，两焦点为a bF,0, _c), F 2(0,C ). 中 a 2二 b 2c 2.1定义平面内到两定点E,F2的距离之差的绝对值等于常数2a(0 2a F,F2)的点的轨迹叫做双曲线若2a=F i F z|，点P的轨迹是两条射线.若2a>|RF2 ,点P 不存在•2标准方程笃-爲=Ka 0，b 0），两焦点为 a b2 2 ______________________________________________F'-cOFGO）.笃一与=1（a 0,b 0），两焦点为F1（0^c）,F2（0,c）.其中 a bc2 =a2 +b2■3几何性质双曲线是轴对称图形，有两条对称轴；双曲线是中心对称图形，对称中心是双曲线的中心. 双曲线的顶点有两个AA，实轴长为2a，虚轴长为2b，双曲线的焦点在实轴上.2 2若双曲线的标准方程为务一％=1（a 0,b 0），则a bx _ -a或x _ a, y R ；若双曲线的标准方程为N-写=Ka 0,b 0），则a by 兰—a或y Ka, x w R .4渐近线双曲线务-占T（a 0，b 0）有两条渐近线y=b x和y二一 5a b a a2 2 __________________________________________双曲线^~2 -^-2=1(a 0，b 0)有两条渐近线y =^x和y —bxa bbb双曲线的渐进线是它的重要几何特征，每一双曲线都对应确定双曲线的渐进线，但对于同一组渐进线却对应无数条双曲线.2 2笃—^Ja 0,b 0）共渐进线的双曲线可表a b_2 2示为笃（，0）・a b直线与双曲线有两个交点的条件，一定要“消元后的方程的二次项系数-0 ”和“0”同时成立 5等轴双曲线：实轴长等于虚轴长的双曲线叫做等轴双曲线.2 2等轴双曲线的标准方程为丄2壬十0）或a ax2=1(a 0).a等轴双曲线的渐近线方程为y -x .6共轭双曲线：实轴为虚轴，虚轴为实轴的双曲线互为共轭双曲线.如：弓丄"(a Qb .O)的共轭双曲线为 a b与双曲线 2y 2 a 22 2占-笃“(a 0,b 0)，它们的焦点到原点的距离相等，ba因而在以原点为圆心，a2b2为半径的圆上.且它们的渐近线都是y=b x禾廿y = -Bx.a a三、抛物线1定义平面内与一个定点F和一条定直线l(F不在l 上)的距离相等的点的轨迹叫做抛物线.定点F叫做抛物线的焦点，定直线l叫做抛物线的准线.2标准方程(1) y2=2px(p 0)，焦点为(f,0)，准线方程为x七，抛物线张口向右.⑵y2=~2px(p>0)，焦点为(-号，0)，准线方程为X = ^ , 抛物线张口向左.(3) x2 =2py(p 0)，焦点为(0申，准线方程为y七，抛物线张口向上.⑷x2=-2py(p>0)，焦点为(喀)，准线方程为y聲，抛物线张口向下.其中p 表示焦点到准线的距离. 3几何性质抛物线是轴对称图形，有一条对称轴.若方程为 y 2=2px(p 0)或y 2=—2px(p ■ 0)，则对称轴是x轴，若方程为x 2=2py(p 0)或x 2=—2py(p 0)，则对称轴是y 轴.若抛物线方程为y 2=2px(p 0)，则x_0,y R . 若抛物线方程为y 2- -2px(p 0)，则x _ 0, y R .若抛物线方程为x^2py(p 0)，则y_0,x R . 若抛物线方程为x 2=—2py(p 0)，则y_0,x R .圆锥曲线的一些重要结论【几个重要结论】2 2 _______________________________________1已知椭圆务 la b 0)的两焦点为F I(-C ,0),F 2(C ,0)，a bP(x °,y °)为椭圆上PF i |=J (x ° +c)2+y ：=阻 +c)2+b 2(1—予)因为一 a 岂x 0岂a ， — c 乞竺空c,0 ：： a — c 乞些 a 乞a c ，aa?占八a)cx°aCX°a所以|PF^c^+a.同理,acx0 PF2 =2a- Ph =a-—0a '2 2已知双曲线冷一爲"（a 0,b .0）的左、右焦点分别为a bFZOEc,。

圆锥曲线知识点总结6篇

圆锥曲线知识点总结6篇第1篇示例：圆锥曲线是解析几何学中非常重要的概念，它们分为三种：椭圆、双曲线和抛物线。

在数学中，圆锥曲线具有丰富的性质和应用，掌握其基本知识对于理解其在几何、物理、工程等多个领域的应用至关重要。

本文将对圆锥曲线的基本性质和特点进行详细总结。

我们从圆锥曲线的定义入手。

圆锥曲线是平面上一点到一个固定点（焦点）和一条直线（准线）的距离之比为常数的点的轨迹。

根据这个定义，椭圆的准线是实直线，双曲线的准线是虚直线，而抛物线的准线是平行于其自身的直线。

椭圆是圆锥曲线中最简单的一种。

椭圆的定义是到焦点和准线的距离之比小于1的点构成的轨迹。

椭圆具有对称性，其焦点到准线的垂直距离之和恒等于两焦距之和，这个性质被称为焦点定理。

椭圆还有面积、周长等重要性质，在几何中有重要的应用。

抛物线是圆锥曲线中最特殊的一种，其定义是到焦点和准线的距离相等的点构成的轨迹。

抛物线具有对称性，其焦点到准线的垂直距离恰好等于焦距。

抛物线是一种非常重要的曲线，常见于物理学和工程学中的抛物线运动、光学、无线电通信等领域。

除了上述基本性质外，圆锥曲线还有许多重要的定理和性质。

焦点、准线、焦距、离心率等概念是理解圆锥曲线的重要基础。

圆锥曲线的方程形式也是研究和应用圆锥曲线的关键，椭圆和双曲线的标准方程分别为x^2/a^2 + y^2/b^2 = 1和x^2/a^2 - y^2/b^2 = 1，而抛物线的标准方程为y^2 = 2px。

圆锥曲线是解析几何学中的重要内容，掌握其基本性质和定理对于理解几何学、物理学和工程学中的问题有重要意义。

通过对圆锥曲线的学习，我们不仅可以深入理解几何形体的性质，还可以应用圆锥曲线的知识解决实际问题，提高数学建模和问题求解的能力。

加强对圆锥曲线知识的学习和应用是十分必要的。

第2篇示例：圆锥曲线是解析几何中最重要的一类曲线，它包括椭圆、双曲线和抛物线这三种。

这些曲线在数学和物理学等领域中有着重要的应用，是我们熟悉的常见数学概念之一。

圆锥曲线（椭圆、双曲线、抛物线）基础知识及常用结论

圆锥曲线（椭圆、双曲线、抛物线）基础知识及常⽤结论圆锥曲线必背⼝诀(红字为⼝诀)-椭圆⼀、椭圆定义定点为焦点，定值为长轴.（定值=2a ）椭圆.定点为焦点，定直线为准线，定值为离⼼率.（定值=e ）定点为短轴顶点，定值为负值. （定值2k e 1=-）⼆、椭圆的性质定理长轴短轴与焦距，形似勾股弦定理①准线⽅程准焦距，a ⽅、b ⽅除以c ②通径等于 2 ep ，切线⽅程⽤代替③焦三⾓形计⾯积，半⾓正切连乘b ④注解：1长轴2a =，短轴2b =，焦距2c =，则：222a b c =+2准线⽅程：2a x c= （a ⽅除以c ）3椭圆的通径d ：过焦点垂直于长轴的直线与椭圆的两交点之间的距离称为椭圆的通径.（通径22c b 2b 2a c ad 2ep =??==）过椭圆上00x y (,)点的切线⽅程，⽤00x y (,)等效代替椭圆⽅程得到.等效代替后的是切线⽅程是：0022x x y y1a b+=4、焦三⾓形计⾯积，半⾓正切连乘b焦三⾓形：以椭圆的两个焦点12F F ,为顶点，另⼀个顶点P 在椭圆上的三⾓形称为焦三⾓形.半⾓是指12F PF θ=∠的⼀半.则焦三⾓形的⾯积为：2S b 2tanθ=证明：设1PF m =，2PF n =，则m n 2a +=由余弦定理：222m n 2mn 4c cos θ+-?=22224a 4b m n 4b ()=-=+-即：22mn 2mn 4b cos θ-?=-，即：22b 1mn (cos )θ=+.即：2122b mn PF PF 1||||cos θ==+故：12F PF 1S m n 2sin θ=??△2212b b 211sin sin cos cos θθθθ=?=++⼜：22221222sin cossin tan cos cosθθθθθθ==+ 所以：椭圆的焦点三⾓形的⾯积为122F PF S b 2tan θ=. 三、椭圆的相关公式切线平分焦周⾓，称为弦切⾓定理①1F2FOxyPmn切点连线求⽅程，极线定理须牢记②弦与中线斜率积，准线去除准焦距③细看中点弦⽅程，恰似弦中点轨迹④注解：1弦切⾓定理：切线平分椭圆焦周⾓的外⾓，平分双曲线的焦周⾓. 焦周⾓是焦点三⾓形中，焦距所对应的⾓.弦切⾓是指椭圆的弦与其切线相交于椭圆上时它们的夹⾓，当弦为焦点弦时（过焦点的弦），那么切线是两个焦点弦的⾓平分线.2若000P x y (,)在椭圆2222x y 1a b+=外，则过0P 作椭圆的两条切线，切点为12P P ,，则点0P 和切点弦12P P ,分别称为椭圆的极点和极线.切点弦12P P 的直线⽅程即极线⽅程是0022x xy y1a b+=（称为极线定理）3弦指椭圆内的⼀弦AB .中线指弦AB 的中点M 与原点O 的连线，即OAB ?得中线.这两条直线的斜率的乘积，等于准线距离2c a x c=-去除准焦距2bp c=，其结果是：2AB OM2c p b k k x a==- 4中点弦AB 的⽅程：在椭圆中，若弦AB 的中点为00M x y (,)，弦AB 称为中点弦，则中点弦的⽅程就是2200002222x x y y x y a b a b+=+，是直线⽅程.弦中点M 的轨迹⽅程：在椭圆中，过椭圆内点000P x y (,)的弦AB ，其中点M 的⽅程就是22002222x x y y x y a b a b+=+，仍为椭圆.这两个⽅程有些相似，要擦亮眼睛，千万不要搞混了.圆锥曲线必背⼝诀(红字为⼝诀)-双曲线⼀、双曲线定义⼆、双曲线的性质定理基本同椭圆，有所区别：实轴虚轴与焦距，形似勾股弦定理①准线⽅程准焦距，a ⽅、b ⽅除以c ②通径等于 2 e p ，切线⽅程⽤代替③焦三⾓形计⾯积，半⾓余切连乘b ④注解：1实轴2a =，虚轴2b =，焦距2c =，则：222a b c +=2准线⽅程2a x c=± （a ⽅除以c ）准焦距p ：焦点到准线的距离：2b pc = （b ⽅除以c ）3通径等于2 e p ，切线⽅程⽤代替双曲线的通径d ：过焦点垂直于长轴的直线与双曲线的两交点之间的距离称为双曲线的通径.（通径22c b 2b 2a c ad 2ep =??==）过双曲线上000P x y (,)点的切线⽅程，⽤000P x y (,)等效代替双曲线⽅程得到，等效代替后的是切线⽅程是：0022x x y y1a b-=4焦三⾓形计⾯积，半⾓余切连乘b焦三⾓形：以双曲线的两个焦点12F F ,为顶点，另⼀个顶点P 在椭圆上的三⾓形称为焦三⾓形.半⾓是指12F PF γ=∠的⼀半.双曲线2222x y 1a b-=的左右焦点分别为12F F ,，点P 为双曲线上异于顶点任意⼀点12F PF γ∠=，则双曲线的焦点三⾓形满⾜：2122b PF PF 1cos γ=- 其⾯积为；122F PF S b co 2t γ=.证明：设21PF m PF n ,==，则m n 2a -=在12F PF ?中，由余弦定理得：222121212PF PF 2PF PF F F cos γ+-=，即：222m n 2mn 4c cos γ+-?=22224a 4b m n 4b ()=+=-+ 即：2222m n 2mn m n 4b cos ()γ+-?=-+即：22mn 2mn 4b cos γ-?=，即：22b mn 1(cos )γ=-即：22b mn 1cos γ=-，即：2122bPF PF 1cos γ=-那么，焦点三⾓形的⾯积为：12F PF 1S mn 2sin γ?=?212b 21sin cos γγ=?-2222b 22b 122sin cossin cos sinγγγγγ==?-2b 2cot γ= 故：122F PF S b 2cot γ= 同时：12F PF 12P P 1S F F y c y 2?=?=?，故：2p b y c 2cot γ=±? 双曲线的焦点三⾓形的⾯积为：122F PF S b co 2t γ=.三、双曲线的相关公式切线平分焦周⾓，称为弦切⾓定理①切点连线求⽅程，极线定理须牢记②弦与中线斜率积，准线去除准焦距③细看中点弦⽅程，恰似弦中点轨迹④注解：1弦切⾓定理：切线平分椭圆焦周⾓的外⾓，平分双曲线的焦周⾓.焦周⾓是焦点三⾓形中，焦距所对应的⾓. 弦切⾓是指双曲线的弦与其切线相交于双曲线上时它们的夹⾓，当弦为焦点弦时（过焦点的弦），那么切线是两个焦点弦的⾓平分线.如图，12F PF ?是焦点三⾓形，12F PF ∠为焦周⾓，PT 为双曲线的切线. 则PT 平分12F PF ∠.2若000P x y (,)在双曲线2222x y 1a b-=外，以包含焦点的区域为内，不包含焦点的区域为外，则过0P 作双曲选的两条切线，切点为1P 、2P ，则点0P 和切点弦12P P 分别称为双曲线的极点和极线，切点弦12P P 的直线⽅程即极线⽅程是0022x xy y1a b-=（称为极线定理）3弦指双曲线内的⼀弦AB .中线指弦AB 的中点M 与原点O 的连线，即OAB ?得中线.这两条直线的斜率的乘积，等于准线距离2c a x c =去除准焦距2b p c=，其结果是：2AB OM2c p b k k x a==4中点弦AB 的⽅程：在双曲线中，若弦AB 的中点为00M x y (,)，称弦AB 为中点弦，则中点弦的⽅程就是：2200002222x x y y x y aba b-=-，它是直线⽅程. 弦中点M 的轨迹⽅程：在双曲线中，过双曲线外⼀点000P x y (,)的弦AB ，其AB 中点M 的⽅程就是22002222x x y y x y a b a b-=-，仍为双曲线.这两个⽅程有些相似，要擦亮眼睛，千万不要搞混了.圆锥曲线必背⼝诀(红字为⼝诀)-抛物线⼀、抛物线定义抛物线，有定义，定点定线等距离12⼆、抛物线性质焦点准线极点线①，两臂点乘积不变②焦弦切线成直⾓，切点就是两端点③端点投影在准线，连结焦点垂直线④焦弦垂直极焦线⑤，切线是⾓平分线⑥直⾓梯形对⾓线，交点就是本原点⑦焦弦三⾓计⾯积，半个p ⽅除正弦⑧注解：1抛物线的焦点和准线是⼀对极点和极线.抛物线⽅程：2y 2px =，焦点(,)p F 02，准线p p x 2=-(抛物线的顶点(,)O 00到定点(,)p F 02和定直线p p x 2=-距离相等) 焦弦：过焦点的直线与抛物线相交于两点A 和B ，则AB 称为焦弦.弦中点(,)M M M x y ，A B M x x x 2+=，A B M y yy 2+= 焦弦⽅程：()p y k x 2=-，k 为斜率. 2焦点三⾓形两边OA 和OB 的点乘积为定值，且夹⾓是钝⾓. 证明：焦弦AB 满⾜的条件()2y 2pxp y k x 2?=??=- ()22p k x 2px 2-=? ()22222k p k x k 2px 04-++=由韦达定理得：2A B px x 4=2A B py y 22p p 2==-=-?=-，即：2A B p x x 4=，2A B y y p =- ①且：2A A B B A B A B 3OA OB x y x y x x y y p 04(,)(,)?=?=+=-<. 故：焦点三⾓形两边之点乘积为定值.3即：焦弦两端点的切线互相垂直. 证明：如图，由抛物线⽅程：2y 2px =得到导数：yy p '=，即：py y'=故：AEA p k y =，BE Bp k y = 于是：2AE BEA B A Bp p p k k y y y y ?=?=将①式2A B y y p =-代⼊上式得：AE BE k k 1?=-即：AE BE ⊥，故焦弦端点在准线的投影点与焦点构成直⾓三⾓形. 4即：焦弦端点在准线的投影点与焦点构成直⾓三⾓形. 证明：坐标B p C y 2(,)-,A p D y 2(,)-则：B CF p y (,)=-，A DF p y (,)=- 于是：2A B CF DF p y y ?=+将①式2A B y y p =-代⼊上式得：CF DF 0?= 故：CF DF ⊥即：焦弦端点A B ,在准线的投影点D C ,，则CF DF ⊥，即：焦弦端点在准线的投影点与焦点构成直⾓三⾓形.5若焦弦AB 对应的极点E ，则EF 为极焦线，于是EF AB ⊥⽤向量⽅法可证.由于M 是AB 的中点，AEB ?为直⾓三⾓形，计算可得E 是DC 的中点，故：ED EF EC == 由向量法可证EF AB 0?=即：焦弦AB 与极焦线EF 互相垂直. 6即：切线平分焦弦的倾⾓(或倾⾓的外⾓) 如图：因为ADE ?和AFE ?都是直⾓三⾓形，且由定义知：AF AD =，AE AE =故ADE AFE ??≌，则对应⾓相等. 即：AE 是DAF ∠的⾓平分线同理，BE 是CBF ∠的⾓平分线 7即：直⾓梯形ABCD 对⾓线相交于原点即：A O C ,,三点共线；B O D ,,三点共线. ⽤向量法证明：OA CO //，OB DO //证明：坐标2A A y A y 2p (,)，2B B y B y 2p (,)，B p C y 2(,)-，A pD y 2(,)-向量：2A A y OA y 2p (,)=，B pCO y 2(,)=-各分量之⽐：2A2x A 2xy OA y 2p p p CO 2()()==，2y A AB A B y OA y y y y y CO ()()==--将①式2A B y y p =-代⼊上式得：22yA A2A By OA y y y y p CO ()()==- 故：y x xyOA OA OACO CO CO()()()()==，即：OA CO // 同理：OB DO //.直⾓梯形ABCD 对⾓线相交于原点. 8即：焦弦三⾓形的⾯积为：sin 2 AOBp S 2α= （α为焦弦的倾⾓）证明：AB AF BF =+A B A B p p x x x x p 22=+ ++=++M p2x 2()=+2EM = 如图：GF 2OF p == 则：2EF GF 1pEM sin sinsin sin αααα==?= E于是：22pAB sin α= 故：AOB1S OF AB 2sin α?=221p 2p p 222sin sin sin ααα==附：圆锥曲线必背----极坐标圆锥曲线的极坐标以准焦距p 和离⼼率e 来表⽰常量，以极径ρ和极⾓θ来表⽰变量.0ρ≥，[,)o 0360θ∈以焦点(,)F 0θ为极点(原点O )，以椭圆长轴、抛物线对称轴、双曲线的实轴为极轴的建⽴极坐标系.故准线是到极点距离为准焦距p 、且垂直于极轴的直线L . 极坐标系与直⾓坐标系的换算关系是：ρ=，arctan y xθ= 或者：cos x ρθ=，sin y ρθ= 特别注意：极坐标系中，以焦点为极点(原点)，⽽直⾓坐标系中以对称点为原点得到标准⽅程. 如图，O 为极点，L 为准线，则依据定义，到定点(极点)和到定直线(准线)的距离之⽐为定值(定值e )的点的轨迹为圆锥曲线. 所以，对极坐标系，请记住：⑴极坐标系的极点O 是椭圆的左焦点、抛物线的焦点、双曲线的右焦点；⑵曲线上的点(,)Pρθ到焦点F的距离是ρ，到准线的距离是cospρθ+，根据定义：cosepρρθ=+即：cosep eρθρ+=，即：cosep eρρθ=-，即：1eρθ=-①这就是极坐标下，圆锥曲线的通式.⑶对应不同的e，呈现不同的曲线. 对双曲线，只是右边的⼀⽀；对抛物线，开⼝向右.将极轴旋转o180，α和θ分别对应变换前后的极⾓，即转⾓为o180θα=+，则极坐标⽅程变换前⽅程为：cosep1eρα=-变换后⽅程为：cosep1eρθ=+②此时的极坐标系下，此时有：⑵对应不同的e，呈现不同的曲线对双曲线，只是左边的⼀⽀；对抛物线，开⼝向左.⑴将极轴顺时针旋转o90，即：o 90θα=+，则情况如图.圆锥曲线的⽅程为：sin ep1e ρθ=- ③此时的极坐标系下：对应于直⾓坐标系下，焦点在y 轴的情况，且极点O 对应于椭圆下⽅的焦点，双曲线上⽅的焦点，抛物线的焦点.对双曲线，只是y 轴上边的⼀⽀；对抛物线，开⼝向上. ⑵如果将极轴逆时针旋转o 90，即：o 90θα=-，则情况如图. 圆锥曲线的⽅程为：sin ep1e ρα=+ ③此时的极坐标系下：对应于直⾓坐标系下，焦点在y 轴的情况，且对应于椭圆上⽅的焦点，双曲线下⽅的焦点，抛物线的焦点.对双曲线，只是y 轴下边的⼀⽀；对抛物线，开⼝向下.⑴在极坐标系中，圆锥曲线的通式为：=cos ep1e ρθ- ①即：cos e ep ρρθ-=，即：cos ep e ρρθ=+即：(cos )(cos )(cos )2222222ep e e p e 2e p ρρθρθρθ=+=++ ②将222x y ρ=+，cos x ρθ=代⼊②式得：2222222x y e p e x 2e px +=++即：()2222221e x 2e px y e p --+= ③当e 1≠时有：()[()]()()22222222222222--++=+---- 即：()()()22222 2222222e p e e p 1e x y e p 11e 1e 1e --+=+=--- 即：()()22222222222e px y 1e1e p e p1e 1e --+=-- ④⑴当e 1<时，令()22222e p a 1e =-，2222e p b 1e=-，22e p c 1e=-则：()222222222e p e p a b 1e 1e-=---[()]()()2222e p e p 11e 1e 1e =--=--⽽：()()2422222222e p e p c a b 1e 1e ===--- 代⼊④式得：()2222x c y 1ab-+= ⑤这是标准的椭圆⽅程. ⑵当e 1>时，令()222 22e p a e 1=-，2222e p b e 1=-，22e p c e 1=-则：()222222222e p e p a b e 1e 1+=+--[()]()()2242e p e p 1e 1e 1e 1=+-=-- ⽽：()()2422222222e p e p c a b e 1e 1===+-- 代⼊④式得：()2222x c y 1ab+-= ⑥这是标准的双曲线⽅程.⑶当e 1=时，由③式()2222221e x 2e px y e p --+=得：222px y p -+=即：()22p y 2px p 2p x 2=+=+ 即：()2p y 2p x 2=+ ⑦这是标准的抛物线⽅程.。

最全圆锥曲线知识点总结

最全圆锥曲线知识点总结的定义是指平面内一个动点P到两个定点F1,F2的距离之和等于常数（PF1+PF2=2a>F1F2），那么这个动点P的轨迹就是椭圆。

这两个定点被称为椭圆的焦点，两焦点的距离被称为椭圆的焦距。

注意：如果PF1+PF2=F1F2，则动点P的轨迹是线段F1F2；如果PF1+PF2<F1F2，则动点P的轨迹无图形。

2）对于椭圆，如果焦点在x轴上，那么它的参数方程是x=acosθ，y=bsinθ（其中θ为参数），如果焦点在y轴上，那么它的参数方程是y=acosθ，x=bsinθ。

如果椭圆的标准方程是x2/a2+y2/b2=1（a>b>0），那么它的范围是−a≤x≤a,−b≤y≤b，焦点是两个点(±c,0)，对称中心是(0,0)，顶点是(±a,0)和(0,±b)，长轴长为2a，短轴长为2b，离心率为e=c/a，椭圆即为0<e<1的情况。

3）关于直线与椭圆的位置关系，如果点P(x,y)在椭圆外，那么a2+b2>1；如果点P(x,y)在椭圆上，那么a2+b2=1；如果点P(x,y)在椭圆内，那么a2+b2<1.4）焦点三角形是指椭圆上的一点与两个焦点构成的三角形。

5）弦长公式是指如果直线y=kx+b与圆锥曲线相交于两点A、B，且x1、x2分别为A、B的横坐标，那么AB=√[1+k2(x1−x2)2]。

如果y1、y2分别为A、B的纵坐标，则AB=√[1+k2(y1−y2)2]。

如果弦AB所在直线方程设为x=ky+b，则AB=√[1+k2(y1−y2)2]。

6）圆锥曲线的中点弦问题可以用“韦达定理”或“点差法”求解。

在椭圆中，以P(x,b2x,y)为中点的弦所在直线的斜率k=−a2y。

1.已知椭圆 $m x^2 + n y^2 = 1$ 与直线 $x+y=1$ 相交于$A,B$ 两点，点 $C$ 是 $AB$ 的中点，且 $AB=2\sqrt{2}$，求椭圆的方程，若 $OC$ 的斜率为 $\frac{1}{2}$，求 $m,n$ 的值。

高考圆锥曲线经验总结及知识点汇总

果切线垂直且相交于 P ，则动点 P 的轨迹为圆 x 2 y 2 a 2 b 2 ．
结论 7：点 M
（
x0
，
y0
）在椭圆
x a
2 2

y2 b2
1（ a b 0 ）上，过点 M
作椭圆的切线方
程为
x0 x a2

y0 y b2
1．
结论 8：点 M
（
x0
，
y0
）在椭圆
x a
2 2
结论
5：过椭圆
x a
2 2

y2 b2
1（ a
b
0 ）上任意不同两点 A ， B 作椭圆的切线，如果切
线垂直且相交于 P ，则动点 P 的轨迹为圆 x 2 y 2 a 2 b 2 ．
结论
6：过双曲线
x a
2 2

y2 b2
1（ a
b
0 ）上任意不同两点 A ， B 作双曲线的切线，如
1（ a 0,b 0 ）外，过点 M
作双曲线
的两条切线，切点分别为
A，B
，则切点弦
AB
的直线方程为
x0 x a2

y0 y b2
1．
结论 10：（补充）点 M
（
x0
，
y0
）在双曲线
x a
2 2

y2 b2
1（ a
0,b 0 ）内，过点 M
作
双曲线的弦 AB （不过双曲线中心），分别过 A、B 作双曲线的切线，则两条切线的交点 P
结论 13：点 M
（
x0
，
y
0
）在椭圆

圆锥曲线知识点总结

圆锥曲线知识点总结圆锥曲线，是由平面上一个动点到两个定点的距离之比为定值的点的轨迹。

圆锥曲线是解析几何的重要内容，广泛应用于数学、物理、工程等领域。

本文将对圆锥曲线的相关知识进行总结，帮助读者更好地理解和掌握这一概念。

一、基本概念1. 定义：圆锥曲线是平面上一个动点到两个定点的距离之比为定值的点的轨迹。

2. 定点：圆锥曲线的两个定点分别称为焦点。

3. 对称轴：通过两个焦点并垂直于准线的直线称为对称轴。

4. 准线：通过两个焦点的直线段称为准线。

二、椭圆1. 定义：椭圆是圆锥曲线的一种，其离心率小于1，且焦点不重合的曲线。

2. 方程：椭圆的标准方程为x^2/a^2 + y^2/b^2 = 1，其中a和b分别是椭圆的半长轴和半短轴。

3. 性质：椭圆具有对称性、渐近线和切线性质等。

4. 应用：椭圆在天文学、建筑学和电子等领域应用广泛。

三、双曲线1. 定义：双曲线是圆锥曲线的一种，其离心率大于1的曲线。

2. 方程：双曲线的标准方程为x^2/a^2 - y^2/b^2 = 1，其中a和b分别是双曲线的半长轴和半短轴。

3. 性质：双曲线具有渐近线和切线性质，且有两个分支。

4. 应用：双曲线在物理学、天文学和通信等领域有重要应用。

四、抛物线1. 定义：抛物线是圆锥曲线的一种，其离心率等于1的曲线。

2. 方程：抛物线的标准方程为y^2 = 4ax，其中a是抛物线的焦点到准线的距离。

3. 性质：抛物线具有对称性、渐近线和切线性质等。

4. 应用：抛物线在物理学、工程学和天文学等领域有广泛应用。

五、圆1. 定义：圆是圆锥曲线的一种，其离心率等于0的曲线。

2. 方程：圆的标准方程为(x-h)^2 + (y-k)^2 = r^2，其中(h, k)是圆心的坐标，r是半径长度。

3. 性质：圆具有对称性、切线性质和切圆定理等。

4. 应用：圆在几何学、物理学和工程学等领域有广泛应用。

总结：圆锥曲线是解析几何的重要内容，包括椭圆、双曲线、抛物线和圆。

圆锥曲线知识点总结

圆锥曲线知识点总结圆锥曲线是代数几何中重要的一部分，它由平面和一个定点的两条曲线组成。

在数学的发展历史中，圆锥曲线的研究经历了漫长的时期，涉及到众多的数学家和学者的努力。

本文将对圆锥曲线的基本概念、性质、分类以及应用等知识点进行总结。

一、圆锥曲线的基本概念1. 圆锥曲线的定义圆锥曲线是由平面与一个定点和这个定点到平面上任意一点的连线组成的图形。

2. 圆锥曲线的基本元素圆锥曲线由定点称为焦点和一条固定的直线称为准线组成。

3. 圆锥曲线的标准方程圆锥曲线可以用一般的二次方程表示，即 Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0，其中A、B、C、D、E和F为常数。

4. 圆锥曲线的焦点和准线焦点是定点到平面上各点的距离与准线到这些点距离之比的极限值。

准线是过焦点且垂直于对称轴的直线。

二、圆锥曲线的性质1. 直线和圆的特例直线是当离心率为1的圆锥曲线，圆是离心率为0的圆锥曲线。

2. 焦准属性圆锥曲线上的任意一点到焦点的距离与到准线的距离之比始终为常数，这就是焦准属性。

3. 长轴和短轴圆锥曲线的焦点和准线确定了两条互相垂直的轴线，这两条轴线分别称为长轴和短轴。

4. 离心率圆锥曲线的离心率是一个反映离心程度的量，离心率为0时曲线为圆，离心率为1时曲线为直线。

5. 对称性圆锥曲线具有平移和对称性，即曲线在对称轴两侧具有相同的形状。

三、圆锥曲线的分类1. 椭圆圆锥曲线的离心率小于1，且大于0，形状近似于椭圆的曲线称为椭圆。

2. 抛物线圆锥曲线的离心率等于1，形状类似于抛物线的曲线称为抛物线。

3. 双曲线圆锥曲线的离心率大于1，形状类似于双曲线的曲线称为双曲线。

四、圆锥曲线的应用1. 天文学圆锥曲线在天文学中有广泛的应用，例如行星和彗星的轨道可以用圆锥曲线描述。

2. 工程学在工程学中，圆锥曲线被用于设计天桥、隧道、公路弯道等工程项目。

3. 经济学圆锥曲线在经济学中有重要的应用，例如需求曲线和供给曲线可以用圆锥曲线表示。

圆锥曲线知识要点及结论个人总结

《圆锥曲线》知识要点及重要结论、椭圆1定义平面内到两定点 F 「F 2的距离的和等于常数2a(2^|F^2)的点P 的轨迹叫做椭圆•若2a = F ,F 2，点P 的轨迹是线段F I F 2・若0 ：：： 2a ：：： F ,F 2，点P 不存在•2 2务与=1(a b 0)，两焦点为 R (_c,0), F 2(c,0). a b2 2X2 =1(ab ■ 0)，两焦点为 F i (0,_c), F 2(0,C ).其中 a 2"2 cla b3几何性质椭圆是轴对称图形，有两条对称轴 .椭圆是中心对称图形，对称中心是椭圆的中心椭圆的顶点有四个，长轴长为2a ，短轴长为2b ，椭圆的焦点在长轴上•2 2若椭圆的标准方程为务•与=1(a b ■ 0)，则- a 空x 空a, -b 曲乞b ； a b2 2若椭圆的标准方程为 =1(a b 0)，则-b 辽x 乞b,-a y 乞a .a 2b 2二、双曲线1定义平面内到两定点 F 1, F 2的距离之差的绝对值等于常数 2a(0 ：：： 2a ：：：R F ?)的点的轨迹叫做双曲线.若2^|F 1F 2，点P 的轨迹是两条射线.若2^|F 1F 2，点P 不存在.2 22 标准方程务一―1(a ■ 0,b0)，两焦点为 F 1(-c,0), F 2(C ,0).a b2 2令…占二“ 0,b 0)，两焦点为 F 1 (0^c ), F 2(0, c ).其中 c 2 二 a 2 b 2. a b 3几何性质双曲线是轴对称图形，有两条对称轴；双曲线是中心对称图形，对称中心是双曲线的中心双曲线的顶点有两个 A 1, A 2，实轴长为2a ，虚轴长为2b ，双曲线的焦点在实轴上2 2J 壬-1(a 0,b 0)，则 x 乞-a 或x — a, y R ；a b2-牛=1(a 0,b 0)，则 y — -a 或 y — a, x R .b 22标准方程若双曲线的标准方程为若双曲线的标准方程为2a4渐近线双曲线的渐进线是它的重要几何特征，每一双曲线都对应确定双曲线的渐进线，但对于同组渐进线却对应无数条双曲线 •2 2 2 2与双曲线笃-与 "(a 0,b ■ 0)共渐进线的双曲线可表示为笃一笃=，(・=0).a ba b直线与双曲线有两个交点的条件，一定要“消元后的方程的二次项系数同时成立•5等轴双曲线：实轴长等于虚轴长的双曲线叫做等轴双曲线•2 2 2 2等轴双曲线的标准方程为务一爲=1(a . 0)或爲-笃 "(a ■ 0).a aa a等轴双曲线的渐近线方程为 y =「x .6共轭双曲线：实轴为虚轴，虚轴为实轴的双曲线互为共轭双曲线2 2 2 2如：笃-与=1(a0,b - 0)的共轭双曲线为每-务=1(a0,b - 0)，它们的焦点到a bb a原点的距离相等，因而在以原点为圆心，.a 2 b 2为半径的圆上.且它们的渐近线都是b b y x 和 y x .aa三、抛物线1定义平面内与一个定点 F 和一条定直线l(F 不在I 上)的距离相等的点的轨迹叫做抛物线.定点F 叫做抛物线的焦点，定直线 I 叫做抛物线的准线. 2标准方程(1) y 2 =2px(p 0)，焦点为(号,0)，准线方程为x = -号，抛物线张口向右.⑵y 2 =-2px(p 0)，焦点为(-p,0)，准线方程为x =号，抛物线张口向左.⑶x 2 =2py (p 0)，焦点为 (0导，准线方程为y = 一号，抛物线张口向上.⑷X 2 - -2 py (p 0)，焦点为 (0』) ，准线方程为y = _p ，抛物线张口向下. 其中p 表示焦点到准线的距离. 3几何性质抛物线是轴对称图形，有一条对称轴.若方程为y 2 = 2 px( p - 0)或y 2 = -2 px( p - 0)，2 2双曲线x y2 -.2ab2 2yx 2.2 a b=1(a 0, b 0)有两条渐近线y=1( a 0, b 0)有两条渐近线y a a x 和yx .即b b 2 2x y=02■ 2ab22yx2.2ab=0” 和“二.0双曲线则对称轴是x 轴，若方程为x 2 =2py(p . 0)或x 2 =_2py(p 0)，则对称轴是y 轴.若抛物线方程为y 2 =2 px( p 0)，则x 亠0, y 尸R . 若抛物线方程为y 2 - -2 px( p .0)，则x _ 0, y• R .2若抛物线方程为x =2py(p . 0)，则y_0,x ・R . 若抛物线方程为x 2 - -2 py( p .0)，贝V y 込0, x 三R .圆锥曲线的一些重要结论【几个重要结论】2 21已知椭圆笃•与 "(a b 0)的两焦点为F !^c,0),F 2(c,0)，P(x °,y °)为椭圆上一a b点，则I PF.H c)*2冷冷心讪1一予)ms 丿丿cx 0 cx 0因为一a _ x 0 _ a ， -c 仝乞 c,0 ：：： a -c 0 a c ，aa所以 |PF^-cx ° +a .同理，PF 2 =2a — PF,| =a —也.a a. b sin a 2a L F!PF 2的面积为b tan .1 +cos^2解：根据椭圆的定义可得|PF_, +|PF 2| =2a ①由余弦定理可得 4c 2 = F J F 2 2 =|PFj 2 +|PF 2 2 — 2PF 」PF 2 COS 。

圆锥曲线知识要点及重要结论

圆锥曲线知识要点及重要结论圆锥曲线是数学中的一个重要概念，它包括椭圆、双曲线和抛物线三种特殊的曲线形状。

本文将介绍圆锥曲线的基本定义、性质和重要结论，以帮助读者更好地理解和应用这一概念。

1. 圆锥曲线的定义圆锥曲线是由一个可移动的点P和两个固定点F1、F2组成的。

对于椭圆和双曲线而言，这两个固定点称为焦点，而抛物线只有一个焦点。

圆锥线还有一个固定的直线L，称为准线，通过焦点F1、F2的垂线交于准线上的点称为顶点。

圆锥曲线的定义可以用以下公式表示：椭圆：PF1 + PF2 = 2a，其中a为椭圆的大半轴长度；双曲线：|PF1 - PF2| = 2a，其中a为双曲线的距离焦点到准线的距离；抛物线：PF = PL，其中P为抛物线上任意一点，F为焦点，L为准线。

2. 圆锥曲线的性质2.1 椭圆椭圆是圆锥曲线中的一种，它的性质如下：- 所有椭圆上的点到焦点的距离之和等于常数2a，其中a为椭圆的大半轴长度；- 椭圆的长轴是焦点的连线，短轴是准线的连线；- 椭圆是一个封闭曲线，对称于长轴和短轴。

2.2 双曲线双曲线是圆锥曲线中的一种，它的性质如下：- 所有双曲线上的点到焦点的距离之差的绝对值等于常数2a，其中a为焦点到准线距离的一半；- 双曲线的两支分别相交于点F1、F2，这两个点称为焦点；- 双曲线是一个非封闭曲线，它与准线之间没有交点。

2.3 抛物线抛物线是圆锥曲线中的一种，它的性质如下：- 抛物线上的点到焦点的距离等于该点到准线的垂直距离；- 抛物线是一个非封闭曲线，它与准线相切于顶点。

3. 圆锥曲线的重要结论3.1 椭圆的离心率椭圆的离心率是用来衡量椭圆形状扁度的指标，其定义为离心距与长轴长度的比值。

离心率的取值范围为0到1，当离心率为0时，椭圆变成了一个圆，而当离心率为1时，椭圆变成了一个线段。

3.2 双曲线的离心率双曲线的离心率也是衡量其形状的指标，其定义为离心距与焦点距离之差的比值。

离心率的取值范围大于1，当离心率趋近于无穷大时，双曲线的形状趋近于两个平行线。

圆锥曲线知识要点及结论个人总结

圆锥曲线知识要点及结论个人总结《圆锥曲线》知识要点及重要结论一、椭圆1 定义平面内到两定点21,F F 的距离的和等于常数)2(221F F a a >的点P 的轨迹叫做椭圆.若212F F a =，点P的轨迹是线段21F F .若2120F F a <<，点P 不存在.2 标准方程)0(12222>>=+b a by a x ，两焦点为)0,(),0,(21c F c F -.)0(12222>>=+b a b x a y ，两焦点为),0(),,0(21c F c F -.其中222c b a+=.3 几何性质椭圆是轴对称图形，有两条对称轴. 椭圆是中心对称图形，对称中心是椭圆的中心.椭圆的顶点有四个，长轴长为a 2，短轴长为b 2，椭圆的焦点在长轴上. 若椭圆的标准方程为)0(12222>>=+b a b y a x ，则by b a x a ≤≤-≤≤-,；若椭圆的标准方程为)0(12222>>=+b a bx a y ，则ay a b x b ≤≤-≤≤-,.二、双曲线1 定义平面内到两定点21,F F 的距离之差的绝对值等于常数)20(221F F a a <<的点的轨迹叫做双曲线.若212F F a =，点P 的轨迹是两条射线.若212F F a >，点P不存在. 2 标准方程)0,0(12222>>=-b a by a x ，两焦点为)0,(),0,(21c F c F -.)0,0(12222>>=-b a b y a x ，两焦点为),0(),,0(21c F c F -.其中222b a c +=.3 几何性质双曲线是轴对称图形，有两条对称轴；双曲线是中心对称图形，对称中心是双曲线的中心. 双曲线的顶点有两个21,A A ，实轴长为a 2，虚轴长为b 2，双曲线的焦点在实轴上. 若双曲线的标准方程为)0,0(12222>>=-b a by a x ，则Ry a x a x ∈≥-≤,或；若双曲线的标准方程为)0,0(12222>>=-b a b x a y ，则Rx a y a y ∈≥-≤,或.4 渐近线双曲线)0,0(12222>>=-b a b y a x 有两条渐近线x a b y =和x aby -=.即02222=-b y a x双曲线)0,0(12222>>=-b a bx a y 有两条渐近线x b a y =和x bay -=.即02222=-bx a y双曲线的渐进线是它的重要几何特征，每一双曲线都对应确定双曲线的渐进线，但对于同一组渐进线却对应无数条双曲线. 与双曲线)0,0(12222>>=-b a b y a x 共渐进线的双曲线可表示为)0(2222≠=-λλby a x .直线与双曲线有两个交点的条件，一定要“消元后的方程的二次项系数0≠”和“0>∆”同时成立. 5 等轴双曲线：实轴长等于虚轴长的双曲线叫做等轴双曲线.等轴双曲线的标准方程为)0(12222>=-a ay a x 或)0(12222>=-a a x a y .等轴双曲线的渐近线方程为x y ±=.6 共轭双曲线：实轴为虚轴，虚轴为实轴的双曲线互为共轭双曲线.如：)0,0(12222>>=-b a b y a x 的共轭双曲线为)0,0(12222>>=-b a ax b y ，它们的焦点到原点的距离相等，因而在以原点为圆心，22b a +为半径的圆上.且它们的渐近线都是x aby =和x ab y -=. 三、抛物线1 定义平面内与一个定点F 和一条定直线F l (不在l 上) 的距离相等的点的轨迹叫做抛物线. 定点F 叫做抛物线的焦点，定直线l 叫做抛物线的准线.2 标准方程 (1) )0(22>=p px y，焦点为)0,2(p ，准线方程为2px -=，抛物线张口向右. (2) )0(22>-=p px y，焦点为)0,2(p -，准线方程为2p x =，抛物线张口向左. (3) )0(22>=p py x，焦点为)2,0(p ，准线方程为2py -=，抛物线张口向上. (4) )0(22>-=p py x，焦点为)2,0(p -，准线方程为2p y =，抛物线张口向下.其中p 表示焦点到准线的距离. 3 几何性质抛物线是轴对称图形，有一条对称轴.若方程为)0(22>=p px y 或)0(22>-=p px y，则对称轴是x 轴，若方程为)0(22>=p py x或)0(22>-=p py x，则对称轴是y 轴. 若抛物线方程为)0(22>=p px y ，则R y x ∈≥,0. 若抛物线方程为)0(22>-=p px y ，则R y x ∈≤,0. 若抛物线方程为)0(22>=p py x ，则R x y ∈≥,0.若抛物线方程为)0(22>-=p py x ，则R x y ∈≤,0.圆锥曲线的一些重要结论【几个重要结论】 1 已知椭圆)0(12222>>=+b a by a x 的两焦点为)0,(),0,(21c F c F -，),(00y x P 为椭圆上一点，则)1()()(22022020201a x b c x y c x PF -++=++=a a cx a a cx a cx a x c +=+=++=020202202)(2因为ax a ≤≤-0，c a a acx c a c acxc +≤+≤-<≤≤-00,，所以a acx PF+=1. 同理，acx a PF a PF0122-=-=.已知双曲线)0,0(12222>>=-b a b y a x 的左、右焦点分别为)0,(),0,(21c F c F -，),(0y x P 为双曲线上一点，则a acx PF+=1，a acx PF -=2.2 椭圆)0(12222>>=+b a b y a x 的两焦点为21,F F ，P 为椭圆上一点，若θ=∠21PFF ，则21PF F ∆的面积为2tancos 1sin 22αααb b =+.解：根据椭圆的定义可得aPF PF 221=+ ①由余弦定理可得αcos 242122212212PF PF PF PF F F c -+== ② 由①②得)cos 1(2442122α+=-PF PF c a.从而αcos 12221+=b PF PF所以，21F PF ∆的面积为2tan cos 1sin sin 212221ααααb b PF PF =+=双曲线)0,0(12222>>=-b a by a x 的两焦点为21,F F ，P 为其上一点，若α=∠21PF F ，则21PF F ∆的面积为2cot cos 1sin sin 212221ααααb b PF PF =-=.3 已知椭圆)0(1:2222>>=+b a by a x C ，N M ,是C 上关于原点对称的两点，点P 是椭圆上任意一点，当直线PNPM ,的斜率都存在，并记为PNPMk k,时，那么PMk 与PNk之积是与点P 位置无关的定值. 解：设),(),,(11y x M y x P ，则),(11y x N --.1010101,x x y y k x x y y k PN PM----=--=，从而2120212001010101x x y y x x y y x x y y k kPNPM--=----⋅--=⋅.又因为),(),,(1100y x M y x P 都在椭圆上，故1,1221221220220=+=+by a x b y a x .两式相减得，02212022120=-+-by y a x x ，因而2221202120ab x x y y -=--即22ab k k PNPM -=⋅.已知双曲线)0,0(12222>>=-b a b y a x .N M ,是C 上关于原点对称的两点，点P 是双曲线上任意一点，当直线PNPM ,的斜率都存在，并记为PNPMk k,时，那么PMk 与PNk之积是与点P 位置无关的定值.【常用方法】1 在求轨迹方程时，若条件满足圆、椭圆、双曲线、抛物线的定义，则可以用定义求轨迹方程，这是常用求轨迹的数学方法，称为定义法. 2本章经常会碰到直线l 与圆锥曲线C 相交于两点的问题，若已知l 过定点),(0y x P ，则可设l 的方程为x x =或)(00x x k yy -=-.然后分两种情况进行研究，一般处理方法是把直线方程代入曲线C 的方程中，整理得到关于x 或y 的一元二次方程(要注意二次项系数是否为零).韦达定理和判别式经常要用到！若l 的条件不明显时，则可设l 的方程为m x =或mkx y +=.3 本章还经常用到“点差法”：设直线l 与圆锥曲线C 交于点),(),,(2211y x B y x A ,则B A ,两点坐标都满足曲线C 的方程，然后把这两个结构相同的式子相减，整理可以得到直线AB 的斜率1212x x y y--的表达式，也经常会出现2121,y y x x++，这样又可以与线段AB 的中点),(00y x P 联系起来！4 若三点),(),,(),,(02211y x P y x B y x A 满足以线段AB 为直径的圆经过点P 或BP AP ⊥时，常用处理方法有： ①根据勾股定理可得222PBPA AB+=；②根据AP 的斜率与BP 的斜率之积为1-，可得120201010-=--⋅--x x y y x x y y ；③根据),(),,(,002020101y y x x y y x x--=--==⋅可得))(())((02010201=--+--y y y y x x x x .5求轨迹方程的方法常见的有：直接法、定义法、待定系数法、代入法（也叫相关点法）.1 椭圆22221(0)x y a b a b +=>>的参数方程是cos sin x a y b θθ=⎧⎨=⎩.离心率c e a ==△PF 1F 2中，记12F PFα∠=, 12PF Fβ∠=,12F F P γ∠=，则有sin sin sin c eaαβγ==+.线到中心的距离为2a c，焦点到对应准线的距离(焦准距)2b p c=。

圆锥曲线知识点总结

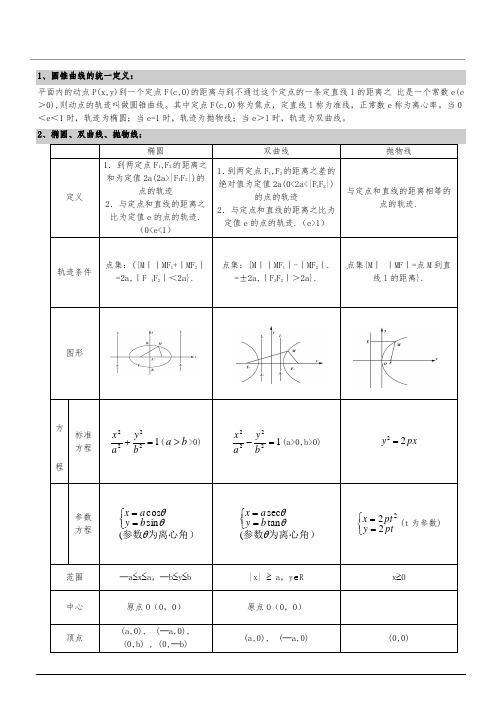
1、圆锥曲线的统一定义：平面内的动点P(x,y)到一个定点F(c,0)的距离与到不通过这个定点的一条定直线l的距离之比是一个常数e(e ＞0),则动点的轨迹叫做圆锥曲线。

其中定点F(c,0)称为焦点，定直线l称为准线，正常数e称为离心率。

当02y2x2=pxy2【备注1】双曲线：⑶等轴双曲线：双曲线222a y x ±=-称为等轴双曲线，其渐近线方程为x y ±=，离心率2=e .⑷共轭双曲线：以已知双曲线的虚轴为实轴，实轴为虚轴的双曲线，叫做已知双曲线的共轭双曲线.λ=-2222by a x 与λ-=-2222b y a x 互为共轭双曲线，它们具有共同的渐近线：02222=-b y a x .⑸共渐近线的双曲线系方程：)0(2222≠=-λλb y a x 的渐近线方程为02222=-b y a x 如果双曲线的渐近线为0=±bya x 时，它的双曲线方程可设为)0(2222≠=-λλby ax .【备注2】抛物线：（1）抛物线2y =2px(p>0)的焦点坐标是(2p ,0)，准线方程x=-2p ，开口向右；抛物线2y =-2px(p>0)的焦点坐标是(-2p ,0)，准线方程x=2p ，开口向左；抛物线2x =2py(p>0)的焦点坐标是(0,2p )，准线方程y=-2p ，开口向上；抛物线2x =-2py （p>0）的焦点坐标是（0,-2p ），准线方程y=2p，开口向下. （2）抛物线2y =2px(p>0)上的点M(x0,y0)与焦点F 的距离20p x MF +=；抛物线2y =-2px(p>0)上的点M(x0,y0)与焦点F 的距离02x pMF -=（3）设抛物线的标准方程为2y =2px(p>0)，则抛物线的焦点到其顶点的距离为2p ，顶点到准线的距离2p ，焦点到准线的距离为p.（4）已知过抛物线2y =2px(p>0)焦点的直线交抛物线于A 、B 两点，则线段AB 称为焦点弦，设A(x1,y1),B(x2,y2)，则弦长AB =21x x ++p 或α2sin 2p AB =(α为直线AB 的倾斜角)，221p y y -=，2,41221p x AF p x x +==(AF 叫做焦半径). 3、椭圆的常用结论：1. 点P 处的切线PT 平分△PF1F2在点P 处的外角.2. PT 平分△PF1F2在点P 处的外角，则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆，除去长轴的两个端点.3. 若000(,)P x y 在椭圆22221x y a b+=上，则过0P 的椭圆的切线方程是00221x x y y a b +=. 4. 若000(,)P x y 在椭圆22221x y a b +=外，则过0P作椭圆的两条切线切点为P 1、P 2，则切点弦P 1P 2的直线方程是00221x x y ya b+=. 5. 椭圆22221x y a b+= (a ＞b ＞0)的左右焦点分别为F 1，F 2，点P 为椭圆上任意一点12F PF γ∠=，则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.6. 椭圆22221x y a b+=（a ＞b ＞0）的焦半径公式10||MF a ex =+,20||MF a ex =-(1(,0)F c - ,2(,0)F c 00(,)M x y ).7. 7、已知椭圆22221x y a b +=（a ＞b ＞0），O 为坐标原点，P 、Q 为椭圆上两动点，且OP OQ ⊥.（1）22221111||||OP OQ a b +=+;（2）|OP|2+|OQ|2的最大值为22224a b a b +;（3）OPQ S ∆的最小值是2222a b a b +.8. 过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点，A 1P 和A 2Q 交于点M ，A 2P 和A 1Q交于点N ，则MF ⊥NF.9. AB 是椭圆22221x y a b +=的不平行于对称轴的弦，M ),(00y x 为AB 的中点，则22OM AB b k k a⋅=-，即202y a x b K AB-=。

圆锥曲线知识点总结

圆锥曲线知识点总结圆锥曲线是解析几何中的重要内容，由平面与一个双曲面、椭圆面或者抛物线面相交而得到。

在高中数学课程中，学习圆锥曲线是必不可少的。

本文将对圆锥曲线的定义、基本方程、性质和应用进行总结。

一、圆锥曲线的定义圆锥曲线就是平面与一个双曲面、椭圆面或者抛物线面相交而得到的曲线，在平面上的图像可以呈现出不同的形状。

二、圆锥曲线的基本方程1. 双曲线：双曲线的基本方程为：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$。

其中，a和b分别为椭圆的两个半轴。

2. 椭圆：椭圆的基本方程为：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$。

其中，a和b分别为椭圆的两个半轴。

3. 抛物线：抛物线的基本方程为：$y^2=2px$。

其中，p为抛物线的焦距。

三、圆锥曲线的性质1. 双曲线的性质：双曲线的两个分支镜像对称于原点，焦点到曲线的距离之差为常数。

双曲线还具有渐近线，即曲线趋近于两根直线。

2. 椭圆的性质：椭圆的两个焦点在椭圆的长轴上，且焦点到任意点的距离之和为常数。

此外，椭圆也具有主轴、短轴和焦距等重要概念。

3. 抛物线的性质：抛物线的焦点位于抛物线的顶点上，且焦点到抛物线上任意点的距离等于焦点到该点的法线距离。

四、圆锥曲线的应用1. 双曲线的应用：双曲线在电磁学中有广泛的应用，例如电磁波的传播、天线的辐射以及电磁场分布等方面。

2. 椭圆的应用：椭圆在力学、天文学和导航等领域有着重要的应用。

例如椭圆轨道运动的物体、天体运动规律的研究以及导航系统中的卫星轨道等。

3. 抛物线的应用：抛物线在物理学和工程学中有着广泛的应用。

例如自由落体运动、射击运动以及卫星的发射轨道等。

综上所述，圆锥曲线是解析几何中的重要内容，通过本文的总结，我们了解了圆锥曲线的定义、基本方程、性质和应用。

在学习过程中，我们需要深入理解每个曲线的特点和应用领域，为解决实际问题提供有力的数学工具。

希望本文对你对圆锥曲线的学习有所帮助。

圆锥曲线知识点全归纳(完整精华版)

圆锥曲线知识点全归纳（精华版）圆锥曲线包括椭圆，双曲线，抛物线。

其统一定义：到定点的距离与到定直线的距离的比e 是常数的点的轨迹叫做圆锥曲线。

当0<e<1时为椭圆：当e=1时为抛物线；当e>1时为双曲线。

一、圆锥曲线的方程和性质：1）椭圆文字语言定义：平面内一个动点到一个定点与一条定直线的距离之比是一个小于1的正常数e。

定点是椭圆的焦点，定直线是椭圆的准线，常数e是椭圆的离心率。

标准方程：1.中心在原点，焦点在x轴上的椭圆标准方程：(x^2/a^2)+(y^2/b^2)=1其中a>b>0，c>0，c^2=a^2-b^2.2.中心在原点，焦点在y轴上的椭圆标准方程：(x^2/b^2)+(y^2/a^2)=1其中a>b>0，c>0，c^2=a^2-b^2.参数方程：X=acosθY=bsinθ(θ为参数，设横坐标为acosθ，是由于圆锥曲线的考虑，椭圆伸缩变换后可为圆此时c=0，圆的acosθ=r)2）双曲线文字语言定义：平面内一个动点到一个定点与一条定直线的距离之比是一个大于1的常数e。

定点是双曲线的焦点，定直线是双曲线的准线,常数e是双曲线的离心率。

标准方程：1.中心在原点,焦点在x轴上的双曲线标准方程：(x^2/a^2)-(y^2/b^2)=1其中a>0,b>0,c^2=a^2+b^2.2.中心在原点,焦点在y轴上的双曲线标准方程：(y^2/a^2)-(x^2/b^2)=1.其中a>0,b>0,c^2=a^2+b^2.参数方程：x=asecθy=btanθ(θ为参数 )3）抛物线标准方程：1.顶点在原点,焦点在x轴上开口向右的抛物线标准方程：y^2=2px 其中 p>02.顶点在原点,焦点在x轴上开口向左的抛物线标准方程：y^2=-2px 其中 p>03.顶点在原点,焦点在y轴上开口向上的抛物线标准方程：x^2=2py 其中 p>04.顶点在原点,焦点在y轴上开口向下的抛物线标准方程：x^2=-2py 其中 p>0参数方程x=2pt^2 y=2pt (t为参数) t=1/tanθ(tanθ为曲线上点与坐标原点确定直线的斜率）特别地，t 可等于0直角坐标y=ax^2+bx+c (开口方向为y轴, a<>0 ） x=ay^2+by+c （开口方向为x轴, a<>0 )圆锥曲线（二次非圆曲线）的统一极坐标方程为ρ=ep/(1-e×cosθ)其中e表示离心率，p为焦点到准线的距离。

完美版圆锥曲线知识点总结

圆锥曲线的方程与性质1.椭圆（1）椭圆概念平面内与两个定点 F i 、F 2的距离的和等于常数 2a （大于IF 1F 2I ）的点的轨迹叫做椭圆。

这两个定点叫做椭圆表示焦点在y 轴上的椭圆。

（2）椭圆的性质-y 代替y 方程不变，所以若点（X, y ）在曲线上时，点（x,-y ）也在曲线上,-X 代替X 方程不变，则曲线关于y 轴对称。

若同时以 -X 代替X ，-y 代替y方程也不变，则曲线关于原点对称。

所以，椭圆关于X 轴、y 轴和原点对称。

这时，坐标轴是椭圆的对称轴，原点是对称中心，椭圆的对称中心叫椭圆的中心;③ 顶点：确定曲线在坐标系中的位置，常需要求出曲线与X 轴、y 轴的交点坐标。

在椭圆的标准方程中，令2 ①范围：由标准方程X2a 2+：2 =1知I XI 兰a , I y I 兰b ,说明椭圆位于直线 X = ±a , y = ±b 所围成的矩形里;的焦点，两焦点的距离2c 叫椭圆的焦距。

若 M 为椭圆上任意一点，则有IMF " 1 + 1 MF 2 |=2a 。

上）。

椭圆的标准方程为:2 2X y—=1 （ a >b 》0 ）（焦点在X 轴上）或（焦点在y 轴注：①以上方程中a,b 的大小 a >b ：>0，其中 b 2 =a 2 -c 2 ；y 2X2分b^"两个方程中都有“b 〉0的条件，要分清焦点的位置，只要看X 2和y 2的分2 2母的大小。

例如椭圆一+仏=1 m n（m >0， n>0，mHn ）当m 》n 时表示焦点在x 轴上的椭圆;当 men 时②对称性：在曲线方程里，若以所以曲线关于X 轴对称，同理，以2 2②对称性：双曲线务-乂〒=1关于每个坐标轴和原点都是对称的，这时，坐标轴是双曲线的对称轴，原点a b2 2是双曲线X-y2 =1的对称中心，双曲线的对称中心叫做双曲线的中心。

a 2 b 222冷亠 =1的方程里，对称轴是 X, y 轴，所a 2b 22 2以令y =0得X = ±a ，因此双曲线和X 轴有两个交点 A （-a,0）A 2（a,0），他们是双曲线 =1的顶点。

高中数学圆锥曲线知识点总结

高中数学中，圆锥曲线是重要的内容之一。

以下是对圆锥曲线的知识点进行总结：1. 圆锥曲线的定义：圆锥曲线是在平面上由一个固定点（焦点）和一个到该点的固定距离之比（离心率）确定的曲线。

2. 椭圆：-定义：椭圆是所有到两个焦点的距离之和等于常数的点的集合。

-基本方程：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$，其中$a$和$b$分别代表椭圆的半长轴和半短轴。

-离心率：$e=\frac{\sqrt{a^2-b^2}}{a}$，离心率满足$0<e<1$。

3. 双曲线：-定义：双曲线是所有到两个焦点的距离之差的绝对值等于常数的点的集合。

-基本方程：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$，其中$a$和$b$分别代表双曲线的半长轴和半短轴。

-离心率：$e=\frac{\sqrt{a^2+b^2}}{a}$，离心率满足$e>1$。

4. 抛物线：-定义：抛物线是所有到一个焦点的距离等于到直线（准线）的距离的点的集合。

-基本方程：$y^2=4ax$，其中$a$为抛物线的焦点到准线的距离的一半。

5. 圆：-定义：圆是到一个固定点的距离等于常数的点的集合。

-基本方程：$(x-h)^2+(y-k)^2=r^2$，其中$(h,k)$为圆心的坐标，$r$为半径的长度。

6. 圆锥曲线的性质：-焦点和准线：椭圆和双曲线有两个焦点和一条准线，抛物线有一个焦点和一条准线，圆只有一个焦点和没有准线。

-对称性：椭圆和双曲线关于$x$轴、$y$轴对称，抛物线关于$y$轴对称。

-焦点与离心率的关系：椭圆和双曲线的离心率小于1，抛物线的离心率等于1，圆的离心率为0。

-焦点与直径的关系：椭圆和双曲线的焦点在直径上，抛物线的焦点在对称轴上。

7. 焦点和准线的性质：-椭圆和双曲线：对于椭圆和双曲线，焦点到准线的距离等于焦点到曲线上任意点的距离之差的一半。

同时，准线也是曲线的对称轴。

高中数学_圆锥曲线知识点小结

高中数学_圆锥曲线知识点小结《圆锥曲线》知识点小结一、椭圆：（1）椭圆的定义：平面内与两个定点F1,F2的距离的和等于常数（大于|其中：两个定点叫做椭圆的焦点，焦点间的距离叫做焦距。

注意：2a |F1F2|表示椭圆；2a |F1F2|表示线段F1F2；2a |F1F2|没有轨迹；（2F1F2|）的点的轨迹。

22xy3．常用结论：（1）椭圆1(a b 0)的两个焦点为F1,F2，过F1的直线交椭圆于A,B两a2b2点，则ABF2的周长= （2）设椭圆x2y22 1(a b 0)左、右两个焦点为F1,F2，过F1且垂直于对称轴的直线2ab交椭圆于P,Q两点，则P,Q的坐标分别是|PQ|二、双曲线：（1）双曲线的定义：平面内与两个定点F1,F2|迹。

其中：两个定点叫做双曲线的焦点，焦点间的距离叫做焦距。

注意：|F1F2|PF1| |PF2| 2a与|PF2| |PF1| 2a（2a |F1F2|）表示双曲线的一支。

2a |F1F2|表示两条射线；2a |F1F2|没有轨迹；（2）双曲线的标准方程、图象及几何性质：标准方程中心在原点，焦点在x轴上中心在原点，焦点在y轴上x2y21(a 0,b 0) a2b2y2x22 1(a 0,b 0) 2ab图形B1(0, a),B2(0,a)顶点对称轴焦点焦距离心率渐近线通径（3）双曲线的渐近线：A1( a,0),A2(a,0)x轴，y轴；虚轴为2b，实轴为2aF1( c,0),F2(c,0)|F1F2| 2c(c 0) ceF1(0, c),F2(0,c)a2 b2c(e 1)（离心率越大，开口越大）aybx a2b2 ayax b2222①求双曲线x y 1的渐近线，可令其右边的1为0，即得x y 0，因式分解得到x y 0。

aba2b2a2b2x2y2x2y2②与双曲线2 2 1共渐近线的双曲线系方程是2 ；2ab（4）等轴双曲线为x2y2 t2，其离心率为yx（4）常用结论：（1）双曲线2 1(a 0,b 0)的两个焦点为F1,F2，过F1的直线交双曲线的2ab同一支于A,B两点，则ABF2的周长x2y22 1(a 0,b 0)左、右两个焦点为F1,F2，过F1且垂直于对称轴的2ab（2）设双曲线直线交双曲线于P,Q两点，则P,Q的坐标分别是|三、抛物线：PQ|（1）抛物线的定义：平面内与一个定点的距离和一条定直线的距离相等的点的轨迹。

高中数学圆锥曲线总结

数学圆锥曲线总结1、圆锥曲线的两个定义：（1）第一定义中要重视“括号”内的限制条件：椭圆中，与两个定点F，F的距离的和等于常数，且此常数一定要大于，当常数等于时，轨迹是线段F F，当常数小于时，无轨迹；双曲线中，与两定点F，F的距离的差的绝对值等于常数，且此常数一定要小于|F F|，定义中的“绝对值”与＜|F F|不可忽视。

若＝|F F|，则轨迹是以F，F为端点的两条射线，若﹥|F F|，则轨迹不存在。

若去掉定义中的绝对值则轨迹仅表示双曲线的一支。

（2）第二定义中要注意定点和定直线是相应的焦点和准线，且“点点距为分子、点线距为分母”，其商即是离心率。

圆锥曲线的第二定义，给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系，要善于运用第二定义对它们进行相互转化。

Attention：（1）在求解椭圆、双曲线问题时，首先要判断焦点位置，焦点F，F的位置，是椭圆、双曲线的定位条件，它决定椭圆、双曲线标准方程的类型，而方程中的两个参数，确定椭圆、双曲线的形状和大小，是椭圆、双曲线的定形条件；在求解抛物线问题时，首先要判断开口方向；（2）在椭圆中，最大，，在双曲线中，最大，。

4.圆锥曲线的几何性质：（1）椭圆（以（）为例）：①范围：；②焦点：两个焦点；③对称性：两条对称轴，一个对称中心（0,0），四个顶点，其中长轴长为2，短轴长为2；④准线：两条准线；⑤离心率：，椭圆，越小，椭圆越圆；越大，椭圆越扁。

（2）（2）双曲线（以（）为例）：①范围：或；②焦点：两个焦点；③对称性：两条对称轴，一个对称中心（0,0），两个顶点，其中实轴长为2，虚轴长为2，特别地，当实轴和虚轴的长相等时，称为等轴双曲线，其方程可设为；④准线：两条准线；⑤离心率：，双曲线，等轴双曲线，越小，开口越小，越大，开口越大；⑥两条渐近线：。

（3）抛物线（以为例）：①范围：；②焦点：一个焦点，其中的几何意义是：焦点到准线的距离；③对称性：一条对称轴，没有对称中心，只有一个顶点（0,0）；④准线：一条准线；⑤离心率：，抛物线。