风与结构的耦合作用及风振响应分析(精)
多因素耦合作用下的结构动力响应分析

多因素耦合作用下的结构动力响应分析结构动力学是土木工程中的一个重要分支,研究结构在外力作用下的振动特性和动力响应。
在实际工程中,结构受到多种因素的耦合作用,如地震、风载、温度变化等,这些因素的共同作用会对结构的动力响应产生影响。
因此,了解多因素耦合作用下的结构动力响应是非常重要的。
首先,我们来讨论地震因素对结构的动力响应的影响。
地震是一种短周期的振动载荷,其频率范围广,能量较大。
当地震发生时,结构会受到地震波的激励,产生振动响应。
地震波的传播路径和结构的固有振动频率密切相关,当地震波的频率接近结构的固有频率时,共振现象就会发生,从而导致结构的振动幅值增大。
因此,在结构设计和抗震设防中,需要对结构的固有频率进行合理选择,以避免共振现象的发生。
其次,风载是另一个重要的结构动力响应影响因素。
风是一种长周期的振动载荷,其频率范围相对较窄,但能量较大。
当风载作用于结构时,会产生风压力,使结构产生振动响应。
风压力的大小与风速、结构形状以及结构表面粗糙度等因素有关。
在设计中,需要根据结构的特点和所处的环境条件来确定风荷载的大小和分布。
此外,结构的抗风性能也是一个重要考虑因素,通过合理的结构形状和防护措施,可以降低结构受到风载的影响。
温度变化也是影响结构动力响应的重要因素之一。
温度变化会导致结构的体积膨胀或收缩,从而产生内应力和变形。
当结构受到温度变化作用时,会产生温度应力和热应力,进而影响结构的稳定性和振动特性。
因此,在结构设计和施工中,需要考虑温度变化对结构的影响,并采取相应的措施来减小温度变形和应力。
除了地震、风载和温度变化,结构的动力响应还受到其他因素的耦合作用。
例如,结构的材料性能、结构的几何形状、结构的支座条件等都会对结构的动力响应产生影响。
在结构设计和分析中,需要综合考虑这些因素,并进行合理的模型建立和分析,以准确预测结构的动力响应。
综上所述,多因素耦合作用下的结构动力响应分析是一个复杂而重要的问题。
风力发电机耦合振动分析

( 2) ( 3)
式中 , B 为桨叶数量 , c为截面弦长 , F 为叶尖和轮 毂损失 , H 为诱导修正因子 , r为叶素半径 , < 为叶素来
动比 ; Tm :高速轴上的扭矩 ; λ:尖速比 ;ρ :空气密度 ; R: 风轮半径 ; U ∞ :上风向风速 ; 高速端传动模型为 : ωg d ( 12 ) Jg = Tm - Te dt 2 其中 : J g : 电机转动惯量 , kgm ,ωg : 电机转动角速 度 , rad / s; Tm 高速轴上的扭矩 , Te 发电机上的反扭矩 。 失速控制风力发电机组采用的电机主要是定速感 应电机 , 其特性由斜率 h 和短路瞬态时间常数 τ 。电机
流角 , ve - op ve - ip为叶素上面内和面外的变形速度 , Ω 为 风轮转速 、 U ∞为来流风速 , C l 、CD 为升阻力系数 , 为 L 和 D 的无因次化量 。进行计算时 , 对给定 a 和 a ′ 初始 值进行迭代计算 , r, c, B , U ∞ , Ω 为已知 , ve - op ve - ip的结 果从结构动力学分析计算而来 , 计算出对应的 Cx , Cy , H, F, < , W , 生成新的 a, a ′ , 当迭代误差达到要求 , 即计 算出 a, a ′ 。 a, a ′ 确定后 , Cx , Cy , H, F, < , W 也相应确 定 , 根据叶素理论 , 叶素上法向力和切向力分别为 : 2 ρ ( 4) dL = 1 / 2 W cCL (α) d r 2 ρ ( 5) dD = 1 / 2 W cCD (α) d r 式中 ,ρ 为空气密度 , W 为相对速度 。 叶素上的推力和转矩分别为 : 1 2 ( 6) dF = ρ W c ( CL cos< + CD sin < ) d r 2 1 2 ( 7) dT = ρ W c ( CL sin < - CD cos< ) d r 2 因此 , 对于第 i个半径为 R 的风轮叶片 , 推力 F、 转 矩 T 和产生的功率 P 分别为 :
考虑土—结构相互作用的大型风力发电结构风—震耦合作用下动力响应分析

考虑土—结构相互作用的大型风力发电结构风—震耦合作用下动力响应分析考虑土—结构相互作用的大型风力发电结构风—震耦合作用下动力响应分析随着全球对可再生能源的需求不断增长,风力发电作为一种环保、可持续的能源形式得到了广泛应用。
大型风力发电结构在风—震耦合作用下的动力响应分析具有重要的工程意义。
针对该问题,本文旨在探索大型风力发电结构在风—震耦合作用下的动力响应,并考虑土—结构相互作用的影响。
首先,本文将介绍大型风力发电结构的基本构造和工作原理。
大型风力发电结构由塔筒、机舱、叶片和基础组成,其中叶片通过转动驱动发电机发电。
风力发电结构的基础在土壤中承受着巨大的力学荷载,因此考虑土—结构相互作用对风力发电结构的动力响应分析具有重要意义。
接下来,本文将详细介绍大型风力发电结构的风—震耦合作用。
风力作为外界激励力引起结构的震荡,而地震则是地面运动引起的振动。
当风和地震共同作用时,风力发电结构的动力响应将受到双重激励影响。
风—震耦合作用是一个复杂的过程,需要考虑风力和地震的频率、振幅、相位和方向等因素。
然后,本文将分析大型风力发电结构在风—震耦合作用下的动力响应。
首先,通过建立结构的数学模型,采用有限元方法进行计算,获得结构受力、位移和振动特性等参数。
其次,通过数值模拟和实验验证,研究风力和地震双重激励对结构的影响。
最后,对不同风速、地震强度和土壤条件下的结构响应进行综合分析和比较。
最后,本文将讨论土—结构相互作用对大型风力发电结构的影响。
土—结构相互作用是指结构与土壤之间的相互作用,包括土壤的刚度、阻尼和耗散能力等因素。
通过考虑土—结构相互作用,可以更准确地预测结构的动力响应,提高结构的抗风、抗震能力。
综上所述,本文通过考虑土—结构相互作用的影响,探索大型风力发电结构在风—震耦合作用下的动力响应分析。
这对于优化风力发电结构设计、提高结构的抗风、抗震能力具有重要的工程应用价值综合上述分析,风-震耦合作用对大型风力发电结构的动力响应具有重要影响。
结构动力学中的风振问题分析

结构动力学中的风振问题分析结构动力学是研究结构在外界力作用下的振动行为的学科,而风振问题则是结构动力学中一个重要的研究方向。
本文将从风振问题的背景和原因、影响因素和评估方法等方面进行详细分析和讨论。
一、背景和原因在风振问题中,结构物在大风环境下会受到风力的作用,引起结构的振动。
风振问题主要存在于高层建筑、长跨度桥梁、烟囱、塔楼等高耸结构中。
这种振动既可能是结构自身的自由振动,也可能是受到风力激励后的强迫振动。
风振问题的产生原因可以归结为以下几点:1. 气象因素:大风引起的气动力是产生风振问题的主要原因之一。
气象因素包括风速、风向、风向变化频率等。
2. 结构刚度:结构刚度的大小将直接影响结构的振动特性,而刚度小的结构更容易受到风力的激励而发生振动。
3. 结构阻尼:结构的阻尼越小,振动越容易发生和持续。
因此,结构的阻尼对于风振问题的研究具有重要意义。
4. 结构质量:结构质量的大小也将影响结构的振动特性,质量越大,振动频率越低,风振问题相对较小。
二、影响因素风振问题的复杂性决定了其受到多个因素的共同影响。
主要的影响因素包括:1. 风速和风向:风速和风向是产生风振问题的主要因素,其中风速对结构振动的影响最为显著。
2. 结构特性:结构的刚度、质量和阻尼等特性将直接影响结构的振动响应。
3. 结构形状和几何尺寸:结构的形状和几何尺寸影响着结构对风力的反应,尤其是在流体作用下的层流和湍流区域。
4. 地面效应:结构与地面之间的交互作用对风振问题也具有重要影响。
三、评估方法针对风振问题,需要进行定量的评估和分析,以寻找有效的风振控制措施。
常用的评估方法包括:1. 数值模拟:通过数值模拟方法,可以模拟结构在大风作用下的振动响应。
常用的数值方法包括有限元法、计算流体力学方法等。
2. 风洞试验:风洞试验可以模拟真实的风场环境,并通过模型的测试来评估结构的振动响应。
风洞试验是评估风振问题最为直观和准确的方法之一。
3. 实测方法:通过实际的结构振动监测数据,可以对结构的风振问题进行评估和分析。
良态风及台风不同风谱对结构风雨振反应对比分析

Ab s t r a c t : No r ma l w i n d a n d t y p h o o n s p e c t r a w e r e u s e d t o g e n e r a t e t i me h i s t o r y c u r v e s o f wi n d a n d r a i n l o a d s i n
关键 词:台风 ; 良态风 ; 雨荷载 ; 风速 谱 ; 输 电塔
中 图分 类 号 :T M 7 5 3 文 献 标 志码 :A D O I : 1 0 . 1 3 4 6 5 / j . c n k i . i V S . 2 0 1 5 . 1 1 . 0 0 2
Co mpa r a t i v e a na l y s i s f o r wi n d a n d r a i n- i n duc e d r ur e s wi t h no r ma l i n w d a nd t y ph o o n s p e c t r a
FU X g,L I Ho n g— n a n ( F a c u l t y o f I n f r a s t r u c t u r e E n g i n e e r i n g ,D a l i a n U n i v e r s i t y o f T e c h n o l o g y ,D a l i a n 1 1 6 0 2 4 , C h i n a )
考虑风与结构耦合作用时电视塔结构的风振响应

毕
() 6
叶 变换 一时频 迭代 法 来求 解结 构 的运 动微 分 方程 , 最后 得 到结 构 的 风振 响应 。计 算 结 果表 明 对 电 视 塔 结构 应考 虑风 与结 构 的耦合 作 用 。
关键 词 : 电视塔 结 构 ; 合 ; 线性 ; 耦 非 凤振 响应
中 图分 类 号 : U3 1 T 1
文章编号 :6 3—0 7 2 0 0 17 4 X(0 6)4—0 2 0 7—0 4
考虑 风 与 结构 耦 合 作 用 时 电视 塔 结构 的风 振 响应
范存新 薛松涛2 陈 , , 镕2唐和生2 ,
(. 1 苏州科技 学院 , 江苏 苏州 2 5 1 ; 1 0 1 2同济大学结 构工程与防灾研究所 , 上海 2 0 9 0 02
文献 标识 码 : A
在 目 的风振响应计算中 , 前 理论分析大多数集中在结构 的顺风向响应上 , 在分析方法上一般可分成在频 率域范 围内以及在时间域范围内这两个方面进行 , 虽然这两方面的计算基本上都趋于成熟 , 但是 由于计算过 程的复杂 , 大多数结构风振响应分析均作了一定 的简化 , 特别是没有考虑风与结构 的耦合作用 , 对基频较小 的高耸结构 、 特别是电视塔结构来说 , 考虑与不考虑结构速度对风速 的耦合作用 , 将产生不 同的结构响应特 征。由于结构速度与风速的耦合将 在运动 方程 中产生非线性项 , 方程难 以用 常规 的振型分 解法解耦 , 文
1 风荷载 的随机 时程模拟
在用时程分析法计算结构的风振响应时 , 首先要进行风荷载的时程模拟 , 时程模拟的主要方法有谐波叠 加法和线性滤波器法。其 中线性滤波器法利用 P阶 自回归过滤器技术来产生脉 动风速时程具有计算量小
风力机结构耦合振动分析

和气动载荷, 计算出的气动载荷作为输入作用在 结构动力学模型上。由于气动载荷的变化 , 引起 结构发生变形 , 计算出的变形又作为输入作用在 空气动力学模型上 , 从而可计算出相应的气动载 荷, 这就是气弹耦合现象。结构动力学模型计算 出的输出扭矩 , 同时作用在传动链模型上, 传统链 模型也对结构动力学模型产生反作用力矩 , 在空 气动力学模型和传动链模型联合作用下 , 通过结 构动力学模型计算出转速。转速又影响空气动力 学模型载荷的气动载荷计算, 生成新的气动载荷, 又作用在结构动力学模型上。各模型之间的关系 如图 1 所示。其中, 空气动力学模型和传动链动 力学模型是在 MA TLAB/ Simulink 下构建的 , 结 构动力学模型是在 ADAMS/ View 下构建的。
重庆大学, 重庆, 400044
摘要 : 采用通用动态尾流理论进行风力机气动力学的计算分析 , 并用 MAT LAB/ Simulink 进行编 程, 建立了风力机传动链的数学模型 。在 MATLAB/ Simulink 中进行传动链系统的编程运算 , 建立了 风力机 ADA MS 柔性多体结构动力学仿真模型 , 并利用 MAT LAB/ Simulink 和 ADAMS 进行风力机振 动性能的联合仿真。 仿真时将气动载荷加载到风力机叶片结构上, 将传动系统模型的反扭矩加到 AD2 AMS 风轮模型上 , 同时考虑风力机的结构变形对气动性能 、 传动性能产生的影响。 仿真最终实现了风 力机系统振动性能耦合分析, 其数据同实验测试数据比较表明, 该联合仿真方法可以较好地模拟风力机 的振动特性。 关键词: 通用动态尾流理论; 联合仿真; 风力发电机 ; 振动 中图分类号 : T K83; TP391 文章编号: 1004 ) 132X( 2008) 01 ) 0009 ) 05 Coupled Vibrat ion Analysis of Wind Turbine Jin Xin H e Yulin Du Jing Liu H ua Chongqing Univer sit y, Chongqing, 400044 Abstr act: T he aer odynamics charact erist ics of wind t ur bine were calculat ed by applying GDW t he2 ory and wer e programmed in MATLAB/ Simulink. T he drive chain was calculat ed by applying st at e space met hod and also progr ammed in MAT LAB/ Simulink. T he model of t he wind t ur bine was built in Adams. T he simulat ion of vibr at ion charact erist ics was car ried out so t hat the aer odynamic loads and t he t orque were applied t o t he st ruct ure of t he rotor. Simult aneously t he defor mat ion of t he str uc2 t ure also affect ed t he loads. The result s show t hat t he met hod has excel lent abilit y t o simulate t he vi2 brat ion charact erist ics almost t he same as t est measur ed. Key words: GDW( generalized dynamic wake) t heory; combined simulat ion; wind t urbine; vibra2 t ion
风荷载与结构的风致响应及解决方法

风荷载与结构的风致响应及解决方法摘要:风是一种为人们所熟知的自然现象,影响着生活的方方面面。
而且,风能作为一种可再生的绿色能源也已越来越被重视。
但是,对于结构而言,风对结构的影响可以说都是不利的。
尤其是对于那些质量轻、柔度大、阻尼小、自振频率低的结构,如:大跨度桥梁、超高层建筑、大跨度悬挑屋盖等,风往往是设计的主要控制因素之一。
根据风压随时间变化的特点,其被分解为平均风压和脉动风压两个分量。
不同的风压分量往往会引起结构的不同类型的破坏。
本文将结合若干工程实例,浅谈其破坏类型,并总结相关设计方法。
关键字:风荷载;风敏感结构;风致响应;抗风设计1.自然风1.1. 风的成因空气是由各种气体分子等组成的混合物,是一种流体。
其运动方向是气压的正梯度方向。
只有存在气压差时,才会形成风。
在自然条件下,气压差往往是由于太阳辐射的不均匀、地球上水陆分布的不均匀使空气产生不均匀的升温而造成的。
太阳光照射在地球表面上,使地表温度升高,地表的空气受热膨胀变轻而往上升。
热空气上升后,低温的冷空气横向流入,上升的空气因逐渐冷却变重而降落,由于地表温度较高又会加热空气使之上升,这种空气的流动就产生了风。
图1-1 全球大气循环1.2. 风的类型根据风的成因的不同,可分为多种类型的风。
以下是一些典型的、对土木工程影响较大的风气候。
大气环流:大气环流是指在全球范围由太阳辐射和地球自传作用形成的大尺度的大气运动,它决定了各地区天气的行程与变化。
其中季风就是由大气环流、海陆分布和大陆地形等多种因素造成的,是以年为周期的一种区域性的大气运动。
这种类型的风作用区域最大、破坏性小,是平时最为常见的一类风。
热带气旋:热带气旋是指在热带或副热带海洋上产生的强烈空气漩涡。
其直径通常为几百千米,厚度为几十千米。
强烈的热带气旋不但形成狂风、巨浪,而且往往伴随发生暴雨、风暴潮,造成严重的灾害。
这种类型的风作用区域较大,持续时间长,而且具有很强的破坏性,是主要的自然灾害之一。
结构风振响应分析

平均风压
脉动风压
50
01——0:;_sec
0、200400600
——U0N/m2)
10
•
由涡旋脱落引起的结构受迫振动。
特点:
1)细长形结构
2)确定性谐波振动
3)风荷载可由风洞试验或正弦激励假定确定
Along-wind
方柱的升力系数和
阻力系数时程
方柱的升力和阻力
功率谱
會3LOW
fB/U
10W
當.3(7电
★风振响应坐标系统
★按响应方向分类•顺风向振动
沿来流风向的振动; 主要由大气来流中的 湍流脉动引起的。
★按响应性质分类
•
由风压脉动引起的结构振动。
特点:
1)受迫振动
2)随机振动,需采用随机振动理论分析3)风荷载通常由风洞试验Fra bibliotek拟定常假定确定
拟定常假定:假定作用在物体表面的脉动 风压与来流风速具有相同的变化规律。
Required Course for Undergraduate Students
4.
武岳孙瑛
Harbi n Institute of T ech no logy
本章内容
4.1结构风振响应类型4.2顺风向风振响应分析
4.3横风向风振响应分析
建筑结构中的风振响应研究

建筑结构中的风振响应研究近年来,建筑工程的安全问题越来越引起人们的关注。
其中,风振响应研究成为了一个热门话题。
此次文章将对建筑结构中的风振响应研究进行探讨。
一、风振响应的概念风振响应是指建筑物在风力作用下所发生的振动。
建筑物所受风荷载的变化将引起结构振动,可能产生结构共振。
随着建筑结构的发展,越来越多的结构形式出现,这些形式的特点会影响结构的风振响应。
二、影响风振响应的因素1. 建筑结构特征:建筑结构的刚度、坚固程度和柔韧性等特征是影响建筑物风振响应的最主要因素之一。
例如,高层建筑的高度和重量是影响风振响应的重要因素。
2. 风荷载的特征:建筑物所受风荷载的变化也会影响风振响应。
例如,风速的大小、风向的变化等都会对建筑物的风振响应产生影响。
3. 地面条件:建筑物所处的地面条件也会影响风振响应。
地形、土壤的属性、地面的起伏程度等都会对结构的振动产生影响。
三、风振响应的研究手段1. 数值分析法:通过有限元分析等数值模拟方法,可以得出建筑物在不同风荷载情况下的振动,从而评估风振响应情况。
2. 实验研究法:通过建造模型、进行风洞试验等实验手段,可以模拟不同风荷载情况下建筑结构的振动,从而获取风振响应的相关数据。
3. 结构优化方法:通过对建筑结构的设计进行优化,可以达到降低风振响应的效果。
四、风振响应的对策1. 提高建筑物的刚度和抗风能力:通过提高建筑物的刚度和抗风能力,可以有效减少风振响应的产生。
2. 选择合适的结构形式:合理选择建筑物的结构形式,可以有效避免结构的风振响应。
3. 采用适当的结构优化方法:通过对建筑物的结构进行优化,可以有效降低风振响应。
总之,对于建筑结构中的风振响应研究,需要考虑多方面的因素,包括建筑结构的特征、风荷载的特征和地面条件等。
研究风振响应的手段也应包括数值分析法、实验研究法和结构优化方法等。
对建筑物进行适当的加强和优化可以有效降低风振响应,确保建筑物的安全性。
风力发电系统结构动力学优化与振动控制

风力发电系统结构动力学优化与振动控制随着对可再生能源的需求不断增长,风力发电系统作为一种清洁、可再生的能源选择,受到了广泛关注。
然而,风力发电系统在实际运行过程中存在着结构动力学问题,特别是振动现象,这对系统的可靠性和性能带来了一定的挑战。
风力发电系统结构动力学是研究系统在外部风载荷和内部激振下的振动特性和响应,并通过优化设计和振动控制来提高系统的可靠性和性能。
本文将针对风力发电系统结构动力学优化与振动控制进行探讨和分析。
首先,风力发电系统的结构动力学优化是通过对系统的结构参数进行优化设计,以提高系统的稳定性和有效性。
通常,优化的目标是减少系统的质量和弯曲刚度,降低系统的固有频率,以便使系统能够更好地抵抗外部风载荷和内部激振,减少结构振动的影响。
此外,还可以通过改变叶片的材料和几何形状,以及调整塔筒的结构参数,来改善系统的动力学特性。
其次,风力发电系统的振动控制是通过采用一系列控制策略和技术,来减小系统振动对系统性能的影响。
在振动控制中,主要应用的方法包括主动振动控制、被动振动控制和半主动振动控制等。
主动振动控制是通过在系统中引入主动控制装置,通过实时监测和反馈控制来减小系统振动。
被动振动控制是通过在系统中引入阻尼装置,通过吸收和分散振动能量来减小系统振动。
半主动振动控制则是综合了主动和被动控制的优点,通过改变控制装置的刚度和阻尼特性,以适应不同的振动条件。
为了实现风力发电系统结构动力学优化与振动控制,需要进行系统的动力学建模和仿真分析。
在动力学建模中,主要包括风力发电机组的机械动力学模型、风力机叶片的结构动力学模型、风载荷的模型等。
通过建立系统的数学模型,可以预测系统在不同条件下的振动响应,并进行结构参数的优化设计和控制策略的选择。
在仿真分析中,可以利用计算机技术和数值计算方法,对系统的振动特性、响应以及优化效果进行评估和验证。
通过仿真分析,可以快速获取系统的动力学响应和优化结果,为系统设计和控制决策提供参考依据。
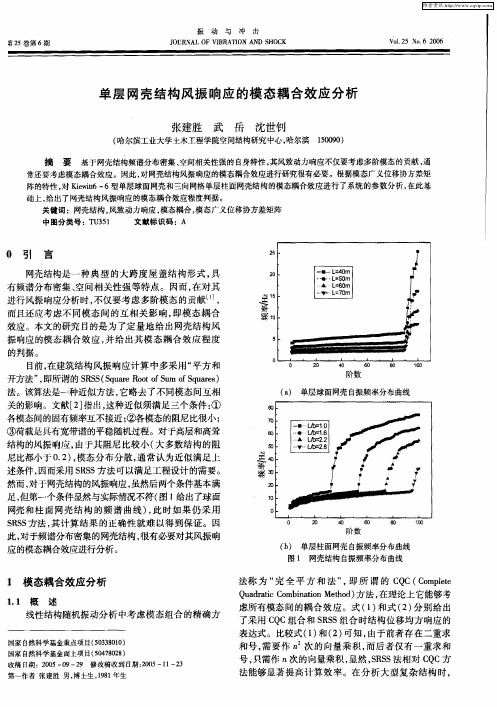
单层网壳结构风振响应的模态耦合效应分析
振
喜2 卷第 6期 5
动
与
冲
击
J U N LO IR I N A D S C O R A F V B AT O N HO K
单层 网壳结 构风 振 响应 的模 态 耦 合效 应分 析
张建胜 武 岳 沈世钊
10 9 ) 5 00
第一作者 张建胜 男 , 博士生 , 8 年生 1 1 9
法称 为 “ 全平 方 和法 ” 即所 谓 的 C C( o p t 完 , Q Cm le e Q art o bntnMe o ) 法 , 理论 上 它能够考 udai Cm iao t d 方 c i h 在 虑所有模态问的耦合效应。式 ( ) 1 和式 ( ) 2 分别给 出 了采用 C C组合和 S S 组合时结构位移均方响应的 Q RS 表达式 。比较式( ) 2 可知 , I 和( ) 由于前者存 在二重求 和号 , 需要作 乃 次 的向量乘积 , 而后者仅有一重求和 号, 只需作 n 次的向量乘积, 显然 ,R S S S 法相对 C C方 Q 法能够显著提高计算效率。在分析大型复杂结构时,
; J帅() ()d ∑ ∞ I ∞ lt ( I s o 2 )
式中,I 为外荷载广义力谱密度矩阵, ( ) [Ⅳ ] s ∞ 为频
响函数 日 ( ) 的共轭复数 。 ∞ 近年来 , 随着计算机技术 的发展 和计算 手段 的提 高,Q C C方法又重新成为研究 的热点。Wio l n等 在地 s 震分析的响应谱法中采用 C C法, Q 给出了比 S S 方法 RS 明显改善的结果;i eh n4、 e d -分别针对多点 Ku gi _ H r i 5 r a J e a 地震支座运动激励下结构响应问题 , 给出了 C C法的具 Q 体表达式 ; 林家浩 则提出了“ 虚拟激励法” Ped x ( s oE- u
基于双向流固耦合的海上风力发电塔架风致响应特性分析

基于双向流固耦合的海上风力发电塔架风致响应特性分析随着全球环保意识的不断提高和能源结构的逐渐优化,风力发电逐渐成为了新能源领域中的一个重要组成部分。
海上风力发电具有风能资源充足、发电效率高以及对环境污染低等优点,正逐渐被人们所重视。
然而,在海上建立风力发电塔架会面临着应力复杂、弹塑性结构特性明显等困难。
本文旨在基于双向流固耦合对海上风力发电塔架的风致响应特性进行研究。
1. 双向流固耦合概述双向流固耦合是指空气与结构之间发生相互作用,在此过程中,气体不断地与结构表面发生接触或离开,同时结构也对空气产生反作用力。
风能是土地和海洋上进行风能开发的基础资源。
在海上风力发电中,架设在水面上的风力发电塔架需要对风场所对应的风压和波浪荷载进行耦合计算。
2. 海上风力发电塔架结构海上风力发电塔架结构主要由桥架、柱子、桅杆、连接处及深基础等组成。
桥架连接塔身和基础,在塔身和基础间起到一个水平承载体系的作用;柱子起到一个立体支撑的作用;桅杆则承担着塔筒的重量和风荷载等荷载分担工作。
连接处则不仅为各基础构件之间的相互连接提供联系,同时也可起到刚性补强的作用。
深基础主要承担着浮力提供不足的部分,并将塔筒的荷载传送到更深的海床土层中。
3. 风致响应特性分析(1)风荷载风荷载是海上风力发电塔架结构中的主要荷载之一。
在气流与塔身相互作用的过程中,风流层内的空气具有强烈的涡旋运动,产生了一系列大小形状不同的涡旋,涡旋进一步导致了气体的剪切和压缩等几何变化。
由于在海上风力发电中,气流运动状态具有一定的随机性,因此风荷载的参数随机性较强。
(2)液体荷载海水波浪荷载是海上风力发电塔架结构中的另一个重要荷载。
海水波浪荷载主要表现为环绕在塔身周围的波浪荷载和塔身底部埋入海床中的波浪荷载。
波浪荷载的不确定性较大,波浪荷载的高度、波长、周期以及入射角等参数难以测量。
(3)动力响应塔筒受到风荷载和波浪荷载时,将产生一系列动力响应,包括位移、速度、加速度等。
建筑结构设计中的风荷载与风力响应分析

建筑结构设计中的风荷载与风力响应分析在建筑结构设计中,风荷载与风力响应分析是至关重要的。
风是自然界中的一种常见力量,它对建筑物产生的压力和力学响应不能忽视。
本文将探讨建筑结构设计中的风荷载与风力响应分析,并提供一些相关的实例和方法。
一、风荷载分析风荷载是指风对建筑物产生的压力和力学效应。
在建筑结构设计中,风荷载是必须考虑的重要因素之一。
首先,我们需要了解风荷载的来源和作用机制。
风荷载的来源主要是大气中的气压差异引起的。
当风经过建筑物时,会在建筑物表面产生压力差,从而产生荷载。
风荷载对建筑结构的影响有两个方面:一个是静风荷载,即常见的静态压力;另一个是动风荷载,即风速引起的动态效应。
对于风荷载的计算,常用的方法是按照国家规范进行计算。
这些规范提供了各种建筑类型和地区的风速概率分布曲线,以及建筑物的风荷载计算方法。
基于这些规范,结构设计师可以确定不同风速下的静风压力,并结合建筑结构的特点进行计算。
二、风力响应分析风力响应分析是指建筑物在受到风荷载时的结构响应分析。
建筑物在受到风荷载时会产生形变和应力,而风力响应分析旨在评估和控制这些响应,确保建筑物的稳定性和安全性。
常见的风力响应分析方法包括静力分析和动力分析。
静力分析是一种简化的方法,通常用于预估建筑物在可能的最大风荷载下的位移和应力。
动力分析则更为复杂,考虑了风荷载的动态效应以及结构的振动特性。
对于静力分析,常用的方法是等效静态法。
该方法的基本思想是将动态风荷载转化为与之等效的静态风荷载,从而简化结构的分析和设计。
这种方法适用于一些简单的建筑结构,但对于复杂的结构则需要考虑动力分析。
动力分析的方法有很多种,其中一种常见的方法是模态分析。
模态分析考虑了建筑物的固有振动特性,通过计算建筑物的模态响应来评估风力响应。
这种方法对于高层建筑等柔性结构尤为适用,能够更准确地预测结构的响应。
三、风荷载与风力响应的实例下面以高层建筑为例,说明风荷载与风力响应的分析过程。
风与结构的耦合作用及风振响应分析(精)

第17卷第5期工程力学Vol.17 No.52000年 10 月ENGINEERING MECHANICSOct. 2000收稿日期修订日期国家自然科学基金资助项目(59578050作者简介女浙江大学土木系副教授主要从事结构工程研究文章编号孙炳楠(浙江大学土木系在目前的风振响应计算中但对于超高层建筑由于基频较低本文基于准定常假定推论出风与结构的耦合作用实质上就是气动阻尼效应就可建立考虑风与结构耦合作用的风振响应模态分析方法确定了风与结构耦合作用所产生的气动阻尼比较了采用Davenport 谱和Kaimal 谱对计算结果的差异性采用Kaimal 谱并考虑风与结构的耦合作用所得计算结果能与风洞试验结果吻合较好风振响应气动阻尼中图分类号A1前言作用于高耸建筑物地震荷载和风荷载结构显得越来越柔性振动频率随之降低建筑物越柔而地震能量集中在高频区因此当建筑物总高度超过某一值时深入分析高耸结构的风振效应就显得十分重要大部分的研究都集中在顺风向的抖振分析上从原理上讲只是在计算过程中针对具体的分析对象有不同的处理方式对结构的计算模式作不同的简化等等频域分析法比较直接方便并且所需机时较长在目前的风振响应计算中这对于一阶频率高于0.5Hz 的悬臂结构是可以接受的[5]¸ßËÊËþΦ½á¹¹ÓÈÆäÊÇ×èÄá½ÏСµÄ¸Ö½á¹¹±¾ÎÄ»ùÓÚ×¼¶¨³£¼Ù¶¨风与结构的耦合作用及风振响应分析17虑风与结构耦合作用的风振响应模态分析方法确定了不同风速下风与结构耦合作用所产生的气动阻尼采用三维离散的桁架单元和梁单元模型并着重探讨了两个问题(2 采用Davenport 谱和Kaimal 谱对结构风振响应的差异性2风振响应频域分析法任一结构采用合适的有限单元离散后在风荷载作用下的运动平衡方程为大气湍流可以看成是一个平稳随机过程为了求得风振响应的均方根值xσ∂™™⊄∂↓• ≥⊂(1进行求解并且对于小阻尼体系得风振响应的功率谱为∑==nj pj j j x S i H S 122 ( ( (ωωϕω (2对于第q 个自由度分别为自由度及振型的序号(ωpj S 为j 振型广义力 (t P j 的自谱密度函数按下式计算∑==nj xj j x 12σωσ&& (5式中xj σ为第j 振型的位移响应均方根值对于第r 个自由度r r r r r A C t v V t F ( (ρ= (6若第r 个自由度位于节点i和r A 分别为i 节点所对应的平均风速r C 为气动力系数, , ( , , ( (11211ωρϕϕωϕϕωk r S A A C C V V k r S S v nr k r k r k r nk kj rj nr F nk kj rj Pj ∑∑∑∑====== (7式中kr k r k r A A C C V V k 个自由度对应的平均风速迎风面积可表示为18工程力学, , ( ( ( , , ( ( (ωωωωk r coh S S k r S k v r v v = (8式中(ωv S 为脉动风速谱至今为止大致可以分为两类另一类是谱密度随高度的增加而减小分别采用了这两类谱中应用较为广泛的Davenport 谱和Kaimal 谱[6]3风与结构的耦合作用及气动阻尼为了考虑风与结构的耦合作用采用风与结构的相对速度来计算抖振力风阻力为假设脉动风速(t V Ïà¶ÔÓÚƽ¾ù·çËÙV 的平方可以忽略不计X AV C t AVv C AV C P D D D D &ρρρ−+= (212 (10 显然式(10中的第一项为平均风力第二项即为脉动风速引起的抖振力若将该非定常阻力引入运动方程(1ʹÎÊÌâ±äµÃ¸´ÔÓ¶øÄÑÒÔÇó½â¸ÃÁ¦Óë½á¹¹Õñ¶¯ËٶȳÉÕý±ÈÒò´Ë¿ÉÒÔ²ÉÓÃÔÚÔ˶¯·½³ÌÖÐÒýÈëÆø¶¯×èÄáµÄ¼ò»¯·½·¨À´¿¼ÂÇ·çÓë½á¹¹µÄñîºÏ×÷ÓÃ固有圆频率为0ω™∨∅ • ⊄∧V作用下的气动阻尼常数为[7]¶à×ÔÓɶȽṹµÄ¶¯Á¦ÏìÓ¦±»¿´×÷Óɸ÷½×ģ̬ÏìÓ¦µü¼ÓµÄ×ܺÍÈçͬµ¥×ÔÓɶÈÒ»°ãÓɴ˿ɼûÆø¶¯×èÄáΪÕý×èÄá¼´¿çÔ½µµ¾àΪ1500米塔体总高达183米居浙江省最高椒江是强台风区最大瞬时风速达45米/秒以上4.1动力特性分析风与结构的耦合作用及风振响应分析19首先分别采用如图2所示二种较严格的计算模式对该高耸输电铁塔(简称椒江塔进行动力特性分析按空间桁架进行计算将塔柱及横隔看作空间梁单元水平斜撑及塔头杆件为空间二力杆单元以下简称半刚架模式计算表明说明该类铁塔完全可以按空间桁架模式计算图1 椒江塔示意图图2 椒江塔计算模式图3为椒江塔x 方向和y 方向的前三阶弯曲振型由于该塔的塔身横截面为正方形y两个方向的频率该塔的一阶扭转频率为4.65Hz ÖµµÃ×¢ÒâµÄÊÇÔÚÀíÂÛ¼ÆËãʱÖÊÁ¿·Ö²¼µÈ¾ùÊÇÀíÏëµØ¶Ô³ÆÓÚxÈôʵ¼Ê½¨³ÉºóµÄËþÉÔÓÐÆ«ÐÄ(a x 方向1~3阶振型 (b y 方向1~3阶振型图3 椒江塔x 方向和y 方向前三阶弯曲振型4.2抖振响应分析采用以上所述的模态分析法进行抖振响应分析还要确定以下主要参数K 和结构阻尼β20工程力学根据椒江塔所处的地貌特征椒江塔主要由薄壁钢管构成钢管为12720×φ在规范中纯钢结构的阻尼比为0.01ÔòÈ¡Ò»½×ÕñÐ͵Ľṹ×èÄá±ÈΪ0.015(2 阻力系数DC 由风洞试验得到该塔在各风向角下的阻力系数如表1所示[8]È¡µ¥Ãæ¼ÆËã±íÃ÷¶þ½×ÒÔÉϵÄÓ°ÏìԼΪ2.5%Òò´Ë¿ÉÒÔ½«½·½-Ëþ¿´×÷ΪÕÔ¹ÌÓÐƵÂÊ1ω振动的单自由度物体其中平均风速V 取塔架中点高度(H =90m处的风速90V 表2椒江塔气动阻尼aβ风速10V (m/s1520253035404550风速90V (m/s20.427.234.040.847.654.461.268.0气动阻尼aβ0.00460.00600.00760.00910.01060.01200.01400.0150根据上述所取参数分别采用Davenport 谱和Kaimal 谱对椒江塔进行了抖振响应计算并以图4图4 顶点位移均方根值与风速10V 的关系图5 顶点加速度均方根值与风速10V 的关系风与结构的耦合作用及风振响应分析 21 表3铁塔顶点风振响应风速 V10 (m/s 15 20 位移均方根值σ x (cm 25 30 35 40 45 50 15 1.55 1.65 1.53 1.61 加速度均方根值σ x (0.01g 20 3.65 3.15 3.39 3.02 25 6.32 5.22 5.68 4.93 30 9.49 7.89 8.21 7.35 35 40 45 50 不计气 Davenport 谱 1.16 2.74 4.74 7.14 10.40 14.64 19.74 25.74 动阻尼Kaimal 谱 1.24 2.36 3.92 5.94 8.46 8.82 7.74 11.54 15.16 19.44 12.18 15.86 20.32 10.34 13.34 16.8 13.84 19.28 26.28 34.25 11.25 15.37 20.17 25.86 11.74 16.20 21.09 27.03 10.29 13.77 17.74 22.35 考虑气 Davenport 谱 1.14 2.54 4.28 6.18 动阻尼 Kaimal 谱1.20 2.28 3.70 5.52 结构风振响应随速度非线性单调增加并且采用 Davenport 谱所得的结构响应明显大于采用 Kaimal 谱所得的结构响应风速越大二者的差距越大考虑气动阻尼后二者的差距虽有所减小但椒江塔在设计风速 V10 = 36.6m/s 下Davenport 谱仍然比 Kaimal 谱所得结果大 15% 图中还反映出气动阻尼或者说风与结构的耦合作用对计算结果有较大的影响在气动稳定的情况下气动阻尼随风速而增大因而其影响程度也随风速的增大而增大当考虑气动阻尼后在风速 V10 = 36.6m/s 时采用 Davenport 谱结构响应可减小 18% 采用 Kaimal 谱则减小 10% 因此对于象钢结构那样柔性并阻尼小的结构气动阻尼的影响是不可忽略的它将减小铁塔风振响应理论计算结果与试验结果的对比如图 6 图 7 所示图 6 为 0o 风向时塔头 170m 高度处顺风向的加速度响应图 7 为 45o 风向时塔身 121m 高度处顺风向的加速度响应图中曲线明显地反映出采用 Kaimal 谱并考虑气动阻尼所得的结果与试验结果较接近当风速达到设计风速时二者吻合得很好而采用 Davenport 谱所得结果偏大尤其是不考虑气动阻尼时计算值比试验值大得多约偏大 20% 因此在输电铁塔风振响应的计算中建议采用 Kaimal 谱并有必要考虑风与结构的耦合作用从图中可以直观地看出图 6 0o 风向角塔头 170m 高度处加速度响应比较图 7 45o 风向角塔身 121m 高度处加速度响应比较5主要结论 1 对于低阻尼的钢结构体系在理论计算中应考虑风与结构的耦合作用这一耦合作用在气动稳定时可转化为气动阻尼的影响文中采用拟单自由度法确定了不同风速下的气动阻尼从而简化了三维多自由度体系风与结构耦合作用的计算 2 在气动弹性稳定时气动阻尼随风速的增大而增大因而其影响程度也随之增大对于象钢结构那样柔性并阻尼较小的结构气动阻尼的影响是不可忽略的它将减少结构22 工程力学的风振响应 3 理论计算与试验结果的对比表明采用 Kaimal 谱所求得的风振响应与试验值吻合较好而采用 Davenport 谱加速度响应偏大达 20%左右尽管目前许多国家(包括我国的规范均采用 Davenport 谱但运用该谱所求得的风振响应偏于保守而 Kaimal 谱比较接近实际参考文献 [1] Ahsom Kareem. Dynamic response of high-rise building to stochastic wind loads[J]. J. Wind Engineering and Industrial Aerodynamics, 1992, 41-44: 1101-1112. [2] H Tsukagoshi, et. al. Response analyses of along-wind and across-wind vibrations of tall buildings in time domain[J]. J. Wind Engineering and Industrial Aerodynamics, 1993, 46-47: 497-506. [3] G Solari. 3-D response of building to wind action[J]. J. Wind Engineering and Industrial Aerodynamics, 1986,23: 379-393. [4] [5] [6] 陈勇,楼文娟,孙炳楠. 基于 windows 的多点脉动风风速时程模拟[J]. 浙江大学学报,1997,31:147-152. 张相庭. 结构风振与风压计算[M]. 同济大学出版社学出版社 1992. [7] [8] (日伯野元彦, 主编, 李明昭, 等译. 土木工程振动手册[M]. 中国铁道出版社 1992. 楼文娟, 孙炳楠, 唐锦春. 大跨越输电铁塔的气动弹性模型及风洞试验[C]. 第二届结构与地基国际学术研讨会论文集, 香港, 1997. 383-388. 1985. 埃米尔希缪, 罗伯特 H 斯坎伦, 著, 刘尚培, 项海帆, 谢霁明, 译. 风对结构的作用[M]. 同济大 WIND-STRUCTURE-COUPLING EFFECTS AND BUFFETING RESPONSES LOU Wen-juan , SUN Bing-nan (Department of Civil Engineering, Zhejing University, Hangzhou 310027 Abstract: It is evident that the interaction between wind and structure is of great importance for structures such as super tall buildings, towers and guyed masts that have a low fundamental natural frequency. However, little research has been carried out to consider the coupling effects. This paper presents a method for analyzing the wind-induced vibration which takes into account windstructure coupling effects. The method is developed based on the quasi-stead theory by treating the wind-structure coupling effect as an aerodynamic damping. The buffeting responses of a tall transmission tower are analyzed in detail to demonstrate the method. Numerical results based on Kaimal spectrum and Davenport spectrum are presented. Wind tunneltests were also carried out. It is shown that numerical predictions based on Kaimal spectrum are in good agreement with experimental observations. The study shows that the wind-structure interaction has a significant effect on the responses of the structure. Key words: wind-induced response; tall structure; aerodynamic damping风与结构的耦合作用及风振响应分析作者:作者单位:刊名:英文刊名:年,卷(期:被引用次数:楼文娟,孙炳楠, LOU Wen-juan, SUN Bing-nan 浙江大学土木系,杭州,310027 工程力学 ENGINEERING MECHANICS 2000,17(5 24次参考文献(8条 1.楼文娟;孙炳楠;唐锦春大跨越输电铁塔的气动弹性模型及风洞试验1997 2.伯野元彦;李明昭土木工程振动手册 1992 3.埃米尔·希缪;罗伯特·H·斯坎伦;刘尚培;项海帆,谢霁明风对结构的作用 1992 4.张相庭结构风振与风压计算 1985 5.陈勇;楼文娟;孙炳楠基于windows的多点脉动风风速时程模拟 1997 6.G Solari 3-D response of building to wind action 1986 7.H Tsukagoshi Response analyses of along-wind and across-wind vibrations of tall buildings in time domain 1993 8.Ahsom Kareem Dynamic response of high-rise building to stochastic wind loads 1992 引证文献(24条 1.范存新.张毅.唐和生考虑桩-土-结构相互作用时高层建筑风振响应分析(Ⅱ[期刊论文]-四川建筑科学研究 2010(1 2.林立孚浅析高层建筑结构的计算分析方法[期刊论文]-中国高新技术企业 2010(22 3.范存新.张毅.唐和生考虑桩-土-结构相互作用时高层建筑风振响应分析(Ⅰ[期刊论文]-四川建筑科学研究 2009(6 4.李春祥.李锦华.于志强输电塔线体系抗风设计理论与发展[期刊论文]-振动与冲击 2009(10 5.王元战.孙熙平.詹水芬.洪宁宁防风网结构设计研究综述[期刊论文]-港工技术 2008(3 6.楼文娟.卢旦.杨毅.余世策开孔建筑屋盖风振响应中的气动阻尼识别[期刊论文]-空气动力学学报 2007(4 7.陈达.张玮风能利用和研究综述[期刊论文]-节能技术 2007(4 8.甘凤林.潘兹勇高层建筑和高耸结构的抗风设计探讨[期刊论文]-山西建筑 2007(8 9.范存新.薛松涛.陈镕.唐和生考虑风与结构耦合作用时电视塔结构的风振响应[期刊论文]-苏州大学学报(工科版) 2006(4 10.刘毛方大跨度屋盖结构脉动风特性及风振响应计算方法的研究[学位论文]硕士 2006 11.辛庆胜.周岱.马骏大跨斜拉网格结构耦合风振响应分析计算的研究现状与发展前景[期刊论文]-振动与冲击 2005(1 12.王世村高耸结构风振响应和风振疲劳研究[学位论文]博士 2005 13.王世村高耸结构风振响应和风振疲劳研究[学位论文]博士 2005 14.唐喜基于ANSYS参数化语言的索膜结构找形优化和荷载分析[学位论文]硕士 2005 15.刘嵩杆式结构风激响应的谱分析[学位论文]硕士 2005 16.章增当.陈水福三管钢筋混凝土烟囱风振响应分析与结构方案评价[期刊论文]-工业建筑 2004(5 17.范存新.薛松涛.陈镕.张毅考虑风-结构-土耦合作用时高层建筑顺风向风振响应分析[期刊论文]-力学季刊 2004(2 18.宋海妍大跨机库网架屋盖的风振响应及风振系数研究[学位论文]硕士 2004 19.秦云结构静力风荷载数值模拟研究[学位论文]博士 2004 20.舒新玲大跨度单层网壳结构风载风振研究[学位论文]硕士 2003 21.舒新玲大跨度单层网壳结构风载风振研究[学位论文]硕士2003 22.舒新玲大跨度单层网壳结构风载风振研究[学位论文]硕士 2003 23.周岱.舒新玲.周笠人大跨空间结构风振响应及其计算与试验方法[期刊论文]-振动与冲击2002(4 24.舒新玲.周岱.王泳芳风荷载测试与模拟技术的回顾及展望[期刊论文]-振动与冲击 2002(3 本文链接:/Periodical_gclx200005003.aspx。
风与建筑结构的相互作用研究

风与建筑结构的相互作用研究风是自然界中一种重要的气象要素,它不仅影响着人类的日常生活,也对建筑结构产生着深远的影响。
风对建筑结构的相互作用研究一直是结构工程领域的重要课题。
本文将探讨风与建筑结构之间的相互作用,以及这种相互作用对建筑设计与安全性的影响。
风与建筑结构的相互作用是一种流体-结构耦合问题。
当风经过建筑物表面时,会产生一系列力的作用,包括压力差、摩擦力和涡旋激发力等。
这些力对于建筑结构来说可能是有益的,比如可以提供降温和通风的效果,也可能是有害的,比如会引发振动和损坏。
因此,深入研究风与建筑结构的相互作用对于建筑的设计、施工和维护至关重要。
首先,风对建筑结构的相互作用在建筑设计中起到了重要的指导作用。
建筑师在进行设计时,需要考虑到建筑物所处地理环境的风速、风向和风压等因素。
这些因素直接影响结构的稳定性和建筑物的使用寿命。
根据风场的情况,设计师可以选择适当的建筑形式、横截面积和材料强度等,以保证建筑物能够在风力作用下具备足够的稳定性。
因此,风与建筑结构的相互作用研究为建筑设计提供了可靠的技术支持。
其次,风与建筑结构的相互作用对建筑安全性具有重要影响。
风对建筑物的高层部分产生的风压力在一定程度上会导致结构产生振动。
当风速超过建筑物所能承受的极限时,振动会变得剧烈,从而可能导致结构疲劳和破坏。
因此,在高风区,建筑物的结构设计和风荷载计算尤为重要。
合理的结构设计和风荷载计算,可以保证建筑物在极端气象条件下的整体完整性和稳定性,从而提高建筑的抗风能力和安全性。
另外,风与建筑结构的相互作用还可以应用于建筑物的能量利用和环境控制。
通过结合建筑物和风场的特性,可以设计出利用风能的建筑形式,提高建筑的能效和环境可持续性。
例如,在建筑立面上设置风能利用装置,可以通过风的作用驱动风轮或风力发电机,为建筑供应部分能源。
此外,通过合理设计建筑的通风系统,可以利用风的自然流动来实现室内空气的更新和调节,降低能耗,提高舒适度。
风雨耦合环境结构荷载与响应的分析及试验研究

风雨耦合环境结构荷载与响应的分析及试验研究作者:赵林等来源:《振动工程学报》2014年第04期摘要:采用理论分析及试验研究方法对风雨共同作用下的结构荷载与响应进行了研究。
首先在确定风雨联合作用概率模型的基础上通过对降雨作用特性的分析,比较了雨滴冲击作用模型和空气密度等效变化模型对建筑结构等效静力的作用性能;其次,基于高精度风雨耦合荷载环境模拟试验设备,进行了风雨定常气动力荷载模型高频天平测力试验,研究了简单几何形体的风雨定常荷载变化规律;然后,采用二维悬挂系统测振试验方法,研究了风雨非定常气动力荷载模型及其结构振动响应特点;最后,对缆索承重桥梁拉索风雨激振现象进行耦合荷载环境参数精细化控制试验,揭示了拉索空间姿态、拉索动力特性、来流风速和不同雨强组合等条件对拉索风雨振的影响规律。
关键词:拉素;风雨共同作用;气动力荷载;结构响应;风洞试验中图分类号:U488.25; TU973.2+1文献标识码: A文章编号: 10044523(2014)040507111概述夏秋两季中国南方大部分地区无论是强季风还是强台风往往都伴随着强降雨,特别是袭击中国东南沿海地区的台风10 min平均风速可达40 m/s以上,伴随的日平均雨强可达到200 mm/24 h;与结构风振极值响应相关的瞬时风速可以达到60 m/s以上,相应的极端雨强亦可达到15 mm/10 min。
目前风雨共同对结构作用研究最关注的问题是斜拉桥拉索的风雨激振,这是一种能够在实际结构中观测到的风雨振动现象[1,2];降雨对基本结构构件气动特性影响的研究虽有初步进展[3,4],但强风袭击极端荷载条件下的降雨效应对于结构静、动态影响行为的系统评价始终处于空白状态。
风雨共同作用主要关注风驱动雨(winddriven rain)对于建筑结构表面的侵蚀效应以及柔性拉索的风雨激振现象(RWIV)。
已有研究证明狂风驱动骤雨对结构形成的强迫动力作用,特殊条件会极大地恶化无雨状态下单纯脉动风的湍流效应。
混凝土结构风振响应分析技术规程

混凝土结构风振响应分析技术规程一、前言混凝土结构在风荷载作用下容易发生振动,如果振动幅度过大,会导致结构的破坏。
因此,对混凝土结构的风振响应进行分析是非常必要的。
本文将介绍混凝土结构风振响应分析技术规程。
二、基本概念1. 风荷载:指风对建筑物产生的作用力。
2. 结构自振频率:指结构在自由振动时的振动频率。
3. 风振:指风荷载作用下结构的振动。
4. 风振响应:指结构在风振作用下的响应。
5. 风振舒适度:指人员在结构内感受到的风振程度。
三、分析方法1. 建立数学模型首先,需要建立混凝土结构的数学模型。
可以采用有限元方法建立结构的数学模型,将结构分成若干个单元,并对每个单元进行建模和分析。
建立好数学模型后,可以通过计算机模拟来进行分析。
2. 确定风荷载在进行混凝土结构风振响应分析之前,需要确定结构所受的风荷载。
可以采用国家规范《建筑结构荷载规范》中的方法来计算风荷载。
3. 计算结构自振频率在进行混凝土结构风振响应分析之前,需要计算结构的自振频率。
可以采用有限元方法来计算结构的自振频率。
4. 计算风振响应在确定风荷载和结构自振频率后,可以计算结构在风振作用下的响应。
可以采用有限元方法进行计算。
计算时需要注意结构与环境的耦合效应,即将结构与风场、地面等环境进行耦合计算。
5. 分析风振舒适度在进行混凝土结构风振响应分析时,需要分析风振舒适度。
可以采用国家规范《建筑抗震设计规范》中的方法来分析风振舒适度。
风振舒适度分为A、B、C三个等级,其中A级为最高级别,C级为最低级别。
四、结论通过以上分析,可以得出混凝土结构在风荷载作用下的振动情况,以及人员在结构内感受到的风振程度。
如果结构的振动幅度过大,需要进行结构加固或采用措施来改善风振舒适度。
五、注意事项1. 在进行混凝土结构风振响应分析时,需要注意选用合适的数学模型和分析方法。
2. 在计算风荷载时,需要按照国家规范中的方法进行计算。
3. 在计算结构自振频率时,需要注意采用合适的有限元方法进行计算。
风力作用下结构物的响应与结构优化

风力作用下结构物的响应与结构优化引言:风是一种常见的自然力量,对于建筑和结构物来说,风力是一种重要的外部荷载。
当风力作用于结构物时,会引起结构物的振动和变形,甚至可能导致结构的破坏。
因此,了解风力作用下结构物的响应规律,并通过结构优化来提高结构的抗风能力,是非常重要的。
一、风力作用下结构物的响应1. 风力的特点风力是由气流运动引起的,具有不稳定性和随机性。
风力的大小与方向都会不断变化,这使得结构物在风力作用下具有不确定性的响应。
2. 结构物的振动当风力作用于结构物时,会引起结构物的振动。
结构物的振动可以分为自由振动和受迫振动两种形式。
自由振动是指结构物在没有外力作用下的振动,而受迫振动是指结构物在外力作用下的振动。
3. 结构物的变形除了振动外,风力还会引起结构物的变形。
结构物的变形主要包括弯曲、扭转和剪切等形式。
这些变形可能导致结构物的破坏,因此需要通过结构优化来提高结构的抗风能力。
二、结构优化的方法1. 结构形式的优化结构形式的优化是通过改变结构的形式和布置来提高结构的抗风能力。
例如,可以采用更加均匀分布的柱网结构,增加结构的刚度和稳定性;或者采用空心结构,减小结构的风阻力。
2. 结构材料的优化结构材料的优化是通过选择合适的材料来提高结构的抗风能力。
例如,可以采用高强度材料,提高结构的抗弯刚度和抗剪切能力;或者采用轻质材料,减小结构的质量和风阻力。
3. 结构连接的优化结构连接的优化是通过改进结构的连接方式和节点设计来提高结构的抗风能力。
例如,可以采用更加牢固的连接方式,增加结构的整体刚度和稳定性;或者采用柔性连接,减小结构的应力集中和疲劳损伤。
4. 结构布局的优化结构布局的优化是通过合理布置结构的构件和部件来提高结构的抗风能力。
例如,可以采用对称布局,均匀分布结构的质量和刚度;或者采用适当的几何形状,减小结构的风阻力和气动力。
结论:风力作用下结构物的响应是一个复杂的问题,需要综合考虑结构的振动和变形等因素。
风雨耦合环境结构荷载与响应的分析及试验研究_赵林

图 3 风速雨强联合分布概率模型 F i . 3 J o i n t r o b a b i l i s t i c m o d e l a b o u t w i n d a n d r a i n g p
时为自然条件最大可能概率出现情况 。
图 2 气象数据收集位置 F i . 2 O b s e r v a t i o n s i t e o f m e t e o r o l o i c a l d a t a g g
2 风雨独立作用理论分析
2. 1 降雨作用特性 如 图 2) 风雨 收集上海市崇明岛侯家镇气象站 ( 历史纪录 ( 包括 1 9 7 1 年到 2 0 0 7 年影响崇明的 4 7组 强台风风速 ( 以小时为时间间隔的1 0m i n最大风 ) 速) 和雨强 ( 小时降雨量 ) 的各个台风的最大风速和 采用不同 最大雨强作为风速 雨 强 联 合 分 布 的 样 本 , 的概率分布模型分别对风速雨强的概率分布参数进 行拟合 , 并作拟 合 优 度 比 较 。 对 风 速 雨 强 联 合 概 率 分布描述 效 果 较 好 的 是 G u m b e l C o u l a函数联合 p 概率分布模型 , 其联合概率分布函数如下
第2 7 卷第 4 期 2 0 1 4年8月
振 动 工 程 学 报
J o u r n a l o f V i b r a t i o n E n i n e e r i n g g
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第17卷第5期工程力学Vol.17 No.52000年 10 月ENGINEERING MECHANICSOct. 2000收稿日期修订日期国家自然科学基金资助项目(59578050作者简介女浙江大学土木系副教授主要从事结构工程研究文章编号孙炳楠(浙江大学土木系在目前的风振响应计算中但对于超高层建筑由于基频较低本文基于准定常假定推论出风与结构的耦合作用实质上就是气动阻尼效应就可建立考虑风与结构耦合作用的风振响应模态分析方法确定了风与结构耦合作用所产生的气动阻尼比较了采用Davenport 谱和Kaimal 谱对计算结果的差异性采用Kaimal 谱并考虑风与结构的耦合作用所得计算结果能与风洞试验结果吻合较好风振响应气动阻尼中图分类号A1前言作用于高耸建筑物地震荷载和风荷载结构显得越来越柔性振动频率随之降低建筑物越柔而地震能量集中在高频区因此当建筑物总高度超过某一值时深入分析高耸结构的风振效应就显得十分重要大部分的研究都集中在顺风向的抖振分析上从原理上讲只是在计算过程中针对具体的分析对象有不同的处理方式对结构的计算模式作不同的简化等等频域分析法比较直接方便并且所需机时较长在目前的风振响应计算中这对于一阶频率高于0.5Hz 的悬臂结构是可以接受的[5]¸ßËÊËþΦ½á¹¹ÓÈÆäÊÇ×èÄá½ÏСµÄ¸Ö½á¹¹±¾ÎÄ»ùÓÚ×¼¶¨³£¼Ù¶¨风与结构的耦合作用及风振响应分析17虑风与结构耦合作用的风振响应模态分析方法确定了不同风速下风与结构耦合作用所产生的气动阻尼采用三维离散的桁架单元和梁单元模型并着重探讨了两个问题(2 采用Davenport 谱和Kaimal 谱对结构风振响应的差异性2风振响应频域分析法任一结构采用合适的有限单元离散后在风荷载作用下的运动平衡方程为大气湍流可以看成是一个平稳随机过程为了求得风振响应的均方根值xσ∂™™⊄∂↓• ≥⊂(1进行求解并且对于小阻尼体系得风振响应的功率谱为∑==nj pj j j x S i H S 122 ( ( (ωωϕω (2对于第q 个自由度分别为自由度及振型的序号(ωpj S 为j 振型广义力 (t P j 的自谱密度函数按下式计算∑==nj xj j x 12σωσ&& (5式中xj σ为第j 振型的位移响应均方根值对于第r 个自由度r r r r r A C t v V t F ( (ρ= (6若第r 个自由度位于节点i和r A 分别为i 节点所对应的平均风速r C 为气动力系数, , ( , , ( (11211ωρϕϕωϕϕωk r S A A C C V V k r S S v nr k r k r k r nk kj rj nr F nk kj rj Pj ∑∑∑∑====== (7式中kr k r k r A A C C V V k 个自由度对应的平均风速迎风面积可表示为18工程力学, , ( ( ( , , ( ( (ωωωωk r coh S S k r S k v r v v = (8式中(ωv S 为脉动风速谱至今为止大致可以分为两类另一类是谱密度随高度的增加而减小分别采用了这两类谱中应用较为广泛的Davenport 谱和Kaimal 谱[6]3风与结构的耦合作用及气动阻尼为了考虑风与结构的耦合作用采用风与结构的相对速度来计算抖振力风阻力为假设脉动风速(t V Ïà¶ÔÓÚƽ¾ù·çËÙV 的平方可以忽略不计X AV C t AVv C AV C P D D D D &ρρρ−+= (212 (10 显然式(10中的第一项为平均风力第二项即为脉动风速引起的抖振力若将该非定常阻力引入运动方程(1ʹÎÊÌâ±äµÃ¸´ÔÓ¶øÄÑÒÔÇó½â¸ÃÁ¦Óë½á¹¹Õñ¶¯ËٶȳÉÕý±ÈÒò´Ë¿ÉÒÔ²ÉÓÃÔÚÔ˶¯·½³ÌÖÐÒýÈëÆø¶¯×èÄáµÄ¼ò»¯·½·¨À´¿¼ÂÇ·çÓë½á¹¹µÄñîºÏ×÷ÓÃ固有圆频率为0ω™∨∅ • ⊄∧V作用下的气动阻尼常数为[7]¶à×ÔÓɶȽṹµÄ¶¯Á¦ÏìÓ¦±»¿´×÷Óɸ÷½×ģ̬ÏìÓ¦µü¼ÓµÄ×ܺÍÈçͬµ¥×ÔÓɶÈÒ»°ãÓɴ˿ɼûÆø¶¯×èÄáΪÕý×èÄá¼´¿çÔ½µµ¾àΪ1500米塔体总高达183米居浙江省最高椒江是强台风区最大瞬时风速达45米/秒以上4.1动力特性分析风与结构的耦合作用及风振响应分析19首先分别采用如图2所示二种较严格的计算模式对该高耸输电铁塔(简称椒江塔进行动力特性分析按空间桁架进行计算将塔柱及横隔看作空间梁单元水平斜撑及塔头杆件为空间二力杆单元以下简称半刚架模式计算表明说明该类铁塔完全可以按空间桁架模式计算图1 椒江塔示意图图2 椒江塔计算模式图3为椒江塔x 方向和y 方向的前三阶弯曲振型由于该塔的塔身横截面为正方形y两个方向的频率该塔的一阶扭转频率为4.65Hz ÖµµÃ×¢ÒâµÄÊÇÔÚÀíÂÛ¼ÆËãʱÖÊÁ¿·Ö²¼µÈ¾ùÊÇÀíÏëµØ¶Ô³ÆÓÚxÈôʵ¼Ê½¨³ÉºóµÄËþÉÔÓÐÆ«ÐÄ(a x 方向1~3阶振型 (b y 方向1~3阶振型图3 椒江塔x 方向和y 方向前三阶弯曲振型4.2抖振响应分析采用以上所述的模态分析法进行抖振响应分析还要确定以下主要参数K 和结构阻尼β20工程力学根据椒江塔所处的地貌特征椒江塔主要由薄壁钢管构成钢管为12720×φ在规范中纯钢结构的阻尼比为0.01ÔòÈ¡Ò»½×ÕñÐ͵Ľṹ×èÄá±ÈΪ0.015(2 阻力系数DC 由风洞试验得到该塔在各风向角下的阻力系数如表1所示[8]È¡µ¥Ãæ¼ÆËã±íÃ÷¶þ½×ÒÔÉϵÄÓ°ÏìԼΪ2.5%Òò´Ë¿ÉÒÔ½«½·½-Ëþ¿´×÷ΪÕÔ¹ÌÓÐƵÂÊ1ω振动的单自由度物体其中平均风速V 取塔架中点高度(H =90m处的风速90V 表2椒江塔气动阻尼aβ风速10V (m/s1520253035404550风速90V (m/s20.427.234.040.847.654.461.268.0气动阻尼aβ0.00460.00600.00760.00910.01060.01200.01400.0150根据上述所取参数分别采用Davenport 谱和Kaimal 谱对椒江塔进行了抖振响应计算并以图4图4 顶点位移均方根值与风速10V 的关系图5 顶点加速度均方根值与风速10V 的关系风与结构的耦合作用及风振响应分析 21 表3铁塔顶点风振响应风速 V10 (m/s 15 20 位移均方根值σ x (cm 25 30 35 40 45 50 15 1.55 1.65 1.53 1.61 加速度均方根值σ x (0.01g 20 3.65 3.15 3.39 3.02 25 6.32 5.22 5.68 4.93 30 9.49 7.89 8.21 7.35 35 40 45 50 不计气 Davenport 谱 1.16 2.74 4.74 7.14 10.40 14.64 19.74 25.74 动阻尼Kaimal 谱 1.24 2.36 3.92 5.94 8.46 8.82 7.74 11.54 15.16 19.44 12.18 15.86 20.32 10.34 13.34 16.8 13.84 19.28 26.28 34.25 11.25 15.37 20.17 25.86 11.74 16.20 21.09 27.03 10.29 13.77 17.74 22.35 考虑气 Davenport 谱 1.14 2.54 4.28 6.18 动阻尼 Kaimal 谱1.20 2.28 3.70 5.52 结构风振响应随速度非线性单调增加并且采用 Davenport 谱所得的结构响应明显大于采用 Kaimal 谱所得的结构响应风速越大二者的差距越大考虑气动阻尼后二者的差距虽有所减小但椒江塔在设计风速 V10 = 36.6m/s 下Davenport 谱仍然比 Kaimal 谱所得结果大 15% 图中还反映出气动阻尼或者说风与结构的耦合作用对计算结果有较大的影响在气动稳定的情况下气动阻尼随风速而增大因而其影响程度也随风速的增大而增大当考虑气动阻尼后在风速 V10 = 36.6m/s 时采用 Davenport 谱结构响应可减小 18% 采用 Kaimal 谱则减小 10% 因此对于象钢结构那样柔性并阻尼小的结构气动阻尼的影响是不可忽略的它将减小铁塔风振响应理论计算结果与试验结果的对比如图 6 图 7 所示图 6 为 0o 风向时塔头 170m 高度处顺风向的加速度响应图 7 为 45o 风向时塔身 121m 高度处顺风向的加速度响应图中曲线明显地反映出采用 Kaimal 谱并考虑气动阻尼所得的结果与试验结果较接近当风速达到设计风速时二者吻合得很好而采用 Davenport 谱所得结果偏大尤其是不考虑气动阻尼时计算值比试验值大得多约偏大 20% 因此在输电铁塔风振响应的计算中建议采用 Kaimal 谱并有必要考虑风与结构的耦合作用从图中可以直观地看出图 6 0o 风向角塔头 170m 高度处加速度响应比较图 7 45o 风向角塔身 121m 高度处加速度响应比较5主要结论 1 对于低阻尼的钢结构体系在理论计算中应考虑风与结构的耦合作用这一耦合作用在气动稳定时可转化为气动阻尼的影响文中采用拟单自由度法确定了不同风速下的气动阻尼从而简化了三维多自由度体系风与结构耦合作用的计算 2 在气动弹性稳定时气动阻尼随风速的增大而增大因而其影响程度也随之增大对于象钢结构那样柔性并阻尼较小的结构气动阻尼的影响是不可忽略的它将减少结构22 工程力学的风振响应 3 理论计算与试验结果的对比表明采用 Kaimal 谱所求得的风振响应与试验值吻合较好而采用 Davenport 谱加速度响应偏大达 20%左右尽管目前许多国家(包括我国的规范均采用 Davenport 谱但运用该谱所求得的风振响应偏于保守而 Kaimal 谱比较接近实际参考文献 [1] Ahsom Kareem. Dynamic response of high-rise building to stochastic wind loads[J]. J. Wind Engineering and Industrial Aerodynamics, 1992, 41-44: 1101-1112. [2] H Tsukagoshi, et. al. Response analyses of along-wind and across-wind vibrations of tall buildings in time domain[J]. J. Wind Engineering and Industrial Aerodynamics, 1993, 46-47: 497-506. [3] G Solari. 3-D response of building to wind action[J]. J. Wind Engineering and Industrial Aerodynamics, 1986,23: 379-393. [4] [5] [6] 陈勇,楼文娟,孙炳楠. 基于 windows 的多点脉动风风速时程模拟[J]. 浙江大学学报,1997,31:147-152. 张相庭. 结构风振与风压计算[M]. 同济大学出版社学出版社 1992. [7] [8] (日伯野元彦, 主编, 李明昭, 等译. 土木工程振动手册[M]. 中国铁道出版社 1992. 楼文娟, 孙炳楠, 唐锦春. 大跨越输电铁塔的气动弹性模型及风洞试验[C]. 第二届结构与地基国际学术研讨会论文集, 香港, 1997. 383-388. 1985. 埃米尔希缪, 罗伯特 H 斯坎伦, 著, 刘尚培, 项海帆, 谢霁明, 译. 风对结构的作用[M]. 同济大 WIND-STRUCTURE-COUPLING EFFECTS AND BUFFETING RESPONSES LOU Wen-juan , SUN Bing-nan (Department of Civil Engineering, Zhejing University, Hangzhou 310027 Abstract: It is evident that the interaction between wind and structure is of great importance for structures such as super tall buildings, towers and guyed masts that have a low fundamental natural frequency. However, little research has been carried out to consider the coupling effects. This paper presents a method for analyzing the wind-induced vibration which takes into account windstructure coupling effects. The method is developed based on the quasi-stead theory by treating the wind-structure coupling effect as an aerodynamic damping. The buffeting responses of a tall transmission tower are analyzed in detail to demonstrate the method. Numerical results based on Kaimal spectrum and Davenport spectrum are presented. Wind tunneltests were also carried out. It is shown that numerical predictions based on Kaimal spectrum are in good agreement with experimental observations. The study shows that the wind-structure interaction has a significant effect on the responses of the structure. Key words: wind-induced response; tall structure; aerodynamic damping风与结构的耦合作用及风振响应分析作者:作者单位:刊名:英文刊名:年,卷(期:被引用次数:楼文娟,孙炳楠, LOU Wen-juan, SUN Bing-nan 浙江大学土木系,杭州,310027 工程力学 ENGINEERING MECHANICS 2000,17(5 24次参考文献(8条 1.楼文娟;孙炳楠;唐锦春大跨越输电铁塔的气动弹性模型及风洞试验1997 2.伯野元彦;李明昭土木工程振动手册 1992 3.埃米尔·希缪;罗伯特·H·斯坎伦;刘尚培;项海帆,谢霁明风对结构的作用 1992 4.张相庭结构风振与风压计算 1985 5.陈勇;楼文娟;孙炳楠基于windows的多点脉动风风速时程模拟 1997 6.G Solari 3-D response of building to wind action 1986 7.H Tsukagoshi Response analyses of along-wind and across-wind vibrations of tall buildings in time domain 1993 8.Ahsom Kareem Dynamic response of high-rise building to stochastic wind loads 1992 引证文献(24条 1.范存新.张毅.唐和生考虑桩-土-结构相互作用时高层建筑风振响应分析(Ⅱ[期刊论文]-四川建筑科学研究 2010(1 2.林立孚浅析高层建筑结构的计算分析方法[期刊论文]-中国高新技术企业 2010(22 3.范存新.张毅.唐和生考虑桩-土-结构相互作用时高层建筑风振响应分析(Ⅰ[期刊论文]-四川建筑科学研究 2009(6 4.李春祥.李锦华.于志强输电塔线体系抗风设计理论与发展[期刊论文]-振动与冲击 2009(10 5.王元战.孙熙平.詹水芬.洪宁宁防风网结构设计研究综述[期刊论文]-港工技术 2008(3 6.楼文娟.卢旦.杨毅.余世策开孔建筑屋盖风振响应中的气动阻尼识别[期刊论文]-空气动力学学报 2007(4 7.陈达.张玮风能利用和研究综述[期刊论文]-节能技术 2007(4 8.甘凤林.潘兹勇高层建筑和高耸结构的抗风设计探讨[期刊论文]-山西建筑 2007(8 9.范存新.薛松涛.陈镕.唐和生考虑风与结构耦合作用时电视塔结构的风振响应[期刊论文]-苏州大学学报(工科版) 2006(4 10.刘毛方大跨度屋盖结构脉动风特性及风振响应计算方法的研究[学位论文]硕士 2006 11.辛庆胜.周岱.马骏大跨斜拉网格结构耦合风振响应分析计算的研究现状与发展前景[期刊论文]-振动与冲击 2005(1 12.王世村高耸结构风振响应和风振疲劳研究[学位论文]博士 2005 13.王世村高耸结构风振响应和风振疲劳研究[学位论文]博士 2005 14.唐喜基于ANSYS参数化语言的索膜结构找形优化和荷载分析[学位论文]硕士 2005 15.刘嵩杆式结构风激响应的谱分析[学位论文]硕士 2005 16.章增当.陈水福三管钢筋混凝土烟囱风振响应分析与结构方案评价[期刊论文]-工业建筑 2004(5 17.范存新.薛松涛.陈镕.张毅考虑风-结构-土耦合作用时高层建筑顺风向风振响应分析[期刊论文]-力学季刊 2004(2 18.宋海妍大跨机库网架屋盖的风振响应及风振系数研究[学位论文]硕士 2004 19.秦云结构静力风荷载数值模拟研究[学位论文]博士 2004 20.舒新玲大跨度单层网壳结构风载风振研究[学位论文]硕士 2003 21.舒新玲大跨度单层网壳结构风载风振研究[学位论文]硕士2003 22.舒新玲大跨度单层网壳结构风载风振研究[学位论文]硕士 2003 23.周岱.舒新玲.周笠人大跨空间结构风振响应及其计算与试验方法[期刊论文]-振动与冲击2002(4 24.舒新玲.周岱.王泳芳风荷载测试与模拟技术的回顾及展望[期刊论文]-振动与冲击 2002(3 本文链接:/Periodical_gclx200005003.aspx。
