随机过程第4章离散部分复习题与参考答案
随机过程习题集-第四章马尔可夫过程

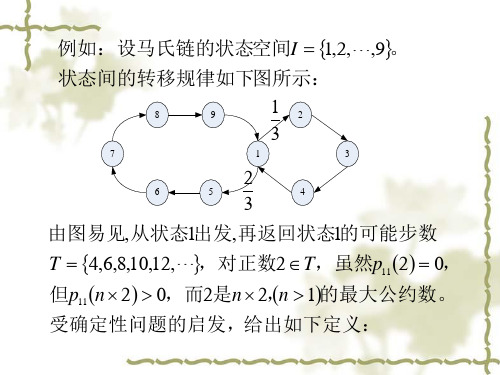
1第四章 马尔可夫过程内容提要1. 马尔可夫过程的概念 (1)马尔可夫过程给定随机过程{}(),X t t T ∈,如果对122,∀≥∀<<<∈n n t t t T ,有11221111{()|(),(),,()}{()|()}n n n n n n n n P X t x X t x X t x X t x P X t x X t x ----<====<=则称{}(),X t t T ∈为马尔可夫过程。
称(){}:,==∈E x X t x t T 为状态空间。
参数集和状态空间都是离散的马尔可夫过程称为离散参数马氏链. 参数连续、状态空间离散的马尔可夫过程称为连续参数马氏链. (2)k 步转移概率设{}(),0,1,2,=X n n 为离散参数马氏链,称()(),(,){|},0,1=+==≥≥i j p n k P X n k j X n i n k为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率,称(),(,)((,)),P =∈i j n k p n k i j E为{}(),0,1,2,=X n n 在时刻n 的k 步转移概率矩阵. 特别地,当1k =时,在时刻n 的一步转移概率和一步转移概率矩阵分别简记为()ij p n 和()n P . (3)初始分布、绝对分布称((0)),,==∈i p P X i i E 为离散参数马氏链{}(),0,1,2,=X n n 的初始分布,记为0P ,称()(){},,==∈j p n P X n j j E 为马尔可夫链{}0n X n ≥的绝对分布,记为P n . (4)离散参数齐次马氏链设{}(),0,1,2,=X n n 是一离散参数马氏链,如果其一步转移概率()ij p n 恒与起始时刻n 无关,记为ij p ,则称{}(),0,1,2,=X n n 为离散参数齐次马氏链。
若{}(),0,1,2,=X n n2是离散参数齐次马氏链,则其k 步转移概率记为(),i j p k ,一步转移概率矩阵和k 转移概率矩阵分别记为P 和().P k(5) 离散参数齐次马氏链的遍历性离散参数齐次马氏链{X (n ) ,n=0,1,2… },若对一切状态i ,j ,存在与i 无关的极限()()lim 0,ij j n p n i j E →+∞=π>∈则称此马氏链具有遍历性.0,1j j j Ej E ππ∈>∈=∑若且则称{},j j E π∈为离散参数齐次马氏链{X (n ) ,n=0,1,2… }的极限分布,或称为最终分布,记为{},j j E ∏=∈π(6)离散参数齐次马氏链的平稳分布离散参数齐次马氏链{X (n ) ,n=0,1,2… },若存在{v j , j ∈E } 满足条件:1)0,2)13)j jj Ej i iji Ev j E vv v p ∈∈≥∈==∑∑则称此马氏链是平稳的,称 { v j , j ∈E } 为此马氏链的平稳分布。
随机过程第四章
pii
(n)
1
i
0
证:(1)如i为零常返则i
,由lim n
pii nd
d
i
0
而当n不能被周期d整除时n 0modd ,
必然有pii
(n)
0,故
lim
n
pii
n
0
反之,若lim n
pii
(n)
0,
而i是正常返,
则由lim n
pii (nd )
d
i
0矛盾.
(2) 如i为遍历,即d 1,由上面定理得
即 Tij minn:X m i, X mn j,n 1
而称:
fij (n) P Tij n
P{X mv j,1 v n 1,X mn j / X m i},n 1 为自状态i出发,经n步首次到达状态j的概率, 简称首达概率。
注:由齐次马氏链性质知,首达概率与出发时刻
p3
① q1 q2
p1
③ q3 ②
p2
求从状态1出发经n步转移首次到达各个状态的概率。
f12
(n)qq11p3 p3源自q m1 1m p1,
q3
,
n 2m, n 2m 1,
m 1 m0
同理:
f13 (n)
p1q2 p1q2
p m1 1
m q1,
p2
,
n 2m, n 2m 1,
m 1 m0
互通关系的状态是同一类型.
定理:如果i j, 则
(1) i与j同为常返或非常返,如为常返,则它们
同为正常返或零常返;
(2) i与j有相同的周期。
1证:因为i j,故存在正整数k与m,使
pij (m) 0, p ji (k ) 0
《随机过程》第四章作业解答

20. 解:由例 4.8 中的结果可知甲最终赢的概率为:
(1)
P (甲最终赢)
=
(
1−p p
)a
−
1
(
1−p p
)a+b
−
1
=
(
2 3
)16
(
2 3
)36
− −
1 ;
1
(2)
P (甲最终赢)
=
(
1−p p
)a
−
1
(
1−p p
)a+b
−
1
=
(
2 3
)4
−
1
(
2 3
)24
−
1
21. 解:(1) 状态空间可以分为三个等价类:{1, 2}, {3, 4}, {5, 6}。其中 {1, 2} 与 {3, 4} 是常 返的,{5, 6} 是瞬时的,而且状态 {1, 2, 3, 4} 是非周期的。从而由推论 4.1 可知:
不妨记 p11 ≥ p12 ≥ · · · ≥ pn1 ≥ 0,若 p11 > p12 严格成立,从而有:
n
n
p11 = p1ipi1 < p11 p1i = p11
i=1
i=1
得到矛盾,从而有 p11 = p12。类似可证:对 ∀j ≤ n,p11 = p1j 均成立。从而类似可证:
对 ∀i, j ≤ n, p1j = pjj。
19.
解:结合概率转移矩阵画出有向图,可以得到: f1(1n) = a,
n=1 , 从而状态{1}是
0, n > 1
如有疏漏,欢迎指正
4
《随机过程》第四章作业解答
随机过程第4章Markov过程(PDF)

第四章 Markov 过程本章我们先讨论一类特殊的参数离散状态空间离散的随机过程,参数为0{0,1,2,}T N ==L ,状态空间为可列{1,2,}I =L 或有限{1,2,,}I n =L 的情况,即讨论的过程为Markov 链。
Markov 链最初由Markov 于1906年引入,至今它在自然科学、工程技术、生命科学及管理科学等诸多领域中都有广泛的应用。
之后我们将讨论另一类参数连续状态空间离散的随机过程,即纯不连续Markov 过程。
§4.1 Markov 链的定义与性质一、Markov 链的定义定义 4.1设随机序列{;0}n X n ≥的状态空间为I ,如果对0n N ∀∈,及0110011,,,,,{,,,}0n n n n i i i i I P X i X i X i +∈===>L L ,有:11001111{,,,}{}n n n n n n n n P X i X i X i X i P X i X i ++++=======L (4.1.0)则称{;0}n X n ≥为Markov 链。
注1:等式(4.1.0)刻画了Markov 链的特性,称此特性为Markov 性或无后效性,简称为马氏性。
Markov 链也称为马氏链。
定义4.2 设{;0}n X n ≥为马氏链,状态空间为I ,对于,i j I ∀∈,称1{}()ˆn n i j P X j X i p n +===为马氏链{;0}n X n ≥在n 时刻的一步转移概率。
注2:一步转移概率满足:()0,,()1,i j i jj Ip n i j Ipn i I ∈≥∈=∈∑若对于,i j I ∀∈,有1{}()ˆn n i j i j P X j X i p n p +===≡即上面式子的右边与时刻n 无关,则称此马氏链为齐次(或时齐的)马氏链。
设{}0()(0),p i P X i i I ==∈,如果对一切i I ∈都有00()0,()1i Ip i p i ∈≥=∑,称0()p i 为马氏链的初始分布。
随机过程课后题答案

第一章习题解答1. 设随机变量X 服从几何分布,即:(),0,1,2,k P X k pq k ===。
求X 的特征函数,EX 及DX 。
其中01,1p q p <<=-是已知参数。
解()()jtxjtkk X k f t E eepq ∞===∑()k jtkk p q e∞==∑ =0()1jt kjtk pp qe qe ∞==-∑又200()kkk k q qE X kpq p kq p p p ∞∞======∑∑222()()[()]q D X E X E X P =-=(其中 00(1)nnn n n n nxn x x ∞∞∞====+-∑∑∑)令 0()(1)n n S x n x ∞==+∑则 1000()(1)1xxnn k n xS t dt n t dt x x∞∞+===+==-∑∑⎰⎰202201()()(1)11(1)1(1)xn n dS x S t dt dxx xnx x x x ∞=∴==-∴=-=---⎰∑同理 2(1)2kkkk k k k k k x k x kx x ∞∞∞∞=====+--∑∑∑∑令20()(1)k k S x k x ∞==+∑ 则211()(1)(1)xkk k k k k S t dt k t dt k xkx ∞∞∞+====+=+=∑∑∑⎰)2、(1) 求参数为(,)p b 的Γ分布的特征函数,其概率密度函数为1,0()0,0()0,0p p bxb x e x p x b p p x --⎧>⎪=>>Γ⎨⎪≤⎩(2) 其期望和方差;(3) 证明对具有相同的参数的b 的Γ分布,关于参数p 具有可加性。
解 (1)设X 服从(,)p b Γ分布,则10()()p jtxp bxX b f t ex e dx p ∞--=Γ⎰ 1()0()p p jt b x b x e dx p ∞--=Γ⎰101()()()()(1)p u p p p p p b e u b u jt b x du jt p b jt b jt b∞----==Γ---⎰ 10(())x p p e x dx ∞--Γ=⎰ (2)'1()(0)X p E X f j b∴== 2''221(1)()(0)X p p E X f j b +== 222()()()PD XE X E X b∴===(4) 若(,)i i X p b Γ 1,2i = 则121212()()()()(1)P P X X X X jt f t f t f t b-++==-1212(,)Y X X P P b ∴=+Γ+同理可得:()()iiP X b f t b jt∑=∑-3、设X 是一随机变量,()F x 是其分布函数,且是严格单调的,求以下随机变量的特征函数。
(解答)《随机过程》第四章习题

第四章 二阶矩过程、平稳过程和随机分析 习题解答1、 设∑=-=Nk k k kn U n X 1)cos(2ασ,其中k σ和k α为正常数,)2,0(~πU U k ,且相互独立,N k ,,2,1 =,试计算},1,0,{ ±=n X n 的均值函数和相关函数,并说明其是否是平稳过程。
解:计算均值函数和相关函数如下0)}{cos(2)cos(2}{)(11=-=⎭⎬⎫⎩⎨⎧-==∑∑==Nk k k k N k k k k n X U n E U n E X E n ασασμ∑∑∑∑∑∑======-=--=--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-⋅⎥⎦⎤⎢⎣⎡-=Ni i i N i i i i i i Ni Nj j j i i j i N j j j j N i i i i X m n U m U n E U m U n E U m U n E m n R 12121111)](cos[)}cos(){cos(2)}cos(){cos(2)cos(2)cos(2),(ασαασαασσασασ因此可知,},1,0,{ ±=n X n 是平稳随机过程。
2、 设有随机过程))(cos()(t t A t X πηω+=,其中0>ω为常数,}0),({≥t t η是泊松过程,A 是与)(t η独立的随机变量,且2/1}1{}1{===-=A P A P 。
(1) 试画出此过程的样本函数,并问样本函数是否连续? (2) 试求此过程的相关函数,并问该过程是否均方连续? 解:(1)样本函数不连续。
(2)令:012≥>t t ,下面求相关函数:)(221)(212210)(1212211212121211212212122112221122121121212cos cos )]}(cos[)]({cos[21!)]([)]}(cos[)]({cos[)1(21))]}()(()(cos[))]()(()(2)({cos[21))]}()(()(cos[))]()(()({cos[21))}(cos())({cos(}{))}(cos())(cos({)}()({),(t t t t k t t k kX e t t e t t t t e k t t t t t t t t t t t t t t t E t t t t t t t t E t t t t E A E t t t t A E t X t X E t t R ----∞=--⋅=⋅-++=⋅-⋅-++-=-+-+-+++=-+-++++=++⋅=++==∑λλλωωωωλωωηηπωηηππηωηηπωηηπωπηωπηωπηωπηω因为:t t t R ωξ2cos ),(=因此该过程是均方连续的随机过程。
随机过程答案

随机过程第三章与第四章习题解答3.1 解:令()N t 表示(0,)t 时间内的体检人数,则()N t 为参数为30的poisson 过程。
以小时为单位。
则((1))30E N =。
4030(30)((1)40)!k k P N e k -=≤=∑。
3.2 解:法一:(1)乘坐1、2路汽车所到来的人数分别为参数为1λ、2λ的poisson 过程,令它们为1()N t 、2()N t 。
1N T 表示1()N t =1N 的发生时刻,2N T 表示2()N t =2N 的发生时刻。
1111111111()exp()(1)!N NN T f t t t N λλ-=-- 2221222222()exp()(1)!N NN T f t t t N λλ-=--1212121221112,12|12211122212(,)(|)()exp()exp()(1)!(1)!N N N N N NNN N T T T T T f t t f t t f t t t t t N N λλλλ--==---- 12212121112211122210012()exp()exp()(1)!(1)!NNt N N N N P T T dt t t t t dt N N λλλλ∞--<=----⎰⎰(2)当1N =2N 、1λ=2λ时,12121()()2N N N N P T T P T T <=>=法二:(1)乘车到来的人数可以看作参数为1λ+2λ的泊松过程。
令1Z 、2Z 分别表示乘坐公共汽车1、2的相邻两乘客间到来的时间间隔。
则1Z 、2Z 分别服从参数为1λ、2λ的指数分布,现在来求当一个乘客乘坐1路汽车后,下一位乘客还是乘坐1路汽车的概率。
212211122210()exp()exp()z p P Z Z dz z z dz λλλλ∞=<=--⎰⎰112λλλ=+。
故当一个乘客乘坐1路汽车后,下一位乘客乘坐2路汽车的概率为1-p 212λλλ=+上面的概率可以理解为:在乘客到来的人数为强度1λ+2λ的泊松过程时,乘客分别以112λλλ+概率乘坐公共汽车1,以212λλλ+的概率乘坐公共汽车2。
随机过程试题及答案

随机过程试题及答案一、选择题1. 关于随机过程的描述,错误的是:A. 随机过程是一种由随机变量组成的集合B. 随机过程是一种在时间上有序排列的随机变量序列C. 随机过程可以是离散的,也可以是连续的D. 随机过程是一种确定性的数学模型答案:D2. 以下哪种过程不是随机过程?A. 白噪声过程B. 马尔可夫过程C. 布朗运动D. 正态分布答案:D3. 随机过程的一阶矩描述的是:A. 均值B. 方差C. 偏度D. 峰度答案:A4. 当随机过程的各个时间点上的随机变量是独立同分布时,该随机过程为:A. 马尔可夫过程B. 马尔可夫链C. 平稳随机过程D. 白噪声过程答案:B5. 下列关于马尔可夫过程的说法中,正确的是:A. 当前状态只与上一状态有关,与历史状态无关B. 当前状态只与历史状态有关,与上一状态无关C. 当前状态只与上一状态和历史状态有关D. 当前状态与所有历史状态均无关答案:A二、填空题1. 随机过程中,时域函数常用的表示方法是__________。
答案:概率分布函数或概率密度函数2. 马尔可夫过程的状态转移概率只与__________相关。
答案:当前状态和下一状态3. 随机过程的时间参数称为__________。
答案:时刻或时间点4. 白噪声过程的自相关函数是一个__________函数。
答案:冲激函数5. 平稳随机过程的自相关函数只与__________相关。
答案:时间差三、解答题1. 请简要解释随机过程的概念。
随机过程是一种由随机变量组成的集合,表示一个在时间上有序排列的随机变量序列。
它可以是离散的,也可以是连续的。
随机过程的描述通常包括概率分布函数或概率密度函数,以及相关的统计特征,如均值、方差等。
随机过程可以用于对随机现象进行建模和分析。
2. 请简要说明马尔可夫过程的特点及应用。
马尔可夫过程是一种具有马尔可夫性质的随机过程,即当前状态只与上一状态有关,与历史状态无关。
其状态转移概率只与当前状态和下一状态相关。
随机过程第四章复习题及其解答马尔科夫链

第四章一、填空1.参数集和状态集均为离散集的马尔可夫过程称为马尔可夫链。
2.设{X n ,n єT}为马尔可夫链,称pj=p{X0=j}为{X n ,n єT}的初始概率,称pj (n )=p{Xn=j}为{X n ,n єT}的绝对概率。
3.设{X n ,n>=0}为马尔可夫链,则一步转移概率p ij =P{X n+1=j|X n =i}4.矩阵()ij a 其元素非负且对每i 有1j=∑ija,称矩阵()ij a 为随机矩阵。
5.f (n)ij =P{T ij =n|X 0=i}=P{X n =j,X k ≠j,1<=k<=n-1|X 0=i}为首达概率。
6.若1=ii f ,称i 为常返状态;若1<ii f ,称i 为非常返状态。
7.状态相通关系为等价关系,具有自反性、对称性、传递性。
8.设马尔可夫链的状态集为E={0,±1,±2,…}或其有限子集,其初始时刻n=0的概率记为p i (0)=P{X(0)=i},i єE,称集合{p i (0)}为该马尔可夫链的初始分布。
9.设马尔可夫链的状态集为E={0,±1,±2,…}或其有限子集,其绝对时刻n 时的概率记为p i (n)=P{X(n)=i},i єE,称集合{p i (n)}为该马尔可夫链的绝对分布。
10.设C ⊂S ,如对任意i ∈C 及j ∉C,都有p ij =0,称C 为闭集。
若C 的状态相通,C 成为不可约的。
11.若平稳齐次马尔可夫链的初始分布为平稳分布,则绝对概率等于初始概率。
12.不可约非周期马尔可夫链是正常返的充要条件是存在平稳分布,且此平稳分布就是极限分布⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∈I j ,u 1j 。
13.马氏链的绝对分布由其初始分布及相应的转移概率唯一确定。
二、1.设昨日、今日都下雨,明日有雨的概率为0.7;昨日无雨,今日有雨、明日有雨的概率为0.5;昨日有雨,今日无雨,明日有雨的概率为0.4;昨日、今日均无雨,明日有雨的概率为0.2。
《随机过程》第4章离散部分习题及参考答案

湖南大学本科课程《随机过程》第4章习题及参考答案主讲教师:何松华 教授30.设X(n)为均值为0、方差为σ2的离散白噪声,通过一个单位脉冲响应为h(n)的线性时不变离散时间线性系统,Y(n)为其输出,试证:2[()()](0)E X n Y n h σ=,2220()Y n h n σσ∞==∑证:根据离散白噪声性质,220()[()()]()0X m R m E X n m X n m m σσδ⎧==+==⎨≠⎩()()()()()m Y n X n h n X n m h m ∞==⊗=-∑220[()()]{()()()][()()]()()()()()(0)m m X m m E X n Y n E X n X n m h m E X n X n m h m R m h m m h m h σδσ∞∞==∞∞===-=-===∑∑∑∑12121222112202121221210000[()]{()()()()][()()]()()[()()]()Y m m m m m m E Y n E X n m h m X n m h m E X n m X n m h m h m m m h m h m σσδ∞∞==∞∞∞∞======--=--=-∑∑∑∑∑∑(对于求和区间内的每个m 1,在m 2的区间内存在唯一的m 2=m 1,使得21()0m m δ-≠)1222110()()()m n h m h m h n σσ∞∞====∑∑(求和变量置换) 31.均值为0、方差为σ2的离散白噪声X(n)通过单位脉冲响应分别为h 1(n)=a n u(n)以及h 2(n)=b n u(n)的级联系统(|a|<1,|b|<1),输出为W(n),求σW 2。
解:该级联系统的单位脉冲响应为121211100()()()()()()()1(/)()1/n m m m m mn n n nnn m m n nm m h n h n h n h n m h m a u n m b u m b b a aba b a a u n a b a a b∞∞-=-∞=-∞+++-===⊗=-=---⎛⎫====⎪--⎝⎭∑∑∑∑参照题30的结果可以得到21122222211212000222222222()[()2()()]()2(1)[]()111(1)(1)(1)n n n n n W n n n a b h n a ab b a b a b a ab b ab a b a ab b a b ab σσσσσσ++∞∞∞+++===⎡⎤-===-+⎢⎥--⎣⎦+=-+=-------∑∑∑32.设离散系统的单位脉冲响应为()() (1)n h n na u n a -=>,输入为自相关函数为2()()X X R m m σδ=的白噪声,求系统输出Y(n)的自相关函数和功率谱密度。
(解答)《随机过程》第四章习题

(2)如果 X ~ N (0,1) ,问过程 (t) 是否均方可微?说明理由。
解:计算随机过程 (t) 的相关函数:
R (s,t) E{ (s) (t)} E{( X cos 2s Y sin 2s)(X cos 2t Y sin 2t)} cos 2s cos 2tE{X 2} sin 2s sin 2tE{Y 2} [cos 2s sin 2t sin 2s cos 2t]E{XY}
4、 设有随机过程 X (t) 2Z sin(t ) , t ,其中 Z 、 是相互独立的随机 变量,Z ~ N (0,1) ,P( / 4) P( / 4) 1/ 2 。问过程 X (t) 是否均方可积
过程?说明理由。
解:由 Z 、 的相互独立性,计算随机过程 X (t) 的均值函数和相关函数: E{X (t)} E{2Z sin(t )} 2E{Z}E{sin(t )} 0
Y (t) 2X (t) 1, t 0 。试求过程{Y (t), t 0} 的相关函数 RY (s,t) 。
解:由相关函数的定义,有:
RY (s,t) E{Y (s)Y (t)} E{(2X (s) 1)(2X (t) 1)} 4E{X (s) X (t)} 2E{X (s)} 2E{X (t)} 1 4E{X (s) X (t)} 4 1
0
T 2 T T E{X (s) X (u)}dsdu m2 00
T 2
T 0
T 0
R
X
(
s
u
)dsdu
m
2
T 2
T 0
T 0
[C
《随机过程答案》第四章习题

第四章 二阶矩过程、平稳过程和随机分析 习题完整答案,请搜淘宝1、 设∑=-=N k k k k n U n X 1)cos(2ασ,其中k σ和k α为正常数,)2,0(~πU U k ,且相互独立,N k ,,2,1 =,试计算},1,0,{ ±=n X n 的均值函数和相关函数,并说明其是否是平稳过程。
2、 设有随机过程))(cos()(t t A t X πηω+=,其中0>ω为常数,}0),({≥t t η是泊松过程,A 是与)(t η独立的随机变量,且2/1}1{}1{===-=A P A P 。
(1) 试画出此过程的样本函数,并问样本函数是否连续?(2) 试求此过程的相关函数,并问该过程是否均方连续?3、 设}0),({≥t t X 是一实的零初值正交增量过程,且),(~)(2t N t X σμ。
令1)(2)(-=t X t Y ,0≥t 。
试求过程}0),({≥t t Y 的相关函数),(t s R Y 。
4、 设有随机过程)sin(2)(Θ+=t Z t X ,+∞<<∞-t ,其中Z 、Θ是相互独立的随机变量,)1,0(~N Z ,2/1)4/()4/(=-=Θ==ΘππP P 。
问过程)(t X 是否均方可积过程?说明理由。
5、 设随机过程t Y t X t 2sin 2cos )(+=ξ,+∞<<∞-t ,其中随机变量X 和Y 独立同分布。
(1) 如果)1,0(~U X ,问过程)(t ξ是否平稳过程?说明理由;(2) 如果)1,0(~N X ,问过程)(t ξ是否均方可微?说明理由。
6、 设随机过程});({+∞<<∞-t t X 是一实正交增量过程,并且0)}({=t X E ,及满足:{}+∞<<∞--=-t s s t s X t X E ,,)]()([2;令:+∞<<∞---=t t X t X t Y ),1()()(,试证明)(t Y 是平稳过程。
随机过程复习题(含答案)

随机过程复习题一、填空题:1.对于随机变量序列}{n X 和常数a ,若对于任意0>ε,有______}|{|lim =<-∞>-εa X P n n ,则称}{n X 依概率收敛于a 。
2.设}),({0≥t t X 是泊松过程,且对于任意012≥>t t , ,则1592}6)5(,4)3(,2)1({-⨯⨯====e X X X P ,618}4)3(|6)5({-===e X X P1532623292!23!2)23(!23}2)3()5({}2)1()3({}2)0()1({}2)3()5(,2)1()3(,2)0()1({}6)5(,4)3(,2)1({----⨯⨯=⨯⨯⨯==-=-=-==-=-=-====e e e e X X P X X P X X P X X X X X X P X X X P66218!26}2)3()5({}4)3(|6)5({--===-===e e X X P X X P3.已知马尔可夫链的状态空间为},,{321=I ,初始分布为),,(412141,⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=43410313131043411)(P ,则167)2(12=P ,161}2,2,1{210====X X X P⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=4831481348436133616367164167165)1()2(2P P 167)2(12=P161314341}2|2{}1|2{}1{}2,1|2{}1|2{}1{}2,2,1{12010102010210=⨯⨯=================X X P X X P X P X X X P X X P X P X X X P4.强度λ的泊松过程的协方差函数),min(),(t s t s C λ= 5.已知平稳过程)(t X 的自相关函数为πττcos )(=X R ,)]()([)(πϖδπϖδπω-++=X S6. 对于平稳过程)(t X ,若)()()(ττX R t X t X >=+<,以概率1成立,则称)(t X 的自相关函数具有各态历经性。
随机过程-习题-第4章-01

4.1 设有一泊松过程(){}0,≥t t N ,求:(1)()(){}2211,k t N k t N P ==,用21t t 、的函数表示之; (2)该过程的均值和相关函数。
问该过程是否为平稳过程? (1) 解:首先,{}{}{}1111222211)()()()(,)(k t N P k t N k t N P k t N k t N P ======根据泊松过程的独立增量性质可知{}{})(1212121211221212!)()]([)()()(t t k k ek k t t k k t t N P k t N k t N P -----=-=-===λλ 于是,{}21122!)(!)()(,)(1211122211t k k k k e k k k t t t k t N k t N P λλ----===(2) 解:该过程的均值为[]()()t k t te e k t k t N E k k t k t k λλλλλλ=⎪⎪⎭⎫ ⎝⎛-==∑∑+∞=--+∞=-110!1!)()( 根据泊松过程的独立增量过程性质可得其相关函数为(12t t >)[]()[])]([)]()([)]([)()()()()()(12121112121t N E t N t N E t N E t N t N t N t N E t N t N E +-=+-=其中,)()]()([1212t t t N t N E -=-λ121212)]([t t t N E λλ+=于是,12t t >时的相关函数为[]12121212121221)()()(t t t t t t t t t N t N E λλλλλ+=++-=同理可得21t t >时的相关函数为[]221221)()(t t t t N t N E λλ+=所以,泊松过程的相关函数为[]{}2121221,min )()(t t t t t N t N E λλ+=所以,泊松过程过程不是平稳过程。
随机过程习题和答案

、1.1设二维随机变量(X , F)的联合概率密度函数为:=—i—[l241-ι>⅛= "k"QTh Xl-JF)1.2 设离散型随机变量X服从几何分布:Hm=(Ip)HPJt=U-试求/的特征函数,并以此求其期望E(X)与方差I K X)¾0 = Efr ir) = ∑e⅛ = *)解:一=⅛α-ri M P=√^∑^α-p)t U O-P) ⅛J1—(I-JI)1—q/(O)=α⅛24(1-小丄0<y<x<l苴它试求:在OJu <■ 1时,求I『F)解:J;240 H)JKfc0<y<l Jj2Jf(I_y)3 0<JF<1P 其它^{θ其它当OJXI 时,Aw)2OT(Xy)y<x<l其它所以:-⅛(0)二丄f PZUr=J Er3-(JEIf)3=^^-^=4PPp2.1袋中有一个白球,两个红球,每隔单位时间从袋中任取一球后放回,对每一个确定的t 对应随机变量x(t^3如果对t时取得红球e t如果对t时取得白球试求这个随机过程的一维分布函数族2.2设随机过程 W 加吨MIF)∙ gZ I叫,其中吗是常数,/与F是相互独立的随机变量,F服从区间(°2刘上的均匀分布,/服从瑞利分布,其概率密度为x>0x≤0试证明Xu)为宽平稳过程。
解:( 1)⑷+F)} q啊诚如+ f)}= 与无关(2)枚F(M 仪加血I(Q/伽说如")汁F(才),f _ t t⅛(Q) =-J PQ ÷g)= -te^t∣Γ÷p ^dt =-2σ1e^i∣Γ=2σ3所以必U)啟0⑴卜"(3)R lM壊M∞¼⅛+Hl∕∞Ψ⅛+y)]}=豺]£{oKs(A +Γ)∞<β(A +Γ)}=2^Jtt 2{α≈(0A + β⅛+ y)-rasfflfc A)I^⅛心’皿叫仏Z L)只与时间间隔有关,所以XU)为宽平稳过程2.3设随机过程 X(t)=Ucos2t,其中U是随机变量,且 E(U)= 5, D(U)= 5.求: (1)均值函数;(2)协方差函数;(3)方差函数2.4设有两个随机过程 X(t)=Ut2, Y(t)=Ut3,其中U是随机变量,且D(U) = 5.试求它们的互协方差函数2.5设代B是两个随机变量,试求随机过程X(t) =At ∙3B,t∙ T =(」:「:)的均值函数和自相关函数若A, B相互独立,且A~ N(1,4), B ~U (0,2),则mχ (t)及Rχ(t1,t2)为多少?3.1 一队学生顺次等候体检。
随机过程试题及答案

一.填空题(每空2分,共20分)1.设随机变量X 服从参数为λ的泊松分布,则X 的特征函数为it (e -1)eλ。
2.设随机过程X(t)=Acos( t+),-<t<ωΦ∞∞ 其中ω为正常数,A 和Φ是相互独立的随机变量,且A 和Φ服从在区间[]0,1上的均匀分布,则X(t)的数学期望为1(sin(t+1)-sin t)2ωω。
3.强度为λ的泊松过程的点间间距是相互独立的随机变量,且服从均值为1λ的同一指数分布。
4.设{}n W ,n 1≥是与泊松过程{}X(t),t 0≥对应的一个等待时间序列,则n W 服从Γ分布。
5.袋中放有一个白球,两个红球,每隔单位时间从袋中任取一球,取后放回,对每一个确定的t对应随机变量⎪⎩⎪⎨⎧=时取得白球如果时取得红球如果t t t e t t X ,,3)(,则 这个随机过程的状态空间212t,t,;e,e 33⎧⎫⎨⎬⎩⎭。
6.设马氏链的一步转移概率矩阵ij P=(p ),n 步转移矩阵(n)(n)ij P (p )=,二者之间的关系为(n)n P P =。
7.设{}n X ,n 0≥为马氏链,状态空间I ,初始概率i 0p P(X =i)=,绝对概率{}j n p (n)P X j ==,n 步转移概率(n)ij p ,三者之间的关系为(n)ji ij i Ip (n)p p ∈=⋅∑。
8.在马氏链{}n X ,n 0≥中,记 {}(n)ij v n 0f P X j,1v n-1,X j X i ,n 1,=≠≤≤==≥(n)ij ij n=1f f ∞=∑,若ii f 1<,称状态i 为非常返的。
9.非周期的正常返状态称为遍历态。
10.状态i 常返的充要条件为(n)iin=0p∞=∑∞。
二.证明题(每题6分,共24分)1.设A,B,C 为三个随机事件,证明条件概率的乘法公式:P(BC A)=P(B A)P(C AB)。
证明:左边=P(ABC)P(ABC)P(AB)P(C AB)P(B A )P(A)P(AB)P(A)===右边2.设{X (t ),t ³0}是独立增量过程, 且X (0)=0, 证明{X (t ),t ³0}是一个马尔科夫过程。
随机过程试题及答案

随机过程试题及答案一、单项选择题(每题2分,共10分)1. 随机过程的数学定义中,通常需要满足哪些条件?A. 样本空间、概率测度、随机变量B. 样本空间、概率测度、随机函数C. 样本空间、随机变量、随机函数D. 概率测度、随机变量、随机函数答案:B2. 马尔可夫链的无记忆性指的是什么?A. 过程的未来状态仅依赖于当前状态B. 过程的未来状态仅依赖于过去的状态C. 过程的未来状态依赖于当前和过去的状态D. 过程的未来状态依赖于所有历史状态答案:A3. 在随机过程中,如果一个过程的任何有限维分布都是联合正态的,则称该过程为什么?A. 正态过程B. 高斯过程C. 联合正态过程D. 多元正态过程答案:B4. 以下哪个不是平稳随机过程的性质?A. 一阶矩不随时间变化B. 任意两个不同时间点的协方差仅依赖于时间差C. 过程的均值随时间变化D. 过程的自相关函数仅依赖于时间差答案:C5. 随机过程的谱密度函数与自相关函数之间的关系是什么?A. 互为傅里叶变换B. 互为拉普拉斯变换C. 互为Z变换D. 互为梅林变换答案:A二、填空题(每题3分,共15分)1. 如果随机过程的样本路径是连续的,则称该过程为_________。
答案:连续过程2. 随机过程的样本函数是定义在时间轴上的_________。
答案:随机变量3. 对于一个平稳过程,其自相关函数R(τ)仅依赖于时间差τ,而不依赖于绝对时间t,即R(t1, t2) = R(t1 - t2) = R(τ),其中τ = t2 - t1。
这种性质称为_________。
答案:时间平移不变性4. 随机过程的遍历性是指过程的_________等于其统计平均。
答案:时间平均5. 随机过程的遍历性分为_________遍历性和_________遍历性。
答案:强,弱三、简答题(每题10分,共20分)1. 简述什么是泊松过程,并给出其概率质量函数。
答案:泊松过程是一种描述在固定时间或空间间隔内随机事件发生次数的随机过程。
随机过程课后习题答案

标准教材:随机过程基础及其应用/赵希人,彭秀艳编著索书号:O211.6/Z35-2备用教材:(这个非常多,内容一样一样的)工程随机过程/彭秀艳编著索书号:TB114/P50历年试题(页码对应备用教材)2007一、习题0.7(1)二、习题1.4三、例2.5.1—P80四、例2.1.2—P47五、习题2.2六、例3.2.2—P992008一、习题0.5二、习题1.4三、定理2.5.1—P76四、定理2.5.6—P80五、1、例2.5.1—P802、例2.2.2—P53六、例3.2.3—P992009(回忆版)一、习题1.12二、例2.2.3—P53三、例1.4.2与例1.5.5的融合四、定理2.5.3—P76五、习题0.8六、例3.2.22010一、习题0.4(附加条件给出两个新随机变量表达二、例1.2.1三、例2.1.4四、例2.2.2五、习题2.6六、习题3.3引理1.3.1 解法纠正 许瓦兹不等式()222E XY E X E Y ⎡⎤⎡⎤≤⎡⎤⎣⎦⎣⎦⎣⎦证明:()()()()222222222220440E X Y E X E XY E Y E XY E X E Y E XY E X E Y λλλ +⎡⎤⎡⎤=++≥⎣⎦⎣⎦∴∆≤⎡⎤⎡⎤∴-≤⎡⎤⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤∴≤⎡⎤⎣⎦⎣⎦⎣⎦例1.4.2 解法详解已知随机过程(){},X t t T ∈的均值为零,相关函数为()121212,,,,0a t t t t et t T a --Γ=∈>为常数。
求其积分过程()(){},t Y t X d t T ττ=∈⎰的均值函数()Y m t 和相关函数()12,Y t t Γ。
解:()0Y m t =不妨设12t t >()()()()()()1212222112121122122100,,Y t t t t t t t t t EY t Y t E X d X d d d τττττττττΓ===Γ⎰⎰⎰⎰()()()()()222121122221222112222212221212121212000220022002200222211||111111||211ττττττττττττττττττττττττ--------------=+-=+=---=+-+⎡=++--⎣⎰⎰⎰⎰⎰⎰⎰⎰t t t a a t t a a a a t t t a a at a t a at t a t t at at ed d ed de d e d a ae d e d a a t t e e a a a a t e e e a a⎤⎦同理当21t t >时()()2112112221,1a t t at at Y t t t e e e a a----⎡⎤Γ=++--⎣⎦ (此处书上印刷有误)例1.5.5解法同上例1.5.6 解法详解 普松过程公式推导:(){}()()()()()()()()()()()1lim !lim 1!!!1lim 1!!lim 1lim !lim lim !第一项可看做幂级数展开:第二项将分子的阶乘进行变换:→∞-→∞-→∞---∆-→∞→∞-→∞→∞===-∆∆-⎡⎤⎡⎤⎡⎤=-∆∆⎢⎥⎢⎥⎣⎦-⎣⎦⎣⎦⎡⎤⎡⎤-∆==⎢⎥⎣⎦⎣⎦⎡⎤⋅∆=∆⎢⎥--⎣⎦N k N N kkN N k kN N kN kq t qtN N k N kk k N N P X t k C P N q t q t k N k N q t q t N k k q t e e N N N q t q t N k N ()()()()()!lim 1!-→∞⎡⎤⎢⎥⎣⎦⎡⎤⎡⎤=∆⋅=⋅=⎢⎥⎣⎦-⎣⎦N k k k k kN k N q t N qt qt N k (){}()()()()!1lim 1!!!N kkN kqt P X t k N q t q t N k k qt ek -→∞-∴=⎡⎤⎡⎤⎡⎤=-∆∆⎢⎥⎢⎥⎣⎦-⎣⎦⎣⎦=例2.1.2 解法详解设(){},X t t -∞<<+∞为零均值正交增量过程且()()2212121,E X t X t t t t t -=->⎡⎤⎣⎦,令()()()1Y t X t X t =--,试证明(){},Y t t -∞<<+∞为平稳过程。
随机过程第四章习题解答

第四章习题解答4.1Y1,Y2,···是来自总体Y的随机变量,与X0独立,h(x,y)是实函数.对于n 1,取X n=h(X n−1,Y n).设{X n}的状态空间为I,验证{X n}是马氏链,给出转移概率p ij.解:由题知,Y k与X1,···,X k−1独立,k 1,∀n,i,j,i1,...,i n−1∈I有,P(X n+1=j|X n=i,X n−1=i n−1, (X0)i0)=P(h(i,Y n+1)=j|X n=i,X n−1=i n−1,···,X0=i0)=P(h(i,Y n+1)=j|X n=i)=P(h(i,Y)=j)=P(h(i,Y1)=j|X0=i)=P(X1=j|X0=i).∴X n是马氏链,P ij=P(h(i,Y)=j).4.2设{X i,i 0}是取非负整数值的独立同分布的随机变量序列,V ar(X0)>0.验证以下随机序列是马氏链:(a){X n,n 0};(b){S n,n 0},其中S n=∑ni=0X i;(c){ξn,n 0},其中ξn=∑ni=0(1+X i).解:∀n,i,j,i0,···,i n−1∈N+,(a).P(X n+1=j|X n=i,X n−1=i n−1,···,X0=i0)=P(X n+1=j)= P(X n+1=j|X n=i)=P(X1=j)=P(X1=j|X0=i).1第四章离散时间马尔可夫链第四章离散时间马尔可夫链(b).P(S n+1=j|S n=i,S n−1=i n−1,···,X0=i0)=P(X n+1=j−i|X n=i−i n−1,···,X0=i0)=P(X n+1=j−i)=P(X n+1=j−i,S n=i|S n=i)=P(S n+1=j|S n=i)=P(X1=j−i)=P(X1=j−i|X0=i)=P(S1=j|S0=i).(c).P(ξn+1=j|ξn=i,ξn−1=i n−1,···,ξ0=i0)=P(X n+1=ji −1)=P(X n+1=ji−1|ξn=i)=P(ξn+1=j|ξn=i)=P(X1=ji −1)=P(X1=ji−1|X0=i)=P(ξ1=j|ξ0=i).4.3马氏链的状态空间是I=(1,2,3,4,5),转移概率矩阵P=0.20.80000.50.5000000.50.500.20.3000.500001界定马氏链的状态。
随机过程复习题(含答案)

随机过程复习题(含答案)随机过程复习题一、填空题:1.对于随机变量序列}{n X 和常数a ,若对于任意0>ε,有______}|{|lim =<-∞>-εa X P n n ,则称}{n X 依概率收敛于a 。
2.设}),({0≥t t X 是泊松过程,且对于任意012≥>t t ,,则1592}6)5(,4)3(,2)1({-??====eX X X P ,618}4)3(|6)5({-===eX X P1532623292!23!2)23(!23}2)3()5({}2)1()3({}2)0()1({}2)3()5(,2)1()3(,2)0()1({}6)5(,4)3(,2)1({----??=?==-=-=-==-=-=-====eeeeX X P X X P X X P X X X X X X P X X X P66218!26}2)3()5({}4)3(|6)5({--===-===eeX X P X X P3.已知马尔可夫链的状态空间为},,{321=I ,初始分布为),,(4 12141,=43410313131043411)(P ,则167)2(12=P ,161}2,2,1{210====X X X P=4831481348436133616367164167165)1()2(2P P 167)2(12=P161314341}2|2{}1|2{}1{}2,1|2{}1|2{}1{}2,2,1{12010102010210=??=================X X P X X P X P X X X P X X P X P X X X P4.强度λ的泊松过程的协方差函数),min(),(t s t s C λ= 5.已知平稳过程)(t X 的自相关函数为πττcos )(=X R ,)]()([)(π?δπ?δπω-++=X S6. 对于平稳过程)(t X ,若)()()(ττX R t X t X >=+<,以概率1成立,则称)(t X 的自相关函数具有各态历经性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学本科课程《随机过程》第4章习题及参考答案主讲教师:何松华 教授30.设X(n)为均值为0、方差为2的离散白噪声,通过一个单位脉冲响应为h(n)的线性时不变离散时间线性系统,Y(n)为其输出,试证:2[()()](0)E X n Y n h σ=,2220()Y n h n σσ∞==∑证:根据离散白噪声性质,220()[()()]()0X m R m E X n m X n m m σσδ⎧==+==⎨≠⎩ 0()()()()()m Y n X n h n X n m h m ∞==⊗=-∑220[()()]{()()()][()()]()()()()()(0)m m X m m E X n Y n E X n X n m h m E X n X n m h m R m h m m h m h σδσ∞∞==∞∞===-=-===∑∑∑∑12121222112202121221210000[()]{()()()()][()()]()()[()()]()Y m m m m m m E Y n E X n m h m X n m h m E X n m X n m h m h m m m h m h m σσδ∞∞==∞∞∞∞======--=--=-∑∑∑∑∑∑(对于求和区间的每个m 1,在m 2的区间存在唯一的m 2=m 1,使得21()0m m δ-≠)1222110()()()m n h m h m h n σσ∞∞====∑∑(求和变量置换) 31.均值为0、方差为2的离散白噪声X(n)通过单位脉冲响应分别为h 1(n)=a n u(n)以及h 2(n)=b n u(n)的级联系统(|a|<1,|b|<1),输出为W(n),求W2。
解:该级联系统的单位脉冲响应为121211100()()()()()()()1(/)()1/n mm m m mn n n nnn m m n nm m h n h n h n h n m h m au n m b u m b b a aba b a a u n a b a a b∞∞-=-∞=-∞+++-===⊗=-=---⎛⎫====⎪--⎝⎭∑∑∑∑参照题30的结果可以得到21122222211212000222222222()[()2()()]()2(1)[]()111(1)(1)(1)n n n n n W n n n a b h n a ab b a b a b a ab b ab a b a ab b a b ab σσσσσσ++∞∞∞+++===⎡⎤-===-+⎢⎥--⎣⎦+=-+=-------∑∑∑32.设离散系统的单位脉冲响应为()() (1)n h n na u n a -=>,输入为自相关函数为2()()X X R m m σδ=的白噪声,求系统输出Y(n)的自相关函数和功率谱密度。
解:根据离散时间随机过程通过离散时间线性系统理论,有1221121212002122100()()()()[()]Y Xm m m mXm m R m Rm m m h m h m m m m m a m a σδ∞∞==∞∞--===-+=-+∑∑∑∑注:对比因果连续系统的输出过程与输入过程相关函数的关系12120()()()()Y X R R h h ττττττ∞∞=-+⎰⎰不妨设0m ≥,则只有当m 1m 时,求和区间存在脉冲点21m m m =-,因此1111111()211222211()()[]m m m Y X m m m m m X m mm mR m m m m a a a m a m m a σσ∞---=∞∞--===-=-∑∑∑令:1111211()m m m mm mx m am q∞∞-====∑∑,则1112(1){}{}1(1)m m m m m m d d q mq m q x q q q dq dq q q +∞=--=⨯=⨯=--∑ 令:111122211()m m m mm my ma mq ∞∞-====∑∑,则11112221223(1){}{}(1)(221)(21)(1)m m m m m m m m d d mq m q y q m q q dq dq q m q m m q m m qq +∞=++--=⨯=⨯----+-+=-∑2212221232124222323(221)(21)(1)()[](1)(1)(1)(1)(1)(1)(1)(1)m m m m m mY X m m mmX X m q m m q m m q m q m m q R m a q q m qm qa m a m a a q a σσσ+++++----+-+--=---+--+--==--考虑到相关函数的偶函数特性,得到:422||23(||1)(||1)()(1)m Y X a m a m R m aa σ-+--=-下面求功率谱密度函数,采用频域法。
-100220()() ()1{}{}1(1)()j nn j nn j n n n n j j n j n j j j n H j h n ena enp e p a d d pe ae p p e p dp dp pe pe a e ωωωωωωωωωω∞∞∞----===--∞----======⨯=⨯==---∑∑∑∑222222222222()|()|()()(|cos()sin()|)[12cos()]j X Y X X j X a ae G H j G a e a j aa a ωωσωωωσωωσω--===--+=+-可以通过相关函数的傅立叶变换进行验证。
典型双边序列的离散时间傅立叶变换对:2||||21 (||1)12cos()m m m a aa a a a ω∞--=-∞-↔=>+-∑ 222||22212(1)cos()4||12cos()[12cos()]m d a a a a m aa da a a a a ωωω-⎛⎫-+-↔-⨯=⎪+-+-⎝⎭ 242242422||||||23232324224222223222322222()()(||1)(||1)()||(1)(1)(1)()()2(1)cos()41(1)[12cos()](1)12cos()[12cos()]m m m X X Y X X X X a a a a a m a m R m am a aa a a a a a a a a a a a a a a a a a a a σσσσσωωωσω----++--==+----++--↔+-+--+-=+-33.序列X(n)和Y(n)满足差分方程()()()Y n X n a X n a =+--其中a 为整常数,试用X(n)的相关函数表示Y(n)的相关函数。
解:1212112212121212(,)[()()]{[()()][()()]}(,)(,)(,)(,)Y X X X X R n n E Y n Y n E X n a X n a X n a X n a R n a n a R n a n a R n a n a R n a n a ==+--+--=++--+-+-+--当X(n)为平稳随机过程时,则Y(n)也为平稳的,且有()2()(2)(2)Y X X X R m R m R m a R m a =---+34.实值一阶自回归过程X(n)满足差分方程1()(1)()X n a X n V n +-=其中a 1为常数,V(n)为方差为2的白噪声,输入从n=0开始,(1)0X -=。
(1)证明:若V(n)均值非零,则X(n)非平稳;(2)证明:若V(n)均值为零、|a 1|<1,则当n 足够大时,2221[()]/(1)V E X n a σ=-;(3)若V(n)均值为零,|a 1|<1,求X(n)的自相关函数的平稳解。
证:(1) 采用Wold 分解方法211123111111100()()(1)()(1)(2)()(1)(2)(3)...()()()(1)()()nnmn m m m X n V n a X n V n a V n a X n V n a V n a V n a X n a V n m a X a V n m +===--=--+-=--+---==--+--=--∑∑1111001[1()][()][()()]()1n nnmmV V m m m a E X n E a V n m a m a +==--=--=-=+∑∑ 显然,若V(n)均值非零,则X(n)的均值函数不是一个常数,是非平稳的。
(2) 若V(n)均值为零,则X(n)的均值为常数0,则210[()][()][()()]nm m E X n Var X n Var a V n m ===--∑根据相互独立随机变量的和的方差等于方差之和的性质,得到2211022(1)2211201[()][()()]()[()][1]()1nnmm m m n nm V V m E X n Var a V n m a Var V n m aa aσσ==+==--=---==-∑∑∑显然,若输入从n=0开始,则即使在V(n)均值为零的情况下,方差也不为常数,X(n)是非平稳的,当|a 1|<1且n 足够大时,渐近平稳,2221[()]1V E X n aσ=-。
(3) 不妨假设时刻差m0,则根据Wold 分解得到121212121212111201112002111200(,)[()()]{[()()][()()]}()()[()()]()()()n mnm m X m m n mnm m m m n mnm m V m m R n m n E X n m X n E a V n m m a V n m a a E V n m m V n m a a m m m σδ+==+==+==+=+=-+---=--+--=---+∑∑∑∑∑∑根据求和区间的脉冲点21m m m =-的存在条件:1n m m m +≥≥,得到:11111()222111122(1)211121(,)()()()()[1]()1n mn mm m m m mX V V m mm mm n mV R n m n a a a aa a a a σσσ++--==+-+=--=--=--∑∑当n 足够大时,输出过程是渐近平稳的,自相关函数的平稳解为:2121()()1mV X a R m a σ-=-35.考察如下的二阶自回归过程X(n)12()(1)(2)()X n a X n a X n V n =----+(1)若已知随机过程的相关函数值(0)X R 、(1)X R 、(2)X R ,试写出用于计算系数a 1,a 2以及零均值白色噪声()V n 的方差2V σ的Yule-Walker 方程;(2)反过来,若已知a 1= -1,a 2=0.5, 20.5V σ=,求(0)X R 、(1)X R 、(2)X R 的值;(3)求相关函数的通解。
