20年6月西南大学机考[0158]《高等代数》参考

合集下载

西南大学20年6月[0917]《高等数学》机考【答案】

西南大学培训与继续教育学院课程考试试题卷学期：2020年春季课程名称【编号】：高等数学【0917】 A卷考试类别:大作业满分：100 分（一）计算题（本大题共9小题，任意选做4个小题，每小题20分，共80分）1. 求.2. 求不定积分.3. 求定积分.4. 求函数的导数.5. 求函数的极值.6. 求函数的二阶偏导数及.7. 计算函数的全微分.8.求微分方程的通解.9. 计算，其中是抛物线及直线所围成的闭区域.（二）证明题（本大题共1小题，必做，共20分）1. 证明方程在区间（-1，0）内有且只有一个实根.计算题；1（1-x)^5*(1+x+x^2)^5=(1-x)^4(1+x+x^2)^4*(1-x)(1+x+x^2)=[(1-x)(1+x+x^2)]^4*(1-x)(1+x+x^2)=(1-x^3)^4*(1-x)(1+x+x^2)=[(1-x^3)^2]^2*(1-x)(1+x+x^2)=[(1-x^3)^2]^2*(1-x^3)=（1-X^3)^52∫x^4/(1+x²)² dx=∫[1+1/(1+x²)²-2/(1+x²)]dx,用综合除法=∫dx+∫dx/(1+x²)²-2∫dx/(1+x²)在第二项,令x=tanp,dx=sec²pdp=∫dx+∫sec²p/(1+tan²p)²-2∫dx/(1+x²)=∫dx+∫sec²p/(sec^4p)-2∫dx/(1+x²)=∫dx+∫cos²pdp-2∫dx/(1+x²)=∫dx+∫(1+cos2p)/2 dp-2∫dx/(1+x²)=∫dx+(1/2)∫dp+(1/4)∫cos2pd(2p)-2∫dx/(1+x²)- 1 -=x+(1/2)p+(1/4)sin2p-2arctanx+C=x+(1/2)p+(1/2)sinpcosp-2arctanx+C=x+(1/2)arctanx+(1/2)[x/√(1+x²)][1/√(1+x²)]-2arctanx+C=x-(3/2)arctanx+(1/2)[x/(1+x²)]=x+x/[2(1+x²)]-(3/2)arctanx+C4y′=2（1+cos2x）（1+cos2x）′=2（1+cos2x）（-sin2x）（2x）′=4（1+cos2x）（-sin2x）=-4sin2x-2sin4x5 令f′(x)=0,解得x1=−1,x2=0,x3=1当x变化时,f′(x),f(x)的变化如下表x (−∞,−1) −1 (−1,0) 0 (0,1) 1 (1,+∞)f′(x) − 0 − 0 + 0 +f(x) 减无极值减极小值增无极值增当x=0时,f(x)有极小值，极小值是0，无极大值二证明题- 2 -。

西南大学高中数学课程标准导读答案

组合公式（m，n2）的证明。
证法1：
证法2：在n个元素中固定一个元a，那么从n个元中取m个元可分为两种情形。一定不取a，共有种取法；一定取a，共有种取法，加起来共个取法。
容易看出证法1依赖于组合符号的定义及烦琐的数字计算，是一种对发现公
式本身丝毫无助的纯验证法。而证法2直观形象，通过这种途径我们不但能够证
发生的程序或秩序的理所当然的了解和理解。在上面的证法2中我们把“从n个
元素的集合中取m个元素的过程分解为两种绝然不同的取法程序，其中一种在所
取的m个元素中不含固定元素a，另中一种在所取的m个元素中含固定元素a，
这样合在一起就是从n个元素的集合中取m个元素的所有可能的情形”。证法2
的合理性建立在这种“程序分划”的模式直观之上。一个非常典型的模式直观的实例是关于
数学文化包括以下几个方面。(1)知识成分:包括数学理论知识、数学问题、数学语言等。(2)能力因素:包括数学应用能力、将问题通过适当途径而数学化的能力、逻辑论证能力、计算能力、问题解决能力、数学表达能力等。(3)数学观念:包括数学思维方式、思想观点、情感态度、价值观念。
虽然数学文化的内容涵盖了一个人数学修养的各个方面，但是它更强调当一个人的数学知识与其它各个领域的知识能力相融合之后所表现出来的综合素质.
强调数学的本质，注意适度形式化。数学课程教学中，需要学习严格的、形式化的逻辑推理方式。但是数学教学，不仅限于形式化数学，学生还必须接触到生动活泼、灵活多变的数学思维过程。要让学生追寻数学发展的历史足迹，体念数学的形成过程和数学中的思想方法。教师应该把高度严格的学术形态的数学转化为学生乐于思考的、兴趣盎然的教学形态。
●必修课程分5个模块，选修系列1、2也由模块组成。每个模块2学分，教学时数36学时。选修系列3、4由若干专题组成，每个专题1学分，教学时数18学时。

西南大学20年6月[0350]数学教育学机考大作业参考答案

西南大学网络与继续教育学院课程考试试题卷
类别：网教2020年5月
课程名称：数学教育学(方法论)【0350】
A卷大作业满分：100 分
要答案：wangjiaofudao
一、简述题（共计30分）
1. 简述教学评价对数学教学的功能。

（10分）
2. 简述数学教学原则中的“渗透数学思想方法原则”（20分）
二、实践与综合运用题（共计70分）
（一）选择以下知识点之一（共计30分）
分数的概念（小学）
平方差公式（初中）
函数的单调性（高中）
（1）分析教材，指出该知识点渗透了哪些数学思想方法（10分）
（2）分析学生学习该知识点的思维障碍或者容易出现的典型错误及原因（10分）（提示：该知识点的“思维障碍”与“典型错误”可选择其中之一进行分析）, （3）提出相应的教学策略（10分）
（没有固定评分标准，根据回答情况酌情给分）（二）根据所提出的教学策略，设计简要的教学过程（40分）
答题提示：教学过程设计具有整体性，各环节衔接自如，结构紧凑；在渗透数学思想方法、突破学生思维障碍或纠正典型错误上与上述（一）的回答有一定的联系。

（没有固定评分标准，根据回答情况酌情给分）。

西南大学20年6月[0135]数学物理方法考试大作业参考答案

西南大学网络与继续教育学院课程考试试题卷
类别：网教
课程名称【编号】：数学物理方法【0135】
A卷大作业满分：100 分
要答案：wangjiaofudao
请对下列五个大题解答，要求写出必要的解题步骤.
一、求解下列各题（共4题，选做3题，每题10分，共30分）
计算计算解方程解方程
二、求解下列各题（共2题，选做1题，共15分）
证明函数在复平面上解析，并求的导数.
2、已知解析函数的虚部为，求.
三、求下列积分（共4题，选做2题，每题10分，共20分）
1、2、3、4、
四、求解下列各题（共3题，每题5分，共15分）
求幂级数的收敛半径.
将函数在内展成的幂级数.
3、把函数在内展成洛朗（Laurent）级数．
五、求解下列各题（共2题，每题10分，共20分）
1、试用分离变量法求解以下定解问题
答题要求：请用分离变量法求解，用其它方法求解不得分，并要求写出必要的解题步骤．
2、求解圆内的定解问题（10分）求解定解问题,
其中A为已知正常数．
答题要求：可用任何方法求解，要求写出必要的解题步骤．。

西南大学网络教育2020年春0158]《高等代数》作业标准答案

1、设多项式f(x)|g(x)，c是一个非零常数，则cf(x)|g(x)。

. A.√.2、一个齐次线性方程组的两个解向量的和仍是该方程组的一个解向量。

. A.√.3、设A是n阶矩阵，若非齐次线性方程组AX=B无解，则|A|=0。

. A.√.4、设A是可逆矩阵，交换A的第一行和第二行得矩阵B，则B也是可逆矩阵。

. A.√.5、设是线性空间V的两个子空间，若。

. B.×6、设W是线性空间V的子空间，。

. A.√.7、设A是n阶矩阵，|A|=0，E是n阶单位矩阵，则|A+E|=1。

.B.×8、若多项式g(x)|f(x)，则g(x)为f(x)与g(x)的一个最大公因式。

. A.√.9、如果一个向量组线性相关，那么它的任一部分组也线性相关。

. B.×10、设为一个向量组，由于，所以线性无关。

. B.×11、如果一个二次型是正定的，那么它的函数值恒大于零。

. B.×12、数域P上两个不可约多项式的积一定是可约多项式。

. A.√.13、如果两个n阶矩阵的秩相同，那么它们一定合同。

. B.×14、设为一个向量组，若，则线性相关。

. A.√.1317、设A为矩阵，B为矩阵，则AB的列数等于。

418、在向量组中，，则的秩等于。

219、20、若2为f(x)的根，且2是的5重根，则2为f(x)的重根。

621、设，则f(x)的所有系数的和等于。

322、若，则c= 。

-123、设为对称矩阵，则a= 。

324、若矩阵不可逆，则a= 。

-4 25、3阶行列式。

-126、计算题.doc1.计算下面的4阶行列式的值： 1111211312254321D -=。

2.设43232()341,()1f x x x x x g x x x x =+---=+--，求((),())f x g x 。

3.设A = 033110123⎛⎫ ⎪ ⎪ ⎪-⎝⎭，且2AB A B =+，求矩阵B 。

[0464]高等几何20年6月西南机考大作业参考答案

西南大学网络与继续教育学院课程考试试题卷
类别：网教
课程名称【编号】：高等几何【0464】
A卷大作业满分：100 分
要答案：wangjiaofudao
一、计算题(共6题，其中6，7题任选一题，总共70分)
1、求联接点（1,2,－1）与二直线[2,1,3]，[1，－1，0]之交点的直线方程. (10分)
2. 设点A（3，1，2），B（3，-1，0）的联线与圆x2+y2－5x－7y＋6=0相交于两点C和D，求交点C，D及交比（AB，CD）(10分)
3. 求射影变换的不变元素. (15分)
4. 若有两个坐标系，同以△A1A2A3为坐标三角形，但单位点不同，那么两种坐标间的转换式为何？(15分)
5. 求二次曲线xy+x+y=0的渐近线方程. (10分)
6. 求二阶曲线的过点的直径及其共轭直径.(10分)
7.求过点A（1,0,2），B（0,1,2），C（0,-1,1）且以, 为切线的二次曲线方程。

(10分)
二、证明题(任选2题，每题15分，总共30分)
1. 设A1,B1,C1三点在一直线上,A2,B2,C2三点在另一直线上,B1C2与B2C1的交点为L,C1A2与C2A1的交点为M,A1B2与A2B1的交点为N,证明,M,N三点共线. (15分)
2. 若有心二次曲线的一条直径通过一定点,则其共轭直径平行于的极线. (15分)
3.在内接于圆的两个三点形与中，设证明三点共线. (15分)。

(9102)《高等数学》西南大学20年6月机考限时答案

西南大学培训与继续教育学院课程一、单项选择题(本大题共15小题，每道题4.0分，共60.0分)1.设()且，则在处 ( )A..B..C..D..2.函数在处( )A.不连续B.连续不可导C.连续且仅有一阶导数D.连续且有二阶导数3.曲线在点处切线斜率等于( )A.8B.12C.-6D.64.设时，与是同阶无穷小，则为( )A.1B.2C.3D.45.设在处可，则( )A..B..C..D..6.函数的反函数是( )A..B..C..D..7.设有二阶连续导数，且，则 ( )A..B..C..D..8.两个无穷小量与之积仍是无穷小量，且与或相比( )A.是高阶无穷小B.是同阶无穷小C.可能是高阶，也可能是同阶无穷小D.与阶数较高的那阶同阶9.若在区间上二次可微，且，，()，则方程在上 ( )A.没有实根B.有重实根C.有无穷多个实根D.有且仅有一个实根10.任意给定，总存在，当时，，则( )A..B..C..D..11.设在上有定义，函数在点左、右极限都存在且相等是函数在点连续的( )A.充分条件B.充分且必要条件C.必要条件D.非充分也非必要条件12.设在内连续，且，则在点处( )A..B..C..D..13.已知函数在任意点处的增量且当时，是的高阶无穷小，，则( )A..B..C..D..14.下列函数中在上满足拉格朗日定理条件的是( )A..B..C..D..15.在下列四个函数中,在上满足罗尔定理条件的函数是( )A..B..C..D..二、计算题(本大题共4小题，每道题5.0分，共20.0分)1.2.求下列函数的自然定义域3.4.求在点(1, 2)处的偏导数三、证明题(本大题共1小题，每道题20.0分，共20.0分) 1.。

西南大学考研参考书目

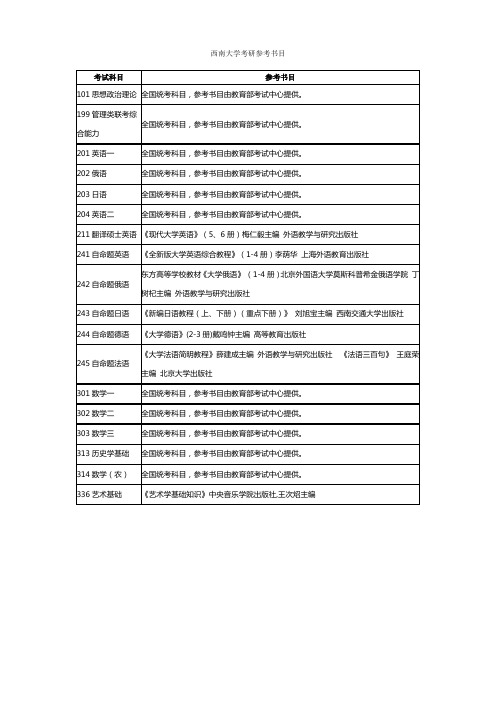
西南大学考研参考书目
考试科目
参考书目
101思想政治理论
全国统考科目，参考书目由教育部考试中心提供。
199管理类联考综合能力
全国统考科目，参考书目由教育部考试中心提供。
201英语一
全国统考科目，参考书目由教育部考试中心提供。
202俄语
全国统考科目，参考书目由教育部考试中心提供。
203日语
全国统考科目，参考书目由教育部考试中心提供。
832工业设计命题设计(3小时)
相关专业期刊杂志\书籍\图集
833建筑构造
《建筑构造》上册第三版李必瑜中国建筑工业出版社,《建筑构造》下册第三版刘建荣中国建筑工业出版社
836环境工程
环境工程学,蒋展鹏主编,高等教育出版社1992年
838物理化学一
《物理化学》肖衍繁、李文斌编,天津大学出版社,2004
《传播学引论》李彬著新华出版社 2003年版
649中外美术史
《中国美术简史》中央美院美术史系编中国青年出版社,2002年版
《外国美术简史》中央美院美术史系编中国青年出版社,2007年版
651建筑物理
《建筑物理》第三版柳孝图中国建筑工业出版社
810理论力学
理论力学(第六版),哈尔滨工业大学理论力学教研室编,高等教育出版社,2004
355建筑学基础
中国建筑工业出版社:《中国建筑史》第五版潘谷西,《外国建筑史》（19世纪末叶以前）第三版陈志华,《外国近现代建筑史》第二版罗小未,《建筑构造》上下册第三版李必瑜、刘建荣,《建筑物理》第三版柳孝图;同济大学出版社:《外国建筑历史图说》罗小未、蔡琬英
357英语翻译基础
《英汉翻译简明教程》庄绎传编外语教学与研究出版社2002；《英汉翻译基础教程》冯庆华、穆雷主编高等教育出版社2008

[0158]《高等代数》西南大学

0158 20191判断题1、一个线性变换的两个不变子空间之和仍是它的不变子空间。

1. A.√2. B.×2、线性空间上的线性变换是单射当且仅当是它满射。

1. A.√2. B.×3、数域P上任何非零多项式的次数都大于零.1. A.√2. B.×4、一个3次实系数多项式至少有一个实根。

1. A.√2. B.×5、与对称矩阵合同的矩阵一定是对称矩阵。

1. A.√2. B.×6、两个有限维线性空间同构的充要条件是它们的维数相等。

1. A.√2. B.×7、交换正交矩阵的任意两列所得到的矩阵仍是正交矩阵。

1. A.√2. B.×8、A为n阶方阵，若A的行列式不等于0，则A一定可逆。

1. A.√2. B.×9、数域P上n阶方阵在初等行变换之下行列式的值不变.1. A.√2. B.×10、欧式空间中保持向量夹角不变的线性变换是正交变换。

1. A.√2. B.×11、若两个向量组的秩相等，则这两个向量组一定等价.1. A.√2. B.×12、若n阶方阵A和B的特征多项式相同, 则A与B相似.1. A.√2. B.×13、对任意实数a，向量(a,0,1)与向量(-1,1,a)都是线性无关的.1. A.√2. B.×14、n维线性空间V中任意n个线性无关的向量都是V的基.1. A.√2. B.×15、如果两个n阶矩阵相似，那么它们一定合同。

1. A.√2. B.×主观题16、高等代数第一次作业.doc参考答案：高等代数第一次作业参考答案.doc17、高等代数第二次作业.doc参考答案：高等代数第二次作业参考答案.doc18、高等代数第三次作业.doc参考答案：高等代数第三次作业参考答案.doc。

新版西南大学基础数学考研经验考研参考书考研真题

回想起去年这个时候，自己还在犹豫是不是要遵从自己的梦想，为了考研奋斗一次。

当初考虑犹豫了很久，想象过所有的可能性，但是最后还是决定放手一搏。

为什么呢？有一个重要的考量，那就是对知识的渴望，这话听来可能过于空洞吧，但事实却是如此。

大家也都可以看到，当今社会的局势，浮躁，变动，不稳定，所以我经常会陷入一种对未来的恐慌中，那如何消除这种恐慌，个人认为便是充实自己的内在，才不至于被一股股混乱的潮流倾翻。

而考研是一条相对比较便捷且回报明显的路，所以最终选择考研。

所幸的是结局很好，也算是没有白费自己将近一年的努力，没有让自己浑浑噩噩的度过大学。

在准备备考的时候，我根据自己的学习习惯，做了一份复习时间规划。

并且要求自己严格按照计划进行复习。

给大家一个小的建议，大家复习的时候一定要踏踏实实的打好我们的基础，复习比较晚的同学也不要觉得时间不够，因为最后的成绩不在于你复习了多少遍，而是在于你复习的效率有多高，所以在复习的时候一定要坚持，调整好心态，保证自己每天都能够有一个好的学习状态，不要让任何事情影响到你，做好自己！在此提醒大家，本文篇幅较长，因为想讲的话实在蛮多的，全部是我这一年奋战过程中的想法、经验以及走过的弯路，希望大家看完可以有所帮助。

最后结尾处会有我在备考中收集到的详细资料，可供各位下载，请大家耐心阅读。

西南大学基础数学的初试科目为：(101)思想政治理论和(201)英语一(615)数学分析和(819)高等代数参考书目为：1.华东师范大学数学系《数学分析》2.北京大学数学系《高等代数》跟大家先说一下英语的复习吧。

学英语免不了背单词这个难关，词汇量上不去，影响的不仅是考试成绩，更是整体英语能力的提升；背单词也是学习者最感到头痛的过程，不是背完了转身就忘，就是背的单词不会用，重点单词主要是在做阅读的时候总结的，我把不认识不熟悉的单词全都挑出来写到旁边，记下来反复背直至考前，总之单词这一块贵在坚持，背单词的日程一定要坚持到考研前一天。

20年6月西南大学课程考试[0158]《高等代数》大作业(资料)

西南大学培训与继续教育学院课程考试试题卷
学期：2020年春季
课程名称【编号】：高等代数【0158】 A卷
考试类别:大作业满分：100 分
一、给出下面两个概念的定义（共2小题，15分/小题，共30分）
1．数域P上多项式p(x)在P上不可约。
答：在数域P上，p(x)无法写成两个次数较低的多项式之乘积的多项式。
可以写为
这样的形式，
即
由于
因此过渡矩阵即为
六、（10分）设是数域P上全体n阶方阵关于矩阵加法及数与矩阵的数乘构成的线性空间，。证明：W是V的子空间。
答：ቤተ መጻሕፍቲ ባይዱ
要证明W是V的子空间，即证明W对于矩阵数乘和矩阵加法运算封闭。
，满足与，若证明，则说明对于矩阵加法运算封闭
由于
得证
若证明，则说明对于矩阵数乘封闭
得证
综上，由于W对于矩阵数乘和矩阵加法都满足，因此W是V的子空间。
，之后将第二行乘-1加到第一行，最后将第三行乘上2加到第二行，乘上-1加到第一行
因此
四、（15分）求下面的齐次线性方程组的一个基础解系
。
答：该方程组可以化为
左边矩阵可以变形为：
，
若设，那么就可以求得一个基础解系
其中
五、（15分）设，，
，
求由基到基的过渡矩阵。
答：
设过渡矩阵为，则依题意有
2．数域P上n维向量组线性相关。
答：若系数满足公式，且不全为0，则称n维向量组线性相关。
二、（15分）设，，求除的商式与余式。
答：
商式：
余式：
三、（15分）设，求。
答：
使用初等行变换，可以得到

西南大学考研参考书目

862影视艺术史论
《影视艺术概论》，周星主编，高等教育出版社，2007年版
《中国电影史纲要》\《外国电影史纲要》，虞吉主编，西南师范大学出版社，2007年版
863舞蹈艺术基础理论
《舞蹈艺术概论》，隆荫培徐尔充主编，上海音乐出版社
864综合音乐理论基础
《艺术学概论》彭吉象著（第三版），北京大学出版社，2006
《音乐基础理论》李重光著人民音乐出版社
《音乐分析基础教程》彭志敏著人民音乐出版社
865设计理论
《设计学概论》（修订版）湖南科技出版社，2009
866新闻传播实务
《新闻写作:思考与训练》黄晓钟著四川大学出版社,2002年版
《法汉翻译教程》许钧主编上海外语教学出版社2007
623基础英语
《现代大学英语》第五、六册，主编：梅仁毅，外语教学与研究出版社
624日汉互译
《日汉互译教程》高宁便主编南开大学出版社；
《新编日汉翻译教程》庞春兰主编北京大学出版社
625数学分析
《数学分析》(第二版)陈纪修等主编高等教育出版社
627德汉互译
相关专业期刊杂志\书籍\图集
519设计学命题设计(6小时)
相关专业期刊杂志\书籍\图集
520工业设计工程命题设计(6小时)
相关专业期刊杂志\书籍\图集
601高等数学
《高等数学》同济大学编第三版,高等教育出版社
616药学基础综合
1.药物化学郑虎主编人民卫生出版社2007年第6版
2.药理学李端主编人民卫生出版社2007年第6版
643中外舞蹈史
《中国舞蹈发展史》，王克芬主编，上海人民出版社
《西方舞蹈发展史》，欧建平主编，上海音乐出版社
645文学概论
《文学理论教程》童庆炳主编高等教育出版社,2005年版

20年6月西南大学机考[0158]《高等代数》参考

2、答：若存在不全为零的数，使得，则称向量组线性所以一般解为：，其中是自由未知数。
基础解系为：。
五、解：观察可得
，。。
所以由基到基的过渡矩阵为
。
六、证明：由于n阶零矩阵在W中，所以W是V的非空子集。
对，有，所以。
对，有，所以。
所以W是V的子空间。
西南大学培训与继续教育学院课程考试试题卷
学期：2020年春季
课程名称【编号】：高等代数【0158】 A卷
考试类别:大作业满分：100 分
一、给出下面两个概念的定义（共2小题，15分/小题，共30分）
1．数域P上多项式p(x)在P上不可约。
2．数域P上n维向量组线性相关。
二、（15分）设，，求除的商式与余式。
三、（15分）设，求。
四、（15分）求下面的齐次线性方程组的一个基础解系
。
五、（15分）设，，
，
求由基到基的过渡矩阵。
六、（10分）设是数域P上全体n阶方阵关于矩阵加法及数与矩阵的数乘构成的线性空间，。证明：W是V的子空间。
一、
1、答：p(x)为数域P上多项式，，如果不能表成数域P上两个次数比的次数低的多项式的积，则称为数域P上不可约多项式。

《高等代数》期末闭卷考试题A

西南财经大学第一学期校内光华试验选拔斑__________本科学号________________ 评定成绩________________(分) 学生姓名________________ 担任教师_线性代数课程组__《高等代数》期末闭卷考试题A(下述一～四题全作100分, 两小时完卷)试题全文一.填空题（将正确答案填在题中括号内。

每小题2分，共10分）1.已知4阶行列式D 的第三行元素分别为;4,2,0,1-第四行元素对应的余子式依次是.4,,10,5a 则=a ( ).2.设方程0111)(112111121112==------n n n n n n a a a a a a x x x x f ΛΛΛΛΛΛΛΛ其中)1,,2,1(-=n i a i Λ为互不相等的实常数,则方程的全部解是( ). 3.设四阶矩阵[][],,,,,,,,432432γγγβγγγα==B A 其中432,,,,γγγβα均为14⨯列矩阵,且巳已知行列式,1,4==B A 则行列式=+B A ( ). 4.设),(21I B A +=则当且仅当=2B ( )時,.2A A =. 5.已知n 阶矩阵滿足关系式,0322=-+I A A 则=+-1)4(I A ( ).二.单项选择题 (每小题仅有一个正确答案, 将正确答案的番号填入下表内.1.设A 为方阵,则0=A 的必要条件是( ) )(A 両行(列)元素对应成比例; )(B 任一列为其它列的线性组合; )(C 必有一列为其它列的线性组合; )(D A 中至少有一列元素全为零.2.设A 为m 阶方阵,B 为n 阶方阵,,⎥⎦⎤⎢⎣⎡=O B A O C 则=C ( ); )(A ;B A )(B ;B A -)(C ;)1(B A n m +- )(D .)1(B A mn -3. 行列式=600300301395200199204100103( ).)(A 1000; )(B -10000; )(C 2000; )(D -2000. 4. A 是n 阶矩阵,k 是非零常数,则=*)(kA ( ). )(A ;1-n Ak )(B ;1-n Ak)(C ;1)1(--n n n A k )(D .11--n n Ak5. 设B A ,为n 阶对称矩阵,则下面四个结论不正确的是( ). )(A B A +也是对称矩阵; )(B AB 也是对称矩阵; )(D ;m m B A + )(D T T AB BA +也是对称矩阵.6. 设B A ,为n 阶方阵, 则下列结论成立的是( ) )(A 00≠⇔≠A AB 且;0≠B )(B ;0O A A =⇔= )(C 00=⇔=A AB 或;0=B (D) .1=⇔=A I A7. 设A 为n 阶可逆矩阵,则( ))(A A 总可以只经过初等行变換变为;I)(B 对分块矩阵A ( )I 施行若干次初等变换,当子块变为I 时,相应地I 变为;1-A)(C 由.BA AX =得;A X = )(D 以上三个结论都不正确.8. 设A 是n m ⨯矩阵,其秩为,r C 是n 阶可逆阵,且B AC =的秩为,1r 则( ) 正确.)(A r ﹥;1r (B) r ﹤;1r)(C ;1r r = (D) r 与1r 的关系依C 而定. 9. 设B A ,为同阶可逆方阵,则( )成立. (A) ;BA AB =(B) 存在可逆阵,P 使;1B AP P =- (C) 存在可逆阵,C 使;B AC C T = (D) 存在可逆阵,,Q P 使.B PAQ =10. 设B A ,为n 阶非零矩阵,且,O AB =则A 和B 的秩( ). )(A 必有一个等于零; )(B 都小于;n )(C 一个小于,n 一个等于;n )(D 都等于.n三、计算题 (每小题9分, 共54分)1. 计算下列行列式:19980000000019970020001000ΛΛΛΛΛΛΛΛΛΛ2. 计算下列n 阶行列式的值:βαβαβαβαβαβαβαβα+++++=ΛΛΛΛΛΛΛΛΛΛΛ00000000000n D3. 设矩阵,111111111111⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=k k k k A 且,3)(=A R 则k 为什么?4. 当⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=21232321A 时,,6I A =求.11A5. 已知矩阵,PQ A =其中[]2,1,2,121-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=Q P ,求矩阵.,,1002A A A6. 设矩阵A 的伴随矩阵,8030010100100001*⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=A 且,311I BA ABA +=--其中I 为4阶单位矩阵,求矩阵.B四﹑证明题 (每小题8分, 共16分)1. 设B A ,是n 阶正交矩阵,且,1-=B A 证明.0=+B A2. 设A为n阶非奇异矩阵,α为n元列,b为常数,记分块矩阵,,*⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-=bAQAAOIPTTααα(1) 计算并化简;PQ(2) 证明:矩阵Q可逆的充分必要条件是.1bAT≠-αα。

20年6月西南大学机考[0158]《高等代数》参考

西南大学20年6月[0917]《高等数学》机考【答案】

西南大学高中数学课程标准导读答案

西南大学20年6月[0350]数学教育学机考大作业参考答案

西南大学20年6月[0135]数学物理方法考试大作业参考答案

西南大学网络教育2020年春0158]《高等代数》作业标准答案

[0464]高等几何20年6月西南机考大作业参考答案

(9102)《高等数学》西南大学20年6月机考限时答案

西南大学考研参考书目

[0158]《高等代数》西南大学

新版西南大学基础数学考研经验考研参考书考研真题

20年6月西南大学课程考试[0158]《高等代数》大作业(资料)

西南大学考研参考书目

20年6月西南大学机考[0158]《高等代数》参考

《高等代数》期末 闭卷考试题A

《高等代数》期末闭卷考试题A